05.参数估计与假设检验_SPSS
参数估计与假设检验SPSS

3
区别
参数估计更侧重于总体参数的估计和推断,而假 设检验更侧重于对总体参数的假设进行验证和决 策。
02
SPSS软件介绍
SPSS软件的特点与优势
强大的统计分析功能
SPSS提供了广泛的统计分析方法,包括描述性统计、推论性统计、 多元统计分析等,能够满足各种数据分析和科学研究的需求。
易用性
SPSS的用户界面友好,操作简单,使得用户可以快速上手,减少了 学习成本。
参数估计与假设检验的应用场景与注 意事项
参数估计与假设检验的应用场景
社会科学研究 在社会科学研究中,参数估计与 假设检验是常用的统计方法,用 于检验理论模型和假设,评估变 量之间的关系。
心理学研究 在心理学研究中,参数估计与假 设检验用于研究人类行为、认知 和情感等方面的规律和特点。
医学研究 在医学研究中,参数估计与假设 检验常用于临床试验和流行病学 研究中,以评估治疗效果、疾病 发病率和风险因素等。
04
05
根据输出结果判断假设是否 成立。
假设检验的实例分析
以一个实际研究问题为例,如比较两组人群的平均身高是否存在显著差异。
在SPSS中实现该实例分析,包括数据导入、选择统计方法、设置参数、运 行统计方法和结果解读等步骤。
根据SPSS的输出结果,判断提出的假设是否成立,并解释结果的实际意义。
05
数据处理技术,提高分析效率和准确性。
多变量分析方法
03
多变量分析方法的发展将促进参数估计与假设检验的进一步应
用,能够更全面地揭示变量之间的关系。
THANKS
感谢观看
使用SPSS进行参数估计,例如使用逻辑回归分 析来估计吸烟与肺癌之间的关系。
04
假设检验在SPSS中的实现
spss假设检验

SPSS假设检验1. 简介SPSS(Statistical Package for the Social Sciences)是一种非常常用的统计软件,被广泛应用于社会科学研究中。
其中,假设检验是SPSS中常用的统计方法之一,用于验证研究者对总体或样本的某种假设。
2. 假设检验的概念假设检验是统计学中的一种重要方法,用于判断一个统计推断是否与样本数据一致。
在假设检验中,通常会提出一个原假设(H0)和一个备择假设(H1),然后根据样本数据对两个假设进行检验,以确定是否拒绝原假设,从而对总体进行推断。
3. SPSS中的假设检验SPSS中提供了丰富的假设检验方法,涵盖了多种统计推断的情况。
下面将介绍几种常见的假设检验方法。
3.1 单样本 t 检验单样本 t 检验用于判断一个样本的均值是否与一个已知的常数有显著性差异。
在SPSS中,进行单样本 t 检验的步骤如下:1.导入数据:在SPSS中打开或导入数据文件。
2.选择变量:选择要进行 t 检验的变量。
3.进行检验:选择菜单栏上的“分析”-“比较均值”-“单样本 t 检验”。
4.设置参数:选择相关的变量和检验参数,点击“确定”进行分析。
5.查看结果:SPSS将显示 t 检验的结果,包括均值、标准差、t 值、自由度和显著性等。
3.2 独立样本 t 检验独立样本 t 检验用于判断两个独立样本的均值是否存在显著性差异。
在SPSS中,进行独立样本 t 检验的步骤如下:1.导入数据:在SPSS中打开或导入数据文件。
2.选择变量:选择需要进行对比的两个变量。
3.进行检验:选择菜单栏上的“分析”-“比较均值”-“独立样本 t 检验”。
4.设置参数:选择相关的变量和检验参数,点击“确定”进行分析。
5.查看结果:SPSS将显示独立样本 t 检验的结果,包括均值、标准差、t 值、自由度和显著性等。
3.3 配对样本 t 检验配对样本 t 检验用于判断同一组个体在两个不同时间点或条件下的均值是否存在显著性差异。
第二部分 参数估计和检验 SPSS操作指导
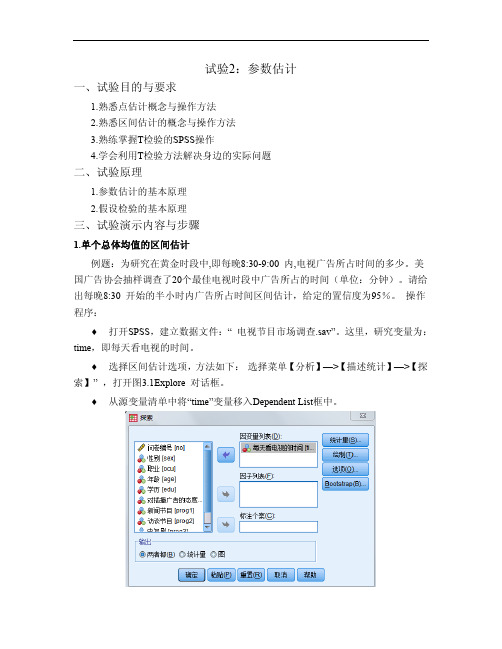
试验2:参数估计一、试验目的与要求1.熟悉点估计概念与操作方法2.熟悉区间估计的概念与操作方法3.熟练掌握T检验的SPSS操作4.学会利用T检验方法解决身边的实际问题二、试验原理1.参数估计的基本原理2.假设检验的基本原理三、试验演示内容与步骤1.单个总体均值的区间估计例题:为研究在黄金时段中,即每晚8:30-9:00 内,电视广告所占时间的多少。
美国广告协会抽样调查了20个最佳电视时段中广告所占的时间(单位:分钟)。
请给出每晚8:30 开始的半小时内广告所占时间区间估计,给定的置信度为95%。
操作程序:♦打开SPSS,建立数据文件:“ 电视节目市场调查.sav”。
这里,研究变量为:time,即每天看电视的时间。
♦选择区间估计选项,方法如下:选择菜单【分析】—>【描述统计】—>【探索】” ,打开图3.1Explore 对话框。
♦从源变量清单中将“time”变量移入Dependent List框中。
图3.1 Explore对话框♦单击上图右方的“统计量”按钮打开“探索:统计量”对话框。
在设置均值的置信水平,如键入95%,完成后单击“继续”按钮回到主窗口。
图3.2 探索统计量设置窗口♦返回主窗口点击ok运行操作。
♦计算结果简单说明:表3.1 描述统计量DescriptiveStatistic Std. Errortime Mean 6.5350.1348095% ConfidenceLower Bound 6.2529Interval for MeanUpper Bound 6.81715% Trimmed Mean 6.5167Median 6.4500Variance .363Std. Deviation .60287Minimum 5.60Maximum 7.80Range 2.20Interquartile Range .95Skewness .295.512Kurtosis -.612.992 ♦如上表显示。
参数估计和假设检验

参数估计和假设检验1.参数估计参数估计是指通过样本数据来推断总体参数的过程。
总体参数是指总体的其中一种性质,比如总体均值、总体方差等。
样本数据是从总体中随机抽取的一部分数据,用来代表总体。
参数估计的目标是使用样本数据来估计总体参数的值。
常见的参数估计方法有点估计和区间估计。
(1)点估计点估计是通过一个统计量来估计总体参数的值。
常见的点估计方法有样本均值、样本方差等。
点估计的特点是简单、直观,但是估计值通常是不准确的。
这是因为样本的随机性导致样本统计量有一定的误差。
因此,点估计通常会伴随着误差界限,即估计值的置信区间。
(2)区间估计区间估计是通过一个统计量构建总体参数的估计区间。
常见的区间估计方法有置信区间和可信区间。
置信区间是指当重复抽样时,包含真实总体参数的概率。
置信区间的计算方法是在样本统计量的基础上,加减一个合适的误差界限,得到一个估计区间。
可信区间是指在一次抽样中,包含真实总体参数的概率。
可信区间的计算方法同样是在样本统计量的基础上,加减一个合适的误差界限,得到一个估计区间。
参数估计的应用非常广泛,可以用于各个领域的数据分析和决策。
例如,经济学家可以通过样本数据估计失业率,政治学家可以通过样本数据估计选举结果,医学研究者可以通过样本数据估计药物的疗效等。
2.假设检验假设检验是指通过样本数据来判断总体参数的其中一种假设是否成立。
在假设检验中,我们先提出一个原假设(H0),然后使用样本数据来检验该假设的合理性。
在假设检验中,我们需要确定一个统计量,该统计量在原假设成立时,其分布是已知的。
然后,我们计算该统计量在样本数据下的取值,并通过比较该取值与已知分布的临界值,来判断原假设是否成立。
假设检验包含两种错误,即第一类错误和第二类错误。
第一类错误是指在原假设成立的情况下,拒绝原假设的错误概率。
第二类错误是指在原假设不成立的情况下,接受原假设的错误概率。
常见的假设检验方法有单样本假设检验、双样本假设检验、方差分析等。
参数估计与假设检验的区别和联系

1.参数估计就是用样本统计量去估计总体的参数,它的方法有点估计和区间估计两种。
点估计是用估计量的某个取值直接作为总体参数的估计值。
点估计的缺陷是没法给出估计的可靠性,也没法说出点估计值与总体参数真实值接近的程度。
区间估计是在点估计的基础上给出总体参数估计的一个估计区间,该区间通常是由样本统计量加减估计误差得到的。
在区间估计中,由样本估计量构造出的总体参数在一定置信水平下的估计区间称为置信区间。
统计学家在某种程度上确信这个区间会包含真正的总体参数。
在区间统计中置信度越高,置信区间越大。
置信水平为1-a,a为小概率事件或者不可能事件,常用的置信水平值为99%,95%,90%,对应的a为0.01,0.05,0.1置信区间是一个随机区间,它会因样本的不同而变化,而且不是所有的区间都包含总体参数。
一个总体参数的区间估计需要考虑总体是否为正态分布,总体方差是否已知,用于估计的样本是大样本还是小样本等(1)来自正态分布的样本均值,不论抽取的是大样本还是小样本,均服从正态分布(2)总体不是正态分布,大样本的样本均值服从正态分布,小样本的服从t 分布(3)不论已判断是正态分布还是t分布,如果总体方差未知,都按t分布来处理(4)t分布要比标准正态分布平坦,那么要比标准正态分布离散,随着自由度的增大越接近(5)样本均数服从的正态分布为N(ua^2/n)远远小于原变量离散程度N (ua^2)2.假设检验是推断统计的另一项重要内容,它与参数估计类似,但角度不同,参数估计是利用样本信息推断未知的总体参数,而假设检验则是先对总体参数提出一个假设值,然后利用样本信息判断这一假设是否成立。
假设检验的基本思想:先提出假设,然后根据资料的特点,计算相应的统计量,来判断假设是否成立,如果成立的可能性是一个小概率的话,就拒绝该假设,因此称小概率的反证法。
最重要的是看能否通过得到的概率去推翻原定的假设,而不是去证实它<2>统计学中假设检验的基本步骤:(1)建立假设,确定检验水准α--假设有零假设(H0)和备择假设(H1)两个,零假设又叫作无效假设或检验假设。
参数估计和假设检验

参数估计和假设检验参数估计和假设检验是统计学中常用的两种方法,用于根据样本数据对总体的特征进行推断和判断。
参数估计是通过样本数据估计总体参数值的方法,而假设检验则是基于样本数据对总体参数假设进行判断的方法。
下面将详细介绍这两种方法以及它们的应用。
1.参数估计参数是指总体特征的度量,比如总体均值、总体方差等。
在实际应用中,我们往往无法得到总体数据,只能通过抽样得到样本数据。
参数估计的目标是利用样本数据去估计总体参数的值。
最常用的参数估计方法是点估计和区间估计:-点估计是使用样本统计量来估计总体参数的值,常用的样本统计量有样本均值、样本方差等。
-区间估计是利用样本数据构建一个置信区间,用来估计总体参数的取值范围。
置信区间的计算方法通常是基于样本统计量的分布进行计算。
在进行参数估计时,需要注意以下几个要点:-选择适当的样本容量和抽样方法,确保样本具有代表性,并满足参数估计的要求。
-选择适当的样本统计量进行参数估计,并对其进行合理的解释与限制。
-利用抽样分布特性和统计理论,计算参数估计的标准误差和置信区间,对参数估计结果进行解释和判断。
2.假设检验假设检验是基于样本数据对总体参数假设进行判断的方法。
在实际问题中,我们常常需要根据样本数据来判断一些总体参数是否达到一些要求或存在其中一种关系。
假设检验的基本步骤:-建立原假设(H0)和备择假设(H1)。
原假设通常是对总体参数取值的一种假设,备择假设则是原假设的对立假设。
-选择适当的统计量用来检验假设,并计算样本统计量的检验统计量。
-根据样本数据计算得出的检验统计量,利用抽样分布特性和统计理论计算P值。
-根据P值与事先设置的显著性水平进行比较,如果P值小于显著性水平,则拒绝原假设;反之,接受原假设。
在进行假设检验时,需要注意以下几个要点:-显著性水平的选择:显著性水平(α)是进行假设检验过程中设置的一个临界值,它反映了能够容忍的错误发生的概率。
常用的显著性水平有0.05和0.01-选择适当的统计量与检验方法:根据问题的性质和数据类型选择适当的统计量和检验方法。
数理统计中的参数估计与置信区间估计及假设检验与拟合优度检验

数理统计中的参数估计与置信区间估计及假设检验与拟合优度检验数理统计是一门研究如何利用数据对未知参数进行估计和进行推断的学科。
本文将介绍数理统计中的参数估计与置信区间估计,以及假设检验与拟合优度检验的基本概念和相关方法。
一、参数估计与置信区间估计在数理统计中,参数是描述总体特征的量,例如总体均值、总体方差等。
参数估计就是利用样本统计量对总体参数进行估计。
常用的参数估计方法有最大似然估计和矩估计。
最大似然估计是一种常用的参数估计方法,其基本思想是选择参数值使得观测到的样本出现的概率最大化。
假设总体服从某个分布,最大似然估计通过优化似然函数来估计参数。
最大似然估计具有良好的性质,例如渐近正态性和无偏性等。
矩估计是另一种常用的参数估计方法,其基本思想是利用样本矩与总体矩的对应关系来估计参数。
例如,样本均值可以用来估计总体均值,样本矩可以通过总体矩的方法进行计算得到。
矩估计具有较好的渐近正态性和无偏性。
参数估计的结果往往带有一定的不确定性,为了评估估计结果的准确性,常使用置信区间估计。
置信区间估计是指通过样本数据得到的区间,该区间包含了未知参数的真值的概率。
常见的置信区间估计方法有正态分布的置信区间估计和大样本下的置信区间估计。
二、假设检验在数理统计中,假设检验是一种推断方法,用于检验总体参数的假设是否成立。
假设检验的基本思想是通过样本数据来判断假设是否得到支持。
常用的假设检验方法有正态总体均值的假设检验、正态总体方差的假设检验和两样本均值的假设检验等。
假设检验包括建立原假设和备择假设,选择适当的检验统计量,并设定显著性水平,进行统计推断。
结果的判断依据是计算得到的检验统计量是否落在拒绝域内。
如果检验统计量落在拒绝域内,拒绝原假设,否则接受原假设。
假设检验的结果可以提供统计学上的证据,用于决策和推断。
三、拟合优度检验拟合优度检验是一种用于检验总体数据是否符合某个特定分布的方法。
在数理统计中,拟合优度检验常用于检验样本数据与给定的分布是否相符。
第4章参数估计和假设检验

第4章参数估计和假设检验第四章参数估计与假设检验掌握参数估计和假设检验的基本思想是正确理解和应⽤其他统计推断⽅法的基础,后⾯将要学习的⽅差分析、⾮参数检验、回归分析、时间序列等统计推断⽅法都是在此基础上展开的。
需要特别指出的是,所有的统计推断都要以随机样本为基础。
如果样本是⾮随机的,统计推断⽅法就不适⽤了。
由于相关知识在先修课程中已经学习过,本章主要在回顾相关知识的基础上,补充讲解必要样本容量的计算、p值、参数估计和假设检验⽅法的软件操作和结果分析等内容。
本章的主要内容包括:(1)参数估计的基本思想和软件实现。
(2)简单随机抽样情况下样本容量的计算。
(3)假设检验的基本原理。
(4)假设检验中的p值。
(5)⼏种常⽤假设检验的软件实现。
第⼀节参数估计⼀、参数估计的基本概念参数估计是指利⽤样本信息对总体数字特征作出的估计。
例如,我们可以通过估计⼀部分产品的合格率对整批产品的合格率作出估计,通过调查⼀个样本的⼈⼝数来对全国的⼈⼝数作出估计,等等。
参数估计可以分为点估计和区间估计。
点估计是指根据样本数据给出的总体未知参数的⼀个估计值。
对总体参数进⾏估计的⽅法可以有多种,例如矩估计法、极⼤似然估计法等,得到的估计量(样本统计量)并不是唯⼀的。
例如我们可以使⽤样本均值对总体均值作出估计,也可以使⽤样本中位数对总体均值进⾏估计。
因此,在参数估计中我们需要对估计量的好坏作出评价,这就涉及到估计量的评价准则问题。
常⽤的估计量评价准则包括⽆偏性、有效性、⼀致性等。
⽆偏性是指估计量的数学期望与总体参数的真实值相等;有效性的含义是,在两个⽆偏估计量中⽅差较⼩的估计量较为有效,⽅差越⼩越有效;⼀致性是指随着样本容量的增⼤,估计量的取值应该越来越接近总体参数。
样本的随机性决定了估计结果的随机性。
由于每⼀个点估计值都来⾃于⼀个随机样本,所以总体参数真值刚好等于⼀个具体估计值的可能性极⼩。
区间估计的⽅法则以概率论为基础,在点估计的基础上给出了⼀个置信区间,并给出了这⼀区间包含总体真值的概率,⽐点估计提供了更多的信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
检验结果
假设检验
(双边检验-等于)
假设检验
(单边检验-大于等于-左侧)
假设检验
(单边检验-大于-右侧)
检验结果
检验结果
假设检验
(双边检验-等于)
假设检验
(单边检验-高出-右侧)
检验结果
检验结果
两个总体均值之差的区间估计
概述-假设检验
原假设 备择假设 统计量 统计量对应的p值 显著性水平 临界值 拒绝域
特别关注: 单边情况
两类错误
假设检验的步骤
假设
· 班长很少骂人。
统计假设就是关于“总体的 某个声明”或“某事是真的之叙 述”。
· 某航空公司的代表声称该公司民航客机的平均机 龄不超过10年。 · 某企业的总经理认为该企业本年度的利润会比去 年的增加2亿美元。
单样本T检验
Analyze
Compare Means
One Sample T test
例一
区间估计
例二
例一
“Employee.sav”资料,计算公司 职工的平均受教育年数。假定该地 区人口平均受教育年数为13年,问: ①公司职工文化程度是否有别于该 地区的居民文化程度? ②公司职工文化程度是否显著性高 于居民文化程度?
配对样本(Paired Sample)或相 关样本(Correlated Sample),指两 个样本的观测值之间彼此关联,如实 验前后的测量,研究者感兴趣的是二 次测量之间是否存在差异。显然对应 个别样本的顺序不可以变化的。 两个配对样本均值之间差异用t 统计量进行检验。
两配对样本平均数差异T检验
对两个总体均值之差的区间估计
Analyze — Compare Means — Paired Sample T Test
假设检验
(双边检验-等于)
某省大学英语四级考试的平均 成绩为65分,现从某校随机抽取 20份试卷,其分数为:72 76 68 78 62 59 64 85 70 75 61 74 87 83 54 76 56 66 68 62。若显著性水平 取0.05,问该校英语水平与全区是 否基本一致。(假定考试成绩服从 正态分布)
假设检验
(单边检验-不高于-右侧)
某省大学英语四级考试的平均 成绩为65分,现从某校随机抽取 20份试卷,其分数为:72 76 68 78 62 59 64 85 70 75 61 74 87 83 54 76 56 66 68 62。若显著性水平 取0.05,问该校英语水平是否不高 于全区水平。(假定考试成绩服从 正态分布)
假设检验
(单边检验-高于-右侧)
某省大学英语四级考试的平均 成绩为65分,现从某校随机抽取 20份试卷,其分数为:72 76 68 78 62 59 64 85 70 75 61 74 87 83 54 76 56 66 68 62。若显著性水平 取0.05,问该校英语水平是否高于 全区水平。(假定考试成绩服从正 态分布)
Compare Means
Independent Sample T test
例一
区间估计
例二
例一
用 “Employee.sav”资料,问: 清洁工、保管员和经理的受教育 年数是否有显著差异?
例二
由以往资料知道,甲、乙两煤 矿煤的含灰率都服从正态分布且方 差相等。从甲矿抽10个样本,从乙 矿抽12个样本,进行测试并得相关 数据。问两矿所采煤的平均含灰率 有无显著差异?
例二
某省大学英语四级考试的平均 成绩为65分,现从某校随机抽取 20份试卷,其分数为:72 76 68 78 62 59 64 85 70 75 61 74 87 83 54 76 56 66 68 62。问该校英语水 平与全区是否基本一致。
对单个总体均值的区间估计
Analyze —
Compare Means —
假设检验
(单边检验-低于-右侧)
某省大学英语四级考试的平均 成绩为65分,现从某校随机抽取 20份试卷,其分数为:72 76 68 78 62 59 64 85 70 75 61 74 87 83 54 76 56 66 68 62。若显著性水平 取0.05,问该校英语水平是否低于 全区水平。(假定考试成绩服从正 态分布)
假设检验
(单边检验-不低于-左侧)
某省大学英语四级考试的平均 成绩为65分,现从某校随机抽取 20份试卷,其分数为:72 76 68 78 62 59 64 85 70 75 61 74 87 83 54 76 56 66 68 62。若显著性水平 取0.05,问该校英语水平是否不低 于全区水平。(假定考试成绩服从 正态分布)
One-Sample T Test Analyze — Descriptives — Explore
例
例一
某区进行英语测验,现从某校 随机抽取20份试卷,其分数为:72 76 68 78 62 59 64 85 70 75 61 74 87 83 54 76 56 66 68 62 根据现有 资料,以95%的置信水平推断该校 英语测试的成绩。(假定学生的考 试成绩是服从正态部分的。)
分层次计算平均数
Analyze — Compare Means — Mean
例一
例一
用“Employee.sav”资料,
(1)计算各工种的平均受教育年数。 (2)计算各工种分性别的平均受教 育年数。
单样本T检验
单样本T检验是指,样本平均与总体 平均数的差异检验。样本平均数( x ) 与总体平均数μ。往往大小不一,这差 异是由于抽样误差造成,还是本质性误 差—样本根本不是来源于该总体。如果 差异显著,则认为样本平均数与总体平 均数μ。的差异已不能完全认为是抽样 误差了。
Analyze
Compare Means
Paired-Samples T test
例一
区间估计
例二
例一
用 “Employee.sav”资料,分 析美国企业现在工资与过去工资 是否有明显差异。
例二
从小学三年级随机抽取10名儿 童作为样本,分别在学期初和学期 末进行了推理能力的测验,看学生 的推理能力是否有所提高。
例三
医生测得18例慢性支气管炎患者及 16例健康人的尿17酮类固醇排出量 (mg/dl)分别为X1和X2,试问两组 的均数有无不同? 数据为data04_13。
对两个总体均值之差的区间估计
Analyze —
Compare Means —
Independent Sample T Test
两配对样本平均数差异T检验
定义
总体参数估计是以样本统计量 (即样本数字特征)作为未知总体 参数(即ቤተ መጻሕፍቲ ባይዱ体数字特征)的估计量, 并通过对样本单位的实际观察取得 样本数据,计算样本统计量的取值 作为被估计参数的估计值。
参数估计中的几个基本概念 总体参数 样本统计量 点估计 点估计的优良性
概率保证程度 (置信度)
置信区间
单个总体均值的区间估计
专题二 参数估计与假设检验
Analyze - Compare Means
分析 - 比较均值 Mean One Sample T test 均值
基本概念
单样本T检验
Independent Sample T test
Paired-Samples T test
独立样本T检验
配对样本T检验
One-Way ANOVA
单因素方差分析
南京财经大学 管于华
基本概念
参数估计和假设检验是统计推断 的二个重要方面。 参数估计是依照一定的概率保证 程度,用样本统计量估计总体参数取 值范围的方法。假设检验是先对研究 总体作出某种假设,然后通过对样本 的观察和试验来决定假设成立与否。
概述-参数估计
1. 几个基本概念 2. 单个总体均值的区间估计 3. 两个总体均值之差的区间估计
解一 解二
解一
解二
两独立样本平均数差异T检验
独立样本(Independent Sample) 是指两个样本彼此独立,没有任何关 联。例如实验组与控制组、男生组与 女生组、高收入组与低收入组、大学 数学系与物理系等。
两个独立样本均值之间差异用t 统计量进行检验。
两独立样本平均数差异T检验
Analyze
单边情况
原始主张受保护;原假设必带等号。
两类错误
显著性水平、临界值与拒绝区
假设检验的步骤
1.根据具体问题的要求,提出原假设H0和 备择假设H1;
2.选择一个合适的检验统计量,并计算之;
3.计算统计量相应的p值;
4.判断:若p值小于显著性水平α,则拒绝 原假设;若大于,则不能拒绝原假设。
单个总体均值的假设检验
