电场强度与梯度优秀课件
合集下载
8-5电场强度与梯度

§8-5 电场强与电势梯度
电场强度和电势都是描述电场性质的物理量,电场强度反映了电场 中力的作用,而电势则从能量的角度反映电场的性质。电场强度可以形 象地用电场线来描述,电势同样也可以用一个形象的图形来描述,这就 是等势面。
8.5.1 等势面 1、等势面:电场中电势相等的点构成的面,称为等势面。 点电荷的等势面 q U 4 0 r 平行板电容器电场的等势面。
dq dS
U U (x)
x dU 1 2 2 1/ 2 (1 ) E Ex 2 2 ( R x ) 2 x 1 2 0 dx R x2 2 0
作业:8-10 8-11
E
θ
P
2
只有 cos 0 即: E dl
Q dl
∴电场线垂直于等势面 (2)等势面较密的地方场强大,稀疏的地方场强小,电场线 指向电势降落的方向。 等势面的规定:任意相邻的两等势面间的电势差相等。
等势面的法线方向:电势增加的方向为正方向。
记
U ab E1 ab
式中
( i j k) x y z
梯度算符
c、场强与电势的关系 ∵电场中某点的场强总可以在等势面的切线方向和法线 方向上分解
E E En E 0 En n0
E E En E 0 En n0
U 又 E 0
En
U dU E n0 n0 U n dn
U n
电势梯度 的负值
说明:沿等势面的法线方向上电势的变化率最大。 例8-10 自看 例8-11 求均匀带电圆盘轴线上一点的电势和电场强度。设 q 圆盘半径为R,带电量为q。 dr R 2 解: ∵dq在P点的电势
电场强度和电势都是描述电场性质的物理量,电场强度反映了电场 中力的作用,而电势则从能量的角度反映电场的性质。电场强度可以形 象地用电场线来描述,电势同样也可以用一个形象的图形来描述,这就 是等势面。
8.5.1 等势面 1、等势面:电场中电势相等的点构成的面,称为等势面。 点电荷的等势面 q U 4 0 r 平行板电容器电场的等势面。
dq dS
U U (x)
x dU 1 2 2 1/ 2 (1 ) E Ex 2 2 ( R x ) 2 x 1 2 0 dx R x2 2 0
作业:8-10 8-11
E
θ
P
2
只有 cos 0 即: E dl
Q dl
∴电场线垂直于等势面 (2)等势面较密的地方场强大,稀疏的地方场强小,电场线 指向电势降落的方向。 等势面的规定:任意相邻的两等势面间的电势差相等。
等势面的法线方向:电势增加的方向为正方向。
记
U ab E1 ab
式中
( i j k) x y z
梯度算符
c、场强与电势的关系 ∵电场中某点的场强总可以在等势面的切线方向和法线 方向上分解
E E En E 0 En n0
E E En E 0 En n0
U 又 E 0
En
U dU E n0 n0 U n dn
U n
电势梯度 的负值
说明:沿等势面的法线方向上电势的变化率最大。 例8-10 自看 例8-11 求均匀带电圆盘轴线上一点的电势和电场强度。设 q 圆盘半径为R,带电量为q。 dr R 2 解: ∵dq在P点的电势
8.5电场强度与电势梯度的关系

E
ds
等势面——规定、性质、梯度
gradU
U n
n
三、 q、E、U 三者关系网
1、 q E
E
1
4 0
dq r3
r
sE
ds
1
0
vdv
2、 q U
U
1
4 0
dq r
U LE dl
3 E U
U LE dl
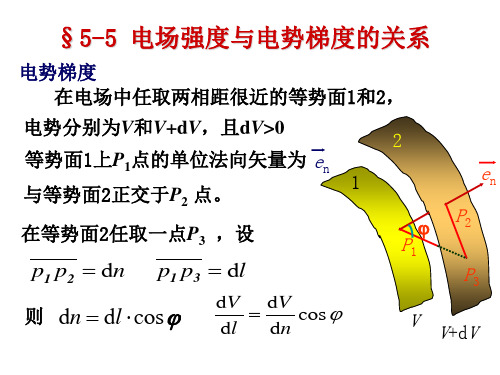
势面2,电场力做功
dA qE dl
qEdl cos
en
1
2
P1
en P2
P3
qEdn
V V+dV
上页 下页 返回 退出
电场力做功等于电势能的减少量 dA q dU
E dU dn
场强也与等势面垂直,但指向电势降低的方向。
E Een 写成矢量形式
E
第一章 真空中静电场小结
一、理论体系:
出发点
:叠 库加 仑原 定理 律
高斯定理 环路定理
电场为有源场 电场是有势场
二、内容:
1、一个定律 : 2、两个定理 :
F
q1q2
4 0
r r3
E
ds
1
dv
s
0 v
l E dl 0
上页 下页 返回 退出
则 dn dl cos
dU dU cos
dl dn
2
P1
en P2
P3
U U+dU
上页 下页 返回 退出
定义电势梯度
电场强度与梯度

△l→0时有
E
V
V d V E l i m l l 0 l d l
电场中某一点的电场强度沿某一方向的分量, 等于这一点的电势沿该方向单位长度上电势变 化率的负值。 V t 电场强度的单位也用V/m。 2 电势梯度 显然电势沿不同方向 V V 的单位长度增量是不同的, 现讨论两个特殊方向上的 情况:切向和法向。
2 21 / 2 p ( 4 x y ) 2 2 E E E x y 2 22 4 ( x y ) 0
x
A点在电偶极矩的延长线上时:
y 0
2p 1 E 4 0 x3
1 E 4 0 y3 p
y
A
A点在电偶极矩的中垂线上时:
r
q o
r
r
q
x 0
r0
y
A
r
r r
r0
q
q o
x
2
V 0
用A点的坐标x,y写成:
x V 4 0 (x2 y2)3/2
2 2 V p y 2 x E x 2 25 / 2 x 4 ( x y ) 0
p
y
A
r
r r
r0
q
V p 3 x y o q E y 2 25 /2 y 4 ( x y ) 0
例2 求电偶极子电场中任意一点V的电势和电场强度。
解
r0 r 2 rr r c o s r r r 0
1 q V 4 0 r 1 q V 4 0 r V V V q r r 4 0 r r
y
x
例3 如图所示,水分子可以近似看作为电偶极矩
E
V
V d V E l i m l l 0 l d l
电场中某一点的电场强度沿某一方向的分量, 等于这一点的电势沿该方向单位长度上电势变 化率的负值。 V t 电场强度的单位也用V/m。 2 电势梯度 显然电势沿不同方向 V V 的单位长度增量是不同的, 现讨论两个特殊方向上的 情况:切向和法向。
2 21 / 2 p ( 4 x y ) 2 2 E E E x y 2 22 4 ( x y ) 0
x
A点在电偶极矩的延长线上时:
y 0
2p 1 E 4 0 x3
1 E 4 0 y3 p
y
A
A点在电偶极矩的中垂线上时:
r
q o
r
r
q
x 0
r0
y
A
r
r r
r0
q
q o
x
2
V 0
用A点的坐标x,y写成:
x V 4 0 (x2 y2)3/2
2 2 V p y 2 x E x 2 25 / 2 x 4 ( x y ) 0
p
y
A
r
r r
r0
q
V p 3 x y o q E y 2 25 /2 y 4 ( x y ) 0
例2 求电偶极子电场中任意一点V的电势和电场强度。
解
r0 r 2 rr r c o s r r r 0
1 q V 4 0 r 1 q V 4 0 r V V V q r r 4 0 r r
y
x
例3 如图所示,水分子可以近似看作为电偶极矩
高二物理竞赛课件:电场强度与电势梯度

4 0 x
40a(a l )
Q
Q a l
(2)球在 x 处电势 V 4 0 x
ln 40 a
2
电场强度和电势梯度 d V:两等位面电势之差。
E
dl
nˆ
d l:两等位面间在P1点处的最短距离。 P1
P2
(等位面间在P1点处的法向距离)
nˆ :P1点处法线方向上的单位矢量,
V V dV
指向电势升高的方向。
r
dr
2 0
4 0
(
R2
r2
)
0
外电场对电偶极子的力矩和取向作用
解:电偶极子受 力偶的作用
F qE F qE
合力: F F F
电矩
0
p ql
l
F
q
q
F E
故偶极子不平动。 合力矩:
M 的方向
M
M
2F
P
l 2
sin qEl
E
M使 p
sin
转向
E
pE
sin
2
电荷在外电场中的静电势能 任何电荷在静电场中都具有势能,叫的静电势能。
E R2
若令V= 0 则
rR V
R2
E dl
r
2 0 r
r
R2 dr 2 0 r
ln 电势发散,无意义!
20 r
R
只能取有限远处电势为零。
r
若令柱面 处 VR=0,则
r > R:V R R2 dr R2 ln R 0
r 20r
20 r
r
r < R:V
R r
W q0 (Vb Va )
2
例、长为L 的均匀带电导线,电荷线密度为 。
40a(a l )
Q
Q a l
(2)球在 x 处电势 V 4 0 x
ln 40 a
2
电场强度和电势梯度 d V:两等位面电势之差。
E
dl
nˆ
d l:两等位面间在P1点处的最短距离。 P1
P2
(等位面间在P1点处的法向距离)
nˆ :P1点处法线方向上的单位矢量,
V V dV
指向电势升高的方向。
r
dr
2 0
4 0
(
R2
r2
)
0
外电场对电偶极子的力矩和取向作用
解:电偶极子受 力偶的作用
F qE F qE
合力: F F F
电矩
0
p ql
l
F
q
q
F E
故偶极子不平动。 合力矩:
M 的方向
M
M
2F
P
l 2
sin qEl
E
M使 p
sin
转向
E
pE
sin
2
电荷在外电场中的静电势能 任何电荷在静电场中都具有势能,叫的静电势能。
E R2
若令V= 0 则
rR V
R2
E dl
r
2 0 r
r
R2 dr 2 0 r
ln 电势发散,无意义!
20 r
R
只能取有限远处电势为零。
r
若令柱面 处 VR=0,则
r > R:V R R2 dr R2 ln R 0
r 20r
20 r
r
r < R:V
R r
W q0 (Vb Va )
2
例、长为L 的均匀带电导线,电荷线密度为 。
5-5 电场强度与电势梯度的关系
2 2
2
2
P 2 2 4 x y 4 0 ( x 2 y 2 ) 2
P(0,y) y E -q
-L/2
讨论:
1. 在X轴上,y=0,则
Ex P 20 x 3 P 40 y
Ey 0
3
2. 在Y轴上,x=0,则
Ex
+q
O
L/2
P(x,0)
Ey 0
E
x
与用叠加原理得到的结果一致。
1 1
E
en
P2
P1
P3
V
V+dV
例1 试由电偶极子的电势分布求其的电场强度。 解: 在直角坐标系中先写出电势的表达式,
1 q 1 q q r r V 40 r 40 r 40 r r
L cos P cos 2 2 40 r 4 0 r Px 40 ( x 2 y 2 ) 3 / 2 q
P3
V
则 dn dl cos
V+dV
定义电势梯度
dV grad V en dn
单位:V/m
其量值为该点电势增加率的最大值。 方向与等势面垂直,并指向电势升高的方向。 电势梯度与电场强度的关系 2
en
电荷q从等势面1移动到等 势面2,电场力做功
1
en P1
dA qE dl qE dl cos qE den
例2 将半径为R2 的圆盘在盘心处挖去半径为R1的小孔,并 使盘均匀带电.试通过用电势梯度求电场强度的方法,计算这 个中空带电圆盘轴线上任一点P处的电场强度.
解:设圆盘上的电荷 面密度为 轴线上任一点p 到中空圆盘的 距离为x,在圆 盘上取半径为r 宽为dr的圆环 ,环上所带电 z 荷为
2
2
P 2 2 4 x y 4 0 ( x 2 y 2 ) 2
P(0,y) y E -q
-L/2
讨论:
1. 在X轴上,y=0,则
Ex P 20 x 3 P 40 y
Ey 0
3
2. 在Y轴上,x=0,则
Ex
+q
O
L/2
P(x,0)
Ey 0
E
x
与用叠加原理得到的结果一致。
1 1
E
en
P2
P1
P3
V
V+dV
例1 试由电偶极子的电势分布求其的电场强度。 解: 在直角坐标系中先写出电势的表达式,
1 q 1 q q r r V 40 r 40 r 40 r r
L cos P cos 2 2 40 r 4 0 r Px 40 ( x 2 y 2 ) 3 / 2 q
P3
V
则 dn dl cos
V+dV
定义电势梯度
dV grad V en dn
单位:V/m
其量值为该点电势增加率的最大值。 方向与等势面垂直,并指向电势升高的方向。 电势梯度与电场强度的关系 2
en
电荷q从等势面1移动到等 势面2,电场力做功
1
en P1
dA qE dl qE dl cos qE den
例2 将半径为R2 的圆盘在盘心处挖去半径为R1的小孔,并 使盘均匀带电.试通过用电势梯度求电场强度的方法,计算这 个中空带电圆盘轴线上任一点P处的电场强度.
解:设圆盘上的电荷 面密度为 轴线上任一点p 到中空圆盘的 距离为x,在圆 盘上取半径为r 宽为dr的圆环 ,环上所带电 z 荷为
高二物理竞赛课件电场强度与电势梯度

荷系。因此任意点电荷系的电场力所做的功,等于
组成此点电荷系的各点电荷的电场力所做功的代数
和:
E Ei
i
W
q0
E dl
l
i
q0 l Ei dl
结论:静电场力做功与路径无关,与始末位置有关.
10.4.2 静电场的环路定理
q0 E dl q0 E dl
ABC
ADC
q0( E dl E dl ) 0
r
dl
rdl
cos
rdr
B
rB
dl
dr
E
r
dW
q0 E
dl
qq0
4π 0r3
r
dl
q rA q0
A
W qq0
4 π0
rB dr r rA 2
qq0 ( 1 1 )
4 π0 rA rB
结果: A 仅与 q0 的始末
位置有关,与路径无关.
任意带电体都可看成由许多点电荷组成的点电
电场强度与电势梯度
电场强度与电势梯度 等势面 电场中电势相等的点所构成的面,叫做等势面。
相邻两个等势面间电势差等于常量。
点电荷的电场线与等势面
一对等量异号点电荷的电 场线和等势面
-
-
+
两平行带电平板的电场线和等势面
++++++++++++
等势面的性质: (1)等势面与电力线处处垂直,电力线的方向是 电势降落的方向。 (2)等势面的疏密反映了场强的强弱。等势面较 密的地方场强大,较疏的地方场强小。
i
j
k
x y z
8-4场强与梯度,带电粒子

M PE sin qlE sin
/2
M max 6 10 N m
3
P
E
A W [W (0) W ( 2)]
q
8-5 、6场强与梯度,带电粒子的运动
第八章 真空中的静电场
三、带电粒子在匀强电场中的运动
例3 将半径分别为R1=10cm和R2=20cm的两个很长的共 轴金属圆筒分别接到直流电源的两极上。今使一电子以 v 5 106 m / s ,沿半径为r(R1<r<R2)的圆周的切线 速率 方向射入两圆筒间。求使电子作圆周运动的电源电压。
q R
o
r
z
P x E
x
电场弱的地方电势低;电场强的地方电势高吗?
V=0 的地方 E 0吗?
E 相等的地方,V 一定等吗?
8-5 、6场强与梯度,带电粒子的运动
第八章 真空中的静电场
§8-6 带电粒子在静电场中的运动
一、带电粒子在匀强场中受力(力矩)
q
F F F qE qE 0
q
0 W p E 能量最低 π /2 W 0 π W p E 能量最高
F
l
q
F
E
从= 角,电场力做多少功?
A W pE cos
8-5 、6场强与梯度,带电粒子的运动
第八章 真空中的静电场
例2 一电偶极子由电量 q 1.5 10 6 C的两个异号电荷 组成,两电荷相距 l 2.0cm 把这电偶极子放在场强 大小为 E 2.0 10 5 N / C 的均匀电场中。试求: (1)电场作用于电偶极子的最大力矩。 (2)电偶极子从受最大力矩的位置转到平衡位置 过程,电场力作的功。 q
/2
M max 6 10 N m
3
P
E
A W [W (0) W ( 2)]
q
8-5 、6场强与梯度,带电粒子的运动
第八章 真空中的静电场
三、带电粒子在匀强电场中的运动
例3 将半径分别为R1=10cm和R2=20cm的两个很长的共 轴金属圆筒分别接到直流电源的两极上。今使一电子以 v 5 106 m / s ,沿半径为r(R1<r<R2)的圆周的切线 速率 方向射入两圆筒间。求使电子作圆周运动的电源电压。
q R
o
r
z
P x E
x
电场弱的地方电势低;电场强的地方电势高吗?
V=0 的地方 E 0吗?
E 相等的地方,V 一定等吗?
8-5 、6场强与梯度,带电粒子的运动
第八章 真空中的静电场
§8-6 带电粒子在静电场中的运动
一、带电粒子在匀强场中受力(力矩)
q
F F F qE qE 0
q
0 W p E 能量最低 π /2 W 0 π W p E 能量最高
F
l
q
F
E
从= 角,电场力做多少功?
A W pE cos
8-5 、6场强与梯度,带电粒子的运动
第八章 真空中的静电场
例2 一电偶极子由电量 q 1.5 10 6 C的两个异号电荷 组成,两电荷相距 l 2.0cm 把这电偶极子放在场强 大小为 E 2.0 10 5 N / C 的均匀电场中。试求: (1)电场作用于电偶极子的最大力矩。 (2)电偶极子从受最大力矩的位置转到平衡位置 过程,电场力作的功。 q
电场强度与梯度页PPT文档

a m F 1 9 ..4 1 3 1 1 1 0 0 1 3 0 1m s 2 1 .5 7 1 0 2 0 m s 2
v a t 1 . 5 7 1 0 2 0 1 0 1 4 m s - 1 1 . 5 7 1 0 6 m s - 1
W a b q 0 ( V a V b ) a b q 0 E d l 0
q 0 0E 0d l 0 Edl
② 等势面密集的地方电场强度大,稀疏的地方电 场强度小。
2 几种电荷分布的电场线
与等势面
⑴ 点电荷的电场线与等势面
q
⑵ 一对等量异号点电荷的电场线和等势面
q
q
⑶ 两平行带电平板的电场线和等势面
++++++++++++++++
二 电场强度与电势梯度 1 电势沿任意方向的增加率
B l A
UAB ( VBVA) El E l
Elcos
E
E c o s E l V V B V A VV V
VEll 即 El V l
与气体分子热运动能量比较
TE p 3.5710 20K2.59103K k 1.3810 23
电子在分子电偶极子电场中所受的力为
F
eE
2e
40
p x3
2 1 .6 0 1 0 1 9
6 .2 1 0 3 01 .4 3 1 0 1 0N
4 8 .8 5 1 0 1 2(5 1 0 1 0)3
4 0 r r
r0 r
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相等吗?
例1 求一均匀带电细圆环轴线上任一点的电场强度。
解 V
q
y
40 (x2 R2 )1 2
E V
qR
r
P
E
Ex
V x
ox
x
z
x410
(x2
q R2)12
1
qx
40 (x2 R2)32
例2 求电偶极子电场中任意一点V的电势和电场强度。
解
V
1
4 0
q r
y
A
V
1
4 0
q r
r r r
解 电子在A点的电势能为
ep
Ep
eV
40
r2
o Hp A
e1.601019C
H
E p 41 .6 8 0 .8 5 1 0 1 1 0 9 1 2(6 5 .2 1 0 1 0 1 0 3 )0 2 3 .5 7 1 0 2 0J
与气体分子热运动能量比较
TE p 3.5710 20K2.59103K k 1.3810 23
电子在分子电偶极子电场中所受的力为
F
eE
2e
40
p x3
2 1 .6 0 1 0 1 9 6 .2 1 0 3 01 .4 3 1 0 1 0N
4 8 .8 5 1 0 1 2(5 1 0 1 0)3
a m F 1 9 ..4 1 3 1 1 1 0 0 1 3 0 1m s 2 1 .5 7 1 0 2 0m s 2
V V V q r r
4 0 r r
q o q x
r0
r0 r
r r r 0 c o s r r r 2
y V q r r q r0 cos
40 rr 4 0 r2
A
1 p cos
4 0 r2
即 V 1 pcos 40 r2
0
V
1
40
p r2
V410ຫໍສະໝຸດ p r2r r r
E E n E t E t 0E
En
dV dln
en
可见:电场强度大小等于电势梯度的负值,
方向由高电势指向第电势处。
⑴
电场强度沿任意方向的分量:E l
dV dl
El Ecos(E,l)Ecos
(gradV)l ddVln cos
dldln EnEl
⑵ 直角坐标系中
Ex V x Ey V y Ez V z
v a t 1 . 5 7 1 0 2 0 1 0 1 4 m s - 1 1 . 5 7 1 0 6 m s - 1
2p 1 y0 E
40 x3
A点在电偶极矩的中垂线上时:
x0 E p 1
40 y3
y
A
r r r
q o q x
r0
例3 如图所示,水分子可以近似看作为电偶极矩
p=6.2×10-30C·m 的电偶极子。有一电子放在电 偶极矩的延长线、距电偶极矩中心O为5×10-10m
的点A上。求电子的势能和作用在电子上的力。
q o q x
r0
V 0
2
用A点的坐标x,y写成:
p
x
V
40 (x2 y2)3/2
yA
V p y22x2
Exx40(x2y2)5/2
r r r
x Ey V y4p0(x2 3xyy2)5/2
q
o
r0
q
p(4x2y2)1/2
EE x 2E y 24 0 (x2y2)2
A点在电偶极矩的延长线上时:
q
q
⑶ 两平行带电平板的电场线和等势面
++++++++++++++++
二 电场强度与电势梯度 1 电势沿任意方向的增加率
B l A
UAB ( VBVA) El E l
Elcos
E
E c o s E l V V B V A VV V
VEll 即 El V l
△l→0时有
V dV
El lil m0 l
电场强度与梯度优秀课件
静电场中电荷沿等势面移动时,电场力作功
W a b q 0 ( V a V b ) a b q 0 E d l 0
q 0 0E 0d l 0 Edl
② 等势面密集的地方电场强度大,稀疏的地方电 场强度小。
2 几种电荷分布的电场线
与等势面
⑴ 点电荷的电场线与等势面
q
⑵ 一对等量异号点电荷的电场线和等势面
E ( ViVjVk) grad V x y z
电场强度与电势梯度关系的物理意义 ① 空间某点电场强度的大小取决于该点领域内
电势V的空间变化率。 ② 电场强度的方向恒指向电势降落的方向。
讨论 ⑴ 电场弱的地方电势低;电场强的地方电势高吗?
⑵ V=0地方, E 0 吗?
⑶ E 相等的地方,V一定相等吗?等势面上 E 一定
dV0 Et 0
⑵ 沿法向
En
dV d ln
dV dln
0
时
E
0
V
V V
E 的方向总是由高电
势指向低电势,即 E 与
e n 反向。则有:E n
dV dln
en
et
dl
A en
d ln
E 低高
电电 势势
式中
d d
V ln
en
称为电势在该电的电势梯度,记作
grad V
dV dln
en
3 电场强度与电势梯度的关系
dl
电场中某一点的电场强度沿某一方向的分量,
等于这一点的电势沿该方向单位长度上电势变
化率的负值。
电场强度的单位也用V/m。 V
2 电势梯度
显然电势沿不同方向 V V
的单位长度增量是不同的,
et
dl
A en
d ln
现讨论两个特殊方向上的
E 低高
情况:切向和法向。
电电 势势
⑴ 沿切向Et d dV lt
例1 求一均匀带电细圆环轴线上任一点的电场强度。
解 V
q
y
40 (x2 R2 )1 2
E V
qR
r
P
E
Ex
V x
ox
x
z
x410
(x2
q R2)12
1
qx
40 (x2 R2)32
例2 求电偶极子电场中任意一点V的电势和电场强度。
解
V
1
4 0
q r
y
A
V
1
4 0
q r
r r r
解 电子在A点的电势能为
ep
Ep
eV
40
r2
o Hp A
e1.601019C
H
E p 41 .6 8 0 .8 5 1 0 1 1 0 9 1 2(6 5 .2 1 0 1 0 1 0 3 )0 2 3 .5 7 1 0 2 0J
与气体分子热运动能量比较
TE p 3.5710 20K2.59103K k 1.3810 23
电子在分子电偶极子电场中所受的力为
F
eE
2e
40
p x3
2 1 .6 0 1 0 1 9 6 .2 1 0 3 01 .4 3 1 0 1 0N
4 8 .8 5 1 0 1 2(5 1 0 1 0)3
a m F 1 9 ..4 1 3 1 1 1 0 0 1 3 0 1m s 2 1 .5 7 1 0 2 0m s 2
V V V q r r
4 0 r r
q o q x
r0
r0 r
r r r 0 c o s r r r 2
y V q r r q r0 cos
40 rr 4 0 r2
A
1 p cos
4 0 r2
即 V 1 pcos 40 r2
0
V
1
40
p r2
V410ຫໍສະໝຸດ p r2r r r
E E n E t E t 0E
En
dV dln
en
可见:电场强度大小等于电势梯度的负值,
方向由高电势指向第电势处。
⑴
电场强度沿任意方向的分量:E l
dV dl
El Ecos(E,l)Ecos
(gradV)l ddVln cos
dldln EnEl
⑵ 直角坐标系中
Ex V x Ey V y Ez V z
v a t 1 . 5 7 1 0 2 0 1 0 1 4 m s - 1 1 . 5 7 1 0 6 m s - 1
2p 1 y0 E
40 x3
A点在电偶极矩的中垂线上时:
x0 E p 1
40 y3
y
A
r r r
q o q x
r0
例3 如图所示,水分子可以近似看作为电偶极矩
p=6.2×10-30C·m 的电偶极子。有一电子放在电 偶极矩的延长线、距电偶极矩中心O为5×10-10m
的点A上。求电子的势能和作用在电子上的力。
q o q x
r0
V 0
2
用A点的坐标x,y写成:
p
x
V
40 (x2 y2)3/2
yA
V p y22x2
Exx40(x2y2)5/2
r r r
x Ey V y4p0(x2 3xyy2)5/2
q
o
r0
q
p(4x2y2)1/2
EE x 2E y 24 0 (x2y2)2
A点在电偶极矩的延长线上时:
q
q
⑶ 两平行带电平板的电场线和等势面
++++++++++++++++
二 电场强度与电势梯度 1 电势沿任意方向的增加率
B l A
UAB ( VBVA) El E l
Elcos
E
E c o s E l V V B V A VV V
VEll 即 El V l
△l→0时有
V dV
El lil m0 l
电场强度与梯度优秀课件
静电场中电荷沿等势面移动时,电场力作功
W a b q 0 ( V a V b ) a b q 0 E d l 0
q 0 0E 0d l 0 Edl
② 等势面密集的地方电场强度大,稀疏的地方电 场强度小。
2 几种电荷分布的电场线
与等势面
⑴ 点电荷的电场线与等势面
q
⑵ 一对等量异号点电荷的电场线和等势面
E ( ViVjVk) grad V x y z
电场强度与电势梯度关系的物理意义 ① 空间某点电场强度的大小取决于该点领域内
电势V的空间变化率。 ② 电场强度的方向恒指向电势降落的方向。
讨论 ⑴ 电场弱的地方电势低;电场强的地方电势高吗?
⑵ V=0地方, E 0 吗?
⑶ E 相等的地方,V一定相等吗?等势面上 E 一定
dV0 Et 0
⑵ 沿法向
En
dV d ln
dV dln
0
时
E
0
V
V V
E 的方向总是由高电
势指向低电势,即 E 与
e n 反向。则有:E n
dV dln
en
et
dl
A en
d ln
E 低高
电电 势势
式中
d d
V ln
en
称为电势在该电的电势梯度,记作
grad V
dV dln
en
3 电场强度与电势梯度的关系
dl
电场中某一点的电场强度沿某一方向的分量,
等于这一点的电势沿该方向单位长度上电势变
化率的负值。
电场强度的单位也用V/m。 V
2 电势梯度
显然电势沿不同方向 V V
的单位长度增量是不同的,
et
dl
A en
d ln
现讨论两个特殊方向上的
E 低高
情况:切向和法向。
电电 势势
⑴ 沿切向Et d dV lt
