管理软件应用——Lingo

合集下载

LINGO使用说明比较简单

LINGO使用说明比较简单
第九步，分析和优化结果。

优化模型求解完成后，你可以通过结果显
示区中的结果表格和图表来分析和优化结果。

LINGO还提供了一些分析工具，如灵敏度分析和场景分析，帮助你深入理解模型的行为和性能。

第十步，保存和导出结果。

在 LINGO 中，你可以保存整个优化模型
及其求解结果，以供将来使用。

通过点击菜单栏中的“文件”选项，选择“保存”或“导出”，就可以将模型和结果保存为不同的文件格式，如LINGO模型文件（.lng）、Excel 文件（.xls）或文本文件（.txt）。

通过上述十个步骤，你可以使用LINGO软件完成一个优化模型的建立、求解和分析。

当然，LINGO还具备其他高级功能和应用，如混合整数规划、随机规划和非线性规划等，可以根据你的具体需求进行进一步学习和应用。

LINGO使用手册和官方网站上有更多详细的说明和案例，可以帮助你更好
地使用和理解LINGO软件。

第三章LINGO软件的使用

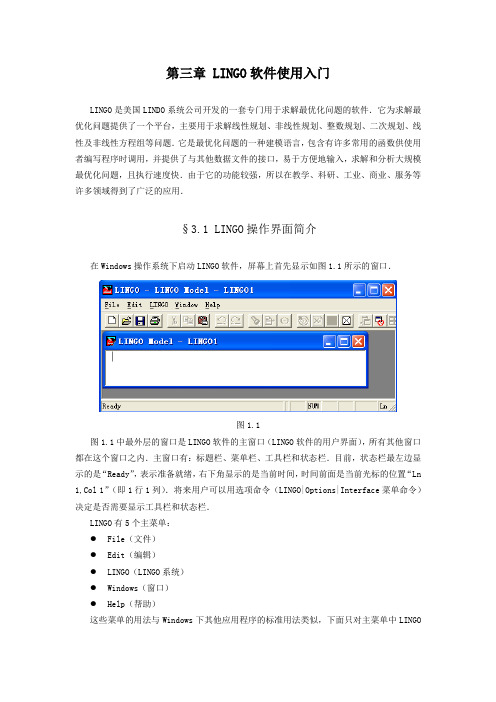
第三章 LINGO软件使用入门LINGO是美国LINDO系统公司开发的一套专门用于求解最优化问题的软件．它为求解最优化问题提供了一个平台，主要用于求解线性规划、非线性规划、整数规划、二次规划、线性及非线性方程组等问题．它是最优化问题的一种建模语言，包含有许多常用的函数供使用者编写程序时调用，并提供了与其他数据文件的接口，易于方便地输入，求解和分析大规模最优化问题，且执行速度快．由于它的功能较强，所以在教学、科研、工业、商业、服务等许多领域得到了广泛的应用．§3.1 LINGO操作界面简介在Windows操作系统下启动LINGO软件，屏幕上首先显示如图1.1所示的窗口．图1.1图1.1中最外层的窗口是LINGO软件的主窗口（LINGO软件的用户界面），所有其他窗口都在这个窗口之内．主窗口有：标题栏、菜单栏、工具栏和状态栏．目前，状态栏最左边显示的是“Ready”，表示准备就绪，右下角显示的是当前时间，时间前面是当前光标的位置“Ln 1,Col 1”（即1行1列）．将来用户可以用选项命令（LINGO|Options|Interface菜单命令）决定是否需要显示工具栏和状态栏．LINGO有5个主菜单：●File（文件）●Edit（编辑）●LINGO（LINGO系统）●Windows（窗口）●Help（帮助）这些菜单的用法与Windows下其他应用程序的标准用法类似，下面只对主菜单中LINGO系统的主要命令进行简要介绍．LINGO系统（LINGO）的主菜单●LINGO|Solve(Ctrl-S)LINGO|Solve(Ctrl-S)（求解）命令对当前模型进行编译并求解．如果当前模型输入有错误，编译时将报告错误．求解时会显示一个求解器运行状态窗口．●LINGO|Solution(Ctrl-O)LINGO|Solution(Ctrl-O)（解答）命令显示当前解．●LINGO|Range(Ctrl-R)LINGO|Range(Ctrl-R)（灵敏度分析）命令显示当前解的灵敏度分析结果．（你必须在此之前求解过当前模型）●LINGO|Options(Ctrl-I)LINGO|Options(Ctrl-I)（选项）命令将打开一个含有7个选项卡的对话框窗口，你可以通过它修改LINGO系统的各种控制参数和选项．修改完以后，你如果单击“应用”按钮，则新的设置马上生效；如果单击“OK”按钮，则新的设置马上生效，并且同时关闭该窗口；如果单击“Save”按钮，则将当前设置变为默认设置，下次启动LINGO时这些设置仍然有效；如果单击“Default”按钮，则恢复LINGO系统定义的原始默认设置；如果单击“Cancel”按钮将废弃本次操作，退出对话框；单击“Help”按钮将显示本对话框的帮助信息．●LINGO|Generate和LINGO|PictureLINGO|Generate和LINGO|Picture命令都是在模型窗口下才能使用，他们的功能是按照LINGO模型的完整形式分别以代数表达式形式和矩阵图形形式显示目标函数和约束．●LINGO|Debug（Ctrl+D）LINGO|Debug（Ctrl+D）命令分析线性规划无解或无界的原因，建议如何修改●LINGO|Model Statistics（Ctrl+E）LINGO|Model Statistics（Ctrl+E）命令显示当前模型的统计信息．●LINGO|Look（Ctrl+L）LINGO|Look（Ctrl+L）命令显示当前模型的文本形式，显示时对所有行按顺序编号．图1.2给出了工具栏的简要功能说明．图1.2当前光标所在的窗口（窗口标题栏上标有“LINGO Model-LINGO1”），就是模型窗口（model windows），也就是用于输入LINGO优化模型（即LINGO程序）的窗口．§3.2 LINGO模型的基本特征LINGO模型（程序）从LINGO模型窗口输入，它以语句“MODEL:”开始，以语句“END”结束．它是由一系列语句组成，每个语句都是以分号“；”结束，语句是组成LINGO模型的基本单位．每行可以写多个语句，为了保持模型的可读性，最好一行只写一个语句，并且按照语句之间的嵌套关系对语句安排适当的缩进，增强层次感．以感叹号“！”开始的语句是注释语句（注释语句也需要以分号“；”结束）．LINGO模型（程序）一般由5个部分（或称5段）组成：（1）集合段（SETS）：这部分要以“SETS：”开始，以“ENDSETS”结束，作用在于定义必要的集合变量（SET）及其元素（member，含义类似于数组的下标）和属性（attribute，含义类似于数组）．格式有基本集和派生集两种．基本集：Setname(集合变量名)[/member_list(元素列表)/][:attribute_list(属性列表)]；元素列表可以全部一一列出，也可以用格式“/元素1..元素N/”列出，例如SETS：STUDENTS/1,2,3,4,5/:NAME,AGE；ENDSETSSETS：STUDENTS/1..5/:NAME,AGE；ENDSETS派生集：Setname(parent_set_list(源集列表))[/member_list/][:attribute_list]；例如SETS:PRODUCT/A B/；MACHINE/M N/；WEEK/1..2/；ALLOWED( PRODUCT,MACHINE,WEEK)；ENDSETS列表可以用逗号“，”分开，也可以用空格分开．（2）数据段（DATA）：这部分要以“DATA：”开始，以“ENDDATA”结束，作用在于对集合的属性（数组）输入必要的常数数据．格式为：attribute_list(属性列表)=value_list(常数列表)；例如SETS:SET1 /A, B, C/: X, Y；ENDSETSDATA:X = 1 2 3；Y = 4 5 6；ENDDATA（3）初始化段（INIT）：这部分要以“INIT：”开始，以“ENDINIT”结束，作用在于对集合的属性（数组）给出初值．格式为：attribute_list(属性列表)=value_list(常数列表)；与数据段的用法类似．（4）计算段（CALC）：这部分要以“CALC：”开始，以“ENDCALC”结束，作用在于对一些原始数据进行计算处理．因为在实际问题中，输入的数据往往是原始数据，不一定能在模型中直接使用，可以在这个段对这些原始数据进行一定的“预处理”，得到模型中真正需要的数据．在计算段中语句是顺序执行的．（5）目标与约束段：这部分没有段的开始和结束标记，作用在于给定目标函数与约束条件．可见除这一段外，其他4个段都有明确的段标记．这一段是模型的主要部分，其他段是为这一段服务的．其他四段可以没有，这一段必须要有．否则不称其为模型．这一段一般要用到LINGO的运算符和各种函数．§3.3 LINGO的运算符和函数LINGO包含有大量的运算符和函数，供程序（建立优化模型）调用，其功能很强．充分利用这些函数，对解决问题将是非常方便的．下面给出部分函数及简要功能介绍，全部函数及详细功能说明可进一步参考LINGO的使用手册．一、运算符及其优先级LINGO的运算符有三类：算数运算符、逻辑运算符和关系运算符．1．算术运算符：LINGO中的算术运算符有以下5种：+（加法），-（减法或负号），*（乘法），/（除法），∧（求幂）．算术运算是数与数之间的运算，运算结果仍是数．2．逻辑运算符：LINGO中的逻辑运算符有以下9种，可以分成两类：（1）#AND#（与），#OR#（或），#NOT#（非）：这三个运算是逻辑值之间的运算，也就是它们操作的对象本身必须已经是逻辑值或逻辑表达式，计算结果也是逻辑值．（2）#EQ#（等于），#NE#（不等于），#GT#（大于），#GE#（大于等于），#LT#（小于），#LE#（小于等于）：这6个操作实际上是“数与数之间”的比较，也就是它们操作的对象本身必须是两个数，而逻辑表达式计算的结果是逻辑值．3．关系运算符：LINGO中的关系运算符有以下3种：＜（即＜＝，小于等于），＝（等于），＞（即＞＝，大于等于）这三个运算符虽然也是“数与数之间”的比较，但在LINGO中只用来表示优化模型的约束条件，所以不是真正意义上的运算．这些运算符的优先级如表3.1所示（同一优先级按左到右的顺序执行；如果有括号“（）”，则括号内的表达式优先进行计算）表3.1二、基本的数学函数在LINGO中写程序时可以调用大量的内部函数，这些函数以“@”符号打头（类似调用命令）．LINGO中数学函数的用法与其它语言中的数学函数的用法类似，主要有以下函数：@ABS(X)：绝对值函数，返回X的绝对值．@COS(X)：余弦函数，返回X的余弦值（X的单位是弧度）．@EXP(X)：指数函数，返回e x的值．@FLOOR(X)：取整函数，返回X的整数部分（向最靠近0的方向取整）．@LGM(X)：返回X的伽马（Gamma）函数的自然对数值．@LOG(X)：自然对数函数，返回X的自然对数值．@MOD(X,Y)：模函数，返回X对Y取模的结果．@POW(X,Y)：指数函数，返回X Y的值．@SIGN(X)：符号函数，返回X的符号值（X＜0时返回-1，X＞＝0返回1）．@SIN(X)：正弦函数，返回X的正弦值．@SMAX(list)：最大值函数，返回列表（list）中的最大值．@SMIN(list)：最小值函数，返回列表（list）中的最小值．@SQR(X)：平方函数，返回X的平方值．@SQRT(X)：平方根函数，返回X的正的平方根的值．@TAN(X)：正切函数，返回X的正切值．三、集合循环函数集合循环函数是指对集合上的元素（下标）进行循环操作的函数，主要有@FOR，@MAX，@MIN，@SUM，@PROD五种,其用法如下：@function(setname[(set_index_list)[|conditional_qualifier]]:expression_list)；其中：Function是集合函数名；Setname是集合名；set_index_list是集合索引列表（不需要使用索引时可以省略）；|conditional_qualifier是用逻辑表达式给出的过滤条件（无条件时可以省略）；:expression_list是一个表达式（对@FOR函数，可以是一组表达式）．下面简要介绍其作用．@FOR(setname[(set_index_list)[|cond_qualifier]]:exp_list)：对集合setname中的每个元素独立地生成由exp_list描述的表达式（通常是优化问题的约束）．@MAX(setname[(set_index_list)[|cond_qualifier]]:exp)：返回集合setname上的表达式exp的最大值．@MIN(setname[(set_index_list)[|cond_qualifier]]:exp)：返回集合setname上的表达式exp的最小值．@SUM(setname[(set_index_list)[|cond_qualifier]]:exp)：返回集合setname上的表达式exp的和．@PROD(setname[(set_index_list)[|cond_qualifier]]:exp)：返回集合setname上的表达式exp的积．四、集合操作函数集合操作函数是指对集合进行操作的函数，主要有@INDEX,@IN,@WRAP,@SIZE四种，下面简要介绍其作用．@INDEX([set_name,]primitive_set_element)：返回元素primitive_set_element在集合set_name中的索引值（即按定义集合时元素出现顺序的位置编号）．如果省略集合名set_name，LINGO按程序定义的集合顺序找到第一个含有元素primitive_set_element的集合，并返回索引值．如果在所有集合中均没有找到该元素，会给出出错信息．@IN(set_name,primitive_index_1[,primitive_index_2 ...])：判断一个集合中是否含有索引值．集合set_name 中包含由索引primitive_index_1[,primitive_index_2...]所表示的对应元素，则返回1（逻辑值“真”），否则返回0（逻辑值“假”）．@WRAP(INDEX,LIMIT)：返回J=INDEX-K*LIMIT,其中J 位于区间[1，LIMIT]，K 为整数．当INDEX 位于区间[1，LIMIT]内时直接返回INDEX ．相当于数学上用INDEX 对LIMIT 取模函数的值+1，即@WRAP(INDEX,LIMIT)=@MOD(INDEX,LIMIT)+1．此函数对LIMIT ＜1无定义．可以想到，此函数的目得之一是防止集合的索引值越界．@SIZE(set_name)：返回集合set_name 的模，即元素的个数．五、变量定界函数变量定界函数是对变量的取值范围加以限制的函数．主要有@BIN, @BND, @FREE, @GIN 四种，下面简要介绍其作用．@BIN(variable)：限制变量variable 为0或1．@BND(lower_bound, variable, upper_bound)：限制lower_bound ＜＝variable ＜＝upper_bound@FREE(variable)：取消对变量variable 的符号限制（即可取负数、0或正数）． @GIN(variable)：限制变量variable 为整数．六、财务会计函数财务会计函数是用于计算净现值的函数．主要有@FPA, @FPL 两种，下面简要介绍其作用． @FPA(I,N)：返回若干时段单位等额回收净现值．其中单位时段利率为I,时段N 个，即∑=+=Nn n I N I FPA 1)1(1),(@ @FPL(I,N)：返回一个时段单位回收净现值．其中单位时段利率为I,时段N ，即N I N I FPL )1(1),(@+=七、概率中的相关函数概率中的相关函数是涉及到概率论和随机过程中的一些函数．主要有以下函数： @PSN(X)：返回标准正态分布的分布函数在X 点的取值．@PSL(X)：标准正态的线性损失函数，即返回MAX(0,Z-X)的期望值，其中Z 为均值为A的Poisson随机变量．@PPS(A,X)：返回均值为A的Poisson分布的分布函数在X点的取值．@PPL(A,X)：Poisson分布的线性损失函数，即返回MAX(0,Z-X)的期望值，其中Z为标准正态随机变量．@PBN(P,N,X)：返回参数为（N,P）的二项分布的分布函数在X点的取值．@PHG(POP,G,N,X)：返回总共有POP个球，其中G个是白球，随机地从中取出N个球，白球不超过X的概率．@PFD(N,D,X)：返回自由度为N和D的F分布的分布函数在X点的取值．分布的分布函数在X点的取值．@PCX(N,X)：返回自由度为N的2@PTD(N,X)：返回自由度为N的t分布的分布函数在X点的取值．@PEB(A,X)：返回当到达负荷（强度）为A，服务系统有X个服务器且允许无穷排队时的Erlang繁忙概率．@PEL(A,X)：返回当到达负荷（强度）为A，服务系统有X个服务器且不允许排队时的Erlang繁忙概率．@PFS(A,X,C)：返回当负荷上限为A，顾客数为C，并行服务器数量为X时，有限源的Poisson服务系统得等待顾客数的期望值．@QRAND(SEED)：返回0与1之间的多个拟均匀随机数，其中SEED为种子，默认时取当前计算机时间为种子．该函数只能用在数据段（DATA-ENDDATA）．@RAND(SEED)：返回0与1之间的一个伪均匀随机数，其中SEED为种子．八、文件输入输出函数文件输入输出函数是指通过文件输入数据和输出结果的函数．主要有以下函数：@FILE('filename')：这个函数提供LINGO与文本文件的接口，用于引用其它ASCII码或文本文件中的数据，其中filename为存放数据的文件名（包括路径，没有指定路径时表示当前目录），该文件中记录之间必须用符号“～”分开．主要用在集合段和数据段，通过文本文件输入数据．@TEXT(['filename'])：用于数据段中将解答结果送到文本文件filename中．@ODBC(['data_source'[,'table_name'[,'col_1'[, 'col_2'...]]]])：这个函数提供LINGO与ODBC（open data base connection,开放式数据库连接）的接口，用于集合段和数据段中引用其它数据库数据或将解答结果送到数据库中．其中data_source是数据库名，table_name是数据表名，col_i是数据列名（数据域名）．@OLE('spreadsheet_file'[,range_name_list])：这个函数提供LINGO与OLE（object linking and embedding，对象链接与嵌入）的借口，用于集合段、数据段和初始段中输入和输出数据库．其中spreadsheet_file是文件名，range_name_list是文件中包含数据的单元范围．@POINTER(N)：在Windows下使用LINGO的动态链接库（dynamic link library ,DLL），直接从共享的内存中传送数据．§3.4 LINGO软件求解案例一、生产管理问题1．问题实例某厂有5种设备A1,A2,…,A5，用来加工7种零部件B1,B2,…,B7，每种设备的数量、每种零部件的单位成本及所需各设备的加工工时（以小时计）见表1表1在其后的半年中，工厂有设备检修计划（停工检修时间一个月）见表2表2工厂在半年中有订单（必须按时交货）见表3表3每种零部件库存最多可到100件，现每种零部件有库存80件，库存费用每件每月为0.5元，，要求到六月底每种零部件有存货50件，每种零部件生产至少50件．工厂每周工作5天，每天2班，每班8小时．试回答如下问题：（1）工厂如何安排各月份各种零部件的加工数量？（2）单位成本有10%的变化，对计划有什么影响？（3）设备各增加1台对计划有什么的影响．2．模型建立设： ij a 为第j 种零部件在第i 种设备上的单位加工工时)7,,2,1,5,,2,1( ==j i ；ik b 为第i 种设备在第k 月的数量)6,,2,1,5,,2,1( ==k i ； kj d 为第k 月第j 种零部件的顶单数量)7,,2,1,6,,2,1( ==j k ； j c 为第j 种零部件的单位收益)7,,2,1( =j ； kj x 为第k 月第j 种零部件的生产数量)7,,2,1,6,,2,1( ==j k ； kj s 为第k 月末第j 种零部件的库存数量)7,,2,1,6,,2,1( ==j k ； 800=j s 为初始库存)7,,2,1( =j假设每月以20天计，有以下模型：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥≥==≥=≤====-+===≤+-=====∑∑∑∑∑)(7,,2,1,6,,2,1,0,07,,2,1,6,,2,1,50)(7,,2,1,100)(7,,2,1,50)(7,,2,1,6,,2,1,)(6,,2,1,5,,2,13205.0min 6(617161617171非负约束生产要求个月末的库存第种零部件的库存月第第种设备的有效工时月第第费用目标））（，库存约束 j k s x j k x j s j s j k d x s s k i b x a s x c kj kj kj kjjkj kj j k kj ik j kj ij k k j kj j kj j j k i k 3．模型求解利用LINGO 软件计算，输入model:sets:cp/1..7/:c;yf/1..6/:;sb/1..5/:;sl1(yf,cp):x,d,s;sl2(sb,cp):a;sl3(sb,yf):b;endsetsdata:a=0.5 0.7 0.0 0.0 0.3 0.2 0.50.1 0.2 0.0 0.3 0.0 0.6 0.00.2 0.0 0.8 0.0 0.0 0.0 0.60.05 0.03 0 0.07 0.1 0 0.080 0 0.01 0 0.05 0 0.05;b=3 4 4 4 3 42 2 1 1 1 23 1 3 3 3 21 1 1 1 1 11 1 1 1 1 1;d=250 500 150 150 400 100 100300 250 100 0 200 150 100150 300 0 0 250 200 100100 150 200 250 100 0 1000 100 250 100 500 150 0250 250 100 300 550 250 100;c=100 60 80 40 110 90 30;enddatamin=@sum(sl1(k,j):c(j)*x(k,j)+0.5*s(k,j));@for(yf(k):@for(sb(i):@sum(cp(j):a(i,j)*x(k,j))<=320*b(i,k))); @for(yf(k)|k#gt#1:@for(cp(j):s(k,j)=s(k-1,j)+x(k,j)-d(k,j))); @for(cp(j):s(1,j)=80+x(1,j)-d(1,j));@for(cp(j):s(6,j)=50);@for(sl1(k,j):s(k,j)<=100);@for(sl1(k,j):x(k,j)>=50);end（1）计算结果有：目标函数：590580 z（2）目标的灵敏度分析：Objective Coefficient Ranges（目标系数的灵敏度分析）Current Allowable AllowableVariable Coefficient Increase Decrease变量目前系数允许增加范围允许减少范围X( 1, 1) 100.0000 INFINITY0.5000000X( 1, 2) 60.00000 INFINITY 0.5000000X( 1, 3) 80.00000 INFINITY 0.5000000X( 1, 4) 40.00000 INFINITY 1.500000X( 1, 5) 110.0000 INFINITY 0.5000000X( 1, 6) 90.00000 INFINITY 0.5000000X( 1, 7) 30.00000 INFINITY 0.5000000X( 2, 1) 100.0000 0.5000000 0.5000000X( 2, 2) 60.00000 0.5000000 0.5000000X( 2, 3) 80.00000 0.5000000 1.000000X( 2, 4) 40.00000 INFINITY 1.000000X( 2, 5) 110.0000 0.5000000 0.5000000X( 2, 6) 90.00000 0.5000000 0.5000000X( 2, 7) 30.00000 0.5000000 0.5000000X( 3, 1) 100.0000 0.5000000 0.5000000X( 3, 2) 60.00000 0.5000000 0.5000000X( 3, 3) 80.00000 INFINITY 0.5000000X( 3, 4) 40.00000 INFINITY 0.5000000X( 3, 5) 110.0000 0.5000000 0.5000000X( 3, 6) 90.00000 0.5000000 1.000000X( 3, 7) 30.00000 0.5000000 0.5000000X( 4, 1) 100.0000 0.5000000 1.000000X( 4, 2) 60.00000 0.5000000 0.5000000X( 4, 3) 80.00000 0.50000000.5000000X( 4, 4) 40.00000 0.5000000 0.5000000X( 4, 5) 110.0000 0.5000000 0.5000000X( 4, 6) 90.00000 INFINITY 0.5000000X( 4, 7) 30.00000 0.5000000 1.000000X( 5, 1) 100.0000 INFINITY 0.5000000X( 5, 2) 60.00000 0.5000000 0.5000000X( 5, 3) 80.00000 0.5000000 0.5000000X( 5, 4) 40.00000 0.5000000 0.5000000X( 5, 5) 110.0000 0.5000000 0.5000000X( 5, 6) 90.00000 0.5000000 0.5000000X( 5, 7) 30.00000 INFINITY 0.5000000X( 6, 1) 100.0000 0.5000000 INFINITYX( 6, 2) 60.00000 0.5000000 INFINITYX( 6, 3) 80.00000 0.5000000 INFINITYX( 6, 4) 40.00000 0.5000000 INFINITYX( 6, 5) 110.0000 0.5000000 INFINITYX( 6, 6) 90.00000 0.5000000 INFINITYX( 6, 7) 30.00000 0.5000000 INFINITY其中INFINITY是无穷．从以上灵敏度分析可见，提高10%,有超出允许范围的，所以对计划有影响．（3）约束条件的灵敏度分析：Righthand Side Ranges（右边常数项的灵敏度分析） Row Current Allowable AllowableRHS Increase Decrease行目前常数项允许增加范围允许减少范围2 960.0000 INFINITY450.00003 640.0000 INFINITY488.00004 960.0000 INFINITY840.00005 320.0000 INFINITY258.00006 320.0000 INFINITY300.80007 1280.000 INFINITY836.00008 640.0000 INFINITY473.00009 320.0000 INFINITY138.000010 320.0000 INFINITY268.400011 320.0000 INFINITY305.500012 1280.000 INFINITY830.000013 320.0000 INFINITY110.000014 960.0000 INFINITY 830.000015 320.0000 INFINITY 267.000016 320.0000 INFINITY 302.000017 1280.000 INFINITY 1035.00018 320.0000 INFINITY 205.000019 960.0000 INFINITY 760.000020 320.0000 INFINITY 282.000021 320.0000 INFINITY 308.500022 960.0000 INFINITY 670.000023 640.0000 INFINITY 525.000024 960.0000 INFINITY 720.000025 320.0000 INFINITY 253.500026 320.0000 INFINITY 290.000027 1280.000 INFINITY 655.000028 640.0000 INFINITY 270.000029 640.0000 INFINITY 410.000030 320.0000 INFINITY 206.000031 320.0000 INFINITY 283.5000从以上灵敏度分析可见，提高1台,没有超出允许范围的，所以对计划没有影响．也可以将数据与模型分离，先准备数据文件exam01.ldt:!单耗;0.5 0.7 0.0 0.0 0.3 0.2 0.50.1 0.2 0.0 0.3 0.0 0.6 0.00.2 0.0 0.8 0.0 0.0 0.0 0.60.05 0.03 0 0.07 0.1 0 0.080 0 0.01 0 0.05 0 0.05~!设备数量;3 4 4 4 3 42 2 1 1 1 23 1 3 3 3 21 1 1 1 1 11 1 1 1 1 1~!需求;250 500 150 150 400 100 100300 250 100 0 200 150 100150 300 0 0 250 200 100100 150 200 250 100 0 1000 100 250 100 500 150 0250 250 100 300 550 250 100~!单位成本;100 60 80 40 110 90 30~再写程序如下：model:sets:cp/1..7/:c;yf/1..6/:;sb/1..5/:;sl1(yf,cp):x,d,s;sl2(sb,cp):a;sl3(sb,yf):b;endsetsdata :a=@file ('exam01.ldt');b=@file ('exam01.ldt');d=@file ('exam01.ldt');c=@file ('exam01.ldt');enddatamin =@sum (sl1(k,j):c(j)*x(k,j)+0.5*s(k,j));@for (yf(k):@for (sb(i):@sum (cp(j):a(i,j)*x(k,j))<=320*b(i,k))); @for (yf(k)|k#gt#1:@for (cp(j):s(k,j)=s(k-1,j)+x(k,j)-d(k,j))); @for (cp(j):s(1,j)=80+x(1,j)-d(1,j));@for (cp(j):s(6,j)=50);@for (sl1(k,j):s(k,j)<=100);@for (sl1(k,j):x(k,j)>=50);end二、下料问题1．问题实例有某种材料一根长19米．现需用其切割4米长毛坯50根、5米长毛坯10根、6米长毛坯20根、8米长毛坯15根．如何切割使其用料最省？要求切割模式不能超过3种．2．模型建立设：4,3,2,1=i 分别表示4米长，5米长，6米长，8米长的毛坯；i a 为第i 种毛坯的长度)4,3,2,1(=i ；i b 为第i 种毛坯的需要量)4,3,2,1(=i ；j x 为第j 种切割模式所用的材料数量)3,2,1(=j ；ij r 为第j 种切割模式切割第i 种毛坯的数量)3,2,1,4,3,2,1(==j i ．一种合理的切割模式应满足：其余料长度不应该大于或等于需要切割毛坯的最小长度．于是有模型如下⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==≥≥=≥=≤=≥=∑∑∑∑====3,2,1,4,3,2,1,0,0(3,2,1,16(3,2,1,19(4,3,2,1,(min 41413131j i r x j r a j r a i b x r x z ij ji ij i i ij i i j j ij j j 且整数合理的下料模式所下毛坯的总长所下毛坯的需要量用料目标））））3．模型求解为了便于运算，我们先来缩小可行域．由于3种切割模式的排列顺序是无关紧要的，所以不妨增加以下约束：321x x x ≥≥又注意到用料的总量有明显的上界和下界．首先，无论如何，用料总量不可能少于2619158206105504=⎥⎥⎤⎢⎢⎡⨯+⨯+⨯+⨯ 其次，考虑一种特殊的下料计划：模式1：切割成4根4米钢管，需13根；模式2：切割成1根5米和2根6米钢管，需10根；模式3：切割成2根8米钢管，需8根．这样需要13+10+8=31于是可得到解的一个上界．所以又可增加约束：3126321≤++≤x x x利用LINGO 软件计算，输入model:sets:needs/1..4/:a,b;cuts/1..3/:x;patterns(needs,cuts):r;endsetsdata:a=4 5 6 8;b=50 10 20 15;enddatamin=@sum(cuts(j):x(j));!用料目标;@for(needs(i):@sum(cuts(j):x(j)*r(i,j))>b(i));!需要量要求;@for(cuts(j):@sum(needs(i):a(i)*r(i,j))<19);!材料总长;@for(cuts(j):@sum(needs(i):a(i)*r(i,j))>16);!合理模式;@sum(cuts(j):x(j))>26;!用料下限;@sum(cuts(j):x(j))<31;!用料上限;@for(cuts(j)|j#lt#@size(cuts):x(j)>x(j+1));!人为约束;@for(cuts(j):@gin(x(j)));!整数约束;@for(patterns(i,j):@gin(r(i,j)));!整数约束;end经过LINGO求解，得到输出如下：Objective value: 28.00000Variable Value Reduced CostX( 1 ) 10.00000 0.000000X( 2 ) 10.00000 2.000000X( 3 ) 8.000000 1.000000R( 1, 1) 3.000000 0.000000R( 1, 2) 2.000000 0.000000R( 1, 3) 0.000000 0.000000R( 2, 1) 0.000000 0.000000R( 2, 2) 1.000000 0.000000R( 2, 3) 0.000000 0.000000R( 3, 1) 1.000000 0.000000R( 3, 2) 1.000000 0.000000R( 3, 3) 0.000000 0.000000R( 4, 1) 0.000000 0.000000R( 4, 2) 0.000000 0.000000R( 4, 3) 2.000000 0.000000即按照模式1、2、3分别切割10、10、8根材料，使用材料总根数为28根．第一种切割模式下1根材料切割3根4米的和1根6米的；第二种切割模式下1根材料切割2根4米的、1根5米的和1根6米的；第三种切割模式下1根材料切割2根8米的．三、投资组合问题1．问题实例有三种股票A,B,C，其前12年的价值每年的增长情况如表所示表中还给出了相应年份的500种股票的价格指数的增长情况．假设目前你有一笔资金准备投资这三种股票，并期望年收益率达到15%，那么你应如何投资？ 2．模型建立设：3,2,1=i 分别表示表示A,B,C 三种股票；i R 为第i 种股票的价值)3,2,1(=i ；ij R 为第i 种股票第j 年的价值)12,,2,1,3,2,1( ==j i ；M 为指数；j M 为第j 年的指数)12,,2,1( =j ；i x 为投资第i 种股票比例)3,2,1(=i ．股票指数反映的是股票市场的大势信息，对每只股票的涨跌是有影响的．假设每只股票的收益与股票指数成线性关系．即i i i i e M b a R ++=或12,,2,1,3,2,1, ==++=j i e M b a R ij j ij ij ij其中ij ij b a ,是待定系数，ij e 是一个随机误差，其均值为0)(=ij e E ，方差为)(2ij ij e D s =，此外假设随机误差ij e 与其他股票和股票指数都是独立的，所以0)()(==j ij kj ij M e E e e E ．先根据所给数据回归计算ij ij b a ,，即使误差的平方和最小：3,2,1,||min12121212=-+=∑∑==i R M b a ej ij j ij ij j ij可用Matlab 软件做该回归计算，也可用LINGO 软件分别来做每只股票的回归计算，输入 model: sets:year/1..12/:M,R,a,b,e; endsets data:R=1.300 1.103 1.216 0.954 0.929 1.056 1.038 1.089 1.090 1.083 1.035 1.176;M=1.258997 1.197526 1.364361 0.919287 1.057080 1.055012 1.187925 1.317130 1.240164 1.183675 0.990108 1.526236; enddata calc:mean0=@sum(year(j):M(j))/@size(year);s20=@sum(year(j):@sqr(M(j)-mean0))/(@size(year)-1); s0=@sqrt(s20); endcalc min=s2;s2=@sum(year(j):@sqr(e(j)))/(@size(year)-2); s=@sqrt(s2);@for(year(j):e(j)=R(j)-a-b*M(j)); @for(year(j):@free(e(j))); @free(a);@free(b);End对上面的程序，注意以下几点：（1）只给了一种股票的价值R ；（2）在CALC 段直接计算了M 的均值mean0和方差s20以及标准差s0（为了使这个估计是无偏估计，分母是11而不是12）；（3）程序中用到平方函数@sqr 和平方根函数@sqrt ；（4）除了计算回归系数外，同时估计了回归误差s2和标准差s ，为了使这个估计是无偏估计，分母是10而不是11和12，这是因为此时已经假设保持误差的均值为0，所以自由度又少了一个；（5）@free(a),@free(b),@free(e)三个语句不能少，因为它们不一定是非负的；运行这个LINGO 模型，结果为：Objective value: 0.5748320E-02Variable Value Reduced CostMEAN0 1.191458 0.000000 S20 0.2873661E-01 0.000000 S0 0.1695188 0.000000 S2 0.5748320E-02 0.000000 S 0.7581767E-01 0.000000 A 0.5639761 0.000000 B 0.4407264 0.000000也就是说：M 的均值191458.10=m ，方差02873661.020=s ，标准差1695188.00=s ，对股票A ，回归系数5639761.01=a ，4407264.01=b ，误差的方差005748320.021=s ，误差的标准差07581767.01=s ．同理，可以得到：对股票B ，回归系数239802.1,2635059.022=-=b a ，误差的方差01564263.022=s ，误差的标准差1250705.02=s ．对股票C ，回归系数523798.1,5809590.033=-=b a ，误差的方差03025165.023=s ，误差的标准差1739300.03=s ．于是，年投资收益为∑∑==++==3131)(i i i i i i i i e M b a x R x R收益的期望为∑∑==+=++=31031)()(i i i i i i i i i m b a x e M b a E x ER收益的方差为∑∑==+=++=3122202312])[()(i i i i i i i i i i s x s b x e M b a D x DR进一步，令∑=ii b x y ，则模型应该为⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≥+==+=∑∑∑∑====015.1)(1 ..)(min 31031313122202ii i i i i ii ii i i i x m b a x x b x y t s s x s y z 3．模型求解利用LINGO 软件计算，输入 model: sets:stocks/1..3/:u,b,s2,x; endsets data:mean0=1.191458; s20=0.02873661;s2=0.005748320,0.01564263,0.03025165; u=0.5639761,-0.2635059,-0.5809590; b=0.4407264,1.239802,1.523798; enddatamin=s20*@sqr(y)+@sum(stocks(i):s2(i)*@sqr(x(i))); @sum(stocks(i):b(i)*x(i))=y; @sum(stocks(i):x(i))=1;@sum(stocks(i):(u(i)+b(i)*mean0)*x(i))>1.15; end运算这个LINGO 模型，输出结果如下Objective value: 0.2465621E-01 Y 0.8453449 0.000000 X( 1) 0.5266052 0.000000 X( 2) 0.3806461 0.000000 X( 3) 0.9274874E-01 0.000000根据运算结果可知：A 大约占初始时刻总资产的53%，B 占38%，C 占9%．四、最小费用最大流问题1．问题实例需要将某地s 的天然气通过管道输送到另一地t ，中间有4个中转站4321,,,v v v v ．由于输气管道的长短粗细不一或地质等原因，使得每条管道上的运输量及费用不同．下图给出了这两地与中转站的连接以及管道的容量、费用：图中括号里第一个数字是管道容量，第二个数字是管道单位运费．考虑s 地到t 地如何输送天然气，使得费用最小流量最大． 2．模型建立设：V 为网络顶点集，A 为网络的弧集；ij f 为弧),(j i 上的流量； ij b 为弧),(j i 上的单位运费； ij c 为弧),(j i 上的容量；)(f v 为发点处的净流量．根据最大流的定义，我们有模型如下：⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧∈≤≤⎪⎩⎪⎨⎧≠=-==-∑∑∑∈∈∈∈∈Aj i c f t s i ti f v s i f v f f t s f v t s f bij ij A i j V j ji A j i V j ij Aj i ijij),(,0, 0 )( ),(..)(max ..min),(),(),( 3．模型求解先考虑最大流模型，LINGO 软件输入如下 model: sets:nodes/s,1,2,3,4,t/;arcs(nodes,nodes)/s,1 s,2 1,2 1,3 2,4 3,2 3,t 4,3 4,t/:c,f;endsetsdata:c=8 7 5 9 9 2 5 6 10;enddatamax=flow;@for(nodes(i)|i#ne#1 #and# i#ne#@size(nodes):@sum(arcs(i,j):f(i,j))-@sum(arcs(j,i):f(j,i))=0);@sum(arcs(i,j)|i#eq#1:f(i,j))=flow;@for(arcs(i,j):@bnd(0,f(i,j),c(i,j)));end计算结果如下：Objective value: 14.00000Variable Value Reduced Cost FLOW 14.00000 0.000000F( S, 1) 7.000000 0.000000F( S, 2) 7.000000 0.000000 F( 1, 2) 2.000000 0.000000 F( 1, 3) 5.000000 0.000000 F( 2, 4) 9.000000 -1.000000 F( 3, 2) 0.000000 0.000000 F( 3, T) 5.000000 -1.000000 F( 4, 3) 0.000000 1.000000 F( 4, T) 9.000000 0.000000 其次考虑最小费用最大流模型，LINGO软件输入如下model:sets:nodes/s,1,2,3,4,t/;arcs(nodes,nodes)/s,1 s,2 1,2 1,3 2,4 3,2 3,t 4,3 4,t/:b,c,f;endsetsdata:b=2 8 5 2 3 1 6 4 7;c=8 7 5 9 9 2 5 6 10;flow=14;enddatamin=@sum(arcs(i,j):b(i,j)*f(i,j));@for(nodes(i)|i#ne#1 #and# i#ne#@size(nodes):@sum(arcs(i,j):f(i,j))-@sum(arcs(j,i):f(j,i))=0);@sum(arcs(i,j)|i#eq#1:f(i,j))=flow;@for(arcs(i,j):@bnd(0,f(i,j),c(i,j)));end计算结果如下：Objective value: 205.0000Variable Value Reduced CostF( S, 1) 8.000000 -1.000000F( S, 2) 6.000000 0.000000F( 1, 2) 1.000000 0.000000F( 1, 3) 7.000000 0.000000F( 2, 4) 9.000000 0.000000F( 3, 2) 2.000000 -3.000000F( 3, T) 5.000000 -8.000000F( 4, 3) 0.000000 11.00000F( 4, T) 9.000000 0.000000附录 LINGO出错信息在LINGO程序求解时，系统首先会对程序进行编译．系统在编译或执行其他命令时，会因程序中的错误或运行错误，弹出一个出错报告窗口，显示其错误代码，并简要指出错误的原因．这些错误报告信息能够提示用户发现程序中的错误，以便能尽快修改．下面我们给出出错信息的一个简要说明，仅供参考．LINGO错误编号及原因对照表习题1．用LINGO 软件求解线性规划问题并作灵敏度分析（1） ⎪⎩⎪⎨⎧≥≤++≤++-++-=0,,9010412203..1355max 321221321321x x x x x x x x x t s x x x （2） ⎪⎩⎪⎨⎧≥≤≤+--≤+---+-=0,,,1035.0125.009825.0..65.02075.0max 3213432143214321x x x x x x x x x x x x t s x x x x z 2．用LINGO 软件求解0-1规划问题⎪⎪⎩⎪⎪⎨⎧=≥+-+≥+++-≥+++-+++=10,,,11424204..4352min 43214321432143214321或x x x x x x x x x x x x x x x x t s x x x x 3．用LINGO 软件求解整数规划问题⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≤≤≤≤=+=-+=-+=-++++++=且整数0,,,,,,20,45,40,3025352515..2.02.02.05.54.51.50.5min 3214321432134323212113214321y y y x x x x x x x x y x y y x y y x y x t s y y y x x x x4．用LINGO 软件求解非线性规划问题 ⎪⎪⎩⎪⎪⎨⎧=≤≤--=+-+=++-+-+-+-+-=5,4,3,2,1,55222223..)()()()()1(min 4232332215544433322211i x x x x x x x t s x x x x x x x x x z i5．用LINGO 软件求解⎪⎩⎪⎨⎧-∈≤+++≤-≤+≤-+=}1,1{,,,2311..21max 432143214321T T x x x x x x x x x x x x t s z Qx x x c 其中T )2,4,8,6(-=c ，Q 是三对角线矩阵，主对角线上元素全为-1，两条次对角线上元素全为2．。

数学软件应用之lingo

注：LINGO不询问对灵敏度进行分析，灵敏度分析需要通过修改系统选项启动灵敏度分析后，再调用 “REPORT|RANGE”菜单命令来实现。我们可以把模型和结果报告保存在文件中。
•运行状态窗口
Variables(变量数量) 变量总数（Total）: 非线性变量数（Nonlinear）: 整数变量数（Integer）: Conatraints(约束数量) 约束总数（Total）: 非线性约束个数（ Nonlinear ）：
返回本节
集循环函数
集循环函数遍历整个集进行操作。其语法为 @function(setname[(set_index_list)[|conditional_qualifier ]]:expression_list); @function相应于下面罗列的四个集循环函数之一；setname是要遍历的集；set_ index_list是集索引列表； conditional_qualifier是用来限制集循环函数的范围，当集循环函数遍历集的每个成员时，LINGO都要对conditional_qualifier 进行评价，若结果为真，则对该成员执行@function操作，否则跳过，继续执行下一次循环。expression_list是被应用到每个集成员的表达式列表，当用的是@for函数时，expression_list可以包含多个表达式，其间用逗号隔开。这些表达式将被作为约束加到模型中。当使用其余的三个集循环函数时，expression_list只能有一个表达式。如果省略set_index_list，那么在 expression_list中引用的所有属性的类型都是setname集。
在LINGO中使用LINGO模型 1、在 LINGO中可以直接使用LINGO语法编写的优化模型（优化程序）。举一个简单例题：在名为 LINGO1.lg4的模型文件中保存了一个LINGO模型，我们现在看看如何打开它（1）选择菜单命令“File|open(F3)”可以看到“打开文件” 对话框。（2）打开“LINGO1.lg4”文件。（3）选择“LINGO|Solve（Ctrl+S）”来运行这个程序。（运行状态窗口如下图）

培训教案——LINGO(一)

培训教案——LINGO(一)LINGO是一款常用的线性规划软件，它能够方便地解决复杂问题。

培训LINGO，需要深入了解软件的使用方法和解决实际问题的能力。

下面就LINGO培训的内容进行分点介绍。

一、LINGO的基础知识LINGO的基础知识包括软件的基本功能和操作。

需要讲解LINGO的界面、工具栏、菜单栏等。

初次接触LINGO的学员需要掌握LINGO的一些基本用法，比如如何输入数据、如何设定优化目标，如何设置约束等，这些都是LINGO的基本操作。

二、LINGO求解模型了解LINGO的基本操作之后，需要讲解LINGO的求解模型。

LINGO的数学模型是LINGO软件解决问题必需的部分。

对于LINGO求解模型的学习，需要学员掌握数学模型的建立方法和标准的数学模型。

培训学员掌握LINGO的求解模型知识是LINGO培训的核心。

三、LINGO的高级应用LINGO的高级应用需要讲授如何利用LINGO解决实际问题，需要讲解如何构建多约束模型来描述现实中的问题，如何设置变量、常数和目标函数等。

高级应用的讲授需要结合实例，让学员深入了解LINGO的实际应用场景，提高解决实际问题的能力。

四、LINGO的调试LINGO的调试是LINGO培训的重要组成部分。

在LINGO求解过程中，有时会出现错误，导致模型不能正常求解。

因此，需要讲解LINGO调试的方法和技巧，使得学员具备调试LINGO模型的能力。

五、LINGO应用举例为了让学员进一步巩固LINGO的知识，需要讲解一些LINGO的应用举例。

举例的内容包括：产品组合问题、生产调度问题、财务规划问题、运输规划问题等。

通过这些示例，让学员对LINGO的应用有更加深刻的理解。

六、LINGO的作业练习培训LINGO需要进行实际操作，软件操作的熟练程度可以通过作业考核来体现。

作业练习的难度需要逐渐增加，从简单到复杂地设置模型，巩固培训成果。

LINGO培训需要根据学员的水平进行分类管理，加强培训的个性化和针对性。

2024年度LINGO软件

结果分析
对求解结果进行分析，验证模型的有效性和可行性。
模型调整
根据结果分析，对模型进行调整和优化，提高模型的实用性和准确性。
24
05 LINGO软件在各个领域的应用案例
2024/3/23
25
生产计划与调度问题
2024/3/23
生产线平衡
LINGO可以用于解决生产线平衡问题，通过优化生产线上各个工位的任务分配，提高生产效率和资源利用率。
一些学术机构和研究团队也会分享他们的 LINGO使用经验和案例，为学习者提供更多的学习资源和合作机会。
37
THANKS
感谢观看
2024/3/23
38
LINGO可用于金融市场预测和决策分析，通过建立预测模型和分析工具
，揭示金融市场的运行规律和趋势，为投资决策提供支持。
29
06 LINGO软件与其他工具的集成与应用
2024/3/23
30
与Excel的集成与应用
2024/3/23
数据交换
LINGO可以直接从Excel中导入数据，也可以将结果导出到Excel ，实现数据的无缝对接。
2024/3/23
28
金融工程与投资组合优化问题
01
投资组合优化
LINGO可以用于解决投资组合优化问题，通过优化投资组合中各个资产
的配置比例，实现风险和收益的平衡。
02
期权定价与风险管理
利用LINGO建立期权定价模型，可以准确计算期权的价值，为风险管理
提供决策依据。
2024/3/23
03
金融市场预测与决策分析
2024/3/23
整数规划算法
分支定界法、割平面法等适用于整数规划问题的求解。

Lingo软件在运筹学中的应用

Lingo软件在运筹学中的应用Lingo软件在运筹学中的应用随着信息技术的不断发展，计算机软件在各个领域中的应用越来越广泛，尤其是在运筹学领域。

运筹学是研究在复杂决策环境下，如何高效地进行决策的学科。

Lingo软件作为一款运筹学建模和求解工具，为运筹学的研究和应用带来了很大的便利和效率。

本文将介绍Lingo软件在运筹学中的应用，并通过实例来说明其实际效果。

首先，Lingo软件在线性规划问题中的应用非常广泛。

线性规划是一种数学优化技术，用于在给定的约束条件下最大化或最小化线性目标函数。

Lingo软件提供了直观的图形用户界面，使得用户可以轻松地建立线性规划模型，并通过内置的求解器进行求解。

用户只需输入决策变量、约束条件和目标函数，Lingo就能自动找到最优解。

这对于一些复杂的决策问题，如生产规划、资源调度和供应链优化等，提供了很大的帮助。

其次，Lingo软件在整数规划和混合整数规划问题中也有着广泛的应用。

整数规划是在线性规划的基础上，将决策变量限制为整数解的优化问题。

混合整数规划在整数规划的基础上，允许部分决策变量取非整数解。

这种类型的决策问题在实际中很常见，如生产工作安排、旅行路线规划和仓储优化等。

Lingo软件提供了强大的分支定界算法和割平面算法，能够有效地求解整数规划和混合整数规划问题。

用户只需调整问题的参数，Lingo就能快速找到最优解，大大减少了优化问题的求解时间。

此外，Lingo软件还可以用于非线性规划问题的建模和求解。

非线性规划是在线性规划的基础上，将决策变量限制为非线性函数的优化问题。

非线性规划在许多实际问题中都有着广泛的应用，如投资组合优化、工程设计和市场定价等。

Lingo软件提供了多种求解算法，如牛顿法、拟牛顿法和遗传算法等，能够有效地求解非线性规划问题。

用户只需选择合适的算法和调整参数，Lingo就能找到最优解或是近似最优解。

最后，Lingo软件还具有灵活的扩展性和集成性。

它可以与其他优化软件和模拟软件进行集成，提供更强大的求解能力和模型分析能力。

《LINGO简介》课件

某些复杂的数学表达可能无法直接在 LINGO中表示。用户可以通过混合编程或使用其他建模语言（如GAMS）来解决这一问题。
对于特定行业或领域的定制化需求， LINGO可能无法直接提供相应的功能。在这种情况下，用户可以通过扩展 LINGO的API或与其他软件的集成来实现定制化需求。
感谢您的观看
目标函数的设置
目标函数定义
在LINGO中，需要定义一个目标函数来描述决策变量的优化目标。
目标函数类型
目标函数可以是最大化或最小化形式，根据实际问题的需求进行选择。
目标函数编辑器
LINGO提供了一个目标函数编辑器，用户可以在其中方便地定义和编辑目标函数。
求解操作
求解器选择
在LINGO中，可以选择不同的求解器来求解模型，根据模型的规模和复杂
LINGO软件广泛应用于生产计划、资源分配、工艺流程优化等方面。
物流运输
LINGO软件用于运输路线规划、车辆调度、仓储优化等问题求解。
金融投资
LINGO软件用于投资组合优化、风险管理、信贷决策等问题求解。
科研领域
LINGO软件在数学建模、统计分析、机器学习等领域有广泛应用。
02
LINGO软件的基本操作
物流配送问题
总结词
物流配送问题是一个复杂的优化问题，LINGO软件能够通过建立有效的数学模型，优化配送路线和成本。
详细描述
物流配送问题涉及到如何合理规划配送路线、分配运输资源，以最小化运输成本并确保及时送达。LINGO软件通过构建配送问题的数学模型，帮助企业找到最优的配送方案，降低运输成本、提高运输效率。
LINGO软件与其他软件的比较与选择
MATLAB
MATLAB在科学计算和数据分析领域具有广泛的应用，但相比之下，LINGO在求解优化问题方面更加专业和高效。

lingo使用手册

lingo使用手册Lingo使用手册本手册旨在帮助用户了解和使用Lingo软件。

Lingo是一种用于程序设计和开发的工具，用于创建交互式应用程序和游戏。

本手册将指导您使用Lingo的各种功能和功能。

目录1、引言1.1 Lingo概述1.2 如何获取Lingo1.3 系统要求2、安装和配置2.1 安装Lingo2.2 激活Lingo许可证2.3 配置Lingo环境3、Lingo基础知识3.1 Lingo语法3.2 变量和数据类型3.3 运算符3.4 控制结构3.5 函数和方法3.6 数组和列表4、交互式应用开发4.1 创建交互式界面4.2 事件处理4.3 用户输入和输出4.4 数据验证和处理4.5 错误处理4.6 数据存储和检索5、游戏开发5.1 创建游戏场景5.2 角色和动画5.3 游戏逻辑与规则5.4 碰撞检测和物理模拟 5.5 游戏音频和视觉效果5.6 游戏性能优化6、调试和测试6.1 Lingo调试工具6.2 单元测试6.3 集成测试6.4 性能优化和代码审查7、常见问题解答7.1 Lingo常见错误和解决方案7.2 常见Lingo编码问题7.3 Lingo资源和社区支持附件本文档涉及的法律名词及注释：1、许可证 - 一种法律文件，规定用户对软件的使用权和限制。

2、事件处理 - 在程序中响应用户操作或系统事件的过程。

3、数据验证 - 确保用户输入满足特定要求或规则的过程。

4、错误处理 - 处理程序中出现的错误和异常情况的过程。

5、碰撞检测 - 在游戏开发中，检测两个对象是否发生碰撞的过程。

6、物理模拟 - 在游戏中模拟物体之间的物理行为，如重力、碰撞等。

7、单元测试 - 在软件开发中，测试单个模块或函数的正确性和性能的过程。

8、集成测试 - 在软件开发中，测试整个应用程序或系统的正确性和性能的过程。

9、代码审查 - 对软件源代码进行系统的检查和评估，以确保质量和可靠性。

本文档涉及的附件请参考附件部分。

LINGO软件介绍

例：邮局一周中每天需要不同数目的雇员，设周一至少20人，周二至少16人，13,16,19,14,12人，又规定应聘者需连续工作5天，问邮局每天聘多少雇员才能既满足需求，又使聘用总人数最少。 min =s1+s2+s3+s4+s5+s6+s7; s1+s4+s5+s6+s7>=20; !周1雇员数; s1+s2+s5+s6+s7>=16; !周2雇员数; s1+s2+s3+s6+s7>=13; !周3雇员数; s1+s2+s3+s4+s7>=16; !周4雇员数; s1+s2+s3+s4+s5>=19; !周5雇员数; s2+s3+s4+s5+s6>=14; !周6雇员数; s3+s4+s5+s6+s7>=12; !周7雇员数;
五个基本的组成部分： 1．变量定义； 2．数据输入； 3．目标函数； 4．约束； 5．变量取值范围。
结束。（1）每条语句后必须使用分号“；”结束。问题）每条语句后必须使用分号“ 模型必须由MODEL命令开始，END结束。命令开始，结束。模型必须由命令开始结束命令来作为输入问题模型的开始，（2）用MODEL命令来作为输入问题模型的开始，）命令来作为输入问题模型的开始格式为MODEL：statement （语句）。语句）。格式为：（3）目标函数必须由“min =”或“max =”开头。开头。）目标函数必须由“ 或开头（4）数字与变量之间变量与变量之间要使用运）数字与变量之间,变量与变量之间要使用运算符。如号等号等) 算符。(如*号等

lingo教程

lingo教程Lingo是一个强大且易于学习的编程语言，用于Adobe Director，一个用于创建互动式多媒体应用程序的软件。

在这个Lingo教程中，我们将介绍一些基本的Lingo语法和使用方法。

首先，让我们从Lingo的变量和数据类型开始。

Lingo支持许多数据类型，包括数字，字符串，布尔值和列表。

要声明一个变量，可以使用“variableName = value”的语法。

例如，要声明一个名为“score”的变量，并将其设置为10，可以使用以下代码：```score = 10```要输出变量的值，可以使用“put”命令。

例如：```put score```这将在屏幕上显示变量的值。

Lingo还支持条件语句和循环。

条件语句用于根据条件执行不同的操作。

例如，以下代码将检查“score”变量的值，并根据其值执行不同的操作：if score > 10 thenput "High score!"elseput "Low score."end if```循环用于重复执行一组操作。

例如，以下代码将显示从1到10的所有数字：```repeat with i = 1 to 10put iend repeat```Lingo还支持函数和自定义命令。

函数用于执行特定的操作并返回一个值。

例如，以下代码定义了一个名为“addNumbers”的函数，它将两个数字相加并返回结果：```function addNumbers(num1, num2)return num1 + num2end addNumbers```要使用这个函数，可以使用以下代码：put addNumbers(5, 3)```这将输出结果为8。

自定义命令用于执行一系列的操作，但不返回任何值。

例如，以下代码定义了一个名为“showMessage”的自定义命令，它将显示一个消息框，并将输入的文本作为参数：```on showMessage(text)alert textend showMessage```要使用这个自定义命令，可以使用以下代码：```showMessage("Hello, world!")```这将显示一个消息框，其中包含文本“Hello, world!”。

LINGO使用说明

LINGO使用说明一、LINGO的基本特性1.建模语言：LINGO使用一种直观的建模语言，被称为LINGO语言，它使用简洁的语法和自然语言类似的表达方式，使用户能够轻松地描述问题。

2.线性优化：LINGO支持线性规划（LP）和整数线性规划（ILP），它的线性优化功能包括线性约束、线性目标函数和变量定义，可以解决诸如生产优化、资源分配等问题。

3.非线性优化：LINGO还支持非线性规划（NLP）和全局优化（GLO），可以解决包括非线性约束和非线性目标函数的问题。

它提供了多种求解方法和算法，如牛顿法、逐次线性规划等。

4.约束和限制：LINGO能够处理各种类型的约束和限制，包括等式约束、不等式约束、逻辑约束等。

用户可以根据具体问题定义约束，LINGO会自动处理约束的完整性和一致性。

5.求解器：LINGO内置了一系列高效的求解器，如线性规划求解器、非线性规划求解器、整数规划求解器等。

用户可以根据问题的复杂程度选择最适合的求解器。

6.结果分析：LINGO可以生成详细的结果报告，包括优化解、约束条件、目标函数值等。

用户可以通过结果报告来分析问题的解决方案，做出决策。

二、LINGO的使用方法2.创建模型：在LINGO中，用户需要先创建一个模型文件，来描述问题。

可以通过鼠标点击“新建模型”按钮或选择文件菜单中的“新建”选项来创建一个新的模型文件。

3.定义变量：在模型文件中，用户可以定义变量。

变量可以是整数、二进制或连续的，并为每个变量分配一个名称、类型和取值范围。

4.定义目标函数：在模型文件中，用户可以定义一个目标函数。

目标函数可以是线性的或非线性的，并定义在变量上。

5.定义约束：在模型文件中，用户可以定义约束。

约束可以是线性的或非线性的，并定义在变量上。

用户需要通过约束来限制变量的取值范围。

6.设置求解器：在模型文件中，用户可以选择合适的求解器来解决问题。

LINGO提供了多种求解器，用户可以根据问题的复杂程度选择最适合的求解器。

LINGO软件介绍

（1） LINGO 软件介绍LINGO 是一种专门用于求解数学规划问题的软件包。

LINGO 主要用于求解线性规划、非线性规划、二次规划、动态规划和整数规划等问题，也可以用于求解一些线性和非线性方程组及代数方程求根等。

LINGO 中包含了一种建模语言和大量的常用函数，可供使用者在建立数学规划问题的模型时调用。

（2）示例例如，用LINGO 求解线性规划问题：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==≥≥+≥+≥+≥+≥+++≥++++++++++=4,3,2,1;2,1,01002001100170010002000..153751511572521min 241423132212211124232221141312112423222114131211j i x x x xx x x x x x x x x x x x x t s x x x x x x x x z ij只需要打开LINGO ，然后按照下面的操作进行即可。

1、模型的输入当打开LINGO 后，屏幕将出现如图1所示的窗口。

标题为“LINGO ”的窗口是主窗口，它包含所有的其他窗口以及所有命令菜单和工具栏。

里面的空白窗口用于输入LINGO 的程序代码，代码格式如下：MODEL:图1min=21*x11+25*x12+7*x13+15*x14+51*x21+51*x22+37*x23+15*x24; x11+x12+x13+x14>=2000; x21+x22+x23+x24>=1000; x11+x21>=1700;x12+x22>=1100;x13+x23>=200; x14+x24>=100; END2、执行从Solve 菜单选择Solve 命令，或者在窗口顶部的工具栏里按Solve 按钮，LINGO 就会先对模型进行编译，检查模型是否具有数学意义以及是否符合语法要求。

如果模型不能通过这一步检查，会看到报错信息，并指出出错的语句。

lingo数学模型

lingo数学模型
"lingo"是一种用于数学建模和优化的软件工具。

它提供了一个
直观的界面，用于建立和求解复杂的数学模型，包括线性规划、整
数规划、非线性规划、多目标规划等。

lingo的使用可以帮助分析
师和决策者在面临复杂的决策问题时进行优化决策。

在数学建模方面，lingo可以用来建立数学模型，包括定义决
策变量、约束条件和目标函数。

用户可以通过lingo的界面直观地
输入模型的各个部分，而无需深入了解数学建模的具体语法和规则。

这使得非专业的用户也能够快速地建立数学模型。

在优化方面，lingo提供了强大的求解算法，可以对各种类型
的数学模型进行求解，以找到最优的决策方案。

lingo支持对模型
进行灵敏度分析，帮助用户了解参数变化对最优解的影响，从而更
好地进行决策。

除了数学建模和优化外，lingo还具有数据可视化功能，可以
直观地展示模型的结果和决策方案。

这有助于用户向决策者传达模
型分析的结果，从而更好地支持决策过程。

总的来说，lingo作为数学建模和优化工具，为用户提供了一
个方便、强大的平台，帮助他们解决复杂的决策问题。

通过lingo，用户可以更好地理解问题、制定决策，并得到最优的解决方案。

lingo基础用法

lingo基础用法Lingo是一种计算机编程语言，它的基础用法包括以下几个方面：1. 变量声明和赋值：可以使用Lingo语言声明变量，并给变量赋值。

例如：```global myVariable -- 声明一个全局变量put 5 into myVariable -- 将值5赋给变量myVariable```2. 条件语句：可以使用条件语句来根据条件执行不同的代码块。

例如：```if myVariable = 5 thenput "It's five!" into messageanswer messageend if```3. 循环语句：可以使用循环语句来反复执行特定的代码块。

例如：```repeat with i = 1 to 10put i into messageanswer messageend repeat```4. 函数和命令：Lingo提供了许多内置的函数和命令，可以执行特定的操作。

例如：```put the date into currentDate -- 获取当前日期get the long name of sprite 1 -- 获取精灵1的长名称```5. 脚本和行为：可以使用Lingo编写脚本和行为，控制多媒体项目的行为。

例如：```on mouseUpgo to the next frameend```上述是Lingo语言的基础用法，只是其中的一小部分。

Lingo 还提供了丰富的功能和特性，包括面向对象编程、多媒体处理等。

要更深入地学习和使用Lingo，建议参考Lingo的官方文档或相关教程。

lingo知识点总结

lingo知识点总结Lingo 是一个用于多媒体和跨平台软件开发的高级编程语言。

它以其简单易用，高效快速的特点，广泛应用于多媒体制作、交互式应用程序开发等领域。

Lingo 语言自身也有许多重要的知识点，包括基本语法、面向对象编程、多媒体处理等内容。

在本文中，将对Lingo 的知识点进行总结和介绍，希望能够帮助大家更好地理解和使用 Lingo 语言。

一、基本语法1. 变量和常量：在 Lingo 语言中，可以通过变量和常量来存储和表示数据。

变量是可以改变数值的，而常量是一旦定义就不可改变的数值。

变量和常量的使用可以帮助我们更好地处理数据和逻辑关系。

2. 数据类型：Lingo 语言支持多种数据类型，包括整型、浮点型、布尔型、字符串等。

不同的数据类型有不同的操作方法和适用范围，熟练掌握数据类型可以帮助我们更好地处理数据。

3. 运算符：Lingo 语言支持多种运算符，包括算术运算符、比较运算符、逻辑运算符等。

运算符的使用可以帮助我们进行数值计算和逻辑判断。

4. 控制语句：Lingo 语言支持多种控制语句，包括条件语句、循环语句、跳转语句等。

控制语句的使用可以帮助我们控制程序的流程和逻辑。

5. 函数和方法：在 Lingo 语言中，可以通过函数和方法来封装和重用代码。

函数和方法的使用可以帮助我们更好地组织和管理代码。

6. 事件处理：Lingo 语言支持事件处理，可以方便地处理用户输入或系统事件。

事件处理的使用可以帮助我们开发交互式应用程序。

二、面向对象编程1. 类和对象：在Lingo 语言中，可以通过类和对象来进行面向对象编程。

类是对象的模板，对象是类的实例。

类和对象的使用可以帮助我们更好地组织和管理代码。

2. 继承和多态：Lingo 语言支持继承和多态，可以方便地重用代码和扩展功能。

继承和多态的使用可以帮助我们更好地设计和组织代码。

3. 封装和抽象：Lingo 语言支持封装和抽象，可以方便地隐藏代码细节和实现复杂功能。

LINGO软件的简介与使用

LINGO软件的使用
运算符的优先级：优先级运算符最高 #NOT# —（负号） ^ * / + —（减法） #EQ# #NE# #GT# #GE# #LT# #LE# #AND# #OR# <(=) = >(=) 最低
LINGO软件的使用
常用函数： ABS(X) 绝对值函数 COS(X) 余弦函数 EXP(X) 指数函数 FLOOR(X) 取整函数 LOG(X) 自然对数函数 MOD(X,Y) 模函数 POW(X,Y) 指数函数 SIGN(X) 符号函数 SIN(X) 正弦函数 SQR(X) 平方函数 SQRT(X) 平方根函数 TAN(X) 正切函数 BIN(X) 限定0-1变量 FREE(X) 取消符号限制 GIN(X) 限制整数等等还有很多~
absx绝对值函数cosx余弦函数expx指数函数floorx取整函数logx自然对数函数modxy模函数powxy指数函数signx符号函数sinx正弦函数sqrx平方函数sqrtx平方根函数tanx正切函数binx限定01变量freex取消符号限制ginx限制整数等等还有很多lingosolverstatus求解程序状态框
LINGO软件的使用
Solver Status 求解程序状态框： Model 模型类型 State 解的状态 Objective 最优值 Infeasibility 不满足约束总数 Iterations 迭代次数
பைடு நூலகம்
LINGO软件的使用
Solution Report 解答报告：解的状态 Objective value 最优值 Extended solver steps 特殊求解程序运行步数 Total solver iterations 迭代次数

LINGO软件介绍

关于LINGO软件的其它介绍
三、LINGO中的集四、集循环函数五、集操作函数
六、运用定义集的方法求解规划问题
由于时间关系所限，更主要是涉及的内容有相当的难度，所以关于LINGO软件的以上四方面的介绍只能从略。有兴趣的读者可以自学有关内容。
21
上机作业
再现教材P165-167的程序文件: ex_1.lg4、 ex_2.lg4 、 ex_3max.lg4 以及 ex_3min.lg4 要求：提交程序文件和相应的截图文件（图形文件格式为 JPG格式，文件名自定）
二、用LINGO解决基本的线性规划问题和二次规划问题
例3 求解二次规划问题：
解法一：直接使用LINGO最大化过程：
max=98*x1+277*x2-x1^2-0.3*x1*x2-2*x2^2; x1 + x2 <= 100; x1 <= 2*x2; @gin(x1);@gin(x2);
15
二、用LINGO解决基本的线性规划问题和二次规划问题
3
一、LINGO介绍
LINGO的主要功能特色为： 1. 既能求解线性规划问题，也有一定求解非线性规划问题的能力； 2. 输入模型简练直观； 3. 运行速度快、计算能力强；
4
一、LINБайду номын сангаасO介绍
LINGO的主要功能特色为： 4. 内置建模语言，提供几十个内部函数，从而能以较少的语句，较直观的方式描述较大规模的优化模型； 5. 将集合的概念引入编程语言，很容易将实际问题转换为LINGO模型； 6. 能方便地与Excel、数据库等其他软件交换数据。
7
二、用LINGO解决基本的线性规划问题和二次规划问题
我们编辑程序并求解后，得到LINGO Model窗口、 Solution report窗口和Solver status窗口如下：

lingo入门教程

lingo入门教程Lingo是一种广泛应用于计算机编程和计算机科学领域的编程语言。

它是用于Adobe Director（一种多媒体应用程序）中的脚本语言，用于控制多媒体元素和动画。

Lingo的语法比较简单易懂，有助于创建交互式和多媒体项目。

下面是一些Lingo的基本概念和用法。

1. 变量（Variables）: 在Lingo中，变量用于存储数据值。

变量可以是数字、文本或其他数据类型。

要创建变量，可以使用关键字`global`或`local`，后跟变量名和初始值（可选）。

例如：```global myVariable = 10local myText = "Hello World"```2. 条件语句（Conditional statements）: 条件语句用于根据条件执行特定的代码块。

常用的条件语句有`if-then`和`if-then-else`。

例如：```if myVariable > 5 thenalert "Value is greater than 5"elsealert "Value is less than or equal to 5"end if```3. 循环（Loops）: 循环用于重复执行一段代码块，直到满足指定条件为止。

Lingo提供了`repeat`和`repeat while`循环语句。

例如：```repeat with i = 1 to 5put iend repeat```4. 函数（Functions）: 函数是一组预定义的代码，用于执行特定的任务。

Lingo提供了许多内置函数，如`alert`、`put`等。

您还可以创建自己的函数。

例如：```on multiplyNumbers(a, b)return a * bend multiplyNumbersput multiplyNumbers(2, 4) -- 输出8```这些只是Lingo的一些基本概念和用法。

数学软件应用之Lingo课件

第1章
计算机基础知识
第二篇
LINGO软件
§1 LINGO 概述 LINGO是一种专门用于求解数学规划问题的软件包。由于LINGO执行速度快，易于方便地输入、求解和分析数学规划问题，因此在教学、科研和工业界得到广泛应用。LINGO主要用于求解线性规划、非线性规划、二次规划和整数规划等问题，也可以用于求解一些线性和非线性方程组及代数方程求根等。 LINGO的最新版本为LINGO10.0，但解密版通常为 4.0和5.0版本，本书就以LINGO5.0为参照而编写。
上一页
下一页
返回本章首页返回本节
第1章
计算机基础知识
3．查看．．．（Look．．．）从LINGO菜单中选用“Look．．．”命令或直接按Ctrl+L组合键可以查看全部的或选中的模型文本内容。 4．灵敏性分析（Range，Ctrl+R）用该命令产生当前模型的灵敏性分析报告：研究当目标函数的费用系数和约束右端项在什么范围（此时假定其它系数不变）时，最优基保持不变。灵敏性分析是在求解模型时作出的，因此在求解模型时灵敏性分析是激活状态，但是默认是不激活的。为了激活灵敏性分析，运行LINGO|Options…，选择General Solver Tab，在Dual Computations列表框中，选择Prices and Ranges选项。灵敏性分析耗费相当多的求解时间，因此当速度很关键时，就没有必要激活它。 5. 模型通常形式．．．（Generate．．．）从LINGO菜单中选用“Generate．．．”命令或直接按Ctrl+G组合键可以创建当前模型的代数形式、LINGO模型或MPS格式文本。
上一页
下一页
返回本章首页返回总目录

Lingo在飞行管理中的应用

Lingo在飞行管理中的应用概述随着航空业的日益发展，航空企业的管理需求也在不断增加。

其中，飞行管理是航空企业中重要的一环。

飞行管理主要包括航班计划安排、机组人员排班、飞机维护计划等。

而这些工作都需要高效的管理系统来支撑。

近年来，航空企业普遍采用了飞行管理软件来实现飞行管理的自动化。

Lingo是一种广泛应用于数学建模的工具。

它可以帮助人们建立数学模型、进行分析和求解，常被应用于生产调度、物流管理、供应链优化等方面。

而在飞行管理中，Lingo同样有着广泛的应用，可以帮助航空企业解决飞行计划、机组排班等问题，提高管理效率。

本文将详细介绍Lingo在飞行管理中的应用。

飞行计划优化飞行计划是飞行管理中最基础的工作之一。

飞行计划涉及航班的起降时间、航线、停靠机场、飞行时长等信息。

而对于航空企业来说，合理的飞行计划可以提高飞行效率、降低飞行成本。

因此，如何优化飞行计划是航空企业中重要的问题。

在传统的飞行计划优化中，往往需要考虑到多种因素，包括航班的数量、起降时间、机组人员等。

由于这些因素之间相互影响，因此很难快速得到一个最优解。

而使用Lingo进行飞行计划优化，可以大大降低这个问题的复杂度，提高优化效率。

Lingo通过建立数学模型来描述飞行计划优化问题。

例如，可以将优化目标设置为最小化航班总飞行时间，同时满足每个航班的飞行约束条件（如最晚到达时间、最早出发时间等）。

通过运行Lingo模型，可以得到一个最优的飞行计划方案，使得目标函数最小。

机组排班问题与飞行计划一样，机组排班也是飞行管理非常重要的一项工作。

机组排班涉及机组人员的任务安排、机组人员的休息时间、机组人员的交替等。

在传统的机组排班中，人工安排的方式容易出现安排不当，导致机组人员出现疲劳情况，从而影响航班安全。

因此，建立一个合理的机组排班系统对于保证航班安全至关重要。

Lingo同样可以用于机组排班问题的求解。

它可以把机组排班问题转化为一个数学优化模型，使得机组人员可以在最短的时间内完成任务，并且保障机组人员的休息时间。