最新n直线分平面,n平面分空间,n圆分平面,n球面分空间
平面分空间

n个平面把空间分割成的部分数最多, 个平面把空间分割成的部分数最多, 其位置关系如何呢? 其位置关系如何呢? 任何两个平面相交; 1)任何两个平面相交; 2)任何三个平面呢? 任何三个平面呢?
任何三个平面, 任何三个平面, 不相交于同一条直线, 不相交于同一条直线, 交线也不能相互平行; 交线也不能相互平行;
与“3条直线分割平面最多有几个部分”类比 条直线分割平面最多有几个部分” 有一部分有限。无限部分是: 有一部分有限。无限部分是: 与三角形有一公共边的有三部分, 与三角形有一公共边的有三部分, 与三角形有一公共顶点的有三部分, 与三角形有一公共顶点的有三部分, 于是,总的分割数是1 于是,总的分割数是1+3+3=7。
…… …… …… …… …… …… …… ……
结论: ♦结论:
维空间分割r维空间得到的最大 用 n个( r-1)维空间分割 维空间得到的最大 维空间数目 个 维空间分割 维空间得到的最大r维空间数目 = 用 (n-1)个( r-1)维空间分割 维空间得到的最大 维空 维空间分割r维空间得到的最大 个 维空间分割 维空间得到的最大r维空 间数目+用 维空间分割(r-1)维空间得到的最 间数目 用 (n-1)个(r-2)维空间分割 个 维空间分割 维空间得到的最 维空间数目. 大(r-1)维空间数目 维空间数目 即对任意的r维空间, 个 即对任意的 维空间,n个(r-1)维超平面最多可以把 r维 维空间 维超平面最多可以把 维 切割成W(n,r)部分,则 部分, 空间 切割成 部分
r 1 2 3 4 5 6 …… n 1 2 2 2 2 2 2 2 3 4 4 4 4 4 3 4 7 8 8 8 8 4 5 11 15 16 16 16 5 6 16 26 31 32 32 6 7 22 42 57 63 64 7 8 29 64 99 120 127 …… …… …… …… …… …… ……
n个平面最多把空间分成几部分

n个平面最多把空间分成几部分
解: (1)先来解决一个问题:n条直线最多把平面分成几个部分呢?不妨记为f(n),易得f(1)=2,f(2)=4,f(3)=7,第n条直线与前n-1条直线两两相交,有n-1个交点,这n-1个交点最多把第n条直线分成n段,这样第n条直线就把原来的平面多分成了n个部分,所以有f(n)=f(n-1)+n (n>=2)通过计算求得f(n)=n(n+1)/2+1=C(n+1,2)+1 -----(I) (2)设n个平面最多能把空间分成g(n)部分,易得g(1)=2 g(2)=4 g(3)=8 g(4)=15 第n个平面与前面n-1平面两两相交,有n-1条直线,这n-1条直线最多把第n个平面分成f(n-1)个部分,每一部分就把原来的空间多分成了一部分,所以有g(n)=g(n-1)+f(n-1) n>=2 -----(II) 利用递推公式(II)公式(I)可得:g(n)=g(1)+f(1)+f(2)+…+f(n-1) =C(2,2)+C(3,2)+…+C(n,2)+n+1 =C(3,3)+C(3,2)+…+C(n,2)+n+1 =C(4,3)+C(4,2)+…+C(n,2)+n+1… =C(n+1,3)+n+1。
平面划分最多问题
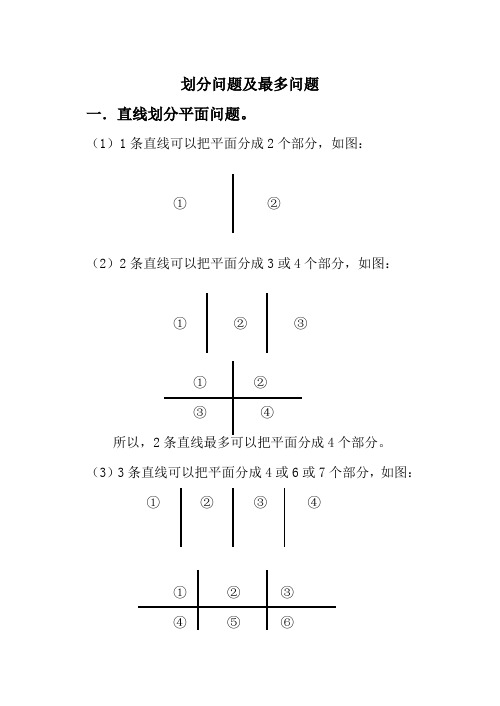
划分问题及最多问题一.直线划分平面问题。
(1)1条直线可以把平面分成2个部分,如图:①②(2)2条直线可以把平面分成3或4个部分,如图:①②③①②③④所以,2条直线最多可以把平面分成4个部分。
(3)3条直线可以把平面分成4或6或7个部分,如图:①②③④①②③④⑤⑥① ② ③④ ⑤ ⑥① ② ③ ④ ⑤ ⑥ ⑦所以,3条直线最多可以把平面分成7个部分。
(4)4条直线呢?最多可以把平面分成几个部分? (5)n 条直线最多可以把平面分成几个部分?分析:要n 条直线最多把平面分成若干部分,必须n 条直线两两相交且无3条过同一点,记n 条直线最多可以把平面分成a n 个部分,第n 条直线与前n-1 条直线最多有n-1个交点,这些交点把第n 条直线分成n 段,每一段把原来对应的部分分为两部分,所以从n-1条直线增加了1条直线共增加了 n 个部分,即a n -a n-1=n (n>1),累加求和得,)2(212++=n n a n二.平面划分空间问题。
(1)1个平面可以把空间分成2个部分,如图:①②(2)23或4个部分,如图:①②③①②③④所以,2个平面最多可以把空间分成4个部分,(3)3个平面可以把空间分成4或6或7或8个部分,如图:①②③④⑤⑥③④⑤⑥⑦⑧所以,3个平面最多可以把空间分成8个部分. (4)4个平面最多可以把空间分成几个部分?(5)n个平面最多可以把空间分成几个部分?分析:记n 个平面最多可以把空间分成a n 部分,第n 个平面与前n-1 个平面最多有n-1条交线,这些交线把第n 个平面分成)2(212+-n n 部分,每部分把对应的空间分为两部分,所以共增加了 )2(212+-n n 部分,a n -a n-1=)2(212+-n n , (n>1)累加求和得,*∈+-+=N n n n n a n ),6)(1(612. n 个平面把空间最多分成)6)(1(612+-+n n n 个部分.①②③④⑤⑥⑦⑧。
n个平面最多可将空间分成多少个部分

--1--空间分成多少个部分问题提出:空间n 个平面最多可将空间分成多少个部分?问题分析:显然,当这n 个平面满足以下条件时,所分割的部分数是最多的。
1、 这n 个平面两两相交;2、 没有三个以上的平面交于一点;3、 这n 个平面的交线任两条都不平行。
对于一般情况一下子不易考虑,我们不妨试着从简单的,特殊的情况入手来寻找规律。
设n 个平面分空间的部分数为n a ,易知当1=n时,2=n a ;当2=n 时,4=n a当3=n 时,8=n a 当4=n 时,情况有些复杂,我们以一个四面体为模型来观察,可知15=n a ;从以上几种情况,很难找出一个一般性的规律,而且当n 的值继续增大时,情况更复杂,看来这样不行。
那么,我们把问题在进一步简单化,将空间问题退化到平面问题:n 条直线最多可将平面分割成多少个部分?(这n 条直线中,任两条不平行,任三条不交于同一点),设n 条直线最多可将平面分割成n b 个部分,那么当3,2,1=n 时,易知平面最多被分为2,4,7个部分。
当k n =时,设k 条直线将平面分成了k b 个部分,接着当添加上第1+k 条直线时,这条直线与前k 条直线相交有k 个交点,这k 个交点将第k 条直线分割成n 段,而每一段将它所在的区域一分为二,从而增加了1+k个区域,故得递推关系式 )1(1++=+k b b k k ,即11+=-+k b b k k显然当1=k时, 21=b ,当1,,2,1-=n k 时,我们得到1-n 个式子:212=-b b323=-b b434=-b b ……n b b n n =--1将这1-n 个式子相加,得)2(212++=n n b n ,即n 条直线最多可将平面分割成)2(212++n n 个部分。
我们来归纳一下解决这个问题的思路:从简单情形入手,确定k b 与1+k b 的递推关系,最后得出结论。
现在,我们回到原问题,用刚才的思路来解决空间的问题,设k 个平面将空间分割成k a 个部分,再添加上第1+k 个平面,这个平面与前k 个平面相交有k 条交线,这k 条交线,任意三条不共点,任意两条不平行,因此这第1+k 个平面就被这k 条直线分割成k b 个部分。
n条直线分平面问题

N 条直线分平面问题1.n 条直线最多能将平面分为多少个区域?设n 条直线最多能将平面分为n a 个区域,则121,4a a ==。
下面来建立1n a +与n a 的关系,设已画出n 条直线的情况,对于n+1条直线,我们看成是在n 条的基础上再增加一条直线所得,设新增直线为L,L 与n 条直线最多有n 个交点,n 个交点将L 分为 n+1个部分,而每个部分均将其在的区域一分为二,所以增一条L ,使在n 条直线的基础上最多增加n+1个区域,从而11n n a a n +=++。
由递推知11221,1,,2n n n n a a n a a n a a ----=-=--= 。
累加得11(1)(2)2(1)12n a a n n n n n -=+-+-++=+- ,故1(1)12n a n n =++。
所以n 条直线最多能将平面分为1(1)12n n ++个区域。
2.平面上n 条直线相交,内部最多能得到多少个区域?方法(1)设n 条直线相交,内部最多能得到n a 个区域,则1230,0,1a a a ===。
下面来建立1n a +与n a 的关系,设已画出n 条直线的情况,对于n+1条直线,我们看成是在n 条的基础上再增加一条直线所得,设新增直线为L,L 与n 条直线最多有n 个交点,n 个交点将L 分为 n+1个部分,而每个部分均将其在的区域一分为二,只有两头两部分没有使所在区域增加一个内部区域,中间n-1个部分使所在区域均增加一个内部区域,所以增一条L ,使在n 条直线的基础上最多增加n-1个内部区域,从而11n n a a n +=+-。
由递推知112212,3,,0n n n n a a n a a n a a ----=--=--= 。
累加得11(2)(3)(4)10(1)(2)2n a a n n n n n -=-+-+-+++=-- ,故1(1)(2)2n a n n =--。
平面最多分割空间问题

平面最多分割空间问题祁阳一中 王勇波高一学了立几后,学生就把思维的灵光扩大到我们所生活的空间,总有同学问我n 个平面最多能把空间分成几部分,我跟他们说,这是切西瓜的问题,几个平面即是几刀去切一个大西瓜,三刀以下学生很好理解,四刀以上就搞不定了。
要弄清这个问题先要学习“数列”“推理证明”等相关的知识点。
一、 首先要弄清直线分割平面的问题直线要最多分割平面的前提条件是:任两条直线都要相交,任何三条直线都不能交于同一点。
设n 条直线最多分割平面为f (n )部分,一条直线分平面为二部分,即f (1)=2,f (2)=4,f (3)=7,…,接下来我们要弄清f (n +1)与f (n )的内在联系(这个我们初中是接触过的)。
我们来看增加的第n +1条直线,按照题目的意思知道,没有任何三条直线交于同一点,这样第n +1条直线与前面n 条直线有n 个交点,而这n 个交点把第n +1条直线分成n +1段,而这n +1段把它所在的区域一分为二,这由n 条直线到n +1条直线平面就增加了n +1个区域,即f (n +1)=f (n )+n +1,故有:f (1)=2 (1)f (2)=f (1)+2 (2)f (3)=f (2)+3 (3)…………f (n )=f (n -1)+n (n )上述n 个式子相加即有f (n )=2+2+3+4+…+n =21()12n n ++ f (1)=2也适合式子 故f (n )=2+2+3+4+…+n =21()12n n ++(此结论后面有用的) 二、 平面最大分割空间这里首先要明白平面最大分割空间要满足什么条件,即是所有平面都相交,任何三个平面都不能交于同一条直线。
我们也仿照上面直线分割平面的方法来处理这个问题。
设n 个平面最多分割空间为F (n )个区域,一条直线分平面为二部分,即F (1)=2,F (2)=4,F (3)=8,…,接下来我们要弄清F (n +1)与F (n )的内在联系。
六年级数学专题:图形区域分割计数

第36章 图形区域分割计数【内容综述】用一些几何图形去分割另一个图形,得到最多区域数是有规律可循的.如用点分直线,直线分平面,三角形分平面,平面分空间等等.下面我们来探索它们的规律,主要是从最简单的情形出发,依次递推,找到相邻两个图形之间的“增量”规律,然后归纳出一般公式.这里出现符号P (n ),表示n 个图形分另一个图形的最多区域数.1、点分直线:n 个点最多把一条直线分成=+=+P n C C n n n 101)(部分.如图,直线上4个点,最多分加 例5部分,n =1 =P 12)( 12n =2=+P 512)(n =3 +=+P 2519)(……当增加第3个角时,与前每个角最多有4个交点,被分成2⨯4+1=9段,增加9部分,所以3个角最多把平面分成2+5+9=16部分.如此类推,得到6个角最多把平面分成2+5+9+13+17+21=67部分.【评注】注意,添加第2个角时,大家很容易发现增加5部分,后面就认为每个都增加5k 部分,就会发生错误,为了不出现错误,还是看新增的角的边被分成了几部分.我们可以归纳出n 个角最多把平面分成:⎣⎦⎡⎤⋯=++++++-+P n n 4152913171)()(例6部分; 部分.=P 12)(=+P 126)( =++P 12612)(3)1个四边形分平面2部分;2个四边形最多把平面分成2+8=10部分,因为当画第2个四边形时,它与前一个四边形最多有8个交点,四边形边界被分成8段,每段都使区域数增加1部分,故最多把平面分成2+8=10部分; 如图,通过归纳得到10个四边形最多把平面分成=P (10)2+8⨯1+8⨯2+8⨯3+⋯+8⨯9=362部分.=12部分; n 个a 变形,最多把平面分成区域数为=-+P n an n (1)2)(.例3. 如果n 个相同的图形最多把平面分成-+an an 22部分,则称这种图形为“a 边形”.例如4个三角形最多把平面分成⨯-⨯+=34342382部分,则称三角形为“3边形”;5个正方形最多把平面分成⨯-⨯+=52825442部分,则称正方形为“4边形”;…….那么根据定义,当a =1时,可以最多把平面分成-+n n 22部分,则称为“1边形”,圆就是一种“1边形”.因此我们猜想:可以最多把平面分n =1 n =3 n =2成-+n n 2222部分的图形称为“2边形”.那么,有没有“2边形”呢?如果有,请举出实例. 【分析】通过例2的学习,我们把圆看作“1边形”,有没有“2边形”?显然“角”分平面不是“2边形”.若是“2边形”,必须=+⨯+⨯+⨯++⨯-=-+⋯P n n n n ()24142434(1)2(1)2. 【解答】一个“2边形”,首先第1个“2边形”分平面为2部分,后面每一个“2边形”都与前面每一个“2边形”相交时,区域数都最多增加4部分.如图,这样的“2边形”可以是椭圆、弓形、梭形、纺锤形等等.例1点,就会增加线1段基本线段.当两点重合时,就会减少1段.因此直线上有n 个点,就会把直线分成=+=+P n C C n n n ()101部分.这n +1部分中,有(n -1)部分为线段,2部分为射线.所以对于直线上有6个点,最多把直线分成1+6=7部分.。
n个平面最多可将空间分成多少个部分

--35--邯郸市一中校刊n 个平面最多可将空间分成多少个部分数学教师 赵新国问题提出:空间n 个平面最多可将空间分成多少个部分?问题分析:显然,当这n 个平面满足以下条件时,所分割的部分数是最多的。
1、 这n 个平面两两相交;2、 没有三个以上的平面交于一点;3、 这n 个平面的交线任两条都不平行。
对于一般情况一下子不易考虑,我们不妨试着从简单的,特殊的情况入手来寻找规律。
设n 个平面分空间的部分数为n a ,易知当1=n时,2=n a ;当2=n 时,4=n a当3=n 时,8=n a 当4=n 时,情况有些复杂,我们以一个四面体为模型来观察,可知15=n a ;从以上几种情况,很难找出一个一般性的规律,而且当n 的值继续增大时,情况更复杂,看来这样不行。
那么,我们把问题在进一步简单化,将空间问题退化到平面问题:n 条直线最多可将平面分割成多少个部分?(这n 条直线中,任两条不平行,任三条不交于同一点),设n 条直线最多可将平面分割成n b 个部分,那么当3,2,1=n 时,易知平面最多被分为2,4,7个部分。
当k n =时,设k 条直线将平面分成了k b 个部分,接着当添加上第1+k 条直线时,这条直线与前k 条直线相交有k 个交点,这k 个交点将第k 条直线分割成n 段,而每一段将它所在的区域一分为二,从而增加了1+k个区域,故得递推关系式 )1(1++=+k b b k k ,即11+=-+k b b k k显然当1=k时, 21=b ,当1,,2,1-=n k 时,我们得到1-n 个式子:212=-b b323=-b b434=-b b ……n b b n n =--1将这1-n 个式子相加,得)2(212++=n n b n ,即n 条直线最多可将平面分割成)2(212++n n 个部分。
我们来归纳一下解决这个问题的思路:从简单情形入手,确定k b 与1+k b 的递推关系,最后得出结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.平面上有n 条直线,最多可把平面分成几部分? 答:2
22++n n 分析:当增加一条直线时,把平面多分割出几部分来呢?
由第n 条直线与前(n-1)条直线有(n-1)个交点,从而把第n 条直线分成n 段,而每一段把所在部分一分为二,于是增加了n 个部分。
由此得n 条直线把平面分割成的最多部分数为
1+(1+2+3+ … +n)=2
22++n n 2.n 个平面将空间分成的部分数为: 答:6
653++n n 分析:若增加1个平面,可把空间多分割出几部分呢?
由于增加的第n 个平面与前(n-1)个平面都相交,于是第n 个平面上有(n-1)条交线, 因此增加的第n 个平面被(n-1)条直线分成[(n-1)2+(n-1)+2]/2=(n2-n+2)/2块,
而每一块把所在的部分空间一分为二,于是增加了(n2-n+2)/2个部分。
因此,n 个平面将空间分成的部分数为:1+[1+2+4+7+11+…+(n2-n+2)/2]=6
653++n n 3.平面上的n 个圆,至多可把平面分成几部分? 答:22+-=n n a n
分析:推导方法是递推,先看多加一个圆后增加了多少个交点,在K 个圆上再加一个圆至多能增加2K 个交点,又增加n 个交点就多了n 块区域,故在K 个圆上再加一个圆至多能增加2K 块区域。
所以一个圆最多分2部分,两个圆最多分2+2=4部分,三个圆最多分4+4=8部分,四个圆最多分8+6=14部分,五个圆最多分14+8=22部分,六个圆最多分22+10=32部分。
推广到n 个圆,n 个圆最多将平面分成: 2+2(1+2+3+…+n -1)=2+n(n-1)= 22
+-n n 部分。
方法2:设n 个圆最多可将平面分成n a 个部分,现增加一个圆,它与前n 个圆有2n 个交点,这些交点将新增的第n 个圆分成2n 段互不相交的弧段,每一段把所在的平面区域
一分为二。
得n a a n n 21+=+ 计算得22+-=n n a n 4.空间中n 个球面,至多可把空间分成几部分? 答:3
8323n n n +- 分析:推导方法是递推,先看多加一个球面后能增加多少个部分,在已有N-1个球面基础上再加一个球面,这个球面至多能被这N-1个球面划分成(N-1)^2-(N-1)+2(参见n 个圆最多将平面分成几部分中的结论)块区域,其中每块区域都将其所在的原来那部分空间一分为二,故在已有N-1个球面基础上再加一个球面,这个球面至多增加(N-1)^2-(N-1)+2块空间区域。
所以一个球面最多分2部分,两个球面最多分2+2=4部分,三个球面最多分4+4=8部分,四个球面最多分8+8=16部分,五个球面最多分16+14=30部分,六个球面最多分30+22=52部
分。
推广到N 个球面,N 个球面最多将空间分成
2+(1^2-1+2)+ (2^2-2+2)+…+ ((N -1)^2-(N-1)+2) =38323n n n +- Excel
电子表格试题
一、单项选择题
1. 在保存新建的Excel2010工作簿的操作过程中,默认的工作簿文件名是()。
A.工作簿1
B.工作表1
C.文档1
D.电子表格1
2. Excel 启动后,系统默认打开的工作表数目是()个。
A.2
B.3
C.4
D.5
3. 如果当前工作簿有4个工作表,此时再插入一个工作表,其默认的工作表名
为()。
A.Sheet4
B.Sheet(4)
C.Sheet5
D.Sheet(5)
4. 对工作表进行添加或删除、复制、重命名等操作后()。
A.无法撤消
B.可以撤消
C.删除不能撤消,其它可以撤消
D.重命名可以撤消,其它不能撤消
5. Excel2010文件的扩展名为()。
A.xcel
B.exls
C.xlsx
D.exlx 6. 工作表是由()行构成。
A.1048576
B.16384
C.65535
D.256
7. 一张工作表是由()列构成。
A.1048576
B.16384
C.65535
D.256
8. 第3行第4列的单元格名字是()。
A.C4
B.C3
C.E3
D.E4
9. 要想复制工作表,可按住()键不放,使用鼠标拖动标签。
A.Alt
B.Ctrl
C.Shift
D.Esc
10. 在Excel 中,输入系统当前日期的快捷键是()。
A.Ctrl+;
B.Ctrl+Shif+;
C.Shift+;
D.Shift+Alt+;
11. 输入系统当前时间的快捷键是()。
A.Ctrl+;
B.Ctrl+Shif+;
C.Shift+;
D.Shift+Alt+; 12. 在Excel2010中,活动工作表有()个。
A.1
B.2
C.3
D.4
13.在一个工作表中,活动单元格有()个。
A.1
B.2
C.3
D.4
14.在Excel2010中,工作表()。
A.可以增加或删除
B.不可以增加或删除
C.只能增加
D.只能删除
15.在Excel2010中,默认情况下,文本型数据()。
A.左对齐
B.居中
C.右对齐
D.两端对齐
16.Excel2010在默认情况下,数字型数据()。
A.左对齐
B.居中
C.右对齐
D.两端对齐
17.在某个单元格中输入“2/4”,按回车后显示()。
A.1/2
B.2/4
C.0.5
D.4月4日
18.在某个单元格中输入“(8)”,按回车后显示()。
A.8
B.(8)
C.-8
D.⑧
19.要在选定的多个单元格中输入相同的数据,在输入第一个数据后按键()。
A.Enter
B.Ctrl+Enter
C.Shift+Enter
D.Alt+Enter。
