专题:质心系概论
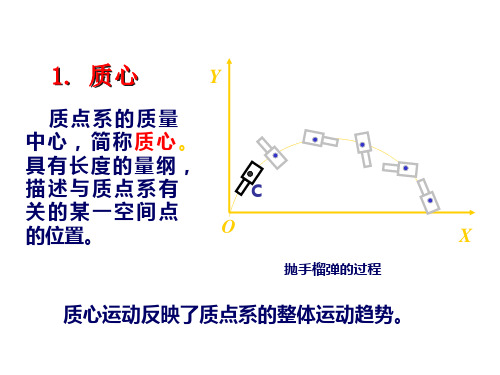
3.3--质心--质心运动定理

x1
l
S
xc
mx1 Mx2 mM
O
x2' S
x
终了时,系统质心位置
xc
mx1 m
Mx2 M
x2
M (x2 x2 ') m(x1'x1)
S
lS
解得 S ml mM
s l S Ml mM
例3 如图 已知:M , m,l ,地面光滑。 m, l o
起初:单摆水平,静止。
mg
求:下摆至 时,车的位移。
i
而
mi m
i
mii P
P mii i
i
C
P mc
mc
m
2. 质心运动定理——质点系的动量定理
F外
m
dc
dt
=mac
ac miai / mi
i
i
dP F外 dt
t2 t1
F外dt
P
dP
P0
讨论
1)质点系动量定理微分和积分形式:
F外 mac
(F外
dP) dt
t2 t1
F外dt
rC
×
C
c
在质心系中考察质点系的运动。 x O
y
由于质心vc=0,所以质心系是一 个零动量参考系
O系为惯性系
知识回顾 Knowledge Review
祝您成功!
d
dm
x Rcos y Rsin
yc
ydm
M
π 0
Rsin M Rd
πR
2R
M
π
O
x
xc 0
说明
几何对称性
(1) 弯曲铁丝的质心并不在铁丝上;
质心参考系

r
' i
rc
(mi
' i
mivc
)
Lo L' Lc
r
' i
mi
' i
rc
mi
' i
mi
r
' i
c
rc
mic
4
第3章动量与角动量
质点系的轨道角动量等于质点系的全部质量集中于质心
处的一个质点对于参考点O的角动量。它反映了整个质
点系绕参考点的旋转运动。 质点系的自旋角动量是以质心为参考点的角动量。与质心 运动无关。它只代表系统的内禀性质 。
mi Fi
质点系整体随质心的运动;
ri ri
各质点相对于质心的运动
ri rC r'i
vi vC v'i
rC
×
C
c
xO
y
(mii ) ( mi )c ( mi )rc (miri )
可得
C 是质心兼质心
mii 0 坐标系原点
miri 0 ,
2
第3章动量与角动量
二、质心系的基本特征
LO LC L
LC rC MvC rC P
L r'i miv'i
3
第3章动量与角动量
质心系中的角动量
z i mi Fi
ri ri
rC
×
C
c
xO
y
对O点 对质心 C 对O
Lo ri (mii )
L ri(mii )
LC rC ( mi )C
可得
Lo ri (mii )
P
rC
dP dt
ri Fi 0 rC Fi
质心系(精心整理)

m1r12 m1 m2
;
的角动量
为: LC
LC r1' p1'r2' p2'
m2r12
u
m1r12
(
u)
m1 m2
r12
u
m1 m2
与一u个的位质矢点为的角r12动,量动相量同为
*计算一个氢原子的角动量时必须用电子—质子系统
mn an
mn
d vn dt
Fn
fn2
fn3
fnn
质心运动定理
对于内力 f12 f21 0, , fin fni 0,
miai
Fi
ac
miai mi
ac
Fi 质心m运i
Fi
于两部分之和: 相对于质心的内动能(固有动能)。
质心平动动能(轨道动能) 。
*一个体系的内能就是指:
内能=质点系各质点 相对于质心的内动能 +质点间相互作用的内势能
*在惯性系中机械能守恒定律的形式在质心系中仍
然成立(质心相对质心的速度为零)。无论质心系 是惯性系还是非惯性系。(证明从略)
所以在质心系中分析问题方便。见刚体力学。20
(m1r1
m2r2 ) vC
rC
(m1
m2 )vC
r L
r L'
r rC
(m1
42--质心-质心运动定理-质心坐标系

zc
zdm dm
,
yc
ydm dm
,
rc
rdm dm
例1、一段均匀铁丝弯成半圆形,其半径为R,求此半 圆形铁丝的质心。
解:如图:建立坐标系,坐标原点为圆心,任取一小 段特丝,长度为dl,质量为dm,ρ为线密度,得到:
y
dm=ρdl
yc
ydm m
ydl
m
由于y=Rsinθ,dl=ds=Rd θ,得到:
解一:以人和船为一个系统,在水平方向不受力,质心速度
为0,质心的坐标值不变。
xc
m1x1 m2 x2 m1 m2
x
' c
m1x'1
m2 x'2
m1 m2
得到:xc=x’c
m2 (x2
x'2 )
m1 ( x1
x
' 1
)
x2-x2’为船移动的距离d,人移动的距离为(l-d)
得到:
d m1 l 50 4 0.8m m1 m2 50 200
Rsin Rd
yc 0
m
2R2
mm Ryc源自2Rdl dθ
θ x
二、质心运动定理
将质心位矢对时间求导:
rc miri / m
i
得
drc
dt
i
mi
dri dt
/
m
或 vc mivc / m
mvc mivc
i
i
根据质点系的动量定理:
t
0
Fidt
mivi
mivi0
质点系
一、质心
质心是与质点系质量分布有关的一个代表点,它 的位置在平均意义上代表着质量分布的中心。
08-质心系

动力学
§3.5 质心参照系
5.1 质心系是零动量参照系 5.2 质点系相对于 L系 、C系的角动量之间的关系 系 系 5.3 相对于一质点系的质心的外力 转) 矩与该质点 相对于一质点系的质心的外力(转 系内部角动量的关系。 系内部角动量的关系。 5.4 质点系统相对于 系、C系的动能间的关系 质点系统相对于L系 系
ɺ ɺ ∴m r '+m r '= 0 1 1 2 2
1 1 1 2 2 2 ∴E = m v ' + m v2' + (m +m )vC k 1 1 2 1 2 2 2 2 de f 质点系相对于质心系 1 1 2 2 E内 ≡ mv ' + m v ' k 1 1 2 2 的动能叫做内动能。 的动能叫做内动能。 2 2 12
r = C
∑mr
i
i i
m
; 不代撇
C系 r C = 系 C
∑mr '
i i
i
m
=0
r '= C
∑mr '
i i i
m
= 0代撇
C系 v = 系 C C
∑mv '
i i i
m
=0
vC'=
∑mv '
i i i
m
= 0代撇
5
5.2 质点系相对于实验室参照系 系)的角动量与它 质点系相对于实验室参照系(L系 的角动量与它 相对于质心参照系(C系 的角动量之间的关系 相对于质心参照系 系)的角动量之间的关系
zm 1
C x' r ' m 2 O 2
r C
r' 1
大学物理力学第六章质心运动定理(一)2024

大学物理力学第六章质心运动定理(一)引言概述:
大学物理力学第六章质心运动定理(一)是研究质点系运动的基本定理之一。
它提供了描述质点系运动的质心运动定理,通过质心的位置和速度来刻画整个质点系的运动状态。
本文将从质心的定义、质心运动的基本性质、运动定理的表达形式、定理的证明过程以及实际应用等五个大点来详细阐述质心运动定理的相关内容。
正文:
一、质心的定义
1. 质心的概念及其物理意义
2. 如何计算质心的位置坐标
二、质心运动的基本性质
1. 质心的速度与质点的速度之间的关系
2. 质心的加速度与质点的加速度之间的关系
3. 质心运动的平稳性及其相关说明
三、质心运动定理的表达形式
1. 质心运动定理的基本公式
2. 质心运动定理的向量形式
3. 质心运动定理的微分形式
四、质心运动定理的证明过程
1. 利用质心的定义和质点系的微分元素进行推导
2. 推导过程中的重要假设和简化处理
3. 将推导结果与实际情况进行对比验证
五、质心运动定理的实际应用
1. 航天器的姿态控制与稳定
2. 运动物体的动量变化分析
3. 天文学中的质心运动定理应用
总结:
本文从质心的定义、质心运动的基本性质、运动定理的表达形式、定理的证明过程以及实际应用等五个大点全面阐述了大学物理力学第六章质心运动定理(一)的相关内容。
这一定理的正确应用,不仅能够帮助我们更好地理解质点系的运动规律,还在实际生活中有着广泛的应用前景,对于提高物体运动控制、动量变化分析、航天器姿态控制等方面都具有重要意义。
通过深入学习和理解质心运动定理,我们能够更好地应用物理学知识解决实际问题,推动科学技术的发展。
质心知识点总结归纳

质心知识点总结归纳质心(Center of Mass)是物体集中质量的平均位置。
在物理学中,质心是描述物体运动的重要概念,对于研究物体的运动、碰撞、转动等现象都有重要的意义。
同时,质心在工程、航天航空等领域也有着广泛的应用。
质心的计算方法有多种,可以通过物体的密度分布、几何形状和其他条件来进行计算。
而质心的运动规律也可以通过牛顿定律和动量定律来描述。
本文将从质心的概念、计算方法、运动规律以及工程应用等方面对质心的知识点进行总结和归纳。
一、质心的概念1. 定义质心是物体所有质点的集中位置,也可以看作是物体的平衡点。
在质心系中,物体的总动量和总角动量相对于质心系均为零。
2. 特点(1)质心不一定位于物体内部,可以位于物体的外部;(2)质心的运动不一定与物体的其他点相同;(3)质心的位置与物体的形状和质量分布有关;(4)质心具有跟随物体运动的特点。
二、质心的计算方法1. 特殊形状物体的质心计算(1)均匀杆对于一根均匀杆,质心位于杆的中点处。
(2)均匀圆环对于一个均匀圆环,质心位于环的中心处。
2. 连续体的质心计算对于连续分布的质量分布,可以通过积分的方法来计算质心。
一般来说可以使用以下公式来计算:\[ x_{cm} = \frac{1}{M} \int x\;dm \]\[ y_{cm} = \frac{1}{M} \int y\;dm \]\[ z_{cm} = \frac{1}{M} \int z\;dm \]其中,\( x_{cm} \)、\( y_{cm} \)、\( z_{cm} \) 分别表示质心在 x、y、z 方向上的位置,M 表示物体的总质量。
三、质心的运动规律1. 质心的运动状态质心的运动状态可以通过牛顿定律和动量定律描述。
在外力作用下,质心会产生加速度,并且质心的加速度与物体的质量成反比。
2. 刚体的平动运动对于刚体的平动运动,可以通过质心的运动来描述整个刚体的运动状态。
刚体的平动运动可以看作是质心的平动运动。
质心系(精心整理)分解
o
riO riC rCO (1)
mi v iO mi v iC mi v CO (2)
10
v iC 表示的第i个质点相对于质心C的位矢和速度。 riC、 因为质心相对于质心的位矢恒为零,即 rCC 0, 所以 在质心系中质心的速度也恒为零 v CC 0
i
m
;不代撇
C系 rCC
mi riC
i
m
mi v iC
i
0
rC '
mi ri '
i
m
mi v i '
i
0 代撇
C系 v CC
m
0
vC '
m
0 代撇
12
2 质点系相对于实验室参照系(L系)的角动量与它相 对于质心参照系(C系)的角动量之间的关系
L ( r1 ' p1 ' r2 ' p2 ') rC ( p1 ' p2 ') (m1r1 m2 r2 ) v C ( p1' p2 ') 0 质心系是零动量参照系
(m1r1 m2 r2 ) v C rC (m1 m2 )vC
以两个质点的系统为例
在L系中质点m1、m 2及其 vC 质心的速度分别为 v1 、 、 v2
z m1
z'
r1 '
在C系中质点m1、m 及其 2 ' 质心的速度分别为 v1 、 ' v 2、
vC ' 0 L r1 p1 r2 p2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
转动惯量小的滚得快!
┫
质心的角动量仍能满足角动量定理的原因。 5
【例】一长为L,质量为m的均匀细棒,水平放 置静止不动,受垂直向上的冲力F作用,冲量 为Ft(t很短),冲力的作用点距棒的质心l 远,求冲力作用后棒的运动状态。
解 (1)质心的运动
l CF
(F mg ) t mv C0
vC 0
F
m m
g
t
质心以vC0的初速做上抛运动。
(2)在上抛过程中棒的转动
绕过质心转轴,列转动定理:
Fl JC JC
d
dt
JC
t
JC
t
Flt
JCLeabharlann 12FltmL2l CF
在上抛过程中,棒以恒定角
速度绕过质心轴转动。
三.刚体的无滑动滚动 瞬时转轴 1.平面平行运动
质心做平面运动+绕过质心垂直轴做转动 只考虑圆柱,球等轴对称刚体的滚动。 2.无滑动滚动: 任意时刻接触点P 瞬时静止
可以证明: L L LC
3
2. 质点系对质心的角动量定理:
d L dt
d
d t
(L
LC
d L (d rC
dt dt
)
P
d
d
t
(
L
rC
rC
dP dt
P )
)
ri
Fi
(0
(ri rC ) Fi
rC
Fi)
ri Fi
M外
即有
M 外
d L dt
—— 质心系中质点对质心的角动量定理 4
一. 质心(参考)系(frame of center of mass) 1. 质心系 讨论天体运动及碰撞等问题时常用到质心系。 质心系是固结在质心上的平动参考系。 质心系不一定是惯性系。 质点系的复杂运动通常可分解为: 质点系整体随质心的运动;
各质点相对于质心的运动 —— 在质心系中考察质点系的运动。
C
R p
ac
vc
无滑动滚动条件:
vC R aC R
【例】两个质量和半径 都相同,但转动惯量不 同的柱体,在斜面上作 无滑动滚动,哪个滚得 快?
C
y
R
f
x
mg
mgsin f maC 质心运动定理
Rf JC 过质心轴转动定理 aC R 纯滚动条件(运动学条件)
mgR sin
JC mR2
尽管质心系可能不是惯性系,但对质心来说,
角动量定理仍然成立。 这再次显示了质心的
特殊之处和选择质心系来讨论问题的优点。
惯设若性质质力心心对加系质速是心度非的为惯力a性矩C 系:, ,则M有则 外M力惯矩C 中 d应dLt包 括
M惯C
ri(miaC)
i
(
mi
ri
)aC
0
i
这正是即使质心系为非惯性系,但质点系对
1
2.质心系的动量
miv i ( mi )vC 0
质心系是零动量参考系。
m1v1
·· m1v10
m2v20
m2v2
质心系中看两粒子碰撞
两质点系统在其 质心系中,总是具有 等值、反向的动量。
2
二. 质心系中的角动量定理
1. 质心系中的角动量
利用x关zOO系系vi:•为r•iv惯vrr•Ciii •性m×Cri系vir•i•iv•FCyirvCC,,对C对CO是质对O是mm点质心O惯iivr心性iiLLL兼系C00质((中r心的Crr坐v一iirCC(标个((mm系m定00)ii)i原vv点)vii。点,)C)
