人教版七校2020届九年级上学期数学期末联考试卷A卷
人教版2020版九年级上学期期末数学试题A卷新版
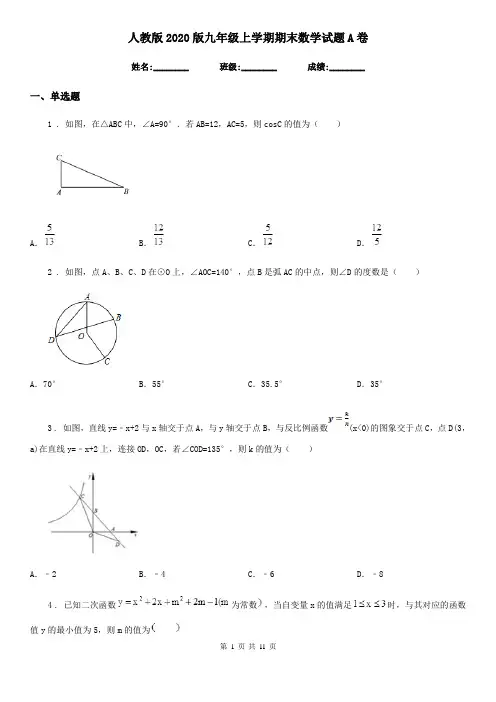
人教版2020版九年级上学期期末数学试题A卷姓名:________ 班级:________ 成绩:________一、单选题1 . 如图,在△ABC中,∠A=90°.若AB=12,AC=5,则cosC的值为()A.B.C.D.2 . 如图,点A、B、C、D在⊙O上,∠AOC=140°,点B是弧AC的中点,则∠D的度数是()A.70°B.55°C.35.5°D.35°3 . 如图,直线y=﹣x+2与x轴交于点A,与y轴交于点B,与反比例函数(x<0)的图象交于点C,点D(3,a)在直线y=﹣x+2上,连接OD,OC,若∠COD=135°,则k的值为()A.﹣2B.﹣4C.﹣6D.﹣84 . 已知二次函数为常数,当自变量x的值满足时,与其对应的函数值y的最小值为5,则m的值为A.1或B.或5C.1或D.1或35 . 下列说法正确的是()A.了解重庆电视台新闻频道的收视率应采用全面调查B.了解我区初一年级学生的视力情况,在甲中学、乙中学的初一年级随机地各抽取10名学生的视力情况C.反映重庆市6月份每天的空气质量的变化情况适合用折线统计图D.商家从一批粽子中抽取200个进行质量检测,200是总体6 . 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=,则“人字梯”的顶端离地面的高度AD是()A.144cm B.180cm C.240cm D.360cm7 . 如图,的半径为5,的内接于,若,则的值为()A.B.C.D.8 . 如图,是的直径,弦于点,,的半径为,则圆心到弦的距离为()A.2.5 cm B.3cm C.3cm D.6cm二、填空题9 . 若将抛物线y=ax2+bx+c-3向上平移4个单位长度后得到的图象如图所示,则c=________.10 . 如图,在直角坐标系中,,边、都在轴的正半轴上,点的坐标为,,.反比例函数的图象经过点,交边于点.则的值为________.11 . 如图所示,∠C=∠E=90°,AC=3,AB=4,AE=2,当AD=___时,Rt△ABC∽Rt△ADE.12 . 如图,点O是△ABC的内切圆的圆心,若∠A=80°,则∠BOC=____°.13 . 已知抛物线,且当时,抛物线与x轴有且只有一个公共点,则c的取值范围是________.14 . 已知两个正整数的和是,设其中一个数为,两个正整数的积为,则的最大值是________.15 . 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°,得到Rt△EFC,若AB=,BC=1,则阴影部分的面积为________.16 . 若二次函数有最小值为,当时,,它的图象的对称轴为直线,则函数的关系式为____________.三、解答题17 . 从甲、乙两台包装机包装的质量为300g的袋装食品中各抽取10袋,测得其实际质量如下(单位:g)甲:301,300,305,302,303,302,300,300,298,299乙:305,302,300,300,300,300,298,299,301,305(1)分别计算甲、乙这两个样本的平均数和方差;(2)比较这两台包装机包装质量的稳定性.18 . 如图,中,,以为直径的与边相交于点,连接,过点作的切线,交边于点,交边的延长线于点.求证:;若,,求的长.19 . 如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设PA=x.(1)求证:△PFA∽△ABE;(2)若以P,F,E为顶点的三角形也与△ABE相似,试求x的值;(3)试求当x取何值时,以D为圆心,DP为半径的⊙D与线段AE只有一个公共点.20 . 计算:.21 . 如图,直线y=x+b(b>0)与x轴、y轴交于点A、B,在直线AB上取一点C,过点C作x轴的垂线,垂足为E,若点E(4,0).(1)若EC=BC,求b的值;(2)在(1)的条件下,有一动点P从点B出发,延着射线BC方向以每秒1个单位的速度运动,以点P为圆心,作半径为的圆,动点Q从点O出发,在线段OE上以每秒1个单位的速度作来回运动,过点Q作直线l垂直x轴,点P与点Q同时从点B、点O开始运动,问经过多少秒后,直线l和⊙P相切.22 . 如图,一个运动员推铅球,铅球在点A处出手,出手时球离地面m.铅球落地点在点B处,铅球运行中在运动员前4 m处(即OC=4 m)达到最高点,最高点D离地面3 m.已知铅球经过的路线是抛物线,根据图示的平面直角坐标系,请你算出该运动员的成绩.23 . 如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF,∠FDC=30°,求∠BEF的度数.24 . 某地铁站口的垂直截图如图所示,已知∠A=30°,∠ABC=75°,AB=BC=4米,求C点到地面AD的距离(结果保留根号).25 . 已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边长作正方形PQMN,使点M落在反比例函数的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点在第二象限;(1)如图所示,点P坐标为(1,0),图中已画出一个符合条件的正方形PQMN,请你在图中画出符合条件的另一个正方形,并写出点的坐标;(2)请你通过改变P点的坐标,对直线M的解析式y﹦kx+b进行探究:①k=;②若点P的坐标为(m,0),则b= ;(3)依据(2)的规律,如果点P的坐标为(8,0),请你求出点和点M的坐标.26 . (重温旧知)圆内接四边形的内角具有特殊的性质.如图①,四边形ABCD是⊙O的内接四边形,若AB=BD,∠ABD=50°,则∠BCD=_______°.(提出问题)圆内接四边形的边会有特殊性质吗?如图②,某数学兴趣小组进行深入研究发现:AB•CD+BC•DA=AC•BD,请按他们的思路继续完成证明.证明:如图③,作∠BAE=∠CAD,交BD于点E.∵∠BAE=∠CAD,∠ABD=∠ACD,∴△ABE∽△ACD,∴即AB•CD=AC•BE(应用迁移)如图 ,已知等边△ABC外接圆⊙O,点P为上一点,且PB=,PC=1,求PA的长.27 . 如图,∠MAN=30°,点C、B分别在射线AM、AN上,AB=6,∠ACB=30°.动点P从点A出发,沿射线AN以每秒3个单位长度的速度运动.过点P作PQ⊥AN交射线AM于点Q,点E是线段AQ的中点,连结PE.设△PQE 与△ABC重叠部分图形的面积为S平方单位,点P的运动时间为t秒(t>O).(1)求PQ的长(用含t的代数式表示).(2)当点Q在边AC上时,求S与t之间的函数关系式.(3)当△PQE与△ABC重叠部分图形是一个面积为的三角形时,求t的值.28 . 在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:若b′=,则称点Q为点P的理想点.例如:点(1,2)的理想点的坐标是(1,﹣2),点(﹣2,3)的理想点的坐标是(﹣2,3).(1)点(,﹣1)理想点的坐标是_____;若点C在函数y=2x2的图象上,则它的理想点是A(1,﹣2),B (﹣1,2)中的哪一个?_____;(2)若点P在函数y=﹣2x+4(﹣2≤x≤k,k>﹣2)的图象上,其理想点为Q:①若其理想点Q的纵坐标b′的取值范围是﹣6≤b′≤10,求k的值;②在①的条件下,若点P的理想点Q都不在反比例函数y=(m<0,x>0)上,求m的取值范围.参考答案一、单选题1、2、3、4、5、6、7、8、二、填空题1、2、3、4、5、6、7、8、三、解答题1、2、3、4、5、6、7、8、9、10、11、12、第11 页共11 页。
人教版2020届九年级上学期数学期末考试试卷 A卷

人教版2020届九年级上学期数学期末考试试卷A卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共10分)1. (1分)下列图案中,不是轴对称图形的是()A .B .C .D .2. (1分)在平面直角坐标系中,将二次函数的图象向上平移2个单位,所得图象的表达式为()A .B .C .D .3. (1分)布袋中装着只有颜色不同的红、黄、黑小球各一个,从中任意摸出一个球,记下颜色后放回搅匀,再摸出一个球,则摸出一个红球,一个黑球的概率是()A .B .C .D .4. (1分)若反比例函数的图象经过点(m,3m),其中,则此反比例函数的图象()A . 第一、二象限B . 第一、三象限C . 第二、四象限D . 第三、四象限5. (1分)正六边形具备而菱形不具备的性质是()A . 对角线互相平分B . 对角线互相垂直C . 对角线相等D . 每条对角线平分一组对边6. (1分)如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为()A . 50°B . 60°C . 75°D . 80°7. (1分)如图,∠AOB是⊙0的圆心角,∠AOB=80°则弧AB所对圆周角∠ACB的度数是()A . 40°B . 45°C . 50°D . 80°8. (1分)如图,点B、C、D在⊙O上,若∠BCD=140°,则∠BOD的度数是()A . 40°B . 50°C . 80°D . 90°9. (1分)已知圆锥的侧面积是8πcm2 ,若圆锥底面半径为R(cm),母线长为l(cm),则R关于l的函数图象大致是()A .B .C .D .10. (1分)关于x的一元二次方程ax2+bx=2(a,b是常数,且a≠0),()A . 若a>0,则方程可能有两个相等的实数根B . 若a>0,则方程可能没有实数根C . 若a<0,则方程可能有两个相等的实数根D . 若a<0,则方程没有实数根二、解答题 (共8题;共15分)11. (2分)用适当方法解下列方程:(1)(x-4)2-81=0;(2)3x(x-3)=2(x-3);(3) .(4)解方程:2x2-10x=3.12. (2分)已知圆O是等边△ABC的外接圆,P是圆上异于A,B,C的一点.(1)如图,若∠PAC=90°,,记直线AP与直线BC的交点为D,连接PC,求PD的长度;(2)若∠APC=∠BPC,猜想PA,PB,PC的数量关系并给予证明.13. (1分)如图,长方体的长为15,宽为10,高为20,点B离点C的距离是5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?14. (2分)一个不透明的布袋里装有三个球,其中2个红球,1个白球,它们除颜色不同外其余都相同:(1)摸出一个球记下颜色后放回,并搅匀,再摸出一个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);(2)现再将n个白球放入布袋中搅匀后使摸出一个球是白球的概率为,求n的值.15. (2分)如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.(1)求该反比例函数的解析式;(2)若△ABC的面积为6,求直线AB的表达式.16. (2分)小王叔叔家是养猪专业户,他们养的藏香猪和土黑猪一直很受市民欢迎.小王今年10月份开店卖猪肉,已知藏香猪肉售价每斤元,土黑猪肉售价每斤元,每天固定从叔叔家进货两种猪肉共斤并且能全部售完.(1)若每天销售总额不低于元,则每天至少销售藏香猪肉多少斤?(2)小王发现10月份每天上午就能将猪肉全部售完,而且消费者对猪肉的评价很高.于是小王决定调整猪肉价格,并增加进货量,且能将猪肉全部销售完.他将藏香猪肉的价格上涨,土黑猪肉的价格下调,销量与(1)中每天获得最低销售总额时的销量相比,藏香猪肉销量下降了,土黑猪肉销量是原来的倍,结果每天的销售总额比(1)中每天获得的最低销售总额还多了元,求的值.17. (1分)在△ABC中,AE⊥BC于点E,∠BAE:∠CAE=4:7,BD平分∠ABC,点F在BC上,∠CDF=70°,∠ABD=25°.(1)求∠CAE的度数;(2)求证:DF⊥BC.18. (3分)如图,二次函数的图象的顶点坐标为(1,),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).(1)求该二次函数的表达式;(2)判断点B是否在此二次函数的图象上,并说明理由.三、填空题 (共8题;共8分)19. (1分)若x=1是关于x的一元二次方程x2+3mx+n=0的解,则6m+2n=________.20. (1分)在平面直角坐标系中,点(-3,5)关于y轴对称的点的坐标为________.21. (1分)如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A 在反比例函数的图象上,若,则k的值为 ________.22. (1分)如图是两个质地均匀的转盘,现转动转盘①和转盘②各一次,则两个转盘指针都指向红的部分的概率为________。
人教版2020届九年级上学期数学期末考试试卷A卷F卷

人教版2020届九年级上学期数学期末考试试卷A卷F卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)下列图案中中心对称图形有()A . 1个B . 2个C . 3个D . 4个2. (2分)下列方程中变形正确的是()①4x+8=0变形为x+2=0;②x+6=5﹣2x变形为3x=﹣1;③ =3变形为4x=15;④4x=2变形为x=2.A . ①④B . ①②③C . ③④D . ①②④3. (2分)向阳村2010年的人均年收入为12000元,2012年的人均年收入为14520元.设人均年收入的平均增长率为x,则下列所列的方程中正确的是()A . 14520(1﹣x2)=12000B . 12000(1+x)2=14520C . 12000(1+x)2=14520D . 12000(1﹣x)2=145204. (2分)下列说法正确的是()A . 掷一枚硬币,正面一定朝上B . 某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖C . 旅客上飞机前的安检应采用抽样调查D . 方差越大,数据的波动越大5. (2分)如图,已知直线a∥b,则∠1+∠2﹣∠3=()A . 180°B . 150°C . 135°D . 90°6. (2分)如图,AB是圆锥的母线,BC为底面直径,已知BC=6cm,圆锥的面积为15πcm2 ,则sin∠ABC的值为()A .B .C .D .7. (2分)意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,……,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如下图),再分别依次从左到右取2个,3个,4个,5个正方形拼成如下长方形并记为①,②,③,④,相应长方形的周长如下表所示:若按此规律继续作长方形,则序号为⑧的长方形周长是()A . 288B . 110C . 1288. (2分)已知如图,菱形ABCD四个顶点都在坐标轴上,对角线AC、BD交于原点O,DF垂直AB交AC于点G,反比例函数,经过线段DC的中点E,若BD=4,则AG的长为()A .B . +2C . 2 +1D . +19. (2分)如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC 的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则()A . DE=EBB . DE=EBC . DE=DO10. (2分)如图,从一块直径是1m的圆形铁皮上剪出一个圆心角为90°的扇形,如果将剪下来的扇形围成一个圆锥,圆锥的底面圆的半径是多少?()A .B .C .D .二、填空题 (共6题;共6分)11. (1分)如图1,有一张矩形纸片ABCD,已知AB=10,AD=12,现将纸片进行如下操作:现将纸片沿折痕BF进行折叠,使点A落在BC边上的点E处,点F在AD上(如图2);然后将纸片沿折痕DH进行第二次折叠,使点C落在第一次的折痕BF上的点G处,点H在BC上(如图3),给出四个结论:①AF的长为10;②△BGH的周长为18;③ = ;④GH的长为5,其中正确的结论有________.(写出所有正确结论的番号)12. (1分)如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PB切⊙O于点B,则PB的最小值是________.13. (1分)如图,量角器的直径与直角三角板ABC的斜边及直角三角板ABD的直角边重合于AB,其中量角器0刻度线的端点与点A重合,点P从A处出发沿AD方向以每秒 cm 的速度移动,CP与量角器的半圆弧交于点E,已知AB=10cm,第5秒时,点E 在量角器上对应的读数是________度.14. (1分)若4x﹣1与7﹣2x的值互为相反数,则x=________.15. (1分)圆内接四边形相邻三个内角之比是3:4:6,则该四边形内角中最大度数是________.16. (1分)已知y是x的反比例函数,当x=3时,y=8,则这个函数关系式为________ .三、解答题 (共9题;共92分)17. (20分)按要求解方程(1)x2﹣4x+1=0(配方法)(2)4x2﹣6x﹣3=0(运用公式法)(3)(2x﹣3)2=5(2x﹣3)(分解因式法)(4)(x+8)(x+1)=﹣12(运用适当的方法)18. (5分)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣4),B(3,﹣2),C(6,﹣3).①画出△ABC关于轴对称的△A1B1C1;②以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 ,使△A2B2C2与△A1B1C1的相似比为2:1.19. (5分)在一个不透明的口袋中,装有分别标有数字2,3,4的3个小球(小球除数字不同外,其余都相同),甲、乙两同学玩摸球游戏,游戏规则如下:先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号,将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数,若该两位数能被4整除,则甲胜,否则乙胜,问这个游戏公平吗?请说明理由.20. (10分)如图,正比例函数的图象与反比例函数在第一象限的图象交于点,过点作轴的垂线,垂足为,已知的面积为1.(1)求反比例函数的解析式;(2)如果为反比例函数在第一象限图象上的点(点与点不重合),且点的横坐标为1,在轴上求一点,使最小.21. (15分)为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:(1)在这项调查中,共调查了多少名学生?(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.22. (5分)如图,∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,求线段DF的长度.23. (10分)对于任意实数a,b,定义关于“⊗”的一种运算如下:a⊗b=2a﹣b.例如:5⊗2=2×5﹣2=8,(﹣3)⊗4=2×(﹣3)﹣4=﹣10.(1)若3⊗x=﹣2011,求x的值;(2)若x⊗3<5,求x的取值范围.24. (15分)如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.(1)求证:AC平分∠DAB;(2)探究线段PC,PF之间的大小关系,并加以证明;(3)若tan∠PCB=,BE= ,求PF的长.25. (7分)阅读下面材料:小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D 在BC边上,CD:BD=1:2,AD与BE相交于点P,求的值.(1)小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:的值为________.(2)参考小昊思考问题的方法,解决问题:如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3.①求的值;(3)②若CD=2,则BP=________.参考答案一、单选题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共6题;共6分)11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共9题;共92分)17-1、17-2、17-3、17-4、18-1、19-1、20-1、20-2、21-1、21-2、21-3、22-1、23-1、23-2、24-1、24-2、24-3、25-1、25-2、25-3、。
人教版2020年九年级上学期期末数学试题A卷精编

人教版2020年九年级上学期期末数学试题A卷姓名:________ 班级:________ 成绩:________一、单选题1 . 下列选项的图形是中心对称图形的是()A.B.C.D.2 . 半径为3的圆中,一条弦长为4,则圆心到这条弦的距离是A.3B.4C.D.3 . 如图,三点在边长为1的正方形网格的格点上,则的度数为()A.B.C.D.4 . 关于的方程的两个实数根互为相反数,则的值是()A.B.C.D.5 . 有10名学生的身高如下(单位):160 170 166 165 170 152 159 175 158 160从中任选一名学生,身高不到161的概率是()A.B.C.D.6 . 已知一元二次方程有一个根为-1,则k的值为()A.2B.-2C.4D.-47 . 下列事件是必然事件的是( ) A .抛掷一枚硬币四次,有两次正面朝上 B .射击运动员射击一次,命中靶心 C .随意翻到一本书的某页,这页的页码是奇数 D .方程必有实数根 8 . 在平面直角坐标系中,抛物线y=-(x+1)2-的顶点是( )A .(-1,-)B .(-1,)C .(1,-)D .(1,)9 . 对抛物线y=-x2+2x -3而言,下列结论正确的是( )A .与x 轴有两个交点B .开口向上C .与y 轴交点坐标是(0,3)D .顶点坐标是(1,2)10 . 如图,以点A (1,)为圆心的⊙A 交y 轴正半轴于B ,C 两点,且OC=+1,点D 是⊙A 上第一象限内的一点,连接OD 、CD .若OD 与⊙A 相切,则CD 的长为( )A .﹣1B .2C .2D. +1 二、填空题11 . 一个正n 边形的每一个内角都是140°,则n =______.12 . 已知,抛物线的部分图象如图,则下列说法:①对称轴是直线;②当时,;③;④方程无实数根,其中正确的有________.13 . 半径为,圆心角为的扇形面积是________(结果保留).14 . 将方程 3x(x-1)= 2 x 2 - x +1 化为一般形式为________________.15 . 如图,将△OAB绕点O按逆时针方面旋转至△OA′B′,使点B恰好落在边A′B′上.已知AB=4cm,BB′=1cm,则A′B长是______cm.三、解答题16 . 在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CA.(1)求证:Rt△ABE≌Rt△CBF;(2)若∠CAE=60°,求∠ACF的度数.17 . 如图,⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BA.(1)由AB,BD,围成的阴影部分的面积是;(2)求线段DE的长.18 . 嘉琪同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的□ABCD,并写出了如下尚不完整的已知和求证.已知:如图,在四边形ABCD中,BC=AD,AB= .求证:四边形ABCD是四边形.(1)补全已知和求证(在方框中填空);(2)嘉琪同学想利用三角形全等,依据“两组对边分别平行的四边形是平行四边形”来证明.请你按她的想法完成证明过程.19 . 盒中有若干枚黑球和白球,这些球除颜色外无其他差别,现让学生进行摸球试验:每次摸出一个球,记下颜色后放回摇匀,重复进行这样的试验得到以下数据:摸棋的次数n1002003005008001000摸到黑棋的次数m38791211963223980.3800.3950.4030.3920.4030.398摸到黑棋的频率(精确到0.001)(1)根据表中数据估计,从盒中摸出一个球是白球的概率是_____(精确到0.01);(2)若盒中黑球与白球共有5枚,某同学连续不放回地摸出两个球,用树状图或表格计算这两个球颜色不同的概率.20 . 解方程(1)2(x+1)2﹣8=0;(2)5x(x﹣3)=6﹣2x.21 . 由于提倡环保节能,自行车已成为市民日常出行的主要工具之一,据某自行车经销店4至6月份统计,某品牌自行车4月份销售200辆,6月份销售338辆,求该品牌自行车销售量的月平均增长率.22 . 在平面直角坐标系中有,为原点,,,将此三角形绕点顺时针旋转得到,抛物线过三点.(1)求此抛物线的解析式及顶点的坐标;(2)直线与抛物线交于两点,若,求的值;(3)抛物线的对称轴上是否存在一点使得为直角三角形.参考答案一、单选题1、2、3、4、5、6、7、8、9、10、二、填空题1、2、3、4、5、三、解答题1、2、3、4、5、6、7、。
陕西人教版七校2020届九年级上学期数学期末联考试卷A卷

陕西人教版七校2020届九年级上学期数学期末联考试卷A卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)在方程x+=2,(3-x)(2+x)=4,x2+x=y,2x-x2=x3中,一元二次方程有()A . 0个B . 1个C . 2个D . 3个2. (2分) (2019九上·利辛月考) 下列函数中,y是x的二次函数的是()A . y=x2-x(x+2)B . y=x2-C . x=y2D . y=(x-1)(x+3)3. (2分) (2018九上·淮阳期中) 关于x的一元二次方程(m-2)x2+(2m+1)x+m -2=0有两个不相等的正实数根,则m的取值范围是()A . m>B . m>且m≠2C . -<m<2D . <m<24. (2分)(2018·象山模拟) 在同一平面直角坐标系内,将函数y=2x2+4x+1的图象沿x轴方向向右平移2个单位长度后再沿y轴向下平移1个单位长度,得到图象的顶点坐标是()A . (﹣1,1)B . (1,﹣2)C . (2,﹣2)D . (1,﹣1)5. (2分) (2018九上·沈丘期末) 二次函数y=ax2+bx+c(a≠0),自变量x与函数y 的对应值如下表:则下列说法正确的是()x…﹣5﹣4﹣3﹣2﹣10…y… 4.90.06﹣2﹣20.06 4.9…A . 抛物线的开口向下B . 当x>﹣3时,y随x的增大而增大C . 二次函数的最大值是6D . 抛物线的对称轴是x=﹣6. (2分) (2019七上·昭通期末) 一元一次方程3 +7=32-2 的解是()A . 1B . 2C . 5D . 67. (2分) (2018九上·江海期末) 用配方法解方程,配方后得到的方程为()A .B .C .D .8. (2分) (2018九上·下城期中) 如图是抛物线y=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),有下列结论:①2a+b=0,②abc >0;③方程ax2+bx+c=3有两个相等的实数根,④当y<0时,﹣2<x<4,其中正确的是()A . ②③B . ①③C . ①③④D . ①②③④9. (2分)(2019·秀洲模拟) 如图,已知二次函数的图像与正比例函数的图像交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2 ,则x的取值范围是()A . 0<x<2B . 0<x<3C . 2<x<3D . x<0或x>310. (2分) (2019九上·贾汪月考) 某工厂一月份的产值是100万元,之后每月产值的平均增长率是x,已知第一季度的总产值是331万元,为了求出x,下列方程正确的是()A . 100(x+1)=331B . 100(x+1) ²=331C . 100+100(x+1)²=331D . 100+100(x+1)+100(x+1)²=33111. (2分) (2018九上·惠阳期中) 将抛物线y=3x2向左平移2个单位,再向下平移1个单位,所得抛物线为()A . y=3(x+2)2﹣1B . y=3(x﹣2)2+1C . y=3(x﹣2)2﹣1D . y=3(x+2)2+112. (2分)已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①a bc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2 .其中正确的结论有()A . 4个B . 3个C . 2个D . 1个二、填空题 (共6题;共6分)13. (1分)(2019·松北模拟) 已知抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,该抛物线与x轴的一个交点为P(4,0),则它与x轴的另一个交点Q的坐标是________,4a﹣2b+c的值为________.14. (1分) (2017九上·淅川期中) 抛物线的顶点关于x轴对称的点的坐标为________.15. (1分) (2018八上·武昌期中) 小华要从长度分别为5cm,6cm,11cm,16cm的四根小木棒中选出三根摆成一个三角形,那么他选的三根木棒形成的三角形的周长为________cm.16. (1分)在平面直角坐标系中,点A、B、C的坐标分别为(0,1)、(4,2)、(2,6).如果P(x,y)是△ABC围成的区域(含边界)上的点,那么当w=xy取得最大值时,点P的坐标是________.17. (1分) (2018九上·松原月考) 如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1=-1,x2=3;③a+b+c>0;④当x>1时,y随x的增大而增大.正确的有:________.18. (1分)(2019·河池模拟) 抛物线的部分图象如图所示,与轴的一个交点坐标为 ,抛物线的对称轴是直线 ,下列结论:① ;② ;③方程有两个不相等的实数根;④抛物线与轴的另一个交点坐标为 ,其中正确的结论有________.三、解答题 (共8题;共70分)19. (10分) (2019九上·三门期末) 解方程:(1) x2﹣9=0(2) x2+8x﹣20=020. (5分) (2017九上·新乡期中) 已知,二次函数的图象的顶点是(4,﹣12),且过(2,0),求此二次函数的解析式.21. (5分)(2019·福田模拟) 先化简,再求值:(1+ )÷ ,其中x是不等式组的整数解.22. (10分) (2019九上·绍兴月考) 如图所示,抛物线y=x2-2x-3与x轴交于A,B两点(A点在B点左侧),与y轴交于点C。
人教版2020届九年级上学期数学期末考试试卷A卷

人教版2020届九年级上学期数学期末考试试卷A卷姓名:________ 班级:________ 成绩:________一、单选题 (共6题;共12分)1. (2分)一元二次方程(x-9)2=0的解是()A . x1=x2=9B . x1=x2=3C . x1=9,x2=-9D . x1=3,x2=-32. (2分)圆心在原点O ,半径为5的⊙O ,则点P(-3,4)与⊙O的位置关系是().A . 在⊙0上B . 在⊙0内C . 在⊙O外D . 不能确定3. (2分)下列特征量不能反映一组数据集中趋势的是()A . 众数B . 中位数C . 方差D . 平均数4. (2分)已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的近似解为()A . x1≈﹣2.1,x2≈0.1B . x1≈﹣2.5,x2≈0.5C . x1≈﹣2.9,x2≈0.9D . x1≈﹣3,x2≈15. (2分)在反比例函数y= 中,当x>0时,y随x的增大而增大,则二次函数y=mx2+mx 的图象大致是图中的()A .B .C .D .6. (2分)如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC,若∠CAB=22.5°,CD=8cm,则⊙O的半径为()A . 8cmB . 4cmC . 4 cmD . 5cm二、填空题 (共10题;共10分)7. (1分)已知,且3a-2b+c=9,则2a+4b-3c=________.8. (1分)某校九年级安全疏散演习中,各班疏散的时间分别是3分钟,2分40秒,3分20秒,3分30秒,2分45秒.这次演习中,疏散时间的极差为________ 秒.9. (1分)已知:a2﹣4ab+5b2﹣2b+1=0,则以a,b为根的一元二次方程为________.10. (1分)某种植物的主干长出若干数目的支干又长出同样数目的小分支,主干、支干和小分支的总数是91.设每个支干长出x个小分支,则可得方程为________.11. (1分)在平面直角坐标系中,把抛物线y=﹣x2+1向上平移3个单位,再向左平移1个单位,则所得抛物线的解析式是________ .12. (1分)圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为________cm2 .13. (1分)在同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距离.如图,在一个路口,一辆长为10m的大巴车遇红灯后停在距交通信号灯20m的停止线处,小张驾驶一辆小轿车跟随大巴车行驶.设小张距大巴车尾x m,若大巴车车顶高于小张的水平视线0.8m,红灯下沿高于小张的水平视线3.2m,若小张能看到整个红灯,则x的最小值为________.14. (1分)抛物线y=2x2+3x+k﹣2经过点(﹣1,0),那么k=________.15. (1分)如图,平行四边形ABCD中,E是边AB的中点,F是对角线BD的中点,若EF=5,则AD=________.16. (1分)如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上一动点(不与B,C 重合),E是AC上一个动点,始终保持∠ADE=∠B,则当△DCE为直角三角形时,BD的长为________.三、解答题 (共11题;共126分)17. (5分)解方程:2(3x﹣1)2=8.18. (10分)请选择适当的方法解下列一元二次方程:(1)(2)19. (10分)今年上半年,住房和城乡建设等9部门决定在全国地级以上城市全面启动生活垃分类工作.圾分类有利于对垃圾进行分流处理,势在必行.为了了解同学们对垃圾分类相关知识的掌握情况,增强同学们的环保意识,西街中学团委对七年级一,二两班各69名学生进行了垃极分类相关知识的测试,并分别抽取了15份成绩,整理分析过程如下,请补充完整.(收集数据)一班15名学生测试成绩统计如下:(满分100分)68,72,89,85,82,85,74,92,80,85,78,85,69,76,80二班15名学生测试成绩统计如下:(满分100分)86,89,83,76,73,78,67,80,80,79,80,84,82,80,83(1)【整理数据】按如下分数段整理、描述这两组样本数据在表中,a=________,b=________.(2)【分析数据】份两组样本数据的平均数、众数、中位数、方差如下表所示:在表中:x=________,y=________.(3)若规定得分在80分及以上(含80分)为合格,请估计二班69名学生中垃极分类及投放相关知识合格的学生有________人.(4)你认为哪个班的学生掌握垃圾分类相关知识的整体水平较好,说明理由.20. (3分)一枚普通的正方体骰子,每个面上分别标有1,2,3,4,5,6,在抛掷一枚普通的正方体骰子的过程中,请用语言描述:(1)一件不可能事件:________(2)一件必然事件:________(3)一件不确定事件:________.21. (10分)如图,已知AB是⊙O的直径,点C是AB延长线上的一点,点D在⊙O上且AD=CD,∠C=30°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版七校2020届九年级上学期数学期末联考试卷A卷
姓名:________ 班级:________ 成绩:________
一、单选题 (共12题;共24分)
1. (2分) (2017九上·武邑月考) 下列方程是关于x的一元二次方程的是()
A . ax2+bx+c=0
B . +x=2
C . x2+2x=x2﹣1
D . 3x2+1=2x+2
2. (2分)下列函数中,属于二次函数的是()
A . y=
B . y=2(x+1)(x﹣3)
C . y=3x﹣2
D . y=
3. (2分) (2019八下·岑溪期末) 已知关于x的一元二次方程x2+2x+k=0有实数根,则k的取值范围是()
A . k≤1
B . k≥1
C . k<1
D . k>1
4. (2分) (2019九上·龙湖期末) 将抛物线向左平移2单位,再向上平移3个单位,则所得的抛物线解析式为()
A .
B .
C .
D .
5. (2分) (2019九上·湖州月考) 如图,抛物线y=-x2+mx的对称轴为直线x=2,若关于x的-元二次方程-x2+mx-t=0 (t为实数)在l<x<3的范围内有解,则t的取值范围是()
A . -5<t≤4
B . 3<t≤4
C . -5<t<3
D . t>-5
6. (2分) (2018七上·天门期末) 若方程2x+1=﹣1的解是关于x的方程1﹣2(x﹣a)=2的解,则a的值为()
A . ﹣1
B . 1
C . ﹣
D . ﹣
7. (2分)把方程x2﹣4x+1=0配方,化为(x+m)2=n的形式应为()
A . (x﹣2)2=﹣3
B . (x﹣2)2=3
C . (x+2)2=﹣3
D . (x+2)2=3
8. (2分) (2017九上·宜昌期中) 若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是()
A . 0<k<4
B . -3<k<1
C . k<-3或k>1
D . k<4
9. (2分) (2018九上·温州开学考) 二次函数y=a +bx+c(a≠0)的图象如图所示,当y>0时,自变量x的取值范是()
A . x<-1
B . x>3
C . x<-1或x>3
D . -1<x<3
10. (2分) (2018九上·钦州期末) 某制药厂2014年正产甲种药品的成本是500元/kg,随着生产技术的进步,2016年生产甲种药品的成本是320元/kg,设该药厂2014﹣2016年生产甲种药品成本的年均下降率为x,则根据题意可列方程为()
A . 500(1﹣x)2=320
B . 500(1+x)2=320
C . 320(1﹣x)2=500
D . 3320(1+x)2=500
11. (2分) (2019九上·中山期末) 抛物线y=3x2向右平移一个单位得到的抛物线是()
A . y=3x2+1
B . y=3x2﹣1
C . y=3(x+1)2
D . y=3(x﹣1)2
12. (2分)(2019·河池) 如图,抛物线y=ax2+bx+c的对称轴为直线x=1,则下列结
论中,错误的是()
A .
B .
C .
D .
二、填空题 (共6题;共6分)
13. (1分) (2018九上·佳木斯期中) 设点(﹣1,y1),(2,y2),(3,y3)是抛物线y=﹣x2+a上的三点,则y1、y2、y3的从小到大排列为________.
14. (1分) (2018九上·宁县期中) 点 A 、B 在二次函数
的图像上,则与的大小关系为 ________ (填“ ).
15. (1分) (2019九上·兴化月考) 一个三角形的两边长为2和9,第三边长是方程x2-14x+48=0的一个根,则三角形的周长为________.
16. (1分)(2019·山西模拟) 如图,在平面直角坐标系中,A(-2,-1),B(-1,-1),若抛物线与线段AB有交点,则的取值范围是________.
17. (1分) (2017九上·淅川期中) 抛物线的顶点关于x轴对称的点的坐标为________.
18. (1分)(2019·河池模拟) 抛物线的部分图象如图所示,与轴的一个交点坐标为 ,抛物线的对称轴是直线 ,下列结论:① ;② ;③方程有两个不相等的实数根;④抛物线与轴的另一个交点坐标为 ,其中正确的结论有________.
三、解答题 (共8题;共70分)
19. (10分) (2019九上·武汉月考) 解方程:
(1) x2-4x-7=0(公式法)
(2) x2-4x-12=0(因式分解法)
20. (5分) (2018九上·瑶海期中) 已知抛物线的图像经过点
和 .求这个二次函数的关系式.
21. (5分)先化简,÷(﹣),再从﹣2<x<3中选一个合适的整数代入求值.
22. (10分)(2019·怀化) 如图,在直角坐标系中有,为坐标原点,
,将此三角形绕原点顺时针旋转,得到,二次函数的图象刚好经过三点.
(1)求二次函数的解析式及顶点的坐标;
(2)过定点的直线与二次函数图象相交于两点.
①若,求的值;
②证明:无论为何值,恒为直角三角形;
③当直线绕着定点旋转时,外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.
23. (10分) (2017九上·潜江期中) 已知关于x的一元二次方程x2-6x+m+4=0有两个实数根x1 , x2 .
(1)求m的取值范围;
(2)若x1,x2满足3x1=|x2|+2,求m的值.
24. (5分) (2018九上·遵义月考) 若一个等腰三角形的三边长均满足方程x2﹣9x+18=0,求此三角形的周长.
25. (10分) (2019九上·长白期中) 某商场销售一种品牌羽绒服和防寒服,其中羽绒服的售价是防寒服售价的5倍还多100元,2014年1月份(春节前期)共销售500件,羽绒服与防寒服销量之比是4:1,销售总收入为58.6万元.
(1)求羽绒服和防寒服的售价;
(2)春节后销售进入淡季,2014年2月份羽绒服销量下滑了6m%,售价下滑了4m%,防寒服销量和售价都维持不变,结果销售总收入下降为16.04万元,求m的值.
26. (15分) (2019九上·吉林月考) 如图,在平面直角坐标系中,抛物线y=ax2-2x+
(a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M,P为抛物线的顶点,直线OP交直线AM于点B,且M为线段AB的中点。
(1)求抛物线的对称轴及点M坐标
(2)求直线OP的解析式
(3)求抛物线的解析式。
参考答案
一、单选题 (共12题;共24分)
1、答案:略
2、答案:略
3、答案:略
4、答案:略
5、答案:略
6、答案:略
7、答案:略
8、答案:略
9、答案:略
10、答案:略
11、答案:略
12、答案:略
二、填空题 (共6题;共6分)
13、答案:略
14、答案:略
15、答案:略
16、答案:略
17、答案:略
18、答案:略
三、解答题 (共8题;共70分)
19、答案:略
20、答案:略
21、答案:略
22、答案:略
23、答案:略
24、答案:略
25、答案:略
26、答案:略。
