量子化学基础
计算化学3-量子化学基础-分子轨道理论与分子轨道法

配合物 1
反应坐标
配合物 2
AB····C
A + BC
AB + C
势能面和反应途径
二维等能量线图
(A⋅⋅⋅⋅ ⋅⋅⋅⋅ ⋅⋅⋅⋅B⋅⋅⋅⋅ ⋅⋅⋅⋅ ⋅⋅⋅⋅C)
T
二维势能曲面
鞍点
势能面无法实验测定。 由量子化学计算给出
如何进行反应途径和过渡态搜索? 如何进行反应途径和过渡态搜索?
反应活化能计算精度取决于
3、分子轨道由原子轨道线性组合而成 在分子中电子的空间运动状态可用相应的分子轨道波 函数ψ来描述 分子轨道可以由分子中原子轨道波函数的线性组合 (linear combination of atomic orbitals,LCAO) 而得到
ψ = a1φ1 + a 2φ 2 + ..... + a n φ n =
2、单电子波函数的近似 单电子近似假定n个电子的运动是彼此独立的,每 一个电子是在m个核和n-1个电子所组成的场中独 立运动,与其它电子无关 若其状态用ψ i来表示,则分子的状态为各单电子 波函数的乘积
ψ =ψ1ψ 2ψ 3 Lψ n
E = E1 + E2 + ... + En
单电子波函数就是分子轨道
维生素C分子的 电子密度与静电势
The electron density around the vitamin C molecule. The colors show the electrostatic potential with the negative areas shaded in red and the positive in blue
∑a φ
k =1 k
n
量子化学第二章 量子力学基础

都是能量算符的本征值为-3.4 eV 的本征函数,
则这些本征函数是简并的。
27
量子化学 第二章
5. 线性算符
若
(a, b为任意常数),
则 为线性算符 。
例:
、
、乘实函数 、积分运算 等
,+c
注:若 和 为线性算符,
则
(c1和c2为常数)为线性算符。
28
例1:
量子化学 第二章
线性算符
量子化学 第二章
1900年,普朗克为 了解释黑体辐射现象,引 入一个“离经叛道”的假 设: 黑体吸收或发射辐射 的能量必须是不连续的. 这一重要事件后来被认为 是量子革命的开端.普朗克 为此获1918年诺贝尔物理 学奖.
4
量子化学 第二章
普朗克(Plank)最先提出了能量量子的概念, 指出
黑体是由谐振子构成, 能量为nh (n=1,2,…3, 为
1929年,德布罗意获 诺贝尔物理学奖.
9
量子化学 第二章
1924年,年轻的法国科学家德布罗意受爱因 斯坦“光子学说”的启发,大胆预言实物微粒也有
波动性, 即一个能量为E、动量为 p 的质点同时也
具有波的性质, 其波长 由动量 p 确定, 频率 则
由能量 E 确定 。 = h h p m
= E h
不是本征方程 ,为本征方程
23
量子化学 第二章
例4:假设体系的状态波函数为 动能算符 试验证该函数是否为动能算符的本征函数?
证明:
结论:该函数是动能算符的本征函数。
24
量子化学 第二章
Notes: ①在状态下,对力学量Q,若存在本征方程 这表明状态下,力学量Q有确定值q。这就是本征方 程的量子力学意义。
化学软件基础-第4章 第3节-量子化学

化学软件基础第四章第三节量子化学Quantum Chemistry卞希慧,田野2015年5月10号目录一:量子化学产生历程 (1)二:量子化学研究内容 (3)三:量子化学计算方法与理论 (3)1:从头算方法 (3)2:半经验法 (4)3:密度泛函理论 (5)4:微扰理论 (5)四:量子化学计算软件 (6)1:建模软件 (6)1)Chemoffice (6)2)GaussView (6)2:计算软件 (7)1)Gaussian (7)2)Materials Studio (7)3)VASP (8)4)Gamess-US (8)5)CASTEP (9)6)ATK (9)五:量子化学的应用 (10)1:在材料科学中的应用 (10)1)在建筑材料方面的应用 (10)2)在金属及合金材料方面的应用 (11)2:在能源研究中的应用 (11)1)在煤裂解的反应机理和动力学性质方面的应用 (11)2)在锂离子电池研究中的应用 (12)3:在生物大分子体系研究中的应用 (12)一:量子化学的产生历程1900年,普朗克提出辐射量子假说,假定电磁场和物质交换能量是以间断的形式(能量子)实现的,能量子的大小同辐射频率成正比,比例常数称为普朗克常数,从而得出黑体辐射能量分布公式,成功地解释了黑体辐射现象。
1905年,爱因斯坦引进光量子(光子)的概念,并给出了光子的能量、动量与辐射的频率和波长的关系,成功地解释了光电效应。
其后,他又提出固体的振动能量也是量子化的,从而解释了低温下固体比热问题。
1913年,玻尔在卢瑟福有核原子模型的基础上建立起原子的量子理论。
按照这个理论,原子中的电子只能在分立的轨道上运动,原子具有确定的能量,它所处的这种状态叫“定态”,而且原子只有从一个定态到另一个定态,才能吸收或辐射能量这个理论虽然有许多成功之处,但对于进一步解释实验现象还有许多困难。
在人们认识到光具有波动和微粒的二象性之后,为了解释一些经典理论无法解释的现象,法国物理学家德布罗意于1923年提出微观粒子具有波粒二象性的假说。
理论化学的基础理论

理论化学的基础理论理论化学是化学的一种重要分支,它研究分子和原子之间的相互作用及其转化,是现代化学研究的基础。
其基础理论包括量子化学、统计力学、分子轨道理论、原子轨道理论等等。
今天,我们就来探究一下理论化学的基础理论。
量子化学是理论化学研究的核心内容,它是量子力学的应用。
量子力学是描述微观世界运动状态的一种物理学理论,研究微观粒子的运动和相互作用。
量子力学中的波函数是描述微观物体运动状态的主要工具,而量子化学则是将波函数理解为电子云,并用它来描述原子和分子结构和性质。
量子化学是非常复杂的,需要高深的数学和理论物理学基础。
但它对于化学的研究和应用有着重要的意义。
在量子化学的基础上,统计力学也是理论化学的重要组成部分。
统计力学是研究物体宏观状态与微观粒子状态之间的关系和转化规律的学问。
它以能量和熵为中心,能够描述物体的微观状态和宏观状态之间的转化过程,从而解释了许多自然现象和化学现象。
在化学中,统计力学理论被广泛应用于理解化学反应动力学和平衡热力学等问题,为化学分析和应用提供了一个统一的基础。
分子轨道理论和原子轨道理论是理论化学中必须了解的两个基础理论。
原子轨道理论主要是研究原子的电子结构和能级,分子轨道理论则是将原子之间的相互作用考虑在内,以描述分子的电子结构、电荷分布和反应能力等性质。
这两个理论的提出奠定了理论化学研究的基础。
除了以上提到的基础理论外,还有许多在化学研究中被广泛应用的理论,如化学键论、配位化学、超分子化学等等。
这些理论有各自的研究方向和应用领域,在实际应用中经常被用于化学设计、分析和生产制造等方面。
理论化学是一门非常重要的学科,它对化学科学的发展和应用有着重要的推动作用。
基础理论的深入探究和研究对化学科学的发展有着重要的推动作用,能够为人类生产、生活和环保等方面提供新的思路和解决方案。
相信随着科技的不断进步,理论化学将会得到更为深入的研究和应用。
量子化学群论基础PPT培训课件

分子的振动与群论
总结词
群论在分子的振动分析中也有重要应用,通过群论可以描述分子的振动模式和频率,进而研究分子的 热力学和反应动力学性质。
详细描述
分子的振动是指分子内部运动模式的总称,包括伸缩振动、弯曲振动、摇摆振动等。群论可以描述分 子的振动模式和频率,将分子振动分类,进而研究分子的热力学和反应动力学性质。此外,群论还可 以用于研究分子的振动光谱和红外光谱等实验现象。
到表示的不可约性。
无限群的表示
03
无限群的表示可以通过函数来表示,通过傅里叶变换可以得到
函数的展开式和表示的不可约性。
03
量子化学中的群论应用
分子对称性与群论
总结词
分子对称性是群论在量子化学中应用的重要领域之一,通过群论可以描述分子的对称性质和对称操作,进而研究 分子的结构和性质。
详细描述
分子对称性是指分子在空间中的对称性质,包括对称面、对称轴、对称中心等。群论是研究对称性的数学工具, 通过群论可以描述分子的对称操作和对称元素,将分子对称性分类,进而研究分子的电子结构和化学键等性质。
分子光谱的解析
分子光谱的解析是群论在量子化学中应用的一个重要方面,通 过群论可以确定分子光谱的能级和光谱项,从而解析出分子的
结构和性质。
群表示理论
群表示的定义
01
群表示是将群元素与线性空间中的向量对应起来的一种方法,
通过群的表示可以研究群的性质和结构。
有限群的表示
02
有限群的表示可以通过矩阵来表示,通过计算矩阵的迹可以得
量子化学群论基础ppt培训课件
目录
• 量子化学简介 • 群论基础 • 量子化学中的群论应用 • 分子光谱与群论 • 量子化学中的群论计算方法 • 总结与展望
结构化学 第一章 量子化学基础 习题

1029
y y y 设 体 系 处 在 状 态 =c1 211+ c2 210 中 , 角 动 量 M2 和 Mz 有 无 定 值 。其值为多少?若无 ,
则求其平均值。
1030
h¶
试 求 动 量 算 符 pˆ x=
的 本 征 函 数 (不 需 归 一 化 )。
i2p ¶x
1031
y 下 列 说 法 对 否 :” =cos x, px 有确 定 值 , p2x 没 有 确 定 值,只有平均值 。” ---------- ( )
(A) 16.5 × 10 -24? J (B) 9.5
× 10 -7 J (C) 1.9
× 10 (E) 1.75 × 10 -50? J
1039 一个在一维势箱中运动的粒子,
(1) 其 能 量 随 着 量 子 数 n 的 增 大 :------------------------ ( ) (A) 越 来 越 小 (B) 越 来 越 大 (C) 不变 (2) 其 能 级 差 En+1-En 随 着 势 箱 长 度 的 增大 : -------------------( ) (A) 越 来 越 小 (B) 越 来 越 大 (C) 不变
(A)
Aˆ U=λU, λ=常数
(B)
Bˆ U=U*
(C)
Cˆ U=U2
(D)
Dˆ U = dU
dx
(E)
Eˆ U=1/ U
1026 物 理 量 xp y- ypx
1027
_____ 。
某 粒 子 的 运 动 状 态 可 用波 函 数y =Ne-ix 来表 示 , 求 其 动 量 算符 pˆ x 的 本 征 值 。
1013
测 不 准 原 理 的 另一 种 形 式 为 Δ E·Δt≥h/2 π。当一个电子从 高能级向低能级跃迁 时,
量子化学概述

量子化学概述
标题:量子化学概述
正文:
量子化学是一门研究原子和分子的物理性质及其变化的学科。
它基于量子力学的原理,通过数学计算和理论模型来描述和解释原子与分子的结构、性质和反应。
首先,量子化学研究的核心是原子和分子的波函数。
根据薛定谔方程,波函数可以描述系统的状态和性质。
通过求解薛定谔方程,我们可以得到原子和分子的能量、振动频率、轨道结构等信息。
其次,量子化学研究的一个重要应用领域是分子结构预测。
通过计算,可以确定分子的几何构型、键长和键角等。
这对于理解分子的稳定性和反应活性具有重要意义。
同时,量子化学还可以预测分子的光谱性质,如吸收光谱和拉曼光谱,进一步揭示物质的结构特征。
此外,量子化学也在解释化学反应机制、催化过程和原子与分子间的相互作用方面发挥重要作用。
通过量子化学计算,可以研究反应的速率常数、中间体的形成和反应物的能垒等。
这对于设计新的催化剂和理解化学反应动力学有着重要意义。
最后,量子化学还与实验研究相结合,通过理论模拟和实验验证相互印证,共同推动科学的进展。
量子化学的发展也为材料科学、生物化学和药物设计等领域提供了理论基础和研究方法。
总结起来,量子化学是一门基于量子力学原理的学科,通过数学模型和计算方法研究原子和分子的性质和反应。
它在预测分子结构、解释化学反应机制和催化过程等方面发挥着重要作用,为化学和相关领域的研究提供了关键的理论支持。
《量子化学基础》习题课
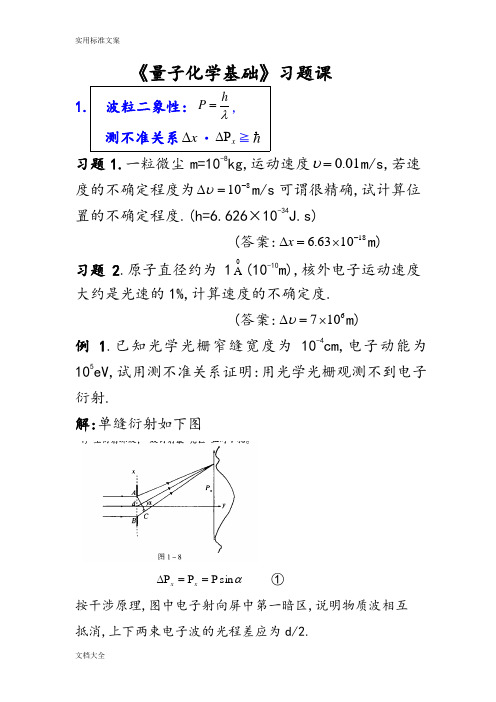
《量子化学基础》习题课 1. 波粒二象性: λhP =,测不准关系x ∆·x ∆P ≧习题1.一粒微尘m=10-8kg,运动速度01.0=υm/s,若速度的不确定程度为810-=∆υm/s 可谓很精确,试计算位置的不确定程度.(h=6.626×10-34J.s)(答案:181063.6-⨯=∆x m)习题2.原子直径约为10A (10-10m),核外电子运动速度大约是光速的1%,计算速度的不确定度.(答案:6107⨯=∆υm)例1.已知光学光栅窄缝宽度为10-4cm,电子动能为105eV,试用测不准关系证明:用光学光栅观测不到电子衍射.解:单缝衍射如下图αsin P =P =∆P x x ①按干涉原理,图中电子射向屏中第一暗区,说明物质波相互抵消,上下两束电子波的光程差应为d/2.λαα=⋅∆=⋅=sin sin x d BC ②这里410-=∆=x d cm,meV h mE h h 22==P =λ (=m 9.11×10-31kg ;=e 1.602×10-19C) 51025.1225.12==V λ=3.87×10-12m 661210101087.3sin ---=⨯==m m d λα 0≈α 证毕. 习题3.计算动能为3000eV 的电子的de Brogle 波长(1eV=1.602×10-19J, V 3000C10602.1J 10602.130001919=⨯⨯⨯=--V ) (答案: 0A 2237.0300025.1225.12===V λ.) 2 .一维势箱: 2228ml h n E =,),2,1( =nx ln C x πsin )(2=ψ 习题4.计算箱宽为5×10-10m 的一维势箱中粒子n=1、2时的能量.及粒子从n=2跃迁到n=1时辐射的波长. (答案:E 1=2.41×10-19J,E 2=9.64×10-19J191023.7-⨯=∆E J 71075.2-⨯=λm) 习题 5.可将原子中的电子粗略的模拟为一维箱中粒子,箱的宽度为原子的尺度.计算在长度10A 的箱中电子两个最低能级之差(eV)和在此两能级间跃迁的光子波长(cm). (答案:21013.1⨯=∆E eV, 8101.1-⨯=λm)例2. 丁二烯(H 2C=CH-CH=CH 2)4个π电子(P z 电子),可以近似地看作长度为大Π键键长(已知:双键长035.1A 、单键长054.1A )的一维势箱中的4个粒子的运动.体系的基态向第一激发态的跃迁为:_______1_______2___________3___________4↑↓=↑↓===n n n n 1_______2________3________4___________=↑↓=↑=↑=n n n n求:体系基态向第一激发态的跃迁能(cm -1).解.箱长:m A A l 10001078.554.1235.12-⨯=⨯+⨯=.)23(888222222222223-=-=∆l m h l m h n l m h n E e e e 21031234)1078.5(1011.985)10626.6(m kg s J ---⨯⨯⨯⨯⨯⋅⨯=J 191002.9-⨯=.14834191054.4/10310626.61002.9----⨯=⨯⨯⋅⨯⨯=∆=cm s m s J J hc E ν 例3.有一个量子数为n 在长度为l 的一维箱中运动的粒子(1)计算在箱的左端41区内找到粒子的几率.(2)n 为何值时该几率最大?(3)计算当n →∞时该几率的极限?解: 2sin 2141)sin 2(2410πππn n dx x l n l P -==⎰⎪⎩⎪⎨⎧==-==8,6,4,2,015,11,7,3,113,9,5,1,12sin n n n n 当当当π 即,n=3时,P 最大.π6141max +=P . 41)2sin 2141(lim =-∞→ππn n n (该式说明:当n →∞时量子力学问题还原为经典(力学)问题,因为经典力学处理一维箱问题在左端1/4处的几率正是1/4.)习题6.有一质量为1g 的小球,在长为10cm 的一维箱中运动小球速度0.1cm/s,试求小球的量子数n 是多少 ? (答案:n=3.018×1026) 3. 一位谐振子:m k πν21=)21(+=υνh E ( 3,2,1,0=υ) 习题7.HI 近红外光谱的基本振动频率22300=-ν.1cm -1,求HI 键的弹力常数k . (答案:k =2.93×105 D.cm -1) 习题8.已知H 2和Cl 2的基本振动频率分别为24.4395)(20=H νcm -1,9.564)(20=Cl νcm -1,求它们的零点能. (答案:E 0(H 2)=6.28kg/mol, E 0(Cl 2)=0.807kg/mol) 例 4.利用简谐振动公式:)sin()(φω+=t C t x ,证明一维谐振子的总能量是常数:221kC E =解:)(sin 21)(cos 2122222φωφωω+++=+=t kC t C m V T E m k =2ω ,带入上式,得: 221kC E =. 习题9.若H 35Cl 基本振动频率13010667.8⨯=νs -1,试求H 37Cl 的基本振动频率,设它们键的力常数相同.(答案:8.660×1013s -1) 4. 刚性转子:)1(22+=l l IE ( 3,2,1,0=l ) )1(2)(+=l B l ν (式中Ic hB 28π=) 例5.由HCl 的远红外光谱数据得知HCl 的转动能级相邻谱线间距为20.74cm -1,求HCl 分子的键长r.解: c r hIc h B 222442μππν===∆24231063.11002.6)45.35008.1(45.35008.1-⨯=⨯+⨯=+⋅=Cl H Cl H m m m m μg/mol 211024227212)2/74.20(1031063.1)1416.3(810626.6)8(][⨯⨯⨯⨯⨯⨯==--cB h r μπ =1.287×10-8cm=1.2870A习题10.从CN 的微波谱知道一系列谱线的间距皆为3.7978cm -1,求该分子的核间距r.(答案:r=1.172×10-10m)习题11.已知CN +的键长是1.290A ,指出CN +微波谱的第一到第四条线的位置.(答案:3.134cm -1,6.268cm -1,9.402cm -1,12.536cm -1 5.算符:),,(t q P F ∧∧其中q i ∂∂-=P ∧与本征函数:∧A )(x f =k )(x f习题12.写出下列物理量的算符:(1)动量P,(2)动量3y p ,(3)x y yp xp -,(4)动能T( 答案(1))(z k y j x i i P ∂∂+∂∂+∂∂-=∧,(2)3333y i P y ∂∂=∧(3))()(x y y x i p y p x L x y z ∂∂-∂∂-=-=∧∧∧ (4) )(22222222z y x m T ∂∂+∂∂+∂∂-=∧) 13.计算算符222kx dx d A -=∧的本征函数2x e α-的本征值(答案:22)24()(222222x x e kx x e kx dx d αααα----=- )14.利用[∧D ,∧x ]=1,(1)计算2)(x D +∧,(2)))((x D x D -+∧∧ (答案:(1)2)(x D +∧1222+++=∧x D x D (2)1))((22--=-+∧∧∧x D x D x D )15.三维箱中粒子的波函数是下列那些算符的本征函数(1)∧x p ,(2)∧2x p ,(3)∧2z p ,(4)∧2x .(答案(2),(3) )6.对易计算以下对易恒等式可方便对易运算:①.],[],[∧∧∧∧-=A B B A②.0],[=∧∧n A A (n=1,2,3…)③.],[],[],[∧∧∧∧∧∧==B A k kB A B kA④],[],[],[∧∧∧∧∧∧∧+=+C A B A C B A⑤ ],[],[],[∧∧∧∧∧∧∧∧∧+=C A B C B A C B A 例6.计算对易子:],[∧x P x ,],[2∧x P x ,],[∧H x ,],[∧∧H P x .解: i i x x i x x i x i x P x x =-=∂∂-=∂∂=∂∂=∧],[],[],[],[ ],[],[],[2∧∧∧∧∧+=x x x x x P x P P P x P xx i i x i i ∂∂⋅+∂∂⋅= x ∂∂=22)](21,[],[)],,(,[],[222∧∧∧∧∧∧++==+=z y x P P P m x T x z y x V T x H x ∧∧=∂∂==x x P mi x m P x m 22],[21 ],[)](,[21],[222V P P P P P m H P x z y x x x ∧∧∧∧∧∧∧+++= x V i V x i V P x ∂∂-=∂∂-==∧],[],[(式中x V f x f V x Vf f x V V x f V x ∂∂=∂∂-∂∂=∂∂-∂∂=∂∂)()(],[)16.计算:],[222c bx ax dx d ++ (答案: ],[222c bx ax dx d ++=dxd b ax a )24(2++. ) 例7.证明:222)(〉〈-〉〈=∆A A A解: 〉〉〈-〈≡≡∆∧222)()(A A A A στψψd A A ⎰〉〈-=∧*2)( τψψτψψτψψτψψd A d A A d A A d A ⎰⎰⎰⎰〉〈+〉〈-〉〈-=*∧*∧*∧*22τψψτψψτψψd A d A A d A A A ⎰⎰⎰*∧*∧*〉〈+〉〈-〉〈-〉〈=22 2222〉〈+〉〈-〉〈-〉〈=A A A A 22〉〈-〉〈=A A 证毕 7. H 原子薛定谔方程的解222204118n R n h e E n -=-=εμ (n=1,2,…),其中22048h e R εμ-=. )()()(,,,θϕθϕψm l l n m l n Y r R r =)()()(,,ϕθm m l l n r R ΦΘ= ϕθim ml na Zr i l l n i i e P e a Zr c C )(cos })({0101--+-=∑= 氢原子波函数受控于三个量子数(m l n ,,)∞=,,2,1 n1,,2,1,0-=n ll m ±±±=,,2,1,0习题17.下列函数(1)2P z ,(2)2P x ,(3)2P 1分别是算符∧H 、∧2L 、∧z L 中哪个的本征函数. (答案:(1)、(3)全是,(2)是∧H 、∧2L 的本征函数) 习题18.对H 原子P 态,测量L Z 的可能值为h 、0、-h,问在下列函数中测量L Z 得到各可能值的几率.(1)Pz 2ψ,(2) Px 2ψ,(3) 12P ψ(答案:(1) 121211210200-⋅+⋅+=ψψψψPz得0值几率为1,得h 、-h 几率为0. (2) 121211*********-++⋅=ψψψψPx 得h 、-h 几率各为21,得0值几率为0.(3) 12P ψ=211ψ,得h 几率为1,其余为0) 例8.已知H 原子)(ϕΦ方程复数解:ϕπϕim m e 21)(=Φ,(1)验证)(ϕm Φ是归一化的.(2)证明)(ϕm Φ是算符ϕ∂∂-=∧ i L z 的本征函数.而)(ϕm Φ线性组合的实函数: ⎪⎪⎩⎪⎪⎨⎧=Φ=Φϕπϕϕπϕm m m msin 1)(cos 1)('`不是∧z L 的本征函数.解:(1)121212020202===ΦΦ=Φ⎰⎰⎰⎰-*ππϕϕπϕπϕπϕϕd d e e d d im im (2) )(21)(ϕπϕϕϕm im m z m e i L Φ±=∂∂-=Φ±∧而 ϕπϕπϕϕm m i m i L m z sin cos 1)( =∂∂-=Φ∧不构成本征方程: )()(ϕϕm m z c L Φ≠Φ∧.例如n=2,l =1的H 原子波函数是p 轨道,有三个状态(m=1,0,-1),其复函数形式为:θθϕψcos )()(0,1,2r r f r = (即:z p p 也是0)ϕθθϕψi e r r f r ±±=sin )()('1,1,2 (即:11-p p 和)其中复函数z p p 等于实函数0,复函数11-p p 和线性组合为实函数y x p p ,,即ϕθθϕϕcos sin )()(sin )(11r R N e e r R N p i i x =+=- ϕθθϕϕsin sin )()(sin )(11r R N e e r R N p i i y =-=- 因此,z p p 和0都是∧z L 的本征函数. 11-p p 和也是∧z L 的本征函数.只有y x p p ,不是∧z L 的本征函数.P 轨道的实函数与复函数形式都是体系的状态函数,但表示图形不一样:例9.对H 原子基态,(1)求2倍玻耳半径之外的电子几率.(2)玻耳半径之内的电子几率. 解:H 原子基态,n=1,0=l ,m=0301,,,1)()()(a r s ml l n m l n eaY r R r -=→=πψθϕθϕψ(1)设P 2为02a 之外的电子几率 ϕθθπτψππd drd re a d P a r a s sin 1122200203021200-⎰⎰⎰⎰==-⎰⎰⎰-=ππϕθθπ2022023sin 10d d dr e r a a r adr e r a a ra 002202304-⎰=ππ利用积分公式][0203020022302)82422(41a a r ara a r ea P ---=--)22(3222b b x b x e dx e x bx bx +-=⎰]4)44448([430303030430a a a a e a +---=- 4131e -= 即: 24.01342==e P(2)设1P 是玻耳半径0a 之内的电子几率,则dr e r a P a r a 02023014-⎰=][00302002230)82422(4a a r a ra a r e a ---=-]4)44242([430303030230a a a a e a +---=-32.0512=-=e例10.已知类氢离子基态波函数 03031a zr s ea z-=πψ,(1) 求半径r 的平均值.(2)r 的最可几值.解:(1)ϕθθπτψψππd drd r ea zd r r a zr ssin 32002030310-∞*⎰⎰⎰⎰==〉〈dr er a za zr 02033034-∞⎰⋅=ππ利用广义积分公式:10!+∞-=⎰n qxn qn dx ex (0,1>->q n )z a a z a z dr e r a z r a zr23)2(!344040303023330=⋅==〉〈⎰∞-(2)径向分布函数: 0223032214)(a zr ser a z r r R D -=⋅=求最可几半径就是求最大径向分布函数时r,0)22(4)(40202230322303=-==---a zr a zr a zr ea z r rea zer dr d a z dr dD020=-r r a z 即, z a r 0=为最可几半径.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Schrödinger证明这个方程与Heisenberge的矩阵理论只是量子力学的不 同表示方法,转向寻求更基本的方程未果,后来不久就转向研究生命是 什么。不过在这场喜剧中de Broglie与Schrödinger都成为诺奖得主而 名垂青史。
乌云罩顶: 乌云罩顶: 黑体辐射:能吸收所有照到它上面的辐射,并将其转化为热辐射,热辐 射光谱特征仅与黑体的温度有关; 光电效应; 原子的线状光谱与稳定性; 固体与分子的低温比热→0:按照经典力学,比热应该是一个常数。 经典力学无法解释这些诡异的现象!
7000K
5000K
紫外灾难
黑体辐射:Max. Planck(1858-1947),1900年提出: 原子“谐振子”能量不连续En=nhν(后来证明是: En=(n+1/2)hν ), 第一次提出“量子”概念;
Heitler W, London F, Wechselwirkung neutraler atome und homöopolare bindung nach der quantenmechanik, Z Physik, 1927, 44:455-472
h2 2 → ˆ − ∇ Ψ + U → Ψ r , t = H Ψ = ξΨ (r) 2µ
Seminal papers on QM
L. de Broglie, Comptes Rendus 177, 507 (1923); Nature 112, 540 (1923) W. Heisenberg, Zeit. Physik 33, 879 (1925) E. Schrödinger, Ann. der Physik 79, 36 (1929); 79, 489 (1926); 80, 437 (1926); 81, 109 (1926); 79, 734 (1926) P. A. M. Dirac, Proc. Roy. Soc. (London) A144, 243 (1927); A144, 710 (1927).
j ≠i
ˆ j ˆ ˆ h(i )φi (r1 ) + ∑ φ * (r2 ) g (r1 , r2 )φ j (r2 )dr2φi (r1 ) − φ * (r2 ) g (r1 , r2 )φi (r2 )dr2φ j (r1 ) = ξiφi (r1 ) j
j ≠i
闭壳层Hartree-Fock方程: 闭壳层Hartree-Fock方程 Hartree 方程 考虑自旋,则可以很轻易地得到闭壳层的形式与开壳层限制性、非限制性 自洽迭代方程。 对于闭壳层,2N个电子的体系(库伦作用与自旋无关;自旋相反的两个电 子交换项为0):
Nobel laureates
Laureate M. Planck A. Einstein N. Bohr L. de Broglie W. Heisenberg E. Schrödinger P. A. M. Dirac W. Pauli M. Born Time 1918 1921 1922 1929 1932 1933 1933 1945 1954 Work Quantum of action Photoelectric effect Atomic structure and radiation Matter wave Matrix mechanics Wave mechanics Relativistic wave mechanics Exclusion principle Statistical interpretation of wave function
ˆ j ˆ ˆ h(i )φi (r1 ) + ∑ φ * (r2 ) g (r1 , r2 )φ j (r2 )dr2φi (r1 ) − φ * (r2 ) g (r1 , r2 )φi (r2 )dr2φ j (r1 ) = ξiφi (r1 ) j
j ≠i
开壳层Hartree-Fock方程: 开壳层Hartree-Fock方程 Hartree 方程 对于开壳层,N个电子的体系p个电子自旋向上,N-p个电子自旋向下, 自旋非限制性HF(SUHF或UHF):
Ψ =| φ1 (r1 )φ2 ( r2 )...φN −1 (rN −1 )φN ( rN ) >
转化为可求解的系列单体波函数方程(Hartree-Fock方程 Hartree-Fock方程): Hartree 方程
ˆ ˆ ˆ h(i )φi (r1 ) + ∑ φ * (r2 ) g (r1 , r2 )φ j (r2 )dr2φi (r1 ) − φ * (r2 ) g (r1 , r2 )φi (r2 )dr2φ j (r1 ) = ξiφi (r1 ) j j
1928年D.R. Hartree提出了Hartree方程,方程将每一个电子都 看成是在其余电子所提供的平均势场中运动的,通过迭代的方法解出每 一个电子的运动方程。1930年, Hartree的学生B.A. Fock和J.C. Slater分别提出了考虑泡利原理的Hartree的自洽场(Self Consistant Field, SCF)迭代方程,称为Hartree-Fock方程。至此,实际求解多体问 题,在理论上成为现实。
N
p
自旋向下: 自旋向下
在Planck与Einstein的光量子理论及Bohr的原子量子论的启发下,考虑 到光具有波粒二象性,de Broglie根据类比的原则,设想实物理子也具 有波粒二象性。
现代量子力学(1923-1927): 现代量子力学(1923-1927): 在普朗克的量子假说、爱因斯坦的光量子理论和玻尔的原子理论基础上, Schrödinger、Feynman、Heisenberg、 Einstein、 Pauli、Fermi、 Bohr、Dirac……一大批大师级物理学家发展出完善的量子力学理论; 量子力学的理论框架,分别被Schrödinger的波函数理论、Feynman的路 径积分与Heisenberg的矩阵理论,这三种等价的形式得到表达。 量子化学主要从Schrödinger的波函数理论出发而建立、发展、完善。 Erenfest等将量子力学与经典力学统一起来,发现经典力学只是量子力 宏观近似。 学的宏观近似 宏观近似
1.
雄心勃勃的经典力学: 雄心勃勃的经典力学: 牛顿力学; 热力学; 统计力学; 电动力学。
量子力学的诞生
“There is nothing new to be discovered 19世纪末20世纪初,经典力学被认为完美无缺 in physics now. All that remains is more and more precise measurements” Lord Kelvin (1900)
3.
量子化学的诞生
h2 2 → ˆ − ∇ Ψ + U → Ψ r , t = H Ψ = ξΨ (r) 2µ
1927年物理学家 W. Heitler和F. London将量子力学通过非常 粗略的近似应用于氢分子,算出其结合能约为实验值的2/3,成功地解释 了两个氢原子能够结合成一个稳定的氢分子的原因,这一成功标志着量 子化学的诞生。
∂ → h2 2 → ˆ ih Ψ r , t = − ∇ Ψ +U → Ψ r,t = H Ψ (r) ∂t 2µ
如果波函数只有一个变量,Schrödinger方程可以手动精确求解。对氢原 子的求解并正确理解结果的含义(Born几率波假设),才使得Schrödinger 方程得到重视。 多体问题的困难: 多体问题的困难 如果系统包含N个电子,波函数ψ中就包含除时间变量t之外的3N个变量, 并且U也不再是local函数,解析求解就变得几乎不可能。 实际的原子、分子、聚合物、晶体如何求解?
20 18
Plank 5000K Plank 7000K Plank 10000K classical 5000K classical 7000K classical 10000K
ε = hν
energy/10 J
15
16 14 12 10 8 6 4 2 0 0 500 1000 1500
8π hν 3 1 Eν = 3 c exp[hν / kT ] − 1
自旋向上: 自旋向上
ˆ ˆ ˆ h(i )φi (r1 ) + ∑ 'φ (r2 ) g (r1 , r2 )φ j (r2 )dr2φi (r1 ) − ∑ 'φ * (r2 ) g (r1 , r2 )φi (r2 )dr2φ j (r1 ) = ξiφi (r1 ) j
j =1 * j j =1
Modern atom (fuzzy orbits)
Wave function instead of orbit !
密度
discrete angular momenta
角向分布 (d)
角向分布 (f)
波有粒子性? 波有粒子性?那就粒子也有 波动性吧! 波动性吧!
Kinetic Work
T
ν0
ν
光电效应:Einstein结合Plank量子的概念,提出了光量子的概念; 固体与分子的低温比热→0:引入量子的概念,比热问题迎刃而解。
原子的线状光谱与稳定性:Bohr提出原子的量子论,允许离散轨道,允 许轨道跃迁,这个模型很好地解释了氢原子。但是经典orbital模型
2.
Schrödinger的量子力学 的量子力学
1926年,de Broglie的那篇只有一页纸的博士论文也送了一份给维也纳 大学,当时主持物理学术活动的是德拜,德拜将它交给年近中年的讲师 Schrödinger。 de Broglie的论文说粒子是波,于是德拜说“那你弄个 波的方程吧!” 于是Schrödinger方程就这样被凑出来了:
