吉林省长春市2009—2010学年度高中毕业班第三次调研测试
2014年长春市高中毕业班第三次调研测试语文试题参考答案与评分标准

长春三模语文参考答案及评分参考一、(9分)1.【参考答案】A【解析】张冠李戴,扩大范围。
实现人文关怀的首要方式,是作者亲身投入经邦治国的大业”,“完善道德修养、塑造完善人格”的途径是“立德”。
【命题立意】本题考查学生对文中主要概念的含义理解的能力。
2.【参考答案】B【解析】“不脱离客观又拉开与客观距离,以宇宙中对立因素的统一为着眼点”是中国画“独具特色的笔墨语言”而非“中国汉字反映的思维方式”。
【命题立意】本题考查学生对文章主要信息的筛选和理解能力。
3.【参考答案】B【解析】A项信息嫁接错误;C项季羡林是以三个和谐来解释“天人合一”,后半句推断过于绝对;D项原文说“只要摆脱20世纪以来全盘西化的遮蔽……就可大有作为。
”【命题立意】本题考查学生对文章的理解分析能力。
二、(36分)(一)(19分)4.(3分)【参考答案】B【解析】谕:告诉,说明。
【命题立意】本题考查学生理解常见文言实词在文中含义的能力。
5.(3分)【参考答案】C【解析】①表现郑侠感念王安石知遇之恩。
⑤是皇帝的命令。
⑥神宗对郑侠的评价。
【命题立意】本题主要考查学生筛选、归纳文章内容的能力。
6.(3分)【参考答案】D【解析】“编管汀州”是因为郑侠“谤讪”,即诽谤罪。
因“党与”(朋党)罪流放英州。
【命题立意】本题主要考查学生分析、概括文章内容的能力。
7.(10分)【参考答案】(1)奏疏呈上后,神宗反复观看所绘之图,长叹几声,将图画揣在袖子里带回宫中。
(2)英州的人无论贫富贵贱,都很尊敬他,争相让子弟跟他学习,并为他建造居室,让他迁居。
【解析】(1)“奏”“数四”“袖”各1分,总体2分;(2)“无”“从学”“迁”各1分,总体2分。
【命题立意】本题主要考查学生理解与翻译的能力。
(二)(11分)8.(6分)【参考答案】这首诗表达了对远方友人的深切思念之情。
(2分)“春堤杨柳发”触景生情,(1分)交代了春天这一时间背景,“杨柳”勾起了诗人对昔日离别情景的回忆,“发”字有绵延生长之感,(或写出了春意盎然的景象)(2分)增添了诗人对远方友人的绵绵不尽的思念之情。
长春市2014届高中毕业班第三次调研测试理科数学试题(含答案解析)(word版)

第 1 页 共 15 页长春市2014届高中毕业班第三次调研测试数学试题(理科) 2014.4本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分 150分,考试时间为120分钟,其中第Ⅱ卷22题—24题为选考题,其它题为必考题。
考试结束后,将试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第Ⅰ卷(选择题,共60分)一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只.有一项...是符合题目要求的,请将正确选项填涂在答题卡上). 1.复数z 满足(1i)2i z +=,则复数z 在复平面内对应的点在A .第一象限B .第二象限C .第三象限D .第四象限2.设集合}421{,,=A ,集合},,|{A b A a b a x x B ∈∈+==,则集合B 中有___个元素 A .4 B .5 C .6 D .73.下列函数中,在(0,)+∞上单调递减,并且是偶函数的是A .2y x =B .3y x =-C .lg ||y x =-D .2x y = 4.观察下面频率等高条形图,其中两个分类变量x y ,之间关系最强的是A .B .C .D .5.如图所示的程序框图,该算法的功能是A .计算012(12)(22)(32)++++++…(12)n n +++的值B .计算123(12)(22)(32)++++++…(2)n n ++的值第5题图。
吉林省长春市高考数学三模试卷理科Word版含解析

2017年吉林省长春市高考数学三模试卷(理科)一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项涂在答题卡上)1.已知复数z=1+2i,则=()A.5ﻩB.5+4i C.﹣3D.3﹣4i2.已知集合A={x|x2﹣2x﹣3<0},,则A∩B=()A.{x|1<x<3} B.{x|﹣1<x<3}C.{x|﹣1<x<0或0<x<3}ﻩD.{x|﹣1<x<0或1<x<3}3.若点P为抛物线y=2x2上的动点,F为抛物线的焦点,则|PF|的最小值为()A.2ﻩB. C.ﻩD.4.某高中体育小组共有男生24人,其50m跑成绩记作ai(i=1,2,…,24),若成绩小于6.8s为达标,则如图所示的程序框图的功能是()A.求24名男生的达标率ﻩB.求24名男生的不达标率C.求24名男生的达标人数ﻩD.求24名男生的不达标人数5.等比数列{a n}中各项均为正数,S n是其前n项和,且满足2S3=8a1+3a2,a4=16,则S4=( )A.9ﻩB.15C.18ﻩD.306.在平面内的动点(x,y)满足不等式,则z=2x+y的最大值是()A.﹣4 B.4 C.﹣2ﻩD.27.某几何体的三视图如图所示,则其表面积为()A.B.ﻩC. D.8.将一枚硬币连续抛掷n次,若使得至少有一次正面向上的概率不小于,则n的最小值为( )A.4ﻩB.5 C.6 D.79.若方程在上有两个不相等的实数解x1,x2,则x1+x2=( )A.ﻩB.ﻩC.ﻩD.10.设n∈N*,则=()A.ﻩB. C. D.11.已知向量,,(m>0,n>0),若m+n∈[1,2],则的取值范围是()A.ﻩB.C.ﻩD.12.对函数f(x)=,若∀a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,则实数m的取值范围是( )A.B.C.D.二、填空题(本大题包括4小题,每小题5分,共20分,把正确答案填在答题卡中的横线上).13.《九章算术》是我国第一部数学专著,下有源自其中的一个问题:“今有金箠(chuí),长五尺,斩本一尺,重四斤,斩末一尺,重二斤.问金箠重几何?”其意思为:“今有金杖(粗细均匀变化)长5尺,截得本端1尺,重4斤,截得末端1尺,重2斤.问金杖重多少?”则答案是.14.函数f(x)=ex•sinx在点(0,f(0))处的切线方程是.15.直线kx﹣3y+3=0与圆(x﹣1)2+(y﹣3)2=10相交所得弦长的最小值为.16.过双曲线﹣=1(a>b>0)的左焦点F作某一渐近线的垂线,分别与两渐近线相交于A,B两点,若,则双曲线的离心率为.三、解答题(本大题包括6小题,共70分,解答应写出文字说明,证明过程或演算步骤).17.(12分)已知点,Q(cosx,sinx),O为坐标原点,函数. (1)求函数f(x)的最小值及此时x的值;(2)若A为△ABC的内角,f(A)=4,BC=3,求△ABC的周长的最大值.18.(12分)某手机厂商推出一款6吋大屏手机,现对500名该手机用户(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:女性用户分值区间[50,60)[60,70)[70,80)[80,90)[90,100]频数2040805010男性用户分值区间[50,60)[60,70)[70,80)[80,90)[90,100]频数4575906030(1)完成下列频率分布直方图,并指出女性用户和男性用户哪组评分更稳定(不计算具体值,给出结论即可);(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.19.(12分)如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点.(1)求证:PD⊥平面ABE;(2)若F为AB中点,,试确定λ的值,使二面角P﹣FM﹣B的余弦值为.20.(12分)已知F1,F2分别是长轴长为的椭圆C:的左右焦点,A1,A2是椭圆C的左右顶点,P为椭圆上异于A1,A2的一个动点,O为坐标原点,点M为线段PA2的中点,且直线PA2与OM的斜率之积恒为.(1)求椭圆C的方程;(2)设过点F1且不与坐标轴垂直的直线C(2,2,0)交椭圆于A,B两点,线段AB的垂直平分线与B(2,0,0)轴交于点N,点N横坐标的取值范围是,求线段AB长的取值范围.21.(12分)已知函数.(1)求f(x)的极值;(2)当0<x<e时,求证:f(e+x)>f(e﹣x);(3)设函数f(x)图象与直线y=m的两交点分别为A(x1,f(x1)、B(x2,f(x2)),中点横坐标为x0,证明:f'(x0)<0.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程选讲](共1小题,满分10分)22.(10分)已知在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴,建立极坐标系.曲线C1的极坐标方程为ρ=4cosθ,直线l:(为参数).(1)求曲线C1的直角坐标方程及直线l的普通方程;(2)若曲线C2的参数方程为(α为参数),曲线P(x0,y0)上点P的极上的动点,求PQ的中点M到直线l距离的最大值.坐标为,Q为曲线C2[选修4-5:不等式选讲](共1小题,满分0分)23.已知a>0,b>0,函数f(x)=|x+a|+|2x﹣b|的最小值为1.(1)求证:2a+b=2;(2)若a+2b≥tab恒成立,求实数t的最大值.2017年吉林省长春市高考数学三模试卷(理科)参考答案与试题解析一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项涂在答题卡上)1.已知复数z=1+2i,则=()A.5 B.5+4iﻩC.﹣3ﻩD.3﹣4i【考点】复数代数形式的乘除运算.【分析】由已知直接利用求解.【解答】解:∵z=1+2i,∴=|z|2=.故选:A.【点评】本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.2.已知集合A={x|x2﹣2x﹣3<0},,则A∩B=()A.{x|1<x<3}ﻩB.{x|﹣1<x<3}C.{x|﹣1<x<0或0<x<3}ﻩD.{x|﹣1<x<0或1<x<3}【考点】集合的表示法.【分析】先化简A,B,再求出其交集即可.【解答】解:由A={x|﹣1<x<3},B={x|x<0,或x>1},故A∩B={x|﹣1<x<0,或1<x<3}.故选D.【点评】本题考查了集合的交集的运算,属于基础题.3.若点P为抛物线y=2x2上的动点,F为抛物线的焦点,则|PF|的最小值为()A.2ﻩB.ﻩC.ﻩD.【考点】抛物线的简单性质.【分析】根据题意,设P到准线的距离为d,则有|PF|=d,将抛物线的方程为标准方程,求出其准线方程,分析可得d的最小值,即可得答案.【解答】解:根据题意,抛物线y=2x2上,设P到准线的距离为d,则有|PF|=d,抛物线的方程为y=2x2,即x2=y,其准线方程为:y=﹣,分析可得:当P在抛物线的顶点时,d有最小值,即|PF|的最小值为,故选:D.【点评】本题考查抛物线的几何性质,要先将抛物线的方程化为标准方程.4.某高中体育小组共有男生24人,其50m跑成绩记作a i(i=1,2,…,24),若成绩小于6.8s为达标,则如图所示的程序框图的功能是()A.求24名男生的达标率 B.求24名男生的不达标率C.求24名男生的达标人数D.求24名男生的不达标人数【考点】程序框图.【分析】由题意,从成绩中搜索出大于6.8s的成绩,计算24名中不达标率.【解答】解:由题意可知,k记录的是时间超过6.8s的人数,而i记录是的参与测试的人数,因此表示不达标率;故选B.【点评】本题考查程序框图的理解以及算法功能的描述.5.等比数列{a n}中各项均为正数,Sn是其前n项和,且满足2S3=8a1+3a2,a4=16,则S4=()A.9 B.15ﻩC.18 D.30【考点】等比数列的前n项和.【分析】设等比数列{a n}的公比为q>0,由2S3=8a1+3a2,可得2(a1+a2+a3)=8a1+3a2,化为:2q2﹣q﹣6=0,解得q,进而得出.【解答】解:设等比数列{an}的公比为q>0,∵2S3=8a1+3a2,∴2(a1+a2+a3)=8a1+3a2,化为:2a3=6a1+a2,可得=6a1+a1q,化为:2q2﹣q﹣6=0,解得q=2.又a4=16,可得a1×23=16,解得a1=2.则S4==30.故选:D.【点评】本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.6.在平面内的动点(x,y)满足不等式,则z=2x+y的最大值是( )A.﹣4ﻩB.4 C.﹣2ﻩD.2【考点】简单线性规划.【分析】画出约束条件的可行域,利用目标函数的几何意义求解最大值即可.【解答】解:不等式组所表示的平面区域位于直线x+y﹣3=0的下方区域和直线x﹣y+1=0的上方区域,根据目标函数的几何意义,可知目标函数经过A时,z取得最大值.由可得A(1,2),所以目标函数z的最大值为4.故选B.【点评】本题主要考查线性规划问题.画出可行域判断目标函数的几何意义是解题的关键.7.某几何体的三视图如图所示,则其表面积为()A.ﻩB.C. D.【考点】由三视图求面积、体积.【分析】通过三视图复原的几何体是正四棱锥,结合三视图的数据,求出几何体的体积.【解答】解:由题意三视图可知,几何体是正四棱锥,底面边长为2的正方形,一条侧棱垂直正方形的一个顶点,长度为2,四棱锥的表面积为.故选D.【点评】本题是基础题,考查三视图复原几何体的表面积的求法,考查计算能力,空间想象能力.8.将一枚硬币连续抛掷n次,若使得至少有一次正面向上的概率不小于,()A.4B.5ﻩC.6ﻩD.7【考点】n次独立重复试验中恰好发生k次的概率.【分析】由题意,1﹣≥,即可求出n的最小值.【解答】解:由题意,1﹣≥,∴n≥4,∴n的最小值为4,故选A.【点评】本题考查概率的计算,考查对立事件概率公式的运用,比较基础.9.若方程在上有两个不相等的实数解x1,x2,则x1+x2=( )A.B.ﻩC.ﻩD.【考点】正弦函数的对称性.【分析】由题意可得2x+∈[,],根据题意可得=,由此求得x1+x2 值.【解答】解:∵x∈[0,],∴2x+∈[,],方程在上有两个不相等的实数解x1,x2,∴=,则x1+x2=,故选:C.【点评】本题主要考查正弦函数的图象的对称性,属于基础题.10.设n∈N*,则=(A.ﻩB. C.D.【考点】归纳推理.【分析】利用数列知识,即可求解.--【解答】解: 故选 A. 【点评】本题主要考查推理证明的相关知识,比较基础.=.11.已知向量,,(m>0,n>0),若 m+n∈[1,2],则的取值范围是( )A.B. ﻩC.D.【考点】简单线性规划;简单线性规划的应用;平面向量数量积的运算.【分析】根据题意,由向量的坐标运算公式可得=(3m+n,m﹣3n),再由向量模的计算公式可得=,可以令 t=,将 m+n∈[1,2]的关系在直角坐标系表示出来,分析可得 t=表示区域中任意一点与原点(0,0)的距离,进而可得t的取值范围,又由= t,分析可得答案.【解答】解:根据题意,向量,,=(3m+n,m﹣3n),则==,令t=,则= t,而 m+n∈[1,2],即 1≤m+n≤2,在直角坐标系表示如图,t=表示区域中任意一点与原点(0,0)的距离,分析可得: ≤t≤2,又由= t,故≤≤2 ;故选:D.----【点评】本题考查简单线性规划问题,涉及向量的模的计算,关键是求出的表达式.12.对函数f(x)=,若∀ a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,则实数 m 的取值范围是( )A.B.C.D.【考点】函数的值. 【分析】当 m=2时,f(a)=f(b)=f(c)=1,是等边三角形的三边长;当m>2 时,只要即可,当 m<2时,只要即可,由此能求出结果.【解答】解:当 m=2时,f(x)==1,此时 f(a)=f(b)=f(c)=1,是等边三角形的三边长,成立;当 m>2 时,,只要即可,解得2<m<5;当 m<2 时,,只要即可,解得,综上.故选:C. 【点评】本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意分类讨论思想 的合理运用.----二、填空题(本大题包括 4 小题,每小题5分,共 20 分,把正确答案填在答题卡中的横线上). 13.《九章算术》是我国第一部数学专著,下有源自其中的一个问题:“今有金箠(chuí), 长五尺,斩本一尺,重四斤,斩末一尺,重二斤.问金箠重几何?”其意思为:“今有金杖(粗细 均匀变化)长 5 尺,截得本端1尺,重4斤,截得末端 1 尺,重 2 斤.问金杖重多少?”则答案是 15 斤. 【考点】等差数列的通项公式. 【分析】由题意可知等差数列的首项和第 5 项,由等差数列的前 n 项和得答案. 【解答】解:由题意可知等差数列中 a1=4,a5=2,则 S5=,∴金杖重 15 斤. 故答案为:15 斤. 【点评】本题考查等差数列的前 n 项和,是基础的计算题.14.函数 f(x)=ex•sinx 在点(0,f(0))处的切线方程是 y=x . 【考点】利用导数研究曲线上某点切线方程. 【分析】先求出 f′(x),欲求出切线方程,只须求出其斜率即可,故先利用导数求出在 x=0处 的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决. 【解答】解:∵f(x)=ex•sinx,f′(x)=ex(sinx+cosx),(2分) f′(0)=1,f(0)=0, ∴函数f(x)的图象在点 A(0,0)处的切线方程为 y﹣0=1×(x﹣0), 即 y=x(4 分). 故答案为:y=x. 【点评】本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程 等基础知识,考查运算求解能力.属于基础题.15.直线kx﹣3y+3=0 与圆(x﹣1)2+(y﹣3)2=10 相交所得弦长的最小值为 2 . 【考点】直线与圆的位置关系.----【分析】由条件可求得直线 kx﹣3y+3=0 恒过圆内定点(0,1),则圆心(1,3)到定点的距 离为 ,因此最短弦长为 . 【解答】解:由条件可求得直线 kx﹣3y+3=0 恒过圆内定点(0,1),则圆心(1,3)到定点(0, 1))的距离为 ,当圆心到直线 kx﹣3y+3=0的距离最大时(即等于圆心(1,3)到定点(0,1))的距离)所得弦长的最小,因此最短弦长为 2=.故答案为:2 . 【点评】题考查直线和圆的位置关系,以及最短弦问题,属于中档题16.过双曲线 ﹣ =1(a>b>0)的左焦点F作某一渐近线的垂线,分别与两渐近线相交于 A,B两点,若,则双曲线的离心率为.【考点】双曲线的简单性质. 【分析】方法一、运用两渐近线的对称性和条件,可得 A 为 BF 的中点,由垂直平分线的性质和等腰三角形的性质,可得 Rt△OAB 中,∠AOB= ,求得渐近线的斜率,运用离心率公式即可得到;方法二、设过左焦点F作的垂线方程为,联立渐近线方程,求得交点 A,B的纵坐标,由条件可得 A 为 BF 的中点,进而得到 a,b的关系,可得离心率.【解答】解法一:由,可知A为 BF的中点,由条件可得,则Rt△OAB中,∠AOB= ,渐近线 OB 的斜率k= =tan = ,即离心率 e= ==.解法二:设过左焦点 F 作的垂线方程为联立,解得,,----联立,解得,,又,∴yB=﹣2yA∴3b2=a2,所以离心率.故答案为: . 【点评】本题考查双曲线的性质和应用,主要是离心率的求法,解题时要认真审题,仔细解答, 注意向量共线的合理运用.三、解答题(本大题包括 6 小题,共 70 分,解答应写出文字说明,证明过程或演算步骤).17.(12 分)(2017•长春三模)已知点,Q(cosx,sinx),O 为坐标原点,函数.(1)求函数 f(x)的最小值及此时 x 的值;(2)若 A 为△ABC 的内角,f(A)=4,BC=3,求△ABC的周长的最大值.【考点】平面向量数量积的运算;基本不等式在最值问题中的应用;余弦定理的应用.【分析】(1)利用向量的数量积以及两角和与差的三角函数化简函数的解析式,然后求解最值.(2)利用函数的解析式求解 A,然后利用余弦定理求解即可,得到bc 的范围,然后利用基本不等式求解最值.【解答】解:(1)∵,∴,∴当时,f(x)取得最小值 2.(2)∵f(A)=4,∴,又∵BC=3,∴,∴9=(b+c)2﹣bc.,∴,----∴,当且仅当 b=c 取等号,∴三角形周长最大值为.【点评】本题考查向量的数量积以及两角和与差的三角函数,三角函数的最值,基本不等式以及余弦定理的应用,考查计算能力.18.(12 分)(2017•长春三模)某手机厂商推出一款 6 吋大屏手机,现对 500 名该手机用户(200 名女性,300 名男性)进行调查,对手机进行评分,评分的频数分布表如下:女性用户 分值区间 [50,60) [60,70) [70,80) [80,90) [90,100]频数2040805010男性用户 分值区间 [50,60) [60,70) [70,80) [80,90) [90,100]频数4575906030(1)完成下列频率分布直方图,并指出女性用户和男性用户哪组评分更稳定(不计算具体值,给出结论即可);(2)根据评分的不同,运用分层抽样从男性用户中抽取 20名用户,在这 20 名用户中,从评 分不低于 80分的用户中任意抽取 3 名用户,求 3 名用户中评分小于 90 分的人数的分布列和 期望. 【考点】离散型随机变量的期望与方差;离散型随机变量及其分布列.【分析】(I)根据已知可得频率,进而得出矩形的高=,即可得出图形.(II)运用分层抽样从男性用户中抽取 20 名用户,评分不低于 8(0 分)有 6 人,其中评分小于 9(0 分)的人数为 4,从 6 人中任取3人,记评分小于 9(0 分)的人数为 X,则 X 取值为1,2,3, 利用超几何分布列的计算公式即可得出. 【解答】解:(Ⅰ)女性用户和男性用户的频率分布表分别如下左、右图:----由图可得女性用户更稳定.(4 分) (Ⅱ)运用分层抽样从男性用户中抽取20 名用户,评分不低于 8(0 分)有6人,其中评分小于 9(0 分)的人数为4,从 6 人中任取3人,记评分小于 9(0分)的人数为 X,则 X 取值为 1,2,3,;P(X=2)==;.所以 X 的分布列为X123P.(12 分) 【点评】本题考查了频率分布直方图的性质、超几何分布列的概率与数学期望计算公式、分 层抽样,考查了推理能力与计算能力,属于中档题.19.(12分)(2017•长春三模)如图,在四棱锥 P﹣ABCD 中,底面ABCD 为正方形,PA⊥底 面 ABCD,AD=AP,E为棱 PD中点. (1)求证:PD⊥平面 ABE;(2)若F为 AB 中点,,试确定 λ 的值,使二面角 P﹣FM﹣B 的余弦值为.【考点】二面角的平面角及求法;直线与平面平行的判定. 【分析】(I)证明 AB⊥平面 PAD,推出 AB⊥PD,AE⊥PD,AE∩AB=A,即可证明 PD⊥平面A----BE.(II) 以 A 为原点,以为x,y,z 轴正方向,建立空间直角坐标系 A﹣BDP,求出相关点的坐标,平面 PFM 的法向量,平面 BFM 的法向量,利用空间向量的数量积求解即可. 【解答】解:(I)证明:∵PA⊥底面 ABCD,AB⊂ 底面 ABCD,∴PA⊥AB, 又∵底面 ABCD 为矩形,∴AB⊥AD,PA∩AD=A,PA⊂ 平面 PAD,AD⊂ 平面 PAD, ∴AB⊥平面PAD,又PD⊂ 平面PAD,∴AB⊥PD,AD=AP,E 为 PD 中点,∴AE⊥PD, AE∩AB=A,AE⊂ 平面ABE,AB⊂ 平面 ABE,∴PD⊥平面 ABE.(II) 以A为原点,以为x,y,z 轴正方向,建立空间直角坐标系A﹣BDP,令|AB|=2,则 A(0 , 0 , 0),B ( 2,0 , 0 ) ,P(0 , 0 ,2 ) , C(2 , 2 , 0 ) , E(0 , 1 , 1) , F(1,0 ,0),,,,M(2λ,2λ,2﹣2λ)设 平 面 P FM 的 法 向 量,,即,设平面 BFM 的法向量,,即,,解得.【点评】本题考查直线与平面垂直的判定定理的应用,二面角的平面角的求法,考查空间想 象能力以及计算能力.----20.(12 分 ) ( 2 0 1 7 • 长 春 三 模 ) 已 知 F 1 , F 2 分 别 是 长 轴 长 为 的 椭 圆 C : 的左右焦点,A1,A2是椭圆 C 的左右顶点,P 为椭圆上异于 A1,A2 的一个动点,O 为坐标原点,点M为线段PA2的中点,且直线 PA2 与 OM 的斜率之积恒为 .(1)求椭圆 C 的方程; (2)设过点 F1且不与坐标轴垂直的直线 C(2,2,0)交椭圆于 A,B两点,线段 AB 的垂直平分线与 B(2,0,0)轴交于点 N,点 N 横坐标的取值范围是,求线段AB 长的取值范围. 【考点】直线与椭圆的位置关系.【 分 析 】 ( 1) 由 已 知 2a=2 , 解 得 a= , 记 点 P(x0,y 0 ) ,kOM =,可得kOM•=•利用斜率计算公式及其点 P(x0,y0)在椭圆上,即可得出.(2)设直线 l:y=k(x+1),联立直线与椭圆方程得(2k2+1)x2+4k2x+2k2﹣2=0,记 A(x1,y1),B(x2,y2).利用根与系数的关系、中点坐标公式、弦长公式即可得出. 【解答】解:(1)由已知 2a=2 ,解得a= ,记点 P(x0,y0),∵kOM=,∴kOM•=•=•=,又点P(x0,y0)在椭圆上,故 + =1,∴kOM•=﹣ =﹣ ,∴,∴b2=1,∴椭圆的方程为.(4分)(2)设直线l:y=k(x+1),联立直线与椭圆方程,得(2k2+1)x2+4k2x+2k2﹣2=0,记 A(x1,y1),B(x2,y2).由韦达定理可得,可得,----故 AB中点,QN 直线方程:,∴,已知条件得:,∴0<2k2<1,∴,∵,∴.(12分)【点评】本题考查了椭圆的定义标准方程及其性质、一元二次方程的根与系数的关系、斜率 计算公式、中点坐标公式、两点之间的距离公式,考查了推理能力与计算能力,属于难题.21.(12 分)(2017•长春三模)已知函数.(1)求 f(x)的极值; (2)当 0<x<e 时,求证:f(e+x)>f(e﹣x); (3)设函数 f(x)图象与直线y=m 的两交点分别为 A(x1,f(x1)、B(x2,f(x2)),中点横 坐标为x0,证明:f'(x0)<0. 【考点】利用导数研究函数的极值;利用导数研究函数的单调性. 【分析】(1)求出函数的导数,解关于导函数的不等式,求出函数的极值即可; (2)问题转化为证明(e﹣x)ln(e+x)>(e+x)ln(e﹣x),设 F(x)=(e﹣x)ln(e+x)﹣(e +x)ln(e﹣x),根据函数的单调性证明即可.【解答】解:(1)f′(x)=,f(x)的定义域是(0,+∞),x∈(0,e)时,f′(x)>0,f(x)单调递增; x∈(e,+∞)时,f'(x)<0,f(x)单调递减.当 x=e 时,f(x)取极大值为 ,无极小值.(2)要证f(e+x)>f(e﹣x),即证:,只需证明:(e﹣x)ln(e+x)>(e+x)ln(e﹣x). 设 F(x)=(e﹣x)ln(e+x)﹣(e+x)ln(e﹣x),----,∴F(x)>F(0)=0, 故(e﹣x)ln(e+x)>(e+x)ln(e﹣x), 即 f(e+x)>f(e﹣x), (3)证明:不妨设 x1<x2,由(1)知 0<x1<e<x2,∴0<e﹣x1<e, 由(2)得 f[e+(e﹣x1)]>f[e﹣(e﹣x1)]=f(x1)=f(x2), 又 2e﹣x1>e,x2>e,且 f(x)在(e,+∞)上单调递减, ∴2e﹣x1<x2,即x1+x2>2e,∴,∴f'(x0)<0.【点评】本小题主要考查函数与导数的知识,具体涉及到导数的运算,用导数来研究函数的 单调性等,考查学生解决问题的综合能力.请考生在 22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4: 坐标系与参数方程选讲](共1小题,满分 10分) 22.(10分)(2017•长春三模)已知在平面直角坐标系 xOy 中,以 O 为极点,x轴的正半轴为极轴,建立极坐标系.曲线 C1 的极坐标方程为 ρ=4cosθ,直线 l:(为参数). (1)求曲线 C1 的直角坐标方程及直线 l 的普通方程;(2)若曲线 C2 的参数方程为(α 为参数),曲线 P(x0,y0)上点 P 的极坐标为 ,Q为曲线 C2 上的动点,求 PQ的中点 M 到直线 l 距离的最大值. 【考点】参数方程化成普通方程;简单曲线的极坐标方程. 【分析】(1)利用三种方程的转化方法,求曲线 C1的直角坐标方程及直线l的普通方程;(2),直角坐标为(2,2),,利用点到直线l的距离公式能求出点M到直线l的最大距离.【解答】解:(1)由曲线 C1 的极坐标方程为 ρ=4cosθ,得直角坐标方程,----直线 l:,消去参数,可得普通方程 l:x+2y﹣3=0.( 2),直角坐标为(2,2),,M 到l的距离 d==,从而最大值为.(10 分) 【点评】本小题主要考查极坐标系与参数方程的相关知识,具体涉及到极坐标方程与平面直 角坐标方程的互化,参数方程的运用.[选修 4-5:不等式选讲](共 1 小题,满分 0 分) 23.(2017•长春三模)已知 a>0,b>0,函数 f(x)=|x+a|+|2x﹣b|的最小值为 1. (1)求证:2a+b=2; (2)若 a+2b≥tab 恒成立,求实数 t 的最大值. 【考点】函数恒成立问题;绝对值不等式的解法.【分析】(1)法一:根据绝对值的性质求出 f(x)的最小值,得到 x= 时取等号,证明结论即可;法二:根据 f(x)的分段函数的形式,求出 f(x)的最小值,证明即可;(2)法一,二:问题转化为≥t 恒成立,根据基本不等式的性质求出的最小值,从而求出 t 的范围即可;法三:根据二次函数的性质判断即可.【解答】解:(1)法一:f(x)=|x+a|+|2x﹣b|=|x+a|+|x﹣ |+|x﹣ |,∵|x+a|+|x﹣ |≥|(x+a)﹣(x﹣ )|=a+ 且|x﹣ |≥0,∴f(x)≥a+ ,当 x= 时取等号,即f(x)的最小值为 a+ ,∴a+ =1,2a+b=2;法二:∵﹣a< ,∴f(x)=|x+a|+|2x﹣b|=,----显然 f(x)在(﹣∞, ]上单调递减,f(x)在[ ,+∞)上单调递增,∴f(x)的最小值为f( )=a+ ,∴a+ =1,2a+b=2.(2)方法一:∵a+2b≥tab 恒成立,∴≥t 恒成立,= + =( + )(2a+b )• = (1+4+ + ),当 a=b= 时,取得最小值 ,∴ ≥t,即实数 t 的最大值为 ;方法二:∵a+2b≥tab 恒成立,∴≥t恒成立,t≤= + 恒成立,+=+ ≥=,∴ ≥t,即实数t的最大值为 ; 方法三:∵a+2b≥tab 恒成立, ∴a+2(2﹣a)≥ta(2﹣a)恒成立, ∴2ta2﹣(3+2t)a+4≥0恒成立, ∴(3+2t)2﹣326≤0, ∴ ≤t≤ ,实数 t 的最大值为 . 【点评】本题考查了绝对值不等式问题,考查绝对值的性质以及二次函数的性质,考查转化 思想,是一道中档题.--。
2014年长春市高中毕业班第三次调研测试地理试题参考答案与评分标准

长春三模文综地理参考答案及评分参考1.【命题立意】本题考查人口增长模式类型问题,意在考查学生在图示中获取和解读地理信息的能力。
【试题解析】该题关键点是“进入现代型的时间”,应是1970年以前。
【参考答案】C2.【命题立意】本题考查生产力对人口增长的影响。
意在考查学生读图的能力。
【试题解析】因为生产力的水平不断提高,由图可知死亡率不断下降,因此呈负相关。
【参考答案】B3.【命题立意】考查工业的区位选择问题。
意在考查学生调动和运用知识的能力和利用图示获取和解读地理信息的能力。
【试题解析】炼铝业为动力导向型,应接近水电站。
【参考答案】A4.【命题立意】考查水库的生态效益,考查诱调动和运用知识的能力。
【试题解析】发电和养殖为经济效益,水库易发地质灾害,上游地区发展畜牧业,并有城市分布,易造成水污染,水库有净化水质的作用。
【参考答案】C5.【命题立意】考查地理信息技术问题,考查调动和运用知识的能力。
【试题解析】题干中的“飞机”“拍照”说明应用遥感技术。
【参考答案】A6.【命题立意】考查影响气象要素变化的原因,考查学生利用图示获取和解读地理信息的能力。
【试题解析】由于海域面积大,水汽充足,云量多;距海岸远,受洋流影响小;所处纬度为20°S—26°S,不受西风的影响,受副高影响,天气晴朗。
【参考答案】A7.【命题立意】考查河湖的相关知识。
考查学生调动和运用知识的能力和利用图示获取和解读地理信息的能力。
【试题解析】读指向标,得出下北上南;读等高线,可知南部河流注入湖泊,河流为内流河,湖泊属于内流湖;北部河流注入海洋,为外流河;由于图示位置为温带海洋性气候,终年温和多雨,雨水补给量大,湖泊为淡水湖,河流径流量变化不大。
【参考答案】D8.【命题立意】考查外力作用对地貌的影响,意在考查学生调动和运用知识的能力和利用图示获取和解读地理信息的能力。
【试题解析】因为题干中问题为自然原因,排除D;该沙丘带向内部陆延伸宽度大,故不受洋流影响该沿海沙丘带处无河流,流故无河流堆积作用。
【恒心】【好卷速递】12年长春市高中毕业班第3次调研测试理综标准答案【东三省专版】【教师专版】【首发】

2012年东北三省四市教研协作体等值诊断联合考试2012年长春市高中毕业班第三次调研测试理科综合能力测试参考答案及评分标准一、选择题:本题共13小题,每小题6分,共78分。
1.【参考答案】C【命题立意】本题考查对细胞结构和有关生理功能知识的理解能力【解析】蓝藻能进行光合作用,但无叶绿体;硝化细菌等能进行有氧呼吸,但无线粒体;有丝分裂是真核细胞进行细胞分裂的方式;原核生物无内质网,但也可以合成蛋白质。
2.【参考答案】B【命题立意】本题考查对细胞分裂有关知识的理解能力【解析】有丝分裂前期核膜解体核仁消失;正常情况下,减数第二次分裂后期没有同源染色体,有2个染色体组。
3.【参考答案】C【命题立意】本题考查对光合作用有关知识的理解和分析能力,以及获取信息的能力。
【解析】在35℃时HB品系植物的光合速率最高,所以耐高温性较好。
30℃时HA 品系植物的光合速率比20℃时的光合速率低。
4.【参考答案】A【命题立意】本题考查对生长素及其他植物激素知识的理解能力【解析】赤霉素能促进细胞的伸长,使植株增高;由于促进扦插枝条生根作用的生长素有一个最适浓度,在低于或高于最适浓度有相同的作用效果。
植物激素的极性运输不受重力影响;侧芽受到抑制的原因是顶芽产生的生长素向下运输,大量积累在侧芽从而抑制侧芽生长。
5.【参考答案】D【命题立意】本题考查对DNA复制,转录和翻译等有关知识的理解能力【解析】DNA的复制是以DNA的二条链为模板,原料是脱氧核苷酸,碱基互补配对的方式是A-T,G-C。
转录是以DNA的一条链为模板,原料是核糖核苷酸,碱基互补配对的方式是A-U,T-A,G-C。
翻译是以mRNA为模板,原料是氨基酸,碱基互补配对的方式是A-U,G-C。
6.【参考答案】D【命题立意】本题考查对植物细胞吸水和吸收矿质离子知识的理解和分析能力,以及获取信息的能力。
【解析】从柱形图中不能分析出番茄对各种离子的吸收与氧气浓度有关。
7.【参考答案】B【命题立意】本题考查有关化学用语的相关内容【解析】原子的原子结构简图最外层最多不超过8个电子, 原子核内有8个质子、10个中子的氧原子的质量数为18。
2024届吉林省长春市高三下学期第三次质量监测语文答案

2024年三模语文参考答案1. D(3分)2. D(3分)3. C(3分)4. A(3分)5. (6分)①故乡是人的精神家园,也是恒产,一点一滴地建设家园依然是农人的理想;②这一传统理念在当今因土地流转政策,农民不需再固守土地,对土地的使用更加灵活;③在当代“人口外泄”体现在农人对美好生活的向往,选择进城务工,寻找更多的发展机会。
6. B(3分)7. C(3分)8. (5分)①写作者的感激与愧疚之情;②有意哄骗孩子,将画片从他们的手中要回;③对自己在孩子面前的行为感到惭愧,反思并认识到自己不如孩子。
9. (6分)①在作者看来,与孩子相比,成人显得狭小、爱算计、不光明,且有着固化的思维与行为;②从孩子们身上,我们看到了高尚的理想、对艺术的偏好以及纯真的品质;③社会文化建设应该是纯粹的,真实的,孩子让我们看到了社会文化建设的未来和希望。
10. B D F(3分)11. B(3分)12. C(3分)13. (8分)(1)修筑壁垒要经过几天时间才能完成,魏军在城内做好了防守准备,其他地方的救兵如果到来,那么就不能攻取(或图谋)了。
(2)国家即使再大,喜好战事就必然灭亡;天下即使太平,忘记战事就必然危险。
14. (3分)李靖侧重攻时攻敌心(知彼)、守时守吾气(知己),唐太宗从攻守两端都强调知己知彼,体现出攻守一道思想。
参考译文:材料一:大凡战争,所说的进攻,是要了解敌方。
只有了解敌方有能被击破的道理,那么派遣军队攻打他,没有不胜利的。
兵法说:了解敌方攻击敌方可以取胜,就去攻打。
三国魏公曹操派遣朱光为庐江太守,朱光率兵驻屯在皖,大力开田种稻,同时又派间谍招募利诱敌方鄱阳的老部下,让他们充当内应。
吴国大将吕蒙说:“皖城郊野的田地肥美,如果稻禾一旦成熟收割,魏军数量必然增加,像这样几年,曹操强大的态势就显现出来了,应当尽早铲除掉。
”就详细地陈述了军队的情况。
于是,孙权亲自出征皖城。
一昼夜就到达这里。
孙权向众将征询攻城之策,大家都建议构筑高垒。
吉林省吉林市2022届高三下学期理综物理第三次调研试卷

1 / 11…………外…………○……………订…学校:_班级:___________ 考…………内…………○……………订…1.(2分)如图所示,两位同学在体育课上进行传接篮球训练,甲同学将篮球从A 点抛给乙(篮球运动的轨迹如图中实线1所示),乙在B 点接住然后又将篮球传给甲(篮球运动的轨迹如图中虚线2所示).已知篮球在空中运动的最大高度恰好相同.若忽略空气阻力,则下列说法中正确的是( )A .篮球沿轨迹1运动的时间较长B .篮球沿轨迹1运动的过程中速度变化较快C .两同学将篮球抛出的速度大小相等D .篮球落到B 点前的瞬间重力做功的功率等于落到C 点(与A 、B 两点高度相同)前的瞬间重力做功的功率2.(2分)如图所示为氢原子能级图,表中给出了六种金属的逸出功,已知可见光光子的能 量范围为1.62~3.11eV ,下列说法正确的是( )C .大量氢原子由n=4能级向基态跃迁时可能放出4种不同频率的可见光D .用大量氢原子由n=5能级向基态跃迁时放出的可见光照射表中金属,能发生光电效应的只有金属铯3.(2分)科技日报北京2017年9月6日电,英国《自然天文学》杂志发表的一篇论文称,某科学家在银河系中心附近的一团分子气体云中发现了一个黑洞.科学研究表明,当天体的逃逸速度(逃逸速度为第一宇宙速度的√2倍)达到光速时,该天体就会成为黑洞.已知某天体与地球的质量之比为k ,地球的半径为R ,地球卫星的环绕速度(第一宇宙速度)为v 1,光速为c ,则要使该天体成为黑洞,其半径为( )A .2v 12Rkc 2B .2kv 12R c 2C .kv 12R 2c 2D .2kc 2R v 124.(2分)绝缘光滑水平面上有ABO 三点,以O 点为坐标原点,向右方向为正方向建立直线坐标轴x轴,A 点坐标为-2m ,B 点坐标为2m ,如图甲所示。
A 、B 两点间的电势变化如图乙,左侧图线为四分之一圆弧,右侧图线为一条倾斜线段。
2013年长春市高中毕业班第三次调研测试文科数学
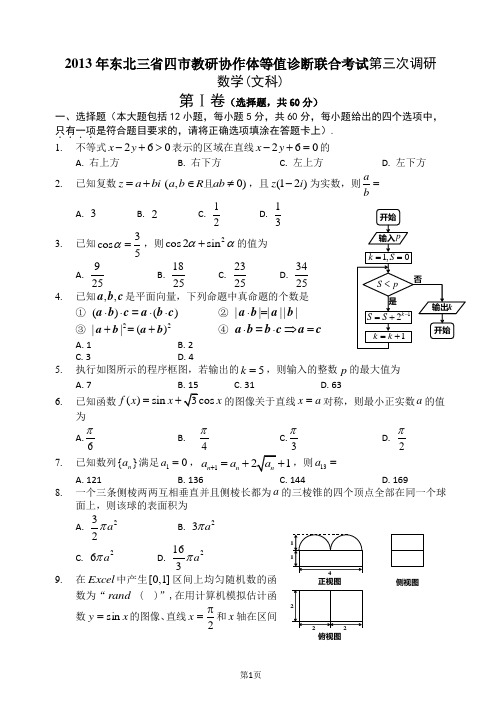
2013年东北三省四市教研协作体等值诊断联合考试第三次调研数学(文科)第Ⅰ卷(选择题,共60分)一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项....是符合题目要求的,请将正确选项填涂在答题卡上). 1. 不等式260x y -+>表示的区域在直线260x y -+=的 A. 右上方 B. 右下方 C. 左上方D. 左下方2. 已知复数z a bi =+(,0)a b R ab ∈≠且,且(12)z i -为实数,则ab= A. 3B. 2C.12D.133. 已知3cos 5α=,则2cos 2sin αα+的值为 A.925B. 1825C. 2325D. 34254. 已知,,a b c 是平面向量,下列命题中真命题的个数是① ()()⋅⋅⋅⋅a b c =a b c ② ||||||⋅= a b a b③ 22||()+=+a b a b ④ ⋅⋅⇒=a b =b c a cA. 1B. 2C. 3D. 45. 执行如图所示的程序框图,若输出的5k =,则输入的整数p 的最大值为A. 7B. 15C. 31D. 636.已知函数()sin f x x x =的图像关于直线x a =对称,则最小正实数a 的值为A.6π B.4π C.3π D.2π 7. 已知数列{}n a 满足10a =,11n n a a +=+,则13a =A. 121B. 136C. 144D. 1698. 一个三条侧棱两两互相垂直并且侧棱长都为a 的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为A.232a πB. 23a πC. 26a π D. 2163a π9. 在Excel 中产生[0,1]区间上均匀随机数的函数为“rand ( )”,在用计算机模拟估计函数x y sin =的图像、直线2π=x 和x 轴在区间正视图侧视图俯视图0,2π⎡⎤⎢⎥⎣⎦上部分围成的图形面积时,随机点11(,)a b 与该区域内的点),(b a 的坐标变换公式为 A. 11,2a ab b π=+= B. 112(0.5),2(0.5)a a b b =-=-C. [0,],[0,1]2a b π∈∈ D. 11,2a ab b π==10. 已知抛物线28y x =的焦点为F ,直线(2)y k x =-与此抛物线相交于,P Q 两点,则11||||FP FQ += A. 12B. 1C. 2D. 411. 如图所示是一个几何体的三视图,则该几何体的体积为A. 162π+B. 82π+C. 16π+D. 8π+12. 若函数()f x 对任意的x ∈R 都有(3)(1)f x f x +=-+,且(1)2013f =,则[(2013)2]1f f ++= A. 2013- B. 2012- C. 2012 D. 2013第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分,第13题-21题为必考题,每个试题考生都必须作答,第22题-24题为选考题,考生根据要求作答. 二、填空题(本大题包括4小题,每小题5分,共20分,把正确答案填在答题卡中的横线上). 13. 函数2()lg(34)f x x x =+-的定义域为____________.14. 若等比数列{}n a 的首项是1a ,公比为q ,n S 是其前n 项和,则n S =_____________.15. 双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为1F 和2F ,左、右顶点分别为1A 和2A ,过焦点2F 与x 轴垂直的直线和双曲线的一个交点为P ,若2112PA 是22PA和2122A A 的等差中项,则该双曲线的离心率为 .16. 已知集合224{(,)|(3)(4)}5A x y x y =-+-=,{(,)|2|3||4|}B x y x y λ=-+-=,若A B ≠∅ ,则实数λ的取值范围是__________. 三、解答题(本大题包括6小题,共70分,解答应写出文字说明,证明过程或演算步骤). 17. (本小题满分12分)在三角形ABC 中,sin 2cos cos 2sin C C C C C ⋅+=⋅+⑴ 求角C 的大小;⑵ 若2AB =,且sin cos sin 2B A A ⋅=,求ABC ∆的面积.18. (本小题满分12分) 2012年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类: 第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,)+∞(单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.⑴ 求该小区居民用电量的中位数与平均数;⑵ 本月份该小区没有第三类的用电户出现,为鼓励居民节约用电,供电部门决定:对第一类每户奖励20元钱,第二类每户奖励5元钱,求每户居民获得奖励的平均值;⑶ 利用分层抽样的方法从该小区内选出5户居民代表,若从该5户居民代表中任选两户居民,求这两户居民用电资费属于不同类型的概率.19. (本小题满分12分)如图,E 是矩形ABCD 中AD 边上的点,F 为CD边的中点,243AB AE AD ===,现将ABE ∆沿BE 边折至PBE ∆位置,且平面PBE ⊥平面BCDE .⑴ 求证:平面PBE ⊥平面PEF ;⑵ 求四棱锥P BEFC -的体积. 20.(本小题满分12分)如图,曲线2:M y x =与曲线222:(4)2(0)N x y m m -+=>相交于A 、B 、C 、D 四个点.⑵ 求m 的取值范围;⑵ 求四边形ABCD 的面积的最大值及此时对角线AC 与BD 的交点坐标.21(本小题满分12分)已知函数()sin xf x e x =.⑴ 求函数()f x 的单调区间; ⑵ 如果对于任意的[0,]2x π∈,()kx f x ≥总成立,求实数k 的取值范围;⑶ 是否存在正实数m ,使得:当(0,)x m ∈时,不等式21()22x f x x <+恒成立?请给出结论并说明理由.PB C D FE (1)(2)请考生在22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分. 22. (本小题满分10分)选修4-1:几何证明选讲. 如图,AB 是O 的直径,弦CD 与AB 垂直,并与AB 相交于点E ,点F 为弦CD 上异于点E 的任意一点,连结BF 、AF 并延长交O 于点M 、N .⑴ 求证:B 、E 、F 、N 四点共圆; ⑵ 求证:22AC BF BM AB +⋅=.23.(本小题满分10分)选修4-4:坐标系与参数方程选讲.在直角坐标系xOy 中,曲线1C 的参数方程为2cos ()1sin x t t y t απαα<=+⎧⎨=+⎩≤是参数,0,以原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2221cos ρθ=+. ⑴ 求曲线1C 的普通方程和曲线2C 的直角坐标方程;⑵ 当4πα=时,曲线1C 和2C 相交于M 、N 两点,求以线段MN 为直径的圆的直角坐标方程.24.(本小题满分10分)选修4-5:不等式选讲.设函数()|1||5|f x x x =++-,∈x R .⑴ 求不等式()10f x x +≤的解集;⑵ 如果关于x 的不等式2()(2)f x a x --≥在R 上恒成立,求实数a 的取值范围.2013年东北三省四市教研协作体等值诊断联合考试2013年长春市高中毕业班第三次调研测试数学(文科)参考答案及评分标准一、选择题(本大题包括12小题,每小题5分,共60分)1.B2.C3.A4.A5.B6.A7.C8.B9.D 10.A 11.B 12.B 简答与提示:1. 【命题意图】本小题主要考查二元一次不等式所表示的区域位置问题,是线性规划的一种简单应用,对学生的数形结合思想提出一定要求. 【试题解析】B 右下方为不等式所表示区域,故选B.2. 【命题意图】本小题主要考查复数的基本运算,特别是共轭复数的乘法运算以及对共轭复数的基本性质的考查,对考生的运算求解能力有一定要求.【试题解析】C 由(12)z i ⋅-为实数,且0z ≠,所以可知(12)z k i =+,0k ≠,则122a kb k ==,故选C. 3. 【命题意图】本小题主要考查同角三角函数的基本关系式以及倍角的余弦公式的应用,对学生的化归与转化思想以及运算求解能力提出一定要求.【试题解析】A由3cos 5α=,得22229cos 2sin 2cos 11cos cos 25ααααα+=-+-==,故选A. 4. 【命题意图】本小题主要考查平面向量的定义与基本性质,特别是对平面向量运算律的全面考查,另外本题也对考生的分析判断能力进行考查.【试题解析】A 由平面向量的基础知识可知①②④均不正确,只有③正确, 故选A.5. 【命题意图】本小题主要通过程序框图的理解考查学生的逻辑推理能力,同时考查学生对算法思想的理解与剖析.【试题解析】B 有程序框图可知:①0S =,1k =;②1S =,2k =;③3S =,3k =;④7S =,4k =; ⑤15S =,5k =. 第⑤步后k 输出,此时15S P =≥,则P 的最大值为15,故选B.6. 【命题意图】本题着重考查三角函数基础知识的应用,对于三角函数的对称性也作出较高要求. 本小题同时也考查考生的运算求解能力与考生的数形结合思想.【试题解析】A函数()sin 2sin()3f x x x x π==+的对称轴为x a =,则32a k πππ+=+,即()6a k k Z ππ=+∈,因此a 的最小正数值为6π. 故选A. 7. 【命题意图】本小题主要考查数列的递推问题,以及等差数列的通项公式,也同时考查学生利用构造思想解决问题的能力以及学生的推理论证能力.【试题解析】C 由11n n a a +=+,可知211)n a +=,1=,故是公差为11212==,则13144a =. 故选C.8.【命题意图】本小题主要考查立体几何中球与球的内接几何体中基本量的关系,以及球表面积公式的应用,本考点是近年来高考中的热点问题,同时此类问题对学生的运算求解能力与空间想象能力也提出较高要求.【试题解析】B 由题可知该三棱锥为一个棱长a的正方体的一角,则该三棱锥与,则球半径为2a,则22244()32S r a aπππ===. 故选B.9.【命题意图】本小题主要考查均匀随机数的定义与简单应用,对于不同尺度下点与点的对应方式也做出一定要求. 本题着重考查考生数据处理的能力,与归一化的数学思想.【试题解析】D. 由于[0,]2aπ∈,[0,1]b∈,而1[0,1]a∈,1[0,1]b∈,所以坐标变换公式为12a aπ=,1b b=. 故选D.10.【命题意图】本小题是定值问题,考查抛物线的定义与基本性质及过焦点的弦的性质. 本题不但对考生的运算求解能力、推理论证能力有较高要求,而且对考生的化归与转化的数学思想也有较高要求.【试题解析】A 设11(,)P x y,22(,)Q x y,由题意可知,1||2PF x=+,2||2QF x=+,则1212121241111||||222()4x xFP FQ x x x x x x+++=+=+++++,联立直线与抛物线方程消去y得,2222(48)40k x k x k-++=,可知124x x=,故121212121244111||||2()42()82x x x xFP FQ x x x x x x+++++===+++++. 故选A.11.【命题意图】本小题主要考查立体几何中的三视图问题,并且对考生的空间想象能力及利用三视图还原几何体的能力进行考查,同时考查简单几何体的体积公式.【试题解析】B 由图可知该几何体是由两个相同的半圆柱与一个长方体拼接而成,因此21241282Vππ=⨯⨯+⨯⨯=+. 故选B.12.【命题意图】本小题着重考查函数的周期性问题,以及复合函数的求值问题,对于不同的表达式,函数周期性的意义也不同,此类问题时高考中常见的重要考点之一,请广大考生务必理解函数的周期与对称问题.本题主要对考生的推理论证能力与运算求解能力进行考查.【试题解析】B 由(3)(1)f x f x+=-+可知函数()f x周期4T=,当0x=时可知,(3)(1)2013f f=-=-,(2013)(1)2013f f==,因此[(2013)2]1(2015)1(3)12012f f f f++=+=+=-. 故选B.二、填空题(本大题包括4小题,每小题5分,共20分)13. (,4)(1,)-∞-+∞14.11(1)111nna qqS qna q⎧-≠⎪=-⎨⎪ =⎩15. 216. 2] 简答与提示:13. 【命题意图】本小题主要考查对数函数的性质与其定义域的求取问题,以及一元二次不等式的解法.本小题着重考查考生的数学结合思想的应用.【试题解析】由题意可知2340x x +->,解得4x <-或1x >,所以函数()f x 的定义域为(,4)(1,)-∞-+∞ .14. 【命题意图】本小题主要考查等比数列的前n 项和公式的推导与应用,同时考查了学生的分类讨论思想.【试题解析】根据等比数列前n 项和公式:11(1)111n n a q q S qna q ⎧- ≠⎪= -⎨⎪ =⎩. 15. 【命题意图】本小题主要考查双曲线中各基本量间的关系,特别是考查通径长度的应用以及相关的计算,同时也对等差中项问题作出了一定要求. 同时对考生的推理论证能力与运算求解能力都有较高要求.【试题解析】由题可知2221212||||2||PA PA A A =+ ,则4422222()()8b b c a c a a a a ++=+-+,化简得248ac a =,故2c e a==. 16. 【命题意图】本小题主要考查曲线与方程的实际应用问题,对学生数形结合与分类讨论思想的应用作出较高要求.【试题解析】 由题可知,集合A 表示圆224(3)(4)5x y -+-=上点的集合,集合B 表示曲线2|3||4|x y λ-+-=上点的集合,此二集合所表示的曲线的中心都在(3,4)处,集合A 表示圆,集合B 则表示菱形,可以将圆与菱形的中心同时平移至原点,如图所示,可求得λ的取值范围是2]. 三、解答题(本大题必做题5小题,三选一选1小题,共70分) 17. (本小题满分12分)【命题意图】本题针对三角变换公式以及解三角形进行考查,主要涉及三角恒等变换,正、余弦定理等内容,对学生的逻辑思维能力提出较高要求.【试题解析】(1)由sin 2cos cos 2sin C C C C C -=,化简得sin C C =,即sin C C +=,即2sin()3C π+= (3分)则sin()32C π+=,故233C ππ+=或3π(舍),则3C π=. (6分)(2) 因为sin cos 2sin cos B A A A =,所以cos 0A =或sin 2sin B A =. (7分)当cos 0A =时,90A =︒,则b =,112223ABC S b c ∆=⋅⋅==; (8分)当sin 2sin B A =时,由正弦定理得2b a =.所以由22222441cos 2222a b c a a C ab a a +-+-===⋅⋅,可知24a =.(10分) 所以211sin 222ABC S b a C a a∆=⋅⋅⋅=⋅⋅==(11分) 综上可知ABC S ∆= (12分)18. (本小题满分12分)【命题意图】本小题主要考查统计与概率的相关知识,其中包括中位数与平均数的求法、对于随机事件出现情况的分析与统计等知识的初步应用. 本题主要考查学生的数据处理能力.【试题解析】解:(1) 因为在频率分布直方图上,中位数的两边面积相等,可得中位数为155. (2分) 平均数为 1200.005201400.075201600.020201800.00520⨯⨯+⨯⨯+⨯⨯+⨯⨯2000.003202200.00220156.8+⨯⨯+⨯⨯=.(4分) (2) 10000.82010000.258002020051710001000⨯⨯+⨯⨯⨯+⨯==(元). (7分)(3) 由题可知,利用分层抽样取出的5户居民中属于第一类的有4户,编为,,,A B C D ,第二类的有1户,编为a . 现从5户中选出2户,所有的选法有aA ,aB ,aC ,aD ,AB ,AC ,AD ,BC ,BD ,CD 共计10种,其中属不同类型的有aA ,aB ,aC ,aD 共计4种.(10分) 因此,两户居民用电资费属不同类型的概率42105P ==.(12分)19. (本小题满分12分)【命题意图】本小题主要考查立体几何的相关知识,具体涉及到线面、面面的垂直关系、空间几何体体积的求取. 本小题对考生的空间想象能力与运算求解能力有较高要求.【试题解析】解:(1) 证明:由题可知,4545ED DF DEF DEF ED DF EF BEAE AB ABE AEB AE AB =⎫⎫∆ ⇒∠=︒⎬⎪⊥⎭⎪⇒⊥⎬=⎫⎪∆ ⇒∠=︒ ⎬⎪⊥⎭⎭中中 (3分)ABE BCDEABE BCDE BE EF PBE PBE PEF EF BE EF PEF ⎫⊥⎫⎪⎪=⇒⊥⎬⎪⇒⊥⎬⎪⊥⎭⎪⎪ ⊂⎭ 平面平面平面平面平面平面平面平面 (6分) (2) 116444221422BEFC ABCD ABE DEF S S S S =--=⨯-⨯⨯-⨯⨯=,则1114333BEFCV S h=⋅⋅=⨯⨯=. (12分) 20.(本小题满分12分)【命题意图】本小题主要考查直线与圆锥曲线的综合应用能力,具体涉及到直线与圆锥曲线的相关知识以及圆锥曲线中极值的求取. 本小题对考生的化归与转化思想、运算求解能力都有很高要求.【试题解析】解:(1) 联立曲线,M N消去y可得22(4)20x x m-+-=,226160x x m-+-=,根据条件可得212212364(16)060160mx xx x m⎧∆=-->⎪+=>⎨⎪=->⎩,4m<<.(4分)(2) 设11(,)A x y,22(,)B x y,21x x>,1y>,2y>则122121()())ABCDS y y x x x x=+-=-==.(6分)令t=,则(0,3)t∈,ABCDS==,(7分) 设32()3927f t t t t=--++,则令22()3693(23)3(1)(3)0f t t t t t t t'=--+=-+-=--+=,可得当(0,3)t∈时,()f x的最大值为(1)32f=,从而ABCDS的最大值为16.此时1t=1=,则215m=. (9分) 联立曲线,M N的方程消去y并整理得2610x x-+=,解得13x=-23x=+,所以A点坐标为(31)-,C点坐标为(31)+,12ACk==-,则直线AC的方程为11)[(32y x--=---,(11分) 当0y=时,1x=,由对称性可知AC与BD的交点在x轴上,即对角线AC与BD交点坐标为(1,0). (12分)21.(本小题满分12分)【命题意图】本小题主要考查函数与导数的综合应用能力,具体涉及到用导数来描述函数的单调性、极值以及函数零点的情况. 本小题主要考查考生分类讨论思想的应用,对考生的逻辑推理能力与运算求解有较高要求.【试题解析】解:(1) 由于()sinxf x e x=,所以'()sin cos (sin cos )sin()4x x x x f x e x e x e x x x π=+=+=+.(2分) 当(2,2)4x k k ππππ+∈+,即3(2,2)44x k k ππππ∈-+时,'()0f x >;当(2,22)4x k k πππππ+∈++,即37(2,2)44x k k ππππ∈++时,'()0f x <.所以()f x 的单调递增区间为3(2,2)44k k ππππ-+()k Z ∈,单调递减区间为37(2,2)44k k ππππ++()k Z ∈.(4分) (2) 令()()sin xg x f x kx e x kx =-=-,要使()f x kx ≥总成立,只需[0,]2x π∈时min ()0g x ≥.对()g x 求导得()(sin cos )xg x e x x k '=+-,令()(sin cos )xh x e x x =+,则()2cos 0xh x e x '=>,((0,)2x π∈)所以()h x 在[0,]2π上为增函数,所以2()[1,]h x e π∈.(6分)对k 分类讨论:① 当1k ≤时,()0g x '≥恒成立,所以()g x 在[0,]2π上为增函数,所以min ()(0)0g x g ==,即()0g x ≥恒成立;② 当21k e π<<时,()0g x '=在上有实根0x ,因为()h x 在(0,)2π上为增函数,所以当0(0,)x x ∈时,()0g x '<,所以0()(0)0g x g <=,不符合题意;③ 当2k e π≥时,()0g x '≤恒成立,所以()g x 在(0,)2π上为减函数,则()(0)0g x g <=,不符合题意.综合①②③可得,所求的实数k 的取值范围是(,1]-∞.(9分)(3) 存在正实数m 使得当(0,)x m ∈时,不等式21()22x f x x <+恒成立. 理由如下:令2()sin 22xx g x e x x =--,要使2()22x f x x <+在(0,)m 上恒成立,只需()0max g x <. (10分)因为()(sin cos )2xg x e x x x '=+--,且(0)10g '=-<,2()(2)022g e πππ'=-+>,所以存在正实数0(0,)2x π∈,使得0()0g x '=,当0(0,)x x ∈时,()0g x '<,()g x 在0(0,)x 上单调递减,即当0(0,)x x ∈时,()(0)0g x g <=,所以只需0(0,)m x ∈均满足:当(0,)x m ∈时,21()22x f x x <+恒成立.(12分)注:因为332.719e e π>>>,22(2)4162π+<=,所以2(2)02e ππ-+>22. (本小题满分10分)【命题意图】本小题主要考查平面几何的证明,具体涉及到四点共圆的证明、圆中三角形相似等内容. 本小题重点考查考生对平面几何推理能力. 【试题解析】解 (1)连结BN ,则AN BN ⊥,又CD AB ⊥, 则90BEF BNF ∠=∠=︒,即180BEF BNF ∠+∠=︒, 则B 、E 、F 、N 四点共圆. (5分)(2)由直角三角形的射影原理可知2AC AE AB =⋅, 由Rt BEF ∆与Rt BMA ∆相似可知:BF BEBA BM=, ()BF BM BA BE BA BA EA ⋅=⋅=⋅-,2BF BM AB AB AE ⋅=-⋅,则22BF BM AB AC ⋅=-,即22AC BF BM AB +⋅=.(10分)23. (本小题满分10分)【命题意图】本小题主要考查极坐标系与参数方程的相关知识,具体涉及到极坐标方程与平面直角坐标方程的互化、平面内直线与曲线的位置关系等内容. 本小题考查考生的方程思想与数形结合思想,对运算求解能力有一定要求. 【试题解析】解:(1)对于曲线1C 消去参数t 得:当2πα≠时,1:1tan (2)C y x α-=-;当2πα=时,1:2C x =.(3分)对于曲线2C :222cos 2ρρθ+=,2222x y x ++=,则222:12y C x +=. (5分)(2) 当4πα=时,曲线1C 的方程为10x y --=,联立12,C C 的方程消去y 得222(1)20x x +--=,即23210x x --=,||MN ====圆心为1212(,)22x x y y ++,即12(,)33-,从而所求圆方程为22128()()339x y -++=.(10分)24. (本小题满分10分)【命题意图】本小题主要考查不等式的相关知识,具体涉及到绝对值不等式及 不等式证明等内容. 本小题重点考查考生的化归与转化思想.【试题解析】解:(1) 24()624x f x x -+⎧⎪=⎨⎪-⎩1155x x x <--≤≤>(2分)当1x <-时,2410x x -+≤+,2x ≥-,则21x -≤<-; 当15x -≤≤时,610x ≤+,4x ≥-,则15x -≤≤; 当 5x >时,2410x x -≤+,14x ≤,则514x <≤. 综上可得,不等式的解集为[2,14]-.(5分)(2) 设2()(2)g x a x =--,由函数()f x 的图像与()g x 的图像可知:()f x 在[1,5]x ∈-时取最小值为6,()f x 在2x =时取最大值为a , 若()()f x g x ≥恒成立,则6a ≤.(10分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
吉林省长春市2009—2010学年度高中毕业班第三次调研测试理科综合试题本试卷分为第I卷(选择题)和第II卷(非选择题)两部分,其中第II卷33~40为选考题,其它题为必答题。
考试结束后,将试卷和答题卡一并交回。
注意事项:1.答题前,考生必须将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠、不要弄破,不准使用涂改液、刮纸刀。
选择题(选择题,共21小题,每小题6分,共126分)以下数据可供解题时参考:相对原子质量(原子量):H:1 N:14 O:16 Fe:56一、选择题:本题共13小题,每小题6分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列有关酶的叙述不正确...的是()A.酶比无机催化剂更能显著降低化学反应的活化能B.淀粉酶被水解的最终产物是氨基酸C.光合作用所需的酶仅存在于叶绿体基质中D.胰岛B细胞的细胞质中有作用于DNA的解旋酶2.右图表示一些概念间的相互关系。
下列与a、b、c、d、e依次相对应的一组概念是()A.生态系统、群落、无机环境、种群、个体B.细胞代谢、细胞呼吸、光合作用、有氧呼吸、丙酮酸彻底氧化分解C.免疫、特异性免疫、非特异性免疫、体液免疫、细胞免疫D.细胞核、染色体、同源染色体、非同源染色体、染色单体3.下列有关种群、群落和生态系统的叙述正确的是()A.现代生物进化理论认为,种群中的个体是生物进化的基本单位B.动物群落的演替与光照条件无关C .水稻田内不规则分布的杂草,体现了群落结构水平方向上的差异D .生态系统中的信息传递和能量流动都是单向的4.下面为人体的细胞凋亡及清除示意图。
据图分析,不正确...的是 ( )A .①过程体现了生物膜的信息传递功能B .细胞凋亡过程是由基因所决定的细胞程序性死亡的过程C .②过程中有新的蛋白质合成D .若凋亡相关基因发生突变,必将导致细胞发生癌变 5.下列有关人体内环境稳态调节的叙述,正确的是 ( ) A .剧烈运动时,由于胰岛素分泌量减少,将导致血糖含量下降 B .肌细胞无氧呼吸产生的乳酸进入血液后,将导致血浆pH 明显降低 C .机体大量产热后,只能通过皮肤内的毛细血管散热 D .吃的食物过咸时,机体分泌的抗利尿激素增加6.生物兴趣小组利用某二倍体农作物①和②两个品种进行了如下实验,下列有关分析不正..确.的是( )A .由⑤×⑥培育出的⑧植株为新物种B .由③到④的育种过程依据的原理是基因突变C .若③的基因型为AaBbdd ,则获得的⑦植株中纯合子约占1/4D .由⑤到⑦过程中可能发生基因突变7.世界气候大会于2009年12月在丹麦首都哥本哈根召开。
会议的主题是“促进低碳经济,减少2CO 的排放”。
下列行为中不符合...这一主题的是 ( )A .开发新能源,如太阳能、风能等,减少对化石能源的依赖B .限制化工发展,关停化工企业,消除污染源头C .加快研发利用二氧化碳合成聚碳酸酯类可降解塑料D .推广煤的气化、液化技术、提供清洁燃料和化工原料 8.下列关于有机物的说法中正确的是 ( )A .淀粉和纤维素互为同分异构体B .蛋白质和淀粉水解的最终产物都是氨基酸C .油脂、纤维素、淀粉在一定条件下均可发生水解反应D .蛋白质、纤维素、蔗糖都是高分子化合物 9.下列叙述正确的是 ( )A .将2CO 通入2BaCl 溶液中至饱和,无沉淀产生;再通入2CO ,产生沉淀B .32()Ca HCO 溶液和2BaCl 溶液混合无沉淀;再加入NaOH 溶液仍无沉淀产生C .向3AlCl 溶液中滴加氨水,产生白色沉淀;再加入4NaHSO 溶液,沉淀消失D .纯锌与稀硫酸反应产生氢气的速率较慢;再加入少量4CuSO 固体,速率不改变10.已知下列反应的热化学方程式为:( )①22()()()C s O g CO g +==;1393.5H kJ mol -∆=-②3222(l)2()2()2(l)CH COOH O g CO g H O +==+;1870.3H kJ mol -∆=-③2221()()(l)2H g O g H O +==;1285.8H kJ mol -∆=- 则反应2232()2()()(l)C s H g O g CH COOH ++==的H ∆为A .1488.3kJ mol -+ B .1488.3kJ mol -- C .1244.15kJ mol --D .1244.15kJ mol -+11.下列离子方程式正确的是( )A .用惰性电极电解饱和食盐水:222H C Cl H O l OH --+↑+↑+电解B .用3FeCl 溶液腐蚀印刷电路板:322Fe Cu FeCu ++++==+C .将3FeCl 饱和溶液滴入沸水中制取3()Fe OH 胶体:3+23()3H O F ()3H Fe e OH +++ 胶体D .向NaClO 溶液中通入过量2SO :22242ClO SO H O Cl SO H ---+++==++12.一定条件下,将X 和Y 两种气体按不同比例通入固定容积的密闭容器中,反应达平衡后,测得X 、Y 的转化率与起始时物质的量之比:()()n X n Y 的关系如下图所示。
改变温度和压强,生成物Z 的百分含量如下表所示,则该反应的化学方程式可表示为 ( )A .3()()4();0X g Y g Z g H +∆>B .()3()4();0X g Y g Z g H +∆>C .3()()3();0X g Y g Z g H +∆<D .()3()3();0X g Y g Z g H +∆<13.关于下列图示的说法中正确的是( )A .图①表示可逆反应“222()()()()CO g H O g CO g H g ++ ”中的H ∆大于0B .图②为电解硫酸铜溶液的装置,两电极产生单质的物质的量之比为1:1C .图③两个装置中通过导线的电子数相同时,消耗负极材料的物质的量也相同D .图④实验装置可完成比较碳酸和硅酸的酸性强弱的实验二、选择题:本题共8小题,每小题6分,共48分。
在每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.在变电站里,经常要用交流电表去监测电网上的高电压,所用的器材叫电压互感器。
如下所示的四个图中,能正确反应其工作原理的是 ( )15.一个物块位于斜面上,受到平行于斜面的水平力F 的作用处于静止状态,如图所示。
如果将外力F 撤去,则物块 ( )A .会沿斜面下滑B .摩擦力的值变大C .摩擦力的值不变D .摩擦力方向一定变化16.如图所示,地面上有两个完全相同的木块A 、B ,在水平推力F 作用下运动,当弹簧长度稳定后,若用μ表示木块与地面间的动摩擦因数,N F 表示弹簧弹力,则 ( ) A .0μ=时,12N F F =B .0μ=时,N F F =C .0μ≠时,12N F F =D .0μ≠时,N F F =17.如图所示为一个实物连接的电路图,电源电动势为E ,内电阻为r 。
两电压表1V 和2V 可看作是理想电表。
当闭合开关,将滑动变阻器的滑片由右端向左滑动时,下列说法中正确的是 ( )A .小灯泡1L 、2L 均变暗B .小灯泡1L 变亮,1V 表的读数变大,C .小灯泡2L 变亮,1V 表的读数变小D .小灯泡1L 变暗,2V 表的读数变大18.“黑洞”是广义相对论引力理论所预言的宇宙中的一种特殊天体。
研究认为,黑洞可能是由于超中子星发生塌缩,而形成的密度极大的宇宙中的奇点,以至于物体以光速绕其运动都无法逃离。
欧洲航天局由卫星观测发现银河系中心存在着一个超大型黑洞并将它命名为:MCG6-30-15r 。
假设银河系中心仅此一个黑洞,已知太阳绕银河系中心做匀速圆周运动,则根据下列哪一组数据可以估算出该黑洞的质量 ( ) A .太阳的质量和绕其运行的速度 B .太阳绕黑洞公转的周期和太阳到黑洞中心的距离 C .已知光速和黑洞的半径可估算黑洞质量的最大值 D .太阳绕黑洞运行速度和黑洞的的半径19.某空间内有高度为d 、宽度足够宽、方向水平向左的匀强电场。
当在该空间内建立如图所示的坐标系后,在x 轴上的P 点沿y 轴正方向连续射入质量和电荷量均相同、且带电性质也相同的带电粒子(不计粒子重力、粒子间相互作用及粒子对电场的影响),由于粒子的入射速率不同, 有的粒子将在电场中直接通过y 轴,有的将穿出电场后 再通过y 轴。
设粒子通过y 轴时,离坐标原点的距离为h ,从P 到y 轴所需的时间为0t ,则 ( )A .由题中条件可以判断出粒子的带电性质B .对h d ≤的粒子,h 越大,0t 越大C .对h d ≤的粒子,在时间0t 内,电场力对粒子做的 功不相等D .对h d >的粒子,h 越大,电场力对粒子做的功越大20.某一空间存在着磁感应强度大小不变、方向随时间周期性变化的磁场(忽略磁场瞬间变化所产生的感应电场),如图甲所示,规定垂直纸面向里的磁场方向为正方向。
为了使静止在该磁场中的带正电的粒子能做横“∞”字曲线运动且逆时针方向通过fgab (轨迹如图乙),已知磁场变化周期T 等于粒子完成一次横“∞”字曲线运动的时间,则可行的办法是(粒子只受磁场力作用,其它力不计) ( )A.若粒子初始位置在g处,12t T=时给粒子一个沿切线方向竖直向下的初速度B.若粒子初始位置在a处,38t T=时给粒子一个沿切线方向水平向右的初速度C.若粒子初始位置在f处,118t T=时给粒子一个沿切线方向水平向左的初速度D.若粒子初始位置在d处,t T=时给粒子一个沿切线方向竖直向上的初速度21.质量为2kg的物体,放在动摩擦因数μ=0.1的水平面上,在水平拉力F的作用下,由静止开始运动,拉力做的功W和物体发生的位移x之间的关系如图所示,g=10m/2s。
则对此物体的说法正确的是()A.此物体在AB段做匀速直线运动B.此物体在AB段做匀加速直线运动C.整个过程中拉力的最大功率为5W。
D.整个过程中拉力的最大功率为15W。
第Ⅱ卷(非选择题,共174分)三、非选择题:包括必考题和选考题两部分。
第22题~第32题为必考题。
每个小题考生都必须做答。
第33题~第40题为选考题,考生根据要求做答。
(一)必考题(11题,共129分)22.(4分)(1)用游标为20分度的游标卡尺测量某物体的长度如图甲,由图可知其长度为mm;(2)用螺旋测微器测量某物体的直径如图乙,由图可知其直径为 mm 。
