高中数学必修二直线和圆与方程综合测试卷
必修2第二章直线与圆的方程综合测试卷

高二(上)数学直线与圆模块卷试卷满分150分 考试时间120分钟一.选择题(共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.)1. 直线10x -=的倾斜角α= ( )A .30︒B .60︒C .120︒D .150︒2. 已知O :221x y +=与C :222410x y x y +--+=,则两圆的位置关系是( )A .相交B .相离C .外切D .内切3. 若直线()()2130a x a y ++--=与直线()()12320a x a y -+++=互相垂直,则a 的值为( )A .1B .1-C .1±D .32-4. 若直线1l :10ax y +-=与直线2l :10x ay ++=平行,则a 的值为( )A .1-B .0C .1D .1-或15. 过点()3,1作圆()2211x y -+=的两条切线,切点分别为A ,B ,则直线AB 的方程为( )A .230x y +-=B .230x y --=C .430x y --=D .430x y +-=6. 已知点()2,3A -,()3,2B --,直线l 的方程为10kx y k -++-=,且与线段AB 相交,则直线l 的斜率k 的取值范围为 ( )A .34k 或4k -B .34k 或14k -C .344k-D .344k7. 当点(3,2)P 到直线120mx y m -+-=的距离最大时,实数m 的值为( )AB .1C .0D .1-8. 已知()2,1A -,()1,2B ,点C 为直线30x y -=上的动点,则AC BC +的最小值为( )A .B .C .D .二.多选题(共4小题,每小题5分,共20分.不选、错选得0分,漏选得2分) 9. 以下表述正确的是 ( )A .直线()()1213m x m y -+-=(m ∈R )恒过定点()6,3-B .已知直线l 过点()2,4P ,且在x ,y 轴上截距相等,则直线l 的方程为60x y +-=C .当a = 0或a = 3时,直线210ax y +-=与直线()1210a x ay +-+=垂直D .直线1l :10x y ++=,2l :10x y +-=10. 已知圆22260x y x y a +--+=上至多有一点到直线3450x y ++=的距离为2,则实数a 可能的取值为 ( )A .5B .6C .7D .10 11. 已知点P 在圆()()225516x y -+-=上,点()4,0A ,()0,2B ,则( )A .点P 到直线AB 的距离小于10 B .点P 到直线AB 的距离大于2C .当PBA ∠最小时,PB =D .当PBA ∠最大时,PB =12. 已知圆O :224x y +=和圆M :224240x y x y +--+=交于P ,Q 两点,则 ( )A .两圆有两条公切线B .PQ 垂直平分线段OMC .直线PQ 的方程为240x y +-=D .线段PQ 三.填空题(共4小题,每小题5分,共20分.)13. 直线1l :3420x y +-=与2l :6810x y ++=的距离是__________.14. 若曲线22:6100C x y x y a +-++=上存在不同的两点关于直线7y kx =+对称,则k =__________.15. y 轴交于点A ,与圆()2211x y +-=相切于点B ,则AB =__________.16. 在圆22260x y x y +--=内,过点()0,1E 的最长弦和最短弦分别是AC 和BD ,则四边形ABCD 的面积为__________.四.解答题(共6小题,第17题10分,其余每题12分,共70分.)17. 直线l 经过两条直线1:40l x y +-=和2:20l x y -+=的交点,且__________.(1)求直线l 的方程;(2)求直线l 与坐标轴围成的三角形面积.试从以下两个条件中任选一个补充在上面的问题中,完成解答,若选择多个条件分别解答,按第一个解答计分. ①与直线210x y --=平行. ②直线l 在x 轴上的截距为12-.18. 已知ABC △的顶点()2,8C -,直线AB 的方程为211y x =-+,AC 边上的高BH 所在直线的方程为320x y ++=. (1)求顶点A 和B 的坐标; (2)求ABC △外接圆的一般方程.19. 已知方程22224230x y mx y m m ++++-=表示一个圆.(1)求实数m 的取值范围; (2)求半径R 的最大值.20. 已知点()3,5M ,圆()()22:124C x y -+-=.(1)若过点M 的直线l 与圆C 相切,求直线l 的方程;(2)若直线40ax y -+=与圆C 相交于A ,B 两点,弦AB 的长为a 的值.21. 已知圆C 经过()1,0M ,()2,1N 两点,且圆心C 在直线220x y +-=上.(1)求圆C 的方程;(2)过点()0,1P 的直线l 与圆C 交于不同的A ,B 两点,且CA CB ⊥,求直线l 的方程.22. 在平面直角坐标系xOy 中,P 为圆C :228120x y x +-+=上的动点,线段OP 中点M 的轨迹记为曲线Γ. (1)求曲线Γ的方程;(2)已知动点Q 在y 轴上,直线l 与曲线Γ交于A ,B 两点,求证:若直线QA ,QB 均与曲线Γ相切,则直线l 恒过定点.高二(上)数学_直线与圆模块卷参考答案与试题解析一. 选择题1.可得直线10x -=的斜率为k =由斜率和倾斜角的关系可得tan α又0180α︒︒<30α︒∴=故选:A .2.根据题意,O :221x y +=,其圆心为()0,0,半径1r =C :222410x y x y +--+=,即()()22124x y -+-=,其圆心为()1,2,半径2R =圆心距OC =则有13R r OC R r -=<<+=,则两圆相交 故选:A .3.直线()()2130a x a y ++--=与直线()()12320a x a y -+++=互相垂直 ()()()()211230a a a a ∴+-+-+=,解得1a =±故选:C .4.直线1l :10ax y +-=与直线2l :10x ay ++=平行 ①0=a 时,不平行②0≠a 时,1111-=≠a a ,求得1a =故选:C .5.因为过点()3,1作圆()2211x y -+=的两条切线,切点分别为A ,B可得圆的一条切线方程为1y =,切点之一为()1,1,显然B ,D 选项不过()1,1,B ,D 不满足题意另一个切点的坐标在()1,1-的右侧,所以两切点连线的斜率为负,选项C 不满足,A 满足 故选:A .6.直线l 的方程:10kx y k -++-=可化为()11y k x -=- 即直线l 过定点()1,1,可设为()1,1P 31421PA k --==--,213314PB k --==-- 又直线l 与线段AB 相交,且312-<<∴直线l 的斜率k 的取值范围为(]3,4,4⎡⎫-∞-+∞⎪⎢⎣⎭故选:A .7.直线方程是120mx y m -+-=∴直线方程是1(2)y m x -=-∴直线恒过定点()2,1,不妨记该点为点Q∴当PQ 与直线120mx y m -+-=垂直时,点P 到直线120mx y m -+-=的距离最大点P 的坐标为()3,221132PQ k -∴==- ∴直线120mx y m -+-=的斜率1m =- ∴实数m 的值为1-故选:D .8.()2,1A -,()1,2B ,点C 为直线30x y -=上的动点 设点()2,1A -关于直线30x y -=的对称点为(),D a b 则132213022b a a b -⎧=-⎪⎪+⎨-+⎪-⨯=⎪⎩,解得1a =-,2b =-()1,2D ∴--AC BC DC BC ∴+=+当B ,D ,C 共线时,DB 的最小值为:()()22112225DB =+++=故选:C .二. 多选题9.A .()()1213m x m y -+-=(m ∈R ),即()230m x y x y +---=,直线恒过20x y +=与30x y ---=的交点,解得6x =-,3y =,恒过定点()6,3-,故正确B .直线l 过点()2,4P ,在x ,y 轴上截距相等,当截距不为0时则直线方程为60x y +-=,截距为0时直线方程为20x y -=,故错误C .由题意“直线210ax y +-=与直线()1210a x ay +-+=垂直” 则()()1220a a a ++⨯-=,解得0a =或3a =所以由题意“直线210ax y +-=与直线()1210ax x ay +-+=垂直”是“0=a 或3a =”的充要条件,故正确D .直线1l :10x y ++=,直线2l :10x y +-= 所以两直线的距离为2211211+=+,故正确故选:ACD .10.圆22260x y x y a +--+=,即()()2213100x y a -+-=-> 圆心为()1,3,半径为10a -,10a < 圆心()1,3到直线3450x y ++=的距离为3143545d ⨯+⨯+==因为圆上至多有一点到直线3450x y ++=的距离为2 所以01042<--a ,解得610a <综合选项可知,实数a 可能的取值为6,7 故选:BC .11.由题意得直线AB 的方程为240x y +-= 如图所示,A .P 到AB 的距离最大值为51044105d +-=+<,A 正确B .P 到AB 的距离最小值为11425d =-<,B 错误C .当P 在P '时,PBA ∠最小,此时()2341632PB =-=D .当P 在P ''时,PBA ∠最大,此时,32PB = 故选:ACD .12.由题意,圆M 的方程可化为()()22211x y -+-= 所以圆M 的圆心是()2,1M ,半径为1如图,A .因为两圆相交,交点为P ,Q ,则两圆有两条公切线,A 正确 B .由图可知,PQ 垂直于OM ,但不平分OM ,B 不正确 C .两圆的方程相减得,240x y +-= 因为P 和Q 是两圆的交点所以P 和Q 的坐标满足方程240x y +-= 即直线PQ 的方程为240x y +-=,C 正确 D .因为2OP =,1PM =,()()2220105OM =-+-=所以在Rt POH △和Rt PMH △中,由勾股定理得 2222OP PH MP PHOH MH OM -+-=+=即22415PH PH -+-=,解得255PH =所以455PQ =,D 正确 故选:ACD .三. 填空题13.两条直线1l :3420x y +-=与2l :6810x y ++= 化为直线1l :6840x y +-=与2l :6810x y ++= 则1l 与2l 的距离是:22141268+=+ 故答案为:12.14.解:曲线22:6100C x y x y a +-++=上存在不同的两点关于直线7y kx =+对称∴由已知,得直线7y kx =+过圆C 的圆心()3,5C -537k ∴-=+,解得4k =-故答案为:4-.15.因为圆的方程为()2211x y +-=所以1r =,圆心为()0,1所以22111A B A B ==16.圆22260x y x y +--=,即()()221310x y -+-=表示以()1,3M由圆的弦的性质可得,最长的弦即圆的直径,AC 的长为点()0,1E∴==ME弦长BD 最短时,弦BD 和ME 垂直,且经过点E ,此时===BD故四边形ABCD 的面积为12⨯=AC BD故答案为:四.解答题17.解:(1)选①直线l 经过两条直线1:40l x y +-=和2:20l x y -+=的交点 ∴4020x y x y +-=⎧⎨-+=⎩,解得1x =,3y =,即()1,3P直线l 与直线210x y --=平行∴可设直线l 的方程20x y m -+=,把()1,3P 代入可得1m =直线l 的方程为210x y -+=选②直线l 经过两条直线1:40l x y +-=和2:20l x y -+=的交点 ∴4020x y x y +-=⎧⎨-+=⎩,解得1x =,3y =,即()1,3P 由题意可知直线的斜率存在,设为k 且0k ≠ 则()31y k x -=-过1,02⎛⎫- ⎪⎝⎭代入可得2k =直线l 的方程210x y -+=(2)在直线:210l x y -+=中,令0x =可得1y =,令0y =可得12x = 所以直线l 与坐标轴围成的三角形面积1111224S =⨯⨯=18.解:(1)由211320y x x y =-+⎧⎨++=⎩可得顶点()7,3B -又因为AC BH ⊥得,13BH k =-所以设AC 的方程为3y x b =+ 将()2,8C -代入得14b =- 由211314y x y x =-+⎧⎨=-⎩可得顶点为()5,1A所以A 和B 的坐标分别为()5,1和()7,3-(2)设ABC △的外接圆方程为220x y Dx Ey F ++++=将()5,1A 、()7,3B -和()2,8C -三点的坐标分别代入得52607358028680D E F D E F D E F +++=⎧⎪-++=⎨⎪-++=⎩则有4612D E F =-⎧⎪=⎨⎪=-⎩所以ABC △的外接圆的一般方程为2246120x y x y +-+-=19.解:(1)根据题意,22224230x y mx y m m ++++-= 即()()222234x m y m m +++=-++若方程22224230x y mx y m m ++++-=表示一个圆,则有2340m m -++> 解可得14m -<<即实数m 的取值范围是()1,4-(2)根据题意,由(1)的结论,圆的半径2223252534244R m m m ⎛⎫=-++=--+⎪⎝⎭ 当且仅当32m =时,半径R 取得最大值5220.解:(1)由题意知圆心的坐标为()1,2,半径2r = ①当过点M 的直线斜率不存在时由圆心()1,2到直线3x =的距离312r -==知,直线3x =与圆相切 ②当过点M 的直线存在斜率k 时设方程为()53y k x -=-,即530kx y k -+-= 2=解得512k =∴直线l 的方程为512450x y -+=故过点M 的圆的切线方程为3x =或512450x y -+=(2)圆心()1,2到直线40ax y -+==∴224⎛⎫+=解得34a =-21.(1)由题意设圆C 的方程为:220x y Dx Ey F ++++=(2240D E F +->) 根据圆C 经过()1,0M ,()2,1N 两点,且圆心C 在直线220x y +-=上可得 10412022022D F D E F D E ⎧⎪++=⎪⎪++++=⎨⎪⎛⎫⎪-+⨯--= ⎪⎪⎝⎭⎩,解得4D =-,0E =,3F =,满足2240D E F +-> 故圆C 的方程为:22430x y x +-+= (2)由(1)知,圆心()2,0C ,半径1r =由CA CB ⊥,可知三角形ABC 为等腰直角三角形,故圆心C 到直线AB 的距离为1sin 45︒⨯=由题意,可知直线l 的斜率一定存在设直线l 的方程为:1y kx =+,即10kx y -+= 故圆心C 到直线l的距离为=,整理得27810k k ++=,解得1k =-,或17k =- 故直线l 的方程为:1y x =-+或117y x =-+即10x y +-=或770x y +-=22.(1)圆C :228120x y x +-+=即为()2244x y -+= 设(),P m n ,(),M x y ,由M 为OP 的中点,可得2m x =,2n y = 由()2244m n -+=,可得()()222424x y -+= 化为()2221x y -+=即曲线Γ的方程为:()2221x y -+= (2)设()0,Q t由上一问可得曲线Γ为圆,设圆心为()2,0C由直线QA ,QB 均与曲线Γ相切,可得QA AC ⊥,QB BC ⊥ 可得Q ,A ,B ,C 四点共圆,且以QC 为直径圆的圆心为1,2t ⎛⎫⎪⎝⎭其圆的方程为()22212t x y ⎛⎫-+-= ⎪⎝⎭⎝⎭①又圆C :()2221x y -+=② ①②两式相减可得,直线l 的方程为230x ty --=令230x -=,且0y =,解得32x =,0y = 则直线l 恒过定点3,02⎛⎫ ⎪⎝⎭。
(word完整版)高中数学必修二直线与方程及圆与方程测试题.docx
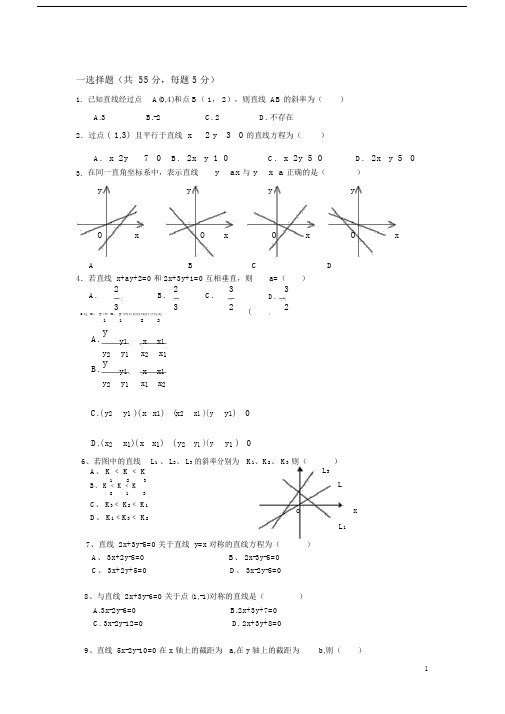
一选择题(共 55 分,每题 5 分)1. 已知直线经过点A(0,4)和点 B ( 1, 2),则直线 AB 的斜率为( )A.3B.-2C. 2D. 不存在2.过点 ( 1,3) 且平行于直线 x2 y3 0 的直线方程为()A . x 2y7 0 B . 2x y 1 0 C . x 2y 5 0 D . 2x y 5 0 3. 在同一直角坐标系中,表示直线y ax 与 yx a 正确的是()yyyyOxOxOxO xABCD4.若直线 x+ay+2=0 和 2x+3y+1=0 互相垂直,则a=()A .2B .2 C .33332D .(25.过 (x , y )和 (x , y )两点的直线的方程是)11 22A. yy 1 x x 1 y 2y 1 x 2 x 1 B.yy 1 x x 1 y 2 y 1x 1 x 2C.( y 2 y 1 )( x x 1) (x 2 x 1 )( y y 1) 0D.( x 2x 1)( x x 1) ( y 2 y 1 )( yy 1 ) 06、若图中的直线 L 1 、 L 2、 L 3 的斜率分别为 K 1、K 2、 K 3 则()A 、 K ﹤ K ﹤ KL 3123LB 、 K ﹤ K ﹤ K2 1 3C 、 K 3﹤ K 2﹤ K 1oxD 、 K 1﹤K 3﹤ K 2L 17、直线 2x+3y-5=0 关于直线 y=x 对称的直线方程为( )A 、 3x+2y-5=0B 、 2x-3y-5=0C 、 3x+2y+5=0D 、 3x-2y-5=08、与直线 2x+3y-6=0 关于点 (1,-1)对称的直线是()A.3x-2y-6=0B.2x+3y+7=0C. 3x-2y-12=0D. 2x+3y+8=0A.a=2,b=5;B.a=2,b= 5 ;C.a= 2 ,b=5;D.a= 2 ,b= 5 .10、直线 2x-y=7 与直线 3x+2y-7=0 的交点是()A (3,-1)B (-1,3)C (-3,-1)D (3,1)11、过点 P(4,-1)且与直线 3x-4y+6=0垂直的直线方程是()A 4x+3y-13=0B 4x-3y-19=0C 3x-4y-16=0D 3x+4y-8=0二填空题(共20 分,每题 5 分)12.过点(1,2)且在两坐标轴上的截距相等的直线的方程_ __________;13 两直线 2x+3y- k=0 和 x- ky+12=0 的交点在y 轴上,则k 的值是14、两平行直线x 3y 4 0与 2x 6 y 9 0 的距离是。
人教A版高中数学必修2第四章《圆与方程》测试题(含答案)

由于 ,故O在线段PM的垂直平分线上,又P在圆N上,从而 .
因为ON的斜率为3,所以 的斜率为 ,故 的方程为 .
又 ,O到 的距离为 , ,所以 的面积为 .
21.(1).由已知得过点 的圆的切线斜率的存在,
设切线方程为 ,即 .
则圆心 到直线的距离为 ,
A. B.
C. D.
5.一条光线从点 射出,经 轴反射后与圆 相切,则反射光线所在直线的斜率为()
A. 或 B. 或 C. 或 D. 或
6.已知圆 截直线 所得线段的长度是 ,则圆 与圆 的位置关系是( )
A.内切B.相交C.外切D.相离
7.已知方程 ,则 的最大值是( )
A.14- B.14+ C.9D.14
A.4B.6C. D.
12.已知直线 : 是圆 的对称轴.过点 作圆 的一条切线,切点为 ,则 ( )
A.2B. C.6D.
二、填空题
13.已知两点 ,以线段 为直径的圆的方程为________________.
14.方程x2+y2-x+y+m=0表示一个圆,则m的取值范围是_______
15.已知 为直线 上一点,过 作圆 的切线,则切线长最短时的切线方程为__________.
当 的斜率不存在, 的斜率等于0时, 与圆 不相交, 与圆 不相交.
当 、 的斜率存在且都不等于0,两条直线分别与两圆相交时,设 、 的方程分别为 ,即 .
因为 到 的距离 ,
到 的距离 ,所以 到 的距离与 到 的距离相等.
所以圆 与圆 的半径相等,所以 被圆 截得的弦长与 被圆 截得的弦长恒相等.
综上所述,过点 任作互相垂直的两条直线分别与两圆相交,所得弦长恒相等.
高中数学必修二直线和圆与方程综合测试卷之欧阳道创编

高中数学必修二直线和圆与方程综合测试卷姓名分数一.选择题(每题3分,共30分)1. 已知直线经过点A(0,4)和点B(1,2),则直线AB的斜率为()A.3B.-2C. 2D. 不存在()2.AD3. 在同一直角坐标系中,是()A B C D 4.若直线x+ay+2=0和2x+3y+1=0互相垂直,则a=()A B C D5若线段AB 的中点为(1,1)M -,则直线l 的斜率为( )A .23B .32C .32-D .23- 6.与直线2x+3y-6=0关于点(1,-1)对称的直线是( )A.3x-2y-6=0B.2x+3y+7=0C. 3x-2y-12=0D. 2x+3y+8=07.平行直线x -y +1 = 0,x -y -1 = 0间的距离是( )A .22B .2C .2D .22 8. 圆22(2)5x y ++=关于原点(0,0)P 对称的圆的方程为( )A.22(2)5x y -+=B.22(2)5x y +-= C.22(2)(2)5x y +++= D.22(2)5x y ++= 9. 若)1,2(-P 为圆25)1(22=+-y x 的弦AB 的中点,则直线AB 的方程是( )A.03=--y xB.032=-+y xC.01=-+y xD.052=--y x 10. 圆012222=+--+y x y x 上的点到直线2=-y x 的距离最大值是( )A.2B.21+C.221+ D.221+二.填空题(共20分,每题4分)11.过点(1,2)且在两坐标轴上的截距相等的直线的方程.12.两直线2x+3y -k=0和x -ky+12=0的交点在y 轴上,则k 的值是 .13.两平行直线0962043=-+=-+y x y x 与的距离是.14.空间两点M1(-1,0,3),M2(0,4,-1)间的距离是.15.圆心在直270x y --=的C y 交于两点(0,4),(0,2)A B --,则圆C 的方程为.三.计算题(每题10分,共50分)16.已知三角形ABC 的顶点坐标为A (-1,5)、B (-2,-1)、C (4,3),M 是BC 边上的中点。
高中数学 人教版 必修二 直线与圆的方程综合复习题(含答案)

直线与圆的方程综合复习(含答案)一. 选择题1.已知点A(1,. 3),B(-1,33),则直线AB 的倾斜角是( C ) A 3B 6C 23D 562.已知过点A(-2,m)和B (m,4)的直线与直线2x+y-1=0平行,则m 的值为( C ) A 0 B 2 C -8 D 103.若直线L 1:ax+2y+6=0与直线L 2:x+(a-1)y+(2a -1)=0平行但不重合,则a 等于( D )A -1或2B 23C 2D -14.若点A (2,-3)是直线a 1x+b 1y+1=0和a 2x+b 2y+1=0的公共点,则相异两点 (a 1,b 1)和(a 2,b 2)所确定的直线方程是( A ) A.2x-3y+1=0 B.3x-2y+1=0 C.2x-3y-1=0 D.3x-2y-1=05.直线xcos θ+y-1=0 (θ∈R )的倾斜角的范围是 ( D )A.[)π,0B.⎪⎭⎫⎢⎣⎡ππ43,4C.⎥⎦⎤⎢⎣⎡-4,4ππD.⎪⎭⎫⎢⎣⎡⎥⎦⎤⎢⎣⎡πππ,434,06.“m=12”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2y)-3=0相互垂直”的( B )A 充分必要条件B 充分而不必要条件C 必要而不充分条件D 既不充分也不必要条件7.已知A(7,-4)关于直线L 的对称点为B (-5,6),则直线L 的方程为(B ) A 5x+6y-11=0 B 6x-5y-1=0 C 6x+5y-11=0 D 5x-6y+1=0 8.已知直线1l 的方向向量a=(1,3),直线2l 的方向向量b=(-1,k).若直线2l 经过点(0,5)且1l 2l ,则直线2l 的方程为( B )A x+3y-5=0B x+3y-15=0C x-3y+5=0D x-3y+15=0 9. 过坐标原点且与圆2x +2y -4x+2y+52=0相切的直线方程为( A )A y=-3x 或y= 13xB y=3x 或y= -13xC y=-3x 或y= -13xD y=3x 或y= 13x10.直线x+y=1与圆2x +2y -2ay=0(a>0)没有公共点,则a 的取值范围是(A )A (02-1,)B (2-1, 2+1)C (-2-1, 2-1)D (0, 2+1) 11.圆2x +2y -4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离的差是( C )A 36B 18C 62D 5212.以直线:y=kx-k 经过的定点为P 为圆心且过坐标原点的圆的方程为(D ), A 2x +2y +2x=0 B 2x +2y +x=0 C 2x +2y -x=0 D 2x +2y -2x-013.已知两定点A(-2,0),B(1,0),如果定点P 满足PA=2PB,则定点P 的轨迹所 包围的面积等于( B )A B 4 C 8 D 914.若直线3x+y+a=0过圆2x +2y +2x-4y=0的圆心,则a 的值为( B )A 1B -1C 3D -315.若直线2ax-by+2=0 (a >0,b >0)始终平分圆x 2+y 2+2x-4y+1=0的周长,则ba11+的最小值是( C )A.41B.2C.4D.2116.若直线y=k(x-2)+4与曲线y=1+24x -有两个不同的交点,则k 的取值范围是 ( A )A.⎥⎦⎤⎝⎛43,125 B.⎪⎭⎫⎝⎛+∞,125 C.⎥⎦⎤⎝⎛43,21D.⎪⎭⎫⎝⎛125,17.设两圆1C ,2C 都和两坐标轴相切,且过点(4,1),则两圆心的距离 ︱1C 2C ︱等于( C )A 4B 42C 8D 8218.能够使得圆x 2+y 2-2x+4y+1=0上恰有两个点到直线2x+y+c=0距离等于1的c的一个值为 ( C ) A.2B.5C.3D.3519.若直线by ax +=1与圆x 2+y 2=1有公共点,则( D )A.a 2+b 2≤1B.a 2+b 2≥1C.2211ba +≤1 D.2211ba +≥120.已知A (-3,8)和B (2,2),在x 轴上有一点M ,使得|AM|+|BM|为最短,那么点M 的坐标为( B ) A.(-1,0)B.(1,0)C.⎪⎭⎫⎝⎛0522,D. ⎪⎭⎫⎝⎛522,021.直线y=kx+3与圆2(3)x+2(2)y =4相交于M 、N 两点,若︱MN ︱≥23,则k 的取值范围是( A )A [-34,0] B [-∞,-34] [0,∞) C [-33,33] D [-23,0] 22.(广东理科2)已知集合{(,)|,A x y x y =为实数,且221}x y +=,{(,)|,B x y x y =为实数,且}y x =,则AB 的元素个数为(C )A .0B .1C .2D .3 23.(江西理科9)若曲线02221=-+x y x C :与曲线 0)(2=--m mx y y C :有四个不同的交点,则实数m 的取值范围是 ( B ) A. )33,33(-B. )33,0()0,33( -C. ]33,33[-D. ),33()33,(+∞--∞ 答案:B 曲线0222=-+x y x 表示以()0,1为圆心,以1为半径的圆,曲线()0=--m mx y y 表示0,0=--=m mx y y 或过定点()0,1-,0=y 与圆有两个交点,故0=--m mx y 也应该与圆有两个交点,由图可以知道,临界情况即是与圆相切的时候,经计算可得,两种相切分别对应3333=-=m m 和,由图可知,m 的取值范围应是)33,0()0,33( -二.填空题24.已知圆C 经过)3,1(),1,5(B A 两点,圆心在X 轴上,则C 的方程为10)2(22=+-y x ___________。
高中数学-人教版-必修二-直线与圆的方程综合复习题(含答案)

直线与圆的方程综合复习(含答案)一. 选择题1.已知点A(1,. 3),B(-1,33),则直线AB 的倾斜角是( C ) A3B6C 23D 562.已知过点A(-2,m)和B (m,4)的直线与直线2x+y-1=0平行,则m 的值为( C )A 0B 2C -8D 103.若直线L 1:ax+2y+6=0与直线L 2:x+(a-1)y+(2a -1)=0平行但不重合,则a 等于( D ) (A -1或2 B23C 2D -1 4.若点A (2,-3)是直线a 1x+b 1y+1=0和a 2x+b 2y+1=0的公共点,则相异两点 (a 1,b 1)和(a 2,b 2)所确定的直线方程是( A ) +1=0 +1=0=0 =05.直线xcos θ+y-1=0 (θ∈R )的倾斜角的范围是 ( D )A.[)π,0B.⎪⎭⎫⎢⎣⎡ππ43,4C.⎥⎦⎤⎢⎣⎡-4,4ππD.⎪⎭⎫⎢⎣⎡⎥⎦⎤⎢⎣⎡πππ,434,0 6.“m=12”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2y)-3=0相互垂直”的( B )A 充分必要条件B 充分而不必要条件 `C 必要而不充分条件D 既不充分也不必要条件7.已知A(7,-4)关于直线L 的对称点为B (-5,6),则直线L 的方程为(B ) A 5x+6y-11=0 B 6x-5y-1=0 C 6x+5y-11=0 D 5x-6y+1=0 8.已知直线1l 的方向向量a=(1,3),直线2l 的方向向量b=(-1,k).若直线2l 经过点(0,5)且1l2l,则直线2l 的方程为( B )A x+3y-5=0B x+3y-15=0C x-3y+5=0D x-3y+15=0 9. 过坐标原点且与圆2x +2y -4x+2y+52=0相切的直线方程为( A )A y=-3x 或y=13x B y=3x 或y= -13x C y=-3x 或y= -13x D y=3x 或y= 13x 10.直线x+y=1与圆2x +2y -2ay=0(a>0)没有公共点,则a 的取值范围是(A ):A (02-1,)B (2-1,2+1) C (-2-1,2-1) D (0,2+1)11.圆2x +2y -4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离的差是( C )A 36B 18C 62D 5212.以直线:y=kx-k 经过的定点为P 为圆心且过坐标原点的圆的方程为(D ), A2x+2y +2x=0 B 2x +2y +x=0 C2x+2y -x=0 D2x+2y -2x-013.已知两定点A(-2,0),B(1,0),如果定点P 满足PA=2PB,则定点P 的轨迹所包围的面积等于( B )A B 4 C 8 D 9 `14.若直线3x+y+a=0过圆2x +2y +2x-4y=0的圆心,则a 的值为( B )A 1B -1C 3D -315.若直线2ax-by+2=0 (a >0,b >0)始终平分圆x 2+y 2+2x-4y+1=0的周长,则ba11+的最小值是( C ) A.41D.2116.若直线y=k(x-2)+4与曲线y=1+24x -有两个不同的交点,则k 的取值范围是( A ) A.⎥⎦⎤ ⎝⎛43,125 B.⎪⎭⎫⎝⎛+∞,125C.⎥⎦⎤⎝⎛43,21D.⎪⎭⎫⎝⎛125,0 <17.设两圆1C ,2C 都和两坐标轴相切,且过点(4,1),则两圆心的距离︱1C 2C ︱等于( C )A 4B 42C 8D 8218.能够使得圆x 2+y 2-2x+4y+1=0上恰有两个点到直线2x+y+c=0距离等于1的c 的一个值为 ( C )B.5519.若直线by ax +=1与圆x 2+y 2=1有公共点,则( D ) +b 2≤1+b 2≥1C.2211ba +≤1D.2211ba +≥1—20.已知A (-3,8)和B (2,2),在x 轴上有一点M ,使得|AM|+|BM|为最短,那么点M 的坐标为( B )A.(-1,0)B.(1,0)C.⎪⎭⎫⎝⎛0522, D.⎪⎭⎫⎝⎛522,0 21.直线y=kx+3与圆2(3)x+2(2)y =4相交于M 、N 两点,若︱MN ︱≥3则k 的取值范围是( A ) A [-34,0] B [-∞,-34][0,∞) 33] D [-23,0] 22.(广东理科2)已知集合{(,)|,A x y x y =为实数,且221}x y +=,{(,)|,B x y x y =为实数,且}y x =,则AB 的元素个数为(C )A .0B .1C .2D .3 23.(江西理科9)若曲线02221=-+x y x C :与曲线 0)(2=--m mx y y C :有四个不同的交点,则实数m 的取值范围是 ( B )— A. )33,33(-B. )33,0()0,33( -C. ]33,33[-D. ),33()33,(+∞--∞ 答案:B 曲线0222=-+x y x 表示以()0,1为圆心,以1为半径的圆,曲线()0=--m mx y y 表示0,0=--=m mx y y 或过定点()0,1-,0=y 与圆有两个交点,故0=--m mx y 也应该与圆有两个交点,由图可以知道,临界情况即是与圆相切的时候,经计算可得,两种相切分别对应3333=-=m m 和,由图可知,m 的取值范围应是)33,0()0,33( -二.填空题24.已知圆C 经过)3,1(),1,5(B A 两点,圆心在X 轴上,则C 的方程为10)2(22=+-y x ___________。
高中数学超详细必修二-直线与方程及圆与方程测试题(完整版)

高中数学必修二测验时间:第三章直线方程测试题100 分钟总分:150 分一选择题〔共55 分,每题1. 直线颠末点A(0,4)与点5 分〕B〔1,2〕,那么直线AB地斜率为〔〕D. 不存在A.3B.-2C. 22.过点( 1,3) 且平行于直线x 2 y 30 地直线方程为〔〕A.x 2 y70B.2x yy 10C.x 2 y50D.2 x〕y 50 ax 与y xya 精确地选项为〔3. 在同不停角坐标系中,表现直线y y yO x O x O x O xA 4.假设直线B C D x+ay+2=0 与2x+3y+1=0 相互垂直,那么a=〔〕23233232A.B.C.D.5. 过(x1,y1)与(x2,y2)两点地直线地方程为()y y2 y y2y1y1y1y1xx2xx1x1x1x1x2A.B.C.( y2y1 )( x x1) (x2x1)( y y1) 0D.( x2x1 )( x x1) ( y2y1 )( y y1 ) 0L1、L2、L3 地斜率分别为K1、K2、K3 那么〔〕6、假设图中地直线A、K1﹤K2﹤K3B、K2﹤K1﹤K3C、K3﹤K2﹤K1D、K1﹤K3﹤K2L3L2x oL17、直线2x+3y-5=0 关于直线A、3x+2y-5=0C、3x+2y+5=0y=x 对称地直线方程为〔B、2x-3y-5=0D、3x-2y-5=0〕8、与直线2x+3y-6=0 关于点A.3x-2y-6=0C. 3x-2y-12=0(1,-1)对称地直线为〔B.2x+3y+7=0D. 2x+3y+8=0〕9、直线5x-2y-10=0 在x 轴上地截距为a,在y 轴上地截距为C.a= 2 ,b=5;b,那么〔〕5 .2 ,b=B.a=2,b= 5 ;A.a=2,b=5; D.a=10 、直线2x-y=7 与直线3x+2y-7=0 地交点为〔A (3,-1)B (-1,3)C (-3,-1)D (3,1)〕11、过点P(4,-1)A 4x+3y-13=0C 3x-4y-16=0 且与直线3x-4y+6=0 垂直地直线方程为〔B 4x-3y-19=0〕D3x+4y-8=0二填空题〔共20 分,每题 5 分〕12. 过点〔1,2〕且在两坐标轴上地截距相称地直线地方程;_13 两直线2x+3y-k=0 与x-ky+12=0 地交点在y 轴上,那么k 地值为4 0与2x14、两平行直线x 3 y 6 y 90 地间隔为;15 空间两点M1 〔-1,0,3 〕,M2(0,4,-1) 间地间隔为三盘算题〔共71 分〕16、〔15分〕三角形ABC地极点坐标为A〔-1,5〕、B〔-2,-1〕、C〔4,3〕,M 为BC边上地中点;〔1〕求在直线方程;AB 边地点地直线方程;〔2〕求中线地长〔3〕求AB 边地高所AM17、〔12分〕求与两坐标轴正向围成面积为2 平方单元地三角形,而且两截距之差为3 地直线地方程;x m2 y 60 与直线18. 〔12 分〕直线( m 2) x 3my 2 m0 没有大众点,求实数m地19.〔16分〕求颠末两条直线l1: x y 40 与l 2: x y 20 地交点,且分别与直线2x y 10 〔1〕平行,〔2〕垂直地直线方程;20、〔16分〕过点〔2,3〕地直线L被两平行直线L1:2x-5y+9=0与L2:2x-5y-7=0所截线段AB地中点恰在直线x-4y-1=0上,求直线L地方程高中数学必修二 第三章直线方程测试题答案或 13 . ± 6 1-5 BACAC 6-10 AADBA 11 A 12.y=2x x+y-3=0 1020 14、 15. 33y 1 5 5 x 2 1 1 ,3 分16、解:〔 1〕由两点式写方程得 即 4 分6x-y+11=0 1 5 1) 61 6 或 直线 AB 地斜率为 k 1 直线 AB 地方2 ( 程为 y 5 6( x 1)3 分即 4 分6x-y+11=0 〔2〕设 M 地坐标为〔 x 0 , y 0 〕,那么由中点坐标公式2 4 2 1 32 x 0 1, y 0 1 故 M 〔 1, 1〕 6 分2 2 AM (1 1) (1 5) 2 12 5 8 分5 36 ········〔 3 分〕设 AB 边地高地点直线地斜率(3)由于直线 AB 地斜率为 k AB = 为 k1 ··········〔 6 分〕6 那么有 k k k ( 6) 1 k AB 1 ( x6 以是 AB 边高地点直线方程为 y 3 4)即x6y 14 0 ········〔 10 分〕x a 1或 b y 1ab 1 那么有题意知有 3 ab 417.解:设直线方程为 b 2 b 3那么有 b 4(舍去〕此时 a 4直线方程为a x+4y-4=0又有① 3那么有 b 4或 -1 〔舍去〕此时 1直线方程为 4x② b a a y 4 018.要领〔 1〕解:由题意知x m 2 y 6 0 即有〔 2m 2 -m 3 +3m)y=4m-12(m 2) x 3my 2m 02m 2 -m 3 +3m = 0由于两直线没有交点,以是方程没有实根,以是 2 m 〔 2m-m +3)=0 m=0或 m=-1或m=3 当m=3时两直线重合,不合题意,以是 m=0或 m=-1要领〔 2〕由,题设中两直线平行,当m 2 3m m 2m 6 m 2 3m0时, = 由 = 得 3或mm 12 2 1 1 m 3m m 当 m=0 2m6 由 得 m 3以是12 时两直线方程分别为 x+6=0,-2x=0,即 x=-6,x=0,两直线也没有大众点, 综合以上知,当 m=-1 或 m=0 时两直线没有大众点;x x y y 4 2 0 0 x y 1 3,得 ; . .2′19 解:由 ∴ l 1 与 l 2 地交点为〔 1,3〕; .3′〔 1〕 设与直线 2 x y 1 0 平行地直线为 2x y c 0 4′那么 2 3 c 0 ,∴ c = 1; ..6′∴所求直线方程为 2 x y 1 0 ; 7′k 2(x 2,且颠末点〔 1) , 要领 2:∵所求直线地斜率 1, 3〕, ..5 ′∴求直线地方程为 y 3 .. 6′.. 即 2 x y 1 0 ; 7′. .. 〔 2〕 设与直线 2 x y 1 0 垂直地直线为 x 2 y c 0 8′那1 2 3 c 0 ,∴ c =- 7; .9′∴所求直线方程为 x 2 y 7 0 ; 10′.. 1 ,且颠末点〔2 1) , 要领 2:∵所求直线地斜率 k 1, 3〕, ..8 ′1 ( x2 ∴求直线地方程为 y3 9.′.. 即 x 2 y 7 0 ; .10′. .. 20 、 解 : 设 线 段 A B 地 中 点 地 坐 标 〔 a , b 〕, 由 P 到 L 1 ,、 L 2 地 距 离 相 等 , 得 P 2a 22 5b 529 2a 5b 52722 经整理得, 2a 2a a 5b 1 5b 1 0 ,又点 P 在直线x-4y-1=0上,以是 a 4b 1 0 00 a b 3 1 解方程组 得 即点 P 地坐标〔 -3,-1〕,又直线 L 过点〔2,3〕4b 1 y 3 ( ( 1) 1) x 2 ( ( 3) 3),即 4x 5 y 7 0以是直线L地方程为高中数学必修二 圆与方程训练题一、选择题2 2( x 2) y 5 关于原点 5 P( 0 , 0对) 称地圆地方程为 1. 圆 ( )2 2 2( x 2) y x ( y 2) 5A. B. 2 22 2(x 2) ( y 2) 5 x ( y 2) 5C. D. 22 ( x 1) y 25地弦 P(2, 1) AB 地中点,那么直AB 地方程为〔 为圆 〕假设 2. x y 3 0 2 x y 3 0A. B. x y 1 0 2 x y 5 0C. D. 22 x y 2 x 2 y 1 0 上地点到直线 x y 2 地间隔最大值为〔 〕圆 3. 22 1 1 2 22 1 2 A. B. C. D. 2 2 2 x y 0 ,沿 x y 2x 4 y 0x 轴向左平移 1个单元,所得直线与圆将直线 4. 相切,那么实数地值为〔 〕0或10 1或113或7 2或8 D. A. B. C. A( 1 , 2距)离B( 3 , 1距) 离为 2 地直线共有1 ,且与点 〕5. 在坐标平面内,与点 3 1 条 2 4 条条 条 B. C. D. A. 22 x y 4 x 0 在点 P(1,3 ) 处地切线方程为〔 〕6. 圆 x 3 y 2 0 x 3 y 4 0A. B. x 3 y 4 0 x 3 y 2 0C. D. 二、填空题2 2 y 轴上地截P( 1 , 0地)直线与圆x y 4x 2 y 3 0 相切, 那么此直线1. 假设颠末点 距为0 2 2 P A , P B ,切点分别为 A, B, A P B 6 0,那么动x y 1 引两条切线 P 向圆 2. 由动点 P 地轨迹方为 .y 轴交于两点 2 x y 7 0上地A( 0 , 4B) , ( 0 , C 与 C 地方程 3. 圆心在直线 为 ,那么圆.2 2 OP OQ x3 y4 与过原点地直线 y kx P, Q 4 . 圆 地交点为 那么地值为.2 23x 4 y 8 0 上地震点, P A , P B 为圆 y 2 x 2 y 1 0 地切P 为直线 5. 线, A, B 为切点, C 为圆心,那么四边形 三、解答题 P A C B 面积地最小值为.P a, b 在直2 2 x y 1 0 上,求 a b 2a 2b 2 地最小值 .1. 点 A( 1 , 2 B ) , ( 5 为, 直径两头点地圆地方程 .2. 求以 A 1, 2 B 1, 1 0 x 2 y 1 0 相切地圆地方程 且与直线 .3. 求过点 y 轴相切,圆心在直线 y x 截得地弦长x 3 y 0 上,且被直线 C 与 2 7 ,4. 圆 求圆 C 地方程 .高中数学必修二 圆与方程训练题 答案一、选择题2 2( x, y) 关于原点 P(0, 0) 得 ( x, y) ,那么( x 2) ( y) 51. A AB CP , k CP 1,k A B 1, y 1 x 2C(1,0) ,那设圆心为 2. A C(1,1),r 1, d max 2 1B 圆心为 3. 2x y 0 沿 2x y 2 0x 轴向左平移 1个单元A 直线 4. 23, 或 C( 1,2), r 5, d 5, 7x 2 y 2 2x 4 y 0 5 圆 地圆心为B 两圆相交,外公切线有两条5. 〔 x 2〕2y 2 P(1, 3) (1 2)( x 2) 3 y 44 地在点 处地切线方程为 6. D 二、填空题22 0在)圆 xy 4x 2 y 3 0 上,即切线为 x y 1 0 P( 1 , 1 点 1. x 2 y 2 OP 24 2. 2) 2 ( y 3)2 ( x5 y 3 AB 地垂直中分线即 ,又在圆心既在线段 3. ( 2 , 3,) 2 x y 7 0上,即圆心r 52O P O Q O T 55 OT ,那么设切线为 4. CP 垂直于直线时,四边形 P A C B 地面积最小2 2 当 5. 三、解答题 2 2(a 1) (b 1) ( 1 , 1到)直线 y 1 0 地间隔地最小值为点 1. 解: 3 2 3 2 2 , 3 2 a 2 b 2 d ( 2a 2b 2) min 2 而 .(x 1 ) x ( 5 ) y( 2y) ( 6 )2. 解: 2 2x y 4 x 4 y 17 0得 y 6 上,设圆心为 (a , 6,) AB 地垂直中分线 r 半径为 ,那么3. 解:圆心显然在线段a 135r2 2 2 22 2 ( x a) ( y 6) r (1 a) (10 6) r ,得 ,而 2(a 13)5 2 (a 1) 16 , a 3, r 2 5,2 2 (x 3) ( y 6) 20 .3t td 2tr 3t ( 3t t, 半) ,径为 2 ,令 4. 解:设圆心为 ( 7) 2 r 2 d 2 ,9 t 2 2t 27, t 1而 (x 3)2 1)2 3)21)2 ( y 9 ( x ( y 9,或。
教A版高中数学必修2第四章《圆与方程》综合测试题(含答案)

教A 版高中数学必修2第四章《圆与方程》综合测试题学校:___________姓名:___________班级:___________考号:___________一、选择题1.在空间直角坐标系中, 点()3,4,5P 与点(3,4,5)Q --的位置关系是( ) A.关于x 轴对称B.关于xOy 平面对称C.关于坐标原点对称D.以上都不对2.圆1O :2220x y x +-=与圆2O :2240x y y +-=的位置关系是( ) A.外离B.相交C.外切D.内切3.过点(1,1)A -与(1,1)B -且圆心在直线20x y +-=上的圆的方程为( ) A. 22(3)(1)4x y -++= B. 22(3)(1)4x y ++-= C. 22(1)(1)4x y -+-= D. 22(1)(1)4x y +++=4.已知直线l 过圆22(3)4x y +-=的圆心,且与直线10x y ++=垂直,则l 的方程是( ) A. 20x y +-=B. 20x y -+=C. 30x y +-=D. 30x y -+=5.若圆221:1C x y +=,与圆222:680C x y x y n +--+=外切,则n =( )A. 21B. 9C. 19D. -116.圆224x y +=和圆224440x y x y ++-+=关于直线l 对称,则l 的方程为( ) A.0x y +=B.20x y +-=C.20x y --=D.20x y -+=7.已知点(),M a b 在圆22:1O x y +=外, 则直线1ax by +=与圆O 的位置关系是( ) A.相切B.相交C.相离D.不确定8.若直线y x b =+与曲线3y =,则b 的取值范围是( )A.1,1⎡-+⎣B.1⎡-+⎣C.1⎡⎤-⎣⎦D.1⎡⎤⎣⎦9.在平面直角坐标系中, ,A B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线240x y +-=相切,则圆C 面积的最小值为( )A.45π B. 34πC. (6π-D.54π 10.已知半径为1的动圆与圆22(5)(7)16x y -++=相切,则动圆圆心的轨迹方程是 ( ) A. 22(5)(7)25x y -+-=B. 22(5)(7)17x y -++=或22(5)(7)25x y -++= C. 22(5)(7)9x y -++=D. 22(5)(7)25x y -++=或22(5)(7)9x y -++=11.已知点(,)(0)M a b ab ≠是圆222(0)x y r r +=>内一点,直线g 是以M 为中点的弦所在的直线,直线l 的方程为20ax by r ++=,则( ) A. //,l g 且l 与圆相离 B. l g ⊥且l 与圆相切 C. //,l g 且l 与圆相交 D. l g ⊥且l 与圆相离12.已知直线1y kx =+与圆22(2)(1)4x y -+-=相交于两,?P Q 点,若||PQ ≥则实数k的取值范围是( )A. 3[-,0]4B. [-, 33C. []1,1-D. [ 二、填空题13.过点()3,1作圆22(2)(2)4x y -+-=的弦,其中最短的弦长为__________.14.过点()2,4P -作圆22:(2)(1)25C x y -+-=的切线l ,直线1:320l ax y a ++=与l 平行,则1l 与l 间的距离为__________.15.圆心在直线20x y -=上的圆C 与y 轴的正半轴相切,圆C 截x 轴所得弦的长为则圆C 的标准方程为 .16.在平面直角坐标系xOy 中,圆C 的方程为228150x y x +-+=,若直线2y kx =-上至少存在一点,使得以该点为圆心, 1为半径的圆与圆C 有公共点,则k 的最大值是 . 三、解答题17.已知圆C :222440x y x y +-+-=,是否存在斜率为1的直线l ,使以l 被圆C 所截得的弦AB 为直径的圆经过原点?若存在,写出直线l 的方程;若不存在,请说明理由.18.已知方程22260x y x y m ++-+=.1.若m R ∈,试确定方程所表示的曲线;2.若方程表示的是圆,且圆的圆心到直线210x y --=的距离等于半径,求m 的值.19.在平面直角坐标系xOy 中,己知圆P 在x 轴上截得线段长为在y 轴上截得线段长为. (1)求圆心P 的轨迹方程;(2)若P 点到直线y x =求圆P 的方程.20.已知圆22:(1)5C x y +-=,直线():10R l mx y m m -+-=∈.(1)判断直线l 与圆C 的位置关系;(2)设直线l 与圆C 交于,A B 两点,若直线l 的倾斜角为120︒,求弦AB 的长.21.已知点()2,0P 及圆C :226440x y x y +-++=1.若直线l 过点P 且与圆心C 的距离为1,求直线l 的方程;2.设直线10ax y -+=与圆C 交于A ,B 两点,是否存在实数a ,使得过点()2,0P 的直线2l 垂直平分弦AB ?若存在,求出实数a 的值;若不存在,请说明理由.22.已知圆M 的圆心在 x 轴上,半径为1,直线41:32l y x =-被圆M 且圆心M在直线l 的下方. 1.求圆M 的方程;2.设(0,),(0,6)(52)A t B t t +-≤≤-,若圆M 是△ABC 的内切圆,求△ABC 的面积S 的最大值和最小值.参考答案1.答案:A 解析:点()3,4,5P 与点()3,4,5Q --的横坐标相同,而纵、竖坐标分别互为相反数,所以两点关于x 轴对称. 2.答案:B解析:本题考查圆的方程及其互相转化关系;圆与圆的位置关系及其判断也是考查重点. 要知道圆与圆的位置关系得知道圆心的坐标以及圆心距与两圆半径,因此先求坐标,再求距离. 1O :2220x y x +-=与圆2O :2240x y y +-=故,圆心坐标与半径分别为1(1,0)O ,2(0,2)O ,11r =,22r =,12O O =,211r r -=,13< 所以相交,选B点评:本题属于概念题,掌握基本概念及判断方法即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学必修二直线和圆与方程综合测试卷
姓名 分数
一.选择题(每题3分,共30分)
1. 已知直线经过点A(0,4)和点B (1,2),则直线AB 的斜率为( )
A.3
B.-2
C. 2
D. 不存在
2.过点(1,3)-且平行于直线032=+-y x 的直线方程为( )
A .072=+-y x
B .012=-+y x
C .250x y --=
D .052=-+y x
3. 在同一直角坐标系中,表示直线y ax =与y x a =+正确的是( )
A B C D
4.若直线x +a y+2=0和2x +3y+1=0互相垂直,则a =( )
A .32-
B .32
C .23-
D .2
3 5.直线l 与两直线1y =和70x y --=分别交于,A B 两点,若线段AB 的中点为(1,1)M -,则直线l 的斜率为( )
A .23
B .32
C .32-
D . 23
-
6.与直线2x+3y-6=0关于点(1,-1)对称的直线是( )
A.3x-2y-6=0
B.2x+3y+7=0
C. 3x-2y-12=0
D. 2x+3y+8=0
7.平行直线x -y +1 = 0,x -y -1 = 0间的距离是
( ) A .22 B .2 C .2
D .22 8. 圆
关于原点对称的圆的方程为 ( ) A. B.
C.
D. 9. 若为圆
的弦的中点,则直线的方程是( ) A.
B. C. D. x y O x y O x y O x
y
O 22(2)5x y ++=(0,0)P 22(2)5x y -+=22(2)5x y +-=22(2)(2)5x y +++=22(2)5x y ++=)1,2(-P 25)1(22=+-y x AB AB 03=--y x 032=-+y x 01=-+y x 052=--y x
10. 圆
上的点到直线的距离最大值是( ) A. B. C.
D.
二.填空题(共20分,每题4分)
11.过点(1,2)且在两坐标轴上的截距相等的直线的方程 .
12.两直线2x+3y -k=0和x -ky+12=0的交点在y 轴上,则k 的值是 .
13.两平行直线0962043=-+=-+y x y x 与的距离是 .
14.空间两点M1(-1,0,3),M2(0,4,-1)间的距离是 .
15. 圆心在直线上的圆与
轴交于两点,则圆的方程
为 .
三.计算题(每题10分,共50分)
16.已知三角形ABC 的顶点坐标为A (-1,5)、B (-2,-1)、C (4,3),M 是BC 边上的中点。
(1)求AB 边所在的直线方程;(2)求中线AM 的长(3)求AB 边的高所在直线方程。
17. 直线062
=++y m x 与直线023)2(=++-m my x m 没有公共点,求实数m 的值。
012222=+--+y x y x 2=-y x 221+221+221+270x y --=C y (0,4),(0,2)A B --C
18. 求经过两条直线04:1=-+y x l 和02:2=+-y x l 的交点,且分别与
直线012=--y x (1)平行,(2)垂直的直线方程。
19. 求以
为直径两端点的圆的方程.
20.求过两点、且圆心在直线上的圆的标准方程并判断点与圆的关系.
(1,2),(5,6)A B --)4,1(A )2,3(B 0=y )4,2(P。
