上海市中考数学综合复习专题动点产生的相似三角形3星(学生版)
2020年上海中考数学相似三角形专题(含答案)
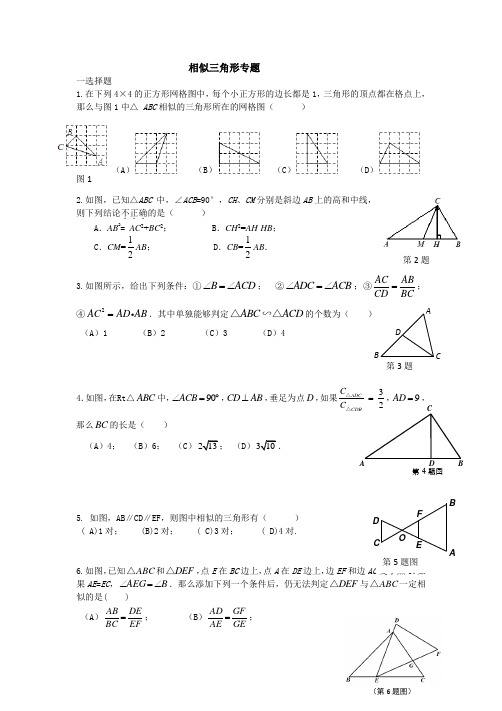
相似三角形专题一选择题1.在下列4×4的正方形网格图中,每个小正方形的边长都是1,三角形的顶点都在格点上,那么与图1中△ ABC 相似的三角形所在的网格图( )(A ) (B ) (C ) (D )2.如图,已知△ABC 中,∠ACB =90°,CH 、CM 分别是斜边AB 上的高和中线,则下列结论不正确...的是( ) A .AB 2= AC 2+BC 2; B .CH 2=AH ·HB ; C .CM =12AB ; D .CB =12AB .3.如图所示,给出下列条件:①B ACD ∠=∠; ②ADC ACB ∠=∠;③AC ABCD BC=;④2AC AD AB =.其中单独能够判定ABC ACD △∽△的个数为( ) (A )1 (B )2(C )3(D )44.如图,在Rt △ABC 中,90ACB ∠=︒,CD AB ⊥,垂足为点D ,如果32ADC CDB C C =△△,9AD =,那么BC 的长是( )(A )4; (B )6; (C )213; (D )310.5. 如图,AB ∥CD ∥EF ,则图中相似的三角形有( ) ( A)1对; (B)2对; ( C)3对; ( D)4对.6.如图,已知ABC △和DEF △,点E 在BC 边上,点A 在DE 边上,边EF 和边AC 交于点G .如果AE =EC ,B AEG ∠=∠.那么添加下列一个条件后,仍无法判定DEF △与ABC △一定相似的是( )(A )EF DE BC AB =; (B )GEGFAE AD =; 图1 第4题图A D CB ACD B 第3题第2题(第6题图)AB C DEF O 第5题图第18题E D C BA (C )EF EG AC AG =; (D )EAEGEF ED =.二填空题7.如果两个三角形相似,其中一个三角形的两个内角分别为50°和60°,那么另一个三角形的最大角为 度.8.如果两个相似三角形的相似比是1:2,那么这两个三角形的周长的比是9.在△ABC 中,点D 、E 分别在边BC 、AC 的延长线上,∠E=∠B ,AC=2,BC=3,CE=6,那么CD= .10 .如果两个相似三角形的对应角平分线比为2︰3,两个三角形的周长的和是100cm ,那么较小的三角形的周长为 cm .11.如图,已知⊿ABC 中,P 是AB 上的一点,∠ACP =∠B ,AB=9,AC=6,那么AP= . 12.如图,在△ABC 中,点D 、E 分别在AB 、AC 上, ADE C ∠=∠,如果=2AE ,△ADE 的面积是4,四边形BCED 的面积是5,那么AB 的长是 .13.如图,R t ΔA B C 中,∠A C B =900,C D ⊥A B ,A C =8,B C =6,则AD=__ _ 14.如图,在△ABC 中,D 、E 分别是边AB 、AC 上的点,如果21==EC AE DB AD ,那么△ADE 与△ABC 面积的比是 .15.已知等腰梯形的上、下两底长分别为4cm 和6cm ,将它的两腰分别延长交于一点,这个交点到上、下两底的距离之比为 .16.△ABC 中,AB =8,AC =6,点D 在AC 上,AD =2,在AB 上找一点E ,使 △ADE 与△ABC 相似,则AE 的长为 . 17.如图,在ABC ∆中,AD 平分BAC ∠交边BC 于点D ,AD BD =,3=AB ,2=AC ,那么AD 的长是 _. 18.如图,点E 是矩形ABCD 的边AD 上一点,且AE=4ED ,且BE ⊥CE ,则AB:BC=______________.三解答题19.如图,已知AB ⊥AD ,BD ⊥DC ,且BC AB BD ⋅=2,求证:∠ABD=∠DBC.E D C BA第12题BACD第14题A 第11题 B CP 第13题 第17题20. 已知:如图,△ABC 中,点E 在中线AD 上, ABC DEB ∠=∠. 求证:(1)DA DE DB ⋅=2; (2)DAC DCE ∠=∠.21如图,在梯形ABCD 中,AD //BC ,点E 在边AD 上, CE 与BD 相交于点F , AD =4,AB =5,BC =BD =6,DE =3.(1)求证:△DFE ∽△DAB ; (2)求线段CF 的长.22.如图, 在AH ABC 中,∆是BC 边上的高,矩形DEFG 内接于ABC ∆(即点G F E D 、、、都在ABC ∆的边上),6,18==AH BC ,矩形DEFG 的周长是20. ACDEBBCD AEF求:DEFG S 矩形的值.23.如图,已知△ABC 中,AB=AC=10,BC=16,点P 、D 分别在边BC 、AC 上, BP=12,∠APD=∠B ,求CD 的长.24.如图:在Rt ⊿ABC 中,∠ACB=90°,CD ⊥AB ,E 是斜边AB 延长 线上一点,且∠ECB=∠BCD (1)求证:⊿ECB ∽⊿EAC ;(2)若AC=,AB=5cm ,求BE 的长.EDBCA相似三角形专题 参考答案一、1、B ,2、D ,3、C ,4、C ,5、C ,6、C二、7、70, 8、1:2 9、4 10、40 11、4,12、3 13、6.4 14、1:9 15 、2:3 16、23或38 17、5103 18、2:5. 三、19、证明Rt△DBC ∽△ABD Rt20、(1)证明∽△ADB △BDE ;(2)由DB=DC 可得DC 2=DE*DA ,可证∽△ADC △CDE 21、(1)由AD//BC 可得21==BF DF BC DE ,∴31=BD DF ,得DF=2, ∴BD DEAD DF =再由BDA EDF ∠=∠可证 (2)由1的结论可求EF=2.5,再可得CF=2EF=522、设AH 与DG 相交于M ,由∽△ABC △ADG 可得AHAMBC DG =可算出DE=4,DG=6 S=2423、证∽△PBA △DCP 可得ABCPBP CD =可得CD=4.8 24、1、证A BCD ECB ∠=∠=∠2、由勾股定理可求BC=5 ,由1的结论可得21===AE EC EC BE AC BC ,可得41=AE BE ,得BE=35。
中考数学专题复习 专题20 相似三角形问题(学生版)

中考专题20 相似三角形问题一、比例1.成比例线段(简称比例线段):对于四条线段a 、b 、c 、d ,如果其中两条线段的长度的比与另两条线段的长度的比相等,即dcb a =(或a :b=c :d),那么,这四条线段叫做成比例线段,简称比例线段。
如果作为比例内项的是两条相同的线段,即cbb a =或a :b=b :c ,那么线段b 叫做线段a ,c 的比例中项。
2.黄金分割:用一点P 将一条线段AB 分割成大小两条线段,若小段与大段的长度之比等于大段与全长之比,则可得出这一比值等于0·618…。
这种分割称为黄金分割,分割点P 叫做线段AB 的黄金分割点,较长线段叫做较短线段与全线段的比例中项。
3.平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
4.两条直线被一组平行线所截,所得的对应线段成比例。
5.平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
二、相似、相似三角形及其基本的理论1. 相似:相同形状的图形叫相似图形。
相似图形强调图形形状相同,与它们的位置、大小无关。
2.相似三角形:对应角相等,对应边成比例的两个三角形叫做相似三角形。
相似多边形对应边的比叫做相似比。
3.三角形相似的判定方法(1)定义法:对应角相等,对应边成比例的两个三角形相似。
(2)平行法:平行于三角形一边的直线和其他两边(或两边延长线)相交,构成的三角形与原三角形相似。
(3)两个三角形相似的判定定理判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,可简述为两角对应相等,两三角形相似。
判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应相等,并且夹角相等,那么这两个三角形相似,可简述为两边对应成比例且夹角相等,两三角形相似。
判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似,可简述为三边对应成比例,两三角形相似。
上海市中考数学综合复习专题动点产生的相似三角形3星(教师版)

专题-动点产生的相似三角形1.掌握相似基本图形中的相似三角形和各种比例式;2.通过观察了解因动点产生的相似三角形问题的特点,熟悉对应的解题方法, 掌握“动中取静,以静窥动”的解题策略;3.学习对图形的直觉能力以及从变化中看到不变实质的数学洞察力;4.学会挖掘题目中的隐藏条件,从未知到已知的一个转变;5.掌握动点产生的相似三角形的分类讨论情况,并能根据题目中的条件进行求解。
知识结构1、相似基本图形:2、相似三角形的基本图形产生的结论: (1)、A 字型:①正A 字型 ②斜A 字型 ③其它A 字型ABCD EABC DEABCEA B C ∽∆∆A D E ACB ∽∆∆ADE ACB ∽∆∆ABEAC AE AB AD = AB AE AC AD = ACABAB AE =AB AE AC AD ⋅=⋅ AC AE AB AD ⋅=⋅ AC AE AB ⋅=2(2)、X 型:①正X 字型 ②斜X 字型ADEBCADEBCA E D ∽∆∆ABC 相似三角形:_________________ABAEAC AD =比例式:_________________ AC AE AB AD ⋅=⋅ 乘积式:_________________ (3)、直角三角形:DCABCDB ∽ACB ∽∆∆∆ADC ①AB AD AC AB ACADC ⋅=⇒=⇒∆∆2AC AD ACB ∽ ②AB BD BC BC BDBDC ⋅=⇒=⇒∆∆2AB BC BCA ∽ ③BD AD CD BDCDADC ⋅=⇒=⇒∆∆2CD AD CDB ∽(4)、直线型(一线三角): (5)、其他基本型:A BCDEFEDABC相似三角形:_________________ 相似三角形:_________________比例式:_________________ 比例式:_________________乘积式:_________________ 乘积式:_________________3、相似三角形方法的选择:(1)已知有一角相等时,可选择方法两角相等和方法两边对应成比例且夹角相等; (2)已知有二边对应成比例时,可选择方法三边对应成比例和方法两边对应成比例且夹角相等;(3)若有平行条件时,可考虑方法基本图形“A 字型和X 型”; (4)有直角三角形时,可考虑方法直角三角形判定方法; (5)不管选择用哪一个方法,先找角度,再根据题目选择。
中考数学压轴题---因动点产生的相似三角形问题[含答案]
![中考数学压轴题---因动点产生的相似三角形问题[含答案]](https://img.taocdn.com/s3/m/52f3b304de80d4d8d15a4fac.png)
因动点产生的相似三角形问题例1(2011年上海市闸北区中考模拟第25题)直线113y x =-+分别交x 轴、y 轴于A 、B 两点,△AOB 绕点O 按逆时针方向旋转90°后得到△COD ,抛物线y =ax 2+bx +c 经过A 、C 、D 三点.(1) 写出点A 、B 、C 、D 的坐标;(2) 求经过A 、C 、D 三点的抛物线表达式,并求抛物线顶点G 的坐标;(3) 在直线BG 上是否存在点Q ,使得以点A 、B 、Q 为顶点的三角形与△COD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.图1满分解答(1)A (3,0),B (0,1),C (0,3),D (-1,0).(2)因为抛物线y =ax 2+bx +c 经过A (3,0)、C (0,3)、D (-1,0) 三点,所以930,3,0.a b c c a b c ++=⎧⎪=⎨⎪-+=⎩ 解得1,2,3.a b c =-⎧⎪=⎨⎪=⎩所以抛物线的解析式为y =-x 2+2x +3=-(x -1)2+4,顶点G 的坐标为(1,4).(3)如图2,直线BG 的解析式为y =3x +1,直线CD 的解析式为y =3x +3,因此CD //BG .因为图形在旋转过程中,对应线段的夹角等于旋转角,所以AB ⊥CD .因此AB ⊥BG ,即∠ABQ =90°. 因为点Q 在直线BG 上,设点Q 的坐标为(x ,3x +1),那么22(3)10BQ x x x =+=±.Rt △COD 的两条直角边的比为1∶3,如果Rt △ABQ 与Rt △COD 相似,存在两种情况: ①当3B Q B A =时,10310x ±=.解得3x =±.所以1(3,10)Q ,2(3,8)Q --.②当13B Q B A=时,101310x ±=.解得13x =±.所以31(,2)3Q ,41(,0)3Q -.图2 图3考点伸展第(3)题在解答过程中运用了两个高难度动作:一是用旋转的性质说明AB ⊥BG ;二是22(3)10BQ x x x =+=±.我们换个思路解答第(3)题:如图3,作GH ⊥y 轴,QN ⊥y 轴,垂足分别为H 、N .通过证明△AOB ≌△BHG ,根据全等三角形的对应角相等,可以证明∠ABG =90°. 在Rt △BGH 中,1sin 110∠=,3cos 110∠=.①当3B Q B A=时,310B Q =.在Rt △BQN 中,sin 13QN BQ =⋅∠=,cos 19BN BQ =⋅∠=. 当Q 在B 上方时,1(3,10)Q ;当Q 在B 下方时,2(3,8)Q --. ②当13B Q B A=时,1103B Q =.同理得到31(,2)3Q ,41(,0)3Q -.例2(2011年上海市杨浦区中考模拟第24题)Rt △ABC 在直角坐标系内的位置如图1所示,反比例函数(0)k y k x =≠在第一象限内的图像与BC 边交于点D (4,m ),与AB 边交于点E (2,n ),△BDE 的面积为2.(1)求m 与n 的数量关系; (2)当tan ∠A =12时,求反比例函数的解析式和直线AB 的表达式;(3)设直线AB 与y 轴交于点F ,点P 在射线FD 上,在(2)的条件下,如果△AEO 与△EFP 相似,求点P 的坐标.图1满分解答(1)如图1,因为点D (4,m )、E (2,n )在反比例函数ky x =的图像上,所以4,2.m k n k =⎧⎨=⎩ 整理,得n =2m .(2)如图2,过点E 作EH ⊥BC ,垂足为H .在Rt △BEH 中,tan ∠BEH =tan ∠A =12,EH =2,所以BH =1.因此D (4,m ),E (2,2m ),B (4,2m +1).已知△BDE 的面积为2,所以11(1)2222B D E H m ⋅=+⨯=.解得m =1.因此D (4,1),E (2,2),B (4,3).因为点D (4,1)在反比例函数k y x=的图像上,所以k =4.因此反比例函数的解析式为4y x=.设直线AB 的解析式为y =kx +b ,代入B (4,3)、E (2,2),得34,22.k b k b =+⎧⎨=+⎩ 解得12k =,1b =.因此直线AB 的函数解析式为112y x =+.图2 图3 图4(3)如图3,因为直线112y x =+与y 轴交于点F(0,1),点D 的坐标为(4,1),所以FD // x 轴,∠EFP =∠EAO .因此△AEO 与△EFP 相似存在两种情况:①如图3,当E A EF A O F P =时,2552FP =.解得FP =1.此时点P 的坐标为(1,1).②如图4,当E A F P A OE F=时,2525F P =.解得FP =5.此时点P 的坐标为(5,1).考点伸展本题的题设部分有条件“Rt △ABC 在直角坐标系内的位置如图1所示”,如果没有这个条件限制,保持其他条件不变,那么还有如图5的情况:第(1)题的结论m 与n 的数量关系不变.第(2)题反比例函数的解析式为12y x=-,直线AB 为172y x =-.第(3)题FD 不再与x 轴平行,△AEO 与△EFP 也不可能相似.图5例3(2010年义乌市中考第24题)如图1,已知梯形OABC ,抛物线分别过点O (0,0)、A (2,0)、B (6,3). (1)直接写出抛物线的对称轴、解析式及顶点M 的坐标;(2)将图1中梯形OABC 的上下底边所在的直线OA 、CB 以相同的速度同时向上平移,分别交抛物线于点O 1、A 1、C 1、B 1,得到如图2的梯形O 1A 1B 1C 1.设梯形O 1A 1B 1C 1的面积为S ,A 1、 B 1的坐标分别为 (x 1,y 1)、(x 2,y 2).用含S 的代数式表示x 2-x 1,并求出当S =36时点A 1的坐标;(3)在图1中,设点D 的坐标为(1,3),动点P 从点B 出发,以每秒1个单位长度的速度沿着线段BC 运动,动点Q 从点D 出发,以与点P 相同的速度沿着线段DM 运动.P 、Q 两点同时出发,当点Q 到达点M 时,P 、Q 两点同时停止运动.设P 、Q 两点的运动时间为t ,是否存在某一时刻t ,使得直线PQ 、直线AB 、x 轴围成的三角形与直线PQ 、直线AB 、抛物线的对称轴围成的三角形相似?若存在,请求出t 的值;若不存在,请说明理由.图1 图2(1)抛物线的对称轴为直线1x =,解析式为21184y x x =-,顶点为M (1,18-).(2) 梯形O 1A 1B 1C 1的面积12122(11)3()62x x S x x -+-⨯3==+-,由此得到1223s x x +=+.由于213y y -=,所以22212211111138484y y x x x x -=--+=.整理,得212111()()384x x x x ⎡⎤-+-=⎢⎥⎣⎦.因此得到2172x x S -=. 当S =36时,212114,2.x x x x +=⎧⎨-=⎩ 解得126,8.x x =⎧⎨=⎩ 此时点A 1的坐标为(6,3).(3)设直线AB 与PQ 交于点G ,直线AB 与抛物线的对称轴交于点E ,直线PQ 与x 轴交于点F ,那么要探求相似的△GAF 与△GQE ,有一个公共角∠G .在△GEQ 中,∠GEQ 是直线AB 与抛物线对称轴的夹角,为定值.在△GAF 中,∠GAF 是直线AB 与x 轴的夹角,也为定值,而且∠GEQ ≠∠GAF . 因此只存在∠GQE =∠GAF 的可能,△GQE ∽△GAF .这时∠GAF =∠GQE =∠PQD . 由于3tan 4G A F ∠=,tan 5DQ t PQD QPt∠==-,所以345t t=-.解得207t =.图3 图4考点伸展第(3)题是否存在点G 在x 轴上方的情况?如图4,假如存在,说理过程相同,求得的t 的值也是相同的.事实上,图3和图4都是假设存在的示意图,实际的图形更接近图3.例4(2010年上海市宝山区中考模拟第24题)如图1,已知点A (-2,4) 和点B (1,0)都在抛物线22y m x m x n =++上.(1)求m 、n ;(2)向右平移上述抛物线,记平移后点A 的对应点为A ′,点B 的对应点为B ′,若四边形A A ′B ′B 为菱形,求平移后抛物线的表达式;(3)记平移后抛物线的对称轴与直线AB ′ 的交点为C ,试在x 轴上找一个点D ,使得以点B ′、C 、D 为顶点的三角形与△ABC 相似.图1满分解答(1) 因为点A (-2,4) 和点B (1,0)都在抛物线22y m x m x n =++上,所以444,20.m m n m m n -+=⎧⎨++=⎩ 解得43m =-,4n =.(2)如图2,由点A (-2,4) 和点B (1,0),可得AB =5.因为四边形A A ′B ′B 为菱形,所以A A ′=B ′B = AB =5.因为438342+--=x x y ()2416133x =-++,所以原抛物线的对称轴x =-1向右平移5个单位后,对应的直线为x =4.因此平移后的抛物线的解析式为()3164342,+--=x y .图2(3) 由点A (-2,4) 和点B ′ (6,0),可得A B ′=45. 如图2,由AM //CN ,可得''''B N B C B MB A=,即2'845B C =.解得'5B C =.所以35AC =.根据菱形的性质,在△ABC 与△B ′CD 中,∠BAC =∠CB ′D .①如图3,当''A B B C A C B D =时,55'35B D=,解得'3B D =.此时OD =3,点D 的坐标为(3,0).②如图4,当''A B B D A CB C=时,5'355B D =,解得5'3B D =.此时OD =133,点D 的坐标为(133,0).图3 图4考点伸展在本题情境下,我们还可以探求△B ′CD 与△ABB ′相似,其实这是有公共底角的两个等腰三角形,容易想象,存在两种情况.我们也可以讨论△B ′CD 与△C B B ′相似,这两个三角形有一组公共角∠B ,根据对应边成比例,分两种情况计算.例5(2009年临沂市中考第26题)如图1,抛物线经过点A (4,0)、B (1,0)、C (0,-2)三点. (1)求此抛物线的解析式;(2)P 是抛物线上的一个动点,过P 作PM ⊥x 轴,垂足为M ,是否存在点P ,使得以A 、P 、M 为顶点的三角形与△OAC 相似?若存在,请求出符合条件的 点P 的坐标;若不存在,请说明理由;(3)在直线AC 上方的抛物线是有一点D ,使得△DCA 的面积最大,求出点D 的坐标.图1满分解答(1)因为抛物线与x 轴交于A (4,0)、B (1,0)两点,设抛物线的解析式为)4)(1(--=x x a y ,代入点C 的 坐标(0,-2),解得21-=a .所以抛物线的解析式为22521)4)(1(212-+-=---=x x x x y .(2)设点P 的坐标为))4)(1(21,(---x x x .①如图2,当点P 在x 轴上方时,1<x <4,)4)(1(21---=x x PM ,x AM -=4.如果2==CO AO PM AM ,那么24)4)(1(21=----xx x .解得5=x 不合题意.如果21==COAO PMAM ,那么214)4)(1(21=----xx x .解得2=x .此时点P 的坐标为(2,1).②如图3,当点P 在点A 的右侧时,x >4,)4)(1(21--=x x PM ,4-=x AM .解方程24)4)(1(21=---x x x ,得5=x .此时点P 的坐标为)2,5(-.解方程214)4)(1(21=---x x x ,得2=x 不合题意.③如图4,当点P 在点B 的左侧时,x <1,)4)(1(21--=x x PM ,x AM -=4.解方程24)4)(1(21=---x x x ,得3-=x .此时点P 的坐标为)14,3(--.解方程214)4)(1(21=---xx x ,得0=x .此时点P 与点O 重合,不合题意.综上所述,符合条件的 点P 的坐标为(2,1)或)14,3(--或)2,5(-.图2 图3 图4(3)如图5,过点D 作x 轴的垂线交AC 于E .直线AC 的解析式为221-=x y .设点D 的横坐标为m )41(<<m ,那么点D 的坐标为)22521,(2-+-m mm ,点E 的坐标为)221,(-m m .所以)221()22521(2---+-=m m mDE m m2212+-=.因此4)221(212⨯+-=∆m mS DAC m m 42+-=4)2(2+--=m .当2=m 时,△DCA 的面积最大,此时点D 的坐标为(2,1).图5 图6考点伸展第(3)题也可以这样解:如图6,过D 点构造矩形OAMN ,那么△DCA 的面积等于直角梯形CAMN 的面积减去△CDN 和△ADM 的面积.设点D 的横坐标为(m ,n ))41(<<m ,那么42)4(21)2(214)22(21++-=--+-⨯+=n m m n n m n S .由于225212-+-=m mn ,所以m m S 42+-=.例6(2009年上海市闸北区中考模拟第25题)如图1,△ABC 中,AB =5,AC =3,cos A =310.D 为射线BA 上的点(点D 不与点B 重合),作DE //BC 交射线CA 于点E ..(1) 若CE =x ,BD =y ,求y 与x 的函数关系式,并写出函数的定义域;(2) 当分别以线段BD ,CE 为直径的两圆相切时,求DE 的长度;(3) 当点D 在AB 边上时,BC 边上是否存在点F ,使△ABC 与△DEF 相似?若存在,请求出线段BF 的长;若不存在,请说明理由.图1 备用图备用图满分解答(1)如图2,作BH⊥AC,垂足为点H.在Rt△ABH中,AB=5,cosA=310A HA B=,所以AH=32=12AC.所以BH垂直平分AC,△ABC 为等腰三角形,AB=CB=5.因为DE//BC,所以A B A CD BE C=,即53y x=.于是得到53y x=,(0x>).(2)如图3,图4,因为DE//BC,所以D E A EB C A C=,M N A NB C A C=,即|3|53D E x-=,1|3|253xM N-=.因此5|3|3xD E-=,圆心距5|6|6xM N-=.图2 图3 图4在⊙M中,115226Mr B D y x===,在⊙N中,1122Nr C E x==.①当两圆外切时,5162x x+5|6|6x-=.解得3013x=或者10x=-.如图5,符合题意的解为3013x=,此时5(3)15313xD E-==.②当两圆内切时,5162x x-5|6|6x-=.当x<6时,解得307x=,如图6,此时E在CA的延长线上,5(3)1537xD E-==;当x>6时,解得10x=,如图7,此时E在CA的延长线上,5(3)3533xD E-==.图5 图6 图7(3)因为△ABC 是等腰三角形,因此当△ABC 与△DEF 相似时,△DEF 也是等腰三角形.如图8,当D 、E 、F 为△ABC 的三边的中点时,DE 为等腰三角形DEF 的腰,符合题意,此时BF =2.5.根据对称性,当F 在BC 边上的高的垂足时,也符合题意,此时BF =4.1.如图9,当DE 为等腰三角形DEF 的底边时,四边形DECF 是平行四边形,此时12534B F =.图8 图9 图10 图11考点伸展第(3)题的情景是一道典型题,如图10,如图11,AH 是△ABC 的高,D 、E 、F 为△ABC 的三边的中点,那么四边形DEHF 是等腰梯形.例7(2008年杭州市中考第24题)如图1,在直角坐标系xOy 中,设点A (0,t ),点Q (t ,b ).平移二次函数2tx y -=的图象,得到的抛物线F 满足两个条件:①顶点为Q ;②与x 轴相交于B 、C 两点(∣OB ∣<∣OC ∣),连结A ,B .(1)是否存在这样的抛物线F ,使得OC OB OA ⋅=2?请你作出判断,并说明理由;(2)如果AQ ∥BC ,且tan ∠ABO =23,求抛物线F 对应的二次函数的解析式.满分解答(1)因为平移2tx y -=的图象得到的抛物线F 的顶点为Q (t ,b ),所以抛物线F 对应的解析式为b t x t y +--=2)(.因为抛物线与x 轴有两个交点,因此0>b t .令0=y ,得-=t OB tb ,+=t OC tb .所以-=⋅t OC OB (|||||tb )( +t tb )|-=2|t22|OA ttb ==.即22b t t t-=±.所以当32t b =时,存在抛物线F 使得||||||2OC OB OA ⋅=.(2)因为AQ //BC ,所以t =b ,于是抛物线F 为t t x t y +--=2)(.解得1,121+=-=t x t x . ①当0>t 时,由||||OC OB <,得)0,1(-t B .如图2,当01>-t 时,由=∠ABO tan 23=||||OB OA =1-t t ,解得3=t .此时二次函数的解析式为241832-+-=x x y .如图3,当01<-t 时,由=∠ABO tan 23=||||OB OA =1+-t t ,解得=t 53.此时二次函数的解析式为-=y 532x +2518x +12548.图2 图3②如图4,如图5,当0<t 时,由||||OC OB <,将t -代t ,可得=t 53-,3-=t .此时二次函数的解析式为=y 532x+2518x -12548或241832++=x x y .图4 图5考点伸展第(2)题还可以这样分类讨论:因为AQ //BC ,所以t =b ,于是抛物线F 为2()y t x t t =--+.由3tan 2O A A B O O B∠==,得23O B O A =.①把2(,0)3B t 代入2()y t x t t =--+,得3t =±(如图2,图5).②把2(,0)3B t -代入2()y t x t t =--+,得35t =±(如图3,图4).。
上海市初三数学相似三角形经典题型(完整资料)

此文档下载后即可编辑相似三角形的判定练习例题分析:例1:已知如图,在△ABC 中,D 是AB 上的一点,连结CD ,∠ACD=∠B,求证:2 AE AD AC =例2:如图,在Rt ΔABC 中,∠ACB=90°,CD ⊥AB ,垂足为D ,(1)求证:△ACD ∽△ABC ∽△CBD(2)求证:222(1) (2) (3)AC AD AB CD AD DB BC BD AB ===例3:已知如图,点D 是AB 上的一点,CA ⊥AB,EB ⊥AB,CD ⊥DE,求证:△ACD ∽△BDE例4:在△ABC 中,AB=6,AC=9,D 为AC 上的一点,AD=3,在AB 上找一点E ,使得△ADE 与△ABC 相似?并求出AE 的长。
两个三角形相似的六种图形:1. 如图在△ABC中,D是BC边的中点,且AD=AC,DE⊥BC,交AB于点E,EC交AD于点F.求证:△ABC∽△FCD;2、已知:如图,△ABC中,∠ACB=900,AB的垂直平分线交AB于D,交BC延长线于F。
求证:CD2=DE·DF3. 如图3,△ABC中,AD平分∠BAC,AD的垂直平分线FE交BC的延长线于E.求证:DE2=BE·CE.4.如图,已知△ABC中,AB=AC,AD是BC边上的中线,CF∥BA,BF交AD于P点,交AC于E点。
求证:BP2=PE·PF。
AEB D CF5.如图,CD是Rt△ABC的斜边AB上的高,∠BAC的平分线分别交BC、CD于点E、F,AC·AE=AF·AB6.如图4,在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中点,ED交AB的延长线于点F.求证:AB DF AC AF.7.已知如图,在平行四边形ABCD中,AC=2AB,求证:△AOB∽△ABC8. 已知:如图,ΔABC中,CE⊥AB,BF⊥AC.求证:(1)△AEC∽△AFB (2) △AEF∽△ACB6.如图5,在△ABC中,∠ACB=90°,CD是斜边AB上的高,G是DC延长线上一点,过B作BE⊥AG,垂足为E,交CD于点F.求证:CD2=DF·DG.7.如图,△ABC中,点DE在边BC上,且△ADE是等边三角形,∠BAC=120°求证:(1)△ADB∽△CEA;(2)DE²=BD·CE;(3)AB·AC=AD·BC.8.如图,平行四边形ABCD中,E为BA延长线上一点,∠D=∠ECA.求证:AD·EC=AC·EB9.如图,E是平行四边形的边DA延长线上一点,EC交AB于点G,交BD于点F,求证:FC²=FG·EF.10.如图,ABCD 为直角梯形,AB ∥CD,AB ⊥BC,AC ⊥BD 。
上海中考数学压轴题专题09 动点产生的相似三角形(原卷版)

上海中考数学压轴题专题09 动点产生的相似三角形教学重难点1.掌握相似基本图形中的相似三角形和各种比例式;2.通过观察了解因动点产生的相似三角形问题的特点,熟悉对应的解题方法, 掌握“动中取静,以静窥动”的解题策略;3.培养学生对图形的直觉能力以及从变化中看到不变实质的数学洞察力;4.培养学生学会挖掘题目中的隐藏条件,从未知到已知的一个转变;5.掌握动点产生的相似三角形的分类讨论情况,并能根据题目中的条件进行求解。
【注意】:1.此部分知识点梳理,先提问学生学过的基本图形,并且画出来,再结合讲义讲解;2.部分基本图形的比例式,可以在白板上先画出基本图形再让学生找相似三角形,并写出比比例式,尤其是第四、五个基本图形一定要让学生写,部分地方让学生填写完,建议8分钟左右完成。
相似三角形的基本图形产生的结论结论: A 字型:① 正A 字型 ②斜A 字型 ③其它A 字型ABC ∽∆∆ADE ACB ∽∆∆ADE ACB ∽∆∆ABEAC AE AB AD = AB AE AC AD = ACABAB AE = AB AE AC AD ⋅=⋅ AC AE AB AD ⋅=⋅ AC AE AB ⋅=2X 型:①正X 字型 ②斜X 字型CCCAED ∽∆∆ABC ADE ∽∆∆ABCAB AE AC AD = ACAEAB AD = AC AE AB AD ⋅=⋅ AB AE AC AD ⋅=⋅直角三角形:CDB ∽ACB ∽∆∆∆ADC①AB AD AC AB ACADC ⋅=⇒=⇒∆∆2AC AD ACB ∽ ②AB BD BC BC BDBDC ⋅=⇒=⇒∆∆2AB BC BCA ∽BD AD CD BDCDADC ⋅=⇒=⇒∆∆2CD AD CDB ∽直线型(一线三角): 其他基本型:CEF ∽∆∆BDE AEB ∽∆∆ADC 和ACB ∽∆∆ADECF BE CE BD = ABAEAC AD = BE CE CF BD ⋅=⋅ AC AE AB AD ⋅=⋅CCCB相似三角形方法的选择:(1)已知有一角相等时,可选择方法两角相等和方法两边对应成比例且夹角相等;(2)已知有二边对应成比例时,可选择方法三边对应成比例和方法两边对应成比例且夹角相等;(3)若有平行条件时,可考虑方法基本图形“A字型和X型”;(4)有直角三角形时,可考虑方法直角三角形判定方法;(5)不管选择用哪一个方法,先找角度,再根据题目选择。
沪教版(上海)2021年中考复习 数学 相似三角形综合复习

FGED CBA AB CDO① ②③④2021年中考复习 数学 相似三角形综合复习一、选择题1.如果两个相似三角形的面积比是1:2,那么它们的周长比是( )(A) 1:2(B) 1:4(C) 1:2(D) 2:12. 已知△ABC 和△DEF 相似,且△ABC 的三边长为3、4、5,如果△DEF 的周长为6,那么下列不可能是△DEF 一边长的是( )(A )1.5; (B )2; (C )2.5; (D )3. 3. 如图,在平行四边形ABCD 中,若E 为CD 中点,且AE 与BD 交于点F ,则△EDF 与△ABF 的周长比为( ) A . 1:2; B . 1:4; C . 1:3;D . 1:9.4. 在△ABC 中,D 、E 分别是边AB 、AC 上的点,下列条件中不能..判定△AED ∽△ABC 是( )A . ∠ADE=∠C ;B .∠AED=∠B ;C . AD AC AEAB=; D .AD ACBCDE=.5. 下列四个命题中,假命题是( )(A )有一个锐角相等的两个等腰三角形相似; (B )有一个锐角相等的两个直角三角形相似; (C )底边和腰对应成比例的两个等腰三角形相似; (D )斜边和直角边对应成比例的两个直角三角形相似. 6.如图,四边形ABCD 的对角线AC 、BD 相交于点O ,且将这个四边形分成①、②、③、④四个三角形,若OA ∶OC = OB ∶OD ,则下列结论中一定正确的是( )A .①和②相似;B .①和③相似;C .①和④相似 ;D .②和④相似; 7.如图,平行四边形ABCD 中,F 是CD 上一点,BF 交AD 的延长线于G ,则图中的相似三角形对数共有( )A .8对;B . 6对;C .4对;D .2对.二、填空题8.已知两个相似三角形的面积比是4:1,则这两个三角形的周长比是 .GDEFC BAFED CBA 9.如果两个相似三角形的对应边上的高之比是2:3,则它们的周长比是 . 10.如果两个相似三角形的周长之比是2︰3,其中小三角形一角的角平分线长是6cm ,那么大三角形对应角的角平分线长是 cm ;11.在Rt △ABC 和Rt △DEF 中,∠ C =∠ F =90°,当AC =3,AB =5,DE =10,EF =8时, Rt △ABC 和Rt △DEF 是 的.(填“相似”或者“不相似”) 12. 如图,在平行四边形ABCD 中,E 为CD 上一点,联结AE 、BD ,且AE 、BD 交于点F ,若DE :EC =2:3, 则S △DEF :S △ABF = .13.如图,在边长为1的正方形网格上有点P 、A 、B 、C ,则图中所形成的三角形中,相似的三角形是 .14.如图,在△ABC 中,若AB =AC =3,D 是边AC 上一点,且BD=BC=2,则线段AD 的长为 .15.如图,在△ABC 与△ADE 中,EDAEBC AB ,要使△ABC 与△ADE 相似,还需添加一个条件,这个条件可以是 .16.在Rt △ABC 中,∠C =90°,CD ⊥AB 于点D ,若AD =9,BD =4,则AC = . 17.如图,在平行四边形ABCD 中,AB =12,AD =18,∠BAD 的平分线交BC 于点E ,交DC 的延长线于点F ,BG ⊥AE ,垂足为G ,BG =82,则△CEF 的周长是 . 18. 新定义:平行于三角形一边的直线被其他两边所截得的线段叫做“三角形的弦”.已知等边三角形的一条弦的长度为2cm ,且这条弦将等边三角形分成面积相等的两个部分,那么这个等边三角形的边长为 cm .19.如图,△ABC 是面积为3的等边三角形,△ADE ∽△ABC ,AB =2AD ,∠BAD =45°,AC 与DE 相交于点F ,则△AEF 的AB CD EACBP DBDCBA面积是 .20.如图,在Rt △ABC 中,∠C =90°,AC =3D 、E 分别是边BC 、AC 上的点,且∠EDC=∠A ,将△ABC 沿DE 对折,若点C 恰好落在边AB 上,则DE 的长为 .21. 如图,矩形ABCD 中,AB =8,BC =9,点P 在BC 边上,CP =3,点Q 为线段AP 上的动点,射线BQ 与矩形ABCD 的一边交于点R ,且AP=BR = . 22.如图,Rt △ABC 中,∠C =90°,AB =5, AC=3,在边AB 上取一点D ,作DE ⊥AB 交BC 于点E .现将△BDE 沿DE 折叠,使点B 落在线段DA 上(不与点A 重合),对应点记为B 1;BD 的中点F 的对应点记为F 1.若△EFB ∽△A F 1E ,则B 1D = .23.的长为 .24.如图,已知等腰△ABC ,AD 是底边BC 上的高,AD :DC =1:3,将△ADC 绕着点D 旋转,得△DEF ,点A 、C 分别与点E 、F 对应,且EF 与直线AB 重合,设AC 与DF 相交于点O = .25.如果将一个三角形绕着它一个角的顶点旋转后使这个角的一边与另一边重叠,再将旋转后的三角形进行相似缩放,使重叠的两条边互相重合,我们称这样的图形变换为三角形转似,这个角的顶点称为转似中心,所得的三角形称为原三角形的转似三角形.如图,在△ABC 中,AB =6,BC =7,AC =5,△A 1B 1C 是△ABC 以点C 为转似中心的其中一个转似三角形,那么以点C 为转似中心的另一个转似三角形△A 2B 2C (点A 2、B 2分别与A 、B 对应)的边A (B 1)A 1EBAABF 1CD EFB 1A2B2的长为.三、解答题1.如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,E.2.如图,点D为△ABC内部一点,点E、F、G分别为线段AB、AC、AD上一点,且EG∥BD,GF∥DC.(1)求证: EF∥BC;(2.3.如图,在△ABC中,∠ACB=90°,AC=BC,点P是△ABC形内一点,且∠APB=∠APC=135°.(1)求证:△CP A∽△APB;(2)试求tan∠PCB的值.BAEC D BAB CP4.如图,已知在直角梯形ABCD 中,∠ADC =90°,AD //BC ,AD =8,DC =6,点E 在BC 上,点F 在AC 上,且DFC AEB ∠=∠,AF =4.(1)求线段CE 的长;(2)若43sin =B ,求线段BE 的长.5.已知:如图,△ABC 中,点D 、E 是边AB 上的点, CD 平分∠ECB ,且2BC BD BA =⋅.(1)求证: △CED ∽△ACD ;(2)求证: AB CEBC ED=.FAC BDF E DCB A6.已知:如图,在△ABC中,已知点D在BC上,联结ADDC=3﹦1﹕2.(1)求AC的值;(2)若将△ADC沿着直线AD翻折,使点C落点E处,AE交边BC于点F,且AB∥DE7.在△ABC中,∠BAC=90°, ∠EAF=90°,(1)求证:△AGC∽△DGB;(2)若点F为CG的中点,AB=3,AC=4求DF的长.AE FGDBC8D 、E 分别在BC 和AC 边上,点G 是BEAG . (1(29.如图,已知CD 是△ABC 中∠ACB 的角平分线,E 是ACAD =6,AE =4.(1) 求证:△BCD ∽△DCE ; (2) 求证:△ADE ∽△ACD ; (3) 求CE 的长.BDAGECABCDE10.如图,已知在等腰△ABC 中,AB =AC ,点E 、点D 是底边所在直线上的两点,联接AE 、AD ,若求证:(1)△ADC ∽△EDA ; (211.在△ABC 中,D 是BC 的中点,且AD=AC ,DE ⊥BC ,与AB 相交于点E , EC 与AD 相交于点F .(1)求证:△ABC ∽△FCD ;(2)若DE =3,BC =8,求△FCD 的面积.BAD。
沪教版九上数学因动点产生的相似三角形问题中考专项练习(word版,含答案)

因动点产生的相似三角形问题中考专项练习1 .如图,在平面直角坐标系xOy中,将抛物线y=x2的对称轴绕着点P (0, 2)顺时针旋转45 后与该抛物线交于A、B两点,点Q是该抛物线上一点.(1)求直线AB的函数表达式;(2)如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值;为顶点的三角形与△ PAT相似时,求所有满足条件的t的值.(3)如图②,若点Q在y轴左侧,且点T (0,t) (t v2)是射线PO上一点,当以P、B、Q图①関②筍用图2 .如图,已知BC是半圆O的直径,BC=8过线段BO上一动点D,作AdL BC交半圆O于点A,联结AQ过点B作BHLAO垂足为点H, BH的延长线交半圆O于点F.(1)求证:AH=BD度.(2)设BD=x BE?BF=y,求y关于x的函数关系式;(3)如图2,若联结FA并延长交CB的延长线于点G,当△卩人丘与厶FBG相似时,求BD 的长3•如图,在平面直角坐标系 xOy 中,直线AB 过点A (3, 0)、B (0, m (m>0), tan /函数y=〒的图象于点F ,分别联结OE OF ,当厶OEI ^A OBE 时,请直接写出满足条件的所有k 2的值.BAO=2(1) 求直线AB 的表达式;k](2) (3) 反比例函数沪*的图象与直线AB 交于第一象限内的C D 两点(v BC ),当AD=2DB 时,求k i的值; 设线段AB 的中点为E ,过点E 作x 轴的垂线,垂足为点M,交反比例4.如图,在Rt △ ABC中,/ ACB=90 , AC=1, BC=7点D是边CA延长线的一点,ALL BD 垂足为点E, AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.(1) 当点E是BD的中点时,求tan / AFB的值;(2) CE?AF的值是否随线段AD长度的改变而变化?如果不变,求出CE?AF的值;如果变化,请说明理由;(3) 当厶BGE^P^ BAF相似时,求线段AF的长分析解答一•解答题(共36小题)【分析】(1)根据题意易得点M P的坐标,利用待定系数法来求直线AB的解析式;(2)如图①,过点Q作x轴的垂线QC交AB于点C,再过点Q作直线AB的垂线,垂足为D,构建等腰直角△ QDC利用二次函数图象上点的坐标特征和二次函数最值的求法进行解答;(3)根据相似三角形的对应角相等推知:△ PBQ中必有一个内角为45°;需要分类讨论:/ PBQ=45和/PQB=45 ;然后对这两种情况下的厶PAT是否是直角三角形分别进行解答.另外,以P、B、Q为顶点的三角形与△ PAT相似也有两种情况:△ Q' PB^A PAT △Q' BP^APAT【解答】解:(1)如图①,设直线AB与x轴的交点为MvZ OPA=45,•••0M=0P=2即M (- 2,0).设直线AB的解析式为y=kx+b (2 0),将M (- 2, 0),P (0,2)两点坐标代入,得r2=kX0+b\o=kX (-2)+b故直线AB的解析式为y=x+2;(2)如图①,过点Q作x轴的垂线QC交AB于点C,再过点Q作直线AB的垂线,垂足为D, 根据条件可知△ QDC为等腰直角三角形,则QD= QC设Q( m m),则C(m m+2.1 29••• QC=m+2m=-( m- .) + ,生生I 2QD=JQC= [-( m- ) +J . f1故当m=时,点Q到直线AB的距离最大,最大值为(3)vZ APT=45 ,中必有一个内角为45°,由图知,/ BPQ=45不合题意.•••△PBQ①如图②,若/ PBQ=45,过点B作x轴的平行线,与抛物线和y轴分别交于点Q、F•此时满足/ PBQ =45°.•- Q (- 2, 4),F (0,4),•••此时△ BPQ是等腰直角三角形,由题意知△ PAT也是等腰直角三角形.(i ) 当/ PTA=90 时,得到:PT=AT=1 此时t=1 ;(ii )当 / PAT=90 时,得到:PT=2,此时t=0 .②如图③,若/ PQB=45,①中是情况之一,答案同上;先以点F为圆心,FB为半径作圆,则P、B、Q都在圆F上,设圆F与y轴左侧的抛物线交于另一点Q'.贝U/ PQ B=Z PQ B=45 (同弧所对的圆周角相等),即这里的交点Q'也是符合要求.设Q'(n, n2) (- 2v n v 0),由FQ' =2,得n2+ (4 - n2) 2=22,即卩n4- 7n2+12=0.解得n2=3或n2=4,而-2v n v O,故n=-/3,即卩Q'(-J^,3).可证△PFQ为等边三角形,所以/ PFQ =60°,又PQ =PQ,所以/ PBQ =1_.则在△ PQ B 中,/ PQ B=45 ,' Z PFQ =30°/ PBQ =30°.(i ) 若厶Q' PB^A PAT则过点A作y轴的垂线,垂足为E.贝U ET= AE=,OE=1 "所以OT^- 1,解得t=1 -V3;(ii ) 若厶Q' B3A PAT则过点T作直线AB垂线,垂足为G.设TG=a贝U PG=TG=, AG= TG= a AP=::,;••• a+a=,解得PT= a=—1晅並/• OT=OP PT=3- 「;,••• t=3 -:.综上所述,所求的t的值为t=1或t=0或t=1 -;或t=3 - ■ :_:.图③图②图①2.【分析】(1)由ADIBC BH L AQ利用垂直的定义得到一对直角相等,再由一对公共角,且半径相等,利用AAS得到三角形ADO与三角形BHO全等,利用全等三角形对应边相等得到OH=O P利用等式的性质化简即可得证;(2)连接AB AF,如图1所示,利用HL得到直角三角形ADB与直角三角形BHA全等,利用全等三角形对应角相等得到一对角相等,再由公共角相等得到三角形ABE与三角形AFB相似,由相似得比例即可确定出y与x的函数解析式;(3)连接OF如图2所示,利用两对角相等的三角形相似得到三角形AFO与三角形FOG 相似,由相似得比例求出BD的长即可.【解答】(1)证明:T AD L BC BH L AQ•••/ ADO M BHO=90 ,在^ ADO^A BHO中,r ZAD0=ZBH0ZAOD=ZBOH:t | ,•••△ ADO^ BHO( AAS ,•••O H=OJD又T OA=OB••• AH=BD(2)解:连接AB AF,如图1所示,T AO是半径,AOL弦BF,•••••• AB=AF二/ ABF W AFB,在Rt△ ADB与Rt△ BHA中, fAH=BDIt AB二BA,••• Rt△ ADB^Rt△ BHA( HL),•••/ ABF玄BAD, •••/ BAD" AFB,BE M-=••• B A=BE?BFT BE?BF=yy=BA ,T Z ADO"ADB=90 ,•AD=AO- DO, AD=AB - BD , • AO- DO=AB- BD , T直径BC=8 BD=x•AB=8x ,则y=8x (O v x v4);方法••• BE?BF=y BF=2BH 二BE?BH=y,•••△BEDT A BOHBE BD•••OB?BD=BE?BH二4x= y,y=8x (O v x v 4);(3)解:连接OF,如图2所示,vZ GFB是公共角,/ FAE>Z G•当厶FA0A FBG时,Z AEF Z GvZ BHA Z ADO=90 ,•Z AEF+Z DAO=9O , Z AOD Z DAO=9O ,•Z AEF Z AOD•Z G=/ AOD•AG=AO=4••••••Z AOD Z AOF•Z G=/ AOF又vZ GFO是公共角,•△FA3A FOGAF OF.•.而而二v AB=8x, AB=AF••• AF=2 二x,;:=-4 4+2逅耳解得:x=3±■,••• 3+ ■> 4,舍去, • BD=3-二.3.【分析】(1)先通过解直角三角形求得A的坐标,然后根据待定系数法即可求得直线AB的解析式;匹型丄(2)作DE//OA根据题意得出OA AB 3==,求得DE即D的横坐标,代入AB的解析式求得纵坐标,然后根据反比例函数图象上点的坐标特征即可求得k i;(3)根据勾股定理求得AB OE进一步求得BE然后根据相似三角形的性质求得EF的长,从而求得FM的长,得出F的坐标,然后根据反比例函数图象上点的坐标特征即可求得k2.【解答】解:(1)v A( 3, 0)、B (0,m (m>0),•OA=3 OB=mOB••• tan / BAO= ' =2,•m=6设直线AB的解析式为y=kx+b,代入A (3, 0)、B (0, 6)得:『0二弘吐t解得:b=6, k=- 2•直线AB的解析式为y= —2x+6;(2)如图1,v AD=2DBDB丄=作DE// OA.匹=BD = 1••• DE= OA=1 • ••D 的横坐标为1,代入 y= - 2x+6 得,y=4, • k i=1 X 4=4; (3)如图 2,v A (3, 0), B (0, 6), • E (一,3), AB=f 匹,'=3 乙 v OE M Rt △ OAB 斜边上的中线,1 .OE= AB=BE=匚v EM Lx 轴, 3• F 的横坐标为二•••△ OEI ^A OBE•空=OE•飯=0B ,3 9 27•-k2=: X =图1 •- D( 1, 4), EF= 8 8' • FM=-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动点产生的相似三角形1.掌握相似基本图形中的相似三角形和各种比例式;2.通过观察了解因动点产生的相似三角形问题的特点,熟悉对应的解题方法,掌握“动中取静,以静窥动”的解题策略;3.培养学生对图形的直觉能力以及从变化中看到不变实质的数学洞察力;4.培养学生学会挖掘题目中的隐藏条件,从未知到已知的一个转变;5.掌握动点产生的相似三角形的分类讨论情况,并能根据题目中的条件进行求解。
知识结构【注意】:1.此部分知识点梳理,先提问学生学过的基本图形,并且画出来,再结合讲义讲解;2.部分基本图形的比例式,可以在白板上先画出基本图形再让学生找相似三角形,并写出比比例式,尤其是第四、五个基本图形一定要让学生写,部分地方让学生填写完,建议8分钟左右完成。
1.相似基本图形:2.相似三角形的基本图形产生的结论结论:(1)、A字型:①正A字型②斜A字型③其它A字型ABCDEABCDEABCEA B C ∽∆∆A D E ACB ∽∆∆ADE ACB ∽∆∆ABEAC AE AB AD = AB AE AC AD = ACABAB AE =AB AE AC AD ⋅=⋅ AC AE AB AD ⋅=⋅ AC AE AB ⋅=2(2)、X 型:①正X 字型 ②斜X 字型A DEBCADEBCA E D ∽∆∆ABC ADE ∽∆∆ABCAB AE AC AD = ACAEAB AD =AC AE AB AD ⋅=⋅ AB AE AC AD ⋅=⋅(3)、直角三角形:DCABCDB ∽ACB ∽∆∆∆ADC ①AB AD AC AB ACADC ⋅=⇒=⇒∆∆2AC AD ACB ∽ ②AB BD BC BC BDBDC ⋅=⇒=⇒∆∆2AB BC BCA ∽ ③BD AD CD BDCDADC ⋅=⇒=⇒∆∆2CD AD CDB ∽ (4)、直线型(一线三角): (5)、其他基本型:A BCDEFEDABCCEF ∽∆∆BDE AEB ∽∆∆ADC 和ACB ∽∆∆ADECF BE CE BD = ABAEAC AD =BE CE CF BD ⋅=⋅ AC AE AB AD ⋅=⋅3.相似三角形方法的选择:(1)已知有一角相等时,可选择方法两角相等和方法两边对应成比例且夹角相等; (2)已知有二边对应成比例时,可选择方法三边对应成比例和方法两边对应成比例且夹角相等;(3)若有平行条件时,可考虑方法基本图形“A 字型和X 型”; (4)有直角三角形时,可考虑方法直角三角形判定方法; (5)不管选择用哪一个方法,先找角度,再根据题目选择。
4.相似三角形的作用:综合使用相似三角形的性质与相似三角形的识别可以解决以下问题: (1)可用来证明线段成比例、角相等、线段相等、垂直、平行等; (2)可用来计算周长、边长、角度等; (3)用来证明线段的平方比、图形面积的比等。
例1.如图,在直角梯形ABCD 中,AD ∥BC ,∠A =90o,BD ⊥DC ,BC =10cm ,CD =6cm .在线段BC 、CD 上有动点F 、E ,点F 以每秒cm 2的速度,在线段BC 上从点B 向点C 匀速运动;同时点E 以每秒cm 1的速度,在线段CD 上从点C 向点D 匀速运动。
当点F 到达点C 时,点E 同时停止运动。
点F 、E 在运动过程中,如CEF ∆与BDC ∆相似,求线段BF 的长。
(★★★)【参考教法】:一.你来找一下题目中有哪些不变的量或者是比较特殊的条件,试试看:1.哪些角为直角?提示:090A ABC BDC ∠=∠=∠=,则BDC ∆为直角三角形; 2.点F 、E 的运动速度和方向怎样? 二.当CEF ∆与BDC ∆相似时:1.CEF ∆与BDC ∆中是否有相等的角度?提示:C ∠为公共角;2.需不需要分类讨论? 提示:题目中没有对应角,应该需要;3.如需要分类讨论,则分哪几种?提示:因为C ∠为公共角,则分两个情况讨论: ①.当0=90FEC BDC ∠=时:则FC ECBC DC=; 【注意】:1.以下每题教法建议,请老师根据学生实际情况参考;2.在讲解时:不宜采用灌输的方法,应采用启发、诱导的策略,并在读题时引导学生发现一些题目中的条件(相等的量、不变的量、隐藏的量等等),使学生在复杂的背景下自己发现、领悟题目的意思;3.可以根据各题的“参考教法”引导学生逐步解题,并采用讲练结合;注意边讲解边让学生计算,加强师生之间的互动性,让学生参与到例题的分析中来;4.例题讲解,可以根据“教法指导”中的问题引导学生分析题目,边讲边让学生书写,每个问题后面有答案提示;5.引导的技巧:直接提醒,问题式引导,类比式引导等等;6.部分例题可以先让学生自己试一试,之后再结合学生做的情况讲评;7.每个题目的讲解时间根据实际情况处理,建议每题7分钟,选讲例题在时间足够的情况下讲解。
D C B A 第1题图第1题备用图 DCB A②.当0=90EFC BDC ∠=时:则FC ECDC BC=。
4求解完了吧!你真厉害,那求解完的答案是否需要舍掉?提示:根据题目条件两个都答案满足要求。
5.终于计算完了,那你觉得“相似三角形的分类讨论”难吗? 【满分解答】: 当︒=∠=∠90FEC BDC ,则FC EC BC DC =,得:10-2106t t=,所以1160=BF cm , 当︒=∠=∠90EFC BDC ,则FC EC DC BC =,得:10-2610t t=,所以13100=BF cm 综上所述:1160=BF cm 或者13100=BF cm我来试一试!(该例题让学生自己先做、之后讲评)练习1.如图,已知等边△ABC 的边长为6,点D 是边BC 上的一个动点,折叠△ABC ,使得点A 恰好与边BC 上的点D 重合,折痕为EF (点E 、F 分别在边AB 、AC 上)。
当以B 、E 、D 为顶点的三角形与△DEF 相似时,求BE 的长.【解法点拨】:1.可以让学生用白纸剪切一个等边三角形进行翻折,体验动态过程;2.注意点A 落在BC 边上的点D 处3.抓住题目中的不变量(相等的角、边等),注意060A D B C ∠=∠=∠=∠=;4.寻找题目中的基本图形,060D B C ∠=∠=∠=,构成一线三角基本图形。
【满分解答】:分两种情况讨论:①当以B 、E 、D 为顶点的三角形与△DEF 相似, 顶点B 、D 、E 分别与D 、E 、F 对应时, 可得BDF DEF ∠=∠ . ∴EF ∥BC∴60AEF B ︒∠=∠=,60DEF AEF ︒∠=∠=.易得△AEF 、△D E F 、△D F C 、△D E B 是四个边长相等的等边三角形. ∴132BE ED EF AE AB =====.②当以B 、E 、D 为顶点的三角形与△DEF 相似,顶点B 、D 、E 分别与D 、F 、E 对应时,可得BDE DFE ∠=∠ 又BDE DFC ∠=∠,DFE AFE ∠=∠,∴1180603AFE DFE DFC ︒︒∠=∠=∠=⨯= 易得△AEF 、△DEF 、△DFC 、△DEB 四个边长相等的等边三角形.∴132BE ED EF AE AB =====.综上所述,当以B 、E 、D 为顶点的三角形与△DEF 相似时,3BE =.例2.如图,已知梯形ABCD ,AD ∥BC ,5AB AD ==,34tan DBC ∠=.E 为射线BD 上一动点,过点E 作EF ∥DC 交射线BC 于点F .联结EC ,联结DF ,若△BDF 与△BDA 相似,试求BF 的长.(★★★)【参考教法】:一.题目看完了吧!我们来看看点E F 、的运动情况和题目中是否有相等的角度? 提示:1.点E 为射线BD 上一动点,点F 为射线BC 上一动点; 2.在点的移动过程中,ADB DBC ∠=∠; 二.当△BDF 与△BDA 相似时:1.是否有相等的角度?提示:ADB DBC ∠=∠;2.需不需要分类讨论? 提示:题目中没有对应角,应该需要;3.如需要分类讨论,则分哪几种?提示:因为ADB DBC ∠=∠为公共角,则分两个情况讨论:①当ABD BDC ∠=∠时,则四边形ABFD 为平行四边形;②当ABD A ∠=∠时,则BFD ABD ADB DBF ∠=∠=∠=∠,所以BD DF =。
4.注意条件的转化,由相似可能会产生新的相似或者是其它更加特殊的条件; 5.这个题目也也讲解完了,你再来看一下“相似三角形的分类讨论”难吗?【满分解答】:过点A 作AH ⊥BD 于点H , ∵AD ∥BC ,5AB AD ==,∴HD BH DBC ADB ABD =∠=∠=∠,.在ABH RT ∆中,∵43tan tan =∠=∠DBC ABD , ∴54cos ==∠AB BH ABD . ∴4==HD BH . ∴8=BD .∵AD∥BC,∴DBCADB∠=∠.∵△BDF与△BDA相似,①ABDF∠=∠,可证四边形ABFD是平行四边形.∴5BF AD==.②ABDBFD∠=∠,∴DB DF=.可求得:564=BF.综上所述,当△BDF与△BDA相似时,BF的长为5或564.(引导学生总结,大概5分钟左右)一.由动点产生的相似三角形的解题方法和策略:1.寻找题目中特殊的条件和不变的量,并找出由条件引发的一些相等角、相等线段等特殊条件;(挖掘题目中的隐藏条件)2.注意分类讨论,先找是否有相等角,再决定分类讨论情况:3.相似三角形的边如果能直接求出列等式最好,如果不能求出,注意转化相似(是否产生新的相似、等腰、平行四边形等更特殊的条件)4.注意三个易忘定理:线段的中垂线定理、角平分线定理、直角三角形的性质。
(该题综合性很强,需要学生在10分钟内独立完成,并给出学生得分,之后老师再讲评)1.已知:Rt ABC∆中,90C∠=︒,4AC=,cot3B=,四边形MNPQ的边MN在AB边上,2MN=,顶点P、Q分别在边BC、AC上,QM AB⊥于M,//PN QM,如图1,设AM x=,PB y=。
(10分)(1)求y关于x的函数关系式,并写出函数定义域;(4分)(2)PCQ∆能与QMA∆相似吗?若能,请求出x的值;若不能,请说明理由。
(6分)(★★★)【解法点拨】:1.注意题目中的特殊条件:030B∠=,2MN=,090C QAM PNB∠=∠=∠=;CA M N BQP(图1)2.在点P 、Q 的运动过程中,注意有三个直角三角形一直相似:AMQ ∆∽ACB ∆∽PNB ∆;3.求解函数关系时,由基本图形即可求解:PB BNPA BC=; 1.当PCQ ∆与QMA ∆相似时,090C QAM ∠=∠=,则分两个情况讨论: ①当60CQP A ∠=∠=︒时,可得CQP ∆∽CAB ∆∽MAQ ∆; ②当30CQP B ∠=∠=︒时,可得CQP ∆∽CBA ∆∽MQA ∆。
