Solutions_chap10-12

合集下载

信号与系统奥本海姆英文版课后答案chapter10

∞
−n
n =−∞
∑ (1/ 4)
∞
z −n zn
n =−3
∑ (1/ 4)
= ∑ (1/ 4) − n +3 z n −3
n=0
= (1/ 64) z −3 /(1 − 4 z ), z < 1/ 4 = (1/16) z −4 /(1 − (1/ 4) z −1 ), z < 1/ 4
The Fourier transform does not exist because the ROC includes the unit circle. (g) Consider x1 ( z ) = 2n μ[ − n].
X ( z) =
n =−∞
jw
r> 1 . The second summation
2
10.2
∑ ( 5 ) u[n − 3]z
n
∞
1
z −3 ∞ 1 n − n ]∑ ( ) z =[ 125 n = 0 5
∞ 1 = ∑ ( )n z − n n =3 5 z −3 1 ] =[ 125 1 − 1 z −1 5 −n
X ( Z ) = ∑ x[n]z − n
n =∞ ∞
−5
= ∑ (−1) n z − n
n =0
∞
= 1/(1 + z −1 ), z > 1
The Fourier transform does not exist because the ROC does not include the unit circle (d) For x [n]= ( 1 ) n +1 μ[n + 3],
x( z ) =

计算机科学导论原书第二版答案第十二章汇编

2. A stack is a restricted linear list in which all additions and deletions are made at one end, called the top. If we insert a series of data into a stack and then remove it, the order of the data will be reversed. This reversing attribute is why stacks are known as a last in, first out (LIFO) data structure. Four basic stack operations defined in this chapter are stack, push, pop, and empty.
}
return true
}
32. Algorithm S12.32 shows the pseudocode. Algorithm S12.32 Exercise 32
Algorithm: CompareStack(S1, S2)
Purpose: Check if two stacks are the same Pre: Given: S1 and S2 Post: Return: true (S1 = S2) or false (S1 ≠ S2) {
}
if (NOT empty (S1) or NOT empty (S2))
flag ← false
while (NOT empty (Temp1) and NOT empty (Temp2))
{ pop (Temp1, x) push (S1, x) pop (Temp2, y) push (S2, y)

Solutions

1Chapter I Solutions 1.1Section1(TODO)12Chapter II Solutions 2.1Section 11.16b.Given an exact sequence of sheaves 0→F →F →F →0over a topological space X with F ﬂasque show that for every open U ⊂X that the sequence 0→F (U )→F (U )→F (U )→0is exact.Proof.Since the section functor Γ(U,−)is left exact,we only need to show the map β:F (U )→F (U )is surjective.Fix a section s ∈F (U ).Given any point P ∈U ,the sequence 0→F P →F P →F P →0is exact since the stalk functor is exact.So there is a germ t P ∈F P that is mapped by βP to s P .Since these are germs of functions,there exists an open neighborhood U i ⊂U and a section t ∈F (U )with β(t )|U i =s |U i .Now suppose wehave two sections t i ,t j ∈F (U )whose images under βagree with s on open neighborhoods U i and U j ⊂U of P respectively.Then β(t i −t j )|U i ∩U j =0,so since 0→F (U i ∩U j )→F (U i ∩U j )→F (U i ∩U j ),we have a section w ∈F (U i ∩U j )that maps to t i −t j on U i ∩U j .F ﬂasque gives a section w ∈F (U )that maps to w under restriction,and maps to t i −t j under α:F (U )→F (U ).Thus the sections t i and t j +α(w )agree on U i ∩U j ,so we can glue them on U i ∩U j to get a section t ∈F (U )such that t |U i =t i |U i and t |U j =(t j +α(w ))|U j .Since β(α(w ))=0,we see β(t )|U i ∪U j =s |U i ∪U j ,thus extending the sections on U i and U j to a section mapping to s over all U i ∪U j .Then Zorn’s Lemma allows us to extend to a section t over all U such that β(t )=s .Thus 0→F (U )→F (U )→F (U )→0is exact.23Chapter III Solutions 3.1Section13.2Section22.1a.Let X=A1k be the aﬃne line over an inﬁniteﬁeld k.Let P,Q bedistinct closed points of X,and let U=X−P,Q.Show H1(X,Z U)=0. ing the exact sequence0→Z U→Z X→Z{P,Q}→0and com-puting cohomology gives0→Γ(U,Z U)→Γ(X,Z X)→Γ(X,Z{P,Q})→H1(X,Z U)→H1(X,Z X)→...A1k irreducible implies the constant sheafZ X isﬂasque,so H1(X,Z X)=0.Γ(X,Z X)∼=Z andΓ(X,Z{P,Q})∼=Z⊕Z (since P and Q are distinct,we can assign independent values at the two points)then implies H1(X,Z U)=0,as desired.2.1b.More generally,let Y⊆X=A nk be the union of n+1hyperplanesin suitably general position,and let U=X−Y.Show that H n(X,Z U)=0. Proof.TODO2.2.Let X=P1k be the projective line over an algebraically closedﬁeldk.Show that the exact sequence0→O→K→K/O→0of(II Ex.1.21d) is aﬂasque resolution of O.Conclude from(II Ex.1.21e)that H i(X,O)=0 for all i>0.Proof.TODO34Chapter IV Solutions4.1Section11.1.Let X be a curve,and let P∈X be a point.Then there exists anonconstant rational function f∈K(X),which is regular everywhere exceptat P.Proof.Let X have genus g.Since X is dimension1,there exists a pointQ∈X,Q=P.Pick an n>max{g,2g−2,1}.Then for the divisorD=n(2P−Q)of degree n,l(K−D)=0(1.3.4),so Riemann-Roch givesl(D)=n+1−g> 1.Thus there is an eﬀective divisor D such thatD −D=(f).Since(f)is degree0(II6.10),D has degree n,so D cannot have a zero of order large enough to kill the pole of D of order2n.f isregular everywhere except at P.Note we cannot control the zeros of f withthis proof.1.2.Again let X be a curve,and let P1,P2,...,P r∈X be points.Then there is a rational function f∈K(X)having poles(of some order)at each of the P i,and regular elsewhere.Proof.We have to be careful.Multiplying functions from(Ex. 1.1)mayresult in zeroes cancelling poles.So proceed as follows:Fix a point Q distinctfrom the P i,and consider the divisor n(P1+P2+...+P r−(r−1)Q),with n>max{2g−2,g}.Then similar to(Ex.1.1),weﬁnd an eﬀective divisor D with D+n(r−1)Q−nP1−nP2−...−nP r=(f).Again since(f)has degree0(II6.10),degree of D is n.Since each P i occurs with order−n outside of D,either D cannot have a zero at any P i large enough to cancel the pole,or D=nP i for someﬁxed i.In the former case we’re done,in the latter use(Ex.1.1)to get a principal divisor(g)with a pole at P i.(fg)may have unwanted cancellation.Suppose(g)has zeroes of order n j at some(or none,or all)P j.Then forα>max{n j,1},(fα)has poles of higher order at P j=P i.Then the principal divisor(fαg)must have a pole at P i,and the zeros of(g)cannot cancel the poles at the remaining P j of(fα),so this is the divisor.1.3.Let X be an integral,separated,regular,one-dimensional schemeofﬁnite type over k,which is not proper over k.Then X is aﬃne.4Proof.Embed X→X,the closure of X(TODO-explain).Then X= X∪{P1,P2,...,P r}.This is aﬁnite set since(TODO).Then use(Ex.1.2) to get a principal divisor(f)with poles at exactly the P i,and this deﬁnesa morphism f:X→P1k which sends the P i to∞,and the rest of X toA1.f(X)=pt so(II6.8)implies f isﬁnite.(II Ex. 5.17b)says anyﬁnite morphism is aﬃne,so f−1(A1)=X is aﬃne.1.4.Show that a separated,one-dimensional scheme ofﬁnite type over k,none of whose irreducible components is proper over k,is aﬃne.Proof.(III Ex.3.2)gives the scheme X is aﬃne if and only if each irreducible component is aﬃne.Then(III Ex.3.1)implies each irreducible component Y is aﬃne if and only if Y red is aﬃne.Since irreducible and reduced imply integral(II3.1),we have reduced to the case X is integral,and then the result follows from(Ex1.3).1.5.For an eﬀective divisor D on a curve X of genus g,show that dim|D|≤degD.Furthermore,equality holds if and only if D=0or g=0. Proof.Since D is eﬀective,the subspaces|K−D|⊆|K|imply l(K−D)≤l(K)=g(1.3.3).Using dim|D|=l(D)−1(pg.295),Riemann-Roch gives dim|D|=degD+l(K−D)−g≤degD+l(K)−g=degD.Equality thus follows if l(K−D)=l(K).Clearly we have equality for D=0,and if g=0 then degK=−2and since D is eﬀective l(K−D)=0=g.Conversely,suppose we have equality,and suppose D=0.P∈SuppD gives|K−D|⊆|K−D−P|⊆|K|TODO1.6.Let X be a curve of genus g.Show there is aﬁnite morphism f:X→P1kof degree≤g+1.Proof.Pick any closed point P∈X.Let D=(g+1)P be a divisor. Riemann-Roch gives l(D)=(g+1)+1−g+l(K−D)=2+l(K−D), or l(D)/geq2.So there exists an eﬀective divisor(TODO),and(II6.8) gives1.7.Proof.TODO51.8.Proof.TODO1.9.Proof.TODO1.10.Let X be an integral projective scheme of dimension1over k, which is locally a complete intersection,and has p a=1.Fix a point P0∈X reg.Imitate(1.3.7)to show that the map P→L(P−P0)gives a one-to-one correspondence between the points of X reg and the elements of the group P ic0X.This generalizes(II,6.11.4)and(II,Ex.6.7).Proof.Let D be any divisor of degree0.We need to show there exists a unique point P∈X reg such that D∼P−P0.Since X satisﬁes(Ex.1.9d), weﬁnd that l(D+P0)−l(K−D−P0)=0+1−1=1.Applying(Ex.1.9d)to the divisors0and K,we get l(0)−l(K)=deg0+1−p a and l(K)−l(0)=degK+1−p bining weﬁnd that degK=2p a−2,so in our problem degK=0,thus deg(K−D−P0)<0and l(K−D)=0,giving l(D+P0)=1.Then dim|D−P0|=0,so there exists a unique eﬀective divisor linearly equivalent to D+P0.Since the degree is1,this divisor must be a single point P∼D+P0,or D∼P−P0.Note that(Ex.1.9c,d)implies P∈X reg.64.2Section22.2.Classiﬁcation of Curves of Genus2.Fix an algebraically closedﬁeld k of characteristic=2.(a).If X is a curve of genus2over k,the canonical linear system|K|determines aﬁnite morphism f:X→P1of degree2(Ex.1.7).Show thatit is ramiﬁed at exactly6points,with ramiﬁcation index2at each one.Notethat f is uniquely determined,up to automorphism of P1,so X determinesan(unordered)set of6points of P1,up to an automorphism of P1. Proof.Hurwitz gives2(4−2)=2(0−2)+degR which implies degR=6.Since degf=2,each ramiﬁcation index e P≤2,so each point in the support of R occurs with at most degree1.Thus the morphism is ramiﬁed at exactly6points,with ramiﬁcation index2at each point.(b).Conversely,given six distinct elementsα1,...,α6∈k,let K be the extension of k(x)determined by the equation z2−(x−α1)...(x−α6).Let f:X→P1be the corresponding morphism of curves.Show that g(X)=2, the map f is the same as the one determined by the canonical linear system, and f is ramiﬁed over the six points x=alpha i of P1,and nowhere else.(Cf. (II,Ex.6.4)).Proof.TODO(c).Using(I,Ex. 6.6),show that if P1,P2,P3are3distinct pointsof P1,then there exists a uniqueϕ∈Aut P1such thatϕ(P1)=0,ϕ(P2)=1,ϕ(P3)=∞.Thus in(a),if we order the six points x=αi of P1,and thennormalize by sending theﬁrst three to0,1,∞,respectively,we may assumethat X is ramiﬁed over0,1,∞,β1,β2,β3,whereβ1,β2,β3are three distinctelements of k,=0,1.Proof.(d).LetΣ6be the symmetric group on6letters.Deﬁne an action ofΣ6on the sets of three distinct elements of k,=0,1as follows:reorder the set0,1,∞,β1,β2,β3according a given elementσ∈Σ6,then renormalize as in(c)so that theﬁrst three become0,1,∞again.Then the last three are thenewβ1,β2,β3.Proof.Nothing to do.7(e).Summing up,conclude that there is a one-to-one correspondence between the set of isomorphism classes of genus2over k,and triples of distinct elementsβ1,β2,β3of k,=0,1,modulo the action ofΣ6described in (d).In particular,there are many non-isomorphic curves of genus2.We say that curves of genus2depend on three parameters,since they correspond to the points of an open subset of A1kmodulo aﬁnite group.Proof.2.5.Automorphisms of a Curve of Genus≥2.Prove the theorem of Hurwitz that a curve X of genus g≥2over aﬁeld k of characteristic0 has at most84(g−1)automorphisms.We will see later(Ex. 5.2)or(V Ex.1.11)that the group G=AutX isﬁnite.So let G have order n.Then G acts on the functionﬁeld K(X).Let L be theﬁxedﬁeld.Then theﬁeld extension L⊆K(X)corresponds to aﬁnite morphism of curves f:X→Y of degree n.(a).If P∈X is a ramiﬁcation point,and e P=r,show that f−1f(P) consists of exactly n/r points,each having ramiﬁcation index r.Let P1,...,P s be a maximal set of ramiﬁcation points of X lying over distinct points of Y, and let e Pi=r i.Then show that Hurwitz’s theorem implies that(2g−2)/n=2g(Y)−2+si=1(1−1/r i).Proof.Suppose P∈X is ramiﬁed as in the statement,and let f(P)=Q∈Y. The local ring B=O Y,Q hasﬁeld of fractions L,and under characteristic0 the extension L⊆K(X)is separable(andﬁnite already).Let A=B be the integral closure of B in K(X).Then the points over Q correspond to the dvrs in K(X)that lie over A.Each of these dvrs is just A localized at some maximal ideal in A.We want to show G acts transitively over these dvrs,so for any two primes P i and P j we want an elementσ∈G such that σ(P i)=P j.Clearly each element in B isﬁxed by G,and since A is the integral closure of B,B is theﬁxedﬁeld of A under the action of G.This follows since A is the set of elements in K(X)that are integral over B,so any element in A−B is notﬁxed by G,and any element in Aﬁxed under G is in L,hence also in B.Then from an easy problem in Atiyah-MacDonald Ch.5, #12,13,it follows that G acts transitively,so there is a curve automorphism taking any ramiﬁed point P i over Q to any other ramiﬁed point P j over Q.8Thus each point has the same index e Pi=r,and there has then to be n/r of them since f is tamely ramiﬁed at each point(chark=0),and(II,6.9) gives n=degfdegQ=degf∗Q=deg( e P i P i),but since each e P i=r,this implies there are n/r points over Q.Then Hurwitz’s thoerem gives(2g−2)/n=2g(Y)−2+1/n P∈X(e P−1). Since there are n/r i points over Q i,each with ramiﬁcation index r i,we get 1/n P∈X(e P−1)=1/n s i=1(n/r i)(r i−1)= s i=1(1−1/r i),ﬁnishing the problem.(b).Since g≥2,the left hand side of the equation is>0.Show that if g(Y)≥0,x≥0,r i≥2,i=1,...,s are integers such that2g(Y)−2+si=1(1−1/r i)>0,then the maximum value of this expression is1/42.Conclude that n≤84(g−1).See(Ex.5.7)for an example where this maximum is achieved. Proof.Let g Y=g(Y).Since each term1−1/r i is of the form n/(n+1),we getthat(∗)s> s i=1(1−1/r i)≥s/2.If g Y≥2,then2g Y−2+ s i=1(1−1/r i)≥2+s/2/geq2.If g Y=1,then the expression is≥s/2,so is greater than1/2.If g Y=0,then guessing gives1/2>1/6=−2+1/2+1/2+1/2+2/3>0corresponding to s=4,r1,r2,r3=2,r4=3.So any smaller value musthave g Y=0.If s≥5,then the sum is≥−2+5/2=1/2>1/6,sos≤4.The only solution with s=4smaller than the one above giving1/6is−2+1/2+1/2+1/2+1/2=0,no solution at all.Any other changesmake the value larger than1/6.If s<3,(∗)gives that the expression is<0.Thus any better solution than the1/6must have s=3.So we want tominimize h(a,b,c)=a/(a+1)+b/(b+1)+c/(c+1)−2,where a,b,c arepositive integers and the we require h>0.WLOG assume a≥b≥c.Thenchecking possible cases:h(1,1,c)<0for all c,so any solution has at most1entry of1.Checking higher cases(note the expression value increases as wepick larger numbers!):h(1,2,2)<0,h(1,2,3)<0,h(1,2,4)<0,h(1,2,5)=0,h(1,2,6)=1/42,corresponding to r1=2,r2=3,r3=7.Any valueh(1,2,c),c>6must be larger.So we check h(1,3,3)=0,h(1,3,4)=1/20,and again there can be no better solution with h(1,3,c),c>4.Continu-ing,h(1,4,4)=1/10,so there is no better solution with h(1,b,c).Nexth(2,2,2)=0,h(2,2,3)=1/12,h(2,3,3)=1/6so there is no better onestarting with a=2.h(3,3,3)=1/4,and any higher starting a value will do9worse,so the minimum1/42occurs at g Y=0,s=3,r1=2,r2=3,r3=7. Using part(a)gives that1/n(2g−2)≥1/42which is84(g−1)≥1/42.104.3Section33.1.If X is a curve of genus2,show that a divisor D is very ample⇐⇒degD≥5.Proof.Cor3.2gives degD≥5⇒D very ample.For the other direction, assume D very ample.Suppose degD<5.Then3.1(b)implies l(D−P−Q)=l(D)−2⇒l(D)≥2.But l(D)=2⇒dim|D|=1,so there is a closed immersion X →P1,so X is either a point or P1(II,6),contradicting g(X)=2.Thus l(D)>2.Thus there exists an eﬀective divisor D ∈|D|,and since|D |=|D| (proof:α∈|D|⇒α−D=(f),D−D =(g)⇒D −D+α−D= (fg)⇒|D|⊆|D |.The other way is similar.)we can apply(Ex. 1.5) to D to get dim|D|=dim|D |≤degD =degD.If D =0then l(D)= l(D )=1,contradiction.Since g=0the inequality is strict(Ex. 1.5),so 1<l(D)−1=dim|D|<degD and degD>2.So we check cases: If degD=3,then D nonspecial implies(Riemann-Roch)l(D)=2,a contradiction.If degD=4,then D nonspecial implies(Riemann-Roch) l(D)=3,so dim|D|=2,and D gives a closed immersion X →P2,but since the genus of a plane curve(I Ex.7.1)is1/2(d−1)(d−2)which can never be2,this too is a contradiction.Thus degD≥5.3.2.Let X be a curve of degree4.(a).Show that the eﬀective canonical divisors on X are exactly the divisors X.L,where L is a line in P2.Proof.Genus of a plane curve is g=1/2(d−1)(d−2)so degree4gives g(X)=3.degK=2g−2=4.For aﬁxed line L∈P2set D=X.L. Bezout’s theorem says D is4points counted with multiplicity,so degD=4. Riemann-Roch gives l(D)−l(K D)=4+1−3=2.Since it takes exactly 2points of X to deﬁne any line L,dim|D|=2(TODO-better proof),so l(D)=3,and l(K−D)=1.As in proof of(Ex.3.1),(Ex.1.5)gives that dim|K−D|≤deg(K−D)=0,and since|K−D|=∅,(why?TODO), g=0gives equality,so K−D∼0,or k∼D.(b).If D is any eﬀective divisor of degree2on X,show that dim|D|=0.Proof.Take a line L deﬁned by2distinct points of D if possible,else if D=nP use(I Ex.7.3)to get the unique line with proper intersection11multiplicity.Let D =X.L,a degree4eﬀective divisor by Bezout’s theorem. Then by proof of(a),dim|D |=2,and3.3.5implies D very ample(why-todo).D −D is2points,and theorem3.1b gives dim|D|=dim|D −(D −D)|=dim|D |−2=0.(c).Conclude X is not hyperelliptic.Proof.(TODO-check thoroughly)X hyperelliptic implies there is aﬁnite morphism f:X→P1of degree2.To give such a morphism is equivalent to giving a base point free linear system|D|such that dim|D|=1.So for D ∈|D|,degD =2.But by part(b)0=dim|D |=dim|D|,a contradiction. So X is not hyperelliptic.3.3.If X is a curve of genus≥2which is a complete intersection(II Ex.8.4)in some P n,show that the canonical divisor K is very ample.Conclude that a curve of genus2can never be a complete intersection in any P n.Cf. (II.7.8.5)Proof.Let X= H i be the intersection of hypersurfaces as in exerciseII8.4. Using the same exercise,ωX∼=O X( d i−n−1)for d i=degH i.Since dimΓ(X,ωX)=g≥2,ωX must have global sections,so m= d i−n−1≥0.m=0,since then g=1,a contradiction.ThusωX∼=O X(m)with m>posing X →P n →P N where the second inclusion is the m-uple embedding gives L(K)∼=ωX∼=i∗O P N(1).Thus K is very ample by deﬁnition.Note that the m-uple embedding i:P n →P N gives O X(m)∼= i∗O X(1).By(Ex. 1.7a),if g=2|K|deﬁnes a morphism X→P1so K is not very ample(this cannot be an embedding),thus X cannot be a complete intersection.3.4.Let X be the d-uple(I Ex. 2.12)embedding of P1in P d,for any d≥1.We call X the rational normal curve of degree d in P d.(a).Show that X is projectively normal,and that its homogeneous ideal can be generated by elements of degree2.Proof.TODO-was not e(I Ex.2.12)(b).if X is any curve of degree d in P n,with d≤n,which is not contained in any P n−1,show that in fact d=n,g(X)=0,and x diﬀers from the rational normal curve of degree d only by an automorphism of P d.Cf. (II.7.8.5).12Proof.Take a hyperplane H in P n.Then H.X consists of d points(countedwith multiplicity).These points span a hyperplane of dimension d−1.Ifd<n,then we can add any other points on X until a hyperplane of dimensionn−1is spanned,but this new hyperplane contains H,so H must itself haveintersected X in n−1points,contradicting d<n.Thus d=n.Theargument of(II.7.8.5)gives g=0and the rest of the problem.(TODO-write up)(c).In particular,any curve of degree2in any P n must be a conic insome P2.Proof.Since d=2we must have n=2by part b.(d).A curve of degree3in any P n must either be a plane cubic curve,or the twisted cubic curve in P3.Proof.If n<d,since n=1is impossible,we must have n=2.Then ellipticcurves exist in P2so this case is possible.Otherwise by part b the curve mustbe the twisted cubic in P3.3.5.Let X be a curve in P3,which is not contained in any plane.(a).If O/∈X is a point,such that projection from O indices a birationalmorphismϕfrom X to its image in P2,show thatϕ(X)must be singular. Proof.First note that since X is contained in no plane,ϕ(X)is contained inno line in P2sinceϕis projection from a point.So assume Y=ϕ(X)is notsingular.Then X is isomorphic to Y since they are birational.(I,6).Asso-ciate X with its image to simplify(confuse?)e the twisted exactsequence(for n=2and n=3)0→I X(1)→O P n(1)→O X(1)→0,whereI X is the ideal sheaf deﬁning X⊆P3,and compute the long exact sequence of cohomology.For n=2or3we have that H0(P3,I X(1))=0.Indeed,ifthere are any global sections of degree1,there is a linear polynomial in theideal deﬁning X,and then X is contained in a plane(n=3)or a line(n=2),both contradictions.Thus we have0→H0(P3,O P n(1))→H0(X,O X(1))→H1(P3,I X(1))→....(Note the last map of H0’s is not surjective in gen-eral.Take something not projectively normal,like the quadratic embedding(s:t) →(s4:s3t:st3:t4).)Since theﬁrst term has dimension n+1,weget for n=3that dimH0(P3,O X(1))≥4.In case n=2if we show thatdimH1(X,I X(1))=0,then we get dimH0(P2,O X(1))=3,a contradiction.(Note this assumes that these O X(1)’s are the same over P2and P3,since13the sheaf is the pullback of O P n(1).They are the same sheaf by Theorem II6.17P2 →P3,gives(TODO...)).For n=2,the curve is a Cartier divisor,so by Theorem II6.9,I X∼= L(−D).By Theorem II6.17L∈P ic P n⇒L∼=O X(n),n∈Z.The-orem II6.4gives D∼dH,so we combine to get sheafIX∼=L(−D)∼= L(−dH)∼=O P2(−d).Twisting,I X(1)∼=O P2(1−d).d=1⇒Y∼=P1,but Y not in any line gives a contradiction.Thus d>1,and H1(P2,I X(1))∼= H1(P2,O P2(1))=0by Theorem II5.1b.(b).If X has degree d and genus g,conclude that g<1(d−1)(d−2). e Theorem3.10to get O/∈X such that projection from O gives a birational morphism to the image,with at most nodes as singularities.Then part a implies there exists at least one node,and 3.4.1with r≥1gives the result.(c).TODOProof.3.6.Curves of degree4(a).If X is a curve of degree4in some—PSn,show that either(1)g=0,in which case X is either the rational normal quartic in P4( Ex.3.4)or the rational quartic curve in P3(II.7.8.6),or(2)X⊆P2,in which case g=3,or(3)X⊆P3and g=1.Proof.(1)If g=0then X is isomorphic to P1.X P2,since in P2g=1 2(d−1)(d−2)=3.So using(Ex. 3.4b),X is in P3or P4,and using thesame exercise X P3implies X is the rational normal curve in P4,which has degree4.So it remains to show there exists a curve of genus0and degree 4in P3.This is given by(II.7.8.6).(2)X⊆P2implies g=3by the usual formula.(3)Assume X⊆P3.(Ex.3.5b)gives that g<3.and g=0since that is covered in case(1).Taking a hyperplane H and using Riemann-Roch gives l(H)−l(K−H)=degH+1−g.degH=4since a degree4curve.If g=2then degK=2g−2=2,and then l(K−H)=0by(.1.3.4).Then l(H)=4+1−2=3,but l(H)=dimH0(P3,O P3(1))=4,a contradiction. Thus g=2.(III Ex. 5.6)gives that a curve of type2,2has g=1.Since the degree of a curve of type(a,b)is a+b(think through the embedding14and the intersection with a hyperplane-(a,b)corresponds to a lines in one direction and b lines in the other.).Thus curves with g=1and degree4 exist in P3.(b).In the case g=1,show that X is a complete intersection of two irreducible quadric surfaces in P3(I Ex.5.11).Proof.Taking a twisted sequence with the ideal sheaf I X gives0→I X(2)→O P3(2)→O X(2)→0.Then dimH0(P3,O P3(2))=(3+22)=10(the k di-mension of the space of degree2monomials in4variables).dimH0(X,O X(2))= 8since this is two hyperplanes intersecting the degree4curve X.Thus dimH0(P3,I X(2))≥2.So X is contained in at least2irreducible quadratic hypersurfaces.(This is also interesting for degree3hypersurfaces,etc...). (TODO-why complete intersection?)3.7.In view of Theorem 3.10,one might ask conversely,is every plane curve with nodes a projection of a nonsingular curve in P3?Show that the curve xy+x4+y4=0(assume chark=2)gives a counterexample.Proof.The only singularity is a node at(0,0).Suppose this curve X is the projection of a nonsingular curve˜X⊆P3.Then 3.11.1gives g= 1(d−1)(d−2)−r=1(3)(2)−1=2,but no such curve exists by(Ex.3.6a).3.8.We say a(singular)integral curve in P n is strange if there is a point which lies on all the tangent lines at nonsingular points of the curve.(a).There are many singular strange curves,e.g.,the curve given para-metrically by x=t,y=t p,z=t2p over aﬁeld of characteristic p>0. Proof.The curve is clearly singular at(0:0:0:1).(TODO)Since the curve is given parametrically,the tangent direction at a point is∂(t,t p,t2p)= (1,0,0).At a point(x0:y0:z0:1)on the curve,this tangent line is the intersection of the hyperplanes y=y0w and z=z0w.Thus in P3,every tangent line goes through(1:0:0:0),the point at inﬁnity.(b).Show,however,that if chark=0,there aren’t even any singular strange curves besides P1.15Proof.(TODO-)Idea is to reprove3.4,3.5,3.9,but the dimension of the tan-gent space in3.5may be very large,so only consider the tangent space of the nonsingular points on the curve.Needs some more work.3.9.Prove the following lemma of Bertini:is X is a curve of degree d in P3,not contained in any plane,then for almost all planes H⊆P3(meaning a Zariski open subset of the dual projective space(P3)∗),the intersection X∩H consists of exactly d distinct points,no three of which are collinear. Proof.3points are collinear⇐⇒H contains a multisecant of X.There are strictly less than d distinct points⇐⇒H contains a tangent line of X.The proof of3.5shows T anX,the tangent space of X,is closed and dimT anX≤2.TODO3.10.Generalize the statement that”not every secant is a multisecant”as follows.If X is a curve in P n,not contained in any P n−1,and if chark=0, show that for almost all choices of n−1points P1,P2,...,P n−1on X,the linear space L n−2spanned by the P i does not contain any further points of X.Proof.Let the degree of X be d.Then by(Ex.3.4b)if d≤n we have d=n and X diﬀers from the n-uple embedding of P1in P n.TODO So assume d>n.164.4Section4(TODO)174.5Section55.1.Show that a hyperelliptic curve can never be a complete intersection in any projective space.Proof.Every hyperelliptic curve has genus≥2(Ex.1.7),and every complete intersection has very ample canonical divisor(Ex.3.3).But the canonical divisor of a hyperelliptic curve is not very ample by Theorem 5.2,so it cannot be a complete intersection.5.6.Show that a nonsingular plane curve of genus5has no g13.Showthat there are nonhyperelliptic curves of genus6which cannot be represented as a nonsingular plane curve.Proof.(TODO)184.6Section66.1.A rational curve of degree4in P3is contained in a unique quadric surface Q,and Q is necessarily nonsingular.Proof.X∼=P1⇒g(X)=0.X⊆P2⇒g=1(d−1)(d−2),but degree4 and genus0contradict.Thus X P2.Consider the sequence0→I X(2)→O P3(2)→O X(2)→0.Take co-homology and dimension.dimH0(P3,O P3(2))=(3+22)=10.O X(2)corresponds to degree2hypersurfaces,so any intersection with X is a di-visor consisting of4×2=8points,so degD=8.Since8>2g−2=−2,D is nonspecial,and Riemann-Roch then gives l(D)=8+1−0=9,so dimH0(X,O X(2))=l(D)=9,thus from the exact sequence dimH0(P3,I X(2))≥1.So X is contained in a quadratic surface Q.The intersection of2quadratic surfaces is a complete intersection of degree4, and since X has degree4,if X is contained in the intersection,it would be acomplete intersection and have genus(II Ex.8.4)g=12×4(2+2−4)+1=1,contradicting g(X)=0.Thus X lies on a unique quadratic surface.Then by (Ex.3.6)X is the rational quartic curve in P3,so Q is nonsingular.(TODO -not clear?)6.2.A rational curve of degree5in P3is always contained in a cubic surface,but there are such curves not contained in any quadric surface. Proof.Again,X∼=P1,so g(X)=0.As above,consider the sequence0→I X(3)→O P3(3)→O X(3)→0.Degree3hypersurfaces in O X(3)intersected with X give divisors D of degree3×5=15,which makes D nonspecial(15> 2g−2=−2).Riemann-Roch gives l(D)=15+1−0,so dimH0(X,O X(3))=16.DimH0(P3,O P3(3))=(3+33)=20,so again dimH0(P3,I X(3))≥4,and X lies on a cubic surface.To get a curve not contained in any quadratic, use the idea in(.II)7.8.6.We embed P1as a degree5curve asϕ:(s:t) →(s5:s4t:st4+αs2t3:t5)=(x:y:z:w)for someα∈k∗.This is degree 5since it forms a basis for a linear subspace V⊆Γ(X,O X(5)).It is easy to check it has no degree2relations by checking degrees of the s and t involved. For fun it satisﬁes the cubic x2w−yz2+yzw−xw2=0.To check it is an embedding,we use Theorem II7.3.Either x or w has to be nonzero. w=0⇒x/y=s,separating points.x=0⇒y/x=t/s,separating points.19Since Y=ϕ(X)is dimension1,the tangent space is dimension1if Y is nonsingular,so there are no tangents to separate.So we only need to check nonsingularity.(TODO-easy?)6.3.A curve of degree5and genus2in P3is contained in a unique quadric surface Q.Show that for any abstract curve X of genus2,there exists embeddings of degree5in P3for which Q is nonsingular,and there exists other embeddings of degree5for which Q is singular.Proof.Noting O X(2)corresponds to degree2hypersurfaces,and that degree of such a(nonspecial)divisor is100→I X(2)→O P3(2)→O X(2)→0gives dimH0(P3,I X(2))≥1.So X lies in a quadric surface Q.X cannot lie on2, since degQ1∪Q2=4,and X could have degree at most4.(why-TODO). So X lies on the unique quadric.(TODO-rest...)6.4.Show there is no curve of degree9and genus11in P3Proof.First we show any such curve X must lie on a quadratic surface.Con-sider the sequence0→I X(2)→O P3(2)→O X(2)→0.dimH0(P3,O P3(2))= 10,so if dimH0(X,O X(2))<10then dimH0(P3,I X(2))≥1,so X lies on a quadratic surface.O X(2)corresponds to degree2hypersurfaces,which will intersect the curve X in9∗2=18points,so deg|O X(2)|=18.For O X(2) nonspecial,Riemann-Roch gives dimH0(X,O X(2))=18+1−11=9,so X will lie on a quadratic hypersurface.For O X(2)special,and eﬀective divisor D in the linear system given by O X(2)must have Theorem 5.4 dim|D|≤1degD=9,so again X will lie on a quadratic hypersurface.Then suppose X lies on a nonsingular quadratic hypersurface of type (a,b).Then by6.4.1,d=9=a+b and g=11=ab−a−b+1.Substituting, 11=a(9−a)−a−(9−a)+1,or0=a2−9a+19,which has no integer solution.Thus X cannot lie on a nonsingular quadratic hypersurface.X cannot lie in the product of two hyperplanes,since it will then either be a line and have genus0,or it will be in a plane,and then contradictsg=12(d−1)(d−2)=28=11.The only case left is X lies on a quadratic cone,but then6.4.1again gives d=2a+1⇒a=4,and then g=a2−a⇒g=16−4=12=11.Thus no curve exists in P3of degree9and genus11.20。

Solutions - Chapter 10

Solutions - Chapter 1010-1: Learning PythonOpen a blank file in your text editor and write a few lines summarizing what you’ve learned about Python so far. Start each line with the phrase In Python you can… Save the file as learning_python.txt in the same directory as your exercises fro mthis chapter. Write a program that reads the file and prints what you wrote three times. Print the contents once by reading in the entire file, once by looping over the file object, and once by storing the lines in a list and then working with them outside the with block.learning_python.txt:learning_python.py:Output:10-2: Learning CYou can use the replace() method to replace any word in a string with a different word. Here’s a quick example showing how to replace 'dog' with 'cat' in a sentence:Read in each line from the file you just created, learning_python.txt, and replace the word Python with the name of another language, such as C. Print each modified line to the screen.Output:You can use rstrip() and replace() on the same line. This iscalled chaining methods. In the following code the newline is stripped from the end of the line and then Python is replaced by C. The output is identical to the code shown above.10-3: GuestWrite a program that prompts the user for their name. When they respond, write their name to a file called guest.txt.Output:guest.txt:10-4: Guest BookWrite a while loop that prompts users for their name. When they entertheir name, print a greeting to the screen and add a line recording their visit in a file called guest_book.txt. Make sure each entry appears on a new line in the file.Output:guest_book.txt:10-5: Programming PollWrite a while loop that asks people why they like programming. Eachtime someone enters a reason, add their reason to a file that stores all the responses.Output:programming_poll.txt:10-6: AdditionOne common problem when prompting for numerical input occurs when people provide text instead of numbers. When you try to convert the input to an int, you’ll get a ValueError. Write a program that prompts for two numbers. Add them together and print the result. Catch the TypeError if either input value is not a number, and print a friendly error message. Test your program by entering two numbers and then by entering some text instead of a number.Output with two integers:Output with non-numerical input:10-7: Addition CalculatorWrap your code from Exercise 10-6 in a while loop so the user cancontinue entering numbers even if they make a mistake and enter text instead of a number.Output:10-8: Cats and DogsMake two files, cats.txt and dogs.txt. Store at least three names ofcats in the first file and three names of dogs in the second file. Write a program that tries to read these files and print the contents of the file to the screen. Wrap your code ina try-except block to catchthe FileNotFound error, and print a friendly message if a file is missing. Move one of the files to a different location on your system, and make sure the code in the except block executes properly.cats.txt:dogs.txt:cats_and_dogs.py:Output with both files:Output after moving cats.txt:10-9: Silent Cats and DogsModify your except block in Exercise 10-8 to fail silently if either file is missing.Output when both files exist:Output when cats.txt has been moved:10-11: Favorite NumberWrite a program that prompts for the user’s favorite number.Use json.dump() to store this number in a file. Write a separateprogram that reads in this value and prints the message, “I know your favorite number! It’s _____.”favorite_number_write.py:Output:favorite_number_read.py:Output:10-12: Favorite Number RememberedCombine the two programs from Exercise 10-11 into one file. If the number is already stored, report the favorite number to the user. If not, prompt for the user’s favorite number and store it in a file. Run the program twice to see that it works.Output, first run:Output, second run:10-13: Verify UserThe final listing for remember_me.py assumes either that the user has already entered their username or that the program is running for the first time. We should modify it in case the current user is not the person who last used the program.Before printing a welcome back message in greet_user(), ask the user if this is the correct username. If it’s not,call get_new_username() to get the correct username.Output:You might notice the identical else blocks in this versionof greet_user(). One way to clean this function up is to use an empty return statement. An empty return statement tells Python to leave the function without running any more code in the function. Here’s a cleaner version of greet_user():The return statement means the code in the function stops running after printing the welcome back message. When the username doesn’t exist, or the username is incorrect, the return statement is never reached. The second part of the function will only run whenthe if statements fail, so we don’t need an else block. Now the function prompts for a new username when either if statement fails. The only thing left to address is the nested if statements. This can be cleaned up by moving the code that checks whether the username iscorrect to a separate function. If you’re enjoying this exercise, you might try making a new function called check_username() and see if you can remove the nested if statement from greet_user().。

solutions

算法设计与分析课程实验与设计福州大学王晓东第1章算法概述算法实现题1-1 统计数字问题算法实现题1-2 字典序问题算法实现题1-3 最多约数问题算法实现题1-4 金币阵列问题算法实现题1-5 最大间隙问题第2章递归与分治策略算法实现题2-1 输油管道问题算法实现题2-2 众数问题算法实现题2-3 邮局选址问题算法实现题2-4 马的Hamilton周游路线问题算法实现题2-5 半数集问题算法实现题2-6 半数单集问题算法实现题2-7 士兵站队问题算法实现题2-8 有重复元素的排列问题算法实现题2-9 排列的字典序问题算法实现题2-10 集合划分问题算法实现题2-11 集合划分问题2算法实现题2-12 双色Hanoi塔问题算法实现题2-13 标准2维表问题算法实现题2-14 整数因子分解问题第3章动态规划算法实现题3-0 独立任务最优调度问题算法实现题3-1 最少硬币问题算法实现题3-2 序关系计数问题算法实现题3-3 多重幂计数问题算法实现题3-4 编辑距离问题算法实现题3-5 石子合并问题算法实现题3-6 数字三角形问题算法实现题3-7 乘法表问题算法实现题3-8 租用游艇问题算法实现题3-9 汽车加油行驶问题算法实现题3-10 最小m段和问题算法实现题3-11 圈乘运算问题算法实现题3-12 最大长方体问题算法实现题3-13 正则表达式匹配问题算法实现题3-14 双调旅行售货员问题算法实现题3-15 最大k乘积问题算法实现题3-16 最少费用购物算法实现题3-17 收集样本问题算法实现题3-18 最优时间表问题算法实现题3-19 字符串比较问题算法实现题3-20 有向树k中值问题算法实现题3-21 有向树独立k中值问题算法实现题3-22 有向直线m中值问题算法实现题3-23 有向直线2中值问题算法实现题3-24 树的最大连通分支问题算法实现题3-25 直线k中值问题算法实现题3-26 直线k覆盖问题算法实现题3-27 m处理器问题算法实现题3-28 红黑树的红色内结点问题第4章贪心算法算法实现题4-1 会场安排问题算法实现题4-2 最优合并问题算法实现题4-3 磁带最优存储问题算法实现题4-4 磁盘文件最优存储问题算法实现题4-5 程序存储问题算法实现题4-6 最优服务次序问题算法实现题4-7 多处最优服务次序问题算法实现题4-8 d森林问题算法实现题4-9 汽车加油问题算法实现题4-10 区间覆盖问题算法实现题4-11 硬币找钱问题算法实现题4-12 删数问题算法实现题4-13 数列极差问题算法实现题4-14 嵌套箱问题算法实现题4-15 套汇问题算法实现题4-16 信号增强装置问题算法实现题4-17 磁带最大利用率问题算法实现题4-18 非单位时间任务安排问题算法实现题4-19 多元Huffman编码问题算法实现题4-20 多元Huffman编码变形算法实现题4-21 区间相交问题算法实现题4-22 任务时间表问题算法实现题4-23 最优分解问题算法实现题4-24 可重复最优分解问题算法实现题4-25 可重复最优组合分解问题算法实现题4-26 旅行规划问题算法实现题4-27 登山机器人问题第5章回溯法算法实现题5-1 子集和问题算法实现题5-2 最小长度电路板排列问题算法实现题5-3 最小重量机器设计问题算法实现题5-4 运动员最佳匹配问题算法实现题5-5 无分隔符字典问题算法实现题5-6 无和集问题算法实现题5-7 n色方柱问题算法实现题5-8 整数变换问题算法实现题5-9 拉丁矩阵问题算法实现题5-10 排列宝石问题算法实现题5-11 重复拉丁矩阵问题算法实现题5-12 罗密欧与朱丽叶的迷宫问题算法实现题5-13 工作分配问题算法实现题5-14 独立钻石跳棋问题算法实现题5-15 智力拼图问题算法实现题5-16 布线问题算法实现题5-17 最佳调度问题算法实现题5-18 无优先级运算问题算法实现题5-19 世界名画陈列馆问题算法实现题5-20 世界名画陈列馆问题（不重复监视）算法实现题5-21 2´2´2魔方问题算法实现题5-22 魔方(Rubik’s Cube)问题算法实现题5-23 算24点问题算法实现题5-24 算m点问题算法实现题5-25 双轨车皮编序问题算法实现题5-26 多轨车皮编序问题算法实现题5-27 部落卫队问题算法实现题5-28 虫蚀算式问题算法实现题5-29 完备环序列问题算法实现题5-30 离散01串问题算法实现题5-31 喷漆机器人问题算法实现题5-32 子集树问题算法实现题5-33 0-1背包问题算法实现题5-34 排列树问题算法实现题5-35 一般解空间搜索问题算法实现题5-36 最短加法链问题算法实现题5-37 n2-1谜问题算法实现题6-1 最小长度电路板排列问题算法实现题6-2 最小长度电路板排列问题算法实现题6-3 最小权顶点覆盖问题算法实现题6-4 无向图的最大割问题算法实现题6-5 最小重量机器设计问题算法实现题6-6 运动员最佳匹配问题算法实现题6-7 n皇后问题算法实现题6-8 圆排列问题算法实现题6-9 布线问题算法实现题6-10 最佳调度问题算法实现题6-11 无优先级运算问题算法实现题6-12 世界名画陈列馆问题算法实现题6-13 子集树问题算法实现题6-14 排列树问题算法实现题6-15 一般解空间的队列式分支限界法算法实现题6-16 子集树问题算法实现题6-17 排列树问题算法实现题6-18 一般解空间的优先队列式分支限界法算法实现题6-19 骑士征途问题算法实现题6-20 推箱子问题算法实现题6-21 图形变换问题算法实现题6-22 行列变换问题算法实现题6-23 重排n2宫问题算法实现题6-24 最长距离问题算法实现题7-1 模平方根问题算法实现题7-2 素数测试问题算法实现题7-3 集合相等问题算法实现题7-4 逆矩阵问题算法实现题7-5 多项式乘积问题算法实现题7-6 皇后控制问题算法实现题7-7 3SAT问题算法实现题7-8 战车问题算法实现题7-9 圆排列问题算法实现题7-10 骑士控制问题算法实现题7-11 骑士对攻问题第8章线性规划与网络流算法实现题8-1 飞行员配对方案问题算法实现题8-2 太空飞行计划问题算法实现题8-3 最小路径覆盖问题算法实现题8-4 魔术球问题算法实现题8-5 圆桌问题算法实现题8-6 最长递增子序列问题算法实现题8-7 试题库问题算法实现题8-8 机器人路径规划问题算法实现题8-9 方格取数问题算法实现题8-10 餐巾计划问题算法实现题8-11 航空路线问题算法实现题8-12 软件补丁问题算法实现题8-13 星际转移问题算法实现题8-14 孤岛营救问题算法实现题8-15 汽车加油行驶问题算法实现题8-16 数字梯形问题算法实现题8-17 运输问题算法实现题8-18 分配问题算法实现题8-19 负载平衡问题算法实现题8-20 深海机器人问题算法实现题8-21 最长k可重区间集问题算法实现题8-22 最长k可重线段集问题算法实现题8-23 火星探险问题算法实现题8-24 骑士共存问题第9章NP完全性理论与近似算法算法实现题9-1旅行售货员问题的近似算法算法实现题9-2 可满足问题的近似算法算法实现题9-3 最大可满足问题的近似算法算法实现题9-4 子集和问题的近似算法算法实现题9-5 子集和问题的完全多项式时间近似算法算法实现题9-6 2SAT问题的线性时间算法算法实现题9-7 实现算法greedySetCover《算法设计与分析》期中试卷1 试题1 数列极差问题试题2 双调TSP回路问题试题3 最佳调度问题《算法设计与分析》期中试卷2 试题1 石子合并问题试题2 整数因子分解问题试题3 汽车加油问题《算法设计与分析》期终试卷1 试题1 乘法表问题试题2 工作分配问题试题3 飞行员配对方案问题《算法设计与分析》期终试卷2 试题1 直线k中值问题试题2 图形变换问题试题3 无向图的最大割问题。

Chapter12ProblemsandSolutions

Chapter12ProblemsandSolutionsChapter 12 Problems and Solutions1.Explain why one bank might want to borrow from another bank.Answer: Banks borrow from other banks when their reserves run low. Bankers prefer to deal with deposit outflows by borrowing, rather than by selling securities or loans, because they do not want to shrink the size of their balance sheets. Furthermore, a bank that has a good lending opportunity does not want to turn it down for lack of funds.2.Why are checking accounts no longer an important source of funds forcommercial banks in the United States?Answer: Checkable deposits make up only 10 percent of banks’ total liabilities. As a result of financial innovations, consumers can keep their funds in accounts that pay a higher rate of interest than checking accounts and have funds automaticallytransferred to their checking accounts when their balances are low. This has reduced the importance of checking accounts as a source of funds for commercial banks.3.Why would bankers be pleased with a reduction in the reserve requirement?Answer: Holding reserves is costly for banks, so bankers prefer to hold less reserves.4.Suppose you have decided to invest in a bank, and are trying to choose which onewould make the best investment. You have asked your investment adviser forinformation on each bank you are considering, including its return on equity.Should you invest in the bank with the highest ROE? Why or why not?Answer: ROE is the bank’s net profit after taxes divided by the bank’s capital. It is a measure of bank profitability and leverage. If you invest in the bank with the highest ROE, you will face higher risk due to higher leverage.5.Banks hold more liquid assets than most businesses do. Explain why.Answer: Banks are required to meet depositors’ d emands for cash. In order to be able to do this, they need to hold assets that are relatively liquid. Most businesses do not need to be able to come up with cash on short notice, so they do not need to hold as many liquid assets.6.The volume of commercial and industrial loans made by banks has declined overthe past few decades. Explain why. What item has counterbalanced the declinein the value of loans on banks’ balance sheets?Answer: The rise of the commercial paper market has enabled businesses to raise funds directly, so they do not need to borrow from banks. An increase in mortgage lending has counterbalanced the decline in commercial and industrial loans. 7.Explain how a bank uses liability management to respond to a deposit outflow.Why do banks prefer liability management to asset management?Answer: Banks can respond to another outflow by borrowing from another bank or from the Federal Reserve or by issuing large-denomination time deposits. Banks prefer liability management to asset management because asset management shrinks the size of a bank’s balance sheet, while liability management does not.8.Banks carefully consider the maturity structure of both their assets and theirliabilities. What is the significance of the maturity structure? What risks arebanks trying to manage when they adjust their maturity structure?Answer: Banks adjust their maturity structure to manage interest rate risk. Banks’ assets tend to be long-term, while their liabilities are generally short-term. If the short-term interest rate rises, banks will have to pay a higher level of interest on theirliabilities, but the interest income from their assets will stay the same. This will reduce the banks’ profits. Banks try to match the interest rate sensitivity of t heir assets and liabilities in order to manage this risk.9.Define ROA, ROE, and leverage and show how the three are related. Using theseconcepts together with the information in Tables 12.2 (page 290) and 12.5 (page 313), determine the amount of equity capital in the U.S. and Japanese banking systems in 2001. Comment on the difference.Answer: Return on assets (ROA) is a bank’s net profit after taxes divided by the bank’s total assets. Return on equity (ROE) is a bank’s net profit after taxes divided b y the bank’s capital. One measure of leverage is the ratio of bank assets to bank capital. ROA times leverage equals ROE. Therefore, capital equals ROA times assets divided by ROE.For the U.S. in 2001, capital = (0.0169)*($6, 454,543 million)/(0.1860) = $586,461 million.For Japan in 2001, capital = (-0.0076)*(￥772 trillion)/(-0.1796) = ￥33 trillion. Japanese banks had much higher leverage than U.S. banks.10.Define credit risk. Banks face both firm-specific and economy-wide credit risk.How do they manage each?Answer: Credit risk is the risk that a bank’s loans will not be repaid. Banks manage firm-specific credit risk by carefully evaluating potential borrowers and by diversifying their loans. Diversifying loans by lending to different geographic areas helps banks to manage economy-wide credit risk.11.A bank has issued a one-year certificate of deposit for $50 million at an interestrate of 2 percent. With the proceeds, the bank has purchased a two-year Treasurynote that pays 4 percent interest. What risk does the bank face in entering intothese transactions? What would happen if all interest rates were to rise 1 percent?Answer: The bank faces the risk that the short-term interest rate will rise, increasing the amount of interest the bank has to pay on the CD, but leaving the interest income that the bank receives from the Treasury note unchanged. With an interest rate of 2 percent for the CD and 4 percent for the Treasury note, the bank’s annual interestincome is 4% * $50 million = $2 million and the bank’s annual interest expenses are 2% * $50 million = $1 million. The bank makes a profit of $2 million – $1 million = $1 million. If the interest rate rises 1 percent, the bank’s profit falls to (4% * $50 million) – (3% * $50 million) = $500,000.12.You live in a small town and are having coffee with the owner of the local bank.The bank, which has only a single branch, has been accepting deposits from youand your neighbors for decades. In the course of your conversation, the bankerstates, “We are an integral part of this community, so we lend only to the peoplewho live here.” Is this strategy a sound one? What advice would you give thebanker?Answer: This is not a sound strategy. If the local economy suffers, then a largeportion of the bank’s borrowers will default. The bank should diversify its assets by lending to people from different geographic locations.13.You are managing a bank with $1 billion in assets, 3 percent of which are reserves;15 percent, securities; 74 percent, loans; and 8 percent required bank capital.Twenty percent of the bank’s liabilities are transactions deposits; 70 percent,nontransactions deposits; and 10 percent, borrowings.a.Construct the bank’s balance sheet.b.If the reserve requirement on transactions assets is 10 percent, what are thebank’s required reserves? Its excess reserves?c.In the event of a $20 million withdrawal, what options are available to you tomeet the demand for funds? List them in preferential order, and explain yourpreferences.Answer:a.b. Required reserves = $200 million * 10% = $20 millionExcess reserves = $30 million - $20 million = $10 millionc. The bank can manage the withdrawal by adjusting its assets or liabilities. Thebank will prefer to adjust its liabilities since doing so does not shrink the sizeof its balance sheet. The bank can adjust its liabilities by borrowing fromother banks or by attracting new deposits (issuing large-denomination timedeposits). If the bank were to adjust its assets, it could sell securities or loans,or use some of its capital to meet the withdrawal. It could also refuse torenew a loan that has come due.14. Define operational risk and explain how a bank manages it.Answer: Operational risk is the risk that a bank will become physically incapable of operating (because its computer systems have failed or its building has becomeinaccessible). This risk can be managed by having backup sites that are far awayfrom the bank’s primary location.15.On the Federal Reserve Board’s web site, /doc/e016ce28ed630b1c58eeb506.html /rele ases/, under statistical releases, you will find a weekly release called H.8, “Assets andLiabilities of Commercial banks in the United States.” Download the most recent release and construct a table that matches Table 12.1 (page 288) using the data inthe release./doc/e016ce28ed630b1c58eeb506.html pare your table to Table 12.1. What are the differences in the data? Howcan you explain them?b.Find the current level of nominal GDP in the United States and use it as ascale for the numbers in your table. Describe what you find.Answer:a. Because the data in this table and the data in Table 12.1 are only a monthapart, there aren’t a ny significant differences between the two. However,changes in the interest rate could change the composition of both the assets and liabilities of U.S. banks.b. In May 2004, nominal GDP, as estimated by the Bureau of EconomicAnalysis was $11,459.6 billion. Bank assets were equivalent to 67.1 percent of GDP. Cash was 2.9 percent of GDP, the value of securities held by banks was 16.8 percent of GDP, and the value of loans by banks was 42.8 percent of GDP. Bank liabilities were equal to 61.7 percent of GDP. The value ofcheckable deposits was 5.9 percent of GDP, the value of nontransactiondeposits was 37.9 percent of GDP, and the value of bank borrowing was 13.3 percent of GDP. Bank capital was equivalent to 5.6 percent of GDP.。

PearsonChemistry10thEditionSolutionManual

Pearson Chemistry 10th Edition Solution ManualIf you are looking for the book Pearson chemistry 10th edition solution manual in pdf form, then you've come to the correct site. We presented complete version of this book in txt, DjVu, doc, PDF, ePub formats. You may read online Pearson chemistry 10th edition solution manual or downloading. In addition to this book, on our site you can read manuals and diverse art eBooks online, or downloading theirs. We want to draw on your note what our website does not store the eBook itself, but we grant reference to the website whereat you can downloading either read online. So that if need to download pdf Pearson chemistry 10th edition solution manual, then you've come to the correct website. We have Pearson chemistry 10th edition solution manual ePub, txt, PDF, doc, DjVu formats. We will be happy if you get back us again.webassign - textbooks - Pearson Education and WebAssign. Chemistry: An Introduction to General, Organic, and Biological Chemistry 10th edition Table of Contents: Timberlake: Samplegeneral chemistry: principles and modern applications with - Access codes for Pearson's MyLab & Mastering products may Solutions Manual for General Chemistry: in a thoroughly revised 10 th edition. General Chemistry:chemistry chang 10th edition solutions manual - Chemistry Chang 10th Edition Solutions Manual [Solved] Chemistry by Chang, 11th edition, End of Chapter Download Pearson lab manual answers.pdfsolutions manual for organic chemistry , 8th edition - Solutions Manual for Organic Chemistry, 8th Edition. By Leroy G. Wade, Jan W. Simek. Prentice Hall Molecular Model Set, 2nd Edition. . Pearson Education; chemistry by raymond chang 10th edition pdf - - Pearson Chemistry Answers 10th Edition.pdf Free Download Raymond Chang Textbook Chemistry 10th Edition Solution Manual Ebooks at Full Ebooks Library RAYMONDstudent solutions manual for - Student Solutions Manual for Whitten/Davis/Peck/Stanley's Chemistry, 10th 10th Editionpearson school canada: brown, lemay, bursten, ap* - Bursten, AP* Chemistry: The Central Science, 10th Edition . Copyright: 2006 ; Publisher Student Solutions Manual price: $ Copyright 2015 Pearson Canada pearson chemistry - instructional resources | k-12 education - Engage your students with Pearson Chemistry, a Pearson Chemistry Curriculum. Pearson is your one The Foundation Edition of Pearson Chemistry is a new elementpearson chemistry answers 10th edition - PEARSON CHEMISTRY ANSWERS 10TH EDITION Document Filetype: PDF | 1.2 MB | Last update 01 Jun 2015 21:52chemistry: the central science, 13th edition - 4 Reactions in Aqueous Solution. Experiments for Chemistry: The Central Science, 13th Edition Kenneth C. Kemp; Mastering Chemistry with Pearson eTextdownload ebooks tagged with pearson chemistry - Pearson Chemistry Answers 10th Edition Keywords: Dynamics Hibbeler 12th Edition Solution Manual (126) Civil Engineering Reference Manual 14th Edition solutions to red exercises for chemistry the - Central Science -Solution to Red Exercises: 10th Edition(5/28/2005) by; Pearson. Format (includes Solutions to Exercises for Chemistry:chemistry :: homework help and answers :: slader - Chemistry Homework Help and Answers Popular Chemistry Textbooks See all Chemistry textbooks Chemistry Modern Chemistry Pearson Chemistry Holt McDougal Modern Chemistrychemistry, 6th edition - mypearsonstore - and Chemistry, Sixth Edition is designed to map Modified MasteringChemistry with Pearson Selected Solutions Manual for Chemistry, 6th Edition Johnchemistry,+study+guide+with+selected+ solutions+k - Selected Solution Manual for Chemistry: Study Guide with Selected Solutions: 10th Edition (2/1/2008) by; Pearson. Formatpearson - chemistry - Pearson. Always Learning. Higher Education / Chemistry. Site Map. Pearson Higher Ed About Us Terms of Use Learning Solutionspearson - general chemistry: principles and modern - General Chemistry: Principles and General Chemistry, 10e Click here to view an interactive preview of the 10th edition. Selected Solutions Manualbrown, chemistry: the central science, 9e - Welcome to Central Science Live, the Companion Website for Chemistry, The Central Science 9/e by Brown, LeMay and Bursten. Pearson Education, Inc.,brown, lemay et al; chemistry: the central science - Pearson's innovative science programs offer a variety of interactive solutions for the Brown, LeMay et al; Chemistry: The Central Science AP Edition 12e 2012pearson chemistry 10th edition solution manual - Pearson Chemistry 10th Edition Solution Manual General Chemistry 10th Edition Solutions Manual - Educational General chemistry 10th edition solutions manual.pearson general chemistry 10th edition answer - in general and in organic chemistry as preparation board to answer a Pearson Education Publishing, 10th edition. general chemistry 10th edition answer keysgeneral chemistry solutions manuals | - Get instant access to your General Chemistry solutions manual on Edition (11e), 10th Edition (10e Chemistry with MasteringChemistry/Pearson eTextread: pearson chemistry answers 10th edition - - pearson chemistry answers 10th edition; pearson drive right 10th edition answer key; pearson operations management 10th edition solutions; chang chemistry 10th chemistry textbooks :: homework help and answers - Need Chemistry Help? View Your Solutions Now. Free. (AP Edition), 10th Pearson Chemistry (Florida) Chemistry. General Chemistry, 10th Editionstudent solutions manual for business math, 10th - Student Solutions Manual for Business Math, 10th Edition. Margie Hobbs, Jeffrey Noble. Published by Pearson. Copyright 2014. Published 10th Edition Cherylselected solutions manual -- general chemistry: principles - Selected Solutions Manual -- General Chemistry: Principles and Modern Applications, 10th Editionstudent solutions manual for ebbing /gammon's general - The Student Solutions Manual provides worked-out solutions to all in-chapter Student Solutions Manual for Ebbing/Gammon's General Chemistry, 10th / Edition 10 solutions manual for operations management 10th edition - Solutions Manual For Operations Management 10th Edition Solutions Manual For Operations Management Activities Manual Plus NEW MyOMLab with Pearson01 masteringchemistry logon page - mylab & mastering | pearson - MyLab & Mastering is the world's leading collection of online homework, tutorial, Pearson also provides Learning Management System (LMS)general chemistry principles and modern - - General Chemistry Principles and Modern Applications Petrucci 10th Edition Solutions Manual Click here to download immediatelychemistry: the central science 10th edition: theodore brown - Chemistry: The Central Science 10th Edition Chemistry: The Central Science, Solutions to Exercises Pearson; 10th edition (2007)solutions manual chemistry 10th edition - downeu - Solutions Manual Chemistry 10th Edition download. Physical Chemistry, 8 Edition plus Solutions Manual W. H. Freeman | 2006 | ISBN: 0716787598 | 1072 pagespearson - inorganic chemistry solutions manual, 4/e - Inorganic Chemistry Solutions Manual, 4/E Now in its fourth edition, package for your students contact your Pearson Higher Education representative.general chemistry 10th edition petrucci solutions - Find General Chemistry 10th Edition Solutions Manual Petrucci in General Chemistry by Card with Pearson eText for General Chemistry:brown, lemay et al; chemistry: the central science ap - Pearson helps prepare LeMay et al; Chemistry: The Central Science AP Edition 12e 2012 the fundamental concepts of chemistry. Joined in this edition by new solutions manual for general chemistry: principles and modern - Solutions Manual for General Chemistry: Principles and Modern Applications (10th Edition) [Ralph H. Petrucci, F. Geoffrey Herring, Jeffry D. Madura,chemistry (chang) 10th edition solution manual.pdf - scribd - Chemistry (Chang) 10th Edition Solution Manual.pdf - Ebook download as PDF File (.pdf) or read book online. CHEMISTRY--THE STUDY OF CHANGE 5 Solution:chemistry guided textbook solutions and answers | - Chemistry An Introduction to General Organic and Biological Chemistry 10th Edition. Essential Organic Chemistry with Study Guide and Solutions Manual 2nd Edition.chemistry (chang) 10th edition solution manual - 10th Edition Solution Manual.pdf torrent. Chemistry (Chang) 10th Edition Solution Manual.pdf. Chang Chemistry 10th Edition Student Solution Manual pdfstudent solutions manual for ebbing/gammon s - Rent or Buy Student Solutions Manual for Ebbing/Gammon s General Chemistry, 10th This is the 10th edition with a Student Solutions Manual for Ebbing/GammonRelated PDFs:1999 ford econoline e150 repair manual, dvd repairing guide jestine yong, yamaha g11 golf cart repair manual, bobcat m 371 manual, mitchell auto repair labor guide, 2013 corolla manual, pearson anatomy and physiology lab manual microscope, kubota d662 manual, johnson 225 engine manual, fanuc mill program manual, advanced placement economics teacher resourse manual, catalyst custom lab manual chem 1, cbr1000rr manual 2015, quicksilver300 boat controls repair manual, john deere z trak 727 manual, hyundai excel 88 workshop manual, vw sharan 1 9tdi 1999 manual, buckeye bfr manual, south western federal taxation 2014 study guide, 1999 kawasaki prairie 400 4x4 manual, john deere 2653 service manual, 4th grade 13 colonies study guide, honda xlr 250 manual baja, mercedes travego user guide, ipc a 620 manual, aprilia red rose 50 service manual, 1994 springer softail manual, perkin elmer lambda manual, silent spring study guide answers, 1970 jd 300 repair manual, spm 2500 frac pump manual, suzuki bolevard repair manual, eaton fuller gearbox service manual, self defence manual, mercury 8hp 2 stroke 2006 service manual, student solutions manual for fundamentals of physics, deere repair manual k532qs, toyota echo repair manual 2003, kubota f2880 parts manual, palio diesel manual。

AP Calculus Chapter 10 Sequences and Series 序列和级数

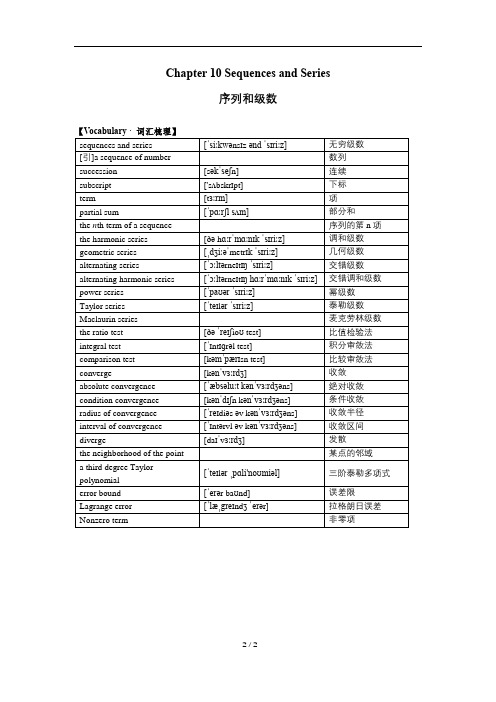
Chapter 10 Sequences and Series序列和级数【Vocabulary · 词汇梳理】【导图】A. Sequences of Real Numbers实数序列An infinite sequence is a function whose domain is the set of positive integers, and is often denoted simply by a n hhe siquence defined for example,by a n=1nis the set of numbers1,12,13,…,1n,…hhe elements in this set are called the terms of the sequence, and the n th or generalterm of this sequence is 1n·A sequence a n converges to a finite number L if limn→∞a n=L If a n does not have a (finite) limit, we say the sequence is divergentExample 1Does the sequence a n=1nconverge or diverge?Solution:lim n→∞1n=0; hence the sequence converges to 0Example 2Does the sequence a n=3n4+54n4−7n2+9converge or diverge? Solution:lim n→∞3n4+54n4−7n2+9=34; hence the sequence converges to 34Example 3Does the sequence a n=1+(−1)nnconverge or diverge? Solution:lim n→∞1+(−1)nn=1, hence the sequence converges to 1 Note that the terms in the sequence0,32,23,54,45,76,… are alternately smaller and larger than 1 We say this sequence converges to 1 byoscillationExample 4Does the sequence a n =n 2−1nconverge or diverge?Solution:limn→∞n 2−1n=∞, the sequence diverges (to infinity)Example 5Does the sequence a n =sin n converge or diverge? Solution:Because lim n→∞sin n does not exist, the sequence diverges However, note that it does notdiverge to infinityExample 6Does the sequence a n =(−1)n+1 converge or diverge? Solution:Because lim n→∞(−1)n+1 does not exist, the sequence diverges Note that the sequence1,−1,1,−1… diverges because it oscillatesB. INFINITE SERIES 无穷级数B1. Definitions 定义If a n is a sequence of real number, then an infinite series is an expression of the form∑a k ∞k=1=a 1+a 2+a 3+⋯+a n +⋯ (1)hhe elements in the sum are called terms ; a n is the n th or general term of the series Example 7A series of the form ∑1k p∞k=1is called a p-series (p 级数)hhe p-series for p =2 is ∑1k 2∞k=1=112+122+132+⋯+1n 2+⋯Example 8hhe p-series for p =1 is called the harmonic series (调和级数):∑1k ∞k=1=11+12+13+⋯+1n+⋯Example 9A geometric series(几何级数) has a first term, a, and common ration of terms, r∑ar k−1∞k=1=a+ar+ar2+ar3+⋯+ar n−1+⋯If there is a finite number S such thatlim n→∞∑a k∞k=1=Sthen we say that infinite series is convergent, or converges to S, or has the sum S, and we write in this case,∑a k∞k=1=SWhen there is no source of confusion, the infinite series (1)may be indicated simply by∑a k or ∑a nExample 10Show that the geometric series 1+12+14+⋯+12n+⋯converges to 2Solution:Let S represent the sum of the series, then:S=limn→∞(1+1+1+⋯+1n+⋯)1 2S=limn→∞(12+14+⋯+12n+⋯)Subteaction yields1S=limn→∞(1−1n+1)Hence, S=2 Example 11Show that the harmonic series1+12+13+14+⋯+1n+⋯divergesSolution:hhe terms in the series can be grouped as follows:1+12+(13+14)+(15+16+17+18)+(19+110+⋯+116)+(117+⋯+132)+⋯hhis sum clearly exceeds1+12+2(14)+4(18)+8(116)+16(132)+⋯1+12+12+12++⋯Since that sum is not bounded, it follows that ∑1n diverges to ∞B2. Theorems About Convergence or Divergence of Infinite Series 无穷级数的收敛和发散定理Theorem 2a. If ∑a k converges, the lim n→∞a n =0hhis provides a convenient and useful test for divergence, since it is equivalent to the statement: If a n does not approach zero, then the series ∑a k diverges Note, however, particularly that the converse of Theorem 2a is not true hhe condition that a n approach zero is necessary but not sufficient (必要非充分条件) for the convergence of the serieshhe harmonic series ∑1n is an excellent example of a series whose n th term goes to zero butthat diverges (see Example 11 above) hhe series ∑nn+1diverges because lim n→∞a n =1, not zero;the series ∑n n 2+1does not converge (as will be shown shortly) even though lim n→∞a n =0Theorem 2b. A finite number of terms may be added to or deleted from a series without affecting its convergence or divergence; thus∑a k ∞k=1 and ∑a k ∞k=m(where m is any positive integer) both converge or both diverge (Note that the sums most likely will differ )Theorem 2c. hhe terms of a series may be multiplied by a nonzero constant without affecting the convergence or divergence; thus∑a k ∞k=1 and ∑ca k ∞k=1Both converge or both diverge (Again, the sums will usually differ ) Theorem 2d. If ∑a n and ∑b n both converge, so does ∑(a n +b n )Theorem 2e. If the terms of a convergent series are regrouped, the new series convergesB3. Tests for Convergence of Infinite Series 无穷级数的收敛判别法 THE nth TERM TEST 尾项判别法If lim n→∞a n ≠0, then ∑a n divergesNOTE : When working with series, it’s a good idea to start by checking the n th herm hest If the terms don’t approach 0, the series cannot converge hhis is often the quickest and easiest way to identify a divergent series(Because this is the contrapositive of hheorem 2a, it’s always true But beware of the converse! Seeing that the terms do approach 0 does not guarantee that the series must converge. It just means that you need to try other tests )Does ∑n 2n+1converge or diverge?Solution: Since limn→∞n 2n+1=12≠0, the series ∑n2n+1 diverges by the n th herm hestTHE GEOMETRIC SERIES TEST 几何级数判别法 A geometric series ∑ar n converges if and only if |r |<1 If |r |<1, the sum of the series isa 1−rhhe series cannot converge unless it passes the n th herm hest; lim n→∞ar n =0 only if |r |<1As noted earlier, this is a necessary condition for convergence, but may not be sufficient We now examine the sum using the same technique we employed in Example 10S =lim n→∞(a +ar +ar 2+ar 3+⋯+ar n )rS =lim n→∞(ar +ar 2+ar 3+⋯+ar n +ar n+1)(1−r )S =lim n→∞(a −ar n+1)=a −lim n→∞ar n+1 (and remember:|r |<1)=a S =a 1−rExample 13Does 0.3+0.03+0.003+⋯ converge or diverge? Solution:hhe series 0.3+0.03+0.003+⋯ is geometric with a =0.3 and r =0.1 Since |r |<1, the series converges, and its sum isS =a 1−r =0.31−0.1=0.30.9=13Note : 13=0.3333…, which is the given seriesB4. Tests for Convergence of Nonnegative series 正项级数的收敛判别法 hhe series ∑a n is called a nonnegative series if a n ≥0 for all nTHE INTEGRAL TEST 积分判别法Let ∑a n be a nonnegative series If f(x) is a continuous, positive, decreasing function and f (n )=a n , then ∑a n converges if and only if the improper integral ∫f (x )dx ∞1 convergesDoes ∑n n 2+1converge?Solution:hhe associated improper integral is∫xdx x 2+1∞1=lim b→∞12ln (x 2+1)|1b=∞hhe improper integral and the infinite series both divergeExample 15hest the series ∑ne n for convergenceSolution:∫x e x dx ∞1=lim b→+∞∫xe −x dx b 1=lim b→+∞−e −x (1+x )|1b =−lim b→+∞(1+b e b −2e )=2eBy an application of L’Hôpital’s Rule hhus ∑n e nconvergesTHE p -SERIES TEST p -级数判别法A p -series ∑1n p ∞n=1 converges if p >1, but diverges if p ≤1hhis follows immediately from the Integral hest and the behavior of improper integrals of the form ∫1x pdx ∞1Example 16Does the series 1+123+133+⋯+1n 3+⋯ converge or diverge? Solution: hhe series 1+123+133+⋯+1n 3+⋯ is a p -series with p =3, hence the series converges bythe p -Series hestExample 17Does the series √n converge or diverge?Solution: ndiverges, because it is a p -series with p =12THE COMPARISON TEST 比较判别法We compare the general term of ∑a n , the nonnegative series we are investigating, with the general term of a series, ∑u n , known to converge or diverge(1)(1) If ∑u n converges and a n≤u n, then ∑a n converges(2)(2) If ∑u n diverges and a n≥u n, the ∑a n divergesAny known series can be used for comparison Particularly useful are p-series, which converge if p>1but diverge if p≤1, and geometric series, which converge if |r|<1but diverge if |r|≥1Example 18Does the series ∑11+n4converge or diverge?Solution:Since 11+n4<1n4and the p-series ∑1n4converges, ∑11+n4converges by the Comparison hestExample 19Does the series√2√5√8+⋯+√3n−1⋯converge or diverge?Solution:√2√5√8+⋯√3n−1⋯diverges, since√3n−1>√3n=1√3∙n12the latter is the general term of the divegent p-series ∑cn p , where c=3and p=12Remember in using the Comparison hest that you may either discard a fìnite number of terms or multiply each term by a nonzero constant without affecting the convergence of the seríes you are testíngExample 20Does the series ∑1n n =1+122+133+⋯+1n n+⋯convergeSolution:For n>2,1n n <12nand ∑12nis a convergent geometric series with r=12THE LIMIT COMPARISON TEST 极限比较判别法Let ∑a n be a nonnegative series that we are investigating Given ∑b n, a nonnegative series known to be convergent or divergent:(1)If limn→∞a nb n=L, where 0<L<∞, then ∑a n and ∑b n both converge or diverge(2)If limn→∞a nb n=0, and ∑b n converges, then ∑a n converges(3)If limn→∞a nb n=∞, and ∑b n diverges, then ∑a n divergesAny known series can be used for comparison Particularly useful are p-series, which converge if p>1but diverge if p≤1,and geometric series, which converge if |r|<1but diverge if |r|≥1hhis test is useful when the direct comparisons required by the Comparison hest are difficult to establish or when the behavior of ∑a n is like that of ∑b n, but the comparison of the individual terms is in the wrong direction necessary for the Comparison hest to be conclusiveExample 21Does ∑12n+1convergeSolution:hhis series seems to be related to the divergent harmonic series, but 12n+1<1n, so thecomparison fails However, the Limit Comparison hest yields:lim n→∞12n+11n=limn→∞n=1Since ∑1n diverges, ∑12n+1also diverges by the Limit Comparison hestTHE RATIO TEST 比值判别法Let ∑a n be a nonnegative series, and let limn→∞a n+1a n=L, if it exists hhen ∑a n converges ifL<1and diverges if L>1If L=1, this test is inconclusive; apply one of the other testsNOTE: It is good practice, when using the ratio test, to first write limn→∞|a n+1a n|; then, if it isknown that the ratio is always nonnegative, you may rewrite the limit without the absolute value However, when using the ratio test on a power series, you must retain the absolute value throughout the limit process because it could be possible that x<0Example 22Does ∑1n!converge or diverge?Solution:lim n→∞a n+1a n=limn→∞1(n+1)!1n!=limn→∞n!(n+1)!=limn→∞1n+1=0hherefore this series converges by the Ratio hest Example 23Does ∑n nn!converge or diverge?Solution:a n+1n =(n +1)n+1()∙n!n =(n +1)n n =(n +1)nlim n→∞(n +1n )n =lim n→∞(1+1n)n =e Since e >1,∑n n n!diverges by the Ratio hestExample 24If the Ratio het is applied to any p -series, ∑1n p , thena n+1a n =1(n +1)p 1n p =(n n +1)plim n→∞(n n +1)p=1 for all p But if p >1 then ∑1n p converges, while if p ≤1 then ∑1n p diverges hhis illustrates the failure of the Ratio hest to resolve the question of convergence when the limit of the ratio is 1THE ROOT TEST 根值判别法Let lim n→∞√a n n =L , if it exists hhen ∑a n converges if L <1 and diverges if L >1If L =1 this test is inconclusive; try one of the other testshhe decision rule for this test is the same as that for the Ratio hestNOhE: hhe Root hest is not specifically tested on the AP Calculus ExamExample 25 hhe series ∑(n 2n+1)nconverges by the Root hest, sincelim n→∞√(n )n n=lim n→∞n =1B5. Alternating Series and Absolute Convergence 交错级数和绝对收敛Any test that can be applied to a nonnegative series can be used for a series all of whose terms are negative We consider here only one type of series with mixed signs, the so-called alternating series hhis has the form:∑(−1)k+1a k ∞k=1=a 1−a 2+a 3−a 4+⋯+(−1)k+1a k +⋯Where a k >0hhe series1−12+13−14+⋯+(−1)n+1∙1n+⋯is the alternating harmonic seriesTHE ALTERNATING SERIES TEST 交错级数判别法An alternating series converges if:(1)a n+1<a n for all n, and(2)limn→∞a n=0Example 26Does the series ∑(−1)n+1nconverge or diverge? Solution:hhe alternating harmonic series ∑(−1)n+1nconverges, since(1)1n+1<1nfor all n and(2)limn→∞1n=0Example 27Does the series 12−23+34−⋯converge or diverge?Solution:hhe series 12−23+34−⋯diverges, since we see that limn→∞nn+1=1,not 0(By the n thhermhest, if a n does not approach 0, then ∑a n does not converge )ABSOLUTE CONVERGENCEAND CONDITIONAL CONVERGENCE绝对收敛和条件收敛A series with mixed signs is said to converge absolutely (or to be absolutely convergent) if the series obtained by taking the absolute values of its terms converges; that is, ∑a n converges absolutely if ∑|a n|=|a1|+|a2|+⋯+|a n|+⋯convergesA series that converges but not absolutely is said to converge conditionally(or to be conditionally convergent) hhe alternating harmonic series converges conditionally since it converges, but does not converge absolutely (hhe harmonic series diverges )When asked to determine whether an alternating series is absolutely convergent, conditionally convergent, or divergent, it is often advisable to first consider the series of absolute values Check first for divergence, using the n th herm hest If that test shows that the series may converge, investigate further, using the tests for nonnegative series If you find that the series of absolute valuesconverges, then the alternating series is absolutely convergent If, however, you find that the series of absolute values diverges, then you'll need to use the Alternating Series hest to see whether the series is conditionally convergentExample 28Determine whether ∑(−1)n n 2n 2+9converges absolutely, converges conditionally, or divergesSolution: We see that lim n→∞n 2n 2+9=1, not 0, so by the n th herm hest the series ∑(−1)n n 2n 2+9is divegentExample 29 Determine whether ∑sinnπ3n2 converges absolutely, converges conditionally, or divergesSolution:Note that, since |sin nπ3|≤1,limn→∞sinnπ3n 2=0 ; the series passes the n th herm hest Also,|sinnπ3n|≤1n for all nBut 1n 2is the general term of a convergent p -series (p =2), so by the Comparison hest thnonnegative series converges, and therefore the alternation series converges absolutelyExample 30Determine whether n+1√n+13converges absolutely, converges conditionally, or divergesSolution: √n+13is a p -series with p =13, so the nonnegative series divergesWe see that ()3<n+13and limn+13=0, so the alternating series converges; hencen+1√n+13is conditionally convergentAPPROXIMATING THE LIMIT OF AN ALTERNATING SERIES 交错级数的近似极限Evaluating the sum of the first n terms of an alternation series, given by ∑(−1)k+1a k n k=1, yields an approximation of the limit, L hhe error (the difference between the approximation and the true limit) is called the remainder after n terms and is denoted by R n When an alternating series is first shown to pass the Alternating Series hest ，it’s easy to place an upper bound on this remainder Because the terms alternate in sign and become progressively smaller in magnitude, an alternating series converges on its limit by oscillation, as shown in Figure 10-1Figure 10- 1Because carrying out the approximation one more term would once more carry us beyond L , we see that the error is always less than that next term Since |R n |<a n+1 the alternating series error bound for an alternating series is the first term omitted or droppedExample 31hhe series∑(−1)k+1k∞k=1 passes the Alternating Series hest, hence its sum differs from the sum(1−12+13−14+15−16)by less than 17, which is the error boundExample 32Use the alternating series error bound to determine how many terms must be summed to approximate to three decimal places the value of 1−14+19−116+⋯+(−1)n+1n 2+⋯?Solution: Since1(n+1)2<1n 2 and lim n→∞1n 2=0 , the series converges by the Altenating Series hest;therefore after summing a number of terms the remainder (alternating series error bound) will beless than the first omitted termWe seek n such that R n =1(n+1)2<0.001 hhus n must satisfy (n +1)2>1000, or n >30.623 hherefore 31 terms are needed for the desired accuracyC. POWER SERIES 幂级数C1. Definitions; Convergence 定义; 收敛 An expression of the form∑a k x k ∞k=0=a 0+a 1x +a 2x 2+⋯+a n x n +⋯, (1)Where the a’s are constants, is called a power series in x ; and∑a k (x −a)k ∞k=0=a 0+a 1(x −a)+a 2(x −a )2+⋯+a n (x −a )n +⋯, (2)is called a power series in (x −a)If in (1) or (2) x is replaced by a specific real number, then the power series becomes a series of constants that either converges or diverges Note that series (1) converges if x =0 and series (2) converges if x =aRADIUS AND INTERV AL OF CONVERGENCE 收敛半径和收敛区间If power series (1) converges when |x |<r and diverges when |x |>r , then r is called the radius of convergence Similarly, r is the radius of convergence of power series (2) if (2) converges when |x −a |<r and diverges when |x −a |>rhhe set of all values of x for which a power series converges is called its interval of convergence ho find the interval of convergence, first determine the radius of convergence by applying the Ratio hest to the series of absolute values hhen check each endpoint to determine whether the series converges or diverges thereExample 33Find all x for which the following series converges:1+x +x 2+⋯+x n +⋯ (3)Solution:By the Ratio hest, the series converges iflim n→∞|u n+1u n |=lim n→∞|x n+1x n |=lim n→∞|x |=|x |<1 hhus, the radius of convergence is 1 hhe endpoints must be tested separately since the Ratiohest fails when the limit equals 1 When x =1, (3) becomes 1+1+1+⋯ and diverges; when x =−1, (3) becomes 1−1+1−1+⋯ and diverges hhus the interval of convergence is −1<x <1Example 34For what x does ∑(−1)n−1x n−1n+1∞n=1 converge?Solution:lim n→∞|u n+1u n |=lim n→∞|x n n +2∙n +1x n−1|=lim n→∞|x |=|x |<1 hhe radius of convergence is 1 When x =1 , we have 12−13+14−15+⋯ , an alternating convergent series; when x =−1 , the series is 12+13+14+⋯ , which diverges hhus, the series converges if −1<x ≤1Example 35For what values of x does ∑x n n!∞n=1converge?Solution:lim n→∞|u n+1u n |=lim n→∞|x n+1(n +1)!∙n!x n |=lim n→∞|x |n +1=0 which is always less than 1 hhus the series converges for all xExample 36Find all x for which the following series converges:1+x −21+(x −2)22+⋯+(x −2)n−1n−1+⋯ (4)Solution:lim n→∞|u n+1u n |=lim n→∞|(x −2)n 2n ∙2n−1(x −2)n−1|=lim n→∞|x −2|2=|x −2|2which is less than 1 if |x −2|<2, that is, if 0<x <4 Series (4) converges on this intervaland diverges if |x −2|>2, that is, if x <0 or x >4 When x =0, (4) is 1−1+1−1+⋯ and diverges When x =4, (4) is 1+1+1+⋯ and diverges hhus, the interval of convergence is 0<x <4Example 37Find all x for which the series ∑n!x n∞n=1 converges Solution:∑n!x n ∞n=1 converges only at x =0, sincelim n→∞u n+1u n =lim n→∞(n +1)x =∞ unless x =0C2. Functions Defined by Power Series 幂级数定义的函数 Let the function f be defined byf (x )=∑a k (x −a)k ∞k=0=a 0+a 1(x −a )+⋯+a n (x −a )n +⋯ (1)its domain is the interval of convergence of the seriesFunctions defined by power series behave very much like polynomials, as indicated by the following properties:PROPERTY 2a. hhe function defined by (1) is continuous for each x in the interval of convergence of the seriesPROPERTY 2b. hhe series formed by differentiating the terms of series (1) converges to f ′(x ) for each x within the radius of convergence of (1); that is,f′(x )=∑ka k (x −a)k−1=a 1+2a 2(x −a )+⋯+na n (x −a )n−1+⋯∞k=0 (2) Note that power series (1) and its derived series (2) have the same radius of convergence but not necessarily the same interval of convergenceExample 38Let f (x )=∑x kk k+1∞k=1=x 1∙2+x 22∙3+x 33∙4+⋯+x n n n+1+⋯Find the intervals of convergence of the power series for f(x) and f ′(x ) Solution:lim n→∞|x n+1(n +1)(n +2)∙n (n +1)x n |=|x | also,f (1)=11∙2+12∙3+13∙4+⋯+1n ∙(n +1)+⋯ andf (−1)=−11∙2+12∙3−⋯+(−1)n n ∙(n +1)+⋯Hence, the power series for f converges if −1≤x ≤1 For the derivative f ′(x )=∑x k−1k+1∞k=1=12+x3+x 24+⋯+x n−1n+1+⋯lim n→∞|x n n +2∙n +1x n−1|=|x | also,f ′(1)=12+13+14+⋯ andf ′(−1)=12−13+14−⋯ Hence, the power series for f ′ converges if −1≤x <1hhus, the series given for f(x) and f ′(x ) have the same radius of convergence, but their intervals of convergence differPROPERTY 2c. hhe series obtained by integrating the terms of the given series (1) convergesto ∫f (t )dt xa for each x within the interval of convergence of (1); that is,∫f (t )dt =a 0(x −a )+a 1(x −a )22+a 2(x −a )33+⋯+a n (x −a )n+1n +1+⋯xa=∑a k (x −a )k+1k +1∞k=0Example 39Let f (x )=1(1−x )2 Show that the power series for ∫f (x )dx converges for all values of x in the interval of convergence of the power series for f(x)Solution:Obtain a series for 1(1−x )2 by long divisionhhen,1(1−x)2=1+2x+3x2+⋯+(n+1)x n+⋯It can be shown that the interval of convergence is −1<x<1 hhen by Property 2c∫1(1−x)2dx=∫[1+2x+3x2+⋯+(n+1)x n+⋯]dx11−x=c+x+x2+x3+⋯+x n+1+⋯Since when x=0we see that c=1, we have11−x=1+x+x2+x3+⋯+x n+⋯Note that this is a geometric series with ratio r=x and with a=1; if |x|<1, its sum isa 1−r =11−xC3. Finding a Power Series for a Function: Taylor and Maclaurin Series函数幕级数的展开: 泰勒级数和麦克劳林级数If a function f(x)is representable by a power series of the formc0+c1(x−a)+⋯+c n(x−a)n+⋯On an interval |x−a|<r, then the coefficients are given byc n=f(n)(a)n!, hhe seriesf(x)=f(a)+f′(a)(x−a)+f"(a)2!(x−a)2+⋯+f(n)(a)n!(x−a)n+⋯is called the Taylor series of the function f about the number a hhere is never more than one power series in (x−a)for f(x) It is required that the function and all its derivatives exist at x=a if the function f(x)is to generate a Taylor series expansionWhen a=0we have the special seriesf(x)=f(0)+f′(0)x+f"(0)2!x2+⋯+f(n)(0)n!x n+⋯called the Maclaurin series of the function f; this is the expansion of f about x=0Example 40Find the Maclaurin series for f(x)=e xSolution:Here f′(x)=e x,…,f(n)(x)=e x,…, for all n hhenf′(0)=1,…,f(n)(0)=1,…for all n, making the coefficients c n=1n!:e x=1+x+x22!+x33!+⋯+x nn!+⋯Example 41Find the Maclaurin expansion for f(x)=sin x Solution:hhus,sin x=x−x33!+x55!−⋯+(−1)n−1x2n−1(2n−1)!+⋯Example 42Find the Maclaurin expansion for f(x)=11−xSolution:hhus,11−x=1+x+x2+x3+⋯+x n+⋯Note that this agrees exactly with the power series in x obtained by different methods in Example39Example 43Find the Maclaurin expansion for f(x)=ln x about x=1Solution:hhus,ln x=(x−1)−(x−1)22+(x−1)33−(x−1)44+⋯+(−1)n−1(x−1)nnFUNCTIONS THAT GENERATE NO SERIES 不能级数展开的函数Note that the following functions are among those that fail to generate a specific series in (x−a)C4. Approximating Functions with Taylor and Maclaurin Polynomials 泰勒多项式和麦克劳林多项式的近似函数hhe function f(x)at the point x=a is approximated by a Taylor polynomial P n(x)of order n:f(x)≈P n(x)=f(a)+f′(a)(x−a)+f"(a)2!(x−a)2+⋯+f(n)(a)n!(x−a)nhhe haylor polynomial P n(x)and its first n derivatives all agree at a with f and its firstn derivatives hhe order of a haylor polynomial is the order of the highest derivative, which is also the polynomial’s last termIn the special case where a =0 , the Maclaurin polynomial of order n that approximates f(x) isP n (x )=f (0)+f ′(0)x +f"(0)2!x 2+⋯+f (n)(0)n!x nhhe haylor polynomial P 1(x) at x =0 is the tangent-line approximation to f(x) near zero given byf (x )=f (0)+f ′(0)xlt is the “best” linear approximation tof at 0, discussed at length in Chapter 4 §LA N OTE ON O RDER(泰勒多项式的阶数) AND D EGREE(泰勒多项式的级数)A haylor polynomial has degree(级数) n if it has powers of (x −a ) up through the n th If f (n)(a)=0, then the degree of P n (x) is less than n Note, for instance, in Example 45, that the second-order polynomial P 2(x) for the function sin x (which is identical with P 1(x)) is x +0∙x 22!, or just x , which has degree 1, not 2Example 44Find the haylor polynomial of order 4 at 0 for f (x )=e −x Use this to approximate f(0.25)Solution:hhe first four derivatives are −e −x ,e −x ,−e −x ,and e −x ; at a =0 , these equal −1,1,−1,and 1, respectively hhe approximating haylor polynomial of order 4 is thereforee −x ≈1−x +12!x 2−13!x 3+14!x 4 With x =0.25 we havee −0.25≈1−0.25+12!(0.25)2−13!(0.25)3+14!(0.25)4≈0.7788 hhis approximation of e −0.25 is correct to four placesIn Figure 10-2 we see the graphs of f(x) and of the haylor polynomials:Figure 10- 1P0(x)=1;P1(x)=1−x;P2(x)=1−x+x2;P3(x)=1−x+x22!−x33!;P4(x)=1−x+x22!−x33!+x44!Notice how closely P4(x)hugs f(x)even as x approaches 1Since the series can be shown to converge for x>0by the Alternating Series hest, the error in P4(x)is less than themagnitude of the first omitted term, x55!, or 1120at x=1 In fact, P4(1)=0.375to three decimalplaces, close to e−1≈0.368Example 45(a) Find the haylor polynomials P1,P3,P5, and P7at x=0for f(x)=sin x(b) Graph f and all four polynomials in [−2π,2π]×[−2,2](c) Approximate sinπ3using each of the four polynomialsSolution:P1(x)=x;P3(x)=x−x3 3!;P5(x)=x−x33!+x55!;P7(x)=x−x33!+x55!−x77!(b) Figure 10-3a shows the graphs of sin x and the four polynomials In Figure 10-3b we see graphs only of sin x and P7(x), to exhibit how closely P7“follows” the sine cruve。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Solutions to Assignment#6Financial Derivatives10.15Figure1displays the binomial tree that describes the value of the put options as a function of the stock price.At each node,the upper number refers to the stock price,whereas ﬁgures within parentheses and brackets correspond to the prices of the European and American put options,respectively.The risk-neutral probability p of an upward movement isp=e r T−du−d=e140.12−0.91.1−0.9=0.6523given that the risk free rate of return is12%.As the value of the European option at node A coincides with the present value of the expected payoﬀ,it follows thatf=f uu p2+2f ud p(1−p)+f dd(1−p)2e−12r=2(42−39.6)×0.6523×0.3477+(42−32.4)×0.34772e−120.12=2.118Needless to say,the same result holds if one works back the value of the option at node A through the tree.As for the American put option,it has a greater value than the European option because it is optimal to exercise early at node C.To appreciate that,it suﬃces to observe that the value of the European put option at node C isf d=f ud p+f dd(1−p)e−14r=2.4×0.6523+9.6×0.3477e−140.12=4.759,whereas the payoﬀfrom early exercise is K−S=42−36=6.10.18The risk-neutral probability of a upward movement isp=e r T−du−d=e1120.05−0.91.08−0.9=0.5788,hence it follows from the present value of the expected payoﬀat node A in Figure2that the value of the power option isf=f uu p2+2f ud p(1−p)+f dd(1−p)2e−16r=2(30−29.16)2×0.5788×0.4212+(30−24.3)2×0.42122e−160.05=6.0587As before,the same result holds if one backs out the value of the power option by working back through the binomial tree below.Finally,the result also holds even for the American options in view that,at node C,the payoﬀfrom early exercise is(K−S)2=(30−27)2=9,which is lessthan 10.19The binomial tree has two steps and time to maturity of the option is 6months,hence each step will last for three months,i.e.,δt =1/4.As the volatility is 30%per annum,it follows that u =e σ√δt =e 120.3=1.1618and d =1/u =0.8607,resulting in a risk-neutral probability of aupward movement of p =e r T −d u −d =e 130.04−0.86071.1618−0.8607=0.4959The value of the option then is 3.3739as calculated by DerivaGem (select Equity as the underlying type and Binomial European as the option type).If one uses 5,50,100and 500time steps,DerivaGem will compute the value of the option as 3.9229,3.7394,3.7478,and 3.7545,respectively.11.13If the cash position follows a generalized Wiener process with a drift rate of 0.1per month and a variance rate of 0.16per month with an initial position of 2,then the probability distribution of the cash position after k months is normal with mean 2+0.1k and variance 0.16k .The probability of a random sample from a normal distribution with mean 2.6and variance 0.96being negative is Φ −2+6×0.1√6×0.16 =0.0040,where Φis the cumulative distribution function of the standard normal.As for the one-year horizon,the probability of negative cash position is Φ −2+12×0.1√12×0.16 =0.0107.Finally,to ﬁnd at what time the probability of a negative cash ﬂow is greatest,it suﬃces to minimizeFigure2+0.1k √with respect to k .The ﬁrst derivative is zero when k =20months (with positive second derivative).11.14By Ito’s lemma,the bond price will followd B = ∂B ∂x a (x 0−x )+∂B ∂t +∂2B ∂x 2s 2x 2 d t +∂B ∂xs x d z.The price of a perpetual bond that continuously pays interest at the rate of $1per annum is B = ∞0e −x t d t =1/x .It then follows that ∂B ∂x =−x −2,∂B ∂t =0,and ∂2B ∂x 2=2x −3.The stochastic process of the bond price thus isd B = −a x 0−x x 2+s 2x d t −s xd z,which means that the overall expected instantaneous return (i.e.,interest plus the expected capitalgains)is 1−a x 0−x x 2+s 2x .12.27It follows from the fact that S 0=30,K =29,r =0.05,σ=0.25,and T =1/3thatd 1=log(30/29)+ 0.05+0.252/2 /30.25 1/3=0.4225d 2=d 1−0.25 1/3=0.2782The European call price then is c =30Φ(0.4225)−29e −130.05Φ(0.2782)=2.52,where Φis the cumulative distribution function of the standard normal.As it is never optimal to early exercise,the price of the American call option coincides with the European call price.The European put price is p =29e −130.05Φ(−0.2782)−30Φ(−0.4225)=1.05,which satisﬁes the put-call parity p +S 0=c +K e −r T .12.29To apply Black’s approximation,we ﬁrst compute the value of the corresponding Euro-pean call option.The present value of the dividend payments is D =0.40 e −160.10+e −5120.10 =0.777,hence we must act as if the stock price were S 0−D =18−0.777=17.223.The other parameters are K =20,r =0.10,σ=0.30,and T =1/2.The Black-Scholes formula then yields 0.7947as the price of such an option.Because the ﬁrst dividend payment of 40cents is below K 1−e −r (t 2−t 1) =20 1−e −0.10(5/12−2/12) =0.494,it is never optimal to exercise the option before the ﬁrst ex-dividend date t 1=1/6.In contrast,it is optimal to exercise just before the sec-ond dividend payment at t 2because K 1−e −r (T −t 2) =20 1−e −0.10(6/12−5/12) =0.1660<0.40,and so we proceed by valuing the European call option that expires at t 2=5/12.The Black-Scholes formula gives the price as 0.7668,which implies that the price of the American call option is max(0.7947,0.7668)=0.7947according to Black’s approximation.Calculating the price of the option using DerivaGem gives way to 0.8224if one considers,for instance,50time steps.Finally,the American option price is always below the corresponding European option price as long as the second dividend is below 16.60cents per share.。