[推荐学习]2018年高考数学总复习课时规范练11函数的图象文新人教A版
最新-2018届高考数学一轮复习 第4讲函数及其表示课件 理 新人教课标A版 精品

第4讲 │ 要点探究
(1)函数 y= kx2-6x+k+8的定义域为 R,则 k 的取值
范围是( )
A.k≥0 或 k≤-9
B.k≥1
C.-9≤k≤1
D.0<k≤1
(2)若函数 f(x)=mx2+x-4m4x+3的定义域为 R,则实数 m 的取值 范围是________.
第4讲 │ 要点探究
(1)B (2)0,34 [解析] (1)∵kx2-6x+k+8≥0 恒成立,k≤0 显然不符,∴kΔ>=0,36-4kk+8≤0, 解得 k≥1.
第4讲 │ 要点探究
(3)当 x>1 或 x<-1 时,x2-1>0, ∴g[f(x)]=g(x2-1)= (x2-1) -1=x2-2. 当-1≤x≤1 时,x2-1≤0, ∴g[f(x)]=g(x2-1)=2-(x2-1)=-x2+3, 故 g[f(x)]=-x2-x2+2,3,x>-1或1≤x<x-≤11,.
B.f(x)= x2x-4,x∈-∞,-2∪2,+∞
C.f(x)=- 4-x x2,x∈-2,0∪0,2
D.f(x)= 4-x x2,x∈-2,0∪0,2
第4讲 │ 要点探究
(3)[2010·合肥模拟] 已知函数 f(2x)定义域是[1,2],则函数
f(log2x)的定义域为________.
[思路] (1)(2)是根据函数解析式求其定义域,只要根据使函数表
(3)∵f(2x)的定义域为[1,2],因此函数 f(x)的定义域为[2,4],由 2≤log2x≤4,解得 4≤x≤16,因此函数 f(log2x)的定义域为[4,16].
[点评] (1)由函数解析式求定义域,关键是列出使函数有意义的条 件,解出各条件中自变量取值范围,并结合数轴求得它们的交集,从 而得到函数的定义域;(2) 若函数 f(x)的定义域为[a,b],则复合函数 y=f[g(x)]的定义域是不等式 a≤g(x)≤b 的解集;(3)函数的定义域应 写成区间或集合的形式.对于已知函数定义域求字母参数问题,可转 化为恒成立问题求解,如下面的变式题.
2018版高考数学(人教A版理)一轮复习课件:重点强化课1 函数的图象与性质

1 1 3 < 2,即|a-1|<2,所以2<a<2.]
高三一轮总复习
☞角度 2 奇偶性与周期性结合 (2017· 贵阳适应性考试(二))若函数 f(x)=asin 2x+btan x+1, 且 f(- 3)=5,则 f(π+3)=________.
-3 [令 g(x)=asin 2x+btan x,则 g(x)是奇函数,且最小正周期是 π,由 f(- 3)=g(-3)+1=5,得 g(-3)=4,则 g(3)=-g(-3)=-4,则 f(π+3)=g(π+3)+1 =g(3)+1=-4+1=-3.]
高三一轮总复习
重点 1
函数图象的应用
则
1 0,2, cos πx,x∈ 已知 f(x)为偶函数,当 x≥0 时,f(x)= 2x-1,x∈1,+∞, 2
1 不等式 f(x-1)≤2的解集为(
) 【导学号:01772064】
高三一轮总复习
1 2 4 7 A.4,3∪3,4 3 1 1 2 B.-4,-3∪4,3 1 3 4 7 C.3,4∪3,4 3 1 1 3 D.-4,-3∪3,4
x∈[1,+
1 a=f(-3)=f(3),b=f4=f(4),所以
b>a>c,故
即根据分段函数中自变量取值范围的界定,代入相应的解析式求解零点,注意取 值范围内的大前提,以及函数性质和数形结合在判断零点个数时的强大功能.
Hale Waihona Puke 高三一轮总复习[对点训练 2] (2017· 石家庄一模)已知函数 y=f(x+2)的图象关于直线 x=-2 对称,且当 x∈(0,+∞)时,f(x)=|log2x|,若 c 的大小关系是( A.a>b>c C.c>a>b ) B.b>a>c D.a>c>b
福建专用2018年高考数学总复习课时规范练19函数y=Asin(ωx+φ)的图象及应用文新人教A版20180315470

课时规范练19 函数y=A sin(ωx+φ)的图象及应用基础巩固组1.将函数y=sin x的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得各点向右平行移动个单位长度,所得图象的函数解析式是()A.y=sinB.y=sinC.y=sinD.y=sin2.已知函数f(x)=cos(ω>0)的最小正周期为π,则该函数的图象()A.关于点对称B.关于直线x=对称C.关于点对称D.关于直线x=对称3.(2017湖南邵阳一模,文6)若将函数f(x)=sin 2x+cos 2x的图象向左平移φ(φ>0)个单位长度,所得的图象关于y轴对称,则φ的最小值是()A. B. C. D.4.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin+k.据此函数可知,这段时间水深(单位:m)的最大值为()A.5B.6C.8D.105.(2017天津,文7)设函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,|φ|<π,若f=2,f=0,且f(x)的最小正周期大于2π,则()A.ω=,φ=B.ω=,φ=-C.ω=,φ=-D.ω=,φ=〚导学号24190738〛6.若函数f(x)=2sin 2x的图象向右平移φ个单位长度后得到函数g(x)的图象,若对满足|f(x1)-g(x2)|=4的x1,x2,有|x1-x2|的最小值为,则φ=()A. B. C. D.7.已知函数f(x)=sin(ωx+φ)的部分图象如图所示,则y=f取得最小值时x的集合为()A.B.C.D.〚导学号24190739〛8.函数y=sin x-cos x的图象可由函数y=2sin x的图象至少向右平移个单位长度得到.9.已知函数y=g(x)的图象由f(x)=sin 2x的图象向右平移φ(0<φ<π)个单位长度得到,这两个函数的部分图象如图所示,则φ=.10.(2017北京,文16)已知函数f(x)=cos-2sin x cos x.(1)求f(x)的最小正周期;(2)求证:当x∈时,f(x)≥-.〚导学号24190740〛综合提升组11.(2017辽宁大连一模,文11)若关于x的方程2sin=m在上有两个不等实根,则m的取值范围是()A.(1,)B.[0,2]C.[1,2)D.[1,]12.已知函数f(x)=cos(2x+φ)的图象关于点对称,若将函数f(x)的图象向右平移m(m>0)个单位长度后得到一个偶函数的图象,则实数m的最小值为.13.已知函数y=3sin.(1)用五点法作出函数的图象;(2)说明此图象是由y=sin x的图象经过怎么样的变化得到的.〚导学号24190741〛创新应用组14.已知曲线C1:y=cos x,C2:y=sin,则下面结论正确的是()A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2〚导学号24190742〛15.如图所示,某地夏天8—14时用电量变化曲线近似满足函数式y=A sin(ωx+φ)+b,ω>0,φ∈(0,π).(1)求这期间的最大用电量及最小用电量;(2)写出这段曲线的函数解析式.答案:1.B由题意,y=sin x的图象进行伸缩变换后得到y=sin x的图象,再进行平移后所得图象的函数为y=sin=sin.故选B.2.D由题意知ω=2,函数f(x)的对称轴满足2x+=kπ(k∈Z),解得x=(k∈Z),当k=1时,x=,故选D.3.C函数f(x)=sin 2x+cos 2x=sin的图象向左平移φ个单位长度,所得函数y=sin的图象关于y轴对称,则有2φ+=kπ+,k∈Z.解得φ=kπ+,k∈Z.由φ>0,则当k=0时,φ的最小值为.故选C.4.C因为sin∈[-1,1],所以函数y=3sin+k的最小值为k-3,最大值为k+3.由题图可知函数最小值为k-3=2,解得k=5.所以y的最大值为k+3=5+3=8,故选C.5.A由题意可知,>2π,,所以≤ω<1.所以排除C,D.当ω=时,f=2sin=2sin=2,所以sin=1.所以+φ=+2kπ,即φ=+2kπ(k∈Z).因为|φ|<π,所以φ=.故选A.6.C由函数f(x)=2sin 2x的图象向右平移φ个单位长度后得到函数g(x)=2sin[2(x-φ)]的图象,可知对满足|f(x1)-g(x2)|=4的x1,x2,有|x1-x2|的最小值为-φ.故-φ=,即φ=.7.B根据所给图象,周期T=4×=π,故π=,即ω=2,因此f(x)=sin(2x+φ).又图象经过,代入有2×+φ=kπ(k∈Z),再由|φ|<,得φ=-,故f=sin,当2x+=-+2kπ(k∈Z),即x=-+kπ(k∈Z)时,y=f取得最小值.8.因为y=sin x-cos x=2sin,所以函数y=sin x-cos x的图象可由函数y=2sin x的图象至少向右平移个单位长度得到.9.函数f(x)=sin 2x的图象在y轴右侧的第一个对称轴为2x=,则x=.x=关于x=对称的直线为x=,由图象可知,通过向右平移之后,横坐标为x=的点平移到x=,则φ=.10.(1)解f(x)=cos 2x+sin 2x-sin 2x=sin 2x+cos 2x=sin.所以f(x)的最小正周期T==π.(2)证明因为-≤x≤,所以-≤2x+.所以sin≥sin=-.所以当x∈时,f(x)≥-.11.C方程2sin=m可化为sin,当x∈时,2x+,画出函数y=f(x)=sin在x∈上的图象如图所示.由题意,得<1,即1≤m<2,∴m的取值范围是[1,2),故选C.12.∵函数的图象关于点对称,∴2×+φ=kπ+,k∈Z,解得φ=kπ-,k∈Z,∴f(x)=cos,k∈Z.∵f (x )的图象平移后得函数y=cos (k ∈Z )为偶函数,∴-2m+k π-=k 1π(k ∈Z ,k 1∈Z ),m=.∵m>0,∴m 的最小正值为,此时k-k 1=1(k ∈Z ,k 1∈Z ).13.解 (1)列表:x-描点、连线,如图所示.(2)(方法一)“先平移,后伸缩”.先把y=sin x 的图象上所有点向右平移个单位长度,得到y=sin 的图象,再把y=sin 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y=sin 的图象,最后将y=sin的图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),就得到y=3sin的图象.(方法二)“先伸缩,后平移”先把y=sin x的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y=sin x的图象,再把y=sin x图象上所有的点向右平移个单位长度,得到y=sin=sin的图象,最后将y=sin的图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),就得到y=3sin的图象.14.D曲线C1的方程可化为y=cos x=sin,把曲线C1上各点的横坐标缩短到原来的倍,纵坐标不变,得曲线y=sin=sin 2,为得到曲线C2:y=sin 2,需再把得到的曲线向左平移个单位长度.15.解 (1)由图象,知这期间的最大用电量为50万千瓦时,最小用电量为30万千瓦时.(2)A=(50-30)=10,b=(50+30)=40,T==2×(14-8)=12,所以ω=,所以y=10sin+40.把x=8,y=30代入上式,得φ=.所以所求解析式为y=10sin+40,x∈[8,14].。
高三数学一轮复习课时作业10 函数的图象及应用 新人教A版 文
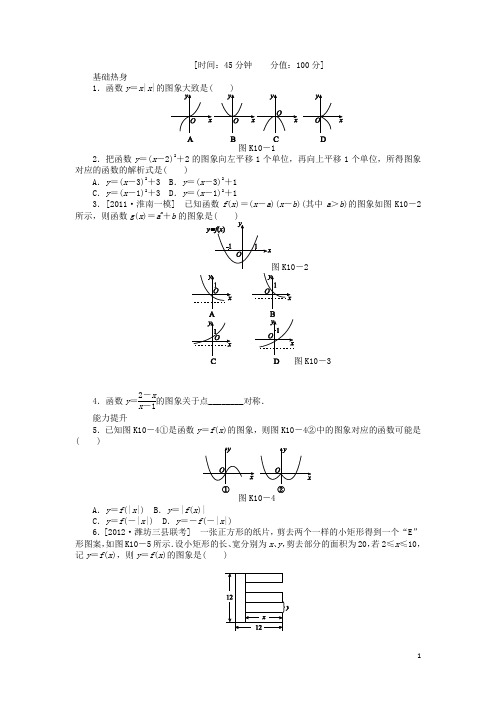
[时间:45分钟 分值:100分]基础热身1.函数y =x |x |的图象大致是( )图K10-2.把函数y =(x -2)2+2的图象向左平移1个单位,再向上平移1个单位,所得图象对应的函数的解析式是( )A .y =(x -3)2+3B .y =(x -3)2+1C .y =(x -1)2+3D .y =(x -1)2+13.[2011·淮南一模] 已知函数f (x )=(x -a )(x -b )(其中a >b )的图象如图K10-2所示,则函数g (x )=a x+b-2图K10-34.函数y =2-xx -1的图象关于点________对称.能力提升5.已知图K10-4①是函数y =f (x )的图象,则图K10-4②中的图象对应的函数可能是( )图A .y =f (|x |) B .y =|f (x )|C .y =f (-|x |)D .y =-f (-|x |) 6.[2012·潍坊三县联考] 一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图K10-5所示.设小矩形的长、宽分别为x 、y ,剪去部分的面积为20,若2≤x ≤10,记y =f (x ),则y =f (x )的图象是( )图K10-5图K10-67.已知f (x )=⎩⎪⎨⎪⎧x +1,x ∈[-1,0,x 2+1,x ∈[0,1],则如图K10-7中函数的图象错误的是( )K10-8.[2011·课标全国卷] 已知函数y =f (x )的周期为2,当x ∈[-1,1]时f (x )=x 2,那么函数y =f (x )的图象与函数y =|lg x |的图象的交点共有( )A .10个B .9个C .8个D .1个9.如图K10-8,正方形ABCD 的顶点A ⎝ ⎛⎭⎪⎫0,22,B 22,0,顶点C 、D 位于第一象限,直线l :x =t (0≤t ≤2)将正方形ABCD 分成两部分,记位于直线l 左侧阴影部分的面积为f (t ),则函数S =f (t )的图象大致是( )图K10-8图K10-910.函数y =f (x )的图象与函数y =e x的图象关于直线y =x 对称,将y =f (x )的图象向左平移2个单位,得到函数y =g (x )的图象,再将y =g (x )的图象向上平移1个单位,得到函数y =h (x )的图象,则函数y =h (x )的解析式是________.11.[2011·岳阳调研] 若函数y =f (x +2)的图象过点P (-1,3),则函数y =f (x )的图象关于原点O 对称的图象一定过点________.12.已知a >0且a ≠1,f (x )=x 2-a x,当x ∈(-1,1)时均有f (x )<12,则实数a 的取值范围是________.13.已知函数y =f (x )和y =g (x )在[-2,2]上的图象如图K10-10所示:则方程f [g (x )]=0有且仅有________个根;方程f [f (x )]=0有且仅有________个根.14.(10分)已知函数f (x )=x 2-2x ,且g (x )的图象与f (x )的图象关于点(2,-1)对称,求函数g (x )的表达式.15.(13分)若关于x 的方程|x 2-4x +3|-a =x 至少有三个不相等的实数根,试求实数a 的取值范围.难点突破16.(12分)已知函数f (x )的图象与函数h (x )=x +1x+2的图象关于点A (0,1)对称.(1)求f (x )的解析式;(2)若g (x )=f (x )+a x,且g (x )在区间(0,2]上为减函数,求实数a 的取值范围.课时作业(十)【基础热身】1.A [解析] 因y =⎩⎪⎨⎪⎧x 2,x ≥0,-x 2,x <0,又y =x |x |为奇函数,结合图象知,选A.2.C [解析] 把函数y =f (x )的图象向左平移1个单位,即把其中x 换成x +1,于是得y =[(x +1)-2]2+2=(x -1)2+2的图象,再向上平移1个单位,即得到y =(x -1)2+2+1=(x -1)2+3的图象.3.A [解析] f (x )的零点为a ,b ,由图可知0<a <1,b <-1,则g (x )是一个减函数,可排除C 、D ;再根据g (0)=1+b <0,可排除B ,故正确选项为A.4.(1,-1) [解析] y =2-x x -1=-1+1x -1,y =2-x x -1的图象是由y =1x的图象先向右平移1个单位,再向下平移1个单位而得到,故对称中心为(1,-1).【能力提升】5.C [解析] 由题图②知,图象对应的函数是偶函数,且当x <0时,对应的函数是y =f (x ),故选C.对于给定函数的图象,要能从图象的左右、上下分布范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性,注意图象与函数解析式中参数的关系.6.A [解析] 依题意y =10x(2≤x ≤10),所以图象为A.7.D [解析] 因f (x )=⎩⎪⎨⎪⎧x +1,x ∈[-1,0,x 2+1,x ∈[0,1],其图象如图,验证知f (x -1),f (-x ),f (|x |)的图象均正确,只有|f (x 8.A [解析] 10个交点.9.C [解析] 当0<t ≤22时,f (t )=12·t ·2t =t 2,当22<t ≤2f (t )=1-12·(2-t )·2(2-t )=-t 2+22t -1,即函数f (t )在⎝ ⎛⎦⎥⎤0,22上是开口向上的抛物线,在⎝ ⎛⎦⎥⎤22,2上是开口向下的抛物线,故选C. 10.y =ln(x +2)+1 [解析] 依题意,f (x )=ln x ,g (x )=ln(x +2),h (x )=ln(x +2)+1.11.(-1,-3) [解析] 依题意得f (-1+2)=3,f (1)=3,即函数f (x )的图象一定过点(1,3),因此函数y =f (x )的图象关于原点O 对称的图象一定经过点(1,3)关于原点O 的对称点(-1,-3).12.12≤a <1或1<a ≤2 [解析] 由题意可知a x >x 2-12在(-1,1)上恒成立, 令y 1=a x ,y 2=x 2-12,由图象知:⎩⎪⎨⎪⎧a -1≥-12-12,a 1≥1-12,a >0且a ≠1,∴12≤a <1或1<a ≤2. 13.6 5 [解析] 上的根有三个,分别为x =0,x =a ∈(-2,-1),x =b ∈(1,2).①f [g (x )]=0等价于g (x )=0或g (x )=a ∈(-2,-1)或g (x )=b ∈(1,2),结合y =g (x )在[-2,2]的图象,可以发现g (x )=0,g (x )=a ∈(-2,-1),g (x )=b ∈(1,2)各有两个解,合计为6个解;②f [f (x )]=0等价于f (x )=0或f (x )=a ∈(-2,-1)或f (x )=b ∈(1,2),结合y =f (x )在[-2,2]的图象,可以发现f (x )=0,f (x )=a ∈(-2,-1),f (x )=b ∈(1,2)的根分别为3个,1个,1个,合计为5个解.14.[解答] 函数f (x )的定义域是R ,在函数f (x )的图象上任取一点(x 0,y 0),它关于点(2,-1)对称的点为(x ,y ),根据两点连线段的中点坐标公式,有⎩⎪⎨⎪⎧x 0=4-x ,y 0=-2-y ,于是-2-y =f (4-x )=(4-x )2-2(4-x )=x 2-6x +8,所以y =-x 2+6x -10.故g (x )=-x 2+6x -10.15.[解答] 原方程变形为|x 2-4x +3|=x +a ,于是,设y 1=|x 2-4x +3|,y 2=x +a ,在同一坐标系下分别作出它们的图象.如图, 则当直线y 2=x +a 过点(1,0)时a =-1;当直线y 2=x +a 与抛物线y 1由⎩⎪⎨⎪⎧y 2=x +a ,y 1=-x 2+4x -3⇒x 2-3x +a +3=0, 由Δ=9-4(3+a )=0,得a =-34.由图象知,a ∈⎣⎢⎡⎦⎥⎤-1,-34时,方程至少有三个根. 【难点突破】 16.[解答] (1)设f (x )图象上任一点P (x ,y ),则点P 关于点(0,1)的对称点P ′(-x,2-y )在h (x )的图象上,则2-y =-x -1x +2,∴y =x +1x.故f (x )=x +1x(x ≠0).(2)g (x )=f (x )+a x =x +a +1x ,g ′(x )=1-a +1x2. ∵g (x )在(0,2]上为减函数,∴1-a +1x2≤0在(0,2]上恒成立,即a +1≥x 2在(0,2]上恒成立,∴a +1≥4, 即a ≥3,故a 的取值范围是[3,+∞).。
人教A版高考总复习一轮数学精品课件 第5章 课时规范练 函数y=Asin(ωx+φ)的图象及应用

C.y=sin(2x-2 )
π
D.y=sin(2x- )
6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
解析 将函数
y=sin(x-3)的图象上所有点的横坐标伸长到原来的
不变),得到图象对应的函数解析式为
1
y=sin(2x-3),将
移3个单位长度,得到的图象对应的函数解析式为
2 倍(纵坐标
1
y=sin(2x-3)的图象向左平
1
1
y=sin(2(x+3)-3)=sin(2x-6).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
2.(2024·青海西宁模拟)把函数 y=f(x)图象上所有点的横坐标伸长到原来的 2
π
倍,纵坐标保持不变,再把所得图象向左平移 个单位长度,得到
解析 因为 ω>0,所以
2π
T=π= ⇒ω=2,当
π
π
π
x= 时,sin( +φ)=0⇒ +φ=kπ(k∈Z).因
4
2
2
π
π
为 0<φ<π,所以 φ= ,所以 f(x)=sin(2x+ )=cos
2
2
2x.将函数 f(x)图象上的所有点的
横坐标伸长为原来的 2 倍(纵坐标不变),可得函数 y=cos x 的图象,再将所得图
2
3
由 θ>0 可知,当 k=1 时,θ
π
取得最小值6.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
2018高考一轮通用人教A版数学文练习第2章 第7节 函数

第七节 函数的图象———————————————————————————————— [考纲传真] 会运用基本初等函数的图象分析函数的性质.1.利用描点法作函数的图象 方法步骤:(1)确定函数的定义域; (2)化简函数的解析式;(3)讨论函数的性质(奇偶性、单调性、周期性、最值等); (4)描点连线.2.利用图象变换法作函数的图象 (1)平移变换(2)对称变换①y =f (x )的图象―――――→关于x 轴对称y =-f (x )的图象; ②y =f (x )的图象――――――→关于y 轴对称y =f (-x )的图象; ③y =f (x )的图象――――――→关于原点对称y =-f (-x )的图象;④y =a x (a >0且a ≠1)的图象――――――――→关于直线y =x 对称y =log a x (a >0且a ≠1)的图象.(3)伸缩变换 ①y =f (x )的图象y=f(ax)的图象;②y=f(x)的图象a>1,纵坐标伸长为原来的a倍,横坐标不变y=af(x)的图象.―――――――――――――――――――――→0<a<1,纵坐标缩短为原来的a,横坐标不变(4)翻转变换x轴下方部分翻折到上方①y=f(x)的图象―――――――――――→y=|f(x)|的图象;x轴及上方部分不变y轴右侧部分翻折到左侧②y=f(x)的图象―――――――――――――→y=f(|x|)的图象.原y轴左侧部分去掉,右侧不变1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)函数y=f(1-x)的图象,可由y=f(-x)的图象向左平移1个单位得到.()(2)函数y=f(x)的图象关于y轴对称即函数y=f(x)与y=f(-x)的图象关于y 轴对称.()(3)当x∈(0,+∞)时,函数y=f(|x|)的图象与y=|f(x)|的图象相同.()(4)若函数y=f(x)满足f(1+x)=f(1-x),则函数f(x)的图象关于直线x=1对称.()[答案](1)×(2)×(3)×(4)√2.(教材改编)甲、乙二人同时从A地赶往B地,甲先骑自行车到两地的中点再改为跑步,乙先跑步到中点再改为骑自行车,最后两人同时到达B地.已知甲骑车比乙骑车的速度快,且两人骑车速度均大于跑步速度.现将两人离开A 地的距离s与所用时间t的函数关系用图象表示,则下列给出的四个函数图象中,甲、乙的图象应该是()①②③④图2-7-1A .甲是图①,乙是图②B .甲是图①,乙是图④C .甲是图③,乙是图②D .甲是图③,乙是图④B [设甲骑车速度为V甲骑,甲跑步速度为V 甲跑,乙骑车速度为V 乙骑,乙跑步速度为V 乙跑,依题意V 甲骑>V 乙骑>V 乙跑>V 甲跑,故选B.]3.函数f (x )的图象向右平移1个单位长度,所得图象与曲线y =e x 关于y 轴对称,则f (x )=( )A .e x +1B .e x -1C .e-x +1D .e-x -1D [依题意,与曲线y =e x 关于y 轴对称的曲线是y =e -x ,于是f (x )相当于y =e -x 向左平移1个单位的结果,∴f (x )=e -(x +1)=e -x -1.]4.(2016·浙江高考)函数y =sin x 2的图象是( )D [∵y =sin(-x )2=sin x 2,∴函数为偶函数,可排除A 项和C 项;当x =π2时,sin x 2=sin π24≠1,排除B 项,故选D.]5.若关于x 的方程|x |=a -x 只有一个解,则实数a 的取值范围是________.【导学号:31222055】(0,+∞) [在同一个坐标系中画出函数y =|x |与y =a -x 的图象,如图所示.由图象知当a >0时,方程|x |=a -x 只有一个解.](1)y =⎝ ⎛⎭⎪⎫12|x |;(2)y =|log 2(x +1)|;(3)y =2x -1x -1;(4)y =x 2-2|x |-1.[解] (1)先作出y =⎝ ⎛⎭⎪⎫12x 的图象,保留y =⎝ ⎛⎭⎪⎫12x 图象中x ≥0的部分,再作出y=⎝ ⎛⎭⎪⎫12x 的图象中x >0部分关于y 轴的对称部分,即得y =⎝ ⎛⎭⎪⎫12|x |的图象,如图①实线部分.3分① ②(2)将函数y =log 2x 的图象向左平移一个单位,再将x 轴下方的部分沿x 轴翻折上去,即可得到函数y =|log 2(x +1)|的图象,如图②.6分(3)∵y =2+1x -1,故函数图象可由y =1x 图象向右平移1个单位,再向上平移2个单位得到,如图③.9分③ ④(4)∵y =⎩⎨⎧x 2-2x -1,x ≥0,x 2+2x -1,x <0,且函数为偶函数,先用描点法作出[0,+∞)上的图象,再根据对称性作出(-∞,0)上的图象,得图象如图④.12分[规律方法] 画函数图象的一般方法(1)直接法.当函数表达式(或变形后的表达式)是熟悉的基本函数时,就可根据这些函数的特征直接作出;(2)图象变换法.若函数图象可由某个基本函数的图象经过平移、翻折、对称得到,可利用图象变换作出.易错警示:注意平移变换与伸缩变换的顺序对变换单位及解析式的影响. [变式训练1] 分别画出下列函数的图象: (1)y =|lg x |;(2)y =sin|x |.[解] (1)∵y =|lg x |=⎩⎨⎧lg x ,x ≥1,-lg x ,0<x <1.∴函数y =|lg x |的图象,如图①.6分(2)当x ≥0时,y =sin|x |与y =sin x 的图象完全相同,又y =sin|x |为偶函数,图象关于y 轴对称,其图象如图②.12分[2,2]( )(2)(2015·全国卷Ⅱ)如图2-7-2,长方形ABCD 的边AB =2,BC =1,O 是AB 的中点.点P 沿着边BC ,CD 与DA 运动,记∠BOP =x .将动点P 到A ,B 两点距离之和表示为x 的函数f (x ),则y =f (x )的图象大致为( )图2-7-2A B C D(1)D (2)B [(1)∵f (x )=2x 2-e |x |,x ∈[-2,2]是偶函数,又f (2)=8-e 2∈(0,1),故排除A ,B.设g (x )=2x 2-e x ,则g ′(x )=4x -e x .又g ′(0)<0,g ′(2)>0,∴g (x )在(0,2)内至少存在一个极值点,∴f (x )=2x 2-e |x |在(0,2)内至少存在一个极值点,排除C.故选D.(2)当点P 沿着边BC 运动,即0≤x ≤π4时, 在Rt △POB 中,|PB |=|OB |tan ∠POB =tan x , 在Rt △P AB 中,|P A |=|AB |2+|PB |2=4+tan 2x ,则f (x )=|P A |+|PB |=4+tan 2x +tan x ,它不是关于x 的一次函数,图象不是线段,故排除A 和C ;当点P 与点C 重合,即x =π4时,由上得f ⎝ ⎛⎭⎪⎫π4=4+tan 2π4+tan π4=5+1,又当点P 与边CD 的中点重合,即x =π2时,△P AO 与△PBO 是全等的腰长为1的等腰直角三角形,故f ⎝ ⎛⎭⎪⎫π2=|P A |+|PB |=2+2=22,知f ⎝ ⎛⎭⎪⎫π2<f ⎝ ⎛⎭⎪⎫π4,故又可排除D.综上,选B.][规律方法] 函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;(2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的周期性,判断图象的循环往复; (5)从函数的特征点,排除不合要求的图象.[变式训练2] (1)已知函数f (x )的图象如图2-7-3所示,则f (x )的解析式可以是( )图2-7-3A .f (x )=ln|x |x B .f (x )=e xx C .f (x )=1x 2-1 D .f (x )=x -1x(2)(2016·河南平顶山二模)函数y =a +sin bx (b >0且b ≠1)的图象如图2-7-4所示,那么函数y =log b (x -a )的图象可能是( )图2-7-4(1)A (2)C [(1)由函数图象可知,函数f (x )为奇函数,应排除B ,C.若函数为f (x )=x -1x ,则x →+∞时,f (x )→+∞,排除D ,故选A.(2)由题图可得a >1,且最小正周期T =2πb <π,所以b >2,则y =log b (x -a )是增函数,排除A 和B ;当x =2时,y =log b (2-a )<0,排除D ,故选C.]☞角度1 研究函数的性质已知函数f (x )=x |x |-2x ,则下列结论正确的是( )A .f (x )是偶函数,递增区间是(0,+∞)B .f (x )是偶函数,递减区间是(-∞,1)C .f (x )是奇函数,递减区间是(-1,1)D .f (x )是奇函数,递增区间是(-∞,0)C [将函数f (x )=x |x |-2x 去掉绝对值得f (x )=⎩⎨⎧x 2-2x ,x ≥0,-x 2-2x ,x <0,画出函数f (x )的图象,如图,观察图象可知,函数f (x )的图象关于原点对称,故函数f (x )为奇函数,且在(-1,1)上单调递减.] ☞角度2 确定函数零点的个数已知f (x )=⎩⎨⎧|lg x |,x >0,2|x |,x ≤0,则函数y =2f 2(x )-3f (x )+1的零点个数是________.5 [方程2f 2(x )-3f (x )+1=0的解为f (x )=12或1.作出y =f (x )的图象,由图象知零点的个数为5.] ☞角度3 求参数的值或取值范围(2016·浙江杭州五校联盟一诊)若直角坐标平面内两点P ,Q 满足条件:①P ,Q 都在函数y =f (x )的图象上;②P ,Q 关于原点对称,则称(P ,Q )是函数y =f (x )的一个“伙伴点组”(点组(P ,Q )与(Q ,P )看作同一个“伙伴点组”).已知函数f (x )=⎩⎨⎧kx -1,x >0,-ln (-x ),x <0有两个“伙伴点组”,则实数k 的取值范围是( )A .(-∞,0)B .(0,1) C.⎝ ⎛⎭⎪⎫0,12 D .(0,+∞)B [根据题意可知,“伙伴点组”的点满足: 都在函数图象上,且关于坐标原点对称.可作出函数y =-ln(-x )(x <0)关于原点对称的函数y =ln x (x >0)的图象, 使它与直线y =kx -1(x >0)的交点个数为2即可.当直线y =kx -1与y =ln x 的图象相切时,设切点为(m ,ln m ),又y =ln x 的导数为y ′=1x ,即km -1=ln m ,k =1m ,解得m =1,k =1,可得函数y =ln x (x >0)的图象过(0,-1)点的切线的斜率为1, 结合图象可知k ∈(0,1)时两函数图象有两个交点.故选B.] ☞角度4 求不等式的解集函数f (x )是定义在[-4,4]上的偶函数,其在[0,4]上的图象如图2-7-5所示,那么不等式f (x )cos x <0的解集为________.图2-7-5⎝ ⎛⎭⎪⎫-π2,-1∪⎝ ⎛⎭⎪⎫1,π2 [在⎝ ⎛⎭⎪⎫0,π2上,y =cos x >0,在⎝ ⎛⎭⎪⎫π2,4上,y =cos x <0. 由f (x )的图象知在⎝ ⎛⎭⎪⎫1,π2上f (x )cos x <0, 因为f (x )为偶函数,y =cos x 也是偶函数, 所以y =f (x )cos x 为偶函数,所以f (x )cos x <0的解集为⎝ ⎛⎭⎪⎫-π2,-1∪⎝ ⎛⎭⎪⎫1,π2.][规律方法] 函数图象应用的常见题型与求解方法 (1)研究函数性质:①根据已知或作出的函数图象,从最高点、最低点,分析函数的最值、极值. ②从图象的对称性,分析函数的奇偶性.③从图象的走向趋势,分析函数的单调性、周期性. ④从图象与x 轴的交点情况,分析函数的零点等.(2)研究方程根的个数或由方程根的个数确定参数的值(范围):构造函数,转化为两函数图象的交点个数问题,在同一坐标系中分别作出两函数的图象,数形结合求解.(3)研究不等式的解:当不等式问题不能用代数法求解,但其对应函数的图象可作出时,常将不等式问题转化为两函数图象的上、下关系问题,从而利用数形结合求解.[思想与方法]1.识图:对于给定函数的图象,要从图象的左右、上下分布范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性,注意图象与函数解析式中参数的关系.2.用图:借助函数图象,可以研究函数的定义域、值域、单调性、奇偶性、对称性等性质.利用函数的图象,还可以判断方程f (x )=g (x )的解的个数,求不等式的解集等.[易错与防范]1.图象变换是针对自变量x 而言的,如从f (-2x )的图象到f (-2x +1)的图象是向右平移12个单位,先作如下变形f (-2x +1)=f ⎝ ⎛⎭⎪⎫-2⎝ ⎛⎭⎪⎫x -12,可避免出错. 2.明确一个函数的图象关于y 轴对称与两个函数的图象关于y 轴对称的不同,前者是自身对称,且为偶函数,后者是两个不同函数的对称关系.3.当图形不能准确地说明问题时,可借助“数”的精确,注重数形结合思想的运用.课时分层训练(十)函数的图象A组基础达标(建议用时:30分钟)一、选择题1.为了得到函数y=2x-2的图象,可以把函数y=2x的图象上所有的点() A.向右平行移动2个单位长度B.向右平行移动1个单位长度C.向左平行移动2个单位长度D.向左平行移动1个单位长度B[因为y=2x-2=2(x-1),所以只需将函数y=2x的图象上所有的点向右平移1个单位长度,即可得到y=2(x-1)=2x-2的图象,故B正确.] 2.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是()【导学号:31222056】A B C DC[出发时距学校最远,先排除A,中途堵塞停留,距离没变,再排除D,堵塞停留后比原来骑得快,因此排除B.]3.(2016·广西桂林高考一调)函数y=(x3-x)2|x|的图象大致是()A B C DB[由于函数y=(x3-x)2|x|为奇函数,故它的图象关于原点对称,当0<x <1时,y<0;当x>1时,y>0,故选B.]4.已知函数f(x)=若关于x的方程f(x)=k有两个不等的实数根,则实数k 的取值范围是( )A .(0,+∞)B .(-∞,1)C .(1,+∞)D .(0,1]D [作出函数y =f (x )与y =k 的图象,如图所示:由图可知k ∈(0,1],故选D.]5.(2017·洛阳模拟)若f (x )是偶函数,且当x ∈[0,+∞)时,f (x )=x -1,则f (x -1)<0的解集是( )A .(-1,0)B .(-∞,0)∪(1,2)C .(1,2)D .(0,2)D [由⎩⎨⎧x ≥0,f (x )<0,得0≤x <1.由f (x )为偶函数.结合图象(略)知f (x )<0的解集为-1<x <1.所以f (x -1)<0⇔-1<x -1<1,即0<x <2.] 二、填空题6.已知函数f (x )的图象如图2-7-6所示,则函数g (x )=log 2f (x )的定义域是________. 【导学号:31222057】图2-7-6(2,8] [当f (x )>0时,函数g (x )=log2f (x )有意义,由函数f (x )的图象知满足f (x )>0时,x ∈(2,8].]7.如图2-7-7,定义在[-1,+∞)上的函数f (x )的图象由一条线段及抛物线的一部分组成,则f (x )的解析式为________.图2-7-7f (x )=⎩⎪⎨⎪⎧x +1,-1≤x ≤0,14(x -2)2-1,x >0 [当-1≤x ≤0时,设解析式为y =kx +b ,则⎩⎨⎧ -k +b =0,b =1,得⎩⎨⎧k =1,b =1,∴y =x +1. 当x >0时,设解析式为y =a (x -2)2-1. ∵图象过点(4,0),∴0=a (4-2)2-1, 得a =14,即y =14(x -2)2-1. 综上,f (x )=⎩⎪⎨⎪⎧x +1,-1≤x ≤0,14(x -2)2-1,x >0.]8.设函数f (x )=|x +a |,g (x )=x -1,对于任意的x ∈R ,不等式f (x )≥g (x )恒成立,则实数a 的取值范围是________.[-1,+∞) [如图,作出函数f (x )=|x +a |与g (x )=x -1的图象,观察图象可知:当且仅当-a ≤1,即a ≥-1时,不等式f (x )≥g (x )恒成立,因此a 的取值范围是[-1,+∞).]三、解答题9.已知函数f (x )=⎩⎨⎧3-x 2,x ∈[-1,2],x -3,x ∈(2,5].(1)在如图2-7-8所示给定的直角坐标系内画出f (x )的图象;图2-7-8(2)写出f (x )的单调递增区间;(3)由图象指出当x 取什么值时f (x )有最值. [解] (1)函数f (x )的图象如图所示.4分(2)由图象可知,函数f (x )的单调递增区间为[-1,0],[2,5].8分 (3)由图象知当x =2时,f (x )min =f (2)=-1, 当x =0时,f (x )max =f (0)=3.12分 10.已知f (x )=|x 2-4x +3|. (1)作出函数f (x )的图象;(2)求函数f (x )的单调区间,并指出其单调性;(3)求集合M ={m |使方程f (x )=m 有四个不相等的实根}. [解] (1)当x 2-4x +3≥0时,x ≤1或x ≥3,∴f (x )=⎩⎨⎧x 2-4x +3,x ≤1或x ≥3,-x 2+4x -3,1<x <3,∴f (x )的图象为:4分(2)由函数的图象可知f (x )的单调区间是(-∞,1],(2,3],(1,2],(3,+∞),其中(-∞,1],(2,3]是减区间;[1,2],[3,+∞)是增区间.8分(3)由f (x )的图象知,当0<m <1时,f (x )=m 有四个不相等的实根,所以M ={m |0<m <1}.12分B 组 能力提升 (建议用时:15分钟)1.(2016·全国卷Ⅱ)已知函数f (x )(x ∈R)满足f (x )=f (2-x ),若函数y =|x 2-2x -3|与y =f (x )图象的交点为(x 1,y 1),(x 2,y 2),…,(x m ,y m ),则∑i =1mx i =( )A .0B .mC .2mD .4mB [∵f (x )=f (2-x ),∴函数f (x )的图象关于直线x =1对称.又y =|x 2-2x -3|=|(x -1)2-4|的图象关于直线x =1对称,∴两函数图象的交点关于直线x =1对称.当m 为偶数时,∑i =1mx i =2×m2=m ;当m 为奇数时,∑i =1mx i =2×m -12+1=m .故选B.]2.已知函数f (x )=若对任意的x ∈R ,都有f (x )≤|k -1|成立,则实数k 的取值范围为________.【导学号:31222058】⎝ ⎛⎦⎥⎤-∞,34∪⎣⎢⎡⎭⎪⎫54,+∞ [对任意的x ∈R ,都有f (x )≤|k -1|成立, 即f (x )max ≤|k -1|.因为f (x )的草图如图所示,观察f (x )=的图象可知,当x =12时,函数f (x )max =14, 所以|k -1|≥14,解得k ≤34或k ≥54.]3.已知函数f (x )的图象与函数h (x )=x +1x +2的图象关于点A (0,1)对称.(1)求函数f(x)的解析式;(2)若g(x)=f(x)+ax,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.[解](1)设f(x)图象上任一点坐标为(x,y),∵点(x,y)关于点A(0,1)的对称点(-x,2-y)在h(x)的图象上,∴2-y=-x+1-x+2,3分∴y=x+1x,即f(x)=x+1x.5分(2)由题意g(x)=x+a+1 x,且g(x)=x+a+1x≥6,x∈(0,2].7分∵x∈(0,2],∴a+1≥x(6-x),即a≥-x2+6x-1.9分令q(x)=-x2+6x-1,x∈(0,2],q(x)=-x2+6x-1=-(x-3)2+8,∴x∈(0,2]时,q(x)max=q(2)=7,故a的取值范围为[7,+∞).12分。
课时规范练11函数的图象

课时规范练11函数的图象基础巩固组1.函数f(x)={3x,x≤1,log13x,x>1,则y=f(x+1)的图象大致是()2.已知f(x)=2x,则函数y=f(|x-1|)的图象为()3.(2019山西吕梁一模,6)函数f(x)=x sin x+ln|x|的图象大致为()4.(2019湖南三湘名校联考一,4)函数f(x)=|x|ln|x|x2的图象大致为()125.函数f (x )的部分图象如图所示,则f (x )的解析式可以是( )A.f (x )=x+sin xB.f (x )=cosxxC.f (x )=x (x -π2)(x -3π2) D.f (x )=x cos x6.已知函数f (x )=x 2+e x -12(x<0)与g (x )=x 2+ln(x+a )的图象上存在关于y 轴对称的点,则a 的取值范围是( ) A.(√e)B.(-∞,√e )C.(√e √e)D.(-√e ,√e )7.(2019河北衡水同卷联考,7)下列函数中,其图象与函数y=log 2x 的图象关于直线y=1对称的是( )A.y=log 22x B.y=log 24x C.y=log 2(2x )D.y=log2(4x )38.(2019湖北省一月模拟,7)已知函数f (x )={x 2,x ≤0,-1x ,x >0,g (x )=-f (-x ),则函数g (x )的图象是( )9.(2019吉林实验中学模拟)函数f (x )=x+1x 的图象与直线y=kx+1交于不同的两点(x 1,y 1),(x 2,y 2),则y 1+y 2= .10.已知函数f (x )={-x 2+2x ,x ≤0,ln (x +1),x >0.若|f (x )|≥ax ,则a 的取值范围是 .综合提升组11.(2019河南郑州三模,5)我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象的特征.如函数f (x )=x 4|4x -1|的图象大致是 ( )12.已知f (x )={|lgx |,x >0,2|x |,x ≤0,则函数y=2f 2(x )-3f (x )+1的零点个数是 .13.(2019山东青岛二中期末)已知f (x )={-2x ,-1≤x ≤0,√x ,0<x ≤1,则下列函数的图象错误的是()414.(2019北师大实验中学模拟)如图,矩形ABCD 的周长为8,设AB=x (1≤x ≤3),线段MN 的两端点在矩形的边上滑动,且MN=1,当N 沿A →D →C →B →A 在矩形的边上滑动一周时,线段MN 的中点P 所形成的轨迹为G ,记G 围成的区域的面积为y ,则函数y=f (x )的图象大致为( )15.(2019福建双十中学模拟)设函数y=f (x+1)是定义在(-∞,0)∪(0,+∞)上的偶函数,在区间(-∞,0)上是减函数,且图象过点(1,0),则不等式(x-1)f (x )≤0的解集为 .创新应用组16.(2019安徽江淮十校联考)若直角坐标系内A ,B 两点满足:(1)点A ,B 都在f (x )图象上;(2)点A ,B 关于原点对称,则称点对(A ,B )是函数f (x )的一个“和谐点对”,(A ,B )与(B ,A )可看作一个“和谐点对”.已知函数f (x )={x 2+2x ,x <0,2ex ,x ≥0,则f (x )的“和谐点对”有( )A.1个B.2个C.3个D.4个17.如图,长方形ABCD的边AB=2,BC=1,O是AB的中点.点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为()参考答案课时规范练11函数的图象1.B将f(x)的图象向左平移一个单位即得到y=f(x+1)的图象.故选B.2.D f(|x-1|)=2|x-1|.当x=0时,y=2.可排除选项A,C.56当x=-1时,y=4.可排除选项B . 故选D .3.D 因函数f (x )为偶函数,可排除A,C;又f (1)=sin 1>0,可排除B,因而选D .4.A 因为f (-x )=|-x |ln |-x |x 2=|x |ln |x |x 2=f (x ),所以f (x )是偶函数,可得图象关于y 轴对称,排除C,D;当x>0时,f (x )=lnxx ,f (1)=0,f (12)<0,排除B,故选A .5.D 由函数的图象可知函数是奇函数,排除C;又f (x )=x+sin x=0,函数只有一个零点,所以A 不正确;函数的图象可知,x=0是函数的零点,而f (x )=cosxx ,x ≠0,所以B 不正确.故选D . 6.B 由已知得与函数f (x )的图象关于y 轴对称的图象的解析式为h (x )=x 2+e -x -12(x>0).令h (x )=g (x ),得ln(x+a )=e -x -12,作函数M (x )=e -x -12(x>0)的图象,显然当a ≤0时,函数y=ln(x+a )的图象与M (x )的图象一定有交点.当a>0时,若函数y=ln(x+a )的图象与M (x )的图象有交点,则ln a<12,则0<a<√e . 综上a<√e .故选B .7.B 设P (x ,y )为所求函数图象上的任意一点,它关于直线y=1对称的点是Q (x ,2-y ),由题意知点Q (x ,2-y )在函数y=log 2x 的图象上,则2-y=log 2x ,即y=2-log 2x=log 24x ,故选B . 8.A 因为g (x )=-f (-x ),所以g (x )图象与f (x )的图象关于原点对称,由f (x )解析式,作出f (x )的图象如图.7从而可得g (x )的图象为A .9.2 因为f (x )=x+1x =1x +1,所以f (x )的图象关于点(0,1)对称,而直线y=kx+1过(0,1)点,故两图象的交点(x 1,y 1),(x 2,y 2)关于点(0,1)对称,所以y 1+y22=1,即y 1+y 2=2. 10.[-2,0] 可画出|f (x )|的图象如图所示.当a=0时,|f (x )|≥ax=0恒成立, 所以a=0满足题意;当a>0时,在x<0时,|f (x )|≥ax=0恒成立,所以只需x>0时,ln(x+1)≥ax 成立.对比对数函数与正比例函数的增长速度发现,一定存在ln(x+1)<ax 的时刻,所以a>0不满足条件;当a<0时,在x>0时满足题意; 当x ≤0时,只需x 2-2x ≥ax 成立,即直线在抛物线下方,即a ≥x-2恒成立,则a ≥-2. 综上,a 的取值范围为[-2,0]. 11.D 根据题意,函数f (x )=x 4|4x -1|,则f (-x )=(-x )4|4-x-1|=x 4·4x|4x -1|,易得f (x )为非奇非偶函数,排除A,B;当x →+∞时,f (x )=x 4x -1→0,排除C .故选D .812.5 方程2f 2(x )-3f (x )+1=0的解为f (x )=1或1.作出y=f (x )的图象,由图象知零点的个数为5.13.D 在坐标平面内画出函数y=f (x )的图象,将函数y=f (x )的图象向右平移1个单位长度,得到函数y=f (x-1)的图象,因此A 正确;作函数y=f (x )的图象关于y 轴的对称图形,得到y=f (-x )的图象,因此B 正确;y=f (x )在[-1,1]上的值域是[0,2],因此y=|f (x )|的图象与y=f (x )的图象重合,C 正确;y=f (|x|)的定义域是[-1,1],且是偶函数,当0≤x ≤1时,y=f (|x|)=√x ,这部分的图象不是一条线段,因此选项D 不正确.故选D .14.D 由题意可知,点P 的轨迹为图中虚线所示,其中四个角均是半径为12的扇形.因为矩形ABCD 的周长为8,AB=x ,则AD=8-2x2=4-x ,所以y=x (4-x )-π4=-(x-2)2+4-π4(1≤x ≤3),显然该函数的图象是二次函数图象的一部分,且当x=2时,y max =4-π4∈(3,4),故选D .15.{x|x ≤0或1<x ≤2} 画出f (x )的大致图象如图所示.不等式(x-1)f (x )≤0可化为{x >1,f (x )≤0,或{x <1,f (x )≥0.由图可知符合条件的解集为{x|x ≤0或1<x ≤2}.16.B 作出函数y=x 2+2x (x<0)的图象关于原点对称的图象,看它与函数y=2e x (x ≥0)的图象的交点个数即可,观察图象可得交点个数为2,即f (x )的“和谐点对”有2个.17.B由题意可得f(π2)=2√2,f(π4)=√5+1,即f(π2)<f(π4),由此可排除C,D项;当3π4≤x≤π时,f(x)=-tan x+2x+4,可知x∈[3π4,π]时,f(x)的图象不是线段,可排除A项,故选B项.9。
福建专用2018年高考数学总复习课时规范练19函数y=Asin(ωx+φ)的图象及应用文新人教A版2

课时规范练19函数y=A sin(ωx+φ)的图象及应用基础巩固组1.将函数y=sin x的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得各点向π右平行移动个单位长度,所得图象的函数解析式是()10A.y=sin(2푥-π10)1 B.y=sin(2푥- π20)C.y=sin(2푥-π5)1 D.y=sin(2푥- π10)π2.已知函数f(x)=cos(휔푥+3)(ω>0)的最小正周期为π,则该函数的图象()πA.关于点(3,0)对称πB.关于直线x=对称4πC.关于点(4,0)对称πD.关于直线x=对称33.(2017湖南邵阳一模,文6)若将函数f(x)=sin 2x+cos 2x的图象向左平移φ(φ>0)个单位长度,所得的图象关于y轴对称,则φ的最小值是()π3ππ5πA. B. C. D.48884.π如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin(6푥+휑)+k.据此函数可知,这段时间水深(单位:m)的最大值为()A.5B.6C.8D.1015π11π5.(2017天津,文7)设函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,|φ|<π,若f(8)=2,f(8)=0,且f(x)的最小正周期大于2π,则()2πA.ω=,φ=312211πB.ω=,φ=-312111πC.ω=,φ=-32417πD.ω=,φ=〚导学号24190738〛324π6.若函数f(x)=2sin 2x的图象向右平移φ(0<휑<2)个单位长度后得到函数g(x)的图象,若π对满足|f(x1)-g(x2)|=4的x1,x2,有|x1-x2|的最小值为,则φ=()6πππ5πA. B. C. D.643127.ππ已知函数f(x)=sin(ωx+φ)(휔>0,|휑|<2)的部分图象如图所示,则y=f(푥+6)取得最小值时x的集合为()A.{푥|푥=푘π-π6,푘∈Z}B.{푥|푥=푘π-π3,푘∈Z}C.{푥|푥=2푘π-π6,푘∈Z}πD.{푥|푥=2푘π- 3,푘∈Z}〚导学号24190739〛8.函数y=sin x- 3cos x的图象可由函数y=2sin x的图象至少向右平移个单位长度得到.9.2已知函数y=g(x)的图象由f(x)=sin 2x的图象向右平移φ(0<φ<π)个单位长度得到,这两个函数的部分图象如图所示,则φ=.π10.(2017北京,文16)已知函数f(x)= 3cos(2푥- 3)-2sin x cos x.(1)求f(x)的最小正周期;ππ1(2)求证:当x∈[- 4]时,f(x)≥- .4,2〚导学号24190740〛综合提升组ππ11.(2017辽宁大连一模,文11)若关于x的方程2sin(2푥+6)=m在[0,2]上有两个不等实根,则m的取值范围是()A.(1, 3)B.[0,2]C.[1,2)D.[1, 3]32π12.已知函数f(x)=cos(2x+φ)的图象关于点(3,0)对称,若将函数f(x)的图象向右平移m(m>0)个单位长度后得到一个偶函数的图象,则实数m的最小值为.1π13.已知函数y=3sin(4).2푥-(1)用五点法作出函数的图象;(2)说明此图象是由y=sin x的图象经过怎么样的变化得到的.4〚导学号24190741〛创新应用组2π14.已知曲线C1:y=cos x,C2:y=sin(2푥+3),则下面结论正确的是()πA.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长6度,得到曲线C2πB.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长12度,得到曲线C21πC.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,26得到曲线C21πD.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,212得到曲线C2〚导学号24190742〛15.如图所示,某地夏天8—14时用电量变化曲线近似满足函数式y=A sin(ωx+φ)+b,ω>0,φ∈(0,π).(1)求这期间的最大用电量及最小用电量;(2)写出这段曲线的函数解析式.答案:11.B由题意,y=sin x的图象进行伸缩变换后得到y=sin x的图象,再进行平移后所得图象的21π1π[2(푥- 10)]=sin(20).故选B.函数为y=sin푥-2π푘ππ2.D由题意知ω=2,函数f(x)的对称轴满足2x+=kπ(k∈Z),解得x=2―(k∈Z),当k=136π时,x=,故选D.35。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时规范练11 函数的图象
基础巩固组
1.已知f(x)=2x,则函数y=f(|x-1|)的图象为()
2.(2017安徽蚌埠一模,文4)函数y=sin(x2)的图象大致是()
3.为了得到函数y=log2-的图象,可将函数y=log2x的图象上所有的点的()
A.纵坐标缩短到原来的,横坐标不变,再向右平移1个单位长度
B.横坐标缩短到原来的,纵坐标不变,再向左平移1个单位长度
C.横坐标伸长到原来的2倍,纵坐标不变,再向左平移1个单位长度
D.纵坐标伸长到原来的2倍,横坐标不变,再向右平移1个单位长度
4.(2017江西南昌模拟)函数y=的图象大致为()
〚导学号24190722〛5.已知函数f(x)=-x2+2,g(x)=log2|x|,则函数F(x)=f(x)·g(x)的大致图象为()
6.(2017浙江,7)函数y=f(x)的导函数y=f'(x)的图象如图所示,则函数y=f(x)的图象可能是()
〚导学号24190723〛
7.已知函数f(x)=x2+e x-(x<0)与g(x)=x2+ln(x+a)的图象上存在关于y轴对称的点,则a的取值范
围是()
A.-
B.(-∞,)
C.
D.-
8.已知函数f(x)(x∈R)满足f(x)=-f(2x),若函数y=|x2-2x-3|与y=f(x)图象的交点为
(x1,y1),(x2,y2),…,(x m,y m),则x i=()
A.0
B.m
C.2m
D.4m〚导学号24190724〛
9.(2017河南洛阳统考)已知函数f(x)=关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是.
10.(2017陕西师范附属二模)已知直线y=x与函数f(x)=的图象恰有三个公共点,则实数m的取值范围是.
11.已知定义在R上的函数f(x)=若关于x的方程f(x)=c(c为常数)恰有3个不同的实
数根x1,x2,x3,则x1+x2+x3=.〚导学号24190725〛
综合提升组
,则y=f(x)的图象大致为()
12.已知函数f(x)=
-
13.函数f(x)=|ln x|-x2的图象大致为()
〚导学号24190726〛14.已知f(x)=则函数y=2f2(x)-3f(x)+1的零点个数是.
15.(2017安徽淮南一模,文16)已知函数f(x)=
-
其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是.
创新应用组
16.(2017山东潍坊一模)已知定义在R上的奇函数f(x)满足f(x+2)=f(2-x),当x∈[0,2]
时,f(x)=-4x2+8x.若在区间[a,b]上,存在m(m≥3)个不同整数x i(i=1,2,…,m),满足-
|f(x i)-
f(x i+1)|≥72,则b-a的最小值为() 〚导学号24190727〛A.15 B.16
C.17
D.18
17.(2017广东、江西、福建十校联考,文12)已知函数f(x)=
-
--
当1<a<2时,则关
于x的方程f-=a的实根个数为()
A.5
B.6
C.7
D.8
答案:
1.D f(|x-1|)=2|x-1|.
当x=0时,y=2.可排除选项A,C.
当x=-1时,y=4.可排除选项B.
故选D.
2.D设f(x)=sin(x2),因为y=f(-x)=sin((-x)2)=sin(x2)=f(x),所以y=f(x)为偶函数,
所以函数y=f(x)的图象关于y轴对称,故排除A,C,当x=时,y=0,故排除B,故选D.
3.A y=log2-=log2(x-1log2(x-1).将y=log2x的图象上所有点的纵坐标缩短到原来的,横坐标不变,可得y=log2x的图象,再向右平移1个单位长度,可得y=log2(x-1)的图象,也即
y=log2-的图象.
4.D当0<x<1时,2x>0,ln x<0,∴y<0,图象在x轴的下方;当x>1时,2x>0,ln x>0,∴y>0,图象在x 轴的上方,当x→+∞时,y→+∞,故选D.
5.B易知函数F(x)为偶函数,故排除选项A,D;当x=时,F-·log2=-<0,故排除选项
C,选B.
6.D设导函数y=f'(x)的三个零点分别为x1,x2,x3,且x1<0<x2<x3.
所以在区间(-∞,x1)和(x2,x3)上,f'(x)<0,f(x)是减函数,
在区间(x1,x2)和(x3,+∞)上,f'(x)>0,f(x)是增函数,
所以函数y=f(x)的图象可能为D,故选D.
7.B由已知得与函数f(x)的图象关于y轴对称的图象的解析式为h(x)=x2+e-x-(x>0).
令h(x)=g(x),得ln(x+a)=e-x-,作函数M(x)=e-x-的图象,显然当a≤0时,函数y=ln(x+a)的图象与M(x)的图象一定有交点.
当a>0时,若函数y=ln(x+a)的图象与M(x)的图象有交点,则ln a<,则0<a<.
综上a<.故选B.
8.B由题意可知,y=f(x)与y=|x2-2x-3|的图象都关于直线x=1对称,所以它们的交点也关于直线x=1对称.
当m为偶数时,x i=2·=m;
当m为奇数时,x i=2·-+1=m,故选B.
9.(1,+∞)问题等价于函数y=f(x)与y=-x+a的图象有且只有一个交点,画出两个函数图象如图,结合函数图象可知a>1.
10.[-1,2)画出函数图象如图所示.
由图可知,当m=-1时,直线y=x与函数图象恰好有3个公共点,
当m=2时,直线y=x与函数图象只有2个公共点,故m的取值范围是[-1,2).
11.0函数f(x)的图象如图,方程f(x)=c有3个不同的实数根,
即y=f (x )与y=c 的图象有3个交点,易知c=1,且一根为0. 由lg |x|=1知另两根为-10和10,故x 1+x 2+x 3=0. 12.B 当x=1时,y=
-
<0,排除A;当x=0时,y 不存在,排除D;f -
-
<0,故选B .
13.C 由函数的定义域为x>0,可知排除选项A;当x>1时,f'(x )=
x=
-
,当1<x<2时,f'(x )>0,
当x>2时,f'(x )<0,即f (x )在(1,2)内单调递增,在(2,+∞)内单调递减,排除选项B,D,故选C . 14.5 方程2f 2
(x )-3f (x )+1=0的解为f (x )=
或1.作出y=f (x )的图象,由图象知零点的个数为5.
15.(3,+∞) 当m>0时,函数f (x )= -
的图象如图所示. ∵当x>m 时,f (x )=x 2-2mx+4m=(x-m )2+4m-m 2>4m-m 2,
∴要使得关于x 的方程f (x )=b 有三个不同的根,必须4m-m 2<m (m>0),
即m 2
>3m (m>0),解得m>3, 故m 的取值范围是(3,+∞).
16.D 由题意得f (x+2+2)=f (2-x-2)=f (-x )=-f (x ),即f (x+4)=-f (x ),
则f (x+8)=-f (x+4)=f (x ).
∴f (x )的周期为8,函数f (x )的图象如图所示.
∵f (-1)=-4,f (0)=0,f (1)=4,f (2)=0,f (3)=4,f (4)=0,……,|f (-1)-f (0)|=4,|f (0)-f (1)|=4,|f (1)-f (2)|=4,|f (2)-f (3)|=4,……,
=18,故b-a 的最小值为18,故选D .
17.B令x+-2=t,则f(t)=a,作出y=f(x)的函数图象如图所示.
由图可知,当1<a<2时,关于t的方程f(t)=a有3个解.
不妨设3个解分别为t1,t2,t3,且t1<t2<t3,
则-24<t1<-4,1<t2<2,2<t3<3,
当x+-2=t1,即x2-(2+t1)x+1=0,
∵-24<t1<-4,
∴Δ=(2+t1)2-4>0,
∴方程x+-2=t1有2解,
同理方程x+-2=t2有2解,x+-2=t3有2解,
∴当1<a<2时,关于x的方程f-=a有6解.故选B.。
