2011中考数学复习课件35直线与圆的位置关系(浙教版)
合集下载
浙教版九年级下册数学《3.1直线与圆的位置关系(3)》PPT课件

AE D F
O
B
C
G
做一做
2、如图,直线AB与⊙O相切于点C,射线AO交⊙O于点D
,E,连结CD,CE.找出图中的一对相似三角形,并说
明理由。
E O
F
D
A
C
B
若已知AC=4cm,⊙O的半径为3cm,能否求出图中其
它线段的长度?
做一做
3、先按要求操作:AB 为⊙O的直径,在⊙O上任取一点
C(不与A、B重合),过点C画⊙O的切线,过点A作过点C的
常用的辅助线是连接半径. 综合性较强,要联系许多其它图形的性质.
挑战自我
如图,在直角梯形ABCD中,∠B=90°,AD∥BC, ∠C= 30°,AD=1,AB=2.
试猜想在BC是否存在一点P,使得⊙P与线段CD、
AB都相切,如存在,请确定⊙P的半径.
A
D
B
30 C
切线的垂线,垂足为D,交BC的延长线于点E。连结AC。
E
根据上述操作及已知条件,在图中
D
找出一些相等的线段和角,并证明
C
你所得到的结论。
A
O
B
做一做
4、如图:已知PA,PB分别切⊙O于A,B两点,如果
∠P=60° ,PA=2,那么AB的长为__2___.
变式1: CD也与⊙O相切,切点为E.交PA于C点,交
杨林中学
汪水明
切线的判定定理: 经过半径的外端并且垂直这条半径的直线是圆的切线
这个定理不仅可以用来判定圆的切线,还可以依据它来画切线.
∵l⊥OA ∴l是⊙O的切线
A O
l
切线的判定方法有: ①直线与圆有唯一个公共点。
②直线到圆心的距离等于圆的半径。 ③切线的判定定理。
直线与圆的位置关系复习课[下学期]--浙教版
![直线与圆的位置关系复习课[下学期]--浙教版](https://img.taocdn.com/s3/m/94671e58d5bbfd0a78567339.png)
教学目标: 知识目标:
1.了解直线与圆的位置关系,能用数量关系判断直线与圆的位置 关系;
2.掌握切线的判定与切线的性质;
3.理解弦切角的概念,能够运用弦切角定理及推论进行角的计算;
4.理解并掌握圆幂定理的内容及图形的变化,并能运用定理进行 圆中比例线段的证明或计算. 能力目标:通过复习培养学生综合运用知识的能力. 情感目标:体会曲线型图形圆与三角形、四边形间的联系. 教学重点:切线的判定和性质的运用及圆中比例线段.
优游 优游
1.如图,AB是⊙O的直径,下列条件,哪一条能 够判定AT是⊙O的切线
(1)AB=3,AT=4,BT=5
B
(2)∠B=380, ∠TAC= 380
(3) ∠TAC= 300 , BC=√3AC (4)∠B= ∠T
CO
T
A
2.已知:直线L的解析式为y=m8 x+m(m为常 数,m≠0),点B(-4,3)在直线L上.
(1)求m的值;
(2)若⊙A的圆心为原点,半径为R,并且⊙ A与直线L有公共点,度求R的取值范围.
3.如图,AB是⊙O的直径,⊙O过AC的中点D, DE⊥BC,垂足为E.
(1)由这些条件,写出四个正确的结论(不添辅 助线).
(2)若∠ABC为直角,其它条件不变,除上述
结论外,再写两个结论,并画出图形.(也不添辅
点M作⊙O1,交⊙O于A,B两点,BA的延长 线交PN于Q点,求MQ:QN:PM的值.
MQ N A
P
O1
O
B
如图,在⊙ O中,弦AB和直径CD相交于P,M是 DC延长线的一点,MN是⊙ O的切线,N为切点. 已知AP=8,PB=6,PD=4,MC=6,求MN.
NA
MC O
1.了解直线与圆的位置关系,能用数量关系判断直线与圆的位置 关系;
2.掌握切线的判定与切线的性质;
3.理解弦切角的概念,能够运用弦切角定理及推论进行角的计算;
4.理解并掌握圆幂定理的内容及图形的变化,并能运用定理进行 圆中比例线段的证明或计算. 能力目标:通过复习培养学生综合运用知识的能力. 情感目标:体会曲线型图形圆与三角形、四边形间的联系. 教学重点:切线的判定和性质的运用及圆中比例线段.
优游 优游
1.如图,AB是⊙O的直径,下列条件,哪一条能 够判定AT是⊙O的切线
(1)AB=3,AT=4,BT=5
B
(2)∠B=380, ∠TAC= 380
(3) ∠TAC= 300 , BC=√3AC (4)∠B= ∠T
CO
T
A
2.已知:直线L的解析式为y=m8 x+m(m为常 数,m≠0),点B(-4,3)在直线L上.
(1)求m的值;
(2)若⊙A的圆心为原点,半径为R,并且⊙ A与直线L有公共点,度求R的取值范围.
3.如图,AB是⊙O的直径,⊙O过AC的中点D, DE⊥BC,垂足为E.
(1)由这些条件,写出四个正确的结论(不添辅 助线).
(2)若∠ABC为直角,其它条件不变,除上述
结论外,再写两个结论,并画出图形.(也不添辅
点M作⊙O1,交⊙O于A,B两点,BA的延长 线交PN于Q点,求MQ:QN:PM的值.
MQ N A
P
O1
O
B
如图,在⊙ O中,弦AB和直径CD相交于P,M是 DC延长线的一点,MN是⊙ O的切线,N为切点. 已知AP=8,PB=6,PD=4,MC=6,求MN.
NA
MC O
浙教版九年级数学直线和圆的位置关系ppt

一、知识的产生
直线与圆有几种位置关系?
1、相离(没有交点) 2、相交(两个交点)
3、相切(一个交点)
探 索
二.知识 的发展
判定直线L:3x +4y-12=0与圆 C:(x-3)2 + (y-2)2=4的位置关 系. 方法一 :代数法
方法二 :几何法
Y
代数法: 3x +4y-12=0 { (x-3)2 + (y-2)2=4
代数法:
Ax+By+C=0 由方程组 (x-a)2+(y-b)2=r2 mx2+nx+p=0(m≠ 0) 方程组有两解 △>0 方程组有一解 △=0 方程组无解 △<0
△= n2-4mp 相交 相切 相离
直线与圆的位置关系的判定
几何方法
直线与圆相离
直线与圆相切 直线与圆相交d>r d=rd<r四.知识的运用
kx y k 1 0 2 2 ( x 3) ( y 4) 4
消去y得:
(k2+1)x2-2(k2+5k+3)x+k2+10k+30=0 ( ※ ) ∴△=4(20k-21)=0
21 k 直 线 方 程 为21x 20 y 41 0 20
若直线斜率不存在,则直线方程为x=1
1 、 过 点 P ( 1 , -1 ) 的 直 线 L 与 圆
M:(x-3)2+(y-4)2=4 (1)、当直线和圆相切时,求切线 方程。 (2)、若直线的斜率为2,求直线被 圆截得的弦AB的长。
解:代数法 (1)若直线有斜率,设为k.则直 线方程为y+1=k(x-1), 即kx-y-k-1=0
直线与圆有几种位置关系?
1、相离(没有交点) 2、相交(两个交点)
3、相切(一个交点)
探 索
二.知识 的发展
判定直线L:3x +4y-12=0与圆 C:(x-3)2 + (y-2)2=4的位置关 系. 方法一 :代数法
方法二 :几何法
Y
代数法: 3x +4y-12=0 { (x-3)2 + (y-2)2=4
代数法:
Ax+By+C=0 由方程组 (x-a)2+(y-b)2=r2 mx2+nx+p=0(m≠ 0) 方程组有两解 △>0 方程组有一解 △=0 方程组无解 △<0
△= n2-4mp 相交 相切 相离
直线与圆的位置关系的判定
几何方法
直线与圆相离
直线与圆相切 直线与圆相交d>r d=rd<r四.知识的运用
kx y k 1 0 2 2 ( x 3) ( y 4) 4
消去y得:
(k2+1)x2-2(k2+5k+3)x+k2+10k+30=0 ( ※ ) ∴△=4(20k-21)=0
21 k 直 线 方 程 为21x 20 y 41 0 20
若直线斜率不存在,则直线方程为x=1
1 、 过 点 P ( 1 , -1 ) 的 直 线 L 与 圆
M:(x-3)2+(y-4)2=4 (1)、当直线和圆相切时,求切线 方程。 (2)、若直线的斜率为2,求直线被 圆截得的弦AB的长。
解:代数法 (1)若直线有斜率,设为k.则直 线方程为y+1=k(x-1), 即kx-y-k-1=0
新浙教版九年级数学下册第二章《直线与圆的位置关系(1)》优课件

置关系?为什么?
(1)r=2
(2)r= 2 2 (3)r=3
• 例2.如图,海中有一个小岛P,该岛四周12海 里内暗礁.今有货轮四由西向东航行,开始 在A点观测P在北偏东60°处, 行驶10海里 后到达B点观测P在北偏东45°处,货轮继续 向东航行.你认为货轮继续向东航行途中会 有触礁的危险吗?
北
• 如图,圆心O到直线l的距离为d与⊙O的半径为r
r ●O ┐d
相交
r ●O
d ┐ 相切
r ●O
d
┐ 相离
直线与圆的位置关系量化
r ●O ┐d
相交
• 直线和圆相交 n 直线和圆相切 n 直线和圆相离
r ●O
d ┐ 相切
nd < r;
nd = r;
nd > r;
r ●O
d
┐ 相离
例1. 在△ABC中,∠A=45°,AC=4,以C为 圆心,r为半径的圆与直线AB有怎样的位
2.1直线与圆的位置关系(1)
直线与圆的位置关系直线与圆的交点个 数可判定它们关系
直线与圆有两个公共点时,叫做直线与圆相交. 直线与圆有惟一公共点时,叫做直线与圆相切,这条直线叫
做圆的切线,这个公共点叫做切点.
直线与圆没有公共点时,叫做直线与圆相离.
●O
●O
●O
相交
相切
相离
直线与圆的位置关系量化
①r=4cm ②r=4.8cm ③r=6cm ④与斜边 AB只有一个公共点,求r的取值范围
3、圆心O到直线l的距离为d,⊙O半径为R,若d、
R是是方程x2﹣9x﹢20=0的两个根,则直线与
圆的位置关系是
,当d、R是方程
x2 ﹣ 4x ﹢ m = 0 的 两 根 , 且 直 线 与 ⊙O 相 切 , 则
(1)r=2
(2)r= 2 2 (3)r=3
• 例2.如图,海中有一个小岛P,该岛四周12海 里内暗礁.今有货轮四由西向东航行,开始 在A点观测P在北偏东60°处, 行驶10海里 后到达B点观测P在北偏东45°处,货轮继续 向东航行.你认为货轮继续向东航行途中会 有触礁的危险吗?
北
• 如图,圆心O到直线l的距离为d与⊙O的半径为r
r ●O ┐d
相交
r ●O
d ┐ 相切
r ●O
d
┐ 相离
直线与圆的位置关系量化
r ●O ┐d
相交
• 直线和圆相交 n 直线和圆相切 n 直线和圆相离
r ●O
d ┐ 相切
nd < r;
nd = r;
nd > r;
r ●O
d
┐ 相离
例1. 在△ABC中,∠A=45°,AC=4,以C为 圆心,r为半径的圆与直线AB有怎样的位
2.1直线与圆的位置关系(1)
直线与圆的位置关系直线与圆的交点个 数可判定它们关系
直线与圆有两个公共点时,叫做直线与圆相交. 直线与圆有惟一公共点时,叫做直线与圆相切,这条直线叫
做圆的切线,这个公共点叫做切点.
直线与圆没有公共点时,叫做直线与圆相离.
●O
●O
●O
相交
相切
相离
直线与圆的位置关系量化
①r=4cm ②r=4.8cm ③r=6cm ④与斜边 AB只有一个公共点,求r的取值范围
3、圆心O到直线l的距离为d,⊙O半径为R,若d、
R是是方程x2﹣9x﹢20=0的两个根,则直线与
圆的位置关系是
,当d、R是方程
x2 ﹣ 4x ﹢ m = 0 的 两 根 , 且 直 线 与 ⊙O 相 切 , 则
直线与圆的位置关系课件(第一课时)(浙教版)
应用:海中有一个小岛P,该岛四周12海里范 围内是一暗礁区.今有货轮自西向东航行,开 始在A点观测P在北偏东600方向, 行驶10海 里后到达B点观测P在北偏东450方向,若货轮 不改变方向继续向东航行.
P
60°
A
45°
B
例题1:已知点P是∠ABC的平分线上的 一点,⊙P与BC相切。求证:⊙P与AB 相切。
并视察发现d与r的不同数量关系对应相应的直 线与圆的位置关系。
把半径r与圆心与直线的距离d作比较,可以判断 直线与圆的位置关系!
直线与圆的位置关系:
r ●O ┐d
相交
• 直线和圆相交 直线和圆相切 直线和圆相离
r ●O
d ┐ 相切
r ●O d ┐ 相离
d < r; d = r; d > r;
(1)课内练习的第1、2题; (2)A组的第3题、第1题。
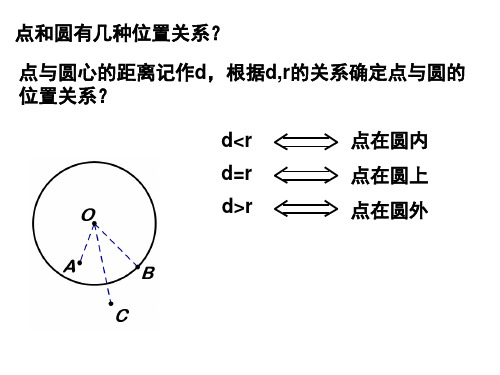
点和圆有几种位置关系?
点与圆心的距离记作d,根据d,r的关系确定点与圆的 位置关系?
d<r
点在圆内
d=r
点在圆上
d>r
点在圆外
千岛湖建兰中学
长大 河漠 落孤 日烟 圆直
天海 涯上 共升 此 时
直线与圆有几种位置关系?
想一想、画一画后填空: 1、过⊙O内一点P作直线l,则直线l与⊙O 的位置关系是 __相__交__ 2、过⊙O外一点P作直线l,则直线l与⊙O 的位置关系是_相__交__、__相__切__或_ 相离 3、过⊙O上一点P作直线l,则直线l与⊙O 的位置关系是 __相__切__或__相__交
4、过⊙O外两点A、B作直线l,则直线l与
⊙O的位置关系是_相__交__、__相_切__或_ 相离
如图,O为直线L外一点,OT⊥L,且OT=d.请以 O为圆心,以任意长为半径画圆.所画的圆与直 线L有什么位置关系?
九年级数学下册:第三章直线与圆、圆与圆的位置关系复习课件(浙教版)

∴AD=1 , AO=2 ∴BO=8
∴t=8 2=4s时,⊙O与 AC相切
②当圆心O在BC上时 作OE⊥ AC于E
∵ OE=r= 3 时⊙O与 AC相切
此时,得CO=AO=2 点O移动距离为22
B
∴t=22 2=11s时,⊙O与 AC相切
∴t = 4s 或 11s 时, ⊙O与 AC相切
A
X
2X D O
A
B
OC
10
探究1 如图, ⊙O的半径为 3 cm,正三角形的边长为10 cm, 圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为 t(s) 问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?
A
BO
10
C
探究1 如图, ⊙O的半径为 3 cm,正三角形的边长为10 cm, 圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为 t(s) 问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
∴AD=1 , AO=2
∴BO=8
∴t=8 2=4s时,⊙O与 AC相切
②当圆心O在BC上时
A
X
2X D O
B
C
10
探究1 如图, ⊙O的半径为 3 cm,正三角形的边长为10 cm, 圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为 t(s) 问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?
A
B
C
10
探究1 如图, ⊙O的半径为 3 cm,正三角形的边长为10 cm, 圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为 t(s) 问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
∴t=8 2=4s时,⊙O与 AC相切
②当圆心O在BC上时 作OE⊥ AC于E
∵ OE=r= 3 时⊙O与 AC相切
此时,得CO=AO=2 点O移动距离为22
B
∴t=22 2=11s时,⊙O与 AC相切
∴t = 4s 或 11s 时, ⊙O与 AC相切
A
X
2X D O
A
B
OC
10
探究1 如图, ⊙O的半径为 3 cm,正三角形的边长为10 cm, 圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为 t(s) 问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?
A
BO
10
C
探究1 如图, ⊙O的半径为 3 cm,正三角形的边长为10 cm, 圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为 t(s) 问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
∴AD=1 , AO=2
∴BO=8
∴t=8 2=4s时,⊙O与 AC相切
②当圆心O在BC上时
A
X
2X D O
B
C
10
探究1 如图, ⊙O的半径为 3 cm,正三角形的边长为10 cm, 圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为 t(s) 问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?
A
B
C
10
探究1 如图, ⊙O的半径为 3 cm,正三角形的边长为10 cm, 圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为 t(s) 问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
直线与圆的位置关系复习课[下学期]--浙教版
![直线与圆的位置关系复习课[下学期]--浙教版](https://img.taocdn.com/s3/m/1938acb252ea551810a687e6.png)
TPM目视管理的推行方法与技巧1.目视管理颜色的使用在很多企业的安全管理工作中,通常用颜色来刺激人的视觉,从而达到警示的目的。 (1)红色——防火、停止、禁止、高度危险的基本色。 如防火标志、消防栓、灭火器、火灾报警器、紧急停止开关、禁止通行、易燃易爆危险品等。 (2)黄色——引起注意的基本色。 如用于标识有冲撞、坠落、易滑倒的地方;吊车、堆高机、卡车、叉车、有冲撞可能的柱子、楼梯外缘、电线的防护具、路障等。 为了衬托黄色,一般以黑色为底色。 目视管理(3)蓝色——勿动的基本色,如除了责任人外,其他人不许随便操作。 (4)白色——基本色,如通道线、转向等。 (5)黑色——用来标识文字、记号和箭头等。 2.实施透明化管理在5S管理活动中,整理、整顿、清扫做得最差的地方,往往是看不到的地方,如藏在铁架或设备护盖背后的部分。 此时,可以利用目视管理,例如,取下护盖便于透明化,或在外部护盖上加装视窗,就可以看到里面的电气控制盘等。 3.状态视觉化如在电风扇上绑布条,可以了解其送风状况;将配水管的一部分使用透明管道,并装上浮标,从而进行目视管理并做好水流管理。 4.使用看板看板的主要要求如下。 (1)板面采用线条或图文分割,做到条理清晰。 (2)主次分明,重点突出。 (3)尽量用量化的数据和直观的图形,形象地说明问题。 (4)尽量用不同颜色的箭头标识动态信息。 (5)适当采用卡通、漫画的形式,目的是活跃版面。 5.标志的使用(1)指示性标志指示性标志是指依据包装物内商品的特性,指示储运过程中的作业人员进行安全、合理的操作的图像及文字。 (2)TPM设备管理咨询公司提出目视管理危险性标志。 它是用来表明包装物内的商品属于哪一类危险品及危险程度的标志,通常用图像和文字来表示。 其作用主要是:警示物流作业人员,加强必要的安全防护措施,保证作业过程中人、财、物的安全。 应将其贴在醒目的位置。 (3)环保标志又称为环境标志、生态标志,是一种反映环保意识的商品包装标志。 (4)目视管理质量认证标志,是认证机构设计并发布的一种专用标志,用以表明该产品已达到某一特定标准或技术规范。
浙教版九年级下册 3.1直线和圆的位置关系 课件

d=r
当直线与圆的位置关系是相交时,
d<r
知识梳理:
直线和圆的 位置关系
图形
公共点 公共点 d 与 r 直线 个数 名称 的关系 名称
相离 相切 相交
没有
d>r
一个 切点 d=r 切线
两个
d< 割线 r
练一练!
1、已知圆的直径为13cm,如果直线和圆心的 距离分别为(1)d=4.5cm (2)d=6.5cm (3)d=8cm, 那么直线和圆有几个公共点? 为什么? 2、已知圆心和直线的距离为4cm,如果圆和 直线的关系分别为以下情况,那么圆的半径 应分别取怎样的值? (1)相交;(2)相切;(3)相离。
例1;
▪ 1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
以点C为圆心作圆,当半径为多长
时,AB与⊙C相切?
A D
┐
C
B
例、在Rt△ABC中,∠C=900,AC=3cm,
(1)B以CA=为4c圆m心. ,3cm为半径的圆与直线BC的位置关系是
;
相切
以A为圆心,2cm为半径的圆与直线BC的位置关系是
d=r 当
时,直线与圆的位置关系是相切
d<r 当
时,直线与圆的位置关系是相交
想一想!
如果已知直线l与圆的位置关系分别是相离、相切、相 交时,圆心O到直线l的距离d与圆的半径r有什么关系?
r
o
d
l
r
o
d
l
o
rd
l
设圆心到直线的距离为d,圆的半径为r:
当直线与圆的位置关系是相离时,
d>r
当直线与圆的位置关系是相切时,
有触礁的危险吗?北
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
类型之一 直线与圆的位置关系的判定 青岛] [2010青岛]如图 青岛 如图35-2,在Rt△ABC中,∠C= 90°, , △ 中 ° 为圆心, ∠B= 30°,BC=4 cm,以点 为圆心,以2 cm的长为半径 ° ,以点C为圆心 的长为半径 作圆, 作圆,则⊙C与AB的位置关系是 ( B) 与 的位置关系是 A.相离 B.相切 相离 相切 C.相交 D.相切或相交 相交 相切或相交
∴ADDB=100.设AD=x,DB=y, 设 , 则xy=100. 由⊙O是△ABC内切圆及切线长定理得 是 内切圆及切线长定理得 AC=x+4,BC=y+4, ∴(x+y)2=(x+4)2+ , 解得x+y=21,即AB的长为 的长为21. 解得 即 的长为 点悟】解三角形内切圆问题,主要是切线长定理的应用, 【点悟】解三角形内切圆问题,主要是切线长定理的应用,解决此类问 常转化到直角三角形中,利用勾股定理列方程来求解. 题,常转化到直角三角形中,利用勾股定理列方程来求解
巩固练习:
A 1、如图,△ABC中,∠A=55度,I是内心 如图, ABC中 A=55度 112.5 BIC=————度 则,∠BIC=————度。
I C A
B
2、如图,△ABC中,∠A=55度, A=55度 如图, ABC中 其内切圆切△ 其内切圆切△ABC 于D、E、F, 67.5 FDE=————度 则∠FDE=————度。
2.圆的切线 圆的切线
性质定理: 的半径. 性质定理:圆的切线垂直于经过切点的半径 性质推论1:经过圆心且垂直于切线的直线必经过切点. 性质推论 :经过圆心且垂直于切线的直线必经过切点 性质推论2:经过切点且垂直于切线的直线必经过圆心. 性质推论 :经过切点且垂直于切线的直线必经过圆心 规律: 规律: (1)当直线与圆的公共点已知时,连半径证垂直; )当直线与圆的公共点已知时,连半径证垂直; (2)当直线与圆的公共点未知时,作垂直证直线到圆心的距离等于 )当直线与圆的公共点未知时, 圆的半径; 圆的半径; (3)连接圆心和切点,构造直角三角形解题 )连接圆心和切点,构造直角三角形解题.
2.圆的切线 圆的切线 判定定理: 这条半径的直线是圆的切线. 判定定理:经过半径的 外端 并且 垂直于 这条半径的直线是圆的切线 注意:判定一条直线是圆的切线的方法还有: 注意:判定一条直线是圆的切线的方法还有: (1)与圆有唯一公共点的直线是圆的切线; )与圆有唯一公共点的直线是圆的切线; (2)圆心到直线的距离等于该圆的半径,则这条直线是圆的切线 )圆心到直线的距离等于该圆的半径,则这条直线是圆的切线. 性质定理: 的半径. 性质定理:圆的切线垂直于经过切点的半径 性质推论1:经过圆心且垂直于切线的直线必经过切点. 性质推论 :经过圆心且垂直于切线的直线必经过切点 性质推论2:经过切点且垂直于切线的直线必经过圆心. 性质推论 :经过切点且垂直于切线的直线必经过圆心 规律: 规律: (1)当直线与圆的公共点已知时,连半径证垂直; )当直线与圆的公共点已知时,连半径证垂直; (2)当直线与圆的公共点未知时,作垂直证直线到圆心的距离等于 )当直线与圆的公共点未知时, 圆的半径; 圆的半径; (3)连接圆心和切点,构造直角三角形解题 )连接圆心和切点,构造直角三角形解题.
解:∵DE是⊙O的直径, ∴∠DBE=90°. ∵∠ABD=30°, ∴∠EBO=∠DBE-∠ABD=90°-30°=60°. ∵AC是⊙O的切线, ∴∠CAO=90°. 又∠AOC=2∠ABD=60°, ∴∠C=180°-∠AOC-∠CAO=180°-60°-90°=30°. 【点悟】“圆的切线垂直于过切点的半径”是构造直角三角形进行证明和 计算的常用方法.
B
F E
D
C
三、特殊三角形外接圆、内切圆半径的求法: 特殊三角形外接圆、内切圆半径的求法:
直角三角形外接圆、内切圆半径的求法
c O
B
R= — 2
c
a I A b C
a+ba+b-c r = ————
2
常用公式:如图 内切于△ 常用公式:如图35-1,⊙I内切于△ABC,切点分别为 、E、F.△ABC ⊙ 内切于 ,切点分别为D、 、 △ 的 三边长为BC=a,AC=b,AB=c,⊙I的半径为 的半径为r. 三边长为 , , , 的半径为
【解析】运用直径所对的圆周角等于90°得∠EBD=90°, 解析】运用直径所对的圆周角等于 ° ° 结合已知的∠ 结合已知的∠ABD=30°可求∠EBO=60°. °可求∠ ° 运用切线的性质知∠ 运用切线的性质知∠CAO=90°,由同弧所对的圆心角与圆 ° 由同弧所对的圆心角与圆 周角的关系得∠AOC=2∠ABD=60°,易求∠C=30° 周角的关系得∠ ∠ ° 易求∠ ° 易求
类型之三 切线的判定 如图35-4,AB是⊙O的直径,BC⊥AB于点 连接 的直径, ⊥ 于点B.连接 如图 , 是 的直径 于点 连接OC交 交 于点E, 于点G. ⊙O于点 ,弦AD∥OC,弦DF⊥AB于点 于点 ∥ , ⊥ 于点 的中点; (1)求证:点E是BD的中点; )求证: 是 的中点 的切线; (2)求证:CD是⊙O的切线; )求证: 是 的切线 的半径为5, 的长. (3)若sin∠BAD= ,⊙O的半径为 ,求DF的长 ) ∠ 的半径为 的长
三角形的外接圆: 三角形的外接圆:
A
O B C
三角形的内切圆: 三角形的内切圆:
A
I
BCΒιβλιοθήκη 三角形的外心与内心1、①外心是指三角形外接圆的圆心; 外心是指三角形外接圆的圆心 外接圆的圆心; 内切圆的圆心。 ②内心是指三角形内切圆的圆心。 内心是指三角形内切圆的圆心
实质
性质
三角形的 三角形各边垂直 到三角形 外心 平分线的交点 各顶点的 距离相等 三角形的 三角形各内角角 到三角形 内心 平分线的交点 各边的距 离相等
(1)当直线与圆的公共点已知时,连半径证垂直; )当直线与圆的公共点已知时,连半径证垂直; (2)当直线与圆的公共点未知时,作垂直证直线到 )当直线与圆的公共点未知时, 圆心的距离等于圆的半径; 圆心的距离等于圆的半径; (3)连接圆心和切点,构造直角三角形解题 )连接圆心和切点,构造直角三角形解题.
【解析】(1)如图,当正方形EFGD的顶点F在⊙M上时,则 GM=MD=12 ,设正方形边长为a ,圆的半径为r,连接EM,则由 MD2+ED2= ,得 ,
(2)连接 、EB, )连接AE、 , 是半圆M的直径 ∵AB是半圆 的直径, 是半圆 的直径, ∴∠AEB为直角 又ED⊥AB, 为直角.又 ∴∠ 为直角 ⊥ , ∴△AED∽△EBD, ∽ , ∴ADED=EDDB, , ∴ED2=ADDB.
2.圆的切线 圆的切线 判定定理: 这条半径的直线是圆的切线. 判定定理:经过半径的 外端并且 垂直于 这条半径的直线是圆的切线 注意:判定一条直线是圆的切线的方法还有: 注意:判定一条直线是圆的切线的方法还有: (1)与圆有唯一公共点的直线是圆的切线; )与圆有唯一公共点的直线是圆的切线; (2)圆心到直线的距离等于该圆的半径,则这条直线是圆的切线 )圆心到直线的距离等于该圆的半径,则这条直线是圆的切线.
类型之二 切线的性质的运用 已知如图35-3,AB是⊙O的直径,CA与⊙O相切于点 , 的直径, 与 相切于点A, 已知如图 , 是 的直径 相切于点 连接CO交⊙O于点 ,CO的延长线交⊙O于点 连接 、 于点D, 的延长线交⊙ 于点 连接BE、 于点E.连接 连接 交 于点 的延长线交 BD,∠ABD=30°,求∠EBO和∠C的度数 的度数. , ° 和 的度数
【解析】 (1)可利用同圆中,圆心角若与圆周角相等,则圆周角所对的弧等于圆心角 所对的弧的2倍,求解证明. (2)连接OD,证OD⊥DC,可通过证△DOC≌△BOC得到. (3)在Rt△ADG中,由sin∠BAD=,令DG=4x,AD=5x得出AG=3x,再在 Rt△ODG中运用勾股定理求出x的值,从而 得到DF的长. 解:(1)证明:∵AD∥OC,∴∠A=∠COB, ∴DB=2BE,∴DE=BE,即点E是BD的中点.
(2)证明:连接OD. 证明:连接 证明 由(1)知∠DOE=∠BOE. 知 ∠ 在△COD和△COB中,CO=CO,OD=OB, 和 中 , ∴△DOC≌△BOC, ≌ , ∴∠CDO=∠B. ∴∠ ∠ 又∵BC⊥AB, ⊥ ∴∠CDO=∠B=90°, ∴∠ ∠ ° 的切线. 即CD是⊙O的切线 是 的切线 (3)在△ADG中,∵DF⊥AB, 在 中∵ ⊥ ∴sin A=DGAD= , 设DG=4x,AD=5x,∴AG=3x. ∴ ∵⊙O的半径为 的半径为5,由 又∵⊙ 的半径为 由OD2=DG2 x2=0(舍去 舍去), 舍去
3.三角形的内切圆 三角形的内切圆 定义:和三角形各边都相切的圆叫做三角形的内切圆, 定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心 叫做三角形的内心,这个三角形叫做圆的外切三角形. 叫做三角形的内心,这个三角形叫做圆的外切三角形 易混点: 易混点:三角形的内心和外心 不要混淆, 不要混淆,列表比较 如下: 如下:
一:点与圆的位置关系
如图34-1,点与圆的位置关系有三种,设点到圆心 的距离为 , 点与圆的位置关系有三种, 的距离为d, 关 系:如图 点与圆的位置关系有三种 设点到圆心O的距离为 圆的半径为r. 圆的半径为 (1)点在圆的外部:点到圆心的距离 )点在圆的外部: 圆的半径, 圆的半径,OP1=d>r; > ; (2)点在圆上:点到圆心的距离 )点在圆上: 圆的半径, 圆的半径,OP2=d=r; ; (3)点在圆的内部:点到圆心的距离 )点在圆的内部: 圆的半径, 圆的半径,OP3=d<r. <
如图35-5,AB为半圆的直径,C是半圆弧上一点,正方形 , 为半圆的直径, 是半圆弧上一点 正方形DEFG的一 是半圆弧上一点, 如图 为半圆的直径 的一 在直径AB上,另一边 的内切圆圆心O,且点E在半圆 边DG在直径 在直径 上 另一边DE过△ABC的内切圆圆心 ,且点 在半圆 过 的内切圆圆心 弧上,( )若正方形的顶点F也在半圆弧上 也在半圆弧上, 弧上,(1)若正方形的顶点 也在半圆弧上,则半圆的半径与正方形边 ,( 长的比是 ;(2)若正方形 ( )若正方形DEFG的面积为 的面积为100,且△ABC的内切圆 的面积为 , 的内切圆 . 半径r=4,则半圆直径 则半圆直径AB= 半径 则半圆直径
