数字电子技术基础I(B)

合集下载

数字电子技术基础第一章逻辑代数与EDA技术的基础知识

(2) 十-二转换：降幂比较法 — 要求熟记 20 ∼ 210 的数值。
20 21 22 23 24 25 26 27 28 29 210 1 2 4 8 16 32 64 128 256 512 1024
(2) 十-二转换：降幂比较法 ( 157 )10 ( 10011101)2
157 ) 128 27
任意(N)进制数展开式的普遍形式： D ki N i
ki — 第 i 位的系数 N i — 第 i 位的权
4. 几种常用进制数之间的转换 (1) 二-十转换：将二进制数按位权展开后相加
( 101. 11 )2 1 22 0 21 1 20 1 21 1 22 4 1 0. 5 0. 25 (5. 75)10
1、数字电路与模拟电路相比主要有下列优点：（1）数字电路是以二值数字逻辑为基础的，只有0和 1两个基本数字，易于用电路来实现。（2）由数字电路组成的数字系统工作可靠，精度较高，抗干扰能力强。
（3）数字电路不仅能完成数值运算，而且能进行逻辑判断和运算，这在控制系统中是不可缺少的。
（4）数字信息便于长期保存，比如可将数字信息存入磁盘、光盘等长期保存。
十-二转换：方法二
※整数部分的转换：除基取余法
用目标数制的基数（R=2）去除十进制数，第一次相
除所得余数为目的数的最低位K0，将所得商再除以基数，
反复执行上述过程，直到商为“0”，所得余数为目的数
的最低位。
( 157 )10 =(？)2
※小数部分的转换：乘基取整法
用小数乘以目标数制的基数（R=2），第一次相乘结
编码：用二进制数表示文字、符号等信息的过程。二进制代码：编码后的二进制数。
二-十进制代码：用二进制代码表示十个数字符号 0 ~ 9，又称为 BCD 码（Binary Coded Decimal ）。 8421码 2421码 5211码

《数字电子技术基本教程第》阎石习题详解

vI/V vO/V
51Ω 1.5KΩ 100KΩ ∞
0
0
0 不定
5
5
5 不定
图 2.44 习题 2-3 电路图
图 2.45
3.16 答案：
RP（m a x）
VCC VOH nIOH IL
5 3.6 2 0.1103 3 20106 5.4K
RP（m in）
VOH mI IH

10106
5 3.5 3 1106
6

41.7K
RP（m in）
VDD VOL IOL(max) mI IL

5 0.3 4103 1106
6
1.2K
图 2.53 习题 2-17 图
3.13 答案：
图 2.44 习题 2-3 电路图
vI1/V 悬空接地 51Ω 3.6 50KΩ 0.2 vI2/V 1.4V 0V 0V 1.4V 1.4V 0.2V
2.7 答案：
0
1
1
0
0
1
高阻态
0 0
1
2.8 答案： 1
1 0
0
1
0 0
1
2.9 答案：
图 2.48 习题 2-9 图
2.12 答案：
F A B AB AB 1 B 1 B B
最多可以接10个同样的门电路
图 2.55 习题 2-19 图
3.20 答案：
IOH(max) 0.4mA
IIH(max) 20 A
IOL(max) 8mA IIH(max) 0.4mA
2nIIH(max) IOH(max)
n
IOH (max) 2I IH(max)

数字电子技术基础(第3版)练习答案

第1章数字电路基础1.1 (1001010)2=1×26+1×23+1×21=(74)10(111001)2=1×25+1×24+1×23+1×20=(57)10 1.2 (54)10=(110110)2 (47)10=(101111)2 5427 13 6 3 1 01……MSB 10 1 1 0……LSB2 4723 11 5 2 1 01……MSB 01 1 1 1……LSB1.3 (58A)16 =(0101 1000 1010)2=1×210+1×28+1×27+1×23+1×21=1024+256+128+10=(1418)10或(58A)16=5×162+8×161+10×160=(1418)10 (CE)16 =(1100 1110)2=27+26+14=128+64+14=(206)10 =(0010 0000 0110)8421BCD 1.4 a 1.5 c 1.6 c 1.7 (×) 1.8 (×) 1.9 (√)1.10 ① 数字信号：在幅值上，时间上离散的（间断的、不连续的脉冲）信号． ② 数字电路：产生、处理、传输、变换数字信号的电路称为数字电路．③ 数字电路的特点：a ）电路处于开关状态. 与二进制信号要求相一致，这两个状态分别用0和1两个数码表示；b ）数字电路的精度要求不高，只要能区分出两种状态就可以；c ）数字电路研究的问题是逻辑问题，一为逻辑分析，是确认给定逻辑电路的功能，二为逻辑设计，是找到满足功能要求的逻辑电路；d ）研究数字电路的方法是逻辑分析方法，其主要工具是逻辑代数．有代数法和卡诺图法等；e ）数字电路能进行逻辑运算、推理、判断，也能进行算术运算．算术运算也是通过逻辑运算实现的．1.11 ① 位置计数法：将表示数值的数码从左到右按顺序排列起来．它有三个要素a ）基数R ，是指相邻位的进位关系，十进制R =10，即逢十进一，二进制R =2，即逢二进一．b ）数码：表示数字的符号，十进制k i 从0~9共十个．二进制k i 是0和1，十六进制k i 从0~9~A~F 共十六个．c ）位权：数码处于不同位置代表不同的位权，用R i表示．以小数点前从右到左为i 的位号分别为0、1、2、3…，小数点后从左到右i 的位号从–1，–2，–3…来确定R i．② 按权展开式是将任何进制数表示为十进制数值公式，是系数乘位权的集合，即(N )10=i i i k R ∞=-∞⨯∑． 1.12 ① (3027)10=3×103+2×101+7×100② (827)=8×102+2×101+7×100③ (1001)2=1×23+1×20④ (11101)2=1×24+1×23+1×22+1×20⑤ (273)16=2×162+7×161+3×160⑥ (4B5)16=4×162+11×161+5×1601.13 ① (6)10=(110)2② (13)=(1101)2 ③ (39)10=(100111)2 ④ (47)10=(101111)2 1.14 ① (1011)2=(11)10② (110101)2=(53)10③ (4A)16=4×161+10×160=(74)10④ (37)16 =3×161+7×160=(55)101.15 ① (1010 1101)2=(010 101 101)2=(255)8=(1010 1101)2=(AD)16② (100101011)2=(100 101 011)2=(453)8 =(0001 0010 1011)2=(12B)16 ③ ()2=(010 110 001 010)2=(2612)8 =(0101 1000 1010)2=(58A)16 1.16 ① (78)16=(0111 1000)2=(1111000)2 ② (EC)16=(1110 1100)2=(1110 1100)2 ③ (274)16=(0010 0111 0100)2=(1001110100)2注：从1.15~1.16均用分组方法，即二进制3位一组可表示1位八进制数；二进制4位一组可表示1位十六进制数．1.17 A =(1011010)2；B =(101111)2； C =(1010100)2；D =(110)2 （1）① A +B =(10001001)2② A –B =(101011)2 1011010 + 101111 100010011011010 – 101111 101011 ③ C ×D =(111111000)2④ C ÷D =(1110)2 1010100× 110 0000000 1010100 + 1010100 1111110001110 110 1010100 110 1001 110 0110110 0（2）A=(1011010)2=(90)10B=(101111)2=(47)10①A+B=(137)10=(10001001)2②A–B=(43)10=(101011)2C=(1010100)2=(84)10D=(110)2=(6)10③C×D=(504)10=(111111000)2这说明十进制四则运算的法则在二进制四则运算中也完全适用，对其它进制也一样．1.18 ① [0]8421BCD=(238)10② [10001]8421BCD=(7951)10③ [0]8421BCD=(640)101.19 ①逻辑函数：反映因果关系的二值逻辑表达式．原因（条件）为逻辑自变量，结果为逻辑因变量，它们都只有两种状态0和1，用以反映存在不存在，成立不成立，所以它们之间的关系称为（二值）逻辑函数．②与逻辑：表明所有的条件都具备结果才会发生这样的基本逻辑关系为“与”逻辑（逻辑乘）．用式Y=A·B·C…表示．如学生成绩合格及不犯罪与能否毕业的关系即为与逻辑．③或逻辑关系：表明诸多条件中只要有1个以上具备结果就会发生，用Y=A+B+…表示．如去银行办理业务（储蓄），持存款证或持银行卡都可以办理．④非逻辑：是否定的因果关系，即条件具备结果就不能发生，用Y=A表示．如：征兵体检“有病”和“入伍”的关系就是非逻辑．“有病”存在，“入伍”就被否定了，有病不能入伍．1.21 由真值表可以写出最小项与或表达式．方法是将使函数Z为1的几种情况下输入变量的取值组合写成乘积项（变量取值为0写反变量因子，变量取值为1写原变量因子），然后将各乘积项相加，得Z=A B C+A B C+A BC+A B C+A B C1.23Z a=AB AB=A B+A B(摩根定理) =A⊕BZ b=B C AB+= (B⊕C)·AB=(BC+B C)AB=ABC1 1 1 0 1 1 1 1 1 11.24 见教材原文1.5节 1.25 a ）Z a =m (0, 2, 3, 5, 6) =A B C +A B C +A BC +A B C +AB C =A C +B C +A B +A B Cb ）Z b =m (0, 2, 7, 13, 15, 8, 10)=A B C D +A B C D +A BCD +A B C D +A B C D +AB C D +ABCD=B D +BCD +ABD1.26 （1）Z =A B +B +A B =A B +B =A +B （2）Z =A B C +A +B +C =A B C +A B C ++ =A B C +A B C =1（3）Z =AB ABC AB AB C +=++ =11AB AB C C +=+= （4）Z =A B CD +ABD +A C D=AD (B C +B +C ) =AD (C +B +C ) =AD ·1 =AD（5）Z =(A +B )(A CD +AD BC +)A B=(A +B )·A B ·(A CD +AD BC +) =0注：(A +B )A B =A A B +A B ·B =0（6）Z =AC (C D +A B )+BC (B AD CE ++)=0+BC ·(B +AD )·CE =BC (C +E )(B +AD ) =(BC E )(B +AD ) =BC E +BC E AD =BC E （7）Z =ABC +AC D +A C +CD=C (AB +A D +D )+A C =C (D +A )+A C =AC +CD +A C =A +CD（8）Z =A +B C +·(A +B +C )(A +B +C )=A +B C (A +B +C )(A +B +C ) ←展开=A +(A B C +B C )(A +B +C )←展开、吸收=A +B C（9）Z =B (A D +A D )+B (AD AD ABCE BC +++)=B (A D +A D )+B (A D +A D ) =A D +A D =A ⊕D（10）Z =AC +A C D +A B E F +B (D ⊕E )+BD E +B D E +BF=A (C +C D )+A B E F +BD E +B D E +BF =AC +AD +F (A B E +B )+B D E +BD E=AC +AD +A E F +BF +BD E +B D E1.27 求反函数Z 和对偶函数Z' （1）Z =AB +C （2）Z =(A +BC )C D Z =(A +B )·C Z =A ·(B +C )+C +DZ'=(A +B )·C Z' =A ·(B +C )+C +D（3）Z =()(+)A C A B AC BC ++ Z =(AC AB A C +++)·(B +C ) Z'=(AC AB A C +++)·(B +C )（4）Z =A D +AC +BCD +CZ =(A +D )·A C +·(B C D ++)·C Z'=(A +D )·A C +·(B C ++D )·C （5）Z =(AC +BD )ABC CD +Z =(A +C )·(B +D )+()()A B C C D +++ Z'=(A +C )·(B +D )+()()A B C C D +++ 1.28 用填卡诺图方法写最小项表达式（1）F 1=A BC +AC +B C =m (1, 3, 5, 7)=ABC +A BC +A B C +ABC（2）F 2=A +B +CD =m (3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15)=ABCD ABCD ABCD ABCD ABCD ABCD ++++++ABCD ABCD ABCD +++ABCD ABCD ABCD ABCD +++题1.28（1）F1卡诺图题1.28（2）F2卡诺图1.29 证明异或关系的正确性（1）A⊕0=A·0+A·0=A得证（2）A⊕1=A·1+A·1=A得证（3）A⊕A=A·A+A·A=0 得证（4）A⊕A=A·A+A·A=1 得证=A+A=1（5）(A⊕B)⊕C =(A⊕B)C+A B C⊕=ABC ABC ABC ABC+++=m(1, 2, 4, 7)A⊕(B⊕C) =A()⊕+⊕B C A B C=A(BC+BC)+A(B C+B C)=ABC ABC ABC ABC+++=m(1, 2, 4, 7)左式=右式，得证（6）右式AB⊕AC=AB·()()+=+++=+AC ABAC AB A C A B AC ABC ABC左式A(B⊕C)=A(B C+B C)=ABC ABC+得证（7）左式A⊕B=A B+AB=AB+AB=中式右式A⊕B⊕1=A⊕(B⊕1)=A⊕B=AB AB AB AB+=+=中式得证．1.30 用卡诺图法将函数化简为与或式．（1）Z ABC ABC ABC ABC=+++（2）1Z A B AB ABC BC=++++=题1.30（1）的卡诺图题1.30（2）的卡诺图（3）Z ABC AB AD C BD=++++填图后，可圈“0”得到Z=Z BCD再对Z取反，得到ZZ Z BCD B C D===++（4）Z(A、B、C)=m(0, 1, 2, 5, 6, 7)Z=AB AC BC++题1.30（3）的卡诺图题1.30（4）的卡诺图（5）Z(A、B、C、D)=m(0, 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 14)Z=B AC AD CD+++（6）Z(A、B、C、D)=m(0, 1, 2, 5, 8, 9, 10, 12, 14)Z=BC+BD+AD ACD+题1.30（5）的卡诺图题1.30（6）的卡诺图（7）Z=A C D ABCD ABCD++++，给定的约束条件为ABCD ABCD ABCD ABCD++++ 0ABCD ABCD+=Z=ACD ABCD ABCD++=ACD BCD AD++（8）Z=()CD A B ABC ACD⊕++给定的约束条件为AB+AC=0AC ACDZ=ABCD ABCD ABC ACD +++=BD ACD +题图1.30（7）的卡诺图题图1.30（8）的卡诺图（9）Z =m (0, 1, 2, 4)+d (3, 5, 6, 7)=1（10）Z =m (2, 3, 7, 8, 11, 14)+d (0, 5, 10, 15) Z =BD CD AC ++题图1.30（9）的卡诺图题图1.30（10）的卡诺图1.31 试用卡诺图法化简下列逻辑图 ① Z a =ABC ABC BC=ABC ABC BC ++ =ABC AC BC ++② Z b ：按逻辑图逐级写函数式，最后得出Z b =A ⊕C +(A +B )()BC AC BD AD +=A ⊕C +(A +B )()()B C AC BD A D +++=A ⊕C +(A +B )ABCD ↓展开为与或式 =A ⊕C +(A +B )(A +B +C +D )=A ⊕C +AB +A C +AD +AB +B +BC +BD=A C +A C +AD +B 填入卡诺图由卡诺图判断：Z b=AC+AC+AD+B该式已为最简与或式．题图1.31（a）的卡诺图题图1.31（b）的卡诺图1.32 化函数式为与非-与非式，并画出对应的逻辑图．（1）Z1 =AB+BC+AC=AB BC AC+++（2）Z2 =ABC AB BC AB=()++ABC AB BC AB=()++++ABC A B BC A BABC=1=ABC题图1.32（1）题图1.32（2）1.33 用最小项性质证明两个逻辑函数的与、或、异或运算可用卡诺图中对应的最小项分别进行与、或、异或运算来实现．解：命题所给出的结论是正确的．因为当输入变量的取值组合使某一最小项为1时，其他最小项均为0，若两函数相“与”，即Y=Y1·Y2，在对应最小项位置上Y1、Y2均为1时必然使Y为1；Y1Y2在该位置上有0，则0·0或1·0，Y必然为0，将所有对应最小项作乘运算就实现了Y=Y1·Y2运算．其他运算（或和异或）也是同样的道理．或运算是对应最小项相加；异或运算是对应最小项相异或．。

数字电子技术基础教材

（1-1）
1.2.2 二进制数表述方法
( N )2 an1 2n1
n 1

ai 2i
im
a1 21 a0 20 a1 21 am 2m
（1-2）
如将 (11010.101)2 写成权展开式为：
(11010.101)2 1 24 1 23 0 22 1 21 0 20 1 21 0 22 1 23
1.2.2 二进制数表述方法
二进制的加法规则是： 0 + 0 = 0 ，1 + 0 = 1 0 + 1 = 1 ，1 + 1 = 10
二进制的乘法规则是： 0 × 0 = 0 ，1 × 0 = 0 0 × 1 = 0 ，1 × 1 = 1
二进制的减法规则是： 0 – 0 = 0， 0 – 1 = 1（有借位） 1 – 0 = 1 ，1 – 1 = 0
表1-3 四位格雷码
格雷码
十进制数二进制码
0000 0001 0011 0010 0110 0111 0101 0100
8
1000
9
1001
10
1010
11
1011
12
1100
13
1101
14
1110
15
1111
格雷码
1100 1101 1111 1110 1010 1011 1001 1000
1.4.1 十进制编码【例1-8】把二进制数1001转换成格雷码。解：
1.4.3 字母数字码
【例1-12】一组信息的ASCII码如下，请问这些信息是什么？
1001000 1000101 1001100 1010000 解：
把每组7位码转换为等值的十六进制数，则有： 48 45 4C 50

数字电子技术基础第三章

二、交流噪声容限
反相器对窄脉冲的噪声容限—交流噪声容限远高于直流噪声容限。
交流噪声容限受电源电压和负载电容的影响。
图3.3.23 CMOS反相器的交流噪声容限
三、动态功耗
动态功耗：当CMOS 反相器从一种稳定工作状态突然转变到另一种稳定的过程中，将产生附加的功耗。
PD=PC+PT PD为总动态功耗 PC为对负载电容充放
图3.3.xx CMOS三态门电路结构之三可连接成总线结构。还能实现数据的双向传输。
3.3.6 CMOS电路的正确使用
一、输入电路的静电防护
1、在存储和运输CMOS器件时最好采用金属屏蔽层作包装材料，避免产生静电。
2、组装、调试时，应使电烙铁和其他工具、仪表、工作台面等良好接地。操作人员的服装、手套等选用无静电的原料制作。
图3.5.34 OC门输出并联的接法及逻辑图
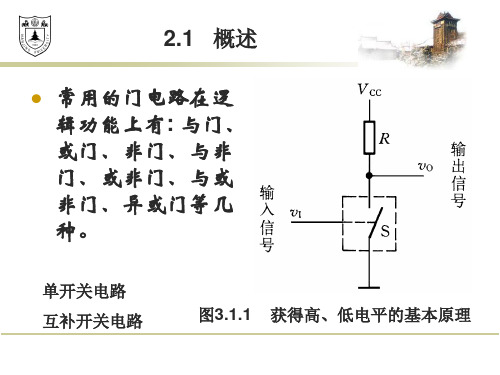
2.1 概述
常用的门电路在逻辑功能上有: 与门、或门、非门、与非门、或非门、与或非门、异或门等几种。
单开关电路互补开关电路
图3.1.1 获得高、低电平的基本原理
图3.1.2 正逻辑与负逻辑
一些概念
1、片上系统（SoC） 2、双极型TTL电路 3、CMOS
1961年美国TI公司,第一片数字集成电路（Integrated Circuits, IC）。
C=1时 Vo=RL*Vi/(RL+RTG) RTG越小越好，并且希望不受输入电压变化。
图3.3.39 CMOS模拟开关接负载电阻的情况
四、三态输出的CMOS门电路
高阻态。此电路结构总是接在集成电路的输出端。
图3.3.40 CMOS三态门电路结构之一

数字电子技术基础ppt课件

RC
例： =30， VCC = VEE
+
=12V， VCES=0.3V， R1 =5.1k， RC =2k, R2
+
V R1
’ i
IC
=20k，当Vi = 0、5V、悬空时，晶体管的静态工
Vi
IB
R2
VO
作状态及Vo的值？
-
-VEE
-
分析：当Vi 悬空时：
Vi'VEE 1V 00.7V
Q位于截止区，Vo=12V
A D1 B D2
Y
A
0
0
1
1
【】内容回顾
BY 00 11 01 11
二极管或门 A
≥1
Y
B
【】 § 2.3 三极管及其构成的非门电路
内容回顾
VCC
三极管工作状态
判断方法：
RC
(1) 判断UBE (2) 计算ICS 和IBS (3) 计算IB
RB
+
Vi IB
-
+
IC
VO
-
(4) 判断IB 是否大于IBS , 若大于则三极管工作于饱和状态，反之，则工作于放大状态。
VCC
例： =30， VCC = VEE
RC
=12V， VCES=0.3V， R1 =5.1k， RC =2k, R2
=20k，当Vi = 0、5V、 +
IB
R1 Vi’
IC
+
悬空时，晶体管的静态工
作状态及Vo的值？
Vi
VO
R2
分析：当Vi =0时：
-
-VEE
-
V i'R 1R 2R 2V iR 1R 1R 2V EE 2.4V0.7V

数字电子技术B——总览

1.数字量和模拟量·数字量：在时间上和数量上都是离散、不连续的。

(存在⼀个最⼩数量单位Δ)·模拟量：数字量以外的物理量。

·数字电路和模拟电路：⼯作信号、研究对象、分析/设计⽅法以及所⽤的数学⼯具都有显著的不同。

2.什么是电⼦技术？是研究电⼦器件以及电⼦器件应⽤的⼀门学科3.电⼦技术的发展·1948 贝尔实验室制成第⼀⽀晶体管·1958 集成电路(4-12-100-1000)·1969 ⼤规模集成电路(10万)·1975 超⼤规模集成电路(15万)·……4.电⼦电路？处理信息、能量转换·模拟电路：⽤连续的模拟电压/流值来表⽰信息·数字电路：⽤⼀个离散的电压序列来表⽰信息第⼀章信息和编码1.信息⼆进制信息2.编码对信息进⾏描述·唯⼀性·编码的效率以及可靠性、安全性·数制：表⽰数量的规则①每⼀位的构成②从低位向⾼位的进位规则·数制：⼆进制、⼋进制、⼗进制、⼗六进制$$⼆进制转⼗进制：v=\sum_{i=0}{n-1}{2ib_i}$$$$转换公式：D=\sum{K_iN^i}{}$$⼆进制数的补码：·算数运算⼆进制数的0/1可以表⽰数量，进⾏加，减，乘，除等运算⼆进制数的正、负号也是⽤0/1表⽰的。

在定点运算中，最⾼位为符号位（0为正，1为负）补码： -8=1000；-1=1111 （-8与-1相差7即111）11010110=-128+64+16+4+2=-42+5=（0 0101）-5=（1 1011）·最⾼位为符号位（0为正，1为负）·整数的补码和它的原码相同·负数的补码 = 数值逐位求反+1+5=（0000 0101）-5=（1111 1011）·两个补码表⽰的⼆进制数相加时的符号位讨论结论：将两个加数的符号位和来⾃最⾼位数字位的进位相加，结果就是和的符号。

《数电》48学时第01章_数制和码制

例：
0.8125
2( k − 2 2 −1 + k −3 2 − 2 + ⋯ + k − m 2 − m +1 ) = k − 2 ( k −3 2 −1 + ⋯ + k − m 2 − m + 2 ) ＋
× 2 ⋯⋯⋯⋯ 整数部分＝ 1 ＝k −1 1.6250 0.6250 × 2 ⋯⋯⋯⋯ 整数部分＝ 1 ＝k − 2 1.2500 0.2500 × 2 ⋯⋯⋯⋯ 整数部分＝ 0 ＝k −3 0.5000 0.5000 × 2 ⋯⋯⋯⋯ 整数部分＝ 1 ＝k − 4 1.000
数字电子技术基础
《数字电子技术基础》（第五版）数字电子技术基础》第五版）
阎石主编高等教育出版社
电子信息工程学院电子工程系李改新高级工程师 ligaixin@ ligaixin@
1
数字电子技术基础
课程介绍
• • • • 前言课程性质教材课程内容
14
数字电子技术基础
不同进制数的对照表
十进制数 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 二进制 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 八进制 00 01 02 03 04 05 06 07 10 11 12 13 14 15 16 17 十六进制 0 1 2 3 4 5 6 7 8 9 A B C D E F
( 0101 ,1110 . 1011 , 0010 ) 2
=( 5
E
. B
2)16
四、十六－二转换（每位16进制数转换成4位二进制数）

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、(20分)选择题，每题2分。

1．有符号位二进制数的原码为（11101），则对应的十进制为（ A ）。

A 、-29
B 、+29
C 、-13
D 、+13
2．逻辑函数)(F E BCD BD A AC Y +++=的最简的与或式（ B ）。

A 、AC+BD ；
B 、BD A A
C + C 、AC+B
D 、A+BD
3. 逻辑函数的F=BC B A B A ++的标准与或式为（ A ）。

A 、∑)7,5,4,3,2(
B 、∑)6,4,3,2,1(
C 、∑)5,3,2,1,0(
D 、∑)7,6,5,4,3(
4．逻辑函数Y （A ，B ，C ）=∑)5,4,2,0(的最简与或非式为（ A ）。

A 、A
B
C A + B 、C A B A +
C 、B A C A +
D 、C B C A B A ++
5．逻辑函数Y （A ，B ，C ，D ）=∑)9,6,5,4,2,1(其约束条件为AB+AC=0则最简
与或式为（ A ）。

A 、D C D C C
B ++ B 、D
C A
D C C B ++ ；
C 、
D C D C D C A ++ D 、C A D B B A ++
6．下图为TTL 逻辑门，其输出Y 为（ A ）
A 、0
B 、 1
C 、B A +
D 、B A ∙
7．下图为OD 门组成的线与电路其输出Y 为（ A ）
A 、1
B 、0
C 、B
D 、B A ∙
8．下图中触发器的次态方程Q n+1为（ A ）。

A 、A
B 、0
C 、Q n
D 、Q n
9．RS触发器要求状态由0→1其输入信号为（ A ）。

A、RS=01
B、RS=×1
C、RS=×0
D、RS=10 10．电源电压为+12V的555定时器、组成施密特触发器，控制端开路，则该触发器的回差电压△V T为（ A ）。

A、4V
B、6V
C、8V
D、12V
(10分)判断题，每题1分。

1．TTL门电路在高电平输入时，其输入电流很小，74LS系列每个输入端的输入电流在40uA以下（ T）
2．三态门输出为高阻时，其输出线上电压为高电平（ F ）
3．超前进位加法器比串行进位加法器速度慢（ F ）
4．译码器哪个输出信号有效取决于译码器的地址输入信号（ T）
5．五进制计数器的有效状态为五个（T）
6．施密特触发器的特点是电路具有两个稳态且每个稳态需要相应的输入条件维持。

（T ）
7、当时序逻辑电路存在无效循环时该电路不能自启动（T ）
8．RS触发器、JK触发器均具有状态翻转功能（F ）
9．D/A的含义是模数转换（F ）
10．构成一个7进制计数器需要3个触发器（T ）
三、(10分)填空题，每空1分。

1．八进制数 (34.2 ) 8 的等值二进制数为（11100.01 ） 2 ；十进制数 98 的8421BCD 码为（10011000 ） 8421BCD 。

2 . TTL 与非门的多余输入端悬空时，相当于输入高电平。

3 .下图所示电路中的最简逻辑表达式为。

AB
4. 一个 JK 触发器有两个稳态，它可存储一位二进制数。

5. 若将一个正弦波电压信号转换成同一频率的矩形波，应采用多谐振荡器电路。

6. 常用逻辑门电路的真值表如表1所示，则 F 1 、 F 2 、 F 3 分别属于何种常用逻辑门。

表 1
A B F 1 F 2 F 3
0 0 1 1 0
0 1 0 1 1
1 0 0 1 1
1 1 1 0 1
F 1 同或；F 2 与非门；F 3 或门。

四、(60分) 分析计算题。

1、（本题15分）
（1）、用代数法化简为最简与或式（7分）B
+
+
=
+
Y∙
CD
AD
B
A
Y=A+B
2、用卡诺图法化简为最简或与式 (8分)
+AB
CD
+
=
B
=约束条件：0
B
A
+
C
D
A
C
Y+
A
B
D
C
D
B
C
A
A
D
用卡诺图圈0的方法可得：Y=（+D）（A+ ）（+ ）
2、如图所示电路在V i＝0.3V和V i＝5V时输出电压V0分别为多少，三极管分别工作于什么区（放大区、截止区、饱和区）。

(10分)
+5V
V 0
解：（1）0.3V V i = 时，三极管截止，工作在截止区，5V V o = ；
（2）5V V i =时，三极管导通，工作在饱和区，V V ce 0V (m ax)o ≈=
3、试用图示3线－8线译码器74LS138和必要的门电路产生如下多输出逻辑函数。

要求：（1）写出表达式的转换过程（7分）；（2）在给定的逻辑符号图上完成最终电路图。

（8分）
⎪⎩⎪⎨⎧+=++=+=C B A C B Y BC
C B A C B A
Y BC AC Y 321
①转换过程 5
4037
43127531m m m Y m m m m Y m m m Y ∙∙=∙∙∙=∙∙=
②连接图
4、试分析同步时序逻辑电路，要求写出各触发器的驱动方程、状态方程，画出完整的状态转换图（按Q 3Q 2Q 1排列）。

（10分）
①驱动方程 ②状态方程
2
13212
321321Q K Q K Q K Q J Q J Q J ======
③状态转换图
2
3232312121213121Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q =+==+=+
=
5、用74LS160及少量的与非门组成能显示00~48的计数器（10分）
D 0 D 1 D 2 D 3 Q 0 Q 1 Q 2 Q 3 EP
ET
CP C LD D R 74160 D 0 D 1 D 2 D 3 Q 0 Q 1 Q 2 Q 3
E P E T C P C LD D R 74160。