2013年中考数学复习考点跟踪训练25梯形(全解全析)
中考数学精练精析 二十五 梯形知能综合检测 鲁教版五四制

【全程复习方略】2013版中考数学精练精析 二十五 梯形知能综合检测 鲁教版五四制(40分钟 60分)一、选择题(每小题5分,共20分)1.(2012·长沙中考)下列四边形中,对角线一定不相等的是( )(A)正方形(B)矩形 (C)等腰梯形 (D)直角梯形2.等腰梯形的上底是2 cm ,腰长是4 cm ,一个底角是60°,则等腰梯形的下底是( )(A)5 cm (B)6 cm (C)7 cm (D)8 cm3.(2012·安徽中考)在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2,4,3,则原直角三角形纸片的斜边长是( )(A)10(B)45 (C)1045或 (D)10217或4.(2012·莱芜中考)如图,在梯形ABCD 中,AD ∥BC ,∠BCD=90°,BC=2AD,F ,E 分别是BA ,BC 的中点.则下列结论不正确的是( )(A)△ABC 是等腰三角形(B)四边形EFAM 是菱形(C)BEF ADC 1S S 2△△(D)DE平分∠FDC二、填空题(每小题5分,共15分)5.(2012·扬州中考)已知梯形的中位线长是4 cm,下底长是5 cm,则它的上底长是________cm.6.如图,在梯形ABCD中,∠C=90°,AB∥CD,AB=25,BC=24,将该梯形折叠,点A恰好与点D重合,BE 为折痕,那么AD的长度为________.7.如图,在四边形ABCD中,已知AB与CD不平行,∠ABD=∠ACD,请你添加一个条件:________,使得加上这个条件后能够推出AD∥BC且AB=CD.三、解答题(共25分)8.(12分)如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD.(1)求证:BE=AD;(2)求证:AC是线段ED的垂直平分线;(3)△DBC是等腰三角形吗?并说明理由.【探究创新】9.(13分)如图,在梯形ABCD中,AD∥BC,BC=20 cm,AD=10 cm,现有两个动点P,Q分别从B,D两点同时出发,点P以每秒2 cm的速度沿BC向终点C移动,点Q以每秒1 cm的速度沿DA向终点A移动,线段PQ 与BD 相交于点E ,过E 作EF ∥BC 交CD 于点F ,射线QF 交BC 的延长线于点H ,设动点P,Q 移动的时间为t(单位:秒,0<t <10).(1)当t 为何值时,四边形PCDQ 为平行四边形?(2)在P,Q 移动的过程中,线段PH 的长是否发生改变?如果不变,求出线段PH 的长;如果改变,请说明理由.答案解析1.【解析】选D.正方形,矩形,等腰梯形的对角线都相等,只有直角梯形的对角线不相等.2.【解析】选B.如图,过D 作DE ∥AB 交BC 于E ,∵DE ∥AB ,AD ∥BC ,∴四边形ABED 是平行四边形,∴AD=BE=2 cm ,DE=AB=4 cm ,∠DEC=∠B=60°,AB=DE=DC ,∴△DEC 是等边三角形,∴EC=CD=4 cm ,∴BC=4+2=6(cm).3.【解析】选C.如图1,22CD 345=+=,∴AB=10;如图2,22CD 2425AB 4 5.=+=∴=,4.【解析】选D.连接AE ,∵点E 是 BC 的中点,BC=2AD ,AD ∥BC ,∴AD=EC, 又AD ∥EC,∴四边形ADCE 为平行四边形.又∵∠BCD=90°,∴平行四边形ADCE 为矩形,∴∠AEC=90°.∴AB=AC.∵AD=EC, AD ∥EC ,点E 为BC 的中点,∴AD=EB, AD ∥EB.∴四边形ADEB 为平行四边形,∴AB ∥DE.∵F ,E 分别是BA ,BC 的中点,∴EF ∥AM ,∴四边形EFAM 是平行四边形.在△AEB 中,∠AEB=90°,F 是BA 的中点,∴EF=FA ,∴四边形EFAM 是菱形.∵EF 是△ABC 的中位线,BEF ABC ABE ADC 111S S S S 422∴===△△△△(△ABE 与△ADC 等底等高).当AD=DC 时,∠EDC=45°,∠EDF <45°,∴DE 平分∠FDC 不成立.综上得选项A ,B ,C 都成立.5.【解析】梯形的中位线=两底和的一半,即142=(5+上底),得上底=3 cm.答案:36.【解析】由折叠后可知AB=BD=25,在△BCD 中,22CD 25247=-=,过点D 作DF ⊥AB 于F ,则CD=BF ,所以AF=25-7=18,在Rt △ADF 中,22AD 241830.=+=答案:307.【解析】由题意可知,∠ABD =∠ACD ,AD =AD,则可以再添加一组角∠DAC =∠ADB 或∠BAD =∠CDA,∴△BAD ≌△CDA,∴BD =AC ,AB =DC,∠BDA=∠CAD,∴OA=OD,∴OB=OC,∴∠OBC=∠OCB.又∠AOD=∠COB,∴∠DAC =∠ACB,∴AD ∥BC,同理可添加∠DBC =∠ACB ,∠ABC =∠DCB ,OB =OC ,OA =OD ,从而推出AD ∥BC 且AB =CD.答案:本题答案不唯一,如∠DAC =∠ADB ,∠BAD =∠CDA ,∠DBC =∠ACB ,∠ABC =∠DCB ,OB =OC ,OA =OD(任选其一)8.【解析】(1)∵∠ABC=90°,BD ⊥EC,∴∠1与∠3互余,∠2与∠3互余,∴∠1=∠2,∵∠ABC=∠DAB=90°,AB=BC,∴△BAD ≌△CBE,∴AD=BE.(2)∵E 是AB 中点,∴EB=EA.由(1)AD=BE,得AE=AD.∵AD ∥BC,∴∠7=∠ACB=45°,∵∠6=45°,∴∠6=∠7.由等腰三角形的性质得:EM=MD,AM ⊥DE ,即AC 是线段ED 的垂直平分线.(3)△DBC 是等腰三角形(CD=BD),理由如下:由(2)得:CD=CE,由(1)得:CE=BD.∴CD=BD.∴△DBC 是等腰三角形.9.【解析】(1)∵AD ∥BC ,BC=20 cm ,AD=10 cm ,点P,Q 分别从B,D 两点同时出发,点P 以每秒2 cm 的速度沿BC 向终点C 移动,点Q 以每秒1 cm 的速度沿DA 向终点A 移动,∴DQ=t ,PC=20-2t , ∵若四边形PCDQ 为平行四边形,则DQ=PC ,∴20-2t=t ,解得20t .3=(2)线段PH 的长不变,∵AD ∥BH ,P,Q 两点的速度比为2∶1,∴QD ∶BP=1∶2,∴QE ∶EP=ED ∶BE=1∶2,∵EF ∥BH ,∴ED ∶DB=EF ∶BC=1∶3,∵BC=20 cm ,20EF cm 3∴=,EFQE1PH QP 3∴=∶,∴PH=20 cm.。
(浙江地区专版)中考数学总复习 梯形考点跟踪突破25(含13年中考真题)(无答案)
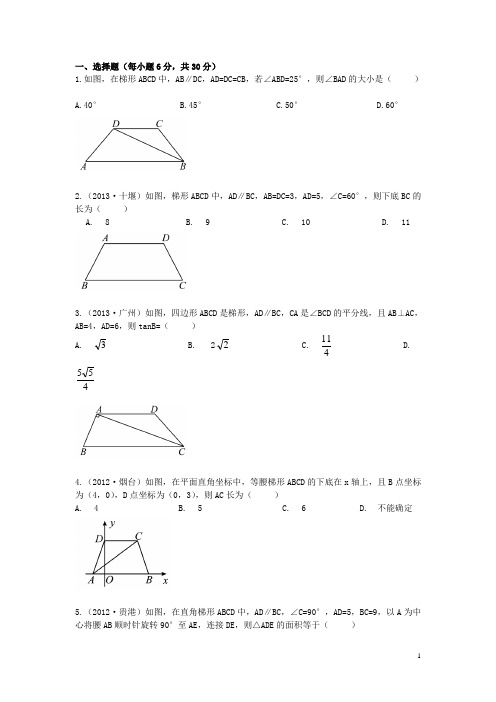
一、选择题(每小题6分,共30分)1.如图,在梯形ABCD 中,AB ∥DC ,AD=DC=CB ,若∠ABD=25°,则∠BAD 的大小是( )A.40°B.45°C.50°D.60°2.(2013·十堰)如图,梯形ABCD 中,AD ∥BC ,AB=DC=3,AD=5,∠C=60°,则下底BC 的长为( ) A.8 B.9 C.10 D.113.(2013·广州)如图,四边形ABCD 是梯形,AD ∥BC ,CA 是∠BCD 的平分线,且AB ⊥AC ,AB=4,AD=6,则tanB=( ) A.3 B.22 C.411D.4554.(2012·烟台)如图,在平面直角坐标中,等腰梯形ABCD 的下底在x 轴上,且B 点坐标为(4,0),D 点坐标为(0,3),则AC 长为( )A.4B.5C. 6D.不能确定5.(2012·贵港)如图,在直角梯形ABCD 中,AD ∥BC ,∠C=90°,AD=5,BC=9,以A 为中心将腰AB 顺时针旋转90°至AE ,连接DE ,则△ADE 的面积等于( )A.10B.11C.12D.13二、填空题(每小题6分,共30分)6.如图,直角梯形ABCD 中,AD ∥BC ,∠C=90°,则∠A+∠B+∠C= 度.7.(2013·曲靖)如图,在直角梯形ABCD 中,AD ∥BC ,∠B=90°,∠C=45°,AD=1,BC=4,则CD= .8.(2012·南通)如图,在梯形ABCD 中,AB ∥CD ,∠A+∠B=90°,AB=7cm ,BC=3cm ,AD=4cm ,则CD= cm.9.(2013·六盘水)如图,梯形ABCD 中,AD ∥BC ,AD=4,AB=5,BC=10,CD 的垂直平分线交BC 于E ,连接DE ,则四边形ABED 的周长等于 .10.(2013·烟台)如图,四边形ABCD 是等腰梯形,∠ABC=60°,若其四边满足长度的众数为5,平均数为425,上、下底之比为1∶2,则BD= .三、解答题(共40分)11.(10分)如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB 中点,EF∥DC交BC于点F,求EF的长.12.(10分)(2012·襄阳)如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED=2,AC与ED相交于点F.(1)求证:梯形ABCD是等腰梯形;(2)当AB与AC具有什么位置关系时,四边形AECD是菱形?请说明理由,并求此时菱形AECD的面积.13.(10分)(2013·南充)如图,等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P 为BC边上一点(不与B,C重合),过点P作∠APE=∠B,PE交CD于E.(1)求证:△APB∽△PEC;(2)若CE=3,求BP的长.14.(10分)(2012·杭州)如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连接AF,DE.(1)求证:AF=DE;(2)若∠BAD=45°,AB=a,△ABE和△DCF的面积之和等于梯形ABCD的面积,求BC的长.。
中考数学专题讲练 梯形(解析版)
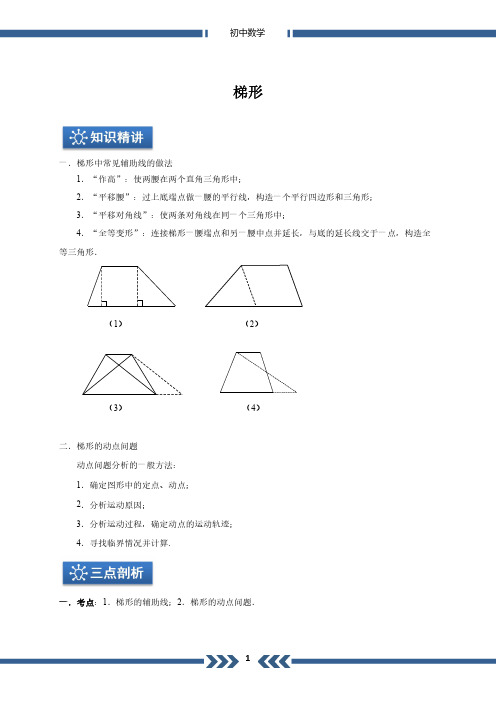
2 2 =2 2 9 s 时,AP=4.5,Q 点在 EC 上 2
4.5 4 =9 2 故答案为:2;9
(2)当 5≤x≤9 时(如图 1)
y=S 梯形 ABCQ﹣S△ABP﹣S△PCQ=
1 1 1 (5+x﹣4)×4 ×5(x﹣5) (9﹣x)(x﹣4) 2 2 2
例 1.1.2 已知:如图,在梯形 ABCD 中,DC∥AB,AD=BC=2,∠A=60°,对角线 BD 平分∠ABC. (1)求对角线 BD 的长; (2)求梯形 ABCD 的面积.
【答案】 (2 ) 3 3 【解析】
(1) 2 3
(1)∵DC∥AB,AD=BC,
∴∠A=∠ABC. ∵BD 平分∠ABC,∠A=60°, ∴∠ABD=
题模一:梯形中的辅助线 例 1.1.1 梯形 ABCD 中,AD∥BC,AD=1,BC=4,∠C=70°,∠B=40°,则 AB 的长为( ) A. 2 B. 3 C. 4 D. 5 【答案】B 【解析】 作 DE∥AB 交 BC 于 E,则四边形 ABED 是平行四边形.∴BE=AD=1,∠CED=∠B=40° ∴∠CDE=70°∴AB=DE=CE=4-1=3
例 1.1.3 如图,梯形 ABCD 中,AD∥BC,点 E 在 BC 上,AE=BE,点 F 是 CD 的中点,且 AF⊥AB,若 AD=2.7,AF=4,AB=6,求 CE 的长.
【答案】 见解析 【解析】 延长 AF、BC 交于点 G.∴△AFD≌△GFC.∴AG=2AF=8,CG=AD=2.7.∵AF⊥AB,AB=6, ∴BG=10.∴BC=BG-CG=7.3.∵AE=BE,∴∠BAE=∠B.∴∠EAG=∠AGE.∴AE=GE.
(2)
梯形练习题及答案

梯形练习题及答案答案一:梯形练习题及答案一、选择题1. 梯形的两边是平行边,且不等长的四边形,其中不等长的一对边称为()。
A. 平行边B. 高C. 长边D. 短边2. 梯形中,非平行边的夹角互补,则该梯形是()。
A. 直角梯形B. 等腰梯形C. 普通梯形D. 等边梯形3. 若梯形的一组对边的夹角为75°,则该梯形的另一组对边的夹角为()A. 15°B. 30°C. 45°D. 60°4. 若梯形的一组对边的夹角为120°,则该梯形的另一组对边的夹角为()A. 60°B. 75°C. 90°D. 105°5. 梯形的高等于上底和下底的差,且上底为10 cm,下底为20 cm,那么该梯形的面积为()㎠。
A. 90B. 100C. 110D. 120二、计算题1. 已知一个梯形的上底长为8 cm,下底长为14 cm,高为6 cm,求该梯形的面积。
解:面积 = (上底长 + 下底长) ×高 ÷ 2= 22 × 6 ÷ 2= 132 ÷ 2= 66 cm²该梯形的面积为66平方厘米。
2. 已知一个梯形的上底长为16 cm,下底长为12 cm,面积为160平方厘米,求该梯形的高。
解:面积 = (上底长 + 下底长) ×高 ÷ 2160 = (16 + 12) ×高 ÷ 2320 = 28 ×高高 = 320 ÷ 28高≈ 11.43 cm该梯形的高约为11.43厘米。
三、综合题在一个梯形中,上底长是下底长的3倍,梯形的高是7 cm,求该梯形的面积。
解:设下底长为x,则上底长为3x。
面积 = (上底长 + 下底长) ×高 ÷ 2= 4x × 7 ÷ 2= 14x ÷ 2= 7x根据题意可得 7x = 7 cm解得 x = 1下底长为1 cm,上底长为3 cm。
2013中考数学复习之函数梯形

2013中考数学复习之函数梯形
中考数学考什么,这是考生和家长最关心的问题。
以往的中考考题主要体现在对知识点的考查上,强调知识点的覆盖面,对能力的考查没有放在一个突出的位置上。
近几年的中考命题发生了明显的变化,既强调了由知识层面向能力层面的转化,又强调了基础知识与能力并重。
注重在知识的交汇处设计命题,对学生能力的考查也提出了较高的要求。
中考数学重点考查学生的数学思维能力已经成为趋势和共识。
初三学生可利用寒假时间对数学思想方法进行梳理、总结,逐个认识它们的本质特征、思维程序和操作程序。
有针对性地通过典型题目进行训练,能够真正适应中考命题。
中考数学复习考点跟踪训练25梯形

考点跟踪训练25 梯形一、选择题1.(·武汉)如图,在梯形ABCD 中,AB ∥DC ,AD =DC =CB ,若∠ABD =25°,则∠BAD 的大小是( )A .40°B .45°C .50°D .60° 答案 C解析 ∵AB ∥DC , ∴∠ABD =∠BDC =25°.∵CD =CB ,∴∠BDC =∠DBC =25°, ∴∠ABC =∠ABD +∠DBC =50°. ∵AB ∥BC ,AD =CB , ∴梯形ABCD 是等腰梯形. ∴∠BAD =∠ABC =50°.2.(·烟台)如图,小区的一角有一块形状为等腰梯形的空地,为了美化小区,社区居委会计划在空地上建一个四边形的水池,使水池的四个顶点恰好在梯形各边的中点上,则水池的形状一定是( )A .等腰梯形B .矩形C .菱形D .正方形 答案 C解析 如图,连接AC 、BD ,因为梯形ABCD 等腰梯形,所以AC =BD .由三角形中位线定理,得EF 綊12AC ,GH 綊12AC ,所以EF 綊GH ,所以四边形EFGH 是平行四边形.又FG=12BD ,EF =12AC ,所以EF =FG ,故▱EFGH 是菱形.3.(·烟台)如图,梯形ABCD 中,AB ∥CD ,点E 、F 、G 分别是BD 、AC 、DC 的中点.已知两底差是6,两腰和是12,则△EFG 的周长是( )A .8B .9C .10D .12 答案 B解析 连接AE 并延长交DC 于H ,易证△ABE ≌△HDE ,AB =DH , ∴CH =CD -DH =CD -AB =6.又∵点E 、F 、G 分别为DB 、AC 、DC 的中点,∴EF =12CH =12×6=3,EG +FG =12BC +12AD =12(BC +AD )=12×12=6,∴△EFG 的周长=EF +EG +FG =3+6=9.4.(·绵阳)如图,在等腰梯形ABCD 中,AB ∥CD ,对角线AC 、BD 相交于O ,∠ABD =30°,AC ⊥BC, AB =8 cm ,则△COD 的面积为( )A.4 33 cm 2B.43 cm 2C.2 33 cm 2D.23 cm 2答案 A解析 分别画CE ⊥AB ,DF ⊥AB ,垂足分别是E 、F .在Rt △ABC 中,∠BAC =∠ABD=30°,AB =8,∴BC =4,BD =AC =4 3,S △ABC =12AC ·BC =12×4 3×4=8 3.在Rt △BCO 中,∠CBO =30°,CB =4,则OC =43 3,OB =83 3,S △BOC =12BC ·OC =12×4×43 3=83 3,∴S △AOB =8 3-83 3=163 3.∵AB ∥CD ,则△DCO ∽△BAO ,S △COD S △AOB=⎝⎛⎭⎫OC OA 2=14,S △COD =14×163 3=433.5.(·福州)梯形ABCD 中AB ∥CD ,∠ADC +∠BCD =90°,以AD 、AB 、BC 为斜边均向形外作等腰直角三角形,其面积分别是S 1、S 2、S 3 ,且S 1+S 3=4S 2,则CD =( )A .2.5AB B .3ABC .3.5ABD .4AB 答案 B解析 过B 画BE ∥AD 交CD 于E ,则四边形ABED 是平行四边形,AD =BE ,∠ADC =BEC ,∴∠BEC +∠BCD =∠ADC +∠BCD =90°,∴∠EBC =90°,BE 2+BC 2=EC 2.而S 1=14AD 2=14BE 2,S 2=14AB 2=14DE 2,S 3=14BC 2.又S 1+S 3=4S 2,得14BE 2+14BC 2=4⎝⎛⎭⎫14DE 2,BE 2+BC 2=4DE 2,∴EC 2=4DE 2,EC =2DE ,CD =DE +EC =3DE =3AB .二、填空题6.(·福州)如图,直角梯形ABCD 中,AD ∥BC ,∠C =90°,则∠A +∠B +∠C =________度.答案 270解析 因为∠A +∠B +∠C +∠D =360°,而∠C =90°,所以∠A +∠B +∠C =270°.7.(·桂林)如图,等腰梯形ABCD 中,AB ∥DC ,BE ∥AD, 梯形ABCD 的周长为26,DE =4,则△BEC 的周长为_________.答案 18解析 由AB ∥DC ,BE ∥AD ,得四边形ABED 是平行四边形,AB =DE =4.又因为梯形ABCD 的周长=AB +BC +CD +DA =26,可知AD +BC +EC =18,所以△BEC 的周长=BE +EC +BC =AD +EC +BC =18.8.(·邵阳)如图所示,在等腰梯形ABCD 中,AB ∥CD ,AD =BC ,AC ⊥BC ,∠B =60°,BC =2 cm ,则上底DC 的长是________cm.答案 2解 ∵∠CAB =90°-60°=30°,又∵在等腰梯形ABCD 中,∠BAD =∠B =60°, ∴∠CAD =∠BAD -∠BAC =30°.又∵CD ∥AB ,∴∠DCA =∠CAB =30°=∠DAC . ∴CD =AD =BC =2 cm.9.(·连云港)一等腰梯形两组对边中点相连线段的平方和为8,则这个等腰梯形的对角线长为_______.答案 2 2解析 如图,易证四边形EGFH 是菱形,在Rt △EOG 中,EG 2=EO 2+GO 2=⎝⎛⎭⎫12EF 2+⎝⎛⎭⎫12GH 2=14()EF 2+GH 2=14×8=2,所以EG =2,又EG =12AC ,所以AC =2EG =2 2.10.(·襄阳)如图,在梯形ABCD 中,AD ∥BC ,AD =6,BC =16,E 是BC 的中点.点P 以每秒1个单位长度的速度从点A 出发,沿AD 向点D 运动;点Q 同时以每秒2个单位长度的速度从点C 出发,沿CB 向点B 运动.点P 停止运动时,点Q 也随之停止运动.当运动时间t =________秒时,以点P 、Q 、E 、D 为顶点的四边形是平行四边形.答案 2或143解析 当四边形PDQE 是平行四边形时,PD =QE ,而PD =6-t ,QE =8-2t ,所以6-t =8-2t ,t =2;当四边形PDEQ 是平行四边形时,PD =EQ ,而PD =6-t ,EQ =2t -8,所以6-t =2t -8,3t =14,t =143;综上,t =2或t =143.三、解答题 11.(·南充)如图,四边形ABCD 是等腰梯形,AD ∥BC ,点E 、F 在BC 上,且BE =CF ,连接DE 、AF .求证:DE =AF .解 证明:∵BE =FC ,∴BE +EF =FC +EF ,即BF =CE . ∵四边形ABCD 是等腰梯形, ∴AB =DC ,∠ B =∠C . 在△DCE 和△ABF 中,⎩⎪⎨⎪⎧DC =AB ,∠C =∠B ,CE =BF ,∴△DCE ≌△ABF (SAS ). ∴DE =AF .12.(·菏泽)如图,在梯形ABCD 中,AD ∥BC ,∠B =90°,∠C =45°,AD =1,BC =4, E 为AB 中点,EF ∥DC 交BC 于点F , 求EF 的长.解 过点A 作AG ∥DC 交BC 于G ,∵AD ∥BC ,∴四边形AGCD 是平行四边形, ∴GC =AD ,∴BG =BC -AD =4-1=3. 在Rt △ABG 中,∠AGB =∠C =45°,AB =BG .∴AG =AB 2+BG 2=2BG 2=2×32=3 2. ∵EF ∥DC ∥AG ,E 是AB 中点, ∴F 是BG 中点,∴EF =12AG =3 22.13.(·重庆)如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°.点E 是DC 的中点,过点E 作DC 的垂线交AB 于点P ,交CB 的延长线于点M .点F 在线段ME 上,且满足CF =AD ,MF =MA .(1)若∠MFC =120°,求证:AM =2MB ;(2)求证:∠MPB =90°-12∠FCM .解 证明:(1)如图,连接MD ,∵点E 是DC 的中点,EM ⊥DC ,∴MD =MC .又∵AD =CF ,MF =MA , ∴△AMD ≌△FMC ,∴∠MAD =∠MFC =120°. ∵AD ∥BC ,∠ABC =90°, ∴∠BAD =90,° ∴∠MAB =30°.在Rt △AMB 中,∠MAB =30°,∴BM =12AM ,即AM =2BM .(2)∵△AMD ≌△FMC , ∴∠ADM =∠FCM , ∵AD ∥BC ,∴∠ADM =∠CMD . ∴∠CMD =∠FCM .∵MD =MC ,ME ⊥DC ,∴∠DME =∠CME =12∠CMD ,∴∠CME =12∠FCM ,∴在Rt △MBP 中,∠MPB =90°-∠CME =90°-12∠FCM .14.(·南充)如图,等腰梯形ABCD 中,AD ∥BC ,AD =AB =CD =2,∠C =600,M 是BC 的中点.(1)求证:△MDC 是等边三角形;(2)将△MDC 绕点M 旋转,当MD (即MD ′)与AB 交于一点E ,MC 即MC ′)同时与AD 交于一点F 时,点E 、F 和点A 构成△AEF .试探究△AEF 的周长是否存在最小值?如果不存在,请说明理由;如果存在,请计算出△AEF 周长的最小值.解 (1)证明:过点D 作DP ⊥BC 于点P ,过点A 作AQ ⊥BC 于点Q , ∵∠C =∠B =60°,∴CP =BQ =12AB ,CP +BQ =AB .又∵ADPQ 是矩形,AD =PQ ,AD =AB ,故BC =2AD . 由已知,点M 是BC 的中点, ∴BM =CM =AD =AB =CD,∴在△MDC 中,CM =CD, ∠C =60°, 故△MDC 是等边三角形.(2)解:△AEF 的周长存在最小值,理由如下:连接AM ,由(1)得▱ABMD 是菱形,△MAB, △MAD 和△MC ′D ′是等边三角形, ∴∠BMA =∠BME +∠AME =60°, ∠EMF =∠AMF +∠AME =60°, ∴∠BME =∠AMF .在△BME 与△AMF 中,BM =AM, ∠EBM =∠F AM =60°,∠BME =∠AMF ,∴△BME ≌△AMF (ASA ).∴BE =AF , ME =MF ,AE +AF =AE +BE =AB . ∵∠EMF =∠DMC =60°,∴△EMF 是等边三角形,EF =MF .∵MF 的最小值为点M 到AD 的距离2·sin60°=3, ∴EF 的最小值是3,∴△AEF 的周长=AE +AF +EF =AB +EF , ∴△AEF 的周长的最小值为2+ 3.15.(2011·杭州)在直角梯形ABCD 中,AB ∥CD ,∠ABC =90°,AB =2BC =2CD ,对角线AC 与BD 相交于点O ,线段OA 、OB 的中点分别为点E 、F .(1)求证:△FOE ≌ △DOC ; (2)求sin ∠OEF 的值;(3)若直线EF 与线段AD 、BC 分别相交于点G 、H ,求AB +CDGH的值.解 (1)证明:∵E 、F 分别为线段OA 、OB 的中点, ∴EF ∥AB ,AB =2EF . ∵AB =2CD ,∴EF =CD . ∵AB ∥CD ,∴EF ∥CD ,∴∠OEF =∠OCD ,∠OFE =∠ODC , ∴△FOE ≌ △DOC .(2)在△ABC 中,∵∠ABC =90°,∴AC =AB 2+BC 2=(2BC )2+BC 2=5BC ,sin ∠CAB =BC AC =55.∵EF ∥AB ,∴∠OEF =∠CAB ,∴sin ∠OEF =sin ∠CAB =55.(3)∵△FOE ≌ △DOC ,∴OE =OC .∵AE =OE ,∴AE =OE =OC ,∴CE CA =23.∵EF ∥AB ,∴△CEH ∽△CAB , ∴EH AB =CE CA =23,∴EH =23AB =43CD . ∵EF =CD ,∴EH =43EF ,FH =13EF =13CD .同理,GE =13CD ,∴GH =53CD ,∴AB +CD GH =2CD +CD 53CD =95.。
中考数学 第25课 梯形复习课件

题型分类 题型二 等腰梯形
知能迁移 2 如图,在梯形 ABCD 中,DC∥AB,AD=BC, BD 平分∠ABC,∠A=60°.过点 D 作 DE⊥AB,过点 C 作 CF⊥BD,垂足分别为 E、F,连接 EF. 求证:△DEF 为等边三角形.
3.梯形的中位线定理:
梯33形..的梯梯中形形位的的线中中平位位行线线于定定上理理、:下:两底,且等于两底和的一半.
梯梯形形的的中中位位线线平平行行于于上上、、下下两两底底,,且且等等于于两两底底和和的的一一 半半..
助学微博
一种联系
平行四边形与梯形的联系:有一组对边平行的四边形有 可能是平行四边形或梯形,关键在于另一组对边的位置或平 行的一组对边的数量关系,梯形只有一组对边平行,而平行 四边形两组对边都平行;平行四边形中平行的一组对边必相 等,梯形平行的一组对边必不相等.
第25课 梯 形
要点梳理
1.一组对边平行而另一组对边不平行的四边形叫梯 1形..一1_组_._对_一_边_组_平_对的行边梯而平形另行叫一而做组另等对一腰边组梯不对形平边.行不的平四行边的形四叫边梯形 形.叫梯 形._两__2__._腰__等__相__腰__等__梯__的的形梯梯的形形判叫叫定做做方等等法腰腰:梯梯形形..
探究提高
涉及直角梯形的问题,常作高构造矩形和直角三角 形来解决问题.
题型分类 题型三 直角梯形
知能迁移 3 如图,在梯形 ABCD 中,已知 AD∥BC,AB= CD,延长线段 CB 到 E,使 BE=AD,连接 AE、AC. (1)求证:△ABE≌△CDA; (2)若∠DAC=40°,求∠EAC 的度数.
又由□ABED,得 AB=DE,
初中中考复习之梯形(精编含答案)

∴AE=EB=BF=FC。
在△ABF和△CBE中,∵AB=CB,∠ABF=∠CBE, BF=BE,
∴△ABF≌△CBE(SAS)。∴∠BAF=∠BCE,AF=CE。
在△AME和△CMF中,
∵∠BAF=∠BCE,∠AME=∠CMF ,AE=CF,
∴△AME≌△CMF(AAS)。∴EM=FM。
在△BEM和△BFM中,∵BE=BF,BM=BM,
点,∴BE=CE。
在△ABE和△DCE中,
∵AB=DC,∠B=∠C
,BE=CE,
∴△ABE≌△DCE(SAS)。∴AE=DE。
7、证明:∵ABCD是等腰梯形,AD∥BC,∴∠B=∠BCD, ∠BCD =∠EDC。
∴∠B=∠EDC。又∵CE=CD。∴∠EDC=∠E。∴∠B=∠E。
8、解:(1)180°-2α。
(1)∠BEF=_____(用含α的代数式表示); (2)当AB=AD时,猜想线段ED、EF的数量关系,并证明你的猜想;
(3)当AB≠AD时,将“点E在AD上”改为“点E在AD的延长线上,且 AE>AB,AB=mDE,AD=nDE”,其他条件不变(如图2),求 的值(用含m、n的代数式表示)。
9.我们知道“连接三角形两边中点的线段叫三角形的中位线”,“三角 形的中位线平行于三角形的第三边,且等于第三边的一半”.类似的, 我们把连接梯形两腰中点的线段叫做梯形的中位线.如图,在梯形ABCD 中,AD∥BC,点E,F分别是AB,CD的中点,那么EF就是梯形ABCD的中位 线.通过观察、测量,猜想EF和AD、BC有怎样的位置和数量关系?并证 明你的结论.
6.如图,在等腰梯形ABCD中,点E为底边BC的中点,连结AE、DE.求 证:AE=DE.
7.如图,等腰梯形ABCD中,AD∥BC,点E是AD延长线上的一点,且 CE=CD,求证:∠B=∠E
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点跟踪训练25 梯形一、选择题 1.(2011·武汉)如图,在梯形ABCD 中,AB ∥DC ,AD =DC =CB ,若∠ABD =25°,则∠BAD 的大小是( )A .40°B .45°C .50°D .60° 答案 C解析 ∵AB ∥DC , ∴∠ABD =∠BDC =25°.∵CD =CB ,∴∠BDC =∠DBC =25°, ∴∠ABC =∠ABD +∠DBC =50°. ∵AB ∥BC ,AD =CB , ∴梯形ABCD 是等腰梯形. ∴∠BAD =∠ABC =50°.2.(2011·烟台)如图,小区的一角有一块形状为等腰梯形的空地,为了美化小区,社区居委会计划在空地上建一个四边形的水池,使水池的四个顶点恰好在梯形各边的中点上,则水池的形状一定是( )A .等腰梯形B .矩形C .菱形D .正方形 答案 C解析 如图,连接AC 、BD ,因为梯形ABCD 等腰梯形,所以AC =BD .由三角形中位线定理,得EF 綊12AC ,GH 綊12AC ,所以EF 綊GH ,所以四边形EFGH 是平行四边形.又FG =12BD ,EF =12AC ,所以EF =FG ,故▱EFGH 是菱形.3.(2011·烟台)如图,梯形ABCD 中,AB ∥CD ,点E 、F 、G 分别是BD 、AC 、DC 的中点.已知两底差是6,两腰和是12,则△EFG 的周长是( )A .8B .9C .10D .12 答案 B解析 连接AE 并延长交DC 于H ,易证△ABE ≌△HDE ,AB =DH , ∴CH =CD -DH =CD -AB =6.又∵点E 、F 、G 分别为DB 、AC 、DC 的中点,∴EF =12CH =12×6=3,EG +FG =12BC +12AD =12(BC +AD )=12×12=6,∴△EFG 的周长=EF +EG +FG =3+6=9.4.(2011·绵阳)如图,在等腰梯形ABCD 中,AB ∥CD ,对角线AC 、BD 相交于O ,∠ABD =30°,AC ⊥BC, AB =8 cm ,则△COD 的面积为( )A.4 33 cm 2B.43 cm 2C.2 33 cm 2D.23 cm 2答案 A解析 分别画CE ⊥AB ,DF ⊥AB ,垂足分别是E 、F .在Rt △ABC 中,∠BAC =∠ABD =30°,AB =8,∴BC =4,BD =AC =4 3,S △ABC =12AC ·BC =12×4 3×4=8 3.在Rt △BCO 中,∠CBO =30°,CB =4,则OC =43 3,OB =83 3,S △BOC =12BC ·OC =12×4×433=83 3,∴S △AOB =8 3-83 3=163 3.∵AB ∥CD ,则△DCO ∽△BAO ,S △COD S △AOB=⎝⎛⎭⎫OC OA 2=14,S △COD =14×163 3=433.5.(2011·福州)梯形ABCD 中AB ∥CD ,∠ADC +∠BCD =90°,以AD 、AB 、BC 为斜边均向形外作等腰直角三角形,其面积分别是S 1、S 2、S 3 ,且S 1+S 3=4S 2,则CD =( )A .2.5AB B .3ABC .3.5ABD .4AB 答案 B解析 过B 画BE ∥AD 交CD 于E ,则四边形ABED 是平行四边形,AD =BE ,∠ADC =BEC ,∴∠BEC +∠BCD =∠ADC +∠BCD =90°,∴∠EBC =90°,BE 2+BC 2=EC 2.而S 1=14AD 2=14BE 2,S 2=14AB 2=14DE 2,S 3=14BC 2.又S 1+S 3=4S 2,得14BE 2+14BC 2=4⎝⎛⎭⎫14DE 2,BE 2+BC 2=4DE 2,∴EC 2=4DE 2,EC =2DE ,CD =DE +EC =3DE =3AB .二、填空题6.(2011·福州)如图,直角梯形ABCD 中,AD ∥BC ,∠C =90°,则∠A +∠B +∠C =________度.答案 270解析 因为∠A +∠B +∠C +∠D =360°,而∠C =90°,所以∠A +∠B +∠C =270°.7.(2011·桂林)如图,等腰梯形ABCD 中,AB ∥DC ,BE ∥AD, 梯形ABCD 的周长为26,DE =4,则△BEC 的周长为_________.答案 18解析 由AB ∥DC ,BE ∥AD ,得四边形ABED 是平行四边形,AB =DE =4.又因为梯形ABCD 的周长=AB +BC +CD +DA =26,可知AD +BC +EC =18,所以△BEC 的周长=BE +EC +BC =AD +EC +BC =18.8.(2011·邵阳)如图所示,在等腰梯形ABCD 中,AB ∥CD ,AD =BC ,AC ⊥BC ,∠B =60°,BC =2 cm ,则上底DC 的长是________cm.答案 2解 ∵∠CAB =90°-60°=30°,又∵在等腰梯形ABCD 中,∠BAD =∠B =60°, ∴∠CAD =∠BAD -∠BAC =30°.又∵CD ∥AB ,∴∠DCA =∠CAB =30°=∠DAC . ∴CD =AD =BC =2 cm. 9.(2011·连云港)一等腰梯形两组对边中点相连线段的平方和为8,则这个等腰梯形的对角线长为_______.答案 2 2解析 如图,易证四边形EGFH 是菱形,在Rt △EOG 中,EG 2=EO 2+GO 2=⎝⎛⎭⎫12EF 2+⎝⎛⎭⎫12GH 2=14()EF 2+GH 2=14×8=2,所以EG =2,又EG =12AC ,所以AC =2EG =2 2.10.(2011·襄阳)如图,在梯形ABCD 中,AD ∥BC ,AD =6,BC =16,E 是BC 的中点.点P 以每秒1个单位长度的速度从点A 出发,沿AD 向点D 运动;点Q 同时以每秒2个单位长度的速度从点C 出发,沿CB 向点B 运动.点P 停止运动时,点Q 也随之停止运动.当运动时间t =________秒时,以点P 、Q 、E 、D 为顶点的四边形是平行四边形.答案 2或143解析 当四边形PDQE 是平行四边形时,PD =QE ,而PD =6-t ,QE =8-2t ,所以6-t =8-2t ,t =2;当四边形PDEQ 是平行四边形时,PD =EQ ,而PD =6-t ,EQ =2t -8,所以6-t =2t -8,3t =14,t =143;综上,t =2或t =143. 三、解答题 11.(2011·南充)如图,四边形ABCD 是等腰梯形,AD ∥BC ,点E 、F 在BC 上,且BE =CF ,连接DE 、AF .求证:DE =AF .解 证明:∵BE =FC ,∴BE +EF =FC +EF ,即BF =CE . ∵四边形ABCD 是等腰梯形, ∴AB =DC ,∠ B =∠C . 在△DCE 和△ABF 中,⎩⎪⎨⎪⎧DC =AB ,∠C =∠B ,CE =BF ,∴△DCE ≌△ABF (SAS ). ∴DE =AF .12.(2011·菏泽)如图,在梯形ABCD 中,AD ∥BC ,∠B =90°,∠C =45°,AD =1,BC =4, E 为AB 中点,EF ∥DC 交BC 于点F , 求EF 的长.解 过点A 作AG ∥DC 交BC 于G ,∵AD ∥BC ,∴四边形AGCD 是平行四边形, ∴GC =AD ,∴BG =BC -AD =4-1=3. 在Rt △ABG 中, ∠AGB =∠C =45°,AB =BG .∴AG =AB 2+BG 2=2BG 2=2×32=3 2. ∵EF ∥DC ∥AG ,E 是AB 中点, ∴F 是BG 中点,∴EF =12AG =3 22.13.(2010·重庆)如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°.点E 是DC 的中点,过点E 作DC 的垂线交AB 于点P ,交CB 的延长线于点M .点F 在线段ME 上,且满足CF =AD ,MF =MA .(1)若∠MFC =120°,求证:AM =2MB ;(2)求证:∠MPB =90°-12∠FCM .解 证明:(1)如图,连接MD ,∵点E 是DC 的中点,EM ⊥DC , ∴MD =MC .又∵AD =CF ,MF =MA , ∴△AMD ≌△FMC ,∴∠MAD =∠MFC =120°. ∵AD ∥BC ,∠ABC =90°, ∴∠BAD =90,° ∴∠MAB =30°.在Rt △AMB 中,∠MAB =30°,∴BM =12AM ,即AM =2BM .(2)∵△AMD ≌△FMC , ∴∠ADM =∠FCM , ∵AD ∥BC ,∴∠ADM =∠CMD . ∴∠CMD =∠FCM .∵MD =MC ,ME ⊥DC ,∴∠DME =∠CME =12∠CMD ,∴∠CME =12∠FCM ,∴在Rt △MBP 中,∠MPB =90°-∠CME =90°-12∠FCM .14.(2011·南充)如图,等腰梯形ABCD 中,AD ∥BC ,AD =AB =CD =2,∠C =600,M 是BC 的中点. (1)求证:△MDC 是等边三角形;(2)将△MDC 绕点M 旋转,当MD (即MD ′)与AB 交于一点E ,MC 即MC ′)同时与AD 交于一点F 时,点E 、F 和点A 构成△AEF .试探究△AEF 的周长是否存在最小值?如果不存在,请说明理由;如果存在,请计算出△AEF 周长的最小值.解 (1)证明:过点D 作DP ⊥BC 于点P ,过点A 作AQ ⊥BC 于点Q , ∵∠C =∠B =60°,∴CP =BQ =12AB ,CP +BQ =AB .又∵ADPQ 是矩形,AD =PQ ,AD =AB ,故BC =2AD . 由已知,点M 是BC 的中点, ∴BM =CM =AD =AB =CD,∴在△MDC 中,CM =CD, ∠C =60°, 故△MDC 是等边三角形.(2)解:△AEF 的周长存在最小值,理由如下:连接AM ,由(1)得▱ABMD 是菱形,△MAB, △MAD 和△MC ′D ′是等边三角形, ∴∠BMA =∠BME +∠AME =60°, ∠EMF =∠AMF +∠AME =60°, ∴∠BME =∠AMF .在△BME 与△AMF 中,BM =AM, ∠EBM =∠F AM =60°,∠BME =∠AMF , ∴△BME ≌△AMF (ASA ).∴BE =AF , ME =MF ,AE +AF =AE +BE =AB .∵∠EMF =∠DMC =60°,∴△EMF 是等边三角形,EF =MF . ∵MF 的最小值为点M 到AD 的距离2·sin60°=3, ∴EF 的最小值是3,∴△AEF 的周长=AE +AF +EF =AB +EF , ∴△AEF 的周长的最小值为2+ 3. 15.(2011·杭州)在直角梯形ABCD 中,AB ∥CD ,∠ABC =90°,AB =2BC =2CD ,对角线AC 与BD 相交于点O ,线段OA 、OB 的中点分别为点E 、F .(1)求证:△FOE ≌ △DOC ; (2)求sin ∠OEF 的值;(3)若直线EF 与线段AD 、BC 分别相交于点G 、H ,求AB +CDGH的值.解 (1)证明:∵E 、F 分别为线段OA 、OB 的中点, ∴EF ∥AB ,AB =2EF . ∵AB =2CD ,∴EF =CD . ∵AB ∥CD ,∴EF ∥CD ,∴∠OEF =∠OCD ,∠OFE =∠ODC , ∴△FOE ≌ △DOC .(2)在△ABC 中,∵∠ABC =90°,∴AC =AB 2+BC 2=(2BC )2+BC 2=5BC ,sin ∠CAB =BC AC =55.∵EF ∥AB ,∴∠OEF =∠CAB ,∴sin ∠OEF =sin ∠CAB =55.(3)∵△FOE ≌ △DOC ,∴OE =OC .∵AE =OE ,∴AE =OE =OC ,∴CE CA =23.∵EF ∥AB ,∴△CEH ∽△CAB , ∴EH AB =CE CA =23,∴EH =23AB =43CD . ∵EF =CD ,∴EH =43EF ,FH =13EF =13CD .同理,GE =13CD ,∴GH =53CD ,∴AB +CD GH =2CD +CD 53CD =95.。
