阶段知能检测(7)—立体几何 shi
立体测试题及答案

立体测试题及答案一、单项选择题(每题2分,共10题)1. 下列哪个选项是立体几何中的基本元素?A. 点B. 线C. 面D. 体答案:D2. 空间中两条直线的位置关系有几种?A. 1种B. 2种C. 3种D. 4种答案:C3. 一个立方体有多少个顶点?A. 6B. 8C. 12D. 14答案:B4. 一个正四面体有多少条棱?A. 6B. 8C. 12D. 16答案:A5. 空间直角坐标系中,点(1,2,3)到原点的距离是多少?A. 1B. 2C. 3D. √14答案:D6. 一个球体的表面积公式是?A. 4πr²B. 2πr²C. πr²D. 4πr³答案:A7. 空间中两个平面的位置关系有哪些?A. 平行B. 相交C. 重合D. 以上都是答案:D8. 一个圆柱体的体积公式是?A. πr²hB. 2πrhC. πr²D. πr³答案:A9. 空间中一个点到一个平面的距离公式是?A. |Ax + By + Cz + D| / √(A² + B² + C²)B. |Ax + By + Cz - D| / √(A² + B² + C²)C. |Ax + By + Cz + D| / √(A² + B²)D. |Ax + By + Cz - D| / √(A² + B²)答案:B10. 空间中一个点到一条直线的距离公式是?A. |Ax + By + Cz + D| / √(A² + B² + C²)B. |Ax + By + Cz - D| / √(A² + B² + C²)C. |(Ax + By + Cz + D) / (A² + B² + C²)| * √(A² + B²)D. |(Ax + By + Cz - D) / (A² + B² + C²)| * √(A² + B²)答案:D二、多项选择题(每题3分,共5题)1. 空间中两个平面相交,它们的交线是?A. 直线B. 曲线C. 点D. 面答案:A2. 空间中一个点到一个平面的距离公式中,A、B、C、D分别代表什么?A. 平面方程的系数B. 平面方程的常数项C. 点的坐标D. 点到平面的距离答案:A, B3. 空间直角坐标系中,点(1,2,3)到点(4,5,6)的距离公式是?A. √((4-1)² + (5-2)² + (6-3)²)B. √((1-4)² + (2-5)² + (3-6)²)C. √((4-1)² + (5-2)² + (6-3)²)D. √((1-4)² + (2-5)² + (3-6)²)答案:A, B4. 空间中一个点到一条直线的距离公式中,A、B、C、D分别代表什么?A. 直线方程的系数B. 直线方程的常数项C. 点的坐标D. 点到直线的距离答案:A, C5. 空间中一个平面的方程可以表示为?A. Ax + By + Cz + D = 0B. Ax + By + Cz = DC. Ax + By + Cz + D = ED. Ax + By + Cz = 0答案:A, D结束语:以上是立体测试题及答案的全部内容,希望对你有所帮助。
(一轮)单元质检卷七空间向量与立体几何含解析新人教A版

单元质检卷七 空间向量与立体几何(时间:100分钟 满分:150分)一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2020河北沧州一中月考)下列说法正确的是( )A.棱柱的各个侧面都是平行四边形B.底面是矩形的四棱柱是长方体C.有一个面为多边形,其余各面都是三角形的几何体是棱锥D.直角三角形绕其一边所在直线旋转一周形成的几何体是圆锥2.(2020辽宁大连高三模拟)已知两条不同的直线l ,m 和一个平面α,下列说法正确的是( ) A.若l ⊥m ,m ∥α,则l ⊥α B.若l ⊥m ,l ⊥α,则m ∥α C.若l ⊥α,m ∥α,则l ⊥mD.若l ∥α,m ∥α,则l ∥m3.(2020广东高三一模(理))已知直三棱柱ABC-A 1B 1C 1的体积为V ,若P ,Q 分别在AA 1,CC 1上,且AP=13AA 1,CQ=13CC 1,则四棱锥B-APQC 的体积是( ) A.16VB.29VC.13VD.79V4.(2020宁夏六盘山高级中学高三模拟)对于不同的直线m ,n 和平面α,β,α⊥β的一个充分条件是( ) A.m ⊥n ,m ∥α,n ∥β B.m ⊥n ,α∩β=m ,n ⊂α C.m ∥n ,n ⊥β,m ⊂α D.m ∥n ,m ⊥α,n ⊥β5.(2020河北博野中学高三开学考试)如图,在棱长为4的正方体ABCD-A 1B 1C 1D 1中,E 为D 1C 1的中点.过点B 1,E ,A 的平面截该正方体所得的截面周长为( ) A.6√2+4√5 B.4√2+2√5 C.5√2+3√5D.8√2+4√56.(2020山东日照五莲丶潍坊安丘、潍坊诸城、临沂兰山高三6月模拟)唐朝的狩猎景象浮雕银杯如图1所示.其浮雕临摹了国画、漆绘和墓室壁画,体现了古人的智慧与工艺.它的盛酒部分可以近似地看作是半球与圆柱的组合体(假设内壁表面光滑,忽略杯壁厚度),如图2所示.已知球的半径为R ,酒杯内壁表面积为143πR 2,设酒杯上部分(圆柱)的体积为V 1,下部分(半球)的体积为V 2,则V1V 2=( )A.2B.32C.1 D.347.(2020全国2,理10)已知△ABC是面积为9√34的等边三角形,且其顶点都在球O的球面上.若球O的表面积为16π,则O到平面ABC的距离为()A.√3B.32C.1 D.√328.(2020山东泰安第二中学月考)菱形ABCD的边长为2,现将△ACD沿对角线AC折起使平面ACD'⊥平面ACB,则此时所成空间四面体体积的最大值为()A.16√327B.5√39C.1D.√34二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.9.在正四面体A-BCD中,E,F,G分别是BC,CD,DB的中点,下面四个结论中正确的是()A.BC∥平面AGFB.EG⊥平面ABFC.平面AEF⊥平面BCDD.平面ABF⊥平面BCD10.如图,已知圆锥的顶点为S,底面圆O的两条直径分别为AB和CD,且AB⊥CD,若平面SAD∩平面SBC=l,则以下结论正确的是()A.AD∥平面SBCB.l∥ADC.若E是底面圆周上的动点,则△SAE的最大面积等于△SAB的面积D.l与平面SCD所成角的大小为45°11.(2020河南洛阳高三模拟)如图,已知正方体ABCD-A1B1C1D1的棱长为2,E为棱CC1的中点,F为棱AA1上的点,且满足A1F∶FA=1∶2,点F,B,E,G,H为过三点B,E,F的平面BMN与正方体ABCD-A1B1C1D1的棱的交点,则下列说法正确的是()A.HF∥BEB.三棱锥B1-BMN的体积为6C.直线MN与平面A1B1BA的夹角是45°D.D1G∶GC1=1∶3.则下列结论正确12.如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=√22的是()A.三棱锥A-BEF的体积为定值B.当E向D1运动时,二面角A-EF-B逐渐变小C.EF在平面ABB1A1内的射影长为12D.当E与D1重合时,异面直线AE与BF所成的角为π4三、填空题:本题共4小题,每小题5分,共20分.13.正三棱锥P-ABC中,PA⊥平面ABC,∠ACB=90°,且PA=AC=BC=a,则异面直线PB与AC所成角的正切值等于.14.(2020辽宁高三二模(理))已知一个圆柱的侧面积等于表面积的一半,且其轴截面的周长是18,则该圆柱的体积是.15.(2020福建福州高三期末)《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的鳖臑P-ABC中,PA⊥平面ABC,∠ACB=90°,CA=4,PA=2,D为AB中点,E为△PAC内的动点(含边界),且PC⊥DE.①当E在AC上时,AE=;②点E的轨迹的长度为.16.(2020新高考全国1,16)已知直四棱柱ABCD-A1B1C1D1的棱长均为2,∠BAD=60°.以D1为球心,√5为半径的球面与侧面BCC1B1的交线长为.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)如图,已知正方体ABCD-A1B1C1D1的棱长为3,M,N分别是棱AA1,AB上的点,且AM=AN=1.(1)证明:M,N,C,D1四点共面;(2)求几何体AMN-DD1C的体积.18.(12分)(2020广西南宁二中高三月考)如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.(1)求证:AD⊥BM;时,试确定点E的位置.(2)点E是线段DB上的一动点,当二面角E-AM-D大小为π319.(12分)(2020全国高三二模(文))如图,扇形AOB的圆心角为90°,半径为2,四边形SOBC为正方形,平⏜于点M,交OA于点N.面SOBC⊥平面AOB,过直线SC作平面SCMN交AB(1)求证:MN ∥OB ;(2)求三棱锥S-MON 体积的最大值. 20.(12分)(2020四川宜宾叙州第二中学高三一模(理))如图,已知三棱柱ABC-A 1B 1C 1中,侧棱与底面垂直,且AA 1=AB=AC=2,AB ⊥AC ,M ,N 分别是CC 1,BC 的中点,点P 在线段A 1B 1上,且A 1P ⃗⃗⃗⃗⃗⃗⃗ =λPB 1⃗⃗⃗⃗⃗⃗⃗ . (1)求证:不论λ取何值,总有AM ⊥PN ;(2)当λ=1时,求平面PMN 与平面ABC 夹角的余弦值. 21.(12分)(2020山东高三联考三模)已知直三棱柱ABC-A 1B 1C 1,AB=AC=AA 1=1,M ,N ,P 分别为A 1C 1,AB 1,BB 1的中点,且AP ⊥MN. (1)求证:MN ∥平面B 1BCC 1; (2)求∠BAC ;(3)求二面角A 1-PN-M 的余弦值.22.(12分)(2020重庆沙坪坝南开中学高三月考)如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAB⊥底面ABCD,E为PC上的点,且BE⊥平面APC.(1)求证:平面PAD⊥平面PBC;(2)当三棱锥P-ABC体积最大时,求二面角B-AC-P的余弦值.参考答案单元质检卷七空间向量与立体几何1.A对于A,根据棱柱的性质可知,棱柱的各个侧面都是平行四边形,故A正确;对于B,底面是矩形,若侧棱不垂直于底面,这时的四棱柱是斜四棱柱,不是长方体,只有底面是矩形的直四棱柱才是长方体,故B错误;对于C,有一个面为多边形,其余各面都是三角形的几何体不一定是棱锥,只有其余各面是有一个公共顶点的三角形的几何体,才是棱锥,故C错误;对于D,直角三角形绕其一条直角边所在直线旋转一周形成的几何体是圆锥,如果绕着它的斜边旋转一周,形成的几何体则是两个具有共同底面的圆锥,故D错误.故选A.2.C对选项A,如图所示,在长方体中,满足l⊥m,m∥α,此时不满足l⊥α,故A错误;对选项B,如图所示,在长方体中,满足l ⊥m ,l ⊥α,此时不满足m ∥α,故B 错误; 对选项C,若l ⊥α,m ∥α,则l ⊥m ,故C 正确. 对选项D,如图所示,在长方体中,满足l ∥α,m ∥α,不满足l ∥m ,故D 错误.故选C . 3.B 在棱BB 1上取一点H ,使BH=13BB 1,连接PH ,QH ,由题意S △PHQ =S △ABC ,BH ⊥平面PHQ ,所以V B-PHQ =13S △PHQ ·BH=13S △ABC ·13BB 1=19V ,V ABC-PHQ =S △ABC ·BH=13S △ABC ·BB 1=13V ,所以V B-APQC =V ABC-PHQ -V B-PHQ =13V-19V=29V.故选B .4.C A 选项中,根据m ⊥n ,m ∥α,n ∥β,得到α⊥β或α∥β,所以A 错误;B 选项中,m ⊥n ,α∩β=m ,n ⊂α,不一定得到α⊥β,所以B 错误;C 选项中,因为m ∥n ,n ⊥β,所以m ⊥β, 又m ⊂α,从而得到α⊥β,所以C 正确;D 选项中,根据m ∥n ,m ⊥α,所以n ⊥α,而n ⊥β,所以得到α∥β,所以D 错误.故选C . 5.A 如图,取DD 1的中点F ,连接AF ,EF ,显然EF ∥AB 1,则四边形AB 1EF 为所求的截面. 因为D 1E=C 1E=2,所以B 1E=√22+42=2√5,AB 1=√42+42=4√2,EF=√22+22=2√2,AF=√42+22=2√5,所以截面的周长为6√2+4√5.6.A 设酒杯上部分(圆柱)的高为h ,球的半径为R ,则酒杯下部分(半球)的表面积为2πR 2,酒杯内壁表面积为143πR 2,得圆柱侧面积为143πR 2-2πR 2=83πR 2,酒杯上部分(圆柱)的表面积为2πR ×h=83πR 2,解得h=43R ,酒杯下部分(半球)的体积V 2=12×43π×R 3=23πR 3,酒杯上部分(圆柱)的体积V 1=πR 2×43R=43πR 3,所以V 1V 2=43πR 323πR 3=2.故选A .7.C 设等边三角形ABC 的边长为a ,球O 的半径为R ,△ABC 的外接圆的半径为r ,则S △ABC =√34a 2=9√34,S 球O =4πR 2=16π,解得a=3,R=2.故r=23×√32a=√3.设O 到平面ABC 的距离为d ,则d 2+r 2=R 2,故d=√R 2-r 2=√4-3=1.故选C . 8.A 设AC 的中点为O ,因为D'C=D'A ,所以D'O ⊥AC.又因为平面ACD'⊥平面ACB ,平面ACD'∩平面ACB=AC ,所以D'O ⊥平面ABC ,设∠ABC=∠ADC=α,α∈(0,π),在△ACD 中,DO=AD cos α2=2cos α2,由题意可知D'O=DO=2cos α2,S △ABC =12×2×2sin α=2sin α,V D'-ABC =13S △ABC ×D'O=43sin αcos α2=83sin α2cos 2α2=83sin α21-sin 2α20<α2<π2.设t=sin α2,则V D'-ABC =83(t-t 3),且0<t<1,所以V'D'-ABC =83(1-3t 2),所以当0<t<√33时,V'D'-ABC >0,当√33<t<1时,V'D'-ABC <0,所以当t=√33时,V D'-ABC 取得最大值16√327,所以四面体D'ABC 体积的最大值为16√327.故选A .9.ABD ∵F ,G 分别是CD ,DB 的中点,∴GF ∥BC ,则BC ∥平面AGF ,故A 正确;∵E ,F ,G 分别是BC ,CD ,DB 的中点,∴CD ⊥AF ,CD ⊥BF ,AF ∩BF=F ,即CD ⊥平面ABF ,∵EG ∥CD , ∴EG ⊥平面ABF ,故B 正确; ∵CD ⊥平面ABF ,CD ⊂平面BCD ,∴平面ABF ⊥平面BCD ,故D 正确,C 错误.故选ABD .10.ABD 由AB 和CD 是圆O 的直径,且AB ⊥CD ,得四边形ABCD 为正方形,则AD ∥BC.BC ⊂平面SBC ,从而AD ∥平面SBC ,故A 正确;又因为AD ⊂平面SAD ,且平面SAD ∩平面SBC=l ,所以l ∥AD ,故B 正确; 因为S △SAE =12SA·SE sin ∠ASE ,当∠ASB 为钝角时,(S △SAE )max >S △SAB , 当∠ASB 为锐角或直角时,(S △SAE )max =S △SAB ,故C 不正确;由l ∥AD ,得l 与平面SCD 所成的角等于AD 与平面SCD 所成的角,即为∠ADO ,又因为∠ADO=45°,故D 正确.故选ABD .11.AD 对于A 选项,由于平面ADD 1A 1∥平面BCC 1B 1,而平面BMN 与这两个平面分别交于HF 和BE ,根据面面平行的性质定理可知HF ∥BE ,故A 正确;由于A 1F ∶FA=1∶2,而E 是CC 1的中点,故MA 1=1,C 1N=2.对于B 选项,V B 1-BMN =V B -M N B 1=13×12×MB 1×NB 1×BB 1=13×12×3×4×2=4,故B 错误;对于C 选项,由于B 1N ⊥平面A 1B 1BA ,所以直线MN 与平面A 1B 1BA 所成的角为∠NMB 1,且tan ∠NMB 1=B 1N B 1M =43≠1,故C 错误;对于D 选项,可知D 1G=12,GC 1=32,故D 正确. 综上可知,正确的为AD,故选AD .12.AC 连接BD ,AC ,交于点O ,由正方体性质知BDD 1B 1是矩形,∴S △BEF =12EF·BB 1=12×√22×1=√24,由正方体性质知AO ⊥平面BDD 1B 1,∴AO 是点A 到平面BDD 1B 1的距离,即AO=√22,∴V A-BEF =13S △BEF ×AO=13×√24×√22=112,∴V A-BEF 是定值,故A 正确;连接A 1C 1与B 1D 1交于点M ,连接AD 1,AB 1,由正方体性质知AD 1=AB 1,M 是B 1D 1中点,∴AM ⊥EF ,又BB 1⊥EF ,BB 1∥AA 1,∴二面角A-EF-B 的平面角即为∠A 1AM ,在直角三角形AA 1M 中,tan ∠MAA 1=√22为定值,故B 不正确;如图,作FH ⊥A 1B 1,EG ⊥A 1B 1,FT ⊥EG ,垂足分别为点H ,G ,T.在直角三角形EFT 中,FT=cos45°×EF=√22×√22=12,∴HG=FT=12,故C 正确;当E 与D 1重合时,F 与M 重合,连接AC 与BD 交于点R ,连接D 1R ,D 1R ∥BM ,异面直线AE 与BF 所成的角,即为直线AD 1与D 1R 所成的角,在△AD 1R 中,AD 1=√2,D 1R=MB=√BB 12+MB 12=√62,AR=√22, 由余弦定理得cos ∠AD 1R=√32,则∠AD 1R=π6,故D 不正确,故选AC .13.√2 如图所示将此三棱锥补成正方体DBCA-D 1B 1C 1P ,则PB 与AC 所成的角的大小即此正方体体对角线PB 与棱BD 所成角的大小,在Rt △PDB 中,tan ∠DBP=PD DB=√2,∴异面直线PB 与AC 所成角的正切值为√2.14.27π 设圆柱的底面圆的半径为r ,高为h.由题意可得{2πrℎ2πr 2+2πrℎ=12,2(2r +ℎ)=18,解得r=h=3,则该圆柱的体积是πr 2h=27π. 15.①2 ②2√55①当E 在AC 上时,因为PA ⊥平面ABC ,故PA ⊥DE ,又PC ⊥DE ,故DE ⊥平面PAC.故DE ⊥AC.又∠ACB=90°,D 为AB 中点,故DE ∥BC ,所以E 为AC 中点.故AE=12AC=2. ②取AC 中点F ,则由①知DF ⊥平面PAC ,故PC ⊥DF ,又PC ⊥DE ,设平面DEF ∩PC=G ,则有PC ⊥平面DGF.故点E 的轨迹为线段FG.又此时CF=2,故sin ∠PCA=√22+42=√55.所以FG=CF·sin ∠PCA=2√55. 16.√22π 如图所示,∵∠B 1C 1D 1=∠B 1A 1D 1=∠BAD=60°,且B 1C 1=C 1D 1,∴△B 1C 1D 1为等边三角形. ∴B 1D 1=2.设点O 1是B 1C 1的中点,则O 1D 1=√3,易证D 1O 1⊥平面BCC 1B 1,设P 是球面与侧面BCC 1B 1交线上任意一点,连接O 1P ,则O 1D 1⊥O 1P ,∴D 1P 2=D 1O 12+O 1P 2,即5=3+O 1P 2,∴O 1P=√2.即P 在以O 1为圆心,以√2为半径的圆上.取BB 1,CC 1的中点分别为E ,F ,则B 1E=C 1F=O 1B 1=O 1C 1=1,EF=2, ∴O 1E=O 1F=√2,O 1E 2+O 1F 2=EF 2=4,∴∠EO 1F=90°, ∴交线EPF⏜=14×2√2×π=√22π. 17.(1)证明∵A 1D 1∥AD ,A 1D 1=AD ,又BC ∥AD ,BC=AD ,∴A 1D 1∥BC ,且A 1D 1=BC ,连接A 1B ,则四边形A 1BCD 1是平行四边形,所以A 1B ∥D 1C.在△ABA 1中,AM=AN=1,AA 1=AB=3,所以AM AA 1=ANAB ,所以MN ∥A 1B ,所以MN ∥D 1C ,所以M ,N ,C ,D 1四点共面. (2)解因为平面ABB 1A 1∥平面DCC 1D 1,又M ,N ,C ,D 1四点共面,所以平面AMN ∥平面DD 1C , 延长CN 与DA 相交于点P ,因为AN ∥DC , 所以AN DC=PA PD,即13=PAPA+3,解得PA=32,同理延长D 1M 与DA 相交于点Q ,可得QA=32,所以点P 与点Q 重合,所以D 1M ,DA ,CN 三线相交于一点,所以几何体AMN-DD 1C 是一个三棱台,所以V AMN -DD 1C =13×12+√12×92+92×3=132. 18.解取AM 的中点O ,AB 的中点N ,则ON ,OA ,OD 两两垂直,以O 为原点建立如图所示的空间直角坐标系,则A (√22,0,0),B -√22,√2,0,M -√22,0,0,D 0,0,√22.(1)证明:由于AD ⃗⃗⃗⃗⃗ =-√22,0,√22,BM ⃗⃗⃗⃗⃗⃗ =(0,-√2,0),则AD ⃗⃗⃗⃗⃗ ·BM ⃗⃗⃗⃗⃗⃗ =0,故AD ⃗⃗⃗⃗⃗ ⊥BM ⃗⃗⃗⃗⃗⃗ ,即AD ⊥BM.(2)解:设存在满足条件的点E ,并设DE ⃗⃗⃗⃗⃗ =N DB ⃗⃗⃗⃗⃗⃗ ,λ∈(0,1],DB⃗⃗⃗⃗⃗⃗ =-√22,√2,-√22,则DE ⃗⃗⃗⃗⃗ =λ-√22,√2,-√22,则点E 的坐标为-√22N ,√2N ,√22−√22N ,λ∈(0,1].易得平面ADM 的法向量可以取n 1=(0,1,0),设平面AME 的法向量为n 2=(x ,y ,z ),则AM ⃗⃗⃗⃗⃗⃗ =(-√2,0,0),AE ⃗⃗⃗⃗⃗ =-√22N -√22,√2N ,√22−√22N ,则{n 2·AM ⃗⃗⃗⃗⃗⃗ =0,n 2·AE ⃗⃗⃗⃗⃗ =0,所以{-√2x =0,(-√22λ-√22)x +√2λy +(√22-√22λ)z =0,故n 2=(0,λ-1,2λ). cos <n 1,n 2>=n 1·n 2|n 1||n 2|=√(λ-1)+4λ2,由于二面角E-AM-D 大小为π3, 故cos π3=√(λ-1)+4λ2=12,由于λ∈(0,1],故解得λ=2√3-3或-2√3-3(舍去). 故当E 位于线段DB 之间,且DE DB=2√3-3时,二面角E-AM-D 大小为π3.19.(1)证明因为SC ∥OB ,SC ⊂平面SCMN ,OB ⊄平面SCMN ,所以OB ∥平面SCMN.又OB ⊂平面AOB ,平面SCMN ∩平面AOB=MN ,所以MN ∥OB. (2)解因为平面SOBC ⊥平面AOB ,平面SOBC ∩平面AOB=OB ,SO ⊥OB ,所以SO ⊥平面AOB ,即线段SO 的长就是三棱锥S-MON 的高. 因为OA ⊥OB ,MN ∥OB , 所以MN ⊥OA.设ON=x (0<x<2),则MN=√4-x 2,所以三棱锥S-MON 的体积为V=13SO ·12ON·MN=13×2×12×x ×√4-x 2=13x ×√4-x 2=13√4x 2-x 4=13√4-(x 2-2)2.所以,当x=√2时,三棱锥S-MON 体积有最大值,V max =23.20.解以点A 为坐标原点,以AB ,AC ,AA 1所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系A-xyz ,A 1(0,0,2),B 1(2,0,2),M (0,2,1),N (1,1,0),则A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(2,0,0),AA 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,2),AN ⃗⃗⃗⃗⃗⃗ =(1,1,0).(1)证明:∵A 1P ⃗⃗⃗⃗⃗⃗⃗ =N PB 1⃗⃗⃗⃗⃗⃗⃗ =λ(A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ −A 1P ⃗⃗⃗⃗⃗⃗⃗ ), ∴A 1P ⃗⃗⃗⃗⃗⃗⃗ =λ1+λA 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(2λ1+λ,0,0), ∵AP ⃗⃗⃗⃗⃗ =AA 1⃗⃗⃗⃗⃗⃗⃗ +A 1P ⃗⃗⃗⃗⃗⃗⃗ =(0,0,2)+2λ1+λ,0,0=2λ1+λ,0,2,PN ⃗⃗⃗⃗⃗⃗ =AN ⃗⃗⃗⃗⃗⃗ −AP ⃗⃗⃗⃗⃗ =(1,1,0)-(2λ1+λ,0,2)=1-λ1+λ,1,-2.∵AM⃗⃗⃗⃗⃗⃗ =(0,2,1),∴AM ⃗⃗⃗⃗⃗⃗ ·PN ⃗⃗⃗⃗⃗⃗ =0+2-2=0,即AM ⃗⃗⃗⃗⃗⃗ ⊥PN ⃗⃗⃗⃗⃗⃗ ,因此,无论λ取何值,都有AM ⊥PN.(2)解:当λ=1时,P (1,0,2),PN⃗⃗⃗⃗⃗⃗ =(0,1,-2),PM ⃗⃗⃗⃗⃗⃗ =(-1,2,-1), 而平面ABC 的法向量n =(0,0,1),设平面PMN 的法向量为m =(x ,y ,z ),则{m ·PM⃗⃗⃗⃗⃗⃗ =0,m ·PN ⃗⃗⃗⃗⃗⃗ =0,∴{-x +2y -z =0,y -2z =0,则m =(3,2,1),设平面PMN 与平面ABC 的夹角为θ,则cos θ=|m ·n ||m ||n |=√1414. 因此,平面PMN 与平面ABC 的夹角的余弦值是√1414. 21.(1)证明取B 1C 1的中点Q ,连接MQ ,NP ,PQ ,则MQ ∥A 1B 1,且MQ=12A 1B 1,PN ∥AB ,且PN=12AB ,又AB ∥A 1B 1,AB=A 1B 1,所以PN ∥MQ ,且PN=MQ , 所以PNMQ 为平行四边形,所以MN ∥PQ. 又MN ⊄平面B 1BCC 1,PQ ⊂平面B 1BCC 1, 所以MN ∥平面B 1BCC 1. (2)解设AB ⃗⃗⃗⃗⃗ =a ,AC ⃗⃗⃗⃗⃗ =b ,AA 1⃗⃗⃗⃗⃗⃗⃗ =c ,∠BAC=θ,由已知可得,|a |=|b |=|c |=1,且a ·c =b ·c =0,则AP ⃗⃗⃗⃗⃗ =a +12c ,NM ⃗⃗⃗⃗⃗⃗⃗ =PQ ⃗⃗⃗⃗⃗ =12BB 1⃗⃗⃗⃗⃗⃗⃗ +12B 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =12c +12b -12a ,因为AP ⊥MN ,所以AP ⃗⃗⃗⃗⃗ ·NM ⃗⃗⃗⃗⃗⃗⃗ =a +12c 12c +12b -12a =12a ·b -12a 2+14c 2=12cos θ-14=0, 所以cos θ=12,即∠BAC=60°.(3)解在平面ABC 内过点A 做射线l 垂直于AB ,易知AB ,l ,AA 1两两垂直,建立如图所示的空间直角坐标系A-xyz ,则P 1,0,12,M14,√34,1,N12,0,12,n 1=(0,1,0)为平面A 1PN 的一个法向量,MN ⃗⃗⃗⃗⃗⃗⃗ =14,-√34,-12,PN⃗⃗⃗⃗⃗⃗ =-12,0,0.设n 2=(x ,y ,z )为平面PMN 的一个法向量,则{n 2·MN ⃗⃗⃗⃗⃗⃗⃗ =0,n 2·PN ⃗⃗⃗⃗⃗⃗ =0,所以{14x -√34y -12z =0,-12x =0,令y=1,则n 2=0,1,-√32,则cos <n 1,n 2>=n 1·n 2|n 1||n 2|=11×√74=2√77,由图知二面角A 1-PN-M 的平面角是锐角,所以二面角A 1-PN-M 的余弦值为2√77. 22.(1)证明∵侧面PAB ⊥底面ABCD ,侧面PAB ∩底面ABCD=AB ,四边形ABCD 为正方形,∴BC ⊥AB ,∴BC ⊥平面PAB ,又AP ⊂平面PAB ,∴AP ⊥BC ,又BE ⊥平面APC ,AP ⊂平面PAC ,∴AP ⊥BE ,∵BC ∩BE=B ,BC ,BE 在平面PBC 中,∴AP ⊥平面PBC ,又AP ⊂平面PAD , ∴平面PAD ⊥平面PBC.(2)解V P-ABC =V C-APB =13×12×PA ×PB ×BC=13×PA ×PB ,求三棱锥P-ABC 体积的最大值,只需求PA ×PB 的最大值.令PA=x ,PB=y ,由(1)知,PA ⊥PB ,∴x 2+y 2=4, 而V P-ABC =13xy ≤13×x 2+y 22=23,当且仅当x=y=√2,即PA=PB=√2时,V P-ABC 的最大值为23.如图所示,分别取线段AB ,CD 中点O ,F ,连接OP ,OF ,以点O 为坐标原点,以OP ,OB 和OF 分别作为x 轴,y 轴和z 轴,建立空间直角坐标系O-xyz. 由已知A (0,-1,0),C (0,1,2),P (1,0,0),∴AP ⃗⃗⃗⃗⃗ =(1,1,0),AC ⃗⃗⃗⃗⃗ =(0,2,2), 令平面PAC 的一个法向量n =(x ,y ,z ),则{n ·AP⃗⃗⃗⃗⃗ =0,n ·AC ⃗⃗⃗⃗⃗ =0,∴{x +y =0,2y +2z =0, ∴n =(1,-1,1).易知平面ABC 的一个法向量m =(1,0,0),设二面角B-AC-P 的平面角为θ,由图知θ为锐角, 则cos θ=|n ·m |n ||m ||=|√3=√33.。
《立体几何》测试及答案

《立体几何》测试及答案(时间:120分钟满分:150分)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有 一项是符合题目要求的.1 .已知平而。
内的一条直线1及平而£,则'3_L £”是“ a_L £”的()A.充分必要条件B.充分不必要条件C.必要不充分条件 D,既不充分也不必要条件 解析根据直线与平面垂直的判定定理,由lu "”可证得“a_L £”,即充分性是 成立的.反之由“ a 工B,k a”不一定得到“AL £”,即必要性不成立.所以是 “。
J_ £ ”的充分不必要条件.故选B.答案B72 .已知圆锥的顶点为凡母线州,所所成角的余弦值为石,以与圆锥底面所成角为45° ,若 O △为5的面积为5仃,则该圆锥的侧面积为() A. 40(72 +1) nB. 40^2 HC.8(4i5 + 5) nD. 8710 n解析设。
为圆锥底而圆的圆心,设底而圆的半径为r.以与圆锥底而所成角为45° ,即/80=45°.所以以=小厂7 7母线闩1,所所成角的余弦值为5即cosN 川沙=小 o o 由 S^=^PA • j^sinZJj^=|x2?X^^=5J15. A?=40, , 2 o v故 S 秘侧=n r • PA — n r • \[2r=y[2 n y = 4(h/2 n .答案B3 .如图,在正四棱柱物/一儿RG 〃中,底而边长为2,直线。
乙与平而月以所成角的正弦值 为今则该正四棱柱的高为()贝I] sinN 川哈、= 7、J15 S 8A. 2B. 3C. 4D. 5解析以〃为坐标系原点,DA, DC 、弧所在直线分别为x, y, z 轴建立空间直角坐标系。
一 xyz,如图所示,设正四棱柱的高为方,则。
(0, 0,0),月(2, 0, 0),。
(0, 2, 0), 〃(0, 0, 血,4(0, 2,a ),五=(0, 0,方),赤=(-2, 2, 0),遨=(0, -2,方).设平而月曲的法n • m —2乂+2%=0,向量为〃=(%,必,%),则j —令二=2,则必=方,&=方,A=(/b h,.n •速=-2%+方冬=0, 2)为平面月四的一个法向量.又直线CG 与平面月8所成角的正弦值为所以cos " CG )答案C4 .设三棱柱 四。
立体几何专题评估测试题及详细答案
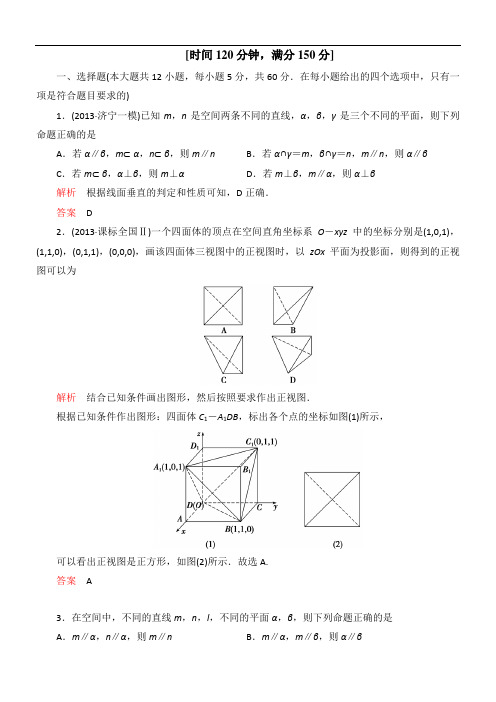
[时间120分钟,满分150分]一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2013·济宁一模)已知m,n是空间两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是A.若α∥β,m⊂α,n⊂β,则m∥n B.若α∩γ=m,β∩γ=n,m∥n,则α∥βC.若m⊂β,α⊥β,则m⊥αD.若m⊥β,m∥α,则α⊥β解析根据线面垂直的判定和性质可知,D正确.答案D2.(2013·课标全国Ⅱ)一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为解析结合已知条件画出图形,然后按照要求作出正视图.根据已知条件作出图形:四面体C1-A1DB,标出各个点的坐标如图(1)所示,可以看出正视图是正方形,如图(2)所示.故选A.答案A3.在空间中,不同的直线m,n,l,不同的平面α,β,则下列命题正确的是A.m∥α,n∥α,则m∥n B.m∥α,m∥β,则α∥βC.m⊥l,n⊥l,则m∥n D.m⊥α,m⊥β,则α∥β答案D4.(2013·大兴一模)已知平面α,β,直线m,n,下列命题中不正确的是A.若m⊥α,m⊥β,则α∥βB.若m∥n,m⊥α,则n⊥αC.若m∥α,α∩β=n,则m∥n D.若m⊥α,m⊂β,则α⊥β解析C中,当m∥α时,m只和过m平面与β的交线平行,所以C不正确.答案C5.(2013·滨州模拟)一个几何体的三视图如图所示,则该几何体的体积为A.1解析由三视图可知,该几何体是四棱锥,以俯视图为底,高为1,俯视图的面积为1×1=1,所以四棱锥的体积为13×1×1=13,选B.答案B6.下列命题正确的是A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内的三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面垂直解析A不正确,满足条件的直线可能相交也可能异面;B不正确,当两个平面相交时也满足条件;由线面平行的性质定理可知C正确;D不正确,垂直于同一个平面的两个平面可能平行,也可能相交.答案C7.某几何体的三视图如图所示,则该几何体的表面积为πB .22πC .(22+1)πD .(22+2)π解析 由三视图可知该几何体是两个高相等、底面完全重合的圆锥,圆锥的底面半径为1,高为1,则该几何体的表面积为2×πrl =2×π×1×2=22π.答案 B8.设m ,n 是不同的直线,α,β,γ是不同的平面,有以下四个命题: ① ⎭⎬⎫α∥βα∥γ⇒β∥γ;② ⎭⎬⎫α⊥βm ∥α⇒m ⊥β; ③⎭⎬⎫m ⊥αm ∥β⇒α⊥β;④⎭⎬⎫m ∥n n ⊂α⇒m ∥α. 其中真命题的是 A .①③B .①④C .②③D .②④解析 ①正确,平行于同一平面的两平面平行;②中m 可能在平面β内,也可能m ∥β,m ⊥β,③正确.④中可能m ⊂α.答案 A9.(2013·临汾模拟)若某几何体的三视图是如图所示的三个直角三角形,则该几何体的外接球的表面积为A .10πB .50πC .25πD .100π解析 由三视图可知该几何体为三棱锥,并且在同一顶点上的三条棱两两垂直,且棱长分别为3、4、5,故该几何体的外接球也就是棱长分别为3、4、5长方体的外接球,则该外接球的半径R =1232+42+52=522,所以S =4πR 2=50π.答案 B10.(2013·太原模拟)几何体ABCDEP 的三视图如图,其中正视图为直角梯形,侧视图为直角三角形,俯视图为正方形,则下列结论中不成立的是A .BD ∥平面PCEB .AE ⊥平面PBC C .平面BCE ∥平面ADPD .CE ∥DP解析 由三视图可知,该几何体的底面是正方形,且棱EB 和PA 都与底面ABCD 垂直.若CE ∥DP ,则CE 在平面PDA 上的射影和DP 平行,这和几何体的侧视图矛盾,故选项D 不成立.答案 D11.若底面边长为a 的正四棱锥的全面积与棱长为a 为正方体的全面积相等,那么这个正四棱锥的侧棱与底面所成角的余弦值为解析 由题意知正四棱锥的每个侧面面积为54a 2.设正四棱锥的侧棱长为x ,则正四棱锥的斜高h ′=x 2-a 24,所以有12x2-a24·a=54a2,解得x=262a.所以正四棱锥的侧棱与底面所有角的余弦值为22a262a=1313.答案C12.如图所示,正方体ABCD-A1B1C1D1中,E、F分别是正方形ADD1A1和ABCD的中心,G是CC1的中点,设GF、C1E与AB所成的角分别是α、β,则α+β等于A.120°B.60°C.75°D.90°解析选BC的中点M,连接FM、MG,则∠GFM为GF与AB所成的角;连接ED1,则∠EC1D1为C1E与AB所成的角.计算出MF,MG,ED1的长度可知C1D1D1E=MGMF,故Rt△GMF∽Rt△C1ED,∴∠GFM+∠EC1D1=90°.选D.答案D二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)13.将边长为2的正方形沿对角线AC折起,以A,B,C,D为顶点的三棱锥的体积最大值等于________.解析如图所示,设O是正方形ABCD的对角线AC和BD的交点,AH是点A到平面BCD的距离,因为S△BCD=2,所以当AH最大时,所求三棱锥的体积就最大,由图可知当点H与点O重合时,AH最大,此时AH=AO=2,则三棱锥的体积最大值为V=13×2×2=223.答案22314.(2013·扬州模拟)正四面体ABCD 中,AO ⊥平面BCD ,垂足为O ,设M 是线段AO 上一点,且∠BMC 是直角,则AMMO 的值为________.解析 如图所示,设正四面体ABCD 的棱长为2,由条件知O 是正三角形BCD 的重心,所以BO =CO =233,AD =22-⎝ ⎛⎭⎪⎫2332=263.设MO =x ,则CM 2=BM 2=x 2+43.又因为∠BMC 是直角,所以BC 2=CM 2+BM 2, 即4=2⎝ ⎛⎭⎪⎫x 2+43,解得x =63,∴MO =63,即MO =12AO , 故AMMO =1. 答案 115.如图,四边形ABCD 为菱形,四边形CEFB 为正方形,平面ABCD ⊥平面CEFB ,CE =1,∠AED =30°,则异面直线BC 与AE 所成的角的大小为________.解析 由题意,正方形和菱形的边长均为1. 又面ABCD ⊥平面CEFB ,所以CE ⊥平面ABCD ,于是CE ⊥CD ,从而DE = 2.在△ADE 中,AD =1,DE =2,∠AED =30°, 由正弦定理得AD sin ∠AED =DEsin ∠EAD,所以sin ∠EAD =DE ·sin ∠AED AD =22, 故∠EAD =45°.又BC ∥AD ,所以异面直线BC 与AE 所成角为∠EAD ,即45°. 答案 45°16.设l ,m ,n 表示不同的直线,α、β、γ表示不同的平面,给出下列四个命题:①若m ∥l ,且m ⊥α,则l ⊥α;②若m ∥l ,且m ∥α,则l ∥α;③若α∩β=l ,β∩γ=m ,γ∩α=n ,则l ∥m ∥n ;④若α∩β=m ,β∩γ=l ,γ∩α=n ,且n ∥β,则l ∥m .其中正确命题的个数为________.解析 ①正确.②中当直线l ⊂α时,不成立.③中,还有可能相交于一点,不成立.④正确,故有2个正确的命题.答案 2三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤) 17.(10分)(2013·济南模拟)如图,斜三棱柱A 1B 1C 1-ABC 中,侧面AA 1C 1C ⊥底面ABC ,底面ABC 是边长为2的等边三角形,侧面AA 1C 1C 是菱形,∠A 1AC =60°,E 、F 分别是A 1C 1、AB 的中点.(1)求证:EC ⊥平面ABC ; (2)求三棱锥A 1-EFC 的体积.解析 (1)证明 在平面AA 1C 1C 内,作A 1O ⊥AC ,O 为垂足. 因为∠A 1AC =60°,所以AO =12AA 1=12AC , 即O 为AC 的中点,所以OC 綊A 1E . 因而EC 綊A 1O .因为侧面AA 1C 1C ⊥底面ABC ,交线为AC ,A 1O ⊥AC , 所以A 1O ⊥底面ABC ,所以EC ⊥底面ABC .(5分)(2)F 到平面A 1EC 的距离等于B 点到平面A 1EC 距离BO 的一半,而BO =3,所以VA1-EFC=VF-A1EC=13S△A1EC·12BO=13·12A1E·EC·32=13·12·3·32=14.(10分)18.(12分)如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.(1)求证:直线A1D⊥B1C1;(2)判断A1B与平面ADC1的位置关系,并证明你的结论.解析(1)证明在直三棱柱ABC-A1B1C1中,AA1⊥面ABC,所以AA1⊥BC.在等边△ABC中,D是BC中点,所以AD⊥BC.因为在平面A1AD中,A1A∩AD=A,所以BC⊥面A1AD.又因为A1D⊂面A1AD,所以,A1D⊥BC.(3分)在直三棱柱ABC-A1B1C1中,四边形BCC1B1是平行四边形,所以B1C1∥BC,所以A1D⊥B1C1.(6分)(2)在直三棱柱ABC-A1B1C1中,四边形ACC1A1是平行四边形,在平行四边形ACC1A1中连接A1C,交于AC1点O,连接DO.则O为A1C中点.在三角形A1CB中,D为BC中点,O为A1C中点,故DO∥A1B.(10分)因为DO⊂平面DAC1,A1B⊄平面DAC1,所以A1B∥面ADC1,故A1B与面ADC1平行.(12分)19.(12分)(2013·门头沟区一模)如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D 是垂足.(1)求证:AB⊥平面PCD;(2)若PC=PD=1,CD=2,试判断平面α与平面β是否垂直,并证明你的结论.解析(1)证明因为PC⊥α,AB⊂α,所以PC⊥AB.同理PD⊥AB.又PC∩PD=P,故AB⊥平面PCD.(5分)(2)平面α与平面β垂直.(6分)证明设AB与平面PCD的交点为H,连接CH、DH.因为PC⊥α,所以PC⊥CH.在△PCD中,PC=PD=1,CD=2,所以CD2=PC2+PD2=2,即∠CPD=90°.在平面四边形PCHD中,PC⊥PD,PC⊥CH,所以PD∥CH.(10分)又PD⊥β,所以CH⊥β,所以平面α⊥平面β.(12分)20.(12分)如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.(1)求证:A1B∥平面ADC1;(2)若AB=BB1=2,求A1D与平面AC1D所成角的正弦值.解析(1)证明因为三棱柱ABC-A1B1C1是直三棱柱,所以四边形A1ACC1是矩形.连接A1C交AC1于O,则O是A1C的中点.又D是BC的中点,所以在△ADC1中,OD∥A1B.(3分)因为A1B⊄平面ADC1,OD⊂平面ADC1,所以A1B∥平面ADC1.(5分)(2)因为△ABC是等边三角形,D是BC的中点,所以AD⊥BC.以D为原点,建立如图所示空间坐标系D-xyz.由已知AB =BB 1=2,得D (0,0,0),A (3,0,0),A 1(3,0,2),C 1(0,-1,2).(6分) 则DA →=(3,0,0),DC 1→=(0,-1,2),设平面ADC 1的法向量为n =(x ,y ,z ). 由⎩⎪⎨⎪⎧n ·DA →=0n ·DC 1→=0,得到⎩⎨⎧3x =0-y +2z =0,令z =1,则x =0,y =2, 所以n =(0,2,1).(8分)又DA 1→=(3,0,2),得n ·DA 1→=0×3+2×0+1×2=2, 所以cos 〈DA 1→,n 〉=25×7=23535. 设A 1D 与平面ADC 1所成角为θ,则sin θ=|cos 〈DA 1→,n 〉|=23535,(11分) 所以A 1D 与平面ADC 1所成角的正弦值为23535.(12分)21.(12分)(2013·南京模拟)如图,在直角梯形ABCP 中,AP ∥BC ,AP ⊥AB ,AB =BC =12AP =2,D 是AP 的中点,E 、F 、G 分别为PC 、PD 、CB 的中点,将△PCD 沿CD 折起,使得PD ⊥平面ABCD .(1)求证:平面PCD ⊥平面PAD ;(2)求面GEF 与面EFD 所成锐二面角的大小. 解析 (1)证明 ∵PD ⊥平面ABCD ,∴PD ⊥CD .∵CD ⊥AD ,∴CD ⊥平面PAD .∵CD ⊂平面PCD ,∴平面PCD ⊥平面PAD .(5分)(2)如图以D 为原点,以DA→,DC →,DP →为方向向量建立空间直角坐标系D -xyz .则有关点及向量的坐标为G (1,2,0),E (0,1,1),F (0,0,1),EF →=(0,-1,0),EG →=(1,1,-1).(7分)设平面EFG 的法向量为n =(x ,y ,z ),∴⎩⎪⎨⎪⎧ n ·EF →=0n ·EG →=0⇒⎩⎨⎧ -y =0x +y -z =0⇒⎩⎨⎧x =z y =0. 取n =(1,0,1)平面EFG 的一个法向量.(10分)∵DA→=(1,0,0)为平面EFD 的法向量, ∴cos 〈DA →,n 〉=DA →·n |DA →|·|n |=22. ∴面GEF 与面EFD 所成锐二面角的大小为45°.(12分)22.(12分)(2013·朝阳一模)如图,在四棱锥P -ABCD 中,平面PAC ⊥平面ABCD ,且PA ⊥AC ,PA =AD =2.四边形ABCD 满足BC ∥AD ,AB ⊥AD ,AB =BC =1,点E ,F 分别为侧棱PB ,PC 上的点,且PE PB =PF PC =λ.(1)求证:EF ∥平面PAD ;(2)当λ=12时,求异面直线BF 与CD 所成角的余弦值;(3)是否存在实数λ,使得平面AFD ⊥平面PCD 若存在,试求出λ的值;若不存在,请说明理由.解析 (1)证明 由已知,PE PB =PF PC =λ,所以EF ∥BC .因为BC ∥AD ,所以EF ∥AD .而EF ⊄平面PAD ,AD ⊂平面PAD ,所以EF ∥平面PAD .(4分)(2)因为平面ABCD ⊥平面PAC ,平面ABCD ∩平面PAC =AC ,且PA ⊥AC ,所以PA ⊥平面ABCD ,所以PA ⊥AB ,PA ⊥AD .又因为AB ⊥AD ,所以PA ,AB ,AD 两两垂直.如图所示,建立空间直角坐标系,因为AB =BC =1,PA =AD =2,所以A (0,0,0),B (1,0,0),C (1,1,0),D (0,2,0),P (0,0,2).当λ=12时,F 为PC 中点,所以F ⎝ ⎛⎭⎪⎫12,12,1, 所以BF →=⎝ ⎛⎭⎪⎫-12,12,1,CD →=(-1,1,0). 设异面直线BF 与CD 所成的角为θ,所以cos θ=|cos 〈BF →,CD →〉|=⎪⎪⎪⎪⎪⎪⎝ ⎛⎭⎪⎫-12,12,1·-1,1,014+14+1×2=33, 所以异面直线BF 与CD 所成角的余弦值为33.(8分)(3)设F (x 0,y 0,z 0),则PF →=(x 0,y 0,z 0-2), PC→=(1,1,-2). 由已知PF →=λPC →,所以(x 0,y 0,z 0-2)=λ(1,1,-2), 所以⎩⎨⎧ x 0=λ,y 0=λ,z 0=2-2λ.所以AF→=(λ,λ,2-2λ). 设平面AFD 的一个法向量为n 1=(x 1,y 1,z 1).因为AD →=(0,2,0),所以⎩⎪⎨⎪⎧ n 1·AF →=0,n 1·AD →=0. 即⎩⎨⎧ λx 1+λy 1+2-2λz 1=0,2y 1=0.令z 1=λ,得n 1=(2λ-2,0,λ).设平面PCD 的一个法向量为n 2=(x 2,y 2,z 2).因为PD→=(0,2,-2),CD →=(-1,1,0), 所以⎩⎪⎨⎪⎧ n 2·PD →=0,n 2·CD →=0.即⎩⎨⎧2y 2-2z 2=0,-x 2+y 2=0. 令x 2=1,则n 2=(1,1,1).若平面AFD ⊥平面PCD ,则n 1·n 2=0,所以(2λ-2)+λ=0,解得λ=23.所以当λ=23时,平面AFD ⊥平面PCD .(12分)]。
2024最新立体几何知识点归纳

2024最新立体几何知识点归纳立体几何是数学中的一个分支,主要研究空间中的点、直线、平面以及它们之间的关系。
下面是2024年最新的一些立体几何知识点的归纳:1.点、直线和平面的基本性质:点是空间中没有大小的.直线是由无数个点无限延伸而成的,直线上的任意两点可以确定一条直线.平面是由无数个点组成的,其中任意三点不在同一条直线上.2.垂直和平行:在空间中,直线或平面可以相互关系,其中垂直是指两条直线或平面相互垂直于其他直线或平面,平行是指两条直线或平面在空间中保持恒定的距离和方向.3.立体角:在空间中,两条相交直线所围成的角称为立体角,立体角的度量单位是弧度.它是一个三维的角度,可以用来描述空间中的物体在不同角度下的相对位置.4.体积和表面积:体积是指物体所占据的空间的大小,可以通过计算物体所包围的空间的体积得到.表面积是指物体外部的曲面的总面积.计算物体的体积和表面积是进行几何计算的重要内容之一.5.球体和圆锥体:球体是由半径相等的所有点组成的空间几何体,圆锥体是由一个圆和这个圆上的一个点出发的所有直线段组成的几何体.计算球体和圆锥体的体积和表面积是应用立体几何的重要内容之一.6.平行四边形和正方体:平行四边形是一个具有平行的对边的四边形,正方体是一个具有相等的边长和直角的立方体.计算平行四边形和正方体的面积和体积是立体几何的应用之一.7.相似与全等:相似是指两个图形在形状上相似,但是尺寸不同.全等是指两个图形在形状和尺寸上完全相同.利用相似与全等的性质可以解决一些几何问题.8.中点定理和切线定理:中点定理是指连接一条三角形两边中点的线段平行于第三边,并且长度等于第三边的一半.切线定理是指一条直线与一个圆相切于点A的切线,那么切线上的切点与圆心A、切点、圆心连线的夹角是直角.9.三视图和投影:三视图是指一个立体物体从不同方向观察到的投影,包括正视图、侧视图和俯视图.投影是指立体物体在一个平面上的投影,可以通过投影图来描述对象在不同角度下的位置和形状.10.空间几何的应用:立体几何的应用广泛,包括建筑设计、工程测量、机械制图等领域.运用立体几何的知识可以帮助解决实际问题,提高设计和测量的精确度.这些是2024年最新的一些立体几何知识点的归纳,掌握这些知识可以帮助我们更好地理解和应用立体几何.当然,立体几何是一个广阔而深奥的领域,还有很多其他的知识点和应用等待我们进一步探究和学习.。
高考数学一轮复习第七章立体几何阶段检测试题(含解析)文(new)

第七章立体几何阶段检测试题时间:120分钟分值:150分一、选择题(每小题5分,共60分)1.关于空间几何体的结构特征,下列说法不正确的是()A.棱柱的侧棱长都相等B.棱锥的侧棱长都相等C.三棱台的上、下底面是相似三角形D.有的棱台的侧棱长都相等解析:根据棱锥的结构特征知,棱锥的侧棱长不一定都相等.答案:B2.在正方体ABCD-A1B1C1D1中,E,F分别是线段BC,CD1的中点,则直线A1B与直线EF的位置关系是()A.相交B.异面C.平行D.垂直解析:由BC綊AD,AD綊A1D1知,BC綊A1D1,从而四边形A1BCD1是平行四边形,所以A1B∥CD1,又EF⊂平面A1C,EF∩D1C=F,则A1B与EF相交.答案:A3.(2017·嘉兴月考)对于空间的两条直线m,n和一个平面α,下列命题中的真命题是( )A.若m∥α,n∥α,则m∥nB.若m∥α,n⊂α,则m∥nC.若m∥α,n⊥α,则m∥nD.若m⊥α,n⊥α,则m∥n解析:对A,直线m,n可能平行、异面或相交,故选项A错误;对B,直线m与n可能平行,也可能异面,故选项B错误;对C,m与n垂直而非平行,故选项C错误;对D,垂直于同一平面的两直线平行,故选项D正确.答案:D4.设P是异面直线a,b外的一点,则过点P与a,b都平行的平面()A.有且只有一个B.恰有两个C.不存在或只有一个D.有无数个解析:过点P作a1∥a,b1∥b,若过a1,b1的平面不经过a,b,则存在一个平面同时与a,b平行;若过a,b1的平面经过a或b,则不存在这样的平面同时与a,b平行.1答案:C5.若平面α∥平面β,点A,C∈α,B,D∈β,则直线AC∥直线BD的充要条件是()A.AB∥CD B.AD∥CBC.AB与CD相交D.A,B,C,D四点共面解析:由平面α∥平面β知,直线AC与BD无公共点,则直线AC∥直线BD的充要条件是A,B,C,D四点共面.答案:D6.已知a,b为两条不同的直线,α,β为两个不同的平面,且a⊥α,b⊥β,则下列命题中的假命题是()A.若a∥b,则α∥βB.若α⊥β,则a⊥bC.若a,b相交,则α,β相交D.若α,β相交,则a,b相交解析:若α,β相交,则a,b可能相交,也可能异面,故D为假命题.答案:D7.一个几何体的侧视图和俯视图如图所示,若该几何体的体积为错误!,则它的正视图为()解析:由几何体的侧视图和俯视图,可知几何体为组合体,由几何体的体积为错误!,可知上方为棱锥,下方为正方体.由俯视图可得,棱锥顶点在底面上的射影为正方形一边上的中点,顶点到正方体上底面的距离为1,所以选B.答案:B8.已知一个几何体的三视图如图所示,则该几何体的体积为()A.27-错误!B.18-错误!C.27-3πD.18-3π解析:由几何体的三视图可知该几何体可以看成是底面是梯形的四棱柱挖去了半个圆柱,所以所求体积为错误!×(2+4)×2×3-错误!π×12×3=18-错误!。
智慧测评新高考人教A版理科数学一轮总复习课时训练7.7立体几何的向量方法(含答案详析)

第七篇 第7节一、选择题1.若直线l 的方向向量为a ,平面α的法向量为n ,有可能使l ∥α的是( ) A .a =(1,0,0),n =(-2,0,0) B .a =(1,3,5),n =(1,0,1) C .a =(0,2,1),n =(-1,0,-1) D .a =(1,-1,3),n =(0,3,1)解析:若l ∥α,则a·n =0. 而选项A 中a·n =-2. 选项B 中a·n =1+5=6. 选项C 中a·n =-1, 选项D 中a·n =-3+3=0, 故选D. 答案:D2.直线l 的方向向量s =(-1,1,1),平面α的法向量为n =(2,x 2+x ,-x ),若直线l ∥平面α,则x 的值为( )A .-2B .- 2C . 2D .±2解析:线面平行时,直线的方向向量垂直于平面的法向量, 故-1×2+1×(x 2+x )+1×(-x )=0,解得x =±2. 答案:D3.如图所示,正方体ABCDA 1B 1C 1D 1中,E 、F 分别在A 1D 、AC 上,且A 1E =23A 1D ,AF =13AC ,则( )A .EF 至多与A 1D ,AC 之一垂直B .EF ⊥A 1D ,EF ⊥AC C .EF 与BD 1相交 D .EF 与BD 1异面解析:以D 点为坐标原点,以DA 、DC 、DD1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,设正方体棱长为1,则A 1(1,0,1),D (0,0,0), A (1,0,0),C (0,1,0),E ⎝⎛⎭⎫13,0,13,F ⎝⎛⎭⎫23,13,0, B (1,1,0),D 1(0,0,1),A 1D →=(-1,0,-1),AC →=(-1,1,0), EF →=⎝⎛⎭⎫13,13,-13,BD 1→=(-1,-1,1), EF →=-13BD 1→,A 1D →·EF →=AC →·EF →=0,从而EF ∥BD 1,EF ⊥A 1D ,EF ⊥AC .故选B. 答案:B4.如图所示,ABCDA 1B 1C 1D 1是棱长为6的正方体,E 、F 分别是棱AB 、BC 上的动点,且AE =BF .当A 1、E 、F 、C 1共面时,平面A 1DE 与平面C 1DF 所成锐二面角的余弦值为( )A .32B .12C .15D .265解析:以D 为原点,DA 、DC 、DD 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,易知当E (6,3,0)、F (3,6,0)时,A 1、E 、F 、C 1共面,设平面A 1DE 的法向量为n 1=(a ,b ,c ),依题意得⎩⎪⎨⎪⎧n 1·DE →=6a +3b =0,n 1·DA 1→=6a +6c =0,可取n 1=(-1,2,1),同理可得平面C 1DF 的一个法向量为n 2=(2,-1,1),故平面A 1DE 与平面C 1DF 所成锐二面角的余弦值为|n 1·n 2||n 1|·|n 2|=12.故选B. 答案:B5.在正三棱柱ABCA 1B 1C 1中,已知AB =1,D 在棱BB 1上,且BD =1,则AD 与平面AA 1C 1C 所成的角的正弦值为( )A .64B .-64C .104D .-104解析:取AC 中点E ,连接BE ,则BE ⊥AC , 如图所示,建立空间直角坐标系B -xyz , 则A ⎝⎛⎭⎫32,12,0,D (0,0,1),则AD →=⎝⎛⎭⎫-32,-12,1.∵平面ABC ⊥平面AA 1C 1C , 平面ABC ∩平面AA 1C 1C =AC , BE ⊥AC ,∴BE ⊥平面AA 1C 1C ,∴BE →=⎝⎛⎭⎫32,0,0为平面AA 1C 1C 的一个法向量,∴cos 〈AD →,BE →〉=-64,设AD 与平面AA 1C 1C 所成的角为α, 则sin α=|cos 〈AD →,BE →〉|=64.故选A. 答案:A6.(2013年高考大纲卷)已知在正四棱柱ABCDA 1B 1C 1D 1中,AA 1=2AB ,则CD 与平面BDC 1所成角的正弦值是( )A .23B .33C .23D .13解析:建立如图所示的空间直角坐标系,设AA 1=2AB =2,则B (1,1,0),C (0,1,0), D (0,0,0),C 1(0,1,2),故DB →=(1,1,0),DC 1→=(0,1,2),DC →=(0,1,0). 设平面BDC 1的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·DB →=0,n ·DC 1→=0,得⎩⎪⎨⎪⎧x +y =0,y +2z =0,令z =1,则y =-2,x =2,所以平面BDC 1的一个法向量为n =(2,-2,1). 设直线CD 与平面BDC 1所成的角为θ, 则sin θ=|cos 〈n ,DC →〉|=n ·DC →|n |·|DC →|=23.故选A.答案:A 二、填空题7.平面α的一个法向量n =(0,1,-1),如果直线l ⊥平面α,则直线l 的单位方向向量是________.解析:直线l 的方向向量平行于平面α的法向量, 故直线l 的单位方向向量是±n|n |=±0,22,-22.答案:0,22,-22或0,-22,228.如图所示,正方体ABCDA 1B 1C 1D 1的棱长为1,E 是A 1B 1上的点,则点E 到平面ABC 1D 1的距离是________.解:法一 以点D 为坐标原点,DA ,DC ,DD1所在射线为x ,y ,z 轴,建立如图所示空间直角坐标系,设点E (1,a,1)(0≤a ≤1), 连接D 1E , 则D 1E →=(1,a,0).连接A 1D ,易知A 1D ⊥平面ABC 1D 1,则DA 1→=(1,0,1)为平面ABC 1D 1的一个法向量. ∴点E 到平面ABC 1D 1的距离是d =|D 1E →·DA 1→||DA 1→|=22.法二 点E 到平面ABC 1D 1的距离,即B 1到BC 1的距离,易得点B 1到BC 1的距离为22. 答案:229.(2014合肥月考)等边三角形ABC 与正方形ABDE 有一公共边AB ,二面角CABD 的余弦值为33,M 、N 分别是AC 、BC 的中点,则EM 、AN 所成角的余弦值等于________.解析:过C 点作CO ⊥平面ABDE ,垂足为O ,取AB 中点F ,连接CF 、OF ,则∠CFO 为二面角CABD 的平面角,设AB =1,则CF =32, OF =CF ·cos ∠CFO =12,OC =22,则O 为正方形ABDE 的中心, 如图所示建立直角坐标系Oxyz , 则E ⎝⎛⎭⎫0,-22,0, M ⎝⎛⎭⎫24,0,24,A ⎝⎛⎭⎫22,0,0,N ⎝⎛⎭⎫0,24,24, EM →=⎝⎛⎭⎫24,22,24,AN →=⎝⎛⎭⎫-22,24,24,cos 〈EM →,AN →〉=EM →·AN →|EM →||AN →|=16.答案:1610.空间中两个有一条公共边AD 的正方形ABCD 与ADEF ,设M ,N 分别是BD ,AE 的中点,给出如下命题:①AD ⊥MN ;②MN ∥平面CDE ;③MN ∥CE ;④MN ,CE 异面.则所有的正确命题为________.解析:如图设AB →=a ,AD →=b ,AF →=c ,则|a |=|c |且a ·b =c ·b =0.MN →=AN →-AM →=12(b +c )-12(a +b )=12(c -a ),MN →·AD →=12(c -a )·b =12(c ·b-a ·b )=0,故AD ⊥MN ;CE →=c -a =2MN →,故MN ∥CE ,故MN ∥平面CDE ,故②③正确;③正确时④一定不正确.答案:①②③ 三、解答题11.(2014陕西西安五校三模)如图,在长方体ABCDA 1B 1C 1D 1中,AD =AA 1=1,AB =2,点E 在棱AB 上.(1)求异面直线D 1E 与A 1D 所成的角;(2)若二面角D 1ECD 的大小为45°,求点B 到平面D 1EC 的距离. 解:建立如图所示的空间直角坐标系.(1)由A 1(1,0,1),得 DA 1→=(1,0,1),设E (1,a,0),又D 1(0,0,1),则D 1E →=(1,a ,-1). ∵DA 1→·D 1E →=1+0-1=0,∴DA 1→⊥D 1E →,则异面直线D 1E 与A 1D 所成的角为90°. (2)m =(0,0,1)为平面DEC 的法向量, 设n =(x ,y ,z )为平面CED 1的法向量,则 cos 〈m ,n 〉=|m·n||m||n|=|z |x 2+y 2+z 2=cos 45°=22, ∴z 2=x 2+y 2①由C (0,2,0),得D 1C →=(0,2,-1), 则n ⊥D 1C →, 即n ·D 1C →=0, ∴2y -z =0②由①、②,可取n =(3,1,2), 又CB →=(1,0,0),所以点B 到平面D 1EC 的距离d =|CB →·n ||n |=322=64.12.(2014福建厦门联考)如图所示,在三棱锥P ABC 中,AB =BC =6,平面P AC ⊥平面ABC ,PD ⊥AC 于点D ,AD =1,CD =3,PD = 3.(1)证明△PBC 为直角三角形;(2)求直线P A 与平面PBC 所成角的正弦值.(1)证明:以点E (AC 中点)为坐标原点,以EB ,EC 所在的直线分别为x 轴,y 轴建立如图所示的空间直角坐标系Exyz ,则B (2,0,0),C (0,2,0),P (0,-1,3).于是BP →=(-2,-1,3),BC →=(-2,2,0). 因为BP →·BC →=(-2,-1,3)·(-2,2,0)=0, 所以BP →⊥BC →,所以BP ⊥BC .所以△PBC 为直角三角形. (2)解:由(1)可得,A (0,-2,0).于是AP →=(0,1,3),PB →=(2,1,-3),PC →=(0,3,-3). 设平面PBC 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·PB →=0,n ·PC →=0.即⎩⎪⎨⎪⎧2x +y -3z =0,3y -3z =0.取y =1,则z =3,x = 2.所以平面PBC 的一个法向量为n =(2,1,3). 设直线AP 与平面PBC 所成的角为θ, 则sin θ=|cos 〈AP →,n 〉|=|AP →·n ||AP →||n |=42×6=63.所以直线AP 与平面PBC 所成角的正弦值为63.。
数学立体几何单元测试

数学立体几何单元测试题目:数学立体几何单元测试正文:题一:计算立方体的体积和表面积。
(10分)解答:立方体是一种特殊的几何体,其六个面都是正方形,每条边长度相等。
设立方体的边长为a,则其体积V为a³,表面积S为6a²。
根据给定条件,我们可以进行如下计算:已知边长a=4cm,则立方体的体积V=4³=64cm³,表面积S=6×4²=96cm²。
题二:判断以下四个几何体是否为正多面体,并说明理由。
(10分)解答:正多面体是指各个面都是正多边形且顶点都相同的几何体。
根据这个定义,我们来判断以下四个几何体是否为正多面体:1. 正方体正方体的六个面都是正方形,并且顶点相同,因此它是正多面体。
2. 正六面体正六面体的六个面都是正六边形,并且顶点相同,因此它是正多面体。
3. 正四面体正四面体的四个面都是正三角形,并且顶点相同,因此它是正多面体。
4. 正二十面体正二十面体的二十个面都是正五边形,并且顶点相同,因此它是正多面体。
综上所述,正方体、正六面体、正四面体和正二十面体都是正多面体。
题三:计算圆柱的体积和表面积,要求保留一位小数。
(10分)解答:圆柱是一种特殊的立体几何体,其底面为圆形,侧面为矩形。
设圆柱的底面半径为r,高度为h,则其体积V为πr²h,表面积S为2πrh+2πr²。
根据给定条件,我们可以进行如下计算:已知底面半径r=5cm,高度h=10cm,则圆柱的体积V=3.14×5²×10=785cm³,表面积S=2×3.14×5×10+2×3.14×5²=471cm²。
题四:根据给定条件,判断以下陈述的真假。
(10分)解答:1. 球体的体积公式是V=4/3πr³,其中r为半径。
(正确)2. 圆锥的侧面积公式是S=πrl,其中r为底面半径,l为斜高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单元检测﹙七﹚——立体几何一、选择题(本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知a=(1,1,0),b=(-1,0,3),且k a+b与2a-b垂直,则k的值为()A.125B.1 C.75D.2【解析】k a+b=(k-1,k,3),2a-b=(3,2,-3),由题意,得(k-1)×3+k×2+3×(-3)=0,解得k=12 5.【答案】 A2.某几何体的正视图如图所示,则该几何体的俯视图不可能...的是()【解析】由正视图知,俯视图不可能是圆与内接四边形,C不正确.【答案】 C3.直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图所示,则其侧视图的面积为()A.4 B. 3 C.2 3 D.2【解析】由正视图和俯视图知,直三棱柱的侧视图是长为3,宽为2的长方形,故侧视图的面积为2 3.【答案】 C4.已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是()A.若α⊥γ,α⊥β,则γ∥βB.若m∥n,m⊂α,n⊂β,则α∥βC.若m∥n,m∥α,则n∥αD.若n⊥α,n⊥β,则α∥β【解析】A错,两平面也可相交;B错,不符合面面平行的判定定理的条件,需两平面内有两条相交直线互相平行;C错,直线n不一定在平面α外;D由空间想象知垂直于同一直线的两平面平行,命题正确.【答案】 D5.如图所示,平行四边形ABCD中,AB⊥BD,沿BD将△ABD折起,使面ABD⊥面BCD,连结AC,则在四面体ABCD的四个面中,互相垂直的平面的对数为() A.1 B.2 C.3 D.4【解析】AB⊥BD,面ABD⊥面BCD,且交线为BD,则AB⊥面BCD,则面ABC⊥面BCD,同理CD⊥面ABD,则面ACD⊥面ABD,因此共有3对互相垂直的平面.【答案】 C6.(2012·茂名调研)如图,在正方体ABCD—A1B1C1D1中,O是底面正方形ABCD的中心,M是DD1的中点,N是A1B1上的动点,则直线ON,AM的位置关系是()A .平行B .相交C .异面垂直D .异面不垂直【解析】 如图所示,取BC 、AD 的中点E 、F ,分别连结B 1E ,EF ,F A 1,则ON ⊂平面A 1FEB 1.∵AM ⊥A 1F ,AM ⊥A 1B 1,∴AM ⊥平面A 1FEB 1,∴AM ⊥ON .【答案】 C7.如图六棱锥P —ABCDEF 的底面是正六边形,P A ⊥平面ABC ,P A =2AB ,则下列结论正确的是( )A .PB ⊥ADB .平面P AB ⊥平面PBCC .直线BC ∥平面P AED .直线PD 与平面ABC 所成的角为45°【解析】 ∵PB 在底面射影为AB ,AB 与AD 不垂直,∴PB 与AD 不垂直,排除A.又BD ⊥AB ,BD ⊥P A ,∴BD ⊥面P AB .但BD 不在面PBC 内,排除B.∵BD ∥AE ,∴BD ∥面P AE ,∴BC 与面P AE 不平行,排除C.又∵PD 与面ABC 所成角为∠PDA ,AD =2AB =P A ,∴∠PDA =45°.【答案】 D8.如图所示,在斜三棱柱ABC —A 1B 1C 1中,∠BAC =90°,BC 1⊥AC ,则C 1在底面ABC 上的射影H 必在( )A .直线AB 上 B .直线BC 上 C .直线AC 上D .△ABC内部【解析】 由已知易推出平面ABC 1⊥平面ABC ,故C 1在底面上的射影H 在两平面交线AB 上.【答案】 A二、填空题(本大题共6小题,每小题5分,满分30分)9.正方体ABCD —A 1B 1C 1D 1中,BB 1与平面ACD 1所成角的余弦值为________.【解析】 如图所示,建立空间直角坐标系,且设正方体的棱长为1,∵DB 1⊥平面ACD 1,∴取平面ACD 1的法向量n =DB 1→=(1,1,1), 又BB 1→=DD 1→=(0,0,1), 若设BB 1与平面ACD 1所成角为θ,则sin θ=|cos 〈n ,DD 1〉|=|n ·DD 1→||n |·|DD 1→|=33,∴cos θ=1-sin 2θ=63. 【答案】 6310.(2011·广东高考改编)如图所示,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则该几何体的体积为________.【解析】 该几何体为一个斜棱柱,其直观图如图所示,由题知该几何体的底面是边长为3的正方形,高为3,故V =3×3×3=9 3.【答案】 9 311.已知直线l ,m ,平面α,β且l ⊥α,m ⊂β,给出四个命题:①若α∥β,则l ⊥m ;②若l ⊥m ,则α∥β;③若α⊥β,则l ∥m ;④若l ∥m ,则α⊥β.其中真命题的个数是________.【解析】 命题①,由l ⊥α,α∥β得l ⊥β,∴l ⊥m ,故①对.命题②,l ⊥mD /⇒l ⊥β,则l ⊥mD /⇒α∥β,故命题②错误.命题③,当α⊥β时,l 与m 也可能相交或异面,故③错误.命题④,由l ⊥α,l ∥m 得m ⊥α,∴α⊥β,故④正确.【答案】 212.(2011·辽宁高考)三棱锥P —ABC 中,P A ⊥底面ABC ,P A =3,底面ABC 是边长为2的正三角形,则三棱锥P —ABC 的体积等于________.【解析】 ∵P A ⊥底面ABC ,∴P A 为三棱锥P —ABC 的高,且P A =3,∵底面ABC 为正三角形且边长为2,∴底面面积为12×22×sin 60°=3,∴V P —ABC =13×3×3= 3.【答案】 313.如图所示,过正方形ABCD 的顶点A ,引P A ⊥平面ABCD .若P A =BA ,则平面ABP 和平面CDP 所成的二面角的大小是________【解析】 建立如图所示的空间直角坐标系,不难求出平面APB与平面PCD 的法向量n 1=(0,1,0),n 2=(0,1,1),故平面ABP 与平面CDP 所成二面角的余弦值为|n 1·n 2||n 1||n 2|=22,故所求的二面角的大小是45°.【答案】 45°14.如图所示,在直三棱柱ABC —A 1B 1C 1中,底面是∠ABC 为直角的等腰直角三角形,AC =2a ,BB 1=3a ,D 是A 1C 1的中点,点F 在线段AA 1上,当AF =________时,CF ⊥平面B 1DF .【解析】 由已知得B 1D ⊥平面AC 1,又CF ⊂平面AC 1,∴B 1D ⊥CF ,故若CF ⊥平面B 1DF ,则必有CF ⊥DF .设AF =x (0<x <3a ),则CF 2=x 2+4a 2,DF 2=a 2+(3a -x )2,又CD 2=a 2+9a 2=10a 2,∴10a 2=x 2+4a 2+a 2+(3a -x )2,解得x =a 或2a .【答案】 a 或2a三、解答题(本大题共6小题,满分80分.解答时需写出文字说明、证明过程和演算步骤)15.(本小题满分12分)如图,在四棱锥P —ABCD 中,PD 垂直于底面ABCD ,底面ABCD 是直角梯形,DC ∥AB ,∠BAD =90°,且AB =2AD =2DC =2PD=4(单位:cm),E 为P A 的中点.(1)证明:DE ∥平面PBC ;(2)证明:DE ⊥平面P AB .【证明】 (1)如图所示,设PB 的中点为F ,连结EF 、CF ,则EF ∥AB ,DC ∥AB ,∴EF ∥DC ,且EF =DC =12AB ,故四边形CDEF 为平行四边形,可得DE ∥CF ,DE ⊄平面PBC ,CF ⊂平面PBC ,故DE ∥平面PBC .(2)PD 垂直于底面ABCD ,AB ⊂平面ABCD ,∴AB ⊥PD ,又AB ⊥AD ,PD ∩AD =D ,∴AB ⊥平面P AD ,ED ⊂平面P AD ,故ED ⊥AB ,又PD =AD ,E 为P A 中点,故ED ⊥P A .P A ∩AB =A ,∴DE ⊥平面P AB .16.(本小题满分13分)(2012·湛江质检)如图所示,四面体ABCD 中,O 、E 分别是BD 、BC 的中点,CA =CB =CD =BD =2,AB =AD = 2.(1)求证:AO ⊥平面BCD ;(2)求异面直线AB 与CD 所成角的余弦值;【解】 (1)证明 连结OC .∵BO =DO ,AB =AD ,∴AO ⊥BD .∵BO =DO ,BC =CD ,∴CO ⊥BD .在△AOC 中,由已知可得AO =1,CO = 3.又AC =2,∴AO 2+CO 2=AC 2.∴∠AOC =90°,即AO ⊥OC .又AO ⊥BD ,BD ∩OC =O ,∴AO ⊥平面BCD .(2)以O 为原点,如图建立空间直角坐标系,则B (1,0,0),D (-1,0,0),C (0,3,0),A (0,0,1),E (12,32,0),BA→=(-1,0,1),CD →=(-1,-3,0).∴cos 〈BA →,CD →〉=BA →·CD →|BA→||CD →|=24. ∴异面直线AB 与CD 所成角的余弦值为24.17.(本小题满分13分)(2011·课标全国卷)如图,四棱锥P —ABCD 中,底面ABCD 为平行四边形,∠DAB =60°,AB =2AD ,PD ⊥底面ABCD .(1)证明:P A ⊥BD ;(2)若PD =AD ,求二面角A —PB —C 的余弦值.【解】 (1)证明 因为∠DAB =60°,AB =2AD ,由余弦定理得BD =3AD .从而BD 2+AD 2=AB 2,故BD ⊥AD .又PD ⊥底面ABCD ,可得BD ⊥PD .所以BD ⊥平面P AD ,故P A ⊥BD .(2)如图,以D 为坐标原点,AD 的长为单位长,射线DA 为x 轴的正半轴,建立空间直角坐标系D —xyz .则A (1,0,0),B (0,3,0),C (-1,3,0),P (0,0,1).AB →=(-1,3,0),PB →=(0,3,-1),BC →=(-1,0,0).设平面P AB 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧ n ·AB →=0,n ·PB →=0.即⎩⎨⎧-x +3y =0,3y -z =0. 因此可取n =(3,1,3).设平面PBC 的法向量为m ,则⎩⎪⎨⎪⎧m ·PB →=0,m ·BC →=0. 可取m =(0,-1,-3).cos 〈m ,n 〉=-427=-277. 故二面角A —PB —C 的余弦值为-277.18.(本小题满分14分)(2012·佛山模拟)如图,P A ⊥平面ABCD ,ABCD 是矩形,P A =AB =1,AD =3,点F 是PB 的中点,点E 在边BC 上移动.(1)求三棱锥E —P AD 的体积;(2)当点E 为BC 的中点时,试判断EF 与平面P AC 的位置关系,并说明理由;(3)证明:无论点E 在边BC 的何处,都有PE ⊥AF .【解】 (1)∵V E —P AD =V P —ADE ,又P A =1,S △ADE =12AD ·AB =32,∴V E -P AB =13P A ·S △ADE =13×1×32=36.(2)当点E 为BC 的中点时,EF 与平面P AC 平行.∵在△PBC 中,E 、F 分别为BC 、PB 的中点,∴EF ∥PC ,又EF ⊄平面P AC ,PC ⊂平面P AC ,∴EF ∥平面P AC .(3)证明 ∵P A ⊥平面ABCD ,BE ⊂平面ABCD ,∴BE ⊥P A ,又BE ⊥AB ,AB ∩P A =A ,∴BE ⊥平面P AB .又AF ⊂平面P AB ,∴AF ⊥BE .又P A =AB =1,点F 是PB 的中点,∴PB ⊥AF ,又∵PB ∩BE =B ,∴AF ⊥平面PBE .∵PE ⊂平面PBE ,∴AF ⊥PE .19.(本小题满分14分)(2011·江西高考)如图,在△ABC中,∠B =π2,AB =BC =2,P 为AB 边上一动点,PD ∥BC交AC 于点D ,现将△PDA 沿PD 翻折至△PDA ′,使平面PDA ′⊥平面PBCD .(1)当棱锥A ′—PBCD 的体积最大时,求P A 的长.(2)若点P 为AB 的中点,E 为A ′C 的中点,求证:A ′B ⊥DE .【解】 (1)令P A =x (0<x <2),则A ′P =PD =x ,BP =2-x .因为A ′P ⊥PD ,且平面A ′PD ⊥平面PBCD ,故A ′P ⊥平面PBCD .∴V A ′—PBCD =13Sh =16(2-x )·(2+x )x =16(4x -x 3).令f (x )=16(4x -x 3),由f ′(x )=16(4-3x 2)=0,得x =233. 当x ∈(0,233)时,f ′(x )>0,f (x )单调递增;当x ∈(233,2)时,f ′(x )<0,f (x )单调递减.所以当x =233时,f (x )取得最大值.故当V A ′—PBCD 最大时,P A =233.(2)证明 设F 为A ′B 的中点,如图所示,连结PF ,FE ,则有EF 綊12BC ,PD 綊12BC .所以EF 綊PD .所以四边形EFPD 为平行四边形.所以DE ∥PF .又A ′P =PB ,所以PF ⊥A ′B ,故DE ⊥A ′B .20.(本小题满分14分)(2011·湖南高考)如图,在圆锥PO中,已知PO =2,⊙O 的直径AB =2,C 是AB 的中点,D 为AC 的中点.(1)证明:平面POD ⊥平面P AC ;(2)求二面角B —P A —C 的余弦值.【解】 (1)证明 如图所示,以O 为坐标原点,OB ,OC ,OP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,则O (0,0,0),A (-1,0,0),B (1,0,0),C (0,1,0),P (0,0,2),D (-12,12,0).设n 1=(x 1,y 1,z 1)是平面POD 的一个法向量,由n 1·OD →=0,n 1·OP →=0,得⎩⎪⎨⎪⎧-12x 1+12y 1=0,2z 1=0. 所以z 1=0,x 1=y 1.取y 1=1,得n 1=(1,1,0).设n 2=(x 2,y 2,z 2)是平面P AC 的一个法向量,由n 2·P A →=0,n 2·PC →=0, 得⎩⎨⎧-x 2-2z 2=0,y 2-2z 2=0.所以x 2=-2z 2,y 2=2z 2,取z 2=1, 得n 2=(-2,2,1).因为n 1·n 2=(1,1,0)·(-2,2,1)=0,所以n 1⊥n 2. 从而平面POD ⊥平面P AC .(2)因为y 轴⊥平面P AB ,所以平面P AB 的一个法向量为n 3=(0,1,0). 由(1)知,平面P AC 的一个法向量为n 2=(-2,2,1). 设向量n 2和n 3的夹角为θ,则cos θ=n 2·n 3|n 2|·|n 3|=25=105. 由图可知,二面角B —P A —C 的平面角与θ相等.所以二面角B —P A —C 的余弦值为105.。
