D磁性物理基础-各向异性
最新磁晶各向异性能教学讲义ppt

磁晶各向异性是由自发磁化强度和晶格之间的相互作用产生的,因而自发 磁化强度的温度关系将导致磁晶各向异性的温度变化。实际上磁晶各向异性 对温度的依赖性比自发磁化强度对温度的依赖强的多。在材料中局域自旋的 方向余弦( 1,2,3 )并不同于总自发磁化强度的方向余弦( 1,2,3 ),它们的 差别随温度的升高而增加。温度为T的立方各向异性为:
每个磁矩方向一致的区域就称为一个磁畴。 不同的磁畴方向不同,两磁畴间的区域就
称为磁畴壁 。
铁磁性的起源----直接交换相互作用
原子间距离太远,表现孤立原子特性
a.b原子核外电子因库仑相互作用相 互排斥,在原子中间电子密度减少。
原子间距离适当时,a原子核将吸引
(1) a(1)
a
b
b(2) (2)
下面介绍 Kittel 的一种简明解释:由于自旋-轨道耦合 作用使非球对称的电子云分布随自旋取向而变化,因而导 致了波函数的交迭程度不同,产生了各向异性的交换作用, 使其在晶体的不同方向上能量不同。
磁晶各向异 性机理的一 种简明解释
见Kittelp240
6. 磁晶各向异性常数的温度依赖性
见姜书p220-221
rab
b原子的外囲电子,同样b原子核将吸引 b原子的外囲电子。原子间电子密度增
a
b
加。电子间产生交换作用,或者说a、b
原子的电子进行交换是等同的,自旋平
行时能量最小。铁磁耦合
a
b
原子间距离再近,这种交换作用使
自旋反平行,a、b原子的电子共用一
个电子轨道,抅成反铁磁耦合
a
b
铁磁相互作用
实验事实:铁磁性物质在居里温度以上是顺磁性;居里温度以下
10
K1 K10
3、磁晶各向异性机理

随着4f电子的数目增加,磁量子
数m=3,2,1,0,-1,-2,-3,电子云的形状 与m的正负无关。m=0的电子云沿 C轴延伸,使C轴成为易轴。因为 L=0总的电子云变成球形。
Tb的轨道矩 L=3为稀土元素 中最大值,轨道面垂直于J 伸 展,形成薄饼状的电子云。
Tb的六角晶格的c/a值为1.59, 它比密堆积的六角晶格的理 想值1.633小的多,也就是说 晶格沿C轴被压缩了。
二重态
在立方晶体中有四个<111>轴, 若离子平均的分布在具有不同的 <111>轴的八面体间隙位。
EA 1 4 N LS cos 1 cos 2 cos 3 cos 4
式中1 ,2 ,3 ,4为自旋磁矩与四个<111>轴的夹角
EA
1 4
N LS cos 1 cos 2 cos 3 cos 4
第三项为起源相同的高价项,称为四极相互作用。磁晶各向
异性可以通过对晶体中所有自旋对的能量相加而计算出来
这模型称为自旋对(spin-pair)模型。
EA
w
i
i
i表示自旋对。仅考虑近邻,最多到次近邻之间的相互作用。
设(1,2,3 )为平行自旋对的方向余弦。 对原子连线方向与x-轴平行的自旋对,cos可以用1代替, 对平行y-,z-轴的自旋对,cos可分别用2和3替代。
2
3 35
) ......
然而真正测得的磁各向异性相应的l 值比此项给出的值大 100到1000倍。因此产生磁晶各向异性的机制不是偶极相互 作用,虽然形式相同,但其系数是来源于磁晶各向异性,这 种相互作用被称为赝偶极相互作用
机理:部分未淬灭的轨道矩与自旋相互耦合,随着磁化强度的
各向异性材料的物理性质

各向异性材料的物理性质各向异性材料是指在其内部结构或分子构成上存在着明显的方向性差异,从而导致其物理性质在不同方向上表现出差异性的材料。
相较于各向同性材料,各向异性材料在很多方面具有独特的性质和应用潜力。
本文将围绕各向异性材料的物理性质展开论述,并介绍其在材料科学领域中的重要性。
一、光学性质各向异性材料在光学性质方面表现出明显差异。
例如,晶体材料具有光学各向异性,这意味着光线传播在不同晶向上的速度不同,产生折射和偏振现象。
这使得晶体材料在光学设备领域中有着广泛的应用,并且成为许多光电器件的基础。
二、磁性性质各向异性材料的磁性性质也具有显著的差异。
磁性材料中存在着磁畴的形成和磁畴壁的运动,而各向异性则会影响磁畴的排列方向和磁畴壁的稳定性。
这使得各向异性材料在磁存储、传感器和磁性材料制备等领域具有重要应用。
三、电子性质在电子性质方面,各向异性材料的电导率、电子迁移率和载流子输运性质等均会受到方向性的影响。
例如,某些有机半导体材料因其分子排列的各向异性特性而表现出不同的电子传导行为。
这使得各向异性材料在有机电子学领域中有着广泛的应用前景。
四、力学性质各向异性材料的力学性质通常会因材料内部的各向异性结构而产生方向性差异。
例如,纤维增强复合材料中的纤维方向和矩阵材料之间的界面结合强度具有方向性差异。
这使得各向异性材料在结构工程、航空航天等领域中广泛应用,能够提供更高的强度和刚度。
五、热学性质各向异性材料的热学性质也会受到方向性的影响。
例如,晶体材料的热导率在不同晶向上会有所不同。
此外,各向异性材料在热膨胀和热收缩等方面也表现出不同的特性。
这使得各向异性材料在热管理和热传导领域有着广泛的应用。
各向异性材料的物理性质不仅在基础科学研究中具有重要作用,而且在工程应用中也具有广泛的潜力。
通过深入研究各向异性材料的物理性质,可以更好地理解材料行为和性能,并为创新材料设计和应用提供有益的指导。
因此,持续深入研究各向异性材料的物理性质对于材料科学和工程领域的发展至关重要。
磁晶各向异性
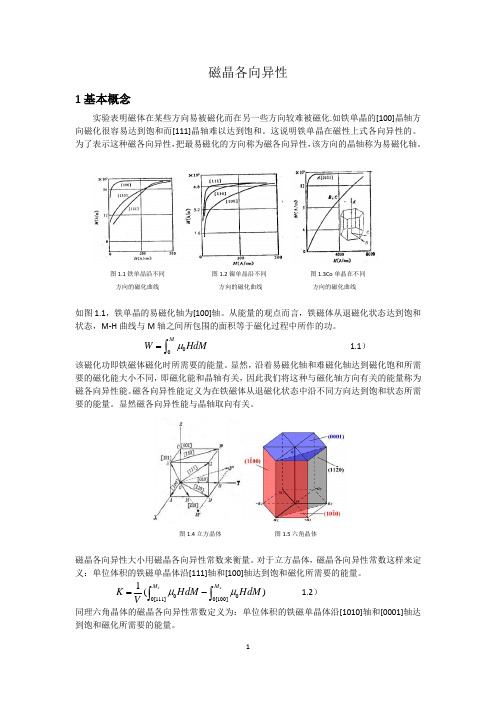
磁晶各向异性1基本概念实验表明磁体在某些方向易被磁化而在另一些方向较难被磁化.如铁单晶的[100]晶轴方向磁化很容易达到饱和而[111]晶轴难以达到饱和。
这说明铁单晶在磁性上式各向异性的。
为了表示这种磁各向异性,把最易磁化的方向称为磁各向异性,该方向的晶轴称为易磁化轴。
图1.1铁单晶沿不同 图1.2镍单晶沿不同 图1.3Co 单晶在不同 方向的磁化曲线 方向的磁化曲线 方向的磁化曲线如图1.1,铁单晶的易磁化轴为[100]轴。
从能量的观点而言,铁磁体从退磁化状态达到饱和状态,M -H 曲线与M 轴之间所包围的面积等于磁化过程中所作的功。
00MW HdM μ=⎰ 1.1)该磁化功即铁磁体磁化时所需要的能量。
显然,沿着易磁化轴和难磁化轴达到磁化饱和所需要的磁化能大小不同,即磁化能和晶轴有关,因此我们将这种与磁化轴方向有关的能量称为磁各向异性能。
磁各向异性能定义为在铁磁体从退磁化状态中沿不同方向达到饱和状态所需要的能量。
显然磁各向异性能与晶轴取向有关。
图1.4立方晶体 图1.5六角晶体磁晶各向异性大小用磁晶各向异性常数来衡量。
对于立方晶体,磁晶各向异性常数这样来定义:单位体积的铁磁单晶体沿[111]轴和[100]轴达到饱和磁化所需要的能量。
000[111]0[100]1()ss M M K HdM HdM V μμ=-⎰⎰ 1.2)同理六角晶体的磁晶各向异性常数定义为:单位体积的铁磁单晶体沿[1010]轴和[0001]轴达到饱和磁化所需要的能量。
000[1010]0[0001]1()ss M M K HdM HdM V μμ=-⎰⎰ 1.3)结合图1.1、图1.2、图1.3可知铁单晶、钴单晶的K 为正值而镍单晶的K 为负值。
2单轴磁晶各向异性磁晶各向异性可以为单轴磁晶各向异性和多轴磁晶各向异性。
单轴各向异性是磁晶各向异性的最简单形式,即自发磁化的稳定方向即易磁化方向平行于某一特殊晶轴。
如六方晶系钴的自发磁化方向平行于 C 轴,这就表现出强的单轴各向异性。
D磁性物理基础-各向异性

2、六角晶系的磁晶各向异性 A、磁晶各向异性能
z
C轴
y
Is
y
C面
C面
°°° ° ° ° ° ° ° ° °° w x
+2/6
六角晶系的特点是在c面有六次对称 轴,与+2n/6,(n=0、1、2…..) 的方向体系的能量是相同的。用, 替代1,2,3 ,计算磁晶各向异性能
z Is x
I s H A sin
HA <111>
E A K1 2 sin(2 2 ) 3 sin(4 4 ) 8
K2 sin( 2 2 ) 4 sin( 4 4 ) 3 sin( 6 6 ) 64
y
4 K H A ( K1 2 ) / I s 3 3
是易轴与磁化强度之间的夹角
H
1
00
如果样品的体积为V,则平衡条件为
VT=L=k1
易轴
Is
适当选择k,使1在较小的范围内变化。如果磁场的转角为(0到 360度),则=-1,由于1很小,就可简化=。
右图为一个典型的转矩曲线, =22.50时sin4=1由转矩曲线公式 1 L( ) K1 sin 4 2 得到:K1=2L(22.50) ~4x105dyn cmcm-3(ergcm-3)
Co:
Ku1=4.53x105Jm-3 Ku2=1.44x105Jm-3
B、磁晶各向异性场:
a. C轴为易磁化轴,用同样的处理方法 E 得到: H A I s sin A b. c面为易磁化面时:
HA 2( K u1 2 K u 2 ) Is
HA
2 K u1 Is
磁晶各向异性能

2.2MBxHmkT
Hm109Am-1(107Oe)
( 分子场 )
一、磁晶各向异性
序言:在磁性物质中,自发磁化主要来源于自旋间的交换作用,这 种交换作用本质上是各向同性的,如果没有附加的相互作用存在,在 晶体中,自发磁化强度可以指向任意方向而不改变体系的内能。实际 上在磁性材料中,自发磁化强度总是处于一个或几个特定方向,该方 向称为易轴。当施加外场时,磁化强度才能从易轴方向转出,此现象 称为磁晶各向异性。
5. 磁晶各向异性的机理:
产生磁晶各向异性的来源比较复杂,一直在研究之中。
目前普遍认为和自旋-轨道耦合与晶场效应有关。经过多 年研究,局域电子的磁晶各向异性理论已经趋于成熟,目 前有两种模型:单离子模型和双离子模型。主要适合于解 释铁氧体和稀土金属的磁晶各向异性。而以能带论为基础 用于解释过渡族金属的巡游电子磁晶各向异性理论进展迟 缓,尚不完备。(见姜书P221-228) 下面介绍 Kittel 的一种简明解释:由于自旋-轨道耦合 作用使非球对称的电子云分布随自旋取向而变化,因而导 致了波函数的交迭程度不同,产生了各向异性的交换作用, 使其在晶体的不同方向上能量不同。
磁畴
磁畴
铁磁性材料所以能使磁化强度显著增大,
在于其中存在着磁畴(Domain)结构 在未受到磁场作用时,磁畴方向是无规的, 因而在整体上净磁化强度为零 每个磁矩方向一致的区域就称为一个磁畴。
不同的磁畴方向不同,两磁畴间的区域就
称为磁畴壁 。
MFM: NG-HD
表面形貌图
Topography
表面磁力图
MFM Phase
Bit size: 150× 30nm
为什么会产生自发磁化?
磁各向异性

Hdi=-Ni/0·Isi=-Ni/µ0·IsI
退磁能
Ed
1 2
IsHd
I
2 s
20
N
2
x1
N
y
2 2
N
2
z3
对x方向的细长针形:Nx=0,Ny=Nz=1/2
z
Ed
Is2
40
(22
32 )
Is2
40
(112 )
I
2 s
40
sin2
y
x
单轴各向异性表达式: EA=Kusin2 ,与Ed比较得
此外还有,轧制磁各向异性,光感生磁各向异性, 交换各向异性。
立方晶系
EA
K1
sin2
1 4
K1
K2
sin 2
2
K1
sin4
K2 4
sin2
2
sin6
立方晶系
z Ms(123)
[001]
[110]
x
几个特征方向的各向异性能:
[100]:1=1,2=0, 3=0
EA=0
[110]: 1 0,2 3 1/ 2 EA=K1/4
y
[111]:1 2 3 1/ 3 EA=K1/3+K2/27
磁各向异性
磁性物理
讲解人 :* 樱
目录
目录 Contents
1 序言 2 磁晶各向异性
3 感生磁各向异性
序言
1 序言
磁各向异性指物质的磁性随方向而变的现 象。主要表现:弱磁体的磁化率及铁磁体的磁 化曲线随磁化方向而变。磁各向异性来源于磁 晶体的各向异性。
自发磁化强度总是处于一个或几个特定方 向,该方向称为易轴。当施加外场时,磁化强 度才能从易轴方向转出,此现象称为磁晶各向 异性。
各向同性与各向异性磁性材料的行为

各向同性与各向异性磁性材料的行为磁性材料是一种在磁场中表现出磁性行为的物质,根据其磁性行为的不同特点,可以将磁性材料分为各向同性和各向异性。
各向同性材料是指在各个方向上其磁性行为都是相同的,而各向异性材料则是指其磁性行为在不同方向上具有差异。
各向同性材料的磁性行为相对简单,没有明显的取向特性。
它们在外加磁场下,磁化强度和磁场强度的关系是线性的,即磁化强度与磁场强度成正比。
这种线性关系可以通过磁化率来描述,磁化率是材料在磁场中磁化强度与磁场强度之比。
不同于各向同性材料,各向异性材料的磁性行为对外磁场的方向有一定的依赖性。
各向异性材料在磁场中会出现磁化方向的取向特性,也就是磁化强度在不同方向上的不同表现。
这种不同方向上的磁化强度之差可以通过磁各向异性来描述。
磁各向异性是材料在磁场中,不同取向上磁化强度的差异。
各向异性的形成主要是由于材料内部存在着有序的磁畴结构。
在各向异性材料中,磁性原子或磁矩会在晶体结构中形成一个或多个排列有序的磁畴,而这些磁畴的磁化方向会随着外磁场的变化而发生旋转或翻转。
这种磁畴结构使得各向异性材料在不同的磁场方向下表现出不同的磁性行为。
各向异性材料的磁性行为对于应用有着重要的意义。
例如,在磁存储器件中,各向异性材料的使用可以实现数据的高密度存储,通过调节外加磁场的方向,可以控制数据的读写操作。
此外,各向异性材料还可以应用于传感器、电动机、磁体等领域。
除了各向同性和各向异性之外,还存在一种特殊的磁性行为,即超顺磁性。
超顺磁性是指在外加磁场中,磁矩远远大于给定温度下的热激励能够产生的磁矩。
这种行为在某些特殊的材料中出现,例如由过渡金属离子组成的配合物。
超顺磁性材料的磁化行为是非线性的,且磁化强度与磁场强度的关系不再是简单的比例关系。
磁化强度的变化可以用磁飘移来描述,磁飘移是材料在外加磁场下磁化强度随时间的演化。
除了磁飘移外,超顺磁性材料还具有磁滞效应和角度依存性等特殊的磁性行为。
各向同性和各向异性材料的研究对于理解和应用磁性材料具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
EA K0 K1 sin 2 K2 sin 4
x
' K3 sin 6 K3 sin 6 cos6
w
通常四次方项作为近似就足够了,因此
EA Ku1 sin 2 Ku 2 sin 4 K 3 sin 6 K 3 sin 6 cos 6
D磁性物理基础
磁晶各向异性与磁致伸缩
一、磁晶各向异性 二、磁晶各向异性常数的测量方法 三、磁晶各向异性的机理 四、磁致伸缩 五、磁致伸缩的机理
六、磁致伸缩的测量方法
七、感生磁各向异性 八、非晶态
一、磁晶各向异性
序言:在磁性物质中,自发磁化主要来源于自旋间的交换作用,这种交 换作用本质上是各向同性的,如果没有附加的相互作用存在,在晶体中,自
右图是用来测量转矩曲线的转矩仪。在自动转 矩仪研制出耒以前,是用光电方法测量。
样品吊在一根弹性金属丝上,样品的转动使吊丝产生一个扭力矩L,
L k1
k是扭力系数(达因.厘米/度),1 为样品的转动角度。
当磁化强度偏离易磁化轴将引起一个力矩T,
吊丝
( Is // H )
E T A
极小 =70021‘,+0.210K1
c. (111)面测定
3K K K 3K K T 1 2 sin 2 1 2 sin 4 2 sin 6 16 64 4 64 8
EA
K1 K E A K 2 ( 2 )(1 cos 6 ) , T sin 6 4 108 18
Wij 2JSi S j 2JS 2 cos
其中,为S自旋的大小,而是Si 和Sj 间的夹角。右 图自旋从a旋转到b所有自旋保持平行,因而=0,交 换能没有改变。故交换能是各向同性。 要解释磁晶各向异性,必须考虑含有晶轴的能量项。 如果假设自旋与原子連线的夹角为,则自旋对的 能量经勒让德多项式展开为
z Is(123)
[001]
K1,K2分别为磁晶各向异性常数,求几个特征方
向的各向异性能,
[100]:1=1,2=0,3=0 [110]:1=0, EA=0 EA=K1/4 EA=K1/3+K2/27
y
[110]
2 3 1 / 2
[111]:
1 2 3 1/ 3
2 2 3 1
,
e)的六次项为:
2 4 2 2 4 6 6 16 2 3 , 12 232 , 122 234 3214 142 232 3412 6 6 2 2 2 2 2 2 16 2 3 122 23 3 12 31223
二、磁晶各向异性常数的测量方法
转矩磁强计的原理是,当样品(片状或 球状)置于强磁场中,使样品磁化到饱和。 若易磁化方向接近磁化强度的方向,则磁 晶各向异性将使样品旋转,以使易轴与磁 化强度方向平行这样就产生一个作用在样 品上的转矩。如果测量转矩与磁场绕垂直 轴转过的角度关系,就可以得到转矩曲线, 并由此可求得磁晶各向异性常数。
2 2 2 2 122 23 3 12
2 1
2 2 2 3
1 2
4 1 4 2 2 3 2 1 2 2 2 2 2 3
2
4 4 2 2 2 2 1 14 2 3 2 12 2 2 3 3 12
EA wi
i i表示自旋对。由于远处自旋对的相互作用很小,仅考虑近邻,最多到次近邻之 间的相互作用。设(1,2,3 )为平行自旋对的方向余弦,对原子連线方向与x-轴 平行的自旋对,cos可以用1代替,对平行y-,z-轴的自旋对,cos可分别用2 和3替代。
1 6 3 1 2 4 EA N l (12 ) q(14 12 ) .... l ( 2 ) q( 2 ..... 3 7 35 3
a.<100>易轴
z Is
y
当从z轴转出角,由于z轴是易磁化轴,等效一个磁 场HA,这样就产生一个转矩 E I s H A sin A 1,2,3用,耒表示,并代入EA,,用上式求HA
x
2 K1 HA Is
K: Jm-3 (m-1.kg.S-2 ) Is: T (kg.S-2.A-1 ) K/Is = Am-1
又由于任意两个i互相交换,表达式也必 须不变,所以对任何l、m、n的组合及任何i、 j、k的交换,i2lj2mk2n形式的项的系数必须 相等。因此,第一项12+22+32=1 。因此EA 可表示为
2 2 2 2 2 2 EA K1 (122 23 3 12 ) K21223
2、六角晶系的磁晶各向异性 A、磁晶各向异性能
z
C轴
y
Is
y
C面
C面
°°° ° ° ° ° ° ° ° °° w x
+2/6
六角晶系的特点是在c面有六次对称 轴,与+2n/6,(n=0、1、2…..) 的方向体系的能量是相同的。用, 替代1,2,3 ,计算磁晶各向异性能
Co:
Ku1=4.53x105Jm-3 Ku2=1.44x105Jm-3
B、磁晶各向异性场:
a. C轴为易磁化轴,用同样的处理方法 E 得到: H A I s sin A b. c面为易磁化面时:
HA 2( K u1 2 K u 2 ) Is
HA
2 K u1 Is
是易轴与磁化强度之间的夹角
H
1
00
如果样品的体积为V,则平衡条件为
VT=L=k1
易轴
Is
适当选择k,使1在较小的范围内变化。如果磁场的转角为(0到 360度),则=-1,由于1很小,就可简化=。
右图为一个典型的转矩曲线, =22.50时sin4=1由转矩曲线公式 1 L( ) K1 sin 4 2 得到:K1=2L(22.50) ~4x105dyn cmcm-3(ergcm-3)
2 2 2 2 2 2 2 2 2 2 2 2 第三项 1 2 1 2 23 2 3 3 1 3 1
2 2 2 2 2 2 122 23 3 12 31223
用到
2 2 12 2 3 1
2 2 12 2 1 3 , ………….
A.立方晶系的转矩曲线
a. (100)面测定
EA K1 cos 4 8 K1 T sin 4 2b.Fra bibliotek(110)面测定
T K1 K (2 sin 2 3 sin 4 ) 2 (sin 2 4 sin 4 3 sin 6 ) 8 64
极大 =25031‘,-0.561K1
c. 易锥面时 (2 Ku1 / Ku 2 )(Ku1 2 K u 2 ) HA Is
附录: EA=( 的0次项 )+( 的一次项 )+( 的二次项 )+……….
a )的0次项0=1,对应于K0。 b)的一次项是奇数项不考虑,为0( 对应于K0 )。 c)的二次项:a112+a222+a332=a( 12+22+32 ) (对六角晶系要考虑二次项) d)的四次项为: 4 4 14 2 3 ,
I s H A sin E A K 1 (2 sin 2 3 sin 4 ) 8 K 2 ( sin 2 4 sin 4 3 sin 6 ) 64
Is x y <110>
H A ( K1
1 K2 ) / Is 2
HA
C. <111>为易轴:
b.<110>易轴:磁化强度的有利转动晶面分别是(100)和(110)面
( 1 )在(100)面上,Is转动求HA z HA
( 100 )
<011>
Is y
I s H A sin
得到
E A K1 sin 4 2
x
z
2 K1 Is ( 2 )在(110)面上,I s从HA转出 角,用转 矩求HA HA
x Fe: Ni: K1=4.72x104Jm-3 K2=-0.075x104Jm-3 K1=-5.7x103Jm-3 K2=-2.3x103Jm-3
图中看到当[100]方 向为易磁化轴和 [111]方向为易磁化 轴的各向异性能的 空间分布状况。
B. 磁晶各向异性场:
在不施加外磁场时,磁化强度的方向处在易磁化轴方向上,因此相当于在 易磁化轴方向上有一个等效磁场HA。
1 6 3 w(cos ) g l (cos 2 ) q(cos 4 cos 2 ) ...... 3 7 35
第一项与无关,对应于交换相互作用,第二项称为 偶极相互作用,因为若系数是 3M 2
l
40 r 3
则它与磁偶极相互作用有相同的形式。然而真正测得的磁各向异性相应的l 值 比此项给出的值大100到1000倍。真正的机理是:部分未淬灭的轨道矩与自旋 相互耦合,随着磁化强度的转动,通过轨道波函数重叠的变化,导致交换能或 静电能发生变化,这种相互作用被称为赝偶极相互作用。第三项为起源相同的 高价项,称为四极相互作用。磁晶各向异性可以通过对晶体中所有自旋对的能 量相加而计算出耒,这模型称为自旋对(spin-pair)模型。
z Is x
I s H A sin
HA <111>
E A K1 2 sin(2 2 ) 3 sin(4 4 ) 8
K2 sin( 2 2 ) 4 sin( 4 4 ) 3 sin( 6 6 ) 64
