综合训练讲义3(适用于外校小升初中)
小升初数学专项训练讲义

2018年小升初数学专项训练之答禄夫天创作第一讲 计算篇一、小升初考试热点及命题方向计算是小学数学的基础,近几年的试卷又以考察分数的计算和巧算为明显趋势(分值年夜体在6分~15分),学生应针对两方面强化练习:一 分数小数混合计算;二 分数的化简和简便运算;二、考试经常使用公式以下是总结的年夜家需要了解和掌握的知识,曾在重要考试中用到过.1.基本公式:()21321+=++n n n 2、()()612121222++=+++n n n n [讲解练习]:20193221⨯++⨯+⨯3、()()412121222333+=++=+++n n n n 4、131171001⨯⨯⨯=⨯=abc abc abcabc 6006610016131177877=⨯=⨯⨯⨯=⨯⇒如:[讲解练习]:2007×20062006-2006×20072007=____.5、()()b a b a b a -+=-22 [讲解练习]:82-72+62-52+42-32+22-12____.时间:二O 二一年七月二十九日6、742851.071 =428571.072 =……[讲解练习]:71化成小数后,小数点后面第2007位上的数字为____.7n化成小数后,小数点后若干位数字和为1992,问n=____.7、1+2+3+4…(n-1)+n+(n-1)+…4+3+2+1=n29、111111111912345679=⨯[讲解练习]:5555555550501111111115091234567945012345679=⨯=⨯⨯=⨯四、典范例题解析1 分数,小数的混合计算【例1】(7185-61511)÷[21514+(4-21514)÷1.35]【例2】)19956.15.019954.01993(22.550276951922.510939519+⨯⨯÷+--+ 2 庞年夜数字的四则运算【例3】19+199+1999+……+919999991个=_________. 【例4】352551855612590921934833344807÷÷=_____ 3 庞年夜算式的四则运算(拆分和裂项的技巧)【例5】42012020141213612211+++++ 【例6】42133011209127657653++++++时间:二O 二一年七月二十九日【例7】21156151051064633312⨯+⨯+⨯+⨯+⨯4 繁分数的化简【例8】已知1811111214x =+++ ,那么x=_________.5 换元法的运用【例9】⎪⎭⎫ ⎝⎛+++⨯⎪⎭⎫ ⎝⎛++++-⎪⎭⎫ ⎝⎛+++⨯⎪⎭⎫ ⎝⎛++++199913121200013121120001312119991312116 其他常考题型【例10】小刚进行加法珠算练习,用1+2+3+……,当数到某个数时,和是1000.在验算时发现重复加了一个数,这个数是___.【拓展】小明把自己的书页码相加,从1开始加到最后一页,总共为1050,不外他发现他重复加了一页,请问是___页.作业题1、)5246.5(402323153236-⨯⨯+÷2、39×148149+148×86149+48×74149 3、有一串数、、、、、、、、4241333231222111它的前1996个数的和是几多?时间:二O 二一年七月二十九日5、将右式写成份数21212121+++第二讲 几何篇(一)一、小升初考试热点及命题方向几何问题是小升初考试的重要内容,分值一般在12-14分(包括1道年夜题和2道左右的小题).尤其重要的就是平面图形中的面积计算,几何从内容方面,可以简单的分为直线形面积(三角形四边形为主),圆的面积以及二者的综合.其中直线形面积近年来考的比力多,值得我们重点学习.从解题方法上来看,有割补法,代数法等,有的题目还会用到有关包括与排除的知识.二、典范例题解析1 等积变换在三角形中的运用首先我们来讨论一下和三角形面积有关的问题,年夜家都知道,三角形的面积=1/2×底×高因此我们有【结论1】等底的三角形面积之比即是对应高的比【结论2】等高的三角形面积之比即是对应底的比【例1】如图,四边形ABCD 中,AC 和BD 相交于O 点,三角形ADO 的时间:二O 二一年七月二十九日面积=5,三角形DOC 的面积=4,三角形AOB 的面积=15,求三角形BOC 的面积是几多?【例2】将下图中的三角形纸片沿虚线折叠获得右图,其中的粗实线图形面积与原三角形面积之比为2:3.已知右图中3个阴影的三角形面积之和为1,那么重叠部份的面积为几多?燕尾定理在三角形中的运用 下面我们再介绍一个非常有用的结论:【燕尾定理】:在三角形ABC 中,AD,BE,CF 相交于同一点O,那么S △ABO:S △ACO=BD:DC【例3】在△ABC 中DC BD =2:1, EC AE =1:3,求OE OB =?2 差不变原理的运用【例4】左下图所示的ABCD 的边BC 长10cm,直角三角形BCE 的直角边EC 长8cm,已知两块阴影部份的面积和比△EFG 的面积年夜10cm 2,求CF 的长.【例5】如图,已知圆的直径为20,S1-S2=12,求BD的长度?3 利用“中间桥梁”联系两块图形的面积关系【例6】如图,正方形ABCD的边长是4厘米,CG=3厘米,矩形DEFG 的长DG为5厘米,求它的宽DE即是几多厘米?【例7】如下图所示,四边形ABCD与DEFG都是平行四边形,证明它们的面积相等.4 其他常考题型【例8】用同样年夜小的22个小纸片摆成下图所示的图形,已知小纸片的长是18厘米,求图中阴影部份的面积和.拓展提高:下图中,五角星的五个顶角的度数和是几多?作业题1、如右图所示,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=2BC;延长CA至F,使AF=3AC,求三角形DEF的面积.2、如图,在三角形ABC中,,D为BC的中点,E为AB上的一点,且BE=13AB,已知四边形EDCA的面积是35,求三角形ABC的面积.3、右图是一块长方形耕地,它由四个小长方形拼合而时间:二O二一年七月二十九日成,其中三个小长方形的面积分别为15、18、30公顷,问图中阴影部份的面积是几多?4、图中AB=3厘米,CD=12厘米,ED=8厘米,AF=7厘米.四边形ABDE 的面积是几多平方厘米.5、三角形ABC中,C是直角,已知AC=2,CD=2,CB=3,AM=BM,那么三角形AMN(阴影部份)的面积为几多?第三讲几何篇(二)一、小升初考试热点及命题方向圆和立体几何近两年虽然不是考试热点,但在小升初考试中也会时常露面.因为立体图形考察学生的空间想象能力,可以反映学生的自己潜能;而另一方面,初中很多知识点都是建立在空间问题上,所以可以说学校考察立体也是为初中选拔知识链接性好的学生.二、典范例题解析1与圆和扇形有关的题型【例1】如下图,等腰直角三角形ABC的腰为10厘米;以A为圆心,EF为圆弧,组成扇形AEF;阴影部份甲与乙的面积相等.求扇形所在的圆面积.【例2】草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈时间:二O二一年七月二十九日的一角用长30米的绳子拴着一只羊(见左下图).问:这只羊能够活动的范围有多年夜?【例3】如图,ABCD是正方形,且FA=AD=DE=1,求阴影部份的面积.(取π=3)与立体几何有关的题型小学阶段,我们除学习平面图形外,还认识了一些简单的立体图形,如长方体、正方体(立方体)、直圆柱体,直圆锥体、球体等,而且知道了它们的体积、概况积的计算公式,归纳如下.见下图.2求不规则立体图形的概况积与体积【例4】用棱长是1厘米的正方块拼成如下图所示的立体图形,问该图形的概况积是几多平方厘米?【例5】如图是一个边长为2厘米的正方体.在正方体的上面的正中向下挖一个边长为1厘米的正方体小洞;接着在小洞的底面正中再向下挖一个边长为1/2厘米的小洞;第三个小洞的挖法与前两个相同,边长为1/4厘米.那么最后获得的立体图形的概况积是几多平方厘米?3水位问题时间:二O二一年七月二十九日时间:二O 二一年七月二十九日【例6】一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈),如下图.已知它的容积为π立方厘米.当瓶子正放时,瓶内的酒精的液面高为6厘米.瓶子倒放时,空余部份的高为2厘米.问:瓶内酒精的体积是几多立方厘米?合几多升?【例7】一个高为30厘米,底面为边长是10厘米的正方形的长方体水桶,其中装有21容积的水,现在向桶中投入边长为2厘米⨯2厘米⨯3厘米的长方体石块,问需要投入几多块这种石块才华使水面恰与桶高相齐?4 计数问题【例8】右图是由22个小正方体组成的立体图形,其中共有几多个年夜年夜小小的正方体?由两个小正方体组成的长方体有几多个?拓展提高:有甲、乙、丙3种年夜小的正方体,棱长比是1:2:3.如果用这三种正方体拼成尽量小的一个正方体,且每种都至少用一个,则最少需要这三种正方体共几多?作业题1、右上图中每个小圆的半径是1厘米,阴影部份的周长是_______厘米.(π=3.14)2、求下图中阴影部份的面积:3、如右图,将直径AB为3的半圆绕A逆时针旋转60°,此时AB达到AC的位置,求阴影部份的面积(取π=3).4、有一个正方体,边长是5.如果它的左上方截去一个边长分别是5、3、2的长方体(如下图),求它的概况积减少的百分比是几多?5、如下图,在棱长为3的正方体中由上到下,由左到右,由前到后,有三个底面积是1的正方形高为3的长方体的洞,求所得形体的概况积是几多?第四讲行程篇(一)一、小升初考试热点及命题方向行程问题是历年小升初的考试重点,各学校都把行程当压轴题处置,可见学校对行程的重视水平,由于行程题自己题干就很长,模型多样,变动众多,所以对学生来说处置起来很头疼,而这也是学校考察的重点,这可以充沛体现学生对题目的分析能力.时间:二O二一年七月二十九日二、基本公式【基本公式】:路程=速度×时间【基本类型】相遇问题:速度和×相遇时间=相遇路程;追及问题:速度差×追及时间=路程差;流水问题:关键是抓住水速对追及和相遇的时间不发生影响;顺水速度=船速+水速逆水速度=船速-水速静水速度=(顺水速度+逆水速度)÷2水速=(顺水速度-逆水速度)÷2(也就是顺水速度、逆水速度、船速、水速4个量中只要有2个就可求另外2个)其他问题:利用相应知识解决,比如和差分倍和盈亏;【复杂的行程】1、屡次相遇问题;2、环形行程问题;3、运用比例、方程等解复杂的题;三、典范例题解析1 典范的相遇问题【例1】甲、乙两人沿400米环形跑道练习跑步,两人同时从跑道的同一地址向相反方向跑去.相遇后甲比原来速度增加2米/秒,乙比原来速度减少2米/秒,结果都用24秒同时回到原地.求甲原来的速度.【例2】小红和小强同时从家里动身相向而行.小红每分走52米,小强每分走70米,二人在途中的A处相遇.若小红提前4分动身,时间:二O二一年七月二十九日且速度不变,小强每分走90米,则两人仍在A处相遇.小红和小强两人的家相距几多米?【例3】甲、乙两车分别从A、B两地同时动身相向而行,6小时后相遇在C点.如果甲车速度不变,乙车每小时多行5千米,且两车还从A、B两地同时动身相向而行,则相遇地址距C点12千米,如果乙车速度不变,甲车每小时多行5千米,且两车还从A、B两地同时动身相向而行,则相遇地址距C点16千米.甲车原来每小时向几多千米?2 典范的追及问题【例4】在400米的环行跑道上,A,B两点相距100米.甲、乙两人分别从A,B两点同时动身,按逆时针方向跑步.甲甲每秒跑5米,乙每秒跑4米,每人每跑100米,都要停10秒钟.那么甲追上乙需要时间是几多秒?3 屡次折返的行程问题【例5】甲、乙两人同时从山脚开始爬山,达到山顶后就立即下山,他们两人的下山速度都是各自上山速度的1.5倍,而且甲比乙速度快.两人动身后1小时,甲与乙在离山顶600米处相遇,当乙达到山顶时,甲恰好到半山腰.那么甲回到动身点共用几多小时?时间:二O二一年七月二十九日4 流水行船问题关键是抓住水速对追及和相遇的时间不发生影响;顺水速度=船速+水速逆水速度=船速-水速静水速度=(顺水速度+逆水速度)÷2水速=(顺水速度-逆水速度)÷2必需熟练运用:水速顺度、逆水速度、船速、水速4个量中只要有2个量求另外2个量公式推导:【例6】一艘轮船顺流航行120千米,逆流航行80千米共用16时;顺流航行60千米,逆流航行120千米也用16时.求水流的速度.【例7】某河有相距45千米的上下两港,每天按时有甲乙两船速相同的客轮分别从两港同时动身相向而行,这天甲船从上港动身失落下一物,此物浮于水面顺水漂下,4分钟后与甲船相距1千米,预计乙船动身后几小时可与此物相遇.【例8】一只小船从甲地到乙地往返一次共用2时,回来时顺水,比去时每时多行驶8千米,因此第2时比第1时多行驶6千米.求甲、乙两地的距离.作业题时间:二O二一年七月二十九日时间:二O 二一年七月二十九日1、在环形跑道上,两人都按顺时针方向跑时,每12分钟相遇一次,如果两人速度不变,其中一人改成按逆时针方向跑,每隔4分钟相遇一次,问两人各跑一圈需要几分钟?2、甲、乙、丙三人行路,甲每分钟走60米,乙每分钟走67.5米,丙每分钟走75米,甲乙从东镇去西镇,丙从西镇去东镇,三人同时动身,丙与乙相遇后,又经过2分钟与甲相遇,求工具两镇间的路程有几多米?3、甲、乙同时从 A, B 两地相向走来.甲每时走 5千米,两人相遇后,乙再走10千米到A 地,甲再走1.6时到B 地.乙每时走几多千米?4千米.4、甲、乙两车同时从A,B 两地相向而行,它们相遇时距A,B 两地中心处8千米,已知甲车速度是乙车的1.2倍,求A,B 两地的距离.5、客车和货车同时从甲、乙两城之间的中点向相反的方向相反的方向行驶,3小时后,客车达到甲城,货车离乙城还有30千米.已知货车的速度是客车的43,甲、乙两城相距几多千米?第五讲 行程篇(二)一、小升初考试热点及命题方向屡次相遇的行程问题是近两年来各个重点中学非常喜爱的出题角度,这类题型往往需要学生结合六年级所学习的比例知识和分数百分数来分析题干条件,考查内容较为全面.二、基本公式【基本公式】:路程=速度×时间【基本类型】相遇问题:速度和×相遇时间=相遇路程;追及问题:速度差×追及时间=路程差;流水问题:关键是抓住水速对追及和相遇的时间不发生影响;顺水速度=船速+水速逆水速度=船速-水速静水速度=(顺水速度+逆水速度)÷2水速=(顺水速度-逆水速度)÷2(也就是顺水速度、逆水速度、船速、水速4个量中只要有2个就可求另外2个)其他问题:利用相应知识解决,比如和差分倍和盈亏;【复杂的行程】1、屡次相遇问题;3、运用比例、方程等解复杂的题;三、典范例题解析1 直线型的屡次相遇问题如果甲乙从A,B两点动身,甲乙第n次迎面相遇时,路程和为全长的2n-1倍,而此时甲走的路程也是第一次相遇时甲走的路程的时间:二O二一年七月二十九日时间:二O 二一年七月二十九日2n-1倍(乙也是如此).【例1】湖中有A,B 两岛,甲、乙二人都要在两岛间游一个来回.两人分别从A,B 两岛同时动身,他们第一次相遇时距A 岛700米,第二次相遇时距B 岛400米.问:两岛相距多远?【例2】甲、乙二人分别从A 、B 两地同时相向而行,乙的速度是甲的32,二人相遇后继续行进,甲到B 地、乙到A 地后立即返回.已知二人第二次相遇的地址距第一次相遇的地址是20千米,那么,A 、B 两地相距___千米.2 环形跑道的屡次相遇问题【例3】在一圆形跑道上,甲从A 点、乙从B 点同时动身反向而行,6分后两人相遇,再过4分甲达到B 点,又过8分两人再次相遇.甲、乙环行一周各需要几多分?.【例4】右图中,外圆周长40厘米,画阴影部份是个“逗号”,两只蚂蚁分别从A,B 同时爬行.甲蚂蚁从A 动身,沿“逗号”四周顺时针爬行,每秒爬3厘米;乙蚂蚁从B 动身,沿外圆圆周顺时针爬行,每秒爬行5厘米.两只蚂蚁第一次相遇时,乙蚂蚁共爬行了几多米?3 与分数百分数相结合的行程问题总结:若两人走的一个全程中甲走1份M 米,则两人走3个全程中甲就走3份M 米.【例5】一辆车从甲地开往乙地.如果车速提高20%,可以比原按时间提前一小时达到;如果以原速行驶120千米后,再将车速提高25%,则可以提前40分钟达到.那么甲乙两地相距几多千米?【例6】学校组织春游,同学们下午一点动身,走了一段平坦的路,爬了一座山,然后按原路返回,下午七点回到学校.已知他们的步行速度平地为4千米/时,上山为3千米/时,下山为6千米/时.问:他们一共走了几多路?作业题1、客车和货车同时从甲、乙两地相向开出,客车行完全程需10时,货车行完全程需15时.两车在中途相遇后,客车又行了90千米,这时客车行完了全程的80%,求甲、乙两地的距离.2、甲、乙两车分别从A、B两地动身,相向而行.动身时,甲、乙的速度比是5:4,相遇后,甲的速度减少20%,乙的速度增加20%,这样,当甲达到B地时,乙离A地还有10千米.那么A、B两地相距几多千米?3、一位少年长跑选手,顺风跑90米用了10秒钟,在同样的风速下,逆风跑70米,也用了10秒钟.问:在无风的时候,他跑100米要用几多秒?时间:二O二一年七月二十九日4、甲、乙两人同时从山脚开始爬山,达到山顶后就立即下山.他们两人下山的速度都是各自上山速度的2倍.甲到山顶时,乙距山顶还有400米;甲回到山脚时,乙刚好下到半山腰.求从山脚到山顶的距离.5、甲,乙两人在一条长100米的直路上来回跑步,甲的速度3米/秒,乙的速度2米/秒.如果他们同时分别从直路的两端动身,当他们跑了10分钟后,共相遇几多次?6、如图,ABCD是一个边长为6米的模拟跑道,甲玩具车从A动身顺时针行进,速度是每秒5厘米,乙玩具车从CD的中点动身逆时针行进,结果两车第二次相遇恰好是在B点,求乙车每秒走几多厘米?第六讲找规律篇一、小升初考试热点及命题方向找规律问题在小升初考试中几乎每年必考,但考题的分值较低,多以填空题型是呈现.在刚刚结束的14年小升初选拔考试中,一八、经纬、郑州中学偶有考察.二、典范例题解析1 与周期相关的找规律问题时间:二O二一年七月二十九日时间:二O 二一年七月二十九日【例1】7n 化小数后,小数点后若干位数字和为1992,求n 为几多? 【例2】、观察下列算式:……用你所发现的规律写出20043的末位数字是__________.2 图表中的找规律问题【例3】自然数如下表的规则排列:求:(1)上起第10行,左起第13列的数;(2)数127应排在上起第几行,左起第几列?【例3】下面是C B A ,,三行按分歧规律排列的,那么当A =32时, B +C =______.【例4】用同样规格的黑白两种颜色的正方形瓷砖按下图方式铺地板,则第(3)个图形中有黑色瓷砖块,第个图形中需要黑色瓷砖块(用含n 的代数式暗示). A 24 6 8 10 …… B 15 9 13 17 …… C2 5 10 17 26 ……3较复杂的数列找规律【例5】下面两个多位数1248624……、6248624……,都是依照如下方法获得的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位.对第2位数字再进行如上把持获得第3位数字……,后面的每一位数字都是由前一位数字进行如上把持获得的.当第1位数字是3时,仍按如上把持获得一个多位数,则这个多位数前100位的所有数字之和是几多?【例6】数学家泽林斯基在一次国际性的数学会议上提出树生长的问题:如果一棵树苗在一年以后长出一条新枝,然后休息一年.再在下一年又长出一条新枝,而且每一条树枝都依照这个规律长出新枝.那么,第1年它只有主干,第2年有两枝,问15年后这棵树有几多分枝(假设没有任何死亡)?【例7】把棱长为a的正方体摆成如图的形状,从上向下数,第一层1个,第二层3个……按这种规律摆放,第五层的正方体的个数是【例8】下面是按规律列的三角形数阵:11 11 2 1时间:二O二一年七月二十九日1 3 3 11 4 6 4 1 1 5 10 10 5 1………………那么第1999行中左起第三个数是______.【例9】一串分数:12123412345612812 ,,,,,,,,,,,,.....,,,......, 33,55557777779991111其中的第2000个分数是.拓展提升:小明每分钟吹-次肥皂泡,每次恰好吹出100个.肥皂泡吹出之后,经过1分钟有-半破了,经过2分钟还有201没有破,经过2分半钟全部肥皂泡都破了·小明在第20次吹出100个新的肥皂泡的时候,没有破的肥皂泡共有个.作业题1、有一堆火柴共 10根,如果规定每次取 1~3根,那么取完这堆火柴共有几多种分歧取法?2、已知一串有规律的数:1,2/3,5/8,13/21,34/55,….那么,在这串数中,从左往右数,第10个数是________.3、用黑白两种颜色的正方形纸片,按黑色纸片数逐渐加1的规律拼成一列图案:时间:二O二一年七月二十九日(1)第4个图案中有白色纸片张;(2)第n个图案中有白色纸片张.4、如图所示,在正六边形A周围画出6个同样的正六边形(阴影部份),围成第1圈;在第1圈外面再画出12个同样的正六边形,围成第2圈;…….按这个方法继续画下去,当画完第9圈时,图中共有______个与A相同的正六边形.5、用火柴棒按下图中的方式搭图形,依照这种方式搭下去,搭第个图形需____________根火柴棒.6、一个人从中央(标有0)的位置动身,向东、向北各走1千米,再(第一个图形)(第二个图形)向西、向南各走2千米,再向东、向北走3千米,向西、向南各走4千米,……,如此继续下去.他每走1千米,就把所走的路程累计数标出(如图),当他走到距中央正东100千米处时,他共走了______千米.第七讲工程篇一、小升初考试热点及命题方向罗巴切夫斯基是俄国数学家.曾有一位承包商向他请教过一个工程问题:某项工程,若甲、乙独自去做,甲比乙多用4天完成;若甲先做2天后,再和乙一起做,则共用7天可完成,问甲、乙时间:二O二一年七月二十九日时间:二O 二一年七月二十九日两人独自做此工程各需几多天完成?谜底:设甲、乙两人每人完成该项工程的一半,以题意,甲、乙两人独自完成,甲比乙多用4天,所以每人独自完成一半时,甲比乙多用2天.另外,已知甲先做2天,然后与乙合作,7天完成,这就是说,甲、乙共同完玉成部工作时(每人做一半),相差刚好2天,那么很明显,甲在7天中正好完成了工程的一半,而乙在5天中也完成了工程的一半.这样,甲独自完成要14天,乙独自完成要10天.工程问题在历届考试中之所以难,是因为工程问题中比例和单元“1” 综合.还有就是学生欠缺一些固定的条件的理解和转化能力.二、知识要点在工程问题中,一般要呈现三个量:工作总量、工作时间(完成工作总量所需的时间)和工作效率(单元时间内完成的工作量).【基本公式】:这三个量之间有下述一些关系式:工作效率×工作时间=工作总量;工作总量÷工作时间=工作效率;工作总量÷工作效率=工作时间. 为叙述方便,把这三个量简称工量、工时和工效.深刻理解公式的用法!三、典范例题解析1 涉及二者的工程问题【例1】一项工程,甲独自做6天完成,乙独自做12天完成.现两人合作,途中乙因病休息了几天,这样用了4.5天才完成任务.乙因病休息了几天?【例2】一项工程,甲、乙两人合作4天后,再由乙独自做5天完成,已知甲比乙每天多完成这项工程的130.甲、乙独自做这项工程各需要几天?【例3】某项工程,甲独自做需要20天,如果与乙合作,12天就可以完成.现在由甲独自做16天,然后由乙继续做完,还需要几天时间?2 涉及三者的工程问题【例4】一项工程,甲队独自做24天完成,乙队独自做30天完成.现在甲、乙两队先合做8天,剩下的由丙队独自做了6天完成了此项工程.如果从开始就由丙队独自做,需要几天?3 涉及多者的工程问题【例5】一项工程,45人可以若干天完成.现在45人工作6天后,调走9人干其他工作.这样,完成这项工程就比原来计划多用了4时间:二O二一年七月二十九日时间:二O 二一年七月二十九日天.原计划完成这项工程用几多天?4 水箱注水的工程问题【例6】水池装置A 、B 、C 、D 、E 五根水管,有的专门放水,有的专门进水.如果每次用两根水管同时工作,注满一池水所用时间如下表所示:如果选用一根水管注水,要尽快把空池注满,问应选用哪根水管?【例7】有甲、乙两根水管,分别同时给两个年夜小相同的水池A和B 注水,在相同时间内甲、乙两管注水量之比7:5.经过312时,A 、B 两池中已注入水之和恰好是一池水.尔后,甲管的注水速度提高25%,乙管的注水速度降低 30%.当甲管注满A 池时,乙管还需多长时间注满B 池?【拓展】“牛吃草”问题例题选讲:有一片牧场,草每天匀速生长,如果牧民在此放24只羊,则6天吃完草;如果放牧21只羊,则8天吃完,每天吃草的量都是相等的.问:1、如果放牧16只羊,则几天可以吃完牧草?2、要是牧草永远吃不完,最多放几只羊?。
2024年小升初语文升学专项阅读训练讲义练习专项3《认识与运用修辞手法》

小升初升学专项阅读训练讲义+练习专项3认识与运用修辞手法课标要求点《语文课程标准(2022年版)》要求:关于语言结构和运用的规律,须让学生在具有比较丰富的语言积累和良好语感的基础上,在实际运用中逐步体会把握。
能分辨常见的修辞手法,根据语境判断运用是否得当,熟练运用各种手法以增强语言的表现力。
因此,掌握常见的修辞手法,并学会体会其在表达上的作用,是一项重要的阅读训练任务。
要点归纳修辞手法,就是通过修饰、调整语句,运用特定的表达形式以提高语言表达作用的方式或方法。
对小学生而言,常见的修辞手法主要有以下几种。
一、比喻与拟人比喻是用与甲事物有相似之处的乙事物来描写或说明甲事物。
比喻一般由本体、喻体和比喻词组成。
用比喻的修辞手法,可使描写的事物生动形象,给人以鲜明深刻的印象。
如《草原》中的“走了许久,远远地望见了一条迂回的明如玻璃的带子——河”。
拟人就是把事物当作人来写,赋予事物以人的行为特点,让读者感到所描写的物体显得更活泼、亲切,使文章更加生动形象。
如《草原》中的“在这境界里,连骏马和大牛有时候都静立不动,好像在回味草原的无限乐趣”。
比喻与拟人的区别:比喻是将一物比作另一物,拟人是将一物当作人去写。
二、夸张夸张就是故意把事物的某一特征进行扩大或缩小,以增强表达效果,给人以深刻的印象。
夸张分为扩大夸张、缩小夸张和超前夸张三种。
是用言过其实的方法,突出事物的本质,引起读者的联想或加强作者的某种感情,如《七律·长征》中的“五岭逶迤腾细浪,乌蒙磅礴走泥丸”。
三、排比排比就是把三个或三个以上结构相似、意思相关、语气一致的句子或句子成分排列在一起。
排比的行文朗朗上口,有极强的说服力,能增强文章的表达效果和气势,如《花之歌》中的“我是诸元素之女:冬将我孕育,春使我开放,夏让我成长,秋令我昏昏睡去”。
四、对偶对偶,结构相同或基本相同、字数相等、意义上密切相连的两个短语或句子,对称地排列。
从形式上看,音节整齐匀称,节奏感强;从内容上看,言简义丰,概括性强,如《七律·长征》中的“金沙水拍云崖暖,大渡桥横铁索寒”。
小升初培训讲义

2013年小升初部分试题(四上——六上内容)
1. 用喜欢的方法计算。
(每小题3分,共18分)
3.2 1.250.25⨯⨯ 5.8[1(2.1 2.09)]⨯+-
31311015050⨯- 1142()23÷+
37175%488⨯+⨯ 7552()()81693
-⨯+
2. 求未知数x 的值(每题3分,共6分) 15(3)13x x +-= 113:(3):226
x +=
3. 我会列式,我会算(每小题3分,共6分)
(1) 甲数的
17等于乙数的23,甲数是112,乙数是多少?
(2)
92乘23的积减去1.5,再除以0.5,商是多少?
一、 解决问题(第1小题4分,第2-7小题每题6分,共40分)
1. 如图所示,求甲比乙的面积少多少平方厘米?
2. 某工程队修一条路,第一天修的比全长的72多2米,第二天修的比剩下部分的3
2少4米,还剩200米没修,这段路全长多少米?
3. 甲乙两车从AB 两地在上午8时同时出发,相向而行,已知甲的速度比乙的速度快2千
米时,到上午10点两车相距36千米,继续前行,又过2小时两车还是相距36千米,求AB 两地的距离?
4. 某商店同时卖出两件商品,每件各卖30元,其中一件盈利20%,另一件亏本20%,
这个商店卖出这两件商品总体上是盈利还是亏本?具体是多少?。
小升初衔接班数学讲义
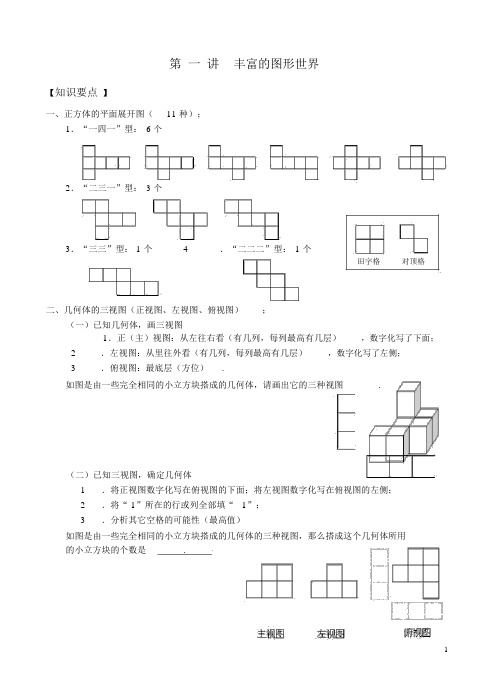
第一讲丰富的图形世界【知识要点】一、正方体的平面展开图(11 种);1.“一四一”型:6 个2.“二三一”型:3 个3.“三三”型: 1 个4.“二二二”型:1 个田字格对顶格二、几何体的三视图(正视图、左视图、俯视图);(一)已知几何体,画三视图1.正(主)视图:从左往右看(有几列,每列最高有几层),数字化写了下面;2.左视图:从里往外看(有几列,每列最高有几层),数字化写了左侧;3.俯视图:最底层(方位).如图是由一些完全相同的小立方块搭成的几何体,请画出它的三种视图.(二)已知三视图,确定几何体1.将正视图数字化写在俯视图的下面;将左视图数字化写在俯视图的左侧;2.将“ 1”所在的行或列全部填“ 1”;3.分析其它空格的可能性(最高值)如图是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是.【新知讲授】1.如图,将标号为A、 B、 C、 D 的正方形沿图中的虚线剪开后得到标号为组图形,则按 A、 B、 C、 D的顺序确定正确对应的图形顺序是 ().(A) P 、M、Q、NA B C(B)Q 、N、M、P(C)M 、P、Q、N(D) N 、Q、P、MP Q M2.在桌子上放着五个薄圆盘 , 如右图所示 . 它们由下到上放置的次序应当是(A)X ,Y, Z,W,V(B)X,W,V,Z,Y(C)Z ,V, W,Y,X(D)Z,Y,W,V,X3.在下列图形中( 每个小正方形皆相同 ) 可以是一个正方体表面展开图的是( ). P、 Q、 M、N 的四DN ( ).(A)(B)(C)(D)4.在下列图形中( 每个小正方形皆相同) 可以是一个正方体表面展开图的是().(A)(B)(C)(D)5.如右图所示的立方体,如果把它展开,可以是下列图形中的().(A)(B)(C)(D)6.正方体的平面展开图是右图,原正方体形如().(A)(B)(C)(D)7.如图所示的几何体是由六个小正方体组合而成的,它的左视图是().8.由几个小立方体搭成的一个几何体如图 1 所示,它的主(正)视图见图2,那么它的俯视图为().(A)(B)(C)(D)9.下面的几何体中,主(正)视图为三角形的是().(A)(B)(C)(D)10.如果用□表示 1 个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下面右图由7 个立方体叠成的几何体,从正前方观察,可画出的平面图形是().(A)(B)(C)(D)11.下图是由一些相同的小正方形构成的几何体的三视图,那么这些相同的小正方形的个数是( ).(A)4 (B)5 (C) 6 (D)712. 已知一个物体由x 个相同的正方体堆成,它的主视图和左视图如图所示,那么x 的最大值是() .(A)13 (B)12 (C)11 (D)10(第 11 题图)(第12题图)(第13题图)13.一个画家有14 个边长为1m的正方体,他在地面上把它们摆成如图所示的形式,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为().(A)19m 2(B)21m 2(C)33m2(D)34m 214.把图中的片沿虚线折起来,便可成为一个正方体,这个正方体 4 号面的对面是_______号面 .(第 14 题图)(第15题图)(第16题图)16.把图 (1) 的正方体表面展开成图(2) 时,有—个面的 4 条棱都没有被剪开,这个面是正方形.(用字母表示).17.由一些相同的小正方体构成一个立体图形,如图是从不同的方向看这个立体图形的平面图形,则构成这个立体图形的小正方形的个数是.C 2B 1A 4主视图左视图俯视图18.如图是一个正方体木块的表面展开图. 若在正方体的各面填上数,使得对面两数之和为7,则 A 处填的数是,B 处填的数是,C 处填的数是.19.一张桌子上摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共摆放有 ________个碟子 .21. 如图都是由边长为 1 的正方体叠成的图形. 例如第( 1)个图形的表面积为 6 个平方单位,第( 2)个图形的表面积为18 个平方单位,第(3)个图形的表面积是36 个平方单位 .(1)依此规律,求第( 5)个图形的表面积是多少个平方单位?(2)第( n)个图形的表面积又是多少个平方单位?22.请在图中用阴影标出六个小正方形,它们是一个正方形的展开图(要求画法各不相同).23.如图是由一些完全相同的小立方块搭成的几何体的三种视图,分别写出搭成这个几何体所用的小立方块的个数 .(1)共用块小立方块;主视图左视图俯视图(2)共用块小立方块;主视图左视图俯视图(3)共用块小立方块;24.如图,是由一些大小相同的小正方体组成的简单的几何体的主视图和俯视图.(1)请你画出这个几何体的一种左视图;(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值 .第二讲线段【知识要点】一、直线、射线、线段;1.区别:直线射线线段图形几何表示直线 AB(直线 BA)射线 AB(射线 BA)线段 AB(线段 BA)同一条直线不同射线同一条线段端点没有 1 个 2 个延伸方向两端延伸一端延伸无延伸长度度量不能不能能2.关系(联系):射线、线段是直线的一部分射线:直线上一点及一旁的部分;线段:直线上两点及两点之间的部分;3 .注意:两点确定一条直线;两点确定两条射线;两点确定一条线段;二、线段的中点;1.定义:将一条线段平均分成相等的两段的点.A P B2.性质:如图, P为线段 AB的中点,则有:①PA=PB;② AB=2PA;③ AB=2PB;④ PA=1AB;⑤ PB=1AB;223.判定 P 为线段 AB的中点:注意点P 是否在线段AB上;..(注意在无图条件下区别:在直线.. AB上);三、线段的有关计算(和、差、倍、分);四、两点间的距离1.定义:连接两点间的线段的长度..;2.能用“两点之间线段最短”来解释生活中的实际问题;3.应用:判断 A、 B、 C 三点共线的方法:AB、 AC、 BC三条线段的长度满足其中两条线段的长等于第三条线段的长. 【新知讲授】O AB1.如图,下列说法不正确的是 ( ).(A) 直线 AB与直线 BA是同一条直线(B) 射线 OA与射线 OB是同一条射线2.下列图形中,能相交的是( ).CDO CAABBBBDAOCAC(A) (B) (C) (D)3.点 C 在线段 AB 上,给出下列关系:① AC+BC=AB ;② AB-AC=BC ;③ AB-BC=AC ;④ AC=BC.其中一定正确的个数是 ( ).(A)0 个(B)1个(C)2 个 (D)3个4. 点 M 在直线 AB 上,下列条件中能判断点M 为线段 AB 的中点的是 ().(A)AM= 1AB(B)AB=2BM(C)AM=BM(D)AM+BM=AB25.下面说法中不正确的是 ( ).(A) 两点之间线段最短(B)两点确定一条直线(C) 直线、射线、线段都有中点(D) 两条不同的直线相交有且只有一个交点6.下面各种情况中, A 、B 、 C 三点在同一条直线上的是 ( ).(A)AB=5cm , AC=4cm , BC=2cm(B)AB=20cm, AC=8cm , BC=15cm (C)AB=16cm , AC=10cm , BC=3cm (D)AB=13cm, AC=16cm , BC=3cm7. C 为线段 AB 延长线上的一点,且 AC=3AB ,则 BC 为 AB 的.8.已知 A 、 B 、C 在同一直线上, AB=8, BC=4,则线段 AC 的长度为. 9.已知 AB=3,AC=9,当 BC= 时,点 A 、B 、 C 在同一条直线上 .10.如图, AC=BC=a , BD=b ,则 AD=.11.如图,已知线段 AB=11,C 、D 为 AB 上的两点,且 AD=8, BC=9,则线段 CD 的长为 .aaBA C DAC D bB12.如图, B 、C 两点把线段 AD 分成 2∶ 3∶ 4 三部分, M 是 AD 的中点, MC=1,则 AD= . 13.如图,已知 B 、C 是线段 AD 上的两点, M 是 AB 的中点, N 是 CD 的中点, MN=a , BC=b ,则线段 AD=.AB M C D A M B C N D14.一质点 P 从距原点 1 个单位的 A 点处向原点方向跳动,第一次跳动到OA 的中点 A 1 处,第二次从 A 1 点跳动到 O A 1 的中点 A 2 处,第三次从 A 2 点跳动到 O A 2 的中点 A 3 处,如 此不断跳动下去,则第 n 次跳动后,该质点到原点 O 的距离为 。
小升初数学复习讲义32.综合应用教案讲义及练习

32.综合应用知识要点梳理一、鸽巢原理1.定义:鸽巢原理又叫抽屉原理,它是组合数学的一个基本原理。
2.类型:(1)吧n+1个元素分成n 类,不管怎么分,则一定有一类有2个或2个以上的元素。
(2)吧m 个元素任意放入n (n ≤m )各集合,则一定有一个集合至少要有k 个元素,其中k=n m (当n 能整除m 时),或k=[n m ]+1(当n 不能整除m 时)这里的[n m ]表示不大于n m 的最大整数。
3.解题的步骤:第一步:分析题意,分清什么是“东西”,什么是“抽屉”。
第二步:制造抽屉。
这是关键的一步,这一步就是如何设计抽屉。
根据题目的条件和结论,结合有关的数学知识,抓住最基本的数量关系,设计和确定解决问题所需的抽屉及其个数,为使用抽屉铺平道路。
第三步:运用抽屉原理。
二、植树问题1.定义:植树问题是指在某个固定图形上,给定点之间的距离或其他条件,在这个图形上最多能分布多少个这样的点的问题。
2.公式:直线植树问题:计算两端点时,树木数=路线长度÷树木间隔+1计算一端点时,树木数=路线长度:树木间隔不计算两端点时,树木数=路线长度÷树木间隔-1圆周植树问题:树木数=路线长度÷树木间隔三、鸡兔同笼问题方法:假设法,方程法,抬脚法,列表法。
假设法解题思路:提出假设一产生差异一分析原因一解决差异。
公式1;(兔的脚数x 总只数一总脚数):(兔的脚数一鸡的脚数)=鸡的只数;总只数-鸡的只数=兔的只数公式2;(总脚数一鸡的脚数x 总只数):(兔的脚数一鸡的脚数)=兔的只数;总只数-兔的只数=鸡的只数公式3;(设兔为x只,鸡为总只数-x)4x + 2(总只数-想)=总脚数考点精讲分析典例精讲考点1 鸽巢原理【例1】张阿姨给孩子买衣服,有红、黄、白三种颜色,但结果总是至少有两个孩子的颜色一样,她至少有( )个孩子。
A.4B.2C.3【精析】把颜色的种类看作“抽屉”,把孩子的数量看作物体的个数,根据抽屉原理得出:孩子的个数至少比颜色的种类多1时,才能至保证少有两个孩子的颜色一样,即3+1=4(个)。
(通用版)小升初小学数学系列综合训练讲义(2)-教学文档

1.计算:11111111()1288244880120168224288+++++++⨯= .2.1111111111111111())()5791179111357911137911+++⨯+++-++++⨯++=()( . 3.由0,1,2,3,4,5组成的没有重复数字的六位数中,百位不是2的奇数有 个.4.新年联欢会上,共有90人参加了跳舞、合唱、演奏三种节目的演出.如果只参加跳舞的人数三倍于只参加合唱的人数;同时参加三种节目的人比只参加合唱的人少7人;只参加演奏的比同时参加演奏、跳舞但没有参加合唱的人多4人;50人没有参加演奏;10人同时参加了跳舞和合唱但没有参加演奏;40人参加了合唱;那么,同时参加了演奏、合唱但没有参加跳舞的有________人.5.已知四位数的个位数与千位数之和为10,个位数既是偶数又是质数,百位数与十位数组成两位数是个质数,又知这个四位数能被36整除,则所有满足条件的四位数中最大的是 .6.已知A 数有7个约数,B 数有12个约数,且A 、B 的最小公倍数[],1728A B =,则B = .7.2008222008+除以7的余数是 .8.设101104107200910k A ⨯⨯⨯⨯=⨯,这里A ,k 都是正整数,那么k 的最大值为 . 【解析】1.原式11111282446681618=++++⨯⨯⨯⨯⨯()2.设111157911A +++=,1117911B ++=,原式111313A B A B ⎛⎫⎛⎫=⨯+-+⨯ ⎪ ⎪⎝⎭⎝⎭111313A B A A B B =⨯+-⨯- 3.由0,1,2,3,4,5组成的没有重复数字的奇六位数,个位可以为1,3,5,有3种选法;个位选定后,十万位不能与个位相同,且不能为0,有4种;十万位选定后万位有4种;……;故由0,1,2,3,4,5组成的没有重复数字的奇六位数的个数为:344321288⨯⨯⨯⨯⨯=个;由0,1,2,3,4,5组成的没有重复数字且百位为2的奇六位数,个位可以为1,3,5,有3种选法;十万位不能与个位相同,且不能为0、2,有3种;十万位选定后万位有3种;……;故由0,1,2,3,4,5组成的没有重复数字且百位为2的奇六位数的个数为:3332154⨯⨯⨯⨯=个;所以,满足条件的数有:28854234-=个.4.设只参加合唱的有x 人,那么只参加跳舞的人数为3x ,由50人没有参加演奏、10人同时参加了跳舞和合唱但没有参加演奏,得到只参加合唱的和只参加跳舞的人数和为501040-=人,即340x x +=,得10x =,所以只参加合唱的有10人,那么只参加跳舞的人数为30人,又由“同时参加三种节目的人比只参加合唱的人少7人”,得到同时参加三项的有3人,所以参加了合唱的人中“同时参加了演奏、合唱但没有参加跳舞的”有:401010317---=人.5.因为个位数既是偶数又是质数,所以个位数字为2,又因为个位数与千位数之和为10,所以千位数字为8,因为这个四位数能被36整除,所以能被4与9整除,由于个位数与千位数之和为10,所以百位数与十位数的和除以9余8,又因为百位数与十位数之和不超过18,所以百位数与十位数的和为8或17.由于能被4整除,所以后两位数能被4整除,由于个位数字为2,所以十位数字只能为1,3,5,7,9,若百位数字为9,由于十位数字为奇数,所以其和不能等于8或17,所以百位数字最大为8,此时个位数字为9,且89是质数,符合题意,故答案为8892.6.63172823=⨯,由于A 数有7个约数,而7为质数,所以A 为某个质数的6次方,由于1728只有2和3这两个质因数,如果A 为63,那么1728不是A 的倍数,不符题意,所以62A =,那么33为B 的约数,设323k B =⨯,则()()13112k +⨯+=,得2k =,所以2323108B =⨯=. 7.328=除以7的余数为1,200836691=⨯+,所以200836691366922(2)2⨯==⨯+,其除以7的余数为:669122⨯=;2019除以7的余数为6,则22008除以7的余数等于26除以7的余数,为1;所以2008222008+除以7的余数为:213+=.8.只要看里面5的因子个数,因为2的因子个数一定足够多.101到2009里面共有(2009101)31637-÷+=个数.其中,这里面的后625个一定含有125个5的倍数,25个25的倍数,5个125的倍数和1个625的倍数;前12个中,110和125共含有4个因子5.所以,含有5的因子个数为12525514160++++=.。
小升初图形综合讲义新完整版

小升初图形综合讲义新 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】英才教育2011东北育才、省实验小升初集训图形训练三一、例题 :1、正方形ABCD 边长为1cm ,依次以A 、B 、C 、D 为圆心,以AD 、BE 、CF 、DG 为半径,画出扇形。
求阴影部分的面积。
2、求右图阴影部分的面积。
(图中单位:cm )3、如右图,O 为圆心,CO 垂直于AB ,三角形ABC 的面积是45cm 2。
求阴影部分的面积。
4、图中阴影甲的面积比阴影乙的面积多28cm 2,AB =40cm , CB 垂直于AB 。
求BC 的长。
5、如图,ACEG 是梯形,BDFG 是正方形。
GE =30cm ,GB =24cm , AC =39cm 。
求梯形ACEG 的面积。
6、如图(1)已知圆的直径为6cm ,求阴影部分的面积。
7、如图(1)所示,求阴影部分的面积。
(图中单位:cm )8、把一个正方形的一边减少20%,相邻的一边增加2cm ,得到一个长方形,它与原来的正方形的面积相等。
求原正方形的面积。
9、边长为10cm 的正方形纸片,正中挖一个正方形的洞,成为宽1cm 的方框放在桌面上成为右图的图案。
问桌面上放这些方框盖住部分的面积是多少cm 2.10、一个直径为4cm 的半圆,让点A 不动,把整个半圆顺时针旋转45。
,此时点B 移至点B 1处,如右图。
求阴影部分面积。
11、草场上有一个长20cm 、宽10cm 的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见右图)。
这只羊能活动的范围有多大?12、把19个棱长为3cm 的正方体重叠起来,如图(1所示),拼成一个立体图形。
求这个立体图形的表面积。
13、将高都是1m ,底面半径分别为1.5m 、1m 、0.5m 的三个圆柱如图所示的方式组成一个立体图形。
求这个立体图形的表面积。
(π取)14、某面粉厂有一容积是24m 3的长方体储粮池,它的宽和高都是长的21。
小升初数学专项训练-讲义汇编(共12讲及配套练习)

小升初数学专项训练-讲义汇编(共12讲及配套练习)
小升初数学考试的考纲中,都会对考试的内容进行详细的规定,从考试题目种类上说,包括填空题、选择题、计算题、应用题等等,而每种题目种类又对应不同的典型题型。
小升初的孩子既要熟知各种题目种类的考察重点,又要掌握不同典型题型的应对方法。
很多家长都担心孩子考不好,如何做好小升初数学考试的总复习?
老师结合自己的教学经验,整理了做好小升初数学考试专项训练-讲义汇编(共12讲及配套练习),希望对家长、孩子有一定的帮助和启发。
为了能进入理想地初中,给小学学习生活划上一个圆满地句号,各位考生正紧张地备战小学毕业考试。
数学是很多考生地弱项,一提起数学考试就会头疼,心理上有种恐惧感。
复习的重要特点就是在系统原理的指导下,对所学知识进行系统的整理,使之形成一个较完整的知识体系,这样有利于知识的系统化
和对其内在联系的把握,便于融合贯通。
做到梳理——训练——拓展,有序发展,真正提高复习的效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中小学1对1课外辅导专家武汉龙文教育学科辅导讲义授课对象 陈晨 授课教师 赵星 授课时间 1月11日 授课题目 综合复习 课 型 复习课使用教具PPT教学目标 综合运用各专题知识 教学重点和难点择校考试综合试题训练参考教材外校模拟试题、各名校往届入校考试试题、分班考试试题教学流程及授课详案择校考试真题训练三 上次课程作业讲解:1. (★★)116.31.41.12136⎡⎤⎛⎫⨯+÷-= ⎪⎢⎥⎝⎭⎣⎦________. 【分析】 遇到这一类问题最好将小数、带分数等都化为分数来处理,并注意乘法分配律的运用.原式6371100710531126⎡⎤⎛⎫=⨯+⨯-= ⎪⎢⎥⎝⎭⎣⎦63262571015286⎡⎤⨯⨯-=⎢⎥⎣⎦632625637101528106⨯⨯-⨯=39147420-=125 2. (★★★)某校六年级有三个班,每班人数一样多,已知一班男生和二班女生一样多,三班男生占全部男生的37,那么该校六年级学生中男、女生比例为 : .【分析】 要找出题目中的比例对应关系,关键是如何使用条件“一班男生和二班女生一样多”. 一班男生和二班女生一样多,说明一班男生和二班男生合起来恰好能凑出1个班的人数,一个班的人数相当于男生人数的34177-=,所以男生人数是总人数的4713712⎛⎫÷⨯= ⎪⎝⎭,所以男女比例为77:17:51212⎛⎫-= ⎪⎝⎭.3. (★★★)有一些五位数,它们至少有3个连续的数位上的数字是相同的,那么这样的五位数一共有个.【分析】 只有3个连续的数位上数字是相同的有:991029992349⨯⨯⨯+⨯⨯=(个);有4个连续的数位上数字是相同的有:992162⨯⨯=(个);有5个连续的数位上数字是相同的有:9个; 一共有234916292520++=(个).4. (★★★)如下图,边长分别为5、7、10的三个正方形放在一起,则其中四边形ABCD 的面积是 .A B C D AB CD【分析】 处理不规则四边形,常规的方法是将它化为两个三角形. 连接AC ,则四边形划分为三角形ABC 、ACD 两个三角形,三角形ABC 的面积55212.5=⨯÷=;三角形ACD 的面积()1075260=⨯+÷=;所以四边形ABCD 的面积是12.56072.5+=.5. (★★★)如下图,以直角三角形ABC 的两条直角边为半径作两个半圆,己知这两段半圆弧的长度之和是37.68厘米,那么三角形ABC 的面积最大是 平方厘米.(π取3.14)A BC 【分析】 与圆弧的长度相关的量是直角边的长度,与直角三角形面积相关的也是直角边的长度.根据条件可知,3.1437.682AB AC +⨯=,所以24AB AC +=,而三角形ABC 的面积为12AB AC ⨯⨯,根据“两数之和一定,差越小,积越大”,可知三角形ABC 的面积最大是1212722⨯=平方厘米.6. (★★)用两个筐装一堆苹果,甲筐装的比总数的60%少8千克,乙筐比甲筐多装5千克. 求甲、乙两筐各装了多少千克? 【分析】 甲、乙两筐构成了总数,它们的和为100%. (法1)如果甲筐装的多上8千克,乙筐装的少上8千克,那么甲筐装的占总数的60%,乙筐装的占总数的40%,甲筐比乙筐多了88511+-=千克,所以这11千克相当于总量的60%40%20%-=,所以两筐总数为1120%55÷=千克,原来甲筐有5560%825⨯-=千克,乙筐有555230+÷=()千克. (法2)将两筐均摊,即从乙筐中转出2.5千克到甲筐,那么甲、乙两筐相等,都占50%,所以比60%少8 2.5 5.5-=千克其实就是50%,两筐总质量为5.560%50%55÷-=()千克.7. (★★★)我们规定两人轮流做一个工程是指,第一个人先做一个小时,第二个人再做一个小时,然后再由第一个人做一个小时,然后又由第二个人做一个小时,如此反复,做完为止.如果甲、乙轮流做一个工程需要9.8小时,而乙、甲轮流做同样的工程只需要9.6小时,那乙单独做这个工程需要多少小时?【分析】 题述过程比较复杂,如果按工作周期来看,题述条件就容易处理了,但要注意最后一个周期是不完整的. 甲、乙轮流做时,甲做了5小时,乙做了4.8小时;乙、甲轮流做时,乙做了5小时,甲做了4.6小时,可见,甲做5 4.60.4-=小时完成的工程等于乙做5 4.80.2-=小时,乙的效率是甲的2倍,甲做5小时完成的任务乙只要2.5小时就能完成.乙单独完成这个工程要2.5 4.87.3+=(小时).8.(★★★)今有若干个底面半径和高均为1的圆柱体和若干个底面半径和高均为2的圆柱体,它们的体积和为50π,表面积和为120π.那么一共有多少个圆柱体?【分析】 一种圆柱体表面积为4π,体积为π,另一种表面积为16π,体积为8π,已知表面积和与体积和,这样的条件关系与“鸡兔同笼”问题非常相似.可以采用“鸡兔同笼”的思想来解.本题也可以采用方程来解.由于两种圆柱体的体积和表面积都不相同,为采用“鸡兔同笼”问题中的假设法,可以先把其中的一组化为相同.比如不妨将8个半径和高均为1的圆柱体看做一个整体,其表面积为32π,体积为8π. 根据“鸡兔同笼”的假设思想,假设全是半径和高均为2的圆柱体,那么其体积和为50π时,表面积为1650π100π8⨯=,那么半径和高均为1的圆柱体整体有()()5120π100π32π16π4-÷-=,由于每个整体有8个,所以实际上有58104⨯=个半径和高均为1的圆柱体,半径和高均为2的圆柱体则有()50ππ108π5-⨯÷=个.9. (★★★)甲、乙两地相距120千米,客车和货车同时从甲地出发驶向乙地,客车到达乙地后立即沿原路返回,在途中的丙地与货车相遇.之后,客车和货车继续前进,各自到达甲地和乙地后又马上折回,结果两车又恰好在丙地相遇.已知两车在出发后的2小时首次相遇,那么客车的速度是每小时多少千米?【分析】 通过画图可以直观的呈现整个行程过程: 丙乙甲第一次相遇,两车合走2个全程,第二次相遇,两车又比第一次相遇时多走2个全程,所以客车、货车第一次相遇时各自走的路程与第一次相遇到第二次相遇时各自走的路程分别相等.两次相遇都在丙点,设乙、丙之间路程为1份,可得甲、丙之间路程为2份,可得乙、丙间路程为120340÷=千米,客车速度为12040280+÷=()(千米/小时).10.(★★★)如图,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲和L 形区域乙、丙.已知三块区域甲、乙、丙的周长之比为4:5:7,并且区域丙的面积为48,求大正方形的面积.【分析】 题目给出了一组周长比例数据和一个面积数据,所以应该通过中间量(正方形边长)将两组数据联系起来.从图中可以看出,甲、乙、丙三块区域的周长分别等于三个正方形的周长,所以这三块区域的周长之比就等于三个正方形的边长之比,设三个正方形的边长分别为4a ,5a ,7a .则22492548a a -=,求出22a =;所以大正方形的面积为24998a =.1.(★★★)甲、乙、丙代表互不相同的3个正整数,并且满足:甲⨯甲=乙+乙=丙135⨯.那么甲最小是.【分析】甲⨯甲=乙+乙=丙135⨯的含义就是:甲的平方是偶数,并且是135的倍数.也就是说甲的平方是270的倍数,3270235=⨯⨯.所以甲最小是223590⨯⨯=.2.(★★★)已知x、y满足方程组76()13072()10x x yy x y+-=⎧⎨--=⎩,则x y-的值是.【分析】将x y-()看作一个整体,上、下两条式子直接相减得到:762120x y x y x y-+-+-=()()(),解得8x y-=.3.(★★)小明的2分硬币比5分硬币多13枚,5分硬币的钱数比2分硬币的钱数多25分.那么5分硬币有枚,2分硬币有枚.【分析】题目给出的硬币数和钱数都不相等,如果将其中一个项目变成相等,条件数据就容易处理了.列方程解应用题也是解此类题目的快捷方法,假设将5分硬币补上13枚,那么小明的2分硬币和5分硬币一样多,不过这时5分硬币的钱数比2分硬币的钱数多2513590+⨯=分,而每一枚硬币5分的比2分的多3分,所以5分和2分的各有905230÷-=()枚,那么原来5分硬币有301317-=枚,2分硬币有30枚.4.(★★★)老师要将20个相同的苹果分给3个小朋友,要求每个小朋友至少分得3个苹果,那么总共有种分配的方法.【分析】相同的苹果分给不同的人,适用插板法.但题目要求的是每人至少分得3个苹果,所以首先应当每人去掉2个苹果,这样共去掉236⨯=个苹果,剩下14个苹果每人至少1个,就相当于在14个苹果的13个间隔之间插两个板,一共有2131312278C=⨯÷=种方法.5.(★★★)如图,P为平行四边形ABCD外一点,已知三角形PAB和三角形PCD的面积分别为7平方厘米和3平方厘米,平行四边形ABCD的面积为平方厘米.PD CBANMPDCBA【分析】 如图,补出一个平行四边形,那么三角形PAB 和三角形PCD 的面积分别等于平行四边形ABNM 和DCNM 面积的一半,而这两个平行四边形的面积的差即为平行四边形ABCD 的面积,所以,7328ABCD S =-⨯=()平方厘米.6. (★★★)从一个长8厘米、宽7厘米、高6厘米的长方体中截下一个最大的正方体(如下图),剩下部分的表面积之和是 平方厘米.68766【分析】 可以将这个图形看作一个八棱柱,表面积和为:87662616661787292⨯-⨯⨯+⨯+++++++=()()(平方厘米).也可以这样想:由于截去后原来的长方体的表面少了3个66⨯的正方形,而新图形凹进去的部分恰好是3个66⨯的正方形,所以新图形的表面积与原图形的表面积相等,为()8786762292⨯+⨯+⨯⨯=(平方厘米).7. (★★)某工厂去年的总产值比总支出多50万元,今年比去年的总产值增加10%,总支出节约20%,如果今年的总产值比总支出多100万元,那么去年的总产值和总支出各是多少万元?【分析】设去年的总支出是x万元,那么总产值就是50()万元.可列方程:x+()+-=1.1501000.8x x解得150x=.所以去年的总支出是150万元,总产值是200万元.8.(★★★)小明跑步的速度是步行速度的3倍,他每天从家到学校都是步行.有一天,由于晚出发10分钟,他不得不跑步行了一半路程,另一半路程步行,这样与平时到达学校的时间一样.那么小明每天步行上学需要多少分钟?【分析】那天小明比平时少走了10分钟,这10分钟是由一半路程跑步而节约来的,如果全部路程跑步,那么应该能节约20分钟,而跑步的速度是步行速度的3倍,也就是说,小明走路所花时间应该是跑步所花时间的3倍,所以小明步行所花的时间为2031330()分钟.÷-⨯=9.(★★★)求所有的正整数x、y,使得满足方程232002-=.x xy【分析】原式化为32002x x y-=(),所以x和3x y-都是2002的约数.2002271113=⨯⨯⨯,而3x x y>-,所以x一定是2002的较大约数,符合条件的x有77、91、143、154、182、286、1001、2002,对应的3x y-是26、22、14、13、11、7、2、1,对应的y的值为17、23、43、47、57、93、333、667.所以满足条件的x、y有:()77,17,()91,23,()143,43,()154,47,()182,57,()286,93,()1001,333,()2002,667.10.(★★★)作家A,B,C,D,E依次坐成一排为同学们签名售书,已知每位同学都恰好找座位相邻的三位作家签名.如果一共有22个同学同时找B和D签名,并且C一共签名38次,A比E多签6次,那么B一共签名几次?【分析】虽然有五个作家,但签名的情况只有3种:ABC、BCD、CDE,同时找B和D签名就是第二种,所以第二种共有22次,C在第二种中签了22次,他共要签38次,所以第一种和第三种共有382216-=次,,而签A的只有第一种,签E的只有第三种,所以第一种的比第三种多6次,第一种有166211+÷=()次,那么签B的有112233+=次.1.(★★)110163.840.063152004200.44⨯+⨯=-⨯________.2.(★★★)已知一个圆柱体的底面积和侧面积相同.如果这个圆柱体的高是5厘米,那么它的体积是立方厘米(π取3.14)3.(★★★)学校给老师发洗衣粉.如果给男老师每人3包,女老师每人4包,那么就会多出8包;如果给男老师每人4包,女老师每人5包,那么就会少7包.已知男老师比女老师多1人,那么一共有多少包洗衣粉?4.(★★)体育商店以30元的价格买进一批足球,按原定价格销售应获得利润3600元,实际全部以8折卖出,获得利润1440元.那么这批足球共有多少个?陈晨家庭作业1月11日1. (★★)2006200720072007200720072006200620062006⨯-⨯=.2.(★★★)21231123123231234223423434⎛⎫⎛⎫⎛⎫⎛⎫+++⨯++-+++⨯+=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.3.(★★)一次考试,参加的学生中有17得优,13得良,12得中,其余的得差,已知参加考试的学生不满50人,那么得差的学生有人.4.(★★)有一城镇共5000户居民,每户的子女不超过2人,一部分家庭有1个孩子,余下的家庭中一半每家有2个孩子,那么此城镇共有孩子人.5.(★★)科学家进行一次实验,每隔5小时作一次记录,他做第12次记录时,时钟正好九点整,问第一次作记录时,时钟是点.6.(★★★)一名学生在计算一道除数是两位数的没有余数的除法时,错把被除数百位上的3看成了8,结果得商383,余17,这商比正确的商大21,那么这道题的被除数是,除数是.7.(★★)1992年爷爷年龄是孙子的10倍,再过12年,爷爷年龄是孙子的4倍,那么1993年孙子是多少岁?8.(★★★)龟兔赛跑,同时出发,全程7000米,乌龟每分钟爬30米,兔子每分钟跑330米,兔子跑了10分钟就停下来睡了215分钟,醒来后立即以原速往前跑,问乌龟和兔子谁先到达终点?先到的到达终点时后到的离终点还有多少米?9.(★★★)如图,正方形边长为2厘米,以圆弧为分界线的甲、乙两部分面积的差(大的减去小的)是多少平方厘米?(圆弧内部的是等腰直角三角形)(π取3.14)甲乙10.(★★★)设@[,](,)=+,其中[,]a b a b a ba b表示a与b的最大公约数,a b表示a与b的最小公倍数,(,)已知12@42x=,求x.家长签名:。
