苏教版六年级数学上册《表面涂色的正方体》课后练习题含答案
苏教版小学六年级数学上册 表面涂色的正方体 单元测试题(含答案)
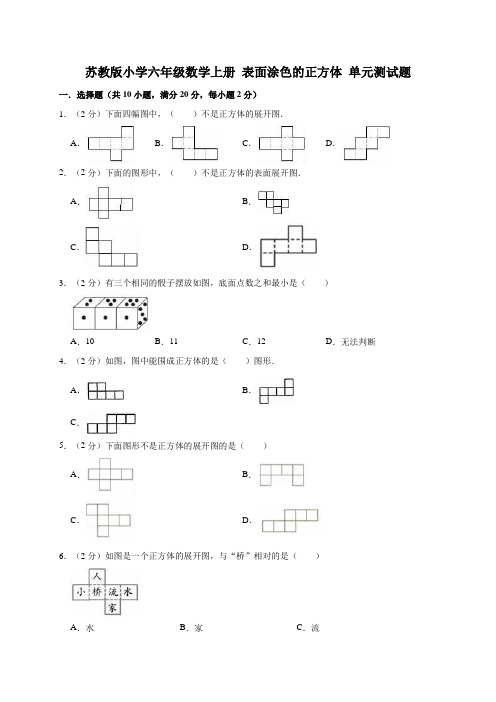
苏教版小学六年级数学上册表面涂色的正方体单元测试题一.选择题(共10小题,满分20分,每小题2分)1.(2分)下面四幅图中,()不是正方体的展开图.A.B.C.D.2.(2分)下面的图形中,()不是正方体的表面展开图.A.B.C.D.3.(2分)有三个相同的骰子摆放如图,底面点数之和最小是()A.10B.11C.12D.无法判断4.(2分)如图,图中能围成正方体的是()图形.A.B.C.5.(2分)下面图形不是正方体的展开图的是()A.B.C.D.6.(2分)如图是一个正方体的展开图,与“桥”相对的是()A.水B.家C.流7.(2分)下列四个图形中,每个小正方形都标上了颜色.若要求一个正方体两个相对面上的颜色都一样,那么不可能是这一个正方体的展开图的是()A.B.C.D.8.(2分)新年到了,依依制作了一个正方体礼品盒(如图),其中,相对的两个面的图案分别相同,那么这个正方体礼品盒可能是由()折叠成的.A.B.C.9.(2分)如图所示是正方体的一种表面展开图,各面都标有数字,则数字﹣4对面的数字是()A.1B.﹣3C.﹣110.(2分)如图中,折叠成正方体后与3相对的是()号面.A.1B.5C.6二.填空题(共9小题,满分10分)11.(2分)如图是一个正方体的展开图,如果3号是底面,那么号是上面.12.(1分)下面是正方体展开图的有(填序号)13.(1分)如图图形不能围成正方体,因为号正方形有两个和它相对的面;而号正方形没有相对的面.14.(1分)如图是一个正方体的展开图.在这个正方体中,与a面相对的是面,与b面相对的是面.15.(1分)如图是一个正方体的展示图.这个正方体中,“5”的对面是;抛下这个正方体,落下后,数朝上的可能性大.(填“奇”或“偶”)16.(1分)如图是一个无盖正方体的展开图,字母A的对面应该是.17.(1分)这是一个正方体的展开图,与1号相对的面是号面.18.(1分)如图是一个正方体的展开图,若相对两个面上标的数字刚好互为倒数,则2a+b=.19.(1分)下面的图形沿虚线折叠后刚好能围成正方体的有.三.判断题(共5小题,满分10分,每小题2分)20.(2分)如图所示形状的图形不能折成正方体..(判断对错)21.(2分)有六块正方形组成的平面图一定可以折成正方体..(判断对错)22.(2分)、、都不能折成一个无盖的正方体.(判断对错)23.(2分)可以折叠成一个正方体..(判断对错)24.(2分)不可以折成一个正方体..(判断对错)四.操作题(共4小题,满分20分,每小题5分)25.(5分)按要求作图.如图是正方体展开图的一部分,请将正方体的展开图补充完整.26.(5分)如图每小格的边长表示1厘米,请在图中画出棱长是2厘米的正方体展开图.27.(5分)如图两幅图是不完整的正方体展开图,请分别把它们补充成完整的正方体展开图.28.(5分)如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图上阴影部分),但是一不小心,少画了一个,请你给他补上一个,可以组成正方体,你有几种画法,在图上用阴影注明.五.解答题(共7小题,满分40分)29.(5分)如图是一个正方体盒展开后的样子,如果再把它折成一个正方体,3号对面是号面.30.(5分)一个正方体的六个面上分别写着1~6六个数字.根据如图摆放的情况,则“2”的对面一定是.31.(6分)如图是正方体的平面展开图,请写出与1号、2号、5号面相对的各是几号面?1号﹣﹣号2号﹣﹣号5号﹣﹣号.32.(6分)如图是边长1厘米的方格图,用阴影部分描出一个棱长1厘米的正方体展开图.33.(6分)有一个正立方体,若在其每一面上依序标上数字1~6,则由前三个图,可判断其展开图的各面数字为何?a=?、b=?、c=?、d=?34.(6分)在一粒骰子的六面上分别刻上最小的六个质数2,3,5,7,11,13,下面两图分别显示从两个不同的角度观看该骰子.如果当刻有「2」的一面向上的时候,问向下的一面刻有那一个数字?35.(6分)请将下面的长方形分成三部分,使每一部分都能折成一个无盖的正方体.参考答案与试题解析一.选择题(共10小题,满分20分,每小题2分)1.解:根据分析可得:A、D、C这三个图属于正方体展开图,能够折成一个正方体;而B图不是正方体展开图.故选:B.2.解:根据分析可得,图A和图D是正方体展开图的“1﹣4﹣1”结构;图B是正方体展开图的“1﹣3﹣2”结构;图C不是正方体的展开图,折叠起来有重合的面.故选:C.3.解:由这三个相同的骰子摆放如图可知,与1(为便于叙述1点说1、2点说2……)相邻的四个面分别是2、3、4、5,从而推出1与6相对,记作:1⇔6;由最右一个骰子可知,与5相邻的是1、4、6,它的对面可能是2或3.假设5的对面是2,则3的对面就是4,即5⇔2,3⇔4,底面点数之和就是5+4+3=12;假设5的对面是3,则2的对面就是4,即5⇔3,2⇔4,底面点数之和就是4+5+2=11.因此,底面点数之和最小是11.故选:B.4.解:根据正方体展开图的特征,选项A不能围成正方体;选项B和选项C都能围成正方体.故选:BC.5.解:A、是141型结构,是正方体的展开图;B、不符合正方体展开图的11种特征,不是正方体的展开图;C、是132型结构,是正方体的展开图;D、是33型结构,是正方体的展开图.故选:B.6.解:如图是一个正方体的展开图,与“桥”相对的是“水”.故选:A.7.解:A、折成正方体后,红与红相对,绿与绿相对,黄与黄相对.符合题意.B、折成正方体后,红与红相对,绿与绿相对,黄与黄相对.符合题意.C、折成正方体后,其中红与绿相对,黄与黄相对.不符合题意.D、折成正方体后,红与红相对,绿与绿相对,黄与黄相对.符合题意.故选:C.8.解:A、两个相同的图案一定不能相邻,故选项错误;B、两个相同的图案一定不能相邻,故选项错误;C、正确.故选:C.9.解:如图是正方体的一种表面展开图,各面都标有数字,则数字﹣4对面的数字是﹣3.故选:B.10.解:如图折叠成正方体后与3相对的是5号面.故选:B.二.填空题(共9小题,满分10分)11.解:如图是一个正方体的展开图,如果3号是底面,那么6号是上面.故答案为:6.12.解:根据正方体展开图的特征可知,(1)(8)属于“1﹣3﹣2”型,能围成正方体;(2)(7)属于“1﹣4﹣1”型,能围成正方体;(3)(6)不属于正方体展开图,不能围成正方体;(4)属于“3﹣3”型,能围成正方体;(5)属于“2﹣2﹣2”型,能围成正方体;所以是正方体展开图的有:(1)(2)(4)(5)(7)(8).故答案为:(1)(2)(4)(5)(7)(8).13.解:如图如图图形不能围成正方体,因为⑤号正方形有两个和它相对的面;而②号正方形没有相对的面.故答案为:⑤,②.14.解:如图在这个正方体中,与a面相对的是d面,与b面相对的是f面.故答案为:D,F.15.解:如图是一个正方体的展示图.这个正方体中,“5”的对面是“4”;抛下这个正方体,落下后奇数数朝上的可能性大.抛下这个正方体,落下后,奇数朝上的可能性大.故答案为:“4”,奇.16.解:如图,把它折成正方体时,字母A的对面应该是E;故答案为:E.17.解:如图这是一个正方体的展开图,与1号相对的面是2号面.故答案为:2.18.解:如图折成正方体后,1与c相对,3与a相对,6与b相对.1的倒数是1,3的倒数是,6的倒数是,由此可知,a=,b=,c=12a+b=2×+=+=故答案为:.19.解:如图①、③、⑤属于正方体展开图的“1﹣4﹣1”结构,都能沿虚线折叠成正方体;②、④不属于正方体展开图,不能沿虚线折叠成正方体.故答案为:①、③、⑤.三.判断题(共5小题,满分10分,每小题2分)20.解:此图虽然不属于正方体展开图,但正面三正方形折成相邻的正方体的三个面,上面三个正方形折成正方体相邻的三个面,合在一起正好是一个正方体,因此,不能折成正方体的说法是错误的.故答案为:×.21.解:有六块正方形组成的平面图一定可以折成正方体是错误的,只有符合正方体展开图11种情况的六块相同的正方形平面图才可以折成正方体.故答案为:×.22.解:根据正方体展开图的特征,图1和图2不能折成一个无盖的正方体,只有图3能折成一个无盖的正方体.原题的说法是错误的.故答案为:×.23.解:可以折叠成一个正方体是正确的.故答案为:√.24.解:不属于正方体展开图四种类型中的任意一种,无法折成一个正方体.故答案为:√.四.操作题(共4小题,满分20分,每小题5分)25.解:按要求作图.如图是正方体展开图的一部分,将正方体的展开图补充完整(补成“1﹣4﹣1”型).26.解:根据题意与分析可得:27.解:如图两幅图是不完整的正方体展开图,分别把它们补充成完整的正方体展开图:28.解:我有四各画法,如图:或五.解答题(共7小题,满分40分)29.解:如图,折成正方体后,1号面与6号面相对;2号面与4号面相对;3号面与5号面相对.故答案为:5.30.解:如图,则“2”的对面数字是4或5或6.故答案为:4或5或6.31.解:如图,根据正方体展开图的特征折叠成正方体后,1号面与6号面相对,2号面与4号面相对,3号面与5号面相对.故答案为:6,4,3.32.解:如图,33.解:根据图一和图二可得:与4相邻的数字是2、3、5、1,所以和4相对的数字是6即a=6;根据图三和图二以及展开图可得:与b=5相邻的数字是1、4、6,所以和5相对的数字是3,即d=3,那么c=2.所以,a=6、b=5、c=2、d=3.故答案为:6,5,2,3.34.解:和5相邻的数是13、7、2、3,所以和5相对的数字是11,那么和2相对的是13,所以向下的一面刻有13这个数字.答:向下的一面刻有13这个数字.35.解:将下面的长方形分成三部分,使每一部分都能折成一个无盖的正方体(每种颜色的都能折成一个无盖的正方体):。
苏教版六年级数学上册 表面涂色的正方体 (2)【新版】

作业提升练
3.一个棱长1分米的正方体木块,表面涂满了红色,把它切成
棱长1厘米的小正方体。在这些小正方体中:
(1)三个面涂色的有多少个?
8个
(2)两个面涂色的有多少个?
96个
(3)一个面涂色的有多少个?
384个
(4)六个面都没有涂色的有多少个? 512个
4.选一选。
把一个外表涂色的大正方体分成若干个相同的小正方体,在
D.5
(4)当正方体的棱长平均分成( D )份时,b<d。
A.3
B.4 C.5
D.6
作业拓展练
5.将一个长6厘米,宽4厘米,高3厘米的长方体的六个面都涂 上红色,然后将它切成棱长为1厘米的小正方体,这些小正 方体中两个面涂色的有几个?
(6-2)×4+(4-2)×4+(3-2)×4=28(个) 答:这些小正方体中两个面涂色的有28个。
2.如果用n表示表面涂色的大正方体每条棱被平均分成的段数, 用a、b、c分别表示2面涂色,1面涂色和6个面都不涂色的小 正方体个数,那么a=( 12(n-2) ),b=( 6(n-2)2 ),c= ( (n-2)3 )。(用含有n的式子表示)
作业提升方向
(1)数量与位置规律的灵活运用 (2)运用规律解决问题
一 长方体和正方体
表面涂色的正方体
六年级上册
作业习题
1.如图是用体积为1 cm3的小正方体拼成的 大正方体,一共用了( 27 )个。在这个大 正方体的表面涂色,小正方体三面涂色的 在大正方体的(顶点)位置,有( 8 )个,两面 涂色的在大正方体的( 棱 )上,有( 12 )个, 一面涂色的在大正方体(每个面中间)的位 置,有( 6 )个,没有涂色的有( 1 )个。
所有小正方体中,3面涂色的有a个,2面涂色的有b个,1面
苏教版六年级上册数学——表面涂色的正方体和长方体练习

表面涂色的正方体和长方体【基础训练】1.一个棱长1分米的正方体木块,表面涂满了红色,把它切成棱长1厘米的小正方体,在这些小正方体中:(1)三个面涂上红色的有多少个?(2)两个面涂上红色的有多少个?(3)一个面涂上红色的有多少个?(4)六个面都没涂色的有多少个?2.把若干个体积相等的小正方体拼成一个大正方体,然后在其表面涂上红色,已知两面涂色的小正方体有24个,那么一面涂色的小正方体有多少个?3.把若干个体积相等的小正方体拼成一个大正方体,然后在其表面涂上红色,已知一面涂色的小正方体有96个,那么两面涂色的小正方体有多少个?4.把若干个体积相等的小正方体拼成一个大正方体,然后在其表面涂上红色,已知六个面都没有涂色的小正方体有27个,那么这些小正方体一共有多少个?5.将一个表面涂有红色的长方体分割成若干个棱长为1厘米的小正方体,其中一点红色都没有涂的小正方体只有3块,原来长方体的表面积是多少平方厘米?6.将一个长6厘米,宽4厘米,高3厘米的长方体的六个面都涂上红色,然后把这个长方体切割成若干个棱长为1厘米的小正方体,这些小正方体中有两个面涂上红色的是多少个?7.有30个棱长为1分米的正方体,在地面上摆成下图的形式,然后把露出的表面涂成红色。
求被涂成红色的表面积是多少平方分米?【拓展提高】1.把两个长、宽、高分别是9厘米、7厘米、4厘米的相同长方体,拼成一个大长方体,这个大长方体的表面积最小是多少?最大是多少?2.有一个长方体模型,它的正面和上面的面积之和是209平方厘米,如果它的长、宽、高都是质数,那么这个长方体的表面积是多少平方厘米?3.如图,是一个棱长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个棱长为1厘米的小正方体,做成一种玩具,它的表面积是多少平方厘米?4.有一个棱长是3厘米的正方体,先从它的每个顶点处挖去一个棱长是1厘米的小正方体,再在它每个面的中央粘上一个棱长是1厘米的小正方体。
2022年苏教版小学数学六年级上册 表面涂色的正方体综合练习

《外表涂色的正方体》综合练习根底练习:1、填空。
如果用n表示把一个外表涂色的大正方体的每条棱长平均分的份数,用a、b、c分别表示2面涂色,1面涂色和6面都不涂色的小正方体个数,那么a=〔〕,b=〔〕,c=〔〕。
〔用含n的字母表示〕2、工艺品厂的工人用棱长为1厘米的小正方体制成了一个魔方〔如图〕。
〔1〕这个魔方的体积是多少立方厘米?〔2〕如果把这个魔方的6个面都涂色,1面涂色的小正方体有几个?2面涂色的小正方体由几个?3面都不涂色的小正方体有几个?综合练习:3、如下图,各个面均涂色,现在按图上线段切开。
〔1〕2个面都涂色均集中在〔〕上。
〔2〕上面一层2面涂色的有〔〕块。
〔3〕中间一层2面涂色的有〔〕块。
〔4〕底层2面涂色的有〔〕块。
〔5〕2面涂色的一共有多少块?4、一个涂色的正方体,把每条棱都平均分成假设干份,得到假设干个小正方体,其中2面涂色的有60块,1面涂色的有多少块?5、下列图是由64个小正方体拼成的一个大正方体,把它的外表全部涂色。
〔1〕3面涂色的一共有〔〕个。
〔2〕2面涂色的一共有12×〔〕=〔〕个。
〔3〕1面涂色的一共有6×〔〕=〔〕个。
〔4〕用64个小正方体-〔〕个涂色的小正方体=〔〕个没有涂色的小正方体。
第二课时一.选择题1、画统计图时,要根据信息的特点来画.在下面的信息中,适合用扇形统计图的是()A.六年级一班女同学的身高B.芳芳612-岁的身高变化 C.大豆的营养成分2、在扇形统计图上,李村的棉花种植面积占总面积的20%,表示棉花种植面积的扇形的圆心角是()A.36︒B.20︒C.72︒D.40︒3、五年〔1〕班有40名学生,参加竞选班长投票,限定每人有且只能投票一次,结果的得票数为:小明20票,小何10票,小阳6票,小新4票.以下四幅图中,()图能准确地表达这一投票结果.A.B. C. D.4、小明统计学校五、六年级的男生和女生人数,制成了下面扇形统计图.请你根据图中反映的男生女生人数的关系判断,下面说法可能正确的()A.五年级 250 人,六年级 200 人B.五年级 200 人,六年级 225人C.五年级 200 人,六年级 160 人D.五年级 160 人,六年级 200 人5、下面分析不合理的是()A.喜欢足球和喜欢篮球的人一样多B.喜欢跳绳的人比喜欢排球的人多C.最不受欢送的体育活动肯定是排球6、如图,以下说法正确的选项是()①面积最大的是亚洲;②南美洲、北美洲、非洲共占总面积的50%;③非洲占总面积13④南美洲的面积是大洋洲面积的2倍.A.①② B.①②③④C.①④ D.①②④7、某学校六年级学生参加课外活动小组的情况如下图,那么参加体育、文艺、美术三类课外兴趣小组的人数比是()A.6:3:1B.1:2:4C.1:3:6D.2:1:0.58、一个圆形花坛内种了三种花〔如下图〕,那么用条形统计图表示各种花占地面积应该是()A.B.C.二.填空题1、常用的统计图有、、,能清楚的看出各种数量的多少的是,能反映出各局部数量同总数之间的关系的是,能反映出各种数量的增减变化情况的是.2、扇形统计图用表示总数,用圆中表示局部所占总数的百分数.3、六〔1〕班体育进行测试,成绩获得优秀的有15人,占全班人数的25%,制成扇形统计图时优秀人数所在扇形的圆心角是︒;成绩获得良好的同学的人数所在圆心角是72︒,那么有人成绩获得良好。
苏教版数学六年级上:1.6《表面涂色的正方体》 (2)

(棱长平均分成的份数-2)2×6
棱长平均分成3份
棱长平均分成4份
棱长平均分成5份
三面涂色 两面涂色 一面涂色
8
88
88
(3-2)×12 (4-2)×12 (5-2)×12
(3-2)2×6 (4-2)2×6 (5-2)2×6
三面涂色的小正方体个数
棱长平均分成
6份
8
两面涂色的小正方体个数 (6-2)×12=48
棱长平均分成3份
棱长平均分成4份
棱长平均分成5份
三面涂色 两面涂色 一面涂色
8
8
8
(3-2)×12 (4-2)×12 (5-2)×12
(3-2)2×6 (4-2)2×6 (5-2)2×6
三面涂色的小正方体个数
棱长平均分成
6份
8
两面涂色的小正方体个数 (6-2)×12=48
如果把每条棱平均分成6份,你能很快算 出3面涂色和2面涂色的小正方体各有多 少个吗?
第一部分小正方体的个数:8+96+384=488
小正方体表面涂色情况表
每条棱 等分数
3面 涂色数
2面 涂色数
1面 涂色数
各面无 涂色数
n
8 12(n-2)6(n-2)2( n-2)3
•
14、抱最大的希望,作最大的努力。2021年5月11日 星期二 2021/5/112021/5/112021/5/11
•
15、一个人炫耀什么,说明他内心缺 少什么 。。2021年5月 2021/5/112021/5/112021/5/115/11/2021
•
16、业余生活要有意义,不要越轨。2021/5/112021/5/11May 11, 2021
苏教版六年级上册数学课程-表面涂色正方体和长方体练习

表面涂色的正方体和长方体【基础训练】1.一个棱长1分米的正方体木块,表面涂满了红色,把它切成棱长1厘米的小正方体,在这些小正方体中:(1)三个面涂上红色的有多少个?(2)两个面涂上红色的有多少个?(3)一个面涂上红色的有多少个?(4)六个面都没涂色的有多少个?2.把若干个体积相等的小正方体拼成一个大正方体,然后在其表面涂上红色,已知两面涂色的小正方体有24个,那么一面涂色的小正方体有多少个?3.把若干个体积相等的小正方体拼成一个大正方体,然后在其表面涂上红色,已知一面涂色的小正方体有96个,那么两面涂色的小正方体有多少个?4.把若干个体积相等的小正方体拼成一个大正方体,然后在其表面涂上红色,已知六个面都没有涂色的小正方体有27个,那么这些小正方体一共有多少个?5.将一个表面涂有红色的长方体分割成若干个棱长为1厘米的小正方体,其中一点红色都没有涂的小正方体只有3块,原来长方体的表面积是多少平方厘米?6.将一个长6厘米,宽4厘米,高3厘米的长方体的六个面都涂上红色,然后把这个长方体切割成若干个棱长为1厘米的小正方体,这些小正方体中有两个面涂上红色的是多少个?7.有30个棱长为1分米的正方体,在地面上摆成下图的形式,然后把露出的表面涂成红色。
求被涂成红色的表面积是多少平方分米?【拓展提高】1.把两个长、宽、高分别是9厘米、7厘米、4厘米的相同长方体,拼成一个大长方体,这个大长方体的表面积最小是多少?最大是多少?2.有一个长方体模型,它的正面和上面的面积之和是209平方厘米,如果它的长、宽、高都是质数,那么这个长方体的表面积是多少平方厘米?3.如图,是一个棱长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个棱长为1厘米的小正方体,做成一种玩具,它的表面积是多少平方厘米?4.有一个棱长是3厘米的正方体,先从它的每个顶点处挖去一个棱长是1厘米的小正方体,再在它每个面的中央粘上一个棱长是1厘米的小正方体。
2022秋六年级数学上册 一 长方体和正方体(表面涂色的正方体)习题课件 苏教版

个,共______8__个。 ②两面涂色的小正方体位于棱上,每条棱上有
__(n__-__ቤተ መጻሕፍቲ ባይዱ_) _个,共_1_2_(_n_-__2_)个。
③一面涂色的小正方体位于面上,每个面中间有 __(n__-__2_)2_个,共_6_(_n_-__2_)2_个。
( 2 )个小正方体。
4.在一个正方体木块的6个面上涂上红色后,把它分割 成若干个棱长是1 cm的小正方体木块,两面涂红色 的小正方体木块共有108个,那么只有一面涂红色 的小正方体木块有多少个? 只有一面涂红色的小正方体木块有486个。
11、凡为教者必期于达到不须教。对人以诚信,人不欺我;对事以诚信,事无不成。 12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 13、在教师手里操着幼年人的命运,便操着民族和人类的命运。2022/1/312022/1/31January 31, 2022 14、孩子在快乐的时候,他学习任何东西都比较容易。 15、纪律是集体的面貌,集体的声音,集体的动作,集体的表情,集体的信念。 16、一个人所受的教育超过了自己的智力,这样的人才有学问。 17、好奇是儿童的原始本性,感知会使儿童心灵升华,为其为了探究事物藏下本源。2022年1月2022/1/312022/1/312022/1/311/31/2022 18 、 人 自 身 有 一 种 力 量, 用 许 多 方 式 按照 本 人意 愿 控 制 和 影 响这 种 力量 , 一 旦 他 这 样做 , 就会 影 响 到 对 他 的教 育 和对 他 发 生 作 用 的环 境 。 2022/1/312022/1/31
④没有涂色的小正方体位于大正方体内部,共有 __(_n_-__2_)3_个。
六年级上册数学一课一练-表面涂色的正方体|苏教版含答案

表面涂色的正方体
1.填一填。
(1)根据图形填写表格并合理推断。
(2)如果用n表示把大正方体的棱平均分的份数,用a,b,c,d分别表示3面涂色、2面涂色、1面涂色和6个面都不涂色的小正方体个数,那么
a=(),b=(),c=(),d=()。
2.一个正方体的表面涂满了红色,然后如下图切开,切开的小正方体中:
(1)三面涂红色的有几个?
(2)两个面涂红色的有几个?
(3)一个面涂红色的有几个?
(4)六个面都没有涂色的有几个?
3.把1立方分米的正方体木块的表面涂上红色,然后切成1立方厘米的小正方体,在这些小正方体中,两面涂色的小正方体共有多少个?
、、
4.将一个表面涂色的正方体分割成若干个体积为1立方厘米的小正方体,其中两面涂色的有36块,原来正方体的体积是多少立方厘米?
表面涂色的正方体
1.(1)略
(2)812(n-2)6(n-2)2(n-2)3
2.(1)8个(2)36个(3)54个(4)27个
3.体积是1立方分米的正方体,棱长是10厘米12×(10-2)=96(个)
4.125立方厘米。
