2014最后三个月冲刺函数零点问题6
函数零点问题解答分析与思考

函数零点问题解答分析与思考函数的零点,即函数在坐标系中与x轴交点的横坐标值。
在数学中,求解函数的零点是一个常见的问题,也是解决方程、求解实际问题的重要一环。
在这篇文章中,我们将对函数零点问题进行一些分析与思考,探讨不同类型函数的零点求解方法,以及如何利用零点求解问题。
一、基本概念我们来回顾一下函数的零点的基本概念。
对于一个函数f(x),其零点即为使得f(x)=0的x值。
通常来说,我们可以通过以下几种方法求解函数的零点:1. 图像法:通过绘制函数的图像,找到函数与x轴的交点;2. 方程法:将函数f(x)化为方程f(x)=0,然后通过解方程求解得到零点;3. 迭代法:利用数值计算方法逼近函数的零点。
这些方法都是常见的零点求解方法,在实际问题中也常常会用到。
下面,我们将结合不同类型的函数,来分析如何利用这些方法求解函数的零点。
二、线性函数的零点求解举个例子来说,我们考虑函数f(x)=2x-3,我们需要求解函数f(x)的零点。
我们可以将函数化为方程2x-3=0,然后通过解方程的方法来求解得到x=3/2。
这样,我们就得到了函数f(x)的零点为x=3/2。
接下来,我们来看一下多项式函数的零点求解。
对于一个n次多项式函数f(x)=anxn+an-1xn-1+...+a1x+a0,其中an≠0,我们可以通过多种方法来求解其零点。
我们也可以利用迭代法来逼近多项式函数的零点。
通过不断迭代计算,我们可以逼近多项式函数的零点。
这在计算机科学和数值计算中经常会用到。
四、三角函数和指数函数的零点求解除了线性函数和多项式函数,我们还可以考虑三角函数和指数函数的零点求解。
对于这两类函数,我们通常会采用迭代法来逼近函数的零点。
对于函数f(x)=sin(x),我们可以通过不断迭代计算,利用泰勒级数展开式来逼近函数的零点。
对于指数函数f(x)=e^x,我们也可以利用迭代法来逼近函数的零点。
五、零点求解在实际问题中的应用我们来思考一下零点求解在实际问题中的应用。
安徽省合肥市合肥六中2014届高三数学冲刺高考(最后一卷)试题 理 新人教A版
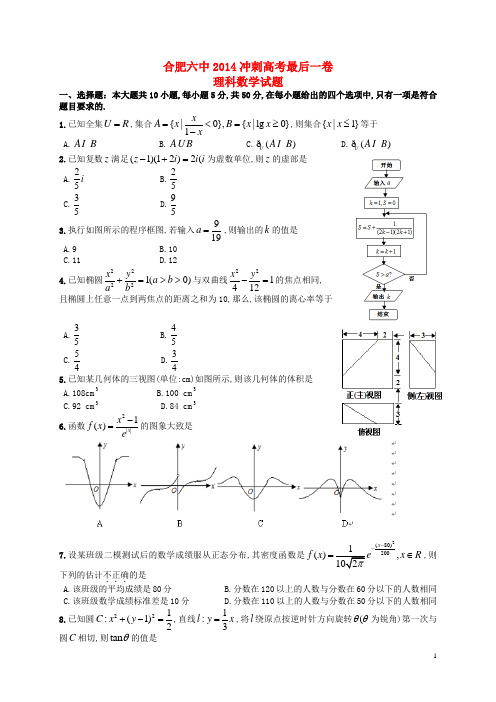
合肥六中2014冲刺高考最后一卷理科数学试题一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U R =,集合{|0},{|lg 0}1xA xB x x x=<=≥-,则集合{|1}x x ≤等于 A.A B B.A B C.()U A B ð D.()U A B ð 2.已知复数z 满足(1)(12)2(z i i i -+=为虚数单位,则z 的虚部是A.25iB.25C.35D.953.执行如图所示的程序框图,若输入919a =,则输出的k 的值是A.9B.10C.11D.124.已知椭圆22221(0)x y a b a b +=>>与双曲线221412x y -=的焦点相同, 且椭圆上任意一点到两焦点的距离之和为10,那么,该椭圆的离心率等于A.35 B.45 C.54 D.345.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是 A.108cm 3B.100 cm 3C.92 cm 3D.84 cm 36.函数2||1()x x f x e-=的图象大致是7.设某班级二模测试后的数学成绩服从正态分布,其密度函数是2(80)200(),x f x x R --=∈,则下列的估计不正确...的是 A.该班级的平均成绩是80分 B.分数在120以上的人数与分数在60分以下的人数相同 C.该班级数学成绩标准差是10分 D.分数在110以上的人数与分数在50分以下的人数相同 8.已知圆221:(1)2C x y +-=,直线1:3l y x =,将l 绕原点按逆时针方向旋转(θθ为锐角)第一次与圆C 相切,则tan θ的值是A.12B.13C.34D.359.若函数()f x 对任意x R ∈满足1()1(1)f x f x +=+,且(0,1)x ∈时,(),()f x xg x mx m ==--在(1,0)(0,1)-上有两个零点,则实数m 的取值范围是A.(1,1)-B.1(0,)2C.(0,1)D.(1,2]-10.如图,正三棱锥A BCD -放置在平面α上,,AD kCD O =是底面BCD ∆的中心,E 是CD 的中点,下列说法中,错误的是A.k >B.当1AD CD ==时,将三棱锥绕直线AO 旋转一周所形成的几何C.动点P 在截面ABE 上运动,且到点B 的距离与到点侧面ACD 的距离相等,则点P 在抛物线弧上D.当12k CD ==时,将该三棱锥绕棱CD 转动,则三棱锥在平面α上投影面积的最大值是2二、填空题:本大题共5小题,每小题5分,共25分,请将答案填写在答题卡的相应位置上.11.10(1)[(1)1]x x x ++-的展开式中,含7x 项的系数是12.设(0,)2x π∈,且21(3)sin cos 3cos 0x x x λ+-+≥恒成立,则实数λ的取值范围是13.如图所示,三棱锥A BCD -中,,E F 分别是棱,AD BC 的中点, 在三棱锥的6条棱及EF 所在的7条直线中,任取2条直线,则这两条直线是异面直线的概率是14.,A B 是椭圆的右顶点及上顶点,由椭圆弧221(0,0)4x y x y +=≥≥ 及线段AB 构成的区域为,P Ω是区域Ω上的任意一点(包括边界),设OP OA OB λμ=+,则动点(,)M λμ所形成区域'Ω的面积是15.定义在R 上的奇函数()f x 当(0,)x ∈+∞是,()0f x >且2()'()0f x xf x +>,有下列命题:①()f x 在R 上是增函数; ②当12x x >时,221122()()x f x x f x >; ③当120x x >>时,221221()()x x f x f x >; ④当120x x +>时,221122()()0x f x x f x +>⑤当12x x >时,221221()()x f x x f x >.则其中正确的命题是 (写出你认为正确的所有命题的序号)三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤. 16(本小题满分12分)如图,在ABC ∆中,D 是BC 上的点,2,C D DAB BAD ∠∠=∠∆的面积与CAD ∆的面积相等,且sin B C =.(Ⅰ)求BAC ∠; (Ⅱ)求::a b c .17(本小题满分12分)如图,多面体ABCPQ 中,PA ⊥平面,,ABC PA AB ABC =∆是等腰直角三角形,90,BAC ∠=,QBC ∆是等边三角形,M 是BC 的中点,二面角Q BC A --的正切值为(Ⅰ)证明://PQ 平面ABC ;(Ⅱ)在线段QM 上是否存在一点N ,使得PN ⊥平面QBC ,如果存在,请求出N 点的位置,如果不存在,请说明理由.,18(本小题满分12分)已知椭圆22122:1(0)x y E a b a b+=>>,椭圆2E 的中心在坐标原点,焦点在x 轴上,长轴长是短轴长的(0,1)λλ>≠.(Ⅰ)求椭圆2E 的方程;并证明椭圆12,E E 的离心率相同;(Ⅱ)当2λ=时,设,M N 是椭圆1E 上的两个点,,OM ON 的斜率分别是,OM ON k k ,且22(OM ONb k k O a⋅=-是坐标原点),若OMPN 是平行四边形,证明:点P 在椭圆2E 上.19(本小题满分13分)已知函数())(0)x f x e x ϕϕπ=+<<且是函数()f x 的一个极值点,'()f x 是函数()f x 的导函数. (Ⅰ)求ϕ的值;(Ⅱ)设()'()g x f x =,求函数()g x 的单调递增区间;(Ⅲ)证明:当0x >时,|'()|x f x <.20(本小题满分13分)在研究 2.5PM (霾的主要成分)形成原因时,某研究人员研究了 2.5PM 与燃烧排放的223,,,CO NO CO O 等物质的相关关系,下图是 2.5PM 与3,CO O 相关性的散点图, (Ⅰ)根据三点图,请你就3,CO O 对 2.5PM 的影响关系作出初步评价;(Ⅱ)以1003为单位,在上述左图中取三个点,如下表所示,求y关于x 的回归方程,并估计当CO 的排放量为200/g m 时, 2.5PM 的值(用最小二乘法求回归方程的系数是(1221,)niii nii x y nx yb a y bx xnx ==⋅-⋅==--∑∑(Ⅲ)雾霾对交通影响较大,某市交通部门发现,在一个月内,当CO 排放量(单位: 3/g m μ)分别是60,120,180时,某路口的交通流量(单位:万辆)依次是800,600,200,在一个月内,CO 排放量是60,120,180的概率依次是,,p q r ,且1,343p q r ≤≤,求该路口一个月的交通流量期望值的最大值.21(本小题满分13分)设正项数列{}n a 的前n 项和为n S ,对任意*n N ∈,都有24410n n S a n --+=且212a a >>. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设12n n a b +=,求证:131321122424221n nb bb b b b b b b b b b -+++<参考答案:1.C2.B3.C4. B.5.B6.C7.B8.A9.B 10.D 11.165 12.(,7]-∞ 13.13 14.142π- 15.②③④ 16.135BAC ∠=::a b c = 17.13MN MQ =18.(略)19.23πϕ=20.(1)CO 与 2.5PM 有正相关关系,而3O 与 2.5PM 没关系(2)9191,,284284b a y x ===+, 544 (3)()800600200200(32)200E X p q r p q =++=++18,321p q ==时,552.38(万辆)21.21n a n =-。
怎样求解函数零点问题

思路探寻函数零点问题的难度通常较大.常见的命题形式有:(1)判断零点的个数;(2)由函数的零点求参数的取值范围;(3)证明与函数零点有关的不等式.那么如何破解这三类函数零点问题呢?下面举例加以探究.一、判断函数零点的个数判断函数零点的个数,实质上是判断函数的图象与x 轴的交点的个数,或求函数为0时的解的个数.因此判断函数零点的个数,往往有两种思路:(1)令函数为0,通过解方程求得零点的个数;(2)判断出函数的单调性、奇偶性、对称性,画出函数的图象,通过研究图象与x 轴的交点,来判断函数零点的个数.例1.已知函数f ()x =ln x -()a -1x +1.(1)若f ()x 存在极值,求a 的取值范围;(2)当a =2,且x ∈()0,π时,证明:函数g ()x =f ()x +sin x 有且仅有2个零点.解:(1)略;(2)当a =2时,g ()x =ln x -x +1+sin x ,得g ′()x =1x-1+cos x ,令h ()x =g ′()x ,因为x ∈()0,π,则h ′()x =-1x2-sin x <0,所以h ()x =g ′()x 在()0,π上单调递减,又因为g ′()π3=3π-1+12=3π-12>0,g ′()π2=2π-1<0,所以g ′()x 在()π3,π2上有唯一的零点α,当x ∈()0,α时,g ′()x >0,当x ∈()α,π时,g ′()x <0,所以g ()x 在()0,α上单调递增,在()α,π上单调递减,可知g ()x 在()0,π存在唯一的极大值点α(π3<α<π2),而g ()α>g ()π2=ln π2-π2+2>2-π2>0,g()1e 2=-2-1e 2+1+sin 1e 2=-1e 2+()sin 1e 2-1<0,g ()π=lnπ-π+1=lnπ-()π-1,令F ()x =ln x -()x -1,F ′()x =1x -1=1-x x ,则x ∈()0,1,F ′()x >0;x ∈()1,+∞,F ′()x <0,所以F ()x 在()0,1上单调递增,在()1,+∞上单调递减,得F ()x max =F ()1=0,故F ()π<F ()1=0,即g ()π=lnπ-()π-1<0,可知g ()x 在()0,α和()α,π上分别有1个零点,所以当x ∈()0,π时,g ()x 有且仅有2个零点.函数式g ()x =f ()x +sin x 中含有对数、三角函数式,我们很难通过画图、解方程求得零点的个数,于是对函数求导,研究函数的单调性、极值,从而画出函数的图象;进而借助函数的图象来确定函数零点的个数.在解答函数零点问题时,经常要用到函数的零点存在性定理,但运用该定理只能判断函数在某个区间上是否含有零点,却不能确定函数在某区间上零点的个数,此时往往需结合函数的图象进行判断.二、由函数的零点求参数的取值范围根据函数的零点求参数的取值范围问题比较常见.在解题时,往往要先通过解方程或画图,利用函数的零点存在性定理,判断函数的零点的存在性和个数,确定零点的范围;然后建立关于参数的关系式,进而求得参数的取值范围.例2.已知函数f ()x =x 2+x ln x .(1)求函数f ()x 在区间[]1,e 上的最大值;(2)若F ()x =f ()x -ax 3有2个零点,求实数a 的取值范围.解:(1)f ()x max =f ()e =e 2+e .(过程略)(2)由题意可知函数f ()x =x 2+x ln x 的定义域为()0,+∞,由f ()x =ax 3可得a =x +ln xx 2,令g ()x =x +ln x x 2,其中x >0,则g ′()x =1-x -2ln xx 3,令h ()x =1-x -2ln x ,其中x >0,则h ′()x =-1-2x<0,所以函数h ()x 在()0,+∞上为减函数,且h ()1=0,当0<x <1时,h ()x >0,则g ′()x >0,所以函数g ()x 在()0,1上单调递增,当x >1时,h ()x <0,则g ′()x <0,所以函数g ()x 在()1,+∞上单调递减,所以g ()x max =g ()1=1,49思路探寻令p ()x =x +ln x ,其中x >0,则p ′()x =1+1x>0,则函数p ()x 在()0,+∞上为增函数,因为p()1e =1e-1<0,p ()1>0,则存在x 0∈()1e,1,使得p ()x 0=0,当0<x <x 0时,f ()x =x ()x +ln x <0;当x >x 0时,f ()x =x ()x +ln x >0.由题意可知,直线y =a 与函数g ()x 的图象有2个交点,如图所示.由图可知,当0<a <1时,直线y =a 与函数g ()x 的图象有2个交点,故实数a 的取值范围是0<a <1.解答本题需抓住关键信息:函数F ()x =f ()x -ax 3有2个零点.于是令F ()x =f ()x -ax 3=0,并将其变形为a =x +ln x x2,再构造新函数,将问题转化为直线y =a 与函数g ()x 的图象有2个交点的问题.利用导数与函数g ()x 单调性的关系判断函数的单调性,并画出函数g ()x 的图象,即可通过讨论直线y =a 与函数g ()x 的图象的位置关系,确定参数a 的取值范围.在求参数的取值范围时,若容易从方程中分离出参数来,往往可以采用分离参数法求参数的取值范围.三、证明与函数零点有关的不等式问题与函数零点有关的不等式问题通常较为复杂,且具有较强的综合性.在解题时,需根据函数零点的分布情况,构造新函数或新方程,再根据导数的性质讨论新函数的性质或方程的根,从而证明不等式.例3.已知函数f ()x =me x -x 2-x +2.(1)若函数f ()x 在R 上单调递增,求m 的取值范围;(2)若m <0,且f ()x 有2个零点x 1,x 2,证明:||x 1-x 2<3+m 3.解:(1)m ≥2e -12;(过程略)(2)不妨设x 1<x 2,由题意可得me x 1-x 21-x 1+2=0,me x 2-x 22-x 2+2=0,即x 1,x 2为方程m =x 2+x -2e x的2个根,因为m <0,所以x 2+x -2<0,解得:-2<x <1,所以x 1,x 2∈(-2,1),设h (x )=x 2+x -2e x(-2<x <1),则h ′(x )=-x 2+x +3e x,令h ′(x )=0得x =1-132,则h (x )在()-2,1-132上单调递减,在()1-132,1上单调递增,而h (x )在()-2,0处的切线方程为y =-3e 2(x +2),设h 1(x )=-3e 2(x +2),则h (x )>h 1(x ),设h (x )在()x 0,x 20+x 0-2ex 0处的切线方程过点(1,0),其切线的斜率为-x 20+x 0+3ex 0,取x 0=-1,则h (x )在()-1,-2e 处的切线斜率为e ,则切线的方程为y +2e =e ()x +1,即y =ex -e ,可知h 2(x )=ex -e 单调递增,可得h (x )≥h 2(x ),记y =m 与y =h 1(x )和y =h 2(x )交点的横坐标分别为x 3,x 4,则h (x 1)=m =h 1(x 3)=-3e 2(x 3+2),故x 3=-2-m3e2,因为h 1(x 3)=h (x 1)>h 1(x 1),所以h 1(x )单调递减,所以x 1>x 3,h (x 2)=m =h 2(x 4)=e (x 4-1),故x 4=1+me,由h 2(x 4)=h (x 2)≥h 2(x 2),知h 2(x )单调递增,所以x 2≤x 4,由于m <0,所以||x 1-x 2=x 2-x 1<x 4-x 3=3+m e +m3e 2=3+m()1e +13e 2<3+m ()13+127<3+m 3.故不等式成立.解答本题,要先将x 1,x 2视为方程m =x 2+x -2e x的两根,根据方程确定两根的取值范围;然后构造新函数h (x ),讨论导函数h ′(x )的性质和几何意义,以确定y =m ,h (x )与其切线y =h 1(x )、y =h 2(x )的交点之间的大小关系,从而证明不等式.函数零点问题一般都可以转化为方程问题或函数单调性问题.因此在解答函数零点问题时,需根据题意构造出相应的方程和函数,灵活运用方程思想和数形结合思想,通过研究该函数的图象与性质、方程的根来求得问题的答案.(作者单位:江苏省如皋市搬经中学)50。
2014高考数学最后冲刺题型突破训练详解6

2014高考数学最后冲刺题型突破训练详解6内容:涉及高中全部内容的创新题 一、选择题1. 对于复数a ,b ,c ,d ,若集合S ={a ,b ,c ,d }具有性质“对任意x ,y ∈S ,必有xy ∈S ”,则当⎩⎪⎨⎪⎧a =1,b 2=1,c 2=b 时,b +c +d 等于 ( )A .1B .-1C .0D .i答案 B解析 若a =1,根据集合的互异性且b 2=1可得b =-1;由c 2=b =-1,可得c =i 或c =-i ,当c =i 时,bc =-i ∈S ,∴d =-i ,同理,当c =-i 时,d =i.故b +c +d =-1+i -i =-1.2. 在R 上定义运算“D ○×”:xD ○×y =(1-x )(1+y ).若不等式(x -a )D ○×(x +a )<1对任意的实数x 都成立,则a 的取值范围是( )A .-1<a <1B .-2<a <0C .0<a <2D .-32<a <12答案 B解析 由题意知,(x -a )D ○×(x +a )=(1-x +a )(1+x +a )=(1+a )2-x 2<1恒成立,即x 2>(1+a )2-1恒成立,故只要(1+a )2-1<0恒成立,即a 2+2a <0,解得-2<a <0. 3. 已知符号函数sgn(x )=⎩⎪⎨⎪⎧1,x >0,0,x =0,-1,x <0.则函数f (x )=sgn(ln x )-ln 2x 的零点个数为 ( )A .1B .2C .3D .4答案 B解析 当x >1时,ln x >0,sgn(ln x )=1, ∴f (x )=1-ln 2x ,令f (x )=0,得x =e 满足. 当x =1时,ln x =0,sgn(ln x )=0, ∴f (x )=-ln 2x ,令f (x )=0,得x =1满足. 当0<x <1时,ln x <0,sgn(ln x )=-1, ∴f (x )=-1-ln 2x <0,f (x )=0无解. ∴函数f (x )的零点为x =1与x =e.4. 定义平面向量之间的一种运算“⊙”如下:对任意的a =(m ,n ),b =(p ,q ),令a ⊙b =mq -np .下面说法错误的是( )A .若a 与b 共线,则a ⊙b =0B .a ⊙b =b ⊙aC .对任意的λ∈R ,有(λa )⊙b =λ(a ⊙b )D .(a ⊙b )2+(a ·b )2=|a |2|b |2 答案 B解析 若a =(m ,n )与b =(p ,q )共线,则mq -np =0,依运算“⊙”知a ⊙b =0,故A 正确.由于a ⊙b =mq -np ,又b ⊙a =np -mq ,因此a ⊙b =-b ⊙a ,故B 不正确.对于C ,由于λa =(λm ,λn ),因此(λa )⊙b =λmq -λnp ,又λ(a ⊙b )=λ(mq -np )=λmq -λnp ,故C 正确.对于D ,(a ⊙b )2+(a ·b )2=m 2q 2-2mnpq +n 2p 2+(mp +nq )2=m 2(p 2+q 2)+n 2(p 2+q 2)=(m 2+n 2)(p 2+q 2)=|a |2|b |2,故D 正确.5. 用min{a ,b }表示a ,b 两数中的最小数,若f (x )=min{|x |,|x +t |}的图象关于直线x =-12对称,则t 的值为 ( ) A .-2B .2C .-1D .1答案 D解析 依题意,y =|x |的图象与y =|x +t |的图象关于直线x =-12对称,y =|x |的图象与y=|x +t |的图象分别关于x =0,x =-t 对称,故x =0,x =-t 也关于x =-12对称,则t =1.6. 对于使-x 2+2x ≤M 成立的所有常数M 中,我们把M 的最小值1叫做-x 2+2x 的“上确界”,若a ,b ∈R +,且a +b =1,则-12a -2b的“上确界”为 ( )A .92B .14C .-92D .-4答案 C解析 由题意知,相当于求-12a -2b的最大值.∵-12a -2b=-⎝⎛⎭⎫12a +2b (a +b ) =-⎝⎛⎭⎫12+2+b 2a +2a b ≤-52-2 b 2a ·2a b =-52-2=-92.7. 定义:F (x ,y )=y x (x >0,y >0),已知数列{a n }满足a n =F (n ,2)F (2,n )(n ∈N *),若对任意正整数n ,都有a n ≥a k (k ∈N *)成立,则a k 的值为( )A .89B .1C .3225D .2答案 A解析 a n =F (n ,2)F (2,n )=2n n2,可以判断{a n }是先减后增的,n =3时,a n =89.8. 函数f (x )=ax 2+bx +c (a ≠0)的图象关于直线x =-b2a对称.据此可推测,对任意的非零实数a ,b ,c ,m ,n ,p ,关于x 的方程m [f (x )]2+nf (x )+p =0的解集不可能是 ( ) A .{1,2} B .{1,4} C .{1,2,3,4}D .{1,4,16,64}答案 D解析 方法一 当p =0,m =2,n =0,a =1,b =-3,c =2时,由2[f (x )]2=0得f (x )=0,即x 2-3x +2=0,得解集{1,2}.当p =0,m =2,n =0,a =1,b =-5,c =4时, 由2[f (x )]2=0得f (x )=0,即x 2-5x +4=0,得解集{1,4}. 当p =0,m =1,n =2,a =1,b =-5,c =4时,由[f (x )]2+2f (x )=0得f (x )=0或f (x )=-2,即x 2-5x +4=0或x 2-5x +4=-2,得解集{1,2,3,4},故选D.方法二 由题意,要使m [f (x )]2+nf (x )+p =0有四个不同解,需mt 2+nt +p =0有两个不同解,设为t 1,t 2,则f (x )=t 1与f (x )=t 2,即ax 2+bx +c =t 1与ax 2+bx +c =t 2也要分别有两个不同解,设ax 2+bx +c =t 1两解为α,β,ax 2+bx +c =t 2两解为p ,q ,则α+β=-b a ,p +q =-ba ,即α+β=p +q .显然D 不适合.9. 已知f (x ),g (x )都是定义在R 上的函数,g (x )≠0,f ′(x )g (x )>f (x )g ′(x ),且f (x )=a x g (x ) (a >0,且a ≠1),f (1)g (1)+f (-1)g (-1)=52.若数列⎩⎨⎧⎭⎬⎫f (n )g (n )的前n 项和大于62,则n 的最小值为 ( ) A .8B .7C .6D .9答案 C 解析 由⎣⎡⎦⎤f (x )g (x )′=f ′(x )g (x )-f (x )g ′(x )g 2(x )>0,知f (x )g (x )在R 上是增函数,即f (x )g (x )=a x 为增函数,所以a >1. 又a +1a =52,∴a =2或a =12(舍).数列⎩⎨⎧⎭⎬⎫f (n )g (n )的前n 项和 S n =21+22+…+2n =2(1-2n)1-2=2n +1-2>62.即2n >32,∴n >5.10.甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a ,再由乙猜甲刚才所想的数字,把乙猜的数字记为b ,其中a ,b ∈{1,2,3,4,5,6},若|a -b |≤1,就称甲、乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为( )A.19B.29C.718D.49 答案 D解析 任意找两人玩这个游戏,共有6×6=36种猜字结果,其中满足|a -b |≤1的有如下情形:①若a =1,则b =1,2;②若a =2,则b =1,2,3;③若a =3,则b =2,3,4;④若a =4,则b =3,4,5;⑤若a =5,则b =4,5,6;⑥若a =6,则b =5,6,总共16种,故他们“心有灵犀”的概率为P =1636=49.11.设A 1,A 2,A 3,A 4是平面直角坐标系中两两不同的四点,若A 1A 3→=λA 1A 2→(λ∈R ),A 1A 4→=μA 1A 2→(μ∈R ),且1λ+1μ=2,则称A 3,A 4调和分割A 1,A 2,已知平面上的点C ,D 调和分割点A ,B ,则下面说法正确的是( )A .C 可能是线段AB 的中点 B .D 可能是线段AB 的中点C .C ,D 可能同时在线段AB 上D .C ,D 不可能同时在线段AB 的延长线上 答案 D解析 依题意,若C ,D 调和分割点A ,B ,则有AC →=λAB →,AD →=μAB →,且1λ+1μ=2.若C是线段AB 的中点,则有AC →=12AB →,此时λ=12.又1λ+1μ=2,所以1μ=0,不可能成立.因此A 不对,同理B 不对.当C ,D 同时在线段AB 上时,由AC →=λAB →,AD →=μAB →知0<λ<1,0<μ<1,此时1λ+1μ>2,与已知条件1λ+1μ=2矛盾,因此C 不对.若C ,D 同时在线段AB 的延长线上,则AC →=λAB →时,λ>1,AD →=μAB →时,μ>1,此时1λ+1μ<2,与已知1λ+1μ=2矛盾,故C ,D 不可能同时在线段AB 的延长线上. 12.函数f (x )的定义域为D ,若满足:①f (x )在D 内是单调函数;②存在[a ,b ]⊆D 使得f (x )在[a ,b ]上的值域为⎣⎡⎦⎤a 2,b 2,则称函数f (x )为“成功函数”.若函数f (x )=log c (c x +t ) (c >0,c ≠1)是“成功函数”,则t 的取值范围为( )A .(0,+∞) B.⎝⎛⎭⎫-∞,14 C.⎝⎛⎭⎫14,+∞D.⎝⎛⎭⎫0,14 答案 D解析 无论c >1还是0<c <1,f (x )=log c(c x+t )都是R 上的单调增函数,故应有⎩⎨⎧f (a )=a2f (b )=b2,则问题可转化为求f (x )=x 2,即log c (c x +t )=x 2,即c x +t =c 在R 上有两个不相等的实数根的问题,令c=m (m >0),则c x +t =c可化为t =m -m 2,问题进一步可转化为求函数y =t 与y =m -m 2 (m >0)的图象有两个交点的问题,结合图形可得t ∈⎝⎛⎭⎫0,14. 二、填空题13.规定记号“”表示一种运算,即a b =ab +a +b (a ,b 为非负实数),若1k =3,则k 的值为________;函数f (x )=k x 的值域为________. 答案 1 [1,+∞)解析 ∵a b =ab +a +b (a ,b 为非负实数),x2 x 2 x 2∴1D ○×k =k +1+k =3(k 为非负实数),求得k =1. 函数f (x )=k x =1x =x +1+x , f 1(x )=x ,则f 1(x )在[0,+∞)上为增函数, f 2(x )=x +1,则f 2(x )在[0,+∞)上也为增函数. 由此可得f (0)=1为最小值,所以f (x )=x +1+x 的值域为[1,+∞).14.对于平面上的点集Ω,如果连接Ω中任意两点的线段必定包含于Ω,则称Ω为平面上的凸集.给出平面上4个点集的图形如下(阴影区域及其边界):其中为凸集的是________(写出所有凸集相应图形的序号). 答案 ②③解析 图①中连接左顶点和右上顶点的线段不在区域内,故不是凸集,图④中两圆的外公切线不在区域内,也不是凸集,②③符合凸集的定义.15.定义在[-2,2]上的连续函数f (x )满足2 012f (-x )=12 012f (x ),且在[0,2]上是增函数, 若f (log 2m )<f (log 4(m +2))成立,则实数m 的取值范围为__________.答案 ⎣⎡⎭⎫14,2解析 2 012f (-x )=12 012f (x ),即2 012f (-x )=2 012-f (x ),可得f (-x )=-f (x ).又因为函数的定义域[-2,2]关于原点对称, 所以函数f (x )为奇函数.由奇函数的性质,可知函数在关于原点对称的两个区间上的单调性是相同的,而已知函数f (x )在[0,2]上是单调递增的,所以函数f (x )在[-2,0]上也是单调递增的. 故由f (log 2m )<f (log 4(m +2)), 可得⎩⎪⎨⎪⎧-2≤log 2m ≤2,-2≤log 4(m +2)≤2,log 2m <log 4(m +2).由-2≤log 2m ≤2,解得14≤m ≤4.由-2≤log 4(m +2)≤2,解得116≤m +2≤16,即-3116≤m ≤14.由log 2m <log 4(m +2),得log 4m 2<log 4(m +2),故有⎩⎪⎨⎪⎧m >0,m +2>0,m 2<m +2,解得0<m <2.综上所述,m 的取值范围是14≤m <2.16.设f (x )和g (x )是定义在同一区间[a ,b ]上的两个函数,若函数y =f (x )-g (x )在x ∈[a ,b ]上有两个不同的零点,则称f (x )和g (x )在[a ,b ]上是“关联函数”,区间[a ,b ]称为“关联区间”.若f (x )=x 2-3x +4与g (x )=2x +m 在[0,3]上是“关联函数”,则m 的取值范围是________.答案 ⎝⎛⎦⎤-94,-2 解析 f (x )=x 2-3x +4为开口向上的抛物线,g (x )=2x +m 是斜率k =2的直线,可先求出g (x )=2x +m 与f (x )=x 2-3x +4相切时的m 值.由f ′(x )=2x -3=2得切点为⎝⎛⎭⎫52,114,此时m =-94,因此f (x )=x 2-3x +4的图象与g (x )=2x +m 的图象有两个交点,只需将g (x )=2x -94向上平移即可.再考虑区间[0,3],可得点(3,4)为f (x )=x 2-3x +4图象上最右边的点,此时m =-2,所以m ∈⎝⎛⎦⎤-94,-2.。
最全函数零点问题处理74页WORD版

最全函数零点问题处理74页WORD版在74页的WORD文档中,我们可以找到最全的函数零点问题处理方法。
函数零点问题是指在一个函数中,寻找让函数取零值的变量值或者变量区间的问题。
这在数学、物理和工程等领域中经常出现,并且在实际问题中具有重要的意义。
以下是一些常见的函数零点问题处理方法:1.图像法:这是一种直观的方法,通过函数的图像来估计函数的零点。
我们可以使用计算机软件或者手绘的方法绘制函数的图像,通过观察图像来判断零点的位置。
这种方法的优点是直观易懂,但是在精确性上可能存在一定的误差。
2. 代数法:这是一种通过代数运算来求解函数零点的方法。
对于一些简单的函数,可以通过代数运算找到确切的零点。
例如,对于一次函数f(x)=ax+b,可以直接解方程ax+b=0来求解零点。
对于高次函数,我们可以使用一些代数方法,如因式分解、配方法等来求解零点。
3.迭代法:这是一种通过不断迭代逼近零点的方法。
迭代法的基本思想是,从一个初始值开始,通过一定的递推公式不断逼近函数的零点。
例如,常见的迭代法有牛顿迭代法、二分法、弦截法等。
这些方法本质上都是通过不断迭代来逼近函数零点,直到满足一定的收敛条件。
4.数值法:这是一种通过数值计算来求解函数零点的方法。
数值法通过一定的数值计算方法,如插值法、拟合法等,根据已知的函数值,求解函数的零点。
数值法的优点是不依赖于函数的解析形式,对于任意函数均可以求解。
但是数值法在精度和计算时间上可能存在一定的限制。
5.综合法:综合法是指综合使用多种方法来求解函数零点的方法。
在实际问题中,往往需要通过多种方法的综合来求解函数的零点。
综合法可以充分发挥各种方法的优点,提高求解的准确性和效率。
在处理函数零点问题时,需要根据具体的问题选择合适的方法。
不同的方法在不同的问题中可能具有不同的适用性和优缺点。
因此,熟悉和掌握各种函数零点问题处理方法是非常重要的。
通过不断的学习和实践,我们可以提高对函数零点问题的处理能力,解决实际问题。
零点问题的类型及解决方法

零点问题的类型及解决方法嘿,咱今儿就来唠唠这零点问题!你说啥是零点问题呀?简单来说,就好比你找一个函数图像和 x 轴交点的时候,那交点不就是零点嘛!零点问题那可是有好些类型呢!就像是不同脾气的小孩。
有的零点问题啊,就像个害羞的孩子,藏得可深了,得你费劲巴拉地去挖掘才能找到它。
还有的呢,就像个调皮鬼,东躲西藏的,让你好一通找。
那咋解决这些让人头疼的零点问题呢?别急呀!咱一个一个说。
比如说,咱可以用画图的办法呀!就像你要找个宝藏,先画个地图,心里不就有底了嘛。
把函数图像一画,零点在哪儿,那不是一目了然嘛!这就好比你在迷宫里有了指南针,一下子就能找到出路啦。
还有啊,代数方法也不错呀!通过各种计算,把零点给算出来。
这就像解谜题一样,一点点地分析,一点点地推导,最后谜底揭开,零点也就现身啦!你想想,那感觉是不是特棒?再或者,咱可以试着把复杂的问题简单化呀!就像你吃一大块肉,一下子咬不下去,那就切成小块嘛。
把复杂的函数拆分成几个简单的部分,分别去研究,不就容易多了嘛。
举个例子吧,有个函数长得特别复杂,一看就头大。
那咱就把它拆成几个小函数,一个一个地去研究它们的零点。
就好像你要打一个大怪兽,先把它的手脚打断,再慢慢收拾它,是不是就轻松多啦?有时候啊,解决零点问题就像爬山,看着那高高的山峰,心里直犯嘀咕,能上去吗?可只要你一步一步地往上爬,总会爬到山顶的呀!遇到难题别退缩,办法总比困难多嘛!咱可不能小瞧了这零点问题呀,它在好多地方都有用呢!比如在数学研究里,那可是重要得很呢!要是搞不清楚零点问题,好多难题都没法解决啦。
所以啊,咱得重视零点问题,学会怎么去解决它。
别觉得难就打退堂鼓,要像个勇士一样,勇敢地去面对!就像那句话说的,世上无难事,只怕有心人嘛!你说是不是?咱只要用心去钻研,就没有解决不了的零点问题!相信自己,一定能行!。
零点问题的类型及解决方法

题型 一 : 函数 零 点 所 在 区 间 的 判 断— — 利 用 零 点 存 在 性 定 理 判 断零 点所 在 区 间
利用零点存在性定理 时 , 函数y ) 在 区间[ a , b ] 上 的图像 必须是连续 曲线 , 并且 在 区间端 点的 函数值符 号
证明: 曲 线 证明: 曲
厂 ( c ) = ( c — a ) ( c — b ) > 0 , 且厂 ( ) 是二次函数 , 所以函数 ) = ( — a ) ( — b ) + ( — b ) ( — c ) + ( — a ) ( — c )的两个零 点分另 U
位于 区间( a , b ) 、 ( b , c ) . 点 评 :运 用 零 点 存 在 性 定 理 判 断零 点 所 在 区 间 , 必
y = ÷ + 1 有唯一的公共点.
点评 : 本 题 要 证 明指 数 函数 与 二 次 函数 的 交 点 个 数
令 厂 ( ) : ( ÷ ) , g ( ) : + 3 ’ 从
而将原题转化成 函数 ) , y = g ( x ) 的交点个数 , 如 图1 所示. 由图可知原方程有 两个解 .
点评 : 将 函 数 的 零 点 问题 转 化 为 两 个 函数 图像 的 交
Hale Waihona Puke 羔问题 来 解 决. 确 定 零 点 个 数.
高 中 版中 敷- ?
研 究
考试
备考指南
2 0 1 4年 3月
题型 四、 复 合 函 数 的 零 点 个 数 问题 — — 通 过 换 元 转 化 为 两 个 函数 图 像 交 点 的个 数
图1
-
问题 , 可把函数交点问题转化为函数零点问题 . 利用函
江苏省南京市2014届高三考前冲刺训练(南京市教研室) 数学 Word版含答案

【答案】 .
【提示】设A(t,2 log2t)(t>1),则B(t2,2 log2t),D(t,log2t),C(t2,2klog2t),则有log2t=2klog2t,
【答案】x+y-2=0.
【说明】本题考查直线与圆相切问题和最值问题.
6.已知双曲线 - =1(a>0,b>0)的离心率等于2,它的右准线过抛物线y2=4x的焦点,则双曲线的方程为.
【答案】 - =1.
【解析】本题主要考查了双曲线、抛物线中一些基本量的意义及求法.
7.在平面直角坐标系xOy中,已知曲线C1、C2、C3依次为y=2log2x、y=log2x、y=klog2x(k为常数,
【答案】π.
【提示】设圆锥的底面半径为r,母线长为l,由题意知 = π,且 ·2πr·l=2 π,解得l=2,r= ,所以圆锥高h=1,则体积V= πr2h=π.
【说明】本题考查圆锥的侧面展开图及体积的计算.
5.设圆x2+y2=2的切线l与x轴正半轴,y轴正半轴分别交于点A,B.当线段AB的长度最小值时,切线l的方程为____________.
当直线过点A时,t最大.由 解得A( , ),
所以tmax= - = .
因此 的取值范围是[- , ].
【说明】本题含三个变量,解题时要注意通过换元减少变量的个数.利用消元、换元等方法进行减元的思想是近年高考填空题中难点和热点,对于层次很好的学校值得关注.
9.已知四数a1,a2,a3,a4依次成等比数列,且公比q不为1.将此数列删去一个数后得到的数列(按原来的顺序)是等差数列,则正数q的取值集合是.
