第4章+习题
第四章(习题答案)

§4-3 戴维宁定理和诺顿定理
(一)戴维宁定理的证明
设流过端口以外的电路中的电流为 i,则据替代定 ,则据替代定 理,外电路可以用一个电流为 i的电流源 iS替代,如图(a)所 替代,如图(a) (a)所 示;则又据 叠加定理,得其相应的分电路 (b),(c): 示;则又据叠加定理 ,得其相应的分电路(b) (c): 叠加定理,得其相应的分电路 (b),
:在线性 线性电路中,任一支路的电流或电 叠加定理 :在 线性 电路中,任一支路的电流或电 压是电路中各个独立电源(激励) 单独作用 时在 压是电路中各个独立电源(激励)单独作用 单独作用时在 该支路中产生的电流或电压的 代数和. 该支路中产生的电流或电压的代数和 代数和.
§4-1 叠加定理
也就是说,只要电路存在唯一解,线性电路中 的任一结点电压,支路电压或支路电流均可表示为 以下形式: y = H 1uS1 + H 2 uS 2 + + H m uSm + K 1 iS1 + K 2 iS 2 + + K n iSn ——表示电路中独立 其中:uSk 表示电路中独立电压源的电压 独立电压源的电压
+ Req + u RL
uS1
NS
uS2
RL
口 含一 源 端
1
戴维宁定理
- -
uoc
维 宁 等 效 电 路
1' i1
RL
isc
1'
1'
u R Geq L
-
+
诺顿定理
诺 顿 等 效 电 路
1'
§4-3 戴维宁定理和诺顿定理
对外电路而言,"含源一端口NS"可以用一条含源支路 对外电路而言," 含源一端口N 可以用一条含源支路 等效替代 戴维宁等效电路和诺顿等效电路称为一端口的等效发电机 戴维宁等效电路和诺顿等效电路称为一端口的等效发电机
第4章课后习题及答案

返 回
第 4 章 供 电 与 用 电
练习题解答
4.1.1 某三相同步发电机,三相绕组联结成星形时的线电压为 10.5kV,若将它联结成三角形,则线电压是多少?若联结成星形 时,L2相绕组的首末端接反了,则三个线电压的有效值U12 , U23 和U31各是多少? · · · · U31= U3 -U1 · -U2 解: 星形联结时UlY = 10.5kV U3 · U 3 UlY 10.5 = kV = 6.06kV ∴UpY = · · U 1=U23 √ 3 √3 · ·-U =U 三角形联结时相电压不变, 2 3 · UlY = UpY =6.06kV L2首末端接反的相量图如图所示:
· · · 0 0 0 IL2 = I2 - I1 ( 8 . 8 30 8 . 8 0 ) A 4 . 56 105 A · · · 0 0 0 IL3 = I3 - I2 ( 8 . 8 30 8 . 8 30 ) A 8 . 8 90 A
XL= Z sin = 77.1×0.6 Ω = 46.3 Ω
返 回 上一题 下一题
第 4 章 供 电 与 用 电
4.3.2 某三相负载,额定相电压为220V,每相负载的电阻为4Ω,感 抗为3Ω,接于线电压为380V的对称三相电源上,试问该负载应
采用什么联结方式?负载的有功功率、无功功率和视在功率?
· I
l2
· I
l3
· I
2
· I
3
-jXC
解: 负载为不对称三相负载
· · 0 U U 220 120 2 23 · 0 I2 = Z = -jX = 8 . 8 30 A -j25 2 C
返 回 上一题 下一题
第4章 习题解答

第4章 习题与答案4-1作简谐振动的物体,每次通过同一位置时,不一定相同的量是 [ ] (A) 位移 ; (B) 速度 ; (C) 加速度; (D) 能量。
[答案:B ]4-2 把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相为 [ ](A) π; (B) π/2; (C) 0; (D) θ [答案:C ]4-3 谐振动的振动曲线如题4-3图所示,则有[ ] (A )A 超前π/2; (B )A 落后π/2; (C )A 超前π; (D )A 落后π。
[答案:A ]4-4 一个质点作简谐振动,振辐为A ,在起始时刻质点的位移为A /2,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为题4-4图 中哪一个? [ ][答案:B ]4-5 两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点恰在最大负位移处。
则第二个质点的振动方程为 [ ] (A) )π21cos(2++=αωt A x ; (B) )π21cos(2-+=αωt A x ; (C) )π23cos(2-+=αωt A x ; (D) )cos(2π++=αωt A x 。
[答案:A ]4-6 已知某简谐振动的振动曲线如题4-6图所示。
则此简谐振动的振动方程(SI )为 [ ](A) 题4-4图题4-3图(A )220.02cos()33x t =π+π;(B )220.02cos()33x t =π-π;(C )420.02cos()33x t =π+π;(D )420.02cos()33x t =π-π。
[答案:C ]4-7 弹簧振子作简谐振动,先后以相同的速度依次通过A 、B 两点,历时1秒,质点通过B 点后再经过1秒又第二次通过B 点,在这2秒内质点通过的总路程为12cm ,则质点的振动周期和振幅分别为 [ ](A )3s 、12cm ; (B )4s 、6cm ; (C )4s 、9cm ; (D )2s 、8cm 。
(完整版)线性代数练习册第四章习题及答案

第四章 线性方程组§4-1 克拉默法则一、选择题1.下列说法正确的是( C )A.n 元齐次线性方程组必有n 组解;B.n 元齐次线性方程组必有1n -组解;C.n 元齐次线性方程组至少有一组解,即零解;D.n 元齐次线性方程组除了零解外,再也没有其他解. 2.下列说法错误的是( B )A 。
当0D ≠时,非齐次线性方程组只有唯一解;B 。
当0D ≠时,非齐次线性方程组有无穷多解;C 。
若非齐次线性方程组至少有两个不同的解,则0D =; D.若非齐次线性方程组有无解,则0D =. 二、填空题1.已知齐次线性方程组1231231230020x x x x x x x x x λμμ++=⎧⎪++=⎨⎪++=⎩有非零解,则λ= 1 ,μ= 0 。
2.由克拉默法则可知,如果非齐次线性方程组的系数行列式0D ≠,则方程组有唯一解i x =iD D. 三、用克拉默法则求解下列方程组 1.832623x y x y +=⎧⎨+=⎩解:832062D ==-≠123532D ==-,2821263D ==-所以,125,62D Dx y D D====- 2.123123123222310x x x x x x x x x -+=-⎧⎪+-=⎨⎪-+-=⎩解:213112112122130355011101r r D r r ---=--=-≠+---11222100511321135011011D r r ---=-+-=---,212121505213221310101101D r r --=-+-=-----, 3121225002112211511110D r r --=+=---所以, 3121231,2,1D D Dx x x D D D ======3.21241832x z x y z x y z -=⎧⎪+-=⎨⎪-++=⎩解:132010012412041200183583D c c --=-+-=≠-13110110014114020283285D c c -=-+=,2322112102112100123125D c c -=-+=--, 31320101241204120182582D c c =-=--所以, 3121,0,1D D Dx y z D D D ====== 4.12341234123412345242235232110x x x x x x x x x x x x x x x x +++=⎧⎪+-+=-⎪⎨---=-⎪⎪+++=⎩解:2131412131111111111214012322315053733121102181231235537013814222180514r r D r r r r r r r r ---=------------+=----=-+---3214212325111511102221422518231523528110121101005110010525182733214210252823522c c D c c c c c c --------=----------+=-----=----212314113231511151112140723222150123733021101518723230132123733031284315181518r r D r r r r r r r r -----=--------------=----=------12342213111512151031224522182325111132283101101002510200251521852974265211228115127c c D c c c c c c -------=---------+=-----=----12432322111152115312125252223121135231200100215215552502714251152604c c D c c r r r r --------=----------+=----=---所以, 312412341,2,3,1D D D Dx x x x D D D D========-§4-2 齐次线性方程组一、选择题1.已知m n ⨯矩阵A 的秩为1n -,12,αα是齐次线性方程组0AX =的两个不同的解,k 为任意常数,则方程组0AX =的通解为( D )。
操作系统习题第四章

第四章互斥、同步与通讯一、单项选择题1.一个正在访问临界资源的进程由于申请等待I/O操作而被中断时,__________.A.可以允许其他进程进入与该进程相关的临界区B.不允许其他进程进入任何临界区C. 可以允许其他就绪进程抢占处理器,继续运行D.不允许任何进程抢占处理器2.两个并发进程之间______A 一定存在互斥关系B 一定存在同步关系C 一定彼此独立无关D 可能存在同步或互斥关系3.为了使两个进程能同步运行,最少需要_______个信号量。
A 一B 二C 三D 四4.共享变量是指__________访问的变量。
A. 只能被系统进程B. 只能被多个进程互斥C. 只能被用户进程D. 可被多个进程5.临界区是指并发进程中访问共享变量的__________.A.管理信息 B.数据 C.信息存储 D.程序段6.设有三个进程共享一个资源,如果每次只允许一个进程使用该资源,则用PV操作管理时信号量S的可能取值是___________A.1,0,-1,-2B.2,0,-1,-2C.1,0,-1D.3,2,1,07.进程的并发执行是指若干个进程__________.A. 同时执行B. 在执行的时间上是重叠的C. 在执行的时间上是不可重叠的D. 共享系统资源8.在进程通信中,__________常用信件交换信息。
A.低级通信 B.高级通信 C.消息通信 D.管道通信9.实现进程同步时,每一个消息与一个信号量对应,进程_________可把不同的消息发送出去。
A.在同一信号量上调用P操作B.在不同信号量上调用P操作C.在同一信号量上调用V操作D.在不同信号量上调用V操作10._________是只能有P和V操作所改变的整形变量。
A.共享变量B.锁C.整型信号量D.记录型信号量11.在执行V操作时,当信号量的值_________时,应释放一个等待该信号量的进程。
A.大于0B.小于0C.大于等于0D.小于等于012.进程和程序的主要区别是__________.A.占用处理器和不占用处理器B.占用主存和不占用主存C.动态和静态D.连续执行和非连续执行13.有三个进程P1,P2,P3共享同一个程序段,而每次最多允许两个进程进入该程序段,则信号量S的初值为___________.A. 0B. 1C. 2D. 314.若P、V操作的信号量S初值为2,当前值为-1,则表示有_________等待进程。
第四章习题及参考答案

第四章习题及参考答案第四章抽样与抽样估计⼀、单项选择题1、实际⼯作中,⼩样本是指()A、样本容量⼤于30的样本B、样本容量⼩于30的样本C、样本容量等于30的样本D、样本容量⼩于等于30的样本2、从5个字母中随机抽取2个字母作为样本,采⽤重复抽样,考虑顺序,则可能的样本个数为()A、10个B、20个C、25个D、30个3、当总体⽅差未知,且样本容量⼩于30时,进⾏正态总体均值的区间估计应采⽤的临界值为()A、F值B、Z值C、t值D、2x值4、当总体⽅差已知,⽆论样本容量n的⼤⼩如何,进⾏正态总体均值的区间估计应采⽤的临界值为()A、F值B、Z值C、t值D、2x值5、在总体内部情况复杂、且各单位之间差异程度⼤、单位数⼜多的情况下,宜采⽤()A、等距抽样B、整群抽样C、简单随机抽样D、类型抽样6、根据重复抽样的资料,甲单位⼯⼈⼯资⽅差为25,⼄单位为100,⼄单位抽的⼈数⽐甲单位多3倍,则抽样平均误差()A、甲单位较⼤B、甲单位较⼤C、⽆法判断D、甲、⼄单位相同7、某学校在全校学⽣中随机重复抽取100⼈调查⾝⾼,计算出抽样平均误差为5cm。
如果改⽤不重复抽样⽅法,在其他条件不变时,其抽样平均误差将会()A、⼤于5cmB、⼩于5cmC、等于5cmD、不确定8、纯随机重复抽样条件下,样本容量扩⼤为原来的9倍,其它条件不变,则()A、抽样允许误差不变B、抽样允许误差缩⼩为原来的九分之⼀C、抽样允许误差缩⼩为原来的三分之⼀D、抽样允许误差增⼤为原来的九倍⼆、多项选择题1、影响抽样平均误差的因素主要有()A、总体⽅差或标准差B、样本容量C、抽样⽅法D、抽样组织⽅式E、抽样的对象2、下列说法中错误的有()A、抽样误差是不可避免的B、抽样误差是可以避免的C、抽样误差可以计算但不能加以控制机D、抽样误差是由于抽样的随机性⽽产⽣的样本估计量与总体参数之间的代表性误差 E、抽样误差是指登记性误差3、评价估计量的优劣常⽤下列三个标准()A、⼀致性B、有效性C、合理性D、代表性E、⽆偏性4、抽样推断过程包括相互联系的三项内容()A、随机抽样B、统计估计C、假设检验D、抽样精度E、置信度5、下列说法正确的有()A、总体参数是唯⼀的、确定的,但⼜是未知的B、总体参数是随机变量C、样本统计量是随机变量D、样本统计量是唯⼀的、确定的E、样本所包含的总体单位个数称为样本容量6、概率抽样最基本的组织⽅式有()A、简单随机抽样B、分层抽样C、等距抽样D、整群抽样E、配额抽样7、抽样估计中的抽样误差()A、⽆法避免B、可以控制C、只能在估计结束才能知道D、可以计算E、不可控制8、抽样平均误差是指()A、所有可能样本的样本指标与总体指标的平均离差B、所有可能样本的样本指标对总体指标的标准差C、已抽出样本的标准差D、等价于极限误差E、已抽出样本的平均差三、填空题1、概率抽样也叫随机抽样,是指按照原则抽取样本。
第4章 习题及答案
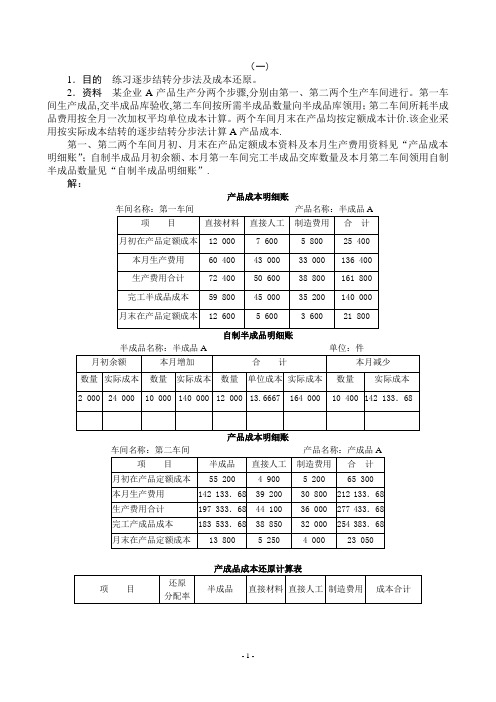
(一)1.目的练习逐步结转分步法及成本还原。
2.资料某企业A产品生产分两个步骤,分别由第一、第二两个生产车间进行。
第一车间生产成品,交半成品库验收,第二车间按所需半成品数量向半成品库领用;第二车间所耗半成品费用按全月一次加权平均单位成本计算。
两个车间月末在产品均按定额成本计价.该企业采用按实际成本结转的逐步结转分步法计算A产品成本.第一、第二两个车间月初、月末在产品定额成本资料及本月生产费用资料见“产品成本明细账”;自制半成品月初余额、本月第一车间完工半成品交库数量及本月第二车间领用自制半成品数量见“自制半成品明细账”.解:产品成本明细账车间名称:第一车间产品名称:半成品A自制半成品明细账半成品名称:半成品A 单位:件产品成本明细账产成品成本还原计算表(二)1.目的练习产品成本计算的综合结转分步法.2.资料某企业生产甲产品,分三个生产步骤进行生产。
该企业设有第一、第二、第三三个基本生产车间,甲产品由这三个车间顺序加工而成。
成本计算采用综合结转法。
原材料在第一车间开始加工时一次投入,半成品不通过中间仓库收发,上一步骤完工后全部交由下一步骤继续加工。
月末在产品按约当产量法计算,各车间月末在产品完工程度均为50%。
该企业本年5月份有关成本计算资料如表1、表2所示。
表1产量记录表2月初在产品成本和本月发生费用表3产品成本计算单135070÷(88+16)=1298。
75 24960÷(88+16×50%)=260 19200÷(88+16×50%)=200表4产品成本计算单173890÷(8050%)=326。
6表5产品成本计算单244450÷(96+4)=2444.5 34300÷(96+4×50%)=350 23520÷(96+4×50%)=240表6(三)1.目的练习产品成本计算的平行结转分步法.2.资料某厂设有三个基本生产车间,第一车间生产甲半成品,交第二车间继续加工,第二车间生产乙半成品,交第三车间生产丙产成品。
第四章习题
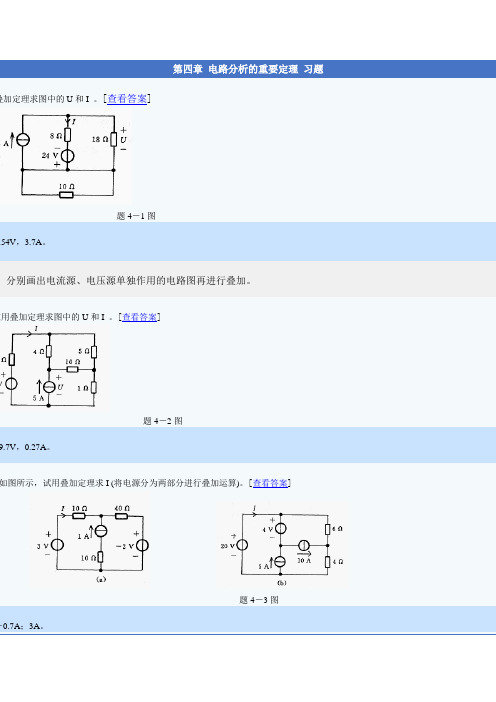
第四章电路分析的重要定理习题叠加定理求图中的U和I 。
[查看答案]题4-1图.54V,3.7A。
:分别画出电流源、电压源单独作用的电路图再进行叠加。
应用叠加定理求图中的U和I 。
[查看答案]题4-2图9.7V,0.27A。
如图所示,试用叠加定理求I (将电源分为两部分进行叠加运算)。
[查看答案]题4-3图-0.7A;3A。
电路如图所示。
若48 V压源突然降为24 V,试求电流I2 有多大变化。
[查看答案]题4-4图.324A:电压源由48V降为24V,相当于一个48V电压源和一个-24V电压源一起作用。
I2=I2原+△I2路如图所示,试用叠加定理求U。
[查看答案]题4-5图5V电路如图所示,N R为线性电阻网络。
已知:当Us=5 V、Is=2 A时,I2=1 A;I S=4 A时,I2=2 A。
求当Us=1 V、Is=1 A时,I2=? [查看答案]题4-6图.5A。
:设I2=αUs+βIs,由已知有5α+2β=12α+4β=2可以得α=0,β=1/2如图所示,N R为线性电阻网络。
当电流源i s和电压源u Sl反向时(u S2不变),电压u ab是原来的0.5倍;向时(u Sl不变),u ab为原来的0.3倍。
问:仅i s反向时(u Sl、u S2均不变),u ab为原来的多少倍?题4-7图.8。
路如图所示。
已知I=1 A,试用替代定理求图(a)中Us和图(b)中R的值。
[查看答案]题4-8图V;4Ω。
电路中,N R为线性电阻网络。
已知:R=R1时,I1=5 A、I2=2 A;4 A、I2=1 A。
求:R=时,I1=? [查看答案]4-9图3A。
图所示各含源二端网络的戴维南等效电路。
[查看答案]题4-10图4—10答案:6V,12.6Ω;-2V,6Ω;14V,2.5Ω;13.3V,2.07kΩ;25V,0.67kΩ;43V,3.1kΩ;14.17V,120.8Ω;;16V,10.67Ω;55V,13.75Ω。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I z = 478.8 × 10 6 mm 4 ;材料为红松,其许用弯曲正应力 [σ ] = 10 MPa ,许用顺纹切应力 [τ ] = 1.1 MPa ; 胶合缝的许用切应力 [τ 胶 ] = 0.35 MPa 。试校核梁的强度。
6. 图示箱形截面简支梁用四块木板胶合而成,受三个集中力作用如图所示。已知横截面对中性轴的惯性矩
任意 x 截面,下边缘的拉应力:
q
A
x
dx
l
B
x
M ( x ) 6M ( x ) σ ( x) = = Wz bh 2
根据胡克定律,任意 x 截面,下边缘的纵向线应变:
y
ε ( x) =
l
σ ( x)
E
=
6 M ( x) Ebh 2
l
于是梁的下边缘的总伸长为:
6 1 1 2 ql 3 Δl = ∫ ε ( x ) d x = ∫ ( qlx − qx ) d x = 0 0 Ebh 2 2 2 2 Ebh 2
4. 图示一矩形截面悬臂梁,在全梁上受集度为 q 的均布荷载作用,其横截面尺寸为 b,h,长度为 l。 (1)试证明在离自由端为 x 处的横截面上切向内力元素 τ d A 的合力等于该截面上的剪力,而法向内力 元素 σ d A 的合力偶矩等于该截面上的弯矩。 (2)如沿梁的中性层截出梁的下半部,如图所示,试问在截开面上的切应力 τ ′ 沿梁长度的变化规律如 何?该面上总的水平剪力有多大?由什么力来平衡?
+ max
+ σmax = 26.2 MPa ,在截面 C 下边缘
9.矩形截面钢条长 l ,总重为 F ,放在刚性水平面上,在钢条 A 端作用 正应力。
F 向上的拉力时,试求钢条内最大 3
F/3 A C
解:在截面 C 处, 有
1 MC = =0 ρ EI F F ( l )2 2l 即 M C = × l A C − × A C = 0, l A C = 3 l 2 3 A C 段可视为受均布载荷 q 作用的简支梁, M max 发生在跨中 σmax = M max q ( l A C )2 / 8 Fl = = 2 W bt / 6 3bt 2
因此有: 由弯曲正应力的强度条件:
D
1 q (l − x) 2 8
σ max =
3
M max 6 M max 6 M max 3M max = = = ≤ [σ ] Wz bh 2 b(2b) 2 2b 3
3M max 3 3 × 3.03 × 10 3 得到: b ≥ = = 0.0769 m = 76.9 mm 2[σ ] 2 × 10 × 10 6 由上可见,矩形截面梁的最小尺寸是宽 77 mm,高 154 mm。
2
正应力沿横截面高度分布为 σ =
于是整个截面的 σ d A 对中性轴的矩是:
M y Iz
∫σ
A
yd A =
M Iz
∫
A
y2 d A =
M ⋅ Iz = M Iz
(2)对此悬臂梁任意 x 截面的剪力为 FS ( x) = q x 。 矩形截面的中性层处的横向切应力为: τ =
根据切应力互等定律,得截开面上切应力 τ 沿梁长度的变化规律为:
则
a= [ FS ] 700 = = 42.4 mm τ ′b 0.33×106 × 50×10−3
q A q 4m 2m 2m 40 kN x 40 kN 40 kN ⋅ m x
40 kN ⋅ m
令
C
20 B 180
100
20
z 82
11.
已知简支梁 q = 20 kN/m ,其截面形状及剪力图和弯 FS
* S za = 20 × 150 × 152 × 10 −9 = 0.456 × 10 −3 m 3
* FS max S za 18 × 10 3 × 0.456 × 10 −3 τa = = = 0.343 × 10 6 Pa = 0.343 MPa < [τ 胶 ] −6 −3 478.8 × 10 × 50 × 10 I zb
q=F/l B
10. 一 根 木 梁 的 两 部 分 用 单 排 钉 连 接 而 成 , 已 知 惯 性 矩
F 87.5 a
I z = 113.5×10−6 m 4 , F = 3 kN ,横截面如图示,每个钉的
许用剪力 [FS ] = 700 N , 试求钉沿梁纵向的间距 a 。 ( C 为形心)
τ ′′ = 3.63 MPa,
危险截面上的正应力及切应力的分布如图所示。 12. T 形截面铸铁梁,承受纯弯曲且弯矩为正,材料的许用拉压应力
30 hc C ht b z
[σ ]+ 1 之比 = ,试求水平翼板的合理宽度 b 。 [σ ]− 4
ht [σ ]+ 1 解:由 = − = , 又 ht + hc = 400 hc [σ ] 4 求得: ht = 80 mm, hc = 320 mm
200 C 50 z
50 200
解:缝间水平切应力
τ′ = τ =
FS ⋅ S z* FS z* = bI z bI z
3 000×[200× 50×(87.5 − 25) + 50×(87.5 − 50)2 / 2]×10−9 = = 0.33 MPa 50×10−3 ×113.5×10−6 τ ′ba = [FS ] = 700 N
7 4
试求梁横截面上的最 矩图如图所示,I z = 3.97 ×10 mm , 大正应力及最大切应力,并绘出危险截面上正应力及切应力的 分布图。 M
40 kN
20
5
解:截面 C:上边缘 σmax = 下边缘 σmin = −σmax ×
M max y max = 118.9 MPa Iz
8.2 = −82.6 MPa 11.8
l l
5.
图示一梁跨度 l = 6 m ,荷载集度 q = 2kN/m ,木梁的许用弯曲正应力
A
q (l − x ) / 2 C l
x B
[σ ] = 10 MPa ,并已知 h = 2 。试求:
b
(1)在用料最经济的情况下,确定支座 C 位置的 x 值; (2)选择矩形截面木梁的尺寸。 解: (1)欲使次梁用料最经济,应使 C 截面与 D 截面的弯矩绝对值相等, 即:
I z=6.013 ×10−5 m 4
解:弯矩如图
4
20 kN . m A M C B D . 10 kN m x
截面 B 的 σ 截面 C 的 σ
+ max
M By 20×103 × 73×10−3 = = = 24.1 MPa Iz 76.013×10−5 M C y 10×103 ×157×10−3 = = = 26.2 MPa Iz 6.013×10−5
qa 2 / 2
M
ql 2 qla − 8 8
注意:本题亦可改为“从弯矩方面考虑,求使梁的两支座间距离最合理的 a 值” 。 2. 试作图示各梁的剪力弯矩图。
4 kN ⋅ m 4 kN/m 4m
FS
FS
20 kN ⋅ m B
A 3m
C
30 kN
15 kN/ m
A
1m
B
0. 5 m
37.5 kN⋅ m
1 2 qx 2 A
C
MD = MC
B
1 1 1 q(l − x ) 2 − qx 2 = qx 2 8 4 2 − 2 + 4 + 20 x= l = 0.29l = 0.29 × 6 = 1.74 m 10 (2)当 x = 1.74 m 时,求得梁的最大弯矩是: 1 1 M max = qx 2 = × 2 × 1.74 2 = 3.03 kN⋅ m 2 2
3FS 3qx = 。 2bh 2bh
τ′ =τ =
3qx 2bh
q B
A
τ′
l
x
其总的水平剪力为:
3qx 3ql 2 dx= 0 0 2h A′ 4h 水平剪力 FS′ 由根部横截面下半部的法向内力元素 σ dA 组成的 x 方向的合力来平衡。 FS′ = ∫ τ ′ d A′ = ∫ τ ′b d x = ∫
3
解:由对称性知
FA = FB = 18 kN (↑) M C = 18 × 1 = 18 kN⋅ m M D = 18 × 2 − 10 × 1 = 26 kN⋅ m
易知最大剪力在 AC 段 (值为 18kN) 及 EB 段 (值 为-18kN) ,最大弯矩在 D 处,值为 26 kN ⋅ m 。 (1) 正应力强度校核
q A B
b z y
x
l
解: (1)矩形截面切应力沿高度分布为:
τ=
* FS S z F b 3FS = S ⋅ (h 2 − 4 y 2 ) = (h 2 − 4 y 2 ) bI z bI z 8 2bh 3
h
于是整个横截面的切向内力构成的合力为:
∫ τ d A = 2b ∫ 2
A
0
3FS (h 2 − 4 y 2 ) d y = FS 3 2bh
又
2
340 60
由
S z = 0 即 60b (80 −
则 b = 510 mm
* S zb = 20 × 50 × 168 × 10 −9 = 0.168 × 10 −3 m 3
τb =Biblioteka * FS max S zb 18 × 103 × 0.168 × 10 −3 = = 0.315 × 10 6 Pa = 0.315 MPa < [τ 胶 ] −6 −3 478.8 × 10 × 20 × 10 I zb
截面 A 中性轴处: 2(20 − 8.2)× 2×(20 − 8.2) S z max = = 278.5×103 mm 3 , 2 FSmaxS z max τ max = = 7 MPa I zb
