ADF检验
adf检验临界值

adf检验临界值adf检验临界值在经济学领域中,我们常常需要对时间序列数据进行分析,以了解其特征及其变化趋势。
而对于非平稳时间序列数据的检验,则需要用到ADF(Augmented Dickey-Fuller)检验方法。
而在ADF检验中,临界值的选择非常重要,因此本文将从概述ADF检验的基本原理、几种常见的ADF检验方法以及临界值选择等方面,来深入解读ADF检验临界值的重要性。
ADF检验简介ADF检验,全称Augmented Dickey-Fuller Test,是检验时间序列数据是否平稳的经典方法之一。
在这个方法中,我们会设置一个基准假设,即时间序列数据是不平稳的。
如果我们找不到反驳这个基准假设的证据,那么我们就确定了时间序列数据是不平稳的。
反之,如果我们找到了证据反驳这个基准假设,那么我们就可以符合地断定时间序列数据是平稳的。
ADF检验方法ADF检验其实有几种常见的方法,这里列举以下:1. ADF-OLS(ordinary least squares)检验:这种方法是最常见的ADF 检验方法。
其适用于没有确定趋势的时间序列数据。
2. ADF-GLS(generalized least squares)检验:这种方法是应用于数据确定趋势的情况下。
它基于一种称为Generalized Least Squares的方法来消除数据中的趋势。
3. ADF-WM(weighted mean)检验:这种方法则可以在数据不平稳的情况下使用,它首先对数据进行标准化,然后使用加权均值来计算数据的趋势,最后通过与残差进行比较确定序列的平稳性。
三种ADF检验方法的原理都非常精妙,各有优缺点,但对于临界值的选择来说,它们都具有相同的依据和标准。
ADF检验临界值在ADF检验中,我们会使用t统计量来衡量我们的样本与平稳随机游走(RW)之间的距离。
在这个过程中,我们需要参照一组临界值来判断我们的样本t统计量所处位置是否超出了这个随机游走的范畴。
adf检验名词解释

ADF检验名词解释1. 什么是ADF检验?ADF(Augmented Dickey-Fuller)检验是一种用于时间序列数据的单位根检验方法。
单位根是指时间序列数据中存在非随机趋势,即数据具有持续性的特征。
ADF检验可以帮助我们判断一个时间序列数据是否具有单位根,从而确定其是否为稳定的平稳过程。
2. 单位根和平稳过程单位根是时间序列数据中的非随机趋势,它表示数据存在长期依赖关系,即过去的值对未来值有预测能力。
相反,平稳过程是指时间序列数据的统计特性在时间上保持不变,不受外部因素影响。
在经济学和金融学中,平稳过程是进行预测和建模的基础。
如果一个时间序列数据包含单位根,则其统计性质会发生变化,使得预测和建模变得困难。
3. ADF检验的原理ADF检验基于Dickey-Fuller回归模型,在该模型中,被解释变量是时间序列数据的差分值(将原始数据进行一阶差分),解释变量包括差分值、滞后差分值以及其他可能影响时间序列数据的因素。
ADF检验的原假设(H0)是存在单位根,即时间序列数据是非平稳的。
备择假设(H1)是不存在单位根,即时间序列数据是平稳的。
通过对回归模型进行估计和假设检验,我们可以判断原假设是否成立,并得出结论。
4. ADF检验的步骤步骤1:提取差分值首先,我们需要对原始时间序列数据进行差分操作,获得一阶差分值。
这样做可以消除数据中的线性趋势。
步骤2:构建ADF回归模型在ADF检验中,我们使用自回归模型(AR)来对差分后的数据进行建模。
这个模型包括一个滞后项和其他可能影响时间序列数据的因素。
步骤3:估计ADF模型参数通过最小二乘法估计ADF模型中的参数,并计算出参数的标准误差。
这些参数和标准误差将用于后续的统计推断。
步骤4:进行假设检验在ADF检验中,我们需要对回归系数进行假设检验。
常见的方法是计算t统计量,并与相应的临界值进行比较。
如果t统计量大于临界值,则可以拒绝原假设,认为时间序列数据是平稳的。
adf检验通俗解释

adf检验通俗解释
ADF检验,即单位根检验(Augmented Dickey-Fuller Test),是一种经济学时间序列分析中常用的统计方法。
它用来判断一个时间序列数据是否存在单位根,即是否存在趋势。
通俗地说,单位根检验用来判断时间序列数据的变化趋势是否随机性的,或者说是否存在长期趋势。
如果数据存在长期趋势,就不能用简单的方法进行分析和预测,因为数据变化是有规律的。
而单位根检验可以帮助我们识别数据是否存在长期趋势,从而选择合适的模型来进行进一步分析。
ADF检验的思路是将时间序列数据拆分成趋势项、季节项、残差项等不同部分,然后分别对这些部分进行统计检验。
如果残差项(即剔除了趋势项和季节项后的数据)不存在单位根,那么我们可以认为原始数据也不存在单位根,即没有长期趋势。
通过ADF检验,我们可以得到一个统计量,根据这个统计量的显著性水平,来判断时间序列是否存在单位根。
如果统计量的值小于某个阈值,即p值小于显著性水平,那么我们可以拒绝存在单位根的假设,认为数据不存在长期趋势。
总之,ADF检验是一种用来判断时间序列数据是否存在长期趋势的方法,通过检验序列的残差项是否存在单位根,来判断原始数据是否存在单位根。
ADF检验

引自Ruey S. Tsay著,王辉、潘家柱译《金融时间序列分析》(第2版)DF检验为了检验资产的对数价格p t是否服从一个随机游动或一个带漂移的随机游动,对模型p t=ϕ1p t−1+e t (1)p t=ϕ0+ϕ1p t−1+e t (2)其中e t为误差项。
考虑原假设H0:ϕ1=1;H1:ϕ1<1,即是一个单位根检验问题。
一个方便的检验统计量就是在原假设下ϕ1的最小二乘估计的t−比。
对(1)式,由最小二乘法得ϕ1=p t−1p tTt=1t−1Tt=1,σe2=p t−ϕ1p t−12Tt=1其中p0=0,T为样本容量。
t−比为DF≡t−比=ϕ1−1ϕ1的标准差=p eTσe p t−12Tt=1这个t−比检验通常称为DF检验。
若e t为一个白噪声序列,其稍高于二阶的矩是有限的,则当T⟶∞时DF统计量趋于一个标准布朗运动的函数。
如果ϕ0=0但我们采用了(2)式,则所得的检验ϕ1=1的t−比将趋于另一种非标准的渐进分布。
上述两种情形都是用模拟方法来得到检验统计量的临界值。
然而如果ϕ0≠0且使用的是(2)式,则用来检验ϕ1=1的t−比是渐进正态的,但此时将需要很大的样本容量来保证渐进正态分布的使用。
ADF检验用x t表示一个AR(p)时间序列,为了验证序列是否存在单位根,通常人们采用ADF检验来验证,即可以用如下回归来进行假设检验(H0:β=1;H1:β<1):x t=c t+βx t−1+ϕiΔx t−i+e tp−1i=1其中c t是关于时间t的确定性函数,Δx j=x j−x j−1是x t的差分序列。
在实际中,c t可以是常数或者c t=ω0+ω1t。
β−1的t−比为ADF−检验=β−1β的标准差其中β为β的最小二乘估计,上述t−比就是著名的ADF检验。
注意到由于一阶差分,上面x t的式子等价于一个带确定性函数c t的AR(p)模型,可以改写为Δx t=c t+βc x t−1+ϕiΔx t−i+e tp−1i=1其中βc=β−1,相应的检验为H0:βc=0;H1:βc<0。
平稳序列检验方法

平稳序列检验方法平稳序列检验是判断一个时间序列是否具有平稳性的方法。
平稳序列是指序列的统计特性在时间上不发生变化,即均值、方差和自协方差与时间无关。
判断一个序列是否平稳很重要,因为只有平稳序列才能进行许多经济和统计分析。
平稳序列检验方法主要有单位根检验、ADF检验和KPSS检验等。
单位根检验是最常用的平稳序列检验方法之一,其基本思想是判断一个序列是否具有单位根。
单位根的存在意味着序列是非平稳的。
ADF检验是单位根检验的一种常用方法,它是在一个线性回归模型的基础上构建的。
具体而言,假设要检验的序列为Yt,则在ADF检验中,我们构建以下的回归模型:Yt = α+ β*t + γ*Yt-1 + δ1(ΔYt-1) + δ2(ΔYt-2) + …+ δp(ΔYt-p) + et其中,ΔYt表示序列的一阶差分,α、β、γ和δ分别是模型中的系数,et是随机误差项。
在ADF检验中,我们假设序列Yt具有单位根,即H0:γ=0,然后通过假设检验来判断是否拒绝原假设。
如果在检验的过程中发现γ显著不等于0,则拒绝原假设,即序列Yt是平稳的。
ADF检验的统计量是基于t统计量计算的,一般会提供临界值用于判断统计量的显著性。
如果统计量的值小于临界值,则拒绝原假设,序列是平稳的。
除了ADF检验外,还有KPSS检验也是一种用于判断平稳序列的方法。
与ADF 检验不同的是,KPSS检验是在原假设下进行的,即假设序列是平稳的。
KPSS检验的原假设是H0:序列是平稳的,备择假设是H1:序列是非平稳的。
具体而言,KPSS检验是基于单位根检验的思想,即检验序列的观测值是否围绕一个常数进行波动。
如果序列的波动围绕一个常数,则序列是平稳的;如果波动围绕着一个随时间增长的函数,则序列是非平稳的。
KPSS检验的统计量也是基于t统计量计算的,一般会提供临界值用于判断统计量的显著性。
如果统计量的值大于临界值,则拒绝原假设,序列是非平稳的。
除了单位根检验,还有一些其他的平稳序列检验方法,如Ljung-Box检验和ARCH检验等。
ADF检验
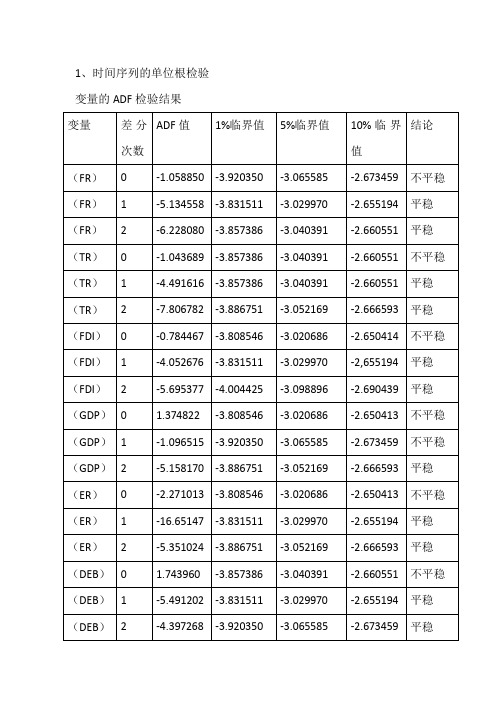
1、时间序列的单位根检验变量的ADF检验结果
说明:差分次数0代表未对数据进行差分;1代表数据的一阶差分;2代表数据的二阶差分
本文运用ADF(Augmented Dickey-Fuller test statistic)对时间序列进行单位根检验,检验Lg(FR)、Lg(TR)、Lg(FDI)、Lg(GDP)、Lg(ER)、Lg(DEB)、Lg(M2)的平稳性,并确定其单整阶数,单位根方程不包括常数项和时间序列项。
具体检验结果如上图所示。
从检验的结果来看,FR、TR、FDI、GDP、ER、DEB、M2均为原阶非平稳,FR、TR、FDI、ER、DEB、M2均为一阶平稳。
但是全体7组数据均为二阶单整。
2、时间序列的协整检验
通过ADF检验得知,FR、TR、FDI、GDP、ER、DEB、M2经过对数变换后都是二阶平稳序列,这是判定Lg(FR)、Lg(TR)、Lg(FDI)、Lg (GDP)、Lg(ER)、Lg(DEB)、Lg(M2)之间是否存在协整关系的前提条件。
adf检验拒绝原假设的条件

adf检验拒绝原假设的条件
ADF检验是判断时间序列数据是否具有平稳性的一种常用方法。
当ADF 检验的统计值小于所设定的临界值时,我们拒绝原假设,即认为该时间序列不存在单位根,即该时间序列是平稳的。
那么ADF检验拒绝原假设的条件有哪些呢?
一、样本容量
首先,在进行ADF检验时,需要确保时间序列的样本容量足够大。
如果样本容量过小,可能会导致统计结果不可靠。
一般来说,样本容量应当大于50,最好是100以上。
二、数据的平稳性
在进行ADF检验之前,需要先对数据进行平稳性检验。
如果数据本身已经是平稳的,那么进行ADF检验的结果显然没有什么意义。
因此,需要对数据进行一定程度的平稳性处理,例如差分或对数变换等。
三、临界值的选择
ADF检验中,临界值的选择非常重要。
不同的置信水平和不同阶数的ADF检验所对应的临界值也不同。
因此,在进行ADF检验时,需要特别注意临界值的选择,以保证检验结果的准确性。
四、模型的选择
在进行ADF检验时,需要选择合适的模型。
如果模型选择不当,可能会影响到检验结果的准确性。
一般来说,需要根据数据的特点选择相应的模型,例如ARIMA模型、VAR模型等。
综上所述,ADF检验拒绝原假设的条件主要包括:样本容量足够大、数据具有一定的平稳性、选择合适的临界值和模型。
只有在以上条件都满足的情况下,我们才能够对时间序列的平稳性进行有效的判断。
ADF检验通俗解释

ADF检验通俗解释
ADF检验,全名为Augmented DickeyFuller检验,是一种用于检验时间序列数据中单位根存在性的统计检验方法。
单位根表示时间序列数据具有非平稳性,即均值或方差可能随时间变化。
以下是对ADF检验的通俗解释:
单位根的概念:在时间序列中,如果一个变量具有单位根,意味着它的变化随时间的推移而保持在某一水平上。
这使得时间序列变量呈现出一种趋势,而不是随机波动。
平稳性的重要性:在统计学和经济学中,我们通常假设数据是平稳的,即它们的均值和方差在时间上是恒定的。
如果时间序列具有单位根,就可能导致违反这个平稳性假设。
ADF检验的目的:ADF检验的目的是确定一个时间序列是否具有单位根,从而判断该序列是否是平稳的。
如果序列是平稳的,就更容易应用许多统计方法,因为这些方法通常基于数据的稳定性。
检验的步骤:
提出假设:ADF检验的零假设是序列具有单位根,即非平稳。
备择假设是序列是平稳的。
进行统计检验:通过比较计算出的检验统计量与临界值,来判断是否拒绝零假设。
如果拒绝了零假设,就认为序列是平稳的。
ADF统计量的解释:ADF检验的统计量反映了单位根的存在性。
如果ADF统计量的值小于某个阈值(即临界值),那么我们可能拒绝
零假设,认为序列是平稳的。
总体而言,ADF检验是一种用于检验时间序列平稳性的工具,它帮助我们判断一个变量是否随时间保持在某一水平上,从而影响到我们在统计建模和分析中如何处理这个变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ADF检验
1数据输入出现以下窗口
输入起始年份和结束年份
点击ok出现以下窗口
在总窗口点击object----new objeck出现如下窗口
选择poold点击ok
在此窗口中另起一行输入n,代表年份点击sheet
输入y? x?后点击ok(两者之间空一格)
点击edit+/-输入数据
.对两组数据取对数,得新的数据:p=log(y),q=log(x)。
可在eviews中点击Genr输入p=log(y)可自动产生对数数列。
对两个时间序列分别做ADF检验。
1.eviews中选取时间序列P4,右键=》open。
在新的窗口中点击view=》unit root test。
2.ADF检验需要对3个模型依次检验,所以在unit root test窗口中先①选:level、trend and intercept。
然后确认=》得到
第一行是所得t值,下面3行是临界值。
t=-2.0665>临界值,因此非平稳。
因此要继续检验②:level、intercept,假设还是非平稳。
继续检验③:level none。
假设还是非平稳,则做一阶差分,即将level换成1st difference,将之前①②③从新来过,一旦t<临界值就可以停止了。
若level时,t值均大于临界值,则为非平稳序列。
若1st difference的一阶差分时,变为平稳的,就是1阶单整,记为I(1),依次类推。
