数字电子技术基础课后答案全解

合集下载

(全)数字电子技术基础课后问题详解夏路易

《数字电子技术基础教程》习题与参考答案（2010．1）第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。

（1）25；（2）43；（3）56；（4）78解：（1）25=（11001）2=（31）8=（19）16（2）43=（101011）2=（53）8=（2B）16（3）56=（111000）2=（70）8=（38）16（4）（1001110）2、（116）8、（4E）16【题1-2】将下列二进制数转换为十进制数。

（1）10110001；（2）10101010；（3）11110001；（4）10001000 解：（1）10110001=177（2）10101010=170（3）11110001=241（4）10001000=136【题1-3】将下列十六进制数转换为十进制数。

（1）FF；（2）3FF；（3）AB；（4）13FF解：（1）（FF）16=255（2）（3FF）16=1023（3）（AB）16=171（4）（13FF）16=5119【题1-4】将下列十六进制数转换为二进制数。

（1）11；（2）9C；（3）B1；（4）AF解：（1）（11）16=（00010001）2（2）（9C）16=（10011100）2（3）（B1）16=（1011 0001）2（4）（AF）16=（10101111）2【题1-5】将下列二进制数转换为十进制数。

（1）1110.01；（2）1010.11；（3）1100.101；（4）1001.0101 解：（1）（1110.01）2=14.25（2）（1010.11）2=10.75（3）（1001.0101）2=9.3125【题1-6】将下列十进制数转换为二进制数。

（1）20.7；（2）10.2；（3）5.8；（4）101.71解：（1）20.7=（10100.1011）2（2）10.2=（1010.0011）2（3）5.8=（101.1100）2（4）101.71=（1100101.1011）2【题1-7】写出下列二进制数的反码与补码（最高位为符号位）。

数字电子技术基础(第3版)练习答案

第1章数字电路基础1.1 (1001010)2=1×26+1×23+1×21=(74)10(111001)2=1×25+1×24+1×23+1×20=(57)10 1.2 (54)10=(110110)2 (47)10=(101111)2 5427 13 6 3 1 01……MSB 10 1 1 0……LSB2 4723 11 5 2 1 01……MSB 01 1 1 1……LSB1.3 (58A)16 =(0101 1000 1010)2=1×210+1×28+1×27+1×23+1×21=1024+256+128+10=(1418)10或(58A)16=5×162+8×161+10×160=(1418)10 (CE)16 =(1100 1110)2=27+26+14=128+64+14=(206)10 =(0010 0000 0110)8421BCD 1.4 a 1.5 c 1.6 c 1.7 (×) 1.8 (×) 1.9 (√)1.10 ① 数字信号：在幅值上，时间上离散的（间断的、不连续的脉冲）信号． ② 数字电路：产生、处理、传输、变换数字信号的电路称为数字电路．③ 数字电路的特点：a ）电路处于开关状态. 与二进制信号要求相一致，这两个状态分别用0和1两个数码表示；b ）数字电路的精度要求不高，只要能区分出两种状态就可以；c ）数字电路研究的问题是逻辑问题，一为逻辑分析，是确认给定逻辑电路的功能，二为逻辑设计，是找到满足功能要求的逻辑电路；d ）研究数字电路的方法是逻辑分析方法，其主要工具是逻辑代数．有代数法和卡诺图法等；e ）数字电路能进行逻辑运算、推理、判断，也能进行算术运算．算术运算也是通过逻辑运算实现的．1.11 ① 位置计数法：将表示数值的数码从左到右按顺序排列起来．它有三个要素a ）基数R ，是指相邻位的进位关系，十进制R =10，即逢十进一，二进制R =2，即逢二进一．b ）数码：表示数字的符号，十进制k i 从0~9共十个．二进制k i 是0和1，十六进制k i 从0~9~A~F 共十六个．c ）位权：数码处于不同位置代表不同的位权，用R i表示．以小数点前从右到左为i 的位号分别为0、1、2、3…，小数点后从左到右i 的位号从–1，–2，–3…来确定R i．② 按权展开式是将任何进制数表示为十进制数值公式，是系数乘位权的集合，即(N )10=i i i k R ∞=-∞⨯∑． 1.12 ① (3027)10=3×103+2×101+7×100② (827)=8×102+2×101+7×100③ (1001)2=1×23+1×20④ (11101)2=1×24+1×23+1×22+1×20⑤ (273)16=2×162+7×161+3×160⑥ (4B5)16=4×162+11×161+5×1601.13 ① (6)10=(110)2② (13)=(1101)2 ③ (39)10=(100111)2 ④ (47)10=(101111)2 1.14 ① (1011)2=(11)10② (110101)2=(53)10③ (4A)16=4×161+10×160=(74)10④ (37)16 =3×161+7×160=(55)101.15 ① (1010 1101)2=(010 101 101)2=(255)8=(1010 1101)2=(AD)16② (100101011)2=(100 101 011)2=(453)8 =(0001 0010 1011)2=(12B)16 ③ ()2=(010 110 001 010)2=(2612)8 =(0101 1000 1010)2=(58A)16 1.16 ① (78)16=(0111 1000)2=(1111000)2 ② (EC)16=(1110 1100)2=(1110 1100)2 ③ (274)16=(0010 0111 0100)2=(1001110100)2注：从1.15~1.16均用分组方法，即二进制3位一组可表示1位八进制数；二进制4位一组可表示1位十六进制数．1.17 A =(1011010)2；B =(101111)2； C =(1010100)2；D =(110)2 （1）① A +B =(10001001)2② A –B =(101011)2 1011010 + 101111 100010011011010 – 101111 101011 ③ C ×D =(111111000)2④ C ÷D =(1110)2 1010100× 110 0000000 1010100 + 1010100 1111110001110 110 1010100 110 1001 110 0110110 0（2）A=(1011010)2=(90)10B=(101111)2=(47)10①A+B=(137)10=(10001001)2②A–B=(43)10=(101011)2C=(1010100)2=(84)10D=(110)2=(6)10③C×D=(504)10=(111111000)2这说明十进制四则运算的法则在二进制四则运算中也完全适用，对其它进制也一样．1.18 ① [0]8421BCD=(238)10② [10001]8421BCD=(7951)10③ [0]8421BCD=(640)101.19 ①逻辑函数：反映因果关系的二值逻辑表达式．原因（条件）为逻辑自变量，结果为逻辑因变量，它们都只有两种状态0和1，用以反映存在不存在，成立不成立，所以它们之间的关系称为（二值）逻辑函数．②与逻辑：表明所有的条件都具备结果才会发生这样的基本逻辑关系为“与”逻辑（逻辑乘）．用式Y=A·B·C…表示．如学生成绩合格及不犯罪与能否毕业的关系即为与逻辑．③或逻辑关系：表明诸多条件中只要有1个以上具备结果就会发生，用Y=A+B+…表示．如去银行办理业务（储蓄），持存款证或持银行卡都可以办理．④非逻辑：是否定的因果关系，即条件具备结果就不能发生，用Y=A表示．如：征兵体检“有病”和“入伍”的关系就是非逻辑．“有病”存在，“入伍”就被否定了，有病不能入伍．1.21 由真值表可以写出最小项与或表达式．方法是将使函数Z为1的几种情况下输入变量的取值组合写成乘积项（变量取值为0写反变量因子，变量取值为1写原变量因子），然后将各乘积项相加，得Z=A B C+A B C+A BC+A B C+A B C1.23Z a=AB AB=A B+A B(摩根定理) =A⊕BZ b=B C AB+= (B⊕C)·AB=(BC+B C)AB=ABC1 1 1 0 1 1 1 1 1 11.24 见教材原文1.5节 1.25 a ）Z a =m (0, 2, 3, 5, 6) =A B C +A B C +A BC +A B C +AB C =A C +B C +A B +A B Cb ）Z b =m (0, 2, 7, 13, 15, 8, 10)=A B C D +A B C D +A BCD +A B C D +A B C D +AB C D +ABCD=B D +BCD +ABD1.26 （1）Z =A B +B +A B =A B +B =A +B （2）Z =A B C +A +B +C =A B C +A B C ++ =A B C +A B C =1（3）Z =AB ABC AB AB C +=++ =11AB AB C C +=+= （4）Z =A B CD +ABD +A C D=AD (B C +B +C ) =AD (C +B +C ) =AD ·1 =AD（5）Z =(A +B )(A CD +AD BC +)A B=(A +B )·A B ·(A CD +AD BC +) =0注：(A +B )A B =A A B +A B ·B =0（6）Z =AC (C D +A B )+BC (B AD CE ++)=0+BC ·(B +AD )·CE =BC (C +E )(B +AD ) =(BC E )(B +AD ) =BC E +BC E AD =BC E （7）Z =ABC +AC D +A C +CD=C (AB +A D +D )+A C =C (D +A )+A C =AC +CD +A C =A +CD（8）Z =A +B C +·(A +B +C )(A +B +C )=A +B C (A +B +C )(A +B +C ) ←展开=A +(A B C +B C )(A +B +C )←展开、吸收=A +B C（9）Z =B (A D +A D )+B (AD AD ABCE BC +++)=B (A D +A D )+B (A D +A D ) =A D +A D =A ⊕D（10）Z =AC +A C D +A B E F +B (D ⊕E )+BD E +B D E +BF=A (C +C D )+A B E F +BD E +B D E +BF =AC +AD +F (A B E +B )+B D E +BD E=AC +AD +A E F +BF +BD E +B D E1.27 求反函数Z 和对偶函数Z' （1）Z =AB +C （2）Z =(A +BC )C D Z =(A +B )·C Z =A ·(B +C )+C +DZ'=(A +B )·C Z' =A ·(B +C )+C +D（3）Z =()(+)A C A B AC BC ++ Z =(AC AB A C +++)·(B +C ) Z'=(AC AB A C +++)·(B +C )（4）Z =A D +AC +BCD +CZ =(A +D )·A C +·(B C D ++)·C Z'=(A +D )·A C +·(B C ++D )·C （5）Z =(AC +BD )ABC CD +Z =(A +C )·(B +D )+()()A B C C D +++ Z'=(A +C )·(B +D )+()()A B C C D +++ 1.28 用填卡诺图方法写最小项表达式（1）F 1=A BC +AC +B C =m (1, 3, 5, 7)=ABC +A BC +A B C +ABC（2）F 2=A +B +CD =m (3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15)=ABCD ABCD ABCD ABCD ABCD ABCD ++++++ABCD ABCD ABCD +++ABCD ABCD ABCD ABCD +++题1.28（1）F1卡诺图题1.28（2）F2卡诺图1.29 证明异或关系的正确性（1）A⊕0=A·0+A·0=A得证（2）A⊕1=A·1+A·1=A得证（3）A⊕A=A·A+A·A=0 得证（4）A⊕A=A·A+A·A=1 得证=A+A=1（5）(A⊕B)⊕C =(A⊕B)C+A B C⊕=ABC ABC ABC ABC+++=m(1, 2, 4, 7)A⊕(B⊕C) =A()⊕+⊕B C A B C=A(BC+BC)+A(B C+B C)=ABC ABC ABC ABC+++=m(1, 2, 4, 7)左式=右式，得证（6）右式AB⊕AC=AB·()()+=+++=+AC ABAC AB A C A B AC ABC ABC左式A(B⊕C)=A(B C+B C)=ABC ABC+得证（7）左式A⊕B=A B+AB=AB+AB=中式右式A⊕B⊕1=A⊕(B⊕1)=A⊕B=AB AB AB AB+=+=中式得证．1.30 用卡诺图法将函数化简为与或式．（1）Z ABC ABC ABC ABC=+++（2）1Z A B AB ABC BC=++++=题1.30（1）的卡诺图题1.30（2）的卡诺图（3）Z ABC AB AD C BD=++++填图后，可圈“0”得到Z=Z BCD再对Z取反，得到ZZ Z BCD B C D===++（4）Z(A、B、C)=m(0, 1, 2, 5, 6, 7)Z=AB AC BC++题1.30（3）的卡诺图题1.30（4）的卡诺图（5）Z(A、B、C、D)=m(0, 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 14)Z=B AC AD CD+++（6）Z(A、B、C、D)=m(0, 1, 2, 5, 8, 9, 10, 12, 14)Z=BC+BD+AD ACD+题1.30（5）的卡诺图题1.30（6）的卡诺图（7）Z=A C D ABCD ABCD++++，给定的约束条件为ABCD ABCD ABCD ABCD++++ 0ABCD ABCD+=Z=ACD ABCD ABCD++=ACD BCD AD++（8）Z=()CD A B ABC ACD⊕++给定的约束条件为AB+AC=0AC ACDZ=ABCD ABCD ABC ACD +++=BD ACD +题图1.30（7）的卡诺图题图1.30（8）的卡诺图（9）Z =m (0, 1, 2, 4)+d (3, 5, 6, 7)=1（10）Z =m (2, 3, 7, 8, 11, 14)+d (0, 5, 10, 15) Z =BD CD AC ++题图1.30（9）的卡诺图题图1.30（10）的卡诺图1.31 试用卡诺图法化简下列逻辑图 ① Z a =ABC ABC BC=ABC ABC BC ++ =ABC AC BC ++② Z b ：按逻辑图逐级写函数式，最后得出Z b =A ⊕C +(A +B )()BC AC BD AD +=A ⊕C +(A +B )()()B C AC BD A D +++=A ⊕C +(A +B )ABCD ↓展开为与或式 =A ⊕C +(A +B )(A +B +C +D )=A ⊕C +AB +A C +AD +AB +B +BC +BD=A C +A C +AD +B 填入卡诺图由卡诺图判断：Z b=AC+AC+AD+B该式已为最简与或式．题图1.31（a）的卡诺图题图1.31（b）的卡诺图1.32 化函数式为与非-与非式，并画出对应的逻辑图．（1）Z1 =AB+BC+AC=AB BC AC+++（2）Z2 =ABC AB BC AB=()++ABC AB BC AB=()++++ABC A B BC A BABC=1=ABC题图1.32（1）题图1.32（2）1.33 用最小项性质证明两个逻辑函数的与、或、异或运算可用卡诺图中对应的最小项分别进行与、或、异或运算来实现．解：命题所给出的结论是正确的．因为当输入变量的取值组合使某一最小项为1时，其他最小项均为0，若两函数相“与”，即Y=Y1·Y2，在对应最小项位置上Y1、Y2均为1时必然使Y为1；Y1Y2在该位置上有0，则0·0或1·0，Y必然为0，将所有对应最小项作乘运算就实现了Y=Y1·Y2运算．其他运算（或和异或）也是同样的道理．或运算是对应最小项相加；异或运算是对应最小项相异或．。

数字电子技术基础第三版课后习题解答与第章

13
【题3-2】解：),=(A田B) C=A⑥B+C}、=AB+(AB)C=AB+(AB+AB)C=AB+ABC+ABC=AB+BC+AC)=A B CY,=AB+(A B)C=AB+BC+AC两个电路功能相同，均为全加器。
14
(2) CDAB 00 01 11o0[ X0111 1 1 X10 1 1
A₃B₃…A₀B₀ 91A₃B₃…A₀B₀A<B.A>R低位 A=B74LS85Fg FxBF,A>B
A₂B₇…A₄B₄A=B74LS85FAn FxnF
【题3-9】解：连线图如图3-26所示。
图3 - 26
27
【题3-10】解：A=A₃A₂A₁A₀ 8421BCD 码 B=B₃B₂B₁B₀ 余3 BCD 码C=C₃C₂C₁C₀ 2421BCD 码 D=D₃D₂D₁D₀ 余 3 循环码(1)卡诺图如图3 - 27所示。B₃=A₃+A₂A₁+A₂A₀=A₂A₂A₁A₂A₀
2
A
B
A
Y'
2
0
0
0
1
0
0
1
1
0
0
1
0
0
0
1
1
1
0
1
)
3-2 解：(1)X=AB;Y=AB+AB=AB+AB;Z=AB。真值表如表3-10所示。表3-10
(2)实现1 位数值比较功能。
3
Y₀=X,④X 。 Y₀=Y₁X₀=X₂X₇X。若令 X₂=B₂ 、X₁=B₁ 、λ₀=B, 则当 K=1 时电路可正确地实现3位二进制码到3位循环码的转换，即有 Y₂=G₂ 、Y,=G₁ 、Y₀=G₀ 。若令X₂=G₂ 、X,=G₁、X₀=G₀, 则当 K=0 时，通过比较可明显看出，只要去掉一个反相器便可实现3位循环码到3位二进制码的转换，即有 Y₂=B₂ 、Y₁=B₁ 、Y₀=B₀。

【数字电子技术基础】课后习题集与参考答案解析

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。

（1）；（2）；（3）；（4）解：（1）=177（2）=170（3）=241（4）=136【题1-3】将下列十六进制数转换为十进制数。

（1）11；（2）9C；（3）B1；（4）AF解：（1）（11）16=（00010001）2（2）（9C）16=（）2（3）（B1）16=（1011 0001）2（4）（AF）16=（）2【题1-5】将下列二进制数转换为十进制数。

（1）；（2）；（3）；（4）解：（1）（）2=（2）（）2=（3）（）2=【题1-6】将下列十进制数转换为二进制数。

（1）；（2）；（3）；（4）解：（1）=（）2（2）=（）2（3）=（）2（4）=（）2【题1-7】写出下列二进制数的反码与补码（最高位为符号位）。

（1）01101100；（2）；（3）；（4）解：（1）01101100是正数，所以其反码、补码与原码相同，为01101100（2）反码为，补码为（3）反码为，补码为（4）反码为，补码为【题1-8】将下列自然二进制码转换成格雷码。

000；001；010；011；100；101；110；111解：格雷码：000、001、011、010、110、111、101、100【题1-9】将下列十进制数转换成BCD码。

数字电子技术基础习题册答案

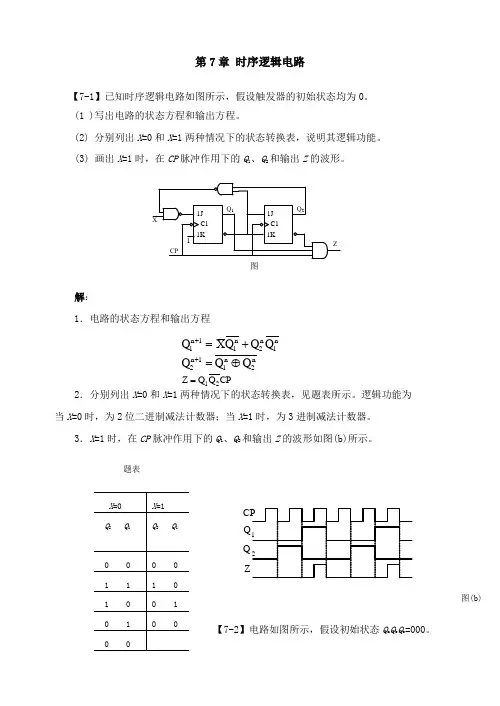
第7章时序逻辑电路【7-1】已知时序逻辑电路如图所示，假设触发器的初始状态均为0。

(1 )写出电路的状态方程和输出方程。

(2) 分别列出X =0和X =1两种情况下的状态转换表，说明其逻辑功能。

(3) 画出X =1时，在CP 脉冲作用下的Q 1、Q 2和输出Z 的波形。

1J 1KC11J 1KC1Q 1Q 2CPXZ1图解：1．电路的状态方程和输出方程n 1n2n 11n 1Q Q Q X Q +=+n 2n 11n 2Q Q Q ⊕=+ CP Q Q Z 21=2．分别列出X =0和X =1两种情况下的状态转换表，见题表所示。

逻辑功能为当X =0时，为2位二进制减法计数器；当X =1时，为3进制减法计数器。

3．X =1时，在CP 脉冲作用下的Q 1、Q 2和输出Z 的波形如图(b)所示。

题表Q Q Z图(b)【7-2】电路如图所示，假设初始状态Q a Q b Q c =000。

(1) 写出驱动方程、列出状态转换表、画出完整的状态转换图。

(2) 试分析该电路构成的是几进制的计数器。

Q c图解：1．写出驱动方程1a a ==K J ncn a b b Q Q K J ⋅== n b n a c Q Q J = n a c Q K = 2．写出状态方程n a 1n a Q Q =+ n a n a n a n a n c n a 1n b Q Q Q QQ Q Q +=+ nc n a n c n b n a 1n b Q Q Q Q Q Q +=+3．列出状态转换表见题表，状态转换图如图(b)所示。

图7.2(b)表7.2状态转换表CP na nbc Q Q Q 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 16 0 0 0n4．由FF a 、FF b 和FF c 构成的是六进制的计数器。

【7-3】在二进制异步计数器中，请将正确的进位端或借位端（Q 或Q ）填入下表解：题表7-3下降沿触发由 Q 端引出进位由Q 端引出借位触发方式加法计数器减法计数器上升沿触发由Q 端引出进位由Q 端引出借位【7-4】电路如图(a)所示，假设初始状态Q 2Q 1Q 0=000。

电子技术基础(数字)康华光课后答案

（A）
（B）
（C）
（D）
解：对于图题 3.1.12（a）所示的 CMOS 电路，当 EN =0 时， TP2 和TN 2 均导通，
TP1 和 TN1 构成的反相器正常工作，L= A ，当 EN =1 时，TP2 和TN 2 均截止，无论
A 为高电平还是低电平，输出端均为高阻状态，其真值表如表题解 3.1.12 所示，该电路是低电平使能三态非门，其表示符号如图题解 3.1.12（a）所示。
A
L
00Βιβλιοθήκη 1010
1
0
1
1
高阻
3.1.12（a）
A
L
0
0
0
0
1
1
1
0
高阻
1
1
高阻
3.1.12（b）
EN A
0
0
L 高阻
0
1
高阻
1
0
0
1
1
1
3.1.12（c
A
L
0
0
1
0
1
0
1
0
高阻
1
1
高阻
3.1.12（d）
3.2.2 为什么说 TTL 与非门的输入端在以下四种接法下，都属于逻辑 1：（1）输入端悬空；（2）输入端接高于 2V 的电源；（3）输入端接同类与非门的输出高电压 3.6V；（4）输入端接 10kΩ 的电阻到地。解：（1）参见教材图 3.2.4 电路，当输入端悬空时，T1 管的集电结处于正偏，Vcc 作用于 T1 的集电结和 T2，T3 管的发射结，使 T2，T3 饱和，使 T2 管的集电极电位 Vc2=VcEs2+VBE3=0.2+0.7=0.9V ，而 T4 管若要导通 VB2=Vc2≥VBE4+VD=0.7+0.7=1.4V，故 T4

数字电子技术基础_第四版_阎石_课后答案[1-6章]

R L (min)
=
Vcc − VOL I LM − m′I IL
= 5 − 0.4 8 − 3× 0.4
≈ 0.68K
∴ 0.68K < RL < 5K
2.8 解：
当VI = VIH时，T必须满足截止条件：I B＝0
同时要满足 Vcc − 0.1 − VOL −VBE
R1
R2 + R3
≤ I LM
(1)Y=A+B
(3)Y=1
(2)Y = ABC + A + B +C 解：Y = BC + A + B +C =C + A + B +C =（1 A＋A＝1）
(5)Y=0
(4)Y = ABCD + ABD + ACD 解：Y = AD(BC + B + C ) = AD(B + C + C) = AD
(4)Y = ABCD+ ABCD+ ABCD+ ABC D+ ABCD + ABCD + ABCD + ABCD (5)Y = LM N + LMN + LMN + LMN + L M N + LMN
1.12 将下列各函数式化为最大项之积的形式 (1)Y = ( A + B + C )( A + B + C)( A + B + C )
=
− 10 5.1 + 20
× 5.1 =
−2V
∴T截止 vo ≈ 10V
当
v
i＝5V时，
I
＝

数字电子技术基础课后习题及参考答案

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。

（1）1110.01；（2）1010.11；（3）1100.101；（4）1001.0101解：（1）（1110.01）2=14.25（2）（1010.11）2=10.75（3）（1001.0101）2=9.3125【题1-6】将下列十进制数转换为二进制数。

数字电子技术基础第四章习题及参考答案

数字电子技术基础第四章习题及参考答案第四章习题1．分析图4-1中所示的同步时序逻辑电路，要求：（1）写出驱动方程、输出方程、状态方程；（2）画出状态转换图，并说出电路功能。

CPY图4-12．由D触发器组成的时序逻辑电路如图4-2所示，在图中所示的CP脉冲及D作用下，画出Q0、Q1的波形。

设触发器的初始状态为Q0=0，Q1=0。

D图4-23．试分析图4-3所示同步时序逻辑电路，要求：写出驱动方程、状态方程，列出状态真值表，画出状态图。

CP图4-34．一同步时序逻辑电路如图4-4所示，设各触发器的起始状态均为0态。

（1）作出电路的状态转换表；（2）画出电路的状态图；（3）画出CP作用下Q0、Q1、Q2的波形图；（4）说明电路的逻辑功能。

图4-45．试画出如图4-5所示电路在CP波形作用下的输出波形Q1及Q0，并说明它的功能（假设初态Q0Q1=00）。

CPQ1Q0CP图4-56．分析如图4-6所示同步时序逻辑电路的功能，写出分析过程。

Y图4-67．分析图4-7所示电路的逻辑功能。

（1）写出驱动方程、状态方程；（2）作出状态转移表、状态转移图；（3）指出电路的逻辑功能，并说明能否自启动；（4）画出在时钟作用下的各触发器输出波形。

CP图4-78．时序逻辑电路分析。

电路如图4-8所示：（1）列出方程式、状态表；（2）画出状态图、时序图。

并说明电路的功能。

1C图4-89．试分析图4-9下面时序逻辑电路：（1）写出该电路的驱动方程，状态方程和输出方程；（2）画出Q1Q0的状态转换图；（3）根据状态图分析其功能；1B图4-910.分析如图4-10所示同步时序逻辑电路，具体要求：写出它的激励方程组、状态方程组和输出方程，画出状态图并描述功能。

1Z图4-1011．已知某同步时序逻辑电路如图4-11所示，试：（1）分析电路的状态转移图，并要求给出详细分析过程。

（2）电路逻辑功能是什么，能否自启动？（3）若计数脉冲f CP频率等于700Hz，从Q2端输出时的脉冲频率是多少?CP图4-1112．分析图4-12所示同步时序逻辑电路，写出它的激励方程组、状态方程组，并画出状态转换图。

数字电子技术基础康华光第五版答案

第一章数字逻辑习题1．1 数字电路与数字信号图形代表的二进制数1．1．4 一周期性数字波形如图题所示，试计算：（1）周期；（2）频率；（3）占空比例MSB LSB0 1 2 11 12 （ms）解：因为图题所示为周期性数字波，所以两个相邻的上升沿之间持续的时间为周期，T=10ms 频率为周期的倒数，f=1/T=1/=100HZ占空比为高电平脉冲宽度与周期的百分比，q=1ms/10ms*100%=10%数制将下列十进制数转换为二进制数，八进制数和十六进制数（要求转换误差不大于24（2）127 （4）解：（2）（127）D= 27 -1=（）B-1=（1111111）B=（177）O=（7F）H（4）（）D=B=O=H二进制代码将下列十进制数转换为 8421BCD 码：（1）43 （3）解：（43）D=（01000011）BCD试用十六进制写书下列字符繁荣ASCⅡ码的表示：P28（1）+ （2）@ （3）you (4)43解：首先查出每个字符所对应的二进制表示的ASCⅡ码，然后将二进制码转换为十六进制数表示。

（1）“+”的ASCⅡ码为 0101011，则（00101011）B=（2B）H（2）@的ASCⅡ码为 1000000,(01000000)B=(40)H(3)you 的ASCⅡ码为本 1111001,1101111,1110101,对应的十六进制数分别为 79,6F,75(4)43 的ASCⅡ码为 0110100,0110011,对应的十六紧张数分别为 34,33逻辑函数及其表示方法在图题 1. 中，已知输入信号 A，B`的波形，画出各门电路输出 L 的波形。

解: (a)为与非， (b)为同或非，即异或第二章逻辑代数习题解答用真值表证明下列恒等式(3)A⊕ =B AB AB+ （A⊕B）=AB+AB由最右边2栏可知，与+AB的真值表完全相同。

用逻辑代数定律证明下列等式(3)A+ABC ACD C D E A CD E++ +( ) = + +解：A+ABC ACD C D E++ +( )=A(1+BC ACD CDE)+ += +A ACD CDE+= +A CD CDE+ = +A CD+ E用代数法化简下列各式 (3)ABC B( +C)解：ABCB( +C)= + +(A B C B C)( + )=AB AC BB BC CB C+ + + + +=AB C A B B+ ( + + +1)=AB C+(6)(A+ + + +B A B AB AB) ( ) ( )()解：(A+ + + +B A B AB AB) () ( )( )= A B?+ A B?+(A+ B A)(+ B)=AB(9)ABCD ABD BCD ABCBD BC+ + + + 解：ABCD ABD BCD ABCBD BC+ + + +=ABC D D ABD BC D C( + +) + ( + ) =B AC AD C D( + + + ) =B A C A D( + + + ) =B A C D( + + ) =AB BC BD+ +画出实现下列逻辑表达式的逻辑电路图，限使用非门和二输入与非门( ))ABCD AB AC+已知函数L（A，B，C，D）的卡诺图如图所示，试写出函数L的最简与或表达式用卡诺图化简下列个式（1）ABCD ABCD AB AD ABC+ + + +解：ABCD ABCD AB AD ABC+ + + +=ABCD ABCD ABC C D D AD B B C C ABC D D++ ( + )( + +)( + )( + +)( + )=ABCD ABCD ABCD ABCD ABCD ABCD ABCD+ + + + + + （6）L A B C D( , , , )=∑m(0,2,4,6,9,13)+∑d(1,3,5,7,11,15)L= +A D（7）L A B C D( , , , )=∑m(0,13,14,15)+∑d(1,2,3,9,10,11)L AD AC AB= + +已知逻辑函数L AB BC CA=+ + ，试用真值表,卡诺图和逻辑图（限用非门和与非门）表示解:1>由逻辑函数写出真值表A B C L0 0 0 00 0 1 10 1 0 10 1 1 11 0 0 11 0 1 11 1 0 11 1 1 02>由真值表画出卡诺图LABBCAC用摩根定理将与或化为与非表达式L = AB + BC + AC = AB BC AC? ?4>由已知函数的与非-与非表达式画出逻辑图第三章习题MOS 逻辑门电路根据表题所列的三种逻辑门电路的技术参数，试选择一种最合适工作在高噪声环境下的门电路。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第3章逻辑代数及逻辑门【3-1】填空 1、与模拟信号相比，数字信号的特点是它的离散性。一个数字信号只有两种取值分别表示为0 和1 。 2、布尔代数中有三种最基本运算：与、或和非，在此基础上又派生出五种基本运算，分别为与非、或非、异或、同或和与或非。 3、与运算的法则可概述为：有“0”出 0 ，全“1”出 1；类似地或运算的法则为有”1”出”1”，全”0”出”0” 。

4、摩根定理表示为：AB=AB ；AB=AB。

5、函数表达式Y=ABCD，则其对偶式为Y=()ABCD。 6、根据反演规则，若Y=ABCDC，则Y()ABCDC 。 7、指出下列各式中哪些是四变量A B C D的最小项和最大项。在最小项后的（）里填入mi，在最大项后的（）里填入Mi，其它填×（i为最小项或最大项的序号）。

(1) A+B+D (× ); (2) ABCD (m7 ); (3) ABC ( × )

(4)AB(C+D) (×); (5) ABCD (M9 ) ; (6) A+B+CD (× ); 8、函数式F=AB+BC+CD写成最小项之和的形式结果应为m(3,6,7,11,12,13,14,15),写成最大项之积的形式结果应为M( 0,1,2,4,5,8,9,10 ) 9、对逻辑运算判断下述说法是否正确，正确者在其后（）内打对号，反之打×。（1）若X+Y=X+Z，则Y=Z；( × ) （2）若XY=XZ，则Y=Z；( × ) （3）若XY=XZ，则Y=Z；(√ ) 【3-2】用代数法化简下列各式

(1) F1 =1ABCAB (2) F2 =ABCDABDACDAD

(3)3FACABCACDCDACD (4) 4()()FABCABCABCABC

【3-3】用卡诺图化简下列各式 (1) 1FBCABABCABC (2) 2FABBCBCAB

(3) 3FACACBCBCABACBC (4) 4FABCABDACDCDABCACDAD 或ABACBC (5) 5FABCACABDABACBD (6) 6FABCDABCADABCABCCD

(7) 7FACABBCDBDABDABCDABDBD (8) 8 FACACBDBDABCDABCDABCDABCD

(9) 9()FACDBCDACDABCDCDCD (10)F10=10FACABBCDBECDECABACBDEC 【3-4】用卡诺图化简下列各式 (1) P1(A,B,C)=(0,1,2,5,6,7)mABACBC

(2) P2(A,B,C,D)=(0,1,2,3,4,6,7,8,9,10,11,14)mACADBCD (3)P3(A,B,C,D)=(0,1,,4,6,8,9,10,12,13,14,15)mABBCADBD (4) P4 (A,B,C,D)=17MMABCBCD• 【3-5】用卡诺图化简下列带有约束条件的逻辑函数（1）1,,,(3,6,8,9,11,12)(0,1,2,13,14,15)()dPABCDmACBDBCDACD或

(2) P2(A,B,C,D)=(0,2,3,4,5,6,11,12)(8,9,10,13,14,15)dmBCBCD (3) P3 =()ACDABCDABCDADACDBCDABD或 AB+AC=0 (4) P4 =ABABCDABCD （A B C D为互相排斥的一组变量，即在任何情况下它们之中不可能两个同时为1）【3-6】已知: Y1 =ABACBD Y2 =ABCDACDBCDBC 用卡诺图分别求出YY12， YY12， YY12。解：先画出Y1和Y2的卡诺图，根据与、或和异或运算规则直接画出YY12，YY12，YY12的卡诺图，再化简得到它们的逻辑表达式： YY12=ABDABCCD

YY12=ABCBD YY12=ABCDABCBCDACD 第4章集成门电路【4-1】填空 1．在数字电路中，稳态时三极管一般工作在开关（放大，开关）状态。在图中，若UI<0，则晶体管截止（截止，饱和），此时UO= （5V，，）；欲使晶体管处于饱和状态，UI需满足的

条件为 b （>0；b.cCCbI7.0RVRU；c. CCIbc0.7VURR）。在电路中其他参数不变的条件下，仅Rb减小时，晶体管的饱和程度加深（减轻，加深，不变）；仅Rc减小时，饱和程度减轻（减轻，加深，不变）。图中C的作用是加速（去耦，加速，隔直）。

+5VRcRbuiuoTC+3V

G1G2A

图图 2．由TTL门组成的电路如图所示，已知它们的输入短路电流为IS＝，高电平输入漏电流IR＝40μA。试问：当A=B=1时，G1的灌（拉，灌）电流为；A=0时，G1的拉（拉，

灌）电流为160A。 3．图中示出了某门电路的特性曲线，试据此确定它的下列参数：输出高电平UOH=3V ；输出低电平UOL= ；输入短路电流IS= ；高电平输入漏电流IR= ；阈值电平UT= ；开门电平UON= ；关门电平UOFF= ；低电平噪声容限UNL= ；高电平噪声容限UNH= ；最大灌电流IOLMax= 15mA ；扇出系数No= 10 。

OUO

0.3V1.5V

UOH

IOH

5mA-1.4

0.02 mAII

O15mA

0.3V

UOL

OmAU

图 4．TTL门电路输入端悬空时，应视为高电平（高电平，低电平，不定）；此时如用万用表测量输入端的电压，读数约为（，0V，）。 5．集电极开路门（OC门）在使用时须在输出与电源（输出与地，输出与输入，输出与电源）之间接一电阻。 6．CMOS门电路的特点：静态功耗极低（很大，极低）；而动态功耗随着工作频率的提高而增加（增加，减小，不变）；输入电阻很大（很大，很小）；噪声容限高（高，低，等）于TTL门【4-2】电路如图(a)～(f)所示，试写出其逻辑函数的表达式。 CMOSAF1

10k

TTLAF2100BCMOSAF3

TTLAF4

100kB

TTLCMOS

AF5

10kB

(a)(b)(c)

(f)(e)(d)



AF6

100kB

 图解：(a) 1FA (b) 21F (c) 3FAB

(d) 4FAB (e) 51F (f) 6FB

【4-3】图中各电路中凡是能实现非功能的要打对号，否则打×。图(a)为TTL 门电路，图(b)为CMOS门电路。解：

A5VA

100A

1M√√√××

(a)

A1MA

BTG

VADD××××

(b) 图【4-4】要实现图中各TTL门电路输出端所示的逻辑关系各门电路的接法是否正确如不正确，请予更正。解： CBACBAF

CDABF

(a)(b)

1ABFX

AΩ100k

XBXAFB

(c)(d)

BACBAF

CDABFC

RCCV××

×√

（改为10Ω）

图【4-5】TTL三态门电路如图(a)所示，在图(b)所示输入波形的情况下，画出F端的波形。

FAB

C A

BC (a) (b) 图

解：当1C时，ABF；当0C时，BABAF。于是，逻辑表达式 CBACABF)( F的波形见解图所示。

ABCF