导热系数预习报告(完整版)
准稳态法测不良导体的导热系数和比热预习报告
准稳态法测不良导体的导热系数和比热预习报告实验目的1. 了解准稳态法测量不良导体的导热系数和比热的原理,并通过快速测量学习掌握该方法;2. 掌握使用温差电偶测量温度的方法。
一. 实验原理1. 热传导物体相邻部分间存在温度差,在各部分之间不发生相对位移的前提下,仅依靠分子、原子及自由电子等微观粒子的热运动而产生的热量传递成为热传导。
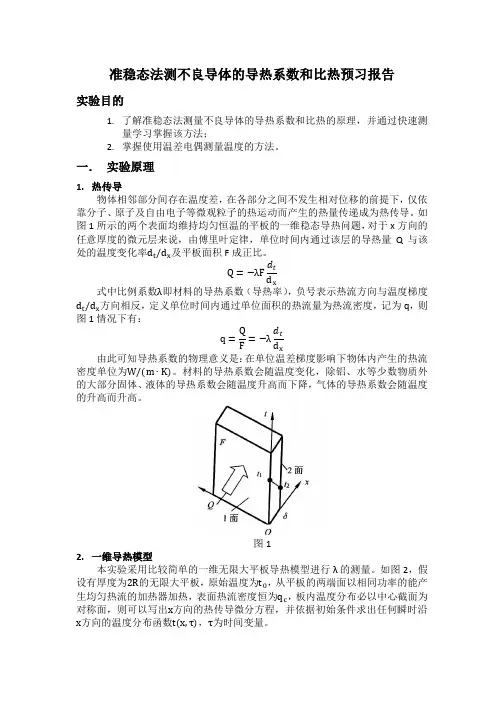
如图1所示的两个表面均维持均匀恒温的平板的一维稳态导热问题,对于x 方向的任意厚度的微元层来说,由傅里叶定律,单位时间内通过该层的导热量Q 与该处的温度变化率d t /d x 及平板面积F 成正比。
Q =−λF d tx式中比例系数λ即材料的导热系数(导热率),负号表示热流方向与温度梯度d t /d x 方向相反,定义单位时间内通过单位面积的热流量为热流密度,记为q ,则图1情况下有:q =Q =−λd t x由此可知导热系数的物理意义是:在单位温差梯度影响下物体内产生的热流密度单位为W/(m ∙K)。
材料的导热系数会随温度变化,除铝、水等少数物质外的大部分固体、液体的导热系数会随温度升高而下降,气体的导热系数会随温度的升高而升高。
图12. 一维导热模型本实验采用比较简单的一维无限大平板导热模型进行λ的测量。
如图2,假设有厚度为2R 的无限大平板,原始温度为t 0,从平板的两端面以相同功率的能产生均匀热流的加热器加热,表面热流密度恒为q c ,板内温度分布必以中心截面为对称面,则可以写出x 方向的热传导微分方程,并依据初始条件求出任何瞬时沿x 方向的温度分布函数t(x,τ),τ为时间变量。
3.热传导方程及求解∂t(x,τ)∂τ=a∂2t(x,τ)∂x(0<x<R,τ>0) (式4)初始条件t(x,τ)τ=0=t0(式5)边界条件q c=λ∂t(x,τ)∂x x=R(式6)λ∂t(x,τ)∂x x=0=0(式7)式中a=λ/cρ为热扩散率(或称热扩散系数),单位为m2/s,c为比热容,单位为J/(kg∙K),ρ为密度,单位为kg/m3。
导热系数实验报告..(20190516150337)

导热系数实验报告..(20190516150337)一、【实验目的】用稳态法测定金属、空气、橡皮的导热系数。
二、【实验仪器】导热系数测定仪、铜-康导热电偶、游标卡尺、数字毫伏表、台秤(公用)、杜瓦瓶、秒表、待测样品(橡胶盘、铝芯)、冰块T 1ABC冰水混合物T 2测1测1 测2表风扇220V电源110V 输入数字电压表调零测2导热系数测定仪FD-TX-FPZ-II 导热系数电压表图4-9-1 稳态法测定导热系数实验装置三、【实验原理】1、良导体(金属、空气)导热系数的测定根据傅里叶导热方程式,在物体内部,取两个垂直于热传导方向、彼此间相距为h、温度分别为θ1、θ2 的平行平面(设θ1>θ2),若平面面积均为S,在t 时间内通过面积S的热量Q 免租下述表达式:Q ( )St h(3-26-1)式中,Qt为热流量;即为该物质的导热系数,在数值上等于相距单位长度的两平面的温度相差1 个单位时,单位时间内通过单位面积的热量,其单位是W (m K )。
在支架上先放上圆铜盘P,在P 的上面放上待测样品B,再把带发热器的圆铜盘 A 放在B 上,发热器通电后,热量从 A 盘传到 B 盘,再传到P 盘,由于A,P 都是良导体,其温度即可以代表B 盘上、下表面的温度θ1、θ2,θ1、θ2 分别插入 A 、P 盘边缘小孔的热电偶E 来测量。
热电偶的冷端则浸在杜瓦瓶中的冰水混合物中,通过“传感器切换”开关G,切换A 、P 盘中的热电偶与数字电压表的连接回路。
由式(3-26-1)可以知道,单位时间内通过待测样品 B 任一圆截面的热流量为Q t ( 1 )2hB2RB(3-26-2)式中,R B 为样品的半径,h B 为样品的厚度。
当热传导达到稳定状态时,θ1 和θ2 的值不变,遇事通过 B 盘上表面的热流量与由铜盘P 向周围环境散热的速率相等,因此,可通过铜盘P 在稳定温度T2 的散热速率来求出热流量Qt。
实验中,在读得稳定时θ1 和θ2 后,即可将B 盘移去,而使 A 盘的底面与铜盘P 直接接触。
对流传热系数与导热系数的测定

mV
蒸汽管外壁温度
℃
套管外壁电位差值
mV
套管外壁温度
℃
⑶实验结果
表四裸管实验结果
冷凝液流量
kg/s
总传热量
W
总传热面积
传热推动力
℃
对流传热系数
(实验值)
W/(m2·℃)
定性温度
℃
定性尺寸
m
空气密度
kg/m3
空气粘度
Pa·s
空气比热容
J/(kg·℃)
空气导热系数
W/(m·℃)
空气体积膨胀系数
1、对流传热系数与导热系数测定实验数据及实验结果列表
(1)操作参数
蒸汽压力计读数R=mm(水柱)
蒸汽压强(绝压)P= Pa
蒸汽温度T=℃
蒸汽冷凝热r=kJ/kg
⑵裸管、固体材料保温管和空气夹层保温管的实验数据。
表一裸管实验数据
实验序号
1
2
室温℃
冷凝液体积mL
受液时间s
冷凝液温度℃
冷凝液密度kg/m³
1/℃
普朗特数
Pr
格拉晓夫数
Gr
Pr·Gr
对流传热系数
(计算值)
W/(m2·℃)
表五固体材料保温管实验结果
冷凝液流量
kg/s
热损失量
W
传热推动力
℃
导热系数
W/(m·℃)
表六空气夹层保温管实验结果
冷凝液流量
kg/s
热损失量
W
传热推动力
℃
等效导热系数
W/(m·℃)
定性温度
℃
定性尺寸
空气密度
kg/m3
空气粘度
综合导热系数实验报告

综合导热系数实验报告实验目的本次实验旨在测量材料的综合导热系数,以了解材料的导热性能,并通过实验数据对比不同材料的导热性能。
实验原理综合导热系数是指材料在单位面积上,单位时间内通过的热量与温度差之比。
可以通过实验测量导热系数,即在相同条件下,测量不同材料的热传导过程,从而得到材料的导热性能。
实验中,我们使用一个导热仪,该仪器由一个热源和两个温度传感器组成,可以测量材料上下表面的温度差,以及通过的热量。
通过对多个材料进行实验,我们可以得到不同材料的导热系数,并进一步了解材料的导热性能。
实验步骤1. 准备不同材料的样品,样品的尺寸和质量应相同,以保证实验条件的一致性。
2. 将待测样品固定在导热仪上,并保证样品与传感器的接触良好,以减小传热阻尼。
3. 打开导热仪,设定初始温度,确保温度稳定在设定值。
4. 记录样品上下表面的温度差,以及通过的热量。
5. 更换待测材料,重复步骤2-4,直到所有材料实验完成。
6. 对实验数据进行处理和分析,计算每个材料的导热系数。
实验数据我们选取了三种常见材料进行实验:铝、铜和玻璃。
实验数据如下表所示:材料温度差()通过的热量(J)-铝10 200铜8 160玻璃 5 100数据处理与分析根据实验数据,我们可以计算每种材料的导热系数。
导热系数(λ)的计算公式如下:λ= (Q ×d) / (A ×ΔT)其中,Q为通过的热量,d为样品的厚度,A为样品的横截面积,ΔT为样品上下表面的温度差。
假设样品的厚度为1cm,横截面积为1平方厘米,则可以得到以下结果:铝的导热系数:λ= (200 ×0.01) / (1 ×10) = 0.2 W/m·K铜的导热系数:λ= (160 ×0.01) / (1 ×8) = 0.2 W/m·K玻璃的导热系数:λ= (100 ×0.01) / (1 ×5) = 0.2 W/m·K根据计算结果可知,铝、铜和玻璃的导热系数均为0.2 W/m·K。
导热系数测定实验报告

导热系数测定实验报告导热系数,作为材料的一项重要物理性质,能够评估材料传导热量的能力。
通过测定导热系数,可以了解材料的导热性能以及在不同工况下的散热能力。
本实验旨在通过实际操作测定不同材料的导热系数,并分析结果对比。
一、实验目的本实验的主要目标是测定不同材料的导热系数,了解热量在材料之间的传导规律,并比较不同材料的导热性能。
通过实验数据的处理和分析,探究导热系数与材料性质之间的关系。
二、实验装置和方法实验所用的装置包括热导率仪和不同材料的试样。
热导率仪由热源、测温探头和显示器组成,用于测量不同材料在不同温度下的热传导情况。
实验的具体步骤如下:1. 准备试样:根据需要测量的材料种类和厚度,制备相应的试样切片。
2. 测量温度:先将测温探头放在设定温度的热源上,进行温度校准,确保准确测量。
3. 安装试样:将试样放置在热导率仪的传热平台上,保持试样与测温探头的接触完全。
4. 测量实验:通过控制热源的温度,使其保持在恒定状态。
记录热导率仪上显示的温度变化情况,并计算得出试样的导热系数。
三、实验数据处理和分析在实验中,我们选择了金属、塑料和木材作为不同材料的代表,分别测量了它们的导热系数,并进行对比分析。
通过实验数据的处理和分析,我们可以得到各材料的导热系数数值。
可以发现,金属材料的导热系数相对较高,这与金属的导电性质有关。
塑料材料的导热系数比金属低,这主要是由于塑料材料结构中有许多绝缘空隙的存在。
木材的导热系数相对较低,并且呈现出随纤维方向变化的趋势,这是因为木材的导热性能与其组织结构有着密切的关系。
导热系数除了与材料的物性有关外,还受到温度的影响。
在不同温度下,导热系数可能会发生变化。
实验中我们选择了不同温度下的测量点,以了解导热系数与温度之间的变化规律。
通过实验数据的分析,我们可以得出导热系数随温度的变化呈现出一定的规律性,不同材料的导热系数随温度变化的趋势可能不同。
四、实验结果与讨论根据实验数据的处理和分析,得出了不同材料在不同温度下的导热系数。
导热系数测定实验报告

导热系数测定实验报告导热系数测定实验报告导热系数是描述物质传导热量能力的物理量,对于研究材料的热传导性质具有重要意义。
本实验旨在通过测定不同材料的导热系数,探究材料的热传导特性,并分析实验结果的意义。
实验仪器与原理本实验使用的仪器主要包括导热系数测定仪、测温仪、样品夹和样品。
导热系数测定仪是一种常用的实验设备,可以测量材料的导热系数。
测温仪则用于测量样品的温度变化。
样品夹用于固定样品,保证测试的准确性。
实验步骤1. 首先,将待测材料切割成相同大小的样品,并清洁表面,确保样品的质量和纯度。
2. 将样品夹住,确保样品与夹具之间没有空隙,以免影响测量结果。
3. 将样品夹放入导热系数测定仪中,并调整仪器参数,确保实验的准确性。
4. 开始实验后,观察样品的温度变化,记录下每个时间点的温度数据。
5. 根据实验数据,计算出样品的导热系数,并进行分析和比较。
实验结果与分析通过实验测得的数据,我们可以计算出不同材料的导热系数,并进行比较。
导热系数的大小反映了材料的热传导能力,数值越大表示材料的热传导能力越强。
在实验中,我们选取了几种常见的材料进行测试,包括金属、塑料和绝缘材料。
结果显示,金属材料的导热系数通常较高,而塑料和绝缘材料的导热系数较低。
这一结果与我们的常识相符。
金属材料由于其内部电子的自由运动,具有较高的导热性能。
而塑料和绝缘材料由于其分子结构的特殊性,导热系数较低。
此外,通过实验还可以发现,导热系数与温度之间存在一定的关系。
随着温度的升高,导热系数通常会增大。
这是因为高温下,物质内部的分子运动加剧,热传导能力增强。
实验的局限性与改进尽管本实验得到了一些有意义的结果,但仍然存在一些局限性。
首先,实验中的样品大小和形状可能对测量结果产生影响。
因此,为了提高实验的准确性,可以选择更多的样品进行测试,并进行多次重复实验。
其次,实验中没有考虑到材料的厚度对导热系数的影响。
在实际应用中,材料的厚度也会对热传导性能产生影响。
导热系数的测量实验报告
导热系数的测量实验报告一、实验目的:1.了解导热系数的概念和定义。
2.掌握导热系数的测量方法。
3.熟悉导热系数的影响因素。
二、实验仪器及材料:1.导热系数测量仪:包括加热装置、温度计、样品支架等。
2.导热系数标准样品:如铜、铝等。
3.测温仪:用于测量样品温度。
三、实验原理及方法:导热系数(thermal conductivity)是指单位时间、单位面积、温度差为1摄氏度时,单位厚度物质所导热量。
常用单位为W/(m·K)。
1.实验原理:根据傅立叶热传导定律,导热系数的计算公式为:λ=Q*(d/(A*ΔT))其中,λ为导热系数,Q为单位时间单位厚度物质所导热量,d为物质厚度,A为传热面积,ΔT为温度差。
2.实验方法:(1)测量导热系数仪的加热功率和样品厚度。
(2)连接加热装置和温度计,将样品放在样品支架上。
(3)将样品置于恒定温度环境下,记录样品初始温度。
(4)通过调节加热功率,使样品温度升高一定值,记录此时的时间。
(5)根据测温仪结果计算出样品的导热系数。
四、实验步骤:1.根据实验原理设置导热系数仪的参数。
2.将所选样品(如铝)放在样品支架上,并记录样品的厚度。
3.连接加热装置和温度计,校准温度计。
4.将样品置于恒定温度环境中,记录样品的初始温度。
5.通过调节加热功率,使样品温度升高一定值(如10℃),记录此时的时间。
6.根据测温仪结果,计算出样品的导热系数。
7.重复2-6步骤,三次测量后取平均值。
五、实验数据及结果:样品:铝厚度:2.5cm初始温度:25℃升温时间:300s根据计算公式,可得到样品的导热系数为:λ=Q*(d/(A*ΔT))=Q*(0.025/(1*10))取三次实验的结果求平均值,最终得到样品铝的导热系数为0.15W/(m·K)。
六、误差分析:1.温度测量误差:由于温度计精度有限,测量结果可能存在误差。
2.加热功率测量误差:加热装置的功率测量也可能存在误差,会影响导热系数测量的准确性。
导热系数测定实验报告
导热系数测定实验报告实验目的:测定给定材料的导热系数。
实验原理:导热系数是描述材料导热能力的物理量,可以通过测量材料的热传导过程来确定。
传导过程中,热量沿着温度梯度从高温区传导到低温区。
根据热传导定律,导热流密度Q/t正比于温度梯度dT/dx,即Q/t = -k(dT/dx),其中k为导热系数。
在本实验中,我们采用平板法进行导热系数的测量。
在稳态条件下,选取一块厚度均匀的材料样品,在两侧施加恒定的温度差,通过测量材料两侧的温度来计算导热系数。
实验器材:1. 导热系数测定设备(包括导热板、温度传感器、温度控制仪等)2. 材料样品3. 温度计4. 计时器实验步骤:1. 准备工作:打开导热系数测定设备,确保设备正常工作。
2. 校准温度传感器:将温度传感器放入恒温水槽中,根据设备要求进行校准。
3. 安装材料样品:将材料样品放置在导热板上,并紧密密封以确保无热能损失。
4. 施加温度差:通过控制仪调节导热板两侧的温度,使其形成恒定的温度差。
5. 记录温度数据:使用温度传感器测量样品两侧的温度,并记录数据。
6. 测量时间:使用计时器测量样品温度变化的时间t。
7. 计算导热系数:利用测得的温度数据及时间t,根据导热定律计算导热系数k。
实验结果与分析:根据实验所得的温度数据及时间信息,计算出材料的导热系数k,并与已知数据进行比较。
分析测量误差的来源,并讨论可能的改进方法。
结论:本实验通过平板法测定了给定材料的导热系数,并得出了相应的结果。
通过分析实验误差与改进方法,进一步提高了实验结果的准确性。
实验存在的问题与建议:1. 实验过程中,温度传感器的校准可能存在误差,建议校准过程更加细致。
2. 材料样品的密封性可能不够好,导致热能损失,建议对样品密封进行改进。
3. 导热板的温度控制可能不够精确,导致温度差过大或过小,建议改进温度控制仪的精度。
参考文献:[1] 吴革南, 金宗俊. 传热学[M]. 高等教育出版社, 2002.[2] 冯德跃. 制冷与空调工程导论[M]. 高等教育出版社, 2004.。
导热系数的测量 实验报告
实验九导热系数的测量一.预习报告。
二.实验数据处理及分析1.数据。
表一散热盘P mp = 0.535kg表二样品B c=0.385 KJ/(K*kg)表三达到稳态时上下板温度读数表四每隔30s记录散热板温度t(s) 0 30 60 90 120 150 180 210 240 T2(°C) 68.9 68 67.2 66.6 65.8 65.1 64.5 63.8 63.1 t(s) 270 300 330 360 390 420 450 480 510 T2(°C) 62.4 61.9 61.3 60.7 60.2 59.5 59 58.4 57.9 t(s) 540 570 600 630 660 690 720 750 780 T2(°C) 57.4 57 56.5 56 55.4 55 54.5 54 53.6 t(s) 810 840 870 900 930 960 990 1020 1050 T2(°C) 53.2 52.7 52.3 51.9 51.5 51.1 50.8 50.5 50.1散热板温度随时间变化折线图2.数据处理。
稳态时:对T1,T2数据取平均值作为稳态温度:T1 = (69.9+69.9+70.0+69.9+70.0+70.0+70.0+70.0+69.9+70.0)/10=69.96 °CT2 = (60.1 +60.1+60.1+ 60.1+60.0+60.0+60.1+60.1 +60.1+60.1)/10= 60.08 °C根据表四及折线图,取原散热板稳定温度的附近值计算,共取了10个数据:利用逐差法计算∆t∆T ∆t = -(60.7+61.3+61.9+62.4+63.1)−(57.9+58.4+59+59.5+60.2)30×5×5= - 14.4750≈ -0.0192 °C/s由公式得:λ= -mc2h p+R p2h p+2R p ∙ 1πR∙ hT1 − T2∙ ∆T∆t= -535×0.385×2×8+492×8+2×49×1π×0.04850×0.00669.96−60.08×(-0.0192)≈ 0.2153 W/m∙K3.数据分析。
导热系数的测量实验实训报告doc
导热系数的测量实验实训报告 .doc 导热系数测量实验实训报告一、实验目的本实验旨在通过测量物质的导热系数,深入理解导热系数的物理意义和影响因素,掌握导热系数测量的基本原理和方法,提高实验操作技能和数据处理能力。
二、实验原理导热系数是描述物质导热性能的重要参数,其大小反映了物质在单位时间内、单位温度差下通过单位面积的热流量。
根据傅里叶导热定律,稳态导热过程中,单位时间内通过单位面积的热流量Q与温度梯度ΔT成正比,与传热面积A和材料热阻R成反比,可用公式表示为:Q = -λAΔT/R其中,λ为导热系数,A为传热面积,R为材料热阻。
因此,通过测量热流量Q、温度梯度ΔT和传热面积A,可以计算出材料的导热系数λ。
三、实验步骤1.准备实验器材:导热系数测量仪、加热器、温度传感器、样品杯、天平、砝码、镊子、电源线等。
2.安装实验器材:将加热器放置在样品杯中央,将温度传感器插入加热器侧壁,将样品杯放置在导热系数测量仪平台上。
3.准备样品:选取具有不同导热系数的物质,如金属、陶瓷、塑料等,将其研磨成粉末,用天平称取一定质量,置于样品杯中。
4.开始测量:连接电源线,打开导热系数测量仪电源开关,设置加热器温度、测量时间等参数,启动测量程序。
5.记录数据:观察实验过程中温度变化情况,记录各个时间点的温度值。
6.数据处理:根据实验数据,计算导热系数,分析实验结果。
四、实验结果与分析1.数据记录:将各个时间点的温度值记录在表格中,计算温度梯度ΔT和热流量Q。
2.导热系数计算:根据公式λ = Q/(AΔT),计算物质的导热系数。
将计算结果记录在表格中。
3.结果分析:比较不同物质的导热系数大小,分析导热系数的影响因素。
可以从物质的结构、分子排列、分子量等方面进行讨论。
例如,金属的导热系数普遍较高,因为金属晶体中存在大量的自由电子,可以快速传递热量;而塑料和陶瓷的导热系数相对较低,因为它们存在大量的分子间空隙和缺陷,阻碍了热量的传递。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一. 实验目的:
a. 掌握稳态法测不良导体的导热系数的方法;
b. 了解物体散热速率和传热速率的关系;
c. 理解温差热电偶特性
二. 实验仪器:
发热盘,传热筒,杜瓦瓶,温差电偶,待测橡胶样品,数字电压表,硅油,停表
三. 实验原理:
当物体内部各处温度不均匀时,就会有热量从温度较高处传向较低处,这种现象称为热传导。
热传导定律指出:如果热量是沿着Z 方向传导,那么在Z 轴上任一位置Zo 处取一个垂直
截面积dS ,以Z d dT
表示在Z 处的温度梯度,以dt dQ 表示该处的传热速率(单位时间内通过截面积dS 的热量),那么热传导定律可表示成:
(1-1)
式中的负号表示热量从高温区向低温区传导(即热传导的方向与温度梯度的方向相反),比例数λ即为导热系数,可见导热系数的物理意义:在温度梯度为一个单位的情况下,单位时间内垂直通过截面单位面积的热量。
利用(1-1)式测量材料的导热系数λ,需解决两个关键的问题:一个是如何在材料内造成一个温度梯度Z d dT
并确定其数值;另一个是如何测量材料内由高温区向低温区的传热速率dt dQ。
1、关于温度梯度Z d dT
为了在样品内造成一个温度的梯度分布,可以把样品加工成平板状,并把它夹在两块良导体——铜板之间,如图1,使两块铜板分别保持在恒定温度T1和T2,就可能在垂直于样品表面的方向上形成温度的梯度分布。
若样品厚度远小于样品直径(D h 《),由于样品侧面积比平板面积小得多,由侧面散去的热量可以忽略不计,可以认为热量是沿垂直于样品平面的方向上传导,即只在此方向上有温度梯度。
由于铜是热的良导体,在达到平衡时,可以认为同一铜板各处的温度相同,样品内同一平行平面上各处的温度也相同。
这样只要测出样品的厚度h 和两块
铜板的温度T1、T2,就可以确定样品内的温度梯度h T T 2
1-。
当然这需要铜板与样品表面紧密接触无缝隙,否则中间的空气层将产生热阻,使得温度梯度测量不准确。
dt ds dz dT dQ Z ⋅-=0)(λ
图1 传热示意图
为了保证样品中温度场的分布具有良好的对称性,把样品及两块铜板都加工成等大的圆形。
2、关于传热速率dt dQ
单位时间内通过某一截面积的热量dt dQ
是一个无法直接测定的量,我们设法将这个量转化为较容易测量的量。
为了维持一个恒定的温度梯度分布,必须不断地给高温侧铜板加热,热量通过样品传到低温侧铜板,低温侧铜板则要将热量不断地向周围环境散出。
当加热速率、传热速率与散热速率相等时,系统就达到一个动态平衡,称之为稳态,此时低温侧铜板的散热速率就是样品内的传热速率。
这样,只要测量低温侧铜板在稳态温度T2下散热的速率,也就间接测量出了样品内的传热速率。
但是,铜板的散热速率也不易测量,还需要进一步作参量转换,我们知道,铜板的散热速率与冷却速率(温度变化率)dt dT
有关,其表达式为
22T dt dT mc dt dQ
T -= (1-2)
式中的m 为铜板的质量,C 为铜板的比热容,负号表示热量向低温方向传递。
因为质量容易直接测量,C 为常量,这样对铜板的散热速率的测量又转化为对低温侧铜板冷却速率的测量。
铜板的冷却速率可以这样测量:在达到稳态后,移去样品,用加热铜板直接对下铜板加热,使其温度高于稳态温度T2(大约高出10℃左右),再让其在环境中自然冷却,直到温度低于T2,测出温度在大于T2到小于T2区间中随时间的变化关系,描绘出T -t 曲线(见图2),曲线在T2处的斜率就是铜板在稳态温度时T2下的冷却速率。
应该注意的是,这样得出的dt dT
是铜板全部表面暴露于空气中的冷却速率,其散热面积为2πRp2+2πRphp (其中Rp 和hp 分别是下铜板的半径和厚度),然而,设样品截面半径为R ,在实验中稳态传热时,铜板的上表面(面积为πRp2)是被样品全部(R=Rp )或部分(R<Rp )覆盖的,由于物体的散热速率与它们的面积成正比,所以稳态时,铜板散热速率的表达式应修正为:
若P R R = ,则 dt dQ
=-p p P p p P h R R h R R dt dT mc ππππ22222++∙ (1-3)
若R <P R , 则 dt dQ
=-
p p P p p P h R R h R R R dt dT m c πππππ2222222++-∙ (1-3′)
根据前面的分析,这个量就是样品的传热速率。
将(1-3)式或(1-3′)式代入热传导定律表达式,考虑到dS=πR2,可以得到导热系数:
λ=
22121222T T p p p p dt
dT T T h R R h R h mc
=∙-∙∙++π (1-4) 或 λ=221222212222T T P p p p p p dt
dT T T h R h R R h R R R m c =∙-∙∙++-π (1-4′)
式中的R 为样品的半径、h 为样品的高度、m 为下铜板的质量、c 为铜的比热容、Rp 和hp 分别是下铜板的半径和厚度。
各项均为常量或直接易测量。
本实验选用铜一康铜热电偶测温度,温差为100℃时,其温差电动势约为4.0mV 。
由于热电偶冷端浸在冰水中,温度为0℃,当温度变化范围不大时,热电偶的温差电动势θ(mV )与待测温度T (℃)的比值是一个常数。
因此,在用(1-4)或(1-4′)式计算时,也可以直接用电动势θ代表温度T 。
四.实验内容与步骤
1、用游标卡尺测量样品、下铜盘的几何尺寸,多次测量取平均值。
2、先放置好待测样品及下铜盘(散热盘),调节下圆盘托架上的三个微调螺丝,使待测样品与上、下铜盘接触良好。
安置圆筒、圆盘时须使放置热电偶的洞孔与杜瓦瓶在同一侧。
热电偶插入铜盘上的小孔时,要抹些硅脂,并插到洞孔底部,使热电偶测温端与铜盘接触良好,热电偶冷端插在杜瓦瓶中的冰水混合物中。
3、根据稳态法,必须得到稳定的温度分布,这就要等待较长时间,为了提高效率,可先将电源电压打到“高”档,几分钟后θ1=4.00mv 即可将开关拨到“低”档,通过调节电热板电压“高”、“低”及“断”电档,使θ1读数在±0.03mv 范围内,同时每隔30秒读θ2的数值,如果在2分钟内样品下表面温度θ2示值不变,即可认为已达到稳定状态。
记录稳态时与θ1,θ2对应的T1,T2值。
需要强调的是,测金属(或陶瓷)的导热系数时,T1、T2值为稳态时金属样品上下两个面的温度,此时散热盘P 的温度为T3。
因此测量P 盘的冷却速率应为: 测T3值时要在T1、T2达到稳定时,将上面测T1或T2的热电偶移下来进行测量。
4、移去样品,继续对下铜盘加热,当下铜盘温度比T2(对金属样品应为T3)高出10℃左右时,移去圆筒,让下铜盘所有表面均暴露于空气中,使下铜盘自然冷却,每隔30秒读一次下铜盘的温度示值并记录,直到温度下降到T2(或T3)以下一定值。
作铜盘的T —t 冷却速率曲线,选取邻近T2(或T3)的测量数据来求出冷却速率。
5、根据(1-4)或(1-4′)式计算样品的导热系数λ。
五.数据记录与数据处理
1.记录橡胶盘,黄铜盘的直径,高度,并给出相应的测量结果。
2. 采用逐差法球散热盘P 在温度为 时的冷却速率。
其中t=120s 。
3.由计算橡胶的导热系数λ,并与橡胶的导热系数标准值0.16W/mk 比较,计算百分百误差,并给出λ测量结果。
∴∆∆=3
T T t T。
