基于Simulink进行系统仿真(微分方程、传递函数)
基于simulink汽车速度控制系统的设计与仿真
基于simulink汽车速度控制系统的设计与仿真摘要：目前许多汽车把汽车速度控制系统作为配属设备或选配设备。
汽车装有汽车速度控制系统后，当驾驶员启动这一装置并进行一些简单的设置后，该装置可自动保持某一恒定速度行驶，而不踩油门。
由于电子系统能准确地控制车辆的速度，从而使高速行驶的车辆更加安全、平稳。
在文中，首先对汽车的运动原理进行分析，建立控制系统简化模型，根据研究对象的物理特性建立起汽车速度控制控制系统的微分方程，再将该微分方程进行线性化处理，运用PID控制理论的方法对汽车速度控制控制系统进行分析和控制。
然后对汽车速度控制系统进行设计分析，在已有的模型下，对设计的汽车速度控制系统进行Matlab语言仿真。
关键词：速度控制系统PID控制仿真指导老师签名:Design and Simulation of the vehicle speedcontrol systemStudent name Class:Supervisor:Abstract:At present, many cars make car speed control system as an attachment device or optional equipment. The car is fitted with the motor speed control system, when the driver start the device and make some simple settings, the device can automatically maintain a constant speed, and do not step on the accelerator. Because the electronic system can accurately control the speed of the vehicle, so that the high-speed vehicles more secure, stable.In this paper, the first principle of the movement of automobile is analyzed, establishing control system is simplified model, based on physical characteristics of the research object to establish the vehicle speed control differential equation of the control system, then the differential equation is linearized by using the method of control theory, analyze and control the motor speed control system. Then the design of the vehicle speed control system, the existing model, to design vehicle speed control system simulation language Matlab.Keyword：Speed control system PID control simulationSignature of Supervisor:目录1绪论 (1)1.1选题的依据及课题意义 (1)1.2汽车速度控制研究概况及发展趋势 (1)2速度控制系统的简述 (3)2.1汽车速度控制系统原理 (3)2.2速度控制系统的分类 (3)2.3速度控制系统的基本用途 (4)2.4电子式多功能速度控制系统功能 (4)3系统模型建立及性能分析 (6)3.1汽车受力分析 (6)3.2行驶汽车仿真模型 (7)3.3 动态性能和稳态性能指标 (8)4 PID控制器 (10)4.1 PID控制简述 (10)4.2 PID控制规律 (10)4.3 PID作用分析 (14)5 系统仿真及结果分析 (15)5.1 SIMULINK简介 (15)5.2实验方案选择 (15)5.2.1采用P控制 (15)5.2.2采用PI控制 (20)5.2.3采用PID控制 (22)5.3实验结果分析 (25)总结 (26)参考文献 (27)致谢 (28)1绪论1.1选题的依据及课题意义随着汽车工业和公路运输业的发展，汽车将走进千家万户，驾驶人员非职业化的特点将突出，车辆驾驶的自动化己成为汽车发展的主要趋势。
基于Simulink的控制系统建模与仿真
第27页/共36页
滑艇速度控制系统模型框图
第28页/共36页
然后设置正确的系统模型参数与仿真参数对此 系统进行仿真，其中Step的Final Value值设置为1000 （即滑艇牵引力）、子系统中增益模块Gain的取值 为1/1000（即1/m）、Fcn模块的expression设置为 u^2-u（求取水的阻力）、系统仿真时间为0至100s。
0.02s。 （2）P、I、D增益模块：取值分别为1、0.01、0。
第15页/共36页
汽车动力机构参数：
（1）Gain模块：取值为1/m，即1/1000。 （2）Gain1模块：取值为b/m，即20/1000。 （3）Integrator模块：初始状态为0，即速度初值为0。 系统仿真参数：
（1）仿真时间范围：从0至1000s。 （2）求解器：使用变步长连续求解器。 4．系统仿真与分析
建模： 根据牛顿第二定律，小车受弹簧的弹性力、
阻尼器的阻尼力、加速度力，运动方程如下：
mx fx kx F x 0.2x 0.4x 0.2F u(t) 0.2F x u(t) 0.2x 0.4x
例exm1。
第1页/共36页
例2 蹦极跳系统 蹦极跳是一种挑战身体极限的运动，蹦极者系
着一根弹力绳从高处的桥梁或山崖等向下跳。在下 落的过程中，蹦极着几乎处于失重状态。应用 Simulink对蹦极跳系统进行仿真研究。
积分环节： x(n) x(n 1) u(n) 微分环节：d(n) u(n) u(n 1) 系统输出： y(n) Pu(n) Ix(n) Dd(n)
第10页/共36页
汽车动力机构 汽车动力机构是行驶控制系统的执行机构。其
基于Simulink状态空间建模的系统分析方法程序实现
基于Simulink状态空间建模的系统分析方法程序实现荆晓莉(陕西理工学院物电学院电子信息科学与技术1101班，陕西汉中723001)指导老师：龙姝明[摘要] 无论用何种方法求高阶连续系统解析解都是十分棘手的问题。
实际上，科学研究和工程应用中更多地需要系统的数值解。
调用Matlab的Simulink工具包，可以用模块图标方法来编程，并通过运行系统模型文件的方法直接给出连续系统的数值解，而不需要将连续系统转换为离散系统再求解。
对于复杂LTI 系统直接写出微分方程再给出状态空间矩阵很困难，我们获得系统状态空间矩阵的方法是：先将系统映射到s 域，列出解（系统输出）函数的像函数满足的代数方程组，解代数方程组给出系统函数H(s),再调用Matlab的函数[a,b,c,d]=tf2ss(num,den)就得到系统的状态空间矩阵，从而完成系统的描述，再创建系统模型文件，写入状态空间矩阵、输入信号、初值条件及运行相关参数，最后编程调用sim()函数运行模型文件给出连续系统的数值解。
[关键字]连续系统;离散化;Simulink;M文件The implementation of the system analysis method based on Simulink state space modelingJing Xiaoli(Grade11,Class1,Major Electronic Information Science and Technology Department of Physics,ShannxiUniversity of Technology,Hanzhong,723001)Tutor: Long ShumingAbstract It is a difficult problem for the higher order continuous system to solve the problem.In fact,the numerical solution of the system is more needed for scientific research and engineering application.Calling Matlab Simulink toolkit can be programmed by using the method of module icon,and the direct method of operation system model file are given continuous system of numerical solution, without the need to convert the continuous system to discrete system, to be solved. Continuous model, mapped to directly write for complex LTI system differential equations and give the state space matrix is very difficult,we obtain the system state space matrix method is: first the system's domain, a list of solutions (output) function as function satisfies the algebraic equation group, the solution of algebraic equations gives the system function H(s), and then call the Matlab function [A,B,C,D]=tf2ss(num,den) system state space matrix,thus completing the system description, and then create a system file, write the state space matrix, input signal, the initial conditions and operating parameters,programming at last call to sim run the model file is system of numerical solutions.Keywords Continuous system,Discrete,Simulink,M file目录1 状态空间分析方法的概述 (1)2 快速创建LTI连续系统状态空间模型的方法 (2)2.1 创建LTI连续系统传递函数的方法 (2)2.2 构造描述LTI连续系统的状态空间模型矩阵 (3)3 用Simulink状态空间建模求解LTI系统数值解的思路 (4)3.1 LTI连续系统的描述 (4)3.2 创建系统的Simulink状态空间模型 (4)3.3 模块内部参数设置及数据存储 (5)4 利用Simulink状态空间建模求解LTI系统的优缺点 (7)4.1 状态空间建模求解LTI系统的优点 (7)4.2 状态空间建模求解LTI系统的缺点 (7)5 连续系统Simulink状态空间建模分析方法程序设计的思路 (7)5.1 调用模型文件及编程求解系统响应 (7)5.2 分析系统的频谱与相位 (9)6 状态空间分析方法的应用实例 (9)6.1 实际连续系统的描述 (9)6.2 在程序中设置参数 (10)6.3 运行程序，求解系统 (10)结语 (11)附录 (13)最近几年科学不断发展，系统的结构也渐渐复杂。
基于Matlab_Simulink数控伺服系统的建模仿真
文章编号:1001-2265(2006)08-0067-03收稿日期:2006-02-27 3基金项目:广东省自然科学基金资助项目(32364);广东省高教厅基金资助项目(Z02067)作者简介:王小东(1981—),男,内蒙古赤峰人,五邑大学机电工程系硕士研究生,研究方向为数控系统及其仿真,(E -mail )wangxiaodong1816@ 。
基于Matlab /Si m ulink 数控伺服系统的建模仿真3王小东,王大承(五邑大学机电工程系,广东 江门 529020)摘要:利用M atlab /Si m ulink 软件,通过对永磁同步电机(P M S M )本体、d /q 坐标系向a /b /c 坐标系转换、三相电流源逆变器等功能模块建立与组合,构建了永磁同步电机控制系统的速度和电流双闭环仿真模型。
根据数控伺服系统的性能要求,进行参数选择及仿真。
仿真结果证明了该系统模型的有效性,为数控伺服控制系统的设计和调试提供了理论基础。
关键词:M atlab /Si m ulink;数控伺服系统;永磁同步电机;仿真中图分类号:TP273 文献标识码:AS i m ul a ti on and M odeli n g of P M S M Ba sed on M a tl abWANG Xiao 2dong,WANG Da 2cheng(Depart m ent of Mechanical and Electrical Engineering,W uyi University,J iang men Guangdong 529020,China )Abstract:I n Matlab /Si m ulink,the bl ocks,such as P MS M bl ock,coordinate transfor mati on f or med q /d t o a /b /c bl ock,three phase current s ource inveter contr oller bl ock,etc .have been modeled .By the organic combi 2nati on of these bl ocks,t w o contr ol l oop s are used .The para meters are chosed by the perf or mance of servo sys 2te m.The reas onability and validity have been testified by si m ulate result and this novel method offers a ne w thought for designing and debugging actual mot or .Key words:Matlab /Si m ulink,NC servo syste m;P MS M ,si m ulati on0 引言数控机床的伺服系统一般由电流环和速度环组成[1]。
simulink建模与仿真
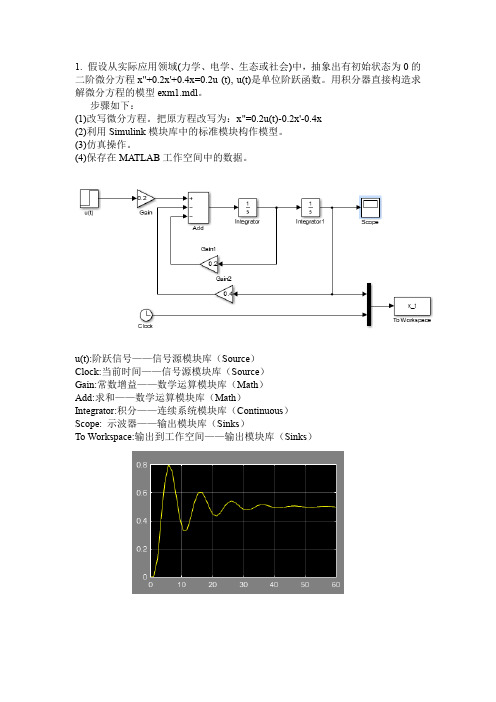
1. 假设从实际应用领域(力学、电学、生态或社会)中，抽象出有初始状态为0的二阶微分方程x"+0.2x'+0.4x=0.2u (t), u(t)是单位阶跃函数。
用积分器直接构造求解微分方程的模型exm1.mdl。
步骤如下：(1)改写微分方程。
把原方程改写为：x"=0.2u(t)-0.2x'-0.4x(2)利用Simulink模块库中的标准模块构作模型。
(3)仿真操作。
(4)保存在MATLAB工作空间中的数据。
u(t):阶跃信号——信号源模块库（Source）Clock:当前时间——信号源模块库（Source）Gain:常数增益——数学运算模块库（Math）Add:求和——数学运算模块库（Math）Integrator:积分——连续系统模块库（Continuous）Scope:示波器——输出模块库（Sinks）To Workspace:输出到工作空间——输出模块库（Sinks）2. 建立二阶系统222)(n n nS S S G ωςωω++=的脉冲响应模型，设ωn=10Hz ，观察当0<ζ<1、ζ=0、ζ=1及ζ>1时系统的响应。
Pulse Generator ：脉冲发生器——信号源模块库（Source ）Transfer Fun ：传递函数——连续系统模块库（Continuous ）Scope ：示波器——输出模块库（Sinks ）ζ=0.2 ζ=0ζ=1 ζ=53．皮球以15米/秒的速度从10米高的地方落下，建立显示球弹跳轨迹的模型。
Gravity：常数——信号源模块库（Source）IC Elasticity：信号的初始值——信号与系统模块库（Signal&Systems）Gain：常数增益——数学运算模块库（Math）Velocity：积分——连续系统模块库（Continuous）Position：有上下边界的有限积分——连续系统模块库（Continuous）Scope：示波器——输出模块库（Sinks）4. 利用使能原理构成一个正弦半波整流器。
第五讲 基于MATLAB-Simulink的建模与仿真
MATLAB软件简介？
MATLAB软件的典型应用领域：
❖科学研究； ❖工程技术应用研究 ❖CAI（Computer Aided Instruct） ❖数学实验（Mathematical Experiment） ❖数学建模（Mathematical Modeling）
模型 Transfer-Fcn：线性传递函数模型 Zero-Pole：以零极点表示的传递
函数模型 Memory：存储上一时刻的状态值 Transport Delay：输入信号延时 一个给定时间再输出 Variable Transport Delay：输入 信号延时一个可变时间再输出
✓ 离散模块（Discrete）
For循环不能用For循环内重新赋值循环变
量n来终止。
在For循环中循环控制量的范围可以是任
何有效的MATLAB矩阵。比如
data=[11 9 45 6; 7 16 -1 5];
for n=data
x=n(1)-n(2)
end 这时程序的输出有四个数值，分别是矩阵
data的两列相减的结果
x = 4 x = -7
x = 46 x = 1
For循环可按需要嵌套，即For循环体内的命 令组中可以出现另一个For循环体，这体现了 For循环体也是命令组。比如 for n=1:5
for m=5:-1:1
A(n,m)=n^2+m^2; End
end
MATLAB软件简介？
While-end循环以不定的次数求一组语句的值。 Whil-end 循环的一般形式是： while expression（控制表达式） {commands} end 只要在控制表达式（expression）里的所有元 素为真，就执行While和end语句之间的命令 串（{commands}）。
SIMULINK_的仿真算法
SIMULINK的仿真算法在SIMULINK的仿真过程中选择合适的算法是很重要的，仿真算法是求常微分方程、传递函数、状态方程解的数值计算方法，这些方法主要有欧拉法(Euler)、阿达姆斯法(Adams)、龙格·库塔法(Rung-Kutta)，这些算法都主要建立在泰勒级数的基础上。
欧拉法是最早出现的一种数值计算方法，它是数值计算的基础，它用矩形面积来近似积分计算，欧拉法比较简单，但精度不高，现在已经较少使用。
阿达姆斯法是欧拉法的改进，它用梯形面积近似积分计算，所以也称梯形法，梯形法计算每步都需要经过多次迭代，计算量较大，采用预报-校正后只要迭代一次，计算量减少，但是计算时要用其他算法计算开始的几步。
龙格-库塔法是间接使用泰勒级数展开式的方法，它在积分区间内多预报几个点的斜率，然后进行加权平均，用作计算下一点的依据，从而构造了精度更高的数值积分计算方法。
如果取两个点的斜率就是二阶龙格-库塔法，取四个点的斜率就是四阶龙格-库塔法。
SIMULINK汇集了各种求解常微分方程数值解的方法，这些方法分为两大类，可变步长类算法和固定步长类算法。
7.1可变步长类算法可变步长(Variable-step)类算法是在解算模型(方程)时可以自动调整步长，并通过减小步长来提高计算的精度。
在SIMULINK的算法中可变步长类算法有如下几种:1.Ode45(Dormand-Prince)基于显式Rung-Kutla(4,5)和Dormand-Prince组合的算法，它是一种一步解法，即只要知道前一时间点的解y(tn-1)，就可以立即计算当前时间点的方程解y(tn)。
对大多数仿真模型来说，首先使用ode45来解算模型是最佳的选择，所以在SIMULINK的算法选择中将ode45设为默认的算法。
2.ode23(Bogacki-Shampine)基于显式Rung-Kutta(2,3)、Bogacki和Shampine相结合的算法，它也是一种一步算法。
Simulink系统仿真原理
仿真效率取决于计算机性能、模型复杂度和数值算法的优化程度。
03
Simulink模型建立
模型元素
模块
Simulink中的模块是构成模型的基本单元， 每个模块代表一个特定的功能或算法。
连接线
连接线用于将不同模块连接起来，表示数据 流或信号流。
参数设置
每个模块都有一些参数可以设置，用于调整 模块的行为或功能。
性能评估
根据仿真结果，评估系统性能指标，如响应时间、超调量、稳态误 差等。
优化设计
基于仿真结果，对系统参数和结构进行优化设计，提高系统性能和 稳定性。
05
模型优化与改进
参数优化
参数优化
在Simulink模型中，参数的选择和调整对仿真结果的影响非常大。通过调整模型中的 参数，可以优化模型的性能，提高仿真的准确性和效率。
通过点击Simulink界面上的“开 始”按钮或使用命令行指令来启 动仿真。
实时监测
02
03
结果导出
在仿真过程中，可以通过 Simulink界面实时监测系统状态、 变量值和输出结果等。
将仿真结果导出为文本、图像或 数据文件，以便进一步分析或与 其他软件进行交互。
模型性能分析
稳定性分析
通过分析仿真结果，判断系统是否稳定，并找出可能的不稳定因素。
特点
支持图形化建模、交互式仿真、动态 系统分析等，适用于多种领域的系统 建模与仿真。
Simulink的历史与发展
1980年代初
由美国MathWorks公司推出Simulink的早期版 本。
1990年代
随着计算机技术的进步，Simulink的功能不断 扩展，支持更多的系统和算法。
2000年代至今
MATLABSimulink与控制系统仿真实验报告
MATLAB/Simulink 与控制系统仿真实验报告姓名：喻彬彬学号：K031541725实验1、MATLAB/Simulink 仿真基础及控制系统模型的建立一、实验目的1、掌握MATLAB/Simulink 仿真的基本知识；2、熟练应用MATLAB 软件建立控制系统模型。
二、实验设备电脑一台；MATLAB 仿真软件一个三、实验内容1、熟悉MATLAB/Smulink 仿真软件。
2、一个单位负反馈二阶系统，其开环传递函数为210()3G s s s =+。
用Simulink 建立该控制系统模型，用示波器观察模型的阶跃响应曲线，并将阶跃响应曲线导入到MATLAB 的工作空间中，在命令窗口绘制该模型的阶跃响应曲线。
3、某控制系统的传递函数为()()()1()Y s G s X s G s =+，其中250()23s G s s s+=+。
用Simulink 建立该控制系统模型，用示波器观察模型的阶跃响应曲线，并将阶跃响应曲线导入到MATLAB 的工作空间中，在命令窗口绘制该模型的阶跃响应曲线。
4、一闭环系统结构如图所示，其中系统前向通道的传递函数为320.520()0.11220s G s s s s s+=+++g ，而且前向通道有一个[-0.2，0.5]的限幅环节，图中用N 表示，反馈通道的增益为1.5，系统为负反馈，阶跃输入经1.5倍的增益作用到系统。
用Simulink 建立该控制系统模型，用示波器观察模型的阶跃响应曲线，并将阶跃响应曲线导入到MATLAB 的工作空间中，在命令窗口绘制该模型的阶跃响应曲线。
四、实验报告要求实验报告撰写应包括实验名称、实验内容、实验要求、实验步骤、实验结果及分析和实验体会。
五、实验思考题总结仿真模型构建及调试过程中的心得体会。
题1、（1）利用Simulink的Library窗口中的【File】→【New】，打开一个新的模型窗口。
（2）分别从信号源库（Sourse）、输出方式库（Sink）、数学运算库（Math）、连续系统库（Continuous）中，用鼠标把阶跃信号发生器（Step）、示波器（Scope）、传递函数（Transfern Fcn）和相加器（Sum）4个标准功能模块选中，并将其拖至模型窗口。
Simulink仿真实例
2014年4月19日星期六
基于MATLAB/SIMULINK的系统建模与 bx 0 M x
构建的模型为
2014年4月19日星期六
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
因有阻尼器存在，故箱子最终会停止运 动。
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
其运动方程式为
M f bx x
拉力作用时间为2s，建构的模型为
2014年4月19日星期六
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
因有摩擦力存在，箱子最终将会停止前 进。
2014年4月19日星期六 基于MATLAB/SIMULINK的系统建模与仿真
2014年4月19日星期六
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
仿真过程中，设绳索长度-30m，起始速 度为0；物体质量为90kg，g为9.8m/s2,弹性 系数k为20，a1和a2均为1.
2014年4月19日星期六
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
仿真曲线为
2014年4月19日星期六
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
假设未伸长时绳索的端部距地面为50m, 为了得到更真实的曲线，将50减去输出位置
2014年4月19日星期六
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2014年4月19日星期六
基于MATLAB/SIMULINK的系统建模与仿真
simulink传递函数单输入多输出simo_概述说明
simulink传递函数单输入多输出simo 概述说明1. 引言1.1 概述在控制系统中，SIMO（Single Input Multiple Output）传递函数是一种常见的模型表示方法。
这种传递函数可以描述系统输入信号与多个输出信号之间的关系。
SIMO传递函数在实际工程中具有广泛的应用，例如机械控制系统、电力系统以及通信系统等。
本文旨在介绍SIMO传递函数的基本概念和相关应用，并重点研究Simulink在SIMO传递函数中的应用。
Simulink是一种流行的图形化仿真环境，可用于建立复杂系统的模型，并进行仿真与分析。
1.2 文章结构本文共分为五个部分，具体内容如下：第一部分为引言部分，主要介绍文章的背景和整体结构。
第二部分详细介绍SIMO传递函数，在2.1节对SIMO系统进行概述，在2.2节定义单输入多输出传递函数，并在2.3节探讨其特点与应用场景。
第三部分将重点关注Simulink在SIMO传递函数中的应用。
首先，在3.1节简要介绍Simulink软件；然后，在3.2节解释如何建立SIMO传递函数模型；最后，在3.3节探讨基于Simulink的模拟与分析方法。
第四部分将介绍SIMO传递函数模型的设计与优化方法。
具体包括参数估计与调整技术在4.1节的应用，系统辨识方法及其应用在4.2节，以及优化算法在SIMO传递函数中的应用在4.3节。
最后，第五部分为结论与展望部分。
5.1节对本文内容进行总结，5.2节展望了未来相关研究方向。
1.3 目的本文的目标是系统地介绍SIMO传递函数以及Simulink在该领域中的应用。
通过本文的阐述，读者将能够了解SIMO传递函数的概念、特点和应用，并能够掌握Simulink软件建立SIMO传递函数模型的方法和基于Simulink进行仿真与分析的技巧。
此外，本文还将介绍SIMO传递函数模型设计与优化所涉及的各种方法和算法，为读者提供理论依据和实践指导。
希望通过这篇文章，读者能够深入了解SIMO传递函数，并将其成功应用于实际工程中。
MATLABsimulink系统仿真分析仿真报告
仿真报告课程名称：自动化技术导论报告题目：MATLAB/simulink系统仿真分析班级姓名学号xxxxxx自动化学院2016年4月软件版本：MATLAB R2010bMATLAB强处理能力MATLAB是一个包含大量计算算法的集合。
其拥有600多个工程中要用到的数学运算函数，可以方便的实现用户所需的各种计算功能。
函数中所使用的算法都是科研和工程计算中的最新研究成果，而且经过了各种优化和容错处理。
在通常情况下，可以用它来代替底层编程语言，如C和C++ 。
在计算要求相同的情况下，使用MATLAB的编程工作量会大大减少。
MATLAB的这些函数集包括从最简单最基本的函数到诸如矩阵，特征向量、快速傅立叶变换的复杂函数。
函数所能解决的问题其大致包括矩阵运算和线性方程组的求解、微分方程及偏微分方程的组的求解、符号运算、傅立叶变换和数据的统计分析、工程中的优化问题、稀疏矩阵运算、复数的各种运算、三角函数和其他初等数学运算、多维数组操作以及建模动态仿真等。
MATLAB图形处理MATLAB自产生之日起就具有方便的数据可视化功能，以将向量和矩阵用图形表现出来，并且可以对图形进行标注和打印。
高层次的作图包括二维和三维的可视化、图象处理、动画和表达式作图。
可用于科学计算和工程绘图。
新版本的MATLAB 对整个图形处理功能作了很大的改进和完善，使它不仅在一般数据可视化软件都具有的功能（例如二维曲线和三维曲面的绘制和处理等）方面更加完善，而且对于一些其他软件所没有的功能（例如图形的光照处理、色度处理以及四维数据的表现等），MATLAB同样表现了出色的处理能力。
同时对一些特殊的可视化要求，例如图形对话等，MATLAB也有相应的功能函数，保证了用户不同层次的要求。
另外新版本的MATLAB还着重在图形用户界面（GUI）的制作上作了很大的改善，对这方面有特殊要求的用户也可以得到满足。
MATLAB对许多专门的领域都开发了功能强大的模块集和工具箱。
Simulink系统仿真课程设计
控制系统设计：用于设计、分析和优化控制系统
信号处理：用于处理和分析信号，如滤波、变换等
通信系统设计：用于设计、分析和优化通信系统
电力系统仿真：用于模拟和分析电力系统的运行状态和性能
基于模型的仿真：通过建立数学模型来模拟真实系统的行为
连续系统与离散系统：Simulink支持连续系统和离散系统的仿真
实践应用：完成了多个仿真项目，提高了解决问题的能力
展望未来：将继续深入学习Simulink，提高仿真能力，为实际工程问题提供解决方案
课程设计目标：掌握Simulink系统仿真的基本原理和操作方法
课程设计内容：包括Simulink的基本操作、模型搭建、仿真分析等
课程设计成果：完成一个完整的Simulink系统仿真项目
确定仿真参数：根据仿真模型确定所需的参数，如时间、空间、物理量等
确定仿真环境：根据仿真模型和参数确定仿真环境，如实验室、现场等
明确仿真目的：确定仿真的目标和需求，如性能优化、故障诊断等
确定仿真模型：根据仿真目的选择合适的模型，如物理模型、数学模型等
确定系统模型：根据实际需求确定系统模型
建立数学方程：根据系统模型建立相应的数学方程
实验分析：对实验结果进行分析和解释
实验结果：展示实验的结果和数据
实验成绩占总成绩的比例
实验报告的质量和完整性
实验操作的熟练程度和准确性
实验结果的分析和解释
实验过程中遇到的问题和解决方法
实验报告的格式和规范性
课程内容：包括Simulink基础、建模、仿真、优化等
学习成果：掌握了Simulink的基本操作和建模技巧
重复仿真：重复步骤1-3，直至得到满意的仿真结果
线性控制系统：由线性元件组成的控制系统
利用simulink进行系统仿真论文
利用simulink进行系统仿真张营湖北科技学院电子信息科学与技术，学号：133621024摘要：Simulink是MATLAB中的一种可视化仿真工具，是一种基于MATLAB的框图设计环境，是实现动态系统建模、仿真和分析的一个软件包，被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中。
Simulink可以用连续采样时间、离散采样时间或两种混合的采样时间进行建模，它也支持多速率系统，也就是系统中的不同部分具有不同的采样速率。
为了创建动态系统模型，Simulink提供了一个建立模型方块图的图形用户接口(GUI) ，这个创建过程只需单击和拖动鼠标操作就能完成，它提供了一种更快捷、直接明了的方式，而且用户可以立即看到系统的仿真结果。
【1】关键词：simulink；仿真；分析引言：Simulink是MATLAB的工具箱，MATLAB R2010a版使用的是simulink7.5,可以用来对动态系统进行建模、仿真和分析，支持连续的、离散的及线性的和非线性的系统，还支持具有多种采样速率的系统。
Simulink是面向框图的仿真软件，具有以下功能。
(1)用绘制方框图代替编写程序，结构和流程清晰。
(2)智能化地建立和运行仿真，仿真仔细，贴近实际。
自动建立各环节的方程，自动在给定精度要求时以最快速度进行系统仿真。
(3)适应面广，包括线性、非线性系统，连续、离散及混合系统，单任务、多任务离散事件系统。
【2】2391 Simulink概述Simulink是MATLAB最重要的组件之一，它提供一个动态系统建模、仿真和综合分析的集成环境。
【3】1.1 Simulink简介Simulink是MATLAB最重要的组件之一，它提供一个动态系统建模、仿真和综合分析的集成环境。
在该环境中，无需大量书写程序，而只需要通过简单直观的鼠标操作，就可构造出复杂的系统。
Simulink具有适应面广、结构和流程清晰及仿真精细、贴近实际、效率高、灵活等优点，并基于以上优点Simulink已被广泛应用于控制理论和数字信号处理的复杂仿真和设计。
simulink微分模块详解
simulink微分模块详解Simulink是一个用于建模、仿真和分析动态系统的工具，微分模块在Simulink中扮演着重要的角色。
微分模块用于描述系统中的微分方程，可以帮助我们建立动态系统的模型，并进行仿真和分析。
下面我将从几个方面详细介绍Simulink中的微分模块。
首先，微分模块在Simulink中通常用于描述动态系统的状态方程。
在实际工程中，许多系统可以通过微分方程来描述其动态行为，比如电路、机械系统、控制系统等。
微分模块可以帮助我们将这些微分方程直接转化为Simulink模型，从而实现对动态系统的建模和仿真。
其次，Simulink中的微分模块可以用于求解微分方程。
通过将微分方程转化为差分方程，Simulink可以利用数值求解方法（如欧拉法、龙格-库塔法等）来对微分方程进行数值求解，从而得到系统的时间响应和状态变化情况。
这对于分析系统的动态行为以及设计控制器非常有帮助。
另外，微分模块还可以用于实现系统的状态空间表示。
在控制系统工程中，状态空间表示是描述动态系统行为的一种常用方法。
Simulink中的微分模块可以帮助我们将系统的状态方程表示为状态空间模型，从而进行状态空间分析和设计。
除此之外，Simulink中的微分模块还可以与其他模块结合，实现更复杂的系统建模和仿真。
比如可以将微分模块与控制器模块、传感器模块等连接起来，构建完整的控制系统模型，进行闭环仿真和分析。
总之，Simulink中的微分模块在动态系统建模和仿真中具有重要作用，可以帮助工程师们更方便地描述和分析动态系统的行为，是Simulink工具中不可或缺的一部分。
希望以上内容能够对你有所帮助。
实验四基于Simulink进行系统仿真(微分方程、传递函数)
实验四 基于Simulink 进行系统仿真（微分方
程、传递函数）
一、 实验目的
1) 熟悉Simulink 的工作环境；
2) 掌握Simulink 数学工具箱的使用；
3) 掌握在Simulink 的工作环境中建立系统仿真模型。
二、 实验内容
系统微分方程：)(10)(10)(10)(8
332
2t u t y dt t dy dt t y d =++
系统传递函数：8
32
8
101010)()()(++==s s s U s Y s G 1)(=t u
1、 仿真电路
用微分方程搭建系统仿真模型
用状态方程搭建系统仿真模型
用传递函数搭建系统仿真模型2、电路元件参数的设置
1）设置Gain参数
2）设置Gain1参数
3）设置Gain2的参数
4）设置State-Space的参数
5）设置Transfer Fcn的参数
3、仿真结果微分方程状态方程
传递函数
4、仿真结果的分析
用微分方程和状态方程搭建系统仿真模型的仿真结果一样，而用传递函数搭建系统仿真模型的仿真结果发散。
连续系统simulink传递函数建模分析方法程序设计
连续系统simulink传递函数建模分析方法程序设计搭建LTI连续系统的时域电路并将其映射到复频域(S域)解出其系统函数H（S），利用H（S）建立Simulink仿真模型,并编写求解连续系统零输入响应、零状态响应和全响应的数值解即MATLAB程序。
选择典型的RLC三阶电路系统，运用所建立的仿真模型和程序求解LTI连续电路系统，并对其进行展示。
目录引言 (1)1 快速计算LTI连续系统S域传递函数的思路 (1)1.1 理论分析方法 (1)1.2 连续系统LTI映射到复频率(S)域的必要性及思路 (1)1.3 连续系统LTI时域映射到复频率域的方法 (2)1.4 导出系统函数的思路 (3)2 利用simulink传递函数仿真模型求解LTI连续系统数值解的思路.. 3 2.1 时域电路系统映射到复频域（S域）的方法 (3)2.2 创建simulink传递函数和状态空间仿真模型文件的思路 (4)3求连续系统simulink传递函数建模分析方法程序设计的思路 (5)3.1 程序设计的思路与技巧 (5)3.2 关键语句分析 (6)4 程序应用实例 (6)4.1 S域电路系统函数和连续系统数值解的思路 (7)4.2 simulink仿真模型及程序求解电路响应 (9)4.2.1 传递函数模型 (9)4.2.2 状态空间模型 (11)4.3 程序运用实例展示 (14)5 结语 (16)参考文献 (17)引言现代社会的发展，诸多领域应用的系统都是连续系统，如科研、生产实践、产品和仪器检测等。
其连续系统中的控制电路都应该满足在一定的频带范围内，具有一定的放大和延迟功能。
连续系统的解法有解析解和数值解两种，相比而言，连续系统的时域解析解法虽然便于理论分析系统响应的变化趋势和系统特性，但实际系统总是多输入多输出的高阶系统，它们的解析微分方程书写困难，时域响应求解极为困难，出错率也较高，即便较低阶系统的解析方程能够得到，其求解也较复杂，耗时耗力[1]。
基于Simulink的OFDM系统仿真
载波采用4-QAM调制，符号周期为1s，用MATLAB画出一个符号周期的调制信 号波形，并比较无频偏解调和存在0.2Hz频偏时的解调结果。 从图1.2和图1.3可以看出，在没有频率偏差时，解调后的结果与原始数据一 致，而存在频率偏差时，解调后的结果与原始数据相比有了较大偏差，在信道噪 声的影响下，容易导致后面的QAM解调产生差错。
f f s N ，所以 f f s N 1 TS ，即这些已调子载波信号频谱 S a ( x) 函数的主
瓣宽度为 2 TS ，间隔为 1 TS 。根据函数性质，知道它们在频域上正交，这就是 正交频分复用（OFDM）名称的由来。 一般的频分复用传输系统的各个子信道之间要有一定的保护频带， 以便在接
1.1 串并变换
数据传输的典型形式是串行数据流，符号被连续传输，每一个数据符号的频 谱可占据整个可利用的带宽。但在并行数据传输系统中，许多符号被同时传输， 减少了那些在串行系统中出现的问题。 在OFDM系统中， 每个传输符号的速率在几十比特每秒到几万比特每秒之间， 所以必须进行串并变换，将输入的串行比特流转换成可以传输的OFDM信号。由 于调制模式可以自适应调节， 所以每个子载波的调制模式是可变化的，因而每个 子载波可传输的比特数也是可变化的， 所以串并变换需要分配给每个子载波的长 度是不一样的。 在接收端执行相反的过程，从各个子载波出来的数据被转换回原 始的串行数据。 当一个OFDM符号在多径无线信道中传输时， 频率选择性衰落会导致某几组 子载波受到相当大的衰减， 从而引起比特错误。这些在信道频率响应上的零点会 造成在附近的子载波上发生的信息受到破坏， 导致在每个符号中出现一连串的比 特错误。 与一大串错误连续出现的情况比较，大多数前向纠错编码在错误均匀分 布的情况下会工作得更加有效。 所以，为了提高系统采用数据加扰作为串并变换 工作的一部分。 这可以通过把每个连续的数据比特随机的分配到各个子载波上来 实现。在接收端，进行一个对应的逆过程还原出原始信号。这样，不仅可以还原
simulink仿真法求解积分
Simulink是一个功能强大的仿真工具，可以用于模拟和求解各种物理系统和数学模型。
在Simulink中，积分求解是一种常用的数值方法，用于求解一阶常微分方程的解。
下面是一个使用Simulink求解积分的基本步骤：1. 建立模型：首先，在Simulink中建立一个包含一阶常微分方程的系统模型。
通常，需要将微分方程作为模型的输入，并将输出连接到需要求解的物理系统或数学模型的输入端。
2. 配置参数：在模型中，需要配置积分器的参数，包括积分器类型、步长、初始值等。
不同的积分器类型适用于不同的微分方程，需要根据实际情况选择合适的积分器类型。
3. 运行仿真：在模型中设置好参数后，可以运行仿真以求解积分。
Simulink会自动使用积分器对微分方程进行求解，并将结果输出到模型的输出端。
4. 结果分析：通过观察仿真结果，可以了解微分方程的解随时间的变化情况。
可以使用Simulink提供的各种工具和图表来可视化仿真结果，以便更好地分析和理解。
下面是一个简单的示例，说明如何使用Simulink求解一阶常微分方程的积分：假设有一阶常微分方程dy/dt = y - 2，可以使用Simulink建立如下模型：* 输入端连接微分方程dy/dt = y - 2的右侧，即y(t) - 2；* 输出端连接到需要求解的物理系统或数学模型的输入端；* 在模型中配置积分器参数为默认的Simulink积分器，并设置合适的步长和初始值；* 运行仿真并观察仿真结果。
在这个例子中，微分方程的解为y(t) = 2e^(-t) + C，其中C 为初始条件。
通过观察仿真结果，可以验证这个解是否正确。
总之，使用Simulink求解积分是一个简单而有效的方法，可以用于模拟和求解各种物理系统和数学模型。
通过建立模型、配置参数、运行仿真和结果分析，可以更好地了解微分方程的解随时间的变化情况，为实际应用提供有价值的参考。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验四 基于Simulink 进行系统仿真（微
分方程、传递函数）
一．实验目的
1) 熟悉Simulink 的工作环境；
2) 掌握Simulink 数学工具箱的使用；
3) 掌握在Simulink 的工作环境中建立系统仿真模型。
二．实验内容
系统微分方程：)(10)(10)
(10)
(83322t u t y dt t dy dt t y d =++
系统传递函数：8328
101010)()()(++==s s s U s Y s G
1)(=t u ，)314sin()(t t u =，)90314sin()(o t t u +=
模型
微分方程时的过程
Ut=1时
t
u 时)(t
314
)
sin(
t
t
u+
=时
)(o
)
sin(
90
314
传递函数时的过程
u时
t
)(=
1
t
u=时
)(t
sin(
314
)
t
t
)(o
=时
u+
)
sin(
90
314
结论及感想
从两种种不同方法的仿真结果，我们可以看出分别用微分方程和传递函数在Simulink中，仿真出来的结果没有很明显的区别，说明两种方法的精度都差不多。
但是，不同的电压源得出的仿真结果不一样，阶跃电源开始时震荡，后来幅度逐渐变小，趋近于1；正弦电源，初相不同时，初始时刻的结果也不相同，有初相时开始震荡会更剧烈，但最后都会变为稳态值，即为正弦值。
通过本次实验，我认识到了建模与仿真的一般性方法，收获甚多，也更进一步了解了
Matlab,Matlab不仅仅在平时的编程方面功能强大，在仿真方面也熠熠生辉。