立体几何练习题及答案
立体几何练习题及答案
立体几何练习题及答案在学习立体几何的过程中，练习题对于巩固知识、提高应用能力起着至关重要的作用。
本文将为大家提供一些立体几何的练习题，并给出详细的答案解析，以帮助读者更好地理解和掌握立体几何的知识。
一、球的表面积和体积1. 某个球的半径为3cm，求其表面积和体积。
解析：球的表面积公式为S = 4πr²，体积公式为V = (4/3)πr³。
将半径r代入公式进行计算即可。
表面积：S = 4π(3)² = 4π(9) ≈ 113.04cm²体积：V = (4/3)π(3)³ = (4/3)π(27)≈ 113.04cm³因此，该球的表面积约为113.04cm²，体积约为113.04cm³。
二、立方体的表面积和体积2. 一个立方体的边长为5cm，求其表面积和体积。
解析：立方体的表面积公式为S = 6a²，体积公式为V = a³。
将边长a代入公式进行计算即可。
表面积：S = 6(5)² = 6(25) = 150cm²体积：V = (5)³ = 5(5)(5) = 125cm³因此，该立方体的表面积为150cm²，体积为125cm³。
三、圆柱的表面积和体积3. 一个圆柱的底面半径为4cm，高度为10cm，求其表面积和体积。
解析：圆柱的表面积公式为S = 2πr² + 2πrh，体积公式为V = πr²h。
将底面半径r和高度h代入公式进行计算即可。
表面积：S = 2π(4)² + 2π(4)(10) = 2π(16) + 2π(40) ≈ 321.2cm²体积：V = π(4)²(10) = π(16)(10) ≈ 502.4cm³因此，该圆柱的表面积约为321.2cm²，体积约为502.4cm³。
高三数学立体几何专项练习题及答案
高三数学立体几何专项练习题及答案一、选择题1. 下列哪个几何体的所有面都是三角形？A. 正方体B. 圆柱体C. 正六面体D. 球体答案：C2. 一个有8个面的多面体，其中6个面是正方形，另外2个面是等边三角形，它的名字是？A. 正八面体B. 正十二面体C. 正二十面体D. 正二十四面体答案：C3. 空间中任意一点到四个角落连线的垂直距离相等的四棱锥称为？A. 正四棱锥B. 圆锥台C. 四棱锥D. 无法确定答案：C4. 任意多面体的面数与顶点数、棱数的关系是？A. 面数 + 顶点数 = 棱数 + 2B. 面数 + 棱数 = 顶点数 + 2C. 顶点数 + 棱数 = 面数 + 2D. 顶点数 + 面数 = 棱数 + 2答案：A5. 求下列多面体的棱数：（1）正六面体（2）正八面体（3）正十二面体答案：（1）正六面体的棱数为 12（2）正八面体的棱数为 24（3）正十二面体的棱数为 30二、填空题1. 下列说法正确的是：一棱锥没有底面时，它的底面是一个______。
答案：点2. 铅垂线是指从一个多面体的一个顶点到与它相对的棱上所作的垂线，它与该棱垂足的连线相交于该多面体的______上。
答案：中点3. 对正八面体，下列说法不正确的是：_____条对角线与_____两两垂直。
答案：六，相邻面三、计算题1. 一个棱锥的底面是一个边长为6cm的正三角形，其高为8cm。
求棱锥体积。
解答：底面积 S = (1/2) ×底边长 ×高 = (1/2) × 6 × 8 = 24 cm²棱锥体积 V = (1/3) × S ×高 = (1/3) × 24 × 8 = 64 cm³所以，棱锥的体积为64 cm³。
2. 一个正四棱锥的底面是一个边长为10cm的正方形，其高为12cm。
求四棱锥的体积。
解答：底面积 S = 边长² = 10² = 100 cm²四棱锥体积 V = (1/3) × S ×高 = (1/3) × 100 × 12 = 400 cm³所以，四棱锥的体积为400 cm³。
高中数学立体几何专项练习题及答案
高中数学立体几何专项练习题及答案一、选择题1. 下面哪个选项不是描述柱体的特点？A. 体积恒定B. 底面形状不限C. 侧面是矩形D. 顶面和底面平行答案：A2. 如果一个四面体的一个顶点的对边垂直于底面，那么这个四面体是什么类型？A. 正方形四面体B. 倒立四面体C. 锥体D. 正方锥体答案：C3. 以下哪个选项正确描述了一个正方体的特点？A. 全部面都是正方形B. 12 条棱长度相同C. 8 个顶点D. 6 个面都是正方形答案：D4. 若长方体的高度是 6cm，底面积是 5cm²，底面对角线长为 a cm，那么 a 的值为多少？A. √11B. √29C. √31D. √41答案：C二、填空题1. 一个正方体的棱长为 4cm，它的体积是多少？答案：64cm³2. 一个球的表面积是100π cm²，那么它的半径是多少？答案：5cm3. 一个圆柱体的底面半径为 3cm，高度为 8cm，它的体积是多少？答案：72π cm³4. 一个圆锥的底面半径为 6cm，高度为 10cm，它的体积是多少？答案：120π cm³三、计算题1. 一个四棱锥的底面是边长为 5cm 的正方形，高度为 8cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算底面积：5cm * 5cm = 25cm²再计算体积：25cm² * 8cm / 3 = 200cm³2. 一个圆柱体的底面直径为 12cm，高度为 15cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算底面半径：12cm / 2 = 6cm再计算底面积：π * 6cm * 6cm = 36π cm²最后计算体积：36π cm² * 15cm = 540π cm³3. 一个球的直径为 8cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算半径：8cm / 2 = 4cm再计算体积：4/3 * π * 4cm * 4cm * 4cm = 268.08π cm³4. 一个圆锥的底面半径为 10cm，高度为 20cm，它的体积是多少？答案：单位为 cm³，计算过程如下：首先计算底面积：π * 10cm * 10cm = 100π cm²最后计算体积：100π cm² * 20cm / 3 = 2000π cm³四、解答题1. 若一个长方体的长度、宽度、高度分别为 a、b、c，它的表面积为多少？答案：单位为 cm²，计算过程如下：首先计算侧面积：2 * (a * b + a * c + b * c)再计算底面积：a * b最后计算表面积：2 * (a * b + a * c + b * c) + a * b2. 一个四棱锥的底面为边长为 a 的正三角形，高度为 h，求这个四棱锥的体积。
高中数学立体几何小题100题(含答案与解析)
立体几何小题100例一、选择题1．如图，已知正方体1111ABCD A B C D -的棱长为4，点E ，F 分别是线段AB ，11C D 上的动点，点P 是上底面1111A B C D 内一动点，且满足点P 到点F 的距离等于点P 到平面11ABB A 的距离，则当点P 运动时，PE 的最小值是（ ）A ．5B ．4C ．42．5【答案】D 【解析】试题分析：因为点P 是上底面1111A B C D 内一动点，且点P 到点F 的距离等于点P 到平面11ABB A 的距离，所以，点P 在连接1111,A D B C 中点的连线上．为使当点P 运动时，PE 最小，须PE 所在平面平行于平面11AA D D ,2244()52PE =+=选D考点：1．平行关系；2．垂直关系；3．几何体的特征．2．如图在一个二面角的棱上有两个点A ，B ，线段,AC BD 分别在这个二面角的两个面内，并且都垂直于棱AB ，=46,AB cm AC cm =， 8,217BD cm CD cm ==，则这个二面角的度数为（ ）A ．30︒B ．60︒C ．90︒D ．120︒ 【答案】B 【解析】试题分析：设所求二面角的大小为θ，则,BD AC θ<>=，因为CD DB BA AC =++，所以22222()222CD DB BA AC DB BA AC DB BA DB AC BA AC =++=+++⋅+⋅+⋅CA DB而依题意可知,BD AB AC AB ⊥⊥，所以20,20DB BA BA AC ⋅=⋅=所以2222||||||||2CD DB BA AC BD AC =++-⋅即222417468286cos θ⨯=++-⨯⨯所以1cos 2θ=，而[0,]θπ∈，所以60θ=︒，故选B. 考点：1.二面角的平面角；2.空间向量在解决空间角中的应用.3．已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm ）可得这 个几何体的体积是（ ）112222侧视图俯视图主视图A ．343cmB ．383cmC ．33cmD ．34cm【答案】B ． 【解析】试题分析：分析题意可知，该几何体为一四棱锥，∴体积382231312=⨯⨯==Sh V ． 考点：空间几何体的体积计算．4．如图，P 是正方体1111ABCD A B C D -对角线1AC 上一动点，设AP 的长度为x ，若PBD ∆的面积为(x)f ，则(x)f 的图象大致是（ ）【答案】A 【解析】试题分析：设AC 与BD 交于点O ,连接OP .易证得BD ⊥面11ACC A ,从而可得BD OP ⊥.设正方体边长为1,在1Rt ACC ∆中126cos 33C AC ∠==.在AOP ∆中 22OA =,设(),03AP x x =≤≤,由余弦定理可得2222226231222362OP x x x x ⎛⎫=+-⋅⨯=-+ ⎪ ⎪⎝⎭,所以223162OP x x =-+.所以()22231262f x x x =-+.故选A. 考点：1线面垂直,线线垂直;2函数图象.5．如图所示，正方体ABCD A B C D ''''-的棱长为1， ,E F 分别是棱AA '，CC '的中点，过直线,E F 的平面分别与棱BB '、DD '交于,M N ，设 BM x =，[0,1]x ∈，给出以下四个命题：（1）平面MENF ⊥平面BDD B ''；（2）当且仅当x=12时，四边形MENF 的面积最小；（3）四边形MENF 周长()L f x =，[0,1]x ∈是单调函数； （4）四棱锥C MENF '-的体积()V h x =为常函数； 以上命题中假命题．．．的序号为（ ） A ．（1）（4） B ．（2） C ．（3） D ．（3）（4） 【答案】C 【解析】试题分析：（1）由于AC EF //，B B AC BD AC '⊥⊥,，则D D B B ''⊥平面AC ，则D D B B EF ''⊥平面，又因为EMFN EF 平面⊂，则平面MENF ⊥平面BDD B ''；（2）由于四边形MENF 为菱形，MN EF S MENF ⋅=21，2=EF ，要使四边形MENF 的面积最小，只需MN 最小，则当且仅当21=x 时，四边形MENF 的面积最小；（3）因为1)21(2+-=x MF ，1)21(4)(2+-=x x f ，)(x f 在]1,0[上不是单调函数；（4）NE C F EC M F MENF C V V V '-'--'+=，ME C S '∆=41121=⋅'E C ，F 到平面ME C '的距离为1，1214131=⋅='-ME C F V ，又41121=⋅'⋅='∆E C S NE C ，1214131=⋅='-NE C F V ，61)(=x h 为常函数.故选（3）考点：1.面面垂直的判定定理；2.建立函数模型.6．已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（ ）（A）4 （B ）4 （C ）4 （D ）34【答案】D. 【解析】试题分析：连接B A 1；11//CC AA ,AB A 1∠∴是异面直线AB 与1CC 所成的角或其补角；在1ADA Rt ∆中，设11=AA ，则21,231==D A AD ；在1BDA Rt ∆中，2121=B A ；在1ABA ∆中，431122111cos 1=⨯⨯-+=∠AB A ；即面直线AB 与1CC 所成的角的余弦值为34. 考点：异面直线所成的角.7．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A ．π312B ．π12C ．π34D ．π3 【答案】D 【解析】试题分析：由三视图可知，该几何体为四棱锥，侧棱垂直底面，底面是正方形，将此四棱锥还原为正方体，则正方体的体对角线即外接球的直径，32=r ，23=∴r ，因此ππ342==r S 表面积，故答案为D. 考点：由三视图求外接球的表面积.8．如图，棱长为1的正方体ABCD-A 1B 1C 1D 1中，P 为线段A 1B 上的动点，则下列结论错误的是（ ）A ．11DC D P ⊥B ．平面11D A P ⊥平面1A APC ．1APD ∠的最大值为90 D ．1AP PD +22+ 【答案】C 【解析】试题分析：111DC D A ⊥ ，11DC B A ⊥，1111A B A D A = ，⊥∴1DC 平面11BCD A ，⊂P D 1平面11BCD A 因此P D DC 11⊥，A 正确；由于⊥11A D 平面11ABB A ，⊂11A D 平面P A D 11，故平面⊥P A D 11平面AP A 1 故B 正确，当2201<<P A 时，1APD ∠为钝角，C 错；将面B AA 1与面11BCD A 沿B A 1展成平面图形，正视图 侧视图俯视图线段1AD 即为1PD AP +的最小值，利用余弦定理解221+=AD ，故D 正确，故答案为C ．考点：棱柱的结构特征． 9．下列命题中，错误的是（ ）A ．一条直线与两个平行平面中的一个相交，则必与另一个平面相交B ．平行于同一平面的两条直线不一定平行C ．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βD ．若直线l 不平行于平面α，则在平面α内不存在与l 平行的直线 【答案】B 【解析】试题分析: 由直线与平面的位置关系右知A 正确;平行于同一个平面的两条直线可以相交、平行或异面，故B 错，所以选B.考点:直线、平面平行与垂直的判定与性质.10．已知如图所示的正方体ABCD ﹣A 1B 1C 1D 1，点P 、Q 分别在棱BB 1、DD 1上，且=，过点A 、P 、Q作截面截去该正方体的含点A 1的部分，则下列图形中不可能是截去后剩下几何体的主视图的是（ ）【答案】A【解析】试题分析：当P 、B 1重合时，主视图为选项B ；当P 到B 点的距离比B 1近时，主视图为选项C ；当P 到B 点的距离比B 1远时，主视图为选项D ，因此答案为A. 考点：组合体的三视图11．一个几何体的三视图及尺寸如图所示，则该几何体的外接球半径为 （ ）A. B. C. D.【答案】C 【解析】试题分析：由三视图可知：该几何体是一个如图所示的三棱锥P-ABC ，它是一个正四棱锥P-ABCD 的一半，其中底面是一个两直角边都为6的直角三角形，高PE=4． 设其外接球的球心为O ，O 点必在高线PE 上，外接球半径为R ， 则在直角三角形BOE 中，BO 2=OE 2+BE 2=（PE-EO ）2+BE 2， 即R 2=（4-R ）2+（32）2，解得：R=174，故选C.考点：三视图，球与多面体的切接问题，空间想象能力12．如右图，在长方体1111ABCD A B C D -中，AB =11，AD =7，1AA =12，一质点从顶点A 射向点()4312E ，，，遇长方体的面反射（反射服从光的反射原理），将1i -次到第i 次反射点之间的线段记为()2,3,4i L i =，1L AE =，将线段1234,,,L L L L 竖直放置在同一水平线上，则大致的图形是（ ）【答案】C 【解析】 试题分析：因为37411>，所以1A E 延长交11D C 于F ，过F 作FM 垂直DC 于.M 在矩形1AA FM 中分析反射情况：由于35105AM =>，第二次反射点为1E 在线段AM 上，此时153E M =,第三次反射点为2E 在线段FM 上，此时24E M =,第四次反射点为3E 在线段1AF 上,由图可知，选C.考点：空间想象能力13．一块石材表示的几何体的三视图如图所示，将该石材切削、打磨、加工成球，则能得到的最大球的半径等于（ ）A.1B.2C.3D.4【答案】B【解析】试题分析：由图可得该几何体为三棱柱,因为正视图,侧视图,俯视图的内切圆半径最小的是正视图(直角三角形)所对应的内切圆,所以最大球的半径为正视图直角三角形内切圆的半径r , 则2286862r r r -+-+⇒=,故选B. 考点：三视图 内切圆 球 三棱柱14．已知二面角l αβ--为60︒，AB α⊂，AB l ⊥，A 为垂足，CD β⊂，C l ∈，135ACD ∠=︒，则异面直线AB 与CD 所成角的余弦值为 A ．14 B ．24 C ．34 D ．12【答案】B. 【解析】试题分析：如图作BE β⊥于E ，连结AE ，过A 作AG ∥CD ，作EG AG ⊥于G ，连结BG ，则.BG AG ⊥设2AB a =．在ABE ∆中，60,90,2,.BAE AEB AB a AE a ∠=︒∠=︒=∴=在Rt AEG ∆中，29045,90,cos 45.2GAE CAG AGE AG a a ∠=︒-∠=︒∠=︒∴=︒=在Rt ABG∆中，222cos 24AG BAG AB a ∠===∴异面直线AB 与CD 所成角的余弦值为24，故选B ．βαElBDACG考点：1.三垂线定理及其逆定理；2. 空间角（异面直线所成角）的计算．15．在空间直角坐标系Oxyz 中,已知(2,0,0)(2,2,0),(0,2,0),(1,1,2)A B C D .若123,,S S S 分别是三棱锥D ABC -在,,xOy yOz zOx 坐标平面上的正投影图形的面积，则（ ）A ．123S S S ==B ．21S S =且23S S ≠C ．31S S =且32S S ≠D ．32S S =且31S S ≠ 【答案】D 【解析】试题分析：三棱锥ABC D -在平面xoy 上的投影为ABC ∆，所以21=S ，设D 在平面yoz 、zox 平面上的投影分别为2D 、1D ，则ABC D -在平面yoz 、zox 上的投影分别为2OCD ∆、1OAD ∆，因为)2,1,0(1D ，)2,0,1(2D ，所以212=-S S ，故选D.考点：三棱锥的性质，空间中的投影，难度中等.16．正方形ABCD 的边长为2，点E 、F 分别在边AB 、BC 上，且1AE =，12BF =，将此正 方形沿DE 、DF 折起，使点A 、C 重合于点P ，则三棱锥P DEF -的体积是（ ） A ．13B 523 D ．23【答案】B【解析】试题分析：解：因为90,DPE DPF ∠=∠=所以,DP PE DP PF ⊥⊥又因为PE ⊂平面PEF ,PF ⊂平面PEF ,且PE PF P =,所以DP ⊥平面PEF在PEF ∆中，22223151,,1222PE PF EF EB BF ⎛⎫===+=+= ⎪⎝⎭所以222351222cos 33212EPF ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭∠==⨯⨯,225sin 133EPF ⎛⎫∠=-= ⎪⎝⎭ 所以11355sin 122234PEF S PE PF EPF ∆=⋅⋅∠=⨯⨯⨯= 115523346PEF P DEF D PEF V V DP S ∆--==⋅⋅=⨯⨯=三棱锥三棱锥 所以应选B.考点：1、直线与平面垂直的判定；2、正弦定理与余弦定理；3、棱锥的体积.17．高为的四棱锥S ﹣ABCD 的底面是边长为1的正方形，点S ，A ，B ，C ，D 均在半径为1的同一球面上，则底面ABCD 的中心与顶点S 之间的距离为（ ）A. B. C. D.【答案】A【解析】试题分析：由题意可知ABCD 是小圆，对角线长为，四棱锥的高为，推出高就是四棱锥的一条侧棱，最长的侧棱就是球的直径，然后利用勾股定理求出底面ABCD 的中心与顶点S 之间的距离．解：由题意可知ABCD 是小圆，对角线长为，四棱锥的高为，点S ，A ，B ，C ，D 均在半径为1的同一球面上，球的直径为2，所以四棱锥的一条侧棱垂直底面的一个顶点，最长的侧棱就是直径，所以底面ABCD 的中心与顶点S 之间的距离为：=故选A点评：本题是基础题，考查球的内接多面体的知识，能够正确推出四棱锥的一条侧棱垂直底面的一个顶点，最长的侧棱就是直径是本题的关键，考查逻辑推理能力，计算能力．18．二面角l αβ--为60°，A 、B 是棱l 上的两点，AC 、BD 分别在半平面,αβ内，AC l ⊥，BD l ⊥，且AB ＝AC ＝a ，BD ＝2a ，则CD 的长为( )A ．2aB ．5aC ．aD ．3a【答案】A【解析】试题分析：根据异面直线上两点间的距离公式2222cos EF d m n mn θ=++± ，对于本题中，d a =，m a =，2n =，60θ=，故()222222cos 602CD a a a a a a =++-⋅⋅⋅=．考点：异面直线上两点间距离,空间想象能力．19．长方体的表面积是24，所有棱长的和是24，则对角线的长是（ ）．Ａ．14 B ．4 C ．32 D ．23【答案】B【解析】试题分析：设出长方体的长、宽、高，表示出长方体的全面积，十二条棱长度之和，然后可得对角线的长度．考点：长方体的结构特征，面积和棱长的关系.20．已知棱长为l 的正方体1111ABCD A B C D -中，E ，F ，M 分别是AB 、AD 、1AA 的中点，又P 、Q 分别在线段11A B 11、A D 上,且11A P=A Q=x,0<x<1，设面MEF 面MPQ=l ，则下列结论中不成立的是( )A ．//l 面ABCDB ．l ⊥ACC ．面MEF 与面MPQ 不垂直D ．当x 变化时，l 不是定直线【答案】D【解析】试题分析：解：连结1111,,,AC BD AC B D ,,AC BD 交于点O 1111,AC B D 交于点1O由正方体的性质知，11111111////,,BD B D AC AC AC BD AC B D ⊥⊥，因为,E F 是,AD AB 的中点，所以//EF BD因为11A P A Q =,所以11//PQ B D所以//PQ EF ,所以//PQ 平面MEF ,//EF 平面MPQ , 由MEF 面MPQ=l ，EF ⊂ 平面MEF ，所以//EF l ，而EF ⊂平面ABCD ,l ⊂/平面ABCD , 所以，//l 面ABCD ，所以选项A 正确；由AC BD ⊥，//EF BD 得EF AC ⊥而//EF l ，所以l ⊥AC ，所以选项B 正确；连111,,MB MD O M ,则11//,O M AC 而1111,//,//AC A B AC BD BD EF A B MF ⊥⊥，所以，11,O M EF O M MF ⊥⊥,所以1O M ⊥平面MEF ，过直线l 与平面MEF 垂直的平面只能有一个，所以面MEF 与面MPQ 不垂直，所以选项C 是正确的；因为//EF l ，M 是定点，过直线外一点有且只有一条直线与已知直线平行，所以直线l 是唯一的，故选项D 不正确．考点：1、直线平面的位置关系；2、直线与直线，直线与平面，平面与平面的平行与垂直的判定及性质．21．如图，等边三角形ABC 的中线AF 与中位线DE 相交于G ，已知ED A '∆是△ADE 绕DE 旋转过程中的一个图形，下列命题中，错误的是( )A ．动点A '在平面ABC 上的射影在线段AF 上B ．恒有平面GF A '⊥平面BCDEC ．三棱锥EFD A -'的体积有最大值D ．异面直线E A '与BD 不可能垂直【答案】D【解析】试题分析：由于',A G DE FG DE ⊥⊥．所以DE ⊥平面'A FG ．经过点'A 作平面ABC 的垂线垂足在AF上．所以A 选项正确．由A 可知B 选项正确．当平面'A DE 垂直于平面BCDE 时，三棱锥EFD A -'的体积最大，所以C 正确．因为BD EF ，设2AC a =．所以'EF A E a ==，当'2A F a =时，32'(')2a A G GF A G GF a <+==．所以异面直线E A '与BD 可能垂直．所以D 选项不正确．考点：1．线面位置关系．2．面面的位置关系．3．体积公式．4．异面直线所成的角．5．空间想象力．22．已知棱长为l 的正方体1111ABCD A B C D -中，E ，F ，M 分别是AB 、AD 、1AA 的中点，又P 、Q 分别在线段11A B 11、A D 上,且11A P=A Q=x,0<x<1，设面MEF 面MPQ=l ，则下列结论中不成立的是( )A ．//l 面ABCDB ．l ⊥ACC ．面MEF 与面MPQ 不垂直D ．当x 变化时，l 不是定直线【答案】D【解析】试题分析：解：连结1111,,,AC BD AC B D ,,AC BD 交于点O 1111,AC B D 交于点1O由正方体的性质知，11111111////,,BD B D AC AC AC BD AC B D ⊥⊥，因为,E F 是,AD AB 的中点，所以//EF BD因为11A P A Q =,所以11//PQ B D所以//PQ EF ,所以//PQ 平面MEF ,//EF 平面MPQ ,由MEF 面MPQ=l ，EF ⊂ 平面MEF ，所以//EF l ，而EF ⊂平面ABCD ,l ⊂/平面ABCD , 所以，//l 面ABCD ，所以选项A 正确；由AC BD ⊥，//EF BD 得EF AC ⊥而//EF l ，所以l ⊥AC ，所以选项B 正确；连111,,MB MD O M ,则11//,O M AC 而1111,//,//AC A B AC BD BD EF A B MF ⊥⊥，所以，11,O M EF O M MF ⊥⊥,所以1O M ⊥平面MEF ，过直线l 与平面MEF 垂直的平面只能有一个，所以面MEF与面MPQ不垂直，所以选项C是正确的；EF l，M是定点，过直线外一点有且只有一条直线与已知直线平行，所以直线l是唯一的，故选因为//项D不正确．考点：1、直线平面的位置关系；2、直线与直线，直线与平面，平面与平面的平行与垂直的判定及性质．23．把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与前三个都相切，求第四个球的最高点与桌面的距离（）A．B．C．D．3【答案】A【解析】由题意，四球心组成棱长为2的正四面体的四个顶点，则正四面体的高．而第四个球的最高点到第四个球的球心距离为求的半径1，且三个球心到桌面的距离都为1，故第四个球的最高点与桌面的距离为，选A．24．如图所示，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA＝AB＝PD.则棱锥Q－ABCD的体积与棱锥P－DCQ的体积的比值是（）A. 2:1B. 1:1C. 1:2D. 1:3【答案】C。
立体几何大题训练及答案
1、如图，正方形所在平面与平面四边形所在平面互相垂直，△是等腰直角三角形，（1）线段的中点为，线段的中点为，求证：；（2）求直线与平面所成角的正切值.解：（1）取的中点为，连,,则,面/面, .............. 分5（2）先证出面，.............. 分8为直线与平面所成角，................ 分11................ 分142、己知多面体ABCDE中，DE平面ACD,, AC=AD=CD=DE=2 AB =1, O 为CD 的中点.（1）求证：AO平面CDE（2）求直线BD与平面CBE所成角的正弦值3、如图，在△中，，，点在上，交于，交于•沿将△翻折成△，使平面平面；沿将△翻折成△ ，使平面平面．（ 1 ）求证：平面；（2 ）若，求二面角的平面角的正切值.解：（1）因为，平面，所以平面.因为平面平面，且，所以平面. …2分同理，平面，所以，从而平面. …4分所以平面平面，从而平面.2)因为，，所以，，，．过E作，垂足为M，连结.由( 1)知，可得，所以，所以.所以即为所求二面角的平面角，可记为.在Rt△中，求得，所以. …4、如图，平面ABC,平面BCD, DE=DA=AB=AC,. M(1) 求直线EM与平面BCD所成角的正弦值；(2) P为线段DM上一点，且DM，求证：AP//DE. (12)分15 分为BC中点.解：(1) 平面,为在平面上的射影,为与平面所成角. …分2平面,, 设,又,. 在△中，，，又为中点，， ,.…5分在△中，，．……………………分 (7)2),为中点, ．又平面, ,平面．又平面,,分11 …分9又，平面. .............. 分13又平面，. .............. 分145、如图，已知ABCD是边长为1的正方形，AF丄平面ABCD, CE// AF,(1)证明：BD丄EF;(2)若AF= 1，且直线BE与平面ACE所成角的正弦值为,求的值.解：(1)连结BD、AC,交点为O. •/ ABCD是正方形/• BD丄AC ……2分•/ AF丄平面ABCD A AF丄BD ……4分••• BD丄平面ACEF (6)A BD丄EF ……7分(2)连结0E,由(1)知，BD丄平面ACEF所以/ BEO即为直线BE与平面ACE所成的角. ……10分•/ AF丄平面ABCD, CE// AF , • CE丄平面ABCD, CE1 BC,•/ BC =1 , AF= 1 ,贝U CE= , BE= , B0=,• RtA BEO 中，，…1盼因为解得. …… 15分6、如图在几何体中平面ABC分别是的中点.(1) 求证：平面CDE；(2) 求二面角的平面角的正切值.解：(1)连接ACR1R交EC于点F ,由题意知四边形ACCR1RE是矩形,贝U F是ACR1R的中连接DF, •/ D是AB的中点，•ABCR1R勺中位线，a BCR1R//DF， 4 分•/ BCR1RF面EDC DF平面EDC,• BCR1R//平面CDE. 7 分(2)作AH丄直线CD,垂足为H ,连接HE,•/ AAR1R丄平面ABC, • AAR1RL DC,CD丄平面AHE,CD丄EH ,••• AHE是二面角E -CD -A的平面角. 11分•/ D是AB的中点，• AH等于点B到CD的距离，在厶BCD中，求得：AH=, 在厶AEH中，即所求二面角的正切值为.7、如图，已知平面与直线均垂直于所在平面，且,( 1 )求证：平面；(2)若，求与平面所成角的正弦值.解：(1)证明：过点作于点，•••平面丄平面，•平面……2分又•••丄平面•- 〃 , ......... 分又•••平面• 〃平面 ......... 分(2) •••平面•,又•/••………………分8•点是的中点，连结，则•平面•//,•四边形是矩形………………分10设得：，又•••，•，从而，过作于点，则：•是与平面所成角…………………………………………分…… •，• 与平面所成角的正弦值为…………………………分14&如图，在直三棱柱中，是等腰直角三角形，，侧棱AA仁2, D, E分别为点，点E在平面ABD上的射影是的重心.(1) 求证：DE// 平面ACB；(2) 求A1B与平面ABD所成角的正弦值.12CC1 与A1B 的中9、如图，在侧棱垂直于底面的三棱柱ABC-A1B1中，底面△ ABC为等腰直角三角形，/ B=90°D为棱BB1的中点。
立体几何大题练习(附答案)
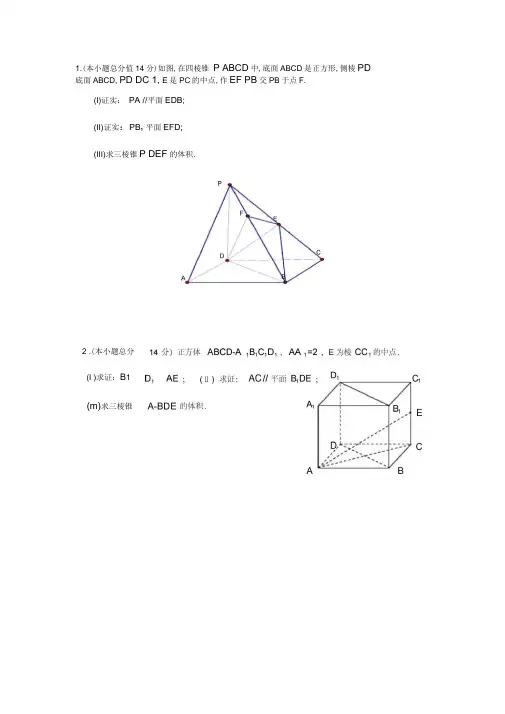
1.(本小题总分值14分)如图,在四棱锥 P ABCD 中,底面ABCD 是正方形,侧棱PD 底面ABCD, PD DC 1, E 是PC 的中点,作EF PB 交PB 于点F.(I)证实： PA //平面EDB; (II)证实：PB ,平面EFD; (III)求三棱锥P DEF 的体积.2 .(本小题总分值(m)求三棱锥(I )求证：B 118.(本小题总分值14分)如右图,在直角梯形ABCD中, B=90 °,1DC//AB,BC=CD= -AB=2 , G 为线段AB 的中点,将VADG 沿GD 2折起,使平面ADG 平面BCDG,得到几何体A-BCDG.(1)假设E,F分别为线段AC,AD的中点,求证：EF//平面ABG;(2)求证：AG 平面BCDG;(3)求V C-ABD 的值.4、(本小题总分值14分)如图4, AA是圆柱的母线, AB是圆柱底面圆的直径,C是底面圆周上异于A,B的任意一点, AA AB 2.(1)求证：BC 平面A〔AC ；(2)求三棱锥A ABC的体积的最大值.图4C (n ) 求证：EF 面PAC;〔出〕求三棱锥B-PAC的体积.6 .〔本小题总分值14分〕如图,平行四边形ABCD中,CD 1, BCD 60,且BD CD ,正方形ADEF 和平面ABCD成直二面角,G, H是DF , BE的中点.〔I〕求证：BD 平面CDE ;〔n〕求证：GH 〃平面CDE；〔出〕求三棱锥D CEF的体积.7.〔本小题总分值14分〕右图是一个直三棱柱〔以A i B i C i为底面〕被一平面所截得到的几何体,截面为ABC.A i B i = B i C i = l, ZAi B i C i = 90 ,AA i = 4,BB i=2, CC i=3.(I)设点O是AB的中点,证实：OC//平面A i B i C i;(II)求此几何体的体积.8 .(本小题总分值i4分)如图,在正方体ABCD—A i B i C i D i中,E、F为棱AD、AB的中点.(i )求证：EF//平面CB i D i；(2)求证：平面CAA i C■平面CB i D i.9 .(本小题总分值i4分)如图i ,在直角梯形ABEF中(图中数字表示线段的长度),将直角梯形DCEF沿CD折起,使平面DCEF 平面ABCD,连结局部线段后围成一个空间几何体,如图2.(I)求证：BE〃平面ADF ;(n)求三棱锥F BCE的体积.图图-10 .(本小题总分值14分)在直三棱柱ABC ABG中,AD 平面ABC,其垂足D落在直线A〔B上.(I )求证：BC A1B ；(n)假设AD J3, AB BC 2, P为AC的中点,求三棱锥P ABC的体积.B1…1 .解：(1)证实：连结AC, AC交BD于O,连结EO••・底面ABCD是正方形,,点O是AC的中点在PAC中,EO是中位线,,PA // EO而EO 平面EDB且PA 平面EDB,所以,PA //平面EDB.(2)证实：PD,底面ABCD 且DC 底面ABCD,,PD DCPD=DC,可知PDC是等腰直角三角形,而DE是斜边PC的中线,.DE PC ①同样由PD,底面ABCD,得PDXBC•••底面ABCD是正方形,有DCXBC,,BC,平面PDC 而DE 平面PDC, BC DE ②由①和②推得DE 平面PBC而PB 平面PBC, . DE PB又EF PB 且DE EF E,所以PB ,平面EFD................................ 8分(3) . PD DC 1,由 PD ,平面 ABCD,PDXBC,又.BCXCD, PDACD = D,BC± PC.-CL 2f在Z^BDE 中,DE -------- , BD22221 DE2 BE 2 BD 2 — 2 而由(2), PB,平面EFD,••.BC,平面 PCD,3 c-一 2 0,即 DEL BE.2PBXDE,因而 DEL 平面 BEF,2在 RtABPD 中,BF BP BD , BF1 1 . V DE EF PF 32 2.解：(I)证实：连结 BD ,那么 BD // B 1D 1,ABCD 是正方形,,AC BD. CE 面 ABCD,,CE BD .又 A .CE C, BD 面 ACE. . AE 面 ACE, . . BD AE ,• .B 1D 1 AE .(n)证实：作BB 1的中点F,连结AF 、CF 、EF.• •・E 、F 是 CC 、BB 1 的中点,,CE?B 1F , • •・四边形B 〔FCE 是平行四边形,, CF// B 1E .E,F 是 CC 、BB 1 的中点,,EF//BC ,又 BC//AD , EF //AD ...............14分136；Rt 革EFEF. AF I CF C , B 1EI ED E ,,平面 ACF 〃面 B 1DE .又 AC 平面 ACF , . . AC 〃面 B 1DE .4证实：二.是底面圆周上异于 A, B 的任意 柱底面圆的直径, •••BCXAC,……2 分,.AA1,平面 ABC , BC i 平面 ABC, . AAiXBC,…… 4 分•.AA i AAC=A , AA 1 i 平面 AA i C, AC i 平面 AA1 C, . EC ,平面AA1C.……6分 (2)解法 1 :设 AC=x ,在 RtMBC 中,BC = J AB 2 AC 2 h x 2(o<x<2),……7 分....1 一 … 1 11 -~~2故 V ARABC = —S VABC AA 1— — AC BC AA 1 _x \ 4x (0<x<2),13 3 23即 V A 「ABC =4“ x 2 1 \/x 2 (4 x 2)：J (x 2~2)2~4 . ……11 分 23 33,-0<x<2 , 0<x 2<4 ,「.当 x 2=2,即 x = 五时, 三棱锥A 1-ABC 的体积的最大值为 -.……14分35(1)证实：在三角形 PBC 中,E 是PC 中点.F 为PB 中点所以 EF//BC , BC 面ABC, EF 面ABC, 所以 EF 〃面ABC ……4分,四边形ADEF 是平行四边形,AF // ED ,(3)S ABD - AB AD 2 •2VA BDE VE ABD1S ~ SABDCE1S3 SABDCE2 3又AB 是.O 的直径,所以BC AC …… ⑵ ……7分 由(1) (2)得 BC 面PAC 因EF//BC BC 面PAC ,所以EF 面PAC ……9分(出)因PA OO 所在的平面,AC 是PC 在面ABC 内的射影,1V B PACV P ABC S ABC PA37 . (1)证实：作OD //.交片81于口,连C 1D .那么 OD // BB 1 // CC 1 .作BH(n) PA BC面ABC 面ABCBC PA所成角 PCA 450,PA=AC11分在Rt ABC 中,E 是PC 中点,BAC -, AC BC 2412分Q O 是AB 的中点,OD1-(AA 1 BB 1) 3 CC 1 .2那么ODCQ 是平行四边形,OC // C 1D .……4分Q C 1D 平面 C 1B 1A 且 OC 平面C1B1A ,OC // 面 A 1B 1C 1.(2)如图,过B 作截面BA 2c 2CC 1 于 A 2,//面ABG,分别交AA1,Q CC 1 面 BA 2c 2, CC 1BH ,那么BH 平面AC .又Q A 2B AB 1 1 , BC 2B 1c l 1 , BH --, 2V B AA 2C 2C1 S A A 2c 2c3BH 1 1 厂J.21 (1 2) '2 -3 2 22PCA 即为PC 与面ABC'.2----- …14分3所求几何体体积为：V V B AACC . 八八 2 J 2 J8 .〔本小题总分值14分〕折叠之后平行关系不变. BC 平面ADF , AD 平面 • .BC//平面 ADF ,V AB|C 1 A2BC 21八, SA A 1B 1C 1BB 1 - 2 1〔1〕证实：连结 BD .在长方体AC i 中, 对角线BD//B 1D 1. 又Q E 、F 为棱AD 、AB 的中点, ・.EF //BD . . .EF //BD 1. 又 B 1D 1 平面 CBD 1, EF 平面 CB 1D 1,,EF//平面 CB 1D 1. (2) Q 在长方体 AC ［中,AA 1,平面 A 1B 1C 1D 1,而 B 1D 1 平面 A 1B 1C 1D 1, . AA iX B i D i . 又Q 在正方形 A 1B 1C 1D 1 中,A 1C 1 XB 1D 1, .. B 1D 1,平面 CAA 1C 1. 又Q B 1D 1 平面 CB 1D 1,,平面 CAA 1C 1,平面 CB 〔D 1. 14分9 .〔本小题总分值14分〕 证实：〔I 〕证法一：取 DF 中点为G,连结AG, EG 中, 八 1一 八 一八.CE — DF ,,EG 〃CD 且 EG CD 2 又•••AB 〃CD 且AB CD,,EG 〃AB 且 EG AB四边形ABEG 为平行四边形,,BE//AG. BE 平面ADF , AG 平面 ADF,. ・BE 〃平面 ADF ,证法二：由图1可知BC // AD , CE//DFV A 1B 1C 1 A 2BC 2同理CE〃平面ADF ................... 4分. BCI CE C , BC , CE 平面BCE ,,平面BCE 〃平面ADF ......... 6分. BE 平面BCE ,,BE 〃平面ADF ......... 7 分(II)解法1：V F BCE V B CEF .................... 8分由图1可知BC CD.平面DCEF 平面ABCD ,平面DCEF I平面ABCD CDBC 平面ABCD,..BC 平面DCEF ,1 1由图 1 可知DC CE 1 S CEF -CE DC .................. ........... 12 分2 2V F BCE V B CEF 3 BC S CEF解法2：由图1可知CD BC , CD CEBCI CE C. .CD 平面BCE ,. DF //DC点F到平面BCE的距离等于点D到平面BCE的距离为1 ,由图1可知BC CE 1 S BCE 1-BC CE 2BCE 1 … c 13 CD S BCE 6解法3:过E作EH FC ,垂足为H , ....................... 8分由图1可知BC CD•••平面DCEF 平面ABCD,平面DCEFI 平面ABCD CD11分A B11分BC 平面 ABCD,. BC 平面 DCEF ,EH 平面 DCEF.BC EH,EH 平面BCF 1 、5S BCF -BC DF —, .......... 12 分 2 2又 BD CD. .BD ¥® CDE(n )证实：连结 EA ,那么G 是AE 的中点••• EAB 中,GH // AB又 AB//CD . GH //CD . .GH 〃平面CDE 11分 由 BC FC , FC .DC 2 DF 2 5, 在 CEF 中,由等面积法可得 EHV F BCE V E BCF EH S BCF13分 14分 6.(本小题总分值14分)(I )证实：平面 ADEF 平面ABCD ,交线为ADED AD• .ED 平面ABCDED BD2〔出〕解：设Rt BCD中BC边上的高为h1 1 -依题意：一2 h 1 32 23• • h —2_ ___ _____ .. 一、. .3即：点C到平面DEF的距离为- ---------------- 10•V D CEF V C DEF .32,33分------- 14 分。
立体几何练习题(含答案)
立几测001试一、选择题：1．a 、b 是两条异面直线，下列结论正确的是（ ）A ．过不在a 、b 上的任一点，可作一个平面与a 、b 都平行B ．过不在a 、b 上的任一点，可作一条直线与a 、b 都相交C ．过不在a 、b 上的任一点，可作一条直线与a 、b 都平行D ．过a 可以且只可以作一个平面与b 平行2．空间不共线的四点，可以确定平面的个数为 ( )Ａ．0 Ｂ．1 Ｃ．1或4 Ｄ．无法确定3．在正方体1111ABCD A B C D -中，M 、N 分别为棱1AA 、1BB 的中点，则异面直线CM 和1D N 所成角的正弦值为 ( ) Ａ．19 Ｂ．2345 254．已知平面α⊥平面β，m 是α内的一直线，n 是β内的一直线，且m n ⊥，则：①m β⊥；②n α⊥；③m β⊥或n α⊥；④m β⊥且n α⊥。
这四个结论中，不正确．．．的三个是 ( )Ａ．①②③ Ｂ．①②④ Ｃ．①③④ Ｄ．②③④5.一个简单多面体的各个面都是三角形，它有6个顶点，则这个简单多面体的面数是( ) A. 4 B. 5 C. 6 D. 86. 在北纬45°的纬度圈上有甲、乙两地，两地经度差为90°，则甲、乙两地最短距离为（设地球半径为R ）( ) A.R π42 B. R 3π C. R 2π D. 3R7. 直线l ⊥平面α，直线m ⊂平面β，有下列四个命题(1)m l ⊥⇒βα// (2)m l //⇒⊥βα (3)βα⊥⇒m l // (4)βα//⇒⊥m l 其中正确的命题是( )A. (1)与(2)B. (2)与(4)C. (1)与(3)D. (3)与(4)8. 正三棱锥的侧面均为直角三角形，侧面与底面所成角为α，则下列不等式成立的是( ) A. 60πα<< B.46παπ<< C.34παπ<< D.23παπ<<9．ABC ∆中，9AB =，15AC =，120BAC ∠=︒，ABC ∆所在平面α外一点P 到点A 、B 、C 的距离都是14，则P 到平面α的距离为( )Ａ．7 Ｂ．9 Ｃ．11 Ｄ．1310．在一个45︒的二面角的一个平面内有一条直线与二面角的棱成角45︒，则此直线与二面角的另一个平面所成角的大小为 ( )Ａ．30︒ Ｂ．45︒ Ｃ．60︒ Ｄ．90︒11. 如图,E, F 分别是正方形SD 1DD 2的边D 1D,DD 2的中点, 沿SE,SF,EF 将其折成一个几何体,使D 1,D,D 2重合,记作 D.给出下列位置关系:①SD ⊥面DEF; ②SE ⊥面DEF;③DF ⊥SE; ④EF ⊥面SED,其中成立的有: ( )Ａ. ①与② B. ①与③ C. ②与③ D. ③与④12. 某地球仪的北纬60度圈的周长为6πcm,则地球仪的表面积为( )A. 24πcm 2B. 48πcm 2C. 144πcm 2D. 288πcm 2二、填空题（本大题共4小题，每小题4分，共16分） 13. 直二面角α—MN —β中，等腰直角三角形ABC 的斜边BC ⊂α，一直角边AC ⊂β，BC 与β所成角的正弦值是46，则AB 与β所成角大小为__________。
高三精选立体几何大题30题(含详细解答)
A BC第1题图ABCD第1题图立体几何大题1．如下图，一个等腰直角三角形的硬纸片ABC中，∠ACB＝90°，AC＝4cm，CD是斜边上的高沿CD 把△ABC折成直二面角．（1）如果你手中只有一把能度量长度的直尺，应该如何确定A，B的位置，使二面角A－CD－B是直二面角？证明你的结论．（2）试在平面ABC上确定一个P，使DP与平面ABC内任意一条直线都垂直，证明你的结论．（3）如果在折成的三棱锥内有一个小球，求出小球半径的最大值．2．如图，已知正四棱柱ABCD—A1B1C1D1的底面边长为3，侧棱长为4，连结A1B过A作AF⊥A1B垂足为F，且AF的延长线交B1B于E。
（Ⅰ）求证：D1B⊥平面AEC；（Ⅱ）求三棱锥B—AEC的体积；（Ⅲ）求二面角B—AE—C的大小的正弦值.3．如图，正三棱柱ABC—A1B1C1的底面边长为1，点M在BC上，△AMC1是以M为直角顶点的等腰直角三角形.（I）求证：点M为BC的中点；（Ⅱ）求点B到平面AMC1的距离；（Ⅲ）求二面角M—AC1—B 的正切值. 4．如图，已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，三角形ACD是正三角形，且AD=DE=2，AB=1，F是CD的中点．（Ⅰ）求证：AF∥平面BCE；（Ⅱ）求多面体ABCDE的体积；（Ⅲ）求二面角C-BE-D 的正切值．5．已知：ABCD是矩形，设PA=a，PA⊥平面ABCD.M、N分别是AB、PC的中点.（Ⅰ）求证：MN⊥AB；（Ⅱ）若PD=AB，且平面MND⊥平面PCD，求二面角P—CD—A的大小；（Ⅲ）在（Ⅱ）的条件下，求三棱锥D—AMN的体积.6．在正方体ABCD—A1B1C1D1中，P、M、N分别为棱DD1、AB、BC的中点。
（I）求二面角B1—MN—B的正切值；（II）证明：PB⊥平面MNB1；（III）画出一个正方体表面展开图，使其满足“有4个正方形面相连成一个长方形”的条件，并求出展开图中P、B两点间的距离。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
…数学立体几何练习题一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个是符合题目要求的． 1．如图，在正方体－A 1B 1C 1D 1中，棱长为a ，M 、N 分别为A 1B 和上的点，A 1M ＝＝，则与平面1C 1C 的位置关系是( ) A ．相交 B ．平行 C ．垂直 D ．不能确定2．将正方形沿对角线折起，使平面⊥平面，E 是中点，则AED ∠的大小为（ ） A.45 B.30 C.60D.90 ]3．，，是从P 引出的三条射线，每两条的夹角都是60º，则直线与平面所成的角的余弦值为（ ）A ．12B 。
32C 。
33D 。
634．正方体—A 1B 1C 1D 1中，E 、F 分别是1与1的中点，则直线与D 1F 所成角的余弦值是A ．15B 。
13C 。
12D 。
325． 在棱长为2的正方体1111D C B A ABCD -中，O 是底面的中心，E 、F 分别是1CC 、的中点，那么异面直线和1FD 所成的角的余弦值等于（ ） A ．510B ．32C ．55 D ．5156．在正三棱柱1B 1C 1中，若2，A A 1=1，则点A 到平面A 1的距离为（ ）A ．43 B ．23 C ．433 D ．3：7．在正三棱柱1B 1C 1中，若1,则1与C 1B 所成的角的大小为（ ）ºB. 90ººD. 75º8．设E ，F 是正方体1的棱和D 1C 1的中点，在正方体的12条面对角线中，与截面A 1成60°角的对角线的数目是（ ） A ．0B ．2C ．4D ．6二、填空题：本大题共6小题，每小题5分，共30分． 9.在正方体－A 1B 1C 1D 1中，M 、N 分别为棱1和1的中点，则〈CM ，1D N 〉的值为.10．如图，正方体的棱长为1，C 、D分别是两条棱的中点， A 、B 、M 是顶点，那么点M 到截面的距离是 .11．正四棱锥的所有棱长都相等，E 为中点，则直线与截面所成的角为 ．12．已知正三棱柱1B 1C 1的所有棱长都相等，D 是A 1C 1的中点，则直线与平面B 1所成角的正弦值为 .：13．已知边长为的正三角形中，E 、F 分别为和的中点，⊥面，且2，设平面α过且与平行，则与平面α间的距离AB|D CABCDP 为 ．14．棱长都为2的直平行六面体—A 1B 1C 1D 1中，∠60°，则对角线A 1C 与侧面1D 1所成角的余弦值为.三、解答题:本大题共6小题，共80分。
解答需写出必要的文字说明、推理过程或计算步骤.15．如图，直三棱柱111C B A ABC -，底面ABC ∆中，＝＝1，90=∠BCA ，棱21=AA ，M 、N 分别A 1B 1、A 1A 是的中点． (1) 求的长； （(2) 求〉〈11,cos CB BA 的值；(3) 求证：N C B A 11⊥．16．如图，三棱锥P —中， ⊥平面，2，，D 是上一点， 且⊥平面．(1) 求证：⊥平面；:(2) 求异面直线与所成角的大小；(3)求二面角的大小的余弦值．xy…17．如图所示，已知在矩形中，1，（a >0），⊥平面，且1．·（1）试建立适当的坐标系，并写出点P 、B 、D 的坐标；（2）问当实数a 在什么范围时，边上能存在点Q ， 使得⊥（3）当边上有且仅有一个点Q 使得⊥时， 求二面角的余弦值大小．.18. 如图，在底面是棱形的四棱锥ABCD P -中，,,60a AC PA ABC ===∠ aPD PB 2==，点E 在PD 上，且PE :(1) 证明 ⊥PA 平面ABCD ；(2) 求以为棱，EAC 与DAC 为面的二面角θ(3) 在棱上是否存在一点F ，使BF ∥平面AEC 证明你的结论．/19. 如图四棱锥P —中，底面是平行四边形，⊥平面，垂足为G ，G 在上，且＝4，GD AG 31=，⊥，＝＝2，E 是的中点．QP DCBA C *(1)求异面直线与所成的角的余弦值；(2)求点D到平面的距离；(3)若F点是棱上一点，且⊥，求FCPF的值．]20.已知四棱锥S－的底面是正方形，⊥底面，E是上的任意一点．(1)求证：平面⊥平面；(2)设＝4，＝2，求点A到平面的距离；&(3)当的值为多少时，二面角B－－D的大小为120°理科立体几何训练题（B）答案一、选择题题号<12345678%答案B D D A D B B-CPA G&CDFEA BC DP xyz二、 填空题9. 10． 11. 45° 12． 4513． 3321443三、解答题15解析：以C 为原点建立空间直角坐标系xyz O -. (1) 依题意得B （0，1，0），M （1，0，1）．(2) 依题意得A 1（1，0，2），B （0，1，0）1，2）.563),2,1,0(),2,1,1(1111===⋅=-=∴CB BA CB BA 1030,cos 11=>=<∴CB BA CB BA . (3) 证明：依题意得C 1（0，0，2），N )0,21,21(),2,1,1(),2,21,21(11=--=∴N C B A . NC B A N C B A 1111,002121⊥∴=++-=⋅∴，16．解析： (1) ∵⊥平面,⊂AB 平面，∴⊥.∵⊥平面，⊂AB 平面，∴⊥．又C CD PC = ，∴⊥平面．(2 由(I) ⊥平面，∵2， 又∵，可求得．以B 为原点， 如图建立坐标系．则Ａ（０,０），Ｂ（0,0,0），C （,０,0），P （,０,2）．AP =(,－,2)，BC =(,0,0)． 则AP BC ⋅×+0+0=2． <x'cos AP,BC <>AP BCAP BC ⋅⋅2222⨯ 21．∴异面直线与所成的角为3π．（3）设平面的法向量为 (x ，y ，z )．AB =(0, －,0)AP (,－,2)，则AB 0,AP 0.⎧⋅=⎪⎨⋅=⎪⎩mm即0,20.z ⎧=⎪-+=解得0,y x =⎧⎪⎨=⎪⎩令 -1,得 (2，0，-1)．由⊥平面易知：平面⊥平面，取的中点E ，连接，则BE →为平面的一个法向量，)0,1,1(22)0,22,22(==→BE ，故平面的法向量也可取为 (1，1，0)．cos ,⋅<>=m nm n m n=33232=⨯. ∴二面角的大小的余弦值为33．>17．解析：（1）以A{别为x 、y 、z ∵1，，∴P （0，0，1），B （1，0，0），D （0，a ，0）．（2）设点Q （1，x ，0），则(1,,0),(1,,1)DQ x a QP x =-=--．由0DQ QP •=，得x 21=0．显然当该方程有非负实数解时，边上才存在点Q ，使得⊥，故只须⊿2-4≥0．)因a >0，故a 的取值范围为a ≥2．（3）易见，当2时，上仅有一点满足题意，此时1，即Q 为的中点．取的中点M ，过M 作⊥，垂足为N ，连结、．则M （0，1，0），P （0，0，1），D （0，2，0）．∵D 、N 、P 三点共线， ∴(0,1,0)(0,1,1)(0,1,)111MD MP MN +λ+λ--λλ===+λ+λ+λ．又(0,2,1)PD =-，且0MN PD •=， 故(0,1,)232(0,2,1)0113-λλ-λ•-==⇒λ=+λ+λ．于是22(0,1,)1233(0,,)25513MN -==+． 故12(1,,)55NQ NM MQ MN AB =+=-+=--．》∵1202()(1)()055PD NQ •=+⨯-+-⨯-=，∴PD NQ ⊥．（资料来源：168） ∴∠为所求二面角的平面角． ∵6cos 6||||NM NQ MNQ NM NQ •∠==注：该题还有很多方法解决各个小问，以上方法并非最简.<18解析：（1）传统方法易得证明（略）（2）传统方法或向量法均易解得 30=θ；（3）解 以A 为坐标原点，直线AP AD ,分别为y 轴、z 轴，过AzyxBCDAPEF 点垂直于平面的直线为x 轴，建立空间直角坐标系（如图）．由题设条件，相关各点的坐标为)0,21,23(),0,21,23(),0,0,0(a a C a a B A -)31,32,0(),,0,0(),0,,0(a a E a P a D所以=AE )31,32,0(a a ，=AC )0,21,23(a a ，=AP ),,0,0(a =PC ),21,23(a a a -点，=BP ),21,23(a a a -，设点F 是棱PC 上的==PC PF λ),21,23(a a a λλλ-，其中10<<λ，则))1(),1(21),1(23(λλλ-+-=+=a a a PF BP BF ．令AE AC BF 21λλ+=得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-+=+=-221131)1(3221)1(2123)1(23λλλλλλλa a a a a a a《解得23,21,2121=-==λλλ，即21=λ时，AE AC BF 2321+-=．亦即，F 是的中点时，AE AC BF ,,共面，又⊄BF 平面AEC ，所以当F 是的中点时，BF ∥平面AEC ．19解析：(1)以G 点为原点，GP GC GB 、、为x 轴、y 轴、 z 轴建立空间直角坐标系，则B (2，0，0)，C (0，2，0)，P (0，0，4)，故E (1，1，0)，GE ＝(1，1，0)， PC＝(0，2，4)。
10102022||||cos =⋅=⋅⋅>=<PC GE PC GE PC GE ，，∴与所成的余弦值为1010．(2)平面的单位法向量n ＝(0，±1，0)PA G B，DFE∵)02323(4343，，-===BC AD GD ， ∴点D 到平面的距离为⋅GD |n |＝23.(3)设F (0，y ，z )，则)2323()02323()0(z y z y DF ，，，，，，-=--=。
∵GCDF⊥，∴0=⋅GC DF ，（资料来源：168）即032)020()2323(=-=⋅-y z y ，，，，，∴23=y , 又PCPFλ=，即(0，23，z －4)＝λ(0，2，－4)， ∴1，故F (0，23，1) ，)1210()3230(-=-=，，，，，FC PF ，∴FC PF 352352PF PC ==。
20解析：(1)∵⊥平面，⊂平面，∴⊥，∵四边形是正方形，∴⊥，∴⊥ 平面， ∵⊂平面，∴平面⊥平面. (2)设∩＝F ，连结，则⊥， ∵＝2，＝4，∴＝2， ＝＝＝3，∴S △＝·＝·2·3＝6， 设点A 到平面的距离为h ，∵⊥平面，∴·S △·h ＝·S △·，∴6·h ＝·2·2·4，∴h ＝，即点A 到平面的距离为.(3)设＝a ，以A 为原点，、、所在直线分别为x 、y 、z 轴建立空间直角坐标系，为计算方便，不妨设＝1，则C (1,1,0)，S (0,0，a )，B (1,0,0)，D (0,1,0)，∴SC ＝(1,1，－a )，SB ＝(1,0，－a )，SD ＝(0,1，－a )，再设平面、平面的法向量分别为n 1＝(x 1，y 1，z 1)，n 2＝(x 2，y 2，z 2)，则111111100n SC x y az n SB x az ⎧=++=⎪⎨=-=⎪⎩∴y 1＝0，从而可取x 1＝a ，则z 1＝1，∴n 1＝(a,0,1)， 222222200n SC x y az n SB x az ⎧=++=⎪⎨=-=⎪⎩ ∴x 2＝0，从而可取y 2＝a ，则z 2＝1，∴n 2＝(0，a,1)， ∴〈n 1，n 2〉＝，要使二面角B －－D 的大小为120°，则＝，从而a ＝1， 即当＝＝1时，二面角B －－D 的大小为120°.。