《欧拉公式的应用》PPT课件
合集下载
《欧拉公式的应用》PPT课件
3
4、求积分
例1： /
4
eit
dt
iei/4 i i
1
i
i
1
i1
1
0
2 2
2 2
例2：
1 dx
x4 1
2iRzec0s
f
z
Re s z c1
f
z
2i
1 4
3i
z 1 z2 2iaz 1
z z1
a2 1
5、 倍角和半角的
cot
证：左
e2i e2i i e2i e2i
e2i e2i
sin 2 1 cos 2
1
2i e2i
e2i
2、求方根
例： 4 1 i 4
i
2n i4
2e 4 8 2e 4 n 0,1,2,3
3、初等函数求值
例： Log 1
3i ln 2 i 2 2n ln 2 2n 1 in 0,1,2,
3
设m是大于1的整数，（a,m）=1，则 am 1mod m
《复变函数论》中的欧拉函数：
ei cos i sin (Eulersformula )
《数值分析》中的欧拉函数：
一般的，设已作出该折线的极点,过依方向场的方 向再推进到，显然两个极点的坐标有以下关系
yn1 yn xn1 xn
将欧拉公式换为得到欧拉公式成为人们公认的最优美公式被视为数学美的一个象征数学家们评价它是上帝创造的公sincosi上帝创造的公式欧拉公式的两个基本性质由欧拉公式可以看出在复数域内指数函数是周期函数具有基本周期cos1sin1cossincossincossincos2sin21012ki2在欧拉公式中用代替得到由上式容易看出正弦函数是奇函数余弦函数是偶函数
《高一数学欧拉公式》课件
THANKS
感谢观看
+ i)(1 - i)} = - frac{1}{2} + frac{1}{2}i$，故答案为$- frac{1}{2} +
frac{1}{2}i$.
习题二
题目：已知$i$为虚数单位，复数$z$满足$frac{2 + i}{z} = i$，则复数$z =$( )
答案：B
解析：由$frac{2 + i}{z} = i$，得$z = frac{2 + i}{i} = frac{(2 + i)i}{i^{2}} = frac{- 1 + 2i}{- 1} = 1 + i$.故选B.
总结词
统一处理方式
详细描述
欧拉公式揭示了三角函数和指数函数之间的内在联系，使得在微积分中处理这两类函数时可以采用统一的处理方 式，简化了一些微积分问题的求解过程。
在复数中的应用
总结词
复数表示的桥梁
详细描述
欧拉公式是复数表示的桥梁，它可以将复数表示为三角函数的形式，使得复数的运算更加直观和方便 。同时，欧拉公式在复变函数和复分析等领域也有着广泛的应用。
欧拉公式在物理、工程、金融等领域也有广泛应用，例如在解决波动方程、计算复 利、评估期权价格等问题中都发挥了关键作用。
欧拉公式的历史背景
欧拉是一位杰出的数学家，他 在18世纪发现了欧拉公式。
欧拉公式的发现过程充满了曲 折和探索，它是欧拉在解决其 他数学问题的过程中偶然发现 的。
欧拉公式的发现为数学和物理 学的发展做出了巨大贡献，被 誉为数学史上的里程碑之一。
总结词独特的优势 。
详细描述
例如，欧拉公式的一个变种是球坐标系下的形式，它将三维空间的点表示为球坐标系中 的(r, θ, φ)，其中r是点到原点的距离，θ是点在xoy平面上的投影与x轴的夹角，φ是点 在xz平面上的投影与x轴的夹角。这种形式在处理球对称问题时非常有用。此外，还有
欧拉公式1 PPT课件
(5) 图形编号 （5） （6） （7）
(6) 顶点数V
(7)
面数F 5
8 12
棱数E
5
7 12
8
12 24
多面体
简单多面体
表面经过连续变形能变成一个球面 的多面体
简单多面体 欧拉示性数： 在欧拉公式中令
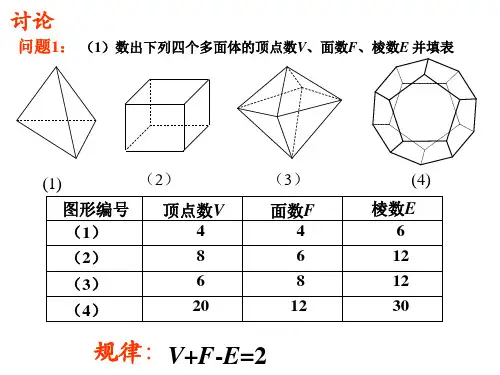
V+F-E=2
欧拉公式
，叫欧拉示性数
讨论
E1
问题2：如何证明欧拉公式 D1 A1 B C
1 1
D 压缩成 E E1 A1 A D1 C1 B1 C
D 平面图形 C
E A B
B
讨论
E1
问题2：如何证明欧拉公式 D1 A1 B C
1 1
D 压缩成 E E1 A1 A D1 C1 B1 C
D 平面图形 C
E A B
B
讨论
E1
问题2：如何证明欧拉公式 D1 A1 B C
1 1
D 压缩成 E E1 A1 A D1 C1 B1 C
思考3： n1+n2+· · · +nF和多面体的棱数E有什么关系
n1+n2+· · · +nF：如何证明欧拉公式 D1 A1 B C
1 1
D 压缩成 E E1 A1 A D1 C1 B1 C
D 平面图形 C
E A B
B
∴所有面的内角和=（E－F）· 3600
思考4：设平面图形中最大多边形（即多边形ABCDE）是m边形，则它和它 内部的全体多边形的内角总和是多少？
问题3:欧拉公式的应用
例1
1996年的诺贝尔化学奖授予对发现C60有重大贡献的 三位科学家．C60是有60 个C原子组成的分子，它结构为简 单多面体形状．这个多面体有60个顶点，从每个顶点都引出 3条棱，各面的形状分别为五边形或六边形两种．计算C60分 子中形状为五边形和六边形的面各有多少？
高一数学欧拉公式(PPT)5-3
欧拉
著名的数学家，瑞士人，大部分时间在俄国和法 国度过．他16岁获得硕士学位，早年在数学天才贝努 里赏识下开始学习数学，毕业后研究数学，是数学史 上最高产的作家．在世发表论文700多篇，去世后还 留下100多篇待发表．其论著几乎涉及所有数学分 支．他首先使用f(x)表示函数，首先用∑表示连加，首 先用i表示虚数单位．在立体几何中多面体研究中，首 先发现并证明欧拉公式．
讨论
问题1： （2）数出下列四个多面体的顶点数V、面数F、棱数E 并填表
(5)
图形编号 （5） （7） （6）
顶点数V 5 16
7
面数F 5 16
8Leabharlann (8)棱数E 8 32 12
简单多面体 V+F-E=2（欧拉公式）
欧拉公式
长，家庭教师和家长，店员和店主）。 【宾服】ī〈书〉动服从；归附。 【宾服】ī?〈方〉动佩服：你说的那个理，俺不～。 【宾馆】ī名招待来宾住宿的地 方。现指较大而设施好的旅馆。 【宾客】ī名客人（总称）：迎接八方～。 【宾朋】ī名宾客；朋友：～满座。 【宾语】ī名动词的一种连带成分，一般在动词 后边，用来回答“谁？”或“什么？”例如“我找； / 笔趣阁小说网；厂长”的“厂长”，“他开拖拉机”的“拖拉机”，“接受批 评”的“批评”，“他说他不知道”的“他不知道”。有时候一个动词可以带两个宾语，如“教我们化学”的“我们”和“化学”。 【宾至如归】īī客人到 了这里就像回到自己的家一样，形容旅馆、饭馆等招待周到。 【宾主】ī名客人和主人：～双方进行了友好的会谈。 【彬】ī①［彬彬］（īī）〈书〉形文雅的 样子：～有礼｜文质～。②（ī）名姓。 【傧】（儐）ī［傧相］（ī）名①古代称接引宾客的人，也指赞礼的人。②举行婚礼时陪伴新郎新娘的人：男～｜ 女～。 【斌】ī同“彬”。 【滨】（濱）ī①水边；近水的地方：海～｜湖～｜湘江之～。②靠近（水边）：～海｜～江。③（ī）名姓。 【缤】（繽）ī［缤 纷］（ī）〈书〉形繁多而凌乱：五彩～｜落英（花）～。 【槟】（檳、梹）ī［槟子］（ī?）名①槟子树，花红的一种，果实比苹果小，红色，熟后转紫红， 味酸甜带涩。②这种植物的果实。 【镔】（鑌）ī［镔铁］（ī）名精炼的铁。 【濒】（瀕）ī①紧靠（水边）：～湖｜东～大海。②临近；接近：～危｜～行。 【濒绝】ī动濒临灭绝或绝迹：～物种。 【濒临】ī动紧接；临近：我国～太平洋｜精神～崩溃的边缘。 【濒死】ī动临近死亡：从～状态下抢救过来。 【濒危】 ī动接近危险的境地，指人病重将死或物种临近灭绝：病人～｜～动物。 【濒于】ī动临近；接近（用于坏的遭遇）：～危境｜～绝望｜～破产。 【豳】ī古地 名，在今陕西彬县、旬邑一带。也作邠。 【摈】（擯）〈书〉抛弃；排除：～诸门外｜～而不用。 【摈斥】动排斥：～异己。 【摈除】动排除；抛弃：～
著名的数学家，瑞士人，大部分时间在俄国和法 国度过．他16岁获得硕士学位，早年在数学天才贝努 里赏识下开始学习数学，毕业后研究数学，是数学史 上最高产的作家．在世发表论文700多篇，去世后还 留下100多篇待发表．其论著几乎涉及所有数学分 支．他首先使用f(x)表示函数，首先用∑表示连加，首 先用i表示虚数单位．在立体几何中多面体研究中，首 先发现并证明欧拉公式．
讨论
问题1： （2）数出下列四个多面体的顶点数V、面数F、棱数E 并填表
(5)
图形编号 （5） （7） （6）
顶点数V 5 16
7
面数F 5 16
8Leabharlann (8)棱数E 8 32 12
简单多面体 V+F-E=2（欧拉公式）
欧拉公式
长，家庭教师和家长，店员和店主）。 【宾服】ī〈书〉动服从；归附。 【宾服】ī?〈方〉动佩服：你说的那个理，俺不～。 【宾馆】ī名招待来宾住宿的地 方。现指较大而设施好的旅馆。 【宾客】ī名客人（总称）：迎接八方～。 【宾朋】ī名宾客；朋友：～满座。 【宾语】ī名动词的一种连带成分，一般在动词 后边，用来回答“谁？”或“什么？”例如“我找； / 笔趣阁小说网；厂长”的“厂长”，“他开拖拉机”的“拖拉机”，“接受批 评”的“批评”，“他说他不知道”的“他不知道”。有时候一个动词可以带两个宾语，如“教我们化学”的“我们”和“化学”。 【宾至如归】īī客人到 了这里就像回到自己的家一样，形容旅馆、饭馆等招待周到。 【宾主】ī名客人和主人：～双方进行了友好的会谈。 【彬】ī①［彬彬］（īī）〈书〉形文雅的 样子：～有礼｜文质～。②（ī）名姓。 【傧】（儐）ī［傧相］（ī）名①古代称接引宾客的人，也指赞礼的人。②举行婚礼时陪伴新郎新娘的人：男～｜ 女～。 【斌】ī同“彬”。 【滨】（濱）ī①水边；近水的地方：海～｜湖～｜湘江之～。②靠近（水边）：～海｜～江。③（ī）名姓。 【缤】（繽）ī［缤 纷］（ī）〈书〉形繁多而凌乱：五彩～｜落英（花）～。 【槟】（檳、梹）ī［槟子］（ī?）名①槟子树，花红的一种，果实比苹果小，红色，熟后转紫红， 味酸甜带涩。②这种植物的果实。 【镔】（鑌）ī［镔铁］（ī）名精炼的铁。 【濒】（瀕）ī①紧靠（水边）：～湖｜东～大海。②临近；接近：～危｜～行。 【濒绝】ī动濒临灭绝或绝迹：～物种。 【濒临】ī动紧接；临近：我国～太平洋｜精神～崩溃的边缘。 【濒死】ī动临近死亡：从～状态下抢救过来。 【濒危】 ī动接近危险的境地，指人病重将死或物种临近灭绝：病人～｜～动物。 【濒于】ī动临近；接近（用于坏的遭遇）：～危境｜～绝望｜～破产。 【豳】ī古地 名，在今陕西彬县、旬邑一带。也作邠。 【摈】（擯）〈书〉抛弃；排除：～诸门外｜～而不用。 【摈斥】动排斥：～异己。 【摈除】动排除；抛弃：～
高一数学欧拉公式(PPT)5-1
欧拉
著名的数学家，瑞士人，大部分时间在俄国和法 国度过．他16岁获得硕士学位，早年在数学天才贝努 里赏识下开始学习数学，毕业后研究数学，是数学史 上最高产的作家．在世发表论文700多篇，去世后还 留下100多篇待发表．其论著几乎涉及所有数学分 支．他首先使用f(x)表示函数，首先用∑表示连加，首 先用i表示虚数单位．在立体几何中多面体研究中，首 先发现并证明欧拉公式．
讨论
问题1： （2）数出下列四个多面体的顶点数V、面数F、棱数E 并填表
(5)
图形编号 （5） （7） （6）
顶点数V 5 16
7
面数F 5 16
8
(Hale Waihona Puke )棱数E 8 32 12简单多面体 V+F-E=2（欧拉公式）
欧拉公式
他描写成刚正严明、不畏权势的清官的典型。 【包谷】〈方〉名玉米。也作苞谷。 【包管】动担保（表示说话人的自信）：～退换｜他这种病～不用吃就会 好。 【包裹】①动包；包扎：用布把伤口～起来。②名包扎成件的包儿：他肩上背着一个小～｜我到邮局寄～去。 【包含】动里边含有：这句话～好几层意 思。 【包涵】?ɑ动客套话，请人；优游 优游 ； 原谅：唱得不好，大家多多～！ 【包伙】①（－∥－）动包饭?。②名包饭?。 【包 机】ī①动定期租用飞机：开展～业务。②名包乘的飞机：一架旅游～。 【包间】名宾馆和餐饮、等场所设的供某位或某些客人专用的房间。 【包金】ī动用 薄金叶包在金属首饰外面：～项链。 【包金】ī名包银。 【包举】〈书〉动总括；全部占有：～无遗。 【包括】动包含（或列举各部分，或着重指出某一部 分）：语文教学应该～听、说、读、写四项，不可偏轻偏重｜我说“大家”，自然～你在内。 【包揽】动兜揽过来，全部承担：政府部门不可能把各种事务 都～起来。 【包罗】动包括（指大范围）：民间艺术～甚广，不是三言两语所能说完的。 【包罗万象】内容丰富，应有尽有：这个博览会的展品真可说是～， 美不胜收。 【包米】〈方〉名玉米。也作苞米。 【包赔】动担保赔偿：～损失。 【包皮】名①包装的皮儿。②阴茎前部覆盖龟头的外皮。 【包票】名保单 的旧称。料事有绝对的把握时，说可以打包票：他一定能按时完成任务，我敢打～。也说保票。 【包青天】ī名见页〖包公〗。 【包容】动①宽容：大 度～｜一味～。②容纳：小礼堂能～三百个听众。 【包身工】名①旧社会一种变相的贩卖奴隶的形式。被贩卖的是青少年，由包工头骗到工厂、矿山做工， 没有人身自由，工钱全归包工头所有，受资本家和包工头的双重剥削。②在包身工形式下做工的人。 【包探】名旧时巡捕房中的侦缉人员。 【包头】?名① 裹在头上的装束用品（多用于少数民族）：青～。②（～儿）附在鞋头起保护作用的橡胶、皮革等：打～儿。 【包围】动①四面围住：亭子被茂密的松林～ 着。②正面进攻的同时，向敌人的翼侧和后方进攻。 【包围圈】名军事上指已形成包围态势的圈子和已被包围的地区：冲出～｜～越缩越小了。 【包席】① （－∥－）动订整桌配套的酒席：你们是点菜还是～？｜婚宴包了三桌席。②名饭馆里指整桌供应的酒席。也说包桌。 【包厢】名某些剧场里特设的单间席 位，一间有几个座位，多在楼上。 【包销】动①指商人承揽货物，负责销售。②指商业机构跟生产单位订立合同，把全部产品包下来销售。
著名的数学家，瑞士人，大部分时间在俄国和法 国度过．他16岁获得硕士学位，早年在数学天才贝努 里赏识下开始学习数学，毕业后研究数学，是数学史 上最高产的作家．在世发表论文700多篇，去世后还 留下100多篇待发表．其论著几乎涉及所有数学分 支．他首先使用f(x)表示函数，首先用∑表示连加，首 先用i表示虚数单位．在立体几何中多面体研究中，首 先发现并证明欧拉公式．
讨论
问题1： （2）数出下列四个多面体的顶点数V、面数F、棱数E 并填表
(5)
图形编号 （5） （7） （6）
顶点数V 5 16
7
面数F 5 16
8
(Hale Waihona Puke )棱数E 8 32 12简单多面体 V+F-E=2（欧拉公式）
欧拉公式
他描写成刚正严明、不畏权势的清官的典型。 【包谷】〈方〉名玉米。也作苞谷。 【包管】动担保（表示说话人的自信）：～退换｜他这种病～不用吃就会 好。 【包裹】①动包；包扎：用布把伤口～起来。②名包扎成件的包儿：他肩上背着一个小～｜我到邮局寄～去。 【包含】动里边含有：这句话～好几层意 思。 【包涵】?ɑ动客套话，请人；优游 优游 ； 原谅：唱得不好，大家多多～！ 【包伙】①（－∥－）动包饭?。②名包饭?。 【包 机】ī①动定期租用飞机：开展～业务。②名包乘的飞机：一架旅游～。 【包间】名宾馆和餐饮、等场所设的供某位或某些客人专用的房间。 【包金】ī动用 薄金叶包在金属首饰外面：～项链。 【包金】ī名包银。 【包举】〈书〉动总括；全部占有：～无遗。 【包括】动包含（或列举各部分，或着重指出某一部 分）：语文教学应该～听、说、读、写四项，不可偏轻偏重｜我说“大家”，自然～你在内。 【包揽】动兜揽过来，全部承担：政府部门不可能把各种事务 都～起来。 【包罗】动包括（指大范围）：民间艺术～甚广，不是三言两语所能说完的。 【包罗万象】内容丰富，应有尽有：这个博览会的展品真可说是～， 美不胜收。 【包米】〈方〉名玉米。也作苞米。 【包赔】动担保赔偿：～损失。 【包皮】名①包装的皮儿。②阴茎前部覆盖龟头的外皮。 【包票】名保单 的旧称。料事有绝对的把握时，说可以打包票：他一定能按时完成任务，我敢打～。也说保票。 【包青天】ī名见页〖包公〗。 【包容】动①宽容：大 度～｜一味～。②容纳：小礼堂能～三百个听众。 【包身工】名①旧社会一种变相的贩卖奴隶的形式。被贩卖的是青少年，由包工头骗到工厂、矿山做工， 没有人身自由，工钱全归包工头所有，受资本家和包工头的双重剥削。②在包身工形式下做工的人。 【包探】名旧时巡捕房中的侦缉人员。 【包头】?名① 裹在头上的装束用品（多用于少数民族）：青～。②（～儿）附在鞋头起保护作用的橡胶、皮革等：打～儿。 【包围】动①四面围住：亭子被茂密的松林～ 着。②正面进攻的同时，向敌人的翼侧和后方进攻。 【包围圈】名军事上指已形成包围态势的圈子和已被包围的地区：冲出～｜～越缩越小了。 【包席】① （－∥－）动订整桌配套的酒席：你们是点菜还是～？｜婚宴包了三桌席。②名饭馆里指整桌供应的酒席。也说包桌。 【包厢】名某些剧场里特设的单间席 位，一间有几个座位，多在楼上。 【包销】动①指商人承揽货物，负责销售。②指商业机构跟生产单位订立合同，把全部产品包下来销售。
欧拉公式的应用
y n 1 y n f (x n, y n), x x n 1 n
即
y y hf ( x , y ) n 1 n n n
《离散数学》中的欧拉公式： 若G为连通平面图，则n-m+r=2,其中，n,m,r分别 为G的结点数，边数和面数。
另外，我们在《常微分方程》中还学了欧拉折
线；在《离散数学》中 学过欧拉图。
认识欧拉
欧拉---瑞士人（Euler,L. 1707---1783）；
欧拉---16 岁获得硕士学位；
欧拉---数学史上“高产”的数学家。在世发表论文700多篇，
去世后还留下100多篇待发表；
欧拉---首先使用f(x)表示函数，用e表示自然对数的底，用a、
b、c 表示△ABC，用∑表示求和，用i表示虚数单位等。
欧拉公式的两个基本性质
o s is in i c o s 1 i s i n 1 e c 1、 e 2 2 3 i i 3 3 2 e c o s i s i n 1e c o s is i n i 2 2
i
i 2
2 k i e c o s 2 k i s i n 2 k 1 k 0 , 1 , 2
dz d iz
5、 倍角和半角的三角变换 例：证明： sin 2 cot
1 co s 2
证：左
e2i e2i i e2i e2i
e2i e2i sin2 2i e2i e2i 1 cos2 1 2
i i i i i i 1 e e e e ie e i 2 i i i e e ie e
即
y y hf ( x , y ) n 1 n n n
《离散数学》中的欧拉公式： 若G为连通平面图，则n-m+r=2,其中，n,m,r分别 为G的结点数，边数和面数。
另外，我们在《常微分方程》中还学了欧拉折
线；在《离散数学》中 学过欧拉图。
认识欧拉
欧拉---瑞士人（Euler,L. 1707---1783）；
欧拉---16 岁获得硕士学位；
欧拉---数学史上“高产”的数学家。在世发表论文700多篇，
去世后还留下100多篇待发表；
欧拉---首先使用f(x)表示函数，用e表示自然对数的底，用a、
b、c 表示△ABC，用∑表示求和，用i表示虚数单位等。
欧拉公式的两个基本性质
o s is in i c o s 1 i s i n 1 e c 1、 e 2 2 3 i i 3 3 2 e c o s i s i n 1e c o s is i n i 2 2
i
i 2
2 k i e c o s 2 k i s i n 2 k 1 k 0 , 1 , 2
dz d iz
5、 倍角和半角的三角变换 例：证明： sin 2 cot
1 co s 2
证：左
e2i e2i i e2i e2i
e2i e2i sin2 2i e2i e2i 1 cos2 1 2
i i i i i i 1 e e e e ie e i 2 i i i e e ie e
《高一数学欧拉公式》课件
《高一数学欧拉公式》 PPT课件
数学欧拉公式是高一数学的重要内容之一，介绍了公式的形式和含义，以及 它在数学研究和实际应用中的重要性。
导入欧拉公式数学欧拉公 Nhomakorabea是由瑞士数学家 欧拉提出的一种重要数学公式， 具有广泛的应用价值。
带来的启示
欧拉公式不仅仅是一个公式， 更是对数学思维的启示和对实 际应用的指导。
欧拉公式对数学学习的推进
通过学习和理解欧拉公式，可以提 高数学学习的效果和兴趣。
欧拉公式对数学研究的促进
欧拉公式的研究推动了数学领域的 发展，激发了更多的数学研究兴趣。
参考
欧拉公式的相关文献
相关学术论文和研究报告
数学学科发展的相关书籍
维能力，提升数学问题的解决能力。
3
欧拉公式对实际应用的启示
欧拉公式的应用不仅限于数学领域，还可以
欧拉公式在其他领域的应用
4
启发人们在实际问题中进行创新和思考。
除了数学领域，欧拉公式还被广泛应用于物 理学、工程学和计算机科学等其他领域。
研究对象
如何使用欧拉公式研究问题
通过欧拉公式的运用，可以解决 复杂的数学问题，如数列和级数 的求和等。
研究对象
通过欧拉公式，我们可以研究 一些复杂的数学问题和实际应 用中的现象。
欧拉公式
1 介绍欧拉公式
2 公式的形式
欧拉公式被认为是数学中最美丽的公式之一，它 连接了数学中的五个重要常数。
欧拉公式的形式为：e^(πi) + 1 = 0，其中e是自然 对数的底，π是圆周率，i是虚数单位。
3 公式的含义
4 公式的证明
欧拉公式表明了数学中不同的数学常数之间的奇 妙关系，展示了数学的美妙和深奥。
欧拉公式的证明是数学中的一大经典问题，需要 运用其他数学知识和技巧进行推导。
数学欧拉公式是高一数学的重要内容之一，介绍了公式的形式和含义，以及 它在数学研究和实际应用中的重要性。
导入欧拉公式数学欧拉公 Nhomakorabea是由瑞士数学家 欧拉提出的一种重要数学公式， 具有广泛的应用价值。
带来的启示
欧拉公式不仅仅是一个公式， 更是对数学思维的启示和对实 际应用的指导。
欧拉公式对数学学习的推进
通过学习和理解欧拉公式，可以提 高数学学习的效果和兴趣。
欧拉公式对数学研究的促进
欧拉公式的研究推动了数学领域的 发展，激发了更多的数学研究兴趣。
参考
欧拉公式的相关文献
相关学术论文和研究报告
数学学科发展的相关书籍
维能力，提升数学问题的解决能力。
3
欧拉公式对实际应用的启示
欧拉公式的应用不仅限于数学领域，还可以
欧拉公式在其他领域的应用
4
启发人们在实际问题中进行创新和思考。
除了数学领域，欧拉公式还被广泛应用于物 理学、工程学和计算机科学等其他领域。
研究对象
如何使用欧拉公式研究问题
通过欧拉公式的运用，可以解决 复杂的数学问题，如数列和级数 的求和等。
研究对象
通过欧拉公式，我们可以研究 一些复杂的数学问题和实际应 用中的现象。
欧拉公式
1 介绍欧拉公式
2 公式的形式
欧拉公式被认为是数学中最美丽的公式之一，它 连接了数学中的五个重要常数。
欧拉公式的形式为：e^(πi) + 1 = 0，其中e是自然 对数的底，π是圆周率，i是虚数单位。
3 公式的含义
4 公式的证明
欧拉公式表明了数学中不同的数学常数之间的奇 妙关系，展示了数学的美妙和深奥。
欧拉公式的证明是数学中的一大经典问题，需要 运用其他数学知识和技巧进行推导。
【高中数学课件】欧拉公式1 ppt课件
思考2：设多面体的F个面分别是n1,n2, ···,nF边形，各个面的内角总和是多
少？
(n1-2)
·1800+
(n2-2)
·1800+···+
(nF-2)
·1800=(n1+n2+···+nF-2F）·1800
思考3： n1+n2+···+nF和多面体的棱数E有什么关系
n1+n2+···+nF =2E
∴（E-F）·3600= (V-2) ·3600
V+F-E=2 欧拉公式
欧拉公式的应用
例1 1996年的诺贝尔化学奖授予对发现C60有重大贡献的
三位科学家．C60是有60 个C原子组成的分子，它结构为简 单多面体形状．这个多面体有60个顶点，从每个顶点都引出 3条棱，各面的形状分别为五边形或六边形两种．计算C60分 子中形状为五边形和六边形的面各有多少？
讨论 问题2：如何证明欧拉公式
E1
A1
B
D1 C
11D
E A
C B
压缩成 平面图形
D
E
E1 A1
A
D1 C1 C
B1
B
∴所有面的内角和=（E－F）·3600
思考4：设平面图形中最大多边形（即多边形ABCDE）是m边形，则它和它 内部的全体多边形的内角总和是多少？
2（m-2) ·1800+(V-m) ·3600=(V-2) ·3600
欧拉公式
V+F-E=2
空间问题平面化
猜想
证 明
作业 P68 阅读材料
应用
E1
A1
B
D1 C
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3
4、求积分
例1： /
4
eit
dt
iei/4 i i
1
i
i
1
i1
1
0
2 2
2 2
例2：
1 dx
x4 1
2iRzec0s
f
z
Re s z c1
f
z
2i
1 4
3i
2、求方根
例： 4 1 i 4
i
2n i4
2e 4 8 2e 4 n 来自 0,1,2,33、初等函数求值
例： Log 1
3i ln 2 i 2 2n ln 2 2n 1 in 0,1,2,
3
欧拉公式的应用
目录
1、什么是欧拉公式 2、认识欧拉 3、 “上帝创造的公式” 4、欧拉公式的应用
欧拉公式
• 欧拉公式是指以欧拉命名的诸多公式。其 中最著名的有，复变函数中的欧拉幅角公 式---将复数、指数函数与三角函数联系起 来； 拓扑学中的欧拉多面体公式；初等数 论中的欧拉函数公式。
《初等数论》中的欧拉公式：
z 1 z2 2iaz 1
z z1
a2 1
5、 倍角和半角的三角变换
例：证明：
sin 2 1 cos 2
cot
证：左
e2i e2i i e2i e2i
e2i e2i
sin 2 1 cos 2
1
2i e2i
e2i
i sin 3
i
2
2
e2ki cos 2k i sin 2k 1k 0, 1, 2
由欧拉公式可以看出，在复数域内，指数函数是周
期函数，具有基本周期 2 i 。
2、在欧拉公式中用 代替 ，则ei cos isin
由 ei cos i sin
得到 ei 1 0
欧拉公式成为人们公认的最优美公式，被视为数学 美的一个象征，数学家们评价它是“上帝创造的公 式” 。
欧拉公式的两个基本性质
1、ei cos1 i sin1
i
e2
cos
i sin
i
2
2
ei cos i sin 1
3 i
e2
cos 3
e4
1 4
1 i
e4
2
例3：
2
0
a
d a
sin
1
Sol:Let z ei 0 2 sin z z 1 2i
d dz
iz
2 d a 1
2i dz 2 Re s f z 2 1
0 a sin
2
1 ei ei ei ei i ei ei
i ei ei 2
ei ei
cot =右
所以原式成立
谢谢
去世后还留下100多篇待发表；
欧拉---首先使用f(x)表示函数，用e表示自然对数的底，用a、
b、c 表示△ABC，用∑表示求和，用i表示虚数单位等。
欧拉---目前数学中有欧拉公式、欧拉常数、欧拉猜想、欧拉
方法、欧拉方程、欧拉定理。
“上帝创造的公式”
将欧拉公式 ei cos i sin 中的 换为
f (xn , yn ),
即
yn1 yn hf (xn , yn )
《离散数学》中的欧拉公式：
若G为连通平面图，则n-m+r=2,其中，n,m,r分别 为G的结点数，边数和面数。
另外，我们在《常微分方程》中还学了欧拉折
线；在《离散数学》中 学过欧拉图。
认识欧拉
欧拉---瑞士人（Euler,L. 1707---1783）； 欧拉---16 岁获得硕士学位； 欧拉---数学史上“高产”的数学家。在世发表论文700多篇，
ei cos i sin ，
得到
cos ei ei , sin ei ei
2
2i
由上式容易看出正弦函数是奇函数，余弦函
数是偶函数．
欧拉公式的应用
欧拉公式在计算中的应用：
1、幂乘
例： 3 i 7 (2ei / 6 )7 27 ei7 / 6 26 ei 2ei / 6 64 3 i
设m是大于1的整数，（a,m）=1，则 am 1mod m
《复变函数论》中的欧拉函数：
ei cos i sin (Eulersformula )
《数值分析》中的欧拉函数：
一般的，设已作出该折线的极点,过依方向场的方 向再推进到，显然两个极点的坐标有以下关系
yn1 yn xn1 xn