两齿轮中心距计算及画法
机械制图--齿轮的画法

2021/6/16
6
已知:一对啮合齿轮Z1=17,Z2=37,中心距A=54。 要求:1)求m及分别计算两齿轮的分度圆、齿顶圆、齿根圆直径;
2)补画主、左视图中所缺少的图线。
左视图画成外形视图。
对于标准齿轮来说,节圆锥面和分度圆锥面, 节圆和分度圆是一致的。
2021/6/16
9
结束语
若有不当之处,请指正,谢谢!
※
6-3 齿轮
轮缘
直
齿
圆
柱 键槽
齿
轮
的
结
轴孔
构
2021/6/16
轮齿 轮毂
幅板(轮幅)
1
一、直齿圆柱齿轮各部分的几何要素和尺寸关系
1、几何要素
齿根 齿顶高ha 齿根高hf
①齿顶圆d a ④齿顶高ha ②分度圆d ⑤齿根高hf
齿顶
③齿根圆d f 齿高h
齿距P
齿距p
齿槽 模数m
C=.d=Z.p
d=—P . Z m=—P
圆已直知径:及直有关齿齿圆轮柱的齿基轮本尺的寸模必数须m直=2接m注m,出Z,=齿17根。圆直径不注。齿轮的模
数要、求齿:数1和)齿计形算角等该参齿数轮在的图分样右度上圆角、的齿参顶数列圆表、中齿列根出圆,齿直面径的;表面粗
糙度代号2注)在补分全度圆主上视。图中所缺少的图线;
齿数
3)标注轮齿部分的尺寸。
模数
齿形角
注意:齿根圆直径不注
齿顶高系数 精度系数
齿轮尺寸计算
Φ38 Φ34
{d= m Z = 34 da= m (Z+2)=38
齿轮的基本知识及其画法
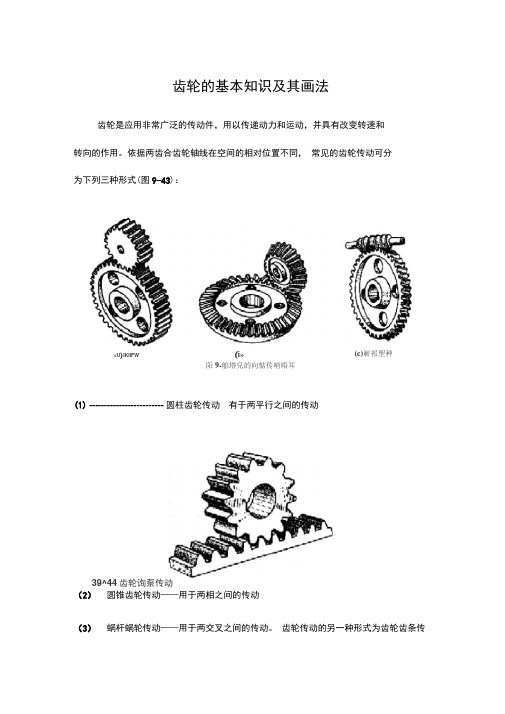
齿轮的基本知识及其画法齿轮是应用非常广泛的传动件,用以传递动力和运动,并具有改变转速和 转向的作用。
依据两齿合齿轮轴线在空间的相对位置不同, 常见的齿轮传动可分 为下列三种形式(图9-43):阳9-舶塔兒的向惦传哨晤耳 (1) ------------------------- 圆柱齿轮传动 有于两平行之间的传动39^44齿轮询泵传动(2) 圆锥齿轮传动——用于两相之间的传动(3) 蜗杆蜗轮传动——用于两交叉之间的传动。
齿轮传动的另一种形式为齿轮齿条传(c)嶄祁聖种<U )IKIIFW (i»动(图9-44 ),可用于转动和移动之间的运动转换。
常见的齿轮轮齿是直齿和斜齿。
齿轮又有标准齿和非标准齿之分,具有标准齿的齿轮称为标准齿轮。
本节介绍具有渐开线齿形的标准齿轮的有关知识与规定画法。
一、直齿圆柱齿轮(直齿轮)(一)直齿圆柱齿轮各部分名称及有关参数(图9-45 )1、齿顶圆(直径d1 )通过圆柱齿轮齿顶的曲面称为齿顶圆柱面。
齿顶圆柱面与端平面的交线称为齿顶圆。
2、齿根圆(直径d2 )通过圆柱齿轮齿根的曲面称为齿根圆柱面。
齿根圆柱面与端平面的交线称为齿根團y -4^ 宜向閒桂齿轮各部分霑称和料号3 .分度圆(直径d)齿轮设计和加工时计算尺寸的基准圆称为分度圆。
它位于齿顶圆和齿根圆之间,是一个约定的假想圆。
4 .节圆(直径d)两齿轮合时,位于连心线00上的两齿廓点P,称为节点。
分别以0 0为圆心,0P为半径所作的两个相切的园称为节圆。
正确安装的标准齿轮的d=d。
5•齿高h轮齿在齿顶圆与齿根圆之间的径向距离称为齿高。
齿高h分为齿顶高hl,齿根高h2 两段(h=h1+h2 )齿顶高h1 :齿顶圆与分度圆之间的径向距离;齿根高h2 :齿根圆与分度圆之间的径向距离;6.齿数z即轮齿的个数,它是齿轮计算的主要参数之一。
8.模数m由于分度圆周长n d=pz,所以d=p/ n z令p/ n=m 贝U d=mz式中m称为齿轮的模数,它等于齿距与圆周率n勺比值。
试求齿轮1的分度圆直径,齿顶圆直径,齿根圆直径,两轮啮合传动的中心距和传动比。

试求齿轮1的分度圆直径,齿顶圆直径,齿根圆直径,两轮啮合传
动的中心距和传动比。
对于两轮啮合传动,我们需要知道齿轮1的模数,齿数和压力角,以及传动比。
传动比可以通过齿数的比值得到。
齿轮1的分度圆直径可以通过以下公式计算:
分度圆直径(D1)= 模数 ×齿数1
齿顶圆直径可以通过以下公式计算:
齿顶圆直径(D1d)= 分度圆直径 + 2 ×模数
齿根圆直径可以通过以下公式计算:
齿根圆直径(D1f)= 分度圆直径 - 2.5 ×模数
两轮啮合传动的中心距可以通过以下公式计算:
中心距(C)= (齿数1 + 齿数2)/ 2 ×模数
传动比可以通过以下公式计算:
传动比(i) = 齿数2 / 齿数1
这些公式可以用来计算齿轮1的分度圆直径、齿顶圆直径、齿根圆直径、两轮啮合传动的中心距和传动比。
两个齿轮啮合的中心距等于分度圆

《两个齿轮啮合的中心距等于分度圆》在机械工程领域中,齿轮传动是一种常见的动力传递方式,而齿轮的啮合是整个传动系统中至关重要的环节。
而在齿轮啮合的设计和制造中,中心距和分度圆是两个十分重要的概念。
本文将从简到繁地介绍这两个概念,并探讨它们在齿轮传动中的作用和意义。
1. 了解中心距和分度圆在谈及齿轮传动时,中心距是一个比较基础的概念。
它指的是两个啮合齿轮的中心线之间的距离。
而分度圆则是指齿轮上的一个虚拟圆周,它的直径等于齿轮的模数。
中心距的确定和分度圆的选择对于齿轮传动的传动比、啮合角等参数都有重要影响。
2. 中心距等于分度圆的意义当两个齿轮的中心距等于分度圆的直径时,意味着它们的啮合条件达到最佳状态。
这种设计可以有效减小齿轮传动的磨损和噪音,并提高传动效率。
这也能够使得齿轮传动更加稳定和可靠,延长使用寿命。
3. 中心距和分度圆对于齿轮传动的影响在齿轮的实际应用中,中心距和分度圆的选择会直接影响到齿轮传动的性能。
过小或过大的中心距都会导致传动系统的不稳定,甚至出现啮合不良的情况。
而分度圆选择不当也会导致齿轮的强度不足或者噪音过大。
合理选择中心距和分度圆对于齿轮传动的正常运行至关重要。
4. 个人观点和总结在我的观点看来,中心距等于分度圆是一种理想的设计状态,它可以使得齿轮传动达到最佳的工作状态。
在实际的工程设计和制造中,我们需要充分考虑中心距和分度圆对于传动系统的影响,以确保设计的齿轮传动能够稳定、高效地工作。
通过不断的学习和实践,我们可以更好地理解和应用这两个概念,从而提高齿轮传动的设计水平和质量。
总结起来,中心距等于分度圆对于齿轮传动来说是十分重要的。
合理选择中心距和分度圆可以有效提高齿轮传动的性能,降低噪音和磨损,保证传动系统的稳定运行。
在实际应用中我们应该深入理解和灵活运用这两个概念,以提升齿轮传动的设计和制造水平。
在文章中详细介绍了中心距和分度圆的概念,并探讨了它们在齿轮传动中的作用和影响。
两个变位齿轮啮合的中心距等于分度圆

两个变位齿轮啮合的中心距等于分度圆标题:深度解读:两个变位齿轮啮合的中心距等于分度圆1. 简介作为机械传动中常见的一种结构,变位齿轮在啮合时具有特殊的啮合特性,其中心距与分度圆的关系更是一个重要的问题。
本文将从深度和广度兼具的角度,全面评估并撰写关于两个变位齿轮啮合中心距等于分度圆的主题内容。
2. 变位齿轮的基本原理2.1 变位齿轮的定义和特点变位齿轮是一种特殊的齿轮传动装置,其啮合面不再是平行而成斜面,这种设计使得变位齿轮啮合更加平稳,噪音更小,传动效率更高。
2.2 变位齿轮的啮合原理变位齿轮的啮合原理涉及到齿轮的分度圆、齿顶圆和齿底圆等参数,其中分度圆是确定齿轮尺寸的基本参考。
3. 两个变位齿轮啮合的中心距等于分度圆3.1 中心距的定义和作用中心距是指两个齿轮啮合时,两个齿轮中心线之间的距离,它直接影响着齿轮传动的工作性能和传动比。
3.2 中心距等于分度圆的原理在两个变位齿轮啮合时,当它们的中心距等于分度圆时,可以实现更加理想的啮合效果和传动性能。
3.3 实际应用中的意义以中心距等于分度圆作为设计和加工的基准,可以更好地保证变位齿轮传动的精度和稳定性。
4. 总结与展望通过对两个变位齿轮啮合中心距等于分度圆的深度解读,我们对变位齿轮的设计和应用有了更深入的理解,同时也揭示了这一设计原理的重要意义。
未来,随着技术的不断发展,对于变位齿轮的研究和应用也将迎来更多的可能性。
5. 个人观点与理解作为文章撰写者,我个人认为两个变位齿轮啮合的中心距等于分度圆确实具有重要的意义,它不仅影响着齿轮传动的性能,还直接关系到齿轮的精度和稳定性。
在实际的设计和制造过程中,我们应该充分重视这一参数,并加以合理的控制和应用。
在本文中,我们对两个变位齿轮啮合中心距等于分度圆的主题进行了全面的评估和深度解读,着重从理论原理到实际应用进行了详细的阐述,并分享了个人的观点和理解。
希望本文能为相关领域的专业人士和爱好者提供一些参考和启发,也欢迎对这一主题进行更深入的探讨和讨论。
变位齿轮中心距计算公式【终于整全了】

目前手册上的跨齿数计算公式大都是近似的,有误差的,并非精确的计算公式,因而有时影响跨齿数的合理性。
就是那些精确的公式,它们在角度变位中也是有不足之处的。
而且至今在手册上似乎还未见到有斜齿精确的跨齿数计算公式。
有人说:“手册上的5.01800+'=n z k α不就是标准斜齿轮跨齿数精确的计算公式吗?”不,它算出的也是近似值(文章后面进行验证)。
笔者已退休多年,精力尚可,因而对此进行了研究、探讨,于是给出一个高度、角度变位都是情况良好的公式。
公式为:5.01)cos sin 2(+--'=παααzinv m xm W k k (用于直齿) (1)5.01)cos sin 2(+'--'=παααn n n n n n n inv z m m x W k (用于斜齿) (1)公式中的'k W 和'n W 当为高度变位直齿时, bKd xm d W 22)2(-+='; 斜齿时, b bn n n d m x d W βcos )2(22-+='。
当为角度变位直齿时, b k d xm d W 22)9.1(-+=';斜齿时, 。
cos )9.1(22b bn n n d m x d W β-+='上列公式中:d ——分度圆直径; b d ——基圆直径;m ——模数,斜齿时为n m ;z —— 齿数;___z '斜齿轮的假想齿数,ntinv inv zz αα=' ; ___α压力角,斜齿轮法面压力角为n αx —— 变位系数,斜齿时法面变位系数为n x ; ___bβ斜齿轮基圆螺旋角;k W '——直齿轮的公法线长度原始计算值 ; n W '——斜齿轮的公法线长度原始计算值 。
2、公式(1)的由来公式(1)是怎么来的?其实它的来历很简单,就是由公法线长度计算公式变换而来的。
公法线长度计算公式为 :[] sin 2)5.0( cos ααπαm x zinv k m W k ++-= (直齿) (2)[] sin 2)5.0cos n n n n n n n m x inv z k m W ααπα+'+-=((斜齿) (2) 将公式(2)中的k 移到等号左边,将k W 和n W 移到等号右边(且变为k W '和n W ')即为公式(1)。
齿轮标准中心距和实际中心距

齿轮标准中心距和实际中心距
齿轮传动是机械传动中常用的一种方式,其重要性不言而喻。
在进行齿轮设计时,中心距的确定是至关重要的一步。
中心距是指两个齿轮中心之间的距离,它的大小直接影响齿轮传动的性能和效率。
在齿轮设计中,标准中心距是一种常见的参数。
标准中心距是根据齿轮模数、齿数和压力角等参数计算得出的理论中心距。
但实际中心距却受到多种因素的影响,包括齿形误差、制造误差、安装误差等等。
因此,在实际应用中,实际中心距往往与标准中心距存在一定的差距。
为了保证齿轮传动的性能和效率,需要尽可能地减小实际中心距与标准中心距之间的差距。
这可以通过在齿轮制造和安装过程中采取一系列措施来实现,比如精确的加工和测量、合理的安装和调整等等。
总之,在齿轮设计和制造中,中心距的确定是一个至关重要的环节。
只有通过精确的计算和控制,才能保证齿轮传动的正常运行和长期稳定性。
- 1 -。
两齿轮啮合节圆等于中心距

两齿轮啮合节圆等于中心距
两齿轮啮合节圆的直径等于两齿轮的中心距。
齿轮中心距是指两个相互啮合的齿轮,其圆心间的距离。
而两齿轮啮合节圆是指两个齿轮在啮合时,其节线相交而形成的圆。
根据齿轮啮合的基本原理,两齿轮啮合节圆的直径等于两齿轮的中心距。
这是因为在齿轮啮合时,两个齿轮的节圆相切于一点,而这个切点的直径就等于两齿轮中心距。
因此,在齿轮设计时,为了保证齿轮的正确啮合和传动,需要准确计算和调整两个齿轮的中心距,使其等于两齿轮啮合节圆的直径。
