您的位置：360文档中心› 北师大版高中数学选修1-1：圆锥曲线与方程综合题专练

北师大版高中数学选修1-1：圆锥曲线与方程综合题专练

合集下载

北师大版高中数学选修1-1第二章 圆锥曲线与方程同步练测.docx

北师大版高中数学选修1-1第二章 圆锥曲线与方程同步练测.docx

高中数学学习材料鼎尚图文*整理制作第二章 圆锥曲线与方程同步练测（北师大版选修1-1）建议用时 实际用时满分 实际得分120分钟150分一、选择题(本题共12小题，每小题5分，共60分)1.已知椭圆2221x y a+=的一个焦点在抛物线24y x=的准线上，则椭圆的离心率为（ ）A.12 B.22 C.13D.332.方程213x y =-表示的曲线是（ ）A.双曲线B.椭圆C.双曲线的一部分D.椭圆的一部分3.已知方程22111x y k k-+-＝表示双曲线，则k 的取值范围是（ ）A.11k -<<B.0k >C.0k ≥D.1k >或1k <-4.以椭圆221139x y +=的左焦点为焦点的抛物线的标准方程是（ ） A. B. C. D.5.已知()P x,y 是中心在原点，焦距为10的双曲线上一点，且y x 的取值范围为3344⎛⎫- ⎪⎝⎭，，则该双曲线的方程是（ ）A.221916x y -=B.221916y x -= C.221169x y -= D.221169y x -= 6.已知定点551,,4,44M N 骣骣鼢珑鼢--珑鼢珑鼢桫桫，给出下列曲线方程：①；②223x y +=；③2212x y +=；④2212x y -=，在曲线上存在点满足||||MP NP =的所有曲线方程是（ ）A.①③B.②④C.①②③D.②③④ 7.已知椭圆22221(0)x y a b a b+=>>，直线交椭圆于两点，△的面积为（为原点），则函数（ ） A.是奇函数 B.是偶函数C.既不是奇函数，也不是偶函数D.奇偶性与有关8.已知椭圆22221(0)x y a b a b+>>＝的左焦点为F ，右顶点为A ，抛物线215()8y a c x =+与椭圆交于B ，C 两点，若四边形ABFC 是菱形，则椭圆的离心率是（ ） A.158 B.415C.23D.129.已知双曲线22221x y a b -=的左焦点为，顶点为1，A ，是双曲线上任意一点，则分别以线段，为直径的两圆的位置关系为( )A.相交B.相切C.相离D.以上情况都有可能 10.已知方程22ax by ab +=和0ax by c ++=，其中0,,0ab a b c 构>,它们所表示的曲线可能是下列图象中的（ ）11.已知抛物线22(0)＝y px p >上一点(1)M ,m (m >0)到其焦点的距离为5，双曲线221－＝x y a的左顶点为，若双曲线的一条渐近线与直线平行，则实数的值是（ ）A .125B .19C .15D .1312.椭圆22221(0)：x yM a b a b+=>>的左、右焦点分别为，为椭圆上任一点，且的最大值在上，其中，则椭圆的离心率的取值范围是（ ） A .⎣⎡⎦⎤14，12 B .⎣⎡⎦⎤12，22 C .⎝⎛⎭⎫22，1 D .⎣⎡⎭⎫12，1 二、填空题(本题共4小题，每小题4分，共16分)13.已知椭圆221x y m n+=与双曲线2x p －2y q 1(，m =)，，n p q +∈R 有共同的焦点，是椭圆和双曲线的一个交点，则12||||PF PF g． 14.双曲线的一条准线方程是，则的值为 ．15.椭圆22162x y +=和双曲线2213x y -=的公共焦点为,,F F P 12是两曲线的一个交点,那么12cos F PF Ð的值是 .16.若过两点(,0)A a 和(0,)B a 的直线与抛物线y =x x 223--没有交点，则实数a 的取值范围是 ．三、解答题（本题共6小题，共74分）17.(本小题满分12分)已知椭圆22221x y a b+＝（a b>＞0）经过点362M ,⎛⎫⎪⎝⎭，焦距为2，它的左、右顶点分别为121A ,A ,P 是该椭圆上的一个动点（非顶点），点2P 是点1P 关于x 轴的对称点，直线11A P 与22A P 相交于点E ． （1）求该椭圆的标准方程；A BC D（2）求点E的轨迹方程．18.(本小题满分12分)已知抛物线方程为22=(0)y pxp>，直线l x y m：过抛物线的焦+=点且被抛物线截得的弦长为3，求p的值．19.(本小题满分12分)设双曲线：x y C a b22221-=(0a >，0)b >的离心率为，若右准线与两条渐近线相交于,P Q 两点，为右焦点，△为等边三 角形．（1）求双曲线离心率的值；（2）若双曲线被直线截得的弦长为22b e a ，求双曲线的方程．20．（本小题满分12分）已知抛物线、椭圆和双曲线都经过点(1,2)M ，它们在x 轴上有共同焦点，椭圆和双曲线的对称轴是坐标轴，抛物线的顶点为坐标原点．（1）求这三条曲线的方程.（2）已知动直线过点(,)P 30，交抛物线于,A B 两点，是否存在垂直于x 轴的直线l ¢被以AP 为直径的圆截得的弦长为定值？若存在，求出l ¢的方程；若不存在，说明理由．21．（本小题满分12分）已知椭圆的中心为坐标原点，焦点在x 轴上，斜率为1且过椭圆右焦点的直线交椭圆于两点，OA OB +uu r uu u r与(3,1)=-a 共线． （1）求椭圆的离心率；（2）设为椭圆上任意一点，且OM λOA μOB uuu r uu r uu u r =+λμR (,)Î，证明22λμ+为定值．22．(本小题满分14分)设分别为椭圆：22221x y a b +=(0)a b >>的左、右两个焦点.（1）若椭圆上的点31,2A ⎛⎫⎪⎝⎭到两点的距离之和等于，求椭圆的方程和焦点坐标.（2）设点是（1）中所得椭圆上的动点，求线段的中点的轨迹方程.（3）已知椭圆具有性质：若是椭圆上关于原点对称的两个点，点是椭圆上任意一点，当直线的斜率都存在时，记为，那么与之积是与点位置无关的定值. 试对双曲线22221x y a b -=写出类似的性质，并加以证明．第二章圆锥曲线与方程同步练测（北师大版选修1-1）答题纸得分：_________一、选择题题号1234567 8 9 10 11 12 答案二、填空题13. 14. 15. 16.三、解答题17.18.19.20.21.22.第二章 圆锥曲线与方程同步练测（北师大版选修1-1）答案一、选择题1.B 解析：由题意知抛物线24y x =的准线方程为1x =-，椭圆2221x y a+=的焦点为(0)c ±，.∵ 椭圆2221x y a+=的一个焦点在抛物线24y x =的准线上，∴ 1c -=-，即1c =．∴ 222112a b c =+=+=.解得2a ＝．∴ 1222c e a ===． 2.D 解析：方程可化为，故表示的曲线是椭圆的一部分.3.A 解析：由双曲线标准方程的形式可知若22111x y k k -+-＝表示双曲线，则有1010k ,k +>⎧⎨->⎩或1010k ,k ,+<⎧⎨-<⎩∴ 11k -<<．4.D 解析：由椭圆的方程知，∴，∴ 抛物线的焦点为（－2，0），∴ 抛物线的标准方程是．5.C 解析：∵ 双曲线22221(0)x y a b a b -=>>的渐近线方程为by x a=±，∴ 动点()P x,y 与原点连线的斜率为y k x =且b b k ,a a ⎛⎫∈- ⎪⎝⎭. 由已知y x 的取值范围为33，44⎛⎫- ⎪⎝⎭，可得34b a =.① ∵ 双曲线的焦距为210c =，即c =5，∴ 22225a b c +==.②联解①②，可得43a ,b ==，∴ 双曲线的方程为221169x y -=.6.D 解析：要使这些曲线上存在点满足，需曲线与的垂直平分线相交．由题意知的中点坐标为302⎛⎫- ⎪⎝⎭，，直线的斜率为101452=， 所以线段的垂直平分线方程为322y x ⎛⎫=-+ ⎪⎝⎭.因为与322y x ⎛⎫=-+ ⎪⎝⎭的斜率相同，所以两直线平行，故两直线无交点，①不符合题意．将与322y x ⎛⎫=-+ ⎪⎝⎭联立，消去，得，，可知②中的曲线与的垂直平分线有交点，②符合题意.将2212x y +=与322y x ⎛⎫=-+ ⎪⎝⎭联立，消去，得，，可知③中的曲线与的垂直平分线有交点，③符合题意. 将2212x y -=与322y x ⎛⎫=-+ ⎪⎝⎭联立，消去，得，，可知④中的曲线与的垂直平分线有交点，④符合题意. 7.B 解析：是直线与椭圆22221x y a b+=相交所得的△的面积，由椭圆的对称性可知 ，所以是偶函数．8.D 解析：∵ 椭圆22221(0)x y a b a b +>>＝的左焦点为F ，右顶点为A ，∴ (0),(0)F c,A a,-.∵ 抛物线215()8y a c x =+与椭圆交于B,C 两点，∴ B,C 两点关于x 轴对称，可设(),()B m,n C m,n -.∵ 四边形ABFC 是菱形，∴ 1()2m a c =-. 将()B m,n 代入抛物线方程，得2215115()()8216•n a c a c b =+-=.∴ 115(),24B a c b ⎛⎫- ⎪ ⎪⎝⎭.将其代入椭圆方程，得2222151()421b a c a b ⎛⎫⎡⎤ ⎪-⎢⎥⎣⎦⎝⎭+＝，即221()1416a c •a -=. 化简、整理，得24830e e -+=，解得12e =312e ⎛⎫=> ⎪⎝⎭舍去9.B 解析：设的中点为1O ，若在双曲线左支上，则()21111112222PF PF P O a a O F ==+=+，即圆心距为两圆半径之和，此时两圆外切；若在双曲线右支上，同理可求得1112a O PF O =-，此时两圆内切，所以两圆的位置关系为相切.10.B 解析：方程可化成221x y b a+=，可化成a c y x b b =--.对于A ，由双曲线可知：，，∴ 0 ＞ab-，即直线的斜率应大于0，故错； 对于C ，由椭圆可知：，，∴ 0＜ab-，即直线的斜率应小于0，故错；同理错.所以选B ．11.B 解析：依题意知152p+=，所以，所以，所以，点的坐标为 又，所以直线的斜率为41a +.由题意得411a a=+，解得19a =.12.B 解析：设，，，则，，.又可看作点到原点的距离的平方，所以，所以＝.由题意知222223≤＝－≤c b a c c ，即21142 ≤≤e ，则1222≤≤e .二、填空题13. 解析：因为椭圆221x y m n+=与双曲线221x y p q -=有共同的焦点12,F F ， 所以其焦点位于轴上.由椭圆及双曲线的对称性不妨设在双曲线的右支上，左、右焦点分别为12,F F ，由椭圆以及双曲线的定义可得， ， 由①②，得，．所以．14.43- 解析：由题意可知双曲线的焦点在轴上，所以.双曲线方程可化为22121y x m m-=--， 因此22a m =-，21b m =-，23c m=-.因为准线方程是，所以，即23m m -=-，解得43m =-. 15.13 解析：由题意知，，联立方程得22221,621,3x y x y ⎧+=⎪⎪⎨⎪-=⎪⎩解得229,21.2x y ⎧=⎪⎪⎨⎪=⎪⎩取点坐标为322,22⎛⎫ ⎪ ⎪⎝⎭，则13222,22PF ⎛⎫=--- ⎪ ⎪⎝⎭，23222,22PF ⎛⎫=-- ⎪ ⎪⎝⎭. ∴ 11222221323212222213||||321321222222•cos ∠PF PF F PF PF PF ⎛⎫⎛⎫--⨯-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭===⎛⎫⎛⎫--+⨯-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭. 16.134∞,⎛⎫--⎪⎝⎭解析：过两点的直线方程为，将其与抛物线方程联立并消去，得．因为直线与抛物线没有交点，所以方程无解，即，解得134a <-． 三、解答题 17.解：（1）由题意得22c =，即1c =，∴ 12(10)(10)F ,,F ,-.∵ 椭圆22221(0)x y a b a b +>>＝经过点362M ,⎛⎫ ⎪⎝⎭，∴ 122MF MF a +==6，∴ 3a =，∴ 2228b a c =-=.∴ 所求椭圆的标准方程为22198x y +＝.（2）12(30),(30)A ,A ,-，设11121111(),(,),(03)P x ,y P x y x x -≠，＜，则11A P 的方程为1133y x y x ++＝.① 22A P 的方程为1133y x y x ---＝.②①×②，得22221199y x y x ---＝.③ ∵ 点111()P x ,y 在椭圆22198x y +＝上，∴ 2211198x y +＝，即22118(9)9x y -＝. 代入③，得22198x y -＝.由111211()()P x ,y ,P x ,y -是椭圆上的非顶点，知3x ≠±，∴ 点()E x,y 的轨迹方程为221(3)98x y x -≠±＝.18.解：由直线l 过抛物线的焦点02p F ,⎛⎫⎪⎝⎭，得直线l 的方程为2p x y +=.由222，，p x y y px ⎧+=⎪⎨⎪=⎩消去，得2220y py p +-=. 由题意得2221212(2)40,2,p p y y p y y p ∆=+>+=-=-.设直线与抛物线交于1122(,),(,)A x y B x y ，1212122(4)22p pAB x x p y y p p y y p =++=-+-+=-+=. ，∴ 解得34p =. 19.解：（1）双曲线的右准线的方程为2a c ，两条渐近线方程为by x a=?．所以两交点坐标为2a ab P c c 骣÷ç÷ç÷ç÷ç桫，，2a ab Q c c 骣÷ç÷ç-÷ç÷ç桫，． 设直线与轴的交点为,因为△为等边三角形，则有3||||2MF PQ =, 所以232a ab abc c c c 骣÷ç÷-=+ç÷ç÷桫×，即223c a abc c-=， 解得3b a =，．所以2ce a==． （2）由（1）得双曲线的方程为222213x y a a -=．把3y ax a =+代入得2222(3)2360a x a x a -++=．依题意得42221230(2430)a a a ,a ,∆=-->⎧-≠⎪⎨⎪⎩所以26a <，且23a ¹． 所以双曲线被直线截得的弦长2222221212121212()()(1)()(1)[()4]d x x y y a x x a x x x x =-+-=+-=++-4222221224(3)(1)(3)a a a a a --=+-g .因为2212b e d a a ==，所以2422227212144(1)(3)a a a a a -=+-×, 整理，得4213771020a a -+=,解得22a =或25113a =． 所以双曲线的方程为22126x y -=或221313151153x y -=．20.解：（1）设抛物线方程为22(0)y px p =>，将(1,2)M 代入方程得2p =，所以抛物线方程为24y x =，则抛物线的焦点坐标为.由题意知椭圆、双曲线的焦点为F F ()()121,0,1,0,-所以.对于椭圆，a MF MF ()（）2222122112112222=+=+++-+=+,所以a 12=+，a ()2212322=+=+，所以222222b a c =-=+，所以椭圆方程为221322222x y +=++.对于双曲线，122222a MF MF ¢=-=-，所以21a ¢=-，2322a ¢=-，所以222222b c a ⅱ?=-=-，所以双曲线方程为221322222x y -=--.（2）设AP 的中点为C ，l ¢的方程为x m =，以AP 为直径的圆交l ¢于,D E 两点，DE 的中点为.H令()11,,A x y 则113,22x y 骣+÷ç÷ç÷ç÷ç桫C ，所以DC AP x y ()221111322==-+，x CH m x m ，()11312322+=-=-+ 所以DH DC CH x y x m m x m m [()()()22222221111113]2323.44轾=-=-+--+=--+犏臌 当m 2=时，2462DH =-+=为定值，所以222DE DH ==为定值，此时l ¢的方程为2x =.21.（1）解：设椭圆方程为22221(0),(,0),x y a b F c a b+=>>22221(0),(,0),x y a b F c a b +=>>则直线的方程为,y x c =-代入22221x y a b +=，消去并整理，得a b x a cx a c a b 22222222()20+-+-=.令1122(,),(,),A x y B x y 则22222121222222,.a c a c a b x x x x a b a b -+==++由1212(,),(3,1),OA OB x x y y OA OB +=++=-+a 与a 共线，得12123()()0.y y x x +++= 又1122,,y x c y x c =-=-所以12123(2)()0,x x c x x +-++=所以1232c x x +=， 即22223,2a c ca b =+所以223.a b =所以226,3a c ab =-=故离心率6.3c e a ==（2）证明：由（1）知223a b =，所以椭圆22221x y ab+=可化为22233x y b +=.设(,),OM x y =uuur由已知得1122(,)(,)(,)x y λx y μx y =+，所以因为点(,)M x y 在椭圆上，所以2221212()3()3λx μx λy μy b +++=，即λx y μx y λμx x y y b 222222*********(3)(3)2(3)3+++++=. ①由（1）知222212331,,222x x c a c b c +===，所以2222212223.8a c ab x xc a b -==+ 所以1212121233()()x x y y x x x c x c +=+--2121243()3x x x x c c =-++22239322c c c =-+0.= 又222222112233,33x y b x y b +=+=，代入①得22 1.λμ+=故22λμ+为定值1.22.解：（1）椭圆的焦点在轴上，由椭圆上的点到两点的距离之和是4，得，即.又点312A ⎛⎫ ⎪⎝⎭，在椭圆上，因此22231212b ⎛⎫⎪⎝⎭+=，解得，于是. 所以椭圆的方程为22143x y +=，焦点，.（2）设椭圆上的动点，则线段的中点满足111,22x yx y -+==， 即，.因此22(21)(2)=143x y ++，即2214123y x ⎛⎫++= ⎪⎝⎭为所求的轨迹方程. （3）类似的性质为：若是双曲线22221x y a b -=上关于原点对称的两个点，点是双曲线上任意一点，当直线的斜率都存在时，记为，那么与之积是与点位置无关的定值. 证明如下：设点的坐标为，则点的坐标为，其中22221m n a b -=.又设点的坐标为，由,PM PN y n y n k k x m x m-+==-+，得•y n y n y n x m x m x m 2222-+-=-+-. 将22222222,b b y x b n a a =-=代入得22b a .。

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(含答案解析)(2)

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(含答案解析)(2)

一、选择题1．已知点12,F F 是椭圆()222210x y a b a b+=>>的左右焦点，椭圆上存在不同两点,A B 使得122F A F B =，则椭圆的离心率的取值范围是（ ） A ．10,3⎛⎫ ⎪⎝⎭B ．10,2⎛⎫ ⎪⎝⎭C ．1,13⎛⎫ ⎪⎝⎭D ．1,12⎛⎫ ⎪⎝⎭2．抛物线：24y x =的过焦点的弦的中点的轨迹方程为（ ） A ．21y x =-B ．212y x =-C ．22(1)y x =-D ．221y x =-3．过抛物线26y x =的焦点作一条直线与抛物线交于()()1122,,,A x y B x y 两点，若123x x +=，则这样的直线（ ）A ．有且只有一条B ．有且只有两条C ．有且只有三条D ．有且只有四条4．已知M 是抛物线2:C x y =上一点，记点M 到抛物线C 的准线的距离为1d ，到直线:3490l x y ++=的距离为2d ，则12d d +的最小值为（ ）A ．1B ．2C ．3D ．45．如图，F 是抛物线28x y =的焦点，过F 作直线交抛物线于A 、B 两点，若AOF 与BOF 的面积之比为1:4，则AOB 的面积为（ ）A ．10B ．8C ．16D ．126．已知1F ，2F 是双曲线()222210,0x y a b a b-=>>的左、右焦点，过1F 的直线l 与双曲线的左、右两支分别交于点A ，B ，若2ABF 为等边三角形，则该双曲线的渐近线的斜率为（ ） A ．2±B 3C ．6D ．77．顶点在原点，经过点()3,6-，且以坐标轴为轴的抛物线的标准方程是（ ） A ．23y x =或212=-x y B ．2123y x =-或212=-x y C ．23y x =或212x y =D ．2123y x =-或212x y =8．已知双曲线()2222:10,0x y C a b a b-=>>的左焦点为1F ，若直线:l y kx =，3,33k ⎡⎤∈⎢⎥⎣与双曲线C 交于M 、N 两点，且11MF NF ⊥，则双曲线C 的离心率的取值范围是（ ） A ．()1,2B ．)2,2⎡⎣C ．2,31⎡⎤+⎣⎦D ．(2,31⎤+⎦9．设双曲线22221(0,0)x y a b a b-=>>的左､右焦点分别为1F ､2F ，点P 在双曲线的右支上，且213PF PF =，则双曲线离心率的取值范围是（ ） A ．(1,2]B ．5(1,]3C ．[2,)+∞D ．4[,)3+∞10．过抛物线24y x =的焦点的直线与抛物线交于A ，B 两点，若AB 的中点的纵坐标为2，则AB 等于（ ） A ．4B ．6C ．8D ．1011．“04a <<”是“方程2214x y a a+=-表示为椭圆”的（ ）A ．充分必要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件12．在抛物线型内壁光滑的容器内放一个球，其通过中心轴的纵剖面图如图所示，圆心在y 轴上，抛物线顶点在坐标原点，已知抛物线方程是24x y =，圆的半径为r ，若圆的大小变化时，圆上的点无法触及抛物线的顶点O ，则圆的半径r 的取值范围是（ ）A ．()2,+∞B ．()1,+∞C ．[)2,+∞D ．[)1,+∞二、填空题13．设F 是抛物线2:2C y x =的焦点，A 、B 是抛物线C 上两个不同的点，若直线AB 恰好经过焦点F ，则4AF BF +的最小值为_______．14．已知双曲线22:143x y C -=的左､右焦点分别12,F F ，P 为双曲线上异于顶点的点，以1PF ，2PF 为直径的圆与直线l 分别相切于A ，B 两点，则12cos ,AB F F <>=___________.15．已知椭圆C 的两个焦点分别为1(2,0)F -，2(2,0)F ，离心率为12e =，点P 在椭圆C 上，且1230F PF ∠=，则12F PF △的面积为__________．16．F 是抛物线24y x =的焦点，过F 的直线l 交抛物线于A 、B 两点，O 为坐标原点，若10AF =，则OAB 的面积为__________.17．在双曲线22221x y a b-=上有一点P ，12,F F 分别为该双曲线的左、右焦点，121290,F PF F PF ∠=︒的三条边长成等差数列，则双曲线的离心率是_______.18．如图，椭圆C ：()222210x y a b a b+=>>的左､右焦点分别为1F ､2F ，B 为椭圆C 的上顶点，若12BF F △的外接圆的半径为23b，则椭圆C 的离心率为________.19．在平面直角坐标系xOy 中，已知椭圆C ：()222210x y a b a b+=>>的焦距为46，直线l 与椭圆C 交于A ，B 两点，且OA OB ⊥，过O 作⊥OD AB 交AB 于点D ，点D 的坐标为()2,1，则椭圆C 的方程为_________．20．如图，两个离心率相等的椭圆1Γ与椭圆2Γ，焦点均在x 轴上A ，B 分别为椭圆2Γ的右顶点和上顶点，过A ，B 分别作椭圆1Γ的切线AC ，BD ，若AC 与BD 的斜率之积为57-，则椭圆1Γ的离心率为__________.三、解答题21．已知椭圆2222:1(0)x y E a b a b +=>>过点P ⎛ ⎝⎭，离心率2e =. （1）求椭圆E 的方程；（2）过点(0,3)M 的直线l 与椭圆E 相交于A ，B 两点. ①当直线OA ，OB 的斜率之和为34时(其中O 为坐标原点)，求直线l 的斜率k ； ②求MA MB ⋅的取值范围.22．已知椭圆2222:1(0)x y E a b a b +=>>的左，右顶点分别为,A B ，离心率2e =，椭圆E 上任意一点M 到两个焦点1F ，2F 的距离之积的最大值为4.（1）求椭圆E 的方程；（2）已知点P 为直线l ：4x =上的任意一点，直线PA 、PB 与椭圆E 分别交于两点C 、D （不同于A 、B 两点），求证：直线CD 经过定点，并求出该定点的坐标，23．已知椭圆()2222:10x y C a b a b+=>>左、右焦点分别为1F 、2F ，上顶点为M ，离心，12MF F△. （1）求椭圆C 的标准方程；（2）过点2F ，的直线l 交椭圆于A 、B 两点，当1ABF 面积最大时，求直线l 的方程.24．已知椭圆2222:1(0)x y C a b a b +=>>(2,1),,A P Q --在椭圆C 上，且,P Q 异于点A ．（1）求椭圆C 的方程；（2）若||||,||||OP OQ AP AQ ==，求直线PQ 的方程．25．已知椭圆()2222:10x y C a b a b+=>>的离心率为1,,2A B 分别是它的左、右顶点，F是它的右焦点，过点F 作直线与C 交于,P Q (异于,A B )两点，当PQ x ⊥轴时，APQ∆的面积为92. （1）求C 的标准方程;（2）设直线AP 与直线BQ 交于点M ，求证:点M 在定直线上.26．设抛物线2:2(0)C y px p =>的焦点为F ，(1,2)M 是抛物线C 上的点. （1）求抛物线C 的方程；（2）若过点(2,0)的直线l 与抛物线C 交于不同的两点,A B ，且13AF BF ⋅=，求直线l 的方程.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】先设点，利用向量关系得到两点坐标之间的关系121223,2x x c y y =-=，再结合点在椭圆上，代入方程，消去222a y 即得2229312c a x c+=，根据题意2x a <，构建,a c 的齐次式，解不等式即得结果. 【详解】设()()1122,,,A x y B x y ，由()()12,0,,0F c F c -得()()112212,,,F A F x c y x c y B -==+，122F A F B =，()()11222,,x c y x c y =∴+-，即121223,2x x c y y =-=，由,A B 在椭圆上，故2222221122222222b x a y a b b x a y a b ⎧+=⎨+=⎩，即()()2222222222222222232b x c a y a b b x a y a b⎧-+=⎪⎨+=⎪⎩， 消去222a y 得，2229312c a x c+=，根据椭圆上点满足a x a -≤≤，又,A B 两点不同，可知2229312c a x a c+=<，整理得22340c ac a -+<，故23410e e -+<，故113e <<.故选：C. 【点睛】 关键点点睛：圆锥曲线中离心率的计算，关键是根据题中条件，结合曲线性质，找到,,a b c 一组等量关系（齐次式），进而求解离心率或范围.2．C解析：C 【分析】设出过焦点的直线方程，与抛物线方程联立求出两根之和，可得中点的坐标，消去参数可得中点的轨迹方程． 【详解】由抛物线的方程可得焦点(1,0)F ，可得过焦点的直线的斜率不为0， 设直线方程为：1x my =+，设直线与抛物线的交点1(A x ，1)y ，2(B x ，2)y ，设AB 的中点(,)P x y ，联立直线与抛物线的方程可得：2440y my --=，124y y m +=，21212()242x x m y y m +=++=+，所以可得2212x m y m⎧=+⎨=⎩，消去m 可得P 的轨迹方程：222y x =-，故选：C ． 【点睛】方法点睛：求轨迹方程的常见方法有：1、定义法；2、待定系数法；3、直接求轨迹法；4、反求法；5、参数方程法等等.3．A解析：A 【分析】由抛物线方程求得焦点F 的坐标，分直线AB 斜率不存在和直线斜率存在，存在时设直线AB 方程与抛物线方程联立，由韦达定理表示出A 、B 两点的横坐标之和，求得k ，即可得结论. 【详解】抛物线26y x =的焦点为3,02F ⎛⎫⎪⎝⎭， 当过焦点的直线斜率不存在时，即为32x =， 1232x x ==，符合123x x +=， 当过焦点的直线斜率存在时设为32y k x ⎛⎫=- ⎪⎝⎭， 与抛物线交于()()1122,,,A x y B x y 两点，由2632y x y k x ⎧=⎪⎨⎛⎫=- ⎪⎪⎝⎭⎩得()222293604k k x k x -++=， 所以2122363k x x k++==，即22363k k +=，所以无解， 则这样的直线有且只有一条. 故选：A. 【点睛】本题考查直线与抛物线的位置关系，解题的时候要注意讨论直线斜率不存在时的情况，以免遗漏，是中档题.4．B解析：B 【分析】作出图形，过点M 分别作抛物线C 的准线l 和直线3490x y ++=的垂线，垂足分别为点B 、A ，由抛物线的定义得出1d MB MF ==，可得出12d d MF MA +=+，利用FM 与直线3490x y ++=垂直时，12d d +取最小值，然后计算出点F 到直线3490x y ++=的距离，即为所求.【详解】 如下图所示：过点M 分别作抛物线C 的准线l 和直线3490x y ++=的垂线，垂足分别为点B 、A ， 由抛物线的定义可得1d MB MF ==，则12d d MF MA +=+， 当且仅当FM 与直线3490x y ++=垂直时，12d d +取最小值， 点F 到直线3490x y ++=的距离为22130494234d ⨯+⨯+==+，因此，12d d +的最小值为2. 故答案为：2. 【点睛】关键点点睛：本题求出抛物线上一点到准线和定直线的距离之和最小值问题，解题的关键就是利用F 、A 、M 三点共线取最小值，结合抛物线的定义转化求解.5．A解析：A 【分析】设直线AB 的方程为2y kx =+，设点()11,A x y 、()11,B x y ，将直线AB 的方程与抛物线的方程联立，列出韦达定理，结合已知条件可得出214x x =-，结合韦达定理求出2k 的值，进而可得出AOB 的面积为1212OAB S OF x x =⋅-△，即可得解. 【详解】易知抛物线28x y =的焦点为()0,2F .若直线AB 与x 轴垂直，此时直线AB 与抛物线28x y =有且只有一个公共点，不合乎题意.设直线AB 的方程为2y kx =+，设点()11,A x y 、()11,B x y ，联立228y kx x y=+⎧⎨=⎩，消去y 并整理得28160x kx --=，由韦达定理可得128x x k +=，1216x x =-，由于AOF 与BOF 的面积之比为1:4，则4BF FA =，则()()2211,24,2x y x y --=-，所以，214x x =-，则12138x x x k +=-=，可得183k x =-， 2221218256441639k k x x x ⎛⎫=-=-⨯-=-=- ⎪⎝⎭，可得2916k =，所以，OAB 的面积为1211222OAB S OF x x =⋅-=⨯△10===.故选：A. 【点睛】方法点睛：利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下： （1）设直线方程，设交点坐标为()11,x y 、()22,x y ；（2）联立直线与圆锥曲线的方程，得到关于x （或y ）的一元二次方程，必要时计算∆； （3）列出韦达定理；（4）将所求问题或题中的关系转化为12x x +、12x x 的形式； （5）代入韦达定理求解.6．C解析：C 【分析】利用双曲线的定义可求得12AF a =，24AF a =，利用余弦定理可求得ca的值，利用公式=b a . 【详解】2ABF 为等边三角形，22AB AF BF ∴==，且260ABF ∠=︒，由双曲线的定义可得121212||BF AB AF a B AF F BF =+-==-，212AF AF a -=，24AF a ∴=，在12AF F △中12AF a =，24AF a =，12120F AF ∠=，由余弦定理可得2212121222cos12027F F c AF AF AF AF a ==+-⋅︒=，即7c a =，所以22222216b b c a c a a a a -⎛⎫===-= ⎪⎝⎭． 因此，该双曲线的渐近线的斜率为6±． 故选：C.【点睛】思路点睛：求解双曲线的渐近线的常用思路：（1）定义法：直接利用a ，b ，求得比值，则焦点在x 轴时渐近线by x a=±，焦点在y 轴时渐近线ay x b=±； （2）构造齐次式，利用已知条件，结合222+=a b c ，构建b a 的关系式（或先构建ca的关系式），再根据焦点位置写渐近线即可.7．D解析：D 【分析】设出抛物线方程为22y mx =或22x ny =，代入点的坐标求出参数值可得．【详解】设抛物线方程为22y mx =，则262(3)m =⋅-，3m =-23y x =-， 或设方程为22x ny =，则2(3)26n =⨯，14n =，方程为212x y =．所以抛物线方程为2y =-或212x y =． 故选：D ． 【点睛】关键点点睛：抛物线的标准方程有四种形式，在不确定焦点位置（或开口方向时），需要分类讨论．象本题在抛物线过一点的坐标，则需要考虑焦点在x 轴和y 轴两种情况，焦点在x 轴上时可以直接设方程为2y mx =，代入点的坐标求出参数值，不必考虑焦点是在x轴正半轴还是在负半轴，焦点在y 轴也类似求解．8．C解析：C 【分析】根据题意，得到()1,0F c -，设(),M x y ，则(),N x y --，由11MF NF ⊥，求出2220x y c +-=与双曲线联立，求出()2222242242222a c a x c c a c a y c ⎧-⎪=⎪⎨-+⎪=⎪⎩，再由2221,33y k x ⎡⎤=∈⎢⎥⎣⎦，列出不等式求解，即可得出结果 【详解】因为点1F 为双曲线()2222:10,0x yC a b a b-=>>的左焦点，则()1,0F c -，设(),M x y ，由题意有(),N x y --，则()1,MF c x y =---，()1,NF c x y =-+，又11MF NF ⊥，所以()()2110MF NF c x c x y ⋅=---+-=，则2220x y c +-=， 又(),M x y 在双曲线上，所以22221x y a b-=，由22222222221x y a b x y c c a b ⎧-=⎪⎪⎪+=⎨⎪=+⎪⎪⎩解得()2222242242222a c a x c c a c ay c ⎧-⎪=⎪⎨-+⎪=⎪⎩，又M 在直线y kx =上，k ∈⎣， 所以()4224424222222222212111,33212c a c a e e e e e a c a y k x -+-+---⎡⎤====-∈⎢⎥⎣⎦，即42424213421e e e e ⎧≥⎪⎪-⎨⎪≤⎪-⎩，整理得42423840840e e e e ⎧-+≥⎨-+≤⎩，解得224e ≤≤+2243e -≤（舍，因为双曲线离心率大于1），1e ≤， 故选：C 【点睛】关键点点睛：本题考查双曲线的性质，考查双曲线的标准方程，解决本题的关键点是把11MF NF ⊥转化为向量数量积的坐标表示，求出点M 的轨迹方程，结合点在双曲线上，求出点的坐标，代入斜率公式求出离心率的范围，考查学生逻辑思维能力和计算能力，属于中档题．9．A解析：A 【分析】根据题中条件，由双曲线的定义，得到2PF a =，13PF a =，根据1212+≥PF PF F F ，即可求出结果. 【详解】因为点P 在双曲线的右支上，由双曲线的定义可得122PF PF a -=， 又213PF PF =，所以222PF a =，即2PF a =，则13PF a =， 因为双曲线中，1212+≥PF PF F F ，即42a c ≥，则2ca≤，即2e ≤， 又双曲线的离心率大于1，所以12e <≤. 故选：A. 【点睛】本题主要考查求双曲线的离心率，熟记双曲线的简单性质即可.10．C解析：C 【分析】先根据抛物线的定义将焦点弦长问题转化为中点到准线距离的两倍，进而用中点横坐标表示，设直线AB 的方程为：1x my =+(m 为常数),与抛物线方程联立消去x ,得到关于y 的一元二次方程，利用中点公式和韦达定理求得m 的值，进而得到中点的横坐标，从而求得线段AB 的长度. 【详解】抛物线24y x =的焦点坐标F (1,0),准线方程:1l x =-,设AB 的中点为M ,过A ,B ,M 作准线l 的垂线，垂足分别为C ,D ,N ,则MN 为梯形ABDC 的中位线，()02|21AB AF BF AC BD MN x ∴=+=+==+,∵直线AB 过抛物线的焦点F ,∴可设直线AB 的方程为：1x my =+(m 为常数), 代入抛物线的方程消去x 并整理得：2440y my --=, 设A ,B 的纵坐标分别为12,y y ,线段AB 中点()00,M x y , 则120222y y y m +===,1m ∴=, ∴直线AB 的方程为1x y =+,001213x y ∴=+=+=,()2318AB ∴=+=，故选：C.【点睛】本题考查抛物线的焦点弦长问题，涉及抛物线的定义，方程，线段中点坐标公式，直线与抛物线的交点问题，属中档题，关键是灵活使用抛物线的定义，将焦点弦长问题转化为中点坐标问题，注意直线方程的设法：过点(a ,0)，斜率不为零的直线方程可以设为x =my +a 的形式，不仅避免了讨论，而且方程组消元化简时更为简洁.11．C解析：C 【分析】根据方程2214x y a a +=-表示椭圆求出实数a 的取值范围，然后利用集合的包含关系可判断出“04a <<”是“方程2214x y a a+=-表示椭圆”的条件.【详解】若方程2214x y a a+=-表示椭圆，则0404a a a a >⎧⎪->⎨⎪≠-⎩，解得02a <<或24a <<， 记为{}02,24A a a a =<<<<或，又记{}04B a a =<<，AB则“04a <<”是“方程2214x y a a+=-表示椭圆”的必要不充分条件.故选：C. 【点睛】关键点点睛：本题的关键是求出方程为椭圆的充分必要条件.12．A解析：A 【分析】设圆心为(0,)P a ，（0a >），半径为r ，(,)Q x y 是抛物线上任一点，求出2PQ ，当2PQ 的最小值在原点处取得时，圆P 过原点，可得此时圆半径的范围，半径不在这个范围内的圆不过原点． 【详解】设圆心为(0,)P a ，（0a >），半径为r ，(,)Q x y 是抛物线上任一点，22222()4()(2)44PQ x y a y y a y a a =+-=+-=-++-，若2PQ 的最小值不在(0,0)O 处取得，则圆P 不过原点，所以20a ->，即2a >，此时圆半径为2r ==>．因此当2r >时，圆无法触及抛物线的顶点O ．故选：A ． 【点睛】关键点点睛：本题考查圆与抛物线的位置关系，题中圆不过原点，说明抛物线上的点到圆心距离的最小值不是在原点处取得，由此得到解法，即设圆心为(0,)P a ，抛物线上点的坐标为(,)Q x y ，求出PQ ，然后确定其最小值，由最小值点不是原点可得结论．二、填空题13．【分析】设点设直线的方程为联立直线与抛物线的方程列出韦达定理推导出利用基本不等式可求得的最小值【详解】若直线与轴重合则直线与抛物线只有一个交点不合乎题意易知抛物线的焦点为准线方程为设点设直线的方程为解析：92【分析】设点()11,A x y 、()22,B x y ，设直线AB 的方程为12x my =+，联立直线AB 与抛物线C 的方程，列出韦达定理，推导出112AF BF+=，利用基本不等式可求得4AF BF +的最小值. 【详解】若直线AB 与x 轴重合，则直线AB 与抛物线C 只有一个交点，不合乎题意. 易知抛物线C 的焦点为1,02F ⎛⎫⎪⎝⎭，准线方程为12x =-，设点()11,A x y 、()22,B x y ，设直线AB 的方程为12x my =+， 联立2122x my y x⎧=+⎪⎨⎪=⎩，整理可得2210y my --=，2440m ∆=+>，由韦达定理可得122y y m +=，121y y =-，()()()12121212211111*********m y y AF BF my my my my x x +++=+=+=++++++()()21222212122222121m y y m m y y m y y m m +++===+++-++， ()4111144522AF BF AF BF AF BF AF BF BF AF ⎛⎫⎛⎫∴+=++=++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭19522⎛≥+= ⎝， 当且仅当2AF BF =时，等号成立，因此，4AF BF +的最小值为92. 故答案为：92. 【点睛】结论点睛：过抛物线的焦点F 的直线与抛物线交于A 、B 两点，则112AF BF p+=. 14．【分析】求得双曲线的设运用双曲线的定义和三角形的中位线定理可得由相切的性质判断四边形为直角梯形过作垂足为运用直角三角形的勾股定理和向量的夹角的定义和直角三角形的余弦函数的定义计算可得所求值【详解】解解析：7【分析】求得双曲线的a ， c ，设1PF m =，2PF n =，运用双曲线的定义和三角形的中位线定理可得MN ，由相切的性质判断四边形ABNM 为直角梯形，过N 作NQ AM ⊥，垂足为Q ，运用直角三角形的勾股定理和向量的夹角的定义和直角三角形的余弦函数的定义，计算可得所求值． 【详解】解：因为双曲线22:143x y C -=，所以2a =，227c a b =+= 依题意画出如下图形，设1PF ，2PF 的中点分别为M ，N ，过点N 作NQ AM ⊥交AM 于点Q ，连接MN ，所以12172MN F F ==，设1PF m =，2PF n =，则24m n a -==所以11122AM PF m ==，21122BN PF n ==，所以()122MQ AM BN m n =-=-=，在Rt MNQ 中223NQ MN MQ =-=，因为//NQ BA ，所以MNQ ∠为12,AB F F 的夹角，所以12321cos ,77QN AB F F MN <>===故答案为：217【点睛】本题考查双曲线的定义、方程和性质，以及直线和圆相切的性质，考查直角三角形的勾股定理和锐角三角函数的定义、向量的夹角的概念，考查方程思想和化简运算能力和推理能力．15．【分析】由椭圆定义得由余弦定理得结合可得的值从而得答案【详解】由已知得所以由椭圆定义得由余弦定理得即则的面积为故答案为：【点睛】本题考查了椭圆的简单的性质关键点是利用余弦定理和三角形的面积公式解题考 解析：243-【分析】由椭圆定义得128F P PF +=，由余弦定理得22212121212cos 2F P PF F F F PF F P PF +-∠=⨯，结合可得12F P PF ⨯的值，从而得答案. 【详解】 由已知得12,2c e ==，所以4a =， 由椭圆定义得12248F P PF +=⨯=， 由余弦定理得222121212123cos cos3022F P PF F F F PF F P PF +-∠===⨯， 即()2121212216F PPF F P PF P PF +-⨯-=⨯，12F P PF⨯=，则12F PF △的面积为12111sin 3024222S F P PF =⨯⨯=⨯=- 故答案为：24- 【点睛】本题考查了椭圆的简单的性质，关键点是利用余弦定理和三角形的面积公式解题，考查了学生分析问题、解决问题的能力.16．【分析】设点为第一象限内的点设点利用抛物线的定义可求得点的坐标可得出直线的方程将直线的方程与抛物线的方程联立列出韦达定理求出的值由此可求得的面积【详解】设点为第一象限内的点设点抛物线的准线方程为由抛 解析：103【分析】设点A 为第一象限内的点，设点()11,A x y 、()22,B x y ，利用抛物线的定义可求得点A 的坐标，可得出直线AB 的方程，将直线AB 的方程与抛物线的方程联立，列出韦达定理，求出12y y -的值，由此可求得OAB 的面积. 【详解】设点A 为第一象限内的点，设点()11,A x y 、()22,B x y ，抛物线24y x =的准线方程为1x =-，由抛物线的定义可得1110AF x =+=，解得19x =，由于点A 为第一象限内的点，则10y >，可得16y ==，即点()9,6A ，直线AF 的斜率为63914AF k ==-，所以，直线AB 的方程为()314y x =-，即413x y =+， 联立24134x y y x⎧=+⎪⎨⎪=⎩，消去x 并整理可得216403y y --=， 由韦达定理可得12163y y +=，21161626333y y ∴=-=-=-， 因此，1211210162233OAB S OF y y =⋅-=⨯⨯+=△. 故答案为：103. 【点睛】方法点睛：利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下： （1）设直线方程，设交点坐标为()11,x y 、()22,x y ；（2）联立直线与圆锥曲线的方程，得到关于x （或y ）的一元二次方程，必要时计算∆； （3）列出韦达定理；（4）将所求问题或题中的关系转化为12x x +、12x x 的形式； （5）代入韦达定理求解.17．5【分析】首先根据双曲线的定义和等差数列的形式可设的三边长表示为最后根据勾股定理得到根据齐次方程求解离心率【详解】设并且的三边成等差数列最长的边为则三边长表示为又整理为两边同时除以得解得：或（舍）所解析：5 【分析】首先根据双曲线的定义和等差数列的形式，可设12PF F △的三边长表示为24,22,2c a c a c --，最后根据勾股定理得到22650c ac a -+=，根据齐次方程求解离心率. 【详解】设12PF PF >，并且122PF PF a -=，12PF F △的三边成等差数列，最长的边为2c ，则三边长表示为24,22,2c a c a c --， 又1290F PF ∠=，()()22224224c a c a c ∴-+-=，整理为22650c ac a -+=，两边同时除以2a 得，2650e e -+=，解得：5e =或1e =（舍），所以双曲线的离心率是5. 故答案为：5 【点睛】方法点睛：本题考查直线与双曲线的位置关系的综合问题，求离心率是圆锥曲线常考题型，涉及的方法包含1.根据,,a b c 直接求，2.根据条件建立关于,a c 的齐次方程求解，3.根据几何关系找到,,a b c 的等量关系求解.18．【分析】由题意可得的外接圆的圆心在线段上可得在中由勾股定理可得：即结合即可求解【详解】由题意可得：的外接圆的圆心在线段上设圆心为则在中由勾股定理可得：即所以即所以所以故答案为：【点睛】方法点睛：求椭 解析：12【分析】由题意可得12BF F △的外接圆的圆心在线段OB 上，1OF c =，123bMF BM ==，可得 13OM b =，在1OMF △中，由勾股定理可得：22211MF OM OF =+，即222233b b c ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，结合222b ac =-即可求解. 【详解】由题意可得：12BF F △的外接圆的圆心在线段OB 上，1OF c =， 设圆心为M ，则2133OM OB BM b b b =-=-=， 在1OMF △中，由勾股定理可得：22211MF OM OF =+，即222233b b c ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭， 所以223b c =，即2223a c c -=，所以2a c =，所以12c e a ==， 故答案为：12. 【点睛】方法点睛：求椭圆离心率的方法： （1）直接利用公式c e a=； （2）利用变形公式221b e a=-； （3）根据条件列出关于,a c 的齐次式，两边同时除以2a ，化为关于离心率的方程即可求解.19．【分析】先利用点坐标和垂直关系求得直线的斜率并写出直线方程联立直线与椭圆利用韦达定理和垂直的向量关系得到的关系式再结合焦距的关系式解出即得方程【详解】依题意椭圆的焦距为即即由点的坐标为知直线OD的斜解析：221 306xy+=【分析】先利用点D坐标和垂直关系求得直线l的斜率，并写出直线方程，联立直线与椭圆，利用韦达定理和垂直的向量关系得到22,a b的关系式，再结合焦距的关系式解出22,a b，即得方程.【详解】依题意，椭圆的焦距为46，即246c=，26c=，即2224a b-=，由点D的坐标为()2,1，知直线OD的斜率101202ODk-==-，又⊥OD AB，知直线l的斜率为2-，即直线l的方程为12(2)y x-=--，即52y x=-.设()()1122,,,A x yB x y联立方程2222152x ya by x⎧+=⎪⎨⎪=-⎩得()2222222420250a b x a x a a b+-+-=，故2222121222222025,44a a a bx x x xa b a b-+==++，即()()()12121212525225104y y x x x x x x=--=-++2222222222222202525425104444a a ab b a ba b a b a b--=-⨯+⨯=+++，由OA OB⊥知，1212OA OB x x y y⋅=+=，即22222222222525444a ab b a ba b a b--+=++，所以222255a b a b+=，又2224a b-=，消去2a得，42141200b b+-=，解得26b=或220b=-（舍去），故2230,6a b==，椭圆C的方程为221306x y+=.故答案为：221306x y +=.【点睛】 思路点睛：求解椭圆中的直线垂直问题时，一般利用直线的斜率之积为-1，或者直线上的向量的数量积为0来处理，再联立直线与椭圆方程，结合韦达定理，即可求出结果.20．【分析】由已知设圆的方程为椭圆的方程为再设出直线AC 的方程为直线BD 的方程为分别与椭圆的方程为联立整理由直线与椭圆相切的条件求得斜率再由已知得由此可求得椭圆的离心率【详解】因为两个椭圆与椭圆的离心率解析：7【分析】由已知设圆1Γ的方程为()()2222+1x y ma mb =，椭圆2Γ的方程为2222+1x y a b =，再设出直线AC 的方程为()1y k x ma =-，直线BD 的方程为2+y k x mb =，分别与椭圆2Γ的方程为2222+1x y a b =联立整理，由直线与椭圆相切的条件0∆=，求得斜率，再由已知得2257b a =，由此可求得椭圆的离心率. 【详解】因为两个椭圆1Γ与椭圆2Γ的离心率相等，所以设椭圆1Γ的方程为()()2222+1x y ma mb =，椭圆2Γ的方程为2222+1x y a b=，设直线AC 的方程为()1y k x ma =-，与椭圆2Γ的方程为2222+1x y a b=联立整理得：()()23422212222211+2+0b mk a x a k xm a a k b --=，因为直线AC 与椭圆2Γ相切，则()()()2222222213241142+0a k m m a a k b a b k --=-=∆，整理化简得()212221k a m b =-，设直线BD 的方程为2+y k x mb =，与椭圆2Γ的方程为2222+1x y a b=联立整理得：()()222222222222+2+0b mk a b a k xm a a x b b --=，因为直线BD 与椭圆2Γ相切，则()()()22222222222242+0a k mk a bm a a b b b -=--=∆，整理化简得()222221m kab -=，又AC 与BD 的斜率之积为57-，所以()()222212222221571mk k a b b a m -⎛⎫⋅=⋅=- ⎪-⎝⎭，整理得2257b a =，所以22222521177c b e a a ==-=-=， 所以椭圆1Γ的离心率为7，故答案为：7. 【点睛】关键点点睛：解决直线与椭圆的位置关系的问题，关键在于联立直线与椭圆的方程，运用方程的根的判别式的正负，满足直线与椭圆相交，相切，相离.三、解答题21．（1）2212x y +=；（2）①3k =-；②808,9⎡⎫⎪⎢⎣⎭．【分析】（1）把点代入方程结合离心率列方程组求解即可；（2）①设直线l 方程为，代入椭圆E 的方程可得，结合判别式与韦达定理，利用直线OA ，OB 的斜率之和为34进而求出直线斜率即可；②当直线l 的斜率不存在时，直线l 的方程为0x =，求得8MA MA ⋅=，当直线l 的斜率存在时，由（2）①得28821MA MB k ⋅=++，从而求得范围．【详解】解：（1）由题意得222221,2c a a b c ⎧=⎪⎨⎪=+⎩，解得222a c =，22b c =.设椭圆E 的方程为222212x y c c +=，又因为点P ⎛ ⎝⎭在椭圆E 上， 所以222211122c c+=，22222,1c a b ===，所以椭圆E 的方程为2212x y +=；（2）①设直线l 方程为：3y kx =+，代入椭圆E 的方程可得，()222112160kx kx +++=因为直线l 与椭圆E 有两个交点，所以216640∆=->k ，即24k >. 设()11,A x y ，()22,B x y ，则1221221k x x k +=-+，1221621x x k ⋅=+， 11223,3y kx y kx =+=+.又()1212121233244OA OB x x y y k k k k x x x x ++=+=+=-=⋅ 解得3k =-，经检验成立.所以，直线l 的斜率3k =-； ②当直线l 的斜率不存在时，直线l 的方程为0x =，将0x =代入2212x y +=，解得1y =±，则(0,1)A ，(0,1)B -，8MA MA ⋅=当直线l 的斜率存在时，由（2）①得()()()()22121212216133121k MA MA x x y y k x x k +⋅=⋅+--=+⋅=+()2228211882121k k k ⎡⎤++⎣⎦==+++因为24k >，所以MA MA ⋅的范围为808,9⎛⎫⎪⎝⎭． 综上，得MA MB ⋅的取值范围是808,9⎡⎫⎪⎢⎣⎭． 【点睛】解决直线与椭圆的综合问题时，要注意：(1)注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件；(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题．22．（1）2214x y +=；（2）证明见解析，()1,0.【分析】（1）利用椭圆的定义可得12|||2|MF MF a =+，根据基本不等式求出2a =，再由离心率求出c =222a b c =+即可求解.（2）当点C 是椭圆上顶点时，求出()4,3P ，进而求出点83,55D ⎛⎫- ⎪⎝⎭，写出直线CD 的方程，得出直线CD 经过定点()1,0N ，设l 上任意点()4,P m ，设(),C C C x y ，(),y D D D x ，写出直线PA 的方程，将直线与椭圆联立，求出2221826,99m m C m m ⎛⎫- ⎪++⎝⎭，同理求出222222,11m m D m m ⎛⎫-- ⎪++⎝⎭，若直线CD 经过定点()1,0N ，只需,,N C D 三点共线，利用向量共线的坐标表示即可求解. 【详解】（1）由椭圆的定义知12|||2|MF MF a =+，所以2122122MF MF MF MF a ⎛+⎫≤= ⎪⎝⎭，已知12||||4MF MF ≤，所以24a =，2a =.因为e =c = 因为222a b c =+，所以1b =，所以椭圆E 的方程为2214x y +=.（2）当点C 是椭圆上顶点时，直线AC 的方程为()122y x =+，可得()4,3P ，则()3:22PB l y x =-与2214x y +=联立解得83,55D ⎛⎫- ⎪⎝⎭，所以直线CD 的方程为：10x y +-=，由椭圆的对称性可知，直线CD 经过x 轴上的定点， 所以直线CD 经过定点()1,0N . 以下证明一般性：设l 上任意点()4,P m ，设(),C C C x y ，(),y D D D x 则直线PA 的方程为()26my x =+ 联立22(2)614m y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩消去y 得()2222944360m x m x m +++-=由韦达定理得2243629C m x m --=+，解得2221826,99m m C m m ⎛⎫- ⎪++⎝⎭因为直线PB 的方程为()22my x =- 联立22(2)214m y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩消去y 得()222214440m x m x m +-+-=由韦达定理得224421D m x m -=+，解得222222,11m m D m m ⎛⎫-- ⎪++⎝⎭ 直线CD 经过定点()1,0N ，即,,N C D 三点共线因为222936,99m m NC m m ⎛⎫-= ⎪++⎝⎭，22232,11m m ND m m ⎛⎫--= ⎪++⎝⎭ 因为222222932639191m m m m m m m m ---⨯-⨯++++ ()()()332218661891m m m m mm -+--=++0=所以//NC ND ，那么,,N C D 三点共线 所以直线CD 经过定点()1,0N ， 【点睛】关键点点睛：本题考查了直线与椭圆的位置关系，解题的关键是利用点C 是椭圆上顶点时，求出定点()1,0N ，再证明一般性，借助,,N C D 三点共线求解，考查了运算求解能力.23．（1）2213x y +=；（2）0x y -=或0x y +=.【分析】（1）由离心率、面积和222a b c =+可得答案；（2）设()11,A x y ，()22,B x y，:l x ty =+11212AF BF F AF F BSSS=+，结合基本不等式，可得答案.【详解】 （1）∵3c e a ==，12MF F S bc ==△222a b c =+，解得a =1b =，c =C 的方程为：2213x y +=.（2）()1F，)2F ，设()11,A x y ，()22,B x y ，已知直线l 的斜率不为0，设直线l：x ty =+2213x ty x y ⎧=+⎪⎨+=⎪⎩，得()22310t y ++-=，故12y y +=，12213y y t =-+，1212121212F F A F F BSSF F y y+=-=23t+，12=≤=，即1t =±时等号成立，所以直线l 的方程为0x y --=或0x y +=. 【点睛】本题考查了椭圆的定义，考查了三角形的面积公式，关键点是利用韦达定理表示1212F F AF F BSS+并利用基本不等式求最值，考查了直线与椭圆的位置关系和计算能力.24．（1）22182x y +=；（2）20x y +=．【分析】（1）由离心率，点的坐标代入椭圆方程及222a b c =+列方程组解得,,a b c 得椭圆方程； （2）已知条件说明直线AO 为线段PQ 的垂直平分线，直线OA 方程为12y x =，这样可设直线PQ 方程为2y x m =-+，代入椭圆方程，应用韦达定理得12x x +，12,x x 即为,P Q的横坐标，求出中点横坐标1202x x x +=，由直线PA 得中点纵坐标0y ，中点坐标代入直线AO 方程可得参数m ，即直线PQ 方程．【详解】（1）依题意，22222411a b a b c c a⎧+=⎪⎪⎪=+⎨⎪⎪=⎪⎩，，解得2282a b ⎧=⎨=⎩，，．故椭圆C 的方程为22182x y +=；（2）∵||||,||||OP OQ AP AQ ==，∴直线AO 为线段PQ 的垂直平分线，则直线OA 的方程为12y x =，设直线PQ 的方程为2y x m =-+， 由221822x y y x m ⎧+=⎪⎨⎪=-+⎩，得：221716480x mx m -+-=， ()22(16)417480m m =-⨯->，解得m <()()1122,,,P x y Q x y ，由韦达定理得121617mx x +=，设PQ 的中点为()00,H x y ， 所以120008,221717x x m m x y x m +===-+=；所以8,1717m m H ⎛⎫⎪⎝⎭． 又8,1717m m H ⎛⎫⎪⎝⎭在直线OA 上，代入得1817217m m =⋅，解得0m =，综上所述，直线PQ 的方程为20x y +=． 【点睛】关键点点睛：本题考查由离心率和一点坐标求椭圆方程，考查直线与椭圆相交问题．在直线与椭圆相交问题时，解题关键是由平面几何知识由条件||||,||||OP OQ AP AQ ==得直线AO 为线段PQ 的垂直平分线，这样用设而不求思想可求得直线PQ 方程．即求出AO 方程，由垂直设出直线PQ 方程，代入椭圆方程应用韦达定理求得PQ 中点坐标，再代入直线AO 方程可得参数值．25．（1）22143x y +=；（2）证明见解析.【分析】（1）根据椭圆离心率和椭圆的性质可知b =，再根据PQ x ⊥轴时，APQ 的面积为 92，由面积公式可知()212922b ac a +⋅=，由此即可求出椭圆方程； （2）设直线PQ 的方程为1x my =+，联立椭圆方程，设1122(,),(,)P x y Q x y ，由韦达定理，可知 12122269,3434m y y y y m m +=-=-++，将直线AP 的方程()112+2y y x x =+与直线 BQ 的方程()2222y y x x =--联立，利用韦达定理，化简计算，即可证明结果. 【详解】 解:（1）由题意知12c a =，所以2a c =，又222a b c =+，所以b =当PQ x ⊥轴时，APQ 的面积为92， 所以()212922b ac a +⋅=解得21,c = 所以224,3a b ==，所以椭圆C 的标准方程为22143x y +=.。

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(有答案解析)(4)

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(有答案解析)(4)

一、选择题1．平面α内有一条直线m ，过平面α外一点P 作直线n 与m 所成角为6π，则直线n 与平面α交点的轨迹是（ ） A ．直线B ．抛物线C ．椭圆D ．双曲线2．光线从椭圆的一个焦点发出，被椭圆反射后会经过椭圆的另一个焦点；光线从双曲线的一个焦点发出，被双曲线反射后的反射光线等效于从另一个焦点射出，如图①，一个光学装置由有公共焦点1F 、2F 的椭圆Γ与双曲线Ω构成，现一光线从左焦点1F 发出，依次经Ω与Γ反射，又回到了点1F ，历时1t 秒；若将装置中的Ω去掉，如图②，此光线从点1F 发出，经Γ两次反射后又回到了点1F ，历时2t 秒；若218t t =，则Γ与Ω的离心率之比为（ ）A ．3:4B ．2:3C ．1:2D ．23．已知双曲线()222210,0x y a b a b-=>>的一条渐近线与圆()2239x y -+=相交于A 、B 两点，若2AB =，则该双曲线的离心率为（ ）A ．5B ．2C ．3D ．44．直线34y kx k =-+与双曲线221169x y -=有且只有一个公共点，则k 的取值有（ ）个A ．1B ．2C ．3D ．45．已知椭圆C 的焦点为()12,0F -，()22,0F ，过2F 的直线与C 交于A ，B 两点，若222AF F B =，1AB BF =，则C 的方程为（ ） A ．221124x y +=B ．2211612x y +=C ．221128x y +=D ．2212016x y +=6．已知直线:(1)(2)230l a x a y a +++--=经过定点P ，与抛物线24x y =交于,A B 两点，且点P 为弦AB 的中点，则直线l 的方程为（ ） A ．230x y +-= B ．210x y -+= C ．210x y -+=D ．20x y +-=7．已知椭圆2221(02)4x y b b+=<<，直线1x y +=与椭圆交于,P Q 两点，若OP OQ ⊥，则椭圆的离心率为（ ）A ．6 B ．7 C ．427D ．278．已知动点(),P x y 满足()()2222522x y x y a a+-+++=+(a 为大于零的常数)﹐则动点P 的轨迹是（ ） A ．线段B ．圆C ．椭圆D ．双曲线9．设1F 、2F 是椭圆()2222:10x y E a b a b +=>>的左、右焦点，P 为直线2ax c=上一点，若21F PF 是底角为30的等腰三角形，则椭圆E 的离心率为（ ） A ．12B ．22C ．34D ．4510．已知抛物线1C 的顶点在坐标原点，焦点F 在y 轴正半轴上．若点F 到双曲线222:126x y C -=的一条渐近线的距离为2，则1C 的标准方程是（ ）A ．2833y x =B ．21633y x =C ．28x y =D ．216x y =11．在抛物线型内壁光滑的容器内放一个球，其通过中心轴的纵剖面图如图所示，圆心在y 轴上，抛物线顶点在坐标原点，已知抛物线方程是24x y =，圆的半径为r ，若圆的大小变化时，圆上的点无法触及抛物线的顶点O ，则圆的半径r 的取值范围是（ ）A ．()2,+∞B ．()1,+∞C ．[)2,+∞D ．[)1,+∞12．已知过点(,0)A a 的直线与抛物线22(0)y px p =>交于M.N 两点，若有且仅有一个实数a ，使得16OM ON ⋅=-成立，则a 的值为（ ） A ．4-B ．2C ．4D ．8二、填空题13．抛物线有一条重要性质：从焦点发出的光线，经过抛物线上的一点反射后.反射光线平行于抛物线的轴.已知抛物线22y x =，平行于x 轴的光线在抛物线上点P 处反射后经过抛物线的焦点F ，在抛物线上点Q 处再次反射，又沿平行于x 轴方向射出，则两平行光线间的最小距离为___________.14．已知双曲线()2222:10,0x y C a b a b-=>>的一条渐近线与圆(224x y +-=相交于A ，B 两点，且2AB =，则双曲线C 的离心率为___________.15．已知双曲线()2222:10,0x y C a b a b-=>>的左、焦点为1F 、2F ，点P 为双曲线C 的渐近线上一点，120PF PF ⋅=，若直线1PF 与圆222x y a +=相切，则双曲线C 的离心率为___________.16．已知椭圆22:143x y C +=的左､右焦点分别为12F F 、，过2F 且倾斜角为π4的直线l 交椭圆C 于A B 、两点，则1F AB 的面积为___________.17．已知直线1:43120l x y -+=和直线2:1l x =-，则抛物线24y x =上一动点P 到直线1l 和直线2l 距离之和的最小值是________．18．在平面直角坐标系xOy 中，已知双曲线22:17y x Γ-=的两个焦点分别为1F ，2F ，以2F 为圆心，12F F 长为半径的圆与双曲线Γ的一条渐近线交于M ，N 两点，若OM ON ≥，则OMON的值为________.19．已知双曲线2222:1(0,0)x y E a b a b-=>>，点F 为E 的左焦点，点P 为E 上位于第一象限内的点，P 关于原点的对称点为Q ，且满足||3||PF FQ =，若||OP b =，则E 的离心率为_________.20．过抛物线24y x =的焦点F 的直线交抛物线于A ，B 两点，点O 是原点，若||3AF =，则AOB 的面积为_______．三、解答题21．已知点M ⎭在椭圆2222:1(0)x y C a b a b +=>>上，且点M 到C 的左，右焦点的距离之和为4． （1）求C 的方程；（2）设O 为坐标原点，若C 的弦AB 的中点在线段OM （不含端点,O M ）上，求OA OB ⋅的取值范围．22．已知椭圆2222:1(0)x y C a b a b+=>>的左顶点和右焦点F 的距离与右焦点F 到椭圆C的右准线的距离相等，且椭圆C 的通径（过椭圆的焦点，且与长轴垂直的弦）长为3. （1）求椭圆C 的方程；（2）设直线l 过点F ，且与坐标轴不垂直，与椭圆C 相交于P ，Q 两点，线段PQ 的垂直平分线与x 轴交于点B . ①当67BF =时，求直线l 的方程； ②求证：PQBF为定值. 23．在平面直角坐标系xOy 中，已知两点()1,0M -，()1,0N ，动点Q 到点M 的距离为，线段NQ 的垂直平分线交线段MQ 于点K ，设点K 的轨迹为曲线E . （1）求曲线E 的方程；（2）已知点()2,0P ，设直线l ：10x my +-=与曲线E 交于A ，B 两点，求证：OPA OPB ∠=∠.24．已知四点1234,1,,(1,1),(0,1)P P P P ⎛⎛- ⎝⎭⎝⎭中恰有三点在椭圆2222:1x y C a b+=上，其中0a b >>． （1）求,a b 的值；（2）若直线l 过定点(2,0)M 且与椭圆C 交于,A B 两点（l 与x 轴不重合），点B 关于x 轴的对称点为点D ．探究：直线AD 是否过定点，若是，求出该定点的坐标；若不是，请说明理由．25．已知椭圆()2222:10x y C a b a b+=>>，A ，B 为椭圆的左、右顶点，点()0,2N -，连接BN 交椭圆C 于点Q ，ABN 为直角三角形，且:3:2NQ QB = （1）求椭圆的方程；（2）过A 点的直线l 与椭圆相交于另一点M ，线段AM 的垂直平分线与y 轴的交点P 满足154PA PM ⋅=，求点P 的坐标.26．已知圆22:4C x y +=，点P 为圆C 上的动点，过点P 作x 轴的垂线，垂足为Q ，设D 为PQ 的中点，且D 的轨迹为曲线E (PQD 三点可重合). （1）求曲线E 的方程；（2）不过原点的直线l 与曲线E 交于M ､N 两点，已知OM ，直线l ，ON 的斜率1k ､k ､2k 成等比数列，记以OM ，ON 为直径的圆的面积分别为S 1，S 2，试探究12S S +是否为定值，若是，求出此值；若不是，说明理由.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】过点P 作PO α⊥，以点O 为坐标原点，OP 为z 轴，以定直线m 为y 轴，建立如图所示的空间直角坐标系，设出坐标，分别表示出直线AB 与PM 的方向向量，利用夹角公式即可得出． 【详解】解：过点P 作PO α⊥，以点O 为坐标原点，OP 为z 轴，以定直线m 为y 轴，建立如图所示的空间直角坐标系．不妨设1OP =，30PBO ∠=︒，OB ∴=．则(0P ，0，1)，B ．设点(Q x ，y ，0)，则(,,1)PQ x y =-，取直线m 的方向向量为(0,1,0)u =． 直线AB 与PQ 所成的角为30，2||cos30||||PQ u PQ u x ∴︒===+ 化为2213y x -=，即为点Q 的轨迹．故选：D ．【点睛】熟练掌握通过建立如图所示的空间直角坐标系利用异面直线的夹角公式求得轨迹的方法是解题的关键．2．A解析：A 【分析】设122F F c =，设椭圆Γ的长轴长为12a ，双曲线Ω的实轴长为22a ，设光速为v ，推导出112a vt =，利用椭圆和双曲线的定义可得出1243a a =，由此可计算得出Γ与Ω的离心率之比. 【详解】设122F F c =，设椭圆Γ的长轴长为12a ，双曲线Ω的实轴长为22a ， 在图②中，1CDF 的周长为111212124CF DF CD CF CF DF DF a vt ++=+++==，所以，1148a vt =，可得112a vt =，在图①中，由双曲线的定义可得2122AF AF a -=，由椭圆的定义可得1212BF BF a +=， 22AF BF AB =-，则2121111222AF AF BF AB AF a BF AB AF a -=--=---=，即()111222a AB AF BF a -++=，由题意可知，1ABF 的周长为111AB AF BF vt ++=，即112111322222a a a a vt a =-=-=， 所以，1243a a =. 因此，Γ与Ω的离心率之比为122112:::3:4c ce e a a a a ===.故选：A. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.3．C解析：C 【分析】设双曲线的渐近线方程为y kx =，其中bk a=±，利用勾股定理可求得k 的值，即可求得b a，再由双曲线的离心率公式e =即可求得双曲线的离心率. 【详解】设双曲线的渐近线方程为y kx =，其中bk a=±， 圆()2239x y -+=的圆心为()3,0C ，半径为3r =，圆心C 到直线y kx =的距离为d =，2AB =，由勾股定理可得2222AB r d ⎛⎫=+ ⎪⎝⎭，即2219+=，解得k =±ba∴=，因此，该双曲线的离心率为3c e a =====. 故选：C. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.4．D解析：D 【分析】将直线方程与双曲线的方程联立，得出关于x 的方程，根据直线与双曲线只有一个公共点，求出对应的k 值，即可得解. 【详解】联立22341169y kx k x y =-+⎧⎪⎨-=⎪⎩，消去y 并整理得()()()2221693243164390k x k k x k ⎡⎤-+-+-+=⎣⎦，由于直线34y kx k =-+与双曲线221169x y -=有且只有一个公共点， 所以，21690k -=或()()()222216903243641694390k k k k k ⎧-≠⎪⎨⎡⎤⎡⎤∆=----+=⎪⎣⎦⎣⎦⎩， 解得34k =±或2724250k k +-=， 对于方程2724250k k +-=，判别式为22447250'∆=+⨯⨯>，方程2724250k k +-=有两个不等的实数解.显然34k =±不满足方程2724250k k +-=. 综上所述，k 的取值有4个. 故选：D. 【点睛】方法点睛：将直线与圆锥曲线的两个方程联立成方程组，然后判断方程组是否有解，有几个解，这是直线与圆锥曲线位置关系的判断方法中最常用的方法，注意：在没有给出直线方程时，要对是否有斜率不存在的直线的情况进行讨论，避免漏解．5．C解析：C 【分析】根据椭圆的定义以及余弦定理，结合221cos cos 0AF O BF F ∠+∠=列方程可解得a ，b ，即可得到椭圆的方程． 【详解】22||2||AF BF =，2||3||AB BF ∴=， 又1||||AB BF =，12||3||BF BF ∴=， 又12||||2BF BF a +=，2||2aBF ∴=， 2||AF a ∴=，13||2BF a =， 12||||2AF AF a +=，1||AF a ∴=， 12||||AF AF ∴=，A ∴在y 轴上．在Rt2AF O 中，22cos AF O a∠=，在12BF F △中，由余弦定理可得22221316()()822cos 2242a a a BF F a a +--∠==⨯⨯． 221cos cos 0AF O BF F ∠+∠=，可得22802a a a -+=，解得212a =．2221248b a c =-=-=．椭圆C 的方程为：221128x y +=．故选：C ． 【点睛】方法点睛：用待定系数法求椭圆方程的一般步骤；①作判断：根据条件判断椭圆的焦点在x 轴上，还是在y 轴上，还是两个坐标轴都有可能；②设方程：根据上述判断设方程()222210x y a b a b +=>>或22221x y b a+=()0a b >>；③找关系：根据已知条件，建立关于a 、b 、c 的方程组；④得方程：解方程组，将解代入所设方程，即为所求.6．B解析：B 【分析】利用点差法求出直线斜率，即可得出直线方程.【详解】由直线:(1)(2)230l a x a y a +++--=得(2)(23)0a x y x y +-++-=所以20230x y x y +-=⎧⎨+-=⎩ 解得11x y =⎧⎨=⎩则()1,1P 设1122(,),(,)A x y B x y ，则21122244x y x y ⎧=⎨=⎩，两式相减得121212()()4()x x x x y y -+=-， 即121212142AB y y x x k x x -+===-， 则直线方程为11(x 1)2y -=-，即210x y -+=. 故选：B. 【点睛】方法点晴：点差法是求解中点弦有关问题的常用方法.7．C解析：C 【分析】设1122(,),(,)P x y Q x y ，把直线1x y +=与椭圆2221(02)4x yb b +=<<，联立，根据OP OQ ⊥计算出b ，直接求出离心率.【详解】设1122(,),(,)P x y Q x y ，由222141x y b x y ⎧+=⎪⎨⎪+=⎩得222(4)8440b x x b +-+-=，所以12221228=444·=4x x b b x x b ⎧+⎪⎪+⎨-⎪⎪+⎩∵OP OQ ⊥，∴12121212=2()10OP OQ x x y y x x x x +=-++=，解得247b =.7e ∴=== 故选：C 【点睛】求椭圆（双曲线）离心率的一般思路：根据题目的条件，找到a 、b 、c 的关系，消去b ，构造离心率e 的方程或（不等式）即可求出离心率．8．C解析：C 【分析】由a 为大于零的常数，可知5a a+的最小值，再根据两点间距离公式得几何意义以及椭圆定义判断轨迹. 【详解】的几何意义为点(),P x y 与点(0,2)A 间的距离，的几何意义为点(),P x y 与点(0,2)B -间的距离，且4AB =又由a 为大于零的常数，可知54a a +≥=>，当且仅当5a a=，即a =54a a=+>， 即动点P 到点A 与到点B 的距离之和为定值，且大于AB ， 所以动点P 的轨迹为椭圆， 故选：C. 【点睛】在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误． 椭圆的定义揭示了椭圆的本质属性，正确理解掌握定义是关键，应注意定义中的常数大于|F 1F 2|，避免了动点轨迹是线段或不存在的情况．9．B解析：B 【分析】设直线2a x c=交x轴于点M ，推导出222PF F M =，可得出关于a 、c 的等式，由此可解得该椭圆的离心率. 【详解】设直线2a x c=交x轴于点M ，21F PF △是底角为30的等腰三角形，260PF M ∠=，2122PF F F c ==，在2Rt PF M 中，290PMF ∠=，230MPF ∠=，222PF F M ∴=，P 为直线2a x c =上一点，222a c c c ⎛⎫∴-= ⎪⎝⎭，即222a c =，22c e a ∴==． 故选：B ． 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.10．D解析：D 【分析】先根据双曲线的方程求解出双曲线的渐近线方程，再根据点到直线的距离公式求解出抛物线方程中的p ，则抛物线方程可求. 【详解】双曲线2C 的渐近线方程是22026x y -=，即3y x =.因为抛物线的焦点()0,02p F p ⎛⎫> ⎪⎝⎭30x y -=的距离为2， 2231p =+，即8p =，所以1C 的标准方程是216x y =，故选：D ． 【点睛】方法点睛：求解双曲线方程的渐近线方程的技巧：已知双曲线方程22221x y a b-=或22221y x a b -=，求解其渐近线方程只需要将方程中的“1”变为“0”，由此得到的y 关于x 的一次方程即为渐近线方程. 11．A【分析】设圆心为(0,)P a ，（0a >），半径为r ，(,)Q x y 是抛物线上任一点，求出2PQ ，当2PQ 的最小值在原点处取得时，圆P 过原点，可得此时圆半径的范围，半径不在这个范围内的圆不过原点． 【详解】设圆心为(0,)P a ，（0a >），半径为r ，(,)Q x y 是抛物线上任一点，22222()4()(2)44PQ x y a y y a y a a =+-=+-=-++-，若2PQ 的最小值不在(0,0)O 处取得，则圆P 不过原点，所以20a ->，即2a >，此时圆半径为2r ==>．因此当2r >时，圆无法触及抛物线的顶点O ．故选：A ． 【点睛】关键点点睛：本题考查圆与抛物线的位置关系，题中圆不过原点，说明抛物线上的点到圆心距离的最小值不是在原点处取得，由此得到解法，即设圆心为(0,)P a ，抛物线上点的坐标为(,)Q x y ，求出PQ ，然后确定其最小值，由最小值点不是原点可得结论．12．C解析：C 【分析】设出直线方程与抛物线方程联立，利用韦达定理得出1212,y y y y +及12x x ，把16OM ON ⋅=-用坐标表示代入上述值结合已知条件可得答案.【详解】设直线MN 的直线方程为x ty a =+，1122(,),(,)M x y N x y ， 由题意得22x ty a y px=+⎧⎨=⎩，整理得2220y pty pa --=， 所以12122,2y y pt y y pa +==-，()()()2212121212x x ty a ty a t y y at y y a =++=+++()()2222t ap at pt a =-++，因为16OM ON ⋅=-，所以121216x x y y +=-， 所以()()2222216tpa at pt a pa -++-=-，22160a pa -+=，因为方程有且仅有一个实数a ，所以()22640p ∆=-=，解得4p =，或4p =-（舍去）， 故选：C.本题考查了直线和抛物线的位置关系，关键点是利用韦达定理求出1212,y y y y +及12x x ，然后16OM ON ⋅=-坐标表示列出等式，考查了学生分析问题、解决问题的能力.二、填空题13．【分析】作出图像设题中问题即为求的最小值设直线联立用韦达定理表示即可得解【详解】根据题意作出图像如图所示设题中问题即为求的最小值设由得所以所以当时最小为2故答案为：2 解析：2【分析】作出图像，设1122(,),(,)A x y B x y ，题中问题即为求12||y y -的最小值，设直线，联立，用韦达定理表示即可得解. 【详解】根据题意作出图像，如图所示，设1122(,),(,)A x y B x y ，题中问题即为求12||y y -的最小值.设1:2AB x ty =+， 由2122x ty y x⎧=+⎪⎨⎪=⎩，得2210y ty --=，所以12122,1y y t y y +==-. 所以22121212||()444y y y y y y t -=+-=+当0t =时，12||y y -最小为2.故答案为：2.14．2【分析】由双曲线圆的方程确定渐近线方程为圆心为半径为根据圆的相交弦与半径弦心距之间的几何关系有结合双曲线参数间的关系即可求其离心率【详解】由题意知：双曲线的渐近线为而圆心为半径为∴圆心到渐近线的距解析：2 【分析】由双曲线、圆的方程确定渐近线方程为by x a=±，圆心为(0,，半径为2r ，根据圆的相交弦与半径、弦心距之间的几何关系有222||4AB r d -=，结合双曲线参数间的关系即可求其离心率. 【详解】由题意知：双曲线的渐近线为by x a=±，而圆心为(0,，半径为2r ，∴圆心到渐近线的距离d ==，而2AB =，∴221r d -=，故222123a a b=+，又222,1c a b c e a +==>， ∴2e =. 故答案为：2. 【点睛】关键点点睛：根据双曲线、圆的标准方程确定渐近线方程、圆心、半径长，结合圆中相交弦的几何性质及双曲线参数关系，列出关于,a c 的齐次方程求离心率.15．【分析】作出图形设与圆相切于点分析出可求得的值进而可得出双曲线的离心率为即可得解【详解】如下图所示设与圆相切于点则则则为的中点则为的中点由直角三角形的性质可得因为为的中点则由于双曲线的两渐近线关于轴 解析：2【分析】作出图形，设1PF 与圆222x y a +=相切于点E ，分析出23POF π∠=，可求得ba的值，进而可得出双曲线C的离心率为e =，即可得解. 【详解】如下图所示，设1PF 与圆222x y a +=相切于点E ，则OE a =，120PF PF ⋅=，则12PF PF ⊥，1OE PF ⊥，则2//OE PF ， O 为12F F 的中点，则E 为1PF 的中点，222PF OE a ∴==，由直角三角形的性质可得1OF OP =，因为E 为1PF 的中点，则1EOF POE ∠=∠， 由于双曲线的两渐近线关于y 轴对称，可得21POF EOF ∠=∠，所以，12EOF POE POF ∠=∠=∠，则1223EOF POE POF POF π∠+∠+∠=∠=， 所以，23POF π∠=，则tan 33b a π==， 因此，双曲线C 的离心率为22222212c c a b b e a a a a +⎛⎫====+= ⎪⎝⎭. 故答案为：2. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.16．【分析】先求出直线的方程与椭圆方程联立消去x 求出|y1-y2|利用即可求出的面积【详解】由题意得:直线:设则有:消去x 得:7y2+6y-9=0∴即的面积为【点睛】求椭圆(双曲线)的焦点弦三角形的面积 解析：1227【分析】先求出直线l 的方程,与椭圆方程联立,消去x ,求出| y 1- y 2|,利用11212|1|||2F AB S F F y y =-△即可求出1F AB 的面积. 【详解】由题意得: 直线l :1y x =-, 设1122(,),(,)A x y B x y ,则有:2213412y x x y =-⎧⎨+=⎩消去x 得:7y 2+6y -9=0, ∴121269,77y y y y +=-=-12211111|||22|222F AB S F F y y -∴=⨯=⨯==△即1F AB 的面积为7【点睛】求椭圆(双曲线)的焦点弦三角形的面积: （1）直接求出弦长|AB |,利用11||2F AB AB d S =△; （2）利用11212|1|||2F AB S F F y y =-△. 17．【分析】作出图像根据抛物线定义和性质将距离之和转化为动点到直线和焦点距离之和最小值数形结合得焦点到直线的距离最小【详解】解：作出图像如下：根据抛物线定义有动点到直线和直线距离之和为当点位于图中的时取 解析：165【分析】作出图像，根据抛物线定义和性质将距离之和转化为动点P 到直线1l 和焦点距离之和最小值，数形结合得焦点F 到直线1l 的距离最小. 【详解】解：作出图像如下：根据抛物线定义有动点P 到直线1l 和直线2l 距离之和为PA PB PB PF +=+ 当点P 位于图中的P '时取得最小值，此时最小值为焦点F 到直线1l 的距离， 由距离公式得：4121655d +== 故答案为：165【点睛】抛物线性质的应用技巧：（1）利用抛物线方程确定及应用其焦点、准线时，关键是将抛物线方程化成标准方程； （2）要结合图形分析，灵活运用平面图形的性质简化运算.18．【分析】求出双曲线的两个焦点坐标和渐近线方程再求圆的方程与渐近线方程联立可得MN 两点的横坐标由即为横坐标的绝对值的比可得答案【详解】由已知得取双曲线的一条渐近线所以圆的方程为由整理得解得取双曲线的另解析：32【分析】求出双曲线的两个焦点坐标和渐近线方程，再求圆的方程与渐近线方程联立可得M ，N 两点的横坐标，由OMON即为横坐标的绝对值的比可得答案.【详解】由已知得2221,7,8a b c ===，242c =，12(22,0),(22,0)F F -，取双曲线的一条渐近线7y x =，所以圆的方程为(22322x y +=-，由(227232y x x y ⎧=⎪⎨-+=⎪⎩整理得22260x x -=，解得3222N M x x ==，323222M NM O x xO N===.取双曲线的另一条渐近线7y x =-，()2272232y xx y ⎧=-⎪⎨-+=⎪⎩整理得22260x x --=与上同，综上32OM ON=. 故答案为：32. 【点睛】关键点点睛：本题考查了直线与双曲线、圆的位置关系，解答本题的关键是求出渐近线与圆的方程然后联立，得到M ，N 两点的横坐标再由绝对值做比值，考查了学生的运算求解能力.19．【分析】由题意设即有由双曲线定义及已知可得且结合点在曲线上联立方程得到关于的齐次方程即可求得离心率【详解】令则且①由题意知：E 的左准线为结合双曲线第二定义知：又∴解得②∵知：∴联立①②得：整理得∴故 解析：3【分析】由题意设00(,)P x y ，即有00(,)Q x y --，由双曲线定义及已知可得22003()a a x x c c +=-且22200x y b +=，结合点在曲线上联立方程得到关于,a c 的齐次方程，即可求得离心率.【详解】令00(,)P x y ，00,0x y >则00(,)Q x y --且2200221x y a b-=①，由题意知：E 的左准线为2a x c =-，结合双曲线第二定义知：20||()a PF e x c=+，20||()a FQ e x c=-，又||3||PF FQ =，∴22003()a a x x c c +=-，解得202a x c=②， ∵||OP b =知：22200x y b +=，∴联立①，②得：42222244(1)a a b b c c+-=，整理得223a c =， ∴e =【点睛】关键点点睛：根据双曲线第二定义：曲线上的点到焦点距离与该点到对应准线的距离之比为常数e ，可得点P 的横坐标为22ac；结合点在曲线上及勾股定理即可得关于,a c 的齐次方程求离心率即可.20．【分析】根据已知条件不妨设在第一象限根据抛物线定义以及方程求出点坐标进而得出直线方程与抛物线方程联立求出点坐标即可求出AOB 的面积【详解】抛物线的焦点为∵∴点A 到准线的距离为3点的横坐标为根据对称性【分析】根据已知条件不妨设A 在第一象限，根据抛物线定义以及方程，求出A 点坐标，进而得出直线AF 方程，与抛物线方程联立，求出B 点坐标，即可求出AOB 的面积. 【详解】抛物线24y x =的焦点为(1,0)F ,∵3AF =，∴点A 到准线:1l x =-的距离为3， 点A 的横坐标为2，根据对称性不妨设点A 在第一象限， 设1122(2,)(0),(,)A y y B x y >，2x =代入抛物线方程得1y =直线AF 方程为1)y x =-，联立21)4y x y x⎧=-⎪⎨=⎪⎩，消去x 得，240y --=，解得12y y ==∴AOB 的面积为12121122S y OF y =⨯⨯==-⨯⨯.故答案为：2. 【点睛】本题考查抛物线的定义，考查三角形的面积的计算，确定相交点的坐标是解题关键，属于中档题.三、解答题21．（1）2214x y +=；（2）861,540⎛⎫- ⎪⎝⎭．【分析】（1）本小题根据已知条件直接求出2a =，1b =，再求出椭圆方程即可.（2）本小题先设A 、B 两点，再将OA OB ⋅转化为只含m 的表达式，最后根据m 的范围确定OA OB ⋅的范围，即可解题. 【详解】解：（1）∵点2M ⎭在椭圆C ：22221x y a b +=（0a b >>）上，∴222112a b+=，又∵24a =， ∴ 2a =，1b =.∴椭圆C 的方程：2214x y +=；（2）设点A 、B 的坐标为11(,)A x y ，22(,)B x y ，则AB 中点1212,22x x y y ++⎛⎫⎪⎝⎭在线段OM 上，且12OM k =，则12122()x x y y +=+， 又221112x y +=，222212x y +=，两式相减得()()()()1212121202x x x x y y y y -++-+=， 易知120x x -≠，120y y +≠，所以()1212121212y y x xx x y y -+=-=--+，则1AB k =-. 设AB 方程为y x m =-+，代入2214xy +=并整理得2258440x mx m -+-=.由216(5)0m ∆=->解得25m <，又由(12425x x m +=∈，则0m <<. 由韦达定理得1285m x x +=，2124(1)5m x x -⋅=，故OA OB ⋅1212x x y y =+()()1212x x x m x m =+-+-+ ()212122x x m x x m =-++()22281855m m m -=-+285m =-又∵. 04m <<∴OA OB ⋅的取值范围是861,540⎛⎫- ⎪⎝⎭．【点睛】解决直线与椭圆的综合问题时，要注意：(1)注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件；(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题．22．（1）22143x y +=；（2）①1y x =-或1y x =-+，②证明见解析.【分析】（1）依题意得到方程组解得即可；（2）设直线l 的方程为()()10y k x k =-≠，()11,P x y ，()22,Q x y ，设线段PQ 的中点为M ，联立直线与椭圆，消元、列出韦达定理，即可表示出线段PQ 的中点M 的坐标，从而得到线段PQ 的垂直平分线方程，表示出B 点坐标，再根据①、②分别计算可得； 【详解】解：（1）由条件得，22,23,a a c c cb a⎧+=-⎪⎪⎨⎪=⎪⎩又222b a c =-，解得2a =，b =1c =，所以椭圆C 的方程为22143x y +=.（2）因为直线l 过点()1,0F ，且与坐标轴不垂直，所以设直线l 的方程为()()10y k x k =-≠，()11,P x y ，()22,Q x y ， 设线段PQ 的中点为M ，由()221,1,43y k x x y ⎧=-⎪⎨+=⎪⎩得()22223484120k x k x k +-+-=，所以2122834k x x k +=+，212241234k x x k-=+所以线段PQ 的中点22243,3434k k M k k ⎛⎫- ⎪++⎝⎭， 所以线段PQ 的垂直平分线方程为2223143434k k y x k k k ⎛⎫+=-- ⎪++⎝⎭， 令0y =，得2234k x k =+，即22,034k B k ⎛⎫ ⎪+⎝⎭①当67BF =时，则2261347k k -=+， 解得1k =±，所以直线l 的方程为1y x =-或1y x =-+.②因为()212212134k PQ x k+=-==+，22223313434k k BF k k+=-=++， 所以4PQBF =为定值. 【点睛】(1)解答直线与椭圆的题目时，时常把两个曲线的方程联立，消去x (或y )建立一元二次方程，然后借助根与系数的关系，并结合题设条件建立有关参变量的等量关系． (2)涉及到直线方程的设法时，务必考虑全面，不要忽略直线斜率为0或不存在等特殊情形．23．（1）2212x y +=；（2）证明见解析.【分析】（1）利用中垂线的性质可得KN KQ =，从而得到2KM KN QM MN +==>=，利用椭圆的定义进行分析求解即可；（2）根据点P 的位置，确定OPA ∠，OPB ∠都是锐角，然后联立直线与椭圆的方程，得到韦达定理，再将问题转化为求证两个角的正切值相等，代入化简求解，即可证明． 【详解】（1）∵线段NQ 的垂直平分线交MQ 于点K ，∴||||KN KQ =，∴||||||||||2||KM KN KM KQ MQ MN +=+==>= ∴点K 的轨迹是以原点为中心，以,M N 为焦点的椭圆.设椭圆方程为22221(0)x y a b a b+=>>，则a =1c =，1b =，所以曲线E 的方程为2212x y +=（2）由221210x y x my ⎧+=⎪⎨⎪+-=⎩消去x 可得()222210m y my +--=.设()11,A x y ，()22,B x y ，则12222m y y m +=+，12212y y m =-+. 易知PA ，PB 的斜率存在，则()()121212121212122221111PA PB y y y y y y my y k k x x my my my my +++=+=+=-------++，又因为121222222022m my y my y m m ++=-=++ 所以0PA PB k k +=，所以OPA OPB ∠=∠. 【点睛】方法点睛：解答直线与椭圆的位置关系的相关问题，其常规思路是先把直线方程与椭圆方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题．涉及弦中点的问题常常用“点差法”解决，往往会更简单.24．（1）1a b ⎧=⎪⎨=⎪⎩2）直线AD 过定点(1,0)Q ．【分析】（1）由于12,1,P P ⎛⎛- ⎝⎭⎝⎭关于原点对称，从而可得12,PP 和4P 在椭圆上，然后将这些点的坐标代入椭圆方程中可求出,a b 的值；（2）由题意可知直线l 的斜率存在，则设直线l 为2(0)x ty t =+≠，与椭圆方程联立成方程组，消去x ，得()222420t y ty +++=，再由根与系数的关系得12122242,22t y y y y t t +=-=++，而直线AD 方程为()()()122112210y y x x x y x y x y ++--+=，代入化简可得答案【详解】因为121,,1,22P P ⎛⎛⎫-- ⎪ ⎪⎝⎭⎝⎭关于原点对称，由题意得12,PP 和4P 在椭圆上， 将14,P P 的坐标代入22221x ya b +=得：222111211a b b ⎧+=⎪⎪⎨⎪=⎪⎩解得：1a b ⎧=⎪⎨=⎪⎩ （2）显然，l 与x 轴不垂直，设l 的方程为：2(0)x ty t =+≠()22222242012x ty t y ty x y =+⎧⎪⇒+++=⎨+=⎪⎩ 设()()1122,,,A x y B x y ，则()22,D x y - 且12122242,22t y y y y t t +=-=++ 直线AD 方程为()()()122112210y y x x x y x y x y ++--+= 令0y =，得()()122112211212121222242214ty y ty y x y x y ty y tx y y y y y y t++++===+=+=+++-，故直线AD 过定点(1,0)Q ． 【点睛】关键点点睛：此题考查椭圆方程的求法，考查直线与椭圆的位置关系，解题的关键是设出直线l 的方程为：2(0)x ty t =+≠，与椭圆方程联立方程组，消元后利用根与系数的关系可得12122242,22t y y y y t t +=-=++，进而可得AD 方程为()()()122112210y y x x x y x y x y ++--+=化简可得答案，属于中档题25．（1）2214x y +=；（2）30,2⎛⎫± ⎪⎝⎭，310,⎛⎫± ⎪ ⎪⎝⎭. 【分析】（1）用待定系数法求椭圆方程；（2）设出直线l ，表示出M 的坐标，利用154PA PM ⋅=，求出点P 的坐标. 【详解】（1）由题意可得：三角形ABN 为等腰直角三角形，所以2a =4，即a =2. 又由()0,2N -，()2,0B ，:3:2NQ QB =所以64,55Q ⎛⎫⎪⎝⎭， 代入22221x y a b+=得：222264()()551a b +=，解得：b =1.所以椭圆的方程为2214x y +=（2）由（1）可知()2,0A -.设M 点的坐标为()11,x y ， 直线l 的斜率显然存在，设为k ，则直线l 的方程为()2y k x =+于是A ，B 两点的坐标满足方程组()22214y k x x y ⎧=+⎪⎨+=⎪⎩，由方程组消去y 并整理， 得()()222214161640kxk x k +++-=由212164214k x k --=+，得2122814k x k-=+，从而12414k y k =+， 设线段AB 是中点为M ，则M 的坐标为22282,1414k k k k ⎛⎫- ⎪++⎝⎭以下分两种情况：①当0k =时，点M 的坐标为()2,0.线段AM 的垂直平分线为y 轴，于是()02,PA y =-，()02,PM y =-由154PA PM ⋅=得0y = ②当0k ≠时，线段AM 的垂直平分线方程为2222181414k k y x k k k ⎛⎫--=+ ⎪++⎝⎭令0x =，解得02614ky k -=+()02,PA y =--，()110PM x y y =⋅- ()()210102222228646214141414k k k k PA PM x y y y k k k k --⎛⎫⋅=---=++ ⎪++++⎝⎭()()422241615115414k k k +-==+ 整理得12k =±，032y =±综上032y =±或02y =±. 点P 的坐标是30,2⎛⎫± ⎪⎝⎭，0,⎛ ⎝⎭. 【点睛】（1）待定系数法可以求二次曲线的标准方程；（2）"坐标法"是解析几何中常见的基本方法，把题目中的条件用坐标翻译出来，把几何条件转化为代数运算.26．（1）2214x y +=；（2）12S S +是否为定值，为54π．证明过程见解析． 【分析】（1）设(,)D x y ，用,x y 表示出P 点坐标，代入圆的方程即可得；（2）设直线l 方程为y kx t =+，1122(,),(,)M x y N x y ，0t ≠，直线方程代入椭圆方程，应用韦达定理得1212,x x x x +，利用率1k ､k ､2k 成等比数列，得2121212y y k k k x x ==可计算出214k =，然后计算12S S +可得证． 【详解】（1）设(,)D x y ，则有(,2)P x y ，又P 在已知不上，∴2244x y +=，所以曲线E 的方程为2214x y +=；（2）设直线l 方程为y kx t =+，1122(,),(,)M x y N x y ，0t ≠， 由2214y kx t x y =+⎧⎪⎨+=⎪⎩得222(14)8440k x ktx t +++-=，2222644(14)(44)0k t k t ∆=-+->，∴122814kt x x k +=-+，21224414t x x k-=+， 111y k x =，222y k x =，∵1k ､k ､2k 成等比数列，∴2121212y y k k k x x ==， ∴2221212121212()()()kx t kx t k x x kt x x t k x x x x +++++==，212()0kt x x t ++=，又0t ≠，∴12()0k x x t ++=，228014k tt k-+=+，解得12k =±． 1228414kt x x kt k +=-=-+，22122442214t x x t k-==-+， 22222222121212()2162(22)4444x x x x x x k t t t t +=+-=--=-+=，22222222121122()()2244OM ON S S OM ON x y x y ππππ⎛⎫⎛⎫+=⨯+⨯=+=+++ ⎪ ⎪⎝⎭⎝⎭， 222222222211221212124()()4()2()2x y x y kx t kx t k x x kt x x t +++=++++=+++++222244825k k t t =+-+=，。

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(含答案解析)(1)

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(含答案解析)(1)

一、选择题1．已知椭圆22221(0)x y C a b a b+=>>：的左､右焦点分别为1F ，2F ，过2F 直线与椭圆C 交于M ，N 两点，设线段1NF 的中点D ，若10MD NF ⋅=，且12//MF DF ，则椭圆C 的离心率为（ ）A ．13B C ．12D ．22．已知抛物线2:2C y px =的焦点为F ，过抛物线上两点A ，B 分别向抛物线C 的准线作垂线，垂足为M ，N ，且()95OBN OAM ABNM S S S +=梯形△△，当直线AB 经过点F 且点F 到抛物线C 准线的距离为4时，直线l 的斜率为（ ）A ．2±B ．±C ．8±D ．±3．过抛物线22y px =焦点(1,0)F 的直线l 与抛物线交于,A B 两点，且(1)AF mFB m =>，25||4AB =，则m =（ ） A ．2B ．3C ．4D ．54．已知双曲线()222210,0x y a b a b-=>>的一条渐近线与圆()2239x y -+=相交于A 、B 两点，若2AB =，则该双曲线的离心率为（ ）A ．5B ．2C ．3D ．45．在正方体1111ABCD A B C D -中，点P 是侧面11BCC B 内一点，且点P 满足到平面11ABB A 的距离等于到点1C 的距离，则点P 的轨迹是（ ）A ．一条线段B ．圆的一部分C ．椭圆的一部分D ．抛物线的一部分6．若椭圆22221(0)x y a b a b +=>>的离心率为3，则213a b +的最小值为（ ）A B C ．2D7．已知双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为F ，直线:l y kx =与C 交于A ，B 两点，以AB 为直径的圆过点F ，若C 上存在点P 满足4=BP BF ，则C 的离心率为（ ）A B C D8．设F 1，F 2是双曲线C ：22221x y a b-=(a >0，b >0)的左、右焦点，P 是双曲线C 右支上一点，若|PF 1|＋|PF 2|＝4a ，且∠F 1PF 2＝60°，则双曲线C 的渐近线方程是（ ） A ．30x y ±= B ．270x y ±= C ．320x y ±=D ．230x y ±=9．已知圆2221:(3)(7)C x y a a ++=>和222:(3)1C x y -+=，动圆M 与圆1C ，圆2C 均相切，P 是12MC C 的内心，且12123PMC PMC PC C S SS+=，则a 的值为（ ）A ．9B ．11C ．17D ．1910．在平面直角坐标系中，双曲线C 的标准方程为2221(0)4x y t t t-=>+，则双曲线的离心率取得最大值时，双曲线的渐近线方程为（ ）A ．2y x =±B ．3y x =±C ．12y x =±D ．13y x =±11．已知过双曲线()2222:1,0x y C a b a b-=>的左焦点F 作圆222x y a +=的切线FT ，交双曲线右支于点P ，点P 到x 轴的距离恰好为34b ，则双曲线离心率为（ ）A ．273+ B ．273+ C ．53D ．212．斜率为14的直线l 与椭圆C ：()222210x y a b a b+=>>相交于A ，B 两点，且l 过C 的左焦点，线段AB 的中点为()2,1M -，C 的右焦点为F ，则AFB △的周长为（ ） A 487 B 247C ．147D ．147二、填空题13．已知双曲线22:143x y C -=的左､右焦点分别12,F F ，P 为双曲线上异于顶点的点，以1PF ，2PF 为直径的圆与直线l 分别相切于A ，B 两点，则12cos ,AB F F <>=___________.14．设1F ，2F 为双曲线()2222:10,0x yC a b a b-=>>的左､右焦点，过2F 的直线l 交双曲线C 的右支于A ､B 两点，且120AF AF ⋅=，2212AF BF =，则双曲线C 的离心率为___________.15．已知双曲线()2222:10,0x y C a b a b-=>>的左、焦点为1F 、2F ，点P 为双曲线C 的渐近线上一点，120PF PF ⋅=，若直线1PF 与圆222x y a +=相切，则双曲线C 的离心率为___________.16．已知椭圆22:143x y C +=的左､右焦点分别为12F F 、，过2F 且倾斜角为π4的直线l交椭圆C 于A B 、两点，则1F AB 的面积为___________.17．已知椭圆T 的中心在坐标原点，左､右焦点分别为1(,0)F c -，2(,0)F c ，(4,3)M -是椭圆上一点，且1MF ，12F F ，2MF 成等差数列，椭圆T 的标准方程________. 18．如图，一种电影放映灯的反射镜面是旋转椭圆面（椭圆绕其对称轴旋转一周形成的曲面）的一部分，过对称轴的截口BAC 是椭圆的一部分，灯丝位于椭圆的一个焦点1F 上，片门位于另一个焦点2F 上.由椭圆一个焦点1F 发出的光线，经过旋转椭圆面反射后集中到另一个焦点2F .已知12BC F F ⊥，1163F B =，124F F =，则截口BAC 所在椭圆的离心率为______.19．已知抛物线2:4C y x =的焦点为F ，准线为l ，过点F 的直线与抛物线交于两点11(,)P x y ，22(,)Q x y .①抛物线24y x =焦点到准线的距离为2； ②若126x x +=，则8PQ =；③2124y y p =-；④过点P 和抛物线顶点的直线交抛物线的准线为点A ，则直线AQ 平行于 抛物线的对称轴；⑤绕点(2,1)-旋转且与抛物线C 有且仅有一个公共点的直线至多有2条. 以上结论中正确的序号为__________.20．直线AB 过抛物线24y x =的焦点F ，且与抛物线交于A 、B 两点，且线段AB 的中点的横坐标是3，则直线AB 的斜率是_____________.三、解答题21．椭圆2212516x y +=上一点P 到左焦点F 的距离为6，若点M 满足1()2OM OP OF =+（O 为坐标原点），则||OM =________．22．如图，已知椭圆22221(0)x y a b a b+=>>的离心率为12，过椭圆右焦点2F 作两条互相垂直的弦AB 与CD ，当直线AB 的斜率为0时，||||7AB CD +=．（Ⅰ）求椭圆的方程；（Ⅱ）求||||AB CD +的取值范围．23．已知椭圆2222:1(0)x y C a b a b+=>>的两个焦点与短轴的一个端点恰好围成面积为3的等边三角形.（1）求C 的方程；（2）如图，设C 的左，右顶点分别为,A B ，右焦点为F ，P 是C 上异于,A B 的动点，直线AP 与直线x a =交于点D ，当点P 运动时，试判断以BD 为直径的圆与直线PF 的位置关系，并加以证明.24．已知抛物线C ：()220y px p =>过点()2,4T -．（1）求抛物线C 的焦点到准线的距离；（2）已知点()4,0A ，过点()4,0B -的直线l 交抛物线C 于点M 、N ，直线MA ，NA分别交直线4x =-于点P 、Q ．求PBBQ的值．25．（1）已知椭圆2222:1(0)x y E a b a b+=>>的焦距为1F 、2F 为左、右焦点，M 为椭圆E 上一点，且123F MF π∠=，123F MF S =△，求椭圆E 的方程． （2）过点()()00P m m a <<,的直线交椭圆E 于A 、B 两点，交直线4x m=于点M ，设MA AP λ=，MB BP μ=，求λμ+的值．26．在平面直角坐标系xOy 中，设动点P 到定点(1,0)F 的距离与到定直线:1l x =-的距离相等，记P 的轨迹为曲线Γ． （1）求曲线Γ的方程；（2）过点F 的直线交曲线Γ于点A 、B （其中点A 在第一象限），交直线l 于点C ，且点F 是AC 的中点，求线段AB 的长．【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】由10MD NF ⋅=得1MD NF ⊥，结合D 是中点，得等腰三角形，由平行线可得2F 是MN 中点，从而MN x ⊥轴，利用勾股定理可得,a c 的关系得离心率． 【详解】因为10MD NF ⋅=，所以1MD NF ⊥，又D 是1NF 中点，所以1MF MN =， 因为12//MF DF ，所以2F 是MN 中点，则22MF NF =，因此MN x ⊥轴， 设2MF m =，则12MF m =，1232MF MF m a +==，23am =，在12MF F △中，由勾股定理得22242()()(2)33m m c +=，变形可得3c e a ==． 故选：B ． 【点睛】关键点点睛：：本题考查求椭圆的离心率，解题关键是确定,,a b c 的等式．解题方法是由向量的数量积得出垂直后，根据三角形的性质得1MF N 的性质（实质上它是等边三角形），特别是MN x ⊥轴，然后结合椭圆定义利用勾股定理可得．2．B解析：B 【分析】根据题意，求得4p =，可得抛物线的方程，因为()95OBN OAM ABNM S S S +=梯形△△，所以49OMN OAB ABMN S S S +=梯形△△，根据面积公式，结合抛物线定义，即可求得AB ，不妨设AB 的斜率为k ，可得直线AB 的方程，与抛物线联立，根据韦达定理，可求得A B x x +的值，代入弦长公式，即可求得答案. 【详解】因为点F 到抛物线C 准线的距离为4，所以4p =，所以28y x =，设抛物线C 的准线与x 轴交于点H ，因为()95OBN OAM ABNM S S S +=梯形△△，所以()()11422192M N A BOMN OABABMNM N OH y y OF y y S S S AM BN y y ⋅-+⋅-+==+⋅-梯形△△，因为2OH OF ==，M N A B y y y y -=-，AM BN AB +=， 所以449OMN OAB ABMN S S S AB +==梯形△△，则9AB =，显然直线AB 的斜率存在，不妨设为k ，则():2AB y k x =-， 与抛物线联立可得：()22224840k x k x k -++=， 从而284A B x x k+=+， 所以28489A B A kB x x =++=+=，解得k =±. 故选：B【点睛】解题的关键是根据面积的关系，得到49OMN OAB ABMN S S S +=梯形△△，结合图象，可求得9AB =，再利用抛物线的弦长公式求解，考查分析计算，化简求值的能力，属中档题.3．C解析：C 【分析】由焦点得2p =，设直线代入抛物线方程结合韦达定理以及已知条件利用弦长公式求得参数值. 【详解】∵焦点(1,0),2F p ∴=，抛物线方程式为24y x =．设直线l 的方程为1(0)x y λλ=+>，代入抛物线方程，得2440y y λ--=．设()()1122,,,A x y B x y ，由韦达定理得124y y =-． 由AF mFB =，得12y my =-．解得212y y m m ==-212y y m m==121,x m x m ∴==．12125||2,44AB x x p m m m ∴=++=++=∴=． 故选：C ． 【点晴】方法点晴：解直线与圆锥曲线位置问题时，通常使用设而不求思想，结合韦达定理运算求解相关参数.4．C解析：C 【分析】设双曲线的渐近线方程为y kx =，其中bk a=±，利用勾股定理可求得k 的值，即可求得b a ，再由双曲线的离心率公式21bea⎛⎫=+ ⎪⎝⎭即可求得双曲线的离心率.【详解】设双曲线的渐近线方程为y kx=，其中bka=±，圆()2239x y-+=的圆心为()3,0C，半径为3r=，圆心C到直线y kx=的距离为231kdk=+，2AB=，由勾股定理可得2222ABr d⎛⎫=+⎪⎝⎭，即2223191kk⎛⎫+=⎪+⎝⎭，解得22k=±，22ba∴=，因此，该双曲线的离心率为22222213c c a b bea a a a+⎛⎫====+=⎪⎝⎭.故选：C.【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a、c的值，根据离心率的定义求解离心率e的值；（2）齐次式法：由已知条件得出关于a、c的齐次方程，然后转化为关于e的方程求解；（3）特殊值法：通过取特殊位置或特殊值，求得离心率.5．D解析：D【分析】由题意画出图形，可知点P到直线BC的距离与点P到点1C的距离相等，所以点P的轨迹为以1C为焦点，以1BB为准线的抛物线．【详解】如图，点P是侧面11BCC B内的一动点，点P到直线1BB的距离即为点P到面11ABB A的距离，因为点P 到直线BC 的距离与点P 到点1C 的距离相等， 所以点P 的轨迹为以1C 为焦点，以1BB 为准线的抛物线， 故选：D ． 【点睛】方法点睛：求动点的轨迹方法之定义法：将动点轨迹化归为某一基本轨迹（圆，椭圆，双曲线，抛物线等），然后利用基本轨迹的定义，直接写出方程.6．C解析：C 【分析】由椭圆的离心率为3和222a b c =+，求得3a b =，化简2219113333a b b b b b ++==+，结合基本不等式，即可求解. 【详解】由题意，椭圆22221(0)x y a b a b +=>>的离心率为3，即3c a =，即3c =，又由222a b c =+，可得2219b a =，即3a b =所以22191132333a b b b b b ++==+≥=，当且仅当133b b=，即13b =时，“=”成立.故选：C. 【点睛】 关键点睛：1、利用基本不等式求最值时，要注意三点：一是各项为正；二是寻求定值；三是考虑等号成立的条件；2、若多次使用基本不等式时，容易忽视等号的条件的一致性，导致错解；3、巧用“拆”“拼”“凑”：在使用基本不等式时，要特别注意“拆”“拼”“凑”等技巧，使其满足基本不等式中的“正、定、等”的条件.7．B解析：B 【分析】由题意设()00,B x y ，(c,0)F ，(,)P m n ，则()00,A x y --，求出BP ，AF ，BF 的坐标，根据4=BP BF 得到,m n ，由点F 在圆上得到22200=+c x y ，把点P ，B 坐标代入双曲线方程联立，可得答案. 【详解】由题意设()00,B x y ，(c,0)F ，(,)P m n ，则()00,A x y --，()00,=--BP m x n y ，()00,=+AF c x y ，()00,=--BF c x y ． 4=BP BF ，()000044,c x m x y n y ⎧-=-∴⎨-=-⎩，00433m c x n y =-⎧⎨=-⎩． 以AB 为直径的圆过点F ，()()00,,0AF BF c x y c x y ∴⋅=+⋅--=，即22200=+c x y ①，点P ，B 均在双曲线上，2200221x y a b ∴-=②，()()2200224331---=c x y a b ③．②-③整理得()()2000222--=-c x x c y a b ，将22200=-y c x 代入，整理得()22220223-=ca x c，于是()2222220233-=-=b ac y c x c ，最后将20x ，20y 代入双曲线方程，整理得22410c a =，所以e ==． 故选：B. 【点睛】本题考查了直线与双曲线的位置关系、圆的有关性质及与向量的结合，关键点是利用4=BP BF 和AF BF ⋅得到点之间的关系，考查了学生分析问题、解决问题的能力.8．C解析：C 【分析】利用双曲线的定义和已知即可得出|PF 1|，|PF 2|，再利用余弦定理找出a,c 的等量关系,从而可求a,b 的比值，即可得出双曲线C 的渐近线方程． 【详解】解：因为F 1、F 2是双曲线的左、右焦点，点P 在双曲线右支上， 所以由双曲线定义可得|PF 1|－|PF 2|＝2a ， 又知|PF 1|＋|PF 2|＝4a ，所以|PF 1|＝3a ，|PF 2|＝a .在△PF 1F 2中，由余弦定理可得222121212||||||cos60=2||||PF PF F F PF PF +-⋅，即222(3)41=232a a c a a +-⨯⨯，所以3a 2＝10a 2－4c 2，即4c 2＝7a 2，又知b 2＋a 2＝c 2，所以223=4b a ，所以双曲线C 的渐近线方程为y x =20y ±=.故选：C. 【点睛】关键点点睛：利用双曲线的定义和已知即可得出|PF 1|，|PF 2|，再利用余弦定理解三角形是解答本题的关键．9．C解析：C 【分析】先判断出圆1C 与2C 内含，根据条件可得动圆M 与圆1C ，圆2C 均相切，从而得出121216MC MC a C C +=+>=，即动点M 的轨迹是以12,C C 为焦点，长轴为1a +的椭圆，又设12MC C 的内切圆的半径为r ' ，由12123PMC PMC PC C SSS+=，有12121113222MC r MC r C C r ''+⨯=⨯⨯⨯'⨯，从而得出答案. 【详解】由圆2221:(3)(7)C x y a a ++=>和222:(3)1C x y -+=，可得圆1C 的圆心()13,0C -，半径为1r a =，圆2C 的圆心()23,0C ，半径为21r = 由121261C C a r r =<-=-所以圆1C 与2C 内含，由动圆M 与圆1C ，圆2C 均相切. 所以动圆M 与圆1C 内切，与圆2C 外切，设动圆M 的半径为R 则11MC r R a R =-=-，221MC r R R =+=+ 所以121216MC MC a C C +=+>=所以动点M 的轨迹是以12,C C 为焦点，长轴为1a +的椭圆，设其方程为22221(0)x y m n m n+=>> 所以12a m +=，设22c m n =-，则3c = 由P 是12MC C 的内心，设12MC C 的内切圆的半径为r ' 由12123PMC PMC PC C SSS+=，有12121113222MC r MC r C C r ''+⨯=⨯⨯⨯'⨯ 即1212318MC MC C C +==，又由椭圆的定义可得121MC MC a +=+ 所以118a +=，则17a = 故选：C 【点睛】本题考查圆与圆的位置关系，考查根据圆与圆的相切求动圆圆心的轨迹，考查椭圆的定义的应用，解答本题的关键的由条件得出圆1C 与2C 内含，由动圆M 与圆1C ，圆2C 均相切，进一步由条件得出121216MC MC a C C +=+>=，即得出动点M 的轨迹，属于中档题.10．C解析：C 【分析】依题意可得c e a ==t ，从而求出双曲线方程，即可求出渐近线； 【详解】解：因为0t >，依题意可得双曲线2221(0)4x y t t t-=>+的离心率2c e a ====≤=当且仅当4t t=即2t =时，等号成立，此时离心率最大， 故双曲线的标准方程为22182y x -=，所以双曲线的渐近线方程为y x =，即12y x =±故选：C 【点睛】在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误．11．A解析：A 【分析】由P 点到x 轴距离（即纵坐标）求出其横坐标，写出直线FP 的方程，然后由原点到切线的距离等于半径可得,,a b c 的等式，变形后可得离心率． 【详解】如图P 在第一象限，因为点P 到x 轴的距离恰好为34b ，即34P y b =，代入双曲线方程得229116P x a -=，解得54P x a =，所以53,44P a b ⎛⎫ ⎪⎝⎭， (,0)F c -，直线FP 方程为34()54b y xc a c =++，化简得3(54)30bx a c y bc -++=， 又直线FP 与圆222x y a +=相切，a=，345bcaa c=+人，变形为4293440160e e e---=，22(342)(348)0e e e e++--=，因为1e>，所以23420e e++>，所以23480e e--=，23e+=去）．故选：A．【点睛】思路点睛：本题考查求双曲线的离心率，解题关键是找到关于,,a b c的齐次等式，本题中由点P到x轴的距离恰好为34b，得出P点坐标，从而可得直线FP方程，由圆心到切线的距离等于半径可得所要关系式，从而转化为离心率e的方程，解之可得．12．C解析：C【分析】由已知得直线l的方程可得c，设()11,A x y()22,B x y代入椭圆的方程做差可得22ba18=，然后利用222b c a=-可得2a，再利用椭圆定义可得答案.【详解】易得直线l的方程为113(2)1442y x x=++=+，当0y=时，6x=-，所以6c=，设()11,A x y，()22,B x y，则22112222222211x ya bx ya b⎧+=⎪⎪⎨⎪+=⎪⎩，则2222212122x x y ya b--+=，整理得222212121222212121y y y y y yba x x x x x x-+-=-=-⋅-+-2221136448aa--=-⨯==，解得a=，则FAB的周长为4a=.故选：C.【点睛】本题考查了椭圆的定义、直线和椭圆的位置关系，在解答平面解析几何中的某些问题时，如果能适时运用点差法，可以达到“设而不求”的目的，同时，还可以降低解题的运算量，优化解题过程，这类问题通常与直线斜率和弦的中点有关或借助曲线方程中变量的取值范围求出其他变量的范围.二、填空题13．【分析】求得双曲线的设运用双曲线的定义和三角形的中位线定理可得由相切的性质判断四边形为直角梯形过作垂足为运用直角三角形的勾股定理和向量的夹角的定义和直角三角形的余弦函数的定义计算可得所求值【详解】解解析：7【分析】求得双曲线的a ， c ，设1PF m =，2PF n =，运用双曲线的定义和三角形的中位线定理可得MN ，由相切的性质判断四边形ABNM 为直角梯形，过N 作NQ AM ⊥，垂足为Q ，运用直角三角形的勾股定理和向量的夹角的定义和直角三角形的余弦函数的定义，计算可得所求值． 【详解】解：因为双曲线22:143x y C -=，所以2a =，c ==依题意画出如下图形，设1PF ，2PF 的中点分别为M ，N ，过点N 作NQ AM ⊥交AM 于点Q ，连接MN ，所以1212MN F F ==，设1PF m =，2PF n =，则24m n a -==所以11122AM PF m ==，21122BN PF n ==，所以()122MQ AM BN m n =-=-=，在Rt MNQ 中NQ =， 因为//NQ BA ，所以MNQ ∠为12,AB F F 的夹角，所以12cos ,7QN AB F F MN <>===故答案为：7【点睛】本题考查双曲线的定义、方程和性质，以及直线和圆相切的性质，考查直角三角形的勾股定理和锐角三角函数的定义、向量的夹角的概念，考查方程思想和化简运算能力和推理能力．14．【分析】利用双曲线的定义分别表示再利用勾股定义和双曲线的定义建立等量关系求双曲线的离心率【详解】设根据双曲线的定义可知即得得中即得根据双曲线的定义即得所以得故答案为：【点睛】方法点睛：本题考查直线与 解析：173【分析】利用双曲线的定义分别表示1212,,,AF AF BF BF ，再利用勾股定义和双曲线的定义建立等量关系，求双曲线的离心率. 【详解】设2AF x =，22BF x =，1AF y =，根据双曲线的定义可知1212AF AF BF BF -=-， 即12y x BF x -=-，得1BF y x =+，120AF AF ⋅=，12AF AF ∴⊥，()()2223y x y x ∴+=+，得4y x =，12Rt AF F △中，222124AF AF c +=，即22174x c =，得217x =，根据双曲线的定义122AF AF a -=，即32x a =，得23x a =，所以2172173a c =，得173c e a ==. 故答案为：17【点睛】方法点睛：本题考查直线与双曲线的位置关系的综合问题，考查学生的转化和计算能力，属于中档题型，求离心率是圆锥曲线常考题型，涉及的方法包含1.根据,,a b c 直接求，2.根据条件建立关于,a c 的齐次方程求解，3.根据几何关系找到,,a b c 的等量关系求解.15．【分析】作出图形设与圆相切于点分析出可求得的值进而可得出双曲线的离心率为即可得解【详解】如下图所示设与圆相切于点则则则为的中点则为的中点由直角三角形的性质可得因为为的中点则由于双曲线的两渐近线关于轴 解析：2【分析】作出图形，设1PF 与圆222x y a +=相切于点E ，分析出23POF π∠=，可求得ba的值，进而可得出双曲线C 的离心率为21b e a ⎛⎫=+ ⎪⎝⎭，即可得解. 【详解】如下图所示，设1PF 与圆222x y a +=相切于点E ，则OE a =，120PF PF ⋅=，则12PF PF ⊥，1OE PF ⊥，则2//OE PF ， O 为12F F 的中点，则E 为1PF 的中点，222PF OE a ∴==，由直角三角形的性质可得1OF OP =，因为E 为1PF 的中点，则1EOF POE ∠=∠， 由于双曲线的两渐近线关于y 轴对称，可得21POF EOF ∠=∠，所以，12EOF POE POF ∠=∠=∠，则1223EOF POE POF POF π∠+∠+∠=∠=，所以，23POF π∠=，则tan 3b a π==，因此，双曲线C 的离心率为2c e a =====. 故答案为：2. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.16．【分析】先求出直线的方程与椭圆方程联立消去x 求出|y1-y2|利用即可求出的面积【详解】由题意得:直线:设则有:消去x 得:7y2+6y-9=0∴即的面积为【点睛】求椭圆(双曲线)的焦点弦三角形的面积解析：7【分析】先求出直线l 的方程,与椭圆方程联立,消去x ,求出| y 1- y 2|,利用11212|1|||2F AB S F F y y =-△即可求出1F AB 的面积. 【详解】由题意得: 直线l :1y x =-, 设1122(,),(,)A x y B x y ,则有:2213412y x x y =-⎧⎨+=⎩消去x 得:7y 2+6y -9=0, ∴121269,77y y y y +=-=-12211111|||22|222F AB S F F y y -∴=⨯=⨯==△即1F AB 的面积为7【点睛】求椭圆(双曲线)的焦点弦三角形的面积: （1）直接求出弦长|AB |,利用11||2F AB AB d S =△; （2）利用11212|1|||2F AB S F F y y =-△. 17．【分析】根据题意结合椭圆定义可得设代解得代回方程即可【详解】解：因为是椭圆上一点且成等差数列所以所以故椭圆方程可设为代解得所以椭圆方程为故答案为：【点睛】椭圆几何性质的应用技巧：（1）与椭圆的几何性解析：2212015x y +=【分析】根据题意结合椭圆定义可得2a c =，设2222143x y c c+=代(4,M 解得25c =代回方程即可.【详解】解：因为M 是椭圆上一点，且1MF ，12F F ，2MF 成等差数列所以2121224MF a MF F F c ===+，所以2a c =，b =故椭圆方程可设为2222143x y c c +=代(4,M 解得25c =所以椭圆方程为2212015x y +=故答案为：2212015x y +=【点睛】椭圆几何性质的应用技巧：（1）与椭圆的几何性质有关的问题要结合图形进行分析，即使不画出图形，思考时也要联想到图形；（2）椭圆相关量的范围或最值问题常常涉及一些不等式．例如：,,01a x a b y b e -≤≤-≤≤<<，三角形两边之和大于第三边，在求椭圆相关量的范围或最值时，要注意应用这些不等关系.18．【分析】取焦点在轴建立平面直角坐标系由题意及椭圆性质有为椭圆通径得结合及解出代入离心率公式计算即可【详解】解：取焦点在轴建立平面直角坐标系由及椭圆性质可得为椭圆通径所以又解得所以截口所在椭圆的离心率解析：13【分析】取焦点在x 轴建立平面直角坐标系，由题意及椭圆性质有BC 为椭圆通径，得2163b a =，结合24c =及222a b c =+解出,,a b c 代入离心率公式计算即可.【详解】解：取焦点在x 轴建立平面直角坐标系，由12BC F F ⊥及椭圆性质可得，BC 为椭圆通径，所以21163b F B a ==，1224F Fc ==又222a b c =+，解得6,2,a c b ===所以截口BAC 所在椭圆的离心率为13故答案为：13【点睛】求椭圆的离心率或其范围的方法：（1）求,,a b c 的值，由22222221c a b b a a a-==-直接求e ； （2）列出含有,,a b c 的齐次方程(或不等式)，借助于222a b c =+消去b ，然后转化成关于e 的方程(或不等式)求解．19．①②④【分析】焦点到准线的距离为即可判断①；利用焦点弦的弦长公式即可判断②；设出直线方程与抛物线方程联立利用韦达定理可判断③；求出两点坐标计算斜率即可判断④；时与抛物线只有一个交点设过点的直线为与抛解析：①②④ 【分析】焦点到准线的距离为p 即可判断①；利用焦点弦的弦长公式即可判断②；设出直线PQ 方程与抛物线方程联立，利用韦达定理可判断③；求出,A Q 两点坐标，计算AQ 斜率即可判断④；1y =时与抛物线只有一个交点，设过点(2,1)-的直线为2x ky k =--，与抛物线方程联立，利用0∆=求出k 的值，即可得出有一个公共点的直线条数，可判断⑤，进而可得正确答案. 【详解】抛物线2:4C y x =可得2p =，()1,0F对于①：抛物线24y x =焦点为()1,0F ，准线l 为1x =-，所以焦点到准线的距离为2，故①正确；对于②：根据抛物线的对义可得：121286222p px x x P p Q x +++=++=+==， 对于③：设直线PQ 方程为：1x ky =+与2:4C y x =联立可得2440y ky --=，可得124y y =-，因为2p =，所以2124y y p ≠-，故③不正确；对于④：11(,)P x y ，所以OP ：11y y x x =，由111y y x x x ⎧=⎪⎨⎪=-⎩可得11y y x =-，所以111,y A x ⎛⎫--⎪⎝⎭，因为22(,)Q x y ，124y y =- 解得：214y y -=，所以214,Q x y ⎛⎫- ⎪⎝⎭， 因为11(,)P x y 在抛物线2:4C y x =上，所以2114y x =，所以21114x y =，1114y x y -=-所以141,A y ⎛⎫--⎪⎝⎭，因为214,Q x y ⎛⎫- ⎪⎝⎭，所以0AQ k =，所以//AQ x 轴，即直线AQ 平行于抛物线的对称轴，故④正确；对于⑤：1y =时，显然与抛物线只有一个交点，设过点(2,1)-的直线为2x ky k =--，由224x ky k y x=--⎧⎨=⎩可得：24480y ky k -++=，令()2164480k k ∆=-+= 可得2k =或1k =-，故过点(2,1)-且与抛物线C 有且仅有一个公共点的直线有3条.，故⑤不正确， 故答案为：①②④ 【点睛】结论点睛：抛物线焦点弦的几个常用结论设AB 是过抛物线22y px =()0p >的焦点F 的弦，若()11,A x y ，()22,B x y ，则：（1）2124p x x =，212y y p =-；（2）若点A 在第一象限，点B 在第四象限，则1cos p AF α=-，1cos pBF α=+，弦长1222sin pAB x x p α=++=，（α为直线AB 的倾斜角）； （3）112||||FA FB p+=； （4）以AB 为直径的圆与准线相切； （5）以AF 或BF 为直径的圆与y 轴相切.20．1或【分析】根据抛物线方程得到设直线方程为与抛物线方程联立得：再根据线段的中点的横坐标为3求得即可得到直线斜率【详解】因为直线AB 过抛物线的焦点F 且与抛物线交于AB 两点所以斜率不为0设直线AB 方程为解析：1或1- 【分析】根据抛物线方程，得到()1,0F ，设直线方程为1x my =+，与抛物线方程联立得：2440y my --=，再根据线段AB 的中点的横坐标为3，126x x +=，求得m ，即可得到直线斜率. 【详解】因为直线AB 过抛物线24y x =的焦点F (1,0)且与抛物线交于A 、B 两点，所以斜率不为0，设直线AB 方程为1x my =+，与抛物线方程联立得：2440y my --=， 由韦达定理得：12124,4y y m y y +=⋅=-， 所以()21212424223x x m y y m +=++=+=⨯，解得1m =±所以直线的方程为1x y =±+， 所以1AB k =±. 故答案为：1或1-三、解答题21．2 【分析】根据222a c b -=求出左焦点F 的坐标，然后设P 的坐标00(,)P x y ，根据两点间的距离公式求出P 到左焦点的距离以及代入椭圆方程中解得P 的坐标，由1()2OM OP OF =+得到M 为PF 的中点，根据中点坐标公式求出M 的坐标，利用两点间的距离公式求出||OM 即可．【详解】由椭圆2212516x y +=得5a =，4b =， 左焦点(3,0)F -，设00(,)P x y ，则()2200336x y ++=又220012516x y +=解得053x =或0553x =-（舍去）；又P 在椭圆上，则将053x =代入到椭圆方程中求出0y =所以点5(3P ，；由点M 满足1()2OM OP OF =+，则得M 为PF 中点，根据中点坐标公式求得2,3M ⎛- ⎝⎭，所以||(2OM =-=故答案为：2. 【点睛】本题考查椭圆的简单几何性质，会利用两点间的距离公式及中点坐标公式、点到直线的距离公式化简求值，同时也考查学生掌握向量的运用法则及向量模的求法，属于中档题．22．（Ⅰ）22143x y +=；（Ⅱ）48,77⎡⎤⎢⎥⎣⎦；【分析】（Ⅰ）通过当直线AB 的斜率为0时可知||2AB a =，22||b CD a =，结合12c e a ==，计算即得结论；（Ⅱ）分别对两条弦的斜率进行讨论，当两条弦中一条斜率为0时、另一条弦的斜率不存在时易得结论；当两条弦斜率均存在且不为0时，通过设直线AB 、CD 的方程并分别与椭圆方程联立，利用韦达定理及两点间距离公式，可得||||AB CD +的表达式，利用换元法及二次函数的性质计算即得结论． 【详解】解：（Ⅰ）当直线AB 的斜率为0时，直线CD 垂直于x 轴，||2AB a ∴=，22||b CD a =，即22||||27b AB CD a a+=+=， 12c e a ==，且222a b c =+，解得：2,a b ==， 所以椭圆方程为22143x y +=；（Ⅱ）①当两条弦中一条斜率为0时，另一条弦的斜率不存在， 由题意可知，||||7AB CD +=；②当两条弦斜率均存在且不为0时，设1(A x ，1)y ，2(B x ，2)y ， 设直线AB 的方程为(1)y k x =-，则直线CD 的方程为1(1)y x k=--，将直线AB 的方程代入椭圆方程中，并整理得：2222(34)84120k x k x k +-+-=， ∴221212228412,3434k k x x x x k k-+==++，∴212212(1)|||34k AB x x k +=-=+，同理，2222112(1)12(1)||4343k k CD k k++==++， ∴2222222212(1)12(1)84(1)||||3434(34)(34)k k k AB CD k k k k ++++=+=++++，令21t k =+，则1t >，∴2222848484||||1149(41)(31)121()24t t AB CD t t t t t +===-++---+，1t >，∴101t<<，∴211494912()244t <--+，∴241111494912()24t <--+， ∴24884711497()24t <--+，∴48||||77AB CD +<， 综合①②可知，||||AB CD +的取值范围为：48,77⎡⎤⎢⎥⎣⎦． 【点睛】(1)解答直线与椭圆的题目时，时常把两个曲线的方程联立，消去x (或y )建立一元二次方程，然后借助根与系数的关系，并结合题设条件建立有关参变量的等量关系． (2)涉及到直线方程的设法时，务必考虑全面，不要忽略直线斜率为0或不存在等特殊情形．23．（1）22143x y +=；（2）相切，证明见解析.【分析】（1）待定系数法求C 的方程；（2）设出直线AP ，求出D 的坐标，表示出以BD 为直径的圆E 的方程，由“设而不求法”表示出E 到直线PF的距离,判断出圆与直线PF 相切.【详解】解：（1）设椭圆半焦距为c ，依题意有122c ⋅=∴1c =，22a c ==，b =故C 的方程为22143x y +=.（2）以BD 为直径的圆与直线PF 相切， 证明如下：易知()2,0A -，()2,0B ，()1,0F . 由题意可设直线AP 的方程为()()20y k x k =+≠. 则点D 坐标为()2,4k ，BD 中点E 的坐标为()2,2k .由()222143y k x x y ⎧=+⎪⎨+=⎪⎩得()2222341616120k x k x k +++-=.设点P 的坐标为()00,x y ，则2021612234k x k--=+.所以2026834k x k -=+，()00212234k y k x k =+=+. ①当12k =±时，点P 的坐标为31,2⎛⎫± ⎪⎝⎭，点D 的坐标为()2,2±.直线PF x ⊥轴，此时以BD 为直径的圆()()22211x y -+±=与直线PF 相切.②当12k ≠时，则直线PF 的斜率0204114PF y k k x k ==--，所以直线PF 的方程为()24114ky x k =--. 点E 到直线PF 的距离322228142||1414k k k d k k k +-===+-. 又因为||4||2BD k d ==，故以BD 为直径的圆与直线PF 相切. 综上，当点P 运动时，以BD 为直径的圆与直线PF 相切. 【点睛】（1）待定系数法、代入法可以求二次曲线的标准方程；（2）“设而不求”是一种在解析几何中常见的解题方法，可以解决直线与二次曲线相交的问题.24．（1）4p =；（2）1. 【分析】（1）求出p 后可得焦点到准线的距离.（2）设直线l 的方程为4x my =-，()11,M x y ，()22,N x y ，可用,M N 的坐标表示PB BQ ，再联立直线l 的方程和抛物线的方程，利用韦达定理化简PB BQ可得所求的值. 【详解】（1）因为()2,4T -在抛物线上，164p =即4p =，抛物线C 的焦点到准线的距离为4p =.（2）显然直线l 的斜率不为0，故设直线l 的方程为4x my =-，由248x my y x=-⎧⎨=⎩得28320y my -+=， 由()228320m ∆=->得216m >，设()11,M x y ，()22,N x y ，则128y y m +=，1232y y =，所以()12124my y y y =+.又114MA y k x =-，224NA y k x =-， 所以直线MA ：()1144y y x x =--，NA ：()2244yy x x =--， 令4x =-，得1184P y y x -=-，2284Q y y x -=-，所以121212124848P QPB y y x y my BQx y my y y --==⋅=⋅-- ()()121121211221221248844184844y y y my y y y y my y y y y y y y +---====-+--．【点睛】思路点睛：直线与圆锥曲线的位置关系中的定点、定值、最值问题，一般可通过联立方程组并消元得到关于x 或y 的一元二次方程，再把要求解的目标代数式化为关于两个的交点横坐标或纵坐标的关系式，该关系中含有1212,x x x x +或1212,y y y y +，最后利用韦达定理把关系式转化为若干变量的方程（或函数），从而可求定点、定值、最值问题.25．（1）22:142x y E +=；（2）0．【分析】（1）首先根据题意得到c =11MF r =，22MF r =，得到122r r a +=，再根据12F MF S =△和余弦定理即可得到24a =，22b =，从而得到椭圆的标准方程. （2）首先设直线x ky m =+，与椭圆联立得到222(2)240k y kmy m +++-=，从而得到1221224y y km y y m +=--，联立4x m x ky m⎧=⎪⎨⎪=+⎩，得到244m M m km ⎛⎫- ⎪⎝⎭,.再根据MA AP λ=，MB BP μ=，得到2141m kmy λ-=-和2241m kmy μ-=-，计算λμ+即可. 【详解】（1）由已知得2c =，即c =设11MF r =，22MF r =，得到122r r a +=. 在12F MF △中，12121sin 23F MF r r S π==△，解得1283r r =. (22212122cos3r r r r π=+-，化简得：()2121283r r r r =+-，288433a =-⨯，解得24a =.。

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测题(包含答案解析)

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测题(包含答案解析)

一、选择题1．已知椭圆2222:1(0)x y E a b a b+=>>，设直线l 与椭圆相交于A ，B 两点，与x 轴，y 轴分别交于C ，D 两点，记椭圆E 的离心率为e ，直线l 的斜率为k ，若C ，D 恰好是线段AB 的两个三等分点，则（ ） A ．221k e -=B ．221k e +=C ．2211e k-= D ．2211e k+= 2．已知点A 为椭圆()2222:10x y C a b a b+=>>的左顶点，(),0F c 为椭圆的右焦点，B 、E 在椭圆上，四边形OABE 为平行四边形（O 为坐标原点），过直线AE 上一点P 作圆()2224b x c y -+=的切线PQ ，Q 为切点，若PQF △面积的最小值大于28b ，则椭圆C的离心率的取值范围是（ ）A ．102⎛- ⎝⎭B ．102⎫-⎪⎪⎝⎭C ．51⎛- ⎝⎭D ．51⎫-⎪⎪⎝⎭3．已知抛物线2:2C y px =的焦点为F ，过抛物线上两点A ，B 分别向抛物线C 的准线作垂线，垂足为M ，N ，且()95OBN OAM ABNM S S S +=梯形△△，当直线AB 经过点F 且点F 到抛物线C 准线的距离为4时，直线l 的斜率为（ ）A ．2±B ．22±C ．8±D ．23±4．已知椭圆22:13620x y C +=的右焦点是F ，直线()0y kx k =≠与椭圆C 交于A 、B 两点，则222AF BF +的最小值是（ ） A ．36B ．48C ．72D ．965．如图，已知曲线2yx 上有定点A ，其横坐标为()0a a >，AC 垂直于x 轴于点C ，M 是弧OA 上的任意一点（含端点），MD 垂直于x 轴于点D ，ME AC ⊥于点E ，OE与MD 相交于点P ，则点P 的轨迹方程是（ ）A ．()310y x x a a=≤≤ B ．()31022ay x x x a a =+≤≤ C ．()220y x ax x a =-≤≤D ．()2022a ay x x x a =+≤≤ 6．已知椭圆()2222:10x y C a b a b+=>>的左右焦点分别是F 1，F 2，过右焦点F 2且斜率为2的直线与椭圆相交于A ，B 两点，若满足223AF F B =，则椭圆的离心率为（ ）A ．35B ．12C ．22D 37．已知M 是抛物线2:C x y =上一点，记点M 到抛物线C 的准线的距离为1d ，到直线:3490l x y ++=的距离为2d ，则12d d +的最小值为（ ）A ．1B ．2C ．3D ．48．设1F 、2F 分别是椭圆22:1259x yC +=的左、右焦点，O 为坐标原点，点P 在椭圆C上且满足4OP =，则12PF F △的面积为（ ） A ．3B ．33C ．6 D ．99．已知1F 、2F 分别是双曲线()2222:10,0x yC a b a b-=>>的左右焦点，点P 在双曲线右支上且不与顶点重合，过2F 作12F PF ∠的角平分线的垂线，垂足为A ，O 为坐标原点，若3OA b =，则该双曲线的离心率为（ ）A 2B ．233C ．2D 510．设F 为双曲线C ：22221(0,0)x y a b a b-=>>的左焦点，O 为坐标原点，以F 为圆心，FO 为半径的圆与C 交于,A B 两点.若55cos 169OFA ⎡⎤∠∈⎢⎥⎣⎦-,，则C 的离心率取值范围为（ ）A ．4,33⎡⎤⎢⎥⎣⎦B ．(1,23⎤⎦C ．5,43⎡⎤⎢⎥⎣⎦D ．[2,23]11．已知直线:(1)(2)230l a x a y a +++--=经过定点P ，与抛物线24x y =交于,A B 两点，且点P 为弦AB 的中点，则直线l 的方程为（ ） A ．230x y +-= B ．210x y -+= C ．210x y -+=D ．20x y +-=12．P 为椭圆22:11713x y C +=上一动点，1F ，2F 分别为左、右焦点，延长1F P 至点Q ，使得2PQ PF =，则动点Q 的轨迹方程为（ ）A ．()22234x y ++= B ．()22268x y ++= C ．()22234x y -+=D ．()22268x y -+=二、填空题13．方程1169x x y y+=表示的曲线为函数()y f x =的图象.对于函数()y f x =，现有如下结论：①函数()y f x =的值域是R ；②()y f x =在R 上单调递减；③()y f x =的图象不经过第三象限；④直线340x y +=与曲线()y f x =没有交点.其中正确的结论是___________.14．过双曲线22221(0,0)x y a b a b-=>>的右顶点且斜率为3的直线，与双曲线的左右两支分别相交，则此双曲线的离心率的取值范围是___________.(用区间表示) 15．已知椭圆C 的两个焦点分别为1(2,0)F -，2(2,0)F ，离心率为12e =，点P 在椭圆C 上，且1230F PF ∠=，则12F PF △的面积为__________．16．已知双曲线2222:1x y C a b-=(0a >，0b >)的两条渐近线与直线1x =-所围成的三角形的面积为4，则双曲线C 的离心率为________.17．已知抛物线2:4C y x =的焦点为F ，准线为l ，过点F 的直线与抛物线交于两点11(,)P x y ，22(,)Q x y .①抛物线24y x =焦点到准线的距离为2； ②若126x x +=，则8PQ =；③2124y y p =-；④过点P 和抛物线顶点的直线交抛物线的准线为点A ，则直线AQ 平行于 抛物线的对称轴；⑤绕点(2,1)-旋转且与抛物线C 有且仅有一个公共点的直线至多有2条. 以上结论中正确的序号为__________.18．在平面直角坐标系xOy 中，设双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为F ，若双曲线的右支上存在一点P ，使得△OPF 是以P 为直角顶点的等腰直角三角形，则双曲线C 的离心率为__________.19．过抛物线24y x =的焦点F 的直线交抛物线于A ，B 两点，点O 是原点，若||3AF =，则AOB 的面积为_______．20．已知下列几个命题：①ABC 的两个顶点为(4,0)A -，(4,0)B ，周长为18，则C 点轨迹方程为221259x y +=； ②“1x >”是“||0x >”的必要不充分条件；③已知命题:33p ≥，:34q >，则p q ∨为真，p q ∧为假，p ⌝为假；④双曲线221916x y -=-的离心率为54．其中正确的命题的序号为_____．三、解答题21．已知椭圆C ：()222210x y a b a b+=>>的左右焦点分别为1F ，2F ，长轴长为离心率为2． （1）求椭圆C 的方程．（2）若过点1F 的两条弦，弦AB 、弦CD ，互相垂直，求四边形ACBD 的面积的最小值．22．已知抛物线C ：()220y px p =>过点()2,4T -．（1）求抛物线C 的焦点到准线的距离；（2）已知点()4,0A ，过点()4,0B -的直线l 交抛物线C 于点M 、N ，直线MA ，NA分别交直线4x =-于点P 、Q ．求PBBQ的值．23．已知点3(1,)-在椭圆2222:1(0)x y E a b a b +=>>上，E的离心率为32． （1）求E 的方程；（2）设过定点(0,2)A 的直线l 与E 交于不同的两点,B C ，且COB ∠为锐角，求l 的斜率的取值范围．24．已知椭圆()2222:10x y M a b a b +=>>经过如下四个点中的三个，1132P ⎛⎫- ⎪⎝⎭，，()20,1P ，3132P ⎛⎫ ⎪⎝⎭，，()43P ，1.（1）求椭圆M 的方程;（2）设直线l 与椭圆M 交于A ，B 两点，且以线段AB 为直径的圆经过椭圆M 的右顶点C (A ，B 均不与点C 重合)，证明:直线l 过定点.25．如图，已知抛物线2:2(0)M x py p =>的焦点为(0,1)F ，过焦点F 作直线交抛物线于A ，B 两点，在A ，B 两点处的切线相交于N ，再分别过A ，B 两点作准线的垂线，垂足分别为C ，D .（1）求证：点N 在定直线上；（2）是否存在点N ，使得BDN 的面积是ACN △的面积和ABN 的面积的等差中项，若存在，请求出点N 的坐标，若不存在，请说明理由.26．已知椭圆C ：22221x y a b +=(0a b >>)的离心率为32，短轴长为2.（1）求椭圆C 的标准方程；（2）过点(1,0)P 的直线l 与椭圆C 交于A ，B 两点若ABO 的面积为35(O 为坐标原点)，求直线l 的方程.【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】首先利用点,C D分别是线段AB的两个三等分点，则211222x xyy=-⎧⎪⎨=⎪⎩，得1112ykx=⋅，再利用点差法化简得2212214y bx a=，两式化简得到选项.【详解】设()11,A x y，()22,B x y，,C D分别是线段AB的两个三等分点，()1,0C x∴-，10,2yD⎛⎫⎪⎝⎭，则112,2yB x⎛⎫-⎪⎝⎭，得211222x xyy=-⎧⎪⎨=-⎪⎩，1121121131232yy y ykx x x x-===⋅-，利用点差法22112222222211x ya bx ya b⎧+=⎪⎪⎨⎪+=⎪⎩，两式相减得()()()()1212121222x x x x y y y ya b+-+-+=，整理得到2212214y bx a=，即222222244b a ck ka a-=⇒=，即221k e+=故选：B【点睛】关键点点睛：本题的关键利用三等分点得到211222x x y y =-⎧⎪⎨=-⎪⎩，再将斜率和离心率表示成坐标的关系，联立判断选项.2．B解析：B 【分析】结合题意先计算直线AE 的表达式，然后运用点到直线的距离计算圆心F 到直线AE 的距离，求出三角形PQF 的面积表达式，结合题意得到不等式，继而计算出椭圆离心率的取值范围. 【详解】因为四边形OABE 是平行四边形，所以//BE AO ，且BE AO a ==，又因为点B 、E关于y 轴对称，所以0,2a E y ⎛⎫ ⎪⎝⎭，将其代入椭圆方程得2202214y a a b+=，解得0y =±，故,22a E ⎛⎫ ⎪ ⎪⎝⎭，(),0A a -，所以()2:32AE l y x a a =+，即30ay -=，故min PF 即为F 到直线AE 的距离，d=，此时PQ ==故2112228PQFb b SPQ R =⋅=⋅>，化简得2212d b >，故()2222231392b ac b b a +>+，即()()222231239a c a c a +>-+，整理得22222142a ac c a c ++>-，分子分母同除以2a ，得2212142e e e ++>-，即23420e e +->，所以23e -<(舍去)或23e >，在椭圆中a c >，所以1e <，所以e ⎫∈⎪⎪⎝⎭故选：B 【点睛】关键点点睛：本题的关键是求出三角形PQF 的面积表达式，结合题意得到不等式进行求解，有一定的计算量，需要把基础知识掌握牢固.3．B解析：B【分析】根据题意，求得4p =，可得抛物线的方程，因为()95OBN OAM ABNM S S S +=梯形△△，所以49OMN OAB ABMN S S S +=梯形△△，根据面积公式，结合抛物线定义，即可求得AB ，不妨设AB 的斜率为k ，可得直线AB 的方程，与抛物线联立，根据韦达定理，可求得A B x x +的值，代入弦长公式，即可求得答案. 【详解】因为点F 到抛物线C 准线的距离为4，所以4p =，所以28y x =，设抛物线C 的准线与x 轴交于点H ，因为()95OBN OAM ABNM S S S +=梯形△△，所以()()11422192M N A BOMN OABABMNM N OH y y OF y y S S S AM BN y y ⋅-+⋅-+==+⋅-梯形△△，因为2OH OF ==，M N A B y y y y -=-，AM BN AB +=，所以449OMN OAB ABMN S S S AB +==梯形△△，则9AB =，显然直线AB 的斜率存在，不妨设为k ，则():2AB y k x =-， 与抛物线联立可得：()22224840k x k x k -++=， 从而284A B x x k +=+， 所以28489A B A k B x x =++=+=，解得22k =±. 故选：B【点睛】解题的关键是根据面积的关系，得到49OMN OAB ABMN S S S +=梯形△△，结合图象，可求得9AB =，再利用抛物线的弦长公式求解，考查分析计算，化简求值的能力，属中档题.4．D解析：D 【分析】求得2AF BF a +=，结合a c BF a c -<<+，利用二次函数的基本性质可求得222AF BF +的最小值.【详解】设椭圆C 的左焦点为F '，在椭圆C 中，6a =，25b =，则224c a b =-=，由题意可知，点A 、B 关于原点对称，且O 为FF '的中点， 所以，四边形AFBF '为平行四边形，所以，BF AF '=，由椭圆的定义可得212AF BF AF AF a '+=+==，0k ≠，a c BF a c ∴-<<+，即210BF <<，()()2222222122324144349696AF BF BFBF BF BF BF ∴+=-+=-+=-+≥，当且仅当4BF =时，等号成立，因此，222AF BF +的最小值为96. 故选：D. 【点睛】关键点点睛：解决本题的关键在于以下几点：（1）问题中出现了焦点，一般利用相应曲线的定义，本题中利用对称性结合椭圆定义可得出AF BF +；（2）利用椭圆的几何性质得出焦半径的取值范围.5．A解析：A 【分析】设点(),P x y ，求出点M 、E 的坐标，利用O 、P 、E 三点共线可得出//OP OE 可求得点P 的轨迹方程.【详解】设点(),P x y ，其中0x a ≤≤，则点()2,M x x，ME 与直线x a =垂直，则点()2,E a x ，因为O 、P 、E 三点共线，则//OP OE ，可得3ay x =，31y x a∴=， 因此，点P 的轨迹方程是()310y x x a a=≤≤. 故选：A. 【点睛】方法点睛：求动点的轨迹方程有如下几种方法：（1）直译法：直接将条件翻译成等式，整理化简后即得动点的轨迹方程；（2）定义法：如果能确定动点的轨迹满足某种已知曲线的定义，则可利用曲线的定义写出方程；（3）相关点法：用动点Q 的坐标x 、y 表示相关点P 的坐标0x 、0y ，然后代入点P 的坐标()00,x y 所满足的曲线方程，整理化简可得出动点Q 的轨迹方程；（4）参数法：当动点坐标x 、y 之间的直接关系难以找到时，往往先寻找x 、y 与某一参数t 得到方程，即为动点的轨迹方程；（5）交轨法：将两动曲线方程中的参数消去，得到不含参数的方程，即为两动曲线交点的轨迹方程.6．D解析：D 【分析】首先设直线2x y c =+，与椭圆方程联立，得到根与系数的关系，同时由条件可得123y y =-，与根与系数的关系联立消元可得22213242a b c +=，求得椭圆的离心率. 【详解】设直线方程为x y c =+，设()11,A x y ，()22,B x y ，与椭圆方程联立得22224102a b y cy b ⎛⎫++-= ⎪⎝⎭，2122212cy y a b +=-+，4122212b y y a b =-+ ① 223AF F B =，()()1122,3,c x y x c y ∴--=-，得123y y =- ②，由①②联立可得，22213242a bc +=即22222323c a b a c =+=-，得2243c a =， 椭圆的离心率32c e a ==. 故选：D 【点睛】方法点睛：本题考查直线与椭圆的位置关系的综合问题，考查学生的转化和计算能力，属于中档题型，求离心率是圆锥曲线常考题型，涉及的方法包含1.根据,,a b c 直接求，2.根据条件建立关于,a c 的齐次方程求解，3.根据几何关系找到,,a b c 的等量关系求解.7．B解析：B 【分析】作出图形，过点M 分别作抛物线C 的准线l 和直线3490x y ++=的垂线，垂足分别为点B 、A ，由抛物线的定义得出1d MB MF ==，可得出12d d MF MA +=+，利用FM 与直线3490x y ++=垂直时，12d d +取最小值，然后计算出点F 到直线3490x y ++=的距离，即为所求.【详解】 如下图所示：过点M 分别作抛物线C 的准线l 和直线3490x y ++=的垂线，垂足分别为点B 、A ， 由抛物线的定义可得1d MB MF ==，则12d d MF MA +=+， 当且仅当FM 与直线3490x y ++=垂直时，12d d +取最小值，点F 到直线3490x y ++=的距离为2d ==，因此，12d d +的最小值为2. 故答案为：2. 【点睛】关键点点睛：本题求出抛物线上一点到准线和定直线的距离之和最小值问题，解题的关键就是利用F 、A 、M 三点共线取最小值，结合抛物线的定义转化求解.8．D解析：D 【分析】设点()00,P x y ，求出20y 的值，由此可求得12PF F △的面积.【详解】在椭圆22:1259x y C +=中，5a =，3b =，则4c ==，所以，1228F F c ==，设点()00,P x y ，则22001259x y +=，可得220025259x y =-，4OP ===，解得208116y =，094y ∴=，因此，12PF F △的面积为1212011989224PF F S F F y =⋅=⨯⨯=△. 故选：D. 【点睛】方法点睛：本题考查椭圆中焦点三角形面积的计算，常用以下两种方法求解： （1）求出顶点P 的坐标，利用三角形面积公式求解；（2）利用余弦定理和椭圆的定义求得12PF PF ⋅的值，利用三角形面积公式求解.9．B解析：B 【分析】延长2F A 交1PF 于点Q ，可得12QF OA ==，结合双曲线的定义可得,a b 的关系，从而求得离心率． 【详解】延长2F A 交1PF 于点Q ，∵PA 是12F PF ∠的平分线，∴2AQ AF =，2PQ PF =， 又O 是12F F 中点，所以1//QFAO ，且12QF OA ==，又11122QF PF PQ PF PF a =-=-=，∴223a b =，222233()a b c a ==-，∴23c e a ==． 故选：B ．【点睛】关键点点睛：本题考查求双曲线的离心率，解题关键是找到关于,,a b c 的关系，解题方法是延长2F A 交1PF 于点Q ，利用等腰三角形的性质、平行线的性质得出123QF b =，然后由双曲线的定义得出关系式，从而求解．10．A解析：A 【分析】根据题意写出,,''AF AF FF ，根据余弦定理表示出cos ∠OFA ，然后根据55cos 169OFA ⎡⎤∠∈⎢⎥⎣⎦-,列出关于e 的不等式，求解范围.【详解】取右焦点F '，连接AF '，因为点A 为圆和双曲线的交点，所以AF OF c ==，则22,2''=+=+=AF AF a c a FF c ，所以22222222224(2)444cos 244''+-+-+--∠==='AF FF AF c c c a c ac a OFA AF FF c c 221111⎛⎫=--=-- ⎪⎝⎭a a c c e e，又因为55cos 169OFA ⎡⎤∠∈⎢⎥⎣⎦-,，所以251151169-≤--≤e e ，即2249902116160e e e e ⎧--≤⎨--≥⎩，解得433≤≤e . 故选：A.【点睛】双曲线的离心率是双曲线最重要的几何性质，求双曲线的离心率（或离心率的取值范围），常见有两种方法： ①求出a ，c ，代入公式c e a=； ②只需要根据一个条件得到关于a ，b ，c 的齐次式，结合222b c a =-转化为a ，c 的齐次式，然后等式（不等式）两边分别除以a 或2a 转化为关于e 的方程（不等式），解方程（不等式）即可得e （e 的取值范围）．11．B解析：B 【分析】利用点差法求出直线斜率，即可得出直线方程. 【详解】由直线:(1)(2)230l a x a y a +++--=得(2)(23)0a x y x y +-++-=所以20230x y x y +-=⎧⎨+-=⎩ 解得11x y =⎧⎨=⎩ 则()1,1P 设1122(,),(,)A x y B x y ，则21122244x y x y ⎧=⎨=⎩，两式相减得121212()()4()x x x x y y -+=-， 即121212142AB y y x x k x x -+===-， 则直线方程为11(x 1)2y -=-，即210x y -+=. 故选：B. 【点睛】方法点晴：点差法是求解中点弦有关问题的常用方法.12．B解析：B 【分析】由椭圆的122PF PF a +==2PQ PF =，所以112PF PQ FQ a +===Q 的轨迹为以()12,0F -为圆心，径的圆，即可求得动点Q 的轨迹方程. 【详解】由2211713x y +=可得：a =，因为122PF PF a +==2PQ PF =，所以112PF PQ FQ a +===所以动点Q 的轨迹为以()12,0F -为圆心， 故动点Q 的轨迹方程为()22268x y ++=. 故选：B. 【点睛】方法点睛：求轨迹方程的常用方法（1）直接法：如果动点满足的几何条件本身就是一些几何量，如（距离和角）的等量关系，或几何条件简单明了易于表达，只需要把这种关系转化为,x y 的等式，就能得到曲线的轨迹方程；（2）定义法：某动点的轨迹符合某一基本轨迹如直线、圆锥曲线的定义，则可根据定义设方程，求方程系数得到动点的轨迹方程；（3）几何法：若所求轨迹满足某些几何性质，如线段的垂直平分线，角平分线的性质，则可以用几何法，列出几何式，再代入点的坐标即可；（4）相关点法（代入法）：若动点满足的条件不变用等式表示，但动点是随着另一动点（称之为相关点）的运动而运动，且相关点满足的条件是明显的或是可分析的，这时我们可以用动点的坐标表示相关点的坐标，根据相关点坐标所满足的方程，求得动点的轨迹方程；（5）交轨法：在求动点轨迹时，有时会出现求两个动曲线交点的轨迹问题，这类问题常常通过解方程组得出交点（含参数）的坐标，再消去参数参数求出所求轨迹的方程.二、填空题13．①②③④【分析】根据方程分别讨论和四种情况得到不同的解析式画出对应的图象即可得答案【详解】当时方程为表示椭圆在第一象限的部分当时方程为表示双曲线在第四象限的部分当时方程为表示双曲线在第二象限的部分当解析：①②③④ 【分析】根据方程，分别讨论0,0x y ≥≥、0,0x y ><、0,0x y <>和0,0x y <<四种情况，得到不同的解析式，画出对应的图象，即可得答案.【详解】当0,0x y ≥≥时，方程为221169x y +=，表示椭圆在第一象限的部分，当0,0x y ><时，方程为221169x y -=，表示双曲线在第四象限的部分， 当0,0x y <>时，方程为221916y x-=，表示双曲线在第二象限的部分，当0,0x y <<时，方程为221916y x --=，无意义，所以()y f x =图象如下所示：所以函数()y f x =的值域是R ；故①正确；()y f x =在R 上单调递减，故②正确； ()y f x =的图象不经过第三象限，故③正确；直线340x y +=为双曲线的渐近线，所以曲线()y f x =没有交点，故④正确. 故答案为：①②③④ 【点睛】解题的关键是根据题意，分类讨论，得到不同的解析式，再画图求解，考查分类讨论，数形结合的能力，属基础题.14．【分析】根据题意构建渐近线的斜率与3的不等关系再利用求得离心率范围即可【详解】过右焦点与渐近线平行的直线与双曲线有一个交点且一条渐近线的斜率为若斜率为的直线与双曲线的左右两支分别相交则则离心率故答案 解析：)10,+∞【分析】根据题意构建渐近线的斜率与3的不等关系，再利用221b e a=+求得离心率范围即可. 【详解】过右焦点与渐近线平行的直线与双曲线有一个交点，且一条渐近线的斜率为b a， 若斜率为3的直线与双曲线的左右两支分别相交，则3ba>，则离心率c e a ===>.故答案为：)+∞.【点睛】求双曲线离心率常见方法：（1）直接法：由a ，c 直接计算离心率ce a=； （2）构建齐次式：利用已知条件和双曲线的几何关系构建关于a ，b ，c 的方程和不等式，利用222b c a =-和ce a=转化成关于e 的方程和不等式，通过解方程和不等式即求得离心率的值或取值范围.15．【分析】由椭圆定义得由余弦定理得结合可得的值从而得答案【详解】由已知得所以由椭圆定义得由余弦定理得即则的面积为故答案为：【点睛】本题考查了椭圆的简单的性质关键点是利用余弦定理和三角形的面积公式解题考解析：24-【分析】由椭圆定义得128F P PF +=，由余弦定理得22212121212cos 2F P PF F F F PF F P PF +-∠=⨯，结合可得12F P PF ⨯的值，从而得答案. 【详解】 由已知得12,2c e ==，所以4a =， 由椭圆定义得12248F P PF +=⨯=， 由余弦定理得222121212123cos cos3022F P PF F F F PF F P PF +-∠===⨯， 即()2121212216F PPF F P PF P PF +-⨯-=⨯，12F PPF ⨯=， 则12F PF △的面积为12111sin 3024222S F P PF =⨯⨯=⨯=- 故答案为：24-【点睛】本题考查了椭圆的简单的性质，关键点是利用余弦定理和三角形的面积公式解题，考查了学生分析问题、解决问题的能力.16．【分析】求出双曲线的渐近线方程求解时的值然后求解三角形的面积推出离心率即可【详解】双曲线的渐近线方程为将代入中解得故故故双曲线的离心率故答案为：【点睛】方法点睛：求圆锥曲线的离心率常用的方法有：（1【分析】求出双曲线的渐近线方程，求解1x =-时，y 的值，然后求解三角形的面积，推出离心率即可． 【详解】双曲线2222:1(0,0)x y C a b a b -=>>的渐近线方程为b y x a=±，将1x =-代入b y x a =±中，解得by a=±， 故12142ba =，故4b a=，故双曲线C 的离心率c e a ===．【点睛】方法点睛：求圆锥曲线的离心率常用的方法有：（1）公式法（求出,a c 的值再代离心率的公式求解）；（2）方程法（根据已知找到关于离心率的方程再解方程得解）.要根据已知条件灵活选择方法求解.17．①②④【分析】焦点到准线的距离为即可判断①；利用焦点弦的弦长公式即可判断②；设出直线方程与抛物线方程联立利用韦达定理可判断③；求出两点坐标计算斜率即可判断④；时与抛物线只有一个交点设过点的直线为与抛解析：①②④ 【分析】焦点到准线的距离为p 即可判断①；利用焦点弦的弦长公式即可判断②；设出直线PQ 方程与抛物线方程联立，利用韦达定理可判断③；求出,A Q 两点坐标，计算AQ 斜率即可判断④；1y =时与抛物线只有一个交点，设过点(2,1)-的直线为2x ky k =--，与抛物线方程联立，利用0∆=求出k 的值，即可得出有一个公共点的直线条数，可判断⑤，进而可得正确答案. 【详解】抛物线2:4C y x =可得2p =，()1,0F对于①：抛物线24y x =焦点为()1,0F ，准线l 为1x =-，所以焦点到准线的距离为2，故①正确；对于②：根据抛物线的对义可得：121286222p px x x P p Q x +++=++=+==， 对于③：设直线PQ 方程为：1x ky =+与2:4C y x =联立可得2440yky --=，可得124y y =-，因为2p =，所以2124y y p ≠-，故③不正确；对于④：11(,)P x y ，所以OP ：11y y x x = ，由111y y x x x ⎧=⎪⎨⎪=-⎩可得11y y x =-， 所以111,y A x ⎛⎫--⎪⎝⎭，因为22(,)Q x y ，124y y =- 解得：214y y -=，所以214,Q x y ⎛⎫- ⎪⎝⎭， 因为11(,)P x y 在抛物线2:4C y x =上，所以2114y x =，所以21114x y =，1114y x y -=-所以141,A y ⎛⎫--⎪⎝⎭，因为214,Q x y ⎛⎫- ⎪⎝⎭，所以0AQ k =，所以//AQ x 轴，即直线AQ 平行于抛物线的对称轴，故④正确；对于⑤：1y =时，显然与抛物线只有一个交点，设过点(2,1)-的直线为2x ky k =--， 由224x ky k y x=--⎧⎨=⎩可得：24480y ky k -++=，令()2164480k k ∆=-+= 可得2k =或1k =-，故过点(2,1)-且与抛物线C 有且仅有一个公共点的直线有3条.，故⑤不正确， 故答案为：①②④ 【点睛】结论点睛：抛物线焦点弦的几个常用结论设AB 是过抛物线22y px =()0p >的焦点F 的弦，若()11,A x y ，()22,B x y ，则：（1）2124p x x =，212y y p =-；（2）若点A 在第一象限，点B 在第四象限，则1cos p AF α=-，1cos pBF α=+，弦长1222sin pAB x x p α=++=，（α为直线AB 的倾斜角）； （3）112||||FA FB p+=； （4）以AB 为直径的圆与准线相切； （5）以AF 或BF 为直径的圆与y 轴相切.18．(或)【分析】先根据的形状先确定出点坐标然后将点坐标代入双曲线方程根据的齐次式求解出离心率的值【详解】因为是以为直角顶点的等腰直角三角形不妨假设在第一象限所以所以所以所以所以所以所以所以又因为所以故【分析】先根据OPF △的形状先确定出P 点坐标，然后将P 点坐标代入双曲线方程，根据,a c 的齐次式求解出离心率的值. 【详解】因为OPF △是以P 为直角顶点的等腰直角三角形， 不妨假设P 在第一象限，所以122P P F c x y x ===，所以,22c c P ⎛⎫ ⎪⎝⎭， 所以2222144c c a b-=，所以2222224c b c a a b -=，所以()()222222224cca c a a c a --=-，所以4224640c a c a -+=，所以42640e e -+=，所以2632e ±==又因为1e >，所以2e ===，. 【点睛】思路点睛：利用齐次式求解椭圆或双曲线的离心率的一般步骤： （1）根据已知条件，先得到关于,,a b c 的方程；（2）结合222a b c =+或222c a b =+将方程中的b 替换为,a c 的形式；（3）方程的左右两边同除以a 的对应次方，由此得到关于离心率e 的方程，从而求解出离心率e 的值.19．【分析】根据已知条件不妨设在第一象限根据抛物线定义以及方程求出点坐标进而得出直线方程与抛物线方程联立求出点坐标即可求出AOB 的面积【详解】抛物线的焦点为∵∴点A 到准线的距离为3点的横坐标为根据对称性解析：2【分析】根据已知条件不妨设A 在第一象限，根据抛物线定义以及方程，求出A 点坐标，进而得出直线AF 方程，与抛物线方程联立，求出B 点坐标，即可求出AOB 的面积. 【详解】抛物线24y x =的焦点为(1,0)F ,∵3AF =，∴点A 到准线:1l x =-的距离为3， 点A 的横坐标为2，根据对称性不妨设点A 在第一象限， 设1122(2,)(0),(,)A y y B x y >，2x =代入抛物线方程得1y =直线AF 方程为1)y x =-，联立21)4y x y x⎧=-⎪⎨=⎪⎩，消去x 得，240y --=，解得12y y ==∴AOB 的面积为12121122S y OF y =⨯⨯==-⨯⨯.故答案为：2. 【点睛】本题考查抛物线的定义，考查三角形的面积的计算，确定相交点的坐标是解题关键，属于中档题.20．③④【分析】根据椭圆定义可对①进行判断；根据必要不充分条件定义可对②进行判断；根据复合命题的真假可对③进行判断；根据双曲线的离心率公式可对④进行判断【详解】①的两个顶点为周长为18则C 点轨迹方程为当解析：③④ 【分析】根据椭圆定义可对①进行判断；根据必要不充分条件定义可对②进行判断；根据复合命题的真假可对③进行判断；根据双曲线的离心率公式可对④进行判断. 【详解】①ABC 的两个顶点为(4,0)A -，(4,0)B ，周长为18，则C 点轨迹方程为221259x y +=(5)x ≠±，当5x =±时，构不成三角形，错误； ②当0.1x =时，1x <，所以||0x >不一定有1x >，错误；③已知命题:33p ≥是真命题，:34q >是假命题，根据复合命题的真假判断，p q ∨为真，p q ∧为假，p ⌝为假，正确；④双曲线221916x y -=-，2216,9a b ==，所以22225c a b =+=，54c e a ==，正确．其中正确的命题的序号是③④， 故答案为：③④. 【点睛】本题考查了椭圆定义、双曲线离心率、必要不充分条件及复合命题真假的判断，属于基础题.三、解答题21．（1）2212x y +=；（2）169.【分析】（1）利用椭圆的长轴长以及离心率求解,a c ，得到b ，即可得到椭圆方程； （2）①当1l x ⊥，2//l x 时，求解四边形的面积；②当1l ，2l 斜率存在时，设1l ：1x my =-，2l ：11x y m=-，分别联立椭圆方程，利用韦达定理以及弦长公式，转化求解四边形的面积，利用基本不等式求解最小值即可. 【详解】（1）得11a b c ⎧=⎪=⎨⎪=⎩，∴椭圆C 的标准方程为2212x y +=；（2）①当1l x ⊥，2//l x 时，22122222b S a b a=⋅⋅⋅==；②当1l ，2l 斜率存在时，设1l ：1x my =-，2l ：11x y m=-， 联立22112x my x y =-⎧⎪⎨+=⎪⎩得()222210m y my +--=， ∴12222m y y m +=+，12212y y m -=+，∴AB ==)2212m m +=+，同理)22221111122m m CD m m ⎫+⎪+⎝⎭==++， ∴()()()()()()()222222222222281414111162292212212212m m m S AB CD m m m m m m +++=⋅=⋅=≥=++++⎛⎫+++ ⎪⎝⎭．当且仅当22221m m +=+即21m =即1m =±时等号成立， 故四边形ACBD 的面积的最小值169． 【点睛】方法点睛：该题考查的是有关椭圆方程的求法，直线与椭圆的综合题，解题方法如下： （1）根据题中所给的条件，建立等量关系，求得,a b 的值，得到椭圆方程；（2）对直线的斜率存在与否进行讨论，根据题意利用适当的形式写出直线的方程，分别与椭圆方程联立，求得弦长，根据四边形面积公式求得四边形的面积，利用基本不等式求得最值，与特殊情况比较，得到结果. 22．（1）4p =；（2）1. 【分析】（1）求出p 后可得焦点到准线的距离.（2）设直线l 的方程为4x my =-，()11,M x y ，()22,N x y ，可用,M N 的坐标表示PB BQ ，再联立直线l 的方程和抛物线的方程，利用韦达定理化简PBBQ可得所求的值. 【详解】（1）因为()2,4T -在抛物线上，164p =即4p =，抛物线C 的焦点到准线的距离为4p =.（2）显然直线l 的斜率不为0，故设直线l 的方程为4x my =-，由248x my y x=-⎧⎨=⎩得28320y my -+=， 由()228320m ∆=->得216m >，设()11,M x y ，()22,N x y ，则128y y m +=，1232y y =，所以()12124my y y y =+. 又114MA y k x =-，224NA y k x =-， 所以直线MA ：()1144y y x x =--，NA ：()2244yy x x =--， 令4x =-，得1184P y y x -=-，2284Q y y x -=-，所以121212124848P QPB y y x y my BQx y my y y --==⋅=⋅-- ()()121121211221221248844184844y y y my y y y y my y y y y y y y +---====-+--．【点睛】思路点睛：直线与圆锥曲线的位置关系中的定点、定值、最值问题，一般可通过联立方程组并消元得到关于x 或y 的一元二次方程，再把要求解的目标代数式化为关于两个的交点横坐标或纵坐标的关系式，该关系中含有1212,x x x x +或1212,y y y y +，最后利用韦达定理把关系式转化为若干变量的方程（或函数），从而可求定点、定值、最值问题.23．（1）22:14x E y +=；（2）32,,2⎛⎛⎫-⎪⎝⎭⎝⎭. 【分析】（1）由点在椭圆上及椭圆离心率的定义列方程可得21a b c ⎧=⎪=⎨⎪=⎩，即可得解；（2）设直线方程，与椭圆方程联立，结合韦达定理，转化条件为0OCOB ⋅>，运算即可得解. 【详解】 （1）点⎛- ⎝⎭在椭圆22221(0)x y a b ab+=>>上，∴221314a b +=，∴ce a ==由222a b c =+解得21a b c ⎧=⎪=⎨⎪=⎩，∴轨迹22:14x E y +=；（2）依题意可知，直线l 的斜率存在且不为零，∴设:2l y kx =+，1122(,),(,)B x y C x y ，∴22214y kx x y =+⎧⎪⎨+=⎪⎩，化简整理有：()221416120k x kx +++=， ∴()221648(14)0k k ∆=-+>得2k >2k <-， 且1221614kx x k +=-+，1221214x x k ⋅=+， 由COB ∠为锐角， ∴2121212122122()414OC OB x x y y k x x k x x k⋅=+=+++++ 22222121232=+40141414k k k k k-+>+++， ∴222212+12324161640k k k k -++=->，∴22k -<<，∴2k -<<2k <<，∴直线l的斜率的范围是32,,222⎛⎛⎫--⎪⎝⎭⎝⎭. 【点睛】关键点点睛：解决本题的关键是由平面数量积的定义转化COB ∠为锐角为0OC OB ⋅>，结合韦达定理运算即可得解.24．（1）2214x y +=；（2）证明见解析.【分析】（1）先分析椭圆M 经过P 1、P 3、P 2，用待定系数法求标准方程；（2）先用联立方程组，设而不求法把以AB 为直径的圆经过C,找到两个参数的关系，证明直线过定点. 【详解】(1)2214x y +=; 由题意，点112P ⎛⎫ ⎪⎝⎭，与点312P ⎫⎪⎭，关于原点对称， 根据椭圆的对称性且椭圆过其中的三个点可知，点112P ⎛⎫ ⎪⎝⎭，和点312P ⎫⎪⎭，都在椭圆上，又因为点312P ⎫⎪⎭，与点)4P 1不可能同时在椭圆上， 即椭圆过点112P ⎛⎫ ⎪⎝⎭，，312P ⎫⎪⎭，，()20,1P ， 所以(2222121a b⎛⎫ ⎪⎝⎭+=， 且2222011a b+=， 故24a =，21b =，所以，椭圆M 的方程为2214x y +=.(2)直线l 恒过点6,05⎛⎫ ⎪⎝⎭.由题意，可设直线AB 的方程()2x ky m m =+≠，。

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(答案解析)(3)

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(答案解析)(3)

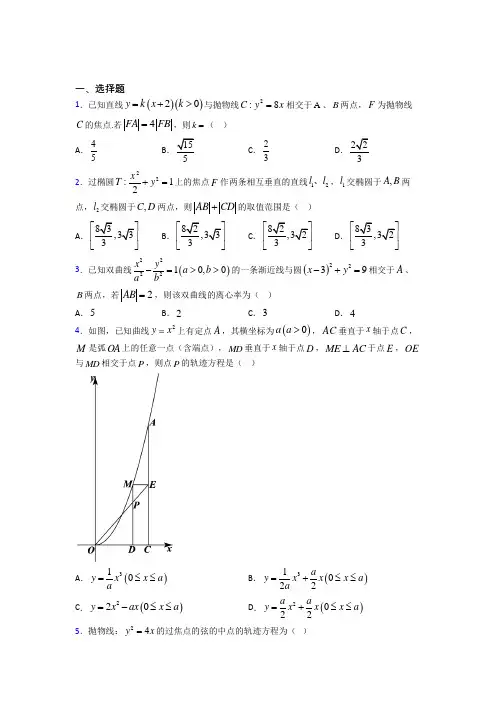
一、选择题1．已知直线()()20y k x k =+>与抛物线2:8C y x =相交于A 、B 两点，F 为抛物线C 的焦点.若4FA FB =，则k =（ ）A ．45B ．15 C ．23D ．222．过椭圆:T 2212x y +=上的焦点F 作两条相互垂直的直线12l l 、，1l 交椭圆于,A B 两点，2l 交椭圆于,C D 两点，则AB CD +的取值范围是（ ）A ．83,333⎡⎤⎢⎥⎣ B ．82,333⎡⎤⎢⎥⎣ C ．82,323⎡⎤⎢⎥⎣ D ．83,323⎡⎤⎢⎥⎣ 3．已知双曲线()222210,0x y a b a b-=>>的一条渐近线与圆()2239x y -+=相交于A 、B 两点，若2AB =，则该双曲线的离心率为（ ）A ．5B ．2C ．3D ．44．如图，已知曲线2yx 上有定点A ，其横坐标为()0a a >，AC 垂直于x 轴于点C ，M 是弧OA 上的任意一点（含端点），MD 垂直于x 轴于点D ，ME AC ⊥于点E ，OE与MD 相交于点P ，则点P 的轨迹方程是（ ）A ．()310y x x a a=≤≤ B ．()31022ay x x x a a =+≤≤ C ．()220y x ax x a =-≤≤D ．()2022a ay x x x a =+≤≤ 5．抛物线：24y x =的过焦点的弦的中点的轨迹方程为（ ）A ．21y x =-B ．212y x =-C ．22(1)y x =-D ．221y x =-6．设抛物线2:4C y x =的焦点为F ，M 为抛物线上异于顶点的一点，且M 在直线1x =-上的射影为N ，若MNF 的垂心在抛物线C 上，则MNF 的面积为（ ） A ．1 B ．2 C ．3 D ．47．已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F ，2F ，()1221,2i i M F M F a i -==，且1M ，2F ，2M 三点共线，点D 在线段21M F 上，且1121F M D M M D ∠=∠1112122M F M F M D +=，则双曲线C 的渐近线方程为（ ）A ．22y x =±B ．2y x =±C ．32y x =±D ．3y x =±8．已知圆2221:(3)(7)C x y a a ++=>和222:(3)1C x y -+=，动圆M 与圆1C ，圆2C 均相切，P 是12MC C 的内心，且12123PMC PMC PC C S SS+=，则a 的值为（ ）A ．9B ．11C ．17D ．199．已知椭圆()222210x y a b a b+=>>上一点A 关于原点的对称点为点B ，F 为其右焦点，若AF BF ⊥，设ABF α∠=，且,124ππα⎛⎫∈ ⎪⎝⎭，则该椭圆的离心率e 的取值范围是（ ）A ．12,23⎛⎫ ⎪⎝⎭B ．26,⎛⎫ ⎪ ⎪⎝⎭C ．222,⎛⎫⎪ ⎪⎝⎭D ．32,3⎛⎫⎪ ⎪⎝⎭10．已知过双曲线()2222:1,0x y C a b a b-=>的左焦点F 作圆222x y a +=的切线FT ，交双曲线右支于点P ，点P 到x 轴的距离恰好为34b ，则双曲线离心率为（ ）A 227+ B 27+C ．53D ．211．已知抛物线2:4C y x =，过点()1,0A -作C 的两条切线，切点分别为B 、D ，则过点A 、B 、D 的圆截y 轴所得弦长为（ ）A ．B ．C ．D ．12．已知抛物线24x y =的焦点为F ，准线为l ，M 是x 轴正半轴上的一点，线段FM 交抛物线于点A ，过A 作l 的垂线，垂足为B .若BF BM ⊥，则FM =（ ） A ．52B ．3C ．72D ．4二、填空题13．已知双曲线()22210y x a a -=>的离心率2e =12,F F 分别是它的下焦点和上焦点，若Р为该双曲线上支上的一个动点，则1PF 与P 到一条渐近线的距离之和的最小值为_________．14．直线l 与抛物线24y x =交于A 、B 两点，O 为坐标原点，直线OA 、OB 的斜率之积为1-，以线段AB 为半径的圆与直线l 交于P 、Q 两点，()6,0M ，则22MP MQ +的最小值为______．15．已知点()1,2A 在抛物线()2:20C y px p =>上，过点()2,2B -的直线交抛物线C 于P ，Q 两点，若直线AP ，AQ 的斜率分别为1k ，2k ，则12k k ⨯等于___________.16．设P 是抛物线28y x =上的一个动点，若点B 为()3,2，则PB PF +的最小值为________________．17．已知圆22:68210C x y x y ++++=，点A 是圆C 上任一点，抛物线28y x =的准线为l ，设抛物线上任意一点Р到直线l 的距离为m ，则m PA +的最小值为_______ 18．如图，一种电影放映灯的反射镜面是旋转椭圆面（椭圆绕其对称轴旋转一周形成的曲面）的一部分，过对称轴的截口BAC 是椭圆的一部分，灯丝位于椭圆的一个焦点1F 上，片门位于另一个焦点2F 上.由椭圆一个焦点1F 发出的光线，经过旋转椭圆面反射后集中到另一个焦点2F .已知12BC F F ⊥，1163F B =，124F F =，则截口BAC 所在椭圆的离心率为______.19．已知双曲线2222:1(0,0)x y E a b a b-=>>，点F 为E 的左焦点，点P 为E 上位于第一象限内的点，P 关于原点的对称点为Q ，且满足||3||PF FQ =，若||OP b =，则E 的离心率为_________.20．对抛物线C ：24x y =，有下列命题：①设直线l ：1y kx =+，则直线l 被抛物线C 所截得的最短弦长为4；②已知直线l ：1y kx =+交抛物线C 于A 、B 两点，则以AB 为直径的圆一定与抛物线的准线相切；③过点()()2,P t t R ∈与抛物线有且只有一个交点的直线有1条或3条；④若抛物线C 的焦点为F ，抛物线上一点()2,1Q 和抛物线内一点()()2,1R m m >，过点Q 作抛物线的切线1l ，直线2l 过点Q 且与1l 垂直，则2l 平分RQF ∠；其中你认为是正确命题的所有命题的序号是______.三、解答题21．椭圆2222:1(0)x y E a b a b +=>>的左焦点为1F ，右焦点为2F ，离心率22e =，过1F 的直线交椭圆于A ，B 两点，且2ABF 的周长为2． （1）求椭圆E 的方程；（2）若直线AB 3，求2ABF 的面积． 22．已知抛物线28y x =的焦点为F ，且A 是抛物线上一点. （1）若4AF =求点A 的坐标；（2）直线l ：y x m =+与抛物线交于两个不同的点P ，Q ，若OP OQ ⊥，求实数m 的值.23．已知椭圆2222:1(0)x y C a b a b +=>>3(2,1),,A P Q --在椭圆C 上，且,P Q 异于点A ．（1）求椭圆C 的方程；（2）若||||,||||OP OQ AP AQ ==，求直线PQ 的方程．24．设抛物线()2:20C y px p =>，恒过定点(),0M m 的直线()0x ky m m =+>与抛物线交于A ，B ，且A 、B 到x 轴距离之积为2m . （1）求抛物线方程； （2）若23AOB π∠=，求实数m 的取值范围. 25．如图，已知抛物线24y x =的焦点为F ，过F 作斜率为(0)k k >的直线交抛物线于()11,A x y 、()22,B x y 两点，且10y >，弦AB 中垂线交x 轴于点T ，过A 作斜率为k -的直线交抛物线于另一点C ．（1）若14y =，求点B 的坐标；（2）记ABT 、ABC 的面积分别为1S 、2S ，若214S S =，求点A 的坐标． 26．已知抛物线C ：22y px =（0p >）的焦点为F ，过点F 的直线l 与抛物线C 交于A ，B 两点，当l x ⊥轴时，4AB =， （1）求p 的值：（2）若2AF BF =，求直线l 的方程.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】 设10m k=>，设点()11,A x y 、()22,B x y ，则直线AB 的方程可表示为2x my =-，将直线AB 的方程与抛物线C 的方程联立，列出韦达定理，由4FA FB =可得出124y y =，代入韦达定理求出正数m 的值，即可求得k 的值.【详解】设10m k=>，设点()11,A x y 、()22,B x y ，则直线AB 的方程可表示为2x my =-，联立228x my y x=-⎧⎨=⎩，整理得28160y my -+=，264640m ∆=->，0m >，解得1m .由韦达定理可得128y y m +=，1216y y =，由4FA FB =得()12242x x +=+，即124my my =，124y y ∴=，12258y y y m ∴+==，可得285m y =，则22122844165m y y y ⎛⎫==⨯= ⎪⎝⎭， 0m >，解得54m =，因此，145k m ==. 故选：A. 【点睛】方法点睛：利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下： （1）设直线方程，设交点坐标为()11,x y 、()22,x y ；（2）联立直线与圆锥曲线的方程，得到关于x （或y ）的一元二次方程，必要时计算∆； （3）列出韦达定理；（4）将所求问题或题中的关系转化为12x x +、12x x 的形式； （5）代入韦达定理求解.2．C解析：C 【分析】当直线12l l 、有一条斜率不存在时，可直接求得32AB CD +=12l l 、的斜率都存在且不为0时，不妨设直线1l 的斜率为k ，则直线2l 的斜率为1k-，则可得直线1l 的方程，与椭圆联立，根据韦达定理及弦长公式，可求得AB 的表达式，同理可求得CD 的表达式，令21k t +=，则可得2112t tAB CD +=+-，令2112y t t =+-，根据二次函数的性质，结合t 的范围，即可求得AB CD +的范围，综合即可得答案. 【详解】当直线12l l 、有一条斜率不存在时，不妨设直线1l 斜率不存在，则直线2l 斜率为0，此时AB =，22b CD a ===所以AB CD +=当直线12l l 、的斜率都存在且不为0时，不妨设直线1l 的斜率为k ，则直线2l 的斜率为1k-， 不妨设直线12l l 、都过椭圆的右焦点(1,0)F ， 所以直线1:(1)l y k x =-，直线21:(1)l y x k=--， 联立1l 与椭圆T 22(1)12y k x x y =-⎧⎪⎨+=⎪⎩，可得2222)202142(-=+-+x k x k k ， 22222(4)4(12)(22)880k k k k ∆=--+-=+>，22121222422,1212k k x x x x k k-+=⋅=++，所以12AB x =-=22)12k k +==+，同理22221))2112k k CD k k ⎛⎫+- ⎪+⎝⎭==+⎛⎫+- ⎪⎝⎭，所以2222))122k k B k C k A D +++=+++， 令21k t +=，因为0k ≠，所以1t >，所以22222))122211(21)(1)k k AB t D k k t t t C +++=+=++--++=+=22211212t t t t =+-+-，令2211119224y t t t ⎛⎫=+-=--+ ⎪⎝⎭， 因为1t >，所以1(0,1)t∈，所以92,4y ⎛⎤∈ ⎥⎦⎝，所以141,92y ⎡⎫∈⎪⎢⎭⎣，所以1AB CD y +=∈⎢⎣， 综上AB CD +的取值范围是3⎡⎢⎣. 故选：C 【点睛】解题的关键是设出直线的方程，结合韦达定理及弦长公式，求得AB CD +的表达式，再根据二次函数性质求解，易错点为需求直线12l l 、中有一个不存在时，AB CD +的值，考查计算求值的能力，属中档题.3．C解析：C 【分析】设双曲线的渐近线方程为y kx =，其中bk a=±，利用勾股定理可求得k 的值，即可求得b a，再由双曲线的离心率公式e =即可求得双曲线的离心率. 【详解】设双曲线的渐近线方程为y kx =，其中bk a=±， 圆()2239x y -+=的圆心为()3,0C ，半径为3r =，圆心C 到直线y kx =的距离为d =，2AB =，由勾股定理可得2222AB r d ⎛⎫=+ ⎪⎝⎭，即2219+=，解得k =±ba∴=，因此，该双曲线的离心率为3c e a =====. 故选：C. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.4．A解析：A 【分析】设点(),P x y ，求出点M 、E 的坐标，利用O 、P 、E 三点共线可得出//OP OE 可求得点P 的轨迹方程. 【详解】设点(),P x y ，其中0x a ≤≤，则点()2,M x x，ME 与直线x a =垂直，则点()2,E a x ，因为O 、P 、E 三点共线，则//OP OE ，可得3ay x =，31y x a∴=， 因此，点P 的轨迹方程是()310y x x a a=≤≤. 故选：A. 【点睛】方法点睛：求动点的轨迹方程有如下几种方法：（1）直译法：直接将条件翻译成等式，整理化简后即得动点的轨迹方程；（2）定义法：如果能确定动点的轨迹满足某种已知曲线的定义，则可利用曲线的定义写出方程；（3）相关点法：用动点Q 的坐标x 、y 表示相关点P 的坐标0x 、0y ，然后代入点P 的坐标()00,x y 所满足的曲线方程，整理化简可得出动点Q 的轨迹方程；（4）参数法：当动点坐标x 、y 之间的直接关系难以找到时，往往先寻找x 、y 与某一参数t 得到方程，即为动点的轨迹方程；（5）交轨法：将两动曲线方程中的参数消去，得到不含参数的方程，即为两动曲线交点的轨迹方程.5．C解析：C 【分析】设出过焦点的直线方程，与抛物线方程联立求出两根之和，可得中点的坐标，消去参数可得中点的轨迹方程． 【详解】由抛物线的方程可得焦点(1,0)F ，可得过焦点的直线的斜率不为0， 设直线方程为：1x my =+，设直线与抛物线的交点1(A x ，1)y ，2(B x ，2)y ，设AB 的中点(,)P x y ， 联立直线与抛物线的方程可得：2440y my --=，124y y m +=，21212()242x x m y y m +=++=+，所以可得2212x m y m⎧=+⎨=⎩，消去m 可得P 的轨迹方程：222y x =-，故选：C ． 【点睛】方法点睛：求轨迹方程的常见方法有：1、定义法；2、待定系数法；3、直接求轨迹法；4、反求法；5、参数方程法等等.6．B解析：B 【分析】设点200,4y M y ⎛⎫⎪⎝⎭，则点()01,N y -，求出MNF 的垂心H 的坐标，再由MH FN ⊥可求得0y 的值，进而可求得MNF 的面积. 【详解】设点200,4y M y ⎛⎫⎪⎝⎭，则点()01,N y -，设点M 在第一象限， 抛物线C 的焦点为()1,0F ，设MNF 的垂心为H ， 由于FHMN ⊥，则点H 的横坐标为1，可得点()1,2H ，MH FN ⊥，则0HM FN ⋅=，2001,24y HM y ⎛⎫=-- ⎪⎝⎭，()02,FN y =-， ()()22200000012122220422y y HM FN y y y y ⎛⎫⋅=--+-=-+=-= ⎪⎝⎭，解得02y =，所以，点M 的坐标为()1,2，所以，2MN =，12222MNF S =⨯⨯=△. 故选：B. 【点睛】关键点点睛：解决本题的关键在于利用已知条件求出点M 的坐标，本题特殊的地方在于MN y ⊥轴，可得出垂心与焦点的连线垂直于x 轴，再结合垂心在抛物线求出垂心的坐标.7．B解析：B 【分析】先取11M F 的中点E ，由题意分析12M F DE 为菱形，得到()()222442c a a =-，从而求出渐近线方程. 【详解】由()1221,2i i M F M F a i -==知：M 1、M 2在双曲线上. 取11M F 的中点E ，连接DE ，2DF ，由111211111222,22,M F M F M D M F M D M F +=∴=-， 即112122,M F F D F D E M =∴=,可知四边形12M F DE 为平行四边形； 又1M D 为112F M F 的角平分线，故四边形12M F DE 为菱形，1212M E F M F D DE ===又21//DE M M 故D 为线段21M F 的中点； 因为211//DF M F ，故2F 为线段12M M 的中点， 故1222M F F M =； 所以21112M F M F =由双曲线的定义：11122M F M F a -=，所以21114,2M F a M F a == 而12M M x ⊥轴，故222121112F F M F M F =-， 故()()222442c a a =-，故3==ce a， 故双曲线C 的渐近线方程为2y x = 故选B ． 【点睛】求双曲线的渐近线的方法:（1）直接令标准方程22221x y a b-=中的1变成0,得到22220x y a b -=,利用平方差公式得到渐近线方程: bxy a=±； （2）根据题意，找到找到a 、b 、c 的关系，消去c ，从而求出渐近线方程.8．C解析：C 【分析】先判断出圆1C 与2C 内含，根据条件可得动圆M 与圆1C ，圆2C 均相切，从而得出121216MC MC a C C +=+>=，即动点M 的轨迹是以12,C C 为焦点，长轴为1a +的椭圆，又设12MC C 的内切圆的半径为r ' ，由12123PMC PMC PC C SSS+=，有12121113222MC r MC r C C r ''+⨯=⨯⨯⨯'⨯，从而得出答案. 【详解】由圆2221:(3)(7)C x y a a ++=>和222:(3)1C x y -+=，可得圆1C 的圆心()13,0C -，半径为1r a =，圆2C 的圆心()23,0C ，半径为21r = 由121261C C a r r =<-=-所以圆1C 与2C 内含，由动圆M 与圆1C ，圆2C 均相切. 所以动圆M 与圆1C 内切，与圆2C 外切，设动圆M 的半径为R 则11MC r R a R =-=-，221MC r R R =+=+ 所以121216MC MC a C C +=+>=所以动点M 的轨迹是以12,C C 为焦点，长轴为1a +的椭圆，设其方程为22221(0)x y m n m n+=>> 所以12a m +=，设22c m n =-，则3c = 由P 是12MC C 的内心，设12MC C 的内切圆的半径为r ' 由12123PMC PMC PC C SSS+=，有12121113222MC r MC r C C r ''+⨯=⨯⨯⨯'⨯ 即1212318MC MC C C +==，又由椭圆的定义可得121MC MC a +=+ 所以118a +=，则17a = 故选：C 【点睛】本题考查圆与圆的位置关系，考查根据圆与圆的相切求动圆圆心的轨迹，考查椭圆的定义的应用，解答本题的关键的由条件得出圆1C 与2C 内含，由动圆M 与圆1C ，圆2C 均相切，进一步由条件得出121216MC MC a C C +=+>=，即得出动点M 的轨迹，属于中档题.9．B解析：B 【分析】由题意设椭圆的左焦点为N ，连接AN ，BN ，因为AF ⊥BF ，所以四边形AFBN 为长方形，再根据椭圆的定义化简得22cos 2sin a c c ＝＋αα，得到离心率关于α的函数表达式，再利用辅助角公式和三角函数的单调性求得离心率的范围. 【详解】由题意椭圆22221x y a b+=()00a b >>，上一点A 关于原点的对称点为点B ，F 为其右焦点，设左焦点为N ，连接AN ，BN ，因为AF ⊥BF ，所以四边形AFBN 为长方形．根据椭圆的定义：2AF AN a +=，由题∠ABF ＝α，则∠ANF ＝α， 所以22cos 2sin a c c αα+＝， 利用2112sin cos 24c e a πααα===+⎛⎫+ ⎪⎝⎭， ∵,124ππα⎛⎫∈ ⎪⎝⎭，∴342πππα<+<，2162324πα<<⎛⎫+ ⎪⎝⎭，即椭圆离心率e 的取值范围是2623⎛⎫⎪ ⎪⎝⎭，故选B . 【点睛】本题主要考查了椭圆的离心率的取值范围问题，其中解答中合理利用椭圆的定义和题设条件，得到22cos 2sin a c c ＝＋αα,再利用三角函数的性质求解是解答的关键，着重考查了推理与运算能力，属于中档试题.10．A解析：A【分析】由P 点到x 轴距离（即纵坐标）求出其横坐标，写出直线FP 的方程，然后由原点到切线的距离等于半径可得,,a b c 的等式，变形后可得离心率． 【详解】如图P 在第一象限，因为点P 到x 轴的距离恰好为34b ，即34P y b =，代入双曲线方程得229116P x a -=，解得54P x a =，所以53,44P a b ⎛⎫ ⎪⎝⎭， (,0)F c -，直线FP 方程为34()54by x c a c =++，化简得3(54)30bx a c y bc -++=，又直线FP 与圆222x y a +=相切，a =，345bc a a c=+人，变形为4293440160e e e ---=，22(342)(348)0e e e e ++--=，因为1e >，所以23420e e ++>，所以23480e e --=，e =（23-去）． 故选：A ． 【点睛】思路点睛：本题考查求双曲线的离心率，解题关键是找到关于,,a b c 的齐次等式，本题中由点P 到x 轴的距离恰好为34b ，得出P 点坐标，从而可得直线FP 方程，由圆心到切线的距离等于半径可得所要关系式，从而转化为离心率e 的方程，解之可得．11．A解析：A 【分析】设出直线方程，与抛物线方程联立，由判别式为零解出B 、D 两点的坐标，进而得出过点A 、B 、D 的圆的方程，求出弦长即可． 【详解】设过点()1,0A -的直线方程为1x my =-， 联立214x my y x=-⎧⎨=⎩，可得2440y my -+=，由216160m ∆=-=，解得1m =± 即2440y y ±+=，2y =±，不妨设()()1,2,1,2B D -，则BD 的中垂线方程为0y =，即圆心在x 轴上又()1,0A -，且点()1,0到点A 、B 、D 的距离都相等，则圆心坐标为()1,0，半径为2圆的方程为()2214x y -+=，令0x =，解得3y =±即圆被y 轴所截得的弦长为23 故选：A 【点睛】关键点点睛：本题考查直线与抛物线的位置关系，考查圆的方程以及直线与圆的位置关系，解决本题的关键点是根据直线与抛物线相切，求出切点的坐标，进而得出圆的方程，求出弦长，考查学生逻辑思维能力和计算能力，属于中档题．12．B解析：B 【分析】先利用方程得求得焦点坐标和准线方程，设点(,0)M m ，()00,A x y ，再利用点()00,A x y 在抛物线与直线上列方程，解出0,x m ，最后利用距离公式计算FM 即可. 【详解】如图所示，抛物线24x y =中，()0,1F ，:1l y =-，依题意设(,0)M m ，()00,A x y ，00x >，则2004x y =，故200,4x A x ⎛⎫⎪⎝⎭，()0,1B x -，因为BF BM ⊥，即BF BM ⊥，而()()00,2,,1BF x BM m x =-=-， 所以()0020BF BM x m x ⋅=-+=，直线:11x y FM m +=，A 在直线上，故200:14x x FM m +=，即02044x m x =-，代入上式即得000024420x x x x ⎛⎫-+= ⎪⎝-⎭，化简整理得4200280x x +-=，即()()2200240x x -+=， 故202x =，而00x >，故02x =422242m ==-(22,0)M ，所以FM =()()22220013-+-=.故选：B. 【点睛】本题解题关键在于利用点()00,A x y 既在抛物线上，又在直线上，构建关系式，求解出点M 即突破难点. 二、填空题13．【分析】根据离心率先求出双曲线的方程得出渐近线方程根据双曲线的定义可得：所以设点到一条渐进线的距离为则从而得出答案【详解】双曲线的离心率所以解得所以双曲线由的双曲线的渐进线方程为由为该双曲线上支上的 解析：5【分析】根据离心率先求出双曲线的方程，得出渐近线方程，根据双曲线的定义可得：1224PF PF a -==，所以124PF PF =+，设点Р到一条渐进线的距离为d ，则124PF d PF d +=++，从而得出答案.【详解】双曲线()22210y x a a -=>的离心率e =所以221514e a =+=，解得2a =，所以((120,,F F 双曲线2214y x -=，由2204y x -=，的双曲线的渐进线方程为2y x =±由Р为该双曲线上支上的一个动点，根据双曲线的定义可得：1224PF PF a -== 所以124PF PF =+，设点Р到渐进线2y x =的距离为d则124PF d PF d +=++，过2F 作渐进线2y x =的垂线，垂足为M ,如图.所以21F M ==所以122445PF d PF d F M +=++≥+=同理1PF 与P 到渐近线2y x =-的距离之和的最小值为5 故答案为：5【点睛】关键点睛：本题考查利用双曲线的定义解决距离之和的最值问题，解答本题的关键是根据双曲线的定义可得：1224PF PF a -==，所以124PFPF =+，设点Р到渐进线2y x =的距离为d ，则124PF d PF d +=++，过2F 作渐进线2y x =的垂线，属于中档题.14．【分析】设直线与抛物线联立方程得韦达定理与代入直线与抛物线表示出与然后根据利用数量积代入求解出从而表示出圆心的坐标根据平行四边形的四边平方和等于对角线平方和代入列式利用二次函数的性质求解最小值【详解 解析：10【分析】设直线AB ，与抛物线联立方程，得韦达定理12y y +与12y y ⋅，代入直线与抛物线表示出12x x +与12x x ⋅，然后根据OA OB ⊥，利用数量积代入求解出4t =，从而表示出圆心的坐标，根据平行四边形的四边平方和等于对角线平方和，代入列式，利用二次函数的性质求解最小值. 【详解】设直线AB 的方程为x my t =+，()11,A x y ，()22,B x y ，由24y x x my t⎧=⎨=+⎩得2440y my t --=，所以()()()22444160m t t m ∆=--=+>， 得124y y m +=，124y y t ，所以()21212242x x m y y t m t +=++=+，222121216y y x x t ⋅==，因为直线OA 、OB 的斜率之积为1-，所以OA OB ⊥，即0OA OB ⋅=，所以2121240x x y y t t +=-=，所以4t =，所以直线AB 的方程为4x my =+，21248x x m +=+，从而圆心为()224,2O m m +'，由平行四边形的四边平方和等于对角线平方和（用向量法易证），得()(222222244MP MQMO PQ MO ''+=+=+()()2222422144148161816202m m m m m ⎛⎫⎡⎤=-++=-++=-+ ⎪⎢⎥⎣⎦⎝⎭， 所以222218102MP MQ m ⎛⎫+=-+ ⎪⎝⎭，所以当2m =±时，22MP MQ +的最小值为10． 故答案为：10 【点睛】解决直线与抛物线的综合问题时，要注意：（1）注意观察应用题设中的每一个条件，明确确定直线、抛物线的条件；（2）强化有关直线与抛物线联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、向量的数量积、三角形的面积等问题．15．【分析】由题意将的坐标代入抛物线的方程可得的值进而求出抛物线的方程设出直线的方程并与抛物线方程联立求出两根之和及两根之积求出直线的斜率之积化简可得定值【详解】由题意将的坐标代入抛物线的方程可得解得所 解析：4-【分析】由题意将()1,2A 的坐标代入抛物线的方程可得p 的值，进而求出抛物线的方程，设出直线PQ 的方程并与抛物线方程联立求出两根之和及两根之积，求出直线AP ，AQ 的斜率之积，化简可得定值4-. 【详解】由题意将()1,2A 的坐标代入抛物线的方程可得42p =，解得2p =， 所以抛物线的方程为24y x =； 由题意可得直线PQ 的斜率不为0，所以设直线PQ 的方程为：(2)2x m y =++，设1(P x ，1)y ，2(Q x ，2)y ， 联立直线与抛物线的方程：2(2)24x m y y x =++⎧⎨=⎩， 整理可得：24880y my m ---=，则124y y m +=，1288y y m =--，由题意可得1212122212122222111144y y y y k k y y x x ----=⋅=⋅---- 1212121616164(2)(2)2()488244y y y y y y m m ====-+++++--+⨯+，所以124k k =-．故答案为：4-. 【点睛】方法点睛：探索圆锥曲线的定值问题常见方法有两种：① 从特殊入手，先根据特殊位置和数值求出定值，再证明这个值与变量无关；② 直接推理、计算，并在计算推理的过程中消去变量，从而得到定值.16．5【分析】求出抛物线的准线方程把到焦点距离转化为它到准线的距离然后利用三点共线得最小值【详解】如图过作与准线垂直垂足为则∴易知当三点共线时最小最小值为∴的最小值为5故答案为：5【点睛】本题考查抛物线解析：5 【分析】求出抛物线的准线方程，把P 到焦点F 距离转化为它到准线的距离，然后利用三点共线得最小值． 【详解】如图，过P 作PM 与准线2x =-垂直，垂足为M ，则PF PM =，∴PF PB PM PB +=+，易知当,,B P M 三点共线时，PM PB +最小，最小值为3(2)5--=．∴PB PF +的最小值为5．故答案为：5．【点睛】本题考查抛物线的定义，考查抛物线上的点到焦点和到定点距离之和的最小值，解题方法是利用抛物线的定义把点到焦点的距离转化为点到准线距离．17．【分析】由抛物线的定义可知结合圆的性质当且仅当三点共线时等号成立取得最值【详解】由圆可得圆心设的焦点为则抛物线上任意一点Р到直线l 的距离为过点作于点则由抛物线的定义可知所以当且仅当三点共线时等号成立 412【分析】由抛物线的定义可知m PF =，m PA PF PA +=+结合圆的性质，当且仅当,,P F C 三点共线时等号成立取得最值.【详解】由圆22:68210C x y x y ++++=可得圆心()3,4C --，2r，设28y x =的焦点为F ，则()2,0F ，:2l x =-，抛物线上任意一点Р到直线l 的距离为m ， 过点P 作PH l ⊥于点H ，则PH m =， 由抛物线的定义可知PH PF =，所以2m PA PH PA PF PA FC r FC +=+=+≥-=-()()223242412=--+-=，当且仅当,,P F C 三点共线时等号成立， 所以m PA +412， 412. 【点睛】关键点点睛：本题解题的关键点是利用抛物线的定义转化为抛物线上一点到焦点的距离与到圆上一点的距离之和的最小值，利用三点共线即可求解.18．【分析】取焦点在轴建立平面直角坐标系由题意及椭圆性质有为椭圆通径得结合及解出代入离心率公式计算即可【详解】解：取焦点在轴建立平面直角坐标系由及椭圆性质可得为椭圆通径所以又解得所以截口所在椭圆的离心率解析：13【分析】取焦点在x 轴建立平面直角坐标系，由题意及椭圆性质有BC 为椭圆通径，得2163b a =，结合24c =及222a b c =+解出,,a b c 代入离心率公式计算即可.【详解】解：取焦点在x 轴建立平面直角坐标系，由12BC F F ⊥及椭圆性质可得，BC 为椭圆通径，所以21163b F B a ==，1224F Fc ==又222a b c =+，解得6,2,42a c b === 所以截口BAC 所在椭圆的离心率为13故答案为：13【点睛】求椭圆的离心率或其范围的方法：（1）求,,a b c 的值，由22222221c a b b a a a-==-直接求e ； （2）列出含有,,a b c 的齐次方程(或不等式)，借助于222a b c =+消去b ，然后转化成关于e 的方程(或不等式)求解．19．【分析】由题意设即有由双曲线定义及已知可得且结合点在曲线上联立方程得到关于的齐次方程即可求得离心率【详解】令则且①由题意知：E 的左准线为结合双曲线第二定义知：又∴解得②∵知：∴联立①②得：整理得∴故 解析：3【分析】由题意设00(,)P x y ，即有00(,)Q x y --，由双曲线定义及已知可得22003()a a x x c c +=-且22200x y b +=，结合点在曲线上联立方程得到关于,a c 的齐次方程，即可求得离心率.【详解】令00(,)P x y ，00,0x y >则00(,)Q x y --且2200221x y a b-=①，由题意知：E 的左准线为2a x c =-，结合双曲线第二定义知：20||()a PF e x c=+，20||()a FQ e x c =-，又||3||PF FQ =，∴22003()a a x x c c +=-，解得202a x c=②， ∵||OP b =知：22200x y b +=，∴联立①，②得：42222244(1)a a b b c c+-=，整理得223a c =， ∴e =【点睛】关键点点睛：根据双曲线第二定义：曲线上的点到焦点距离与该点到对应准线的距离之比为常数e ，可得点P 的横坐标为22ac；结合点在曲线上及勾股定理即可得关于,a c 的齐次方程求离心率即可.20．①②④【分析】①将抛物线与直线联立消去利用根与系数关系求出再由弦长公式即可求出弦长进而可求出弦长的最小值即可判断①的正误；②利用中点坐标公式求出以为直径的圆的圆心的纵坐标判断圆心到直线的距离与半径的解析：①②④ 【分析】①将抛物线与直线联立消去y ，利用根与系数关系求出12x x +，12x x ，再由弦长公式即可求出弦长，进而可求出弦长的最小值，即可判断①的正误；②利用中点坐标公式，求出以AB 为直径的圆的圆心的纵坐标，判断圆心到直线的距离121y y ++与半径||2AB r =的大小关系，即可判断②的正误； ③将2x =代入24x y =，可得()2,1P 在抛物线上，此时当直线的斜率不存在时，只有一个交点，当直线与抛物线相切时，也只有一个交点，故与抛物线只有一个交点的直线有可能有2条，可判断③错误；④设1l 的方程为()12y k x -=-，将直线与抛物线联立消去y ，利用判别式即可求出k ，进而可求出直线1l 的倾斜角，即可判断④的正误. 【详解】①联立方程241x yy kx ⎧=⎨=+⎩，消去y 可得2440x kx --=，216160k ∆=+>恒成立，设两交点坐标分别为()11,A x y ，()22,B x y ， 所以由根与系数的关系得124x x k +=，124x x ⋅=-，故AB ==2444k =+≥，当0k =时，AB 取得最小值4，所以最短弦长为4，故①正确，②由①可知124x x k +=，则21212242y y kx kx k +=++=+，故以AB 为直径的圆的圆心坐标为()22,21k k +，半径2222ABr k ==+， 抛物线24x y =的准线方程为1y =-，故圆心到准线1y =-的距离2221122d k k r =++=+=， 所以以AB 为直径的圆一定与抛物线的准线相切，故②正确，③将2x =代入24x y =，解得1y =，所以当1t =时，即()2,1P 在抛物线上， 当直线的斜率不存在时，方程为2x =，此时只有一个交点()2,1，当直线斜率存在且只与抛物线只有一个交点时，当且仅当该直线为切线时满足条件， 所以过点()2,P t 只与抛物线只有一个交点的直线有可能有2条，故③错误， ④因为抛物线的焦点为()0,1F ，又()2,1Q ，()2,R m ， 所以三角形FQR 为直角三角形且过()2,1Q 的切线斜率一定存在， 设1l 的方程为()12y k x -=-，代入24x y =，可得24840x k k -+-=，由()2164840k k ∆=--=可得1k =，即直线1l 的倾斜角为45︒，因为直线2l 过点Q 且与1l 垂直，所以一定平分RQF ∠，故④正确. 故答案为：①②④ 【点睛】思路点睛：直线与抛物线交点问题的解题思路：(1)求交点问题，通常解直线方程与抛物线方程组成的方程组； (2)与交点相关的问题通常借助根与系数的关系或用向量法解决．三、解答题21．（1）2212x y +=；（2.【分析】（1）根据椭圆的定义，由2ABF 的周长为a ，再根据离心率求出c ，进而可求出2b ，从而可得椭圆方程；（2）先直线AB 的方程为1)y x =+，()11,A x y ，()22,B x y ，联立直线与椭圆方程，根据韦达定理，结合三角形面积公式，即可求出结果. 【详解】（1）因为过1F 的直线交椭圆于A ，B 两点，且2ABF 的周长为得2211224AB AF BF AF BF AF BF a ++=+++==a =又e =，所以c a =，1c =， 所以21b =，所以椭圆E 的方程为2212x y +=；（2）设直线AB的方程为1)y x =+，()11,A x y ，()22,B x y由221)12y x x y ⎧=+⎪⎨+=⎪⎩消去y ，整理得271240x x ++=， 所以12127x x +=-，1247x x ⋅=，所以12127y y x -=-==．所以2121ABF Sc y y =⋅-==． 【点睛】 思路点睛:求解圆锥曲线中的面积问题时，一般需要联立直线与曲线方程，结合韦达定理，弦长公式，以及三角形面积公式，（有时也需要点到直线距离公式），即可求解. 22．（1）点A 的坐标为()()2,4,2,4-；（2）8-. 【分析】（1）由4AF =根据焦半径公式求出点A 的横坐标，再代入抛物线方程求得纵坐标； （2）由28y x m y x=+⎧⎨=⎩得22(28)0x m x m +-+=，利用韦达定理，结合向量垂直的坐标表示，列方程可求实数m 的值. 【详解】（1）设()00,A x y ，042p AF x =+=，22p=，02x ∴= 所以20082164y y =⨯=⇒=±，∴点A 的坐标为()()2,4,2,4-.（2）由28y x m y x=+⎧⎨=⎩得22(28)0x m x m +-+=，设()11,P x y ，()22,Q x y ，则1282x x m +=-，212x x m =，121228y y x x m ∴+=++=，()()()2121212128y y x m x m x x m x x m m =++=+++=，又OP OQ ⊥，0OP OQ ∴⋅=，2121280x x y y m m ∴+=+=，0m ∴=或8m =-，经检验，当0m =时，直线与抛物线交点中有一点与原点O 重合：不符合题意，当8m =-时，2(24)4640∆=--⨯>，符合题意.综上，实数m 的值为8-. 【点睛】方法点睛：解决直线与抛物线的位置关系的相关问题，其常规思路是先把直线方程与抛物线方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题．涉及弦中点的问题常常用“点差法”解决，往往会更简单.23．（1）22182x y +=；（2）20x y +=．【分析】（1）由离心率，点的坐标代入椭圆方程及222a b c =+列方程组解得,,a b c 得椭圆方程； （2）已知条件说明直线AO 为线段PQ 的垂直平分线，直线OA 方程为12y x =，这样可设直线PQ 方程为2y x m =-+，代入椭圆方程，应用韦达定理得12x x +，12,x x 即为,P Q的横坐标，求出中点横坐标1202x x x +=，由直线PA 得中点纵坐标0y ，中点坐标代入直线AO 方程可得参数m ，即直线PQ 方程．【详解】（1）依题意，22222411a b a b c c a⎧+=⎪⎪⎪=+⎨⎪⎪=⎪⎩，，解得2282a b ⎧=⎨=⎩，，．故椭圆C 的方程为22182x y +=；（2）∵||||,||||OP OQ AP AQ ==，∴直线AO 为线段PQ 的垂直平分线，则直线OA 的方程为12y x =，设直线PQ 的方程为2y x m =-+， 由221822x y y x m ⎧+=⎪⎨⎪=-+⎩，得：221716480x mx m -+-=， ()22(16)417480m m =-⨯->，解得m <()()1122,,,P x y Q x y ，由韦达定理得121617mx x +=，设PQ 的中点为()00,H x y ，。

北师大版高二数学选修1-1圆锥曲线方程测试题及答案

北师大版高二数学选修1-1圆锥曲线方程测试题及答案

高二数学选修1-1圆锥曲线方程检测题姓名：_________班级：________ 得分：________一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1、设定点()10,3F -，()20,3F ，动点(),P x y 满足条件a PF PF =+21(a＞)0，则动点P 的轨迹是（ ）.A. 椭圆B. 线段C. 不存在D.椭圆或线段或不存在2、抛物线21y x m = 的焦点坐标为（ ） . A ．⎪⎭⎫ ⎝⎛0,41m B ． 10,4m ⎛⎫ ⎪⎝⎭ C ． ,04m ⎛⎫ ⎪⎝⎭ D ．0,4m ⎛⎫⎪⎝⎭3、双曲线221mx y +=的虚轴长是实轴长的2倍，则m 的值为（ ）. A ．14-B ．4-C ．4D ．144、设双曲线的焦点在x 轴上，两条渐近线为y=±x 21，则该双曲线的离心率e 为（ ） （A ）5 （B ）5 （C ）25 （D ）45 5、线段∣AB ∣=4，∣PA ∣+∣PB ∣=6，M 是AB 的中点，当P 点在同一平面内运动时，PM 的长度的最小值是（ ） （A ）2 （B ）2（C ）5（D ）56、若椭圆13222=++y m x 的焦点在x 轴上，且离心率e=21，则m 的值为（ ）（A ）2（B ）2 （C ）－2（D ）±27、过原点的直线l 与双曲线42x －32y =－1有两个交点，则直线l 的斜率的取值范围是 A.(－23，23) B.(－∞,－23)∪(23,+∞) C.［－23,23］ D.(－∞,－23］∪［23,+∞)8、如图，在正方体ABCD －A1B1C1D1中，P 是侧面BB1C1C 内一动点，若P 到直线BC 与直线C1D1的距离相等，则动点P 的轨迹所在的曲线是（ ）. A.直线B. 抛物线C.双曲线D. 圆9、已知椭圆x 2sin α－y 2cos α=1（0＜α＜2π）的焦点在x 轴上，则α的取值范围是（ ）（A ）（43π，π） （B ）（4π，43π） （C ）（2π，π） （D ）（2π，43π）10、 F 1、F 2是双曲线116922=-y x 的两个焦点，点P 在双曲线上且满足∣P F 1∣·∣P F 2∣=32，则∠F 1PF 2是（ ）（A ） 钝角 （B ）直角 （C ）锐角 （D ）以上都有可能BA 1C 111、与椭圆1251622=+y x 共焦点，且过点（－2，10）的双曲线方程为（ ）（A ）14522=-x y （B ）14522=-y x （C ）13522=-x y （D ）13522=-y x12．若点 到点 的距离比它到直线 的距离小1，则 点的轨迹方程是（ ）A ．B ．C ．D ．二、填空题：本大题共4小题，每小题4分，共16分.13、已知双曲线的渐近线方程为y=±34x，则此双曲线的离心率为________.14．在抛物线 上有一点 ，它到焦点的距离是20，则 点的坐标是_________．15．抛物线上的一点到 轴的距离为12，则与焦点间的距离=______．.16、椭圆具有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.今有一个水平放置的椭圆形台球盘,点A 、B 是它的焦点,长轴长为2a,焦距为2c,静放在点A 的小球(小球的半径忽略不计)从点A 沿直线出发,经椭圆壁反射后第一次回到点A 时,小球经过的路程是_____________.三、解答题：本大题共6小题，共60分，解答应写出文字说明，证明过程或演算步骤. 17. (本小题满分15分)椭圆短轴的一个端点与两个焦点组成一个正三角形，焦点到椭圆长轴端点的最短距离为3，求此椭圆的标准方程。

新北师大版高中数学选修1-1第二章《圆锥曲线与方程》测试卷(含答案解析)

新北师大版高中数学选修1-1第二章《圆锥曲线与方程》测试卷(含答案解析)

一、选择题1．设O 为坐标原点，1F ，2F 是椭圆22221x y a b+=（0a b >>）的左、右焦点，若在椭圆上存在点P 满足123F PF π∠=，且OP ，则该椭圆的离心率为（ ）A ．12B ．14C ．12D ．22．已知()5,0F 是双曲线()2222:=10,0x y C a b a b->>的右焦点，点(A .若对双曲线C 左支上的任意点M ，均有10MA MF +≥成立，则双曲线C 的离心率的最大值为（ ）A B ．5C ．52D ．63．已知椭圆221124y x +=，圆22:4O x y +=，过椭圆上任一与顶点不重合的点G 引圆的两条切线，切点分别为,P Q ，直线PQ 与x 轴，y 轴分别交于点,M N ，则2231OMON+=（ ）A ．54 B ．45C ．43D ．344．双曲线()2222:10,0x y C a b a b-=>>的一条渐近线被圆()2223x y -+=截得的弦长为2，则C 的离心率为（ ）A ．3B ．2C D5．已知点A 是抛物线24x y =的对称轴与准线的交点，点F 为抛物线的焦点，点P 在抛物线上，且满足||||PA m PF =，则m 的最大值是（ ）A ．1BC ．2D ．46．过抛物线26y x =的焦点作一条直线与抛物线交于()()1122,,,A x y B x y 两点，若123x x +=，则这样的直线（ ）A ．有且只有一条B ．有且只有两条C ．有且只有三条D ．有且只有四条7．已知抛物线22(0)y px p =>的焦点为F ，过点F 的直线分别交抛物线于A ，B 两点，若4AF =，1BF =，则p =（ ） A ．165B ．2C ．85D ．18．已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F ，2F ，()1221,2i i M F M F a i -==，且1M ，2F ，2M 三点共线，点D 在线段21M F 上，且1121F M D M M D ∠=∠1112122M F M F M D +=，则双曲线C 的渐近线方程为（ ）A ．22y x =±B ．2y x =±C ．3y x =±D ．3y x =±9．已知点P 是抛物线22y x =上的一个动点，则点P 到点32,32D ⎛⎫⎪⎝⎭的距离与点P 到y 轴的距离之和的最小值为（ ） A ．2B ．52C ．3D ．7210．设双曲线2214y x -=的左、右焦点分别为12,F F ，若点P 在双曲线上，且12F PF △为锐角三角形，则12PF PF +的取值范围是（ ） A ．(42,6)B ．(6,8)C ．(42,8)D ．(6,10)11．已知抛物线1C 的顶点在坐标原点，焦点F 在y 轴正半轴上．若点F 到双曲线222:126x y C -=的一条渐近线的距离为2，则1C 的标准方程是（ ）A ．2833y x =B ．21633y x =C ．28x y =D ．216x y =12．在抛物线型内壁光滑的容器内放一个球，其通过中心轴的纵剖面图如图所示，圆心在y 轴上，抛物线顶点在坐标原点，已知抛物线方程是24x y =，圆的半径为r ，若圆的大小变化时，圆上的点无法触及抛物线的顶点O ，则圆的半径r 的取值范围是（ ）A ．()2,+∞B ．()1,+∞C ．[)2,+∞D ．[)1,+∞二、填空题13．已知双曲线()22210y x a a -=>的离心率5e =，点12,F F 分别是它的下焦点和上焦点，若Р为该双曲线上支上的一个动点，则1PF 与P 到一条渐近线的距离之和的最小值为_________．14．已知双曲线()2222:10,0x y C a b a b-=>>的一条渐近线与圆()22234x y +-=相交于A ，B 两点，且2AB =，则双曲线C 的离心率为___________.15．已知圆22:68210C x y x y ++++=，点A 是圆C 上任一点，抛物线28y x =的准线为l ，设抛物线上任意一点Р到直线l 的距离为m ，则m PA +的最小值为_______ 16．点P 为椭圆C 上一动点，过点P 作以椭圆短轴为直径的圆的两条切线，切点分别为M ，N ，若60MPN ∠=︒，则椭圆C 的离心率的取值范围是______.17．已知椭圆22:143x y C +=的左､右焦点分别为12F F 、，过2F 且倾斜角为π4的直线l交椭圆C 于A B 、两点，则1F AB 的面积为___________. 18．已知抛物线218y x =的焦点为F ，过F 的直线l 与抛物线交于A 、B 两点，抛物线的准线与y 轴交于点M ，当AMAF最大时，弦AB 长度是___________. 19．若M ，P 是椭圆2214x y +=两动点，点M 关于x 轴的对称点为N ，若直线PM ，PN 分别与x 轴相交于不同的两点A (m ，0)，B (n ，0)，则mn =_________.20．如图所示，已知M ，N 为双曲线22221(0,0)x y a b a b-=>>上关于原点对称的两点，点M与点Q 关于x 轴对称，2516ME MQ =，直线NE 交双曲线右支于点P ，若2NMP π∠=，则e =_____________．三、解答题21．已知椭圆具有如下性质：若椭圆的方程为()222210x y a b a b+=>>，则椭圆在其上一点()'',A x y 处的切线方程为''221x y x ya b+=，试运用该性质解决以下问题：在平面直角坐标系xOy 中，已知椭圆C ：()222210x y a b a b +=>>的离心率为2，且经过点21,2A ⎛⎫ ⎪ ⎪⎝⎭. （1）求椭圆C 的方程；（2）设F 为椭圆C 的右焦点，直线l 与椭圆C 相切于点P (点P 在第一象限)，过原点O 作直线l 的平行线与直线PF 相交于点Q ，问：线段PQ 的长是否为定值？若是，求出定值；若不是，说明理由.22．在平面直角坐标系xOy 中，已知直线y x =被抛物线2:2(0)C y px p =>截得的弦长为2l 与抛物线C 相交于点M ，N ，点()1,2A ，且直线AM ，AN 的斜率之和为4.（1）求抛物线C 的方程；（2）求证：直线l 过定点，并求出定点坐标.23．A B 是抛物线24y x =上两个不同的点，A 、B 纵坐标之和为4． （1）求直线AB 的斜率；（2）O 为原点，若OA OB ⊥，求直线AB 的方程．24．已知点A 、B 坐标分别是(2,0)-，(22,0)，直线AP 、BP 相交于点P ，且它们斜率之积是12-． （1）试求点P 的轨迹Γ的方程；（2）已知直线:4l x =-，过点()2,0F -的直线（不与x 轴重合）与轨迹Γ相交于M ．N 两点，过点M 作MD l ⊥于点D ．求证：直线ND 过定点，并求出定点的坐标． 25．已知点1F 、2F 分别是椭圆C 的左、右焦点，离心率为22，点P 是以坐标原点O 为圆心的单位圆上的一点，且120PF PF ⋅=．（1）求椭圆C 的标准方程；（2）设斜率为k 的直线l （不过焦点）交椭圆于M ，N 两点，若x 轴上任意一点到直线1MF 与1NF 的距离均相等，求证：直线l 恒过定点，并求出该定点的坐标．26．已知椭圆2222:1(0)x y C a b a b+=>>的长轴长为4，焦距为23，点P 为椭圆C 上一动点，且直线,AP BP 的斜率之积为14-．（1）求椭圆C 的标准方程；（2）设,A B 分别是椭圆C 的左右顶点，若点,M N 是C 上不同于,A B 的两点，且满//,//AP OM BP ON ，求证：MON △的面积为定值．【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】根据中线向量可得()1212PO PF PF =+，平方后结合椭圆的定义可得212PF PF a ⋅=，在焦点三角形中再利用余弦定理可得224c a =，从而可求离心率. 【详解】因为O 为12F F 的中点，故()1212PO PF PF =+， 所以()2221212124PO PF PF PF PF =++⋅，故22212123112442a PF PF PF PF ⎛⎫=++⋅⋅ ⎪⎝⎭， 故()2222121212123a PF PF PF PF PF PF PF PF =++⋅=+-⋅，所以212PF PF a ⋅=，又22212121422c PF PF PF PF =+-⋅⋅， 故()2222212124343c PF PF PF PF a a a =+-⋅=-=，故12e =. 故选：A. 【点睛】方法点睛：与焦点三角形有关的计算问题，注意利用椭圆的定义来转化，还要注意利用余弦定理和向量的有关方法来计算长度、角度等.2．C解析：C 【分析】设E 是双曲线的左焦点，利用双曲线的定义把MF 转化为ME 后易得MA ME +的最小值，从而得a 的最小值，由此得离心率的最大值． 【详解】设E 是双曲线的左焦点，M 在左支上，则2MF ME a -=，2MF ME a =+，22MA MF MA ME a EA a +=++≥+，当且仅当E A M ,,三点共线时等号成立．则222(5)(11)210EA a a +=-++≥，2a ≥，所以552c e a a ==≤． 故选：C ．【点睛】思路点睛：本题考查双曲线的定义的应用．在涉及双曲线上的点与一个焦点和另外一个定点距离和或差的最值时，常常利用双曲线的定义把到已知焦点的距离转化为到另一焦点的距离，从而利用三点共线取得最值求解．3．D解析：D 【分析】设112233(,),(,),(,)P x y Q x y G x y ，则可得切线,GP GQ 的方程，即可得到直线PQ 的方程，进而可求出点点,M N 的坐标，再结椭圆方程可求出2231OMON+的值【详解】解：设112233(,),(,),(,)P x y Q x y G x y ，则切线GP 的方程为114x x y y +=，切线GQ 的方程为224x x y y +=， 因为点G 在切线,GP GQ 上，所以13134x x y y +=，23234x x y y +=， 所以直线PQ 的方程为334x x y y +=， 所以3344(,0),(0,)M N x y ， 因为点33(,)G x y 在椭圆221124y x+=上，所以2233312x y +=，所以22223333223311123(3)161616164x y x y OM ON+=+=+==， 故选：D 【点睛】关键点点睛：此题考查椭圆的标准方程，以及简单性质有应用，解题的关键是设点33(,)G x y ，再由已知条件得到直线PQ 的方程为334x x y y +=，从而可得,M N 的坐标，进而可得答案，考查计算能力和转化能力，属于中档题4．D解析：D 【分析】设双曲线C 的渐近线方程为y kx =，其中bk a=±，利用圆的半径、渐近线截圆所得弦长的一半、弦心距三者满足勾股定理可求得k的值，再利用e =可求得双曲线C 的离心率e 的值. 【详解】设双曲线C 的渐近线方程为y kx =，其中b k a=±， 圆()2223x y -+=的圆心坐标为()2,0，半径为r =圆心到直线y kx =的距离为d =另一方面，由于圆的半径、渐近线截圆所得弦长的一半、弦心距三者满足勾股定理， 可得2212d r =-=，即2221k k =+，解得1k =±，1ba∴=， 因此，双曲线C 的离心率为22222212c c a b b e a a a a +⎛⎫====+= ⎪⎝⎭. 故选：D. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.5．B解析：B 【分析】由抛物线的对称性可不妨设P 在第一象限或为原点，过P 作准线1y =-的垂线，垂足为E ，利用抛物线的定义可得1sin PAE m=∠，求出sin PAE ∠的最小值后可得m 的最大值. 【详解】由抛物线24x y =可得准线方程为：1y =-，故()0,1A -.如图，由抛物线的对称性可不妨设P 在第一象限或为原点， 过P 作准线1y =-的垂线，垂足为E ，则PE PF =，故1||||sin ||||PF PE PAE m PA PA ===∠， 当直线AP 与抛物线相切时，PAE ∠最小， 而当P 变化时，02PAE π<∠≤，故当直线AP 与抛物线相切时sin PAE ∠最小，设直线:1AP y kx =-，由241x yy kx ⎧=⎨=-⎩得到2440x kx -+=，216160k ∆=-=，故1k =或1k =-（舍），所以直线AP 与抛物线相切时4PAE π∠=，故1m的最小值为2即m， 故选：B. 【点睛】方法点睛：与抛物线焦点有关的最值问题，可利用抛物线的定义把到焦点的距离问题转化为到准线的距离问题.6．A解析：A 【分析】由抛物线方程求得焦点F 的坐标，分直线AB 斜率不存在和直线斜率存在，存在时设直线AB 方程与抛物线方程联立，由韦达定理表示出A 、B 两点的横坐标之和，求得k ，即可得结论. 【详解】抛物线26y x =的焦点为3,02F ⎛⎫⎪⎝⎭， 当过焦点的直线斜率不存在时，即为32x =， 1232x x ==，符合123x x +=， 当过焦点的直线斜率存在时设为32y k x ⎛⎫=- ⎪⎝⎭， 与抛物线交于()()1122,,,A x y B x y 两点，由2632y x y k x ⎧=⎪⎨⎛⎫=- ⎪⎪⎝⎭⎩得()222293604k k x k x -++=， 所以2122363k x x k++==，即22363k k +=，所以无解， 则这样的直线有且只有一条. 故选：A. 【点睛】本题考查直线与抛物线的位置关系，解题的时候要注意讨论直线斜率不存在时的情况，以免遗漏，是中档题.7．C解析：C 【分析】直接设出直线方程，用“设而不求法”表示出AF ，BF ，利用性质可解. 【详解】由题意可知直线AB的斜率一定存在，设为k ，联立2,22,p y k x y px ⎧⎛⎫=-⎪ ⎪⎝⎭⎨⎪=⎩消去y 可得()22222204k p k x k px -++=，设()11,A x y ，()22,B x y ，所以2124p x x =.又根据抛物线的定142p x +=，212p x +=，所以241224p p p ⎫⎫⎛⎛--= ⎪⎪⎝⎝⎭⎭，解得85p =.故选：C 【点睛】"设而不求"是一种在解析几何中常见的解题方法，可以解决直线与二次曲线相交的问题.8．B解析：B 【分析】先取11M F 的中点E ，由题意分析12M F DE 为菱形，得到()()222442c a a =-，从而求出渐近线方程. 【详解】由()1221,2i i M F M F a i -==知：M 1、M 2在双曲线上. 取11M F 的中点E ，连接DE ，2DF ，由111211111222,22,M F M F M D M F M D M F +=∴=-， 即112122,M F F D F D E M =∴=,可知四边形12M F DE 为平行四边形； 又1M D 为112F M F 的角平分线，故四边形12M F DE 为菱形，1212M E F M F D DE ===又21//DE M M 故D 为线段21M F 的中点； 因为211//DF M F ，故2F 为线段12M M 的中点， 故1222M F F M =； 所以21112M F M F =由双曲线的定义：11122M F M F a -=，所以21114,2M F a M F a == 而12M M x ⊥轴，故222121112F F M F M F =-，故()()222442c a a =-，故==ce a，故双曲线C 的渐近线方程为y = 故选B ． 【点睛】求双曲线的渐近线的方法:（1）直接令标准方程22221x y a b-=中的1变成0,得到22220x y a b -=,利用平方差公式得到渐近线方程: bxy a=±； （2）根据题意，找到找到a 、b 、c 的关系，消去c ，从而求出渐近线方程.9．B解析：B 【分析】利用抛物线的定义，把P 到y 轴的距离转化为1||2PF -,利用几何法求最值 【详解】抛物线22y x =的焦点1,02F ⎛⎫ ⎪⎝⎭,准线1:2l x =-，如图示：过P 作PP 1⊥y 轴于P 1,作PP 2⊥l于P 2,则211||||2PP PP -= 所以点P 到点332D ⎛ ⎝的距离与点P 到y 轴的距离之和为 1211||||||||||||22PD PP PD PP PD PF +=+-=+- 由图示，易知，当P 落在Q 时，DPF 三点共线，||||||PD PF DF +=, 其他位置，都有||||||PD PF DF +> 所以点P 到点332D ⎛⎝的距离与点P 到y 轴的距离之和的最小值为： 221111335||||||||||2022222PD PP PD PF DF ⎛⎫⎛⎫+=+-≥-=-+-= ⎪ ⎪ ⎪⎝⎭⎝⎭当D 、P 、F 三点共线时取最小值. 故选：B 【点睛】解析几何问题解题的关键：解析几何归根结底还是几何，根据题意画出图形，借助于图形寻找几何关系可以简化运算．10．D解析：D 【分析】由题意画出图形，不妨设P 在第一象限，P 点在1P 与2P 之间运动，求出112F PF ∠和122F F P ∠ 为直角时12PF PF +的值，可得12F PF △ 为锐角三角形时12PF PF +的取值范围． 【详解】12F PF △为锐角三角形，不妨设P 在第一象限，P 点在1P 与2P 之间运动，如图，当P 在1P 处，11290F PF∠=，又1,2,5a b c ===由222111212|||||20|PF PF F F =+=，1112||||2PFPF -=， 可得1112||||8PF PF ⋅=， 此时 1112||||6PF PF +=；当P 在2P 处，12290F F P ∠=，25P x = 易知24P y = 则224P F =此时12222222||||||2||10P F P F P F a P F +=++=∴12F PF △为锐角三角形，则12PF PF +的取值范围是()6,10， 故选：D ． 【点晴】关键点点晴：本题的关键在于求出112F PF ∠和122F F P ∠ 为直角时12PF PF +的值.11．D解析：D 【分析】先根据双曲线的方程求解出双曲线的渐近线方程，再根据点到直线的距离公式求解出抛物线方程中的p ，则抛物线方程可求. 【详解】双曲线2C 的渐近线方程是22026x y -=，即3y x =.因为抛物线的焦点()0,02p F p ⎛⎫> ⎪⎝⎭30x y -=的距离为2，2=，即8p =，所以1C 的标准方程是216x y =，故选：D ． 【点睛】方法点睛：求解双曲线方程的渐近线方程的技巧：已知双曲线方程22221x y a b-=或22221y x a b -=，求解其渐近线方程只需要将方程中的“1”变为“0”，由此得到的y 关于x 的一次方程即为渐近线方程. 12．A解析：A 【分析】设圆心为(0,)P a ，（0a >），半径为r ，(,)Q x y 是抛物线上任一点，求出2PQ ，当2PQ 的最小值在原点处取得时，圆P 过原点，可得此时圆半径的范围，半径不在这个范围内的圆不过原点． 【详解】设圆心为(0,)P a ，（0a >），半径为r ，(,)Q x y 是抛物线上任一点，22222()4()(2)44PQ x y a y y a y a a =+-=+-=-++-，若2PQ 的最小值不在(0,0)O 处取得，则圆P 不过原点，所以20a ->，即2a >，此时圆半径为2r ==>．因此当2r >时，圆无法触及抛物线的顶点O ．故选：A ． 【点睛】关键点点睛：本题考查圆与抛物线的位置关系，题中圆不过原点，说明抛物线上的点到圆心距离的最小值不是在原点处取得，由此得到解法，即设圆心为(0,)P a ，抛物线上点的坐标为(,)Q x y ，求出PQ ，然后确定其最小值，由最小值点不是原点可得结论．二、填空题13．【分析】根据离心率先求出双曲线的方程得出渐近线方程根据双曲线的定义可得：所以设点到一条渐进线的距离为则从而得出答案【详解】双曲线的离心率所以解得所以双曲线由的双曲线的渐进线方程为由为该双曲线上支上的 解析：5【分析】根据离心率先求出双曲线的方程，得出渐近线方程，根据双曲线的定义可得：1224PF PF a -==，所以124PF PF =+，设点Р到一条渐进线的距离为d ，则124PF d PF d +=++，从而得出答案.【详解】双曲线()22210y x a a -=>的离心率5e =所以221514e a =+=，解得2a =，所以()()120,5,0,5F F - 双曲线2214y x -=，由2204y x -=，的双曲线的渐进线方程为2y x =±由Р为该双曲线上支上的一个动点，根据双曲线的定义可得：1224PF PF a -== 所以124PF PF =+，设点Р到渐进线2y x =的距离为d则124PF d PF d +=++，过2F 作渐进线2y x =的垂线，垂足为M ,如图.所以225112F M ==+所以122445PF d PF d F M +=++≥+=同理1PF 与P 到渐近线2y x =-的距离之和的最小值为5 故答案为：5【点睛】关键点睛：本题考查利用双曲线的定义解决距离之和的最值问题，解答本题的关键是根据双曲线的定义可得：1224PF PF a -==，所以124PFPF =+，设点Р到渐进线2y x =的距离为d ，则124PF d PF d +=++，过2F 作渐进线2y x =的垂线，属于中档题.14．2【分析】由双曲线圆的方程确定渐近线方程为圆心为半径为根据圆的相交弦与半径弦心距之间的几何关系有结合双曲线参数间的关系即可求其离心率【详解】由题意知：双曲线的渐近线为而圆心为半径为∴圆心到渐近线的距解析：2 【分析】由双曲线、圆的方程确定渐近线方程为by x a=±，圆心为(0,，半径为2r ，根据圆的相交弦与半径、弦心距之间的几何关系有222||4AB r d -=，结合双曲线参数间的关系即可求其离心率. 【详解】由题意知：双曲线的渐近线为by x a=±，而圆心为(0,，半径为2r ，∴圆心到渐近线的距离d ==，而2AB =，∴221r d -=，故222123a a b=+，又222,1c a b c e a +==>， ∴2e =. 故答案为：2. 【点睛】关键点点睛：根据双曲线、圆的标准方程确定渐近线方程、圆心、半径长，结合圆中相交弦的几何性质及双曲线参数关系，列出关于,a c 的齐次方程求离心率.15．【分析】由抛物线的定义可知结合圆的性质当且仅当三点共线时等号成立取得最值【详解】由圆可得圆心设的焦点为则抛物线上任意一点Р到直线l 的距离为过点作于点则由抛物线的定义可知所以当且仅当三点共线时等号成立2【分析】由抛物线的定义可知m PF =，m PA PF PA +=+结合圆的性质，当且仅当,,P F C 三点共线时等号成立取得最值. 【详解】由圆22:68210C x y x y ++++=可得圆心()3,4C --，2r，设28y x =的焦点为F ，则()2,0F ，:2l x =-，抛物线上任意一点Р到直线l 的距离为m ， 过点P 作PH l ⊥于点H ，则PH m =， 由抛物线的定义可知PH PF =，所以2m PA PH PA PF PA FC r FC +=+=+≥-=-()()223242412=--+-=，当且仅当,,P F C 三点共线时等号成立， 所以m PA +412， 412. 【点睛】关键点点睛：本题解题的关键点是利用抛物线的定义转化为抛物线上一点到焦点的距离与到圆上一点的距离之和的最小值，利用三点共线即可求解.16．【分析】根据题意找到abc 的关系求出离心率的范围【详解】设椭圆的中心为因为所以所以所以椭圆上的点到原点距离最远的是长轴端点所以即所以离心率所以故答案为：【点睛】求椭圆（双曲线）离心率的一般思路：根据解析：32⎫⎪⎢⎪⎣⎭【分析】根据题意，找到a 、b 、c 的关系，求出离心率的范围 【详解】设椭圆的中心为O ，因为60MPN ∠=︒，所以60POM ∠=︒，所以||2||OP OM =，所以2OP b =，椭圆上的点到原点距离最远的是长轴端点，所以2a b ≥，即12b a ≤，2222211,,44b ac a a -∴≤∴≤所以离心率2c e a ==≥=，所以⎫∈⎪⎪⎣⎭e .故答案为：⎫⎪⎪⎣⎭【点睛】求椭圆（双曲线）离心率的一般思路：根据题目的条件，找到a 、b 、c 的关系，消去b ，构造离心率e 的方程或（不等式）即可求出离心率．17．【分析】先求出直线的方程与椭圆方程联立消去x 求出|y1-y2|利用即可求出的面积【详解】由题意得:直线:设则有:消去x 得:7y2+6y-9=0∴即的面积为【点睛】求椭圆(双曲线)的焦点弦三角形的面积【分析】先求出直线l 的方程,与椭圆方程联立,消去x ,求出| y 1- y 2|,利用11212|1|||2F AB S F F y y =-△即可求出1F AB 的面积. 【详解】由题意得: 直线l :1y x =-, 设1122(,),(,)A x y B x y ,则有:2213412y x x y =-⎧⎨+=⎩消去x 得:7y 2+6y -9=0, ∴121269,77y y y y +=-=-12211111|||227|2227F AB S F F y y -∴=⨯=⨯⨯==△即1F AB 的面积为7【点睛】求椭圆(双曲线)的焦点弦三角形的面积: （1）直接求出弦长|AB |,利用11||2F AB AB d S =△; （2）利用11212|1|||2F AB S F F y y =-△. 18．【分析】作出图形过点作垂直于抛物线的准线于点可得出可知当取最小值时即直线与抛物线相切时最大可求出直线的斜率求出点的坐标利用对称性可求得点的坐标抛物线的焦点弦长公式进而可求得弦的长度【详解】设点为第一 解析：8【分析】作出图形，过点A 作AE 垂直于抛物线218y x =的准线于点E ，可得出1sin AM AF AME=∠，可知当AME ∠取最小值时，即直线AM 与抛物线相切时，AM AF 最大，可求出直线AM 的斜率，求出点A 的坐标，利用对称性可求得点B 的坐标，抛物线的焦点弦长公式，进而可求得弦AB 的长度. 【详解】设点A 为第一象限内的点，过点A 作AE 垂直于抛物线218y x =的准线于点E ，如下图所示：由抛物线的定义可得AE AF =，则1sin AM AM AF AE AME==∠， 可知当AME ∠取最小值时，即直线AM 与抛物线相切时，AMAF最大， 抛物线218y x =的焦点为()0,2F ，易知点()0,2M -. 当直线AM 与抛物线218y x =相切时，直线AM 的斜率存在， 设直线AM 的方程为2y kx =-，联立228y kx x y=-⎧⎨=⎩，消去y 得28160x kx -+=，264640k ∆=-=，因为点A 在第一象限，则0k >，解得1k =，方程为28160x x -+=，解得4x =，此时，228x y ==，即点()4,2A ，此时AB y ⊥轴，由对称性可得()4,2B -，因此，448AB =+=. 故答案为：8 【点睛】方法点睛：有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式12AB x x p =++或12AB y y p =++，若不过焦点，则必须用一般弦长公式．19．4【分析】设出的坐标写出坐标满足的关系式根据题意写出直线的方程求出的横坐标计算得出的值【详解】解：设则则所以直线的方程为令可得同理有直线的方程为令可得则故答案为：【点睛】圆锥曲线中求定值问题常见的方解析：4 【分析】设出,,M N P 的坐标，写出坐标满足的关系式.根据题意，写出直线PM ，PN 的方程，求出,A B 的横坐标，计算得出mn 的值. 【详解】解：设(),M a b ，则(),N a b -，(),P c d ，则2214a b +=，2214c d +=所以PM d bk c a-=- 直线PM 的方程为()d b y b x a c a --=--，令0y =可得ad bcm d b-=-同理有PM d bk c a+=- 直线PN 的方程为()d b y b x a c a ++=--，令0y =可得ad bcn d b+=+ 则222222ad bc ad bc a d b c mn d b d b d b -+-⎛⎫⎛⎫== ⎪⎪-+-⎝⎭⎝⎭222222111144111144a c c a c a ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=⎛⎫--- ⎪⎝⎭()2222414a c a c -==-故答案为：4 【点睛】圆锥曲线中求定值问题常见的方法有两种：(1)从特殊入手，求出定值，再证明这个值与变量无关．(2)直接推理、计算，并在计算推理的过程中消去变量，从而得到定值．20．【分析】设利用点差法得到即可求出离心率；【详解】解：设则由得从而有又所以又由从而得到所以所以故答案为：【点睛】双曲线的离心率是双曲线最重要的几何性质求双曲线的离心率(或离心率的取值范围)常见有两种方解析：54【分析】设()()1122,,,M x y P x y 利用点差法得到22PM PN b k k a⋅=，即可求出离心率； 【详解】解：设()()1122,,,M x y P x y ，则()()1111,,,N x y Q x y ---．由2516ME MQ =，得1117,8E x y ⎛⎫- ⎪⎝⎭，从而有11119,16MN PN ENy y k k k x x ===-，又1190,MN yNMP k x ∠==，所以11MP x k y =-， 又由()()()()22112212121212222222221111x y a bx x x x y y y y ab x y a b ⎧-=⎪⎪⇒+-=+-⎨⎪-=⎪⎩， 从而得到22PM PNb k k a⋅=所以211211991616PM PN x y b k k y x a ⎛⎫⋅=-⋅-== ⎪⎝⎭，所以54e ==．故答案为：54【点睛】双曲线的离心率是双曲线最重要的几何性质，求双曲线的离心率(或离心率的取值范围)，常见有两种方法： ①求出a ，c ，代入公式c e a=； ②只需要根据一个条件得到关于a ，b ，c 的齐次式，结合b 2＝c 2－a 2转化为a ，c 的齐次式，然后等式(不等式)两边分别除以a 或a 2转化为关于e 的方程(不等式)，解方程(不等式)即可得e (e 的取值范围)．三、解答题21．（1）2212x y +=；（2.【分析】（1）根据椭圆离心率为2，以及椭圆经过点2A ⎛⎫ ⎪ ⎪⎝⎭，结合椭圆的性质列方程求解即可；（2）设()00,P x y ，题意可知，切线l 的方程为0022x x y y +=，过原点O 且与l 平行的直线'l 的方程为0020x x y y +=，求出Q 的坐标，表示出PQ 的长，再化简即可得结论. 【详解】（1）由题意知2222221112c aa b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩1a b ⎧=⎪⇒⎨=⎪⎩ ∴椭圆C 的方程为2212x y +=.（2）设()00,P x y ，题意可知，切线l 的方程为0022x x y y +=， 过原点O 且与l 平行的直线'l 的方程为0020x x y y +=， 椭圆C 的右焦点()1,0F ，所以直线PF 的方程为()00010y x x y y ---=，联立()000001020y x x y y x x y y ⎧---=⎨+=⎩，所以2000002,22y x y Q x x ⎛⎫-⎪--⎝⎭，所以PQ =====为定值. 【点睛】方法点睛：探索圆锥曲线的定值问题常见方法有两种：① 从特殊入手，先根据特殊位置和数值求出定值，再证明这个值与变量无关；② 直接推理、计算，并在计算推理的过程中消去变量，从而得到定值.22．（1）24y x =；（2）直线l 过定点，定点坐标为()0,1-，证明见解析. 【分析】（1）联立直线方程和抛物线方程，求出交点的坐标后利用弦长公式可求p 的值，从而可求抛物线的方程.（2）设直线l 的方程为x my b =+，联立直线方程和抛物线方程，消去x 后利用韦达定理化简斜率之和，从而可得b m =，故可求定点坐标.我们也可以设211,4y M y ⎛⎫⎪ ⎪⎝⎭，222,4y N y ⎛⎫⎪⎝⎭，用坐标表示斜率之和，再用该两点的坐标表示直线l ，化简后可得直线过定点. 【详解】 （1）由2,2,y x y px =⎧⎨=⎩解得10x =，22x p =， 因为直线y x =被抛物线()2:20C y px p =>截得的弦长为0p -=，0p >，解得2p =， 所以抛物线C 的方程为24y x =.（2）法一： 设直线l 的方程为x my b =+，()11,M x y ，()22,N x y ， 由2,4,x my b y x =+⎧⎨=⎩得2440y my b --=， 所以124y y m +=，124y y b =-，因为点()1,2A ，且直线AM ，AN 的斜率之和为4，所以121222411y y x x --+=--，而2114y x =，2224y x =，化简得12120y y y y ++=， 所以440m b -=，即b m =， 所以直线l 的方程为()1x m y =+， 所以直线l 过定点，定点坐标为()0,1-.法二： 设211,4y M y ⎛⎫ ⎪ ⎪⎝⎭，222,4y N y ⎛⎫ ⎪⎝⎭， 因为点()1,2A ，且直线AM ，AN 的斜率之和为4，所以1222122241144y y y y --+=--，即12120y y y y ++=， ①当210y y +≠时，直线l 的方程为221112221444y yy y y x y y ⎛⎫--=- ⎪⎝⎭-即2141y x y y =--， 所以直线l 过定点，定点坐标为()0,1-；②当210y y +=时，120y y =，所以120y y ==，不满足题意. 所以直线l 过定点，定点坐标为()0,1-. 【点睛】方法点睛：. 直线与抛物线的位置关系中的定点、定值、最值问题，一般可通过联立方程组并消元得到关于x 或y 的一元二次方程，再把要求解的目标代数式化为关于两个的交点横坐标或纵坐标的关系式，该关系中含有1212,x x x x +或1212,y y y y +，最后利用韦达定理把关系式转化为若干变量的方程（或函数），从而可求定点、定值、最值问题，也可以设出交点坐标，用交点坐标表示目标代数式，从而解决定点、定值、最值问题. 23．（1）1；（2）y x =或4y x =-． 【分析】（1）法一：设()11,A x y ，()22,B x y 代入抛物线方程相减结合斜率公式即可求得；法二：设直线方程与抛物线联立结合韦达定理求得结果；（2）由OA OB ⊥得0OA OB ⋅=即12120x x y y +=结合两根关系可求得m ，即可求直线方程. 【详解】（1）法一：设()11,A x y ，()22,B x y ，则2112224,4,y x y x ⎧=⎨=⎩两式相减得()()()1212124y y y y x x +-=-． ∵124y y +=，∴()()121244y y x x -=-． 根据题意可知12x x ≠，∴12121AB y y k x x -==-， ∴直线AB 的斜率为1．法二：据题意直线AB 斜率存在，可设直线AB 的方程为y kx m =+， 与24y x =联立得204k m y y -+=，则1244y y k+==， ∴1k =，∴直线AB 的斜率为1．（2）由（1）得，124y y +=，124y y m ⋅=， 由题意，0OA OB ⋅=，即()221212121214016x x y y y y y y m m +=+=+=， 解得，0m =或4m =-．所以，直线AB 的方程为y x =或4y x =-． 【点睛】解答直线与抛物线的题目时，时常把两个曲线的方程联立，消去x (或y )建立一元二次方程，然后借助根与系数的关系，并结合题设条件建立有关参变量的等量关系．24．（1）221(84x y x +=≠±；（2）证明见解析，()3,0-.【分析】（1）首先设点(),P x y ，利用12PA PB k k ⋅=-，转化为关于,x y 的方程；（2）方法一，首先由椭圆的对称性可知定点必在x 轴上，设:2MN x my =-，与椭圆方程联立，由根与系数的关系得到()1212my y y y =-+，并求出直线ND 的方程，求与x 轴的交点；方法二，直线:2MN x my =-与椭圆方程联立后，利用求根公式求得两个交点的纵坐标，再代入直线ND 的方程，化简，求定点的坐标. 【详解】（1）设(),P x y ，由题意得：12PA PB k k ⋅=-12=-，化简得22184x y +=．又x ≠±，∴点P的轨迹方程为221(84x y x +=≠±．（2）方法一：由椭圆的对称性知，直线ND 过的定点必在x 轴上， 由题意得直线MN 的斜率不为0，设:2MN x my =-，与22184x y +=联立消去x 得：()222440m y my +--=， ()23210m ∆=+>恒成立，设()11,M x y ，()22,N x y ，则()14,D y -，12242m y y m +=+，12242y y m -=+， ∴()1212my y y y =-+，2112:(4)4y y ND y x y x -=+++，令0y =， ∴()()12122121424y x y my x y y y y +++=-=---()1211212121221y y y my y y y y y y -+++=-=-=--，3x =-，∴直线ND 过定点()3,0-．方法二：由题意可得直线MN 的斜率不为0，设:2MN x my =-，与22184x y +=联立消去x 得：()222440m y my +--=， ()23210m ∆=+>恒成立，设()11,M x y ，()22,N x y ，则()14,D y -，12242m y y m +=+，12242y y m -=+，()12422m y m -=+，()22422m y m +=+， ()2112121122(4)2:(4)42y y x my y y y y ND y x y x my -+++-=++=++2244)2222m x m m m my -+++++=+2222(4)222x m m my +-++==+∴3x =-时0y =， ∴直线ND 过定点()3,0-. 【点睛】关键点点睛：本题考查椭圆中直线过定点问题，第一个关键是首先判断定点在x 轴上，方法一的关键是利用根与系数的关系得到()1212my y y y =-+，再代回直线方程求交点，方法二的关键是变形，化简.25．（1）22121x y +=；（2）证明见解析，（-2,0）.【分析】（1）根据离心率为2，点P 是以坐标原点O 为圆心的单位圆上的一点，且120PF PF ⋅=,可用待定系数法求椭圆的标准方程;（2）先用设而不求法表示出1212,x x x x +，然后分析得到110MF NF k k +=，代入，求出2m k =，即可证明直线过定点（-2，0）. 【详解】(1)设椭圆的标准方程为()22221,,x y P x y a b+=由题意可得2222221(,)(,)0c a x y x c y x c y b c a ⎧=⎪⎪⎪+=⎨⎪-⋅+=⎪+=⎪⎩解得：222211a b c ⎧=⎪=⎨⎪=⎩即椭圆C 的标准方程：22121x y +=.(2)设直线l ：1122,(,),(,)y kx m M x y N x y =+ 则1111221122,1111MF NF y kx m y kx mk k x x x x ++====++++ 有22121x y y kx m ⎧+=⎪⎨⎪=+⎩，消去 y 得：222(12)4220k x mkx m +++-=， 所以2221222122168(1)(12)04122212k m m k mk x x k m x x k ⎧⎪∆=--+>⎪-⎪+=⎨+⎪⎪-=⎪+⎩因为x 轴上任意一点到直线1MF 与1NF 的距离均相等， 所以x 轴为直线1MF 与1NF 的角平分线， 所以111212011MF NF kx m kx mk k x x +++=+=++，即 12122()()20kx x m k x x m ++++= 所以2222242()201212m mkk m k m k k--+++=++ 整理化简得：2m k =即直线l ：2(2)y kx m kx k k x =+=+=+ 故直线恒过定点（-2,0）. 【点睛】（1）待定系数法可以求二次曲线的标准方程；（2）"设而不求"是一种在解析几何中常见的解题方法，可以解决直线与二次曲线相交的问题.26．（1）2214x y +=；（2）定值为1，证明见解析【分析】（1）根据题意可得2a =，c =222a b c =+即可求解.（2）设1122(,),(,)M x y N x y ，且直线MN 的方程为：x my t =+，由题意可得14OM ON k k ⋅=-，联立直线MN 和椭圆方程，利用韦达定理可得2224t m =+，再由121||||2S t y y =-，化简整理即可求解.【详解】（1）由题意可得222242a c a b c =⎧⎪=⎨⎪=+⎩解得1b =，∴椭圆C 的标准方程为2214xy +=（2）证明：设1122(,),(,)M x y N x y ，直线MN 的方程为：x my t =+ 由1//,//,,4AP BP AP OM BP ON k k ⋅=-得14OM ON k k ⋅=- 即121214y y x x ⋅=-， 联立直线MN 和椭圆方程：2214x my tx y =+⎧⎪⎨+=⎪⎩，。

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》测试题(包含答案解析)

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》测试题(包含答案解析)

一、选择题1．已知斜率为16的直线l 与双曲线22221(0,0)x y C a b a b-=>>:相交于B 、D 两点，且BD 的中点为(1,3)M ，则C 的离心率为（ ）A ．2B C ．3 D 2．已知双曲线()222210,0x y a b a b-=>>的一条渐近线与圆()2239x y -+=相交于A 、B 两点，若2AB =，则该双曲线的离心率为（ ）A ．5B ．2C ．3D ．43．过抛物线()2:20C y px p =>的焦点F 且倾斜角为锐角的直线l 与C 交于,A B 两点，过线段AB 的中点N 且垂直于l 的直线与C 的准线交于点M ，若AB =，则直线l 的倾斜角为（ ） A ．15︒B ．30C ．45︒D ．60︒4．设抛物线2:4C y x =的焦点为F ，M 为抛物线上异于顶点的一点，且M 在直线1x =-上的射影为N ，若MNF 的垂心在抛物线C 上，则MNF 的面积为（ ）A ．1B ．2C ．3D ．45．已知点P 是抛物线22y x =上的一个动点，则点P 到点D ⎛⎝的距离与点P 到y 轴的距离之和的最小值为（ ） A ．2B ．52C ．3D ．726．已知圆2221:(3)(7)C x y a a ++=>和222:(3)1C x y -+=，动圆M 与圆1C ，圆2C 均相切，P 是12MC C 的内心，且12123PMC PMC PC C S SS+=，则a 的值为（ ）A ．9B ．11C ．17D ．197．顶点在原点，经过点()，且以坐标轴为轴的抛物线的标准方程是（ ）A ．2y =或212=-x y B ．2y =-或212=-x yC ．2y =或212x y =D ．2y =-或212x y =8．已知过双曲线()2222:1,0x y C a b a b-=>的左焦点F 作圆222x y a +=的切线FT ，交双曲线右支于点P ，点P 到x 轴的距离恰好为34b ，则双曲线离心率为（ ）A ．273+ B ．273+ C ．53D ．29．已知直线l 的方程为1y kx =-，双曲线C 的方程为221x y -=.若直线l 与双曲线C 的右支相交于不同的两点，则实数k 的取值范围是（ ） A ．(2,2)B ．2)C ．[2,2]D ．2)10．已知椭圆2221(02)4x y b b+=<<，直线1x y +=与椭圆交于,P Q 两点，若OP OQ ⊥，则椭圆的离心率为（ ）A ．67B 7C 42D ．7711．已知抛物线24x y =的焦点为F ，准线为l ，M 是x 轴正半轴上的一点，线段FM 交抛物线于点A ，过A 作l 的垂线，垂足为B .若BF BM ⊥，则FM =（ ） A ．52B ．3C ．72D ．412．已知过点(,0)A a 的直线与抛物线22(0)y px p =>交于M.N 两点，若有且仅有一个实数a ，使得16OM ON ⋅=-成立，则a 的值为（ ） A ．4-B ．2C ．4D ．8二、填空题13．已知ABC 中，()1,0B -、()1,0C ，1k 、2k 分别是直线AB 和AC 的斜率.关于点A 有如下四个命题：①若A 是双曲线2212y x -=上的点，则122k k ⋅=；②若122k k ⋅=-，则A 是椭圆2212x y +=上的点；③若121k k ，则A 是圆221x y +=上的点；④若2AB AC =，则A 点的轨迹是圆. 其中所有真命题的序号是__________．14．过双曲线M ：221 3xy-=的右焦点F作圆C：221(1)2x y++=的切线，此切线与M的右支交于A，B两点，则||AB=___________.15．设1F，2F为双曲线()2222:10,0x yC a ba b-=>>的左､右焦点，过2F的直线l交双曲线C的右支于A､B两点，且12AF AF⋅=，2212AFBF=，则双曲线C的离心率为___________.16．在“中国花灯之乡”——广东省兴宁市，流传600多年的兴宁花灯历史文化积淀浓厚，集艺术性、观赏性、民俗性于一体，扎花灯是中国一门传统手艺，逢年过节时常常在大街小巷看到各式各样的美丽花灯，一大批中小学生花灯爱好者积极参与制作花灯．现有一个花灯，它外围轮廓是由两个形状完全相同的抛物线绕着其对称轴旋转而来（如图），花灯的下顶点为A，上顶点为B，8AB=分米，在它的内部放有一个半径为1分米的球形灯泡，球心C在轴AB上，且2AC=分米．已知球形灯泡的球心C到四周轮廓上的点的最短距离是在下顶点A处取到，建立适当的坐标系可得其中一支抛物线的方程为2(0)y ax a=>，则实数a的取值范围是_______17．已知椭圆222:1(06)6x yG bb+=<<的两个焦点分别为1F和2F，短轴的两个端点分别为1B和2B，点P在椭圆G上，且满足1212PB PB PF PF+=+．当b变化时，给出下列三个命题：①点P的轨迹关于y轴对称；②存在b使得椭圆G上满足条件的点P仅有两个；③||OP的最小值为2，其中，所有正确命题的序号是___________．18．椭圆22221(0)x ya ba b+=>>上一点A关于原点的对称点为B，F为椭圆的右焦点，若AF BF ⊥，设ABF α∠=，且,124ππα⎡⎤∈⎢⎥⎣⎦，则该椭圆离心率的最大值为______． 19．已知抛物线C : y 2=2px (p >0)，直线l ：y = 2x + b 经过抛物线C 的焦点，且与C 相交于A 、B 两点．若|AB | = 5，则p = ___．20．设椭圆()2222:10x y C a b a b +=>>的左右焦点为12F F ，，过2F 作x 轴的垂线与C 交于A B ，两点，若1ABF 是等边三角形，则椭圆C 的离心率等于________.三、解答题21．已知抛物线2:2(0)C y px p =>的焦点为F ，准线为l ，若点P 在C 上，点E 在l 上，且PEF 是边长为4的正三角形． （1）求C 的方程；（2）过F 作直线m ，交抛物线C 于A ，B 两点，若直线AB 中点的纵坐标为1-，求直线m 的方程．22．已知椭圆22221(0)x y E a b a b+=>>：的左右焦点分别为1F ，2F ，离心率为12，直线():0l y kx t t =+>与以12F F 为直径的圆相切于点P ，当1k =时，12PF F △的面积为； （1）求E 的方程；（2）直线l 与椭圆交于A ，B 两点，设0k >时，线段AB 的垂直平分线与x 轴交于点(),0M m ，求m 的取值范围.23．已知椭圆()2222:10x y C a b a b+=>>左右焦点分别为()12(,0),,0F c F c -，点Р为椭圆C 上一点，满足1290F PF ∠=︒，且12F PF △的面积为2c .（1）求椭圆C 的离心率； （2）已知直线()122y x =-与椭圆C 交于,M N 两点，点Q 坐标为()2,0，若3MQ NQ =，求椭圆C 的方程.24．在平面直角坐标系xOy 中，已知A ，B 两点是椭圆22:19x E y +=的左、右顶点，P 为直线6x =上的动点，PA 与椭圆E 的另一交点为Q ，当点P 不为点()6,0时，过P作直线PH QB ⊥，垂足为H . （1）证明：直线PH 过定点M ；（2）过（1）中的定点M 作斜率为k 的直线与椭圆E 交于C ，D 两点，设直线AC ，AD 的斜率分别为1k ，2k ，试判断()12k k k ⋅+是否为定值？如果是定值，求出定值.25．已知椭圆2222:1(0)x y E a b a b +=>>的左，右顶点分别为,A B，离心率2e =，椭圆E 上任意一点M 到两个焦点1F ，2F 的距离之积的最大值为4.（1）求椭圆E 的方程；（2）已知点P 为直线l ：4x =上的任意一点，直线PA 、PB 与椭圆E 分别交于两点C 、D （不同于A 、B 两点），求证：直线CD 经过定点，并求出该定点的坐标，26．（1）已知椭圆2222:1(0)x y E a b a b+=>>的焦距为1F 、2F 为左、右焦点，M 为椭圆E 上一点，且123F MF π∠=，12F MF S =△，求椭圆E 的方程． （2）过点()()00P m m a <<,的直线交椭圆E 于A 、B 两点，交直线4x m=于点M ，设MA AP λ=，MB BP μ=，求λμ+的值．【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】设()()1122,,B x y D x y 、，用“点差法”表示出a 、b 的关系，即可求出离心率 【详解】设()()1122,,B x y D x y 、,则22112222222211x y a b x y a b ⎧-=⎪⎪⎨⎪-=⎪⎩， 两式作差得：22221212220x x y y a b ---=，整理得：()()()()2121221212y y y y b a x x x x +-=+-BD 的中点为(1,3)M ，且直线l 的斜率为16 ，代入有：22611262b a =⨯=即22212c a a -=，解得62ce a . 故选：D【点睛】求椭圆（双曲线）离心率的一般思路：根据题目的条件，找到a 、b 、c 的关系，消去b ，构造离心率e 的方程或（不等式）即可求出离心率．2．C解析：C 【分析】设双曲线的渐近线方程为y kx =，其中bk a=±，利用勾股定理可求得k 的值，即可求得b a，再由双曲线的离心率公式e =即可求得双曲线的离心率. 【详解】设双曲线的渐近线方程为y kx =，其中bk a=±， 圆()2239x y -+=的圆心为()3,0C ，半径为3r =，圆心C 到直线y kx =的距离为d =，2AB =，由勾股定理可得2222AB r d ⎛⎫=+ ⎪⎝⎭，即2219+=，解得k =±ba∴=，因此，该双曲线的离心率为3c e a =====. 故选：C. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.3．D解析：D 【分析】设直线l 的斜率为k (0k >)，直线方程为()2y k x π=-，1122(,),(,)A x y B x y ，代入抛物线方程应用韦达定理得12x x +，12AB x x p =++， 求出AB 中点N 的坐标，写出MN的方程，由MN =MN ，然后由己知条件可求得斜率k ，得倾斜角．【详解】 由题意(,0)2p F ，设直线l 的斜率为k (0k >)，直线方程为()2y k x π=-，1122(,),(,)A x y B x y ，由22()2y pxp y k x ⎧=⎪⎨=-⎪⎩得22222(2)04k p k x p k x -++=， 2122(2)p k x x k++=，2124p x x =， 221222(2)2(1)++=++=+=p k p k AB x x p p k k， 2122(2)22N x x p k x k ++==，22()22N N p p y k x k =-=，即222(2)2,22p k p N k k ⎛⎫+ ⎪⎝⎭， 直线MN 的方程为1()N N y y x x k-=--，MN ===，∵AB =，∴222(1)p k k += 整理得23k =，∵0k >，∴k =∴倾斜角为60︒．故选：D ． 【点睛】本题考查直线与抛物线相交问题，解题方法是设而不求的思想方法，设交点坐标，设直线方程代入抛物线方程应用韦达定理，求得中点坐标及焦点弦长，写出直线l 垂线方程，求得MN ，然后由已知条件求得结论．4．B解析：B 【分析】设点200,4y M y ⎛⎫⎪⎝⎭，则点()01,N y -，求出MNF 的垂心H 的坐标，再由MH FN ⊥可求得0y 的值，进而可求得MNF 的面积. 【详解】设点200,4y M y ⎛⎫⎪⎝⎭，则点()01,N y -，设点M 在第一象限， 抛物线C 的焦点为()1,0F ，设MNF 的垂心为H ， 由于FHMN ⊥，则点H 的横坐标为1，可得点()1,2H ，MH FN ⊥，则0HM FN ⋅=，2001,24y HM y ⎛⎫=-- ⎪⎝⎭，()02,FN y =-，()()22200000012122220422y y HM FN y y y y ⎛⎫⋅=--+-=-+=-= ⎪⎝⎭，解得02y =，所以，点M 的坐标为()1,2，所以，2MN =，12222MNF S =⨯⨯=△. 故选：B. 【点睛】关键点点睛：解决本题的关键在于利用已知条件求出点M 的坐标，本题特殊的地方在于MN y ⊥轴，可得出垂心与焦点的连线垂直于x 轴，再结合垂心在抛物线求出垂心的坐标.5．B解析：B 【分析】利用抛物线的定义，把P 到y 轴的距离转化为1||2PF -,利用几何法求最值 【详解】抛物线22y x =的焦点1,02F ⎛⎫ ⎪⎝⎭,准线1:2l x =-，如图示：过P 作PP 1⊥y 轴于P 1,作PP 2⊥l于P 2,则211||||2PP PP -=所以点P 到点D ⎛ ⎝的距离与点P 到y 轴的距离之和为 1211||||||||||||22PD PP PD PP PD PF +=+-=+- 由图示，易知，当P 落在Q 时，DPF 三点共线，||||||PD PF DF +=, 其他位置，都有||||||PD PF DF +>所以点P 到点D ⎛⎝的距离与点P 到y 轴的距离之和的最小值为：1115||||||||||222PD PP PD PF DF +=+-≥-== 当D 、P 、F 三点共线时取最小值. 故选：B 【点睛】解析几何问题解题的关键：解析几何归根结底还是几何，根据题意画出图形，借助于图形寻找几何关系可以简化运算．6．C解析：C 【分析】先判断出圆1C 与2C 内含，根据条件可得动圆M 与圆1C ，圆2C 均相切，从而得出121216MC MC a C C +=+>=，即动点M 的轨迹是以12,C C 为焦点，长轴为1a +的椭圆，又设12MC C 的内切圆的半径为r ' ，由12123PMC PMC PC C SSS+=，有12121113222MC r MC r C C r ''+⨯=⨯⨯⨯'⨯，从而得出答案. 【详解】由圆2221:(3)(7)C x y a a ++=>和222:(3)1C x y -+=，可得圆1C 的圆心()13,0C -，半径为1r a =，圆2C 的圆心()23,0C ，半径为21r = 由121261C C a r r =<-=-所以圆1C 与2C 内含，由动圆M 与圆1C ，圆2C 均相切. 所以动圆M 与圆1C 内切，与圆2C 外切，设动圆M 的半径为R 则11MC r R a R =-=-，221MC r R R =+=+ 所以121216MC MC a C C +=+>=所以动点M 的轨迹是以12,C C 为焦点，长轴为1a +的椭圆，设其方程为22221(0)x y m n m n+=>>所以12a m +=，设22c m n =-，则3c = 由P 是12MC C 的内心，设12MC C 的内切圆的半径为r ' 由12123PMC PMC PC C SSS+=，有12121113222MC r MC r C C r ''+⨯=⨯⨯⨯'⨯ 即1212318MC MC C C +==，又由椭圆的定义可得121MC MC a +=+ 所以118a +=，则17a = 故选：C 【点睛】本题考查圆与圆的位置关系，考查根据圆与圆的相切求动圆圆心的轨迹，考查椭圆的定义的应用，解答本题的关键的由条件得出圆1C 与2C 内含，由动圆M 与圆1C ，圆2C 均相切，进一步由条件得出121216MC MC a C C +=+>=，即得出动点M 的轨迹，属于中档题.7．D解析：D 【分析】设出抛物线方程为22y mx =或22x ny =，代入点的坐标求出参数值可得．【详解】设抛物线方程为22y mx =，则262(m =⋅，m =-2y =-，或设方程为22x ny =，则2(26n =⨯，14n =，方程为212x y =．所以抛物线方程为2y =-或212x y =． 故选：D ． 【点睛】关键点点睛：抛物线的标准方程有四种形式，在不确定焦点位置（或开口方向时），需要分类讨论．象本题在抛物线过一点的坐标，则需要考虑焦点在x 轴和y 轴两种情况，焦点在x 轴上时可以直接设方程为2y mx =，代入点的坐标求出参数值，不必考虑焦点是在x轴正半轴还是在负半轴，焦点在y 轴也类似求解．8．A解析：A 【分析】由P 点到x 轴距离（即纵坐标）求出其横坐标，写出直线FP 的方程，然后由原点到切线的距离等于半径可得,,a b c 的等式，变形后可得离心率． 【详解】如图P 在第一象限，因为点P 到x 轴的距离恰好为34b ，即34P y b =，代入双曲线方程得229116P x a -=，解得54P x a =，所以53,44P a b ⎛⎫ ⎪⎝⎭， (,0)F c -，直线FP 方程为34()54b y xc a c =++，化简得3(54)30bx a c y bc -++=， 又直线FP 与圆222x y a +=相切，a =，345bc a a c=+人，变形为4293440160e e e ---=，22(342)(348)0e e e e ++--=，因为1e >，所以23420e e ++>，所以23480e e --=，e =去）． 故选：A ． 【点睛】思路点睛：本题考查求双曲线的离心率，解题关键是找到关于,,a b c 的齐次等式，本题中由点P 到x 轴的距离恰好为34b ，得出P 点坐标，从而可得直线FP 方程，由圆心到切线的距离等于半径可得所要关系式，从而转化为离心率e 的方程，解之可得．9．D解析：D 【分析】联立直线方程1y kx =-和双曲线方程221x y -=，化为22(12)20k x kx --=+，由于直线1y kx =-与双曲线221x y -=的右支交于不同两点，可得210k -≠，由2248(1)0k k ∆=+->，1k <，解得即可【详解】解：联立直线方程1y kx =-和双曲线方程221x y -=，化为22(12)20k x kx --=+， 因为直线1y kx =-与双曲线221x y -=的右支交于不同两点， 所以210k -≠，且2248(1)0k k ∆=+->，1k <，解得1k <<，所以实数k的取值范围为， 故选：D 【点睛】关键点点睛：此题考查直线与双曲线的位置关系，解题的关键是直线方程和双曲线方程联立方程组，消元后结合题意可得2248(1)0k k ∆=+->，1k <，从而可得答案10．C解析：C 【分析】设1122(,),(,)P x y Q x y ，把直线1x y +=与椭圆2221(02)4x yb b+=<<，联立，根据OP OQ ⊥计算出b ，直接求出离心率.【详解】设1122(,),(,)P x y Q x y ，由222141x y b x y ⎧+=⎪⎨⎪+=⎩得222(4)8440b x x b +-+-=，所以12221228=444·=4x x b b x x b ⎧+⎪⎪+⎨-⎪⎪+⎩∵OP OQ ⊥，∴12121212=2()10OP OQ x x y y x x x x +=-++=，解得247b =. 224442747c e a-∴=== 故选：C 【点睛】求椭圆（双曲线）离心率的一般思路：根据题目的条件，找到a 、b 、c 的关系，消去b ，构造离心率e 的方程或（不等式）即可求出离心率．11．B解析：B 【分析】先利用方程得求得焦点坐标和准线方程，设点(,0)M m ，()00,A x y ，再利用点()00,A x y 在抛物线与直线上列方程，解出0,x m ，最后利用距离公式计算FM 即可. 【详解】如图所示，抛物线24x y =中，()0,1F ，:1l y =-，依题意设(,0)M m ，()00,A x y ，00x >，则2004x y =，故200,4x A x ⎛⎫⎪⎝⎭，()0,1B x -，因为BF BM ⊥，即BF BM ⊥，而()()00,2,,1BF x BM m x =-=-， 所以()0020BF BM x m x ⋅=-+=，直线:11x y FM m +=，A 在直线上，故200:14x x FM m +=，即02044x m x =-，代入上式即得000024420x x x x ⎛⎫-+= ⎪⎝-⎭，化简整理得4200280x x +-=，即()()2200240x x -+=， 故202x =，而00x >，故0x =()24m ==-M ，所以FM =3=.故选：B. 【点睛】本题解题关键在于利用点()00,A x y 既在抛物线上，又在直线上，构建关系式，求解出点M 即突破难点. 12．C解析：C 【分析】设出直线方程与抛物线方程联立，利用韦达定理得出1212,y y y y +及12x x ，把16OM ON ⋅=-用坐标表示代入上述值结合已知条件可得答案.【详解】设直线MN 的直线方程为x ty a =+，1122(,),(,)M x y N x y ， 由题意得22x ty a y px=+⎧⎨=⎩，整理得2220y pty pa --=， 所以12122,2y y pt y y pa +==-，()()()2212121212x x ty a ty a t y y at y y a =++=+++ ()()2222t ap at pt a =-++，因为16OM ON ⋅=-，所以121216x x y y +=-， 所以()()2222216tpa at pt a pa -++-=-，22160a pa -+=，因为方程有且仅有一个实数a ，所以()22640p ∆=-=，解得4p =，或4p =-（舍去）， 故选：C.【点睛】本题考查了直线和抛物线的位置关系，关键点是利用韦达定理求出1212,y y y y +及12x x ，然后16OM ON ⋅=-坐标表示列出等式，考查了学生分析问题、解决问题的能力.二、填空题13．①③【分析】设点可得出结合斜率公式可判断A 选项的正误；求出动点的轨迹方程可判断②的正误；根据求出点的轨迹方程可判断③的正误；由求出点的轨迹方程可判断④的正误【详解】设动点的坐标为对于①由于点是双曲线解析：①③ 【分析】设点(),A x y ，可得出2212y x =+，结合斜率公式可判断A 选项的正误；求出动点A 的轨迹方程，可判断②的正误；根据121k k ，求出点A 的轨迹方程，可判断③的正误；由2AB AC =求出点A 的轨迹方程，可判断④的正误. 【详解】设动点A 的坐标为(),A x y .对于①，由于点A 是双曲线2212y x -=上的点，则2212y x =+，所以，22122221112y y y y k k y x x x =⋅===+--，①正确；对于②，21222111y y y k k x x x =⋅==-+--，化简可得2212y x +=，②错误；对于③，21221111y y y k k x x x =⋅==-+--，化简可得221x y +=，③正确；对于④，由2AB AC ==化简可得2251639x y ⎛⎫-+= ⎪⎝⎭， 当点A 为圆2251639x y ⎛⎫-+= ⎪⎝⎭与x 轴的交点时，A 、B 、C 三点无法构成三角形，④错误.故答案为：①③. 【点睛】方法点睛：求动点的轨迹方程有如下几种方法：（1）直译法：直接将条件翻译成等式，整理化简后即得动点的轨迹方程；（2）定义法：如果能确定动点的轨迹满足某种已知曲线的定义，则可利用曲线的定义写出方程；（3）相关点法：用动点Q 的坐标x 、y 表示相关点P 的坐标0x 、0y ，然后代入点P 的坐标()00,x y 所满足的曲线方程，整理化简可得出动点Q 的轨迹方程；（4）参数法：当动点坐标x 、y 之间的直接关系难以找到时，往往先寻找x 、y 与某一参数t 得到方程，即为动点的轨迹方程；（5）交轨法：将两动曲线方程中的参数消去，得到不含参数的方程，即为两动曲线交点的轨迹方程.14．【分析】首先设出直线利用直线与圆相切求直线方程再利用弦长公式求弦长【详解】因为直线过双曲线的右焦点且与圆相切所以直线的斜率存在设直线方程为()由直线与圆相切知解得或当时双曲线的一条渐近线的斜率是该直解析：【分析】首先设出直线，利用直线与圆相切，求直线方程，再利用弦长公式求弦长AB . 【详解】因为直线过双曲线的右焦点且与圆相切，所以直线的斜率存在，设直线方程为0y k -=(2x -)2=，解得1k =或17k =，当17k =时，双曲线的一条渐近线的斜率是3，17<，该直线不与双曲线右支相交于两点，故舍去；所以直线方程为2y x =-，联立双曲线方程，消元得2212150x x -+=.设()11,A x y ，()22,B x y ，则126x x +=，12152x x =，所以12||AB x =-===.故答案为：【点睛】易错点点睛：利用直线与圆相切，得到两个斜率1k =或17k =，需舍去一个，否则出现增根.15．【分析】利用双曲线的定义分别表示再利用勾股定义和双曲线的定义建立等量关系求双曲线的离心率【详解】设根据双曲线的定义可知即得得中即得根据双曲线的定义即得所以得故答案为：【点睛】方法点睛：本题考查直线与解析：3【分析】利用双曲线的定义分别表示1212,,,AF AF BF BF ，再利用勾股定义和双曲线的定义建立等量关系，求双曲线的离心率. 【详解】设2AF x =，22BF x =，1AF y =，根据双曲线的定义可知1212AF AF BF BF -=-， 即12y x BF x -=-，得1BF y x =+，120AF AF ⋅=，12AF AF ∴⊥，()()2223y x y x ∴+=+，得4y x =，12Rt AF F △中，222124AF AF c +=，即22174x c =，得x =，根据双曲线的定义122AF AF a -=，即32x a =，得23x a =，所以2173a c =，得3c e a ==.【点睛】方法点睛：本题考查直线与双曲线的位置关系的综合问题，考查学生的转化和计算能力，属于中档题型，求离心率是圆锥曲线常考题型，涉及的方法包含1.根据,,a b c 直接求，2.根据条件建立关于,a c 的齐次方程求解，3.根据几何关系找到,,a b c 的等量关系求解.16．【分析】设出抛物线上任意一点的坐标根据两点间的距离公式求得球心到四周轮廓上的点的距离根据最短距离是在下顶点处取到结合二次函数的性质求得的取值范围【详解】建立如图所示直角坐标系其中为坐标原点得抛物线方解析：10,4⎛⎤⎥⎝⎦【分析】设出抛物线上任意一点的坐标，根据两点间的距离公式求得球心C 到四周轮廓上的点的距离，根据最短距离是在下顶点A 处取到，结合二次函数的性质，求得a 的取值范围. 【详解】建立如图所示直角坐标系，其中A 为坐标原点，得抛物线方程2(0)y axa =>，(0,2)C ，设抛物线上任一点的坐标为200(,)x ax ，由两点距离公式得()22224200002(14)4=+-=+-+d x ax a x a x ，令20(0)=≥t x t ，则22(14)4(0)=+-+≥y a t a t t 的开口向上，对称轴为2412-=a t a ， 当对称轴24102a a -≤时，在0t =处取得最小值，此时d 的最小值为4=2=d ， 当对称轴24102a a ->时，最小值在对称轴处取得，即d 的最小值小于2，不符合题意. 故由24102a a -≤，解得10,4a ⎛⎤∈ ⎥⎝⎦. 故答案为：10,4⎛⎤ ⎥⎝⎦【点睛】关于平面图形或者空间几何体中一些边长或者距离的最值计算一般转化为函数问题，可以通过二次函数、反比例函数的性质求解最值，或者有时可以利用基本不等式，较难的问题则需要通过导数判断单调性从而求出最值.17．①③【分析】运用椭圆的定义可得也在椭圆上分别画出两个椭圆的图形即可判断①正确；通过的变化可得②不正确；由图象可得当的横坐标和纵坐标的绝对值相等时的值取得最小即可判断③【详解】解：椭圆的两个焦点分别为解析：①③ 【分析】运用椭圆的定义可得P 也在椭圆222166y x b+=-上，分别画出两个椭圆的图形，即可判断①正确；通过b 的变化，可得②不正确；由图象可得当P 的横坐标和纵坐标的绝对值相等时，||OP 的值取得最小，即可判断③．【详解】解：椭圆222:1(06)6x y G b b+=<<的两个焦点分别为21(6F b -，0)和22(6F b --，0)，短轴的两个端点分别为1(0,)B b -和2(0,)B b ，设(,)P x y ，点P 在椭圆G 上，且满足1212||||||||PB PB PF PF +=+， 由椭圆定义可得，12||||2262PB PB a b +==>，即有P 在椭圆222166y x b+=-上． 对于①，将x 换为x -方程不变，则点P 的轨迹关于y 轴对称， 故①正确；对于②，由图象可得轨迹关于x ，y 轴对称，且06b <<，则椭圆G 上满足条件的点P 有4个，不存在b 使得椭圆G 上满足条件的点P 仅有两个，故②不正确；对于③，点P 靠近坐标轴时(0b →或6)b →，||OP 越大，点P 远离坐标轴时，||OP 越小，所以226b b -=，即23b =时，取得最小值，此时22:163x y G +=，与22163y x += 两方程相加得22222222x y x y +=⇒+=，即||OP 的最小值为 2，故③正确．故答案为：①③．【点睛】本题考查椭圆的对称性及由椭圆上的点到焦点的距离之和等于到短轴的顶点距离之和可得另一个椭圆，及到定点距离的最值的判断．18．【分析】设左焦点为根据椭圆的定义有且O 是直角三角形斜边的中点所以离心率由角的范围可求得离心率的最大值【详解】因为关于原点对称所以B 也在椭圆上设左焦点为根据椭圆的定义：又因为所以O 是直角三角形斜边的中解析：3【分析】设左焦点为F '，根据椭圆的定义有，||||2AF BF a +=，且O 是直角三角形ABF 斜边的中点，所以||2,||2sin ,||2cos AB c AF c BF c αα===，离心率11sin cos 4c a πααα==+⎛⎫+ ⎪⎝⎭，由角的范围可求得离心率的最大值. 【详解】因为,B A 关于原点对称，所以B 也在椭圆上，设左焦点为F '，根据椭圆的定义：||2AF AF a '+=，又因为||BF AF '=，所以||||2AF BF a +=，O 是直角三角形ABF 斜边的中点，所以||2,||2sin ,||2cos AB c AF c BF c αα===，所以2(sin cos )2c a αα+=，所以11sin cos 4c a πααα==+⎛⎫+ ⎪⎝⎭， 由于,124ππα⎡⎤∈⎢⎥⎣⎦，所以当12πα=时，离心率的最大值为：3,故答案为：3. 【点睛】关键点点睛：求椭圆的离心率关键在于由椭圆的定义，善于利用平面几何中的边、角关系建立关于,,a b c 的等式或不等式.19．2【分析】法1：首先利用直线过焦点得再利用直线与抛物线方程联立利用根与系数的关系表示计算求得；法2：由已知求得的值再利用弦长公式求的值【详解】法1：由题意知直线即直线经过抛物线的焦点即直线的方程为设解析：2 【分析】法1：首先利用直线过焦点，得b p =-，再利用直线与抛物线方程联立，利用根与系数的关系表示12AB x x p =++，计算求得p ；法2：由已知tan 2θ=，求得sin θ的值，再利用弦长公式22sin pAB θ=，求p 的值. 【详解】法1：由题意知，直线:2l y x b =+，即22b y x ⎛⎫=+⎪⎝⎭．直线l 经过抛物线()2:20C y px p =>的焦点，22b p∴-=，即b p =-．∴直线l 的方程为2y x p =-． 设()11,A x y 、()22,B x y ，联立222y x p y px=-⎧⎨=⎩，消去y 整理可得22460x px p -+=，由韦达定理得1232p x x +=，又5AB =，12552x p p x ∴++==，则2p =.法2：设直线的切斜角为θ，则tan 2k θ==，得sin θ=，∴22225sin p pAB θ===，得2p =.故答案为：2 【点睛】结论点睛：当直线过抛物线的焦点时，与抛物线交于,A B 两点，AB 称为焦点弦长，有如下的性质：直线与抛物线交于()()1122,,,A x y B x y ，①221212,4p y y p x x =-=；②12AB x x p =++；③11AF BF +为定值2p ；④弦长22sin p AB θ= （θ为直线AB 的倾斜角）；⑤以AB 为直径的圆与准线相切；⑥焦点F 对,A B 在准线上射影的张角为90.20．【分析】利用已知条件推出的关系然后求解椭圆的离心率即可【详解】解：椭圆的左右焦点为过作轴的垂线与交于两点若是等边三角形如图：可得可得即可得解得故答案为：【点睛】本题考查椭圆的简单性质的应用离心率的求解析：3【分析】利用已知条件．推出a 、b 、c 的关系，然后求解椭圆的离心率即可． 【详解】解：椭圆2222:1(0)x y C a b a b+=>>的左右焦点为1F ，2F ，过2F 作x 轴的垂线与C 交于A ，B 两点，若1ABF 是等边三角形，如图：可得2|c AB =，2(,0)F c ，可得22||b AB a=，即2222ac ==，220e +=，(0,1)e ∈解得3 3e=．故答案为：33．【点睛】本题考查椭圆的简单性质的应用，离心率的求法，考查计算能力，属于中档题．三、解答题21．（1）24y x=；（2）220x y+-=.【分析】（1）设l与x轴交于点D，根据PEF是边长为4的正三角形．得到PE l⊥，60PEF EFD∠=∠=︒，然后由||cos60p DF EF==求解.(2)设()11,A x y，()22,B x y，根据点A，B在抛物线上，由21122244y xy x⎧=⎨=⎩，根据线段AB中点的纵坐标为1-，利用“点差法”求解.【详解】（1）因为PEF是边长为4的正三角形．则||||PE PF=，所以PE l⊥，设l与x轴交于点D，则60PEF EFD∠=∠=︒，||4EF=，所以||cos602p DF EF===所以抛物线的方程为24y x=．（2）由（1）得抛物线C的方程为24y x=，焦点(1,0)F，设A，B两点的坐标分别为()11,A x y，()22,B x y，由21122244y xy x⎧=⎨=⎩，得()121212124y yx xx x y y-=≠-+，因为线段AB中点的纵坐标为1-，所以直线m 的斜率21442(1)2AB k y y ==-+-⨯=， 所以直线m 的方程为02(1)y x -=--， 即220x y +-=． 【点睛】方法点睛：解决直线与曲线的位置关系的相关问题，往往先把直线方程与曲线方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题．涉及弦中点的问题常常用“点差法”解决，往往会更简单．22．（1）22143x y +=；（2）1,04⎛⎫- ⎪⎝⎭.【分析】（1）由直线l 斜率为1且圆相切，得14POF π∠=(O 为原点)，从而12PF F △的面积可用c 表示出来，从而求得c ，再由离心率求得a ，然后可得b ，得椭圆方程；（2）设()11,A x y ，()22,B x y ，将直线方程代入椭圆方程应用韦达定理求得12x x +，从而可得AB 中点坐标，写出AB 中垂线方程，令0y =可得m ，由直线与圆相切得,k t 关系，这样m 可化为一元函数，再用换元法可求得取值范围． 【详解】解：（1）设1(,0)F c -，2(,0)F c =，当1k =时，14POF π∠=(O 为原点)，从而1212222PF F Sc c =⋅⋅=， 从而解得1c =， 又离心率12c e a ==， 所以2a =，从而b =因此E 的方程为22143x y +=；（2）设()11,A x y ，()22,B x y ，将()0,0y kx t k t =+>>，代入椭圆方程22143x y +=，消去y ，得()2224384120k x ktx t +++-=，从而122843kt x x k -+=+，212241243t x x k -=+，① 设AB 的中点为()00,Q x y ，则02443kt x k -=+，02343ty k =+，从而AB 的中垂线方程为223144343t kt y x k k k -⎛⎫-=-- ⎪++⎝⎭，令0y =，解得243ktm k -=+， 由线l 与以12F F1=，即t =从而m ==2130,344n k ⎛⎫=∈ ⎪⎝⎭+，则m =由函数2314101623y n n n ⎛⎫=--+<< ⎪⎝⎭取值范围为()0,1， 得m 的取值范围为1,04⎛⎫- ⎪⎝⎭. 【点睛】关键点点睛：本题考查由离心率求椭圆方程，考查直线与椭圆相交中的范围问题．解题关键建立m 与参数的函数式，方法是：由直线方程代入椭圆方程应用韦达定理得弦中心坐标得弦垂直平分线方程，从而可求得m ，利用直线与圆相切得参数,k t 关系后可得所需要的函数式，换元后可求得取值范围． 23．（1）2；（2）答案见解析. 【分析】（1）利用椭圆定义122PF PF a +=和1290F PF ∠=︒求得2122PF PF b =，再根据12F PF △的面积为2c 求解；（2）椭圆方程2222x y a +=与直线1(2)2y x =-联立，由韦达定理得到2121244,36a y y y y -+=-=，再根据3MQ NQ =，分3MQ NQ =和3MQ NQ =-求解. 【详解】（1）由椭圆定义可得122PF PF a +=，① 又1290F PF ∠=，所以222124PF PF c +=，②①和②可得2122PF PF b ⋅=，所以12F PF △的面积为2b ，所以22b c =，即222a c =，所以椭圆C的离心率为2；（2）椭圆方程可化为2222x y a +=，与1(2)2y x =-联立可得： 226840y y a ++-=，由()2642440a ∆=-->可得243a >，设()()1122,,,M x y N x y ，所以2121244,36a y y y y -+=-=，③又直线1(2)2y x =-过点Q ，且3MQ NQ =，()112,MQ x y =--，()222,NQ x y =--.（i ）当3MQ NQ =时，即123y y =时，则122443y y y +==-，可得213y =-，则2212214336a y y y -===，可得2423a =>，所以椭圆C 的方程为2212x y +=；（ii ）当3MQ NQ =-，即123y y =-时，则122423y y y +=-=-，则223y =，可得22212224433336a y y y -⎛⎫=-=-⨯=-= ⎪⎝⎭，解得24123a =>，所以椭圆C 的方程为221126x y +=.【点睛】方法点睛：求椭圆的标准方程有两种方法：①定义法：根据椭圆的定义，确定2a 、2b 的值，结合焦点位置可写出椭圆方程； ②待定系数法：若焦点位置明确，则可设出椭圆的标准方程，结合已知条件求出a 、b ；若焦点位置不明确，则需要分焦点在x 轴上和y 轴上两种情况讨论，也可设椭圆的方程为()2210,0,Ax By A B A B +=>>≠．24．（1）证明见解析；（2）是，定值为112-. 【分析】（1）设()00 ,Q x y ，()()6,0P t t ≠，法一：根据椭圆方程求得19QA QB k k ⋅=-，根据9QA PA tk k ==，即可求得QB k ，根据PH QB ⊥，可求得PH k ，可得直线PH 的方程，即可得答案；法二：根据9AP QA tk k ==，可得直线AP 的方程，与椭圆联立，根据韦达定理，可得Q 点坐标，根据PH QB ⊥，可求得PH k ，可得直线PH 的方程，即可得答案；。

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》测试卷(包含答案解析)

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》测试卷(包含答案解析)

一、选择题1．光线从椭圆的一个焦点发出，被椭圆反射后会经过椭圆的另一个焦点；光线从双曲线的一个焦点发出，被双曲线反射后的反射光线等效于从另一个焦点射出，如图①，一个光学装置由有公共焦点1F 、2F 的椭圆Γ与双曲线Ω构成，现一光线从左焦点1F 发出，依次经Ω与Γ反射，又回到了点1F ，历时1t 秒；若将装置中的Ω去掉，如图②，此光线从点1F 发出，经Γ两次反射后又回到了点1F ，历时2t 秒；若218t t =，则Γ与Ω的离心率之比为（ ）A ．3:4B ．2:3C ．1:2D ．22．已知抛物线2:2C y px =的焦点为F ，过抛物线上两点A ，B 分别向抛物线C 的准线作垂线，垂足为M ，N ，且()95OBN OAM ABNM S S S +=梯形△△，当直线AB 经过点F 且点F 到抛物线C 准线的距离为4时，直线l 的斜率为（ ）A ．2±B ．22±C ．8±D ．23±3．已知点12,F F 是椭圆()222210x y a b a b+=>>的左右焦点，椭圆上存在不同两点,A B 使得122F A F B =，则椭圆的离心率的取值范围是（ ） A ．10,3⎛⎫ ⎪⎝⎭B ．10,2⎛⎫ ⎪⎝⎭C ．1,13⎛⎫ ⎪⎝⎭D ．1,12⎛⎫ ⎪⎝⎭4．设双曲线2222:1(0,0)x y C a b a b-=>>的左焦点为F ，直线250x y -=过点F 且与双曲线C 在第一象限的交点为P ，O 为坐标原点，||||OP OF =，则双曲线的离心率为（ ） A 2B 3C ．2D 55．斜率为1的直线l 经过抛物线24y x =的焦点F ，且与抛物线相交于A 、B 两点，则线段AB 的长为（ ）A ．42B ．62C ．82D ．86．已知椭圆222:14x y C b+=的右焦点为F ，O 为坐标原点，C 上有且只有一个点P 满足||||OF FP =，则b =（ ）A ．3B ．3C ．45D ．257．设抛物线2:4(0)C x y p =>的焦点为F ，准线为l ，过点F 的直线交抛物线C 于,M N 两点，交l 于点P ，且PF FM =，则||MN =（ ）A ．2B ．83C ．5D ．1638．已知直线:(1)(2)230l a x a y a +++--=经过定点P ，与抛物线24x y =交于,A B 两点，且点P 为弦AB 的中点，则直线l 的方程为（ ） A ．230x y +-= B ．210x y -+= C ．210x y -+=D ．20x y +-=9．己知直线l 过抛物线y 2=4x 的焦点F ，并与抛物线交于A ，B 两点，若点A 的纵坐标为4，则线段AB 的长为（ ） A ．253B ．496C ．436D ．25410．设1F 、2F 是椭圆1C 和双曲线2C 的公共焦点，P 是它们的一个公共点，且1PF <2PF ，线段1PF 垂直平分线经过2F ，若1C 和2C 的离心率分别为1e 、2e ，则129e e +的最小值（ ）A ．2B ．4C ．6D ．811．已知动点(),P x y ()()2222522x y x y a a+-++=+(a 为大于零的常数)﹐则动点P 的轨迹是（ ） A ．线段B ．圆C ．椭圆D ．双曲线12．已知抛物线1C 的顶点在坐标原点，焦点F 在y 轴正半轴上．若点F 到双曲线222:126x y C -=的一条渐近线的距离为2，则1C 的标准方程是（ ）A ．23y x =B ．23y x =C ．28x y =D ．216x y =二、填空题13．在平面直角坐标系xOy 中，1F ，2F 是椭圆2222:1(0)x y C a b a b+=>>的焦点.若椭圆C 上存在点P ，使得12|1|||2PO F F =，则椭圆C 的离心率的取值范围为________.14．已知双曲线()2222:10,0x y C a b a b-=>>的一条渐近线与圆(224x y +-=相交于A ，B 两点，且2AB =，则双曲线C 的离心率为___________.15．知直线m 过抛物线()220y px p =>的焦点F ，且交抛物线于A 、B 两点，交其准线l于点C .若6AF =，2CB BF =，则p =____________16．已知椭圆22:143x y C +=的左、右焦点分别为1F 、2F ，点()4,4M ，若点P 为椭圆C 上的一个动点，则1PM PF -的最小值为____________.17．已知双曲线M ：22221x y a b-=（0a >，0b >），ABC 为等边三角形．若点A 在y轴上，点B ，C 在双曲线M 上，且双曲线M 的实轴为ABC 的中位线，则双曲线M 的离心率为________．18．已知双曲线2222:1(0,0)x y E a b a b-=>>，点F 为E 的左焦点，点P 为E 上位于第一象限内的点，P 关于原点的对称点为Q ，且满足||3||PF FQ =，若||OP b =，则E 的离心率为_________.19．直线AB 过抛物线24y x =的焦点F ，且与抛物线交于A 、B 两点，且线段AB 的中点的横坐标是3，则直线AB 的斜率是_____________.20．过抛物线24y x =的焦点F 的直线交抛物线于A ，B 两点，点O 是原点，若||3AF =，则AOB 的面积为_______．三、解答题21．已知椭圆2222:1(0)x y E a b a b +=>>过点P ⎛ ⎝⎭，离心率2e =. （1）求椭圆E 的方程；（2）过点(0,3)M 的直线l 与椭圆E 相交于A ，B 两点. ①当直线OA ，OB 的斜率之和为34时(其中O 为坐标原点)，求直线l 的斜率k ； ②求MA MB ⋅的取值范围.22．已知抛物线()2:20C y px p =>的焦点为F ，过点()2,0A 的直线l 交C 于M ，N两点，当MN 与x 轴垂直时，MNF 的周长为9. （1）求C 的方程：（2）在x 轴上是否存在点P ，使得OPM OPN ∠=∠恒成立(O 为坐标原点)？若存在求出坐标，若不存在说明理由.23．在平面直角坐标系xOy 中，已知A ，B 两点是椭圆22:19x E y +=的左、右顶点，P 为直线6x =上的动点，PA 与椭圆E 的另一交点为Q ，当点P 不为点()6,0时，过P作直线PH QB ⊥，垂足为H . （1）证明：直线PH 过定点M ；（2）过（1）中的定点M 作斜率为k 的直线与椭圆E 交于C ，D 两点，设直线AC ，AD 的斜率分别为1k ，2k ，试判断()12k k k ⋅+是否为定值？如果是定值，求出定值.24．已知抛物线1C ：()220x py p =>和圆2C ：22120x x y -+=交于O ，P 两点，且1OP k =，其中O 为坐标原点.（1）求1C 的方程；（2）过1C 的焦点F 且不与坐标轴平行的直线l 与1C 交于A ，B 两点，AB 的中点为M ，1C 的准线为0l ，且0MQ l ⊥，垂足为Q .证明直线AB ，OQ 的斜率之积T 为定值，并求该定值.25．如图，点(1,0)F 为椭圆2222:1(0)x y E a b a b+=>>的右焦点，过F 且垂直于x 轴的直线与椭圆E 相交于C ､D 两点(C 在D 的上方)，||3CD =.（1）求椭圆E 的方程；（2）设点A ､B 是椭圆E 上位于直线CD 两侧的动点，且满足ACD BCD ∠=∠，试问直线AB 的斜率是否为定值，请说明理由. 26．已知是抛物线2:2C y px=(0)p >的焦点，(1,)M t 是抛物线上一点，且（1）求抛物线C 的方程；（2）过点O （坐标原点）分别作,OA OB 交抛物线C 于,A B 两点(,A B 不与O 重合)，且.2OA OB k k =.求证：直线AB 过定点.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】设122F F c =，设椭圆Γ的长轴长为12a ，双曲线Ω的实轴长为22a ，设光速为v ，推导出112a vt =，利用椭圆和双曲线的定义可得出1243a a =，由此可计算得出Γ与Ω的离心率之比. 【详解】设122F F c =，设椭圆Γ的长轴长为12a ，双曲线Ω的实轴长为22a ， 在图②中，1CDF 的周长为111212124CF DF CD CF CF DF DF a vt ++=+++==，所以，1148a vt =，可得112a vt =，在图①中，由双曲线的定义可得2122AF AF a -=，由椭圆的定义可得1212BF BF a +=， 22AF BF AB =-，则2121111222AF AF BF AB AF a BF AB AF a -=--=---=，即()111222a AB AF BF a -++=，由题意可知，1ABF 的周长为111AB AF BF vt ++=，即112111322222a a a a vt a =-=-=， 所以，1243a a =. 因此，Γ与Ω的离心率之比为122112:::3:4c ce e a a a a ===.【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.2．B解析：B 【分析】根据题意，求得4p =，可得抛物线的方程，因为()95OBN OAM ABNM S S S +=梯形△△，所以49OMN OAB ABMN S S S +=梯形△△，根据面积公式，结合抛物线定义，即可求得AB ，不妨设AB 的斜率为k ，可得直线AB 的方程，与抛物线联立，根据韦达定理，可求得A B x x +的值，代入弦长公式，即可求得答案. 【详解】因为点F 到抛物线C 准线的距离为4，所以4p =，所以28y x =，设抛物线C 的准线与x 轴交于点H ，因为()95OBN OAM ABNM S S S +=梯形△△，所以()()11422192M N A BOMN OABABMNM N OH y y OF y y S S S AM BN y y ⋅-+⋅-+==+⋅-梯形△△，因为2OH OF ==，M N A B y y y y -=-，AM BN AB +=，所以449OMN OAB ABMN S S S AB +==梯形△△，则9AB =，显然直线AB 的斜率存在，不妨设为k ，则():2AB y k x =-， 与抛物线联立可得：()22224840k x k x k -++=， 从而284A B x x k+=+， 所以28489A B A kB x x =++=+=，解得k =±. 故选：B【点睛】解题的关键是根据面积的关系，得到49OMN OAB ABMN S S S +=梯形△△，结合图象，可求得9AB =，再利用抛物线的弦长公式求解，考查分析计算，化简求值的能力，属中档题.3．C解析：C 【分析】先设点，利用向量关系得到两点坐标之间的关系121223,2x x c y y =-=，再结合点在椭圆上，代入方程，消去222a y 即得2229312c a x c+=，根据题意2x a <，构建,a c 的齐次式，解不等式即得结果. 【详解】设()()1122,,,A x y B x y ，由()()12,0,,0F c F c -得()()112212,,,F A F x c y x c y B -==+，122F A F B =，()()11222,,x c y x c y =∴+-，即121223,2x x c y y =-=，由,A B 在椭圆上，故2222221122222222b x a y a b b x a y a b ⎧+=⎨+=⎩，即()()2222222222222222232b x c a y a b b x a y a b⎧-+=⎪⎨+=⎪⎩， 消去222a y 得，2229312c a x c+=，根据椭圆上点满足a x a -≤≤，又,A B 两点不同，可知2229312c a x a c+=<，整理得22340c ac a -+<，故23410e e -+<，故113e <<.故选：C. 【点睛】 关键点点睛：圆锥曲线中离心率的计算，关键是根据题中条件，结合曲线性质，找到,,a b c 一组等量关系（齐次式），进而求解离心率或范围.4．D解析：D 【分析】焦点三角形1PFF 满足||||OP OF =，可根据三角形一边的中线是该边的一半，可判断该三角形是直角三角形.算出该三角形的中位线OH ，可得到12PF =，根据双曲线定义和勾股定理计算出,a c 求解. 【详解】直线20x y -+=过点F，可得()F 设右焦点为1F ，PF 的中点为H .因为O 是1FF 的中点，且||||OP OF =，故三角形1PFF 为直角三角形.1PF PF ⊥，故OH PF ⊥由点到直线距离公式有1OH ==故12PF =，12PF PF a -=，(2222112PF PF F F +== 故()2222220a ++=. 可得1a =ce a== 故选：D 【点睛】双曲线的离心率是双曲线最重要的几何性质，求双曲线的离心率(或离心率的取值范围)，常见有两种方法： ①求出a ，c ，代入公式c e a=； ②只需要根据一个条件得到关于a ，b ，c 的齐次式，结合b 2＝c 2－a 2转化为a ，c 的齐次式，然后等式(不等式)两边分别除以a 或a 2转化为关于e 的方程(不等式)，解方程(不等式)即可得e (e 的取值范围)．5．D解析：D 【分析】写出直线l 的方程，设点()11,A x y 、()22,B x y ，联立直线l 与抛物线的方程，列出韦达定理，利用抛物线的焦点弦长公式可求得AB . 【详解】抛物线24y x =的焦点()1,0F ，直线l 的方程为1y x =-，设点()11,A x y 、()22,B x y联立214y x y x=-⎧⎨=⎩，可得2610x x -+=，2640∆=->，所以，126x x +=，由抛物线的焦点弦长公式得1228AB x x =++=. 故选：D. 【点睛】方法点睛：有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式12AB x x p =++，若不过焦点，则必须用一般弦长公式．6．B解析：B 【分析】首先由椭圆的对称性得到点P 的位置，再求解,c b 的值. 【详解】根据椭圆的对称性可知，若椭圆上只有一个点满足OF FP =，这个点只能是右顶点，即2a c c a c -=⇒=，由条件可知242a a =⇒=，则1c =，那么b ==故选：B 【点睛】关键点点睛：本题的关键是确定点P 的位置，从而得到2a c =这个关键条件.7．D解析：D 【分析】由题意作出MD 垂直于准线l ，然后得2PM MD =，得30∠=︒DPM ，写出直线方程，联立方程组，得关于y 的一元二次方程，写出韦达定理，代入焦点弦公式计算. 【详解】如图，过点M 做MD 垂直于准线l ，由抛物线定义得MF MD =，因为PF FM =，所以2PM MD =，所以30∠=︒DPM ，则直线MN方程为1)x y =-，联立21)4x y x y ⎧=-⎪⎨=⎪⎩，，消去x 得，231030y y -+=，设()()1122,,,M x y N x y ，所以121210,13y y y y +==，得121016||2233MN y y =++=+=. 故选：D.【点睛】（1）直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系；（2）有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式12||=++AB x x p 或12||=++AB y y p ，若不过焦点，则必须用一般弦长公式．8．B解析：B 【分析】利用点差法求出直线斜率，即可得出直线方程. 【详解】由直线:(1)(2)230l a x a y a +++--=得(2)(23)0a x y x y +-++-= 所以20230x y x y +-=⎧⎨+-=⎩ 解得11x y =⎧⎨=⎩ 则()1,1P设1122(,),(,)A x y B x y ，则21122244x y x y ⎧=⎨=⎩，两式相减得121212()()4()x x x x y y -+=-， 即121212142AB y y x x k x x -+===-， 则直线方程为11(x 1)2y -=-，即210x y -+=. 故选：B. 【点睛】方法点晴：点差法是求解中点弦有关问题的常用方法.9．D解析：D 【分析】首先利用,,A F B 三点共线，求点B 的坐标，再利用焦点弦长公式求AB .【详解】4y =时，1644x x =⇒=，即()4,4A ，()1,0F ，设2,4y B y ⎛⎫ ⎪⎝⎭，利用,,A F B 三点共线可知24314y y =-，化简得2340y y --=，解得：1y =-或4y =（舍）当1y =-时，14x =，即()4,4A ，1,14B ⎛⎫- ⎪⎝⎭， 所以121254244AB x x p =++=++=. 故选：D 【点睛】关键点点睛：本题考查直线与抛物线相交，焦点弦问题，重点是求点B 的坐标.10．D解析：D 【分析】设椭圆和双曲线的方程，由题意可得2122PF F F c ==，再利用椭圆和双曲线的定义分别求出1PF ，即可得122a a c +=，计算12112e e +=，()121212111992e e e e e e ⎛⎫+=++ ⎪⎝⎭展开后利用基本不等式即可求最值. 【详解】设椭圆1C 的方程为2222111x y a b +=，则222111c a b =-，设双曲线2C 的方程为2222221x y a b -=，则222222c a b =+，因为椭圆1C 和双曲线2C 的焦点相同，所以2212c c =，设12c c c ==即22221122a b a b -=+，因为P 是椭圆1C 和双曲线2C 的一个公共点， 所以1212+=PF PF a ，2122PF PF a -=，因为线段1PF 垂直平分线经过2F ，所以2122PF F F c ==，所以1122PF a c =-，且1222PF c a =-， 所以122222a c c a -=-，可得122a a c +=， 所以11c e a =，22c e a =，所以1212121122a a a a ce e c c c c++=+===，所以()211212121291111991022e e e e e e e e e e ⎛⎫⎛⎫+=++=++ ⎪ ⎪⎝⎭⎝⎭()11101023822⎛≥+=+⨯= ⎝， 当且仅当21129e e e e =，即213e e =时等号成立， 故选：D. 【点睛】关键点点睛：本题解题的关键点是利用已知条件得出122a a c +=，进而可得12112e e +=， 再利用基本不等式可求最值.11．C解析：C 【分析】由a 为大于零的常数，可知5a a+的最小值，再根据两点间距离公式得几何意义以及椭圆定义判断轨迹. 【详解】的几何意义为点(),P x y 与点(0,2)A 间的距离，的几何意义为点(),P x y 与点(0,2)B -间的距离，且4AB =又由a为大于零的常数，可知54a a +≥=>， 当且仅当5aa=，即a =54a a=+>， 即动点P 到点A 与到点B 的距离之和为定值，且大于AB ， 所以动点P 的轨迹为椭圆， 故选：C. 【点睛】在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误． 椭圆的定义揭示了椭圆的本质属性，正确理解掌握定义是关键，应注意定义中的常数大于|F 1F 2|，避免了动点轨迹是线段或不存在的情况．12．D解析：D 【分析】先根据双曲线的方程求解出双曲线的渐近线方程，再根据点到直线的距离公式求解出抛物线方程中的p ，则抛物线方程可求. 【详解】双曲线2C 的渐近线方程是22026x y -=，即y =.因为抛物线的焦点()0,02p F p ⎛⎫> ⎪⎝⎭0y -=的距离为2，2=，即8p =，所以1C 的标准方程是216x y =，故选：D ． 【点睛】方法点睛：求解双曲线方程的渐近线方程的技巧：已知双曲线方程22221x y a b-=或22221y x a b -=，求解其渐近线方程只需要将方程中的“1”变为“0”，由此得到的y 关于x 的一次方程即为渐近线方程. 二、填空题13．【分析】先分析出得到消去b 整理出ac 的齐次式求出离心率的范围【详解】由落在椭圆上则又得：∴由得：即解得：又∴故答案为：【点睛】求椭圆（双曲线）离心率的一般思路：根据题目的条件找到abc 的关系消去b 构解析：⎫⎪⎪⎣⎭【分析】先分析出||b PO a ≤≤，得到b c a ≤<，消去b ，整理出a 、c 的齐次式，求出离心率的范围. 【详解】由P 落在椭圆2222:1(0)x y C a b a b +=>>上，则||b PO a ≤≤.又12|1|||2PO F F =得：||PO c = ∴b c a ≤<由b c ≤得：22b c ≤，即222a c c -≤，解得：2c e a =≥又1e <，∴12e ≤<故答案为：2⎫⎪⎪⎣⎭【点睛】求椭圆（双曲线）离心率的一般思路：根据题目的条件，找到a 、b 、c 的关系，消去b ，构造离心率e 的方程或（不等式）即可求出离心率．14．2【分析】由双曲线圆的方程确定渐近线方程为圆心为半径为根据圆的相交弦与半径弦心距之间的几何关系有结合双曲线参数间的关系即可求其离心率【详解】由题意知：双曲线的渐近线为而圆心为半径为∴圆心到渐近线的距解析：2 【分析】由双曲线、圆的方程确定渐近线方程为by x a=±，圆心为(0,，半径为2r ，根据圆的相交弦与半径、弦心距之间的几何关系有222||4AB r d -=，结合双曲线参数间的关系即可求其离心率. 【详解】由题意知：双曲线的渐近线为by x a=±，而圆心为(0,，半径为2r ，∴圆心到渐近线的距离d ==，而2AB =，∴221r d -=，故222123a a b=+，又222,1c a b c e a +==>， ∴2e =. 故答案为：2. 【点睛】关键点点睛：根据双曲线、圆的标准方程确定渐近线方程、圆心、半径长，结合圆中相交弦的几何性质及双曲线参数关系，列出关于,a c 的齐次方程求离心率.15．3【分析】过作准线的垂线垂足分别为过作的垂线垂足为根据结合抛物线的定义可得据此求出再根据抛物线的定义可求出【详解】如图：过作准线的垂线垂足分别为过作的垂线垂足为因为所以因为所以所以所以在直角三角形中解析：3 【分析】过A 、B 作准线l 的垂线，垂足分别为,N M ，过F 作AN 的垂线，垂足为D ，根据2CB BF =结合抛物线的定义可得30DFA MCB ∠=∠=，据此求出||3AD =，再根据抛物线的定义可求出p . 【详解】如图：过A 、B 作准线l 的垂线，垂足分别为,N M ，过F 作AN 的垂线，垂足为D ，因为2CB BF =，所以||2||CB BF =， 因为||||BF BM =，所以||2||CB BM =， 所以30MCB ∠=，所以30DFA ∠=，在直角三角形ADF 中，因为||6AF =，所以||3AD =， 因为||||6AN AF ==，且||||3AN AD p p =+=+， 所以63p =+，所以3p =. 故答案为：3 【点睛】关键点点睛：利用抛物线的定义求解是解题关键.16．1【分析】根据已知可以转化为然后由三点共线即两点之间线段最短可得答案【详解】由已知得因为所以所以所以当三点共线时最小即故答案为：1【点睛】本题考查了椭圆上的点到焦点和定点距离和的问题解题关键是利用定解析：1 【分析】根据已知可以转化为124PM PF PM PF -=+-，然后由三点共线即两点之间线段最短可得答案. 【详解】由已知得222224,3,1a b c a b ===-=，2(1,0)F ， 因为2124PF PF a +==，所以124PF PF =-， 所以()12244PM PF PM PF PM PF -=--=+-， 所以当三点2M P F 、、共线时，24PM PF +-最小， 即2222443441PM PF MF +-=-=+=. 故答案为：1.【点睛】本题考查了椭圆上的点到焦点和定点距离和的问题，解题关键是利用定义转化为两点之间线段最短的问题，考查了学生分析问题、解决问题的能力.17．【分析】可根据实轴为的中位线得出再根据对称性及为等边三角形表示出的坐标代入双曲线方程得到关系式求解离心率【详解】实轴长为则关于轴对称不妨设在双曲线左支则其横坐标为根据为等边三角形可得故将的坐标代入双【分析】可根据实轴为ABC 的中位线，得出BC ，再根据对称性及ABC 为等边三角形，表示出B 的坐标，代入双曲线方程，得到,a b 关系式求解离心率. 【详解】实轴长为2a ，则4BC a =，BC 关于y 轴对称不妨设B 在双曲线左支，则其横坐标为2a ，根据ABC 为等边三角形，60ABC ∠=可得B y =故()2,B a ，()2,C a -，将B 的坐标代入双曲线方程有2222431a a a b-=，则a b =，则c =故e =【点睛】双曲线的离心率是双曲线最重要的几何性质，求双曲线的离心率(或离心率的取值范围)，常见有两种方法： ①求出a ，c ，代入公式ce a=； ②只需要根据一个条件得到关于a ，b ，c 的齐次式，结合b 2＝c 2－a 2转化为a ，c 的齐次式，然后等式(不等式)两边分别除以a 或a 2转化为关于e 的方程(不等式)，解方程(不等式)即可得e (e 的取值范围)．18．【分析】由题意设即有由双曲线定义及已知可得且结合点在曲线上联立方程得到关于的齐次方程即可求得离心率【详解】令则且①由题意知：E 的左准线为结合双曲线第二定义知：又∴解得②∵知：∴联立①②得：整理得∴故【分析】由题意设00(,)P x y ，即有00(,)Q x y --，由双曲线定义及已知可得22003()a a x x c c +=-且22200x y b +=，结合点在曲线上联立方程得到关于,a c 的齐次方程，即可求得离心率.【详解】令00(,)P x y ，00,0x y >则00(,)Q x y --且2200221x y a b-=①，由题意知：E 的左准线为2a x c =-，结合双曲线第二定义知：20||()a PF e x c=+，20||()a FQ e x c =-，又||3||PF FQ =，∴22003()a a x x c c +=-，解得202a x c=②， ∵||OP b =知：22200x y b +=，∴联立①，②得：42222244(1)a a b b c c+-=，整理得223a c =， ∴3e = 3【点睛】关键点点睛：根据双曲线第二定义：曲线上的点到焦点距离与该点到对应准线的距离之比为常数e ，可得点P 的横坐标为22ac；结合点在曲线上及勾股定理即可得关于,a c 的齐次方程求离心率即可.19．1或【分析】根据抛物线方程得到设直线方程为与抛物线方程联立得：再根据线段的中点的横坐标为3求得即可得到直线斜率【详解】因为直线AB 过抛物线的焦点F 且与抛物线交于AB 两点所以斜率不为0设直线AB 方程为解析：1或1- 【分析】根据抛物线方程，得到()1,0F ，设直线方程为1x my =+，与抛物线方程联立得：2440y my --=，再根据线段AB 的中点的横坐标为3，126x x +=，求得m ，即可得到直线斜率. 【详解】因为直线AB 过抛物线24y x =的焦点F (1,0)且与抛物线交于A 、B 两点， 所以斜率不为0，设直线AB 方程为1x my =+，与抛物线方程联立得：2440y my --=， 由韦达定理得：12124,4y y m y y +=⋅=-， 所以()21212424223x x m y y m +=++=+=⨯，解得1m =±所以直线的方程为1x y =±+， 所以1AB k =±. 故答案为：1或1-20．【分析】根据已知条件不妨设在第一象限根据抛物线定义以及方程求出点坐标进而得出直线方程与抛物线方程联立求出点坐标即可求出AOB 的面积【详解】抛物线的焦点为∵∴点A 到准线的距离为3点的横坐标为根据对称性解析：2【分析】根据已知条件不妨设A 在第一象限，根据抛物线定义以及方程，求出A 点坐标，进而得出直线AF 方程，与抛物线方程联立，求出B 点坐标，即可求出AOB 的面积. 【详解】抛物线24y x =的焦点为(1,0)F ,∵3AF =，∴点A 到准线:1l x =-的距离为3， 点A 的横坐标为2，根据对称性不妨设点A 在第一象限， 设1122(2,)(0),(,)A y y B x y >，2x =代入抛物线方程得1y =直线AF 方程为1)y x =-，联立21)4y x y x⎧=-⎪⎨=⎪⎩，消去x 得，240y --=，解得12y y ==∴AOB的面积为1211122S y OF y =⨯⨯==-⨯⨯故答案为：2. 【点睛】本题考查抛物线的定义，考查三角形的面积的计算，确定相交点的坐标是解题关键，属于中档题.三、解答题21．（1）2212x y +=；（2）①3k =-；②808,9⎡⎫⎪⎢⎣⎭．【分析】（1）把点代入方程结合离心率列方程组求解即可；（2）①设直线l 方程为，代入椭圆E 的方程可得，结合判别式与韦达定理，利用直线OA ，OB 的斜率之和为34进而求出直线斜率即可；②当直线l 的斜率不存在时，直线l 的方程为0x =，求得8MA MA ⋅=，当直线l 的斜率存在时，由（2）①得28821MA MB k ⋅=++，从而求得范围．【详解】解：（1）由题意得222221,2c a a b c ⎧=⎪⎨⎪=+⎩，解得222a c =，22b c =.设椭圆E 的方程为222212x y c c +=，又因为点P ⎛ ⎝⎭在椭圆E 上， 所以222211122c c+=，22222,1c a b ===，所以椭圆E 的方程为2212x y +=；（2）①设直线l 方程为：3y kx =+，代入椭圆E 的方程可得，()222112160kx kx +++=因为直线l 与椭圆E 有两个交点，所以216640∆=->k ，即24k >. 设()11,A x y ，()22,B x y ，则1221221k x x k +=-+，1221621x x k ⋅=+， 11223,3y kx y kx =+=+.又()1212121233244OA OBx x y y k k k k x x x x ++=+=+=-=⋅ 解得3k =-，经检验成立.所以，直线l 的斜率3k =-； ②当直线l 的斜率不存在时，直线l 的方程为0x =，将0x =代入2212x y +=，解得1y =±，则(0,1)A ，(0,1)B -，8MA MA ⋅=当直线l 的斜率存在时，由（2）①得()()()()22121212216133121k MA MA x x y y k x x k +⋅=⋅+--=+⋅=+()2228211882121k k k ⎡⎤++⎣⎦==+++因为24k >，所以MA MA ⋅的范围为808,9⎛⎫⎪⎝⎭． 综上，得MA MB ⋅的取值范围是808,9⎡⎫⎪⎢⎣⎭． 【点睛】解决直线与椭圆的综合问题时，要注意：(1)注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件；(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题．22．（1）22y x =；（2）存在，P 点坐标为()2,0-. 【分析】（1）利用焦半径公式表示||||MF NF =，代入坐标2x =，求MN 的长度，并表示MNF 的周长，求p ；（2）假设存在点()0,0P x ，设:2l x my =+，与抛物线方程联立，利用根与系数的关系表示0MP NP k k +=，求定点0x 的值. 【详解】（1）当MN 与x 轴垂直时，||||22pMF NF ==+，||MN =，从而有49p ++= 解得1p =，所以C 的方程为22y x =；（2）设()0,0P x ，()11,M x y ，()22,N x y ，由题可知直线l 斜率不为零，设:2l x my =+，代入抛物线方程22y x =消去x ，得2240y my --=，从而122y y m +=，124y y =-，①由OPM OPN ∠=∠可得0MP NP k k +=， 而121020MP NP y y k k x x x x +=+--12102022y y my x my x =++-+-()()()()1201210202222my y x y y my x my x +-+=+-+-将①代入，从而得()()102042022m mx my x my x --=+-+-恒成立，所以02x =-，因此存在点P 满足题意，P 点坐标为()2,0-.【点睛】思路点睛：定点问题解决步骤：（1）设直线代入二次曲线方程，整理成一元二次方程；（2）韦达定理列出两根和及两根积；（3）写出定点满足的关系，整体代入两根和及两根积；（4）整理（3）所得表达式探求其恒成立的条件.23．（1）证明见解析；（2）是，定值为112-. 【分析】（1）设()00 ,Q x y ，()()6,0P t t ≠，法一：根据椭圆方程求得19QA QB k k ⋅=-，根据9QA PA t k k ==，即可求得QB k ，根据PH QB ⊥，可求得PH k ，可得直线PH 的方程，即可得答案；法二：根据9AP QA t k k ==，可得直线AP 的方程，与椭圆联立，根据韦达定理，可得Q 点坐标，根据PH QB ⊥，可求得PH k ，可得直线PH 的方程，即可得答案； （2）设()11,C x y ，()22,D x y ，则直线CD 的方程为()5y k x =-，与椭圆联立，根据韦达定理，可得1212,x x x x +⋅表达式，即可得()12k k k ⋅+的表达式，化简整理，即可得答案.【详解】（1）法一：由题意得：(3,0),(3,0)A B -，设()00 ,Q x y ，()()6,0P t t ≠，则220019x y += ∴00001339QA QB y y k k x x ⋅=⋅=-+-，9QA PA t k k == ∴1QB k t=-∵PH QB ⊥，∴1PH QB k k ⋅=-，∴PH k t =，直线PH 的方程为()6y t t x -=-，即()5y t x =-，所以过定点()5,0M ，法二：由题意得：(3,0),(3,0)A B -，设()00,Q x y ，()()6,0P t t ≠， 9AP QA t k k == ∴直线AP 的方程为()39t y x =+，由()223919t y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩，得()2222969810t x t x t +++-=. ∴20298139t x t--⋅=+，∴2022739t x t -=+，()0023699t y t t x +=+=， ∴2222736,99t t Q t t ⎛⎫- ⎪++⎝⎭，∴222619 27339QB t t k t t t+==---+. ∵PH QB ⊥，∴1PH QB k k ⋅=-，∴PH k t =，∴PH 的方程为()6y t t x -=-，即()5y t x =-，所以过定点()5,0M（2）设()11,C x y ，()22,D x y ，则直线CD 的方程为()5y k x =-由()22519y k x x y ⎧=-⎪⎨+=⎪⎩.得()2222199022590k x k x k +-+-=， ∴22221222122(90)4(19)(2259)0901*******k k k k x x k k x x k ⎧⎪∆=--+->⎪⎪+=⎨+⎪⎪-=⎪+⎩∴()()()()()()()122121121222153533333x x x x y y k k k k k x x x x -++-+⎛⎫⋅+=⋅+= ⎪+⎭⋅+++⎝ ()()1212222121222304813957612x x x x k k x x x x k -⋅+--++⋅===-+为定值 【点睛】 解题的技巧为：根据椭圆方程可得19QA QB k k ⋅=-，根据QA PA k k =，可直接求得QB k ，简化计算，提高正确率，考查计算化简的能力，属中档题. 24．（1）26x y =；（2）证明见解析，定值为12-. 【分析】（1）由题意写出直线OP 的方程，代入圆的方程，求出点P 的坐标，再代入抛物线方程即可；（2）设直线l 的方程，与抛物线方程联立方程组，得韦达定理，即可得点M 的横坐标，进而得点Q ，表示出OQ k ，计算O AB Q k k ⋅可得定值.【详解】（1）解：由O 为坐标原点，且1OP k =，得直线OP 的方程为y x =，代入圆2C 的方程，得22120x x x -+=，解得0x =或6x =，则()6,6P .将点P 的坐标代入1C 的方程，得2626p =⨯，则3p =，故1C 的方程为26x y =.（2）证明：由（1）可知30,2F ⎛⎫ ⎪⎝⎭，0l ：32y =-. 由题意值，直线l 的斜率存在，设直线l 的方程为3(0)2y kx k =+≠， 联立2632x y y kx ⎧=⎪⎨=+⎪⎩，整理得2690x kx --=， 236360k ∆=+>.设()11,A x y ，()22,B x y ，则126x x k +=，所以点M 的横坐标为3k ，则3(3,)2Q k - 则31232OQ k k k -==-， 所以1122AB OQ T k k k k ⎛⎫=⋅=⋅-=- ⎪⎝⎭，故T 是定值，且定值为12-. 【点睛】思路点睛：解决直线与抛物线的综合问题时，要注意：（1）注意观察应用题设中的每一个条件，明确确定直线、抛物线的条件；（2）强化有关直线与抛物线联立得出一元二次方程后的运算能力，重视根与系数之间的关系、焦点弦、斜率、三角形的面积等问题．25．（1）22143x y +=；（2）是定值，理由见解析. 【分析】（1）由焦点及通经长，用待定系数法求椭圆的标准方程；（2）设出直线AB ：y kx m =+，与椭圆联立，用“设而不求法”表示ACD BCD ∠=∠，整理得12k =. 【详解】 （1）由2321b a c ⎧=⎪⎨⎪=⎩得：24a =，23b =∴椭圆E 的方程：22143x y += （2）依题意知直线AB 的斜率存在，设AB 方程：y kx m =+()11,A x y ，()22,B x y 代入椭圆方程22143x y +=得：()2224384120k x kmx m +++-=(*) 122843km x x k ∴+=-+，212241243m x x k -=+ 由ACD BCD ∠=∠得0AC BC k k += 31,2C ⎫⎛ ⎪⎝⎭，121212123333222201111y y kx m kx m x x x x --+-+-∴+=+=---- ()1212322302kx x m k x x m ⎫⎛∴+--+-+= ⎪⎝⎭22241238223043243m km k m k m k k -⎛⎫⎛⎫∴⋅+----+= ⎪⎪++⎝⎭⎝⎭整理得：(63)(223)0k k m -+-=2230k m ∴+-=或630k -=当2230k m +-=时，直线AB 过定点31,2C ⎛⎫ ⎪⎝⎭，不合题意 630k ∴-=，12k =，∴直线AB 的斜率是定值12 另解：设直线AB 的方程为3(1)12m x n y ⎫⎛-+-= ⎪⎝⎭椭圆E 的方程即：22333[(1)1]41222x y ⎡⎤⎫⎛-++-+= ⎪⎢⎥⎝⎭⎣⎦ 即：22334126(1)3(1)022y y x x ⎫⎫⎛⎛-+-+-+-= ⎪ ⎪⎝⎝⎭⎭ 联立得：233(412)(126)22n y m n y ⎫⎫⎛⎛+-++- ⎪ ⎪⎝⎝⎭⎭2(1)(63)(1)0x m x -++-= 即23322(412)(126)(63)011y y n m n m x x ⎛⎫-- ⎪+++++= ⎪-- ⎪⎝⎭ ∴由ACD BCD ∠=∠得121233(126)22011(412)AC BC y y m n k k x x n --++=+=-=--+即：2n m =-∴直线AB 的斜率为12m n -=，是定值. 【点睛】 （1）待定系数法可以求二次曲线的标准方程；（2）"设而不求"是一种在解析几何中常见的解题方法，可以解决直线与二次曲线相交的问题.26．（1）24y x =；（2）直线AB 过定点(2,0)-，证明见解析.【分析】（1）由抛物线的定义求得p ，得抛物线方程；（2）设直线AB 方程为x my b =+， 11(,)A x y ，22(,)B x y ，直线方程代入抛物线方程，由判别式大于0得参数满足的条件，应用韦达定理得1212,y y y y +，计算由2OA OB k k =可得128y y =，从而求得参数b ，并可得出m 的范围．此时由直线方程可得定点坐标．【详解】（1）由抛物线定义可知：122p +=，则2p =， 所以抛物线C 的方程为24y x =（2）设直线AB 方程为x my b =+， 11(,)A x y ，22(,)B x y联立24y x x my b⎧=⎨=+⎩得2440y my b --=， 则216160m b ∆=+>即20()m b +>*且124y y m +=，124y y b =- .2OA OB k k =，所以12122y y x x =， 又2114y x =，2224y x =，因此可得128y y =即48b -=，2b =- 代入()*得220m ->，m ∴<m >所以直线AB 方程为2x my =-，由此可知直线AB 过定点(2,0)-.【点睛】 方法点睛：本题考查主要考查抛物线中直线过定点问题，解题方法是设而不求的思想方程，即设直线方程为x my b =+，设交点坐标为11(,)A x y ，22(,)B x y ，直线方程代入抛物线方程后应用韦达定理得1212,y y y y +，代入已知求出参数值，然后由直线方程得定点坐标．。

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(有答案解析)(3)

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(有答案解析)(3)

一、选择题1．已知直线()()20y k x k =+>与抛物线2:8C y x =相交于A 、B 两点，F 为抛物线C 的焦点.若4FA FB =，则k =（ ）A ．45B C ．23D 2．已知点()P m n ,是抛物线214y x =-上一动点，则A．4B ．5C D ．63．过抛物线22y px =焦点(1,0)F 的直线l 与抛物线交于,A B 两点，且(1)AF mFB m =>，25||4AB =，则m =（ ） A ．2B ．3C ．4D ．54．直线34y kx k =-+与双曲线221169x y -=有且只有一个公共点，则k 的取值有（ ）个A ．1B ．2C ．3D ．45．已知F 是双曲线2222:1(0)x y E a b a b-=>>的左焦点，过点F 的直线与双曲线E 的左支和两条渐近线依次交于,,A B C 三点，若||||||FA AB BC ==，则双曲线E 的离心率为（ ）A BC ．2D 6．已知抛物线22(0)y px p =>的焦点为F ，过点F 的直线分别交抛物线于A ，B 两点，若4AF =，1BF =，则p =（ ） A ．165B ．2C ．85D ．17．设1F 、2F 分别是椭圆22:1259x yC +=的左、右焦点，O 为坐标原点，点P 在椭圆C上且满足4OP =，则12PF F △的面积为（ ）A ．3B ．C ．6D ．98．已知双曲线()2222:10,0x y C a b a b-=>>的左右焦点分别为1F ，2F ，实轴长为4，点P 为其右支上一点，点Q 在以()0,4为圆心、半径为1的圆上，若1PF PQ +的最小值为8，则双曲线的渐近线方程为（ ）A ．12y x =±B ．y x =±C ．2y x =±D ．2y x =±9．已知直线:(1)(2)230l a x a y a +++--=经过定点P ，与抛物线24x y =交于,A B 两点，且点P 为弦AB 的中点，则直线l 的方程为（ ） A ．230x y +-= B ．210x y -+= C ．210x y -+=D ．20x y +-=10．己知直线l 过抛物线y 2=4x 的焦点F ，并与抛物线交于A ，B 两点，若点A 的纵坐标为4，则线段AB 的长为（ ） A ．253B ．496C ．436D ．25411．已知动点(),P x y 5a a=+(a 为大于零的常数)﹐则动点P 的轨迹是（ ） A ．线段B ．圆C ．椭圆D ．双曲线12．已知抛物线1C 的顶点在坐标原点，焦点F 在y 轴正半轴上．若点F 到双曲线222:126x y C -=的一条渐近线的距离为2，则1C 的标准方程是（ ）A ．2y x =B ．2y x =C ．28x y =D ．216x y =二、填空题13．已知抛物线22y px =上三点(2,2),,A B C ，直线,AB AC 是圆22(2)1x y -+=的两条切线，则直线BC 的方程为___________.14．设F 是抛物线2:2C y x =的焦点，A 、B 是抛物线C 上两个不同的点，若直线AB 恰好经过焦点F ，则4AF BF +的最小值为_______．15．过双曲线22221(0,0)x y a b a b-=>>的右顶点且斜率为3的直线，与双曲线的左右两支分别相交，则此双曲线的离心率的取值范围是___________.(用区间表示)16．在平面直角坐标系xOy 中，双曲线()2222:10,0x y C a b a b-=>>的右焦点为F ，过点F 且与x 轴垂直的直线与双曲线的一条渐近线交于第一象限内的点A ，过点F 且平行于OA 的直线交另一条渐近线于点B ，若AB OB ⊥，则双曲线C 的离心率为____________.17．过双曲线M ：2213x y -=的右焦点F 作圆C ：221(1)2x y ++=的切线，此切线与M 的右支交于A ，B 两点，则||AB =___________.18．已知点A ，B 为抛物线C ：24y x =上不同于原点O 的两点，且OA OB ⊥，则OAB 的面积的最小值为__________.19．在平面直角坐标系xOy 中，已知双曲线22:17y x Γ-=的两个焦点分别为1F ，2F ，以2F 为圆心，12F F 长为半径的圆与双曲线Γ的一条渐近线交于M ，N 两点，若OM ON ≥，则OMON的值为________.20．在平面直角坐标系xOy 中，设双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为F ，若双曲线的右支上存在一点P ，使得△OPF 是以P 为直角顶点的等腰直角三角形，则双曲线C 的离心率为__________. 三、解答题21．已知抛物线()2:20C y px p =>的焦点为F ，过点()2,0A 的直线l 交C 于M ，N两点，当MN 与x 轴垂直时，MNF 的周长为9. （1）求C 的方程：（2）在x 轴上是否存在点P ，使得OPM OPN ∠=∠恒成立(O 为坐标原点)？若存在求出坐标，若不存在说明理由.22．在平面直角坐标系xOy 中，已知直线y x =被抛物线2:2(0)C y px p =>截得的弦长为l 与抛物线C 相交于点M ，N ，点()1,2A ，且直线AM ，AN 的斜率之和为4.（1）求抛物线C 的方程；（2）求证：直线l 过定点，并求出定点坐标.23．已知点A 、B 坐标分别是(-，0)，直线AP 、BP 相交于点P ，且它们斜率之积是12-． （1）试求点P 的轨迹Γ的方程；（2）已知直线:4l x =-，过点()2,0F -的直线（不与x 轴重合）与轨迹Γ相交于M ．N 两点，过点M 作MD l ⊥于点D ．求证：直线ND 过定点，并求出定点的坐标．24．已知点(-在椭圆2222:1(0)x y E a b a b +=>>上，E 的离心率为2． （1）求E 的方程；（2）设过定点(0,2)A 的直线l 与E 交于不同的两点,B C ，且COB ∠为锐角，求l 的斜率的取值范围．25．已知点()11,A x y ，()22,B x y 是抛物线C ：24x y =上的两点，满足OA OB ⊥，O 是坐标原点.（1）求证：1216x x =-；（2）若⊥OD AB 于点D ，求点D 的轨迹方程.26．在平面直角坐标系xOy 中，设动点P 到定点(1,0)F 的距离与到定直线:1l x =-的距离相等，记P 的轨迹为曲线Γ． （1）求曲线Γ的方程；（2）过点F 的直线交曲线Γ于点A 、B （其中点A 在第一象限），交直线l 于点C ，且点F 是AC 的中点，求线段AB 的长．【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】 设10m k=>，设点()11,A x y 、()22,B x y ，则直线AB 的方程可表示为2x my =-，将直线AB 的方程与抛物线C 的方程联立，列出韦达定理，由4FA FB =可得出124y y =，代入韦达定理求出正数m 的值，即可求得k 的值.【详解】 设10m k=>，设点()11,A x y 、()22,B x y ，则直线AB 的方程可表示为2x my =-，联立228x my y x=-⎧⎨=⎩，整理得28160y my -+=，264640m ∆=->，0m >，解得1m .由韦达定理可得128y y m +=，1216y y =，由4FA FB =得()12242x x +=+，即124my my =，124y y ∴=，12258y y y m ∴+==，可得285m y =，则22122844165m y y y ⎛⎫==⨯= ⎪⎝⎭， 0m >，解得54m =，因此，145k m ==. 故选：A. 【点睛】方法点睛：利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下： （1）设直线方程，设交点坐标为()11,x y 、()22,x y ；（2）联立直线与圆锥曲线的方程，得到关于x （或y ）的一元二次方程，必要时计算∆； （3）列出韦达定理；（4）将所求问题或题中的关系转化为12x x +、12x x 的形式； （5）代入韦达定理求解.2．D解析：D 【分析】 先把抛物线214y x =-化为标准方程，求出焦点F (0,-1),运用抛物线的定义，找到2222(1)(4)(5)m n m n +++-++的几何意义，数形结合求最值.【详解】 由214y x =-，得24x y =-． 则214y x =-的焦点为()0,1F -．准线为:1l y =． 2222(1)(4)(5)m n m n +++-++几何意义是点()P m n ,到()0,1F-与点()4,5A -的距离之和，如图示：根据抛物线的定义点()P m n ,到()0,1F -的距离等于点()P m n ,到l 的距离，|PF |+|PA |=|PP 1|+|PA |,所以当P 运动到Q 时，能够取得最小值. 最小值为：|AQ 1|=()156--=． 故选：D. 【点睛】解析几何问题解题的关键：解析几何归根结底还是几何，根据题意画出图形，借助于图形寻找几何关系可以简化运算．3．C解析：C 【分析】由焦点得2p =，设直线代入抛物线方程结合韦达定理以及已知条件利用弦长公式求得参数值. 【详解】∵焦点(1,0),2F p ∴=，抛物线方程式为24y x =．设直线l 的方程为1(0)x y λλ=+>，代入抛物线方程，得2440y y λ--=．设()()1122,,,A x y B x y ，由韦达定理得124y y =-． 由AF mFB =，得12y my =-．解得21y y ==-21y y ==121,x m x m ∴==．12125||2,44AB x x p m m m ∴=++=++=∴=． 故选：C ． 【点晴】方法点晴：解直线与圆锥曲线位置问题时，通常使用设而不求思想，结合韦达定理运算求解相关参数.4．D解析：D 【分析】将直线方程与双曲线的方程联立，得出关于x 的方程，根据直线与双曲线只有一个公共点，求出对应的k 值，即可得解. 【详解】联立22341169y kx k x y =-+⎧⎪⎨-=⎪⎩，消去y 并整理得()()()2221693243164390k x k k x k ⎡⎤-+-+-+=⎣⎦，由于直线34y kx k =-+与双曲线221169x y -=有且只有一个公共点， 所以，21690k -=或()()()222216903243641694390k k k k k ⎧-≠⎪⎨⎡⎤⎡⎤∆=----+=⎪⎣⎦⎣⎦⎩， 解得34k =±或2724250k k +-=， 对于方程2724250k k +-=，判别式为22447250'∆=+⨯⨯>，方程2724250k k +-=有两个不等的实数解.显然34k =±不满足方程2724250k k +-=. 综上所述，k 的取值有4个. 故选：D. 【点睛】方法点睛：将直线与圆锥曲线的两个方程联立成方程组，然后判断方程组是否有解，有几个解，这是直线与圆锥曲线位置关系的判断方法中最常用的方法，注意：在没有给出直线方程时，要对是否有斜率不存在的直线的情况进行讨论，避免漏解．5．B解析：B 【分析】可设出直线AB ，与两渐近线方程联立，解出,B C y y ，利用两者的关系式求出直线的斜率.进而表示出A 的坐标，代入双曲线方程，得到,,a b c 的关系式，从而求得离心率. 【详解】||||||FA AB BC ==，故有1123A B C y y y == 故32B C y y =设过点F 的直线方程为：()y k x c =+联立()y k x c b y x a ⎧=+⎪⎨=-⎪⎩，解之得C C kc x bk a b kc a y b k a -⎧=⎪+⎪⎪⎨⎪=⎪⎪+⎩同理联立()y k x c by x a ⎧=+⎪⎨=⎪⎩解之得B B kc x bk a b kc a y b k a ⎧=⎪-⎪⎪⎨⎪=⎪⎪-⎩由32B C y y =有23b bkc kca ab b k k a a =+-，故3232b b k k a a +=- 解之得5bk a=-直线为：()5by x c a=-+ 则1212A B bc y y a -==，又()5A A b y x c a =-+ 故712A cx =-又A 在双曲线上可得：2222491144144c c a a -= 得2213c a =故ca =故选：B 【点睛】双曲线的离心率是双曲线最重要的几何性质，求双曲线的离心率(或离心率的取值范围)，常见有两种方法： ①求出a ，c ，代入公式c e a=； ②只需要根据一个条件得到关于a ，b ，c 的齐次式，结合b 2＝c 2－a 2转化为a ，c 的齐次式，然后等式(不等式)两边分别除以a 或a 2转化为关于e 的方程(不等式)，解方程(不等式)即可得e (e 的取值范围)．6．C解析：C 【分析】直接设出直线方程，用“设而不求法”表示出AF ，BF ，利用性质可解. 【详解】由题意可知直线AB 的斜率一定存在，设为k ，联立2,22,p y k x y px ⎧⎛⎫=-⎪ ⎪⎝⎭⎨⎪=⎩消去y 可得()22222204k p k x k px -++=，设()11,A x y ，()22,B x y ，所以2124p x x =.又根据抛物线的定142p x +=，212p x +=，所以241224p p p ⎫⎫⎛⎛--= ⎪⎪⎝⎝⎭⎭，解得85p =.故选：C 【点睛】"设而不求"是一种在解析几何中常见的解题方法，可以解决直线与二次曲线相交的问题.7．D解析：D 【分析】设点()00,P x y ，求出20y 的值，由此可求得12PF F △的面积.【详解】在椭圆22:1259x y C +=中，5a =，3b =，则4c ==，所以，1228F F c ==，设点()00,P x y ，则22001259x y +=，可得220025259x y =-，4OP ===，解得208116y =，094y ∴=，因此，12PF F △的面积为1212011989224PF F S F F y =⋅=⨯⨯=△. 故选：D. 【点睛】方法点睛：本题考查椭圆中焦点三角形面积的计算，常用以下两种方法求解： （1）求出顶点P 的坐标，利用三角形面积公式求解；（2）利用余弦定理和椭圆的定义求得12PF PF ⋅的值，利用三角形面积公式求解.8．D解析：D 【分析】设设()0,4E ，由12224PF PF a PF =+=+，可得124P PF PQ PQ F +++=，当且仅当,P Q ，()0,4E 和2F 四点共线时取得最小值，进而可得25EF =，设()2,0F c 即可求出c 的值，进而可求出b 的值，由by x a=±可得渐近线方程.【详解】设()0,4E ，由双曲线的定义可知：12224PF PF a PF =+=+， 所以124P PF PQ PQ F +++=，当,P Q 在圆心()0,4E 和2F 连线上时，1PF PQ +最小，()2mi 2n 1PFPQ EF =-+，所以2418EF +-=，解得25EF =， 设()2,0F c ()0c >5=，解得3c =，因为2a =，所以b =， 所以双曲线的渐进线为：b y x x a =±=， 故选：D 【点睛】关键点点睛：本题解题的关键点是由双曲线的定义可得124P PF PQ PQ F +++=，利用2,,,P Q E F 共线时()2mi 2n1PF PQEF =-+求出25EF =.9．B解析：B 【分析】利用点差法求出直线斜率，即可得出直线方程. 【详解】由直线:(1)(2)230l a x a y a +++--=得(2)(23)0a x y x y +-++-= 所以20230x y x y +-=⎧⎨+-=⎩ 解得11x y =⎧⎨=⎩则()1,1P设1122(,),(,)A x y B x y ，则21122244x y x y ⎧=⎨=⎩，两式相减得121212()()4()x x x x y y -+=-， 即121212142AB y y x x k x x -+===-， 则直线方程为11(x 1)2y -=-，即210x y -+=. 故选：B. 【点睛】方法点晴：点差法是求解中点弦有关问题的常用方法.10．D解析：D【分析】首先利用,,A F B 三点共线，求点B 的坐标，再利用焦点弦长公式求AB . 【详解】4y =时，1644x x =⇒=，即()4,4A ，()1,0F ，设2,4y B y ⎛⎫ ⎪⎝⎭，利用,,A F B 三点共线可知24314y y =-，化简得2340y y --=，解得：1y =-或4y =（舍）当1y =-时，14x =，即()4,4A ，1,14B ⎛⎫- ⎪⎝⎭， 所以121254244AB x x p =++=++=. 故选：D 【点睛】关键点点睛：本题考查直线与抛物线相交，焦点弦问题，重点是求点B 的坐标.11．C解析：C 【分析】由a 为大于零的常数，可知5a a+的最小值，再根据两点间距离公式得几何意义以及椭圆定义判断轨迹. 【详解】的几何意义为点(),P x y 与点(0,2)A 间的距离，的几何意义为点(),P x y 与点(0,2)B -间的距离，且4AB =又由a为大于零的常数，可知54a a +≥=>， 当且仅当5a a=，即a =54a a=+>， 即动点P 到点A 与到点B 的距离之和为定值，且大于AB ， 所以动点P 的轨迹为椭圆， 故选：C. 【点睛】在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误． 椭圆的定义揭示了椭圆的本质属性，正确理解掌握定义是关键，应注意定义中的常数大于|F 1F 2|，避免了动点轨迹是线段或不存在的情况．12．D解析：D 【分析】先根据双曲线的方程求解出双曲线的渐近线方程，再根据点到直线的距离公式求解出抛物线方程中的p ，则抛物线方程可求. 【详解】双曲线2C 的渐近线方程是22026x y -=，即y =.因为抛物线的焦点()0,02p F p ⎛⎫> ⎪⎝⎭0y -=的距离为2，2=，即8p =，所以1C 的标准方程是216x y =，故选：D ． 【点睛】方法点睛：求解双曲线方程的渐近线方程的技巧：已知双曲线方程22221x y a b-=或22221y x a b -=，求解其渐近线方程只需要将方程中的“1”变为“0”，由此得到的y 关于x 的一次方程即为渐近线方程. 二、填空题13．【分析】先利用点求抛物线方程利用相切关系求切线再分别联立直线和抛物线求出点即求出直线方程【详解】在抛物线上故即抛物线方程为设过点与圆相切的直线的方程为：即则圆心到切线的距离解得如图直线直线联立得故由 解析：3640x y ++=【分析】先利用点(2,2)A 求抛物线方程，利用相切关系求切线,AB AC ，再分别联立直线和抛物线求出点,B C ，即求出直线BC 方程. 【详解】(2,2)A 在抛物线22y px =上，故2222p =⨯，即1p =，抛物线方程为22y x =，设过点(2,2)A 与圆22(2)1x y -+=相切的直线的方程为：()22y k x -=-，即220kx y k -+-=，则圆心()2,0到切线的距离1d ==，解得k =，如图，直线):22AB y x -=-，直线):22AC y x -=-.联立)22322y x y x⎧-=-⎪⎨=⎪⎩，得()23431416830x x ++-=，故1683A B x x -=，由2A x =得843B x -=，故236B y -= 联立)22322y x y x⎧-=-⎪⎨=⎪⎩，得()23431416830x x -++=，故1633A C x x +=，由2A x =得8433C x +=，故2363C y -=， 故2362364B C y y ---+==-，又由,B C 在抛物线上可知， 直线BC 的斜率为22221114222B C B C BC B C B C B C y y y y k x x y y y y --=====--+--，故直线BC 的方程为2361843323y x ⎛--=-- ⎝⎭，即3640x y ++=. 故答案为：3640x y ++=14．【分析】设点设直线的方程为联立直线与抛物线的方程列出韦达定理推导出利用基本不等式可求得的最小值【详解】若直线与轴重合则直线与抛物线只有一个交点不合乎题意易知抛物线的焦点为准线方程为设点设直线的方程为解析：92【分析】设点()11,A x y 、()22,B x y ，设直线AB 的方程为12x my =+，联立直线AB 与抛物线C 的方程，列出韦达定理，推导出112AF BF+=，利用基本不等式可求得4AF BF +的最小值. 【详解】若直线AB 与x 轴重合，则直线AB 与抛物线C 只有一个交点，不合乎题意.易知抛物线C 的焦点为1,02F ⎛⎫⎪⎝⎭，准线方程为12x =-，设点()11,A x y 、()22,B x y ，设直线AB 的方程为12x my =+， 联立2122x my y x⎧=+⎪⎨⎪=⎩，整理可得2210y my --=，2440m ∆=+>，由韦达定理可得122y y m +=，121y y =-，()()()12121212211111*********m y y AF BF my my my my x x +++=+=+=++++++()()21222212122222121m y y m m y y m y y m m +++===+++-++， ()4111144522AF BF AF BF AF BF AF BF BF AF ⎛⎫⎛⎫∴+=++=++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭19522⎛≥+= ⎝， 当且仅当2AF BF =时，等号成立，因此，4AF BF +的最小值为92. 故答案为：92. 【点睛】结论点睛：过抛物线的焦点F 的直线与抛物线交于A 、B 两点，则112AF BF p+=. 15．【分析】根据题意构建渐近线的斜率与3的不等关系再利用求得离心率范围即可【详解】过右焦点与渐近线平行的直线与双曲线有一个交点且一条渐近线的斜率为若斜率为的直线与双曲线的左右两支分别相交则则离心率故答案解析：)+∞【分析】根据题意构建渐近线的斜率与3的不等关系，再利用e =求得离心率范围即可. 【详解】过右焦点与渐近线平行的直线与双曲线有一个交点，且一条渐近线的斜率为b a， 若斜率为3的直线与双曲线的左右两支分别相交，则3ba>，则离心率c e a ===>.故答案为：)+∞.【点睛】求双曲线离心率常见方法：（1）直接法：由a ，c 直接计算离心率ce a=； （2）构建齐次式：利用已知条件和双曲线的几何关系构建关于a ，b ，c 的方程和不等式，利用222b c a =-和ce a=转化成关于e 的方程和不等式，通过解方程和不等式即求得离心率的值或取值范围.16．【分析】设双曲线半焦距为双曲线的渐近线方程为则设直线的方程为然后直线的方程和另一渐近线方程联立求出点从而可求出直线的斜率再由可得两直线的斜率乘积为从而得进而可求出双曲线的离心率【详解】解：设双曲线半解析：3【分析】设双曲线半焦距为c ，双曲线的渐近线方程为b y x a =±，则(,0),(,)bcF c A c a，设直线BF 的方程为()by x c a=-，然后直线BF 的方程和另一渐近线方程联立，求出点,22c bc B a ⎛⎫- ⎪⎝⎭，从而可求出直线AB 的斜率，再由AB OB ⊥，可得两直线的斜率乘积为1-，从而得2213b a =，进而可求出双曲线的离心率【详解】解：设双曲线半焦距为c ，双曲线的渐近线方程为b y x a =±，则(,0),(,)bc F c A c a， 设直线BF 的方程为()by x c a=-， 由()b y x c a b y x a ⎧=-⎪⎪⎨⎪=-⎪⎩，得22c x bc y a ⎧=⎪⎪⎨⎪=-⎪⎩，所以,22c bc B a ⎛⎫- ⎪⎝⎭， 所以直线AB 的斜率为322AB bc bcb a a kc a c --==-，因为AB OB ⊥，所以3()1AB OB b bk k a a⋅=⨯-=-， 所以2213b a =，所以双曲线的离心率为3e ==故答案为：3【点睛】关键点点睛：此题考查直线与双曲线的位置关系，考查求双曲线的离心率的方法，解题的关键是灵活运用双曲线的几何性质，考查计算能力，属于中档题17．【分析】首先设出直线利用直线与圆相切求直线方程再利用弦长公式求弦长【详解】因为直线过双曲线的右焦点且与圆相切所以直线的斜率存在设直线方程为()由直线与圆相切知解得或当时双曲线的一条渐近线的斜率是该直解析：【分析】首先设出直线，利用直线与圆相切，求直线方程，再利用弦长公式求弦长AB . 【详解】因为直线过双曲线的右焦点且与圆相切，所以直线的斜率存在，设直线方程为0y k -=(2x -)2=，解得1k =或17k =，当17k =时，双曲线的一条渐近线的斜率是3，173<，该直线不与双曲线右支相交于两点，故舍去；所以直线方程为2y x =-，联立双曲线方程，消元得2212150x x -+=.设()11,A x y ，()22,B x y ，则126x x +=，12152x x =，所以12||AB x =-===.故答案为：【点睛】易错点点睛：利用直线与圆相切，得到两个斜率1k =或17k =，需舍去一个，否则出现增根.18．【分析】设利用可得即可求得利用两点间距离公式求出面积利用基本不等式即可求最值【详解】设由可得解得：所以当且仅当时等号成立所以的面积的最小值为故答案为：【点睛】关键点点睛：本题解题的关键点是设坐标采用 解析：16【分析】设211,4y A y ⎛⎫ ⎪⎝⎭，222,4y B y ⎛⎫⎪⎝⎭，利用OA OB ⊥可得0OA OB ⋅=即可求得1216y y =-，利用两点间距离公式求出OA 、OB ，面积12OABS OA OB =，利用基本不等式即可求最值. 【详解】设211,4y A y ⎛⎫ ⎪⎝⎭，222,4y B y ⎛⎫⎪⎝⎭， 由OA OB ⊥可得2212121212104416y y y y OA OB y y y y ⎛⎫⋅=⨯+=+= ⎪⎝⎭， 解得：1216y y =-，1OA y ==OB y ==11122OABSO y O y A B ==12⨯=≥=，22221212216161616y y y y +=+≥=，所以16OABS≥==，当且仅当12y y =时等号成立， 所以OAB 的面积的最小值为16， 故答案为：16. 【点睛】关键点点睛：本题解题的关键点是设A ，B 坐标，采用设而不求的方法，将OA OB ⊥转化为0OA OB ⋅=，求出参数之间的关系，再利用基本不等式求12OABSOA OB =的最值. 19．【分析】求出双曲线的两个焦点坐标和渐近线方程再求圆的方程与渐近线方程联立可得MN 两点的横坐标由即为横坐标的绝对值的比可得答案【详解】由已知得取双曲线的一条渐近线所以圆的方程为由整理得解得取双曲线的另解析：32【分析】求出双曲线的两个焦点坐标和渐近线方程，再求圆的方程与渐近线方程联立可得M ，N 两点的横坐标，由OMON即为横坐标的绝对值的比可得答案.【详解】由已知得2221,7,8a b c ===，2c =，12(F F -，取双曲线的一条渐近线y =，所以圆的方程为(2232x y +=-，由(2232y x y ⎧=⎪⎨-+=⎪⎩整理得2260x -=，解得2N M x x ==，32M NM O x x O N===.取双曲线的另一条渐近线y =，(2232y x y ⎧=⎪⎨-+=⎪⎩整理得2260x -=与上同，综上32OM ON=. 故答案为：32. 【点睛】关键点点睛：本题考查了直线与双曲线、圆的位置关系，解答本题的关键是求出渐近线与圆的方程然后联立，得到M ，N 两点的横坐标再由绝对值做比值，考查了学生的运算求解能力.20．(或)【分析】先根据的形状先确定出点坐标然后将点坐标代入双曲线方程根据的齐次式求解出离心率的值【详解】因为是以为直角顶点的等腰直角三角形不妨假设在第一象限所以所以所以所以所以所以所以所以又因为所以故【分析】先根据OPF △的形状先确定出P 点坐标，然后将P 点坐标代入双曲线方程，根据,a c 的齐次式求解出离心率的值. 【详解】因为OPF △是以P 为直角顶点的等腰直角三角形， 不妨假设P 在第一象限，所以122P P F c x y x ===，所以,22c c P ⎛⎫ ⎪⎝⎭， 所以2222144c c a b-=，所以2222224c b c a a b -=，所以()()222222224cca c a a c a --=-，所以4224640c a c a -+=，所以42640e e -+=，所以23e ==又因为1e >，所以e ===，2）. 【点睛】思路点睛：利用齐次式求解椭圆或双曲线的离心率的一般步骤： （1）根据已知条件，先得到关于,,a b c 的方程；（2）结合222a b c =+或222c a b =+将方程中的b 替换为,a c 的形式；（3）方程的左右两边同除以a 的对应次方，由此得到关于离心率e 的方程，从而求解出离心率e 的值.三、解答题21．（1）22y x =；（2）存在，P 点坐标为()2,0-. 【分析】（1）利用焦半径公式表示||||MF NF =，代入坐标2x =，求MN 的长度，并表示MNF 的周长，求p ；（2）假设存在点()0,0P x ，设:2l x my =+，与抛物线方程联立，利用根与系数的关系表示0MP NP k k +=，求定点0x 的值. 【详解】（1）当MN 与x 轴垂直时，||||22pMF NF ==+，||MN =，从而有49p ++= 解得1p =，所以C 的方程为22y x =；（2）设()0,0P x ，()11,M x y ，()22,N x y ，由题可知直线l 斜率不为零，设:2l x my =+，代入抛物线方程22y x =消去x ，得2240y my --=，从而122y y m +=，124y y =-，①由OPM OPN ∠=∠可得0MP NP k k +=， 而121020MP NP y y k k x x x x +=+--12102022y y my x my x =++-+-()()()()1201210202222my y x y y my x my x +-+=+-+-将①代入，从而得()()102042022m mx my x my x --=+-+-恒成立，所以02x =-， 因此存在点P 满足题意，P 点坐标为()2,0-. 【点睛】思路点睛：定点问题解决步骤：（1）设直线代入二次曲线方程，整理成一元二次方程； （2）韦达定理列出两根和及两根积；（3）写出定点满足的关系，整体代入两根和及两根积； （4）整理（3）所得表达式探求其恒成立的条件.22．（1）24y x =；（2）直线l 过定点，定点坐标为()0,1-，证明见解析. 【分析】（1）联立直线方程和抛物线方程，求出交点的坐标后利用弦长公式可求p 的值，从而可求抛物线的方程.（2）设直线l 的方程为x my b =+，联立直线方程和抛物线方程，消去x 后利用韦达定理化简斜率之和，从而可得b m =，故可求定点坐标.我们也可以设211,4y M y ⎛⎫⎪ ⎪⎝⎭，222,4y N y ⎛⎫⎪⎝⎭，用坐标表示斜率之和，再用该两点的坐标表示直线l ，化简后可得直线过定点. 【详解】（1）由2,2,y x y px =⎧⎨=⎩解得10x =，22x p =，因为直线y x =被抛物线()2:20C y px p =>截得的弦长为0p -=，0p >，解得2p =， 所以抛物线C 的方程为24y x =.（2）法一： 设直线l 的方程为x my b =+，()11,M x y ，()22,N x y ，由2,4,x my b y x =+⎧⎨=⎩得2440y my b --=，所以124y y m +=，124y y b =-，因为点()1,2A ，且直线AM ，AN 的斜率之和为4，所以121222411y y x x --+=--，而2114y x =，2224y x =，化简得12120y y y y ++=， 所以440m b -=，即b m =， 所以直线l 的方程为()1x m y =+， 所以直线l 过定点，定点坐标为()0,1-.法二： 设211,4y M y ⎛⎫ ⎪ ⎪⎝⎭，222,4y N y ⎛⎫⎪⎝⎭， 因为点()1,2A ，且直线AM ，AN 的斜率之和为4，所以1222122241144y y y y --+=--，即12120y y y y ++=， ①当210y y +≠时，直线l 的方程为221112221444y yy y y x y y ⎛⎫--=- ⎪⎝⎭-即2141y x y y =--， 所以直线l 过定点，定点坐标为()0,1-；②当210y y +=时，120y y =，所以120y y ==，不满足题意. 所以直线l 过定点，定点坐标为()0,1-. 【点睛】方法点睛：. 直线与抛物线的位置关系中的定点、定值、最值问题，一般可通过联立方程组并消元得到关于x 或y 的一元二次方程，再把要求解的目标代数式化为关于两个的交点横坐标或纵坐标的关系式，该关系中含有1212,x x x x +或1212,y y y y +，最后利用韦达定理把关系式转化为若干变量的方程（或函数），从而可求定点、定值、最值问题，也可以设出交点坐标，用交点坐标表示目标代数式，从而解决定点、定值、最值问题.23．（1）221(84x y x +=≠±；（2）证明见解析，()3,0-.【分析】（1）首先设点(),P x y ，利用12PA PB k k ⋅=-，转化为关于,x y 的方程；（2）方法一，首先由椭圆的对称性可知定点必在x 轴上，设:2MN x my =-，与椭圆方程联立，由根与系数的关系得到()1212my y y y =-+，并求出直线ND 的方程，求与x 轴的交点；方法二，直线:2MN x my =-与椭圆方程联立后，利用求根公式求得两个交点的纵坐标，再代入直线ND 的方程，化简，求定点的坐标. 【详解】（1）设(),P x y ，由题意得：12PA PB k k ⋅=-12=-，化简得22184x y +=．又x ≠±，∴点P的轨迹方程为221(84x y x +=≠±．（2）方法一：由椭圆的对称性知，直线ND 过的定点必在x 轴上， 由题意得直线MN 的斜率不为0，设:2MN x my =-，与22184x y +=联立消去x 得：()222440m y my +--=， ()23210m ∆=+>恒成立，设()11,M x y ，()22,N x y ，则()14,D y -，12242m y y m +=+，12242y y m -=+， ∴()1212my y y y =-+，2112:(4)4y y ND y x y x -=+++，令0y =， ∴()()12122121424y x y my x y y y y +++=-=---()1211212121221y y y my y y y y y y -+++=-=-=--，3x =-，∴直线ND 过定点()3,0-．方法二：由题意可得直线MN 的斜率不为0，设:2MN x my =-，与22184x y +=联立消去x 得：()222440m y my +--=， ()23210m ∆=+>恒成立，设()11,M x y ，()22,N x y ，则()14,D y -，12242m y y m +=+，12242y y m -=+，()12422m y m -=+，()22422m y m +=+， ()2112121122(4)2:(4)42y y x my y y y y ND y x y x my -+++-=++=++2244)2222m x m m m my -+++++=+2222(4)222x m m my +-++==+ ∴3x =-时0y =， ∴直线ND 过定点()3,0-. 【点睛】关键点点睛：本题考查椭圆中直线过定点问题，第一个关键是首先判断定点在x 轴上，方法一的关键是利用根与系数的关系得到()1212my y y y =-+，再代回直线方程求交点，方法二的关键是变形，化简.24．（1）22:14x E y +=；（2）32,,2⎛⎛⎫-⎪⎝⎭⎝⎭. 【分析】（1）由点在椭圆上及椭圆离心率的定义列方程可得21a b c ⎧=⎪=⎨⎪=⎩，即可得解；（2）设直线方程，与椭圆方程联立，结合韦达定理，转化条件为0OC OB⋅>，运算即可得解. 【详解】 （1）点⎛- ⎝⎭在椭圆22221(0)x y a b ab+=>>上，∴221314a b +=，∴ce a ==由222a b c =+解得21a b c ⎧=⎪=⎨⎪=⎩，∴轨迹22:14x E y +=；（2）依题意可知，直线l 的斜率存在且不为零，∴设:2l y kx =+，1122(,),(,)B x y C x y ，∴22214y kx x y =+⎧⎪⎨+=⎪⎩，化简整理有：()221416120k x kx +++=， ∴()221648(14)0k k ∆=-+>得k >k <， 且1221614kx x k+=-+，1221214x x k ⋅=+， 由COB ∠为锐角， ∴2121212122122()414OC OB x x y y k x x k x x k ⋅=+=+++++ 22222121232=+40141414k k k k k -+>+++， ∴222212+12324161640k k k k -++=->， ∴22k -<<，∴2k -<<2k <<，∴直线l的斜率的范围是32,,2⎛⎛⎫-⎪⎝⎭⎝⎭. 【点睛】关键点点睛：解决本题的关键是由平面数量积的定义转化COB ∠为锐角为0OC OB ⋅>，结合韦达定理运算即可得解.25．（1）证明见解析；（2）()2224x y +-=. 【分析】（1）设出直线方程与抛物线方程联立，由OA OB ⊥转化为坐标形式再利用韦达定理表示可得答案；（2）判断出直线AB 过定点()0,4M ，由⊥OD AB 于点D ，得到点D 在以OM 为直径的圆上可得答案. 【详解】（1）证明：由题意直线AB 的斜率存在，可设方程为y kx b =+，0b ≠，由24y kx b x y=+⎧⎨=⎩可得2440x kx b --=， 所以1x ，2x 是该方程的两根，所以216160k b ∆=+>， 且124x x k +=，124x x b =-，OA OB ∴⊥，12120x x y y ∴+=，即()()()()221212121210x x kx b kx b kx xbk x x b +++=++++=，可得()2224140kb k b b-+++=，0b ≠，解得4b =，此时216160k b ∆=+>成立，12416x x b ∴=-=-.（2）由（1）可得直线AB 的方程为4y kx =+， 所以直线AB 过定点()0,4M ，又⊥OD AB 于点D ，所以点D 在以OM 为直径的圆上， 可得点D 的轨迹方程为()2224x y +-=. 【点睛】本题考查了直线与抛物线的位置关系，利用韦达定理解决问题时注意判别式的范围，要熟练掌握基础知识及转化能力. 26．（1）24y x =；（2）16||3AB =． 【分析】（1）根据抛物线定义可得答案；（2）由点F 是AC 的中点可得A 点的坐标，设出直线AB 方程与抛物线方程联立，利用韦达定理再得B 点坐标，再由两点间的距离公式可得答案． 【详解】（1）因为动点P 到定点(1,0)F 的距离与到定直线:1l x =-的距离相等， 由抛物线定义可得曲线Γ为抛物线，设其方程为22(0)y px p =>，则12p=， 所以2p =，曲线Γ的方程为24y x =.（2）设过点F 的直线方程为1x my =+，设1122(,),(,)A x y B x y ，且120,0y y ><，0(1,)C y -， 由214x my y x=+⎧⎨=⎩整理得，2440y my --=，所以124y y =-， 因为点F 是AC 的中点，所以1112x -=，解得13x =，所以211412y x ==，得1y =(3,A ，又因为124y y =-，所以23y =-，代入抛物线方程得213x =，所以1,3B ⎛ ⎝⎭，所以163AB ===. 【点睛】本题考查了抛物线方程、直线与抛物线的位置关系及弦长，关键点是由点F是AC的中点可得A点的坐标，利用韦达定理再得B点坐标，考查了学生的基础知识、基本技能.。

北师大版高中数学选修1-1第二章《圆锥曲线与方程》测试题(有答案解析)(1)

北师大版高中数学选修1-1第二章《圆锥曲线与方程》测试题(有答案解析)(1)

一、选择题1．已知()5,0F 是双曲线()2222:=10,0x y C a b a b->>的右焦点，点(A .若对双曲线C 左支上的任意点M ，均有10MA MF +≥成立，则双曲线C 的离心率的最大值为（ ）A B ．5C ．52D ．62．已知抛物线2:2C y px =的焦点为F ，过抛物线上两点A ，B 分别向抛物线C 的准线作垂线，垂足为M ，N ，且()95OBN OAM ABNM S S S +=梯形△△，当直线AB 经过点F 且点F 到抛物线C 准线的距离为4时，直线l 的斜率为（ ）A ．2±B ．±C ．8±D ．±3．双曲线()2222:10,0x y C a b a b-=>>的一条渐近线被圆()2223x y -+=截得的弦长为2，则C 的离心率为（ ）A ．3B ．2C D4．已知双曲线22221x y a b -=的两个焦点分别为21(,0)(,0)(0)F c F c c ->，过点2,0a P c ⎛⎫ ⎪⎝⎭的直线与双曲线的左右两支分别交于,A B 两点，且122F A F B =-，求双曲线的离心率（ ）A BC D5．设直线l 与圆C ：22(2)3x y -+=相切于N ，与抛物线22(0)y px p =>交于,A B 两点，且N 是线段AB 的中点，若直线l 有且只有4条，则p 的取值范围是（ ）A ．B ．(1,3)C ．(0,3)D ．6．已知斜率为(0)k k >的直线l 与抛物线2:4C y x =交于,A B 两点，O 为坐标原点，M 是线段AB 的中点，F 是C 的焦点，OFM ∆的面积等于3，则k =（ ）A ．14B ．13C ．12D 7．已知F 是双曲线2222:1(0)x y E a b a b-=>>的左焦点，过点F 的直线与双曲线E 的左支和两条渐近线依次交于,,A B C 三点，若||||||FA AB BC ==，则双曲线E 的离心率为（ ）A BC ．2D 8．已知椭圆()2222:10x y C a b a b+=>>的左右焦点分别是F 1，F 2，过右焦点F 2且斜率为的直线与椭圆相交于A ，B 两点，若满足223AF F B =，则椭圆的离心率为（ ）A ．35B ．12C．2D．29．已知M 是抛物线2:C x y =上一点，记点M 到抛物线C 的准线的距离为1d ，到直线:3490l x y ++=的距离为2d ，则12d d +的最小值为（ ）A ．1B ．2C ．3D ．410．顶点在原点，经过点()，且以坐标轴为轴的抛物线的标准方程是（ ） A．2y =或212=-x y B．2y =-或212=-x y C．2y =或212x y =D．2y =-或212x y =11．已知抛物线2:C x y =，点()2,0A ，()0,2B -，点P 在抛物线上，则满足PAB △为直角三角形的点P 的个数有（ ） A ．2B ．4C ．6D ．812．“04a <<”是“方程2214x y a a+=-表示为椭圆”的（ ）A ．充分必要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件二、填空题13．已知椭圆22221(0)x y a b a b+=>>的短轴长为8，上顶点为A ，左顶点为B ，12,F F 分别是椭圆的左､右焦点，且1F AB 的面积为4，点P 为椭圆上的任意一点，则1211PF PF +的取值范围为___________. 14．已知椭圆C 的两个焦点分别为1(2,0)F -，2(2,0)F ，离心率为12e =，点P 在椭圆C 上，且1230F PF ∠=，则12F PF △的面积为__________．15．在双曲线22221x y a b-=上有一点P ，12,F F 分别为该双曲线的左、右焦点，121290,F PF F PF ∠=︒的三条边长成等差数列，则双曲线的离心率是_______.16．已知双曲线2222:1(0,0)y x C a b a b-=>>，直线x b =与C 的两条渐近线分别交于A ，B 两点，过A 作圆222:(2)M x b y b ++=的切线，D 为其中一个切点若||||AD AB =，则C 的离心率为__________．17．已知曲线22:1(0)x y C mn m n+=≠.给出下列四个命题：①曲线C 过坐标原点；②若0m n =>，则C 是圆，其半径为m ； ③若0m n >>，则C 是椭圆，其焦点在x 轴上；④若0mn <，则C 是双曲线，其渐近线方程为y =. 其中所有真命题的序号是___．18．已知抛物线y 2=4x 的焦点为F ，过点F 的直线AB 交抛物线于A ,B 两点，交准线于点C ，若|BC |=2|BF |，则|AB |=_____.19．在平面直角坐标系xOy 中，设双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为F ，若双曲线的右支上存在一点P ，使得△OPF 是以P 为直角顶点的等腰直角三角形，则双曲线C 的离心率为__________.20．已知下列几个命题：①ABC 的两个顶点为(4,0)A -，(4,0)B ，周长为18，则C 点轨迹方程为221259x y +=； ②“1x >”是“||0x >”的必要不充分条件；③已知命题:33p ≥，:34q >，则p q ∨为真，p q ∧为假，p ⌝为假；④双曲线221916x y -=-的离心率为54．其中正确的命题的序号为_____．三、解答题21．已知抛物线2:2(0)C y px p =>的焦点为F ，准线为l ，若点P 在C 上，点E 在l 上，且PEF 是边长为4的正三角形． （1）求C 的方程；（2）过F 作直线m ，交抛物线C 于A ，B 两点，若直线AB 中点的纵坐标为1-，求直线m 的方程．22．已知动圆M 过点1(2,0),F - 且动圆M 内切于定圆2F ：22(2)32,x y -+= 记动圆M 圆心的轨迹为曲线Γ. （1）求曲线Γ的方程；（2）若A 、B 是曲线Γ上两点，点20,3P ⎛⎫⎪⎝⎭满足20,PF PA PB ++= 求直线AB 的方程.23．已知动圆与直线1x =-相交于,A B 两点，且||AB =． （1）当动圆过定点(2,0)时，求动圆圆心C 的轨迹方程；（2）过点(1,0)-的直线l 交（1）中动圆圆心C 的轨迹于,M N 两点，点P 为,M N 的中点，过点P 垂直于直线l 的直线交x 轴于点Q ，求点Q 的横坐标的取值范围．24．已知椭圆2222:1(0)x y C a b a b+=>>的两个焦点与短轴的一个端点恰好围成面积为3的等边三角形.（1）求C 的方程；（2）如图，设C 的左，右顶点分别为,A B ，右焦点为F ，P 是C 上异于,A B 的动点，直线AP 与直线x a =交于点D ，当点P 运动时，试判断以BD 为直径的圆与直线PF 的位置关系，并加以证明.25．已知椭圆()2222:10x y C a b a b+=>>的左右焦点分别为1F 、2F ，点M 为短轴的一个端点，离心率为12，12MF F △的面积3S = （1）求椭圆C 的方程；（2）设A 是椭圆上的一点，B 是点A 关于x 轴的对称点，P 是椭圆C 上异于A 、B 的任意一点，且直线PA 、PB 分别于x 轴交于不同的点C 、D ，O 为坐标原点，求POC POD S S ⋅△△的最大值，并求出此时P 点的坐标26．在平面直角坐标系xOy 中，设动点P 到定点(1,0)F 的距离与到定直线:1l x =-的距离相等，记P 的轨迹为曲线Γ． （1）求曲线Γ的方程；（2）过点F 的直线交曲线Γ于点A 、B （其中点A 在第一象限），交直线l 于点C ，且点F 是AC 的中点，求线段AB 的长．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C【分析】设E 是双曲线的左焦点，利用双曲线的定义把MF 转化为ME 后易得MA ME +的最小值，从而得a 的最小值，由此得离心率的最大值． 【详解】设E 是双曲线的左焦点，M 在左支上，则2MF ME a -=，2MF ME a =+，22MA MF MA ME a EA a +=++≥+，当且仅当E A M ,,三点共线时等号成立．则222(5)(11)210EA a a +=-++≥，2a ≥，所以552c e a a ==≤． 故选：C ．【点睛】思路点睛：本题考查双曲线的定义的应用．在涉及双曲线上的点与一个焦点和另外一个定点距离和或差的最值时，常常利用双曲线的定义把到已知焦点的距离转化为到另一焦点的距离，从而利用三点共线取得最值求解．2．B解析：B 【分析】根据题意，求得4p =，可得抛物线的方程，因为()95OBN OAM ABNM S S S +=梯形△△，所以49OMN OAB ABMN S S S +=梯形△△，根据面积公式，结合抛物线定义，即可求得AB ，不妨设AB 的斜率为k ，可得直线AB 的方程，与抛物线联立，根据韦达定理，可求得A B x x +的值，代入弦长公式，即可求得答案. 【详解】因为点F 到抛物线C 准线的距离为4，所以4p =，所以28y x =，设抛物线C 的准线与x 轴交于点H ，因为()95OBN OAM ABNM S S S +=梯形△△，所以()()11422192M N A BOMN OABABMNM N OH y yOF y y S S S AM BN y y ⋅-+⋅-+==+⋅-梯形△△，因为2OH OF ==，M N A B y y y y -=-，AM BN AB +=，所以449OMN OAB ABMN S S S AB +==梯形△△，则9AB =，显然直线AB 的斜率存在，不妨设为k ，则():2AB y k x =-， 与抛物线联立可得：()22224840k x k x k -++=， 从而284A B x x k+=+， 所以28489A B A kB x x =++=+=，解得22k =±. 故选：B【点睛】解题的关键是根据面积的关系，得到49OMN OAB ABMN S S S +=梯形△△，结合图象，可求得9AB =，再利用抛物线的弦长公式求解，考查分析计算，化简求值的能力，属中档题.3．D解析：D 【分析】设双曲线C 的渐近线方程为y kx =，其中bk a=±，利用圆的半径、渐近线截圆所得弦长的一半、弦心距三者满足勾股定理可求得k 的值，再利用21b e a ⎛⎫=+ ⎪⎝⎭可求得双曲线C 的离心率e 的值. 【详解】设双曲线C 的渐近线方程为y kx =，其中b k a=±， 圆()2223x y -+=的圆心坐标为()2,0，半径为3r =，圆心到直线y kx =的距离为221k d k =+，另一方面，由于圆的半径、渐近线截圆所得弦长的一半、弦心距三者满足勾股定理， 可得2212d r =-=，即2221k k =+，解得1k =±，1ba∴=， 因此，双曲线C 的离心率为22222212c c a b b e a a a a +⎛⎫====+= ⎪⎝⎭. 故选：D. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.4．B解析：B 【分析】先根据题意画出图形，再根据122F A F B=-，得到21F AF B B P ∽，根据相似比得到222a a c c c c ⎛⎫+=⨯- ⎪⎝⎭，即可求出离心率. 【详解】 解：如图所示：122F A F B =-，12//F A F B ∴，12AF B BF P ∴∽，且122F PF P=, 即222a a c c c c ⎛⎫+=⨯- ⎪⎝⎭， 两边同时除以a 得2a c c a c a a c ⎛⎫+=⨯- ⎪⎝⎭， 即122e e e e+=-， 又1e >，解得：e = 故选：B. 【点睛】关键点点睛：本题解题的关键是利用三角形相似比得到,a c 的关系式，进而求得离心率.5．B解析：B 【分析】根据l 有且只有4条，易知直线l 的斜率不存在时，有两条，得到直线l 斜率存在时，有两条，根据N 是线段AB 的中点，利用点差法得到0ky p =，再根据直线l 与圆C ：22(2)3x y -+=相切于N ，得到012y x k=--，结合得到02x p =-，2203y p =-再根据点N 在抛物线内部求解. 【详解】设()()()112200,,,,,A x y B x y N x y ， 因为l 有且只有4条，当直线l的斜率不存在时，有两条，即2=±x 所以直线l 斜率存在时，有两条， 因为AB 在抛物线上，所以21122222y px y px ⎧=⎨=⎩，两式相减得()2212122y y p x x -=-，因为N 是线段AB 的中点， 所以1202y y y +=， 所以12121202y y p pk x x y y y -===-+， 即0ky p =，因为直线l 与圆C ：22(2)3x y -+=相切于N ，所以0012y x k=--，即002x ky p -=-=-， 所以02x p =-，代入抛物线22y px =，得()222y p p =-，因为点N 在抛物线内部，所以()2022y p p <-，因为点N 在圆上，所以2200(2)3x y -+=，即2203p y +=， 所以2203y p =-，所以()220322y p p p =-<-，即2430p p -+<，解得13p <<， 故选：B 【点睛】方法点睛：解决直线与曲线的位置关系的相关问题，往往先把直线方程与曲线方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题．涉及弦中点的问题常常用“点差法”解决，往往会更简单．6．B解析：B 【分析】先求出F ,设出A 、B 、M ，用“点差法”找出121202y y k x x y -==-，利用OFM ∆的面积等于3计算出0y ，求出斜率k . 【详解】由抛物线2:4C y x =知：焦点()1,0F设()()()112200,,,,,,A x y B x y M x y因为M 是线段AB 的中点，所以0121222x x x y y y =+⎧⎨=+⎩将2114y x =和2224y x =两式相减可得：()2212124y y x x -=-，即121202y y k x x y -==- ∵000k y >∴>∴00113,62OFM S y y ∆=⨯⨯=∴=, 022163k y ∴===.故选：B 【点睛】“中点弦”问题通常用“点差法”处理.7．B解析：B 【分析】可设出直线AB ，与两渐近线方程联立，解出,B C y y ，利用两者的关系式求出直线的斜率.进而表示出A 的坐标，代入双曲线方程，得到,,a b c 的关系式，从而求得离心率. 【详解】||||||FA AB BC ==，故有1123A B C y y y == 故32B C y y =设过点F 的直线方程为：()y k x c =+联立()y k x c b y x a ⎧=+⎪⎨=-⎪⎩，解之得C C kc x bk a b kc a y b k a -⎧=⎪+⎪⎪⎨⎪=⎪⎪+⎩ 同理联立()y k x c by x a ⎧=+⎪⎨=⎪⎩解之得B B kc x bk a b kc a y b k a ⎧=⎪-⎪⎪⎨⎪=⎪⎪-⎩由32B C y y =有23b bkc kca ab b k k a a =+-，故3232b b k k a a +=- 解之得5bk a =-直线为：()5by x c a=-+则1212A B bc y y a -==，又()5A A b y x c a =-+ 故712A cx =-又A 在双曲线上可得：2222491144144c c a a -=得2213c a =故ca =故选：B 【点睛】双曲线的离心率是双曲线最重要的几何性质，求双曲线的离心率(或离心率的取值范围)，常见有两种方法： ①求出a ，c ，代入公式c e a=； ②只需要根据一个条件得到关于a ，b ，c 的齐次式，结合b 2＝c 2－a 2转化为a ，c 的齐次式，然后等式(不等式)两边分别除以a 或a 2转化为关于e 的方程(不等式)，解方程(不等式)即可得e (e 的取值范围)．8．D解析：D 【分析】首先设直线2x y c =+，与椭圆方程联立，得到根与系数的关系，同时由条件可得123y y =-，与根与系数的关系联立消元可得22213242a b c +=，求得椭圆的离心率. 【详解】设直线方程为2x y c =+，设()11,A x y ，()22,B x y ，与椭圆方程联立得22224102a b y cy b ⎛⎫++-= ⎪⎝⎭，2122212cy y a b+=-+，4122212b y y a b =-+ ① 223AF F B =，()()1122,3,c x y x c y ∴--=-， 得123y y =- ②，由①②联立可得，22213242a bc +=即22222323c a b a c =+=-，得2243c a =， 椭圆的离心率3c e a ==.故选：D 【点睛】方法点睛：本题考查直线与椭圆的位置关系的综合问题，考查学生的转化和计算能力，属于中档题型，求离心率是圆锥曲线常考题型，涉及的方法包含1.根据,,a b c 直接求，2.根据条件建立关于,a c 的齐次方程求解，3.根据几何关系找到,,a b c 的等量关系求解.9．B解析：B 【分析】作出图形，过点M 分别作抛物线C 的准线l 和直线3490x y ++=的垂线，垂足分别为点B 、A ，由抛物线的定义得出1d MB MF ==，可得出12d d MF MA +=+，利用FM 与直线3490x y ++=垂直时，12d d +取最小值，然后计算出点F 到直线3490x y ++=的距离，即为所求.【详解】 如下图所示：过点M 分别作抛物线C 的准线l 和直线3490x y ++=的垂线，垂足分别为点B 、A ， 由抛物线的定义可得1d MB MF ==，则12d d MF MA +=+， 当且仅当FM 与直线3490x y ++=垂直时，12d d +取最小值， 点F 到直线3490x y ++=的距离为22130494234d ⨯+⨯+==+，因此，12d d +的最小值为2. 故答案为：2. 【点睛】关键点点睛：本题求出抛物线上一点到准线和定直线的距离之和最小值问题，解题的关键就是利用F 、A 、M 三点共线取最小值，结合抛物线的定义转化求解.10．D解析：D 【分析】设出抛物线方程为22y mx =或22x ny =，代入点的坐标求出参数值可得． 【详解】设抛物线方程为22y mx =，则262(3)m =⋅-，63m =-，方程为2123y x =-， 或设方程为22x ny =，则2(3)26n -=⨯，14n =，方程为212x y =． 所以抛物线方程为2123y x =-或212x y =． 故选：D ． 【点睛】关键点点睛：抛物线的标准方程有四种形式，在不确定焦点位置（或开口方向时），需要分类讨论．象本题在抛物线过一点的坐标，则需要考虑焦点在x 轴和y 轴两种情况，焦点在x 轴上时可以直接设方程为2y mx =，代入点的坐标求出参数值，不必考虑焦点是在x轴正半轴还是在负半轴，焦点在y 轴也类似求解．11．B解析：B 【分析】分三个角为直角分别进行讨论，通过数形结合即得结果. 【详解】(1)若APB ∠为直角，如下图，即以AB 为直径的圆与抛物线的交点为P ，易见有O ，P 两个点符合题意；（2）若PAB ∠为直角，则过A 作直线垂直AB ，如下图，易见有P ，P '两个点符合题意；（3）若PBA ∠为直角，则过B 作直线垂直AB ，如上图，易见无交点，不存在点P 符合题意.综上，共有4个点符合题意. 故选：B. 【点睛】 关键点点睛：本题的解题关键在于对三个角为直角进行分类讨论，再结合数形结合思想即突破难点.12．C解析：C 【分析】根据方程2214x y a a +=-表示椭圆求出实数a 的取值范围，然后利用集合的包含关系可判断出“04a <<”是“方程2214x y a a+=-表示椭圆”的条件.【详解】若方程2214x y a a+=-表示椭圆，则0404a a a a >⎧⎪->⎨⎪≠-⎩，解得02a <<或24a <<， 记为{}02,24A a a a =<<<<或， 又记{}04B a a =<<，AB则“04a <<”是“方程2214x y a a+=-表示椭圆”的必要不充分条件.故选：C. 【点睛】关键点点睛：本题的关键是求出方程为椭圆的充分必要条件.二、填空题13．【分析】先根据的面积和短轴长得出abc的值求得的范围再通分化简为关于的函数利用二次函数求得最值即得取值范围【详解】由已知得故∵的面积为∴∴又故∴∴又而即∴当时最大为；当或时最小为即∴即即的取值范围为解析：25, 58⎡⎤⎢⎥⎣⎦【分析】先根据1F AB的面积和短轴长得出a，b，c的值，求得1PF的范围，再通分化简1211PF PF+为关于1PF的函数，利用二次函数求得最值，即得取值范围．【详解】由已知得28b=，故4b=，∵1F AB的面积为4，∴()142a c b-=，∴2a c-=，又()()22216a c a c a c b-=-+==，故8a c+=，∴5a=，3c=，∴12121211PF PFPF PF PF PF++=()()()22 1111111210101021010525aPF a PF PF PF PF PF PF====---+--+，又而1a c PF a c-≤≤+，即128PF≤≤，∴当15PF=时，()21525PF--+最大，为25；当12=PF或8时，()21525PF--+最小，为16，即()211652525PF≤--+≤，∴121011102516PF PF≤+≤，即12211558PF PF≤+≤.即1211PF PF+的取值范围为25,58⎡⎤⎢⎥⎣⎦.故答案为：25,58⎡⎤⎢⎥⎣⎦.关键点点睛：本题解题关键在于熟练掌握椭圆的性质1a c PF a c -≤≤+，结合椭圆定义和二次函数最值求法，即突破难点.14．【分析】由椭圆定义得由余弦定理得结合可得的值从而得答案【详解】由已知得所以由椭圆定义得由余弦定理得即则的面积为故答案为：【点睛】本题考查了椭圆的简单的性质关键点是利用余弦定理和三角形的面积公式解题考解析：24-【分析】由椭圆定义得128F P PF +=，由余弦定理得22212121212cos 2F P PF F F F PF F P PF +-∠=⨯，结合可得12F P PF ⨯的值，从而得答案. 【详解】 由已知得12,2c e ==，所以4a =， 由椭圆定义得12248F P PF +=⨯=， 由余弦定理得222121212123cos cos302F P PF F F F PF F P PF +-∠===⨯， 即()2121212216F P PFF P PF P PF +-⨯-=⨯，12F P PF⨯=， 则12F PF △的面积为12111sin 3024222S F P PF =⨯⨯=⨯=- 故答案为：24- 【点睛】本题考查了椭圆的简单的性质，关键点是利用余弦定理和三角形的面积公式解题，考查了学生分析问题、解决问题的能力.15．5【分析】首先根据双曲线的定义和等差数列的形式可设的三边长表示为最后根据勾股定理得到根据齐次方程求解离心率【详解】设并且的三边成等差数列最长的边为则三边长表示为又整理为两边同时除以得解得：或（舍）所解析：5 【分析】首先根据双曲线的定义和等差数列的形式，可设12PF F △的三边长表示为24,22,2c a c a c --，最后根据勾股定理得到22650c ac a -+=，根据齐次方程求解离心率.设12PF PF >，并且122PF PF a -=，12PF F △的三边成等差数列，最长的边为2c ，则三边长表示为24,22,2c a c a c --， 又1290F PF ∠=，()()22224224c a c a c ∴-+-=，整理为22650c ac a -+=，两边同时除以2a 得，2650e e -+=，解得：5e =或1e =（舍），所以双曲线的离心率是5. 故答案为：5 【点睛】方法点睛：本题考查直线与双曲线的位置关系的综合问题，求离心率是圆锥曲线常考题型，涉及的方法包含1.根据,,a b c 直接求，2.根据条件建立关于,a c 的齐次方程求解，3.根据几何关系找到,,a b c 的等量关系求解.16．【分析】将代入C 的渐近线方程可得点坐标利用两点间的距离根式可求导根据勾股定理可得再由可得代入即可【详解】将代入C 的渐近线方程得则不妨假设半径为因为是圆的切线所以即则因为所以即故故答案为：【点睛】本题解析：4【分析】将x b =代入C 的渐近线方程可得A 点坐标，利用两点间的距离根式可求导||AM ．根据勾股定理可得||AD ，再由||||AD AB =可得2238b a =，代入e =即可． 【详解】将x b =代入C 的渐近线方程ay x b=±，得y a =±，则||2AB a =． 不妨假设(),A b a ， (2,0)M b -，半径为b DM =， 222||(2)AM b b a =++，因为AD 是圆的切线，所以222||AD DMAM +=，即则||AD =因为||||AD AB =2a =，即2238b a =，故e ==．.【点睛】本题考查双曲线的简单的几何性质，考查直线与圆的位置关系，关键点是用,,b a c 表示||||AD AB =，考查了学生分析问题、解决问题的能力及计算能力.17．③④【分析】对于①根据点在曲线上的充分必要条件即可作出判定；对于②利用圆的标准方程可求得半径为的圆故错误；对于③利用椭圆的标准方程可以判定；对于④利用双曲线的标准方程可以作出判定将双曲线方程中的等号解析：③④ 【分析】对于①，根据点在曲线上的充分必要条件即可作出判定；对于②，利用圆的标准方程可m ③，利用椭圆的标准方程可以判定；对于④，利用双曲线的标准方程可以作出判定，将双曲线方程中的等号右边的常数改为0，得到220x y m n +=，整理即可得到渐近线方程. 【详解】对于①，将原点坐标(0,0)代入曲线22:1(0)x y C mn m n+=≠的方程，显然不成立，故曲线C 不过坐标原点，故错误；对于②，若0m n =>，曲线22:1(0)x y C mn m n+=≠的方程为222x y m m+==,对m 的圆，故错误；对于③，若0m n >>，则曲线22:1(0)x y C mn m n+=≠表示半长轴,a m =半短轴b n =x 轴，即焦点在x 轴上的椭圆，故正确；对于④，若0mn <，曲线22:1(0)x y C mn m n+=≠表示双曲线，渐近线方程为220x y m n+=，即n y x m =-，故正确.故答案为：③④. 【点睛】本题考查圆，椭圆，双曲线的标准方程和性质，难度不大，要熟练准确掌握圆，椭圆，双曲线的标准方程，注意若0mn <，曲线22:1(0)x y C mn m n+=≠表示双曲线，渐近线方程可用220x y m n+=表示.18．【分析】分别过作准线的垂线利用抛物线的定义将到焦点的距离转化到准线的距离利用已知和相似三角形的相似比建立关系式求解可算得弦长【详解】设可知如图作垂直于准线分别于则又解得故答案为：【点睛】1本题体现了解析：163【分析】分别过,A B 作准线的垂线，利用抛物线的定义将,A B 到焦点的距离转化到准线的距离，利用已知和相似三角形的相似比，建立关系式，求解,AF BF 可算得弦长. 【详解】设242y x px ==，可知2p =如图，作AM ,BN 垂直于准线分别于,M N ，则BN BF =，又2BC BN =，23CB CF =，23BN p ∴= 43BN =，83BC =，4CF ∴= 2CF AM CA=，244CF AM CA AM ∴==+，解得4AM =4AF ∴=416433AB AF BF ∴=+=+= 故答案为：163【点睛】1.本题体现了数形结合，解析几何问题，一定要注意对几何图形的研究，以便简化计算2. 抛物线方程中，字母p 的几何意义是抛物线的焦点F 到准线的距离，2p等于焦点到抛物线顶点的距离．牢记它对解题非常有益．19．(或)【分析】先根据的形状先确定出点坐标然后将点坐标代入双曲线方程根据的齐次式求解出离心率的值【详解】因为是以为直角顶点的等腰直角三角形不妨假设在第一象限所以所以所以所以所以所以所以所以又因为所以故【分析】先根据OPF △的形状先确定出P 点坐标，然后将P 点坐标代入双曲线方程，根据,a c 的齐次式求解出离心率的值. 【详解】因为OPF △是以P 为直角顶点的等腰直角三角形， 不妨假设P 在第一象限，所以122P P F c x y x ===，所以,22c c P ⎛⎫ ⎪⎝⎭， 所以2222144c c a b-=，所以2222224c b c a a b -=，所以()()222222224cca c a a c a --=-，所以4224640c a c a -+=，所以42640e e -+=，所以2632e ±==又因为1e >，所以2e ===，. 【点睛】思路点睛：利用齐次式求解椭圆或双曲线的离心率的一般步骤： （1）根据已知条件，先得到关于,,a b c 的方程；（2）结合222a b c =+或222c a b =+将方程中的b 替换为,a c 的形式；（3）方程的左右两边同除以a 的对应次方，由此得到关于离心率e 的方程，从而求解出离心率e 的值.20．③④【分析】根据椭圆定义可对①进行判断；根据必要不充分条件定义可对②进行判断；根据复合命题的真假可对③进行判断；根据双曲线的离心率公式可对④进行判断【详解】①的两个顶点为周长为18则C 点轨迹方程为当解析：③④ 【分析】根据椭圆定义可对①进行判断；根据必要不充分条件定义可对②进行判断；根据复合命题的真假可对③进行判断；根据双曲线的离心率公式可对④进行判断. 【详解】①ABC 的两个顶点为(4,0)A -，(4,0)B ，周长为18，则C 点轨迹方程为221259x y +=(5)x ≠±，当5x =±时，构不成三角形，错误； ②当0.1x =时，1x <，所以||0x >不一定有1x >，错误；③已知命题:33p ≥是真命题，:34q >是假命题，根据复合命题的真假判断，p q ∨为真，p q ∧为假，p ⌝为假，正确；④双曲线221916x y -=-，2216,9a b ==，所以22225c a b =+=，54c e a ==，正确． 其中正确的命题的序号是③④， 故答案为：③④. 【点睛】本题考查了椭圆定义、双曲线离心率、必要不充分条件及复合命题真假的判断，属于基础题.三、解答题21．（1）24y x =；（2）220x y +-=. 【分析】（1）设l 与x 轴交于点D ，根据PEF 是边长为4的正三角形．得到PE l ⊥，60PEF EFD ∠=∠=︒，然后由||cos60p DF EF ==求解.(2)设()11,A x y ，()22,B x y ，根据点A ，B 在抛物线上，由21122244y x y x ⎧=⎨=⎩，根据线段AB 中点的纵坐标为1-，利用“点差法”求解. 【详解】（1）因为PEF 是边长为4的正三角形． 则||||PE PF =，所以PE l ⊥，设l 与x 轴交于点D ，则60PEF EFD ∠=∠=︒，||4EF =， 所以||cos602p DF EF === 所以抛物线的方程为24y x =．（2）由（1）得抛物线C 的方程为24y x =，焦点(1,0)F ， 设A ，B 两点的坐标分别为()11,A x y ，()22,B x y ，由21122244y x y x ⎧=⎨=⎩，得()121212124y y x x x x y y -=≠-+， 因为线段AB 中点的纵坐标为1-，所以直线m 的斜率21442(1)2AB k y y ==-+-⨯=， 所以直线m 的方程为02(1)y x -=--， 即220x y +-=． 【点睛】方法点睛：解决直线与曲线的位置关系的相关问题，往往先把直线方程与曲线方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题．涉及弦中点的问题常常用“点差法”解决，往往会更简单．22．（1）22184x y +=；（2）230x y -+=.【分析】（1）根据两圆内切，以及圆过定点1(2,0),F -列式求轨迹方程；（2）利用重心坐标公式可知122x x +=-，122y y +=，再设直线AB 的方程为,y kx m =+与椭圆方程联立，利用根与系数的关系求解直线方程. 【详解】（1）由已知可得12MF rMF r⎧=⎪⎨=⎪⎩，两式相加可得12124,MF MF F F +=>= 则点M的轨迹是以1F 、2F 为焦点，长轴长为2,a c == 因此曲线Γ的方程是22 1.84y x +=(2)因为20PF PA PB ++=， 则点20,3P ⎛⎫⎪⎝⎭是2F AB 的重心， 易得直线AB 的斜率存在，设直线AB 的方程为()()1122,,,,y kx m A x y B x y =+，121212122020,,2,2333x x y y x x y y ++++∴==∴+=-+= 联立 22,184y kx m x y =+⎧⎪⎨+=⎪⎩ 消 y 得： ()222214280k x kmx m +++-=()()()2222222216421288840,840k m k m k m k m ∴∆=-+-=-+>∴-+>且 1224221kmx x k -+==-+① ()1211122222y y kx m kx m k x x m k m ∴+=+++=++=-+=②由①②解得 13,,22k m == 则直线AB 的方程为 13,22y x =+ 即 230.x y -+=【点睛】本题考查直线与椭圆的问题关系，本题的关键是根据20,PF PA PB ++=求得122x x +=-，122y y +=.23．（1）26y x =；（2）(4,)+∞. 【分析】（1）首先设圆心(),C x y ，利用条件表示半径，列等式求圆心的轨迹方程；（2）首先设直线:(1)MN y k x =+，与（1）的轨迹方程联立，利用根与系数的关系求得中点坐标，并表示过点P 的垂线方程，求与x 轴的交点Q 的坐标，并求范围. 【详解】解：（1）设(,)C x y ，则222(1)3(2)x x y ++=-+即26y x =，所以圆心C 的轨迹方程为：26y x = （2）设过点(1,0)-直线:(1)MN y k x =+，联立26(1)y x y k x ⎧=⎨=+⎩，消y 得：()2222260k x k x k +-+=所以()2242640k k ∆=-->，即232k <设()()1122,,,M x y N x y ，根据韦达定理得：1212262,1x x x x k+=-= 所以MN 的中点2331,P k k ⎛⎫-⎪⎝⎭过点P 的垂线为23131y x k k k ⎡⎤⎛⎫-=--- ⎪⎢⎥⎝⎭⎣⎦令0y =，则2324x k =+>， 所以点Q 的横坐标的取值范围(4,)+∞.【点睛】关键点点睛：本题的关键是第二问直线与抛物线方程联立后，不要忘记0∆>这个条件，否则求点Q 横坐标的取值范围就会出错.24．（1）22143x y +=；（2）相切，证明见解析.（1）待定系数法求C 的方程；（2）设出直线AP ，求出D 的坐标，表示出以BD 为直径的圆E 的方程，由“设而不求法”表示出E 到直线PF 的距离,判断出圆与直线PF 相切. 【详解】解：（1）设椭圆半焦距为c，依题意有122c ⋅= ∴1c =，22a c ==，b =故C 的方程为22143x y +=.（2）以BD 为直径的圆与直线PF 相切， 证明如下：易知()2,0A -，()2,0B ，()1,0F . 由题意可设直线AP 的方程为()()20y k x k =+≠. 则点D 坐标为()2,4k ，BD 中点E 的坐标为()2,2k .由()222143y k x x y ⎧=+⎪⎨+=⎪⎩得()2222341616120k x k x k +++-=.设点P 的坐标为()00,x y ，则2021612234k x k--=+. 所以2026834k x k -=+，()00212234k y k x k =+=+. ①当12k =±时，点P 的坐标为31,2⎛⎫± ⎪⎝⎭，点D 的坐标为()2,2±.直线PF x ⊥轴，此时以BD 为直径的圆()()22211x y -+±=与直线PF 相切. ②当12k ≠时，则直线PF 的斜率0204114PF y k k x k ==--， 所以直线PF 的方程为()24114ky x k =--. 点E 到直线PF 的距离322228142||1414k k k d k k k +-===+-. 又因为||4||2BD k d ==，故以BD 为直径的圆与直线PF 相切. 综上，当点P 运动时，以BD 为直径的圆与直线PF 相切.（1）待定系数法、代入法可以求二次曲线的标准方程；（2）“设而不求”是一种在解析几何中常见的解题方法，可以解决直线与二次曲线相交的问题.25．（1）22143x y+=；（2）POC PODS S⋅△△的最大值为3，此时P点坐标为(0,和(.【分析】（1）由面积得bc=,,a b c，得椭圆方程；（2）设()00,A x y，则()00,B x y-，不妨设y>，设()11,P x y，写出直线,PA PB方程，求得,C D两点的横坐标，计算C Dx x⋅，注意点,A P是椭圆上的点由此可得4C Dx x⋅=为常数，这样可计算出POC PODS S⋅△△＝2Py，最大值易得．【详解】解：（1）由12ca=，2a c=，得b=，又12122MF FS c b=⨯⨯=△所以1c=，2a=，b=所以椭圆C的方程为22143x y+=（2）设()00,A x y，则()00,B x y-，不妨设y>，设()11,P x y则直线PA的方程为：()011101y yy y x xx x--=--，令y=，得100101Cx y x yxy y-=-，同理100101Dx y x yxy y+=+，所以222210012201C Dx y x yx xy y-⋅=-，又点A与点P均在椭圆上，故220413yx⎛⎫=-⎪⎝⎭，2211413yx⎛⎫=-⎪⎝⎭，得()222212201012222010141414334C Dyyy yy yx xy y y y⎛⎫⎛⎫---⎪⎪-⎝⎭⎝⎭⋅===--，所以4C DOC CD x x⋅=⋅=为定值，因为221114224POC POD P p p pS S OC y OD y y y⋅=⋅⋅⋅=⨯⨯=△△由P 为椭圆上的一点，所以要使POC POD S S ⋅△△最大，只要2p y 最大 而2p y 最大为3，所以POC POD S S ⋅△△的最大值为3，此时P 点坐标为(0,和(. 【点睛】关键点点睛：本题考查由离心率求椭圆方程，考查椭圆中的最值问题，解题方法是解析几何的基本方程：设点,A P 坐标，：求直线方程，求交点坐标，计算面积之积，得出结论：即设点,A P 坐标，求出直线,AP BP 方程，求出交点,C D 的坐标（横坐标，纵坐标为0），而2111224POC POD P p C D p S S OC y OD y x x y ⋅=⋅⋅⋅=⨯⋅⨯△△，再计算CD x x ⋅可得最大值时P 点位置．26．（1）24y x =；（2）16||3AB =． 【分析】（1）根据抛物线定义可得答案；（2）由点F 是AC 的中点可得A 点的坐标，设出直线AB 方程与抛物线方程联立，利用韦达定理再得B 点坐标，再由两点间的距离公式可得答案． 【详解】（1）因为动点P 到定点(1,0)F 的距离与到定直线:1l x =-的距离相等， 由抛物线定义可得曲线Γ为抛物线，设其方程为22(0)y px p =>，则12p=， 所以2p =，曲线Γ的方程为24y x =.（2）设过点F 的直线方程为1x my =+，设1122(,),(,)A x y B x y ，且120,0y y ><，0(1,)C y -，由214x my y x=+⎧⎨=⎩整理得，2440y my --=，所以124y y =-， 因为点F 是AC 的中点，所以1112x -=，解得13x =，所以211412y x ==，得1y =(3,A ，又因为124y y =-，所以2y =，代入抛物线方程得213x =，所以1,3B ⎛ ⎝⎭，所以163AB ===. 【点睛】。

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测题(含答案解析)

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测题(含答案解析)

一、选择题1．已知抛物线2:2C y px =的焦点为F ，过抛物线上两点A ，B 分别向抛物线C 的准线作垂线，垂足为M ，N ，且()95OBN OAM ABNM S S S +=梯形△△，当直线AB 经过点F 且点F 到抛物线C 准线的距离为4时，直线l 的斜率为（ ）A ．2±B ．±C ．8±D ．±2．已知点()P m n ,是抛物线214y x =-上一动点，则A ．4B ．5C D ．63．设1F 、2F 分别是椭圆22:1259x yC +=的左、右焦点，O 为坐标原点，点P 在椭圆C上且满足4OP =，则12PF F △的面积为（ ）A ．3B ．C ．6D ．94．已知F 是抛物线2:4E y x =的焦点，若直线l 过点F ，且与抛物线E 交于B ，C 两点，以BC 为直径作圆，圆心为A ，设圆A 与y 轴交于点M ，N ，则MAN ∠的取值范围是（ ）A ．20,3π⎛⎫ ⎪⎝⎭B ．20,3π⎛⎤ ⎥⎝⎦C ．2,33ππ⎛⎤⎥⎝⎦D ．2,33ππ⎡⎤⎢⎥⎣⎦5．已知椭圆222:14x y C b +=的右焦点为F ，O 为坐标原点，C 上有且只有一个点P 满足||||OF FP =，则b =（ ）A ．3BC ．5D 6．已知直线:(1)(2)230l a x a y a +++--=经过定点P ，与抛物线24x y =交于,A B 两点，且点P 为弦AB 的中点，则直线l 的方程为（ ） A ．230x y +-= B ．210x y -+= C ．210x y -+=D ．20x y +-=7．已知椭圆22:11612x y C +=的左焦点为F ，点P 是椭圆C 上的动点，点Q 是圆()22:21T x y -+=上的动点，则PF PQ的最小值是（ ）A ．12B ．27C ．23D8．设双曲线22221(0,0)x y a b a b-=>>的左､右焦点分别为1F ､2F ，点P 在双曲线的右支上，且213PF PF =，则双曲线离心率的取值范围是（ ） A ．(1,2]B ．5(1,]3C ．[2,)+∞D ．4[,)3+∞9．设1F 、2F 是椭圆1C 和双曲线2C 的公共焦点，P 是它们的一个公共点，且1PF <2PF ，线段1PF 垂直平分线经过2F ，若1C 和2C 的离心率分别为1e 、2e ，则129e e +的最小值（ ）A ．2B ．4C ．6D ．810．已知动点(),P x y 5a a=+(a 为大于零的常数)﹐则动点P 的轨迹是（ ） A ．线段B ．圆C ．椭圆D ．双曲线11．已知抛物线1C 的顶点在坐标原点，焦点F 在y 轴正半轴上．若点F 到双曲线222:126x y C -=的一条渐近线的距离为2，则1C 的标准方程是（ ）A ．2y x =B ．2y x =C ．28x y =D ．216x y =12．已知过点(,0)A a 的直线与抛物线22(0)y px p =>交于M.N 两点，若有且仅有一个实数a ，使得16OM ON ⋅=-成立，则a 的值为（ ） A ．4-B ．2C ．4D ．8二、填空题13．已知中心在原点，对称轴为坐标轴的椭圆，其中一个焦点坐标为()2,0F ，椭圆被直线:3l y x =+所截得的弦的中点横坐标为2-，则此椭圆的标准方程为______.14．F 是抛物线24y x =的焦点，过F 的直线l 交抛物线于A 、B 两点，O 为坐标原点，若10AF =，则OAB 的面积为__________.15．已知双曲线()2222:10,0x y C a b a b-=>>的离心率为e ，直线:l y x =与双曲线C 交于,M N 两点，若MN =，则e 的值是___________.16．如图，椭圆C ：()222210x y a b a b+=>>的左､右焦点分别为1F ､2F ，B 为椭圆C 的上顶点，若12BF F △的外接圆的半径为23b，则椭圆C 的离心率为________.17．已知椭圆T 的中心在坐标原点，左､右焦点分别为1(,0)F c -，2(,0)F c ，(4,3)M -是椭圆上一点，且1MF ，12F F ，2MF 成等差数列，椭圆T 的标准方程________.18．设双曲线()2222:10,0x y C a b a b-=>>的右焦点为F ，点P 在C 的右支上，O 为坐标原点，若存在点P ，使PF OF =，且1cos 4OFP ∠=，则双曲线的离心率为___________．19．椭圆()222210x y a b a b+=>>的左焦点为F ，(),0A a -，()0,B b ，()0,C b -分别为其三个顶点.直线CF 与AB 交于点D ，若椭圆的离心率13e =，则tan BDC ∠=___________.20．若M ，P 是椭圆2214x y +=两动点，点M 关于x 轴的对称点为N ，若直线PM ，PN 分别与x 轴相交于不同的两点A (m ，0)，B (n ，0)，则mn =_________. 三、解答题21．如图，已知椭圆22221(0)x y a b a b+=>>的离心率为12，过椭圆右焦点2F 作两条互相垂直的弦AB 与CD ，当直线AB 的斜率为0时，||||7AB CD +=．（Ⅰ）求椭圆的方程；（Ⅱ）求||||AB CD +的取值范围．22．在平面直角坐标系xOy 中，已知A ，B 两点是椭圆22:19x E y +=的左、右顶点，P 为直线6x =上的动点，PA 与椭圆E 的另一交点为Q ，当点P 不为点()6,0时，过P作直线PH QB ⊥，垂足为H . （1）证明：直线PH 过定点M ；（2）过（1）中的定点M 作斜率为k 的直线与椭圆E 交于C ，D 两点，设直线AC ，AD 的斜率分别为1k ，2k ，试判断()12k k k ⋅+是否为定值？如果是定值，求出定值. 23．已知椭圆()2222:10x y C a b a b +=>>过点421,3P ⎛⎫ ⎪ ⎪⎝⎭，离心率为53.（1）求椭圆C 的方程；（2）直线l 与圆22:1O x y +=相切，且与椭圆C 交于M ，N 两点，Q 为椭圆C 上一个动点(点O ，Q 分别位于直线l 两侧)，求四边形OMQN 面积的最大值. 24．已知是抛物线2:2C y px=(0)p >的焦点，(1,)M t 是抛物线上一点，且||2MF =.（1）求抛物线C 的方程；（2）过点O （坐标原点）分别作,OA OB 交抛物线C 于,A B 两点(,A B 不与O 重合)，且.2OA OB k k =.求证：直线AB 过定点.25．已知椭圆2222:1(0)x y C a b a b +=>>的焦点在圆223x y +=上，且离心率为32.（1）求椭圆C 的方程；（2）过原点O 的直线l 与椭圆C 交于,A B 两点，F 为右焦点，若FA 垂直于AB ，求直线l 的斜率.26．已知抛物线()2:20E y px p =>的焦点F ，抛物线E 上一点()3,t 到焦点的距离为4.（1）求抛物线E 的方程；（2）过点F 作直线l ，交抛物线E 于,A B 两点，若线段AB 中点的纵坐标为1-，求直线l 的方程.【参考答案】***试卷处理标记，请不要删除一、选择题1．B 解析：B 【分析】根据题意，求得4p =，可得抛物线的方程，因为()95OBN OAM ABNM S S S +=梯形△△，所以49OMN OAB ABMN S S S +=梯形△△，根据面积公式，结合抛物线定义，即可求得AB ，不妨设AB 的斜率为k ，可得直线AB 的方程，与抛物线联立，根据韦达定理，可求得A B x x +的值，代入弦长公式，即可求得答案. 【详解】因为点F 到抛物线C 准线的距离为4，所以4p =，所以28y x =，设抛物线C 的准线与x 轴交于点H ，因为()95OBN OAM ABNM S S S +=梯形△△，所以()()11422192M N A BOMN OABABMNM N OH y y OF y y S S S AM BN y y ⋅-+⋅-+==+⋅-梯形△△，因为2OH OF ==，M N A B y y y y -=-，AM BN AB +=，所以449OMN OAB ABMN S S S AB +==梯形△△，则9AB =，显然直线AB 的斜率存在，不妨设为k ，则():2AB y k x =-， 与抛物线联立可得：()22224840k x k x k -++=， 从而284A B x x k+=+， 所以28489A B A kB x x =++=+=，解得22k =±. 故选：B【点睛】解题的关键是根据面积的关系，得到49 OMN OABABMNS SS+=梯形△△，结合图象，可求得9AB=，再利用抛物线的弦长公式求解，考查分析计算，化简求值的能力，属中档题.2．D解析：D【分析】先把抛物线214y x=-化为标准方程，求出焦点F(0,-1),运用抛物线的定义，找到2222(1)(4)(5)m n m n+++-++的几何意义，数形结合求最值.【详解】由214y x=-，得24x y=-．则214y x=-的焦点为()0,1F-．准线为:1l y=．2222(1)(4)(5)m n m n+++-++几何意义是点()P m n,到()0,1F-与点()4,5A-的距离之和，如图示：根据抛物线的定义点()P m n,到()0,1F-的距离等于点()P m n,到l的距离，2222(1)(4)(5)m n m n++-++|PF|+|PA|=|PP1|+|PA|,所以当P运动到Q时，能够取得最小值.最小值为：|AQ1|=()156--=．故选：D.【点睛】解析几何问题解题的关键：解析几何归根结底还是几何，根据题意画出图形，借助于图形寻找几何关系可以简化运算．3．D解析：D 【分析】设点()00,P x y ，求出20y 的值，由此可求得12PF F △的面积.【详解】在椭圆22:1259x y C +=中，5a =，3b =，则4c ==，所以，1228F F c ==，设点()00,P x y ，则22001259x y +=，可得220025259x y =-，4OP ===，解得208116y =，094y ∴=，因此，12PF F △的面积为1212011989224PF F S F F y =⋅=⨯⨯=△. 故选：D. 【点睛】方法点睛：本题考查椭圆中焦点三角形面积的计算，常用以下两种方法求解： （1）求出顶点P 的坐标，利用三角形面积公式求解；（2）利用余弦定理和椭圆的定义求得12PF PF ⋅的值，利用三角形面积公式求解.4．B解析：B 【分析】设设()11,B x y ，()22,C x y BC 的中点()00,A x y ，直线l ：()1y k x =-与 2:4E y x =联立可得()2222240k x k x k -++=，由韦达定理计算12x x +，12x x ，再求以BC 为直径作圆的半径12r BC =，求出圆心A 点横坐标，设MN 的中点为D ，则12MAD MAN ∠=∠，由圆的性质可得0cos x MAD r∠=并求出其范围，进而可得MAD ∠的范围，再讨论斜率不存在时MAD ∠的值，即可求解. 【详解】由抛物线2:4E y x =可知，焦点()1,0F ，设()11,B x y ，()22,C x y BC 的中点()00,A x y 设直线l ：()1y k x =-代入2:4E y x =可得()2222240k x k x k -++=，所以212224k x x k++= ，121=x x()()22222121212241612444k k x x x x x x k k +⎛⎫+-=+-=-= ⎪⎝⎭， ()()()2222212416111k BC k x x k k+=+-=+⨯，所以()2241k BC k +=，以BC 为直径作圆的半径()222112k r BC k+==，圆心为BC 的中点()20122122k x x x k+=+=， 设MN 的中点为D ，则12MAD MAN ∠=∠， 则()()()22202222221111cos 1222212121k x k k MAD r k k k k ++∠====+<+=+++ 且1cos 2MAD ∠>，所以03MAD π<∠<， 当k 不存在时，1,2x y ==±，此时2r ，01x =，1cos 2MAD ∠=，3MAD π∠=，所以03MAD π<∠≤可得203MAN π<∠≤， 所以MAN ∠的取值范围是20,3π⎛⎤⎥⎝⎦故选：B 【点睛】关键点点睛：本题解题的关键点是联立直线与抛物线的方程，求出圆的半径和圆心坐标，由圆的性质知圆心与弦中点的连线与弦垂直可求出12MAN ∠的范围，进而可计算MAN ∠的范围.5．B解析：B 【分析】首先由椭圆的对称性得到点P 的位置，再求解,c b 的值. 【详解】根据椭圆的对称性可知，若椭圆上只有一个点满足OF FP =，这个点只能是右顶点，即2a c c a c -=⇒=，由条件可知242a a =⇒=，则1c =，那么b ==故选：B 【点睛】关键点点睛：本题的关键是确定点P 的位置，从而得到2a c =这个关键条件.6．B解析：B 【分析】利用点差法求出直线斜率，即可得出直线方程. 【详解】由直线:(1)(2)230l a x a y a +++--=得(2)(23)0a x y x y +-++-= 所以20230x y x y +-=⎧⎨+-=⎩ 解得11x y =⎧⎨=⎩ 则()1,1P设1122(,),(,)A x y B x y ，则21122244x y x y ⎧=⎨=⎩，两式相减得121212()()4()x x x x y y -+=-， 即121212142AB y y x x k x x -+===-， 则直线方程为11(x 1)2y -=-，即210x y -+=. 故选：B. 【点睛】方法点晴：点差法是求解中点弦有关问题的常用方法.7．B解析：B 【分析】作出图形，利用椭圆的定义以及圆的几何性质可求得PF PQ的最小值.【详解】 如下图所示：在椭圆22:11612x y C +=中，4a =，23b =222c a b -，圆心()2,0T 为椭圆C 的右焦点，由椭圆定义可得28PF PT a +==，8PF PT ∴=-，由椭圆的几何性质可得a c PT a c -≤≤+，即26PT ≤≤，由圆的几何性质可得1PQ PT QT PT ≤+=+， 所以，899211111617PF PF PT PQPT PT PT -≥==-≥-=++++. 故选：B. 【点睛】关键点点睛：解本题的关键在于以下几点：（1）问题中出现了焦点，一般利用相应圆锥曲线的定义，本题中注意到2PF PT a +=，进而可将PF 用PT 表示；（2）利用圆的几何性质得出PT r PQ PT r -≤≤+，可求得PQ 的取值范围； （3）利用椭圆的几何性质得出焦半径的取值范围：a c PT a c -≤≤+.8．A解析：A 【分析】根据题中条件，由双曲线的定义，得到2PF a =，13PF a =，根据1212+≥PF PF F F ，即可求出结果. 【详解】因为点P 在双曲线的右支上，由双曲线的定义可得122PF PF a -=， 又213PF PF =，所以222PF a =，即2PF a =，则13PF a =， 因为双曲线中，1212+≥PF PF F F ，即42a c ≥，则2ca≤，即2e ≤， 又双曲线的离心率大于1，所以12e <≤. 故选：A. 【点睛】本题主要考查求双曲线的离心率，熟记双曲线的简单性质即可.9．D解析：D 【分析】设椭圆和双曲线的方程，由题意可得2122PF F F c ==，再利用椭圆和双曲线的定义分别求出1PF ，即可得122a a c +=，计算12112e e +=，()121212111992e e e e e e ⎛⎫+=++ ⎪⎝⎭展开后利用基本不等式即可求最值. 【详解】设椭圆1C 的方程为2222111x y a b +=，则222111c a b =-，设双曲线2C 的方程为2222221x y a b -=，则222222c a b =+，因为椭圆1C 和双曲线2C 的焦点相同，所以2212c c =，设12c c c ==即22221122a b a b -=+，因为P 是椭圆1C 和双曲线2C 的一个公共点， 所以1212+=PF PF a ，2122PF PF a -=，因为线段1PF 垂直平分线经过2F ，所以2122PF F F c ==，所以1122PF a c =-，且1222PF c a =-， 所以122222a c c a -=-，可得122a a c +=， 所以11c e a =，22c e a =，所以1212121122a a a a ce e c c c c++=+===， 所以()211212121291111991022e e e e e e e e e e ⎛⎫⎛⎫+=++=++ ⎪ ⎪⎝⎭⎝⎭()11101023822⎛≥+=+⨯= ⎝， 当且仅当21129e e e e =，即213e e =时等号成立， 故选：D.【点睛】关键点点睛：本题解题的关键点是利用已知条件得出122a a c +=，进而可得12112e e +=， 再利用基本不等式可求最值.10．C解析：C 【分析】由a 为大于零的常数，可知5a a+的最小值，再根据两点间距离公式得几何意义以及椭圆定义判断轨迹. 【详解】的几何意义为点(),P x y 与点(0,2)A 间的距离，的几何意义为点(),P x y 与点(0,2)B -间的距离，且4AB =又由a为大于零的常数，可知54a a +≥=>， 当且仅当5aa=，即a =54a a=+>， 即动点P 到点A 与到点B 的距离之和为定值，且大于AB ， 所以动点P 的轨迹为椭圆， 故选：C. 【点睛】在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误． 椭圆的定义揭示了椭圆的本质属性，正确理解掌握定义是关键，应注意定义中的常数大于|F 1F 2|，避免了动点轨迹是线段或不存在的情况．11．D解析：D 【分析】先根据双曲线的方程求解出双曲线的渐近线方程，再根据点到直线的距离公式求解出抛物线方程中的p ，则抛物线方程可求. 【详解】双曲线2C 的渐近线方程是22026x y -=，即y =.因为抛物线的焦点()0,02p F p ⎛⎫> ⎪⎝⎭0y -=的距离为2，2=，即8p =，所以1C 的标准方程是216x y =，故选：D ． 【点睛】方法点睛：求解双曲线方程的渐近线方程的技巧：已知双曲线方程22221x y a b-=或22221y x a b -=，求解其渐近线方程只需要将方程中的“1”变为“0”，由此得到的y 关于x 的一次方程即为渐近线方程. 12．C解析：C 【分析】设出直线方程与抛物线方程联立，利用韦达定理得出1212,y y y y +及12x x ，把16OM ON ⋅=-用坐标表示代入上述值结合已知条件可得答案.【详解】设直线MN 的直线方程为x ty a =+，1122(,),(,)M x y N x y ，由题意得22x ty a y px=+⎧⎨=⎩，整理得2220y pty pa --=，所以12122,2y y pt y y pa +==-，()()()2212121212x x ty a ty a t y y at y y a =++=+++ ()()2222t ap at pt a =-++，因为16OM ON ⋅=-，所以121216x x y y +=-， 所以()()2222216tpa at pt a pa -++-=-，22160a pa -+=，因为方程有且仅有一个实数a ，所以()22640p ∆=-=，解得4p =，或4p =-（舍去）， 故选：C. 【点睛】本题考查了直线和抛物线的位置关系，关键点是利用韦达定理求出1212,y y y y +及12x x ，然后16OM ON ⋅=-坐标表示列出等式，考查了学生分析问题、解决问题的能力.二、填空题13．【分析】设椭圆方程为代入直线方程整理就后应用韦达定理结合弦中点横坐标求得关系再由可得得椭圆方程【详解】设椭圆方程为由得所以由题意又所以椭圆方程为故答案为：【点睛】方法点睛：本题考查求椭圆的标准方程解解析：22184x y +=【分析】设椭圆方程为22221(0)x y a b a b+=>>，代入直线方程整理就后应用韦达定理结合弦中点横坐标求得,a b 关系，再由2c =可得,a b 得椭圆方程．【详解】设椭圆方程为22221(0)x ya b a b +=>>，由222213x y a b y x ⎧+=⎪⎨⎪=+⎩，得2222222()690a b x a x a a b +++-=，所以212226a x x a b +=-+，由题意222622a a b-=-⨯+，222a b =， 又2c =，所以22224a b b c -===，28a =，椭圆方程为22184x y +=．故答案为：22184x y +=．【点睛】方法点睛：本题考查求椭圆的标准方程．解题方法是韦达定理．由直线方程与椭圆方程联立方程组，消元后应用韦达定理可得出弦中点坐标，从而得出,a b 的关系．然后结论半焦距c 可求解．14．【分析】设点为第一象限内的点设点利用抛物线的定义可求得点的坐标可得出直线的方程将直线的方程与抛物线的方程联立列出韦达定理求出的值由此可求得的面积【详解】设点为第一象限内的点设点抛物线的准线方程为由抛解析：103【分析】设点A 为第一象限内的点，设点()11,A x y 、()22,B x y ，利用抛物线的定义可求得点A 的坐标，可得出直线AB 的方程，将直线AB 的方程与抛物线的方程联立，列出韦达定理，求出12y y -的值，由此可求得OAB 的面积. 【详解】设点A 为第一象限内的点，设点()11,A x y 、()22,B x y ，抛物线24y x =的准线方程为1x =-，由抛物线的定义可得1110AF x =+=，解得19x =，由于点A 为第一象限内的点，则10y >，可得16y ==，即点()9,6A ，直线AF 的斜率为63914AF k ==-，所以，直线AB 的方程为()314y x =-，即413x y =+， 联立24134x y y x⎧=+⎪⎨⎪=⎩，消去x 并整理可得216403y y --=， 由韦达定理可得12163y y +=，21161626333y y ∴=-=-=-， 因此，1211210162233OAB S OF y y =⋅-=⨯⨯+=△. 故答案为：103. 【点睛】方法点睛：利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下： （1）设直线方程，设交点坐标为()11,x y 、()22,x y ；（2）联立直线与圆锥曲线的方程，得到关于x （或y ）的一元二次方程，必要时计算∆； （3）列出韦达定理；（4）将所求问题或题中的关系转化为12x x +、12x x 的形式； （5）代入韦达定理求解.15．【分析】联立方程组求出M 的坐标利用整理得求出离心率【详解】不妨设点在第一象限联立得又∴则整理得所以故答案为：【点睛】求椭圆（双曲线）离心率的一般思路：根据题目的条件找到abc 的关系消去b 构造离心率e【分析】联立方程组求出M的坐标，利用MN =，整理得225b a =，求出离心率.【详解】不妨设点(),M x y 在第一象限，联立22221x y a b y x⎧-=⎪⎨⎪=⎩，得222222a b x y b a ==-，又MN =，∴2222b x y +=，则2222222a b b b a =-，整理得225b a =，所以==e故答案为：6 【点睛】求椭圆（双曲线）离心率的一般思路：根据题目的条件，找到a 、b 、c 的关系，消去b ，构造离心率e 的方程或（不等式）即可求出离心率．16．【分析】由题意可得的外接圆的圆心在线段上可得在中由勾股定理可得：即结合即可求解【详解】由题意可得：的外接圆的圆心在线段上设圆心为则在中由勾股定理可得：即所以即所以所以故答案为：【点睛】方法点睛：求椭 解析：12【分析】由题意可得12BF F △的外接圆的圆心在线段OB 上，1OF c =，123bMF BM ==，可得 13OM b =，在1OMF △中，由勾股定理可得：22211MF OM OF =+，即222233b b c ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，结合222b ac =-即可求解. 【详解】由题意可得：12BF F △的外接圆的圆心在线段OB 上，1OF c =， 设圆心为M ，则2133OM OB BM b b b =-=-=， 在1OMF △中，由勾股定理可得：22211MF OM OF =+，即222233b b c ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，所以223b c =，即2223a c c -=，所以2a c =，所以12c e a ==， 故答案为：12. 【点睛】方法点睛：求椭圆离心率的方法： （1）直接利用公式c e a=； （2）利用变形公式221be a=-；（3）根据条件列出关于,a c 的齐次式，两边同时除以2a ，化为关于离心率的方程即可求解.17．【分析】根据题意结合椭圆定义可得设代解得代回方程即可【详解】解：因为是椭圆上一点且成等差数列所以所以故椭圆方程可设为代解得所以椭圆方程为故答案为：【点睛】椭圆几何性质的应用技巧：（1）与椭圆的几何性解析：2212015x y +=【分析】根据题意结合椭圆定义可得2a c =，设2222143x y c c+=代(4,M 解得25c =代回方程即可.【详解】解：因为M 是椭圆上一点，且1MF ，12F F ，2MF 成等差数列所以2121224MF a MF F F c ===+，所以2a c =，b =故椭圆方程可设为2222143x y c c +=代(4,M 解得25c =所以椭圆方程为2212015x y +=故答案为：2212015x y +=【点睛】椭圆几何性质的应用技巧：（1）与椭圆的几何性质有关的问题要结合图形进行分析，即使不画出图形，思考时也要联想到图形；（2）椭圆相关量的范围或最值问题常常涉及一些不等式．例如：,,01a x a b y b e -≤≤-≤≤<<，三角形两边之和大于第三边，在求椭圆相关量的范围或最值时，要注意应用这些不等关系.18．2【分析】在焦点三角形中由余弦定理求得关系再求离心率【详解】设双曲线的左焦点为在中由余弦定理得故答案为：2【点晴】求离心率的关键是得的关系本题是由余弦定理得出解析：2 【分析】在焦点三角形中由余弦定理求得,a c 关系，再求离心率. 【详解】设双曲线的左焦点为E ，在EFP △中，2EF c =，2PF c PE a c ==+，，1cos 4EFP ∠=. 由余弦定理()222421cos 224c c c a EFP c c+-+∠==⋅⋅ ，得2c e a ==. 故答案为：2 【点晴】求离心率的关键是得,,a b c 的关系，本题是由余弦定理得出.19．【分析】做出图像可知：利用两角和的正切表示有根据离心率可求出代入正切公式即可求出结果【详解】由图像可知：所以因为离心率可设那么极有代入上式得故答案为：【点睛】本题考查了椭圆的基本性质与平面几何的转化 解析：825-【分析】做出图像可知：BDC BAO CFO ∠=∠+∠，利用两角和的正切表示tan BDC ∠，有tan ,tan b b BAO CFO a c ∠=∠=，根据离心率可求出22b a =，22b c=，代入正切公式即可求出结果. 【详解】 由图像可知：BDC BAO DFA BAO CFO ∠=∠+∠=∠+∠所以tan tan tan tan()1tan tan 1b b BAO CFOa c BDC BAO CFOb bBAO CFO a c+∠+∠∠=∠+∠==-∠∠-⋅因为离心率13c e a ==，可设3a m =，c m =，那么22b m =，极有22b a =，22b c =，代入上式得22228235221223+=--⨯． 故答案为：82-【点睛】本题考查了椭圆的基本性质与平面几何的转化，考查了两角和的正切公式的应用，属于中档题型，思路点睛：（1）根据平面几何将所求角进行转化，BDC BAO CFO ∠=∠+∠； （2）结合两角和的正切公式，直角三角形内求角的正切，将问题转化为,,a b c 的比值问题．（3）根据离心率求出,,a b c 的比值，代入可求.20．4【分析】设出的坐标写出坐标满足的关系式根据题意写出直线的方程求出的横坐标计算得出的值【详解】解：设则则所以直线的方程为令可得同理有直线的方程为令可得则故答案为：【点睛】圆锥曲线中求定值问题常见的方解析：4 【分析】设出,,M N P 的坐标，写出坐标满足的关系式.根据题意，写出直线PM ，PN 的方程，求出,A B 的横坐标，计算得出mn 的值. 【详解】解：设(),M a b ，则(),N a b -，(),P c d ，则2214a b +=，2214c d +=所以PM d bk c a-=-直线PM 的方程为()d b y b x a c a --=--，令0y =可得ad bcm d b-=- 同理有PM d b k c a+=- 直线PN 的方程为()d b y b x a c a ++=--，令0y =可得ad bcn d b+=+ 则222222ad bc ad bc a d b c mn d b d b d b -+-⎛⎫⎛⎫== ⎪⎪-+-⎝⎭⎝⎭222222111144111144a c c a c a ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=⎛⎫--- ⎪⎝⎭()2222414a c a c -==-故答案为：4 【点睛】圆锥曲线中求定值问题常见的方法有两种：(1)从特殊入手，求出定值，再证明这个值与变量无关．(2)直接推理、计算，并在计算推理的过程中消去变量，从而得到定值．三、解答题21．（Ⅰ）22143x y +=；（Ⅱ）48,77⎡⎤⎢⎥⎣⎦；【分析】（Ⅰ）通过当直线AB 的斜率为0时可知||2AB a =，22||b CD a =，结合12c e a ==，计算即得结论；（Ⅱ）分别对两条弦的斜率进行讨论，当两条弦中一条斜率为0时、另一条弦的斜率不存在时易得结论；当两条弦斜率均存在且不为0时，通过设直线AB 、CD 的方程并分别与椭圆方程联立，利用韦达定理及两点间距离公式，可得||||AB CD +的表达式，利用换元法及二次函数的性质计算即得结论． 【详解】解：（Ⅰ）当直线AB 的斜率为0时，直线CD 垂直于x 轴，||2AB a ∴=，22||b CD a =，即22||||27b AB CD a a+=+=， 12c e a ==，且222a b c =+，解得：2,a b ==， 所以椭圆方程为22143x y +=；（Ⅱ）①当两条弦中一条斜率为0时，另一条弦的斜率不存在，由题意可知，||||7AB CD +=；②当两条弦斜率均存在且不为0时，设1(A x ，1)y ，2(B x ，2)y ， 设直线AB 的方程为(1)y k x =-，则直线CD 的方程为1(1)y x k=--，将直线AB 的方程代入椭圆方程中，并整理得：2222(34)84120k x k x k +-+-=， ∴221212228412,3434k k x x x x k k-+==++，∴212212(1)|||34k AB x x k +=-=+，同理，2222112(1)12(1)||4343k k CD k k++==++， ∴2222222212(1)12(1)84(1)||||3434(34)(34)k k k AB CD k k k k ++++=+=++++，令21t k =+，则1t >，∴2222848484||||1149(41)(31)121()24t t AB CD t t t t t +===-++---+，1t >，∴101t<<，∴211494912()244t <--+，∴241111494912()24t <--+， ∴24884711497()24t <--+，∴48||||77AB CD +<， 综合①②可知，||||AB CD +的取值范围为：48,77⎡⎤⎢⎥⎣⎦． 【点睛】(1)解答直线与椭圆的题目时，时常把两个曲线的方程联立，消去x (或y )建立一元二次方程，然后借助根与系数的关系，并结合题设条件建立有关参变量的等量关系． (2)涉及到直线方程的设法时，务必考虑全面，不要忽略直线斜率为0或不存在等特殊情形．22．（1）证明见解析；（2）是，定值为112-. 【分析】（1）设()00 ,Q x y ，()()6,0P t t ≠，法一：根据椭圆方程求得19QA QB k k ⋅=-，根据9QA PA tk k ==，即可求得QB k ，根据PH QB ⊥，可求得PH k ，可得直线PH 的方程，即可得答案；法二：根据9AP QA tk k ==，可得直线AP 的方程，与椭圆联立，根据韦达定理，可得Q 点坐标，根据PH QB ⊥，可求得PH k ，可得直线PH 的方程，即可得答案； （2）设()11,C x y ，()22,D x y ，则直线CD 的方程为()5y k x =-，与椭圆联立，根据韦达定理，可得1212,x x x x +⋅表达式，即可得()12k k k ⋅+的表达式，化简整理，即可得答案. 【详解】（1）法一：由题意得：(3,0),(3,0)A B -，设()00 ,Q x y ，()()6,0P t t ≠，则220019x y += ∴00001339QA QB y y k k x x ⋅=⋅=-+-，9QA PA t k k == ∴1QB k t=-∵PH QB ⊥，∴1PH QB k k ⋅=-，∴PH k t =，直线PH 的方程为()6y t t x -=-， 即()5y t x =-，所以过定点()5,0M ，法二：由题意得：(3,0),(3,0)A B -，设()00,Q x y ，()()6,0P t t ≠，9AP QA tk k ==∴直线AP 的方程为()39ty x =+， 由()223919t y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩，得()2222969810t x t x t +++-=. ∴20298139t x t--⋅=+，∴2022739t x t -=+，()0023699t y t t x +=+=， ∴2222736,99t t Q tt ⎛⎫-⎪++⎝⎭，∴222619 27339QBtt k t tt+==---+. ∵PH QB ⊥，∴1PH QB k k ⋅=-， ∴PH k t =，∴PH 的方程为()6y t t x -=-，即()5y t x =-，所以过定点()5,0M（2）设()11,C x y ，()22,D x y ，则直线CD 的方程为()5y k x =-由()22519y k x x y ⎧=-⎪⎨+=⎪⎩.得()2222199022590k x k x k +-+-=， ∴22221222122(90)4(19)(2259)0901*******k k k k x x k k x x k ⎧⎪∆=--+->⎪⎪+=⎨+⎪⎪-=⎪+⎩∴()()()()()()()122121121222153533333x x x x y y k k k k k x x x x -++-+⎛⎫⋅+=⋅+= ⎪+⎭⋅+++⎝ ()()1212222121222304813957612x x x x k k x x x x k -⋅+--++⋅===-+为定值 【点睛】解题的技巧为：根据椭圆方程可得19QA QB k k ⋅=-，根据QA PA k k =，可直接求得QB k ，简化计算，提高正确率，考查计算化简的能力，属中档题.23．（1）22194x y +=；（2）最大值为.【分析】（1）将1,3P ⎛ ⎝⎭的坐标代入椭圆方程中，再结合3c a =和222a b c =+可求出,a b 的值，进而可求得椭圆的方程；（2）当MN 斜率存在时，设MN 与圆O 的切线为y kx n =+，要使四边形OMQN 的面积最大，则Q 到MN 距离要最大，此时过Q 点MN 的平行线必与椭圆C 相切，设为y kx m =+，易得Q 到MN 距离与O 到MN 距离之和等于O 到直线y kx m =+的距离，然后利用点到直线的距离公式求出O 到直线y kx m =+的距离d ，利用弦长公式求出MN 的值，从而有12OMN QMN OMQN S S S MN d =+=⨯四边形△△，化简可求得其范围，当MN 斜率不存在时，直接可得OMQN S =四边形 【详解】（1）因为椭圆C过点1,3P ⎛⎫⎪ ⎪⎝⎭，所以2213219a b +=，c a = 又222a b c =+，所以得22194x y +=；（2）（i ）当MN 斜率存在时，设MN 与圆O 的切线为y kx n =+，要使四边形OMQN 的面积最大，则Q 到MN 距离要最大，此时过Q 点MN 的平行线必与椭圆C 相切，设为y kx m =+，易得Q 到MN 距离与O 到MN 距离之和等于O 到直线y kx m =+的距离，设O 到直线y kx m =+的距离记为d，则d =，联立22,1,94y kx n x y =+⎧⎪⎨+=⎪⎩，消去y 得()()2229418940k x knx n +++-=，设()11,M x y ，()22,N x y ，1221894kn x x k +=-+，()21229494n x x k -=+，所以12294MN x k =-=+， 因为y kx n =+与圆O1=，因为y kx m =+与椭圆相切，所以2294k m +=，2112294OMN QMNOMQN S S S MN d k =+=⨯=⨯+四边形△△=== 可得OMQN S 四边形随k的增大而增大，即OMQN S <四边形（ii ）当MN斜率不存在时，不妨取M ⎛ ⎝⎭，1,N ⎛ ⎝⎭，此时()3,0Q ，OMQN S =四边形综上所得四边形OMQN的面积的最大值为【点睛】关键点点睛：此题考查椭圆方程的求法，考查直线与椭圆的位置关系，考查计算能力，解题的关键是当MN 斜率存在时，设MN 与圆O 的切线为y kx n =+，要使四边形OMQN的面积最大，则Q 到MN 距离要最大，此时过Q 点MN 的平行线必与椭圆C 相切，设为y kx m =+，易得Q 到MN 距离与O 到MN 距离之和等于O 到直线y kx m =+的距离，从而可得2112294OMN QMNOMQN S S S MN d k =+=⨯=⨯+四边形△△，化简可得结果，属于中档题24．（1）24y x =；（2）直线AB 过定点(2,0)-，证明见解析. 【分析】（1）由抛物线的定义求得p ，得抛物线方程；（2）设直线AB 方程为x my b =+， 11(,)A x y ，22(,)B x y ，直线方程代入抛物线方程，由判别式大于0得参数满足的条件，应用韦达定理得1212,y y y y +，计算由2OA OB k k =可得128y y =，从而求得参数b ，并可得出m 的范围．此时由直线方程可得定点坐标． 【详解】（1）由抛物线定义可知：122p+=，则2p =， 所以抛物线C 的方程为24y x =（2）设直线AB 方程为x my b =+， 11(,)A x y ，22(,)B x y联立24y x x my b⎧=⎨=+⎩得2440y my b --=，则216160m b ∆=+>即20()m b +>* 且124y y m +=，124y y b =-.2OA OB k k =，所以12122y y x x =， 又2114y x =，2224y x =，因此可得128y y =即48b -=，2b =- 代入()*得220m ->，m ∴<m >所以直线AB 方程为2x my =-，由此可知直线AB 过定点(2,0)-.【点睛】方法点睛：本题考查主要考查抛物线中直线过定点问题，解题方法是设而不求的思想方程，即设直线方程为x my b =+，设交点坐标为11(,)A x y ，22(,)B x y ，直线方程代入抛物线方程后应用韦达定理得1212,y y y y +，代入已知求出参数值，然后由直线方程得定点坐标．25．(1) 2214x y +=；(2) 【分析】(1)由焦点在圆上解得c=2a=，2221b a c=-=，方程可求；(2)因为FA垂直于AB可知点A为椭圆与圆的交点，联立方程求得坐标，则直线斜率可求.【详解】解：（1）椭圆2222:1(0)x yC a ba b+=>>的焦点在圆223x y+=上，所以203c+=，即c=，因为2cea==得2a=，2221b a c=-=，故椭圆方程为2214xy+=（2）因为FA垂直于AB ，即点A既在椭圆上又在以OF为直径的圆上，所以22221434xyx y⎧+=⎪⎪⎨⎛⎪-+=⎪⎝⎭⎩解得xy⎧=⎪⎪⎨⎪=⎪⎩所以A⎝⎭故AlAykx==所以直线l的斜率为【点睛】关键点点晴：本题的关键在于求出点A的坐标点.26．（1）24y x=；（2）220x y+-=.【分析】（1）抛物线的定义可得342p⎛⎫--=⎪⎝⎭，即可求出p得值，进而可得抛物线E的方程；（2）设()11,A x y、()22,B x y，则21122244y xy x⎧=⎨=⎩，利用点差法可求直线l的斜率，再求出点()1,0F，利用点斜式即可求出直线l的方程.【详解】（1）由抛物线()2:20E y px p=>可得准线方程为：2px=-，由抛物线的定义可得：342p⎛⎫--=⎪⎝⎭，解得：2p=，所以抛物线E的方程为24y x=，（2）设()11,A x y、()22,B x y，则21122244y xy x⎧=⎨=⎩，两式相减可得()2212124y y x x-=-，所以()()()1212124y y y y x x-+=-，因为线段AB中点的纵坐标为1-，所以122y y+=-，所以直线l 的斜率1212124422y y k x x y y -====--+-， 因为()1,0F ，所以直线l 的方程为：()21y x =--， 即220x y +-=. 【点睛】思路点睛：对于中点弦问题，多采用设而不求的方法，利用整体代入的思想求出直线的斜率，再结合直线所过的点即可得直线的方程.。

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》测试(有答案解析)(4)

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》测试(有答案解析)(4)

一、选择题1．光线从椭圆的一个焦点发出，被椭圆反射后会经过椭圆的另一个焦点；光线从双曲线的一个焦点发出，被双曲线反射后的反射光线等效于从另一个焦点射出，如图①，一个光学装置由有公共焦点1F 、2F 的椭圆Γ与双曲线Ω构成，现一光线从左焦点1F 发出，依次经Ω与Γ反射，又回到了点1F ，历时1t 秒；若将装置中的Ω去掉，如图②，此光线从点1F 发出，经Γ两次反射后又回到了点1F ，历时2t 秒；若218t t =，则Γ与Ω的离心率之比为（ ）A ．3:4B ．2:3C ．1:2D ．22．已知椭圆22221(0)x y C a b a b+=>>：的左､右焦点分别为1F ，2F ，过2F 直线与椭圆C 交于M ，N 两点，设线段1NF 的中点D ，若10MD NF ⋅=，且12//MF DF ，则椭圆C 的离心率为（ ） A ．13B 3C ．12D ．223．已知双曲线22221x y a b -=的两个焦点分别为21(,0)(,0)(0)F c F c c ->，过点2,0a P c ⎛⎫ ⎪⎝⎭的直线与双曲线的左右两支分别交于,A B 两点，且122F A F B =-，求双曲线的离心率（ ） A 2B 3C 5D 64．已知双曲线()222210,0x y a b a b-=>>的一条渐近线与圆()2239x y -+=相交于A 、B 两点，若2AB =，则该双曲线的离心率为（ ）A ．5B ．2C ．3D ．45．已知椭圆()2222:10x y C a b a b+=>>的左焦点为F ，上顶点为A ，右顶点为B ，若FAB 为直角三角形，则椭圆C 的离心率为（ ）A ．22B ．312- C ．51- D ．326．若1F ，2F 是双曲线22221(0,0)y xa b a b-=>>与椭圆2251162x y +=的共同焦点，点P 是两曲线的一个交点，且12PF F △为等腰三角形，则该双曲线的渐近线方程是（ ） A ．22y x =±B ．24y x =±C ．7y x =±D ．37y x =±7．已知M 是抛物线2:C x y =上一点，记点M 到抛物线C 的准线的距离为1d ，到直线:3490l x y ++=的距离为2d ，则12d d +的最小值为（ ）A ．1B ．2C ．3D ．48．如图，F 是抛物线28x y =的焦点，过F 作直线交抛物线于A 、B 两点，若AOF 与BOF 的面积之比为1:4，则AOB 的面积为（ ）A ．10B ．8C ．16D ．129．设F 1，F 2是双曲线C ：22221x y a b-=(a >0，b >0)的左、右焦点，P 是双曲线C 右支上一点，若|PF 1|＋|PF 2|＝4a ，且∠F 1PF 2＝60°，则双曲线C 的渐近线方程是（ ）A 30x y ±=B ．270x =C 320x y ±=D ．230x ±=10．在平面直角坐标系中，双曲线C 的标准方程为2221(0)4x y t t t-=>+，则双曲线的离心率取得最大值时，双曲线的渐近线方程为（ ）A ．2y x =±B ．3y x =±C ．12y x =±D ．13y x =±11．设双曲线22221(0,0)x y a b a b-=>>的左､右焦点分别为1F ､2F ，点P 在双曲线的右支上，且213PF PF =，则双曲线离心率的取值范围是（ ）A ．(1,2]B ．5(1,]3C ．[2,)+∞D ．4[,)3+∞12．设双曲线2214y x -=的左、右焦点分别为12,F F ，若点P 在双曲线上，且12F PF △为锐角三角形，则12PF PF +的取值范围是（ ） A．B ．(6,8)C．D ．(6,10)二、填空题13．设P 是抛物线28y x =上的一个动点，若点B 为()3,2，则PB PF +的最小值为________________．14．已知椭圆22:143x y C +=的左、右焦点分别为1F 、2F ，点()4,4M ，若点P 为椭圆C 上的一个动点，则1PM PF -的最小值为____________.15．设1F ，2F 为双曲线()2222:10,0x yC a b a b-=>>的左､右焦点，过2F 的直线l 交双曲线C 的右支于A ､B 两点，且120AF AF ⋅=，2212AF BF =，则双曲线C 的离心率为___________.16．已知双曲线()2222:10,0x y C a b a b-=>>的左、焦点为1F 、2F ，点P 为双曲线C 的渐近线上一点，120PF PF ⋅=，若直线1PF 与圆222x y a +=相切，则双曲线C 的离心率为___________.17．在平面直角坐标系xOy 中，已知椭圆C ：()222210x y a b a b+=>>的焦距为，直线l 与椭圆C 交于A ，B 两点，且OA OB ⊥，过O 作⊥OD AB 交AB 于点D ，点D 的坐标为()2,1，则椭圆C 的方程为_________．18．已知双曲线2222:1(0,0)x y E a b a b-=>>，点F 为E 的左焦点，点P 为E 上位于第一象限内的点，P 关于原点的对称点为Q ，且满足||3||PF FQ =，若||OP b =，则E 的离心率为_________.19．已知椭圆2212x y +=上存在相异两点关于直线y x t =+对称，则实数t 的取值范围是______.20．已知抛物线C : y 2=2px (p >0)，直线l ：y = 2x + b 经过抛物线C 的焦点，且与C 相交于A 、B 两点．若|AB | = 5，则p = ___．三、解答题21．已知椭圆具有如下性质：若椭圆的方程为()222210x y a b a b+=>>，则椭圆在其上一点()'',A x y 处的切线方程为''221x y x ya b+=，试运用该性质解决以下问题：在平面直角坐标系xOy 中，已知椭圆C ：()222210x y a b a b +=>>的离心率为22，且经过点21,2A ⎛⎫ ⎪ ⎪⎝⎭. （1）求椭圆C 的方程；（2）设F 为椭圆C 的右焦点，直线l 与椭圆C 相切于点P (点P 在第一象限)，过原点O 作直线l 的平行线与直线PF 相交于点Q ，问：线段PQ 的长是否为定值？若是，求出定值；若不是，说明理由.22．椭圆2222:1(0)x y E a b a b +=>>的左焦点为1F ，右焦点为2F ，离心率2e =，过1F 的直线交椭圆于A ，B 两点，且2ABF 的周长为2． （1）求椭圆E 的方程；（2）若直线AB 3，求2ABF 的面积．23．已知椭圆C ：22221(0)x y a b a b+=>>的离心率为12，点31,2P ⎛⎫ ⎪⎝⎭在椭圆C 上． （1）求C 的方程；（2）若椭圆C 的左右焦点分别为12,F F ，过点1F 的直线l 与C 交于A 、B 两点，12AF F △与12BF F △的面积分别为12,S S ，122S S =，求直线l 的斜率．24．如图，已知抛物线2:2(0)M x py p =>的焦点为(0,1)F ，过焦点F 作直线交抛物线于A ，B 两点，在A ，B 两点处的切线相交于N ，再分别过A ，B 两点作准线的垂线，垂足分别为C ，D .（1）求证：点N 在定直线上；（2）是否存在点N ，使得BDN 的面积是ACN △的面积和ABN 的面积的等差中项，若存在，请求出点N 的坐标，若不存在，请说明理由.25．设抛物线2:4C y x =，点()4,0A ，()4,0B -，过点A 的直线l 与C 交于M ，N 两点．（1）当l 与x 轴垂直时，求直线BM 的方程； （2）证明：ABM ABN ∠=∠．26．已知抛物线()2:20E y px p =>的焦点F ，抛物线E 上一点()3,t 到焦点的距离为4.（1）求抛物线E 的方程；（2）过点F 作直线l ，交抛物线E 于,A B 两点，若线段AB 中点的纵坐标为1-，求直线l 的方程.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】设122F F c =，设椭圆Γ的长轴长为12a ，双曲线Ω的实轴长为22a ，设光速为v ，推导出112a vt =，利用椭圆和双曲线的定义可得出1243a a =，由此可计算得出Γ与Ω的离心率之比. 【详解】设122F F c =，设椭圆Γ的长轴长为12a ，双曲线Ω的实轴长为22a ， 在图②中，1CDF 的周长为111212124CF DF CD CF CF DF DF a vt ++=+++==，所以，1148a vt =，可得112a vt =，在图①中，由双曲线的定义可得2122AF AF a -=，由椭圆的定义可得1212BF BF a +=， 22AF BF AB =-，则2121111222AF AF BF AB AF a BF AB AF a -=--=---=，即()111222a AB AF BF a -++=，由题意可知，1ABF 的周长为111AB AF BF vt ++=，即112111322222a a a a vt a =-=-=， 所以，1243a a =. 因此，Γ与Ω的离心率之比为122112:::3:4c ce e a a a a ===. 故选：A. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.2．B解析：B 【分析】由10MD NF ⋅=得1MD NF ⊥，结合D 是中点，得等腰三角形，由平行线可得2F 是MN 中点，从而MN x ⊥轴，利用勾股定理可得,a c 的关系得离心率． 【详解】因为10MD NF ⋅=，所以1MD NF ⊥，又D 是1NF 中点，所以1MF MN =， 因为12//MF DF ，所以2F 是MN 中点，则22MF NF =，因此MN x ⊥轴， 设2MF m =，则12MF m =，1232MF MF m a +==，23am =， 在12MF F △中，由勾股定理得22242()()(2)33m m c +=，变形可得c e a ==． 故选：B ． 【点睛】关键点点睛：：本题考查求椭圆的离心率，解题关键是确定,,a b c 的等式．解题方法是由向量的数量积得出垂直后，根据三角形的性质得1MF N 的性质（实质上它是等边三角形），特别是MN x ⊥轴，然后结合椭圆定义利用勾股定理可得．3．B解析：B 【分析】先根据题意画出图形，再根据122F A F B=-，得到21F AF B B P ∽，根据相似比得到222a a c c c c ⎛⎫+=⨯- ⎪⎝⎭，即可求出离心率. 【详解】 解：如图所示：122F A F B =-，12//F A F B ∴，12AF B BF P ∴∽，且122F PF P=, 即222a a c c c c ⎛⎫+=⨯- ⎪⎝⎭， 两边同时除以a 得2a c c a c a a c ⎛⎫+=⨯- ⎪⎝⎭， 即122e e e e+=-， 又1e >，解得：3e = 故选：B. 【点睛】关键点点睛：本题解题的关键是利用三角形相似比得到,a c 的关系式，进而求得离心率.4．C解析：C 【分析】设双曲线的渐近线方程为y kx =，其中bk a=±，利用勾股定理可求得k 的值，即可求得b a，再由双曲线的离心率公式e =即可求得双曲线的离心率. 【详解】设双曲线的渐近线方程为y kx =，其中bk a=±， 圆()2239x y -+=的圆心为()3,0C ，半径为3r =，圆心C 到直线y kx =的距离为d =，2AB =，由勾股定理可得2222AB r d ⎛⎫=+ ⎪⎝⎭，即2219+=，解得k =±ba∴=，因此，该双曲线的离心率为3c e a =====. 故选：C. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.5．C解析：C 【分析】作出图形，可知FAB 是以FAB ∠为直角的直角三角形，可得出0AF AB ⋅=，可得出a 、b 、c 的齐次等式，进而可求得椭圆C 的离心率.【详解】如下图所示，可知AFB ∠、ABF ∠均为锐角， 所以，FAB 是以FAB ∠为直角的直角三角形，由题意可知，点(),0F c -、()0,A b 、(),0B a ，则(),AF c b =--，(),AB a b =-，20AF AB ac b ⋅=-+=，可得220a c ac --=，即220c ac a +-=，在等式220c ac a +-=的两边同时除以2a 可得210e e +-=，01e <<，解得512e =. 故选：C. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.6．B解析：B 【分析】由题意可得双曲线22221(0,0)y x a b a b-=>>中223,9c a b =+=，由12PF F △为等腰三角形，所以2126PF F F ==,从而可求得1221064PF a PF =-=-=，再利用双曲线的定义可求得在双曲线中1a =，22b =，进而可求出双曲线的渐近线方程 【详解】解：因为椭圆2251162x y +=的焦点坐标为(0,3)，所以双曲线22221(0,0)y x a b a b-=>>中223,9c a b =+=，设点P 为两曲线在第一象限的交点，由于在椭圆中，12PF F △为等腰三角形，所以2126PF F F ==, 所以1221064PF a PF =-=-=，在双曲线中，212642a PF PF =-=-=，所以1a =，代入229a b +=，得22b =，所以该双曲线的渐近线方程为2422ay x x x b=±=±=±，故选：B【点睛】关键点点睛：此题考查椭圆、双曲线的定义的应用，解题的关键由12PF F△为等腰三角形和椭圆的定义求出21,PF PF的值，属于中档题7．B解析：B【分析】作出图形，过点M分别作抛物线C的准线l和直线3490x y++=的垂线，垂足分别为点B、A，由抛物线的定义得出1d MB MF==，可得出12d d MF MA+=+，利用FM与直线3490x y++=垂直时，12d d+取最小值，然后计算出点F到直线3490x y++=的距离，即为所求.【详解】如下图所示：过点M分别作抛物线C的准线l和直线3490x y++=的垂线，垂足分别为点B、A，由抛物线的定义可得1d MB MF==，则12d d MF MA+=+，当且仅当FM与直线3490x y++=垂直时，12d d+取最小值，点F到直线3490x y++=的距离为22130494234d⨯+⨯+==+，因此，12d d+的最小值为2.故答案为：2. 【点睛】关键点点睛：本题求出抛物线上一点到准线和定直线的距离之和最小值问题，解题的关键就是利用F 、A 、M 三点共线取最小值，结合抛物线的定义转化求解.8．A解析：A 【分析】设直线AB 的方程为2y kx =+，设点()11,A x y 、()11,B x y ，将直线AB 的方程与抛物线的方程联立，列出韦达定理，结合已知条件可得出214x x =-，结合韦达定理求出2k 的值，进而可得出AOB 的面积为1212OAB S OF x x =⋅-△，即可得解. 【详解】易知抛物线28x y =的焦点为()0,2F .若直线AB 与x 轴垂直，此时直线AB 与抛物线28x y =有且只有一个公共点，不合乎题意.设直线AB 的方程为2y kx =+，设点()11,A x y 、()11,B x y ，联立228y kx x y=+⎧⎨=⎩，消去y 并整理得28160x kx --=，由韦达定理可得128x x k +=，1216x x =-，由于AOF 与BOF 的面积之比为1:4，则4BF FA =，则()()2211,24,2x y x y --=-，所以，214x x =-，则12138x x x k +=-=，可得183k x =-， 2221218256441639k k x x x ⎛⎫=-=-⨯-=-=- ⎪⎝⎭，可得2916k =， 所以，OAB 的面积为1211222OAB S OF x x =⋅-=⨯△10===.故选：A. 【点睛】方法点睛：利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下： （1）设直线方程，设交点坐标为()11,x y 、()22,x y ；（2）联立直线与圆锥曲线的方程，得到关于x （或y ）的一元二次方程，必要时计算∆； （3）列出韦达定理；（4）将所求问题或题中的关系转化为12x x +、12x x 的形式； （5）代入韦达定理求解.9．C解析：C 【分析】利用双曲线的定义和已知即可得出|PF 1|，|PF 2|，再利用余弦定理找出a,c 的等量关系,从而可求a,b 的比值，即可得出双曲线C 的渐近线方程． 【详解】解：因为F 1、F 2是双曲线的左、右焦点，点P 在双曲线右支上， 所以由双曲线定义可得|PF 1|－|PF 2|＝2a ， 又知|PF 1|＋|PF 2|＝4a ，所以|PF 1|＝3a ，|PF 2|＝a .在△PF 1F 2中，由余弦定理可得222121212||||||cos60=2||||PF PF F F PF PF +-⋅，即222(3)41=232a a c a a +-⨯⨯，所以3a 2＝10a 2－4c 2，即4c 2＝7a 2，又知b 2＋a 2＝c 2，所以223=4b a ，所以双曲线C 的渐近线方程为2y x =±20y ±=.故选：C.【点睛】关键点点睛：利用双曲线的定义和已知即可得出|PF 1|，|PF 2|，再利用余弦定理解三角形是解答本题的关键．10．C解析：C 【分析】依题意可得c e a ==t ，从而求出双曲线方程，即可求出渐近线； 【详解】解：因为0t >，依题意可得双曲线2221(0)4xy t t t-=>+的离心率c e a ====≤=当且仅当4t t=即2t =时，等号成立，此时离心率最大， 故双曲线的标准方程为22182y x -=，所以双曲线的渐近线方程为y x =，即12y x =±故选：C 【点睛】在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误．11．A解析：A 【分析】根据题中条件，由双曲线的定义，得到2PF a =，13PF a =，根据1212+≥PF PF F F ，即可求出结果. 【详解】因为点P 在双曲线的右支上，由双曲线的定义可得122PF PF a -=， 又213PF PF =，所以222PF a =，即2PF a =，则13PF a =， 因为双曲线中，1212+≥PF PF F F ，即42a c ≥，则2ca≤，即2e ≤， 又双曲线的离心率大于1，所以12e <≤. 故选：A. 【点睛】本题主要考查求双曲线的离心率，熟记双曲线的简单性质即可.12．D解析：D 【分析】由题意画出图形，不妨设P 在第一象限，P 点在1P 与2P 之间运动，求出112F PF ∠和122F F P ∠ 为直角时12PF PF +的值，可得12F PF △ 为锐角三角形时12PF PF +的取值范围． 【详解】12F PF △为锐角三角形，不妨设P 在第一象限，P 点在1P 与2P 之间运动，如图，当P 在1P 处，11290F PF∠=，又1,2,5a b c ===由222111212|||||20|PF PF F F =+=，1112||||2PFPF -=， 可得1112||||8PF PF ⋅=， 此时 1112||||6PF PF +=；当P 在2P 处，12290F F P ∠=，25P x = 易知24P y = 则224P F =此时12222222||||||2||10P F P F P F a P F +=++=∴12F PF △为锐角三角形，则12PF PF +的取值范围是()6,10， 故选：D ． 【点晴】关键点点晴：本题的关键在于求出112F PF ∠和122F F P ∠ 为直角时12PF PF +的值.二、填空题13．5【分析】求出抛物线的准线方程把到焦点距离转化为它到准线的距离然后利用三点共线得最小值【详解】如图过作与准线垂直垂足为则∴易知当三点共线时最小最小值为∴的最小值为5故答案为：5【点睛】本题考查抛物线解析：5 【分析】求出抛物线的准线方程，把P 到焦点F 距离转化为它到准线的距离，然后利用三点共线得最小值． 【详解】如图，过P 作PM 与准线2x =-垂直，垂足为M ，则PF PM =，∴PF PB PM PB +=+，易知当,,B P M 三点共线时，PM PB +最小，最小值为3(2)5--=．∴PB PF +的最小值为5．故答案为：5．【点睛】本题考查抛物线的定义，考查抛物线上的点到焦点和到定点距离之和的最小值，解题方法是利用抛物线的定义把点到焦点的距离转化为点到准线距离．14．1【分析】根据已知可以转化为然后由三点共线即两点之间线段最短可得答案【详解】由已知得因为所以所以所以当三点共线时最小即故答案为：1【点睛】本题考查了椭圆上的点到焦点和定点距离和的问题解题关键是利用定解析：1 【分析】根据已知可以转化为124PM PF PM PF -=+-，然后由三点共线即两点之间线段最短可得答案. 【详解】由已知得222224,3,1a b c a b ===-=，2(1,0)F ， 因为2124PF PF a +==，所以124PF PF =-， 所以()12244PM PF PM PF PM PF -=--=+-， 所以当三点2M P F 、、共线时，24PM PF +-最小， 即2222443441PM PF MF +-=-=+=. 故答案为：1. 【点睛】本题考查了椭圆上的点到焦点和定点距离和的问题，解题关键是利用定义转化为两点之间线段最短的问题，考查了学生分析问题、解决问题的能力.15．【分析】利用双曲线的定义分别表示再利用勾股定义和双曲线的定义建立等量关系求双曲线的离心率【详解】设根据双曲线的定义可知即得得中即得根据双曲线的定义即得所以得故答案为：【点睛】方法点睛：本题考查直线与 解析：173【分析】利用双曲线的定义分别表示1212,,,AF AF BF BF ，再利用勾股定义和双曲线的定义建立等量关系，求双曲线的离心率. 【详解】设2AF x =，22BF x =，1AF y =，根据双曲线的定义可知1212AF AF BF BF -=-， 即12y x BF x -=-，得1BF y x =+，120AF AF ⋅=，12AF AF ∴⊥，()()2223y x y x ∴+=+，得4y x =，12Rt AF F △中，222124AF AF c +=，即22174x c =，得17x =，根据双曲线的定义122AF AF a -=，即32x a =，得23x a =，23a =，得c e a ==.故答案为：3【点睛】方法点睛：本题考查直线与双曲线的位置关系的综合问题，考查学生的转化和计算能力，属于中档题型，求离心率是圆锥曲线常考题型，涉及的方法包含1.根据,,a b c 直接求，2.根据条件建立关于,a c 的齐次方程求解，3.根据几何关系找到,,a b c 的等量关系求解.16．【分析】作出图形设与圆相切于点分析出可求得的值进而可得出双曲线的离心率为即可得解【详解】如下图所示设与圆相切于点则则则为的中点则为的中点由直角三角形的性质可得因为为的中点则由于双曲线的两渐近线关于轴 解析：2【分析】作出图形，设1PF 与圆222x y a +=相切于点E ，分析出23POF π∠=，可求得ba的值，进而可得出双曲线C 的离心率为e =，即可得解. 【详解】如下图所示，设1PF 与圆222x y a +=相切于点E ，则OE a =，120PF PF ⋅=，则12PF PF ⊥，1OE PF ⊥，则2//OE PF ， O 为12F F 的中点，则E 为1PF 的中点，222PF OE a ∴==，由直角三角形的性质可得1OF OP =，因为E 为1PF 的中点，则1EOF POE ∠=∠， 由于双曲线的两渐近线关于y 轴对称，可得21POF EOF ∠=∠，所以，12EOF POE POF ∠=∠=∠，则1223EOF POE POF POF π∠+∠+∠=∠=， 所以，23POF π∠=，则tan 33b a π==， 因此，双曲线C 的离心率为22222212c c a b b e a a a a +⎛⎫====+= ⎪⎝⎭. 故答案为：2. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.17．【分析】先利用点坐标和垂直关系求得直线的斜率并写出直线方程联立直线与椭圆利用韦达定理和垂直的向量关系得到的关系式再结合焦距的关系式解出即得方程【详解】依题意椭圆的焦距为即即由点的坐标为知直线OD 的斜解析：221306x y += 【分析】先利用点D 坐标和垂直关系求得直线l 的斜率，并写出直线方程，联立直线与椭圆，利用韦达定理和垂直的向量关系得到22,a b 的关系式，再结合焦距的关系式解出22,a b ，即得方程. 【详解】依题意，椭圆的焦距为46，即246c =，26c =，即2224a b -=，由点D 的坐标为()2,1，知直线OD 的斜率101202OD k -==-，又⊥OD AB ，知直线l 的斜率为2-，即直线l 的方程为12(2)y x -=--，即52y x =-.设()()1122,,,A x y B x y 联立方程2222152x y a by x ⎧+=⎪⎨⎪=-⎩得()2222222420250ab x a x a a b +-+-=，故2222121222222025,44a a a b x x x x a b a b -+==++， 即()()()12121212525225104y y x x x x x x =--=-++2222222222222202525425104444a a a b b a b a b a b a b --=-⨯+⨯=+++， 由OA OB ⊥知，12120OA OB x x y y ⋅=+=，即222222222225254044a a b b a b a b a b --+=++，所以222255a b a b +=，又2224a b -=，消去2a 得，42141200b b +-=，解得26b =或220b =-（舍去），故2230,6a b ==，椭圆C 的方程为221306x y +=.故答案为：221306x y +=.【点睛】 思路点睛：求解椭圆中的直线垂直问题时，一般利用直线的斜率之积为-1，或者直线上的向量的数量积为0来处理，再联立直线与椭圆方程，结合韦达定理，即可求出结果.18．【分析】由题意设即有由双曲线定义及已知可得且结合点在曲线上联立方程得到关于的齐次方程即可求得离心率【详解】令则且①由题意知：E 的左准线为结合双曲线第二定义知：又∴解得②∵知：∴联立①②得：整理得∴故 3【分析】由题意设00(,)P x y ，即有00(,)Q x y --，由双曲线定义及已知可得22003()a a x x c c +=-且22200x y b +=，结合点在曲线上联立方程得到关于,a c 的齐次方程，即可求得离心率.【详解】令00(,)P x y ，00,0x y >则00(,)Q x y --且2200221x y a b-=①，由题意知：E 的左准线为2a x c =-，结合双曲线第二定义知：20||()a PF e x c=+，20||()a FQ e x c =-，又||3||PF FQ =，∴22003()a a x x c c +=-，解得202a x c=②， ∵||OP b =知：22200x y b +=，∴联立①，②得：42222244(1)a a b b c c+-=，整理得223a c =， ∴3e = 3【点睛】关键点点睛：根据双曲线第二定义：曲线上的点到焦点距离与该点到对应准线的距离之比为常数e ，可得点P 的横坐标为22ac；结合点在曲线上及勾股定理即可得关于,a c 的齐次方程求离心率即可.19．【分析】设对称的两点为直线的方程为与联立可得利用根与系数的关系以及中点坐标公式可求的中点利用判别式以及在直线上即可求解【详解】设椭圆存在关于直线对称的两点为根据对称性可知线段被直线直平分且的中点在直解析：33⎛ ⎝⎭【分析】设对称的两点为()11,A x y ，()22,B x y ，直线AB 的方程为y x b =-+与2212x y +=联立可得利用根与系数的关系以及中点坐标公式可求AB 的中点()00,M x y ，利用判别式0∆>以及()00,M x y 在直线y x t =+上即可求解.【详解】设椭圆2212x y +=存在关于直线y x t =+对称的两点为()11,A x y ，()22,B x y ，根据对称性可知线段AB 被直线y x t =+直平分， 且AB 的中点()00,M x y 在直线y x t =+上，且1AB k =-， 故可设直线AB 的方程为y x b =-+， 联立方程2222y x bx y =-+⎧⎨+=⎩，整理可得2234220x bx b -+-=， ∴1243b x x +=，()1212223b y y b x x +=-+=，由()221612220b b ∆=-->，可得b <<， ∴120223x x b x +==，12023y y b y +==， ∵AB 的中点2,33b b M ⎛⎫⎪⎝⎭在直线y x t =+上，∴233b b t =+，可得3b t =-，33t -<<.故答案为：⎛ ⎝⎭. 【点睛】关键点点睛：本题的关键点是利用直线AB 与直线y x t =+垂直可得直线AB 的斜率为1-，可设直线AB 的方程为y x b =-+，代入2212x y +=可得关于x 的一元二次方程，利用判别式0∆>，可以求出b 的范围，利用韦达定理可得AB 的中点()00,M x y 再代入y x t =+即可t 与b 的关系，即可求解.20．2【分析】法1：首先利用直线过焦点得再利用直线与抛物线方程联立利用根与系数的关系表示计算求得；法2：由已知求得的值再利用弦长公式求的值【详解】法1：由题意知直线即直线经过抛物线的焦点即直线的方程为设解析：2 【分析】法1：首先利用直线过焦点，得b p =-，再利用直线与抛物线方程联立，利用根与系数的关系表示12AB x x p =++，计算求得p ；法2：由已知tan 2θ=，求得sin θ的值，再利用弦长公式22sin pAB θ=，求p 的值. 【详解】法1：由题意知，直线:2l y x b =+，即22b y x ⎛⎫=+⎪⎝⎭．直线l 经过抛物线()2:20C y px p =>的焦点，22b p∴-=，即b p =-．∴直线l 的方程为2y x p =-． 设()11,A x y 、()22,B x y ，联立222y x p y px=-⎧⎨=⎩，消去y 整理可得22460x px p -+=，由韦达定理得1232p x x +=，又5AB =，12552x p p x ∴++==，则2p =.法2：设直线的切斜角为θ，则tan 2k θ==，得sin θ=，∴22225sin p pAB θ===，得2p =.故答案为：2 【点睛】结论点睛：当直线过抛物线的焦点时，与抛物线交于,A B 两点，AB 称为焦点弦长，有如下的性质：直线与抛物线交于()()1122,,,A x y B x y ，①221212,4p y y p x x =-=；②12AB x x p =++；③11AF BF +为定值2p ；④弦长22sin p AB θ= （θ为直线AB 的倾斜角）；⑤以AB 为直径的圆与准线相切；⑥焦点F 对,A B 在准线上射影的张角为90.三、解答题21．（1）2212x y +=；（2.【分析】（1）根据椭圆离心率为2，以及椭圆经过点2A ⎛⎫ ⎪ ⎪⎝⎭，结合椭圆的性质列方程求解即可；（2）设()00,P x y ，题意可知，切线l 的方程为0022x x y y +=，过原点O 且与l 平行的直线'l 的方程为0020x x y y +=，求出Q 的坐标，表示出PQ 的长，再化简即可得结论. 【详解】（1）由题意知2222221112c aa b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩1a b ⎧=⎪⇒⎨=⎪⎩∴椭圆C 的方程为2212x y +=.（2）设()00,P x y ，题意可知，切线l 的方程为0022x x y y +=， 过原点O 且与l 平行的直线'l 的方程为0020x x y y +=， 椭圆C 的右焦点()1,0F ，所以直线PF 的方程为()00010y x x y y ---=，联立()000001020y x x y y x x y y ⎧---=⎨+=⎩，所以2000002,22y x y Q x x ⎛⎫-⎪--⎝⎭，所以PQ =====为定值. 【点睛】方法点睛：探索圆锥曲线的定值问题常见方法有两种：① 从特殊入手，先根据特殊位置和数值求出定值，再证明这个值与变量无关；② 直接推理、计算，并在计算推理的过程中消去变量，从而得到定值.22．（1）2212x y +=；（2）7.【分析】（1）根据椭圆的定义，由2ABF 的周长为a ，再根据离心率求出c ，进而可求出2b，从而可得椭圆方程；（2）先直线AB 的方程为1)y x =+，()11,A x y ，()22,B x y ，联立直线与椭圆方程，根据韦达定理，结合三角形面积公式，即可求出结果. 【详解】（1）因为过1F 的直线交椭圆于A ，B 两点，且2ABF的周长为得2211224AB AF BF AF BF AF BF a ++=+++==a =又2e =，所以2c a =，1c =， 所以21b =，所以椭圆E 的方程为2212x y +=；（2）设直线AB的方程为1)y x =+，()11,A x y ，()22,B x y由221)12y x x y ⎧=+⎪⎨+=⎪⎩消去y ，整理得271240x x ++=， 所以12127x x +=-，1247x x ⋅=，所以12127y y x -=-==．所以212177ABF Sc y y =⋅-=⨯=． 【点睛】 思路点睛:求解圆锥曲线中的面积问题时，一般需要联立直线与曲线方程，结合韦达定理，弦长公式，以及三角形面积公式，（有时也需要点到直线距离公式），即可求解.23．（1）22143x y +=；（2）2±. 【分析】（1）由已知条件可得12c e a ==，将点31,2P ⎛⎫⎪⎝⎭代入椭圆的方程结合222a b c =+即可求得,,a b c 的值，进而可得椭圆C 的方程；（2）设:1l x ty =-，设11(,)A x y ，22(,)B x y ，联立直线与椭圆的方程消去x 可得关于y 的一元二次方程，由韦达定理可得12y y +，12y y ，利用122S S =可得122y y =-，即可解出k 的值，进而可求出直线l 的斜率. 【详解】（1）由题意可得：22222121914c a a b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩得2243a b ⎧=⎨=⎩，故C 的方程为22143x y +=.（2）1(1,0)F -，显然l 与y 轴不垂直，故可设:1l x ty =-，设11(,)A x y ，22(,)B x y ，由221143x ty x y =-⎧⎪⎨+=⎪⎩消去x 得22(34)690t y ty +--=，则122634t y y t +=+，122934y y t -=+， 由122S S =得122y y =-， 所以122262034ty y y t +=+=+，可得22634t y t -=+， 由122934y y t -=+可得2229234y t --=+， 消去2y 可得()222236923434t t t--⨯=++ ，整理可得：245t =t =:1l x y =-，所以直线l：)1y x =+， 所以直线l的斜率为. 【点睛】关键点点睛：本题解题的关键是由面积之比得出纵坐标122y y =-，联立直线与椭圆的方程消去x 可得关于y 的一元二次方程，由韦达定理可得12y y +，12y y ，可求t 的值，注意求直线的斜率.24．（1）证明见解析；（2）存在，12N ⎛⎫±- ⎪ ⎪⎝⎭. 【分析】（1）由题意设直线:1AB y kx =+，()11,A x y ，()22,B x y ，将直线与抛物线方程联立求出两根之和、两根之积，求出直线121:24x x AN y x =-以及直线222:24x x BN y x =-，将两直线联立求出交点即证.（2）由（1）知点N 为CD 的中点，取AB 的中点E ，则2AC BDEN +=，利用抛物线的定义可得2AB EN =，ABNAENBENSSS=+，2ACNAF CNS⋅=，2BDNBF CNS ⋅=，根据2BDN ACN ABN S S S =+△△△，可得2BF AF AB =+，即212x x =-，结合韦达定理即可求解. 【详解】解（1）由题知2p =所以2:4M x y =设直线:1AB y kx =+，()11,A x y ，()22,B x y联立214y kx x y=+⎧⎨=⎩得2440x kx --=所以121244x x k x x +=⎧⎨=-⎩对24x y =求导得2x y '=所以直线AN 的斜率为12AN x k =所以直线()111:2x AN y y x x -=-即121:24x x AN y x =-① 同理直线222:24x x BN y x =-② 联立①和②得12122214x x x k x x y +⎧==⎪⎪⎨⎪==-⎪⎩所以点N 的坐标为(2,1)k -，即点N 在定直线1y =-上 （2）由（1）知点N 为CD 的中点 取AB 的中点E ，则2AC BDEN += 由题知AC BD AB += 所以2AB EN =所以22222ABN AEN BEN EN CN EN DN EN CN AB CNS S S ⋅⋅⋅⋅=+=+=⨯=△△△ 而22ACN AC CN AF CN S ⋅⋅==△，22BDN BD DN BF CNS ⋅⋅==△ 若存在点N 满足题意则2BDN ACN ABN S S S =+△△△ 即2BF AF AB =+所以()2121200x x x x -=-+-即212x x =-③ 又因为121244x x kx x +=⎧⎨=-⎩④将③代入④解得=k ±由（1）知(2,1)N k -即1N ⎛⎫- ⎪ ⎪⎝⎭经检验，存在12N ⎛⎫±- ⎪ ⎪⎝⎭满足题意. 【点睛】关键点点睛：本题考查了直线与抛物线的位置关系，解题的关键是由()11,A x y ，()22,B x y ，求出点N 的坐标为(2,1)k -以及212x x =-，考查了计算能力、推理能力.25．（1）122y x =+或122y x =--；（2）见解析. 【分析】（1）首先根据l 与x 轴垂直，且过点A ，求得直线l 的方程为4x =，代入抛物线方程求得点M 的坐标为()4,4或()4,4-，利用两点式求得直线BM 的方程；（2）设直线l 的方程为4x ty =+，点()11,M x y 、()22,N x y ，将直线l 的方程与抛物线的方程联立，列出韦达定理，由斜率公式并结合韦达定理计算出直线BM 、BN 的斜率之和为零，从而得出所证结论成立. 【详解】（1）当l 与x 轴垂直时，l 的方程为4x =，可得M 的坐标为()4,4或()4,4-， 所以直线BM 的方程为122y x =+或122y x =--； （2）设l 的方程为4x ty =+，()11,M x y 、()22,N x y ，由244x ty y x=+⎧⎨=⎩，得24160y ty --=，可知124y y t +=，1216y y =-， 直线BM 、BN 的斜率之和为 ()()()()()()()()21122112121212124488444444BM BN x y x y ty y ty y y yk k x x x x x x +++++++=+==++++++()()()()()()12121212282168404444ty y y y t tx x x x ++⨯-+⨯===++++，所以0BM BN k k +=，可知BM 、BN 的倾斜角互补， 所以ABM ABN ∠=∠. 【点睛】该题考查的是有关直线与抛物线的问题，涉及到的知识点有直线方程的两点式、直线与抛物线相交的综合问题、关于角的大小用斜率来衡量；在解题的过程中，第一问求直线方程的时候，需要注意方法比较简单，需要注意的就是应该是两个，关于第二问，涉及到直线与曲线相交都需要联立方程组，之后韦达定理写出两根和与两根积，借助于斜率的关系来得到角是相等的结论.。

北师大版高中数学选修1-1第二章《圆锥曲线与方程》测试卷(含答案解析)

北师大版高中数学选修1-1第二章《圆锥曲线与方程》测试卷(含答案解析)

一、选择题1．已知斜率为16的直线l 与双曲线22221(0,0)x y C a b a b-=>>:相交于B 、D 两点，且BD 的中点为(1,3)M ，则C 的离心率为（ ）A ．2B ．5 C ．3 D ．6 2．直线34y kx k =-+与双曲线221169x y -=有且只有一个公共点，则k 的取值有（ ）个A ．1B ．2C ．3D ．43．已知点A 是抛物线24x y =的对称轴与准线的交点，点F 为抛物线的焦点，点P 在抛物线上，且满足||||PA m PF =，则m 的最大值是（ ） A ．1B ．2C ．2D ．44．已知双曲线E ：22221(0,0)x y a b a b-=>>的左，右焦点为1F ，2F ，过2F 作一条渐近线的垂线，垂足为M ，若16MF OM =，则E 的离心率为（ ）A 3B ．2C 5D 25．已知12,F F 分别为双曲线22221(0,0)x y a b a b-=>>的左，右焦点，过1F 的直线交双曲线的左支于,A B 两点，若113AF F B =，23cos 5AF B ∠=，则双曲线的离心率e =（ ） A 5B ．52C ．102D ．536．已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为12F F ，，点M 在双曲线C 的渐近线上，若212211221cos 12cos ,3MF F MF F F MF MF F ∠+=∠∠=∠，则双曲线C 的离心率为（ ） A ．3B 3C ．22D ．27．设F 1，F 2是双曲线C ：22221x y a b-=(a >0，b >0)的左、右焦点，P 是双曲线C 右支上一点，若|PF 1|＋|PF 2|＝4a ，且∠F 1PF 2＝60°，则双曲线C 的渐近线方程是（ ）A 0y ±=B ．20x =C 20y ±=D ．20x ±=8．已知双曲线()222210,0x y a b a b-=>>的左、右焦点分别为1F 、2F ，若双曲线右支上存在一点P ，使得2F 关于直线1PF 的对称点恰在y 轴上，则该双曲线的离心率e 的取值范围为（ ）A ．13e <<B ．eC ．e >D ．1e <<9．已知双曲线C ：22221x y a b-=(0a >，0b >)的左右焦点分别为1F ，2F ，过1F 的直线交双曲线左支于P ，交渐近线by x a=于点Q ，点Q 在第一象限，且12FQ F Q ⊥，若12PQ PF =，则双曲线的离心率为（ ）A B ．12+ C 1 D 110．设双曲线22221(0,0)x y a b a b-=>>的左､右焦点分别为1F ､2F ，点P 在双曲线的右支上，且213PF PF =，则双曲线离心率的取值范围是（ ） A ．(1,2]B ．5(1,]3C ．[2,)+∞D ．4[,)3+∞11．已知抛物线24x y =的焦点F 和点(1,8),A P -为抛物线上一点，则||||PA PF +的最小值是（ ） A ．3B ．9C ．12D ．612．已知过点(,0)A a 的直线与抛物线22(0)y px p =>交于M.N 两点，若有且仅有一个实数a ，使得16OM ON ⋅=-成立，则a 的值为（ ） A ．4-B ．2C ．4D ．8二、填空题13．设椭圆()2222:10x y C a b a b+=>>的左焦点为F ，直线x m =与椭圆C 相交于A ，B两点.当ABF 的周长最大时，ABF 的面积为2b ，则椭圆C 的离心率e =________． 14．设P 是双曲线22:13y x Γ-=上任意一点，Q 与P 关于x 轴对称，1F 、2F 分别为双曲线的左、右焦点，若有121PF PF ⋅≥，则1F P 与2F Q 夹角的取值范围是__________. 15．如图，椭圆C ：()222210x y a b a b+=>>的左､右焦点分别为1F ､2F ，B 为椭圆C 的上顶点，若12BF F △的外接圆的半径为23b，则椭圆C 的离心率为________.16．设双曲线()2222:10,0x y C a b a b-=>>的右焦点为F ，点P 在C 的右支上，O 为坐标原点，若存在点P ，使PF OF =，且1cos 4OFP ∠=，则双曲线的离心率为___________．17．如图，一种电影放映灯的反射镜面是旋转椭圆面（椭圆绕其对称轴旋转一周形成的曲面）的一部分，过对称轴的截口BAC 是椭圆的一部分，灯丝位于椭圆的一个焦点1F 上，片门位于另一个焦点2F 上.由椭圆一个焦点1F 发出的光线，经过旋转椭圆面反射后集中到另一个焦点2F .已知12BC F F ⊥，1163F B =，124F F =，则截口BAC 所在椭圆的离心率为______.18．已知双曲线()222210,0x y a b a b-=>>的右焦点为F ，若过点F 且倾斜角为6π的直线与双曲线的右支有且只有一个公共点，则该双曲线的离心率的取值范围___________. 19．对抛物线C ：24x y =，有下列命题：①设直线l ：1y kx =+，则直线l 被抛物线C 所截得的最短弦长为4；②已知直线l ：1y kx =+交抛物线C 于A 、B 两点，则以AB 为直径的圆一定与抛物线的准线相切；③过点()()2,P t t R ∈与抛物线有且只有一个交点的直线有1条或3条；④若抛物线C 的焦点为F ，抛物线上一点()2,1Q 和抛物线内一点()()2,1R m m >，过点Q 作抛物线的切线1l ，直线2l 过点Q 且与1l 垂直，则2l 平分RQF ∠；其中你认为是正确命题的所有命题的序号是______.20．椭圆22221(0)x y a b a b+=>>上一点A 关于原点的对称点为B ，F 为椭圆的右焦点，若AF BF ⊥，设ABF α∠=，且,124ππα⎡⎤∈⎢⎥⎣⎦，则该椭圆离心率的最大值为______． 三、解答题21．已知点22,2M ⎛⎫ ⎪ ⎪⎭在椭圆2222:1(0)x y C a b a b +=>>上，且点M 到C 的左，右焦点的距离之和为4． （1）求C 的方程；（2）设O 为坐标原点，若C 的弦AB 的中点在线段OM （不含端点,O M ）上，求OA OB ⋅的取值范围．22．在平面直角坐标系xOy 中，已知A ，B 两点是椭圆22:19x E y +=的左、右顶点，P 为直线6x =上的动点，PA 与椭圆E 的另一交点为Q ，当点P 不为点()6,0时，过P作直线PH QB ⊥，垂足为H . （1）证明：直线PH 过定点M ；（2）过（1）中的定点M 作斜率为k 的直线与椭圆E 交于C ，D 两点，设直线AC ，AD 的斜率分别为1k ，2k ，试判断()12k k k ⋅+是否为定值？如果是定值，求出定值. 23．已知椭圆()2222:10x y C a b a b+=>>左、右焦点分别为1F 、2F ，上顶点为M ，离心率为63，12MF F△的面积为2. （1）求椭圆C 的标准方程；（2）过点2F ，的直线l 交椭圆于A 、B 两点，当1ABF 面积最大时，求直线l 的方程. 24．已知点()11,A x y ，()22,B x y 是抛物线C ：24x y =上的两点，满足OA OB ⊥，O 是坐标原点.（1）求证：1216x x =-；（2）若⊥OD AB 于点D ，求点D 的轨迹方程. 25．已知是抛物线2:2C y px=(0)p >的焦点，(1,)M t 是抛物线上一点，且||2MF =.（1）求抛物线C 的方程；（2）过点O （坐标原点）分别作,OA OB 交抛物线C 于,A B 两点(,A B 不与O 重合)，且.2OA OB k k =.求证：直线AB 过定点.26．如图，已知抛物线24y x =的焦点为F ，过F 作斜率为(0)k k >的直线交抛物线于()11,A x y 、()22,B x y 两点，且10y >，弦AB 中垂线交x 轴于点T ，过A 作斜率为k -的直线交抛物线于另一点C ．（1）若14y =，求点B 的坐标；（2）记ABT 、ABC 的面积分别为1S 、2S ，若214S S =，求点A 的坐标．【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】设()()1122,,B x y D x y 、，用“点差法”表示出a 、b 的关系，即可求出离心率 【详解】设()()1122,,B x y D x y 、,则22112222222211x y a bx y a b ⎧-=⎪⎪⎨⎪-=⎪⎩， 两式作差得：22221212220x x y y a b---=， 整理得：()()()()2121221212y y y y b a x x x x +-=+-BD 的中点为(1,3)M ，且直线l 的斜率为16 ，代入有：22611262b a =⨯=即22212c a a -=，解得6ce a . 故选：D 【点睛】求椭圆（双曲线）离心率的一般思路：根据题目的条件，找到a 、b 、c 的关系，消去b ，构造离心率e 的方程或（不等式）即可求出离心率．2．D解析：D 【分析】将直线方程与双曲线的方程联立，得出关于x 的方程，根据直线与双曲线只有一个公共点，求出对应的k 值，即可得解. 【详解】联立22341169y kx k x y =-+⎧⎪⎨-=⎪⎩，消去y 并整理得()()()2221693243164390k x k k x k ⎡⎤-+-+-+=⎣⎦，由于直线34y kx k =-+与双曲线221169x y -=有且只有一个公共点， 所以，21690k -=或()()()222216903243641694390k k k k k ⎧-≠⎪⎨⎡⎤⎡⎤∆=----+=⎪⎣⎦⎣⎦⎩， 解得34k =±或2724250k k +-=， 对于方程2724250k k +-=，判别式为22447250'∆=+⨯⨯>，方程2724250k k +-=有两个不等的实数解.显然34k =±不满足方程2724250k k +-=. 综上所述，k 的取值有4个. 故选：D. 【点睛】方法点睛：将直线与圆锥曲线的两个方程联立成方程组，然后判断方程组是否有解，有几个解，这是直线与圆锥曲线位置关系的判断方法中最常用的方法，注意：在没有给出直线方程时，要对是否有斜率不存在的直线的情况进行讨论，避免漏解．3．B解析：B 【分析】由抛物线的对称性可不妨设P 在第一象限或为原点，过P 作准线1y =-的垂线，垂足为E ，利用抛物线的定义可得1sin PAE m=∠，求出sin PAE ∠的最小值后可得m 的最大值. 【详解】由抛物线24x y =可得准线方程为：1y =-，故()0,1A -.如图，由抛物线的对称性可不妨设P 在第一象限或为原点， 过P 作准线1y =-的垂线，垂足为E ，则PE PF =， 故1||||sin ||||PF PE PAE m PA PA ===∠， 当直线AP 与抛物线相切时，PAE ∠最小， 而当P 变化时，02PAE π<∠≤，故当直线AP 与抛物线相切时sin PAE ∠最小，设直线:1AP y kx =-，由241x yy kx ⎧=⎨=-⎩得到2440x kx -+=，216160k ∆=-=，故1k =或1k =-（舍），所以直线AP 与抛物线相切时4PAE π∠=，故1m 2即m 2， 故选：B. 【点睛】方法点睛：与抛物线焦点有关的最值问题，可利用抛物线的定义把到焦点的距离问题转化为到准线的距离问题.4．A解析：A 【分析】由点到直线的距离公式可得2||MF b =，由勾股定理可得||OM a =，则16MF a =，1cos aFOM c∠=-，由此利用余弦定理可得到a ，c 的关系，由离心率公式计算即可得答案． 【详解】由题得2(,0)F c ，不妨设:0l bx ay -=，则2||MF b ==，OM a ==，1MF =，12cos cos aFOM F OM c ∠=-∠=-， 由余弦定理可知222222111||||622OM OF MF a c a a OM OF ac c+-+-==-⋅，化为223c a =，即有==ce a故选：A ． 【点睛】方法点睛：离心率的求解在圆锥曲线的考查中是一个重点也是难点，一般求离心率有以下几种情况：①直接求出,a c ，从而求出e ；②构造,a c 的齐次式，求出e ；③采用离心率的定义以及圆锥曲线的定义来求解；④根据圆锥曲线的统一定义求解．5．C解析：C 【分析】设1133AF F B m ==，利用双曲线定义求出232AF m a =+，22F B m a =+，利用余弦定理写出,a m 关系，推知焦点三角形12F BF 是直角三角形，利用勾股定理求出,a c 关系式，从而求出离心率. 【详解】设1133AF F B m ==，则4AB m =，则由双曲线定义有232AF m a =+，22F B m a =+，在2AF B 中，由余弦定理有()()()()()22242232223m a m a m a m a m =+++-⋅++ 整理得22320m am a --=，解得m a = 故4AB a =，25AF a =，23F B a = 故2AF B 为直角三角形，290ABF ∠=在12Rt F BF △中，2221122F B F B F F +=，则()()22232a a c +=，故22252c e a ==故e =故选：C 【点睛】双曲线的离心率是双曲线最重要的几何性质，求双曲线的离心率(或离心率的取值范围)，常见有两种方法： ①求出a ，c ，代入公式c e a=； ②只需要根据一个条件得到关于a ，b ，c 的齐次式，结合b 2＝c 2－a 2转化为a ，c 的齐次式，然后等式(不等式)两边分别除以a 或a 2转化为关于e 的方程(不等式)，解方程(不等式)即可得e (e 的取值范围)．6．D解析：D 【分析】根据角的关系计算出12216030MF F MF F ∠=︒∠=︒，，从而求出渐近线方程为y =，得到ba=. 【详解】因为21221cos 12cos MF F MF F ∠+=∠，故1221cos cos 2MF F MF F ∠=∠，即12212MF F MF F ∠=∠，而12213F MF MF F ∠=∠，故12216030MF F MF F ∠=︒∠=︒，，则三角形1MF O 为等边三角形，故双曲线C 的渐近线方程为y =，则2e ==，故选D ．【点睛】求椭圆（双曲线）离心率的一般思路：根据题目的条件，找到a 、b 、c 的关系，消去b ，构造离心率e 的方程或（不等式）即可求出离心率．7．C解析：C 【分析】利用双曲线的定义和已知即可得出|PF 1|，|PF 2|，再利用余弦定理找出a,c 的等量关系,从而可求a,b 的比值，即可得出双曲线C 的渐近线方程． 【详解】解：因为F 1、F 2是双曲线的左、右焦点，点P 在双曲线右支上， 所以由双曲线定义可得|PF 1|－|PF 2|＝2a ， 又知|PF 1|＋|PF 2|＝4a ，所以|PF 1|＝3a ，|PF 2|＝a .在△PF1F2中，由余弦定理可得222 121212||||||cos60=2||||PF PF F FPF PF+-⋅，即222(3)41=232a a ca a+-⨯⨯，所以3a2＝10a2－4c2，即4c2＝7a2，又知b2＋a2＝c2，所以223=4ba，所以双曲线C的渐近线方程为3y x=±，即320x y±=.故选：C.【点睛】关键点点睛：利用双曲线的定义和已知即可得出|PF1|，|PF2|，再利用余弦定理解三角形是解答本题的关键．8．B解析：B【分析】设点()2,0F c，设点P在第一象限，设2F关于直线1PF的对称点为点M，推导出12MF F△为等边三角形，可得出tan30ba>，再由公式21bea⎛⎫=+ ⎪⎝⎭可求得该双曲线离心率的取值范围.【详解】如下图所示：设点()2,0F c，设点P在第一象限，由于2F关于直线1PF的对称点在y轴上，不妨设该点为M，则点M在y轴正半轴上，由对称性可得21122MF MF F F c===，22113MO MF OF c=-=，所以，1260MF F∠=，则1230PF F∠=，所以，双曲线的渐近线b y x a =的倾斜角α满足30α>，则12tan 3b PF F a >∠=因此，该双曲线的离心率为3c e a ====>. 故选：B. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.9．A解析：A 【分析】由12FQ F Q ⊥得出OQ c =，求出Q 点坐标为(,)a b ，利用12PQ PF =表示出P 点坐标，代入双曲线方程得关于,,a b c 的等式，变形后可求得e ． 【详解】∵12FQ F Q ⊥，O 是12F F 中点，∴OQ c =， 设(,)Q x y （0,0x y >>），则222y bx a x y c⎧=⎪⎨⎪+=⎩，又222a b v +=，故解得x a y b =⎧⎨=⎩，即(,)Q a b ，12PQ PF =，则12QP PF =，(,)2(,)P P P P x a y b c x y --=---，解得233P P a c x b y -⎧=⎪⎪⎨⎪=⎪⎩， 又P 在双曲线上，∴2222(2)199a c b a b --=，解得12e =（12舍去）． 故选：A ． 【点睛】关键点点睛：本题考查求双曲线的离心率，解题关键是找到关于,a c 的齐次式，本题利用P 在双曲线上列式，由12FQ F Q ⊥得(,)Q a b ，由12PQ PF =表示出P 点坐标，代入双曲线方程即可求解．10．A解析：A【分析】根据题中条件，由双曲线的定义，得到2PF a =，13PF a =，根据1212+≥PF PF F F ，即可求出结果. 【详解】因为点P 在双曲线的右支上，由双曲线的定义可得122PF PF a -=， 又213PF PF =，所以222PF a =，即2PF a =，则13PF a =， 因为双曲线中，1212+≥PF PF F F ，即42a c ≥，则2ca≤，即2e ≤， 又双曲线的离心率大于1，所以12e <≤. 故选：A. 【点睛】本题主要考查求双曲线的离心率，熟记双曲线的简单性质即可.11．B解析：B 【分析】根据抛物线的标准方程求出焦点坐标和准线方程，利用抛物线的定义可得||||||||PA PF PA PF AM +=+≥，故AM 为所求【详解】解：由题意得2p =，焦点(0,1)F ，准线方程为1y =-， 设P 到准线的距离为PM ，（即PM 垂直于准线，M 为垂足），则||||||||9PA PF PA PF AM +=+≥=，（当且仅当,,P A M 共线时取等号）， 所以||||PA PF +的最小值是9， 故选：B 【点睛】关键点点睛：此题考查抛物线的定义、标准方程，以及简单性质的应用，解题的关键是由题意结合抛物线定义得||||||||PA PF PA PF AM +=+≥，从而可得结果12．C解析：C 【分析】设出直线方程与抛物线方程联立，利用韦达定理得出1212,y y y y +及12x x ，把16OM ON ⋅=-用坐标表示代入上述值结合已知条件可得答案.【详解】设直线MN 的直线方程为x ty a =+，1122(,),(,)M x y N x y ，由题意得22x ty a y px=+⎧⎨=⎩，整理得2220y pty pa --=，所以12122,2y y pt y y pa +==-，()()()2212121212x x ty a ty a t y y at y y a =++=+++()()2222t ap at pt a =-++，因为16OM ON ⋅=-，所以121216x x y y +=-， 所以()()2222216tpa at pt a pa -++-=-，22160a pa -+=，因为方程有且仅有一个实数a ，所以()22640p ∆=-=，解得4p =，或4p =-（舍去）， 故选：C. 【点睛】本题考查了直线和抛物线的位置关系，关键点是利用韦达定理求出1212,y y y y +及12x x ，然后16OM ON ⋅=-坐标表示列出等式，考查了学生分析问题、解决问题的能力.二、填空题13．【分析】首先根据椭圆定义分析分析当的周长最大时直线的位置再求的面积得到椭圆的离心率【详解】设椭圆的右焦点为当直线过右焦点时等号成立的周长此时直线过右焦点得故答案为：【点睛】关键点点睛：本题考查椭圆内 解析：12【分析】首先根据椭圆定义分析，分析当ABF 的周长最大时，直线AB 的位置，再求ABF 的面积，得到椭圆的离心率. 【详解】设椭圆的右焦点为F '，AF BF AB ''+≥，当直线AB 过右焦点F '时，等号成立，∴ABF 的周长4l AF BF AB AF BF AF BF a ''=++≤+++=，此时直线AB 过右焦点，22b AB a =，221222ABFb Sc b a=⨯⨯=，得12c e a ==.故答案为：12【点睛】关键点点睛：本题考查椭圆内的线段和的最值问题，关键是利用两边和大于第三边，只有三点共线时，两边和等于第三边，再结合椭圆的定义，求周长的最值.14．【分析】设由求出的取值范围再由平面向量的数量积计算出与夹角的余弦的取值范围从而得夹角的范围【详解】设则又双曲线中即∴又即代入上式得设与夹角为则∵∴∴∵∴故答案为：【点睛】关键点点睛：本题考查依托双曲解析：25,arccos 37ππ⎛⎤⎥⎝⎦- 【分析】设00(,)P x y ，由121PF PF ⋅≥求出20x 的取值范围，再由平面向量的数量积计算出1F P 与2F Q 夹角的余弦的取值范围，从而得夹角的范围．【详解】设00(,)P x y ，则00(,)Q x y -，又双曲线22:13y x Γ-=中2c ==，即12(2,0),(2,0)F F -，∴2212000000(2,)(2,)41PF PF x y x y x y ⋅=---⋅--=-+≥， 又220013y x -=，即220033=-y x ，代入上式得204341x --≥，202x ≥．100(2,)F P x y =+，200(2,)F Q x y =--，2212004F P F Q x y ⋅=--， 设1F P 与2F Q 夹角为θ，则2222221212cos (F P F Q F P F Qθ⋅====∵202x ≥，∴cos θ20202141x x +=--，2200222000132211322414122(41)x x x x x -++==+---， 20417x -≥，203302(41)14x <≤-，201135222(41)7x <+≤-， ∴51cos 72θ-≤<-，∵[0,]θπ∈，∴25arccos 37πθπ<≤-． 故答案为：25,arccos 37ππ⎛⎤ ⎥⎝⎦-．【点睛】关键点点睛：本题考查依托双曲线求平面向量夹角的取值范围．解题方法是设00(,)P x y ，利用P 点满足的条件求出0x 的范围，然后求出向量夹角的余弦值，余弦值的范围，从而得出角的范围．15．【分析】由题意可得的外接圆的圆心在线段上可得在中由勾股定理可得：即结合即可求解【详解】由题意可得：的外接圆的圆心在线段上设圆心为则在中由勾股定理可得：即所以即所以所以故答案为：【点睛】方法点睛：求椭 解析：12【分析】由题意可得12BF F △的外接圆的圆心在线段OB 上，1OF c =，123bMF BM ==，可得 13OM b =，在1OMF △中，由勾股定理可得：22211MF OM OF =+，即222233b b c ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，结合222b ac =-即可求解. 【详解】由题意可得：12BF F △的外接圆的圆心在线段OB 上，1OF c =， 设圆心为M ，则2133OM OB BM b b b =-=-=， 在1OMF △中，由勾股定理可得：22211MF OM OF =+，即222233b b c ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，所以223b c =，即2223a c c -=，所以2a c =，所以12c e a ==， 故答案为：12. 【点睛】方法点睛：求椭圆离心率的方法： （1）直接利用公式c e a=； （2）利用变形公式221b e a=-； （3）根据条件列出关于,a c 的齐次式，两边同时除以2a ，化为关于离心率的方程即可求解.16．2【分析】在焦点三角形中由余弦定理求得关系再求离心率【详解】设双曲线的左焦点为在中由余弦定理得故答案为：2【点晴】求离心率的关键是得的关系本题是由余弦定理得出解析：2 【分析】在焦点三角形中由余弦定理求得,a c 关系，再求离心率. 【详解】设双曲线的左焦点为E ，在EFP △中，2EF c =，2PF c PE a c ==+，，1cos 4EFP ∠=. 由余弦定理()222421cos 224c c c a EFP c c +-+∠==⋅⋅ ，得2c e a ==. 故答案为：2 【点晴】求离心率的关键是得,,a b c 的关系，本题是由余弦定理得出.17．【分析】取焦点在轴建立平面直角坐标系由题意及椭圆性质有为椭圆通径得结合及解出代入离心率公式计算即可【详解】解：取焦点在轴建立平面直角坐标系由及椭圆性质可得为椭圆通径所以又解得所以截口所在椭圆的离心率解析：13【分析】取焦点在x 轴建立平面直角坐标系，由题意及椭圆性质有BC 为椭圆通径，得2163b a =，结合24c =及222a b c =+解出,,a b c 代入离心率公式计算即可.【详解】解：取焦点在x 轴建立平面直角坐标系，由12BC F F ⊥及椭圆性质可得，BC 为椭圆通径，所以21163b F B a ==，1224F Fc ==又222a b c =+，解得6,2,a c b ===所以截口BAC 所在椭圆的离心率为13故答案为：13【点睛】求椭圆的离心率或其范围的方法：（1）求,,a b c 的值，由22222221c a b b a a a-==-直接求e ； （2）列出含有,,a b c 的齐次方程(或不等式)，借助于222a b c =+消去b ，然后转化成关于e 的方程(或不等式)求解．18．【分析】作出图形根据已知条件可得出与的大小关系再利用公式可求得双曲线的离心率的取值范围【详解】如下图所示双曲线的渐近线方程为由于过点且倾斜角为的直线与双曲线的右支有且只有一个公共点由图可知直线的倾斜解析：23,3⎡⎫+∞⎪⎢⎪⎣⎭【分析】作出图形，根据已知条件可得出b a 与tan 6π的大小关系，再利用公式21b e a ⎛⎫=+ ⎪⎝⎭可求得双曲线的离心率的取值范围. 【详解】如下图所示，双曲线()222210,0x y a b a b-=>>的渐近线方程为b y x a =±，由于过点F 且倾斜角为6π的直线与双曲线的右支有且只有一个公共点， 由图可知，直线b y x a =的倾斜角6πα≥，所以，3tan 63b a π≥=， 因此，222222231c c a b b e a a a a +⎛⎫====+≥ ⎪⎝⎭ 所以，该双曲线的离心率为取值范围是23⎫+∞⎪⎪⎣⎭. 故答案为：233⎡⎫+∞⎪⎢⎪⎣⎭. 【点睛】方法点睛：求双曲线离心率或离心率范围的两种方法：一种是直接建立e 的关系式求e 或e 的范围；另一种是建立a 、b 、c 的齐次关系式，将b 用a 、e 表示，令两边同除以a 或2a 化为e 的关系式，进而求解．19．①②④【分析】①将抛物线与直线联立消去利用根与系数关系求出再由弦长公式即可求出弦长进而可求出弦长的最小值即可判断①的正误；②利用中点坐标公式求出以为直径的圆的圆心的纵坐标判断圆心到直线的距离与半径的解析：①②④ 【分析】①将抛物线与直线联立消去y ，利用根与系数关系求出12x x +，12x x ，再由弦长公式即可求出弦长，进而可求出弦长的最小值，即可判断①的正误；②利用中点坐标公式，求出以AB 为直径的圆的圆心的纵坐标，判断圆心到直线的距离121y y ++与半径||2AB r =的大小关系，即可判断②的正误； ③将2x =代入24x y =，可得()2,1P 在抛物线上，此时当直线的斜率不存在时，只有一个交点，当直线与抛物线相切时，也只有一个交点，故与抛物线只有一个交点的直线有可能有2条，可判断③错误；④设1l 的方程为()12y k x -=-，将直线与抛物线联立消去y ，利用判别式即可求出k ，进而可求出直线1l 的倾斜角，即可判断④的正误. 【详解】①联立方程241x yy kx ⎧=⎨=+⎩，消去y 可得2440x kx --=，216160k ∆=+>恒成立，设两交点坐标分别为()11,A x y ，()22,B x y ， 所以由根与系数的关系得124x x k +=，124x x ⋅=-，故AB ==2444k =+≥，当0k =时，AB 取得最小值4，所以最短弦长为4，故①正确，②由①可知124x x k +=，则21212242y y kx kx k +=++=+，故以AB 为直径的圆的圆心坐标为()22,21k k +，半径2222ABr k ==+， 抛物线24x y =的准线方程为1y =-，故圆心到准线1y =-的距离2221122d k k r =++=+=， 所以以AB 为直径的圆一定与抛物线的准线相切，故②正确，③将2x =代入24x y =，解得1y =，所以当1t =时，即()2,1P 在抛物线上， 当直线的斜率不存在时，方程为2x =，此时只有一个交点()2,1，当直线斜率存在且只与抛物线只有一个交点时，当且仅当该直线为切线时满足条件，所以过点()2,P t 只与抛物线只有一个交点的直线有可能有2条，故③错误， ④因为抛物线的焦点为()0,1F ，又()2,1Q ，()2,R m ， 所以三角形FQR 为直角三角形且过()2,1Q 的切线斜率一定存在， 设1l 的方程为()12y k x -=-，代入24x y =，可得24840x k k -+-=，由()2164840k k ∆=--=可得1k =，即直线1l 的倾斜角为45︒，因为直线2l 过点Q 且与1l 垂直，所以一定平分RQF ∠，故④正确. 故答案为：①②④ 【点睛】思路点睛：直线与抛物线交点问题的解题思路：(1)求交点问题，通常解直线方程与抛物线方程组成的方程组； (2)与交点相关的问题通常借助根与系数的关系或用向量法解决．20．【分析】设左焦点为根据椭圆的定义有且O 是直角三角形斜边的中点所以离心率由角的范围可求得离心率的最大值【详解】因为关于原点对称所以B 也在椭圆上设左焦点为根据椭圆的定义：又因为所以O 是直角三角形斜边的中【分析】设左焦点为F '，根据椭圆的定义有，||||2AF BF a +=，且O 是直角三角形ABF 斜边的中点，所以||2,||2sin ,||2cos AB c AF c BF c αα===，离心率11sin cos 4c a πααα==+⎛⎫+ ⎪⎝⎭，由角的范围可求得离心率的最大值. 【详解】因为,B A 关于原点对称，所以B 也在椭圆上，设左焦点为F '，根据椭圆的定义：||2AF AF a '+=，又因为||BF AF '=，所以||||2AF BF a +=，O 是直角三角形ABF 斜边的中点，所以||2,||2sin ,||2cos AB c AF c BF c αα===，所以2(sin cos )2c a αα+=，所以11sin cos 4c a πααα==+⎛⎫+ ⎪⎝⎭， 由于,124ππα⎡⎤∈⎢⎥⎣⎦，所以当12πα=时，离心率的最大值为：3,. 【点睛】关键点点睛：求椭圆的离心率关键在于由椭圆的定义，善于利用平面几何中的边、角关系建立关于,,a b c 的等式或不等式.三、解答题21．（1）2214x y +=；（2）861,540⎛⎫- ⎪⎝⎭．【分析】（1）本小题根据已知条件直接求出2a =，1b =，再求出椭圆方程即可.（2）本小题先设A 、B 两点，再将OA OB ⋅转化为只含m 的表达式，最后根据m 的范围确定OA OB ⋅的范围，即可解题. 【详解】解：（1）∵点2M ⎭在椭圆C ：22221x y a b +=（0a b >>）上，∴222112a b +=，又∵24a =， ∴ 2a =，1b =.∴椭圆C 的方程：2214x y +=；（2）设点A 、B 的坐标为11(,)A x y ，22(,)B x y ，则AB 中点1212,22x x y y ++⎛⎫⎪⎝⎭在线段OM 上，且12OM k =，则12122()x x y y +=+， 又221112x y +=，222212x y +=，两式相减得()()()()1212121202x x x x y y y y -++-+=， 易知120x x -≠，120y y +≠，所以()1212121212y y x x x x y y -+=-=--+，则1AB k =-. 设AB 方程为y x m =-+，代入2214xy +=并整理得2258440x mx m -+-=.由216(5)0m ∆=->解得25m <，又由(12425x x m +=∈，则0m <<. 由韦达定理得1285m x x +=，2124(1)5m x x -⋅=，故OA OB ⋅1212x x y y =+()()1212x x x m x m =+-+-+ ()212122x x m x x m =-++()22281855m m m -=-+285m =-又∵. 04m <<∴OA OB ⋅的取值范围是861,540⎛⎫- ⎪⎝⎭．【点睛】解决直线与椭圆的综合问题时，要注意：(1)注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件；(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题． 22．（1）证明见解析；（2）是，定值为112-. 【分析】（1）设()00 ,Q x y ，()()6,0P t t ≠，法一：根据椭圆方程求得19QA QB k k ⋅=-，根据9QA PA tk k ==，即可求得QB k ，根据PH QB ⊥，可求得PH k ，可得直线PH 的方程，即可得答案；法二：根据9AP QA tk k ==，可得直线AP 的方程，与椭圆联立，根据韦达定理，可得Q 点坐标，根据PH QB ⊥，可求得PH k ，可得直线PH 的方程，即可得答案； （2）设()11,C x y ，()22,D x y ，则直线CD 的方程为()5y k x =-，与椭圆联立，根据韦达定理，可得1212,x x x x +⋅表达式，即可得()12k k k ⋅+的表达式，化简整理，即可得答案. 【详解】（1）法一：由题意得：(3,0),(3,0)A B -，设()00 ,Q x y ，()()6,0P t t ≠，则220019x y += ∴00001339QA QB y y k k x x ⋅=⋅=-+-，9QA PA t k k == ∴1QB k t=-∵PH QB ⊥，∴1PH QB k k ⋅=-，∴PH k t =，直线PH 的方程为()6y t t x -=-，即()5y t x =-，所以过定点()5,0M ，法二：由题意得：(3,0),(3,0)A B -，设()00,Q x y ，()()6,0P t t ≠，9AP QA tk k ==∴直线AP 的方程为()39ty x =+， 由()223919t y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩，得()2222969810t x t x t +++-=. ∴20298139t x t --⋅=+，∴2022739t x t -=+，()0023699t y t t x +=+=， ∴2222736,99t t Q tt ⎛⎫- ⎪++⎝⎭，∴222619 27339QBtt k t tt +==---+. ∵PH QB ⊥，∴1PH QB k k ⋅=-， ∴PH k t =，∴PH 的方程为()6y t t x -=-，即()5y t x =-，所以过定点()5,0M（2）设()11,C x y ，()22,D x y ，则直线CD 的方程为()5y k x =-由()22519y k x x y ⎧=-⎪⎨+=⎪⎩.得()2222199022590k x k x k +-+-=， ∴22221222122(90)4(19)(2259)0901*******k k k k x x k k x x k ⎧⎪∆=--+->⎪⎪+=⎨+⎪⎪-=⎪+⎩∴()()()()()()()122121121222153533333x x x x y y k k k k k x x x x -++-+⎛⎫⋅+=⋅+= ⎪+⎭⋅+++⎝ ()()1212222121222304813957612x x x x k k x x x x k -⋅+--++⋅===-+为定值 【点睛】解题的技巧为：根据椭圆方程可得19QA QB k k ⋅=-，根据QA PA k k =，可直接求得QB k ，简化计算，提高正确率，考查计算化简的能力，属中档题.23．（1）2213x y +=；（2）0x y -=或0x y +=.【分析】（1）由离心率、面积和222a b c =+可得答案；（2）设()11,A x y ，()22,B x y，:l x ty =+11212AF BF F AF F BSSS=+，结合基本不等式，可得答案.【详解】 （1）∵3c e a ==，12MF F S bc ==△222a b c =+，解得a =1b =，c =C 的方程为：2213x y +=.（2）()1F，)2F ，设()11,A x y ，()22,B x y ，已知直线l 的斜率不为0，设直线l：x ty =+2213x ty x y ⎧=+⎪⎨+=⎪⎩，得()22310t y ++-=，故12y y +=，12213y y t =-+，1212121212F F A F F BSSF F y y+=-=23t+，12=≤=，即1t =±时等号成立，所以直线l 的方程为0x y --=或0x y +=. 【点睛】本题考查了椭圆的定义，考查了三角形的面积公式，关键点是利用韦达定理表示1212F F AF F BSS+并利用基本不等式求最值，考查了直线与椭圆的位置关系和计算能力.24．（1）证明见解析；（2）()2224x y +-=. 【分析】（1）设出直线方程与抛物线方程联立，由OA OB ⊥转化为坐标形式再利用韦达定理表示可得答案；（2）判断出直线AB 过定点()0,4M ，由⊥OD AB 于点D ，得到点D 在以OM 为直径的圆上可得答案.【详解】（1）证明：由题意直线AB 的斜率存在，可设方程为y kx b =+，0b ≠，由24y kx b x y=+⎧⎨=⎩可得2440x kx b --=， 所以1x ，2x 是该方程的两根，所以216160k b ∆=+>， 且124x x k +=，124x x b =-，OA OB ∴⊥，12120x x y y ∴+=，即()()()()221212121210x x kx b kx b k x xbk x x b +++=++++=， 可得()2224140kb k b b-+++=，0b ≠，解得4b =，此时216160k b ∆=+>成立，12416x x b ∴=-=-.（2）由（1）可得直线AB 的方程为4y kx =+， 所以直线AB 过定点()0,4M ，又⊥OD AB 于点D ，所以点D 在以OM 为直径的圆上， 可得点D 的轨迹方程为()2224x y +-=. 【点睛】本题考查了直线与抛物线的位置关系，利用韦达定理解决问题时注意判别式的范围，要熟练掌握基础知识及转化能力.25．（1）24y x =；（2）直线AB 过定点(2,0)-，证明见解析. 【分析】（1）由抛物线的定义求得p ，得抛物线方程；（2）设直线AB 方程为x my b =+， 11(,)A x y ，22(,)B x y ，直线方程代入抛物线方程，由判别式大于0得参数满足的条件，应用韦达定理得1212,y y y y +，计算由2OA OB k k =可得128y y =，从而求得参数b ，并可得出m 的范围．此时由直线方程可得定点坐标． 【详解】（1）由抛物线定义可知：122p+=，则2p =， 所以抛物线C 的方程为24y x =（2）设直线AB 方程为x my b =+， 11(,)A x y ，22(,)B x y联立24y x x my b⎧=⎨=+⎩得2440y my b --=，则216160m b ∆=+>即20()m b +>* 且124y y m +=，124y y b =-.2OA OB k k =，所以12122y y x x =， 又2114y x =，2224y x =，因此可得128y y =即48b -=，2b =- 代入()*得220m ->，m ∴<m >所以直线AB 方程为2x my =-，由此可知直线AB 过定点(2,0)-.【点睛】方法点睛：本题考查主要考查抛物线中直线过定点问题，解题方法是设而不求的思想方程，即设直线方程为x my b =+，设交点坐标为11(,)A x y ，22(,)B x y ，直线方程代入抛物线方程后应用韦达定理得1212,y y y y +，代入已知求出参数值，然后由直线方程得定点坐标．26．（1）1,14B ⎛⎫- ⎪⎝⎭；（2）(3,A . 【分析】（1）设直线AB ，然后联立方程组，根据韦达定理，代入14y =，即可求出2y ，再代入抛物线方程即可得点B 的坐标；（2）设()33,C x y ，表示出直线AB 与AC 的斜率，然后相加为零得3122=--y y y ，表示出直线AB 的中垂线方程，求出点T 的坐标，将214S S =转化为4=C T d d ，列式计算.【详解】（1）设直线AB 方程为1x my =+∴21212214404,44x my y my y y y y m y x=+⎧⇒--=⇒=-+=⎨=⎩ ∵1221414y y x =⇒=-⇒=即1,14B ⎛⎫- ⎪⎝⎭（2）设()33,C x y∵12122212121244--===--+AB y y y y k y y x x y y ，同理：134AC k y y =+，因为直线AB 与AC 的斜率分别为,k k -，∴1213312121344002y y y y y y y y y y y +=⇒+++=⇒=--++ 又∵直线AB 方程为：()()1112124440y y x x x y y y y y -=-⇒-+-=+ 直线AB 中垂线方程为：。

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(含答案解析)

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(含答案解析)

一、选择题1．光线从椭圆的一个焦点发出，被椭圆反射后会经过椭圆的另一个焦点；光线从双曲线的一个焦点发出，被双曲线反射后的反射光线等效于从另一个焦点射出，如图①，一个光学装置由有公共焦点1F 、2F 的椭圆Γ与双曲线Ω构成，现一光线从左焦点1F 发出，依次经Ω与Γ反射，又回到了点1F ，历时1t 秒；若将装置中的Ω去掉，如图②，此光线从点1F 发出，经Γ两次反射后又回到了点1F ，历时2t 秒；若218t t =，则Γ与Ω的离心率之比为（ ）A ．3:4B ．2:3C ．1:2D ．22．已知椭圆22221(0)x y C a b a b+=>>：的左､右焦点分别为1F ，2F ，过2F 直线与椭圆C 交于M ，N 两点，设线段1NF 的中点D ，若10MD NF ⋅=，且12//MF DF ，则椭圆C 的离心率为（ ） A ．13B 3C ．12D ．223．已知()5,0F 是双曲线()2222:=10,0x y C a b a b->>的右焦点，点(11A .若对双曲线C 左支上的任意点M ，均有10MA MF +≥成立，则双曲线C 的离心率的最大值为（ ） A 11B ．5C ．52D ．64．已知点12,F F 是椭圆()222210x y a b a b+=>>的左右焦点，椭圆上存在不同两点,A B 使得122F A F B =，则椭圆的离心率的取值范围是（ ）A ．10,3⎛⎫ ⎪⎝⎭B ．10,2⎛⎫ ⎪⎝⎭C ．1,13⎛⎫ ⎪⎝⎭D ．1,12⎛⎫ ⎪⎝⎭5．设直线l 与圆C ：22(2)3x y -+=相切于N ，与抛物线22(0)y px p =>交于,A B 两点，且N 是线段AB 的中点，若直线l 有且只有4条，则p 的取值范围是（ ）A ．B ．(1,3)C ．(0,3)D ．6．已知12,F F 分别是双曲线2214x y -=的左、右焦点，P 为双曲线右支上异于顶点的任意一点，若12PF F △内切圆圆心为I ，则圆心I 到圆22(1)1y x +-=上任意一点的距离最小值为（ ）A ．2B 1C ．1D 27．过抛物线26y x =的焦点作一条直线与抛物线交于()()1122,,,A x y B x y 两点，若123x x +=，则这样的直线（ ）A ．有且只有一条B ．有且只有两条C ．有且只有三条D ．有且只有四条8．已知1F 、2F 分别是双曲线()2222:10,0x yC a b a b-=>>的左右焦点，点P 在双曲线右支上且不与顶点重合，过2F 作12F PF ∠的角平分线的垂线，垂足为A ，O 为坐标原点，若OA =，则该双曲线的离心率为（ ）A B C ．2 D 9．在平面直角坐标系中，双曲线C 的标准方程为2221(0)4x y t t t-=>+，则双曲线的离心率取得最大值时，双曲线的渐近线方程为（ ）A ．2y x =±B ．3y x =±C ．12y x =±D ．13y x =±10．已知直线:(1)(2)230l a x a y a +++--=经过定点P ，与抛物线24x y =交于,A B 两点，且点P 为弦AB 的中点，则直线l 的方程为（ ） A ．230x y +-= B ．210x y -+= C ．210x y -+=D ．20x y +-=11．已知椭圆22:11612x y C +=的左焦点为F ，点P 是椭圆C 上的动点，点Q 是圆()22:21T x y -+=上的动点，则PF PQ的最小值是（ ）A ．12B ．27C ．23D12．已知动点(),P x y 5a a=+(a 为大于零的常数)﹐则动点P 的轨迹是（ ） A ．线段B ．圆C ．椭圆D ．双曲线二、填空题13．已知F 是双曲线2222:1(0,0)x y C a b a b-=>>的右焦点，O 为坐标原点，过F 的直线与C 的两条渐近线的交点分别为,M N ，若0OM MF ⋅=，||MN b =，则C 的离心率为________.14．过双曲线M ：2213x y -=的右焦点F 作圆C ：221(1)2x y ++=的切线，此切线与M 的右支交于A ，B 两点，则||AB =___________.15．已知双曲线()2222:10,0x y C a b a b-=>>的左、焦点为1F 、2F ，点P 为双曲线C 的渐近线上一点，120PF PF ⋅=，若直线1PF 与圆222x y a +=相切，则双曲线C 的离心率为___________.16．已知椭圆22:143x y C +=的左､右焦点分别为12F F 、，过2F 且倾斜角为π4的直线l 交椭圆C 于A B 、两点，则1F AB 的面积为___________.17．已知双曲线2222:1x y C a b-=(0a >，0b >)的两条渐近线与直线1x =-所围成的三角形的面积为4，则双曲线C 的离心率为________.18．双曲线()2222:10,0x y C a b a b-=>>的左焦点为F ，A ､B 分别为C 的左，右支上的点，O 为坐标原点，若四边形ABOF 为菱形，则C 的离心率为______.19．设A 、B 是双曲线22221(0,0)x y a b a b-=>>的左、右顶点，F 是右焦点，M 是双曲线上异于A 、B 的动点，过点B 作x 轴的垂线与直线MA 交于点P ，若直线OP 与BM 的斜率之积为4，则双曲线的离心率为_________．20．设椭圆()2222:10x y C a b a b +=>>的左右焦点为12F F ，，过2F 作x 轴的垂线与C 交于A B ，两点，若1ABF 是等边三角形，则椭圆C 的离心率等于________.三、解答题21．在平面直角坐标系xOy 中，已知两点()1,0M -，()1,0N ，动点Q 到点M 的距离为，线段NQ 的垂直平分线交线段MQ 于点K ，设点K 的轨迹为曲线E .（1）求曲线E 的方程；（2）已知点()2,0P ，设直线l ：10x my +-=与曲线E 交于A ，B 两点，求证：OPA OPB ∠=∠.22．已知椭圆C ：22221(0)x y a b a b+=>>的离心率为12，点31,2P ⎛⎫ ⎪⎝⎭在椭圆C 上．（1）求C 的方程；（2）若椭圆C 的左右焦点分别为12,F F ，过点1F 的直线l 与C 交于A 、B 两点，12AF F △与12BF F △的面积分别为12,S S ，122S S =，求直线l 的斜率．23．已知抛物线1C ：()220x py p =>和圆2C ：22120x x y -+=交于O ，P 两点，且1OP k =，其中O 为坐标原点.（1）求1C 的方程；（2）过1C 的焦点F 且不与坐标轴平行的直线l 与1C 交于A ，B 两点，AB 的中点为M ，1C 的准线为0l ，且0MQ l ⊥，垂足为Q .证明直线AB ，OQ 的斜率之积T 为定值，并求该定值.24．如图，已知抛物线21:2C y x =直线2y kx =+交抛物线C 于A ，B 两点，O 为坐标原点.（1）证明：OA OB ⊥；（2）设抛物线C 在点A 处的切线为1l ，在点B 处的切线为2l ，证明：1l 与2l 的交点M 在一定直线上.25．如图，已知抛物线2:2(0)M x py p =>的焦点为(0,1)F ，过焦点F 作直线交抛物线于A ，B 两点，在A ，B 两点处的切线相交于N ，再分别过A ，B 两点作准线的垂线，垂足分别为C ，D .（1）求证：点N 在定直线上；（2）是否存在点N ，使得BDN 的面积是ACN △的面积和ABN 的面积的等差中项，若存在，请求出点N 的坐标，若不存在，请说明理由.26．已知椭圆2222:1(0)x y C a b a b +=>>的焦点在圆223x y +=3（1）求椭圆C 的方程；（2）过原点O 的直线l 与椭圆C 交于,A B 两点，F 为右焦点，若FA 垂直于AB ，求直线l 的斜率.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】设122F F c =，设椭圆Γ的长轴长为12a ，双曲线Ω的实轴长为22a ，设光速为v ，推导出112a vt =，利用椭圆和双曲线的定义可得出1243a a =，由此可计算得出Γ与Ω的离心率之比. 【详解】设122F F c =，设椭圆Γ的长轴长为12a ，双曲线Ω的实轴长为22a ， 在图②中，1CDF 的周长为111212124CF DF CD CF CF DF DF a vt ++=+++==，所以，1148a vt =，可得112a vt =，在图①中，由双曲线的定义可得2122AF AF a -=，由椭圆的定义可得1212BF BF a +=，22AF BF AB =-，则2121111222AF AF BF AB AF a BF AB AF a -=--=---=，即()111222a AB AF BF a -++=，由题意可知，1ABF 的周长为111AB AF BF vt ++=，即112111322222a a a a vt a =-=-=， 所以，1243a a =. 因此，Γ与Ω的离心率之比为122112:::3:4c ce e a a a a ===. 故选：A. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.2．B解析：B 【分析】由10MD NF ⋅=得1MD NF ⊥，结合D 是中点，得等腰三角形，由平行线可得2F 是MN 中点，从而MN x ⊥轴，利用勾股定理可得,a c 的关系得离心率． 【详解】因为10MD NF ⋅=，所以1MD NF ⊥，又D 是1NF 中点，所以1MF MN =， 因为12//MF DF ，所以2F 是MN 中点，则22MF NF =，因此MN x ⊥轴， 设2MF m =，则12MF m =，1232MF MF m a +==，23am =， 在12MF F △中，由勾股定理得22242()()(2)33m m c +=，变形可得3c e a ==． 故选：B ． 【点睛】关键点点睛：：本题考查求椭圆的离心率，解题关键是确定,,a b c 的等式．解题方法是由向量的数量积得出垂直后，根据三角形的性质得1MF N 的性质（实质上它是等边三角形），特别是MN x ⊥轴，然后结合椭圆定义利用勾股定理可得．3．C解析：C【分析】设E 是双曲线的左焦点，利用双曲线的定义把MF 转化为ME 后易得MA ME +的最小值，从而得a 的最小值，由此得离心率的最大值． 【详解】设E 是双曲线的左焦点，M 在左支上，则2MF ME a -=，2MF ME a =+，22MA MF MA ME a EA a +=++≥+，当且仅当E A M ,,三点共线时等号成立．则222(5)(11)210EA a a +=-++≥，2a ≥，所以552c e a a ==≤． 故选：C ．【点睛】思路点睛：本题考查双曲线的定义的应用．在涉及双曲线上的点与一个焦点和另外一个定点距离和或差的最值时，常常利用双曲线的定义把到已知焦点的距离转化为到另一焦点的距离，从而利用三点共线取得最值求解．4．C解析：C 【分析】先设点，利用向量关系得到两点坐标之间的关系121223,2x x c y y =-=，再结合点在椭圆上，代入方程，消去222a y 即得2229312c a x c+=，根据题意2x a <，构建,a c 的齐次式，解不等式即得结果. 【详解】设()()1122,,,A x y B x y ，由()()12,0,,0F c F c -得()()112212,,,F A F x c y x c y B -==+，122F A F B =，()()11222,,x c y x c y =∴+-，即121223,2x x c y y =-=，由,A B 在椭圆上，故2222221122222222b x a y a b b x a y a b ⎧+=⎨+=⎩，即()()2222222222222222232b x c a y a b b x a y a b ⎧-+=⎪⎨+=⎪⎩，消去222a y 得，2229312c a x c+=，根据椭圆上点满足a x a -≤≤，又,A B 两点不同，可知2229312c a x a c+=<，整理得22340c ac a -+<，故23410e e -+<，故113e <<.故选：C. 【点睛】 关键点点睛：圆锥曲线中离心率的计算，关键是根据题中条件，结合曲线性质，找到,,a b c 一组等量关系（齐次式），进而求解离心率或范围.5．B解析：B 【分析】根据l 有且只有4条，易知直线l 的斜率不存在时，有两条，得到直线l 斜率存在时，有两条，根据N 是线段AB 的中点，利用点差法得到0ky p =，再根据直线l 与圆C ：22(2)3x y -+=相切于N ，得到0012y x k=--，结合得到02x p =-，2203y p =-再根据点N 在抛物线内部求解. 【详解】设()()()112200,,,,,A x y B x y N x y ， 因为l 有且只有4条，当直线l的斜率不存在时，有两条，即2=±x 所以直线l 斜率存在时，有两条， 因为AB 在抛物线上，所以21122222y px y px ⎧=⎨=⎩，两式相减得()2212122y y p x x -=-，因为N 是线段AB 的中点， 所以1202y y y +=， 所以12121202y y p pk x x y y y -===-+， 即0ky p =，因为直线l 与圆C ：22(2)3x y -+=相切于N ， 所以0012y x k=--，即002x ky p -=-=-，所以02x p =-，代入抛物线22y px =，得()222y p p =-，因为点N 在抛物线内部，所以()2022y p p <-，因为点N 在圆上，所以2200(2)3x y -+=，即2203p y +=， 所以2203y p =-，所以()220322y p p p =-<-，即2430p p -+<，解得13p <<， 故选：B 【点睛】方法点睛：解决直线与曲线的位置关系的相关问题，往往先把直线方程与曲线方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题．涉及弦中点的问题常常用“点差法”解决，往往会更简单．6．C解析：C 【分析】设12PF F △内切圆与12PF F △的三边1PF ､2PF ､12F F 的切点分别为D ､N ､M ，根据圆的切线性质，可得2OM =，即可得答案. 【详解】设12PF F △的内切圆分别与12,PF PF 切于点,A B ，与12F F 切于点M ，则11||||,||||PA PB F A F M ==，22||||F B F M =．又点P 在双曲线右支上， 12||||2PF PF a ∴-=，即12(||||)(||||)2PA F A PB F B a +-+=， 12||||2F M F M a ∴-= ①，又12||||2F M F M c += ②， 由①＋②，解得1||F M a c =+， 又1||OF c =，则(,0)M a ，因为双曲线2214x y -=的2a =，所以内切圆圆心I 与在直线2x =上，设0(2,)I y ， 设圆22(1)1y x +-=的圆心为C ，则(0,1)C ，所以()220||21CI y =+-，当01y =时，min ||2CI =，此时圆22(1)1y x +-=上任意一点的距离最小值为min ||1211CI -=-=．故选： C ．【点睛】本题考查双曲线的定义和性质，关键点是由定义和已知得到12||||2F M F M a -=和12||||2F M F M c +=，考查了学生分析问题、解决问题的能力，属于中档题.7．A解析：A 【分析】由抛物线方程求得焦点F 的坐标，分直线AB 斜率不存在和直线斜率存在，存在时设直线AB 方程与抛物线方程联立，由韦达定理表示出A 、B 两点的横坐标之和，求得k ，即可得结论. 【详解】抛物线26y x =的焦点为3,02F ⎛⎫⎪⎝⎭， 当过焦点的直线斜率不存在时，即为32x =， 1232x x ==，符合123x x +=， 当过焦点的直线斜率存在时设为32y k x ⎛⎫=- ⎪⎝⎭， 与抛物线交于()()1122,,,A x y B x y 两点，由2632y x y k x ⎧=⎪⎨⎛⎫=- ⎪⎪⎝⎭⎩得()222293604k k x k x -++=， 所以2122363k x x k++==，即22363k k +=，所以无解， 则这样的直线有且只有一条. 故选：A. 【点睛】本题考查直线与抛物线的位置关系，解题的时候要注意讨论直线斜率不存在时的情况，以免遗漏，是中档题.8．B解析：B 【分析】延长2F A 交1PF 于点Q ，可得1223QF OA b ==，结合双曲线的定义可得,a b 的关系，从而求得离心率． 【详解】延长2F A 交1PF 于点Q ，∵PA 是12F PF ∠的平分线，∴2AQ AF =，2PQ PF =， 又O 是12F F 中点，所以1//QF AO ，且1223QF OA b ==， 又11122QF PF PQ PF PF a =-=-=，∴223a b =，222233()a b c a ==-，∴233c e a ==． 故选：B ．【点睛】关键点点睛：本题考查求双曲线的离心率，解题关键是找到关于,,a b c 的关系，解题方法是延长2F A 交1PF 于点Q ，利用等腰三角形的性质、平行线的性质得出123QF b =，然后由双曲线的定义得出关系式，从而求解．9．C解析：C 【分析】依题意可得2244c t te a t ++==+t ，从而求出双曲线方程，即可求出渐近线； 【详解】解：因为0t >，依题意可得双曲线2221(0)4x y t t t-=>+的离心率2c e a ====≤=当且仅当4t t=即2t =时，等号成立，此时离心率最大， 故双曲线的标准方程为22182y x -=，所以双曲线的渐近线方程为y x =，即12y x =±故选：C 【点睛】在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误．10．B解析：B 【分析】利用点差法求出直线斜率，即可得出直线方程. 【详解】由直线:(1)(2)230l a x a y a +++--=得(2)(23)0a x y x y +-++-=所以20230x y x y +-=⎧⎨+-=⎩ 解得11x y =⎧⎨=⎩则()1,1P 设1122(,),(,)A x y B x y ，则21122244x y x y ⎧=⎨=⎩，两式相减得121212()()4()x x x x y y -+=-， 即121212142AB y y x x k x x -+===-， 则直线方程为11(x 1)2y -=-，即210x y -+=. 故选：B. 【点睛】方法点晴：点差法是求解中点弦有关问题的常用方法.11．B解析：B 【分析】作出图形，利用椭圆的定义以及圆的几何性质可求得PF PQ的最小值.【详解】如下图所示：在椭圆22:11612x y C +=中，4a =，23b =222c a b -，圆心()2,0T 为椭圆C 的右焦点，由椭圆定义可得28PF PT a +==，8PF PT ∴=-，由椭圆的几何性质可得a c PT a c -≤≤+，即26PT ≤≤，由圆的几何性质可得1PQ PT QT PT ≤+=+， 所以，899211111617PF PF PT PQPT PT PT -≥==-≥-=++++. 故选：B. 【点睛】关键点点睛：解本题的关键在于以下几点：（1）问题中出现了焦点，一般利用相应圆锥曲线的定义，本题中注意到2PF PT a +=，进而可将PF 用PT 表示；（2）利用圆的几何性质得出PT r PQ PT r -≤≤+，可求得PQ 的取值范围； （3）利用椭圆的几何性质得出焦半径的取值范围：a c PT a c -≤≤+.12．C解析：C 【分析】由a 为大于零的常数，可知5a a+的最小值，再根据两点间距离公式得几何意义以及椭圆定义判断轨迹. 【详解】()222x y +-的几何意义为点(),P x y 与点(0,2)A 间的距离，的几何意义为点(),P x y 与点(0,2)B -间的距离，且4AB =又由a 为大于零的常数，可知54a a +≥=>，当且仅当5a a=，即a =54a a=+>， 即动点P 到点A 与到点B 的距离之和为定值，且大于AB ， 所以动点P 的轨迹为椭圆， 故选：C. 【点睛】在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误． 椭圆的定义揭示了椭圆的本质属性，正确理解掌握定义是关键，应注意定义中的常数大于|F 1F 2|，避免了动点轨迹是线段或不存在的情况．二、填空题13．2【分析】首先根据可得可计算结合可得是等腰三角形且再由渐进线的斜率可计算出点坐标即可求出点坐标利用结合可得之间的关系即可求解【详解】因为所以即所以为点到渐近线的距离所以可得点为的中点又因为所以所以设解析：2 【分析】首先根据0OM MF ⋅=可得⊥OM MF ，可计算MF b =，结合||MN b =可得OFN △是等腰三角形，且ON c =，再由渐进线的斜率可计算出点N 坐标，即可求出点M 坐标，利用OM a =结合222b c a =-可得,a c 之间的关系，即可求解. 【详解】因为0OM MF ⋅=，所以OM MF ⊥，即⊥OM MF 所以MF 为点(),0F c 到渐近线0bx ay -=的距离，22bcMF b cb a ===+， 所以MF MN b ==，可得点M 为NF 的中点， 又因为⊥OM MF ，所以ON OF c ==， 所以222OM c b a =-=，设双曲线的左焦点为1F ，1FON θ∠=，(),N x y 则()tan tan tan bFON FON aθπ=-∠=-∠=， 因为222c a b =+，所以cos acθ=，sin b c θ=所以cos a x ON c a c θ=-=-⋅=-，sin by ON c b cθ==⋅=， 所以(),N a b -，因为M 为NF 中点，所以,22a M c b -⎛⎫⎪⎝⎭， 222222c a b OM a -⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭，将222b c a =-代入整理可得：()22224c a c a a -+-= 即222240c ac a --=，所以220e e --=，可得()()210e e -+=， 解得：2e =或1e =-（舍）， 故答案为：2 【点睛】方法点睛：求椭圆离心率的方法： （1）直接利用公式c e a=；（2）利用变形公式e =； （3）根据条件列出关于,a c 的齐次式，两边同时除以2a ，化为关于离心率的方程即可求解.14．【分析】首先设出直线利用直线与圆相切求直线方程再利用弦长公式求弦长【详解】因为直线过双曲线的右焦点且与圆相切所以直线的斜率存在设直线方程为()由直线与圆相切知解得或当时双曲线的一条渐近线的斜率是该直解析：【分析】首先设出直线，利用直线与圆相切，求直线方程，再利用弦长公式求弦长AB . 【详解】因为直线过双曲线的右焦点且与圆相切，所以直线的斜率存在，设直线方程为0y k -=(2x -)2=，解得1k =或17k =，当17k =17<，该直线不与双曲线右支相交于两点，故舍去；所以直线方程为2y x =-，联立双曲线方程，消元得2212150x x -+=.设()11,A x y ，()22,B x y ，则126x x +=，12152x x =，所以12||AB x =-===.故答案为：【点睛】易错点点睛：利用直线与圆相切，得到两个斜率1k =或17k =，需舍去一个，否则出现增根.15．【分析】作出图形设与圆相切于点分析出可求得的值进而可得出双曲线的离心率为即可得解【详解】如下图所示设与圆相切于点则则则为的中点则为的中点由直角三角形的性质可得因为为的中点则由于双曲线的两渐近线关于轴 解析：2【分析】作出图形，设1PF 与圆222x y a +=相切于点E ，分析出23POF π∠=，可求得ba的值，进而可得出双曲线C 的离心率为21b e a ⎛⎫=+ ⎪⎝⎭，即可得解. 【详解】如下图所示，设1PF 与圆222x y a +=相切于点E ，则OE a =，120PF PF ⋅=，则12PF PF ⊥，1OE PF ⊥，则2//OE PF ， O 为12F F 的中点，则E 为1PF 的中点，222PF OE a ∴==，由直角三角形的性质可得1OF OP =，因为E 为1PF 的中点，则1EOF POE ∠=∠， 由于双曲线的两渐近线关于y 轴对称，可得21POF EOF ∠=∠，所以，12EOF POE POF ∠=∠=∠，则1223EOF POE POF POF π∠+∠+∠=∠=， 所以，23POF π∠=，则tan 33b a π==， 因此，双曲线C 的离心率为22222212c c a b b e a a a a +⎛⎫====+= ⎪⎝⎭. 故答案为：2. 【点睛】方法点睛：求解椭圆或双曲线的离心率的方法如下：（1）定义法：通过已知条件列出方程组，求得a 、c 的值，根据离心率的定义求解离心率e 的值；（2）齐次式法：由已知条件得出关于a 、c 的齐次方程，然后转化为关于e 的方程求解； （3）特殊值法：通过取特殊位置或特殊值，求得离心率.16．【分析】先求出直线的方程与椭圆方程联立消去x 求出|y1-y2|利用即可求出的面积【详解】由题意得:直线:设则有:消去x 得:7y2+6y-9=0∴即的面积为【点睛】求椭圆(双曲线)的焦点弦三角形的面积【分析】先求出直线l 的方程,与椭圆方程联立,消去x ,求出| y 1- y 2|,利用11212|1|||2F AB S F F y y =-△即可求出1F AB 的面积. 【详解】由题意得: 直线l :1y x =-, 设1122(,),(,)A x y B x y ,则有:2213412y x x y =-⎧⎨+=⎩消去x 得:7y 2+6y -9=0, ∴121269,77y y y y +=-=-12211111|||227|2227F AB S F F y y -∴=⨯=⨯⨯==△即1F AB 【点睛】求椭圆(双曲线)的焦点弦三角形的面积: （1）直接求出弦长|AB |,利用11||2F AB AB d S =△; （2）利用11212|1|||2F AB S F F y y =-△. 17．【分析】求出双曲线的渐近线方程求解时的值然后求解三角形的面积推出离心率即可【详解】双曲线的渐近线方程为将代入中解得故故故双曲线的离心率故答案为：【点睛】方法点睛：求圆锥曲线的离心率常用的方法有：（1【分析】求出双曲线的渐近线方程，求解1x =-时，y 的值，然后求解三角形的面积，推出离心率即可． 【详解】双曲线2222:1(0,0)x y C a b a b -=>>的渐近线方程为b y x a=±，将1x =-代入b y x a =±中，解得by a=±， 故12142ba =，故4b a=，故双曲线C 的离心率22117c b e a a==+=． 故答案为：17 【点睛】方法点睛：求圆锥曲线的离心率常用的方法有：（1）公式法（求出,a c 的值再代离心率的公式求解）；（2）方程法（根据已知找到关于离心率的方程再解方程得解）.要根据已知条件灵活选择方法求解.18．【分析】先根据四边形为菱形及双曲线的性质求的度数再根据双曲线的定义找的关系最后由离心率的计算公式求结论【详解】设右焦点为连接过作轴于因为双曲线关于轴对称四边形为菱形所以所以所以所以根据双曲线的定义可解析：31+. 【分析】先根据四边形ABOF 为菱形，及双曲线的性质，求AFO ∠的度数，再根据双曲线的定义找,a c 的关系，最后由离心率的计算公式求结论. 【详解】设右焦点为'F ，连接'AF ，过A 作AH x ⊥轴于H ，因为双曲线C 关于y 轴对称，四边形ABOF 为菱形， 所以AB OF AF c ===，2cOH FH ==， 所以60AFO ∠=︒，所以'AF AF ⊥，所以'3AF c =， 根据双曲线的定义可得'32AF AF c c a -=-=， 所以3131e ==+-， 31. 【点睛】方法点睛：该题考查的是有关双曲线离心率的求解问题，对于求解圆锥曲线离心率的值或范围的解题方法如下：（1）一般不直接求出的值，而是根据题目给出的圆锥曲线的集合特征建立关于参数,,c a b 的方程组或不等式组，通过解方程组或不等组求得离心率的值或范围； （2）通常从两个方面入手研究，一是考虑几何关系，二是考虑代数关系； （3）注意用好定义.19．【分析】设代入双曲线方程变形为再根据MPA 共线利用斜率相等求得点P 然后再直线与的斜率之积为4得到ab 的关系求解【详解】设则即设又且MPA 共线所以解得则的斜率为的斜率为又直线与的斜率之积为4所以即所以【分析】设(),M m n ，代入双曲线方程变形为22222n b m a a=-，再根据M ，P ，A 共线，利用斜率相等，求得点P ，然后再直线OP 与BM 的斜率之积为4，得到a ，b 的关系求解. 【详解】设(),M m n ，则22221m n a b -=，即22222n b m a a=-， 设(),P a t ，又(),0A a -，且M ，P ，A 共线， 所以2n tm a a=+， 解得2ant m a=+， 则OP 的斜率为2nm a+， BM 的斜率为nm a-， 又直线OP 与BM 的斜率之积为4，所以22222224a n b m a ==-，即222b a =，所以c e a ===【点睛】本题主要考查双曲线的离心率的求法以及点的双曲线上和斜率公式的应用，还考查了运算求解的能力，属于中档题.20．【分析】利用已知条件推出的关系然后求解椭圆的离心率即可【详解】解：椭圆的左右焦点为过作轴的垂线与交于两点若是等边三角形如图：可得可得即可得解得故答案为：【点睛】本题考查椭圆的简单性质的应用离心率的求解析：33【分析】利用已知条件．推出a 、b 、c 的关系，然后求解椭圆的离心率即可． 【详解】解：椭圆2222:1(0)x y C a b a b+=>>的左右焦点为1F ，2F ，过2F 作x 轴的垂线与C 交于A ，B 两点，若1ABF 是等边三角形，如图：可得32||c AB =，2(,0)F c ，可得22||b AB a=， 即2222333ac b a c ==-， 可得23230e e +-=，(0,1)e ∈ 解得3e =． 故答案为：3．【点睛】本题考查椭圆的简单性质的应用，离心率的求法，考查计算能力，属于中档题．三、解答题21．（1）2212x y +=；（2）证明见解析.【分析】（1）利用中垂线的性质可得KN KQ =，从而得到22KM KN QM MN +==>=，利用椭圆的定义进行分析求解即可；（2）根据点P 的位置，确定OPA ∠，OPB ∠都是锐角，然后联立直线与椭圆的方程，得到韦达定理，再将问题转化为求证两个角的正切值相等，代入化简求解，即可证明． 【详解】（1）∵线段NQ 的垂直平分线交MQ 于点K ，∴||||KN KQ =，∴||||||||||2||KM KN KM KQ MQ MN +=+==>= ∴点K 的轨迹是以原点为中心，以,M N 为焦点的椭圆.设椭圆方程为22221(0)x y a b a b+=>>，则a =1c =，1b =，所以曲线E 的方程为2212x y +=（2）由221210x y x my ⎧+=⎪⎨⎪+-=⎩消去x 可得()222210m y my +--=.设()11,A x y ，()22,B x y ，则12222m y y m +=+，12212y y m =-+. 易知PA ，PB 的斜率存在，则()()121212121212122221111PA PB y y y y y y my y k k x x my my my my +++=+=+=-------++，又因为121222222022m my y my y m m ++=-=++ 所以0PA PB k k +=，所以OPA OPB ∠=∠. 【点睛】方法点睛：解答直线与椭圆的位置关系的相关问题，其常规思路是先把直线方程与椭圆方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题．涉及弦中点的问题常常用“点差法”解决，往往会更简单.22．（1）22143x y +=；（2）. 【分析】（1）由已知条件可得12c e a ==，将点31,2P ⎛⎫⎪⎝⎭代入椭圆的方程结合222a b c =+即可求得,,a b c 的值，进而可得椭圆C 的方程；（2）设:1l x ty =-，设11(,)A x y ，22(,)B x y ，联立直线与椭圆的方程消去x 可得关于y 的一元二次方程，由韦达定理可得12y y +，12y y ，利用122S S =可得122y y =-，即可解出k 的值，进而可求出直线l 的斜率. 【详解】（1）由题意可得：22222121914c a a b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩得2243a b ⎧=⎨=⎩，故C 的方程为22143x y +=.（2）1(1,0)F -，显然l 与y 轴不垂直，故可设:1l x ty =-，设11(,)A x y ，22(,)B x y ，由221143x ty x y =-⎧⎪⎨+=⎪⎩消去x 得22(34)690t y ty +--=，则122634t y y t +=+，122934y y t -=+， 由122S S =得122y y =-， 所以122262034ty y y t +=+=+，可得22634t y t -=+， 由122934y y t -=+可得2229234y t --=+， 消去2y 可得()222236923434t t t--⨯=++ ，整理可得：245t =t =:1l x y =-，所以直线l：)1y x =+， 所以直线l的斜率为. 【点睛】关键点点睛：本题解题的关键是由面积之比得出纵坐标122y y =-，联立直线与椭圆的方程消去x 可得关于y 的一元二次方程，由韦达定理可得12y y +，12y y ，可求t 的值，注意求直线的斜率.23．（1）26x y =；（2）证明见解析，定值为12-. 【分析】（1）由题意写出直线OP 的方程，代入圆的方程，求出点P 的坐标，再代入抛物线方程即可；（2）设直线l 的方程，与抛物线方程联立方程组，得韦达定理，即可得点M 的横坐标，进而得点Q ，表示出OQ k ，计算O AB Q k k ⋅可得定值. 【详解】（1）解：由O 为坐标原点，且1OP k =，得直线OP 的方程为y x =， 代入圆2C 的方程，得22120x x x -+=，解得0x =或6x =，则()6,6P .将点P 的坐标代入1C 的方程，得2626p =⨯，则3p =，故1C 的方程为26x y =. （2）证明：由（1）可知30,2F ⎛⎫ ⎪⎝⎭，0l ：32y =-. 由题意值，直线l 的斜率存在，设直线l 的方程为3(0)2y kx k =+≠，联立2632x y y kx ⎧=⎪⎨=+⎪⎩，整理得2690x kx --=，236360k ∆=+>.设()11,A x y ，()22,B x y ，则126x x k +=， 所以点M 的横坐标为3k ，则3(3,)2Q k -则31232OQk k k -==-，所以1122AB OQ T k k k k ⎛⎫=⋅=⋅-=- ⎪⎝⎭，故T 是定值，且定值为12-. 【点睛】思路点睛：解决直线与抛物线的综合问题时，要注意：（1）注意观察应用题设中的每一个条件，明确确定直线、抛物线的条件；（2）强化有关直线与抛物线联立得出一元二次方程后的运算能力，重视根与系数之间的关系、焦点弦、斜率、三角形的面积等问题． 24．（1）证明见解析；（2）证明见解析. 【分析】 （1）设211,12A x x ⎛⎫ ⎪⎝⎭，222,12B x x ⎛⎫ ⎪⎝⎭，联立直线与抛物线方程，消元、列出韦达定理，即可得到0OA OB ⋅=，从而得证；（2）对函数求导，利用导数的几何意义求出过点A 、B 的切线1l 、1l 的方程，即可得到12122y x x ==-，即可得证； 【详解】 解：（1）设211,12A x x ⎛⎫ ⎪⎝⎭，222,12B x x ⎛⎫ ⎪⎝⎭， 把2y kx =+代入212y x =，得2240x kx --=. 由韦达定理得122x x k +=，124x x =-.()22211221212111,,0224OA OB x x x x x x x x ⎛⎫⎛⎫∴⋅=⋅=+= ⎪ ⎪⎝⎭⎝⎭. 所以OA OB ⊥ （2）212y x =，y x '∴=，故经过点211,12A x x ⎛⎫ ⎪⎝⎭的切线1l 的方程为：()211112y x x x x -=-， 即21112y x x x =-，①同理，经过点222,12B x x ⎛⎫ ⎪⎝⎭的切线2l 的方程为：22212y x x x =-，②21x x ⨯-⨯①②，得12122y x x ==-. 即点M 在直线:2l y =-上. 【点睛】(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系；(2)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB |＝x 1＋x 2＋p ，若不过焦点，则必须用一般弦长公式． 25．（1）证明见解析；（2）存在，12N ⎛⎫±- ⎪ ⎪⎝⎭. 【分析】（1）由题意设直线:1AB y kx =+，()11,A x y ，()22,B x y ，将直线与抛物线方程联立求出两根之和、两根之积，求出直线121:24x x AN y x =-以及直线222:24x x BN y x =-，将两直线联立求出交点即证.（2）由（1）知点N 为CD 的中点，取AB 的中点E ，则2AC BDEN +=，利用抛物线的定义可得2AB EN =，ABNAENBENSSS=+，2ACNAF CNS⋅=，2BDNBF CNS ⋅=，根据2BDN ACN ABN S S S =+△△△，可得2BF AF AB =+，即212x x =-，结合韦达定理即可求解. 【详解】解（1）由题知2p = 所以2:4M x y =设直线:1AB y kx =+，()11,A x y ，()22,B x y联立214y kx x y=+⎧⎨=⎩得2440x kx --=所以121244x x kx x +=⎧⎨=-⎩对24x y =求导得2x y '=所以直线AN 的斜率为12AN x k =所以直线()111:2x AN y y x x -=-即121:24x x AN y x =-① 同理直线222:24x x BN y x =-② 联立①和②得12122214x x x k x x y +⎧==⎪⎪⎨⎪==-⎪⎩所以点N 的坐标为(2,1)k -，即点N 在定直线1y =-上 （2）由（1）知点N 为CD 的中点 取AB 的中点E ，则2AC BDEN += 由题知AC BD AB += 所以2AB EN =所以22222ABN AEN BEN EN CN EN DN EN CN AB CNS S S ⋅⋅⋅⋅=+=+=⨯=△△△ 而22ACN AC CN AF CN S ⋅⋅==△，22BDN BD DN BF CNS ⋅⋅==△ 若存在点N 满足题意则2BDN ACN ABN S S S =+△△△ 即2BF AF AB =+所以()2121200x x x x -=-+-即212x x =-③又因为121244x x kx x +=⎧⎨=-⎩④ 将③代入④解得=k ±由（1）知(2,1)N k -即12N ⎛⎫±- ⎪ ⎪⎝⎭经检验，存在12N ⎛⎫±- ⎪ ⎪⎝⎭满足题意. 【点睛】关键点点睛：本题考查了直线与抛物线的位置关系，解题的关键是由()11,A x y ，()22,B x y ，求出点N 的坐标为(2,1)k -以及212x x =-，考查了计算能力、推理能力. 26．(1) 2214x y +=；(2) 2±【分析】(1)由焦点在圆上解得c =2a =，2221b a c =-=，方程可求；(2)因为FA 垂直于AB 可知点A 为椭圆与圆的交点，联立方程求得坐标，则直线斜率可求.【详解】解：（1）椭圆2222:1(0)x y C a b a b +=>>的焦点在圆223x y +=上，所以203c +=，即c =，因为c e a == 得2a =，2221b a c =-=，故椭圆方程为2214x y +=（2）因为FA 垂直于AB ，即点A 既在椭圆上又在以OF 为直径的圆上，所以22221434x y x y ⎧+=⎪⎪⎨⎛⎪-+= ⎪⎝⎭⎩解得33x y ⎧=⎪⎪⎨⎪=±⎪⎩所以33A ⎛± ⎝⎭故2A l A y k x ==±所以直线l的斜率为2±. 【点睛】关键点点晴：本题的关键在于求出点A 的坐标点.。

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(有答案解析)

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(有答案解析)

一、选择题1．已知斜率为16的直线l 与双曲线22221(0,0)x y C a b a b-=>>:相交于B 、D 两点，且BD 的中点为(1,3)M ，则C 的离心率为（ ）A ．2B ．5 C ．3 D ．6 2．斜率为1的直线l 经过抛物线24y x =的焦点F ，且与抛物线相交于A 、B 两点，则线段AB 的长为（ ） A ．42B ．62C ．82D ．83．已知12,F F 分别是双曲线2214x y -=的左、右焦点，P 为双曲线右支上异于顶点的任意一点，若12PF F △内切圆圆心为I ，则圆心I 到圆22(1)1y x +-=上任意一点的距离最小值为（ ） A ．2B ．51-C ．1D ．52-4．如图所示，一隧道内设有双行线公路，其截面由一个长方形的三条边和抛物线的一段构成.为保证安全，要求行驶车辆顶部（假设车顶为平顶）与隧道顶部在竖直方向上高度之差至少要有0.6m ，已知行车道总宽度7m AB =，则车辆通过隧道的限制高度为（ ）A ．3.90mB ．3.95mC ．4.00mD ．4.05m5．抛物线：24y x =的过焦点的弦的中点的轨迹方程为（ ） A ．21y x =-B ．212y x =-C ．22(1)y x =-D ．221y x =-6．已知1F 、2F 分别是双曲线()2222:10,0x yC a b a b-=>>的左右焦点，点P 在双曲线右支上且不与顶点重合，过2F 作12F PF ∠的角平分线的垂线，垂足为A ，O 为坐标原点，若3OA b =，则该双曲线的离心率为（ ）A B ．3C ．2D 7．设F 1，F 2是双曲线C ：22221x y a b-=(a >0，b >0)的左、右焦点，P 是双曲线C 右支上一点，若|PF 1|＋|PF 2|＝4a ，且∠F 1PF 2＝60°，则双曲线C 的渐近线方程是（ ）A 0y ±=B ．20x =C 20y ±=D ．20x ±=8．已知抛物线2:C x y =，点()2,0A ，()0,2B -，点P 在抛物线上，则满足PAB △为直角三角形的点P 的个数有（ ） A ．2B ．4C ．6D ．89．设1F 、2F 是椭圆1C 和双曲线2C 的公共焦点，P 是它们的一个公共点，且1PF <2PF ，线段1PF 垂直平分线经过2F ，若1C 和2C 的离心率分别为1e 、2e ，则129e e +的最小值（ ）A ．2B ．4C ．6D ．810．已知抛物线2:4C y x =，过点()1,0A -作C 的两条切线，切点分别为B 、D ，则过点A 、B 、D 的圆截y 轴所得弦长为（ ）A ．B ．C ．D ．11．已知抛物线24x y =的焦点F 和点(1,8),A P -为抛物线上一点，则||||PA PF +的最小值是（ ） A ．3B ．9C ．12D ．612．设双曲线2214y x -=的左、右焦点分别为12,F F ，若点P 在双曲线上，且12F PF △为锐角三角形，则12PF PF +的取值范围是（ ）A ．B ．(6,8)C ．D ．(6,10)二、填空题13．已知ABC 中，()1,0B -、()1,0C ，1k 、2k 分别是直线AB 和AC 的斜率.关于点A 有如下四个命题：①若A 是双曲线2212y x -=上的点，则122k k ⋅=；②若122k k ⋅=-，则A 是椭圆2212x y +=上的点；③若121k k ，则A 是圆221x y +=上的点；④若2AB AC =，则A 点的轨迹是圆. 其中所有真命题的序号是__________．14．已知双曲线()2222:10,0x y C a b a b-=>>的一条渐近线与圆(224x y +-=相交于A ，B 两点，且2AB =，则双曲线C 的离心率为___________.15．设1A 、2A 为椭圆()222210x y a b a b+=>>的左、右顶点，若在椭圆上存在异于1A 、2A 的点P ，使得10PO PA ⋅=，其中O 为坐标原点，则椭圆的离心率e 的取值范围是_____. 16．已知抛物线218y x =的焦点为F ，过F 的直线l 与抛物线交于A 、B 两点，抛物线的准线与y 轴交于点M ，当AMAF最大时，弦AB 长度是___________. 17．已知点F 为抛物线2:2C x y =的焦点，过点F 作两条互相垂直的直线1l ，2l ，直线1l 与C 交于A ，B 两点，直线2l 与C 交于D ，E 两点，则4AB DE +的最小值为_________.18．已知点A ，B 为抛物线C ：24y x =上不同于原点O 的两点，且OA OB ⊥，则OAB 的面积的最小值为__________.19．已知椭圆22:1168x y C +=的左､右焦点分别为12,F F ，直线(44)x m m =-<<与椭圆C 相交于点A ，B .给出下列三个命题：①存在唯一一个m ，使得12AF F △为等腰直角三角形； ②存在唯一一个m ，使得1ABF 为等腰直角三角形； ③存在m ，使1ABF 的周长最大. 其中，所有真命题的序号为_________.20．如果点12310,,,P P P P ，是抛物线22y x =上的点，它们的横坐标依次为12310,,,,x x x x ，F 是抛物线的焦点，若123105x x x x ++++=，则1210PF P F P F +++=___.三、解答题21．已知椭圆22:11612x y E +=，1F 、2F 为左、右焦点，()2,3A .（1）求12tan F AF ∠及12F AF ∠的角平分线所在直线l 的方程；（2）在椭圆E 上是否存在关于直线l 对称的相异两点？若存在，请找出：若不存在，说明理由．22．如图，已知椭圆22221(0)x y a b a b+=>>的离心率为12，过椭圆右焦点2F 作两条互相垂直的弦AB 与CD ，当直线AB 的斜率为0时，||||7AB CD +=．（Ⅰ）求椭圆的方程；（Ⅱ）求||||AB CD +的取值范围．23．已知动圆与直线1x =-相交于,A B 两点，且||23AB =． （1）当动圆过定点(2,0)时，求动圆圆心C 的轨迹方程；（2）过点(1,0)-的直线l 交（1）中动圆圆心C 的轨迹于,M N 两点，点P 为,M N 的中点，过点P 垂直于直线l 的直线交x 轴于点Q ，求点Q 的横坐标的取值范围． 24．已知抛物线C ：()220y px p =>过点()2,4T -．（1）求抛物线C 的焦点到准线的距离；（2）已知点()4,0A ，过点()4,0B -的直线l 交抛物线C 于点M 、N ，直线MA ，NA 分别交直线4x =-于点P 、Q ．求PBBQ的值． 25．已知是抛物线2:2C y px=(0)p >的焦点，(1,)M t 是抛物线上一点，且||2MF =.（1）求抛物线C 的方程；（2）过点O （坐标原点）分别作,OA OB 交抛物线C 于,A B 两点(,A B 不与O 重合)，且.2OA OB k k =.求证：直线AB 过定点.26．如图，已知抛物线()2:20C y px p =>，焦点为F ，过点()2,0G p 作直线l 交抛物线C 于A 、B 两点，设()11,A x y 、()22,B x y .（1）若124x x ⋅=，求抛物线C 的方程；（2）若直线l 与x 轴不垂直，直线AF 交抛物线C 于另一点M ，直线BF 交抛物线C 于另一点N .求证：直线l 与直线MN 斜率之比为定值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】设()()1122,,B x y D x y 、，用“点差法”表示出a 、b 的关系，即可求出离心率 【详解】设()()1122,,B x y D x y 、,则22112222222211x y a b x y a b ⎧-=⎪⎪⎨⎪-=⎪⎩， 两式作差得：22221212220x x y y a b---=， 整理得：()()()()2121221212y y y y b a x x x x +-=+-BD 的中点为(1,3)M ，且直线l 的斜率为16 ，代入有：22611262b a =⨯=即22212c a a -=，解得62cea . 故选：D 【点睛】求椭圆（双曲线）离心率的一般思路：根据题目的条件，找到a 、b 、c 的关系，消去b ，构造离心率e 的方程或（不等式）即可求出离心率．2．D解析：D 【分析】写出直线l 的方程，设点()11,A x y 、()22,B x y ，联立直线l 与抛物线的方程，列出韦达定理，利用抛物线的焦点弦长公式可求得AB . 【详解】抛物线24y x =的焦点()1,0F ，直线l 的方程为1y x =-，设点()11,A x y 、()22,B x y联立214y x y x=-⎧⎨=⎩，可得2610x x -+=，2640∆=->，所以，126x x +=，由抛物线的焦点弦长公式得1228AB x x =++=. 故选：D. 【点睛】方法点睛：有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式12AB x x p =++，若不过焦点，则必须用一般弦长公式．3．C解析：C 【分析】设12PF F △内切圆与12PF F △的三边1PF ､2PF ､12F F 的切点分别为D ､N ､M ，根据圆的切线性质，可得2OM =，即可得答案. 【详解】设12PF F △的内切圆分别与12,PF PF 切于点,A B ，与12F F 切于点M ，则11||||,||||PA PB F A F M ==，22||||F B F M =．又点P 在双曲线右支上， 12||||2PF PF a ∴-=，即12(||||)(||||)2PA F A PB F B a +-+=， 12||||2F M F M a ∴-= ①，又12||||2F M F M c += ②， 由①＋②，解得1||F M a c =+， 又1||OF c =，则(,0)M a ，因为双曲线2214x y -=的2a =，所以内切圆圆心I 与在直线2x =上，设0(2,)I y ， 设圆22(1)1y x +-=的圆心为C ，则(0,1)C ，所以||CI =01y =时，min ||2CI =，此时圆22(1)1y x +-=上任意一点的距离最小值为min ||1211CI -=-=．故选： C ．【点睛】本题考查双曲线的定义和性质，关键点是由定义和已知得到12||||2F M F M a -=和12||||2F M F M c +=，考查了学生分析问题、解决问题的能力，属于中档题.4．B解析：B 【分析】设抛物线的方程为2x ay =，可知点()5,5-在该抛物线上，求出a 的值，将 3.5x =代入抛物线方程，求出y 的值，即可得解. 【详解】设抛物线的方程为2x ay =，可知点()5,5-在该抛物线上，则255a -=，解得5a =-，所以，抛物线的方程为25x y =-，将 3.5x =代入抛物线方程得25 3.5y -=，解得 2.45y =-， 因此，车辆通过隧道的限制高度为()7 2.450.6 3.95m --=. 故选：B. 【点睛】关键点点睛：本题考查抛物线的实际应用，设出抛物线的方程，分析出抛物线上的点的坐标，求出抛物线的方程是解题的关键，同时要注意车辆限高的意义.5．C解析：C 【分析】设出过焦点的直线方程，与抛物线方程联立求出两根之和，可得中点的坐标，消去参数可得中点的轨迹方程． 【详解】由抛物线的方程可得焦点(1,0)F ，可得过焦点的直线的斜率不为0， 设直线方程为：1x my =+，设直线与抛物线的交点1(A x ，1)y ，2(B x ，2)y ，设AB 的中点(,)P x y ， 联立直线与抛物线的方程可得：2440y my --=，124y y m +=，21212()242x x m y y m +=++=+，所以可得2212x m y m⎧=+⎨=⎩，消去m 可得P 的轨迹方程：222y x =-，故选：C ． 【点睛】方法点睛：求轨迹方程的常见方法有：1、定义法；2、待定系数法；3、直接求轨迹法；4、反求法；5、参数方程法等等.6．B解析：B 【分析】延长2F A 交1PF 于点Q ，可得1223QF OA b ==，结合双曲线的定义可得,a b 的关系，从而求得离心率． 【详解】延长2F A 交1PF 于点Q ，∵PA 是12F PF ∠的平分线，∴2AQ AF =，2PQ PF =， 又O 是12F F 中点，所以1//QF AO ，且1223QF OA b ==， 又11122QF PF PQ PF PF a =-=-=，∴223a b =，222233()a b c a ==-，∴23c e a ==． 故选：B ．【点睛】关键点点睛：本题考查求双曲线的离心率，解题关键是找到关于,,a b c 的关系，解题方法是延长2F A 交1PF 于点Q ，利用等腰三角形的性质、平行线的性质得出123QF b =，然后由双曲线的定义得出关系式，从而求解．7．C解析：C 【分析】利用双曲线的定义和已知即可得出|PF 1|，|PF 2|，再利用余弦定理找出a,c 的等量关系,从而可求a,b 的比值，即可得出双曲线C 的渐近线方程．【详解】解：因为F1、F2是双曲线的左、右焦点，点P在双曲线右支上，所以由双曲线定义可得|PF1|－|PF2|＝2a，又知|PF1|＋|PF2|＝4a，所以|PF1|＝3a，|PF2|＝a.在△PF1F2中，由余弦定理可得222 121212||||||cos60=2||||PF PF F FPF PF+-⋅，即222(3)41=232a a ca a+-⨯⨯，所以3a2＝10a2－4c2，即4c2＝7a2，又知b2＋a2＝c2，所以223=4ba，所以双曲线C的渐近线方程为32y x=±，即320x y±=.故选：C.【点睛】关键点点睛：利用双曲线的定义和已知即可得出|PF1|，|PF2|，再利用余弦定理解三角形是解答本题的关键．8．B解析：B【分析】分三个角为直角分别进行讨论，通过数形结合即得结果.【详解】(1)若APB∠为直角，如下图，即以AB为直径的圆与抛物线的交点为P，易见有O，P两个点符合题意；（2）若PAB∠为直角，则过A作直线垂直AB，如下图，易见有P，P'两个点符合题意；（3）若PBA ∠为直角，则过B 作直线垂直AB ，如上图，易见无交点，不存在点P 符合题意.综上，共有4个点符合题意. 故选：B. 【点睛】 关键点点睛：本题的解题关键在于对三个角为直角进行分类讨论，再结合数形结合思想即突破难点.9．D解析：D 【分析】设椭圆和双曲线的方程，由题意可得2122PF F F c ==，再利用椭圆和双曲线的定义分别求出1PF ，即可得122a a c +=，计算12112e e +=，()121212111992e e e e e e ⎛⎫+=++ ⎪⎝⎭展开后利用基本不等式即可求最值. 【详解】设椭圆1C 的方程为2222111x y a b +=，则222111c a b =-，设双曲线2C 的方程为2222221x y a b -=，则222222c a b =+，因为椭圆1C 和双曲线2C 的焦点相同，所以2212c c =，设12c c c ==即22221122a b a b -=+，因为P 是椭圆1C 和双曲线2C 的一个公共点， 所以1212+=PF PF a ，2122PF PF a -=，因为线段1PF 垂直平分线经过2F ，所以2122PF F F c ==，所以1122PF a c =-，且1222PF c a =-， 所以122222a c c a -=-，可得122a a c +=， 所以11c e a =，22c e a =，所以1212121122a a a a ce e c c c c++=+===， 所以()211212121291111991022e e e e e e e e e e ⎛⎫⎛⎫+=++=++ ⎪ ⎪⎝⎭⎝⎭()11101023822⎛≥+=+⨯= ⎝， 当且仅当21129e e e e =，即213e e =时等号成立，【点睛】关键点点睛：本题解题的关键点是利用已知条件得出122a a c +=，进而可得12112e e +=， 再利用基本不等式可求最值.10．A解析：A 【分析】设出直线方程，与抛物线方程联立，由判别式为零解出B 、D 两点的坐标，进而得出过点A 、B 、D 的圆的方程，求出弦长即可． 【详解】设过点()1,0A -的直线方程为1x my =-，联立214x my y x=-⎧⎨=⎩，可得2440y my -+=，由216160m ∆=-=，解得1m =±即2440y y ±+=，2y =±，不妨设()()1,2,1,2B D -，则BD 的中垂线方程为0y =，即圆心在x 轴上又()1,0A -，且点()1,0到点A 、B 、D 的距离都相等，则圆心坐标为()1,0，半径为2 圆的方程为()2214x y -+=，令0x =，解得y =即圆被y轴所截得的弦长为故选：A 【点睛】关键点点睛：本题考查直线与抛物线的位置关系，考查圆的方程以及直线与圆的位置关系，解决本题的关键点是根据直线与抛物线相切，求出切点的坐标，进而得出圆的方程，求出弦长，考查学生逻辑思维能力和计算能力，属于中档题．11．B解析：B 【分析】根据抛物线的标准方程求出焦点坐标和准线方程，利用抛物线的定义可得||||||||PA PF PA PF AM +=+≥，故AM 为所求【详解】解：由题意得2p =，焦点(0,1)F ，准线方程为1y =-， 设P 到准线的距离为PM ，（即PM 垂直于准线，M 为垂足），则||||||||9PA PF PA PF AM +=+≥=，（当且仅当,,P A M 共线时取等号）， 所以||||PA PF +的最小值是9，【点睛】关键点点睛：此题考查抛物线的定义、标准方程，以及简单性质的应用，解题的关键是由题意结合抛物线定义得||||||||PA PF PA PF AM +=+≥，从而可得结果12．D解析：D 【分析】由题意画出图形，不妨设P 在第一象限，P 点在1P 与2P 之间运动，求出112F PF ∠和122F F P ∠ 为直角时12PF PF +的值，可得12F PF △ 为锐角三角形时12PF PF +的取值范围． 【详解】12F PF △为锐角三角形，不妨设P 在第一象限，P 点在1P 与2P 之间运动，如图，当P 在1P 处，11290F PF∠=，又1,2,5a b c ===由222111212|||||20|PF PF F F =+=，1112||||2PFPF -=， 可得1112||||8PF PF ⋅=， 此时 1112||||6PF PF +=；当P 在2P 处，12290F F P ∠=，25P x = 易知24P y = 则224P F =此时12222222||||||2||10P F P F P F a P F +=++=∴12F PF △为锐角三角形，则12PF PF +的取值范围是()6,10， 故选：D ． 【点晴】关键点点晴：本题的关键在于求出112F PF ∠和122F F P ∠ 为直角时12PF PF +的值.二、填空题13．①③【分析】设点可得出结合斜率公式可判断A 选项的正误；求出动点的轨迹方程可判断②的正误；根据求出点的轨迹方程可判断③的正误；由求出点的轨迹方程可判断④的正误【详解】设动点的坐标为对于①由于点是双曲线解析：①③ 【分析】设点(),A x y ，可得出2212y x =+，结合斜率公式可判断A 选项的正误；求出动点A 的轨迹方程，可判断②的正误；根据121k k ，求出点A 的轨迹方程，可判断③的正误；由2AB AC =求出点A 的轨迹方程，可判断④的正误. 【详解】设动点A 的坐标为(),A x y .对于①，由于点A 是双曲线2212y x -=上的点，则2212y x =+，所以，22122221112y y y y k k y x x x =⋅===+--，①正确；对于②，21222111y y y k k x x x =⋅==-+--，化简可得2212y x +=，②错误；对于③，21221111y y y k k x x x =⋅==-+--，化简可得221x y +=，③正确；对于④，由2AB AC ==化简可得2251639x y ⎛⎫-+= ⎪⎝⎭， 当点A 为圆2251639x y ⎛⎫-+= ⎪⎝⎭与x 轴的交点时，A 、B 、C 三点无法构成三角形，④错误.故答案为：①③. 【点睛】方法点睛：求动点的轨迹方程有如下几种方法：（1）直译法：直接将条件翻译成等式，整理化简后即得动点的轨迹方程；（2）定义法：如果能确定动点的轨迹满足某种已知曲线的定义，则可利用曲线的定义写出方程；（3）相关点法：用动点Q 的坐标x 、y 表示相关点P 的坐标0x 、0y ，然后代入点P 的坐标()00,x y 所满足的曲线方程，整理化简可得出动点Q 的轨迹方程；（4）参数法：当动点坐标x 、y 之间的直接关系难以找到时，往往先寻找x 、y 与某一参数t 得到方程，即为动点的轨迹方程；（5）交轨法：将两动曲线方程中的参数消去，得到不含参数的方程，即为两动曲线交点的轨迹方程.14．2【分析】由双曲线圆的方程确定渐近线方程为圆心为半径为根据圆的相交弦与半径弦心距之间的几何关系有结合双曲线参数间的关系即可求其离心率【详解】由题意知：双曲线的渐近线为而圆心为半径为∴圆心到渐近线的距解析：2 【分析】由双曲线、圆的方程确定渐近线方程为by x a=±，圆心为(0,，半径为2r ，根据圆的相交弦与半径、弦心距之间的几何关系有222||4AB r d -=，结合双曲线参数间的关系即可求其离心率. 【详解】由题意知：双曲线的渐近线为by x a=±，而圆心为(0,，半径为2r ，∴圆心到渐近线的距离d ==，而2AB =，∴221r d -=，故222123a a b=+，又222,1c a b c e a +==>， ∴2e =. 故答案为：2. 【点睛】关键点点睛：根据双曲线、圆的标准方程确定渐近线方程、圆心、半径长，结合圆中相交弦的几何性质及双曲线参数关系，列出关于,a c 的齐次方程求离心率.15．【分析】设点由可得出求出函数在区间上的零点为化简得出进而可解得的取值范围【详解】设点则可知点设则函数在区间上存在零点则为方程的一根设函数在区间内的零点为由韦达定理可得所以即整理可得即解得因此椭圆的离解析：2⎛⎫⎪ ⎪⎝⎭【分析】设点(),P x y ，由10PO PA ⋅=可得出2220e x ax b ++=，求出函数()f x 在区间(),0a -上的零点为22ab c-，化简得出2201b c <<，进而可解得e 的取值范围.【详解】设点(),P x y ，则22222b y b x a=-，可知点()1,0A a -，(),PO x y =--，()1,PA a x y =---，()()22222222221220b c PO PA x a x y x y ax x b x ax x ax b a a⋅=---+-=++=+-+=++=，设()222f x e x ax b =++，则函数()f x 在区间(),0a -上存在零点，()2220f a c a b -=-+=，则a -为方程2220e x ax b ++=的一根，设函数()f x 在区间(),0a -内的零点为1x ，由韦达定理可得222122b a b ax e c -==，212ab x c∴=-，所以，220ab a c -<-<，即2201b c<<，整理可得2222a c b c -=<，222a c ∴<，即221e >，01e <<，解得12e <<.因此，椭圆的离心率e 的取值范围是2⎛⎫⎪ ⎪⎝⎭.故答案为：,12⎛⎫⎪ ⎪⎝⎭. 【点睛】方法点睛：椭圆的离心率是椭圆最重要的几何性质，求椭圆的离心率（或离心率的取值范围），常见有两种方法：①求出a 、c ，代入公式c e a=； ②只需要根据一个条件得到关于a 、b 、c 的齐次式，结合222b a c =-转化为a 、c 的齐次式，然后等式（不等式）两边分别除以a 或2a 转化为关于e 的方程（或不等式），解方程（或不等式）即可得e （e 的取值范围）．16．【分析】作出图形过点作垂直于抛物线的准线于点可得出可知当取最小值时即直线与抛物线相切时最大可求出直线的斜率求出点的坐标利用对称性可求得点的坐标抛物线的焦点弦长公式进而可求得弦的长度【详解】设点为第一 解析：8【分析】作出图形，过点A 作AE 垂直于抛物线218y x =的准线于点E ，可得出1sin AM AF AME=∠，可知当AME ∠取最小值时，即直线AM 与抛物线相切时，AM AF 最大，可求出直线AM 的斜率，求出点A 的坐标，利用对称性可求得点B 的坐标，抛物线的焦点弦长公式，进而可求得弦AB 的长度. 【详解】设点A 为第一象限内的点，过点A 作AE 垂直于抛物线218y x =的准线于点E ，如下图所示：由抛物线的定义可得AE AF =，则1sin AM AM AF AE AME==∠， 可知当AME ∠取最小值时，即直线AM 与抛物线相切时，AMAF最大，抛物线218y x =的焦点为()0,2F ，易知点()0,2M -. 当直线AM 与抛物线218y x =相切时，直线AM 的斜率存在， 设直线AM 的方程为2y kx =-，联立228y kx x y=-⎧⎨=⎩，消去y 得28160x kx -+=， 264640k ∆=-=，因为点A 在第一象限，则0k >，解得1k =，方程为28160x x -+=，解得4x =，此时，228x y ==，即点()4,2A ，此时AB y ⊥轴，由对称性可得()4,2B -， 因此，448AB =+=. 故答案为：8 【点睛】方法点睛：有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式12AB x x p =++或12AB y y p =++，若不过焦点，则必须用一般弦长公式．17．18【分析】设直线的方程为联立方程组分别求得和结合基本不等式即可求得的最小值得到答案【详解】由题抛物线的焦点准线方程为设直线的方程为联立方程组则设可得由抛物线的定义可得由可将上式中的换为可得则当且仅解析：18 【分析】设直线1l 的方程为12y kx =+，联立方程组，分别求得222AB k =+和22||2DE k=+，结合基本不等式，即可求得4AB DE +的最小值，得到答案. 【详解】由题，抛物线2:2C x y =的焦点10,2F ⎛⎫⎪⎝⎭，准线方程为12y 设直线1l 的方程为12y kx =+，0k ≠， 联立方程组2212x y y kx ⎧=⎪⎨=+⎪⎩，则2210x kx --=，设()11,A x y ，()22,B x y ，可得122x x k +=，()21212121112122y y kx kx k x x k +=+++=++=+由抛物线的定义可得212||122AB y y k =++=+， 由12l l ⊥，可将上式中的k 换为1k -，可得22||2DE k=+，则224102102184AB DE k k ⎛⎫+=++≥+⨯= ⎪⎝⎭，当且仅当k = 则4AB DE +的最小值为18 故答案为：18 【点睛】方法点睛：本题考查抛物线的焦点弦，考查基本不等式的应用，与抛物线的焦点有关问题的解题策略：1、与抛物线的焦点有关的问题，一般情况下都与抛物线的定义有关：“看到准线想焦点，看到焦点想准线”，这是解决与过抛物线焦点的弦有关问题的重要途径；2、特别提醒：主要灵活运用抛物线上一点(,)P x y 到焦点F 的距离：2PF p x =+或2PF p y =+. 18．【分析】设利用可得即可求得利用两点间距离公式求出面积利用基本不等式即可求最值【详解】设由可得解得：所以当且仅当时等号成立所以的面积的最小值为故答案为：【点睛】关键点点睛：本题解题的关键点是设坐标采用 解析：16【分析】设211,4y A y ⎛⎫ ⎪⎝⎭，222,4y B y ⎛⎫⎪⎝⎭，利用OA OB ⊥可得0OA OB ⋅=即可求得1216y y =-，利用两点间距离公式求出OA 、OB ，面积12OABS OA OB =，利用基本不等式即可求最值. 【详解】设211,4y A y ⎛⎫ ⎪⎝⎭，222,4y B y ⎛⎫ ⎪⎝⎭，由OA OB ⊥可得2212121212104416y y y y OA OB y y y y ⎛⎫⋅=⨯+=+= ⎪⎝⎭， 解得：1216y y =-，1OA y ==OB y ==11122OABSO y O y A B ==12⨯=≥=，22221212216161616y y y y +=+≥=，所以16OABS≥==，当且仅当12y y =时等号成立， 所以OAB 的面积的最小值为16，故答案为：16. 【点睛】关键点点睛：本题解题的关键点是设A ，B 坐标，采用设而不求的方法，将OA OB ⊥转化为0OA OB ⋅=，求出参数之间的关系，再利用基本不等式求12OABSOA OB =的最值. 19．①③【分析】首先根据题意得到设对①分类讨论和以及即可判断①为真命题对②根据椭圆的对称性可知利用解方程即可判断②为假命题对③利用椭圆的定义即可判断③为真命题【详解】由题知：设对①若则此时则所以满足为等解析：①③ 【分析】首先根据题意得到4a =，b c ==()1F -，()2F ，设(),A m y ，(),B m y -.对①，分类讨论12AF AF =，1290F AF ∠=，和1290AF F ∠=，以及2190AF F ∠=，即可判断①为真命题.对②，根据椭圆的对称性可知，11AF BF =，利用11AF k ==，解方程即可判断②为假命题，对③，利用椭圆的定义即可判断③为真命题. 【详解】由题知：4a =，b c ==()1F -，()2F ， 设(),A m y ，(),B m y -.对①，若12AF AF =，则0m =，此时(0,A .11AF k ==，21AF k ==-，则121AF AF k k ⋅=-，所以1290F AF ∠=，满足12AF F △为等腰直角三角形.若1290AF F ∠=，则()2A -，此时12AF =，12F F =.若2190AF F ∠=，则()2A ，此时22AF =，12F F =.所以存在唯一一个m ，使得12AF F △为等腰直角三角形，故①为真命题. 对②，根据椭圆的对称性可知，11AF BF =，满足等腰三角形. 当190AF B ∠=时，根据椭圆的对称性可知：直线1AF 的倾斜角为45，11AF k ==，即y m =+又因为221168m y +=，所以(22216m m ++=，解得0m =或3m =-，都在44m -<<内， 故存在唯一一个m ，使得1ABF 为等腰直角三角形为假命题. 对③，1ABF 的周长为11AB AF BF ++， 又因为128AF AF =-，128BF BF =-， 所以()112216AF BF AF BF +=-+， 即1ABF 的周长为()2216AB AF BF +-+，又因为22AF BF AB +≥，当且仅当m =时取等号， 所以()22AF BF AB -+≤-，即1ABF 的周长为()22161616AB AF BF AB AB +-+≤+-=.当且仅当m =时，1ABF 的周长最大. 故③为真命题. 故答案为：①③ 【点睛】关键点点睛：本题主要考查椭圆的定义，解决本题①的关键为分类讨论12AF AF =，1290F AF ∠=，和1290AF F ∠=，以及2190AF F ∠=，②的关键为代入椭圆的对称性，③的关键为椭圆的定义，属于中档题.20．10【分析】利用抛物线上的点到焦点的距离把整体代入中即可求解【详解】解：由抛物线的定义可知抛物线上的点到焦点的距离在中所以故答案为：10【点睛】关键点点睛：利用抛物线的焦半径公式整体代入中是解决本题解析：10 【分析】利用抛物线()220y px p =>上的点()000,P x y 到焦点,02p F ⎛⎫⎪⎝⎭的距离002p P F x =+，把123105x x x x ++++=整体代入1210PF P F P F +++中即可求解.【详解】解：由抛物线的定义可知，抛物线()220y px p =>上的点()000,P x y 到焦点,02p F ⎛⎫⎪⎝⎭的距离002p P F x =+，在22y x =中，1p =，所以12121031055510PF P F P F x x xx p +++=+++++=+=.故答案为：10 【点睛】关键点点睛：利用抛物线的焦半径公式整体代入1210PF P F P F +++中是解决本题的关键.三、解答题21．（1）124tan 3F AF ∠=，直线l 的方程为210x y --=；（2）不存在，理由见解析. 【分析】（1）分析得出2AF x ⊥轴，进而可得出12122tan F F F AF AF ∠=，设122F AF θ∠=，求出tan θ的值，可得出直线l 的斜率，进而可得出直线l 的方程；（2）假设椭圆E 上存在关于直线l 对称的相异两点()11,M x y 、()22,N x y ，进而可设直线MN 的方程为2xy t =-+，与椭圆E 的方程联立，列出韦达定理，求出线段MN 的中点P 的坐标，根据点P 在直线l 上，求出t 的值，可得出点P 的坐标，由此可得出结论.【详解】（1）在椭圆E 中，4a =，23b =，2c =，则()12,0F -、()22,0F ，因为222311612+=，即点A 在椭圆E 上，且2AF x ⊥轴，121224tan 3F F F AF AF ∠==，设122F AF θ∠=，则22tan 4tan 21tan 3θθθ==-，整理可得22tan 3tan 20θθ+-=， 易知θ为锐角，则tan 0θ>，解得1tan 2θ=，设直线l 的倾斜角为α，则sin cos 12tan tan 22sin tan cos2πθπθαθπθθθ⎛⎫- ⎪⎛⎫⎝⎭=-==== ⎪⎛⎫⎝⎭- ⎪⎝⎭，因此，直线l 的方程为()322y x -=-，即210x y --=；（2）假设椭圆E 上是否存在关于直线l 对称的相异两点()11,M x y 、()22,N x y ， 则直线MN 的斜率为12-，设直线MN 的方程为2xy t =-+， 联立22123448y x t x y ⎧=-+⎪⎨⎪+=⎩，整理可得22120x tx t -+-=， 由韦达定理可得12x x t +=，则()121213222y y x x t t +=-++=， 所以，线段MN 的中点为3,24t t P ⎛⎫⎪⎝⎭， 点P 在直线l 上，所以，32110244t t t⨯--=-=，解得4t =， 所以点()2,3P ，此时，点P 与点A 重合，不合乎题意. 因此，椭圆E 上不存在关于直线l 对称的相异两点. 【点睛】思路点睛：圆锥曲线中的探索性问题求解思路如下： 第一步：假设结论存在．第二步：结合已知条件进行推理求解．第三步：若能推出合理结果，经验证成立即可肯定正确；若推出矛盾，即否定假设． 第四步：反思回顾，查看关键点、易错点及解题规范．22．（Ⅰ）22143x y +=；（Ⅱ）48,77⎡⎤⎢⎥⎣⎦； 【分析】（Ⅰ）通过当直线AB 的斜率为0时可知||2AB a =，22||b CD a =，结合12c e a ==，计算即得结论；（Ⅱ）分别对两条弦的斜率进行讨论，当两条弦中一条斜率为0时、另一条弦的斜率不存在时易得结论；当两条弦斜率均存在且不为0时，通过设直线AB 、CD 的方程并分别与椭圆方程联立，利用韦达定理及两点间距离公式，可得||||AB CD +的表达式，利用换元法及二次函数的性质计算即得结论． 【详解】解：（Ⅰ）当直线AB 的斜率为0时，直线CD 垂直于x 轴，||2AB a ∴=，22||b CD a =，即22||||27b AB CD a a+=+=， 12c e a ==，且222a b c =+，解得：2,a b ==， 所以椭圆方程为22143x y +=；（Ⅱ）①当两条弦中一条斜率为0时，另一条弦的斜率不存在， 由题意可知，||||7AB CD +=；②当两条弦斜率均存在且不为0时，设1(A x ，1)y ，2(B x ，2)y ， 设直线AB 的方程为(1)y k x =-，则直线CD 的方程为1(1)y x k=--，将直线AB 的方程代入椭圆方程中，并整理得：2222(34)84120k x k x k +-+-=， ∴221212228412,3434k k x x x x k k-+==++，∴212212(1)|||34k AB x x k +=-=+，同理，2222112(1)12(1)||4343k k CD k k++==++， ∴2222222212(1)12(1)84(1)||||3434(34)(34)k k k AB CD k k k k ++++=+=++++，令21t k =+，则1t >，∴2222848484||||1149(41)(31)121()24t t AB CD t t t t t +===-++---+，1t >，∴101t<<，∴211494912()244t <--+，∴241111494912()24t <--+， ∴24884711497()24t <--+，∴48||||77AB CD +<， 综合①②可知，||||AB CD +的取值范围为：48,77⎡⎤⎢⎥⎣⎦． 【点睛】(1)解答直线与椭圆的题目时，时常把两个曲线的方程联立，消去x (或y )建立一元二次方程，然后借助根与系数的关系，并结合题设条件建立有关参变量的等量关系． (2)涉及到直线方程的设法时，务必考虑全面，不要忽略直线斜率为0或不存在等特殊情形．23．（1）26y x =；（2）(4,)+∞. 【分析】（1）首先设圆心(),C x y ，利用条件表示半径，列等式求圆心的轨迹方程；（2）首先设直线:(1)MN y k x =+，与（1）的轨迹方程联立，利用根与系数的关系求得中点坐标，并表示过点P 的垂线方程，求与x 轴的交点Q 的坐标，并求范围. 【详解】解：（1）设(,)C x y ，则222(1)3(2)x x y ++=-+即26y x =，所以圆心C 的轨迹方程为：26y x = （2）设过点(1,0)-直线:(1)MN y k x =+，联立26(1)y x y k x ⎧=⎨=+⎩，消y 得：()2222260k x k x k +-+=所以()2242640k k ∆=-->，即232k <设()()1122,,,M x y N x y ，根据韦达定理得：1212262,1x x x x k+=-= 所以MN 的中点2331,P kk ⎛⎫-⎪⎝⎭ 过点P 的垂线为23131y x k k k ⎡⎤⎛⎫-=--- ⎪⎢⎥⎝⎭⎣⎦令0y =，则2324x k=+>， 所以点Q 的横坐标的取值范围(4,)+∞.【点睛】关键点点睛：本题的关键是第二问直线与抛物线方程联立后，不要忘记0∆>这个条件，否则求点Q 横坐标的取值范围就会出错. 24．（1）4p =；（2）1. 【分析】（1）求出p 后可得焦点到准线的距离.（2）设直线l 的方程为4x my =-，()11,M x y ，()22,N x y ，可用,M N 的坐标表示PB BQ ，再联立直线l 的方程和抛物线的方程，利用韦达定理化简PBBQ可得所求的值. 【详解】（1）因为()2,4T -在抛物线上，164p =即4p =，抛物线C 的焦点到准线的距离为4p =.（2）显然直线l 的斜率不为0，故设直线l 的方程为4x my =-， 由248x my y x=-⎧⎨=⎩得28320y my -+=， 由()228320m ∆=->得216m >，设()11,M x y ，()22,N x y ，则128y y m +=，1232y y =，所以()12124my y y y =+. 又114MA y k x =-，224NA y k x =-，所以直线MA ：()1144y y x x =--，NA ：()2244yy x x =--， 令4x =-，得1184P y y x -=-，2284Q y y x -=-，所以121212124848P QPB y y x y my BQx y my y y --==⋅=⋅-- ()()121121211221221248844184844y y y my y y y y my y y y y y y y +---====-+--．【点睛】思路点睛：直线与圆锥曲线的位置关系中的定点、定值、最值问题，一般可通过联立方程组并消元得到关于x 或y 的一元二次方程，再把要求解的目标代数式化为关于两个的交点横坐标或纵坐标的关系式，该关系中含有1212,x x x x +或1212,y y y y +，最后利用韦达定理把关系式转化为若干变量的方程（或函数），从而可求定点、定值、最值问题. 25．（1）24y x =；（2）直线AB 过定点(2,0)-，证明见解析. 【分析】（1）由抛物线的定义求得p ，得抛物线方程；（2）设直线AB 方程为x my b =+， 11(,)A x y ，22(,)B x y ，直线方程代入抛物线方程，由判别式大于0得参数满足的条件，应用韦达定理得1212,y y y y +，计算由2OA OB k k =可得128y y =，从而求得参数b ，并可得出m 的范围．此时由直线方程可得定点坐标． 【详解】（1）由抛物线定义可知：122p+=，则2p =， 所以抛物线C 的方程为24y x =（2）设直线AB 方程为x my b =+， 11(,)A x y ，22(,)B x y联立24y x x my b⎧=⎨=+⎩得2440y my b --=，则216160m b ∆=+>即20()m b +>*。

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(有答案解析)(2)

(常考题)北师大版高中数学选修1-1第二章《圆锥曲线与方程》检测卷(有答案解析)(2)

一、选择题1．直线3y x与曲线2||194y x x -=的公共点的个数是（ ）A ．1B ．2C ．3D ．42．已知椭圆2222:1(0)x y E a b a b+=>>，设直线l 与椭圆相交于A ，B 两点，与x 轴，y 轴分别交于C ，D 两点，记椭圆E 的离心率为e ，直线l 的斜率为k ，若C ，D 恰好是线段AB 的两个三等分点，则（ ） A ．221k e -=B ．221k e +=C ．2211e k -= D ．2211e k += 3．已知点12,F F 是椭圆()222210x y a b a b+=>>的左右焦点，椭圆上存在不同两点,A B 使得122F A F B =，则椭圆的离心率的取值范围是（ ） A ．10,3⎛⎫ ⎪⎝⎭B ．10,2⎛⎫ ⎪⎝⎭C ．1,13⎛⎫ ⎪⎝⎭D ．1,12⎛⎫ ⎪⎝⎭4．斜率为1的直线l 经过抛物线24y x =的焦点F ，且与抛物线相交于A 、B 两点，则线段AB 的长为（ ）A ．B ．C ．D ．85．已知椭圆C 的焦点为()12,0F -，()22,0F ，过2F 的直线与C 交于A ，B 两点，若222AF F B =，1AB BF =，则C 的方程为（ ） A ．221124x y +=B ．2211612x y +=C ．221128x y +=D ．2212016x y +=6．抛物线：24y x =的过焦点的弦的中点的轨迹方程为（ ） A ．21y x =-B ．212y x =-C ．22(1)y x =-D ．221y x =-7．设1F 、2F 是双曲线()2222:10,0x yC a b a b-=>>的左、右焦点，P 是双曲线C 右支上一点.若126PF PF a +=，且122PF F S =△，则双曲线C 的渐近线方程是（ ）A 0y ±=B ．0x ±=C 20y ±=D ．20x =8．顶点在原点，经过点()，且以坐标轴为轴的抛物线的标准方程是（ ）A ．2y =或212=-x y B ．2y =-或212=-x yC ．2y =或212x y =D ．2y =-或212x y =9．如果直线1y kx =-与双曲线224x y -=只有一个交点，则符合条件的直线有（ ） A ．1条B ．2条C ．3条D ．4条10．设1F 、2F 是椭圆1C 和双曲线2C 的公共焦点，P 是它们的一个公共点，且1PF <2PF ，线段1PF 垂直平分线经过2F ，若1C 和2C 的离心率分别为1e 、2e ，则129e e +的最小值（ ）A ．2B ．4C ．6D ．811．已知直线l 的方程为1y kx =-，双曲线C 的方程为221x y -=.若直线l 与双曲线C 的右支相交于不同的两点，则实数k 的取值范围是（ ） A ．(2,2)-B ．[1,2)C ．[2,2]-D ．(1,2)12．在抛物线型内壁光滑的容器内放一个球，其通过中心轴的纵剖面图如图所示，圆心在y 轴上，抛物线顶点在坐标原点，已知抛物线方程是24x y =，圆的半径为r ，若圆的大小变化时，圆上的点无法触及抛物线的顶点O ，则圆的半径r 的取值范围是（ ）A ．()2,+∞B ．()1,+∞C ．[)2,+∞D ．[)1,+∞二、填空题13．F 是抛物线22y px =（0p >）的焦点，过点F 的直线与抛物线的一个交点为A ，交抛物线的准线于B ，若2BA AF =，且4BA =，则P =______．14．设F 是抛物线2:2C y x =的焦点，A 、B 是抛物线C 上两个不同的点，若直线AB 恰好经过焦点F ，则4AF BF +的最小值为_______．15．知直线m 过抛物线()220y px p =>的焦点F ，且交抛物线于A 、B 两点，交其准线l于点C .若6AF =，2CB BF =，则p =____________16．设点P 是抛物线2:4C y x =上一动点，F 是抛物线的焦点，O 为坐标原点，则OPPF的最大值为___________.17．已知椭圆222:1(06)6x y G b b+=<<的两个焦点分别为1F 和2F ，短轴的两个端点分别为1B 和2B ，点P 在椭圆G 上，且满足1212PB PB PF PF +=+．当b 变化时，给出下列三个命题：①点P 的轨迹关于y 轴对称；②存在b 使得椭圆G 上满足条件的点P 仅有两个；③||OP 的最小值为2，其中，所有正确命题的序号是___________．18．已知椭圆22:1168x y C +=的左､右焦点分别为12,F F ，直线(44)x m m =-<<与椭圆C 相交于点A ，B .给出下列三个命题：①存在唯一一个m ，使得12AF F △为等腰直角三角形； ②存在唯一一个m ，使得1ABF 为等腰直角三角形； ③存在m ，使1ABF 的周长最大. 其中，所有真命题的序号为_________.19．如图，一种电影放映灯的反射镜面是旋转椭圆面（椭圆绕其对称轴旋转一周形成的曲面）的一部分，过对称轴的截口BAC 是椭圆的一部分，灯丝位于椭圆的一个焦点1F 上，片门位于另一个焦点2F 上.由椭圆一个焦点1F 发出的光线，经过旋转椭圆面反射后集中到另一个焦点2F .已知12BC F F ⊥，1163F B =，124F F =，则截口BAC 所在椭圆的离心率为______.20．设A 、B 是双曲线22221(0,0)x y a b a b-=>>的左、右顶点，F 是右焦点，M 是双曲线上异于A 、B 的动点，过点B 作x 轴的垂线与直线MA 交于点P ，若直线OP 与BM 的斜率之积为4，则双曲线的离心率为_________．三、解答题21．已知点A 、B 坐标分别是(2,0)-，(22,0)，直线AP 、BP 相交于点P ，且它们斜率之积是12-．（1）试求点P 的轨迹Γ的方程；（2）已知直线:4l x =-，过点()2,0F -的直线（不与x 轴重合）与轨迹Γ相交于M ．N 两点，过点M 作MD l ⊥于点D ．求证：直线ND 过定点，并求出定点的坐标．22．已知椭圆2222:1(0)x y E a b a b +=>>的左右顶点分别为A ，B ，离心率为3，且过点22,2D ⎛⎫⎪ ⎪⎭．（1）求椭圆E 的标准方程;（2）过点()4,0P 作与x 轴不重合的直线l 与椭圆E 相交于M ，N 两点(N 在P ，M 之间)．证明:直线MB 与直线NA 的交点的横坐标是定值．23．设曲线()22:10,0C mx ny m n +=>>过()()2,3,22,6M N 两点，直线():2l y k x =-与曲线C 交于,P Q 两点，与直线8x =交于点R .（1）求曲线C 的方程；（2）记直线,,MP MQ MR 的斜率分别为123,,k k k ，求证：123k k k λ+=，其中λ为定值.24．已知椭圆2222:1(0)x y C a b a b +=>>的离心率为3,(2,1),,2A P Q --在椭圆C 上，且,P Q 异于点A ．（1）求椭圆C 的方程；（2）若||||,||||OP OQ AP AQ ==，求直线PQ 的方程．25．荷兰数学家舒腾(F.van Shooten ，1615-1660)设计了一种画椭圆的工具，如图1所示，两根等长的带槽的直杆AC 和BF 的一端各用钉子固定在点A 和B 上(但分别可以绕钉子转动)，4AC BF ==，另一端用铰链与杆FC 连接，2FC AB ==，AC 和BF 的交点为E ，转动整个工具，交点E 形成的轨迹为椭圆Γ.以线段AB 中点O 为原点，AB 所在的直线为x 轴建立如图2的平面直角坐标系.（1）求椭圆Γ的标准方程；（2）经过B 点的直线l 交椭圆Γ于不同的两点M N 、，设点P 为椭圆的右顶点，当PNM △的面积为627时，求直线l 的方程. 26．已知点1F 、2F 分别是椭圆C 的左、右焦点，离心率为22，点P 是以坐标原点O 为圆心的单位圆上的一点，且120PF PF ⋅=．（1）求椭圆C 的标准方程；（2）设斜率为k 的直线l （不过焦点）交椭圆于M ，N 两点，若x 轴上任意一点到直线1MF 与1NF 的距离均相等，求证：直线l 恒过定点，并求出该定点的坐标．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】由于已知曲线函数中含有绝对值符号， 将x 以0为分界进行分类讨论，当x ≥0时，曲线为焦点在y 轴上的双曲线，当x <0时，曲线为焦点在y 轴上的椭圆，进而在坐标系中作出直线与曲线的图像，从而可得出交点个数. 【详解】当0x ≥时，曲线2194x xy -=的方程为22194y x -=当0x <时，曲线2194x xy -=的方程为22194y x +=，∴曲线2194x xy -=的图象如图，在同一坐标系中作出直线3y x的图象，可得直线与曲线交点个数为3个．故选：C【点晴】本题讨论曲线类型再利用数形结合法求交点个数是解题的关键．2．B解析：B【分析】首先利用点,C D分别是线段AB的两个三等分点，则211222x xyy=-⎧⎪⎨=⎪⎩，得1112ykx=⋅，再利用点差法化简得2212214y bx a=，两式化简得到选项.【详解】设()11,A x y，()22,B x y，,C D分别是线段AB的两个三等分点，()1,0C x∴-，10,2yD⎛⎫⎪⎝⎭，则112,2yB x⎛⎫-⎪⎝⎭，得211222x xyy=-⎧⎪⎨=-⎪⎩，1121121131232yy y ykx x x x-===⋅-，利用点差法22112222222211x ya bx ya b⎧+=⎪⎪⎨⎪+=⎪⎩，两式相减得()()()()1212121222x x x x y y y ya b+-+-+=，整理得到2212214y bx a=，即222222244b a ck ka a-=⇒=，即221k e+=故选：B【点睛】关键点点睛：本题的关键利用三等分点得到211222x x y y =-⎧⎪⎨=-⎪⎩，再将斜率和离心率表示成坐标的关系，联立判断选项.3．C解析：C 【分析】先设点，利用向量关系得到两点坐标之间的关系121223,2x x c y y =-=，再结合点在椭圆上，代入方程，消去222a y 即得2229312c a x c+=，根据题意2x a <，构建,a c 的齐次式，解不等式即得结果. 【详解】设()()1122,,,A x y B x y ，由()()12,0,,0F c F c -得()()112212,,,F A F x c y x c y B -==+，122F A F B =，()()11222,,x c y x c y =∴+-，即121223,2x x c y y =-=，由,A B 在椭圆上，故2222221122222222b x a y a b b x a y a b ⎧+=⎨+=⎩，即()()2222222222222222232b x c a y a b b x a y a b ⎧-+=⎪⎨+=⎪⎩， 消去222a y 得，2229312c a x c+=，根据椭圆上点满足a x a -≤≤，又,A B 两点不同，可知2229312c a x a c+=<，整理得22340c ac a -+<，故23410e e -+<，故113e <<.故选：C. 【点睛】 关键点点睛：圆锥曲线中离心率的计算，关键是根据题中条件，结合曲线性质，找到,,a b c 一组等量关系（齐次式），进而求解离心率或范围.4．D解析：D 【分析】写出直线l 的方程，设点()11,A x y 、()22,B x y ，联立直线l 与抛物线的方程，列出韦达定理，利用抛物线的焦点弦长公式可求得AB . 【详解】抛物线24y x =的焦点()1,0F ，直线l 的方程为1y x =-，设点()11,A x y 、()22,B x y联立214y x y x=-⎧⎨=⎩，可得2610x x -+=，2640∆=->，所以，126x x +=，由抛物线的焦点弦长公式得1228AB x x =++=. 故选： D. 【点睛】方法点睛：有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式12AB x x p =++，若不过焦点，则必须用一般弦长公式．5．C解析：C 【分析】根据椭圆的定义以及余弦定理，结合221cos cos 0AF O BF F ∠+∠=列方程可解得a ，b ，即可得到椭圆的方程． 【详解】22||2||AF BF =，2||3||AB BF ∴=， 又1||||AB BF =，12||3||BF BF ∴=， 又12||||2BF BF a +=，2||2aBF ∴=， 2||AF a ∴=，13||2BF a =， 12||||2AF AF a +=，1||AF a ∴=， 12||||AF AF ∴=，A ∴在y 轴上．在Rt2AF O 中，22cos AF O a∠=，在12BF F △中，由余弦定理可得22221316()()822cos 2242a a a BF F a a +--∠==⨯⨯． 221cos cos 0AF O BF F ∠+∠=，可得22802a a a -+=，解得212a =．2221248b a c =-=-=．椭圆C 的方程为：221128x y +=．故选：C ． 【点睛】方法点睛：用待定系数法求椭圆方程的一般步骤；①作判断：根据条件判断椭圆的焦点在x 轴上，还是在y 轴上，还是两个坐标轴都有可能；②设方程：根据上述判断设方程()222210x y a b a b +=>>或22221x y b a+=()0a b >>；③找关系：根据已知条件，建立关于a 、b 、c 的方程组；④得方程：解方程组，将解代入所设方程，即为所求.6．C解析：C 【分析】设出过焦点的直线方程，与抛物线方程联立求出两根之和，可得中点的坐标，消去参数可得中点的轨迹方程． 【详解】由抛物线的方程可得焦点(1,0)F ，可得过焦点的直线的斜率不为0， 设直线方程为：1x my =+，设直线与抛物线的交点1(A x ，1)y ，2(B x ，2)y ，设AB 的中点(,)P x y ， 联立直线与抛物线的方程可得：2440y my --=，124y y m +=，21212()242x x m y y m +=++=+，所以可得2212x m y m⎧=+⎨=⎩，消去m 可得P 的轨迹方程：222y x =-，故选：C ． 【点睛】方法点睛：求轨迹方程的常见方法有：1、定义法；2、待定系数法；3、直接求轨迹法；4、反求法；5、参数方程法等等.7．A解析：A 【分析】利用双曲线的定义、余弦定理以及三角形的面积公式可求得123F PF π∠=，利用双曲线的定义以及126PF PF a +=可求得14PF a =，22PF a =，再利用余弦定理可得出ba的值，由此可求得双曲线C 的渐近线方程. 【详解】设12F PF θ∠=，由双曲线的定义可得122PF PF a -=， 在12PF F △中，由余弦定理可得2221212122cos F F PF PF PF PF θ=+-⋅，即()()()22212121212222cos 421cos c PF PF PF PF PF PF a PF PF θθ=-+⋅-⋅=+⋅-，所以，222122221cos 1cos c a b PF PF θθ-⋅==--，1222221222sin cos1sin 22sin 21cos tan112sin 22PF F b b b S PF PF θθθθθθθ⋅=⋅====-⎛⎫-- ⎪⎝⎭△，tan2θ∴=0θπ<<，可得022θπ<<，26θπ∴=，所以，3πθ=，由已知可得121226PF PF a PF PF a ⎧-=⎪⎨+=⎪⎩，解得1242PF a PF a ⎧=⎪⎨=⎪⎩，由余弦定理可得2221212122cos F F PF PF PF PF θ=+-⋅，即222221416416122c a a a a =+-⨯=，则223c a =，即2223a b a +=，b ∴=， 因此，双曲线C的渐近线方程为by x a=±=0y ±=. 故选：A. 【点睛】思路点睛：求解双曲线的渐近线的常用思路：（1）转化已知条件，得到a 、b 、c 中任意两个量的等量关系；（2）若得到a 、b 的等量关系，则渐近线方程可得；若已知a 、c 或b 、c 之间的等量关系，结合222+=a b c 可求得ba的值，则渐近线方程可求. 8．D解析：D 【分析】设出抛物线方程为22y mx =或22x ny =，代入点的坐标求出参数值可得．【详解】设抛物线方程为22y mx =，则262(m =⋅，m =-2y =-， 或设方程为22x ny =，则2(26n =⨯，14n =，方程为212x y =．所以抛物线方程为2y =-或212x y =．故选：D ． 【点睛】关键点点睛：抛物线的标准方程有四种形式，在不确定焦点位置（或开口方向时），需要分类讨论．象本题在抛物线过一点的坐标，则需要考虑焦点在x 轴和y 轴两种情况，焦点在x 轴上时可以直接设方程为2y mx =，代入点的坐标求出参数值，不必考虑焦点是在x轴正半轴还是在负半轴，焦点在y 轴也类似求解．9．D解析：D 【分析】直线方程与双曲线方程联立方程组，由方程组只有一解确定． 【详解】 由2214y kx x y =-⎧⎨-=⎩，得22(1)250k x kx -+-=， 若210k -=，即1k =±，1k =时，52x =，方程组只有一解；1k =-时，52x =-，方程组只有一解； 210k -≠时，22420(1)0k k ∆=+-=，k = 方程组只有一解，即直线与双曲线只有一个交点．因此这样的直线有4条． 故选：D ． 【点睛】关键点点睛：直线与曲线的交点问题，可能通过解方程组确定，直线与曲线方程组成的方程组的解的个数就是它们交点的个数．这是代数方法．也可从几何角度考虑，如本题直线与双曲线相切的有两条，与渐近线平行的有两条共4条直线与双曲线只有一个交点．10．D解析：D 【分析】设椭圆和双曲线的方程，由题意可得2122PF F F c ==，再利用椭圆和双曲线的定义分别求出1PF ，即可得122a a c +=，计算12112e e +=，()121212111992e e e e e e ⎛⎫+=++ ⎪⎝⎭展开后利用基本不等式即可求最值. 【详解】设椭圆1C 的方程为2222111x y a b +=，则222111c a b =-，设双曲线2C 的方程为2222221x y a b -=，则222222c a b =+，因为椭圆1C 和双曲线2C 的焦点相同，所以2212c c =，设12c c c ==即22221122a b a b -=+，因为P 是椭圆1C 和双曲线2C 的一个公共点， 所以1212+=PF PF a ，2122PF PF a -=，因为线段1PF 垂直平分线经过2F ，所以2122PF F F c ==，所以1122PF a c =-，且1222PF c a =-， 所以122222a c c a -=-，可得122a a c +=， 所以11c e a =，22c e a =，所以1212121122a a a a ce e c c c c++=+===， 所以()211212121291111991022e e e e e e e e e e ⎛⎫⎛⎫+=++=++ ⎪ ⎪⎝⎭⎝⎭()11101023822⎛≥+=+⨯= ⎝， 当且仅当21129e e e e =，即213e e =时等号成立， 故选：D. 【点睛】关键点点睛：本题解题的关键点是利用已知条件得出122a a c +=，进而可得12112e e +=， 再利用基本不等式可求最值.11．D解析：D 【分析】联立直线方程1y kx =-和双曲线方程221x y -=，化为22(12)20k x kx --=+，由于直线1y kx =-与双曲线221x y -=的右支交于不同两点，可得210k -≠，由2248(1)0k k ∆=+->，1k <，解得即可【详解】解：联立直线方程1y kx =-和双曲线方程221x y -=，化为22(12)20k x kx --=+， 因为直线1y kx =-与双曲线221x y -=的右支交于不同两点， 所以210k -≠，且2248(1)0k k ∆=+->，1k <，解得1k <<，所以实数k的取值范围为， 故选：D【点睛】关键点点睛：此题考查直线与双曲线的位置关系，解题的关键是直线方程和双曲线方程联立方程组，消元后结合题意可得2248(1)0k k ∆=+->，1k <，从而可得答案12．A解析：A 【分析】设圆心为(0,)P a ，（0a >），半径为r ，(,)Q x y 是抛物线上任一点，求出2PQ ，当2PQ 的最小值在原点处取得时，圆P 过原点，可得此时圆半径的范围，半径不在这个范围内的圆不过原点． 【详解】设圆心为(0,)P a ，（0a >），半径为r ，(,)Q x y 是抛物线上任一点，22222()4()(2)44PQ x y a y y a y a a =+-=+-=-++-，若2PQ 的最小值不在(0,0)O 处取得，则圆P 不过原点，所以20a ->，即2a >，此时圆半径为2r ==>．因此当2r >时，圆无法触及抛物线的顶点O ．故选：A ． 【点睛】关键点点睛：本题考查圆与抛物线的位置关系，题中圆不过原点，说明抛物线上的点到圆心距离的最小值不是在原点处取得，由此得到解法，即设圆心为(0,)P a ，抛物线上点的坐标为(,)Q x y ，求出PQ ，然后确定其最小值，由最小值点不是原点可得结论．二、填空题13．3【分析】设过的直线为与抛物线交于点过两点作垂直准线于点根据抛物线的定义可得即可求出再联立直线与抛物线方程消元列出韦达定理即可得到再由焦半径公式计算可得；【详解】解：因为是抛物线的焦点所以准线为设过解析：3 【分析】设过F 的直线为2p y k x ⎛⎫=-⎪⎝⎭，与抛物线交于点()11,A x y ，()22,C x y ，过A 、B 两点作AM ，CN 垂直准线于M ，N 点，根据抛物线的定义可得CN CF =，AM AF =，即可求出30ABM ∠=︒，6CN CF ==，再联立直线与抛物线方程，消元、列出韦达定理即可得到2124p x x =，再由焦半径公式计算可得；【详解】解：因为F 是抛物线22y px =的焦点，所以,02p F ⎛⎫⎪⎝⎭，准线为2p x =-，设过F 的直线为2p y k x ⎛⎫=- ⎪⎝⎭，与抛物线交于点()11,A x y ，()22,C x y ，过A 、B 两点作AM ，CN垂直准线于M，N 点，所以CN CF =，AM AF =，因为2BA AF =，所以2BA AF =，所以2BA AM =，所以30ABM ∠=︒，又因为4BA =，所以2AM AF ==，且2CN CB BA AF FC BA AM CN ==--=--，所以26CN CN =+，所以6CN CF ==，联立直线与抛物线222p y k x y px ⎧⎛⎫=-⎪ ⎪⎝⎭⎨⎪=⎩，消去y 得22224p k x px px ⎛⎫ ⎪⎭=⎝-+，所以()22222204k p k x k p p x -++=，所以21222k p px x k++=-，2124p x x =，又因为1>0x ，20x >，且122p x AM +==，262p x CN +==，所以2212261242244p p p p x x p ⎛⎫⎛⎫=--=-+= ⎪⎪⎝⎭⎝⎭，所以3p =故答案为：3【点睛】(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系；(2)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB |＝x 1＋x 2＋p ，若不过焦点，则必须用一般弦长公式．14．【分析】设点设直线的方程为联立直线与抛物线的方程列出韦达定理推导出利用基本不等式可求得的最小值【详解】若直线与轴重合则直线与抛物线只有一个交点不合乎题意易知抛物线的焦点为准线方程为设点设直线的方程为解析：92【分析】设点()11,A x y 、()22,B x y ，设直线AB 的方程为12x my =+，联立直线AB 与抛物线C 的方程，列出韦达定理，推导出112AF BF+=，利用基本不等式可求得4AF BF +的最小值. 【详解】若直线AB 与x 轴重合，则直线AB 与抛物线C 只有一个交点，不合乎题意.易知抛物线C 的焦点为1,02F ⎛⎫ ⎪⎝⎭，准线方程为12x =-，设点()11,A x y 、()22,B x y ，设直线AB 的方程为12x my =+， 联立2122x my y x⎧=+⎪⎨⎪=⎩，整理可得2210y my --=，2440m ∆=+>，由韦达定理可得122y y m +=，121y y =-，()()()12121212211111*********m y y AF BF my my my my x x +++=+=+=++++++()()21222212122222121m y y m m y y m y y m m +++===+++-++， ()4111144522AF BF AF BF AF BF AF BF BF AF ⎛⎫⎛⎫∴+=++=++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭19522⎛≥+= ⎝， 当且仅当2AF BF =时，等号成立，因此，4AF BF +的最小值为92. 故答案为：92. 【点睛】结论点睛：过抛物线的焦点F 的直线与抛物线交于A 、B 两点，则112AF BF p+=. 15．3【分析】过作准线的垂线垂足分别为过作的垂线垂足为根据结合抛物线的定义可得据此求出再根据抛物线的定义可求出【详解】如图：过作准线的垂线垂足分别为过作的垂线垂足为因为所以因为所以所以所以在直角三角形中解析：3 【分析】过A 、B 作准线l 的垂线，垂足分别为,N M ，过F 作AN 的垂线，垂足为D ，根据2CB BF =结合抛物线的定义可得30DFA MCB ∠=∠=，据此求出||3AD =，再根据抛物线的定义可求出p . 【详解】如图：过A 、B 作准线l 的垂线，垂足分别为,N M ，过F 作AN 的垂线，垂足为D ，因为2CB BF =，所以||2||CB BF =， 因为||||BF BM =，所以||2||CB BM =， 所以30MCB ∠=，所以30DFA ∠=，在直角三角形ADF 中，因为||6AF =，所以||3AD =， 因为||||6AN AF ==，且||||3AN AD p p =+=+， 所以63p =+，所以3p =. 故答案为：3 【点睛】关键点点睛：利用抛物线的定义求解是解题关键.16．【分析】设点则则可得出令利用二次函数的基本性质求出二次函数的最大值即可得出的最大值【详解】设点则则抛物线的准线方程为由抛物线的定义可得所以令当且仅当时函数取得最大值因此的最大值为故答案为：【点睛】方 解析：233【分析】设点(),P x y ，则24y x =，则0x ≥，可得出OP PF=(]10,11t x =∈+，利用二次函数的基本性质求出二次函数2321y t t =-++的最大值，即可得出OP PF的最大值.【详解】设点(),P x y ，则24y x =，则0x ≥，抛物线C 的准线方程为1x =-，由抛物线的定义可得1PF x =+，所以，OPPF ==== 0x ≥，令(]10,11t x =∈+，221443213333y t t t ⎛⎫=-++=--+≤ ⎪⎝⎭， 当且仅当13t =时，函数2321y t t =-++取得最大值43，因此，OP PF. 【点睛】方法点睛：圆锥曲线中的最值问题解决方法一般分两种：一是几何法，特别是用圆锥曲线的定义和平面几何的有关结论来求最值；二是代数法，常将圆锥曲线的最值问题转化为二次函数或三角函数的最值问题，然后利用基本不等式、函数的单调性或三角函数的有界性等求最值．17．①③【分析】运用椭圆的定义可得也在椭圆上分别画出两个椭圆的图形即可判断①正确；通过的变化可得②不正确；由图象可得当的横坐标和纵坐标的绝对值相等时的值取得最小即可判断③【详解】解：椭圆的两个焦点分别为解析：①③ 【分析】运用椭圆的定义可得P 也在椭圆222166y x b+=-上，分别画出两个椭圆的图形，即可判断①正确；通过b 的变化，可得②不正确；由图象可得当P 的横坐标和纵坐标的绝对值相等时，||OP 的值取得最小，即可判断③．【详解】解：椭圆222:1(06)6x y G b b+=<<的两个焦点分别为21(6F b -，0)和22(6F b --，0)，短轴的两个端点分别为1(0,)B b -和2(0,)B b ，设(,)P x y ，点P 在椭圆G 上，且满足1212||||||||PB PB PF PF +=+， 由椭圆定义可得，12||||2262PB PB a b +==>，即有P 在椭圆222166y x b+=-上． 对于①，将x 换为x -方程不变，则点P 的轨迹关于y 轴对称， 故①正确；对于②，由图象可得轨迹关于x ，y 轴对称，且06b <<，则椭圆G 上满足条件的点P 有4个，不存在b 使得椭圆G 上满足条件的点P 仅有两个，故②不正确；对于③，点P 靠近坐标轴时(0b →或6)b →，||OP 越大，点P 远离坐标轴时，||OP 越小，所以226b b -=，即23b =时，取得最小值，此时22:163x y G +=，与22163y x += 两方程相加得22222222x y x y +=⇒+=，即||OP 的最小值为 2，故③正确．故答案为：①③．【点睛】本题考查椭圆的对称性及由椭圆上的点到焦点的距离之和等于到短轴的顶点距离之和可得另一个椭圆，及到定点距离的最值的判断．18．①③【分析】首先根据题意得到设对①分类讨论和以及即可判断①为真命题对②根据椭圆的对称性可知利用解方程即可判断②为假命题对③利用椭圆的定义即可判断③为真命题【详解】由题知：设对①若则此时则所以满足为等解析：①③ 【分析】首先根据题意得到4a =，b c ==()1F -，()2F ，设(),A m y ，(),B m y -.对①，分类讨论12AF AF =，1290F AF ∠=，和1290AF F ∠=，以及2190AF F ∠=，即可判断①为真命题.对②，根据椭圆的对称性可知，11AF BF =，利用11AF k ==，解方程即可判断②为假命题，对③，利用椭圆的定义即可判断③为真命题. 【详解】由题知：4a =，b c ==()1F -，()2F ， 设(),A m y ，(),B m y -.对①，若12AF AF =，则0m =，此时(0,A .11AF k ==，21AF k ==-，则121AF AF k k ⋅=-，所以1290F AF ∠=，满足12AF F △为等腰直角三角形.若1290AF F ∠=，则()2A -，此时12AF =，12F F =.若2190AF F ∠=，则()2A ，此时22AF =，12F F =.所以存在唯一一个m ，使得12AF F △为等腰直角三角形，故①为真命题. 对②，根据椭圆的对称性可知，11AF BF =，满足等腰三角形. 当190AF B ∠=时，根据椭圆的对称性可知：直线1AF 的倾斜角为45，11AF k ==，即y m =+又因为221168m y +=，所以(22216m m ++=，解得0m =或3m =-，都在44m -<<内， 故存在唯一一个m ，使得1ABF 为等腰直角三角形为假命题. 对③，1ABF 的周长为11AB AF BF ++， 又因为128AF AF =-，128BF BF =-，所以()112216AF BF AF BF +=-+， 即1ABF 的周长为()2216AB AF BF +-+，又因为22AF BF AB +≥，当且仅当m =时取等号， 所以()22AF BF AB -+≤-，即1ABF 的周长为()22161616AB AF BF AB AB +-+≤+-=.当且仅当m =时，1ABF 的周长最大. 故③为真命题. 故答案为：①③ 【点睛】关键点点睛：本题主要考查椭圆的定义，解决本题①的关键为分类讨论12AF AF =，1290F AF ∠=，和1290AF F ∠=，以及2190AF F ∠=，②的关键为代入椭圆的对称性，③的关键为椭圆的定义，属于中档题.19．【分析】取焦点在轴建立平面直角坐标系由题意及椭圆性质有为椭圆通径得结合及解出代入离心率公式计算即可【详解】解：取焦点在轴建立平面直角坐标系由及椭圆性质可得为椭圆通径所以又解得所以截口所在椭圆的离心率解析：13【分析】取焦点在x 轴建立平面直角坐标系，由题意及椭圆性质有BC 为椭圆通径，得2163b a =，结合24c =及222a b c =+解出,,a b c 代入离心率公式计算即可.【详解】解：取焦点在x 轴建立平面直角坐标系，由12BC F F ⊥及椭圆性质可得，BC 为椭圆通径，所以21163b F B a ==，1224F Fc ==又222a b c =+，解得6,2,a c b ===所以截口BAC 所在椭圆的离心率为13故答案为：13【点睛】求椭圆的离心率或其范围的方法：（1）求,,a b c 的值，由22222221c a b b a a a-==-直接求e ；（2）列出含有,,a b c 的齐次方程(或不等式)，借助于222a b c =+消去b ，然后转化成关于e 的方程(或不等式)求解．20．【分析】设代入双曲线方程变形为再根据MPA 共线利用斜率相等求得点P 然后再直线与的斜率之积为4得到ab 的关系求解【详解】设则即设又且MPA 共线所以解得则的斜率为的斜率为又直线与的斜率之积为4所以即所以【分析】设(),M m n ，代入双曲线方程变形为22222n b m a a=-，再根据M ，P ，A 共线，利用斜率相等，求得点P ，然后再直线OP 与BM 的斜率之积为4，得到a ，b 的关系求解. 【详解】设(),M m n ，则22221m n a b -=，即22222n b m a a =-，设(),P a t ，又(),0A a -，且M ，P ，A 共线， 所以2n tm a a=+， 解得2ant m a=+， 则OP 的斜率为2nm a+， BM 的斜率为nm a-， 又直线OP 与BM 的斜率之积为4，所以22222224a n b m a ==-，即222b a=，所以c e a ===【点睛】本题主要考查双曲线的离心率的求法以及点的双曲线上和斜率公式的应用，还考查了运算求解的能力，属于中档题.三、解答题21．（1）221(84x y x +=≠±；（2）证明见解析，()3,0-.【分析】（1）首先设点(),P x y ，利用12PA PB k k ⋅=-，转化为关于,x y 的方程；（2）方法一，首先由椭圆的对称性可知定点必在x 轴上，设:2MN x my =-，与椭圆方程联立，由根与系数的关系得到()1212my y y y =-+，并求出直线ND 的方程，求与x 轴的交点；方法二，直线:2MN x my =-与椭圆方程联立后，利用求根公式求得两个交点的纵坐标，再代入直线ND 的方程，化简，求定点的坐标. 【详解】（1）设(),P x y ，由题意得：12PA PB k k ⋅=-12=-，化简得22184x y +=．又x ≠±，∴点P的轨迹方程为221(84x y x +=≠±．（2）方法一：由椭圆的对称性知，直线ND 过的定点必在x 轴上， 由题意得直线MN 的斜率不为0，设:2MN x my =-，与22184x y +=联立消去x 得：()222440m y my +--=， ()23210m ∆=+>恒成立，设()11,M x y ，()22,N x y ，则()14,D y -，12242m y y m +=+，12242y y m -=+， ∴()1212my y y y =-+，2112:(4)4y y ND y x y x -=+++，令0y =， ∴()()12122121424y x y my x y y y y +++=-=---()1211212121221y y y my y y y y y y -+++=-=-=--，3x =-，∴直线ND 过定点()3,0-．方法二：由题意可得直线MN 的斜率不为0，设:2MN x my =-，与22184x y +=联立消去x 得：()222440m y my +--=， ()23210m ∆=+>恒成立，设()11,M x y ，()22,N x y ，则()14,D y -，12242m y y m +=+，12242y y m -=+，()12422m y m -=+，()22422m y m +=+， ()2112121122(4)2:(4)42y y x my y y y y ND y x y x my -+++-=++=++222244(4)2222m m x m m m my --++++++=+224)3)2222x x m m my my ++++==++ ∴3x =-时0y =， ∴直线ND 过定点()3,0-. 【点睛】关键点点睛：本题考查椭圆中直线过定点问题，第一个关键是首先判断定点在x 轴上，方法一的关键是利用根与系数的关系得到()1212my y y y =-+，再代回直线方程求交点，方法二的关键是变形，化简.22．（1）2214x y +=；（2）证明见解析.【分析】（1）待定系数法求椭圆标准方程；（2）用“设而不求法”表示出M 、N ，，从而表示出直线MB ，NA , 证明直线MB 与直线NA 的交点的横坐标是定值． 【详解】 （1）因为c e a ==12b a =椭圆过点2D ⎫⎪⎪⎭，所以2221142b b +=， 所以2a =，1b =，所以椭圆E 的方程为2214x y +=（2）设直线:4l x my =+，设()11,M x y ，()22,N x y联立22414x my x y =+⎧⎪⎨+=⎪⎩得：()2248120m y my +++= 2161920m ∆=->，m >m <-由韦达定理得：12284m y y m -+=+，122124y y m =+ 由题意得：直线11:(2)2y MB y x x =--，直线22:(2)2y NA y x x =++ 所以()()12212(2)2(2)y x x y x x +-=-+即()()12112212121262262x my y y my y y my y y y my y +--=+++ 整理得()()121221622226x y y my y y y -=++， 即()()121221622326x y y y y y y -=-+++⎡⎤⎣⎦ 即()()12126262x y y y y -=-若213y y =，则1m =±，此时2161920m ∆=-<， 所以12620y y -≠ 所以1x = 【点睛】（1）待定系数法是求二次曲线的标准方程的常用方法；（2）“设而不求”是一种在解析几何中常见的解题方法，可以解决直线与二次曲线相交的问题.23．（1）2211612x y +=；（2）证明见解析.【分析】（1）由已知建立方程组可求得曲线C 的方程；（2）令8x =，则()8,6R k ，联立整理得()()222243161630k x k x k +-+-=，设()()1122,,,P x y Q x y ，()2212122216316,4343k k x x x x k k -+==++，表示12k k +，3k ，可求得定值． 【详解】解：（1）由已知得491861m n m n +=⎧⎨+=⎩，解得116112m n ⎧=⎪⎪⎨⎪=⎪⎩，所以曲线C 的方程为2211612x y +=；（2）令8x =，则()8,6R k ，联立()22116122x y y k x ⎧+=⎪⎨⎪=-⎩，整理得()()222243161630kx k x k +-+-=，设()()1122,,,P x y Q x y ，则()2212122216316,4343k k x x x x k k -+==++， ∴12121212121233113232222y y y y k k x x x x x x ⎛⎫--+=+=+-+ ⎪------⎝⎭， ()()221222121222164443232321241633244343k x x k k k k x x x x k k k k -+-+=-⨯=-⨯=--++--+++， 又3631822k k k -==--， ∴1232k k k +=，∴λ等于定值2，得证.【点睛】关键点点睛：本题考查直线与椭圆的综合问题，关键在于由直线的方程与椭圆的方程联立后，由根与系数的关系表示直线的斜率，求得定值．24．（1）22182x y +=；（2）20x y +=．【分析】（1）由离心率，点的坐标代入椭圆方程及222a b c =+列方程组解得,,a b c 得椭圆方程； （2）已知条件说明直线AO 为线段PQ 的垂直平分线，直线OA 方程为12y x =，这样可设直线PQ 方程为2y x m =-+，代入椭圆方程，应用韦达定理得12x x +，12,x x 即为,P Q的横坐标，求出中点横坐标1202x x x +=，由直线PA 得中点纵坐标0y ，中点坐标代入直线AO 方程可得参数m ，即直线PQ 方程．【详解】（1）依题意，222224112a b a b c c a⎧+=⎪⎪⎪=+⎨⎪⎪=⎪⎩，，解得2282a b ⎧=⎨=⎩，，．故椭圆C 的方程为22182x y +=；（2）∵||||,||||OP OQ AP AQ ==，∴直线AO 为线段PQ 的垂直平分线，则直线OA 的方程为12y x =，设直线PQ 的方程为2y x m =-+， 由221822x y y x m ⎧+=⎪⎨⎪=-+⎩，得：221716480x mx m -+-=， ()22(16)417480m m =-⨯->，解得m <()()1122,,,P x y Q x y ，由韦达定理得121617mx x +=，设PQ 的中点为()00,H x y ， 所以120008,221717x x m m x y x m +===-+=；所以8,1717m m H ⎛⎫⎪⎝⎭． 又8,1717m m H ⎛⎫⎪⎝⎭在直线OA 上，代入得1817217m m =⋅，解得0m =，综上所述，直线PQ 的方程为20x y +=． 【点睛】关键点点睛：本题考查由离心率和一点坐标求椭圆方程，考查直线与椭圆相交问题．在直线与椭圆相交问题时，解题关键是由平面几何知识由条件||||,||||OP OQ AP AQ ==得直线AO 为线段PQ 的垂直平分线，这样用设而不求思想可求得直线PQ 方程．即求出AO 方程，由垂直设出直线PQ 方程，代入椭圆方程应用韦达定理求得PQ 中点坐标，再代入直线AO 方程可得参数值．25．（1）22143x y +=；（2）1x y =±+.【分析】（1）设椭圆Γ的标准方程为22221x y a b+=，连接AF ，由AFB AFC ≌，得到ABE FCE △≌△，再利用椭圆定义求解.（2）设直线l 的方程为：1x my =+,联立221143x my x y =+⎧⎪⎨+=⎪⎩，结合韦达定理得到12y y -,然后由PNM △的面积为7求解. 【详解】 （1）如图所示：。

相关主题
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高中数学学习材料金戈铁骑整理制作圆锥曲线与方程综合题专练1．(2015·湖南文，20)已知抛物线C 1：x 2＝4y 的焦点F 也是椭圆C 2：y 2a 2＋x 2b 2＝1(a >b >0)的一个焦点，C 1与C 2的公共弦的长为2 6.过点F 的直线l 与C 1相交于A ，B 两点，与C 2相交于C ，D 两点，且A C →与B D →同向．(1)求C 2的方程；(2)若|AC |＝|BD |，求直线l 的斜率．[解析] (1)由C 1：x 2＝4y 知其焦点F 的坐标为(0,1)，因为F 也是椭圆C 2的一个焦点，所以a 2－b 2＝1 ①；又C 1与C 2的公共弦长为26，C 1与C 2都关于y 轴对称，且C 1的方程为：x 2＝4y ，由此易知C 1与C 2的公共点的坐标为(±6，32)， ∴94a 2＋6b 2＝1②， 联立①②得a 2＝9，b 2＝8，故C 2的方程为y 29＋x 28＝1. (2)如图，设A (x 1，y 1)，B (x 2，y 2)，C (x 3，y 3)，D (x 4，y 4)，因AC →与BD →同向，且|AC |＝|BD |，所以AC →＝BD →，从而x 3－x 1＝x 4－x 2，即x 3－x 4＝x 1－x 2，于是(x 3＋x 4)2－4x 3x 4＝(x 1＋x 2)2－4x 1x 2 ③设直线l 的斜率为k ，则l 的方程为y ＝kx ＋1，由⎩⎪⎨⎪⎧y ＝kx ＋1，x 2＝4y 得x 2－4kx －4＝0， 由x 1，x 2是这个方程的两根，∴x 1＋x 2＝4k ，x 1x 2＝－4 ④由⎩⎪⎨⎪⎧y ＝kx ＋1，x 28＋y 29＝1，得(9＋8k 2)x 2＋16kx －64＝0，而x 3，x 4是这个方程的两根，x 3＋x 4＝－16k 9＋8k 2，x 3x 4＝－649＋8k 2⑤ 将④、⑤代入③，得16(k 2＋1)＝162k 2(9＋8k 2)2＋4×649＋8k 2. 即16(k 2＋1)＝162×9(k 2＋1)(9＋8k 2)2， 所以(9＋8k 2)2＝16×9，解得k ＝±64， 即直线l 的斜率为±64. 2．(2015·安徽文，20)设椭圆E 的方程为x 2a 2＋y 2b2＝1(a >b >0)，点O 为坐标原点，点A 的坐标为(a,0)，点B 的坐标为(0，b )，点M 在线段AB 上，满足|BM |＝2|MA |，直线OM 的斜率为510. (1)求E 的离心率e ；(2)设点C 的坐标为(0，－b )，N 为线段AC 的中点，证明：MN ⊥AB .[解析] (1)∵|BM |＝2|MA |且A (a,0)，B (0，b )，∴M (23a ，13b )．又∵OM 的斜率为510， ∴13b 23a ＝510⇒b 2a 2＝15⇒a 2－c 2a 2＝15 ⇒c 2a 2＝45⇒e ＝255.(2)由题意可知N 点的坐标为(a 2，－b 2)， ∴k MN ＝13b ＋12b 23a －a 2＝5b 6a 6＝5b a ，k AB ＝b －a ， ∴k MN ·k AB ＝－5b 2a 2＝－1.∴MN ⊥AB .3．(2015·广东文，20)已知过原点的动直线l 与圆C 1：x 2＋y 2－6x ＋5＝0相交于不同的两点A ，B .(1)求圆C 1的圆心坐标；(2)求线段AB 的中点M 的轨迹C 的方程；(3)是否存在实数k ，使得直线L ：y ＝k (x －4)与曲线C 只有一个交点？若存在，求出k 的取值范围；若不存在，说明理由．[解析] (1)圆C 1：x 2＋y 2－6x ＋5＝0化为(x －3)2＋y 2＝4，所以圆C 1的圆心坐标为(3,0)．(2)设线段AB 的中点M (x 0，y 0)，由圆的性质可得C 1M 垂直于直线l .设直线l 的方程为y ＝mx (易知直线l 的斜率存在)，所以kC 1M ·m ＝－1，y 0＝mx 0，所以y 0x 0－3·y 0x 0＝－1，所以x 20－3x 0＋y 20＝0，即⎝⎛⎭⎫x 0－322＋y 20＝94. 因为动直线l 与圆C 1相交，所以|3m |m 2＋1＜2，所以m 2＜45， 所以y 20＝m 2x 20＜45x 20，所以3x 0－x 20＜45x 20，解得x 0＞53或x 0＜0，又因为0＜x 0≤3，所以53＜x 0≤3.所以M (x 0，y 0)满足⎝⎛⎭⎫x 0－322＋y 20＝94⎝⎛⎭⎫53＜x 0≤3， 即M 的轨迹C 的方程为⎝⎛⎭⎫x －322＋y 2＝94⎝⎛⎭⎫53＜x ≤3. (3)由题意知直线L 表示过定点T (4,0)，斜率为k 的直线． 结合图形，⎝⎛⎭⎫x 0－322＋y 20＝94⎝⎛⎭⎫53＜x 0≤3表示的是一段关于x 轴对称，起点为⎝⎛⎭⎫53，－253按逆时针方向运动到⎝⎛⎭⎫53，253的圆弧．根据对称性，只需讨论在x 轴下方的圆弧．设P ⎝⎛⎭⎫53，－253，则k PT ＝2534－53＝257，而当直线L 与轨迹C 相切时，|3k 2－4k |k 2＋1＝32，解得k ＝±34.在这里暂取k ＝34，因为257＜34，所以k PT ＜k .可得对于x 轴下方的圆弧，当0≤k ≤257或k ＝34时，直线L 与x 轴下方的圆弧有且只有一个交点，根据对称性可知－257≤k ≤257或k ＝±43. 综上所述：当－257≤k ≤257或k ＝±43时，直线L ：y ＝k (x －4)与曲线C 只有一交点． 4．(2015·陕西文，20)如图，椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)经过点A (0，－1)，且离心率为22.(1)求椭圆E 的方程；(2)经过点(1,1)，且斜率为k 的直线与椭圆E 交于不同的两点P ，Q (均异于点A )，证明：直线AP 与AQ 的斜率之和为2.[解析] (1)由题意知c a ＝22，b ＝1，综合a 2＝b 2＋c 2，解得a ＝2，所以，椭圆的方程为x 22＋y 2＝1. (2)由题设知，直线PQ 的方程为y ＝k (x －1)＋1(k ≠2)，代入x 22＋y 2＝1，得 (1＋2k 2)x 2－4k (k －1)x ＋2k (k －2)＝0，由已知Δ＞0，设P (x 1，y 1)，Q (x 2，y 2)，x 1x 2≠0，则x 1＋x 2＝4k (k －1)1＋2k 2，x 1x 2＝2k (k －2)1＋2k 2， 从而直线AP 与AQ 的斜率之和k AP ＋k AQ ＝y 1＋1x 1＋y 2＋1x 2 ＝kx 1＋2－k x 1＋kx 2＋2－k x 2＝2k ＋(2－k )(1x 1＋1x 2) ＝2k ＋(2－k )x 1＋x 2x 1x 2＝2k ＋(2－k )4k (k －1)2k (k －2)＝2k －2(k －1)＝2.5．(2015·天津文，19)已知椭圆x 2a 2＋y 2b2＝1(a >b >0)的上顶点为B ，左焦点为F ，离心率为55. (1)求直线BF 的斜率；(2)设直线BF 与椭圆交于点P (P 异于点B )，过点B 且垂直于BP 的直线与椭圆交于点Q (Q 异于点B )，直线PQ 与y 轴交于点M ，|PM |＝λ|MQ |.(i)求λ的值；(ii)若|PM |sin ∠BQP ＝759，求椭圆的方程． [解析] (1)F (－c,0)，由已知离心率c a ＝55及a 2＝b 2＋c 2，可得a ＝5c ，b ＝2c ，又因为B (0，b )，F (－c,0)故直线BF 的斜率k ＝b －00－(－c )＝b c＝2. (2)设点P (x P ，y P )，Q (x Q ，y Q )，M (x M ，y M )．(i)由(1)可得椭圆方程为x 25c 2＋y 24c2＝1， 直线BF 的方程为y ＝2x ＋2c ，两方程联立消去y ，得3x 2＋5cx ＝0，解得x P ＝－5c 3. 因为BQ ⊥BP ，所以直线BQ 的方程为y ＝－12x ＋2c ， 与椭圆方程联立，消去y ，得21x 2－40cx ＝0，解得x Q ＝40c 21. 又因为λ＝|PM ||MQ |，及x M ＝0， 得λ＝|x M －x P ||x Q －x M |＝|x P ||x Q |＝78. (ii)由(i)得|PM ||MQ |＝78， 所以|PM ||PM |＋|MQ |＝77＋8＝715， 即|PQ |＝157|PM |， 又因为|PM |sin ∠BQP ＝759， 所以|BP |＝|PQ |sin ∠BQP ＝157|PM |sin ∠BQP ＝553.又因为y P ＝2x P ＋2c ＝－43c ， 所以|BP |＝⎝⎛⎭⎫0＋5c 32＋⎝⎛⎭⎫2c ＋4c 32＝553c ， 因此553c ＝553，c ＝1， 所以椭圆方程为x 25＋y 24＝1. 6．(2015·新课标Ⅱ卷文，20)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，点(2，2)在C 上．(1)求C 的方程；(2)直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M .证明：直线OM 的斜率与直线l 的斜率的乘积为定值．[解析] (1)由题意有a 2－b 2a ＝22，4a 2＋2b2＝1，解得a 2＝8，b 2＝4，所以椭圆C 的方程为x 28＋y 24＝1. (2)设直线l ：y ＝kx ＋b (k ≠0，b ≠0)，A (x 1，y 1)，B (x 2，y 2)，M (x M ，y M )，把y ＝kx ＋b 代入x 28＋y 24＝1， 得(2k 2＋1)x 2＋4kbx ＋2b 2－8＝0.故x M ＝x 1＋x 22＝－2kb 2k 2＋1，y M ＝kx M ＋b ＝b 2k 2＋1，于是直线OM 的斜率k OM ＝y M x M ＝－12k ，即k OM ·k ＝－12，所以直线OM 的斜率与直线l 的斜率乘积为定值．。

相关文档
最新文档