高一数学人教版A版必修二练习4.2.2 圆与圆的位置关系 Word版含解析
【成才之路】高中数学人教A版必修2练习:4.2.2圆与圆的位置关系(含答案解析)

第四章 4.2 4.2.2一、选择题1.圆x2+y2=1和圆x2+y2-6y+5=0的位置关系是导学号92181004()A.外切B.内切C.外离D.内含[答案] A[解析]圆x2+y2=1的圆心C1(0,0),半径r1=1,圆x2+y2-6y+5=0的圆心C2(0,3),半径r2=2,∴两圆心的距离|C1C2|=-2+-2=3,∴|C1C2|=r1+r2=3,故两圆外切.2.圆x2+y2-2x-5=0和圆x2+y2+2x-4y-4=0的交点为A、B,则线段AB的垂直平分线方程为导学号92181005()A.x+y-1=0 B.2x-y+1=0C.x-2y+1=0 D.x-y+1=0[答案] A[解析]直线AB的方程为:4x-4y+1=0,因此线段AB的垂直平分线斜率为-1,过圆心(1,0),方程为y=-(x-1),故选D.3.已知圆C1:(x+1)2+(y-3)2=25,圆C2与圆C1关于点(2,1)对称,则圆C2的方程是导学号92181006()A.(x-3)2+(y-5)2=25B.(x-5)2+(y+1)2=25C.(x-1)2+(y-4)2=25D.(x-3)2+(y+2)2=25[答案] B[解析]设⊙C2上任一点P(x,y),它关于(2,1)的对称点(4-x,2-y)在⊙C1上,∴(x-5)2+(y+1)2=25.4.若圆(x-a)2+(y-b)2=b2+1始终平分圆(x+1)2+(y+1)2=4的周长,则a、b应满足的关系式是导学号92181007()A.a2-2a-2b-3=0B.a2+2a+2b+5=0C.a2+2b2+2a+2b+1=0D.3a2+2b2+2a+2b+1=0[答案] B[解析]利用公共弦始终经过圆(x+1)2+(y+1)2=4的圆心即可求得.两圆的公共弦所在直线方程为:(2a+2)x+(2b+2)y-a2-1=0,它过圆心(-1,-1),代入得a2+2a+2b+5=0.5.两圆x2+y2=16与(x-4)2+(y+3)2=r2(r>0)在交点处的切线互相垂直,则r=导学号92181008()A.5 B.4C.3 D.2 2[答案] C[解析]设一个交点P(x0,y0),则x20+y20=16,(x0-4)2+(y0+3)2=r2,∴r2=41-8x0+6y0,∵两切线互相垂直,∴y0x0·y0+3x0-4=-1,∴3y0-4x0=-16.∴r2=41+2(3y0-4x0)=9,∴r=3.6.半径长为6的圆与y轴相切,且与圆(x-3)2+y2=1内切,则此圆的方程为导学号92181009()A.(x-6)2+(y-4)2=6B.(x-6)2+(y±4)2=6C.(x-6)2+(y-4)2=36D.(x-6)2+(y±4)2=36[答案] D[解析]半径长为6的圆与x轴相切,设圆心坐标为(a,b),则a=6,再由b2+32=5可以解得b=±4,故所求圆的方程为(x-6)2+(y±4)2=36.二、填空题7.若点A(a,b)在圆x2+y2=4上,则圆(x-a)2+y2=1与圆x2+(y-b)2=1的位置关系是________.导学号92181010[答案]外切[解析]∵点A(a,b)在圆x2+y2=4上,∴a2+b2=4.又圆x2+(y-b)2=1的圆心C1(0,b),半径r1=1,圆(x -a)2+y 2=1的圆心C 2(a,0),半径r 2=1,则d =|C 1C 2|=a 2+b 2=4=2,∴d =r 1+r 2.∴两圆外切.8.与直线x +y -2=0和圆x 2+y 2-12x -12y +54=0都相切的半径最小的圆的标准方程是________.导学号 92181011[答案] (x -2)2+(y -2)2=2[解析] 已知圆的标准方程为(x -6)2+(y -6)2=18,则过圆心(6,6)且与直线x +y -2=0垂直的方程为x -y =0.方程x -y =0分别与直线x +y -2=0和已知圆联立得交点坐标分别为(1,1)和(3,3)或(-3,-3).由题意知所求圆在已知直线和已知圆之间,故所求圆的圆心为(2,2),半径为2,即圆的标准方程为(x -2)2+(y -2)2=2.三、解答题9.求以圆C 1:x 2+y 2-12x -2y -13=0和圆C 2:x 2+y 2+12x +16y -25=0的公共弦为直径的圆C 的方程.导学号 92181012[解析] 解法一:联立两圆方程⎩⎪⎨⎪⎧x 2+y 2-12x -2y -13=0x 2+y 2+12x +16y -25=0, 相减得公共弦所在直线方程为4x +3y -2=0.再由⎩⎪⎨⎪⎧4x +3y -2=0x 2+y 2-12x -2y -13=0, 联立得两圆交点坐标(-1,2)、(5,-6).∵所求圆以公共弦为直径,∴圆心C 是公共弦的中点(2,-2),半径为 12+2+-6-2=5.∴圆C 的方程为(x -2)2+(y +2)2=25.解法二:由解法一可知公共弦所在直线方程为4x +3y -2=0.设所求圆的方程为x 2+y 2-12x -2y -13+λ(x 2+y 2+12x +16y -25)=0(λ为参数).可求得圆心C(-12λ-12+,-16λ-2+). ∵圆心C 在公共弦所在直线上,∴4·--++3·--+-2=0,解得λ=12.∴圆C的方程为x2+y2-4x+4y-17=0.10.判断下列两圆的位置关系.导学号92181013(1)C1:x2+y2-2x-3=0,C2:x2+y2-4x+2y+3=0;(2)C1:x2+y2-2y=0,C2:x2+y2-23x-6=0;(3)C1:x2+y2-4x-6y+9=0,C2:x2+y2+12x+6y-19=0;(4)C1:x2+y2+2x-2y-2=0,C2:x2+y2-4x-6y-3=0. [解析](1)∵C1:(x-1)2+y2=4,C2:(x-2)2+(y+1)2=2.∴圆C1的圆心坐标为(1,0),半径r1=2,圆C2的圆心坐标为(2,-1),半径r2=2,d=|C1C2|=-2+-2= 2.∵r1+r2=2+2,r1-r2=2-2,∴r1-r2<d<r1+r2,两圆相交.(2)∵C1:x2+(y-1)2=1,C2:(x-3)2+y2=9,∴圆C1的圆心坐标为(0,1),r1=1,圆C2的圆心坐标为(3,0),r2=3,d=|C1C2|=3+1=2.∵r2-r1=2,∴d=r2-r1,两圆内切.(3)∵C1:(x-2)2+(y-3)2=4,C2:(x+6)2+(y+3)2=64.∴圆C1的圆心坐标为(2,3),半径r1=2,圆C2的圆心坐标为(-6,-3),半径r2=8,∴|C1C2|=+2++2=10=r1+r2,∴两圆外切.(4)C1:(x+1)2+(y-1)2=4,C2:(x-2)2+(y-3)2=16,∴圆C1的圆心坐标为(-1,1),半径r1=2,圆C2的圆心坐标为(2,3),半径r2=4,∴|C1C2|=2+12+3-12=13.∵|r1-r2|<|C1C2|<r1+r2,∴两圆相交.一、选择题1.已知M 是圆C :(x -1)2+y 2=1上的点,N 是圆C′:(x -4)2+(y -4)2=82上的点,则|MN|的最小值为导学号 92181014( ) A .4B .42-1C .22-2D .2 [答案] D[解析] ∵|CC′|=5<R -r =7,∴圆C 内含于圆C′,则|MN|的最小值为R -|CC′|-r =2.2.过圆x 2+y 2=4外一点M(4,-1)引圆的两条切线,则经过两切点的直线方程为导学号 92181015( )A .4x -y -4=0B .4x +y -4=0C .4x +y +4=0D .4x -y +4=0 [答案] A[解析] 以线段OM 为直径的圆的方程为x 2+y 2-4x +y =0,经过两切点的直线就是两圆的公共弦所在的直线,将两圆的方程相减得4x -y -4=0,这就是经过两切点的直线方程.3.已知两圆相交于两点A(1,3),B(m ,-1),两圆圆心都在直线x -y +c =0上,则m +c 的值是导学号 92181016( )A .-1B .2C .3D .0 [答案] C[解析] 两点A ,B 关于直线x -y +c =0对称,k AB =-4m -1=-1. ∴m =5,线段AB 的中点(3,1)在直线x -y +c =0上,∴c =-2,∴m +c =3.4.(2016·山东文)已知圆M :x 2+y 2-2ay =0(a>0)截直线x +y =0所得线段的长度是22,则圆M 与圆N :(x -1)2+(y -1)2=1的位置关系是导学号 92181017( )A .内切B .相交C .外切D .相离 [答案] B[解析] 由题知圆M :x 2+(y -a)2=a 2,圆心(0,a)到直线x +y =0的距离d =a 2,所以2a 2-a 22=22,解得a =2.圆M 、圆N 的圆心距|MN|=2,两圆半径之差为1、半径之和为3,故两圆相交.二、填空题5.圆x 2+y 2+6x -7=0和圆x 2+y 2+6y -27=0的位置关系是________.导学号 92181018[答案] 相交[解析] 圆x 2+y 2+6x -7=0的圆心为O 1(-3,0),半径r 1=4,圆x 2+y 2+6y -27=0的圆心为O 2(0,-3),半径为r 2=6,∴|O 1O 2|=-3-2++2=32,∴r 2-r 1<|O 1O 2|<r 1+r 2,故两圆相交.6.若圆x 2+y 2=4与圆x 2+y 2+2ay -6=0(a >0)的公共弦长为23,则a =________.导学号 92181019[答案] 1[解析] 两个圆的方程作差,可以得到公共弦的直线方程为y =1a ,圆心(0,0)到直线y =1a的距离d =|1a |,于是由(232)2+|1a|2=22,解得a =1. 三、解答题7.已知圆A :x 2+y 2+2x +2y -2=0,若圆B 平分圆A 的周长,且圆B 的圆心在直线l :y =2x 上,求满足上述条件的半径最小的圆B 的方程.导学号 92181020[解析] 解法一:考虑到圆B 的圆心在直线l 上移动,可先写出动圆B 的方程,再设法建立圆B 的半径r 的目标函数.设圆B 的半径为r.∵圆B 的圆心在直线l :y =2x 上,∴圆B 的圆心可设为(t,2t),则圆B 的方程是(x -t)2+(y -2t)2=r 2,即x 2+y 2-2tx -4ty +5t 2-r 2=0.①∵圆A 的方程是x 2+y 2+2x +2y -2=0,②∴②-①,得两圆的公共弦方程为(2+2t)x +(2+4t)y -5t 2+r 2-2=0.③∵圆B 平分圆A 的周长,∴圆A 的圆心(-1,-1)必在公共弦上,于是,将x =-1,y =-1代入方程③并整理,得r 2=5t 2+6t +6=5(t +35)2+215≥215. ∴当t =-35时,r min =215. 此时,圆B 的方程是(x +35)2+(y +65)2=215. 解法二:也可以从图形的几何性质来考虑,用综合法来解.如图,设圆A ,圆B 的圆心分别为A ,B ,则A(-1,-1),B 在直线l :y =2x 上,连接AB ,过A 作MN ⊥AB ,且MN 交圆于M ,N 两点.∴MN 为圆A 的直径. ∵圆B 平分圆A ,∴只需圆B 经过M ,N 两点.∵圆A 的半径是2,设圆B 的半径为r ,∴r =|MB|=|AB|2+|AM|2 =|AB|2+4.欲求r 的最小值,只需求|AB|的最小值.∵A 是定点,B 是l 上的动点,∴当AB ⊥l ,即MN ∥l 时,|AB|最小.于是,可求得直线AB 方程为y +1=-12(x +1), 即y =-12x -32,与直线l :y =2x 联立可求得B(-35,-65),r min =215. ∴圆B 的方程是(x +35)2+(y +65)2=215. 8.已知圆M :x 2+y 2-2mx -2ny +m 2-1=0与圆N :x 2+y 2+2x +2y -2=0交于A 、B 两点,且这两点平分圆N 的圆周,求圆心M 的轨迹方程.导学号 92181021[解析] 两圆方程相减,得公共弦AB 所在的直线方程为2(m +1)x +2(n +1)y -m 2-1=0,由于A 、B 两点平分圆N 的圆周,所以A 、B 为圆N 直径的两个端点,即直线AB 过圆N 的圆心N ,而N(-1,-1),所以-2(m +1)-2(n +1)-m 2-1=0,即m 2+2m +2n +5=0,即(m +1)2=-2(n +2)(n≤-2),由于圆M 的圆心M(m ,n),从而可知圆心M 的轨迹方程为(x +1)2=-2(y +2)(y≤-2).。
高一数学人教A版必修2课后训练:4.2.2圆与圆的位置关系 Word版含解析

4.2.2 圆与圆的位置关系练习1.圆C 1:x 2+y 2=1与圆C 2:(x -3)2+(y -4)2=16的位置关系是( )A .外离B .相交C .内切D .外切2.圆C 1:x 2+y 2+4x +8y -5=0与圆C 2:x 2+y 2+4x +4y -1=0的位置关系为( )A .相交B .外切C .内切D .外离3.圆C 1:(x -1)2+(y -2)2=4与圆C 2:(x +2)2+(y +2)2=1的位置关系是( )A .外离B .外切C .相交D .内切4.若圆(x -a )2+(y -a )2=4上,总存在不同的两点到原点的距离等于1,则实数a 的取值范围是( )A .22⎛ ⎝⎭B . ⎛ ⎝⎭C . ,22⎛-- ⎝⎭∪22⎛⎫ ⎪ ⎪⎝⎭D . 22⎛⎫- ⎪ ⎪⎝⎭5.已知A ={(x ,y )|x 2+y 2=1},B ={(x ,y )|(x -5)2+(y -5)2=4},则A ∩B 等于( )A .B .{(0,0)}C .{(5,5)}D .{(0,0),(5,5)}6.圆C 1:x 2+y 2-12x -2y -13=0和圆C 2:x 2+y 2+12x +16y -25=0的公共弦所在的直线方程是______.7.若点A (a ,b )在圆x 2+y 2=4上,则圆(x -a )2+y 2=1与圆x 2+(y -b )2=1的位置关系是__________.8.与直线x +y -2=0和圆x 2+y 2-12x -12y +54=0都相切的半径最小的圆的标准方程是__________.9.求和圆(x -2)2+(y +1)2=4相切于点(4,-1)且半径为1的圆的方程.10.一动圆与圆C 1:x 2+y 2+6x +8=0外切,与圆C 2:x 2+y 2-6x +8=0内切,求动圆圆心的轨迹方程.参考答案1.答案:D2.答案:C3.答案:A4.答案:C5.答案:A6.答案:4x+3y-2=07.答案:外切8.答案:(x-2)2+(y-2)2=29.解:设所求圆的圆心为P(a,b),则1.①(1)1+2=3.②由①②,解得a=5,b=-1,所以所求圆的方程为(x-5)2+(y+1)2=1.(2)2-1=1.③由①③,解得a=3,b=-1,所以所求圆的方程为(x-3)2+(y+1)2=1.综上,可知所求圆的方程为(x-5)2+(y+1)2=1或(x-3)2+(y+1)2=1.10. 解:圆C1:(x+3)2+y2=1,所以圆心(-3,0),半径r1=1;圆C2:(x-3)2+y2=1,所以圆心(3,0),半径r2=1.设动圆圆心为(x,y),半径为r,由题意得=r+1r-1,=2,化简并整理,得8x2-y2=8(x>0).所以,动圆圆心的轨迹方程是8x2-y2=8(x>0).。
人教A版数学必修二第四章第四课时同步练习4.2.2圆与圆的位置关系

§4.2.2圆与圆的位置关系一、填空题:1. 判断下列两个圆的位置关系:2222(1)(3)(2)1(7)(1)36x y x y -++=-+-=与位置关系是_________.2222(2)2232030x y x y x y x y +-+=+--=与3位置关系是_________.2. 若圆22x y m +=与圆2268x y x y ++-110-=相交,实数m 的取值范围是________.3.一个圆经过圆221:890C x y x +--=和圆222:8150C x y y +-+=的两个交点,且圆心在直线210x y --=上,则该圆的方程为_______________________________.4.已知一个圆经过直线240x y ++=与圆222410x y x y ++-+=的两个交点,并且有最小面积,则此圆的方程为__________________________.二、解答题:5. 判断下列两圆的位置关系:2222(1)(2)(2)1(2)(5)16x y x y ++-=-+-=与222226706270x y x x y y ++-=++-=()与6. 求过点(0,6)A 且与圆22:10100C x y x y +++=切于原点的圆的方程.7. 已知圆221:2610C x y x y ++-+=,圆222:42110C x y x y +-+-=,求两圆的公共弦所在的直线方程及公共弦长.8.求过两圆22640x y x ++-=和 226280x y y ++-=的交点,且圆心在直线40x y --=上的圆的方程.参考答案一、填空题:1. 答案:(1)内切,(2)相交.2. 答案:1121m <<.3.答案:22101412033x y x y +---=. 4.答案:221364()()555x y ++-=. 二、解答题:5. 【解】(1)根据题意得,两圆的半径分别为1214r r ==和,两圆的圆心距5.d ==因为 12d r r =+,所以两圆外切.(2)将两圆的方程化为标准方程,得2222(3)16,(3)36x y x y ++=++=. 故两圆的半径分别为1246r r ==和,两圆的圆心距d ==.因为1212||r r d r r -<<+,所以两圆相交.点评:判断两圆的位置关系,不仅仅要判断d 与12r r +的大小,有时还需要判断d 与12r r -的关系.6. 分析:如图,所求圆经过原点和(0,6)A ,且圆心应在已知圆的圆心与原点的连线上.根据这三个条件可确定圆的方程.【解】将圆C 化为标准方程,得22(5)(5)50x y +++=,则圆心为(5,5)C --,半径为0x y -=.设所求圆的方程为222()()x a y b r -+-=.由题意知,(0,0),(0,6)O A 在此圆上,且圆心(,)M a b 在直线0x y -=上,则有222222(0)(0),3,(0)(6),3,0a b r a a b r b a b r ⎧-+-=⎧=⎪⎪-+-=⇒=⎨⎨⎪⎪-==⎩⎩于是所求圆的方程是22(3)(3)18x y -+-=.点评:此题还可以通过弦的中垂线必过圆心这一性质来解题,由题意,圆心必在直线3y =上,又圆心在直线0x y -=,从而圆心坐标为(3,3),r =,所以所求圆的方程为22(3)(3)18x y -+-=.7. 分析:因两圆的交点坐标同时满足两个圆方程,联立方程组,消去2x 项、2y 项,即得两圆的两个交点所在的直线方程,利用勾股定理可求出两圆公共弦长.【解】设两圆交点为11(,)A x y 、22(,)B x y ,则A B 、两点坐标满足方程组 22222610,(1)42110,(2)x y x y x y x y ⎧++-+=⎪⎨+-+-=⎪⎩,(1)(2)-得3460x y -+=. 因为,A B 、两点坐标都满足此方程,所以,3460x y -+=即为两圆公共弦所在的直线方程.易知圆1C 的圆心(1,3)-,半径3r =.又1C到直线的距离为95d ==.所以,245AB ===.即两圆的公共弦长为245. 点评:本题较为复杂,要讨论的情况比较多,解题过程中要 注重分析.8.分析:所求圆圆心是两已知圆连心线和已知直线的交点,再利用弦心距、弦长、半径之间的关系求圆半径【解】(法一)可求得两圆连心线所在直线的方程为30x y++=.由40,30,x yx y--=⎧⎨++=⎩得圆心17(,)22-.利用弦心距、弦长、半径之间的关系可求得公共弦长d=所以,圆半径22217|()4|89()22dr⎛⎫--+⎪=+=.所以,所求圆方程为221789()()222x y-++=,即227320x y x y+-+-=(法二)设所求圆的方程为222264(628)0x y x x y yλ++-+++-=即2266428111x y x yλλλλλ++++-=+++.故此圆的圆心为33(,)11λλλ--++,它在直线40x y--=上,所以334011λλλ--+-=++,所以7λ=-.所以所求圆方程为227320x y x y+-+-=点评:“解法二”中设出的经过两已知圆交点的圆方程叫做经过两已知圆的圆系方程.。
高一数学人教A版必修2练习4.2.2 圆与圆的位置关系 Word版含解析
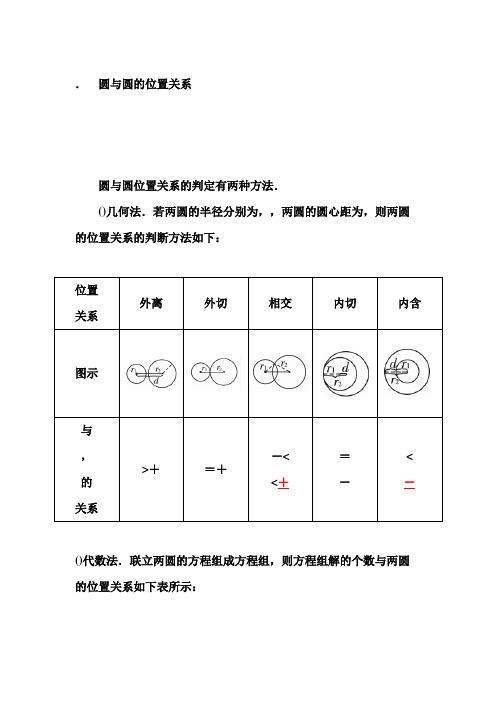
.圆与圆的位置关系
圆与圆位置关系的判定有两种方法.
()几何法.若两圆的半径分别为,,两圆的圆心距为,则两圆的位置关系的判断方法如下:
()代数法.联立两圆的方程组成方程组,则方程组解的个数与两圆的位置关系如下表所示:
两圆的位置关系有相切、相交、相离.
两圆的半径分别为,,圆心距设为.
当>+时,两圆外离;
当=+时,两圆外切;
当-<<+时,两圆相交;
当=-时,两圆内切;
当<-时,两圆内含.
如何根据圆的方程,判断它们之间的位置关系?
答案:联立圆的方程组,当交点个数为时,则外离或内含;
当交点个数为时,则外切或内切;当交点个数为时,则相交.
►思考应用
两圆的公切线有几条?
解析:当两圆内切时有一条公切线;当两圆外切时,有三条公切线:两条外公切线、一条内公切线;当两圆相交时,有两条外公切线;当两圆相离时有四条公切线:两条外公切线、两条内公切线;当两圆内含时,没有公切线.。
人教版数学必修二4.2.2圆与圆的位置关系

课堂小结
1.本节课你收获了什么? (1)知识方面:
判断圆与圆的位置关系的两种方法,以及这两种方法的优劣。 求圆与圆相交弦所在直线方程的方法。 求圆与圆相交弦的弦长的方法。
(2)数学思想方面:
数形结合的思想,等价转化的思想,类比思想。
复习回顾 构建新知 例题讲授 总结反思 变式探究 跟踪训练 课堂小结 拓展训练
|r1-r2|< c1c2 < |r1+r2| c1c2 = |r1-r2| c1c2 < |r1-r2|
复习回顾 构建新知 例题讲授 总结反思 变式探究 跟踪训练 课堂小结 拓展训练
例题讲解
例1.已知圆C1 : x2+y2+2x+8y-8=0和圆C2 : x2+y2-4x-4y-2=0,试判断圆C1与圆C2的 位置关系.
普通高中课程准实验教科书
数 学2 必修
A 人民教育出版社 版
4.2.2 圆与圆的位置关系
复习回顾
1. 平面中直线和圆的位置关系的判断有哪两种方法?
(1)几何法:
r o
d l
r o
dl
r
od
l
(1)直线l 和⊙O相离 d>r
(2)直线l 和⊙O相切
d=r
(3)直线l 和⊙O相交
d<r
复习回顾 构建新知 例题讲授 总结反思 变式探究 跟踪训练 课堂小结 拓展训练
复习回顾 构建新知 例题讲授 总结反思 变式探究 跟踪训练 课堂小结 拓展训练
例题讲解
例1.已知圆C1 : x2+y2+2x+8y-8=0和圆C2 : x2+y2-4x-4y-2=0,试判断圆C1与圆C2的 位置关系.
高一数学人教A版必修2:4-2-2 圆与圆的位置关系

圆系方程表示的是满足某些条件的圆的集合,在处理有 关问题时,利用圆系可使问题得到简化.同心圆系中半径变 化,可得圆心相同的一系列的圆;在方程(x-a)2+(y-b)2=r2 中,a,b变化,就得到半径相等的一系列的圆;而过直线与 圆的交点的圆系方程是常用的.在过两圆交点的圆系方程x2+ y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1,λ∈ R)中,要注意参数λ的取值以及此方程不能包括第二个圆,但 可以包括第一个圆(λ=0).
第四章
圆的方程
第四章 圆的方程
第四章
4.2 直线、圆的位置关系
第四章 圆的方程
第四章
4.2.2 圆与圆的位置关系
第四章 圆的方程
课前自主预习 课堂基础巩固 思路方法技巧 课后强化作业 名师辨误做答
第四章
4.2
4.2.2
课前自主预习
第四章
4.2
4.2.2
温故知新 1.圆与圆的位置关系
大于 (1)外离⇔圆心距______两圆半径长之和; 等于 (2)外切⇔圆心距______两圆半径长之和; 大于 (3)相交⇔圆心距_____两圆半径长之差的绝对值小于两圆
第四章
4.2
4.2.2
由①-②得x+2y+1=0. ③ 由③得x=-2y-1,把此式代入①,并整理得y2-1=0, ④ 方程④的判别式Δ=02-4×1×(-1)=4>0, 所以圆C1与圆C2有两个不同的交点,即两圆是相交的位置 关系.
第四章
4.2
4.2.2
规律总结:利用几何法判断两圆的位置关系,直观,容 易理解,但不能求出交点坐标;利用代数法判断两圆的位置 关系,不能准确地判断位置关系(如Δ=0仅能说明两圆只有一 个公共点,但确定不了是内切还是外切;Δ<0仅能说明两圆没 有公共点,但确定不了是外离还是内含,所以必须借助于图 形).
人教版数学高一-必修二(人教A)练习 4.2.2圆与圆的位置关系

4.2.2圆与圆的位置关系一、选择题(本大题共7小题,每小题5分,共35分)1.圆x2+y2=1和x2+y2-6y+5=0的位置关系为()A.外切B.内切C.外离D.内含2.两圆x2+y2-6x+16y-48=0与x2+y2+4x-8y-44=0的公切线条数为()A.4条B.3条C.2条D.1条3. 已知圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则AB的垂直平分线的方程为()A.x+y+3=0 B.2x-y-5=0C.3x-y-9=0 D.4x-3y+7=04.已知圆C1:x2+y2-m=0,圆C2:x2+y2+6x-8y-11=0.若圆C1与圆C2有公共点,则实数m的取值范围是()A.m<1 B.m>121C.1≤m≤121 D.1<m<1215.设r>0,圆(x-1)2+(y+3)2=r2与圆x2+y2=16的位置关系不可能是()A.相切B.相交C.内切和内含D.外切和外离6.半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程是()A.(x-4)2+(y-6)2=6B.(x±4)2+(y-6)2=6C.(x-4)2+(y-6)2=36D.(x±4)2+(y-6)2=367.已知集合M={(x,y)|y=9-x2,y≠0},n={(x,y)|y=x+b},若M∩N≠∅,则实数b的取值范围是()A.[-3 2,3 2] B.[-3,3]C.(-3,3 2] D.[-3 2,3)二、填空题(本大题共4小题,每小题5分,共20分)8.与圆x2+y2=5外切于点P(-1,2),且半径为2 5的圆的方程为________________.9.两圆x2+y2+2x-4y+3=0与x2+y2-4x+2y+3=0上的点的最短距离是________.10.经过两圆x2+y2=9和(x+4)2+(y+3)2=8的交点的直线方程为________________.11.已知⊙O方程为x2+y2=4,定点A(4,0),则过点A且和⊙O相切的动圆圆心的轨迹方程为________________.三、解答题(本大题共2小题,共25分)12.(12分)已知圆C的圆心在直线x-y-4=0上,且圆C过圆C1:x2+y2-4x-3=0和圆C2:x2+y2-4y-3=0的交点,求圆C的方程.13.(13分)已知两圆x2+y2-2x-6y-1=0和x2+y2-10x-12y+m=0.(1)m取何值时两圆外切?(2)m取何值时两圆内切?(3)求当m=45时,两圆的公共弦所在直线的方程和公共弦的长.14.(5分)已知圆C1:x2+y2+4x+1=0和圆C2:x2+y2+2x+2y+1=0,则以圆C1与圆C2的公共弦为直径的圆的方程为________________.15.(15分)已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且|PQ|=|PA|.(1)求实数a,b间满足的等量关系;(2)若以点P为圆心所作的圆P与圆O有公共点,试求半径取最小值时圆P的方程.4.2.2 圆与圆的位置关系1.A [解析] 因为两圆心间的距离d =r 1+r 2=3,所以圆x 2+y 2=1和x 2+y 2-6y +5=0的位置关系为外切.2.C [解析] 设⊙O 1为(x -3)2+(y +8)2=121,O 1(3,-8),r =11,⊙O 2为(x +2)2+(y -4)2=64,O 2(-2,4),R =8,∴|O 1O 2|=(3+2)2+(-8-4)2=13, ∴r -R <|O 1O 2|<R +r , ∴两圆相交. ∴公切线有2条.3.C [解析] x 2+y 2-4x +6y =0可化为()x -22+()y +32=13,圆心为(2,-3);x 2+y 2-6x =0可化为()x -32+y 2=9,圆心为(3,0).因为圆x 2+y 2-4x +6y =0和圆x 2+y 2-6x =0交于A ,B 两点,所以AB 的垂直平分线即为过两圆圆心的直线,即为3x -y -9=0.4.C [解析] 圆C 1的方程可化为x 2+y 2=m ,则圆心C 1(0,0),半径r 1=m ;圆C 2的方程可化为(x +3)2+(y -4)2=36,则圆心C 2(-3,4),半径r 2=6.∵圆C 1与圆C 2有公共点,∴|r 1-r 2|≤|C 1C 2|≤r 1+r 2, 即|m -6|≤(-3-0)2+(4-0)2≤m +6, ∴⎩⎨⎧|m -6|≤5,m +6≥5,解得1≤m ≤121. 5.D [解析] 两圆圆心之间的距离d =10,而r 1+r 2=4+r >4, ∴d <r 1+r 2,∴两圆不可能外切或外离.6.D [解析] 根据圆的半径为6,可排除A ,B ,再通过验证知圆心是(±4,6),半径是6的圆与圆x 2+(y -3)2=1内切.7.C [解析] 由M ∩N ≠∅,知直线y =x +b 与半圆x 2+y 2=9(y >0)相交,所以画图(图略)可知-3<b ≤3 2.8.(x +3)2+(y -6)2=20 [解析] 设所求圆的圆心为O 1(a ,b ),则所求圆的方程为(x -a )2+(y -b )2=20.∵两圆外切于点P ,且两圆的半径分别为5,2 5,∴-1=0+a 3,2=0+b3,∴a =-3,b =6,∴所求圆的方程为(x +3)2+(y -6)2=20.9.2 [解析] 圆x 2+y 2+2x -4y +3=0可化为()x +12+(y -2)2=2,圆心为(-1,2),半径为 2.x 2+y 2-4x +2y +3=0可化为(x -2)2+()y +12=2,圆心为(2,-1), 半径为2.所以两圆圆心距为32,所以两圆上的点的最短距离是 2.10.4x +3y +13=0 [解析] 由两圆的方程相减,得4x +3y +13=0,所以过两圆交点的直线方程为4x +3y +13=0.11.(x -2)2-y 23=1 [解析] 设动圆圆心为P (x ,y ).因为动圆过定点A ,所以|PA |即为动圆半径.当动圆P 与⊙O 外切时,|PO |=|PA |+2.当动圆P 与⊙O 内切时,|PO |=|PA |-2. 综合这两种情况,得||PO |-|PA ||=2,即|x 2+y 2-(x -4)2+y 2|=2,化简可得(x -2)2-y 23=1.12.解:因为圆C 过两圆的交点,所以设圆C 的方程为x 2+y 2-4x -3+λ(x 2+y 2-4y -3)=0,即 (1+λ)(x 2+y 2)-4x -4λy -3λ-3=0,即 x 2+y 2-4x1+λ-4λy 1+λ-3=0,所以圆C 的圆心为⎝⎛⎭⎫21+λ,2λ1+λ. 因为圆C 的圆心在直线x -y -4=0上,所以21+λ-2λ1+λ-4=0,解得λ=-13,故所求圆的方程为x 2+y 2-6x +2y -3=0.13.解:两圆的标准方程分别为(x -1)2+(y -3)2=11, (x -5)2+(y -6)2=61-m ,圆心分别为M (1,3),N (5,6),半径分别为11和61-m . (1)当两圆外切时,(5-1)2+(6-3)2=11+61-m , 解得m =25+10 11.(2)当两圆内切时,因为定圆的半径11小于两圆圆心之间的距离5, 所以61-m -11=5,解得m =25-10 11. (3)两圆的公共弦所在直线的方程为(x 2+y 2-2x -6y -1)-(x 2+y 2-10x -12y +45)=0, 圆心4x +3y -23=0,则公共弦长为2 (11)2-⎝⎛⎭⎪⎫|4+3×3-23|42+322=2 7.14.(x +1)2+(y +1)2=1 [解析] 由两圆的方程相减,得公共弦所在直线的方程即为x -y =0.∵圆C 1:(x +2)2+y 2=3,圆C 2:(x +1)2+(y +1)2=1, 圆心C 1(-2,0),C 2(-1,-1),∴两圆连心线所在直线的方程为y -0-1-0=x +2-1+2,即x +y +2=0.由⎩⎪⎨⎪⎧x -y =0,x +y +2=0,得所求圆的圆心为(-1,-1). 又圆心C 1(-2,0)到公共弦所在直线x -y =0的距离 d =|-2-0|2=2,∴所求圆的半径r =(3)2-(2)2=1,∴所求圆的方程为(x +1)2+(y +1)2=1.15.解:(1)连接OP .∵Q 为切点,∴PQ ⊥OQ ,∴|PQ |2=|OP |2-|OQ |2. 又|PQ |=|PA |,故|PA |2=|PO |2-1,即(a 2+b 2)-1=(a -2)2+(b -1)2.整理得2a +b -3=0. (2)设圆P 的半径为R .∵圆P 与圆O 有公共点,且半径最小,∴|OP |=a 2+b 2=a 2+(-2a +3)2=5a -652+95,故当a =65时,|OP |取得最小值355.此时,b =-2a +3=35,R 取得最小值355-1.所以当半径取最小值时,圆P 的方程为x -652+y -352=35 5-12.。
高一数学人教A版必修2课后导练:4.2.2圆与圆的位置关系含解析

课后导练基础达标1 两圆 x2+y 2+6x-4y+9=0 和 x2+y2-6x+12y-19=0 的地点关系是()A. 外切B. 内切C.订交D. 外离分析:两圆方程配方得(x+3) 2+(y-2) 2=4 和( x-3)2+(y+6) 2=64,则两圆的圆心,分别为O1( -3,2)、 O2( 3, -6),半径 r1=2,r 2=8,则 |O1O2|= 36 64 =10=r 1+r2,∴两圆外切 .答案: A2 两圆 x2+y 2=r2与 (x-3) 2+(y+1) 2=r2(r>0) 外切 ,则 r 的值是()A. 10 10B.5C.5D.10 2分析:两圆的圆心距为9110 ,由 10 =2r,得r=110 .答案: D23 两圆 C1 :x2+y 2+4x-4y+7=0,C2:x2+y2-4x-10y+13=0的公切线的条数是()A.1B.2C.3D.4分析:配方得 (x+2) 2+(y-2) 2=1,(x-2) 2 +(y-5) 2=16,∴ C1(-2,2),C 2(2,5),r1=1,r2=4,则|C1C2|=5=r1 +r2,∴两圆外切,有 3 条公切线 .答案: C4 已知半径为 1 的动圆与圆 (x-5) 2+(y+7) 2=16 相切,则动圆圆心的轨迹方程是()A.(x-5) 2+(y+7) 2 =25B.(x-5) 2+(y+7) 2=17 或(x-5) 2+(y+7) 2=15C.(x-5) 2+(y+7) 2=9D.(x-5) 2+(y+7) 2 =25 或 (x-5) 2+(y+7) 2=9分析:设动圆圆心为(x,y ),半径 r1=1,已知圆的圆心为M( 5, -7),半径为 r2=4.①若两圆相切,则( x5)2( y7)2122+(y+7)2=25.=r+r =5, 即( x-5 )②若两圆内切,则( x5)2( y7) 2=r2-r1=3,即( x-5)2+(y+7) 2=9.答案: D5 两圆 x2+y 2+4x-4y=0;x2+y 2+2x-12=0 订交于 A , B 两点,则直线AB 方程为 ________.分析:两圆方程相减得x-2y+6=0.答案: x-2y+6=06 圆 x2+y 2-2x+10y-24=0与圆 x2+y 2+2x+2y-8=0的交点坐标是 ___________.分析:两圆方程相减得x-2y+4=0, 代入 x2+y 2+2x+2y-8=0消 x 得 y2 -2y=0,∴y0, 或 y2,x 4 x0.答案:( -4, 0)和( 0, 2)7 不论 m 取何实数,圆x2+y2+mx+my-5-m=0恒过两定点,则这两个定点的坐标为_______.分析:圆方程可化为x2+y2 -5+m(x+y-1)=0.由x 2 y 25, 得 x 2, 或 x 1, xy 10, y1 y2.答案:( 2, -1)和( -1, 2)8 点 P 在圆 A :x 2+(y+3) 2 =4 上 ,点 Q 在圆 B : (x-6) 2+y 2=16 上,则 |PQ|的最小值为 _________.分析: A ( 0, -3), B ( 6,0), r a =2,r b =4,∴|AB|= 3 5 >r a +r b , ∴两圆相离,∴|PQ|最小值为 |AB|-r a -r b = 3 5 -6.答案: 3 5-6 综合运用9 圆( x-a ) 2+(y-b) 2=b 2+1 一直均分圆( x+1 )2+(y+1) 2=4 的周长,则 a,b 关系是()A.a 2-2a-2b-3=0B.a 2+2a+2b+5=0C.a 2+ab 2+2a+ab+1=0D.3a 2+ab 2+2a+2b+1=0分析: 设两圆的交点为 A 、B ,由条件知弦 AB 为圆( x+1 )2+(y+1) 2=4 的直径,两圆方程相减得( 2+2a )x+(2+2b)y-a 2-1=0 必过圆心( -1, -1)代入得 a 2+2a+2b+5=0. 答案: B10 已知线段 AB 长为 10,动点 P 到 A 、B 距离的平方和为 122,则动点 P 的轨迹为 ________.分析: 以 AB 所在直线为 x 轴, AB 的中垂线为 y 轴,成立平面直角坐标系,设A ( -5,0),B ( 5, 0), P ( x,y ),则 |AP|2+|BP|2=122. 即( x-5) 2+y 2+(x+5) 2+y 2=122. 化简得 x 2+y 2=36.答案: 以 AB 中点为圆心,以6 为半径的圆11 假如一个圆与圆 A :x 2+y 2-2x=0 相外切,并与直线 x+3y=0 相切于点 M(3 ,-3),求这个圆的方程 .分析: 设所求圆的圆心 B ( a,b ),半径为 r ,则 r=| a3b | (a 3) 2(b3)2 ,又知2直线 BM 与直线 x+ 3 y=0 垂直 .∴b3? (3) =-1 ,即 b= 3a 4 3 .a3 3∴r=| 4a 12 |=2|a-3|.2又 A ( 1, 0), r a(a 1) 2b 2a=1, ∴ =r +r ,即 (a1)2 ( 3a 4 3)2 =1+2|a-3|.当 a≥3时,平方得 a=4,b=0,r=2.当 a<3 时,平方得 a=0,b= 4 3 ,r=6.故所求圆方程为x2+(y+ 4 3 )2=36或(x-4)2+y2=4.拓展研究12 有一种大型商品, A 、B 两地都有销售,且价钱同样,某地居民从两地之一购得商品后,回运的花费是:每单位距离 A 地的运费是 B 地运费的 3 倍,已知A、B 两地距离10 公里,顾客选 A 或 B 地购置这件商品的标准是:包含运费和价钱的总花费较低.求 A、B 两地的售货地区的分界限的曲线形状,并指出曲线上、曲线内、曲线外的居民应怎样选择购货地址.分析:如图,以A、 B 所确立的直线为x 轴, A 、 B 中点 O 为坐标原点,成立直角坐标系,则 A ( -5, 0), B( 5, 0).设某地 P 的坐标为( x,y ),且 P 地居民选择 A 地购置商品廉价并设 A 地的运费为3a 元 /公里,B 地的运费为 a 元 /公里 .P 地到 A 地运费≤P地到 B 地运费,即3a ( x 5) 2y 2 a ( x 5) 2y 2∵a>0,∴ 3 ( x 5) 2y2(x 5)2y2,25)15即( x+2+y2≤( )2.425415为半径的圆是这两地购货的分界限.∴以点 C(, 0)为圆心,44圆 C 内的居民从 A 地购货廉价 ; 圆C 外的居民从 B 地购货廉价 ;圆 C 上的居民从 A 、 B 两地购货的总花费相等,所以,可任意从 A 、 B 两地之一购货.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆与圆的位置关系
【课时目标】.掌握圆与圆的位置关系及判定方法..会利用圆与圆位置关系的判断方法进行圆与圆位置关系的判断..能综合应用圆与圆的位置关系解决其他问题.
圆与圆位置关系的判定有两种方法:
.几何法:若两圆的半径分别为、,两圆的圆心距为,则两圆的位置关系的判断方法如下:
位置
关系
外离外切相交内切内含
图示
与、
的关系=+
-<
<
<
.代数法:通过两圆方程组成方程组的公共解的个数进行判断.一元二次方程
一、选择题
.两圆(+)+(-)=和(-)+(+)=的位置关系是()
.外切.内切.相交.相离
.两圆+-++=与++--=的公切线有()
.条.条.条.条
.圆+-+=和圆+-=交于、两点,则的垂直平分线的方程是()
.++=.--=
.--=.-+=
.圆:(-)+(+)=与圆:(+)+(-)=外切,则的值为()
..-
.或-.不确定
.已知半径为的动圆与圆(-)+(+)=相切,则动圆圆心的轨迹方程是()
.(-)+(+)=
.(-)+(+)=或(-)+(+)=
.(-)+(+)=
.(-)+(+)=或(-)+(+)=
.集合={(,)+≤},={(,)(-)+(-)≤,>},且∩=,则的取值范围是()
.(,-) .(]
.(-] .(]
二、填空题
.两圆+=和(+)+(-)=相切,则实数的值为.
.两圆交于()及(,-),两圆的圆心均在直线-+=上,则+的值为.
.两圆+-+-=和+=的公共弦长为.
三、解答题
.求过点()且与圆:+++=切于原点的圆的方程.
.点在圆心为的方程++-+=上,点在圆心为的方程++++=上,求的最大值.。
