2018届高三数学第28练函数y=Asinωx+φ的图象与性质练习
2018届高三数学理一轮复习课后作业第3章 第4节 y=Asin

课时作业 A 组 基础对点练1.(2016·高考四川卷)为了得到函数y =sin ⎝ ⎛⎭⎪⎫2x -π3的图象,只需把函数y =sin 2x的图象上所有的点( ) A .向左平行移动π3个单位长度 B .向右平行移动π3个单位长度 C .向左平行移动π6个单位长度 D .向右平行移动π6个单位长度 解析:∵y =sin ⎝ ⎛⎭⎪⎫2x -π3=sin 2⎝ ⎛⎭⎪⎫x -π6,∴将函数y =sin 2x 的图象向右平行移动π6个单位长度,可得y =sin ⎝ ⎛⎭⎪⎫2x -π3的图象.答案:D2.(2017·长沙模拟)将函数y =cos 2x 的图象向左平移π4个单位长度,得到函数y =f (x )·cos x 的图象,则f (x )的表达式可以是( ) A .f (x )=-2sin x B .f (x )=2sin xC .f (x )=22sin 2xD .f (x )=22(sin 2x +cos 2x )解析:由题意得,将函数y =cos 2x 的图象向左平移π4个单位长度后,所得图象对应的函数解析式为y =cos 2(x +π4)=cos ⎝ ⎛⎭⎪⎫2x +π2=-sin 2x =-2sin x ·cos x ,故f (x )的表达式可以是f (x )=-2sin x ,故选A. 答案:A3.(2015·高考陕西卷)如图,某港口一天6时到18时的水深变化曲线近似满足函数y =3sin ⎝ ⎛⎭⎪⎫π6x +φ+k .据此函数可知,这段时间水深(单位:m)的最大值为( )A .5B .6C .8D .10解析:由题图可知-3+k =2,k =5,y =3sin ⎝ ⎛⎭⎪⎫π6x +φ+5,∴y max =3+5=8.答案:C4.(2017·辽宁五校联考)函数f (x )=sin(ωx +φ)(其中|φ|<π2,ω>0)的图象如图所示,为了得到y =sin ωx 的图象,只需把y =f (x )的图象上所有点( )A .向右平移π6个单位长度 B .向右平移π12个单位长度 C .向左平移π6个单位长度 D .向左平移π12个单位长度解析:由题中图象知T 4=7π12-π3,∴T =π.又π=2πω,∴ω=2.由f ⎝ ⎛⎭⎪⎫π3=0得2×π3+φ=k π(k ∈Z ),即φ=k π-2π3(k ∈Z ).∵|φ|<π2,∴φ=π3,即f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3=sin[2(x+π6)],故选A. 答案:A5.(2017·贵阳监测)已知函数f (x )=sin(ωx +φ)(ω>0,|φ|<π2)的部分图象如图所示,如果x 1,x 2∈⎝ ⎛⎭⎪⎫-π6,π3,且f (x 1)=f (x 2),则f (x 1+x 2)=( )A.12 B .32 C.22D .1解析:由题图可知,T 2=π3-⎝ ⎛⎭⎪⎫-π6=π2,则T =π,ω=2,又-π6+π32=π12, ∴f (x )的图象过点⎝ ⎛⎭⎪⎫π12,1,即sin ⎝ ⎛⎭⎪⎫2×π12+φ=1,得φ=π3,∴f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3.而x 1+x 2=-π6+π3=π6,∴f (x 1+x 2)=f ⎝ ⎛⎭⎪⎫π6=sin ⎝ ⎛⎭⎪⎫2×π6+π3=sin 2π3=32.答案:B6.(2017·邢台摸底)先把函数f (x )=sin ⎝ ⎛⎭⎪⎫x -π6的图象上各点的横坐标变为原来的12(纵坐标不变),再把新得到的图象向右平移π3个单位,得到y =g (x )的图象.当x ∈⎝ ⎛⎭⎪⎫π4,3π4时,函数g (x )的值域为( ) A.⎝ ⎛⎦⎥⎤-32,1 B .⎝ ⎛⎦⎥⎤-12,1C.⎝ ⎛⎭⎪⎫-32,32D .[-1,0)解析:依题意得g (x )=sin ⎣⎢⎡⎦⎥⎤2(x -π3)-π6=sin(2x -5π6),当x ∈⎝ ⎛⎭⎪⎫π4,3π4时,2x -5π6∈⎝ ⎛⎭⎪⎫-π3,2π3,sin ⎝ ⎛⎭⎪⎫2x -5π6∈⎝ ⎛⎦⎥⎤-32,1,此时g (x )的值域是⎝ ⎛⎦⎥⎤-32,1,选A. 答案:A7.(2017·湖南调研)已知函数f (x )=sin(ωx +φ)(ω>0,-π<φ<0)的最小正周期是π,若将函数f (x )的图象向左平移π3个单位长度后所得的函数图象过点P (0,1),则函数f (x )=sin(ωx +φ)( ) A .在区间⎣⎢⎡⎦⎥⎤-π6,π3上单调递减B .在区间⎣⎢⎡⎦⎥⎤-π6,π3上单调递增C .在区间⎣⎢⎡⎦⎥⎤-π3,π6上单调递减D .在区间⎣⎢⎡⎦⎥⎤-π3,π6上单调递增解析:依题意得ω=2,f (x )=sin(2x +φ),平移后得到函数y =sin ⎝ ⎛⎭⎪⎫2x +φ+2π3的图象,且过点P (0,1),所以sin ⎝ ⎛⎭⎪⎫φ+2π3=1,因为-π<φ<0,所以φ=-π6,所以f (x )=sin ⎝ ⎛⎭⎪⎫2x -π6,易知函数f (x )在⎣⎢⎡⎦⎥⎤-π6,π3上单调递增,故选B. 答案:B8.(2017·邯郸模拟)下列函数同时具有性质“(1)最小正周期是π;(2)图象关于直线x =π6对称;(3)在⎣⎢⎡⎦⎥⎤π6,π3上是减函数”的是( )A .y =sin ⎝ ⎛⎭⎪⎫x 2+5π12B .y =sin(2x -π3) C .y =cos(2x +2π3) D .y =sin ⎝ ⎛⎭⎪⎫2x +π6解析:易知函数y =sin ⎝ ⎛⎭⎪⎫x 2+5π12的最小正周期为4π,故排除A ;当x =π6时,y =sin ⎝ ⎛⎭⎪⎫2x -π3=0,故排除B ;当x ∈⎣⎢⎡⎦⎥⎤π6,π3时,2x +2π3∈⎣⎢⎡⎦⎥⎤π,4π3,函数y =cos ⎝ ⎛⎭⎪⎫2x +2π3单调递增,故排除C ;对于函数y =sin(2x +π6),可知其最小正周期T =2π2=π,将x =π6代入得,y =sin ⎝ ⎛⎭⎪⎫2×π6+π6=1,是最大值,可知该函数的图象关于直线x=π6对称,令π2+2k π≤2x +π6≤3π2+2k π(k ∈Z ),化简整理可得π6+k π≤x ≤2π3+k π(k ∈Z ),可知函数y =sin(2x +π6)在⎣⎢⎡⎦⎥⎤π6,π3上是减函数,故选D.答案:D9.(2017·江南十校联考)已知函数f (x )=sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,|φ|<π2的最小正周期为4π,且f ⎝ ⎛⎭⎪⎫π3=1,则f (x )图象的一个对称中心是( )A.⎝ ⎛⎭⎪⎫-2π3,0 B .⎝ ⎛⎭⎪⎫-π3,0C.⎝ ⎛⎭⎪⎫2π3,0 D .⎝ ⎛⎭⎪⎫5π3,0解析:由f (x )=sin(ωx +φ)的最小正周期为4π,得ω=12,∵f ⎝ ⎛⎭⎪⎫π3=1,∴12×π3+φ=π2+2m π(m ∈Z ),即φ=π3+2m π(m ∈Z ).由|φ|<π2,得φ=π3,故f (x )=sin ⎝ ⎛⎭⎪⎫12x +π3.令12x +π3=k π(k ∈Z ),得x =2k π-2π3(k ∈Z ),故f (x )图象的对称中心为⎝ ⎛⎭⎪⎫2k π-2π3,0(k ∈Z ),当k =0时,f (x )的对称中心为⎝ ⎛⎭⎪⎫-2π3,0,故选A.答案:A10.(2017·河南六市联考)将奇函数f (x )=A sin(ωx +φ)⎝ ⎛⎭⎪⎫A ≠0,ω>0,-π2<φ<π2的图象向左平移π6个单位得到的图象关于原点对称,则ω的值可以为( ) A .6 B .3 C .4D .2解析:由函数为奇函数得φ=k π(k ∈Z ),又-π2<φ<π2,∴φ=0,y =A sin ωx .由函数图象向左平移π6个单位得到函数y =A sin ⎣⎢⎡⎦⎥⎤ω⎝ ⎛⎭⎪⎫x +π6=A sin ⎝ ⎛⎭⎪⎫ωx +π6ω,其图象关于原点对称,∴有π6ω=k π(k ∈Z ),即ω=6k (k ∈Z ),故选A. 答案:A11.已知函数f (x )=3sin ⎝ ⎛⎭⎪⎫ωx -π6(ω>0)和g (x )=3cos(2x +φ)的图象完全相同,若x ∈⎣⎢⎡⎦⎥⎤0,π2,则f (x )的值域是________.解析:f (x )=3sin ⎝ ⎛⎭⎪⎫ωx -π6=3cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫ωx -π6=3cos ⎝ ⎛⎭⎪⎫ωx -2π3,易知ω=2,则f (x )=3sin ⎝ ⎛⎭⎪⎫2x -π6, ∵x ∈⎣⎢⎡⎦⎥⎤0,π2,∴-π6≤2x -π6≤5π6,∴-32≤f (x )≤3. 答案:⎣⎢⎡⎦⎥⎤-32,312.(2017·郑州质量预测)如图,函数f (x )=A sin(ωx +φ)(其中A >0,ω>0,|φ|≤π2)的图象与坐标轴的三个交点P 、Q 、R 满足P (1,0),∠PQR =π4,M (2,-2)为线段QR 的中点,则A 的值为________.解析:依题意得,点Q 的横坐标是4,R 的纵坐标是-4,T =2πω=2|PQ |=6,ω=π3,因为f ⎝⎛⎭⎪⎫1+42=A sin ⎝ ⎛⎭⎪⎫π3×52+φ=A >0,即sin ⎝ ⎛⎭⎪⎫5π6+φ=1,又|φ|≤π2,π3≤5π6+φ≤4π3,因此5π6+φ=π2,φ=-π3,又点R (0,-4)在f (x )的图象上,所以A sin ⎝ ⎛⎭⎪⎫-π3=-4,A =833. 答案:83313.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y =a +A cos ⎣⎢⎡⎦⎥⎤π6(x -6)(x =1,2,3,…,12,A >0)来表示,已知6月份的月平均气温最高,为28 ℃,12月份的月平均气温最低,为18 ℃,则10月份的平均气温值为________℃.解析:由题意得⎩⎨⎧ a +A =28,a -A =18,∴⎩⎨⎧a =23,A =5, ∴y =23+5cos ⎣⎢⎡⎦⎥⎤π6(x -6),当x =10时,y =23+5×⎝ ⎛⎭⎪⎫-12=20.5.答案:20.514.(2017·武汉模拟)把函数y =sin 2x 的图象沿x 轴向左平移π6个单位,纵坐标伸长到原来的2倍(横坐标不变)后得到函数y =f (x )的图象,对于函数y =f (x )有以下四个判断:①该函数的解析式为y =2sin ⎝ ⎛⎭⎪⎫2x +π6;②该函数图象关于点⎝ ⎛⎭⎪⎫π3,0对称;③该函数在⎣⎢⎡⎦⎥⎤0,π6上是增函数; ④函数y =f (x )+a 在⎣⎢⎡⎦⎥⎤0,π2上的最小值为3,则a =2 3.其中,正确判断的序号是________.解析:将函数向左平移π6得到y =sin 2⎝ ⎛⎭⎪⎫x +π6=sin ⎝ ⎛⎭⎪⎫2x +π3,然后纵坐标伸长到原来的2倍得到 y =2sin ⎝ ⎛⎭⎪⎫2x +π3,即y =f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π3,所以①不正确;y =f ⎝ ⎛⎭⎪⎫π3=2sin ⎝ ⎛⎭⎪⎫2×π3+π3=2sin π=0,所以函数图象关于点⎝ ⎛⎭⎪⎫π3,0对称,所以②正确;由-π2+2k π≤2x +π3≤π2+2k π,k ∈Z ,得-5π12+k π≤x ≤π12+k π,k ∈Z ,即函数的单调增区间为⎣⎢⎡⎦⎥⎤-5π12+k π,π12+k π,k ∈Z ,当k =0时,增区间为⎣⎢⎡⎦⎥⎤-5π12,π12,所以③不正确;y =f (x )+a =2sin ⎝⎛⎭⎪⎫2x +π3+a ,当0≤x ≤π2时,π3≤2x +π3≤4π3,所以当2x +π3=4π3时,函数值最小为y =2sin 4π3+a =-3+a =3,所以a =23,所以④正确.所以正确的命题为②④. 答案:②④B 组 能力提速练1.(2017·南昌调研)要得到函数f (x )=cos ⎝ ⎛⎭⎪⎫2x +π3的图象,只需将函数g (x )=sin ⎝ ⎛⎭⎪⎫2x +π3的图象( ) A .向左平移π2个单位长度 B .向右平移π2个单位长度 C .向左平移π4个单位长度 D .向右平移π4个单位长度 解析:因为f (x )=cos ⎝ ⎛⎭⎪⎫2x +π2-π6=sin ⎝ ⎛⎭⎪⎫π6-2x =sin ⎝ ⎛⎭⎪⎫2x +5π6 =sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x +π4+π3, 所以要得到函数f (x )=cos ⎝ ⎛⎭⎪⎫2x +π3的图象,只需将函数g (x )=sin ⎝ ⎛⎭⎪⎫2x +π3的图象向左平移π4个单位长度,故选C. 答案:C2.(2017·武汉武昌区调研)已知函数f (x )=2sin(ωx +π6)-1(ω>0)的图象向右平移2π3个单位长度后与原图象重合,则ω的最小值是( ) A .3 B .32 C.43D .23解析:将f (x )的图象向右平移2π3个单位长度后得到图象的函数解析式为y =2sin ⎣⎢⎡⎦⎥⎤ω⎝⎛⎭⎪⎫x -2π3+π6-1=2sin ⎝ ⎛⎭⎪⎫ωx -2ωπ3+π6-1,所以2ωπ3=2k π,k ∈Z ,所以ω=3k ,k ∈Z ,因为ω>0,k ∈Z ,所以ω的最小值为3,故选A. 答案:A3.已知函数f (x )=3sin(ωx +φ)(ω>0,|φ|≤π2)的部分图象如图所示,A 、B 两点之间的距离为10,且f (2)=0,若将函数f (x )的图象向右平移t (t >0)个单位长度后所得函数图象关于y 轴对称,则t 的最小值为( )A .1B .2C .3D .4解析:由题图知可设A (x 1,3),B (x 2,-3),所以|AB |=(x 1-x 2)2+62=10,解得|x 1-x 2|=8,所以T =2|x 1-x 2|=16,故2πω=16,解得ω=π8.所以f (x )=3sin ⎝ ⎛⎭⎪⎫π8x +φ,由f (2)=0得3sin ⎝ ⎛⎭⎪⎫π4+φ=0,又-π2≤φ≤π2,所以φ=-π4.故f (x )=3sin ⎝ ⎛⎭⎪⎫π8x -π4,将f (x )的图象向右平移t (t >0)个单位长度,所得图象对应的函数解析式为g (x )=f (x -t )=3sin ⎣⎢⎡⎦⎥⎤π8(x -t )-π4=3sin ⎣⎢⎡⎦⎥⎤π8x -⎝⎛⎭⎪⎫π8t +π4.由题意得,函数g (x )的图象关于y 轴对称,所以π8t +π4=k π+π2(k ∈Z ),解得t =8k +2(k ∈Z ),故正数t 的最小值为2,选B. 答案:B4.(2017·成都七中调研)已知函数f (x )=3sin x cos x -cos 2x -12.(1)求f (x )在区间⎣⎢⎡⎦⎥⎤-π12,2π3上的最大值和最小值及相应的自变量x 的值;(2)在直角坐标系中作出函数f (x )在区间[0,π]上的图象.解析:(1)f (x )=32sin 2x -12cos 2x -1=sin ⎝ ⎛⎭⎪⎫2x -π6-1,当x ∈⎣⎢⎡⎦⎥⎤-π12,2π3时,2x-π6∈⎣⎢⎡⎦⎥⎤-π3,7π6.故当2x -π6=π2,即x =π3时,f (x )在区间⎣⎢⎡⎦⎥⎤-π12,2π3上取得最大值0,当2x -π6=-π3,即x =-π12时,f (x )在区间⎣⎢⎡⎦⎥⎤-π12,2π3上取得最小值-32-1. (2)当x ∈[0,π]时,2x -π6∈⎣⎢⎡⎦⎥⎤-π6,11π6.列表:5.(2016·高考山东卷)设f (x )=23sin(π-x )sin x -(sin x -cos x )2. (1)求f (x )的单调递增区间;(2)把y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移π3个单位,得到函数y =g (x )的图象,求g ⎝ ⎛⎭⎪⎫π6的值.解析:(1)f (x )=23sin(π-x )sin x -(sin x -cos x )2 =23sin 2x -(1-2sin x cos x ) =3(1-cos 2x )+sin 2x -1 =sin 2x -3cos 2x +3-1=2sin ⎝ ⎛⎭⎪⎫2x -π3+3-1, 由2k π-π2≤2x -π3≤2k π+π2(k ∈Z ),得k π-π12≤x ≤k π+5π12(k ∈Z ),所以f (x )的单调递增区间是⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12(k ∈Z )⎝ ⎛⎭⎪⎫或⎝ ⎛⎭⎪⎫k π-π12,k π+5π12(k ∈Z ). (2)由(1)知f (x )=2sin ⎝ ⎛⎭⎪⎫2x -π3+3-1, 把y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y =2sin ⎝ ⎛⎭⎪⎫x -π3+3-1的图象, 再把得到的图象向左平移π3个单位,得到y =2sin x +3-1的图象,即g (x )=2sin x +3-1,所以g ⎝ ⎛⎭⎪⎫π6=2sin π6+3-1= 3.。
高考数学(理)一轮规范练【21】函数y=Asin(ωx φ)的图象与性质(含答案)

课时规范练21 函数y=Asin(ωx+φ)的图象与性质课时规范练第37页一、选择题1.若把函数f(x)=sinωx的图象向左平移个单位,恰好与函数y=cosωx的图象重合,则ω的值可能是( )A. B. C. D.答案:D解析:将函数y=sinωx的图象向左平移个单位长度,则得到函数y=sinω=sin的图象,因为y=cosωx=cos(-ωx)=sin,所以+2kπ,ω=+6k,k∈Z,所以当k=0时,ω=,选D.2.(2018四川高考)函数f(x)=2sin(ωx+φ)ω>0,-<φ<的部分图象如图所示,则ω,φ的值分别是( )A.2,-B.2,-C.4,-D.4,答案:A解析:由图象可得,∴T=π,则ω==2,再将点代入f(x)=2sin(2x+φ)中得sin=1,[:令+φ=2kπ+,k∈Z,解得,φ=2kπ-,k∈Z,又∵φ∈,则取k=0,[:∴φ=-.故选A.3.已知函数y=2sin(ωx+θ)为偶函数(0<θ<π),其图象与直线y=2的某两个交点的横坐标为x1,x2,若|x2-x1|的最小值为π,则( )A.ω=2,θ=B.ω=,θ=C.ω=,θ=D.ω=2,θ=答案:A解析:∵y=2sin(ωx+θ)为偶函数,0<θ<π,∴θ=.∵图象与直线y=2的两个交点的横坐标为x1,x2,|x2-x1|min=π,∴=π,ω=2.故选A.4.若把函数y=cos x-sin x+1的图象向右平移m(m>0)个单位长度,使点为其对称中心,则m的最小值是( )A.πB.C.D.答案:D解析:y=cos x-sin x+1=2cos+1,把该函数图象向右平移m(m>0)个单位后所得函数的解析式为y=2cos+1,由平移后为其对称中心得1=2cos+1,∴cos=0,∴-m=kπ+(k∈Z),解得m=-kπ+(k∈Z),故m的最小值是.5.函数f(x)=sin,给出下列三个其中正确的是( )A.①③B.①②C.②③D.①②③答案:B[:数理化]解析:∵≤x≤,∴≤2x+,∴f(x)在上是减函数,故①正确.fsin,故②正确.y=sin2x向左平移个单位得y=sincos2x≠f(x),故③不正确.故选B.6.已知函数f(x)=Mcos(ωx+φ)(M>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,AC=BC=,∠C=90°,则f的值为( )A.-B.C.-D.答案:A解析:依题意,△ABC是直角边长为的等腰直角三角形,因此其边A B上的高是,函数f(x)的最小正周期是2,故M==2,ω=π,f(x)=cos(πx+φ).又函数f(x)是奇函数,于是有φ=kπ+,其中k∈Z.由0<φ<π得φ=,故f(x)=-sinπx,f=-sin=-,选A.二、填空题7.将函数y=sin x的图象上所有的点向右平移个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是.答案:y=sin解析:函数y=sin x的图象上的点向右平移个单位长度可得函数y=sin的图象;再把各点的横坐标伸长到原来的2倍(纵坐标不变)可得函数y=sin的图象,所以所求函数的解析式是y=sin.8.已知f(x)=sin(ω>0),f=f且f(x)在区间内有最小值,无最大值,则ω= .答案:解析:∵f=f且f(x)在区间上有最小值,无最大值,∴f(x)在x=处取得最小值.∴ω+=2kπ-(k∈Z).∴ω=8k-(k∈Z).∵ω>0,∴当k=1时,ω=8-;当k=2时,ω=16-,此时函数在区间内已存在最大值.故ω=.9.已知函数y=sinωx(ω>0)在一个周期内的图象如图所示,要得到函数y=sin的图象,则需将函数y=sinωx的图象向平移个单位长度.答案:左[:解析:由图象知函数y=sinωx的周期为T=3π-(-π)=4π,[:∴ω=,故y=sinx.又y=sin=sin,∴将函数y=sinx的图象向左平移个单位长度,即可得到函数y=sin的图象.三、解答题10.函数y=sin(ωx+φ)(ω>0,0<φ<π)的最小正周期为π,且函数图象关于点对称,求函数的解析式.解:由题意知最小正周期T=π=,故ω=2.又∵2×+φ=kπ(k∈Z),∴φ=kπ+(k∈Z).又∵0<φ<π,∴φ=,∴y=sin.11.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π)的图象如图所示:(1)求ω,φ的值;(2)设g(x)=f(x)f,求函数g(x)的单调递增区间.解:(1)由图可知T=4=π,ω==2,又由f=1,得sin(π+φ)=1,sinφ=-1.∵|φ|<π,∴φ=-.(2)由(1)知f(x)=sin=-cos2x.∵g(x)=-cos2x=cos2xsin2x=sin4x,∴2kπ-≤4x≤2kπ+(k∈Z),即≤x≤(k∈Z).故函数g(x)的单调递增区间为(k∈Z).12.如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长).现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积S1与种花的面积S2的比值称为“草花比y”.(1)设∠DAB=θ,将y表示成θ的函数关系式.(2)当BE为多长时,y有最小值?最小值是多少?解:(1)因为BD=atanθ,所以△ABD的面积为a2tanθ.设正方形BEFG的边长为t,则由,得,解得t=,则S2=,所以S1=a2tanθ-S2=a2tanθ-,则y=-1.(2)因为tanθ∈(0,+∞),所以y=-1=≥1,当且仅当tanθ=1时取等号,此时BE=t=.所以当BE长为时,y有最小值1.。
【高考复习】2018年高考数学 必修4 三角函数y=Asin(ωx+φ)的图象性质 复习题(含答案)

2018年高考数学 必修4 三角函数y=Asin(ωx +φ)的图象性质复习题1.求函数sin()y A x ωϕ=+的值域,最值,周期,单调区间,对称轴、对称中心等 ,会用五点法作sin()y A x ωϕ=+简图:五点分别为:、 、 、 、 。
2.图象的基本变换:相位变换:sin sin()y x y x ϕ=⇒=+ 周期变换:sin()sin()y x y x ϕωϕ=+⇒=+ 振幅变换:sin()sin()y x y A x ωϕωϕ=+⇒=+ 3.函数sin()y A x ωϕ=+的解析式:即求A 由最值确定,ω有周期确定,φ有特殊点确定。
4.函数sin y x =象到函数sin()(0,0)y A x A ωϕω=+>>的图象变换.5.三角函数最值类型:(1)y =a sin x +b cos x 型函数最值的求法:常转化为:y =x +ϕ)(2)y =a sin 2x +b sin x +c 型:常通过换元法(令sinx=t ,[]1,1t ∈-)转化为y =at 2+bt +c 型: (3)同一问题中出现sin cos ,sin cos ,sin cos x x x x x x +-∙,求它们的范围时,一般是令sin cos x x t +=或21sin cos sin cos 2t x x t x x --=⇒∙=或21sin cos 2t x x -∙=-,转化为关于t 的二次函数来解决例1.基础练习: 1、函数2sin(3)7y x π=+的振幅是 ,相位是 ,初相是 ,周期是 .2、为了得到函数R x x y ∈+=),3cos(的图象,只需把余弦曲线上所有的点向 (左或右)平行移动 个单位长度.3、要得到函数sin(2)3y x π=-的图象,只要sin 2y x =的图象向 (左或右)平行移动 个单位长度.4、把函数sin(2)6y x π=+的图象向右平移3π个单位后,所得图象对应函数解析式为 .5、要得到函数sin()26x y π=-+的图象,可由sin()2xy =-的图象向 (左或右)平行移动 个单位长度.6、把函数sin y x =的图象上所有的点的纵坐标变为原来的13倍(横坐标不变)所得图象的解析式为 .7、将函数sin y x =的图象上所有点向左平移3π个单位长度,再把所得图象上各点横坐标变为原来的5倍,则最后所得图象的解析式为 .例2.已知函数f(x)=sin(3π-2x) (x ∈R ).(1)求f(x)的单调减区间;(2)经过怎样的图象变换使f(x)的图象关于y 轴对称?(仅叙述一种方案即可).例3.如图为函数y 1=Asin(ωx +φ) (|φ|<2π)的一个周期内的图象.(1)写出y 1的解析式;(2)若y 2与y 1的图象关于直线x=2对称,写出y 2的解析式; (3)指出y 2的周期、频率、振幅、初相.例4.已知函数)32sin(21)(π-+=x x f ,x ∈[2,4ππ,].(1)求f(x)的最大值和最小值;(2)若不等式f(x)-m<2在x ∈[2,4ππ,]上恒成立,求实数m 的取值范围.例5.已知函数f(x)=Asin(ωx +φ)(A >0,ω>0)的一个周期的图象如图所示. (1)求f(x)的解析式;(2)若函数g(x)与f(x)的图象关于直线x=2对称,求g(x)的解析式; (3)求函数g(x)的单调区间.三角函数y =Asin(ωx +φ)的图象性质 测试题一、选择题:1.函数y=2sin(421π-x )的振幅、周期和初相分别是( )A.2,π41,-4πB.2,π41,4π C.2,4π,-4π D.±2,4π,-4π2.函数y=sin(2x-3π)在区间[-2π,π]的简图是( )3.函数y=2sin(2x+3π)图象的一条对称轴方程为( ) A.x=-6π B.x=-125ππ C.x=2π D.x=6π4.将函数y=sin x 的图象上所有的点向右平移10π个单位长度,再把所得各点的横坐标变为原来的2倍(纵坐标不变),所得图象的函数解析式是( )A.y=sin(2x-10π)B.y=sin(2x-20π)C.y=sin(1021π-x )D.y=sin(2021π-x )5.将函数y=sin4x 的图像向左平移12π个单位,得到函数y=sin(4x+ϕ)的图像,则ϕ的值为( ) A.12π- B.3π- C.3π D.12π6.将函数y=sin x 的图象向左平移2π个单位长度,得到函数y=f(x)的图象,则下列说法正确的是( )A.y=f(x)是奇函数B.y=f(x)的周期为πC.y=f(x)的图象关于直线x=2π对称D.y=f(x)的图象关于点(-2π,0)对称7.函数y=2sin(1x 23π+)在一个周期内的三个零点可能是( ) A.511,,333πππ- B.2410,,333πππ- C.1123,,666πππ- D.25,,333πππ- 二、填空题: 8.函数 y=51sin(3x-3π) 的定义域是_________,值域是________,周期是________,振幅是________,频率是________,初相是_________.9.要得到y=sin2x-cos2x 的图象,只需将函数y=sin2x+cos2x 的图象沿x 轴向____移___________个单位.10.设函数y=1-3sin(2x+3π)(其中2π-≤x ≤0),当x=_______时,函数的最大值为4.11.把函数y=sin(3x+6π)的图像向左平移3π个单位,再将图像上各点的横坐标缩短为原来的12,那么所得的图像的函数表达式为_______.12.已知函数f(x)=Atan(ωx+ ϕ)(ω>0, ||2πϕ<),y=f(x)的部分图像如下图,则f(24π)=_____.13.已知ω>0,0<φ<π,直线x=4π和x=45π是函数f(x)=sin(ωx +φ)图象的两条相邻的对称轴,则φ=________.三、解答题:14.已知函数f(x)=Asin(ωx+ ϕ)(A>0,ω>0,| ϕ |<π,x ∈R)的部分图像如图所示. (1)求函数f(x)的解析式;(2)求函数y=f(-x)的单调区间及在x ∈[-2,2]上的最值,并求出相应的x 的值.15.已知曲线y=Asin(ωx +φ) (A>0,ω>0)上的一个最高点的坐标为(2,8,π),此点到相邻最低点间的曲线与x 轴交于点(83π,0),若φ∈(-2π,2π).(1)试求这条曲线的函数表达式;(2)用“五点法”画出(1)中函数在[0,π]上的图象.16.已知函数f(x)=sin(ωx +φ) (ω>0,0≤φ≤π)是R 上的偶函数,其图象关于点M(43π,0)对称,且在区间[0,2π]上是单调函数,求φ和ω的值.17.已知函数f(x)=-2asin(2x+6π)+2a+b,x ∈[3,44ππ],是否存在常数a,b ∈Z ,使得f(x)的值域为[].若存在,求出a,b 的值;若不存在,请说明理由.参考答案例2.解:例3.解:例4.解:例5.测试题参考答案1.答案为:C2.答案为:A3.答案为:B4.答案为:C5.选C.【解析】将函数y=sin4x 的图像向左平移12π个单位,得到函数y=sin [4(x+12π)]=sin(4x+3π)的图像,所以ϕ的值为3π. 6.答案为:D 7.选B.【解析】23π-是y=2sin(1x 23π+)的一个零点,y=2sin(1x 23π+)周期T=4π,T2=2π, 所以410,33ππ也是零点. 8.答案为:(-∞,+ ∞),(-15 ,15 ), 2π3 ,15 ,15 ,32π ,-π3 ;9.答案为:右,π2;10.答案:512π-;【解析】由2π-≤x ≤0知22x 333πππ-≤+≤, 当2x 32ππ+=-, 即5x 12π=-时,y=sin(2x+3π)取最小值-1,故y=1-3sin(2x+3π)取最大值4.11.答案:y=-sin(6x+6π);【解析】把函数y=sin(3x+6π)的图像向左平移3π个单位长度,得到函数y sin 3(x )sin(3x )366πππ=++=-+[]的图像,再将图像上各点的横坐标缩短为原来的12,纵坐标不变,得到函数y=-sin(6x+6π)的图像.12.答案【解析】如图可知T 3288ππ=-,即24ππ=ω,所以ω=2, 再结合图像可得2k 82ππ⨯+ϕ=π+,k ∈Z ,即|k |42ππϕ=π+<,所以31k 44-<<,只有k=0,所以4πϕ=,又图像过点(0,1),代入得Atan 4π=1,所以A=1,函数的解析式为f(x)=tan(2x+ 4π),则f ()tan 243ππ==13.答案为:4π;14.解:(1)由图像知A=2.T=8,∵2T 8π==ω,∴4πω=,又图像经过点(1,2), ∴2sin(4π+ϕ)=2,2k 42ππ+ϕ=π+,(k ∈Z),即2k 4πϕ=π+,(k ∈Z).∵|ϕ|<π,∴4πϕ=,∴f(x)=2sin(x 44ππ+).(2)y=f(-x)=2sin(x 44ππ-+)=-2sin(x 44ππ-)由2k x 2k 2442πππππ-≤-≤π+,得8k-1≤x ≤8k+3,k ∈Z ,故y=f(-x)在[8k-1,8k+3],k ∈Z 上是减少的;同理,函数在[8k+3,8k+7],k ∈Z 上是增加的.∵x ∈[-2,2],由上可知当x=-1时,y=f(-x)取最大值2;当x=2时,y=f(-x)取最小值15.解:16.解:17.解:∵3x 44ππ≤≤∴3252x 2x 22363πππππ≤≤≤+≤,∴1sin(2x )62π-≤+≤ (1)当a>0时-2a<0由题意得2a 2a b 12a 2a b 32⎧++=⎪⎨-++=-⎪⎩ ,解得a 1b 5=⎧⎪⎨=⎪⎩.∵a,b ∈Z 舍去. (2)当a<0时-2a>0由题意得2a 2a b 32a 2a b 1++=-⎧⎪⎨-++=⎪⎩解得a 1b 1=-⎧⎨=⎩符合题意.。
2018高考一轮数学浙江专版练习第3章 第4节 函数y=Asin

第四节 函数y =A sin(ωx +φ)的图象及三角函数模型的简单应用1.y =A sin (ωx +φ)的有关概念表所示先平移后伸缩 先伸缩后平移⇓ ⇓1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”) (1)利用图象变换作图时“先平移,后伸缩”与“先伸缩,后平移”中平移的单位长度一致.( )(2)将y =3sin 2x 的图象左移π4个单位后所得图象的解析式是y =3sin ⎝ ⎛⎭⎪⎫2x +π4.( )(3)函数f (x )=A sin(ωx +φ)的图象的两个相邻对称轴间的距离为一个周期.( )(4)函数y =A cos(ωx +φ)的最小正周期为T ,那么函数图象的两个相邻对称中心之间的距离为T2.( )[答案] (1)× (2)× (3)× (4)√2.为了得到函数y =sin ⎝ ⎛⎭⎪⎫x +π3的图象,只需把函数y =sin x 的图象上所有的点( )A .向左平行移动π3个单位长度 B .向右平行移动π3个单位长度 C .向上平行移动π3个单位长度 D .向下平行移动π3个单位长度A [把函数y =sin x 的图象上所有的点向左平行移动π3个单位长度就得到函数y =sin ⎝ ⎛⎭⎪⎫x +π3的图象.]3.若函数y =sin(ωx +φ)(ω>0)的部分图象3-4-1如图,则ω=( )图3-4-1A .5B .4C .3D .2B [由图象可知,T 2=x 0+π4-x 0=π4,所以T =π2=2πω,所以ω=4.]4.将函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为( )A.3π4 B.π4 C .0D .-π4B [把函数y =sin(2x +φ)沿x 轴向左平移π8个单位后得到函数y =sin 2⎝ ⎛⎭⎪⎫x +φ2+π8=sin ⎝ ⎛⎭⎪⎫2x +φ+π4为偶函数,则φ的一个可能取值是π4.] 5.(教材改编)电流I (单位:A)随时间t (单位:s)变化的函数关系式是I =5sin ⎝ ⎛⎭⎪⎫100πt +π3,t ∈[0,+∞),则电流I 变化的初相、周期分别是________.【导学号:51062109】π3,150 [由初相和周期的定义,得电流I 变化的初相是π3,周期T =2π100π=150.]已知函数f (x )=3sin ⎝ ⎛⎭⎪⎫12x -π4,x ∈R .(1)画出函数f (x )在一个周期的闭区间上的简图;(2)将函数y =sin x 的图象作怎样的变换可得到f (x )的图象? [解] (1)列表取值:(2)先把y =sin x 的图象向右平移π4个单位,然后把所有点的横坐标扩大为原来的2倍,再把所有点的纵坐标扩大为原来的3倍,得到f (x )的图象.15分[规律方法] 1.变换法作图象的关键是看x 轴上是先平移后伸缩还是先伸缩后平移,对于后者可利用ωx +φ=ω⎝ ⎛⎭⎪⎫x +φω确定平移单位.2.用“五点法”作图,关键是通过变量代换,设z =ωx +φ,由z 取0,π2,π,32π,2π来求出相应的x ,通过列表,描点得出图象.如果在限定的区间内作图象,还应注意端点的确定.[变式训练1] (1)(2016·全国卷Ⅰ)将函数y =2sin ⎝ ⎛⎭⎪⎫2x +π6的图象向右平移14个周期后,所得图象对应的函数为( )A .y =2sin ⎝ ⎛⎭⎪⎫2x +π4B .y =2sin ⎝ ⎛⎭⎪⎫2x +π3C .y =2sin ⎝ ⎛⎭⎪⎫2x -π4D .y =2sin ⎝ ⎛⎭⎪⎫2x -π3(2)函数y =sin x -3cos x 的图象可由函数y =2sin x 的图象至少向右平移________个单位长度得到. 【导学号:51062110】(1)D (2)π3 [(1)函数y =2sin ⎝ ⎛⎭⎪⎫2x +π6的周期为π,将函数y =2sin ⎝ ⎛⎭⎪⎫2x +π6的图象向右平移14个周期即π4个单位长度,所得图象对应的函数为y =2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x -π4+π6=2sin ⎝ ⎛⎭⎪⎫2x -π3,故选D.(2)∵y =sin x -3cos x =2sin ⎝ ⎛⎭⎪⎫x -π3,∴函数y =sin x -3cos x 的图象可由函数y =2sin x 的图象向右平移π3个单位长度得到.]图3-4-2A .y =2sin ⎝ ⎛⎭⎪⎫2x -π6B .y =2sin ⎝ ⎛⎭⎪⎫2x -π3C .y =2sin ⎝ ⎛⎭⎪⎫x +π6D .y =2sin ⎝ ⎛⎭⎪⎫x +π3(2)已知函数y =A sin(ωx +φ)+b (A >0,ω>0)的最大值为4,最小值为0,最小正周期为π2,直线x =π3是其图象的一条对称轴,则下面各式中符合条件的解析式为( )A .y =4sin ⎝ ⎛⎭⎪⎫4x +π6B .y =2sin ⎝ ⎛⎭⎪⎫2x +π3+2C .y =2sin ⎝ ⎛⎭⎪⎫4x +π3+2D .y =2sin ⎝ ⎛⎭⎪⎫4x +π6+2(1)A (2)D [(1)由图象知T 2=π3-⎝ ⎛⎭⎪⎫-π6=π2,故T =π,因此ω=2ππ=2.又图象的一个最高点坐标为⎝ ⎛⎭⎪⎫π3,2,所以A =2,且2×π3+φ=2k π+π2(k ∈Z ),故φ=2k π-π6(k ∈Z ),结合选项可知y =2sin ⎝ ⎛⎭⎪⎫2x -π6.故选A.(2)由函数y =A sin(ωx +φ)+b 的最大值为4,最小值为0,可知b =2,A =2.由函数的最小正周期为π2,可知2πω=π2,得ω=4.由直线x =π3是其图象的一条对称轴,可知4×π3+φ=k π+π2,k ∈Z ,从而φ=k π-5π6,k ∈Z ,故满足题意的是y =2sin ⎝ ⎛⎭⎪⎫4x +π6+2.][规律方法] 确定y =A sin(ωx +φ)+b (A >0,ω>0)的步骤和方法 (1)求A ,b :确定函数的最大值M 和最小值m ,则A =M -m 2,b =M +m2;(2)求ω:确定函数的周期T ,则可得ω=2πT ; (3)求φ:常用的方法有:①代入法:把图象上的一个已知点代入(此时A ,ω,b 已知)或代入图象与直线y =b 的交点求解(此时要注意交点在上升区间上还是在下降区间上).②五点法:确定φ值时,往往以寻找“五点法”中的某一个点为突破口.“第一点”(即图象上升时与x 轴的交点)时ωx +φ=0;“第二点”(即图象的“峰点”)时ωx +φ=π2;“第三点”(即图象下降时与x 轴的交点)时ωx +φ=π;“第四点”(即图象的“谷点”)时ωx +φ=3π2;“第五点”时ωx +φ=2π.[变式训练2] (2017·浙江名校(镇海中学)交流卷一)函数f (x )=A sin(ωx +φ)⎝ ⎛⎭⎪⎫A >0,ω>0,|φ|<π2的部分图象如图3-4-3所示,则A =________,ω=________,φ=________.图3-4-31 3 π4 [显然A =1;周期T =4⎝ ⎛⎭⎪⎫5π12-π4=2π3,则ω=2πT =3; 由sin ⎝ ⎛⎭⎪⎫3×5π12+φ=-1和|φ|<π2,得φ=π4.]已知函数f (x )=4tan x sin ⎝ ⎛⎭⎪π2-x ·cos ⎝ ⎭⎪⎫x -π3- 3. (1)求f (x )的定义域与最小正周期; (2)讨论f (x )在区间⎣⎢⎡⎦⎥⎤-π4,π4上的单调性.[解](1)f (x )的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠π2+k π,k ∈Z.2分f (x )=4tan x cos x cos ⎝ ⎛⎭⎪⎫x -π3- 3=4sin x cos ⎝ ⎛⎭⎪⎫x -π3- 3=4sin x ⎝ ⎛⎭⎪⎫12cos x +32sin x - 3=2sin x cos x +23sin 2x - 3 =sin 2x +3(1-cos 2x )- 3 =sin 2x -3cos 2x =2sin ⎝ ⎛⎭⎪⎫2x -π3.所以f (x )的最小正周期T =2π2=π.7分(2)令z =2x -π3,则函数y =2sin z 的单调递增区间是⎣⎢⎡⎦⎥⎤-π2+2k π,π2+2k π,k∈Z .由-π2+2k π≤2x -π3≤π2+2k π, 得-π12+k π≤x ≤5π12+k π,k ∈Z .12分设A =⎣⎢⎡⎦⎥⎤-π4,π4,B =x ⎪⎪⎪-π12+k π≤x ≤5π12+k π,k ∈Z ,易知A ∩B =⎣⎢⎡⎦⎥⎤-π12,π4. 所以当x ∈⎣⎢⎡⎦⎥⎤-π4,π4时,f (x )在区间⎣⎢⎡⎦⎥⎤-π12,π4上单调递增,在区间⎣⎢⎡⎦⎥⎤-π4,-π12上单调递减.15分[规律方法] 讨论函数的单调性,研究函数的周期性、奇偶性与对称性,都必须首先利用辅助角公式,将函数化成一个角的一种三角函数.[变式训练3] 设函数f (x )=32-3sin 2ωx -sin ωx cos ωx (ω>0),且y =f (x )图象的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值;(2)求f (x )在区间⎣⎢⎡⎦⎥⎤π,3π2上的最大值和最小值.[解] (1)f (x )=32-3sin 2ωx -sin ωx cos ωx =32-3·1-cos 2ωx 2-12sin 2ωx=32cos 2ωx -12sin 2ωx =-sin ⎝ ⎛⎭⎪⎫2ωx -π3.4分 因为图象的一个对称中心到最近的对称轴的距离为π4,又ω>0,所以2π2ω=4×π4,因此ω=1.7分(2)由(1)知f (x )=-sin ⎝ ⎛⎭⎪⎫2x -π3.9分 当π≤x ≤3π2时,5π3≤2x -π3≤8π3,所以-32≤sin ⎝⎛⎭⎪⎫2x -π3≤1,则-1≤f (x )≤32.13分 故f (x )在区间⎣⎢⎡⎦⎥⎤π,3π2上的最大值和最小值分别为32,-1.15分数关系:f (t )=10-3cos π12t -sin π12t ,t ∈[0,24).(1)求实验室这一天的最大温差;(2)若要求实验室温度不高于11 ℃,则在哪段时间实验室需要降温? [解] (1)因为f (t )=10-2⎝ ⎛⎭⎪⎫32cos π12t +12sin π12t=10-2sin ⎝ ⎛⎭⎪⎫π12t +π3,2分又0≤t <24,所以π3≤π12t +π3<7π3,-1≤sin ⎝ ⎛⎭⎪⎫π12t +π3≤1.4分 当t =2时,sin ⎝ ⎛⎭⎪⎫π12t +π3=1;当t =14时,sin ⎝ ⎛⎭⎪⎫π12t +π3=-1.于是f (t )在[0,24)上取得最大值12,取得最小值8.故实验室这一天最高温度为12 ℃,最低温度为8 ℃,最大温差为4 ℃.7分 (2)依题意,当f (t )>11时实验室需要降温. 由(1)得f (t )=10-2sin ⎝ ⎛⎭⎪⎫π12t +π3,故有10-2sin ⎝ ⎛⎭⎪⎫π12t +π3>11, 即sin ⎝ ⎛⎭⎪⎫π12t +π3<-12.12分又0≤t <24,因此7π6<π12t +π3<11π6,即10<t <18. 故在10时至18时实验室需要降温.15分[规律方法] 1.三角函数模型在实际中的应用体现在两个方面:一是用已知的模型去分析解决实际问题,二是把实际问题抽象转化成数学问题,建立三角函数模型解决问题,其关键是合理建模.2.建模的方法是认真审题,把问题提供的“条件”逐条地“翻译”成“数学语言”,这个过程就是数学建模的过程.[变式训练4] 如图3-4-4,某港口一天6时到18时的水深变化曲线近似满足函数y =3sin ⎝ ⎛⎭⎪⎫π6x +φ+k .据此函数可知,这段时间水深(单位:m)的最大值为( )图3-4-4A .5B .6C .8D .10C[根据图象得函数的最小值为2,有-3+k=2,k=5,最大值为3+k=8.][思想与方法]1.由图象确定函数解析式由图象确定y=A sin(ωx+φ)时,φ的确定是关键,尽量选择图象的最值点代入;若选零点代入,应根据图象升降确定“五点法”作图中的第几个零点.2.对称问题函数y=A sin(ωx+φ)的图象与x轴的每一个交点均为其对称中心,经过该图象上坐标为(x,±A)的点与x轴垂直的每一条直线均为其图象的对称轴,这样的最近两点间横坐标的差的绝对值是半个周期(或两个相邻对称中心的距离).[易错与防范]1.要弄清楚是平移哪个函数的图象,得到哪个函数的图象.2.要注意平移前后两个函数的名称是否一致,若不一致,应先利用诱导公式化为同名函数.3.由y =sin x 的图象变换到y =A sin(ωx +φ)的图象,先相位变换再周期变换(伸缩变换),平移的量是|φ|个单位;而先周期变换(伸缩变换)再相位变换,平移的量是|φ|ω(ω>0)个单位.原因是相位变换和周期变换都是针对x 而言的.4.函数y =A sin(ωx +φ)在x ∈[m ,n ]上的最值可先求t =ωx +φ的范围,再结合图象得出y =A sin t 的值域.课时分层训练(十八) 函数y =A sin(ωx +φ)的图象及三角函数模型的简单应用A 组 基础达标 (建议用时:30分钟)一、选择题1.为了得到函数y =sin 3x +cos 3x 的图象,可以将函数y =2cos 3x 的图象( )A .向右平移π12个单位 B .向右平移π4个单位 C .向左平移π12个单位D .向左平移π4个单位A [由于y =sin 3x +cos 3x =2sin ⎝ ⎛⎭⎪⎫3x +π4,y =2cos 3x =2sin ⎝ ⎛⎭⎪⎫3x +π2,因此只需将y =2cos 3x 的图象向右平移π12个单位,即可得到y =2sin ⎣⎢⎡⎦⎥⎤3⎝⎛⎭⎪⎫x -π12+π2=2sin ⎝ ⎛⎭⎪⎫3x +π4的图象.] 2.(2017·浙江测试卷)为得到函数y =2sin ⎝ ⎛⎭⎪⎫2x +π4的图象,只需将函数y =2cos2x 的图象( ) 【导学号:51062111】A .向左平移π4个单位 B .向右平移π4个单位C .向左平移π8个单位 D .向右平移π8个单位D [将函数y =2cos 2x 的图象向右平移π8个单位,可得函数y =2cos 2⎝ ⎛⎭⎪⎫x -π8=2cos ⎝ ⎛⎭⎪⎫2x -π4=2sin ⎝ ⎛⎭⎪⎫2x +π4的图象.]3.函数f (x )=2sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,-π2<φ<π2的部分图象如图3-4-5所示,则ω,φ的值分别是( )图3-4-5A .2,-π3 B .2,-π6 C .4,-π6 D .4,π3A [∵T 2=1112π-512π,∴T =π.由T =2πω=π,得ω=2.∵5π12×2+φ=π2+2k π,k ∈Z ,∴φ=-π3+2k π.又∵φ∈⎝ ⎛⎭⎪⎫-π2,π2,∴φ=-π3.]4.已知函数f (x )=3sin ωx +cos ωx (ω>0),y =f (x )的图象与直线y =2的两个相邻交点的距离等于π,则f (x )的单调递增区间是( )A.⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12,k ∈Z B.⎣⎢⎡⎦⎥⎤k π+5π12,k π+11π12,k ∈Z C.⎣⎢⎡⎦⎥⎤k π-π3,k π+π6,k ∈ZD.⎣⎢⎡⎦⎥⎤k π+π6,k π+2π3,k ∈Z C [由题设知f (x )=2sin ⎝ ⎛⎭⎪⎫ωx +π6,f (x )的周期为T =π,所以ω=2,由2k π-π2≤2x +π6≤2k π+π2,k ∈Z 得,k π-π3≤x ≤k π+π6,k ∈Z .]5.若将函数y =2sin 2x 的图象向左平移π12个单位长度,则平移后图象的对称轴为( )A .x =k π2-π6(k ∈Z ) B .x =k π2+π6(k ∈Z ) C .x =k π2-π12(k ∈Z )D .x =k π2+π12(k ∈Z )B [将函数y =2sin 2x 的图象向左平移π12个单位长度,得到函数y =2sin2⎝ ⎛⎭⎪⎫x +π12=2sin ⎝ ⎛⎭⎪⎫2x +π6的图象.由2x +π6=k π+π2(k ∈Z ),得x =k π2+π6(k ∈Z ),即平移后图象的对称轴为x =k π2+π6(k ∈Z ).]二、填空题6.若函数f (x )=3sin ⎝ ⎛⎭⎪⎫ωx -π3(ω>0)的最小正周期为π2,则f ⎝ ⎛⎭⎪⎫π3=________.0 [由f (x )=3sin ⎝ ⎛⎭⎪⎫ωx -π3(ω>0)的最小正周期为π2,得ω=4,所以f ⎝ ⎛⎭⎪⎫π3=3sin ⎝ ⎛⎭⎪⎫4×π3-π3=0.] 7.已知函数y =cos x 与y =sin(2x +φ)(0≤φ<π),它们的图象有一个横坐标为π3的交点,则φ的值是________.π6 [由题意cos π3=sin⎝ ⎛⎭⎪⎫2×π3+φ, 即sin ⎝ ⎛⎭⎪⎫2π3+φ=12,2π3+φ=k π+(-1)k ·π6(k ∈Z ).因为0≤φ<π,所以φ=π6.] 8.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y =a +A cos ⎣⎢⎡⎦⎥⎤π6(x -6)(x =1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28 ℃,12月份的月平均气温最低,为18 ℃,则10月份的平均气温值为________ ℃.【导学号:51062112】20.5 [依题意知,a =28+182=23,A =28-182=5,∴y =23+5cos ⎣⎢⎡⎦⎥⎤π6(x -6),当x =10时,y =23+5cos ⎝ ⎛⎭⎪⎫π6×4=20.5.]三、解答题9.已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫2x -π4+1. (1)求它的振幅、最小正周期、初相; (2)画出函数y =f (x )在⎣⎢⎡⎦⎥⎤-π2,π2上的图象.[解] (1)振幅为2,最小正周期T =π,初相为-π4.6分 (2)图象如图所示.15分10.已知函数y =A sin(ωx +φ)(A >0,ω>0)的图象过点P ⎝ ⎛⎭⎪⎫π12,0,图象上与点P 最近的一个最高点是Q ⎝ ⎛⎭⎪⎫π3,5.(1)求函数的解析式;(2)求函数f (x )的递增区间. 【导学号:51062113】 [解] (1)依题意得A =5,周期T =4⎝ ⎛⎭⎪⎫π3-π12=π,2分∴ω=2ππ=2.故y =5sin(2x +φ),又图象过点P ⎝ ⎛⎭⎪⎫π12,0,4分∴5sin ⎝ ⎛⎭⎪⎫π6+φ=0,由已知可得π6+φ=0,∴φ=-π6,∴y =5sin ⎝ ⎛⎭⎪⎫2x -π6.7分 (2)由-π2+2k π≤2x -π6≤π2+2k π,k ∈Z , 得-π6+k π≤x ≤π3+k π,k ∈Z ,10分故函数f (x )的递增区间为⎣⎢⎡⎦⎥⎤k π-π6,k π+π3(k ∈Z ).15分 B 组 能力提升 (建议用时:15分钟)1.将函数y =sin ⎝ ⎛⎭⎪⎫2x -π3图象上的点P ⎝ ⎛⎭⎪⎫π4,t 向左平移s (s >0)个单位长度得到点P ′.若P ′位于函数y =sin 2x 的图象上,则( )A .t =12,s 的最小值为π6 B .t =32,s 的最小值为π6 C .t =12,s 的最小值为π3 D .t =32,s 的最小值为π3A [因为点P ⎝ ⎛⎭⎪⎫π4,t 在函数y =sin ⎝ ⎛⎭⎪⎫2x -π3的图象上,所以t =sin ⎝ ⎛⎭⎪⎫2×π4-π3=sin π6=12.所以P ⎝ ⎛⎭⎪⎫π4,12.将点P 向左平移s (s >0)个单位长度得P ′⎝ ⎛⎭⎪⎫π4-s ,12.因为P ′在函数y =sin 2x 的图象上,所以sin 2⎝ ⎛⎭⎪⎫π4-s =12,即cos 2s =12,所以2s =2k π+π3或2s =2k π+53π,即s =k π+π6或s =k π+5π6(k ∈Z ),所以s 的最小值为π6.]2.若函数y =cos 2x +3sin 2x +a 在⎣⎢⎡⎦⎥⎤0,π2上有两个不同的零点,则实数a的取值范围为________.(-2,-1] [由题意可知y =2sin ⎝ ⎛⎭⎪⎫2x +π6+a ,该函数在⎣⎢⎡⎦⎥⎤0,π2上有两个不同的零点,即y =-a ,y =2sin ⎝ ⎛⎭⎪⎫2x +π6在⎣⎢⎡⎦⎥⎤0,π2上有两个不同的交点.结合函数的图象可知1≤-a <2,所以-2<a ≤-1.]3.函数f (x )=A sin(ωx +φ)⎝ ⎛⎭⎪⎫A >0,ω>0,0<φ<π2的部分图象如图3-4-6所示.图3-4-6(1)求f (x )的解析式; (2)设g (x )=⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫x -π122,求函数g (x )在x ∈⎣⎢⎡⎦⎥⎤-π6,π3上的最大值,并确定此时x 的值.[解] (1)由题图知A =2,T 4=π3,则2πω=4×π3,2分 ∴ω=32.又f ⎝ ⎛⎭⎪⎫-π6=2sin ⎣⎢⎡⎦⎥⎤32×⎝ ⎛⎭⎪⎫-π6+φ =2sin ⎝ ⎛⎭⎪⎫-π4+φ=0,∴sin ⎝ ⎛⎭⎪⎫φ-π4=0.4分∵0<φ<π2, ∴-π4<φ-π4<π4,∴φ-π4=0,即φ=π4,∴f (x )的解析式为f (x )=2sin ⎝ ⎛⎭⎪⎫32x +π4.7分(2)由(1)可得f ⎝ ⎛⎭⎪⎫x -π12=2sin ⎣⎢⎡⎦⎥⎤32⎝⎛⎭⎪⎫x -π12+π4 =2sin ⎝ ⎛⎭⎪⎫32x +π8,10分∴g (x )=⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫x -π122=4×1-cos ⎝ ⎛⎭⎪⎫3x +π42=2-2cos ⎝ ⎛⎭⎪⎫3x +π4.12分∵x ∈⎣⎢⎡⎦⎥⎤-π6,π3,∴-π4≤3x +π4≤5π4,∴当3x +π4=π,即x =π4时,g (x )max =4.15分。
2018高考数学考点突破三角函数与解三角形:函数y=Asin
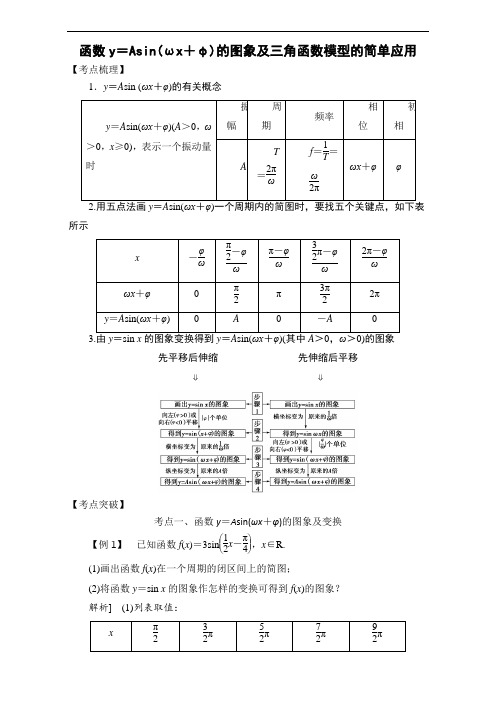
函数y =Asin(ωx +φ)的图象及三角函数模型的简单应用【考点梳理】1.y =A sin (ωx +φ)的有关概念所示先平移后伸缩 先伸缩后平移⇓ ⇓【考点突破】考点一、函数y =A sin(ωx +φ)的图象及变换【例1】 已知函数f (x )=3sin ⎝ ⎛⎭⎪⎫12x -π4,x ∈R.(1)画出函数f (x )在一个周期的闭区间上的简图;(2)将函数y =sin x 的图象作怎样的变换可得到f (x )的图象? 解析] (1)列表取值:(2)先把y =sin x 的图象向右平移π4个单位,然后把所有点的横坐标扩大为原来的2倍,再把所有点的纵坐标扩大为原来的3倍,得到f (x )的图象.【类题通法】1.变换法作图象的关键是看x 轴上是先平移后伸缩还是先伸缩后平移,对于后者可利用ωx +φ=ω⎝ ⎛⎭⎪⎫x +φω确定平移单位. 2.用“五点法”作图,关键是通过变量代换,设z =ωx +φ,由z 取0,π2,π,32π,2π来求出相应的x ,通过列表,描点得出图象.如果在限定的区间内作图象,还应注意端点的确定.【对点训练】1. (1)将函数y =2sin ⎝ ⎛⎭⎪⎫2x +π6的图象向右平移14个周期后,所得图象对应的函数为( )A .y =2sin ⎝ ⎛⎭⎪⎫2x +π4B .y =2sin ⎝ ⎛⎭⎪⎫2x +π3C .y =2sin ⎝ ⎛⎭⎪⎫2x -π4D .y =2sin ⎝ ⎛⎭⎪⎫2x -π3(2)函数y =sin x -3cos x 的图象可由函数y =2sin x 的图象至少向右平移________个单位长度得到.答案] (1)D (2)π3解析] (1)函数y =2sin ⎝ ⎛⎭⎪⎫2x +π6的周期为π,将函数y =2sin ⎝ ⎛⎭⎪⎫2x +π6的图象向右平移14个周期即π4个单位长度,所得图象对应的函数为y =2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x -π4+π6=2sin ⎝ ⎛⎭⎪⎫2x -π3,故选D.(2)∵y =sin x -3cos x =2sin ⎝ ⎛⎭⎪⎫x -π3,∴函数y =sin x -3cos x 的图象可由函数y =2sin x 的图象向右平移π3个单位长度得到.考点二、求函数y =A sin(ωx +φ)的解析式【例2】 (1)函数y =A sin(ωx +φ)的部分图象如图所示,则( ) A .y =2sin ⎝ ⎛⎭⎪⎫2x -π6 B .y =2sin ⎝ ⎛⎭⎪⎫2x -π3C .y =2sin ⎝ ⎛⎭⎪⎫x +π6D .y =2sin ⎝ ⎛⎭⎪⎫x +π3(2)已知函数y =A sin(ωx +φ)+b (A >0,ω>0)的最大值为4,最小值为0,最小正周期为π2,直线x =π3是其图象的一条对称轴,则下面各式中符合条件的解析式为( )A .y =4sin ⎝ ⎛⎭⎪⎫4x +π6B .y =2sin ⎝ ⎛⎭⎪⎫2x +π3+2C .y =2sin ⎝ ⎛⎭⎪⎫4x +π3+2D .y =2sin ⎝ ⎛⎭⎪⎫4x +π6+2答案] (1)A (2)D解析] (1)由图象知T 2=π3-⎝ ⎛⎭⎪⎫-π6=π2,故T =π,因此ω=2ππ=2.又图象的一个最高点坐标为⎝ ⎛⎭⎪⎫π3,2,所以A =2,且2×π3+φ=2k π+π2(k ∈Z),故φ=2k π-π6(k ∈Z),结合选项可知y =2sin ⎝ ⎛⎭⎪⎫2x -π6.故选A.(2)由函数y =A sin(ωx +φ)+b 的最大值为4,最小值为0,可知b =2,A =2.由函数的最小正周期为π2,可知2πω=π2,得ω=4.由直线x =π3是其图象的一条对称轴,可知4×π3+φ=k π+π2,k ∈Z ,从而φ=k π-5π6,k ∈Z ,故满足题意的是y =2sin ⎝ ⎛⎭⎪⎫4x +π6+2.【类题通法】确定y =A sin(ωx +φ)+b (A >0,ω>0)的步骤和方法(1)求A ,b :确定函数的最大值M 和最小值m ,则A =M -m 2,b =M +m2; (2)求ω:确定函数的周期T ,则可得ω=2πT ; (3)求φ:常用的方法有:①代入法:把图象上的一个已知点代入(此时A ,ω,b 已知)或代入图象与直线y =b 的交点求解(此时要注意交点在上升区间上还是在下降区间上).②五点法:确定φ值时,往往以寻找“五点法”中的某一个点为突破口.“第一点”(即图象上升时与x 轴的交点)时ωx +φ=0;“第二点”(即图象的“峰点”)时ωx +φ=π2;“第三点”(即图象下降时与x 轴的交点)时ωx +φ=π;“第四点”(即图象的“谷点”)时ωx +φ=3π2;“第五点”时ωx +φ=2π.【对点训练】2.函数f (x )=A sin(ωx +φ)(A >0,ω>0)的部分图象如图所示,则f ⎝ ⎛⎭⎪⎫11π24的值为( )A .-62B .-32C .-22 D .-1答案] D解析] 由图象可得A =2,最小正周期T =4⎝ ⎛⎭⎪⎫7π12-π3=π,则ω=2πT =2.又f ⎝ ⎛⎭⎪⎫7π12=2sin ⎝ ⎛⎭⎪⎫7π6+φ=-2,解得φ=-5π3+2k π(k ∈Z),即k =1,φ=π3,则f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π3,f ⎝ ⎛⎭⎪⎫11π24=2sin ⎝ ⎛⎭⎪⎫11π12+π3=2sin 5π4=-1,故选D. 考点三、函数y =A sin(ωx +φ)图象与性质的应用【例3】 已知函数f (x )=4tan x sin ⎝ ⎛⎭⎪⎫π2-x ·cos ⎝ ⎛⎭⎪⎫x -π3- 3.(1)求f (x )的定义域与最小正周期; (2)讨论f (x )在区间⎣⎢⎡⎦⎥⎤-π4,π4上的单调性.解析](1)f (x )的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠π2+k π,k ∈Z. f (x )=4tan x cos x cos ⎝ ⎛⎭⎪⎫x -π3- 3=4sin x cos ⎝ ⎛⎭⎪⎫x -π3- 3=4sin x ⎝ ⎛⎭⎪⎫12cos x +32sin x - 3=2sin x cos x +23sin 2x - 3 =sin 2x +3(1-cos 2x )- 3 =sin 2x -3cos 2x =2sin ⎝ ⎛⎭⎪⎫2x -π3.所以f (x )的最小正周期T =2π2=π.(2)令z =2x -π3,则函数y =2sin z 的单调递增区间是⎣⎢⎡⎦⎥⎤-π2+2k π,π2+2k π,k ∈Z.由-π2+2k π≤2x -π3≤π2+2k π,得-π12+k π≤x ≤5π12+k π,k ∈Z.设A =⎣⎢⎡⎦⎥⎤-π4,π4,B =x ⎪⎪⎪-π12+k π≤x ≤5π12+k π,k ∈Z ,易知A ∩B =⎣⎢⎡⎦⎥⎤-π12,π4.所以当x ∈⎣⎢⎡⎦⎥⎤-π4,π4时,f (x )在区间⎣⎢⎡⎦⎥⎤-π12,π4上单调递增,在区间⎣⎢⎡⎦⎥⎤-π4,-π12上单调递减.【类题通法】讨论函数的单调性,研究函数的周期性、奇偶性与对称性,都必须首先利用辅助角公式,将函数化成一个角的一种三角函数.【对点训练】3.设函数f (x )=32-3sin 2ωx -sin ωx cos ωx (ω>0),且y =f (x )图象的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值;(2)求f (x )在区间⎣⎢⎡⎦⎥⎤π,3π2上的最大值和最小值.解析] (1)f (x )=32-3sin 2ωx -sin ωx cos ωx =32-3·1-cos 2ωx 2-12sin 2ωx=32cos 2ωx -12sin 2ωx =-sin ⎝ ⎛⎭⎪⎫2ωx -π3.因为图象的一个对称中心到最近的对称轴的距离为π4,又ω>0,所以2π2ω=4×π4,因此ω=1.(2)由(1)知f (x )=-sin ⎝ ⎛⎭⎪⎫2x -π3.当π≤x ≤3π2时,5π3≤2x -π3≤8π3,所以-32≤sin ⎝ ⎛⎭⎪⎫2x -π3≤1,则-1≤f (x )≤32.故f (x )在区间⎣⎢⎡⎦⎥⎤π,3π2上的最大值和最小值分别为32,-1.考点四、三角函数模型的简单应用【例4】 某实验室一天的温度(单位:℃)随时间t (单位:h)的变化近似满足函数关系:f (t )=10-3cos π12t -sin π12t ,t ∈0,24).(1)求实验室这一天的最大温差;(2)若要求实验室温度不高于11 ℃,则在哪段时间实验室需要降温? 解析] (1)因为f (t )=10-2⎝ ⎛⎭⎪⎫32cos π12t +12sin π12t=10-2sin ⎝ ⎛⎭⎪⎫π12t +π3,又0≤t <24,所以π3≤π12t +π3<7π3,-1≤sin ⎝ ⎛⎭⎪⎫π12t +π3≤1. 当t =2时,sin ⎝ ⎛⎭⎪⎫π12t +π3=1;当t =14时,sin ⎝ ⎛⎭⎪⎫π12t +π3=-1.于是f (t )在0,24)上取得最大值12,取得最小值8.故实验室这一天最高温度为12 ℃,最低温度为8 ℃,最大温差为4 ℃. (2)依题意,当f (t )>11时实验室需要降温. 由(1)得f (t )=10-2sin ⎝ ⎛⎭⎪⎫π12t +π3,故有10-2sin ⎝ ⎛⎭⎪⎫π12t +π3>11,即sin ⎝ ⎛⎭⎪⎫π12t +π3<-12.又0≤t <24,因此7π6<π12t +π3<11π6,即10<t <18. 故在10时至18时实验室需要降温. 【类题通法】1.三角函数模型在实际中的应用体现在两个方面:一是用已知的模型去分析解决实际问题,二是把实际问题抽象转化成数学问题,建立三角函数模型解决问题,其关键是合理建模.2.建模的方法是认真审题,把问题提供的“条件”逐条地“翻译”成“数学语言”,这个过程就是数学建模的过程.【对点训练】4.如图,某港口一天6时到18时的水深变化曲线近似满足函数y =3sin ⎝ ⎛⎭⎪⎫π6x +φ+k .据此函数可知,这段时间水深(单位:m)的最大值为( )A .5B .6C .8D .10答案] C解析] 根据图象得函数的最小值为2,有-3+k =2,k =5,最大值为3+k =8.。
高三数学 函数y=Asinωx+φ的图象与性质期末复习测试卷 文

函数y=Asin(ωx+φ)的图象与性质(40分钟)一、选择题1.函数f(x)=sin的图象的一条对称轴是( )A.x=B.x=C.x=-D.x=-2.(2013·浙江高考)函数f(x)=sinxcosx+cos2x的最小正周期和振幅分别是( )A.π,1B.π,2C.2π,1D.2π,23.函数y=2cos2-1是( )A.最小正周期为π的奇函数B.最小正周期为π的偶函数C.最小正周期为的奇函数D.最小正周期为的偶函数4.(2013·兰州模拟)已知函数f(x)=sin(ωx+φ)-cos(ωx+φ),其图象相邻的两条对称轴方程为x=0与x=,则( )A.f(x)的最小正周期为2π,且在 (0,π)上为单调递增函数B.f(x)的最小正周期为2π,且在(0,π)上为单调递减函数C.f(x)的最小正周期为π,且在上为单调递增函数D.f(x)的最小正周期为π,且在上为单调递减函数5.设函数f(x)=tan(ωx+φ)(ω>0),条件p:“f(0)=0”;条件q:“f(x)为奇函数”,则p是q的( )A.充分不必要条件B.既不充分也不必要条件C.必要不充分条件D.充分必要条件6.(2013·山东高考)将函数y=sin(2x +φ)的图象沿x轴向左平移个单位后,得到一个偶函数的图象,则φ的一个可能取值为( )A. B. C.0 D.-二、填空题7.(2013·江西高考)设f(x)=sin3x+cos3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是.8.将函数y=f(x)图象上所有点的纵坐标变为原来的4倍,横坐标变为原来的2倍,然后把所得图象上的所有点沿x轴向左平移个单位长度,这样得到的曲线和函数y=2sinx的图象相同,则函数y=f(x)的解析式为.9.(2013·重庆高考)设0≤α≤π,不等式8x2-(8sinα)x+cos 2α≥0对x∈R恒成立,则α的取值范围为.三、解答题10.已知f(x)=sin+sin+2cos2x-1,x∈R.(1)求函数f(x)的最小正周期.(2)求函数f(x)在区间上的最大值和最小值.11.已知函数f(x)=2acos2x+bsinxcosx-,且f(0)=,f=.(1)求f(x)的单调递减区间.(2)函数f(x)的图象经过怎样的平移才能使所得图象关于原点对称?12.(2013·宿州模拟)已知函数f(x)=2sinx-2cosx.(1)若x∈[0,π],求f(x)的最大值和最小值.(2)若f(x)=0,求.答案解析1.【解析】选C.函数f(x)=sin的图象的对称轴是x-=kπ+,k∈Z,即x=kπ+,k∈Z.当k=-1时,x=-π+=-.2.【解析】选A.f(x)=sinxcosx+cos2x=sin2x+cos2x=sin ,所以A=1,T=π.3.【解析】选A.y=2cos 2-1=cos=sin2x 为奇函数,T==π.4.【解析】选C.f(x)=2sin,由题意知函数f(x)的周期为T=π,则ω==2,由x=0为f(x)的对称轴,f(0)=2sin ()3πϕ-且|φ|<知φ=-,因此,f(x)=2sin =-2cos2x,故选C.5.【解析】选A.f(0)=0,则tan φ=0,所φ=k π(k ∈Z),所以f(x)=tan(ωx+k π)=tan ωx(k ∈Z),故f(x)为奇函数;而φ=时f(x)为奇函数,但是f(0)≠0, 故p 是q 的充分不必要条件.6.【解析】选 B.将函数y=sin(2x +φ)的图象沿x 轴向左平移个单位,得到函数y=sin =sin,因为此时函数为偶函数,所以+φ=+k π,k ∈Z,即φ=+k π,k ∈Z.【变式备选】为了使变换后的函数的图象关于点成中心对称,只需将原函数y=sin 2x+的图象( ) A.向左平移个单位长度B.向左平移个单位长度C.向右平移个单位长度D.向右平移个单位长度 【解析】选C.函数y=sin 的图象的对称中心为(k ∈Z),其中离点最近的对称中心为,故只需将原函数的图象向右平移个单位长度即可.7.【解析】由于f(x)=sin3x+cos3x=2sin,则|f(x)|=2≤2,要使|f(x)|≤a 恒成立,则a ≥2. 答案:[2,+∞)8.【解析】本题只需将函数y=2sinx逆过来思考即可,即先将函数y=2sinx图象上的所有点向右平移个单位长度,再将纵坐标变为原来的,横坐标变为原来的即可.答案:y=sin9.【解析】因为不等式8x2-(8sinα)x+cos2α≥0对x∈R恒成立,所以Δ=64sin2α-32cos2α≤0,即64sin2α-32+64sin2α≤0,解得0≤sinα≤(0≤α≤π).因为0≤α≤π,所以α∈∪.答案:∪10.【解析】(1)f(x)=sin2x·cos+cos2x·sin+ sin2x·cos- cos2x·sin+cos2x=sin2x+cos2x=sin,所以f(x)的最小正周期T==π.(2)因为f(x)在区间上是增函数,在区间上是减函数,又f=-1,f=,f=1,故函数f(x)在区间上的最大值为,最小值为-1.11.【解析】(1)由f(0)=,得2a-=,故a=.由f=,得+-=,所以b=1.可得f(x)=cos2x+sinxcosx-=cos2x+sin2x=sin.由+2kπ≤2x+≤+2kπ,k∈Z,得+kπ≤x≤+kπ,k∈Z.所以f(x)的单调递减区间是(k∈Z).(2)因为f(x)=sin2,所以由奇函数y=sin2x的图象向左平移个单位即得到y=f(x)的图象,故函数f(x)的图象向右平移+π(k∈Z)个单位或向左平移+π(k∈Z)个单位后,对应的函数即成为奇函数,图象关于原点对称.【方法总结】三角函数的性质问题的解题策略(1)三角函数的性质问题,往往都要先化成f(x)=Asin(ωx+φ)的形式再求解.(2)要正确理解三角函数的性质,关键是记住三角函数的图象,根据图象并结合整体代入的基本思想即可求三角函数的单调性、最值与周期.12.【解析】(1)f(x)=2sinx-2cosx=4=4sin,又因为x∈[0,π],所以,-≤x-≤,所以,-2≤4sin≤4,所以f(x)max=4,f(x)min=-2.(2)由f(x)=0,所以2sinx=2cosx,得tanx=,=====2-.。
2018届高考数学复习-三角函数:(四)函数y=Asin(ωx+φ)的图象变换及应用(试题版)-4

题型1:函数y =Asin(ωx +φ)的图象及变换 【典型例题】[例1]已知函数y =2sin(2x +π3).(1)求它的振幅、周期、初相;(2)用“五点法”作出它在一个周期内的图象;(3)说明y =2sin(2x +π3)的图象可由y =sin x 的图象经过怎样的变换而得到.[例2]►(1)要得到函数y =3sin(x +π4)的图象,只需将函数y =3sin 2x 的图象向________平移________个单位.►(2)把函数y =sin(5x -π2)的图象向右平移π4个单位,再把所得函数图象上各点的横坐标缩短为原来的12,所得的函数解析式为( )A.y =sin(10x -3π4)B.y =sin(10x -7π2)C.y =sin(10x -3π2)D.y =sin(10x -7π4)►(3)[2014·浙江]为了得到函数y =sin 3x +cos 3x 的图像,可以将函数y =2cos 3x 的图像( ) A.向右平移π12个单位 B.向右平移π4个单位 C.向左平移π12个单位 D.向左平移π4个单位►(4)(2016全国III 理)函数y =sin x -3cos x 的图像可由函数y =sin x +3cos x 的图像至少向右平移________个单位长度得到.[例3]►(1)为了得到函数y=sin(2x -π6)的图象,可以将函数y=cos2x 的图象 ( )A.向右平移π6个单位长度B.向右平移π3个单位长度C.向左平移π6个单位长度D.向左平移π3个单位长度►(2)要得到函数y =2cos x 的图象,只需将函数y =2sin(2x +π4)的图象上所有的点的( )A.横坐标伸长到原来的2倍,再向左平移π4个单位长度 B.横坐标伸长到原来的2倍,再向右平移π8个单位长度 C.横坐标缩短到原来的12倍,再向右平移π4个单位长度 D.横坐标缩短到原来的12倍, 再向左平移π8个单位长度►(3)[2013课标Ⅱ]函数y =cos(2x +φ)(-π≤φ<π)的图像向右平移π2个单位后与函数y =sin(2x +π3)的图像重合,则φ=___.[例4]►(1)[2014·安徽]若将函数f (x )=sin 2x +cos 2x 的图像向右平移φ个单位,所得图像关于y 轴对称,则φ的最小正值是( )A.π8B.π4C.3π8D.3π4►(2)(2013·山东改编)将函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为( ). A.3π4 B.π4 C.3π8 D.-π4►(3)(2013·合肥质检)将函数f (x )=A sin(ωx +φ)(A >0,ω>0)的图象向左平移π2个单位,所得函数的图象与函数y =f (x )的图象关于x 轴对称,则ω的值不可能是( ). A.2 B.4 C.6 D.10►(4)(2016全国II 理)若将函数y =2sin2x 的图像向左平移π12个单位长度,则平移后图象的对称轴为( ) A.x =k π2-π6(k ∈Z) B.x =k π2+π6(k ∈Z)C.x =k π2-π12(k ∈Z)D.x =k π2+π12(k ∈Z)[例5]►(1)[2014重庆]将函数f (x )=sin(ωx +φ)(ω>0),(-π2≤φ<π2)图像上每一点的横坐标缩短为原来的一半,再向右平移π6个单位长度得到y =sin x 的图像,则f (π6)=____.►(2)将函数y =sin x 的图象向左平移φ (0≤φ<2π)个单位后,得到函数y =sin(x -π6)的图象,则φ等于( ) A .π6 B.5π6 C.7π6 D.11π6►(3)设函数f (x )=cos ωx (ω>0),将f (x )的图象向右平移π3个单位长度后所得的图象与原图象重合,则ω的最小值=( ) A.13 B.3 C.6 D.9►(4)[2014·辽宁]将函数y =3sin(2x +π3)的图像向右平移π2个单位长度,所得图像对应的函数( )A.在[π12,7π12]上单调递减B.在[π12,7π12]上单调递增 C.在[-π6,π3]上单调递减 D.在[-π6,π3]上单调递增►(5)[2017全国III 理]设函数f (x )=cos(x +π3),则下列结论错误的是( )A.f (x )的一个周期为-2πB.f (x )的图像关于直线x =8π3对称C.f (x +π)的一个零点为x =π6D.f (x )在(π2,π)单调递减【变式训练】 1.(2016四川文)为了得到函数y=sin(x +π3)的图象,只需把函数y=sin x 的图象上所有的点( )A.向左平移π3个单位长度B.向右平移π3个单位长度C.向上平移π3个单位长度D.向下平移π3个单位长度2.(2012·浙江)把函数y =cos 2x +1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图象是( )3.(2016全国III 文)函数y =sin x -3cos x 的图象可由函数y =2sin x 的图象至少向右平移_____个单位长度得到.4.(2014·湖州二模)将函数y =sin 2x +cos 2x 的图象向左平移π4个单位长度,所得图象对应的函数解析式可以是( ). A.y =cos 2x +sin 2x B.y =cos 2x -sin 2x C.y =sin 2x -cos 2x D.y =sin x cos x 5.(2015·烟台市检测)将函数y =f (x )图象向上平移一个单位长度,再向左平移π4个单位长度,则所得图象对应的函数y =2cos 2x ,则f (x )=________.6.(2013湖北文)将函数y =3cos x +sin x (x ∈R)的图象向左平移m (m >0)个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是( ) A.π12 B.π6 C.π3 D.5π67.[2014·福建]将函数y =sin x 的图像向左平移π2个单位,得到函数y =f (x )的图像,则下列说法正确的是( ) A.f (x )是奇函数 B.f (x )的图像关于直线x =π2对称 C.f (x )的周期为π D.f (x )的图像关于点(-π2,0)对称8.[2017全国I 理]已知曲线C 1:y =cos x , C 2:y =sin (2x +2π3),则下面结论正确的是( )A.把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2. B.把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2. C.把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2.D.把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2. 题型2:求函数y =Asin(ωx +φ)的解析式【典型例题】[例1]►(1)(2013四川)函数f (x )=2sin(ωx +φ)(-π2<φ<π2)的部分图象如图所示,则ω,φ的值分别是( ) A.2,-π3 B.2,-π6 C.4,-π6 D.4,π3►(2)(2011·江苏)已知f (x )=A sin(ωx +φ) (A ,ω,φ为常数,A >0,ω>0)的部分图象如图所示,则f (0)的值是______.►(3)已知函数f (x )=A sin(ωx +φ)+h (ω>0,0<φ<π2)的图象如图所示,则f (x )=( )A.4sin(x 2+π4)+2 B.-4sin(x2-π4)+2 C.2sin(x2+π4)+4 D.-2sin(x2+π4)+4[例2]►(1)已知函数f (x )=A sin(ωx +φ) (A >0,|φ|<π2,ω>0)的部分图象如图所示,则该函数的解析式为 .►(2)(2011·辽宁)已知函数f (x )=A tan(ωx +φ)(ω>0,|φ|<π2),y =f (x )的部分图象如图所示,则f (π24)等于 ( ) A.2+ 3 B. 3 C.33 D.2- 3►(3)(2013大纲文)若函数y =sin(ωx +φ)(ω>0)的部分图象如图所示,则ω=( )A.5B.4C.3D.2[例3]►(1)(2015·陕西文理)如图,某港口一天6时到18时的水深变化曲线近似满足函数y =3sin(π6x +φ)+k .据此函数可知,这段时间水深(单位:m )的最大值为( )A.5B.6C.8D.10►(2)如图所示,某地夏天从8~14时用电量变化曲线近似满足函数y =A sin(ωx +φ)+b ,φ∈(0,π).①求这一天的最大用电量及最小用电量; ②写出这段曲线的函数解析式.[例4]►(1)已知f (x )=sin(ωx +π3) (ω>0),f (π6)=f (π3),且f (x )在区间(π6,π3)上有最小值,无最大值,则ω=________.►(2)已知函数f (x )=sin(ωx +φ) (ω>0,-π2≤φ≤π2)的图象上的两个相邻的最高点和最低点的距离为22,且过点(2,-12),则函数解析式f (x )=_______________. ►(3)[2017天津理]设函数f (x )=2sin(ωx +φ),x ∈R ,其中ω>0,|φ|<π.若f(5π8)=2,f(11π8)=0,且f(x)的最小正周期大于2π,则()A.ω=23,φ=π12B.ω=23,φ=-11π12C.ω=13,φ=-11π24D.ω=13,φ=7π24►(4)函数y=A sin(ωx+φ)(A>0,ω>0)的图象过点P(π12,0),图象上与点P最近的一个最高点是Q(π3,5).①求函数的解析式;②求函数f(x)的递增区间.【变式训练】1.函数f(x)=A sin(2x+φ)(A>0,φ∈R)的部分图象如图所示,那么f(0)=()A.-12B.-32C.-1D.- 32.函数y=A sin(ωx+φ) (A,ω,φ为常数,A>0,ω>0)在闭区间[-π,0]上的图象如图所示,则ω=________.3.(2016全国Ⅱ文)函数y=A sin(ωx+φ)的部分图象如图所示,则()A.y=2sin(2x-π6) B.y=2sin(2x-π3)C.y=2sin(x+π6) D.y=2sin(x+π3)4.已知函数y=A sin(ωx+φ)+b(A>0,ω>0)的最大值为4,最小值为0,最小正周期为π2,直线x=π3是其图象的一条对称轴,则下面各式中符合条件的解析式为()A.y=4sin(4x+π6)B.y=2sin(2x+π3)+2C.y=2sin(4x+π3)+2 D.y=2sin(4x+π6)+25.电流强度I(安)随时间t(秒)变化的函数I=A sin(ωt+φ)(A>0,ω>0,0<φ<π2)的图象如图所示,则当t=1100秒时,电流强度是()A.-5安B.5安C.53安D.10安6.[2014·湖北]某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:f(t)=10-3cosπ12t-sinπ12t,t∈[0,24).(1)求实验室这一天上午8时的温度;(2)求实验室这一天的最大温差.7.(2015湖南理)将函数f(x)=sin 2x的图像向右平移φ(0<φ<π2)个单位后得到函数g(x)的图像,若对满足|f(x1)-g(x2)|=2的x1,x2,有|x1-x2|min=π3,则φ=()A.5π12B.π3C.π4D.π68.[2017全国I文]函数y=sin 2x1-cos x的部分图像大致为( )。
高考数学专题复习 专题4 三角函数、解三角形 第27练

(江苏专用)2018版高考数学专题复习 专题4 三角函数、解三角形第27练 函数y =Asin(ωx +φ)的图像与性质练习 文训练目标 (1)三角函数图象的简图;(2)三角函数图象的变换.训练题型(1)“五点法”作简图;(2)已知函数图象求解析式;(3)三角函数图象变换;(4)三角函数图象的应用.解题策略 (1)y =A sin(ωx +φ)的基本画法“五点法”作图;(2)求函数解析式时φ可采用“代点法”;(3)三角函数图象每一次变换只针对“x ”而言;(4)利用图象可解决方程解的个数、不等式问题等.1.(2016·徐州模拟)函数y =2sin(2x +6)在x ∈(0,2)上的值域为________.2.(2016·南通二模)若函数f (x )=2sin(ωx +π3)(ω>0)的图象与x 轴相邻两个交点间的距离为2,则实数ω的值为________.3.(2016·苏锡常一模)将函数y =3sin(2x +π4)的图象向左平移φ(0<φ<π2)个单位长度后,所得函数图象关于原点中心对称,则φ=________.4.(2016·长春三调)函数f (x )=sin(2x +φ)⎝⎛⎭⎪⎫|φ|<π2的图象向左平移π6个单位后关于原点对称,则函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上的最小值为________.5.(2016·安庆第二次模拟)已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2)的部分图象如图所示,则f (x )的递增区间为______________________.6.(2016·扬州期中)将函数f (x )=A sin(ωx +φ)(A >0,ω>0,-π2<φ<π2)图象上每一点的横坐标变为原来的2倍(纵坐标不变),然后把所得图象上的所有点沿x 轴向右平移π3个单位,得到函数y =2sin x 的图象,则f (φ)=________.7.若函数y =A sin(ωx +φ)⎝⎛⎭⎪⎫A >0,ω>0,|φ|<π2在一个周期内的图象如图所示,M ,N 分别是这段图象的最高点与最低点,且OM →·ON →=0,则A ·ω=________.8.(2016·昆明测试)函数y =sin(πx +φ)(φ>0)的部分图象如图所示,设P 是图象的最高点,A ,B 是图象与x 轴的交点,则tan ∠APB =________.9.(2016·开封第一次摸底)已知函数f (x )=sin 2x cos φ+cos 2x sin φ(x ∈R ),其中φ为实数,且f (x )≤f ⎝⎛⎭⎪⎫2π9对任意实数R 恒成立,记p =f ⎝ ⎛⎭⎪⎫2π3,q =f ⎝ ⎛⎭⎪⎫5π6,r =f ⎝ ⎛⎭⎪⎫7π6,则p 、q 、r 的大小关系是______________.10.(2016·宿迁、徐州三模)在平面直角坐标系xOy 中,直线y =1与函数y =3sinπ2x (0≤x ≤10)的图象所有交点的横坐标之和为________.11.(2016·辽源联考)若0≤x ≤π,则函数y =sin ⎝ ⎛⎭⎪⎫π3+x ·cos ⎝ ⎛⎭⎪⎫π2+x 的单调递增区间为__________.12.(2015·陕西改编)如图,某港口一天6时到18时的水深变化曲线近似满足函数y =3sin ⎝ ⎛⎭⎪⎫π6x +φ+k ,据此函数可知,这段时间水深(单位:m)的最大值为________.13.关于x 的方程3sin 2x +cos 2x =k +1在⎣⎢⎡⎦⎥⎤0,π2内有两相异实根,则k 的取值范围是__________.14.(2016·皖北协作区联考)已知函数f (x )=sin x +3cos x ,则下列命题正确的是__________.(写出所有正确命题的序号)①f (x )的最大值为2;②f (x )的图象关于点⎝ ⎛⎭⎪⎫-π6,0对称;③f (x )在区间⎝ ⎛⎭⎪⎫-5π6,π6上单调递增;④若实数m 使得方程f (x )=m 在[0,2π]上恰好有三个实数解x 1,x 2,x 3,则x 1+x 2+x 3=7π3;⑤f (x )的图象与g (x )=2sin ⎝ ⎛⎭⎪⎫x -2π3的图象关于x 轴对称.答案精的1.(-1,2] 2.π2 3.3π8 4.-325.[k π-π12,k π+5π12](k ∈Z )6.0解析 由题设可得f (x )=2sin(2x +π3),所以φ=π3,从而f (π3)=2sin π=0.7.76π 解析 由题中图象知T 4=π3-π12,∴T =π,∴ω=2.∵M ⎝ ⎛⎭⎪⎫π12,A ,N ⎝ ⎛⎭⎪⎫712π,-A , 由OM →·ON →=0,得7π2122=A 2,∴A =712π,∴A ·ω=76π. 8.8解析 函数y =sin(πx +φ)的周期T =2ππ=2,最大值为1,过点P 作PD ⊥x 轴于D ,则AD 是四分之一个周期,即AD =12,DB =32,DP =1,在Rt△APD 中,tan ∠APD =12;在Rt△BPD中,tan ∠BPD =32,所以tan ∠APB =tan(∠APD +∠BPD )=12+321-12×32=8.9.p <q <r解析 ∵f (x )=sin 2x cos φ+cos 2x sin φ=sin(2x +φ), ∴f (x )的最小正周期T =π.∵f (x )≤f ⎝ ⎛⎭⎪⎫2π9,∴f ⎝⎛⎭⎪⎫2π9是最大值.∴f (x )=sin ⎝⎛⎭⎪⎫2x +π18, ∴p =sin 25π18,q =sin 31π18,r =sin 7π18,∴p <q <r . 10.30解析 y =3sin π2x 的周期为4,如图,作出函数在区间[0,10]上的图象,与直线y =1共有六个交点,根据图象关于直线x =5对称可知,x 1+x 6=x 2+x 5=x 3+x 4=10,所以六个交点的横坐标之和为30.11.⎣⎢⎡⎦⎥⎤π3,5π6解析 y =sin ⎝ ⎛⎭⎪⎫π3+x cos ⎝ ⎛⎭⎪⎫π2+x=⎝⎛⎭⎪⎫32cos x +12sin x ·(-sin x )=-12sin ⎝ ⎛⎭⎪⎫2x -π6-14,令2k π+π2≤2x -π6≤2k π+3π2,解得k π+π3≤x ≤k π+5π6(k ∈Z ),又0≤x ≤π,则函数的单调递增区间为⎣⎢⎡⎦⎥⎤π3,5π6.12.8解析 由图象知y min =2,因为y min =-3+k ,所以-3+k =2,解得k =5,所以这段时间水深的最大值是y max =3+k =3+5=8. 13.[0,1) 解析3sin 2x +cos 2x=2sin ⎝ ⎛⎭⎪⎫2x +π6,x ∈⎣⎢⎡⎦⎥⎤0,π2,令t =2x +π6∈⎣⎢⎡⎦⎥⎤π6,7π6,作出函数y =2sin t ,t ∈⎣⎢⎡⎦⎥⎤π6,7π6和y =k +1的大致图象如图所示,由图象易知当1≤k +1<2,即0≤k <1时,方程有两相异实根. 14.①③④⑤解析 f (x )=sin x +3cos x =2⎝ ⎛⎭⎪⎫12sin x +32cos x=2sin ⎝⎛⎭⎪⎫x +π3,所以①正确; 因为将x =-π6代入f (x ),得f ⎝ ⎛⎭⎪⎫-π6=2sin(-π6+π3)=1≠0,所以②不正确; 由2k π-π2≤x +π3≤2k π+π2,k ∈Z ,得2k π-5π6≤x ≤2k π+π6,k ∈Z ,所以f (x )在区间⎝ ⎛⎭⎪⎫-5π6,π6上单调递增,所以③正确;若实数m 使得方程f (x )=m 在[0,2π]上恰好有三个实数解,结合函数f (x )=2sin ⎝ ⎛⎭⎪⎫x +π3及y =m 的图象可知,必有x =0,x =2π,此时f (x )=2sin ⎝⎛⎭⎪⎫x +π3=3,另一解为x =π3,即x 1,x 2,x 3满足x 1+x 2+x 3=7π3,所以④正确;因为f (x )=2sin ⎝⎛⎭⎪⎫x +π3=2sin ⎝⎛⎭⎪⎫x +π-2π3 =-2sin ⎝⎛⎭⎪⎫x -2π3=-g (x ),所以⑤正确.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第28练 函数y=Asin (ωx +φ)的图象与性质
一、选择题
1.已知f (x )=sin 2x +3cos 2x ,在直角坐标系下利用“五点法”作f (x )在区间
⎣
⎢⎡⎦⎥⎤-π3,2π3上的图象,应描出的关键点的横坐标依次是()
A .0,π2,π,3π
2,2π
B .-π3,0,π2,2π
3,π
C .-π3,-π6,π
12,π3,7π12,2π3
D .-π3,0,π2,π,3π2,5π3
2.已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π
2)的部分图象如图所示,则函数f (x )
的解析式为()
A .f (x )=2sin(2x +π
3)
B .f (x )=2sin(2x +π
6)
C .f (x )=2sin(2x +π
3
)
D .f (x )=2sin(2x +π
6
)
3.已知f (x )=cos ⎝ ⎛⎭⎪⎫ωx +π3(ω>0)的图象与y =1的图象的两相邻交点间的距离为π,要得到y =f (x )的图象,只需把y =sin ωx 的图象() A .向左平移5
12π个单位
B .向右平移5
12π个单位
C .向左平移11
12
π个单位
D .向右平移11
12
π个单位
4.(2016·长春三调)函数f (x )=sin(2x +φ)⎝
⎛⎭⎪⎫|φ|<π2的图象向左平移π6个单位后关于原
点对称,则函数f (x )在⎣
⎢⎡⎦⎥⎤0,π2上的最小值为()
A .-32
B .-12
C.1
2
D.32
5.(2016·南阳期中)如图所示,M ,N 是函数y =2sin(ωx +φ)(ω>0)的图象与x 轴的交点,点P 在M ,N 之间的图象上运动,当△MPN 的面积最大时PM →·PN →
=0,则ω等于()
A.π4
B.π3
C.π2
D .8
6.(2017·郑州质检)如图,函数f (x )=A sin(ωx +φ)(其中A >0,ω>0,|φ|≤π
2)与坐标
轴的三个交点P 、Q 、R 满足P (1,0),∠PQR =π
4,M (2,-2)为线段QR 的中点,则A 的值为
()
A .2 3 B.73
3
C.833
D .4 3
7.(2016·开封第一次摸底)已知函数f (x )=sin 2x cos φ+cos 2x sin φ(x ∈R ),其中φ为实数,且f (x )≤f ⎝
⎛⎭⎪⎫2π9对任意实数R 恒成立,记p =f ⎝ ⎛⎭⎪⎫2π3,q =f ⎝ ⎛⎭⎪⎫5π6,r =f ⎝ ⎛⎭
⎪⎫7π6,则
p 、q 、r 的大小关系是()
A .r <p <q
B .q <r <p
C .p <q <r
D .q <p <r
二、填空题。
