高考数学一轮复习 第七章 不等式、推理与证明 7.1 二元一次不等式(组)与简单的线性规划问题课件
2020版高考数学大一轮复习第七章不等式推理与证明7.2二元一次不等式(组)与简单的线性规划问题课件

A.1 B.2 C.3 D.4
关闭
由已知条件可以得到可行域,要使目标函数的最小值为2,则需要满足直线
过x+2y=1与x+y=a的交点,易知该交点为(2a-1,1-a),将其代入目标函数
z=2x+6y中,可求得a=1.
关闭
A
解析
答-案20-
考点一
考点二
考点三
������ + ������ ≥ 1, 关闭
7.2 二元一次不等式(组)与 简单的线性规划问题
-2-
年份 2018
2017 2016
2015
2014
简单的
3,5 分(理) 14,4 分(理) 13,4 分(理)
线性规 12,4 分 划
4,4 分 4,5 分(文) 14,4 分(文) 12,4 分(文)
考查要 求
1.了解二元一次不等式的几何意义. 2.掌握平面区域与二元一次不等式组之间的关系,并会 求解简单的二元线性规划问题.
-6-
知识梳理 双击自测
1.不等式x-2y+6<0表示的区域在直线x-2y+6=0的 ( ) A.右上方 B.右下方 C.左上方 D.左下方
画出图形(图略),可知该区域在直线x-2y+6=0的左上方. C
关闭 关闭
解析 答案
-7-
知识梳理 双击自测
2.不等式组 ������������--3���������+��� +26≥<00,表示的平面区域是(
线性规划问 在线性约束条件下求线性目标函数的最大值 或
题
最小值 问题
-5-
知识梳理 双击自测
3.应用 利用线性规划求最值,一般用图解法求解,其步骤是: (1)在平面直角坐标系内作出可行域. (2)考虑目标函数的几何意义,将目标函数进行变形. (3)确定最优解:在可行域内平行移动目标函数变形后的直线,从 而确定最优解. (4)求最值:将最优解代入目标函数即可求出最大值或最小值.
高考数学一轮复习 第七章 不等式 推理与证明 72 一元二次不等式及其解法课件 文

第
七
不等式 推理与证明
章
12/11/2021
第一页,共四十七页。
第二节
一元二次不等式及其解法
12/11/2021
第二页,共四十七页。
高考概览 1.会从实际情境中抽象出一元二次不等式模型;2.通过函数图 象了解一元二次不等式与相应的二次函数、一元二次方程的关系; 3.会解一元二次不等式,对给定的一元二次不等式,会设计求解 的程序框图.
[思路引导] fx的值域为[0,+∞ → fxmin=0 → 得出a、b的关系 → 写出fx<c的解集 → 消去m求出c
利用“三个二次”之间的关系,将不等式、函数、方程之间 相互转化.
12/11/2021
第三十页,共四十七页。
[解析] 由题意知 f(x)=x2+ax+b =x+a22+b-a42. ∵f(x)的值域为[0,+∞),∴b-a42=0,即 b=a42, ∴f(x)=x+a22. 又∵f(x)<c,∴x+a22<c,
12/11/2021
第八页,共四十七页。
(2)解分式不等式时注意准确转化,如:不等式xx- +21≤0 的解 集是 {x|-1<x≤2} .
提示:由xx- +21≤0,得(x+1)(x-2)≤0 且 x≠-1,解得-1<x≤2. 故填{x|-1<x≤2}.
12/11/2021
第九页,共四十七页。
高考数学一轮复习 第七章 不等式、推理与证明 7.2 一元二次不等式及其解法教学案 理 新人教A版-
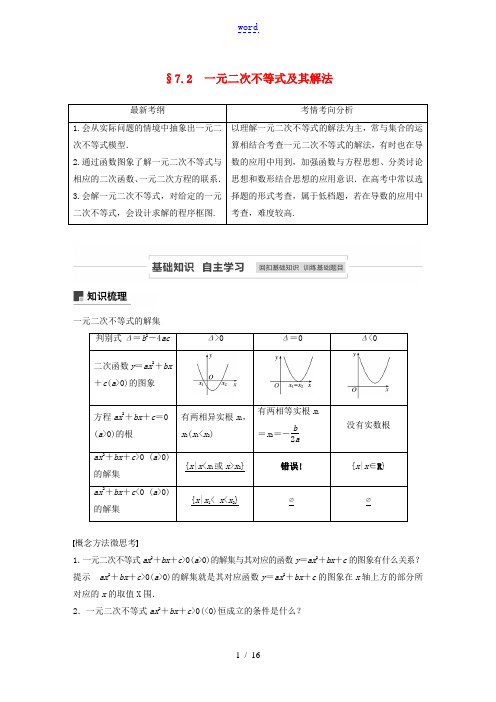
§7.2一元二次不等式及其解法最新考纲考情考向分析1.会从实际问题的情境中抽象出一元二次不等式模型.2.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.3.会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图. 以理解一元二次不等式的解法为主,常与集合的运算相结合考查一元二次不等式的解法,有时也在导数的应用中用到,加强函数与方程思想、分类讨论思想和数形结合思想的应用意识.在高考中常以选择题的形式考查,属于低档题,若在导数的应用中考查,难度较高.一元二次不等式的解集判别式Δ=b2-4ac Δ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象方程ax2+bx+c=0 (a>0)的根有两相异实根x1,x2(x1<x2)有两相等实根x1=x2=-b2a没有实数根ax2+bx+c>0 (a>0)的解集{x|x<x1或x>x2} 错误!{x|x∈R} ax2+bx+c<0 (a>0)的解集{x|x1< x<x2} ∅∅概念方法微思考1.一元二次不等式ax2+bx+c>0(a>0)的解集与其对应的函数y=ax2+bx+c的图象有什么关系?提示ax2+bx+c>0(a>0)的解集就是其对应函数y=ax2+bx+c的图象在x轴上方的部分所对应的x的取值X围.2.一元二次不等式ax2+bx+c>0(<0)恒成立的条件是什么?提示 显然a ≠0.ax2+bx +c >0恒成立的条件是⎩⎪⎨⎪⎧a >0,Δ<0;ax 2+bx +c <0恒成立的条件是⎩⎪⎨⎪⎧a <0,Δ<0.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)若不等式ax 2+bx +c <0的解集为(x 1,x 2),则必有a >0.( √ )(2)若方程ax 2+bx +c =0(a ≠0)没有实数根,则不等式ax 2+bx +c >0的解集为R .( × ) (3)不等式ax 2+bx +c ≤0在R 上恒成立的条件是a <0且Δ=b 2-4ac ≤0.( × ) (4)若二次函数y =ax 2+bx +c 的图象开口向下,则不等式ax 2+bx +c <0的解集一定不是空集.( √ ) 题组二 教材改编2.已知集合A ={x |x 2-x -6>0},则∁R A 等于( ) A .{x |-2<x <3} B .{x |-2≤x ≤3} C .{x |x <-2或x >3} D .{x |x ≤-2或x ≥3} 答案 B解析 ∵x 2-x -6>0,∴(x +2)(x -3)>0,∴x >3或x <-2,即A ={x |x >3或x <-2}.在数轴上表示出集合A ,如图所示.由图可得∁R A ={x |-2≤x ≤3}. 故选B.3.y =log 2(3x 2-2x -2)的定义域是________________. 答案 ⎝ ⎛⎭⎪⎫-∞,1-73∪⎝ ⎛⎭⎪⎫1+73,+∞解析 由题意,得3x 2-2x -2>0,令3x 2-2x -2=0,得x 1=1-73,x 2=1+73,∴3x 2-2x -2>0的解集为 ⎝ ⎛⎭⎪⎫-∞,1-73∪⎝ ⎛⎭⎪⎫1+73,+∞.题组三 易错自纠4.不等式-x 2-3x +4>0的解集为________.(用区间表示) 答案 (-4,1)解析 由-x 2-3x +4>0可知,(x +4)(x -1)<0, 得-4<x <1.5.若关于x 的不等式ax 2+bx +2>0的解集是⎝ ⎛⎭⎪⎫-12,13,则a +b =________.答案 -14解析 ∵x 1=-12,x 2=13是方程ax 2+bx +2=0的两个根,∴⎩⎪⎨⎪⎧a 4-b2+2=0,a 9+b 3+2=0,解得⎩⎪⎨⎪⎧a =-12,b =-2,∴a +b =-14.6.不等式(a -2)x 2+2(a -2)x -4<0,对一切x ∈R 恒成立,则实数a 的取值X 围是________.答案 (-2,2]解析 当a -2≠0时,由⎩⎪⎨⎪⎧a -2<0,Δ<0,得-2<a <2;当a =2时,原式化为-4<0,不等式恒成立, ∴-2<a ≤2.即实数a 的取值X 围是(-2,2].一元二次不等式的求解命题点1 不含参的不等式例1 (2019·某某模拟)已知集合A ={x |x 2-4x <5},则下列选项中正确的是( ) A .-1.2∈A B .30.9∉AC .log 230∈AD .A ∩N ={1,2,3,4} 答案 C解析 因为A ={x |-1<x <5},-1.2∉A ,所以选项A 错误;1<30.9<3,30.9∈A ,所以选项B 错误;0<log 230<log 232=5,log 230∈A ,所以选项C 正确;A ∩N ={0,1,2,3,4},所以选项D 错误.故选C.命题点2 含参不等式例2 解关于x 的不等式ax 2-(a +1)x +1<0(a >0). 解 原不等式变为(ax -1)(x -1)<0,因为a >0,所以⎝⎛⎭⎪⎫x -1a (x -1)<0.所以当a >1时,解得1a<x <1; 当a =1时,解集为∅; 当0<a <1时,解得1<x <1a.综上,当0<a <1时,不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪1<x <1a ; 当a =1时,不等式的解集为∅;当a >1时,不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪1a <x <1. 思维升华 对含参的不等式,应对参数进行分类讨论 (1)根据二次项系数为正、负及零进行分类. (2)根据判别式Δ与0的关系判断根的个数. (3)有两个根时,有时还需根据两根的大小进行讨论.跟踪训练1 (1)(2019·市海淀区期末)不等式x 2+2x -3<0的解集为( ) A .{x |x <-3或x >1}B .{x |x <-1或x >3} C .{x |-1<x <3}D .{x |-3<x <1} 答案 D解析 由x 2+2x -3<0得(x +3)(x -1)<0,解得-3<x <1.故选D. (2)已知不等式ax 2-bx -1>0的解集是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-12<x <-13,则不等式x 2-bx -a ≥0的解集是________.答案 {x |x ≥3或x ≤2}解析 由题意,知-12,-13是方程ax 2-bx -1=0的两个根,且a <0,所以⎩⎪⎨⎪⎧-12+⎝ ⎛⎭⎪⎫-13=ba ,-12×⎝ ⎛⎭⎪⎫-13=-1a,解得⎩⎪⎨⎪⎧a =-6,b =5.故不等式x 2-bx -a ≥0为x 2-5x +6≥0, 解得x ≥3或x ≤2.(3)解不等式12x 2-ax >a 2(a ∈R ). 解 原不等式可化为12x 2-ax -a 2>0, 即(4x +a )(3x -a )>0,令(4x +a )(3x -a )=0,解得x 1=-a 4,x 2=a3.当a >0时,不等式的解集为⎝ ⎛⎭⎪⎫-∞,-a 4∪⎝ ⎛⎭⎪⎫a3,+∞;当a =0时,不等式的解集为(-∞,0)∪(0,+∞); 当a <0时,不等式的解集为⎝ ⎛⎭⎪⎫-∞,a 3∪⎝ ⎛⎭⎪⎫-a4,+∞. 一元二次不等式恒成立问题命题点1 在R 上的恒成立问题例3 已知函数f (x )=mx 2-mx -1.若对于x ∈R ,f (x )<0恒成立,某某数m 的取值X 围. 解 当m =0时,f (x )=-1<0恒成立.当m ≠0时,则⎩⎪⎨⎪⎧m <0,Δ=m 2+4m <0,即-4<m <0.综上,-4<m ≤0,故m 的取值X 围是(-4,0]. 命题点2 在给定区间上的恒成立问题例4 已知函数f (x )=mx 2-mx -1.若对于x ∈[1,3],f (x )<5-m 恒成立,某某数m 的取值X 围.解 要使f (x )<-m +5在x ∈[1,3]上恒成立,即m ⎝ ⎛⎭⎪⎫x -122+34m -6<0在x ∈[1,3]上恒成立.有以下两种方法:方法一 令g (x )=m ⎝ ⎛⎭⎪⎫x -122+34m -6,x ∈[1,3].当m >0时,g (x )在[1,3]上是增函数, 所以g (x )max =g (3),即7m -6<0, 所以m <67,所以0<m <67;当m =0时,-6<0恒成立;当m <0时,g (x )在[1,3]上是减函数, 所以g (x )max =g (1),即m -6<0, 所以m <6,所以m <0.综上所述,m 的取值X 围是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫m ⎪⎪⎪m <67. 方法二 因为x 2-x +1=⎝ ⎛⎭⎪⎫x -122+34>0,又因为m (x 2-x +1)-6<0,所以m <6x 2-x +1.因为函数y =6x 2-x +1=6⎝ ⎛⎭⎪⎫x -122+34在[1,3]上的最小值为67,所以只需m <67即可. 所以m 的取值X 围是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫m ⎪⎪⎪m <67. 若将“f (x )<5-m 恒成立”改为“f (x )<5-m 无解”,如何求m 的取值X 围?解 若f (x )<5-m 无解,即f (x )≥5-m 恒成立, 即m ≥6x 2-x +1恒成立,又x ∈[1,3]时,⎝⎛⎭⎪⎫6x 2-x +1max=6,得m ≥6,即m 的取值X 围为[6,+∞).若将“f (x )<5-m 恒成立”改为“存在x ,使f (x )<5-m 成立”,如何求m的取值X 围?解 由题意知f (x )<5-m 有解, 即m <6x 2-x +1有解,则m <⎝ ⎛⎭⎪⎫6x 2-x +1max,又x ∈[1,3],得m <6,即m 的取值X 围为(-∞,6). 命题点3 给定参数X 围的恒成立问题例5 若mx 2-mx -1<0对于m ∈[1,2]恒成立,某某数x 的取值X 围.解 设g (m )=mx 2-mx -1=(x 2-x )m -1,其图象是直线,当m ∈[1,2]时,图象为一条线段,则⎩⎪⎨⎪⎧g 1<0,g 2<0,即⎩⎪⎨⎪⎧x 2-x -1<0,2x 2-2x -1<0,解得1-32<x <1+32,故x 的取值X 围为⎝⎛⎭⎪⎫1-32,1+32.思维升华 解决恒成立问题一定要搞清谁是主元,谁是参数,一般地,知道谁的X 围,谁就是主元,求谁的X 围,谁就是参数. 跟踪训练2 函数f (x )=x 2+ax +3.(1)若当x ∈R 时,f (x )≥a 恒成立,某某数a 的取值X 围; (2)若当x ∈[-2,2]时,f (x )≥a 恒成立,某某数a 的取值X 围;(3)若当a ∈[4,6]时,f (x )≥0恒成立,某某数x 的取值X 围. 解 (1)∵当x ∈R 时,x 2+ax +3-a ≥0恒成立, 需Δ=a 2-4(3-a )≤0,即a 2+4a -12≤0, 解得-6≤a ≤2,∴实数a 的取值X 围是[-6,2].(2)由题意可转化为x 2+ax +3-a ≥0在x ∈[-2,2]上恒成立, 则(x 2+ax +3-a )min ≥0(x ∈[-2,2]). 令g (x )=x 2+ax +3-a ,x ∈[-2,2], 函数图象的对称轴方程为x =-a2.当-a 2<-2,即a >4时,g (x )min =g (-2)=7-3a ≥0,解得a ≤73,舍去;当-2≤-a2≤2,即-4≤a ≤4时,g (x )min =g ⎝ ⎛⎭⎪⎫-a 2=-a 24-a +3≥0,解得-6≤a ≤2,∴-4≤a ≤2;当-a2>2,即a <-4时,g (x )min =g (2)=7+a ≥0, 解得a ≥-7,∴-7≤a <-4.综上可得,满足条件的实数a 的取值X 围是[-7,2]. (3)令h (a )=xa +x 2+3.当a ∈[4,6]时,h (a )≥0恒成立.只需⎩⎪⎨⎪⎧h 4≥0,h 6≥0,即⎩⎪⎨⎪⎧x 2+4x +3≥0,x 2+6x +3≥0,解得x ≤-3-6或x ≥-3+ 6. ∴实数x 的取值X 围是(-∞,-3-6]∪[-3+6,+∞).设方程ax 2+bx +c =0(a ≠0,Δ>0)有不相等的两根为x 1,x 2,且x 1<x 2,相应的二次函数为f (x )=ax 2+bx +c ,方程的根即为二次函数的图象与x 轴交点的横坐标,它们的分布情况见下面各表(每种情况对应的均是充要条件). 表一:(两根与0的大小比较即根的正负情况)分布情况两个负根即两根都小于0(x 1<0,x 2<0)两个正根即两根都大于0(x 1>0,x 2>0) 一正根一负根即一个根小于0,一个根大于0(x 1<0<x 2)大致图象(a >0)得出的结论错误!错误! f (0)<0大致图象(a<0)得出的结论错误!错误! f (0)>0 综合结论(不讨论a)错误!错误!a·f (0)<0 表二:(两根与k的大小比较)分布情况两根都小于k即x1<k,x2<k两根都大于k即x1>k,x2>k一个根小于k,一个根大于k即x1<k<x2大致图象(a>0)得出的结论错误!错误! f (k)<0大致图象(a<0)得出的结论错误!错误! f (k)>0 综合结论(不讨论a)错误!错误!a·f (k)<0 表三:(根在区间上的分布)分布情况两根都在(m,n)内两根有且仅有一根在(m,n)内(图象有两种情况,只画了一种)一根在(m,n)内,另一根在(p,q)内,m<n<p<q大致图象(a>0)得出的结论错误! f (m)·f (n)<0 错误!或错误!大致图象(a <0)得出的结论 错误! f (m )·f (n )<0 错误!或错误!综合结论(不讨论a ) 错误!f (m )·f (n )<0错误!根在区间上的分布还有一种情况:两根分别在区间(m ,n )外,即在区间两侧x 1<m ,x 2>n ,(图形分别如下)需满足的条件是(1)a >0时,⎩⎪⎨⎪⎧fm <0,f n <0;(2)a <0时,⎩⎪⎨⎪⎧fm >0,f n >0.对以上的根的分布表中,两根有且仅有一根在(m ,n )内有以下特殊情况:(ⅰ)若f (m )=0或f (n )=0,则此时f (m )·f (n )<0不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间(m ,n )内,从而可以求出参数的值.如方程mx 2-(m +2)x +2=0在区间(1,3)上有一根,因为f (1)=0,所以mx 2-(m +2)x +2=(x -1)(mx -2),另一根为2m ,由1<2m <3得23<m <2即为所求;(ⅱ)方程有两个相等的根,且这个根在区间(m ,n )内,即Δ=0,此时由Δ=0可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数.如方程x 2-4mx +2m +6=0有且只有一根在区间(-3,0)内,求m 的取值X 围.分析:①由f (-3)·f (0)<0即(14m +15)(m +3)<0得出-3<m <-1514;②由Δ=0即16m 2-4(2m +6)=0得出m =-1或m =32,当m =-1时,根x =-2∈(-3,0),即m=-1满足题意;当m =32时,根x =3∉(-3,0),故m =32不满足题意.综上分析,得出-3<m <-1514或m =-1. 例1 已知二次方程(2m +1)x 2-2mx +(m -1)=0有一正根和一负根,某某数m 的取值X 围. 解 设f (x )=(2m +1)x 2-2mx +(m -1),由(2m +1)·f (0)<0,即(2m +1)(m -1)<0, 解得-12<m <1,即m 的取值X 围为⎝ ⎛⎭⎪⎫-12,1. 例2 已知方程2x 2-(m +1)x +m =0有两个不等正实根,某某数m 的取值X 围. 解 设f (x )=2x 2-(m +1)x +m ,由⎩⎪⎨⎪⎧Δ>0,--m +12×2>0,f 0>0⇒⎩⎪⎨⎪⎧m +12-8m >0,m >-1,m >0⇒⎩⎨⎧m <3-22或m >3+22,m >0⇒0<m <3-22或m >3+22,即m 的取值X 围为(0,3-22)∪(3+22,+∞).例3 已知二次函数f (x )=(m +2)x 2-(2m +4)x +3m +3与x 轴有两个交点,一个大于1,一个小于1,某某数m 的取值X 围. 解 由(m +2)·f (1)<0,即(m +2)·(2m +1)<0⇒-2<m <-12,即m 的取值X 围为⎝⎛⎭⎪⎫-2,-12.1.(2019·某某调研)已知集合A ={x |x 2-x -2<0},B ={x |x 2+3x <0},则A ∩B 等于( ) A .(0,2) B .(-1,0) C .(-3,2) D .(-1,3) 答案 B解析 A ={x |-1<x <2},B ={x |-3<x <0},∴A ∩B =(-1,0).故选B.2.(2019·某某调研)已知函数f (x )=(ax -1)(x +b ),如果不等式f (x )>0的解集为(-1,3),那么不等式f (-2x )<0的解集为( ) A.⎝ ⎛⎭⎪⎫-∞,-32∪⎝ ⎛⎭⎪⎫12,+∞B.⎝ ⎛⎭⎪⎫-32,12C.⎝ ⎛⎭⎪⎫-∞,-12∪⎝ ⎛⎭⎪⎫32,+∞ D.⎝ ⎛⎭⎪⎫-12,32答案 A解析 由f (x )=(ax -1)(x +b )>0的解集是(-1,3),则a <0,故1a=-1,-b =3,即a =-1,b =-3.∴f (x )=-x 2+2x +3, ∴f (-2x )=-4x 2-4x +3,由-4x 2-4x +3<0,解得x >12或x <-32,故不等式f (-2x )<0的解集是⎝ ⎛⎭⎪⎫-∞,-32∪⎝ ⎛⎭⎪⎫12,+∞.故选A.3.(2020·永州模拟)“不等式x 2-x +m >0在R 上恒成立”的充要条件是( ) A .m >14B .m <14C .m <1D .m >1 答案 A解析 ∵不等式x 2-x +m >0在R 上恒成立, ∴Δ=(-1)2-4m <0,解得m >14,又∵m >14,∴Δ=1-4m <0,∴“m >14”是“不等式x 2-x +m >0在R 上恒成立”的充要条件.故选A.4.若不等式x 2-(a +1)x +a ≤0的解集是[-4,3]的子集,则a 的取值X 围是( ) A .[-4,1]B .[-4,3] C .[1,3]D .[-1,3] 答案 B解析 原不等式为(x -a )(x -1)≤0,当a <1时,不等式的解集为[a ,1],此时只要a ≥-4即可,即-4≤a <1;当a =1时,不等式的解为x =1,此时符合要求;当a >1时,不等式的解集为[1,a ],此时只要a ≤3即可,即1<a ≤3,综上可得-4≤a ≤3. 5.若不等式x 2+ax -2>0在区间[1,5]上有解,则a 的取值X 围是( )A.⎝ ⎛⎭⎪⎫-235,+∞B.⎣⎢⎡⎦⎥⎤-235,1C .(1,+∞) D.⎝ ⎛⎦⎥⎤-∞,-235 答案 A解析 由Δ=a 2+8>0知方程恒有两个不等实根,又因为x 1x 2=-2<0,所以方程必有一正根,一负根,对应二次函数图象的示意图如图.所以不等式在区间[1,5]上有解的充要条件是f (5)>0,解得a >-235,故选A.6.在关于x 的不等式x 2-(a +1)x +a <0的解集中至多包含1个整数,则a 的取值X 围是( ) A .(-3,5) B .(-2,4) C .[-1,3]D .[-2,4] 答案 C解析 因为关于x 的不等式x 2-(a +1)x +a <0可化为(x -1)(x -a )<0, 当a >1时,不等式的解集为{x |1<x <a }, 当a <1时,不等式的解集为{x |a <x <1}, 当a =1时,不等式的解集为∅,要使得解集中至多包含1个整数,则a =1或1<a ≤3或-1≤a <1, 所以实数a 的取值X 围是a ∈[-1,3],故选C.7.(2020·市石景山区模拟)已知集合A ={-5,-1,2,4,5},请写出一个一元二次不等式,使得该不等式的解集与集合A 有且只有一个公共元素,这个不等式可以是______________. 答案 (x +4)(x -6)>0(答案不唯一)解析 因为不等式(x +4)(x -6)>0解集为{x |x >6或x <-4},解集中只有-5在集合A 中.8.(2019·市顺义区模拟)满足关于x 的不等式(ax -b )(x -2)>0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12<x <2,则满足条件的一组有序实数对(a ,b )的值可以是________. 答案 (-2,-1)(答案不唯一)解析 不等式(ax -b )(x -2)>0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12<x <2, ∴方程(ax -b )(x -2)=0的实数根为12和2,且⎩⎪⎨⎪⎧a <0,b a =12,即a =2b <0,则满足条件的一组有序实数对(a ,b )的值可以是(-2,-1).9.(2019·某某省宜丰中学月考)在R 上定义运算⊗:x ⊗y =x (1-y ),若不等式(x -a )⊗(x +a )<1对任意实数x 恒成立,则实数a 的取值X 围为________.答案 ⎝ ⎛⎭⎪⎫-12,32 解析 由题意,可知不等式(x -a )⊗(x +a )<1对任意实数x 都成立, 又由(x -a )⊗(x +a )=(x -a )(1-x -a ), 即x 2-x -a 2+a +1>0对任意实数x 都成立, 所以Δ=1-4(-a 2+a +1)<0,即4a 2-4a -3<0, 解得-12<a <32.10.(2019·市丰台区模拟)已知定义域为R 的奇函数f (x ),当x >0时,f (x )=-(x -1)2+1.①当x ∈[-1,0]时,f (x )的取值X 围是________;②当函数f (x )的图象在直线y =x 的下方时,x 的取值X 围是________. 答案 [-1,0] (-1,0)∪(1,+∞)解析 因为f (x )为奇函数,故可以求函数在[0,1]上的值域,当x >0时,f (x )=-(x -1)2+1在[0,1]上的值域为[0,1],故在x ∈[-1,0]上的值域为x ∈[-1,0];如图所示,当函数f (x )的图象在直线y =x 的下方时,得x 的取值X 围是(-1,0)∪(1,+∞).11.(2019·某某第十三中学质检)已知关于x 的不等式-x 2+ax +b >0. (1)若该不等式的解集为(-4,2),求a ,b 的值; (2)若b =a +1,求此不等式的解集.解 (1)根据题意得⎩⎪⎨⎪⎧2-4=a ,2×-4=-b ,解得a =-2,b =8.(2)当b =a +1时,-x 2+ax +b >0⇔x 2-ax -(a +1)<0, 即[x -(a +1)](x +1)<0.当a +1=-1,即a =-2时,原不等式的解集为∅; 当a +1<-1,即a <-2时,原不等式的解集为(a +1,-1); 当a +1>-1,即a >-2时,原不等式的解集为(-1,a +1).综上,当a <-2时,不等式的解集为(a +1,-1);当a =-2时,不等式的解集为∅;当a >-2时,不等式的解集为(-1,a +1).12.甲厂以x 千克/小时的速度匀速生产某种产品(生产条件要求1≤x ≤10),每小时可获得的利润是100⎝ ⎛⎭⎪⎫5x +1-3x 元.(1)要使生产该产品2小时获得的利润不低于3000元,求x 的取值X 围;(2)要使生产900千克该产品获得的利润最大,则甲厂应该选取何种生产速度?并求最大利润.解 (1)根据题意,得200⎝ ⎛⎭⎪⎫5x +1-3x ≥3000,整理得5x -14-3x≥0,即5x 2-14x -3≥0,又1≤x ≤10,可解得3≤x ≤10.故要使生产该产品2小时获得的利润不低于3000元,x 的取值X 围是[3,10]. (2)设利润为y 元,则y =900x·100⎝ ⎛⎭⎪⎫5x +1-3x=9×104⎝ ⎛⎭⎪⎫5+1x -3x 2=9×104⎣⎢⎡⎦⎥⎤-3⎝ ⎛⎭⎪⎫1x -162+6112,故当x =6时,y max =457500.故甲厂以6千克/小时的生产速度生产900千克该产品时获得的利润最大,最大利润为457 500元.13.设a <0,(4x 2+a )(2x +b )≥0在(a ,b )上恒成立,则b -a 的最大值为( ) A.12B.13C.14D.22 答案 C解析 由题意知a <0,a <b ,则 ①当b <0时,∀x ∈(a ,b ),2x +b <0,所以(4x 2+a )(2x +b )≥0在(a ,b )上恒成立可转化为∀x ∈(a ,b ),a ≤-4x 2, 所以a ≤-4a 2,所以-14≤a <0,所以0<b -a <14;②当b >0时,(4x 2+a )(2x +b )≥0在(a ,b )上恒成立, 当x =0时,(4x 2+a )(2x +b )=ab <0,不符合题意; ③当b =0时,由题意知x ∈(a ,0),(4x 2+a )2x ≥0恒成立, 所以4x 2+a ≤0,所以-14≤a <0,所以0<b -a ≤14.综上所述,b -a 的最大值为14.14.已知对于任意的x ∈(-∞,1)∪(5,+∞),都有x 2-2(a -2)x +a >0,则实数a 的取值X 围是________. 答案 (1,5]解析 设f (x )=x 2-2(a -2)x +a , 当Δ=4(a -2)2-4a <0,即1<a <4时,f (x )>0对x ∈R 恒成立,符合题意; 当a =1时,f (-1)=0,不符合题意; 当a =4时,f (2)=0符合题意;当Δ>0时,由⎩⎪⎨⎪⎧Δ>0,1<a -2<5,f 1≥0,f 5≥0,得⎩⎪⎨⎪⎧a <1或a >4,3<a <7,a ≤5,a ≤5,即4<a ≤5.综上所述,实数a 的取值X 围是(1,5].15.(2020·某某市金山区模拟)若集合A ={x ∈Z |x 2-(a +2)x +2-a <0}中有且只有一个元素,则正实数a 的取值X 围是________.答案 ⎝ ⎛⎦⎥⎤12,23解析 f (x )=x 2-(a +2)x +2-a <0, 即x 2-2x +1<a (x +1)-1, 分别令y 1=x 2-2x +1,y 2=a (x +1)-1,易知y 2过定点(-1,-1),在同一坐标系中画出两个函数的图象,如图所示,若集合A ={x ∈Z |f (x )<0}中有且只有一个元素,结合图象可得,即点(0,1)和点(2,1)在直线上或者在直线上方,点(1,0)在直线下方,∴⎩⎪⎨⎪⎧a -1≤1,2a -1>0,3a -1≤1,解得12<a ≤23.16.(2019·某某六校联考)已知函数f (x )=x 2-2ax +2a -1.若对任意的a ∈(0,3),存在x 0∈[0,4],使得t ≤|f (x 0)|成立,某某数t 的取值X 围.解 ∵f (x )=x 2-2ax +2a -1的对称轴为x =a ,且a ∈(0,3), ∴函数f (x )=x 2-2ax +2a -1在[0,a ]上是减函数, 在[a ,4]上是增函数;∴函数f (x )=x 2-2ax +2a -1在[0,4]上的最小值为f (a )=-(a -1)2∈(-4,0],|f (a )|=(a -1)2,①当2≤a <3时,函数f (x )=x 2-2ax +2a -1(x ∈[0,4])在x =0时取得最大值,且最大值为2a -1,由于此时2≤a <3,则3≤2a -1<5, 易知当2≤a <3时,(a -1)2<2a -1,所以|f (x )|max =max{|f (a )|,|f (0)|}=|f (0)|=2a -1∈[3,5). ∴t ≤3.②当0<a <2时,函数f (x )=x 2-2ax +2a -1(x ∈[0,4])在x =4时取得最大值,且最大值为42-8a +2a -1=15-6a ,由于此时0<a <2,所以3<15-6a <15,且15-6a >(a -1)2,|f (x )|max =max{|f (a )|,|f (4)|}=|f (4)|=15-6a ∈(3,15), ∴t ≤3.综上,t 的取值X 围是(-∞,3].。
高考数学一轮复习 第七章 不等式 推理与证明 73 二元

七
不等式 推理与证明
章
第三节
二元一次不等式(组)与简单的线性规划
高考概览 1.会从实际情境中抽象出二元一次不等式组;2.了解二元一次 不等式的几何意义,能用平面区域表示二元一次不等式组;3.会 从实际情境中抽象出一些简单的二元线性规划问题,并能加以解 决.
吃透教材 夯双基
填一填 记一记 厚积薄发
[答案] D
x-1≥0,
5.(2015·全国卷Ⅰ)若 x,y 满足约束条件x-y≤0,
则
x+y-4≤0,
yx的最大值为________.
[解析] 由约束条件可画出可行域,利用yx的几何意义求解. 画出可行域如图阴影所示,∵yx表示过点(x,y)与原点(0,0)的 直线的斜率, ∴点(x,y)在点 A 处时xy最大.
x+y-1≤0 B.x-2y+2≤0
x-y+1≥0 C.x+2y+2≥0
x+y-1>0 D.x-2y+2>0
x-y≥0, (2)(2018·河北衡水中学五调)若不等式组2y≥x+0y,≤2,
x+y≤a
表示
的平面区域的形状是三角形,则 a 的取值范围是( )
A.a≥43
B.0<a≤1
C.1≤a≤43
[跟踪演练]
x≤0, 已知由不等式组yy≥-0kx,≤2,
y-x-4≤0
确定的平面区域 Ω 的面积为
7,则 k 的值为( ) A.-3 B.-1 C.3 D.1
[解析]
x≤0, 作出不等式组y≥0,
y-x-4≤0
所表示的平面区域,如
图阴影部分所示,可知该区域是等腰直角三角形且面积为 8.由于
直线 y=kx+2 恒过点 B(0,2),且原点的坐标恒满足ห้องสมุดไป่ตู้y-kx≤2,当
2023年高考数学(文科)一轮复习课件——二元一次不等式(组)与简单的线性规划问题

索引
考试要求
1.会从实际情境中抽象出二元一次不等式组;2.了解二元一次不等式 的几何意义,能用平面区域表示二元一次不等式组;3.会从实际情 境中抽象出一些简单的二元线性规划问题,并能加以解决.
内容 索引
知识诊断 基础夯实
考点突破 题型剖析
分层训练 巩固提升
知识诊断 基础夯实
方加1,
结合图形得到 zmin=
12+|1(+-1| 1)22+1=3.
索引
角度3 求参数值或取值范围
x≥2,
例 3 已知 x,y 满足x+y≤4, 若目标函数 z=3x+y 的最大值为 10,则实数 2x-y-m≤0.
m 的值为___5_____. 解析 作出可行域,如图中阴影部分所示.作出 直线3x+y=0,并平移可知,当直线过点A时, z取得最大值为10,当直线过点B时,z取得最 小值.
索引
(2)(2022·南昌模拟)已知变量
x,y
x-2y+4≤0,
满足x≥2,
则
x+y-6≥0,
k=xy+-13的取值范围是
__(_-__∞__,__-__5_]∪___12_,__+__∞____.
解析 由题意作出可行域如图阴影部分所示,
由于 k=xy+-13=y-(x--31)表示动点 M(x,y)与
索引
(2)电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?
解 设总收视人次为z万 ,则目标函数为z=60x+25y.
ZHISHIZHENDUANJICHUHANGSHI
知识梳理
1.二元一次不等式(组)表示的平面区域
不等式
表示区域
Ax+By+C>0 直线Ax+By+C=0某一侧的
高考数学一轮复习 第七章 不等式 推理与证明 7-3 二元一次不等式(组)与简单的线性规划课件 文

x-1≥0,
5.(2015·全国卷Ⅰ)若 x,y 满足约束条件x-y≤0,
则
x+y-4≤0,
yx的最大值为________.
[解析] 由约束条件可画出可行域,利用yx的几何意义求解. 画出可行域如图阴影所示,∵yx表示过点(x,y)与原点(0,0)的 直线的斜率, ∴点(x,y)在点 A 处时xy最大.
[跟踪演练]
x≤0, 已知由不等式组yy≥-0kx,≤2,
y-x-4≤0
确定的平面区域 Ω 的面积为
7,则 k 的值为( ) A.-3 B.-1 C.3 D.1
[解析]
x≤0, 作出不等式组y≥0,
y-x-4≤0
所表示的平面区域,如
图阴影部分所示,可知该区域是等腰直角三角形且面积为 8.由于
[答案] -23,23
3 . (2018·山 东 聊 城 期 末 ) 如 果 点 P(x , y) 在 平 面 区 域
2x-y+2≥0, x-2y+1≤0, x+y-2≤0
上,则 x2+(y+1)2 的最大值和最小值分别是
()
A.3,
3 5
B.9,95
C.9,2
∴zmax=2×6-(-3)=15.
[答案] 15
[ 拓 展 探 究 2] ________.
本
例
条
件
不
变
,
求
y+6 x-2
的
取
值
范
围
是
[解析] 如图,yx+ -62的几何意义为可行域内的点 M(x,y)与点 P(2,-6)连线的斜率,由本例知 B(6,-3),A(-6,-3),∴kPB =-63-+26=34,kPA=- -36+ -62=-38.
(福建专用)2019高考数学一轮复习-第七章 不等式、推理与证明 7.2 基本不等式及其应用课件 理

考点1
考点2
考点3
(2)∵a+b=1,
1
1
1
∴ + + =2
1
+
1
.
∵a+b=1,a>0,b>0,
1
1
+
1
1
∴ + =
1
+
+
1
=2+ + ≥2+2=4,当且仅当 a=b=2时,等号成立.
1
∴ + + ≥8,当且仅当 a=b=2时,等号成立.
考点1
意等号能否取到.
考点1
考点2
考点3
对点训练 1 已知 a>0,b>0,a+b=1,求证: 1 +
1
1+
=2+ .
+
证明: (方法一)∵a>0,b>0,a+b=1,∴1+ =1+
1
1
1
≥9.
同理,1+ =2+ .
1
1
∴ 1+
1+ = 2+
当且仅当 = ,
1
即 a=b=2时,等号成立.
2 = 22 ,
1
4 = ,
即
2 =
2 =
2
2
2
,
时取等号.
4
(2)因为 x>2,所以 x-2>0.
1
1
1
高考数学一轮复习 第七章 不等式 推理与证明 7-2 一元二次不等式及其解法课件 文

3>0},则 A∩B=( )
A.-3,-32 C.1,32
B.-3,32 D.32,3
[解析] 由 x2-4x+3<0,得(x-1)(x-3)<0,所以 1<x<3;由
2x-3>0,得 x>32.所以
A={x|1<x<3},B=xx>32
[跟踪演练] 1.不等式(x2+x+1)(-3x2-2x+8)≥0 的解集是________. [解析] 因为 x2+x+1 中 Δ=1-4<0, ∴x2+x+1>0 恒成立, ∴-3x2-2x+8≥0,即 3x2+2x-8≤0,解得-2≤x≤43,所 以原不等式的解集是-2,43. [答案] -2,43
(2) 正负去分母 → 再求并集 对二次项系 分别得出
(3) 分解因式 → 数分类讨论 → 不等式解集
[解析] (1)集合 A={x|x2-2x-3>0}={x|x>3 或 x<-1},∁UA = {x| - 1≤x≤3} , ∴ ( ∁ UA)∩B = {x| - 1≤x≤3}∩{x|2<x<4} = {x|2<x≤3},故选 C.
2.(2017·河北八所重点中学一模)不等式 2x2-x-3>0 的解集 >0
即为(x+1)·(2x-3)>0,解得
3 x>2
或 x<-1.所以不等式 2x2-x-3>0 的解集为{xx>32或x<-1.故选
B.
[答案] B
3.(2016·全国卷Ⅰ)设集合 A={x|x2-4x+3<0},B={x|2x-
(2)(2018·安徽桐城中学月考)不等式x-4 2≤x-2 的解集是
