proe 齿轮渐开线方程
PROE中各种曲线的方程

38.螺旋曲线
r=t*(10*180)+1
theta=10+t*(20*180)
z=t
39.圆
x = cos ( t *(5*180))
y = sin ( t *(5*180))
z = 0
40.封闭球形环绕曲线
rho=2
theta=360*t
phi=t*360*10
a=1.1
b=0.666
c=sin(theta)
f=1
x = (a*a+f*f*c*c)*cos(theta)/a
y = (a*a-2*f+f*f*c*c)*sin(theta)/b
18.Rhodonea 曲线
采用笛卡尔坐标系
方程:theta=t*360*4
x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta)
61.正弦周弹簧
笛卡尔:
ang1=t*360
ang2=t*360*20
x=ang1*2*pi/360
y=sin(ang1)*5+cos(ang2)
z=sin(ang2)
62.环形螺旋线
x=(50+10*sin(t*360*15))*cos(t*360)
y=(50+10*sin(t*360*15))*sin(t*360)
s=2*pi*r*t
x0=s*cos(ang)
y0=s*sin(ang)
x=x0+s*sin(ang)
y=y0-s*cos(ang)
z=0
6.螺旋线.
Proe各种曲线方程(如齿轮的渐开线方程)

PROE曲线方程第一个:参数方程1.卡笛尔坐标下的渐开线参数方程卡笛尔坐标系下的渐开线参数方程如下(设压力角afa 由0到60度,基圆半径为10):afa=60*tx=10*cos(afa)+pi*10*afa/180 * sin(afa)y=10*sin(afa)-pi*10*afa/180 * cos(afa)z=02.圆柱坐标下的渐开线参数方程圆柱坐标系下的渐开线参数方程如下(设基圆半径为10,压力角afa 从0到60度):afa = 60*tr = (10^2 + (pi*10*afa/180)^2)^0.5theta = afa-atan((pi*10*afa/180)/10)z = 0在Pro/ENGINEER 里使用 Feature > Creat > Datum > Curve > From Equation 命令,选择一个坐标系,然后选择坐标类型(卡笛尔坐标/圆柱坐标/球坐标),在窗口里输入以上方程即可生成一段精确的渐开线。
69. 圆柱齿轮齿廓的渐开线方程:afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注:afa为压力角,取值范围是0到60,10为基圆半径。
第一:参数方程圆渐开线方程:x=R*(cos(t*360)+t*2*pi*sin(t*360))y=R*(sin(t*360)-t*2*pi*cos(t*360))z=0t (将从0变到1) R为基圆半径pi=3.1415921.卡笛尔坐标下的渐开线参数方程卡笛尔坐标系下的渐开线参数方程如下(设压力角afa 由0到60度,基圆半径为10):afa=60*tx=10*cos(afa)+pi*10*afa/180 * sin(afa)y=10*sin(afa)-pi*10*afa/180 * cos(afa)2.圆柱坐标下的渐开线参数方程圆柱坐标系下的渐开线参数方程如下(设基圆半径为10,压力角afa 从0到60度):afa = 60*tr = (10^2 + (pi*10*afa/180)^2)^0.5theta = afa-atan((pi*10*afa/180)/10)z = 0proe曲线方程大全1.碟形弹簧圓柱坐标r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t2.葉形线笛卡儿坐標标a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))3.螺旋线(Helical curve)圆柱坐标(cylindrical)r=ttheta=10+t*(20*360)z=t*34.蝴蝶曲线球坐标rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 85.渐开线笛卡尔坐标系r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=06.螺旋线.笛卡儿坐标x = 4 * cos ( t *(5*360)) y = 4 * sin ( t *(5*360)) z = 10*t7.对数曲线笛卡尔坐标系z=0x = 10*ty = log(10*t+0.0001)8.球面螺旋线球坐标系rho=4theta=t*180phi=t*360*209.双弧外摆线卡迪尔坐标l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360) Y=3*b*sin(t*360)+l*sin(3*t*360)10.星行线卡迪尔坐标a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^311.心脏线圓柱坐标a=10r=a*(1+cos(theta))theta=t*36012.圆内螺旋线柱座标系r=10+10*sin(6*theta)z=2*sin(6*theta)13.正弦曲线笛卡尔坐标系x=50*ty=10*sin(t*360)z=014.太阳线柱坐标r=1.5*cos(50*theta)+1theta=t*360z=015.费马曲线(有点像螺纹线)数学方程:r*r = a*a*theta圓柱坐标方程1: theta=360*t*5a=4r=a*sqrt(theta*180/pi)方程2: theta=360*t*5a=4r=-a*sqrt(theta*180/pi)由于Pro/e只能做连续的曲线,所以只能分两次做16.Talbot 曲线卡笛尔坐标theta=t*360a=1.1c=sin(theta)f=1x = (a*a+f*f*c*c)*cos(theta)/ay = (a*a-2*f+f*f*c*c)*sin(theta)/b18.Rhodonea 曲线笛卡尔坐标系theta=t*360*4x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta) y=25+(10-6)*sin(theta)-6*sin((10/6-1)*theta)19. 抛物线笛卡儿坐标x =(4 * t)y =(3 * t) + (5 * t ^2)z =020.螺旋线圓柱坐标r = 5theta = t*1800z =(cos(theta-90))+24*t21.三叶线圆柱坐标a=1theta=t*380b=sin(theta)r=a*cos(theta)*(4*b*b-1)22.外摆线迪卡尔坐标theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta) y=(a+b)*sin(theta)-b*sin((a/b+1)*theta) z=023. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta)24.长短幅圆内旋轮线卡笛尔坐标a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta) y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)25.长短幅圆外旋轮线卡笛尔坐标theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta) y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)26. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360))y = a*(2*sin(t*360)-sin(2*t*360))27.概率曲线!笛卡儿坐标x = t*10-5y = exp(0-x^2)28.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)29.阿基米德螺线柱坐标a=100theta = t*400r = a*theta30.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)31.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x32.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)33.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/234.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/235.双曲正切x = 6*t-3y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x)) 36.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+137.八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 038.螺旋曲线r=t*(10*180)+1theta=10+t*(20*180)z=t39.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 040.封闭球形环绕曲线rho=2theta=360*tphi=t*360*1041.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180)) y = 100*t * sin ( t *(5*180)) z = 042.蛇形曲线x = 2 * cos ( (t+1) *(2*180)) y = 2 * sin ( t *(5*360))z = t*(t+1)43.8字形曲线柱坐标theta = t*360r=10+(8*sin(theta))^244.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)45.梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*2.5))^246.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^247.改一下就成为空间感更强的花曲线了;)theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^248.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*1249.甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2z = t*1650 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+ttheta=t*360*10z=t*1051 长命锁曲线笛卡尔方程:a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c) y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)52 簪形线球坐标rho=200*ttheta=900*tphi=t*90*1053.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3z=t^3*(t+1)54.蘑菇曲线球坐标rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*2055. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360) Y=b*sin(t*360)+a*sin(3*t*360)56.梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)57.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*1058.碟形弹簧圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+2459 环形二次曲线笛卡儿方程:x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)60 蝶线球坐标:rho=4*sin(t*360)+6*cos(t*360^2) theta=t*360phi=log(1+t*360)*t*36061.正弦周弹簧笛卡尔:ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)62.环形螺旋线笛卡尔:x=(50+10*sin(t*360*15))*cos(t*360) y=(50+10*sin(t*360*15))*sin(t*360) z=10*cos(t*360*5)63.内接弹簧笛卡尔:x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*664.多变内接式弹簧笛卡尔:x=3*cos(t*360*8)-1.5*cos(t*480*8)y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*865.柱面正弦波线柱坐标r=30theta=t*360z=5*sin(5*theta-90)66.漩涡线球坐标:rho=t*20^2theta=t*log(30)*60phi=t*720067. 手把曲线笛卡尔:thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1)x=r*cos(thta0)y=r1*sin(thta1)z=068.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*569. 圆柱齿轮齿廓的渐开线方程:笛卡尔坐标afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注:afa为压力角,取值范围是0到60,10为基圆半径。
ProE中渐开线齿轮画法讲解

(7)完成后的曲线如图3-14所示;
图3-14 完成后的渐开线
4.镜像渐开线
(1)在工具栏内单击 按钮,或者依次在主菜单上单击 “插入”→ “模型基准”→ “点”→ “点”,系统弹出“基准点”对话框,如图3-15所示;
图3-15“基准点”对话框
(2)单击分度圆曲线作为参照,按住Ctrl键,单击渐开线作为参照,如图3-16所示。在“基准点”对话框内单击【确定】,完成基准点“PNT0”的创建;
D12=da
其中D12为圆的直径尺寸代号,da为用户自定义的参数,即为齿顶圆直径。通过该关系式创建的圆即为齿顶圆;
(13)重复7—12步骤,创建另外两个齿轮的基本圆,分别为齿根圆和基圆,基中齿根圆的尺寸关系式为:
D13=df
基圆的尺寸代号为:
D14=db
完成后的基本圆曲线如图3-8所示,完成后的“关系”对话框如图3-9所示。
图3-8 完成后的基本圆曲线
图3-9 完成后的关系式
3.创建渐开线
(1)依次在主菜单上单击 “插入”→ “模型基准”→ “曲线”,或者在工具栏上单击 按钮,系统弹出“曲线选项”菜单管理器,如图3-10所示;
图3-10 “曲线选项”菜单管理器
(2)在“曲线选项”菜单管理器上依次单击 “从方程”→ “完成”,弹出“得到坐标系”菜单管理器,如图3-11所示;
(5)在工具栏内单击 按钮,或者依次在主菜单上单击 “插入”→ “模型基准”→ “平面”,系统弹出“基准平面”对话框;
(6)在绘图区单击选取“A_1”轴作为参照,按住Ctrl键,继续单击基准点“PNT0”作为参照,如图3-17所示;
图3-17“基准平面”对话框
(7)继续在工具栏内单击 按钮,或者依次在主菜单上单击 “插入”→ “模型基准”→ “平面”,系统弹出“基准平面”对话框,如图3-18所示;
ProE中渐开线齿轮画法讲解

齿轮传动是最重要的机械传动之一。
齿轮零件具有传动效率高、传动比稳定、结构紧凑等优点。
因而齿轮零件应用广泛,同时齿轮零件的结构形式也多种多样。
根据齿廓的发生线不同,齿轮可以分为渐开线齿轮和圆弧齿轮。
根据齿轮的结构形式的不同,齿轮又可以分为直齿轮、斜齿轮和锥齿轮等。
本章将详细介绍用Pro/E创建标准直齿轮、斜齿轮、圆锥齿轮、圆弧齿轮以及蜗轮蜗杆的设计过程。
3.1直齿轮的创建3.1.1渐开线的几何分析图3-1 渐开线的几何分析渐开线是由一条线段绕齿轮基圆旋转形成的曲线。
渐开线的几何分析如图3-1所示。
线段s绕圆弧旋转,其一端点A划过的一条轨迹即为渐开线。
图中点(x1,y1)的坐标为:x1=r*cos(ang),y1=r*sin(ang) 。
(其中r为圆半径,ang为图示角度)对于Pro/E关系式,系统存在一个变量t,t的变化范围是0~1。
从而可以通过(x1,y1)建立(x,y)的坐标,即为渐开线的方程。
ang=t*90s=(PI*r*t)/2x1=r*cos(ang)y1=r*sin(ang)x=x1+(s*sin(ang))y=y1-(s*cos(ang))z=0以上为定义在xy平面上的渐开线方程,可通过修改x,y,z的坐标关系来定义在其它面上的方程,在此不再重复。
3.1.2直齿轮的建模分析本小节将介绍参数化创建直齿圆柱齿轮的方法,参数化创建齿轮的过程相对复杂,其中要用到许多与齿轮有关的参数以及关系式。
直齿轮的建模分析(如图3-2所示):(1)创建齿轮的基本圆这一步用草绘曲线的方法,创建齿轮的基本圆,包括齿顶圆、基圆、分度圆、齿根圆。
并且用事先设置好的参数来控制圆的大小。
(2)创建渐开线用从方程来生成渐开线的方法,创建渐开线,本章的第一小节分析了渐开线方程的相关知识。
(3)镜像渐开线首先创建一个用于镜像的平面,然后通过该平面,镜像第2步创建的渐开线,并且用关系式来控制镜像平面的角度。
(4)拉伸形成实体拉伸创建实体,包括齿轮的齿根圆实体和齿轮的一个齿形实体。
proe直齿渐开线圆柱齿轮制作
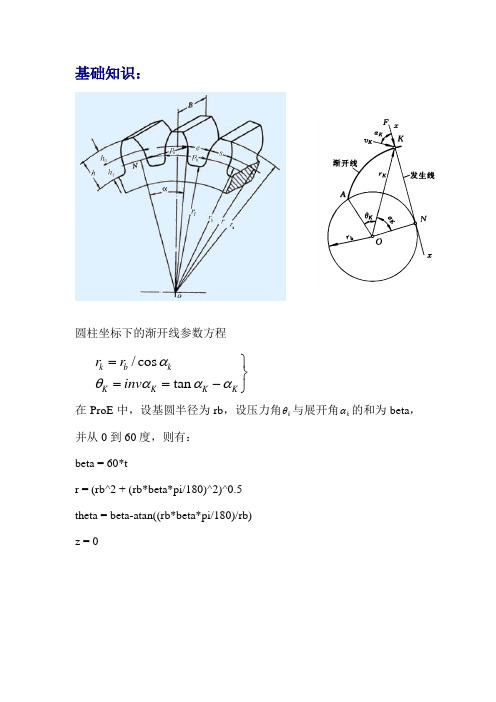
基础知识:圆柱坐标下的渐开线参数方程在ProE 中,设基圆半径为rb ,设压力角k θ与展开角k α的和为beta ,并从0到60度,则有: beta = 60*tr = (rb^2 + (rb*beta*pi/180)^2)^0.5 theta = beta-atan((rb*beta*pi/180)/rb) z = 0/cos tan k b kK K K K r r inv αθααα=⎫⎬==-⎭1、设计参数打开参数窗口,向模型中添加的参数主要有齿数(z),模数(m),压力角(alpha),齿顶高系数(ha),顶隙系数(c),分度圆直径(d),基圆直径(db),齿顶圆直径(da),齿根圆直径(df),齿宽(b)。
确定具体参数时分度圆直径、基圆直径、齿顶圆直径、齿根圆直径、齿宽值设置为零、并通过关系式进行计算。
示例见表1。
说明:1.本表适用于渐开线圆柱齿轮。
对斜齿轮是指法面模数。
2.选用模数时,应优先选用第一系列,其次是第二系列,括号内的模数尽可能不用。
压力角标准值:我国规定标准值一般为20°。
某些行业也采用14.5°,15°。
齿顶高系数ha*齿顶高ha用齿顶高系数ha*与模数的乘积表示:顶隙系数c*齿根高hf用齿顶高系数ha*与顶隙系数c*之和乘以模数表示:齿顶高系数与顶隙系数的标准值正常齿制当m≥1mm时,ha*=1, c*=0.25当m<1mm时,ha*=1, c*=0.35短齿制ha*=0.8, c*=0.32、创建基本曲线通过关系式生成基本曲线,首先草绘四个圆形,分别为齿顶圆、基圆、分度圆、齿根圆曲线,随意设置圆的直径数值,其具体数值将通过关系式确定。
打开关系窗口,选择特征项,选中刚刚绘制的曲线将其尺寸标注切换为符号显示形式( d0, d1, d2)。
在关系的编辑窗口中建立如下约束条件。
d=m*zdb=m*z*cos(alpha)ha=1IF m<1c=0.35elsec=0.25ENDIFda=m*(z+2*ha )df=m*z-2*m*(ha+c)d0=dfd1=dbd2=dd3=da完成关系式的输入后,执行/校验关系并按关系创建新参数。
渐开线齿轮方程

下图为渐开线在极坐标下的推导:所以渐开线的圆柱座标方程为:R=Rb*sqrt(1+ω^2)θ=ω-atan(ω)注意此方程的角度为弧度制在Pro/E中若以Datum Curve=>From Equation绘出渐开线的话,应该将ω转成十进制。
于是有:A= t * 45 ----假设滚动角ω为0-45度,要留意滚动角也就是以后齿轮的压力角了R= Rb * sqrt( 1+ ( A*pi/180)^2 )theta = A- atan ( A* pi/180 )z = 0上面是推导上最简单的方法,下面是输入最省事的方法。
m=3(模数)z=20(齿数)alfa=20(压力角)rb=m*z*cos(alfa)/2(基圆半径)ang(angle简写,尽量用自己能看懂的简写命名变量,所有规则与C语言一样)=t*90(基圆半径生成角度即第一图中的w)s=pi*rb*t/2(指得是弧BC,也等于直线AB,约分之前为s=(pi*2*rb)*(ang/360))xc=rb*cos(ang)()yc=rb*sin(ang)(以B为基点,确定渐开线上点A,线就是点集,而w是按角度增加变化的,不同角度对应不同的点,整个角度变化完后,所有点生成完毕,集合成为所描绘的曲线。
我们只需确定A相对与B的横纵坐标的增量与W间规律。
如图所标出的两个角度,推出横坐标增量为+s*sin(ang))注意为正。
纵坐标增量为-s*cos(ang)注意为负)x=xc+s*sin(ang)(最终的A点的横坐标)y=yc-s*cos(ang)(最终的A点的横坐标)z=0(平面上故z=0)将上程序合并一下为:m=3z=20alfa=20rb=m*z*cos(alfa)/2ang=t*90s=pi*rb*t/2x= rb*cos(ang)+s*sin(ang)y= rb*sin(ang)-s*cos(ang)z=0下面是进入输入程序界面的介绍/* For cartesian coordinate system(笛卡尔坐标系), enter parametric equation(输入坐标方程)/* in terms of t (which will vary from 0 to 1) for x, y and z (这里的意思是t是一个软件已设好的变量,范围是0 ~ 1如:x=t*2,表示X从0~2变化。
PROE齿轮画法大全---直齿轮

3.1直齿轮的创建3.1.1渐开线的几何分析图3-1 渐开线的几何分析渐开线是由一条线段绕齿轮基圆旋转形成的曲线。
渐开线的几何分析如图3-1所示。
线段s绕圆弧旋转,其一端点A划过的一条轨迹即为渐开线。
图中点(x1,y1)的坐标为:x1=r*cos(ang),y1=r*sin(ang) 。
(其中r为圆半径,ang为图示角度)对于Pro/E关系式,系统存在一个变量t,t的变化范围是0~1。
从而可以通过(x1,y1)建立(x,y)的坐标,即为渐开线的方程。
ang=t*90s=(PI*r*t)/2x1=r*cos(ang)y1=r*sin(ang)x=x1+(s*sin(ang))y=y1-(s*cos(ang))z=0以上为定义在xy平面上的渐开线方程,可通过修改x,y,z的坐标关系来定义在其它面上的方程,在此不再重复。
3.1.2直齿轮的建模分析本小节将介绍参数化创建直齿圆柱齿轮的方法,参数化创建齿轮的过程相对复杂,其中要用到许多与齿轮有关的参数以及关系式。
直齿轮的建模分析(如图3-2所示):(1)创建齿轮的基本圆这一步用草绘曲线的方法,创建齿轮的基本圆,包括齿顶圆、基圆、分度圆、齿根圆。
并且用事先设置好的参数来控制圆的大小。
(2)创建渐开线用从方程来生成渐开线的方法,创建渐开线,本章的第一小节分析了渐开线方程的相关知识。
(3)镜像渐开线首先创建一个用于镜像的平面,然后通过该平面,镜像第2步创建的渐开线,并且用关系式来控制镜像平面的角度。
(4)拉伸形成实体拉伸创建实体,包括齿轮的齿根圆实体和齿轮的一个齿形实体。
这一步是创建齿轮的关键步骤。
(5)阵列轮齿将上一步创建的轮齿进行阵列,完成齿轮的基本外形。
这一步同样需要加入关系式来控制齿轮的生成。
(6)创建其它特征创建齿轮的中间孔、键槽、小孔等特征,并且用参数和关系式来控制相关的尺寸。
图3-2 齿轮的建模分析3.1.3直齿轮的建模过程1.输入基本参数和关系式(1)单击,在新建对话框中输入文件名“gear”,然后单击;(2)在主菜单上单击“工具”→“参数”,系统弹出“参数”对话框,如图3-3所示;图3-3 “参数”对话框(3)在“参数”对话框内单击按钮,可以看到“参数”对话框增加了一行,依次输入新参数的名称、值、和说明等。
Proe齿轮建模参数及关系

Proe齿轮建模参数及关系(渐开线方程)1、直齿圆柱齿轮建模参数:M------------------------齿轮模数Z------------------------齿轮齿数B------------------------齿轮宽度ALPHA-----------------------齿轮压力角HAX-----------------------齿轮的齿顶高系数CX------------------------齿轮的齿根高系数D11----------------------齿根过度圆弧半径参数关系:d=M*Z 分度圆直径db=d*cos(ALPHA) 基圆直径Ha=Hax*M齿顶高Hf=(Hax+Cx)*M 齿根高DA=D+2*Ha 齿顶圆直径DF=D-2*Hf齿根圆直径D11=0.38*m笛卡尔坐标渐开线方程:r=DB/2Theta=t*45X=r*cos(theta)+r*sin(theta)*theta*pi/180Z=r*sin(theta)-r*cos(theta)*theta*pi/1802、直齿圆柱变位齿轮建模参数:M------------------------齿轮模数Z-------------------------齿轮齿数X-------------------------变位系数B-------------------------齿轮宽度ALPHA-------------------------齿轮压力角HAX-------------------------齿轮的齿顶高系数CX--------------------------齿轮的齿根高系数D11------------------------齿根过度圆弧半径参数关系:D=Z*M 分度圆直径db=D*cos(ALPHA)基圆直径T_D=(PI/2+2*X*tan(ALPHA))*M分度圆上的齿厚DA=D+(HAX+X)*M*2齿顶圆的直径DF=d-((hax+cx)-X)*M*2齿根圆的直径INV_PHI=tan(ALPHA)- ALPHA*PI/180渐开线函数T_DB=(T_D+M*Z*INV_PHI)*cos(ALPHA)基圆上的齿厚SITA=180*(1/Z-T_DB/(PI*db))基圆上的齿槽所对应圆心角度数的一半D1=B 圆柱坯料宽度等于齿宽D3=360/ZDTM1与FRONT面的夹角柱坐标渐开线方程r=db/2/cos(45*t)theta=tan(45*t)*180/pi-45*t+sitaz=03、斜齿圆柱变位齿轮建模参数:M_N-----------------------齿轮法向模数Z_N-----------------------齿轮的法向变位系数Z------------------------齿轮齿数B-----------------------齿轮宽度BETA-----------------------齿轮的螺旋角ALPHA------------------------齿轮压力角HAX------------------------齿轮的齿顶高系数CX-------------------------齿轮的齿根高系数D11-------------------------齿根过度圆弧半径关系:M_T=M_N/cos(beta)齿轮端面模数a_t=ATAN(tan(alpha)/cos(beta))齿轮端面压力角x_t=x_n*cos(beta)齿轮端面变位系数d=z*m_t分度圆直径db=d*cos(a_t)基圆直径T_D=(pi/2+2*x_t*tan(a_t))*m_t分度圆齿厚DA=d+(hax*cos(beta)+x_t)*m_t*2齿顶圆直径df=d-((hax+cx)*cos(beta)-x_t)*m_t*2齿根圆直径INV_PHI=tan(a_t)-a_t*pi/180渐开线函数T_DB=(T_D+m_n*z*inv_phi)*cos(a_t)基圆齿厚sita=180*(1/z-t_db/(pi*db))基圆上的齿槽所对应圆心角度数的一半D1=b+20*m_n圆柱坯料的长度D3=360/z DTM1与FRONT面的夹角圆柱渐开线方程:r=db/2/cos(45*t)theta=tan(45*t)*180/pi-45*t+sitaz=0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一组关系式 sd17=df/2
sd16=db/2 sd15=d/2 sd12=da/2 sd18=b sd11=delta sd10=90
第二组关系式 sd0=d/cos(delta) sd1=da/cos(delta) sd2=db/cos(delta) sd3=df/cos(delta)
第三组关系式 sd0=(d-2*b*sin(delta))/cos(delta) sd1=(da-2*ba*sin(delta_a))/cos(delta) sd2=(db-2*bb*sin(delta_b))/cos(delta) sd3=(df-2*bf*sin(delta_f))/cos(delta)
斜齿齿轮齿廓渐开线生成方程为笛卡儿坐标系输入参数方 程,根据 t (将从0变到1) 对 x, y 和 z 例如:对在 x-y 平面的一个圆,中心在原点 , 半径 = 4,参数方程将是:
x = 4*cos(t*360) y = 4*sin(t* 360) z=0 delta=atan(z/z_asm) d=m*z db=d*cos(alpha) da=d+2*ha*cos(delta) df=d-2*hf*cos(delta) hb=(d-db)/(2*cos(delta)) rx=d/(2*sin(delta)) theta_a=atan(ha/rx) theta_b=atan(hb/rx) delta_a=delta+theta_a delta_b=delta-theta_b delta_f=delta-theta_f ba=b/cos(theta_a) bb=b/cos(theta_b) bf=b/cos(theta_f) d1=d/(2*tan(delta))
直齿圆锥齿轮(大圆)齿廓渐开线生成 方程
/* 为笛卡儿坐标系输入参数方程 /* 根据 t (将从0变到1) 对 x, y 和 z /* 例如:对在 x-y 平面的一个圆,中心在原点 /* 半径 = 4,参数方程将是: /* x = 4*cos(t*36 z=0 /*------------------------------------------------r=df/2 theta=t*55 x=r*cos(theta)+r*sin(theta)* theta*pi/180 y=r*sin(theta)-r*cos(theta)* theta*pi/180 z=0 斜齿轮关系式 ha=(hax+x)*mn hf=(hax+cx-x)*mn d=mn*z/cos(beta) da=d+2*ha db=d*cos(alpha) df=d-2*hf
