【最新】人教版七年级数学下册第五章《同位角、内错角、同旁内角》优质公开课课件 (4).ppt
合集下载
新人教版七年级数学下册第五章《同位角内错角同旁内角》公开课课件

l3
截线同侧
l1 l2
被截线之间
其它的同旁内角有: ∠4与∠5;
同位角
内错角 同旁内
l3 l3
l2 l2 l1
l2 l1
l3
l1
同位角、内错角和同旁内角的结构特征:
l3
2 1 3 4 6 5 7 8
同位角
l1
l2
内错角 同旁内角
l3 l1 l
哪几对 在两被 在截线 结构 截线的 的位置 特征 位置
直线 l1 ,l 2 相交于O,图中有几个小于平角 的角?它们有什么位置关系?在数量上有 什么关系? 直线 l 2 和直线 l3 被
l1
1 2 4o 3
5 6 8 7
l2
直线 l1 所截
l3
从位置方面观察, ∠1与∠5
右侧 ,在被截线l1, 在截线 l3的______ ____ l2 的上方
l3
截线同侧
l1 l2
被截线同侧
其它的同位角有: ∠2与∠6; ∠4与∠8; ∠3与∠7.
从位置方面观察, ∠3与∠5 两旁 ,在被截线l , 之间 在截线 l3的______ ____ l 1 2
l3
截线两侧
l1 l2
被截线之间
其它的内错角有: ∠4与∠6;
从位置方面观察, ∠3与∠6 左侧 ,在被截线l , 之间 在截线 l3的______ ____ 1 l2
F
C
如图,∠1与哪个角是内错角, 与哪个角是同 旁内角?它们分别是哪两条直线被哪一条直线 所截形成的?
∠1的内错角是∠DAB
∠1的同旁内角有: ∠EAB,∠CAB,∠2
D
A
E
B
1
2
人教版中学数学公开课优质课件精选同位角内错角同旁内角

A 7 5 6 4 3 1 2 B 8
D
F
两条直线AB和CD被第三条直线 EF所截成的小于平角的角共有 E 几个?
A
这两个角分别 在两条直线AB、CD 之间,且在第三条 直线EF的两侧, C 像这样的一对角叫
7 5 6 4 3 1 2 B
8
D
内错角。
F
两条直线AB和CD被第三条直线 EF所截成的小于平角的角共有 E 几个? 这两个角都 在两条直线AB、 CD之间,且在第 三条直线EF的同 旁,像这样的一 对角叫同旁内
练习
⌒
填空题: 1. ∠BAD与∠ CDA是直线__和__被__所截,构成的同旁内角。 2. ∠ 1和∠ 2是直线__和__被__所截,构成的内错角。 3. ∠ 3和∠ 4是直线__和__被__所截,构成的内错角。 4. ∠ DCE与∠ ABC是直线__和__被__所截,构成的同位角。
练习
找出下列图中所有的 同位角 内错角 同旁内角.
被哪一条直线截成的?
∠1和∠2是同位角,是由直线CD、FE被直线AB截成的; ∠2和∠3是内错角,是由直线AB、CD被直线EF截成的;
∠4和∠5是同旁内角,是由直线AB 、EF被直线CD截成的。
例2.看图填空: (1)若ED,BF被AB所截, 则∠ 1与 ∠2 是同位角; E 1 2
A
(2)若ED,BC被AF所截, 则∠3与 ∠4 是内错角;
b
c
1
2
3
4
a
能力挑战: 看图填空
A E
2 1 3
D
4
B
F
C
(1)若ED,BF被AB所截, 则∠1与_____ ∠2 是同位角。
谢谢观看
请指导
D
F
两条直线AB和CD被第三条直线 EF所截成的小于平角的角共有 E 几个?
A
这两个角分别 在两条直线AB、CD 之间,且在第三条 直线EF的两侧, C 像这样的一对角叫
7 5 6 4 3 1 2 B
8
D
内错角。
F
两条直线AB和CD被第三条直线 EF所截成的小于平角的角共有 E 几个? 这两个角都 在两条直线AB、 CD之间,且在第 三条直线EF的同 旁,像这样的一 对角叫同旁内
练习
⌒
填空题: 1. ∠BAD与∠ CDA是直线__和__被__所截,构成的同旁内角。 2. ∠ 1和∠ 2是直线__和__被__所截,构成的内错角。 3. ∠ 3和∠ 4是直线__和__被__所截,构成的内错角。 4. ∠ DCE与∠ ABC是直线__和__被__所截,构成的同位角。
练习
找出下列图中所有的 同位角 内错角 同旁内角.
被哪一条直线截成的?
∠1和∠2是同位角,是由直线CD、FE被直线AB截成的; ∠2和∠3是内错角,是由直线AB、CD被直线EF截成的;
∠4和∠5是同旁内角,是由直线AB 、EF被直线CD截成的。
例2.看图填空: (1)若ED,BF被AB所截, 则∠ 1与 ∠2 是同位角; E 1 2
A
(2)若ED,BC被AF所截, 则∠3与 ∠4 是内错角;
b
c
1
2
3
4
a
能力挑战: 看图填空
A E
2 1 3
D
4
B
F
C
(1)若ED,BF被AB所截, 则∠1与_____ ∠2 是同位角。
谢谢观看
请指导
人教版七年级数学下册第五章《 同位角、内错角、同旁内角》优课件

在截线的_同__侧__
基本图形 图形结构特征 形如字母“__F_” 形如字母“__Z_” 形如字母“__U_”
下图中的∠1与∠2哪些是内错角? 哪些是同旁内角?
1 2 (1)
1 2
(5)
1 2
(2)
1 2 (6)
2 1 (3)
1
2
(7)
12
(4)
1
2
(8)
例题 : 如图,直线DE、BC被直线AB所截.
第五章 相交线与平行线
5.1 相交线
5.1.3 同位角、内错角、同旁内角
两条直线相交构成的4个角中,任意 两个角都有什么关系?
E
两对对顶角:∠1和∠3、 A
∠2和∠4,它们分别相等.
21
O3 4 B
四对邻补角: ∠1和∠2、
∠2和∠3、 ∠3和∠4、
∠4和∠1,它们分别互补.
F
E
A 21
O3 4
l
a
1
练习3:打开课本第7页,做练习题.
总结归纳
1.同位角、内错角、同旁内角 的位置特征及结构特征.
2.识别同位角、内错角、同 旁内角的方法.
Z、xxk
布置作业
1.习题5.1第12题.
2.在下图中,如果直线AB绕着与截线EF 的交
点O 旋转(转动时直线AB不与截线EF重合), ∠1与∠5的同位角关系是否发生改变?两条 被截直线有没有不相交的位置?
谢谢观赏
You made my day!
我们,还在路上……
E
A 21 O3 4 B
65 78
F
❖1、书籍是朋友,虽然没有热情,但是非常忠实。2022年2月14日星期一2022/2/142022/2/142022/2/14 ❖2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于 独立思考的人,给那些具有锲而不舍的人。2022年2月2022/2/142022/2/142022/2/142/14/2022 ❖3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/2/142022/2/14February 14, 2022 ❖4、享受阅读快乐,提高生活质量。2022/2/142022/2/142022/2/142022/2/14
基本图形 图形结构特征 形如字母“__F_” 形如字母“__Z_” 形如字母“__U_”
下图中的∠1与∠2哪些是内错角? 哪些是同旁内角?
1 2 (1)
1 2
(5)
1 2
(2)
1 2 (6)
2 1 (3)
1
2
(7)
12
(4)
1
2
(8)
例题 : 如图,直线DE、BC被直线AB所截.
第五章 相交线与平行线
5.1 相交线
5.1.3 同位角、内错角、同旁内角
两条直线相交构成的4个角中,任意 两个角都有什么关系?
E
两对对顶角:∠1和∠3、 A
∠2和∠4,它们分别相等.
21
O3 4 B
四对邻补角: ∠1和∠2、
∠2和∠3、 ∠3和∠4、
∠4和∠1,它们分别互补.
F
E
A 21
O3 4
l
a
1
练习3:打开课本第7页,做练习题.
总结归纳
1.同位角、内错角、同旁内角 的位置特征及结构特征.
2.识别同位角、内错角、同 旁内角的方法.
Z、xxk
布置作业
1.习题5.1第12题.
2.在下图中,如果直线AB绕着与截线EF 的交
点O 旋转(转动时直线AB不与截线EF重合), ∠1与∠5的同位角关系是否发生改变?两条 被截直线有没有不相交的位置?
谢谢观赏
You made my day!
我们,还在路上……
E
A 21 O3 4 B
65 78
F
❖1、书籍是朋友,虽然没有热情,但是非常忠实。2022年2月14日星期一2022/2/142022/2/142022/2/14 ❖2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于 独立思考的人,给那些具有锲而不舍的人。2022年2月2022/2/142022/2/142022/2/142/14/2022 ❖3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/2/142022/2/14February 14, 2022 ❖4、享受阅读快乐,提高生活质量。2022/2/142022/2/142022/2/142022/2/14
【最新】人教版七年级数学下册第五章《同位角、内错角、同旁内角》公开课课件

第五章
写出来.
相交线与平行线
5.如图,∠1~∠10这些角中,同位角、内错角、同旁内角各几对,请分别
解:同位角有4对:∠1与∠3,∠2与∠9,∠5与∠8,∠5与∠10;
内错角有6对:∠1与∠7,∠2与∠8,∠2与∠10,∠3与∠6,∠4与∠7,∠5 与∠9;
同旁内角有7对:∠1与∠8,∠2与∠7,∠2与∠3,∠3与∠7,∠4与 ∠5,∠4与∠6,∠5与∠6.
第五章
相交线与平行线
探究一:同位角、内错角、同旁内角的识别
【例1】 如图,三条直线两两相交于三点.
(1)∠1与∠4是什么角?是哪两条直线被哪条直
线所截而形成的?
(2)∠1与∠3,∠3与∠4呢? 【导学探究】 同位角、内错角、同旁内角都是成对出现的,同时满足两个条件:(1)必 须是 两 条直线被 第三条直线 所截形成的角.(2)必须是没有公共 顶点的角. 解:(1)∠1与∠4是两直线a,b被直线c所截而形成的同位角. (2)∠1与∠3是两直线b,c被直线a所截而形成的内错角; ∠3与∠4是两直线a,c被直线b所截而形成的同旁内角.
∵∠3=∠4,
∴∠4=70°,
∵∠2+∠4=180°,
∴∠2=110°.
第五章
相交线与平行线
1.如图所示,能与∠α 构成同位角的角有( (A)4个 (B)3个 (C)2个 (D)1个
B
)
解析:与∠α构成同位角的有∠1,∠2,∠3.即共有 3 个, 故选 B.
第五章
(A)∠1 (B)∠2 (C)∠4 (D)∠5
解析:图中的内错角有∠ADE 和∠BED,∠BDE 和∠DEC,共 2 对.
第五章
相交线与平行线
变式训练1-3: a , b 被直线 c 所截得到的 同旁内角;∠3和∠2是直线 a , c 被直线 b 所截得到的 内错 角; ∠1和∠2是直线 b , c 被直线 a 所截得到的 同位 角.
新人教版七年级数学下册第五章《同位角,内错角,同旁内角2》公开课课件
B∠1和∠2是同旁内角
C∠2和∠5是内错角 D∠4和∠5是同旁内角
1 2 4 5 3
请你说出下面说法错误的一个( )
E
A∠1和∠B是同位角
B∠B和∠2是同位角
C∠C和∠2是内错角
B
A
1 2
D
⌒
D∠BAD和∠B是同旁内角
C
勇攀高峰 如图,∠B与哪个角是同旁内角?它们分别 是有哪两条直线被哪一条直线截成的?
5 8
F
∠4和∠6
形 状 如 “ Z”
牛刀小试
下列图形中∠1,∠2是否为内错角
1 2
2 1
2⌒
1
2 1
( 1)
( 2)( 3)Fra bibliotek( 4)
是 是 是 是 内错角的边的特点:两角的边所在直线一共有3 条,其中两角有一条边共线,另两条边不共线, 共线两边所在直线为截线,不共线两边所在直 线为被截直线。
大显身手
大显身手
E
1、(2010.广西桂林) 如图直线AB、CD被直 线EF所截,则∠3的同 旁内角是( B )
A C
5
B
3 4
D
A、∠1
C、∠3
B、∠2
D、∠4
F
2、如图四边形ABCD是梯形,请你判断下列 说法是否正确。
正确 ①∠A和∠B是同旁内角( ) 正确 ②∠A和∠D是同旁内角( )
B A D
C
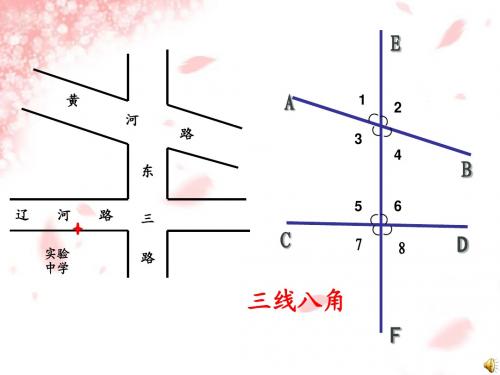
E
黄
河
A
路
东
1 3
2 4
B D
辽
河
实验 中学
路
三 路
5
6
C
7
8
三线八角
F
①在截线EF的同侧
人教版七年级数学下册第五章《同位角、内错角、同旁内角 》优课件

观察∠1和∠5两角:
同位角:一边在截线 的同一侧,另一边在 被截线的同一方.形状 学科网 5 像F.同位角 内错角 同旁内角 举例 练习 结束
图中的同位角除∠1和∠5外,还有…… c
b
87
56
a
43
12
复习 同位角 内错角 同旁内角 举例 练习 结束
下列各图中 1与2哪些是
l1
内错角
65
l2
78
同旁内角
找出图中的同位角、内错角、同旁内角:
b
c
2 34
a
复习 同位角 内错角 同旁内角 举例 练习 结束
能力挑战: 看图填空
A
E1 3D
B2
4
F
C
(2)若ED,BC被AF所截,
则∠3与_∠_4___是内错角。
能力挑战: 看图填空
A
E1 3D
B2
4
F
C
(3)∠1与∠3是AB和AF被 __D_E__所截构成的__内__错___角。
You made my day!
我们,还在路上……
找出图中与∠1构成同旁内角的角?
2 复习 同位角 内错角 同旁内角 举例 练习 结束
图中与∠1是同旁内角的角:
2
复习 同位角 内错角 同旁内角 举例 练习 结束
图中∠2的同旁内角的角:
2
开始 同位角 内错角 同旁内角 举例 练习 结束
当堂反馈:
DA
1 4
5
E
23 F
B
C
(2)如果把图看成是直线CD,EF被直线AB所截, 那么∠1与∠5是一对什么角? ∠4与∠5呢?
5.1.3 同位角、内错角、同旁内角
学科网
【最新】人教版七年级数学下册第五章《同位角、内错角、同旁内角》优质公开课课件 (3).ppt

知识点二 一
解:∠B与∠DAB是内错角; ∠B与∠BAE, ∠BAC, ∠C是同旁内角. ∠C与∠EAC是内 错角;∠C与∠DAC, ∠BAC, ∠B是同旁内角.
四、归纳小结
1、归纳总结同位角、内错角、同旁内角的 特征: 同位角:“ F ” 字型,“同旁同侧” 内错角:“ Z ” 字型,“之间两侧” 同旁内角:“ U ” 字型,“之间同侧”
新课引入 学习目标 研读课文 归纳小结 强化训练
引导学生读懂数学书课题 读书之法,在循序而渐进,熟读而精思.
——朱熹
研究成果配套课件
5.1.3同位角、内错角、同旁内角
一、新课引入
1 、直线AB、CD相交于O小于平角的角有 ___4__个?有____2_对对顶角?有_____对4角、 内错角和同旁内角的应用
例2 如图,直线DE,BC被直线AB所截 (1)∠1和∠2,∠1和∠3,∠1和∠4各是
什么位置关系的角? (2)如果∠1=∠4,那 么∠1和∠2相等吗? ∠1和∠3互补吗? 为什么?
.
知识点二同位角、 内错角和同旁内角的应用
答:(1)__∠_1___和__∠_2__是内错角, _∠__1__和_∠_3__是同旁内角,__∠_1___和 __∠_4__是同位角.
五、学习反思
__________________________________ __________________________________ __________________________________ __________________________________ __________________________________ __________________________________
人教版七年级数学下册第五章《 同位角内错角同旁内角》公开课课件

1
B
C
1与3是同旁内角。
例 如图,直线DE,BC被直线AB所截.
A (1)1与2,1与3, 1与4各
4
是什么角?
D2
E 3
答: 1与2是内错角。
1
B
C
1与3是同旁内角。 1与4是同位角。
例 如图,直线DE,BC被直线AB所截.
A (2)如果1=4,那么1与2 相等吗?
4 D 2 3E
1
B
C
例 如图,直线DE,BC被直线AB所截.
1与 2是直线AB,BC被直 线AC所截成的。
2
A
B
E
CD
12
A
B
答: 1与DCB是内错 角。
是直线AB,DE被直线BC所 截成的。
练习10: 1与哪些同旁内角?它们分别是由哪两条 直线被哪一条直线截成的?
E CD
2
A
B
答: 1与DCA,B, 2是 同旁内角。
答:1与 DCB是直线AB,DE被 直线AC所截成的。
1与B是直线AC,BC被直 线 AB所截成的。 E CD
A
C
1 42
3
D
B
1. 1与3,2与4是什么位 置的角?它们的大 小有什么关系?
A
C
1 42
3
答: 1与3是对顶角, 2与 4是对顶角。并且 1=3 ,2=4。
D
B
2. 1 与2, 4是什么位置的角 ?它们的大 小有什么关 系?
A
C
答: 1与2, 4是邻补角,
并且有 1+ 2=180°,或
1
者1+ 4=180°。
E B
A
C D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l
a
b
对三条直线相交按交点的个数分为三种情况:
(1)三条直线交点的个数有一个,即三条直线交于 一点;
(2)三条直线交点的个数有两个,即两条直线平行 且被第三条直线所截;
(3)三条直线交点的个数有三个,即三条直线两两
相交.
l
a b
对三条直线相交分为两种情况: (1)三条直线交于一点;
(2)两条直线被第三条直线所截.
c
同位角:∠l与∠5, ∠2与∠6.
内错角:∠4与∠6, ∠3与∠5.
同旁内角:∠4与∠5 , ∠3与∠6.
同位角:∠l与∠3, ∠2与∠4.
内错角:无.
同旁内角:∠2与 ∠3.
例.如图,直线DE、BC被直线AB所截, (1)∠l与∠2,∠1与∠3,∠1与∠4各是什么
关系的角?
∠l与∠2是内错角, ∠1与∠3是同旁内角, ∠1与∠4是同位角.
(1)除了∠1和∠5是同 位角,还有∠2和∠6,∠3 和∠7, ∠4和∠8也构成 同位角.
(2)共有4对同位角.
问题5:观察图中的∠3和∠5,它们有怎样的位置 关系?
内错角:如图,像∠3 和∠5,两个角都在直 线AB、CD之间,并且 分别在直线EF两侧.具 有这种位置关系的一对 角叫做内错角.
问题6: (1)你能找出图中还有哪几对角构成内错角? (2)两条直线被第三条直线所截构成的八个角中, 共有几对内错角?
(三)归纳小结
1.你能总结一下同位角、内错角、同旁内角分 别具有哪些特征吗? 2.你认为在图形中识别同位角、内错角、同旁 内角的关键是什么?
(三)布置作业
教科书 习题5.1 第11题,复习题5 第7题
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2021/1/112021/1/11Monday, January 11, 2021
• 10、人的志向通常和他们的能力成正比例。2021/1/112021/1/112021/1/111/11/2021 1:44:30 PM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2021/1/112021/1/112021/1/11Jan-2111-Jan-21 • 12、越是无能的人,越喜欢挑剔别人的错儿。2021/1/112021/1/112021/1/11Monday, January 11, 2021 • 13、志不立,天下无可成之事。2021/1/112021/1/112021/1/112021/1/111/11/2021
。2021年1月11日星期一2021/1/112021/1/112021/1/11
• 15、会当凌绝顶,一览众山小。2021年1月2021/1/112021/1/112021/1/111/11/2021
• 16、如果一个人不知道他要驶向哪头,那么任何风都不是顺风。2021/1/112021/1/11January 11, 2021
•
THE END 17、一个人如果不到最高峰,他就没有片刻的安宁,他也就不会感到生命的恬静和光荣。2021/1/112021/1/112021/1/112021/1/11
(1)除了∠3和∠5是内 错角,还有∠4和∠6 也 构成内错角.
(2)共有2对 内错角.
问题7: (1)如图,我们称∠3和∠6为同旁内角,你能根 据两个角的特征,描述一下同旁内角的定义吗?
同旁内角:如图,像 ∠3和∠6,两个角都 在直线AB、CD之间, 并且都在直线EF的 同一旁.具有这种位 置关系的一对角叫做 同旁内角.
5.1.3 同位角、内错角、同旁内角
课件说明
学习目标: (1)了解同位角、内错角、同旁内角的概念. (2)通过在图形中识别同位角、内错角、同旁内角, 提高识图能力,体会分类的思想.
学习重点: 同位角、内错角、同旁内角的识别.
(一)复习引入
问题1:如图,直线AB与EF相交,你能说出其中的对 顶角与邻补角吗?
l
a b
l
a b
问题3:观察图中的∠1和∠5,它们具有怎样的位 置关系?
同位角:如图,像 ∠1和∠5,两个角分 别在直线AB、CD的 同一方,并且都在直 线EF的同侧.具有 这种位置关系的一对 角叫做同位角.
问题4: (1)你能找出图中还有哪几对角构成同位角? (2)两条直线被第三条直线所截构成的八个角 中,共有几对同位角?
对顶角: ∠1和∠3,∠2和∠4.
邻补角: ∠1和∠2,∠2和∠3, ∠3和∠4,∠4和∠1.
(二)探索与思考
问题2:三条直线相交可以分为哪些情况?
对三条直线相交按交点的个数分为三种情况: (1)三条直线交点的个数有一个,即三条直线交于 一点;
l
a
b
对三条直线相交按交点的个数分为三种情况: (1)三条直线交点的个数有一个,即三条直线交于 一点; (2)三条直线交点的个数有两个,即两条直线平行 且被第三条直线所截;
问题7: (2)你能找出图中还有哪几对角构成同旁内角? (3)两条直线被第三条直线所截构成的八个角中, 共有几对同旁内角?
(1)除了∠4和∠5是 同旁内角,还有∠3和 ∠6 也构成同旁内角.
(2)共有2对 同旁内角.
练习:分别指出下列图中的同位角、内源自角、同旁内角.ba
a
b
5
14
c
23
6
12 34
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
例.如图,直线DE、BC被直线AB所截, (1)∠l与∠2,∠1与∠3,∠1与∠4各是什么
关系的角? (2)如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?
如果∠1=∠4,由对顶角相等, 得∠2=∠4,那么∠1=∠2.
因为∠4与∠3互补,得 ∠4+∠3=180º,, 又因为∠1=∠4, 所以∠1+∠3 =180º, 即∠1和∠3互补.
a
b
对三条直线相交按交点的个数分为三种情况:
(1)三条直线交点的个数有一个,即三条直线交于 一点;
(2)三条直线交点的个数有两个,即两条直线平行 且被第三条直线所截;
(3)三条直线交点的个数有三个,即三条直线两两
相交.
l
a b
对三条直线相交分为两种情况: (1)三条直线交于一点;
(2)两条直线被第三条直线所截.
c
同位角:∠l与∠5, ∠2与∠6.
内错角:∠4与∠6, ∠3与∠5.
同旁内角:∠4与∠5 , ∠3与∠6.
同位角:∠l与∠3, ∠2与∠4.
内错角:无.
同旁内角:∠2与 ∠3.
例.如图,直线DE、BC被直线AB所截, (1)∠l与∠2,∠1与∠3,∠1与∠4各是什么
关系的角?
∠l与∠2是内错角, ∠1与∠3是同旁内角, ∠1与∠4是同位角.
(1)除了∠1和∠5是同 位角,还有∠2和∠6,∠3 和∠7, ∠4和∠8也构成 同位角.
(2)共有4对同位角.
问题5:观察图中的∠3和∠5,它们有怎样的位置 关系?
内错角:如图,像∠3 和∠5,两个角都在直 线AB、CD之间,并且 分别在直线EF两侧.具 有这种位置关系的一对 角叫做内错角.
问题6: (1)你能找出图中还有哪几对角构成内错角? (2)两条直线被第三条直线所截构成的八个角中, 共有几对内错角?
(三)归纳小结
1.你能总结一下同位角、内错角、同旁内角分 别具有哪些特征吗? 2.你认为在图形中识别同位角、内错角、同旁 内角的关键是什么?
(三)布置作业
教科书 习题5.1 第11题,复习题5 第7题
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2021/1/112021/1/11Monday, January 11, 2021
• 10、人的志向通常和他们的能力成正比例。2021/1/112021/1/112021/1/111/11/2021 1:44:30 PM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2021/1/112021/1/112021/1/11Jan-2111-Jan-21 • 12、越是无能的人,越喜欢挑剔别人的错儿。2021/1/112021/1/112021/1/11Monday, January 11, 2021 • 13、志不立,天下无可成之事。2021/1/112021/1/112021/1/112021/1/111/11/2021
。2021年1月11日星期一2021/1/112021/1/112021/1/11
• 15、会当凌绝顶,一览众山小。2021年1月2021/1/112021/1/112021/1/111/11/2021
• 16、如果一个人不知道他要驶向哪头,那么任何风都不是顺风。2021/1/112021/1/11January 11, 2021
•
THE END 17、一个人如果不到最高峰,他就没有片刻的安宁,他也就不会感到生命的恬静和光荣。2021/1/112021/1/112021/1/112021/1/11
(1)除了∠3和∠5是内 错角,还有∠4和∠6 也 构成内错角.
(2)共有2对 内错角.
问题7: (1)如图,我们称∠3和∠6为同旁内角,你能根 据两个角的特征,描述一下同旁内角的定义吗?
同旁内角:如图,像 ∠3和∠6,两个角都 在直线AB、CD之间, 并且都在直线EF的 同一旁.具有这种位 置关系的一对角叫做 同旁内角.
5.1.3 同位角、内错角、同旁内角
课件说明
学习目标: (1)了解同位角、内错角、同旁内角的概念. (2)通过在图形中识别同位角、内错角、同旁内角, 提高识图能力,体会分类的思想.
学习重点: 同位角、内错角、同旁内角的识别.
(一)复习引入
问题1:如图,直线AB与EF相交,你能说出其中的对 顶角与邻补角吗?
l
a b
l
a b
问题3:观察图中的∠1和∠5,它们具有怎样的位 置关系?
同位角:如图,像 ∠1和∠5,两个角分 别在直线AB、CD的 同一方,并且都在直 线EF的同侧.具有 这种位置关系的一对 角叫做同位角.
问题4: (1)你能找出图中还有哪几对角构成同位角? (2)两条直线被第三条直线所截构成的八个角 中,共有几对同位角?
对顶角: ∠1和∠3,∠2和∠4.
邻补角: ∠1和∠2,∠2和∠3, ∠3和∠4,∠4和∠1.
(二)探索与思考
问题2:三条直线相交可以分为哪些情况?
对三条直线相交按交点的个数分为三种情况: (1)三条直线交点的个数有一个,即三条直线交于 一点;
l
a
b
对三条直线相交按交点的个数分为三种情况: (1)三条直线交点的个数有一个,即三条直线交于 一点; (2)三条直线交点的个数有两个,即两条直线平行 且被第三条直线所截;
问题7: (2)你能找出图中还有哪几对角构成同旁内角? (3)两条直线被第三条直线所截构成的八个角中, 共有几对同旁内角?
(1)除了∠4和∠5是 同旁内角,还有∠3和 ∠6 也构成同旁内角.
(2)共有2对 同旁内角.
练习:分别指出下列图中的同位角、内源自角、同旁内角.ba
a
b
5
14
c
23
6
12 34
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
例.如图,直线DE、BC被直线AB所截, (1)∠l与∠2,∠1与∠3,∠1与∠4各是什么
关系的角? (2)如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?
如果∠1=∠4,由对顶角相等, 得∠2=∠4,那么∠1=∠2.
因为∠4与∠3互补,得 ∠4+∠3=180º,, 又因为∠1=∠4, 所以∠1+∠3 =180º, 即∠1和∠3互补.
