2009年考研数一试题
四川大学2009年数学分析考研真题与解答

四川大学2009数学分析考研真题与解析1·求下列极限。
(a )∑=∞→nk k nn Cn2.ln 1lim解: 原极限=()221111121ln ln limln 1limnn C C Cn n k nk kn k n n k nnk n ++-=∑∑∑+==+∞→=∞→=∑=∞→-++nk n k n nn 11ln 121lim =∑=∞→∞→--⋅+n k n n nk n n n 1111ln 1lim 12lim =⎰=--1021)1ln(21dx x(b)().sin lim 22n n n +∞→π解: 原极限=nn n nn n n n n ++=-+∞→∞→22sinlim )sin(lim πππ=12sin 111limsin ==⎪⎪⎭⎫ ⎝⎛++∞→ππn n (c )().sin sin lim2302dtt t t tdtx x x ⎰⎰-→解: 原极限=()().1262limsin sin 2lim 53302230=⎥⎦⎤⎢⎣⎡+--=-⋅→→x x x x x x x x x x x x ο (d )xx xe x x cos 11lim 0----+→ 解: 原极限=()()()⎥⎦⎤⎢⎣⎡++--⎥⎦⎤⎢⎣⎡+--++→222222024218212lim x x x x x x x x x οοο =.32418121-=--2·计算下列积分。
(a ),222dxdy y x yx D⎰⎰--+其中{()}1;R ,222≤+∈=y x y x D 解: 原积分=rdr r r r d ⎰⎰-+12202sin cos θθθπ=dr r r d 220104sin ⎰⎰-⎪⎭⎫⎝⎛+ππθθ=()()θθθπθθd dr r r dr r r ⎰⎰⎰⎥⎦⎤⎢⎣⎡-+-201sin 23sin 032sin sin=θθθπd ⎰⎪⎪⎭⎫ ⎝⎛+-204413sin 6sin =85π(b) ⎰l yzds ,其中l 是球面⎪⎪⎭⎫ ⎝⎛>=++332222a a z y x 与平面1=++z y x 的交线.解: 原积分=()ds z z ds zx yz l l ⎰⎰-=+121)(21 =()()ds z y x ds z y x l l ⎰⎰++-++2226161 =⎰-l ds a 612 =().3131312612222--=-⋅-a a a a ππ(c )设()x f 在()+∞∞-,内有连续导函数,求积分()()[]dy xy f y y x dx y xy f y L11222-++⎰,其中L 是从点⎪⎭⎫⎝⎛32,3A 到()2,1B 的直线段。
2009年全国考研数学一真题及答案.doc
以 X ,Y , Z 分别表示两次取球所取得的红球、黑球与白球的个数。
(Ⅰ)求 p X 1 Z 0 ;
(Ⅱ)求二维随机变量 X , Y 概率分布。
第 4 页 共 24 页
9. (本题满分 11 分)
设总体 X 的概率密度为 f ( x)
2xe x , x 0 ,其中参数 (
0,其他
0) 未知, X 1 ,
S1
an , S2
a2 n 1 ,求 S1 与 S2 的值。
n1
n1
3.
x2 (本题满分 11 分)椭球面 S1 是椭圆
y2 1 绕 x 轴旋转而成,圆锥面 S2 是过点
43
第 3 页 共 24 页
x2 4,0 且与椭圆
4
y2 1
3
相切的直线绕 x 轴旋转而成。
(Ⅰ)求 S1及 S2 的方程
(Ⅱ)求 S1与 S2 之间的立体体积。
2z
9. 设函数 f u, v 具有二阶连续偏导数, z f x, xy ,则
。
xy
10. 若二阶常系数线性齐次微分方程
y ay by 0 的通解为 y C1 C2 x ex ,则非齐
次方程 y ay by x 满足条件 y 0 2, y 0 0的解为 y
。
11. 已知曲线 L : y x2 0 x
均值和样本方差。若 X kS2 为 np 2 的无偏估计量,则 k
。
三、解答题( 15- 23 小题,共 94 分 .请将解答写在答题纸指定的位置上 明、证明过程或演算步骤 .)
.解答应写出文字说
1. (本题满分 9 分)求二元函数 f ( x, y) x2 2 y2 y ln y 的极值。
2. (本题满分 9 分)设 an 为曲线 y xn 与 y xn 1 n 1,2,..... 所围成区域的面积,记
2009年计算机综合考研真题 (附答案解析)

2009年计算机统考真题解析(含答案)一、单项选择题,每小题 2 分,共 80 分。
1.为解决计算机与打印机之间速度不匹配的问题,通常设置一个打印数据缓冲区,主机将要输出的数据依次写入该缓冲区,而打印机则依次从该缓冲区中取出数据。
该缓冲区的逻辑结构应该是A.栈B.队列C.树D.图2.设栈 S 和队列 Q 的初始状态均为空,元素 abcdefg 依次进入栈 S。
若每个元素出栈后立即进入队列Q,且 7 个元素出队的顺序是 bdcfeag,则栈 S 的容量至少是A.1 B.2 C.3 D.43.给定二叉树图所示。
设 N 代表二叉树的根,L 代表根结点的左子树,R 代表根结点的右子树。
若遍历后的结点序列为 3,1,7,5,6,2,4,则其遍历方式是A.LRN B.NRL C.RLN D.RNL4.下列二叉排序树中,满足平衡二叉树定义的是5.已知一棵完全二叉树的第 6 层(设根为第 1 层)有 8 个叶结点,则完全二叉树的结点个数最多是A.39 B.52 C.111 D.1196.将森林转换为对应的二叉树,若在二叉树中,结点 u 是结点 v 的父结点的父结点,则在原来的森林中,u 和 v 可能具有的关系是I.父子关系 II.兄弟关系 III. u 的父结点与 v 的父结点是兄弟关系A.只有 IIB.I 和 IIC.I 和 IIID.I、II 和 III7.下列关于无向连通图特性的叙述中,正确的是 I.所有顶点的度之和为偶数 II.边数大于顶点个数减 1III.至少有一个顶点的度为 1A.只有 IB. 只有 IIC.I 和 IID.I 和 III8.下列叙述中,不符合m阶B 树定义要求的是A.根节点最多有 m 棵子树 B.所有叶结点都在同一层上 C.各结点内关键字均升序或降序排列 D.叶结点之间通过指针链接9.已知关键序列 5,8,12,19,28,20,15,22 是小根堆(最小堆),插入关键字 3,调整后得到的小根堆是A.3,5,12,8,28,20,15,22,19B. 3,5,12,19,20,15,22,8,28C.3,8,12,5,20,15,22,28,19D. 3,12,5,8,28,20,15,22,1910.若数据元素序列 11,12,13,7,8,9,23,4,5 是采用下列排序方法之一得到的第二趟排序后的结果,则该排序算法只能是A.起泡排序 B.插入排序 C.选择排序 D.二路归并排序11.冯•诺依曼计算机中指令和数据均以二进制形式存放在存储器中,CPU 区分它们的依据是A.指令操作码的译码结果 B.指令和数据的寻址方式 C.指令周期的不同阶段 D.指令和数据所在的存储单元12.一个 C 语言程序在一台 32 位机器上运行。
2009年计算机考研真题及答案(统考)

2009年计算机统考真题参考答案一.选择题 8 二.综合应用题 8 2010年全国研究生考试计算机统考试题及答案2009年统考计算机考研真题一.单项选择题,每小题2分,共80分。
1.为解决计算机与打印机之间速度不匹配的问题,通常设置一个打印数据缓冲区,主机将要输出的数据依次写入该缓冲区,而打印机则依次从该缓冲区中取出数据。
该缓冲区的逻辑结构应该是A.栈B.队列C.树D.图2.设栈S和队列Q的初始状态均为空,元素abcdefg依次进入栈S。
若每个元素出栈后立即进入队列Q,且7个元素出队的顺序是bdcfeag,则栈S的容量至少是A.1 B.2 C.3 D.43.给定二叉树图所示。
设N代表二叉树的根,L代表根结点的左子树,R代表根结点的右子树。
若遍历后的结点序列为3,1,7,5,6,2,4,则其遍历方式是A.LRN B.NRL C.RLN D.RNLB. 4.下列二叉排序树中,满足平衡二叉树定义的是5.已知一棵完全二叉树的第6层(设根为第1层)有8个叶结点,则完全二叉树的结点个数最多是A.39 B.52 C.111 D.1196.将森林转换为对应的二叉树,若在二叉树中,结点u是结点v的父结点的父结点,则在原来的森林中,u和v可能具有的关系是 I.父子关系 II.兄弟关系 III. u的父结点与v的父结点是兄弟关系A.只有IIB.I和IIC.I和IIID.I、II和III7.下列关于无向连通图特性的叙述中,正确的是 I.所有顶点的度之和为偶数 II.边数大于顶点个数减1 III.至少有一个顶点的度为1A.只有IB. 只有IIC.I和IID.I和III8.下列叙述中,不符合m阶B树定义要求的是 A.根节点最多有m棵子树 B.所有叶结点都在同一层上C.各结点内关键字均升序或降序排列 D.叶结点之间通过指针链接9.已知关键序列5,8,12,19,28,20,15,22是小根堆(最小堆),插入关键字3,调整后得到的小根堆是A.3,5,12,8,28,20,15,22,19 B. 3,5,12,19,20,15,22,8,28C.3,8,12,5,20,15,22,28,19 D. 3,12,5,8,28,20,15,22,1910.若数据元素序列11,12,13,7,8,9,23,4,5是采用下列排序方法之一得到的第二趟排序后的结果,则该排序算法只能是A.起泡排序 B.插入排序 C.选择排序 D.二路归并排序11.冯·诺依曼计算机中指令和数据均以二进制形式存放在存储器中,CPU区分它们的依据是A.指令操作码的译码结果 B.指令和数据的寻址方式 C.指令周期的不同阶段 D.指令和数据所在的存储单元12.一个C语言程序在一台32位机器上运行。
2009考研数一真题及解析
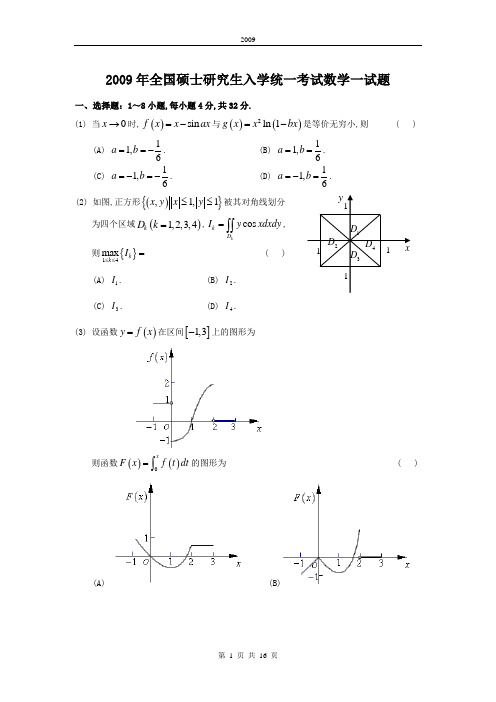
2009年全国硕士研究生入学统一考试数学一试题一、选择题:1~8小题,每小题4分,共32分.(1) 当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则 ( )(A) 11,6a b ==-. (B) 11,6a b ==. (C) 11,6a b =-=-. (D) 11,6a b =-=.(2) 如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max k k I ≤≤= ( )(A) 1I .(B) 2I .(C) 3I .(D) 4I .(3) 设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为 ( )(A) (B)(C)(D)(4) 设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则 ( )(A) 当1nn b∞=∑收敛时,1n nn a b∞=∑收敛. (B) 当1nn b∞=∑发散时,1n nn a b∞=∑发散.(C) 当1nn b∞=∑收敛时,221n nn a b∞=∑收敛. (D) 当1nn b∞=∑发散时,221n nn a b∞=∑发散.(5) 设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23ααα到基122331,,αααααα+++的过渡矩阵为 ( )(A) 101220033⎛⎫ ⎪ ⎪ ⎪⎝⎭.(B) 120023103⎛⎫⎪⎪ ⎪⎝⎭.(C) 111246111246111246⎛⎫- ⎪ ⎪ ⎪-⎪ ⎪ ⎪- ⎪⎝⎭.(D) 111222111444111666⎛⎫-⎪ ⎪⎪- ⎪ ⎪ ⎪- ⎪⎝⎭. (6) 设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为 ( ) (A) **32O B A O ⎛⎫⎪⎝⎭. (B) **23O B A O ⎛⎫⎪⎝⎭.(C) **32O A BO ⎛⎫⎪⎝⎭.(D) **23OA BO ⎛⎫⎪⎝⎭.(7) 设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,其中()x Φ为标准正态分布的分布函数,则EX = ( ) (A) 0. (B) 0.3. (C) 0.7. (D) 1.(8) 设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====.记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为 ( ) (A) 0. (B) 1. (C) 2. (D) 3.二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9) 设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2zx y∂=∂∂ .(10) 若二阶常系数线性齐次微分方程0y ay by '''++=的通解为()12xy C C x e =+,则非齐次方程y ay by x '''++=满足条件()()02,00y y '==的解为y = .(11) 已知曲线(2:0L y x x =≤≤,则Lxds =⎰ .(12) 设(){}222,,1x y z xy z Ω=++≤,则2z dxdydz Ω=⎰⎰⎰ .(13) 若3维列向量,αβ满足2Tαβ=,其中T α为α的转置,则矩阵T βα的非零特征值为.(14) 设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量,则k = .三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值.(16)(本题满分9分)设n a 为曲线n y x =与()11,2,n y xn +== 所围成区域的面积,记11,n n S a ∞==∑2211n n S a ∞-==∑,求1S 与2S 的值.(17)(本题满分11分)椭球面1S 是椭圆22143x y +=绕x 轴旋转而成,圆锥面2S 是由过点()4,0且与椭圆22143x y +=相切的直线绕x 轴旋转而成. (Ⅰ)求1S 及2S 的方程; (Ⅱ)求1S 与2S 之间的立体体积. (18)(本题满分11分)(Ⅰ)证明拉格朗日中值定理:若函数()f x 在[],a b 上连续,在(,)a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-.(Ⅱ)证明:若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.(19)(本题满分10分)计算曲面积分()32222xdydz ydzdx zdxdyI xy z∑++=++⎰⎰,其中∑是曲面222224x y z ++=的外侧.(20)(本题满分11分)设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭(Ⅰ)求满足22131,A A ξξξξ==的所有向量23,ξξ; (Ⅱ)对(Ⅰ)中的任意向量23,ξξ,证明:123,,ξξξ线性无关. (21)(本题满分11分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-(Ⅰ)求二次型f 的矩阵的所有特征值;(Ⅱ)若二次型f 的规范形为2212y y +,求a 的值. (22)(本题满分11分)袋中有1个红球,2个黑球与3个白球.现有放回地从袋中取两次,每次取一个球,以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数.(Ⅰ)求{}10P X Z ==;(Ⅱ)求二维随机变量(),X Y 的概率分布. (23)(本题满分11 分)设总体X 的概率密度为2,0,()0,x xe x f x λλ-⎧>=⎨⎩其他, 其中参数(0)λλ>未知,12,,,n X X X 是来自总体X 的简单随机样本.(Ⅰ) 求参数λ的矩估计量;(Ⅱ )求参数λ的最大似然估计量.2009年全国硕士研究生入学统一考试数学一试题一、选择题:1~8小题,每小题4分,共32分. (1) 【答案】(A)【解析】()sin f x x ax =-与()()2ln 1g x x bx =-是0x →时的等价无穷小,则2200232000330()sin sin limlim lim ()ln(1)()sin 1cos sin lim lim lim 36sin lim 1,66x x x x x x x f x x ax x axg x x bx x bx x ax a ax a axbx bx bxa ax ab axb →→→→→→→--=-⋅---=---⎛⎫=-=-= ⎪⎝⎭等洛洛 即36a b =-,故排除B,C.另外,201cos lim3x a axbx→--存在,蕴含了1cos 0a ax -→()0x →,故1,a =排除D. 所以本题选A.(2) 【答案】(A)【解析】本题利用二重积分区域的对称性及被积函数的奇偶性.令(,)cos f x y y x =,24,D D 两区域关于x 轴对称,(,)cos (,)f x y y x f x y -=-=-,即被积函数是关于y 的奇函数,所以240I I ==;13,D D 两区域关于y 轴对称,(,)cos()cos (,)f x y y x y x f x y -=-==,即被积函数是关于x 的偶函数,所以{}{}1(,),013(,),012cos 0,2cos 0.x y y x x x y y x x I y xdxdy I y xdxdy ≥≤≤≤-≤≤=>=<⎰⎰⎰⎰所以正确答案为(A). (3) 【答案】(D)【解析】此题为定积分的应用知识考核,由()y f x =的图形可以看出,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出下面几个方面的特征:① []1,0x ∈-时,()0F x ≤为线性函数,单调递增; ② []0,1x ∈时,()0F x ≤,且单调递减;③ []1,2x ∈时,()F x 单调递增; ④ []2,3x ∈时,()F x 为常函数; ⑤ ()F x 为连续函数. 结合这些特点,可见正确选项为(D). (4) 【答案】C【解析】解法1 举反例:取(1)nn n a b ==-,则lim 0n n a →∞=,1n n b ∞=∑是收敛的,但111n n n n a b n ∞∞===∑∑发散,排除(A);取1n n a b n ==,则lim 0n n a →∞=,1n n b ∞=∑是发散的,但2111n n n n a b n ∞∞===∑∑收敛,排除(B);取1n n a b n ==,则lim 0n n a →∞=,1n n b ∞=∑是发散的,但224111n n n n a b n∞∞===∑∑收敛,排除(D),故答案为(C).解法2 因为lim 0,n n a →∞=则由定义可知1,N ∃使得1n N >时,有1n a <;又因为1nn b∞=∑收敛,可得lim 0,n n b →∞=则由定义可知2,N ∃使得2n N >时,有1n b <,从而,当12n N N >+时,有22n nn a b b <,则由正项级数的比较判别法可知221n nn a b∞=∑收敛.(5) 【答案】(A)【解析】根据过渡矩阵的定义,知由基12311,,23ααα到122331,,αααααα+++的过渡矩阵M 满足:()12233112312311,,,,2310111,,220,23033M αααααααααααα⎛⎫+++= ⎪⎝⎭⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭所以此题选(A). (6) 【答案】(B)【解析】分块矩阵O A B O ⎛⎫⎪⎝⎭的行列式221236O A A B B O⨯=-=⨯=(),即分块矩阵可逆,且1116112366.1132O A O A O A O B B O B O B O A O O B O B B O B A O A O A O A *---******⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫ ⎪ ⎪⎛⎫⎪=== ⎪ ⎪ ⎪ ⎪⎝⎭⎪ ⎪⎝⎭⎝⎭故答案为(B).(7) 【答案】(C)【解析】因为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,所以 ()()0.710.322x F x x -⎛⎫'''=Φ+Φ ⎪⎝⎭, 因此, ()()10.30.352x EX xF x dx x x dx +∞+∞-∞-∞⎡-⎤⎛⎫'''==Φ+Φ ⎪⎢⎥⎝⎭⎣⎦⎰⎰()10.30.352x x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ ⎪⎝⎭⎰⎰.由于()x Φ为标准正态分布的分布函数,所以()0x x dx +∞-∞'Φ=⎰,()()()()11221222222,x x x dx u u u du u u du u du +∞+∞-∞-∞+∞+∞-∞-∞--⎛⎫''Φ=+Φ ⎪⎝⎭''=Φ+Φ=⎰⎰⎰⎰()10.30.3500.3520.72x EX x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ=+⨯= ⎪⎝⎭⎰⎰.(8) 【答案】(B)【解析】(){}{0}{0}{1}{1}11{0}{1}2211{00}{1},22Z F z P XY z P XY z Y P Y P XY z Y P Y P XY z Y P XY z Y P X z Y P X z Y =≤=≤==+≤===≤=+≤==⋅≤=+≤=由于,X Y 相互独立,所以11(){0}{}22Z F z P X z P X z =⋅≤+≤. (1) 当0z <时,1()()2Z F z z =Φ;(2) 当0z ≥时,11()()22Z F z z =+Φ,因此,0z =为间断点,故选(B).二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9) 【答案】12222xf f xyf '''''++ 【解析】12zf f y x∂''=+⋅∂, 21222212222zxf f yx f xf f xyf x y∂''''''''''=++⋅=++∂∂. (10) 【答案】(1)2x x e -+【解析】由常系数线性齐次微分方程0y ay by '''++=的通解为()12xy C C x e =+可知1x y e =,2x y xe =为其两个线性无关的解,代入齐次方程,有111222(1)010,[2(1)]020,x xy ay by a b e a b y ay by a a b x e a '''++=++=⇒++='''++=++++=⇒+=从而可见2,1a b =-=,非齐次微分方程为2y y y x '''-+=.设特解*y Ax B =+,代入非齐次微分方程,得2A Ax B x -++=,即11(2)202A A Ax A B x A B B ==⎧⎧+-+=⇒⇒⎨⎨-+==⎩⎩所以特解*2y x =+,通解()122xy C C x e x =+++.把()()02,00y y '==代入通解,得120,1C C ==-.所以所求解为2(1)2x x y xe x x e =-++=-+.(11)【答案】136【解析】由题意可知,2,0y x x =≤≤,则ds ==,所以()21148Lxds x ==+⎰11386==. (12) 【答案】415π 【解析】解法1:()212222002124013500sin cos cos cos cos 42.3515z dxdydz d d d d d d πππππθϕρϕρϕρθϕϕρρϕρππΩ==-⎛⎫=⋅-⋅= ⎪⎝⎭⎰⎰⎰⎰⎰⎰⎰⎰⎰解法2:由轮换对称性可知2z dxdydz Ω=⎰⎰⎰2x dxdydz Ω=⎰⎰⎰2y dxdydz Ω⎰⎰⎰所以,()212222400011sin 33z dxdydz x y z dxdydz d d r dr ππϕθϕΩΩ=++=⎰⎰⎰⎰⎰⎰⎰⎰⎰ 14002214sin sin 33515d r dr d ππππϕϕϕϕπ==⋅⋅=⎰⎰⎰. (13) 【答案】2 【解析】2Tαβ=,()2T T βαββαββ∴==⋅,又由于0β≠,T βα∴的非零特征值为2.(14) 【答案】1-【解析】由于2X kS +为2np 的无偏估计量,所以22()E X kS np +=,即2222()()()E X kS np E X E kS np +=⇒+=2(1)1(1)(1)1 1.np knp p np k p pk p p k ⇒+-=⇒+-=⇒-=-⇒=-三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)【解析】 2(,)2(2)x f x y x y '=+,2(,)2ln 1y f x y x y y '=++.令(,)0,(,)0,x y f x y f x y ⎧'=⎪⎨'=⎪⎩解得唯一驻点1(0,)e .由于212(0,)1(0,)21(0,)11(0,)2(2)2(2),1(0,)40,11(0,)(2),xxexye yy eA f y e eB f xy eC f x e e y ''==+=+''===''==+= 所以 2212(2)0,B AC e e -=-+<且0A >. 从而1(0,)f e 是(,)f x y 的极小值,极小值为11(0,)f e e=-.(16)(本题满分9分)【解析】曲线n y x =与1n y x +=的交点为(0,0)和(1,1),所围区域的面积112111111()()001212n n n n n a x x dx x x n n n n +++=-=-=-++++⎰, 111lim 1111111lim()lim(),2312222Nn nN n n N N S a a N N N ∞→∞==→∞→∞===-++-=-=+++∑∑22111211111111(1)22123456n n n n n S a n n n ∞∞∞-=====-=-+-++=-+∑∑∑ ().考查幂级数1(1)n nn x n ∞=-∑,知其收敛域为(1,1]-,和函数为ln(1)x -+.因为2(1)()ln(1)n nn S x x x x n ∞=-==-+∑,令1x =,得2211(1)1ln 2n n S a S ∞-====-∑.(17)(本题满分11分)【解析】(I)椭球面1S 的方程为222143x y z ++=. 设切点为00(,)x y ,则22143x y +=在00(,)x y 处的切线方程为00143x x y y +=. 将4,0x y ==代入切线方程得01x =,从而032y ==±. 所以切线方程为142x y ±=,从而圆锥面2S 的方程为222(1)44x y z +-=,即222(4)440x y z ---=.(II)1S 与2S 之间的体积等于一个底面半径为32、高为3的锥体体积94π与部分椭球体体积V 之差,其中22135(4)44V x dx ππ=-=⎰. 故所求体积为9544πππ-=.(18)(本题满分11分) 【解析】(Ⅰ)取()()()()()f b f a F x f x x a b a-=---,由题意知()F x 在[],a b 上连续,在(),a b 内可导,且()()()()()(),()()()()()().f b f a F a f a a a f a b af b f a F b f b b a f a b a -=--=--=--=-根据罗尔定理,存在(),a b ξ∈,使得()()()()0f b f a F f b aξξ-''=-=-,即()()()()f b f a f b a ξ'-=-.(Ⅱ)对于任意的(0,)t δ∈,函数()f x 在[]0,t 上连续,在()0,t 内可导,由右导数定义及拉格朗日中值定理()()000()0()0lim lim lim ()0t t t f t f f tf f t tξξ++++→→→-'''===-,其中()0,t ξ∈. 由于()0lim t f t A +→'=,且当0t +→时,0ξ+→,所以0lim ()t f A ξ+→'=,故(0)f +'存在,且(0)f A +'=.(19)(本题满分10分)【解析】取2221:1x y z ∑++=的外侧,Ω为∑与1∑之间的部分.()()()11322223322222222.xdydz ydzdx zdxdyI xy zxdydz ydzdx zdxdyxdydz ydzdx zdxdyxy zxy z∑∑-∑∑++=++++++=+++++⎰⎰⎰⎰⎰⎰根据高斯公式()13222200xdydz ydzdx zdxdydxdydz x y z∑-∑Ω++==++⎰⎰⎰⎰⎰ .()1122232222134.x y z xdydz ydzdx zdxdyxdydz ydzdx zdxdyxy zdxdydz π∑∑++≤++=++++==⎰⎰⎰⎰⎰⎰⎰所以4I π=.(20)(本题满分11分)【解析】(Ⅰ)对矩阵1()A ξ 施以初等行变换()11110221111111111012204220000A ξ⎛⎫-- ⎪---⎛⎫ ⎪⎪ ⎪=-→ ⎪ ⎪ ⎪--- ⎪⎝⎭ ⎪ ⎪⎝⎭可求得 2122122k kk ξ⎛⎫-+ ⎪ ⎪ ⎪=- ⎪ ⎪⎪ ⎪⎝⎭,其中k 为任意常数.又2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭,对矩阵21()A ξ 施以初等行变换()211110220122201000044020000A ξ⎛⎫-⎪-⎛⎫ ⎪ ⎪=--→ ⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭,可求得 312a a b ξ⎛⎫-- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,其中,a b 为任意常数.(Ⅱ)解法1 由(Ⅰ)知12311122211,,102222ka ka kbξξξ--+--=-=-≠-, 所以123,,ξξξ线性无关.解法2 由题设可得10A ξ=.设存在数123,,k k k ,使得1122330k k k ξξξ++=, ①等式两端左乘A ,得22330k A k A ξξ+=,即21330k k A ξξ+=, ②等式两端再左乘A ,得2330k A ξ=,即310k ξ=.由于10ξ≠,于是30k =,代入②式,得210k ξ=,故20k =.将230k k ==代入①式,可得10k =,从而1,ξ23,ξξ线性无关.(21)(本题满分11分) 【解析】(Ⅰ)二次型f 的矩阵101111a A a a ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭.由于01||01()((1))((2))111aE A aa a a a λλλλλλλ---=-=--+----+, 所以A 的特征值为123,1,2a a a λλλ==+=-.(Ⅱ)解法1 由于f 的规范形为2212y y +,所以A 合同于100010000⎛⎫ ⎪ ⎪ ⎪⎝⎭,其秩为2,故 1230A λλλ==,于是0a =或1a =-或2a =.当0a =时,1230,1,2λλλ===-,此时f 的规范形为2212y y -,不合题意. 当1a =-时,1231,0,3λλλ=-==-,此时f 的规范形为2212y y --,不合题意. 当2a =时,1232,3,0λλλ===,此时f 的规范形为2212y y +. 综上可知,2a =.解法2 由于f 的规范形为2212y y +,所以A 的特征值有2个为正数,1个为零. 又21a a a -<<+,所以2a =.(22)(本题满分11分)【解析】(Ⅰ) 12211{1,0}463(10)1{0}9()2C P X Z P X Z P Z ⋅========. (Ⅱ)由题意知X 与Y 的所有可能取值均为0,1,2.()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0,461112,0,0,1,36311,1,2,10,910,2,91,20,2,20,C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======故(,)X Y 的概率分布为(23)(本题满分11 分) 【解析】(Ⅰ)2202().x EX xf x dx x e dx λλλ+∞+∞--∞===⎰⎰令X EX =,即2X λ=,得λ的矩估计量为 12Xλ=. (Ⅱ)设12,,,(0,1,2,,)n i x x x x i n >= 为样本观测值,则似然函数为()12121,,,;,nii nx nn i i L x x x ex λλλ=-=∑=⋅∏11ln 2ln ln n ni i i i L n x x λλ===-+∑∑,由1ln 20n i i d L n x d λλ==-=∑,得λ的最大似然估计量为 22Xλ=.。
中山大学考研数学分析2009年真题及答案

中山大学2009年数学分析真题题目一、(每小题6分,共48分) (1) 求lim x→∞(x −x 2ln (1+1x ));(2)求∫1−lnx ln 2xdx ;(3) {x =cos(t 2)y =∫sinuu du t 20,求dydx; (4) 求∫|x −a |e x dx 1−1,|a |<1;(5) 设z =uv +sint,u =e t ,v =cost,求dzdt ;(6) u =φ(x +ψ(y )), 其中φ,ψ二阶可微,x,y 为自变量,求d 2u ;(7) 求级数∑cos nx ∞n=1在收敛域上的和函数;(8)判断级数∑1n1+1n∞n=1的敛散性.二、将区间[1,2]做n 等分。
分点为1=x 0<⋯<x n =2,求lim n→∞√x 1x 2…x n n 。
三、计算I =∫(x+y )dx+(y−x)dyx 2+y 2L,其中L 是从点A (-1,0)到点B (1,0)的一条不经过原点的光滑曲线:y =f (x ),x =[−1,1],且当xϵ(−1,1)时,f(x)>0。
四、计算∬x 2dydz +y 2dzdx +z 2dxdy S ,其中S 为曲面x 2+y 2=z 2介于平面z =0和z =h(h >0)之间的部分取下侧。
五、设f (x)在(1,+∞)上连续,f ′′(x)≤0,f (1)=2,f ′(1)=−3,证明f (x)=0在(1,+∞)上有且仅有一个实根。
六、设函数f (x)在(−∞,+∞)上连续,试证:对一切x 满足f (2x )=f(x)e x 的充要条件是f (x )=f(0)e x 。
七、求椭球面x 2a 2+y 2b 2+z 2c 2=1在第一卦限部分的切平面与三坐标平面围成的四面体的最小体积。
八、讨论级数∑cos(π2lnn)n∞n=1的敛散性。
参考答案一、 (1) lim x→∞(x −x 2ln (1+1x ))=lim x→∞x 2[1x −ln (1+1x )]=12limx→∞x 2x 2=12.(2)∫1−lnx ln 2xdx =∫1−y y 2de y=∫e y (1−y)y 2dy =∫e y (y −1)d 1y =(y−1)e yy−∫d (y−1)e yy=−e y y +C =−x lnx+C .(3) dy dx =dy dt dx dt=2tsint 2t 2−2tsint 2=−1t2.(4)∫|x −a |e x dx 1−1=∫(a −x)e x dx a −1+∫(x −a )e x dx =(a +1−x)e x |−1a 1a +(x −a −1)e x |a 1=2e a −(a +2)e−1−ae . (5) z =uv +sint,u =e t ,v =cost ,故z =e t cost +sint,dz dt=e t (cost −sint )+cost .(6)u =φ(x +ψ(y )),φ,ψ二阶可微,故du =φ′(x +ψ(y ))[dx +ψ′(y)dy]d 2u =dφ′(x +ψ(y ))[dx +ψ′(y )dy]+φ′(x +ψ(y ))d [dx +ψ′(y )dy]=φ′′(x +ψ(y ))[dx +ψ′(y )dy]2+φ′(x +ψ(y ))ψ′′(y )(dy)2(7) ∑cos n x ∞n=1=cosx 1−cosx ,其收敛域为{x ||cosx |<1}={x|x ≠kπ,kϵZ}。
【合集打印】1987-2009年考研数学一真题【 72页 】

九、(本题满分8分) 问a,b为何值时,线性方程组
X1 + X2 + x3 + X4 = 0, x2 + 2x3 + 2x4 = 1, -x2 + (a-3)x3 -2x4 = b, 3x1 + 2x2 + x3 + ax4 = - l 有唯一 解,无解, 有无穷多组解?并求出有无穷多组解时的通解.
(D)某邻域内单调减少.
(3)设有空间区域fl1 :x2 +y2 +z2�R2,z�0 ; 及[12 :X2 十广+z2�R2'X�0'y�0,z�0'则( )
(A)fJJxdv = 4fJJxdv.
il1
纺
(B)fjJydv = 4fjJydv.
il1
{Ji
(C)fJJzdv = 4fJJzdv.
6
1989年真题
1989年全国硕士研究生招生考试试题
(试卷I)
-、填空题(本题共5小题,每小题3分,满分15分)
(1)已知f
'(3)
= 2,则lim h----+O
f(3
-h) -f(3)
2h
(2)设八x)是连续函数,且j(X) = X +2rj(t)dt,则J(x) =
.
Ji J (3)设平面 曲线L为下半圆y =- 二了,则曲线积分 (x2 +y2)ds =
1987年真题
率等于
.已知取出的球是自球,此球属于第二个箱子的概率为
.
7, (3)已知连续型随机变量X的概率密度函数为f(x) = 了 卫心-1' 则X的数学期望为
方差为
,X的
+-、(本题满分6分)
考研数学真题 2009年1月

2009年1月真题解析一、问题求解:第1~15小题,每小题3分,共45分.下列每题给出的A 、B 、C 、D 、E 五个选项中,有一项是符合试题要求的.请在答题卡上将所选项的字母涂黑.1.一家商店为回收资金,把甲、乙两件商品均以480元一件卖出,已知甲商品赚了20%,乙商品亏了20%,则商店盈亏结果为().(A )不亏不赚(B )亏了50元(C )赚了50元(D )赚了40元(E )亏了40元【答案】E【考点】盈亏问题【解析】设甲、乙两件商品的成本价分别为,x y 元,则(120%)480,(120%)480,x y +=⎧⎨-=⎩解得400,600,x y =⎧⎨=⎩所以甲、乙两件商品的成本之和为1000x y +=元,而实际卖得的价格为480+480=960元,商店亏了1000-960=40元.2.某国参加北京奥运会的男女运动员比例原为19:12,由于先增加若干名女运动员,使男女运动员比例变为20:13.后又增加了若干名男运动员,于是男女运动员比例最终变为30:19.如果后增加的男运动员比先增加的女运动员多3人,则最后运动员的总人数为().(A )686(B )637(C )700(D )661(E )600【答案】B【考点】比例问题【解析】方法1:设先增加了x 名女运动员,后增加了3x +名男运动员,最初男女运动员分别有19k 和12k 人则有1920121319(3)301219kk x k x k x⎧=⎪⎪+⎨++⎪=⎪+⎩,解得7,20x k ==所以总人数为1920(73)12207637⨯+++⨯+=(人).方法2:原来男:女19:12=;增加女运动员后,男:女20:13=,在该过程中男运动员数量没变,故男运动员数能被20和19整除,增加女运动员后,男:女20:13=,再增加男运动员后,男:女30:19=;在该过程中女运动员数量没变,故女运动员数能被13和19整除,.最小就1319247⨯=;又男:女30:19=⇒男1330390=⨯=,390247637+=.3.某工厂定期购买一种原料,已知该厂每天需用该原料6吨,每吨价格1800元.原料的保管费用平均每吨3元,每次购买原料支付运费900元.若该厂要使平均每天支付的总费用最省,则应该每()天购买一次原料.(A )11(B )10(C )9(D )8(E )7【答案】B【考点】均值不等式【解析】设应该每隔n 天购买一次原料则总费用1800663(12)900108009(1)900S n n n n n =⨯+⨯⨯++++=+++ ,所以平均每天的费用900108099S n n =++,根据平均值不等式可知当且仅当9009n n=即10n =时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
* *
)
⎛1 2 0⎞ ⎟ ( B) ⎜ ⎜ 0 2 3⎟ . ⎜1 0 3⎟ ⎝ ⎠ ⎛ 1 ⎜ 2 ⎜ 1 ( D) ⎜ ⎜ 4 ⎜ 1 ⎜ ⎜− ⎝ 6 − 1 2 1 4 1 6 1 ⎞ 2 ⎟ ⎟ 1⎟ − . 4⎟ ⎟ 1 ⎟ ⎟ 6 ⎠
2
)
1 . 6 1 ( C ) a = −1, b = − . 6
( A ) a = 1, b = −
1 . 6 1 ( D ) a = −1, b = . 6
( B ) a = 1, b =
y
1
(2)如图,正方形
{( x, y ) x ≤ 1, y ≤ 1} 被其对角线划分为
∫∫ y cos xdxdy ,
(19) (本题满分 10 分)计算曲面积分 I =
� ∫∫
∑
xdydz + ydzdx + zdxdy
(x
2
+y +z
2
3 2 2
,其中
)
∑
是曲面
2 x 2 + 2 y 2 + z 2 = 4 的外侧。
(20) (本题满分 11 分)
⎛ 1 −1 −1 ⎞ ⎜ 设 A = −1 1 1⎟ ⎜ ⎟ ⎜ 0 −4 −2 ⎟ ⎝ ⎠
( A) 0 .
( B ) 0.3 .
( C ) 0.7 .
( D ) 1.
( 8 )设随机变量 X 与 Y 相互独立,且 X 服从标准正态分布 N ( 0,1) , Y 的概率分布为
P {Y = 0} = P {Y = 1} =
1 , 记 FZ ( z ) 为 随 机 变 量 Z = XY 的 分 布 函 数 , 则 函 数 2
D2 , D4 两区域关于 x 轴对称,而 f ( x, − y ) = − y cos x = − f ( x, y ) ,即被积函数是关于 y 的
奇函数,所以 I 2 = I 4 = 0 ;
D1, D3 两区域关于 y 轴对称,而 f (− x, y ) = y cos(− x) = y cos x = f ( x, y ) ,即被积函数是
2
(C ) ⎜
⎛ O 3 A* ⎞ ⎟. * O ⎠ ⎝ 2B
( D) ⎜
⎛ O * ⎝ 3B
考研资料下载中心
(7)设随机变量 X 的分布函数为 F ( x ) = 0.3Φ ( x ) + 0.7Φ ⎜ 态分布函数,则 EX = ( )
⎛ x −1 ⎞ ⎟ ,其中 Φ ( x ) 为标准正 ⎝ 2 ⎠
2
(16) (本题满分 9 分)设 an 为曲线 y = x n 与 y = x
∞ ∞
n +1
( n = 1, 2,.....) 所围成区域的面积,记
S1 = ∑ an , S 2 = ∑ a2n −1 ,求 S1 与 S2 的值。
n =1 n =1
(17) (本题满分 11 分)椭球面 S1 是椭圆
n =1
∞
( C ) 当 ∑ bn
n =1
收敛时,
∑a b
n =1
2 2 n n
收敛.
( D ) 当 ∑ bn
n =1
发散时,
∑a b
n =1
2 2 n n
发散.
(5)设 α1 , α 2 , α 3 是 3 维向量空间 R 的一组基,则由基 α1 , α 2 , α 3 到基
3
1 2
1 3
α1 + α 2 , α 2 + α 3 , α 3 + α1 的过渡矩阵为(
1 . 6 1 ( C ) a = −1, b = − . 6 【答案】 A
( A) a = 1, b = −
1 . 6 1 ( D ) a = −1, b = . 6
( B ) a = 1, b =
【解析】 f ( x) = x − sin ax, g ( x) = x ln(1 − bx) 为等价无穷小,则
x2 y 2 + = 1 绕 x 轴旋转而成,圆锥面 S2 是过点 4 3
3
考研资料下载中心
( 4, 0 ) 且与椭圆
x2 y 2 + =1 4 3
相切的直线绕 x 轴旋转而成。
(Ⅰ)求 S1 及 S2 的方程 (Ⅱ)求 S1 与 S 2 之间的立体体积。 (18) (本题满分 11 分) (Ⅰ)证明拉格朗日中值定理:若函数 f ( x ) 在 [ a, b ] 上连续,在 (a, b) 可导,则存在
考研资料下载中心
2009 年全国硕士研究生入学统一考试数学一试题
一、选择题(1~8 小题,每小题 4 分,共 32 分,下列每小题给出的四个选项中,只有一项 符合题目要求,把所选项前的字母填在题后的括号内.) (1)当 x → 0 时, f ( x ) = x − sin ax 与 g ( x ) = x ln (1 − bx ) 等价无穷小,则(
ξ ∈ ( a, b ) ,使得 f ( b ) − f ( a ) = f ′ (ξ )( b − a )
( Ⅱ ) 证 明 : 若 函 数 f ( x ) 在 x = 0 处 连 续 , 在 ( 0, δ )(δ > 0 ) 内 可 导 , 且
x → 0+
lim f ′ ( x ) = A ,则 f +′ ( 0 ) 存在,且 f +′ ( 0 ) = A 。
}
四个区域 Dk ( k = 1, 2,3, 4 ) , I k = 则 max { I k } =
1≤ k ≤ 4
∫∫ y cos xdxdy ,
Dk
D1
-1
D2 D3
-1
D4
1
x
( A) I1 .
( B ) I2 .
( C ) I3 .
( D ) I4 .
【答案】A 【解析】本题利用二重积分区域的对称性及被积函数的奇偶性。
(Ⅰ)求参数 λ 的矩估计量; (Ⅱ)求参数 λ 的最大似然估计量
5
考研资料下载中心
2009 年全国硕士研究生入学统一考试 数学一试题答案解析
一、选择题:1~8 小题,每小题 4 分,共 32 分,下列每小题给出的四个选项中,只有一项 符合题目要求,把所选项前的字母填在题后的括号内. (1)当 x → 0 时, f ( x ) = x − sin ax 与 g ( x ) = x 2 ln (1 − bx ) 等价无穷小,则
。
(10)若二阶常系数线性齐次微分方程 y′′ + ay′ + by = 0 的通解为 y = ( C1 + C2 x ) e ,则非 齐次方程 y′′ + ay′ + by = x 满足条件 y ( 0 ) = 2, y ′ ( 0 ) = 0 的解为 y = (11)已知曲线 L : y = x (12)设 Ω =
2
x
。 。 。
( 0 ≤ x ≤ 2 ) ,则 ∫ xds =
L
{( x, y, z ) x
。
2
+ y 2 + z 2 ≤ 1 ,则 ∫∫∫ z 2 dxdydz =
Ω
}
(13)若 3 维列向量 α , β 满足 α T β = 2 ,其中 α 为 α 的转置,则矩阵 βα T 的非零特征值 为
T
(14)设 X 1 , X 2 ,⋯ , X m 为来自二项分布总体 B ( n, p ) 的简单随机样本, X 和 S 分别为样本
Dk
四个区域 Dk ( k = 1, 2,3, 4 ) , I k = 则 max { I k } = (
1≤ k ≤ 4
D1
-1
)
D2 D3
-1
D4
1
x
( A ) I1 .
( B ) I2 .
( C ) I3 .
( D ) I4 .
(3)设函数 y = f ( x ) 在区间 [ −1,3] 上的图形为:
2
均值和样本方差。若 X + kS 为 np 的无偏估计量,则 k =
2
2
。
三、解答题(15-23 小题,共 94 分.请将解答写在答题纸指定的位置上.解答应写出文字说 明、证明过程或演算步骤.) (15) (本题满分 9 分)求二元函数 f ( x, y ) = x
2
( 2 + y ) + y ln y 的极值。
2
f ( x) x − sin ax x − sin ax 1 − a cos ax a 2 sin ax lim = lim 2 = lim 2 洛 lim 洛 lim x →0 g ( x ) x →0 x ln(1 − bx ) x →0 x ⋅ (−bx ) x →0 x →0 −3bx 2 −6bx a 2 sin ax a3 = lim =− =1 x →0 6b 6b − ⋅ ax a
2
3
x
-2
0 -1 )
∞
1
2
3
x
(C ) .
n →∞
( D) .
(4)设有两个数列 {an } , {bn } ,若 lim an = 0 ,则(
∞ ∞
∞
( A ) 当 ∑ bn 收敛时, ∑ anbn 收敛.
n =1 n =1
∞ ∞
( B ) 当 ∑ bn 发散时, ∑ anbn 发散.
n =1
∞
4
