【苏教版】六年级复习思维导图
苏教版六年级上册知识点思维导图

一、数与代数1.1分数乘法1.1.1分数乘法算式的意义(1)一个数乘分数表示求这个数的几分之几是多少,求一个数的几分之几是多少用乘法计算。
比如3×53表示3个53相加的和是多少,也可以表示3的53是多少? 典型例题:①把一根3米长的绳子平均分成8份。
每份占总长的( )( ),每份长( )米;两份长( )米,相当于1米的( )( )②填空:甲数是乙数的35 。
( )×35=( );1.1.2分数乘法计算法则(1)分数与整数相乘:用整数与分数的分子相乘的积作为分子,分数的分母作为分母,最后约分成最简分数。
或者先将整数与分数的分母进行约分,再计算。
(2)分数与分数相乘:用分子相乘的积作为分子,用分母相乘的积作为分母,过程中能约分的要约分。
注意:任何整数都可以看作为分母是1的分数,因而分数乘整数与分数乘分数计算方法本质是一样的。
(3)分数连乘:用分子相乘的积作为分子,用分母相乘的积作为分母,过程中能约分的要约分。
注意:约分时要一组一组约,一组约分后,再约下一组。
典型例题:①计算:49×421219×8 (132+725)×25 13×25×(225+213)②一个数是56,它的47是();120千米的23是()。
③红花有100朵,黄花的朵数是红花的五分之二,黄花有多少朵?④男生有 30 人,女生比男生多五分之一,女生比男生多多少人?女生有多少人?⑤小明看一本书,已经看了72页,剩下的是已看的34,这本书共有多少页?⑥一堆煤共有10吨,第一天用去25,第二天比第一天多用去14吨,两天共用去多少吨?⑦小明阅读一本80页的科学书,第一天看了全书的15少2页,小明第二天从第几页开始看起?1.1.3倒数的认识(1)乘积是1的两个数互为倒数。
(2)1的倒数是1,0没有倒数。
(3)一个数乘真分数(比1小的数)积比原数小;一个数乘比1大的假分数(比1大的数)积比原数大。
苏版六年级数学(下册)知识结构图

六年级数学知识结构图一、扇形统计图第1课时:认识扇形统计图1.结合实例认识扇形统计图,了解扇形统计描述数据的特点扇形统计图 2.联系百分数意义,能对扇形统计图的数据作简单的分析3.根据扇形统计图,进行简单的计算第2课时:选择统计图1.条形统计图统计图 2.折线统计图了解各自的不同特点,根据不同统计图从不同角度分析3.扇形统计图根据实际需要选择合适的统计图二、圆柱和圆锥第1课时,圆柱的认识、圆锥的认识1.特征:上下一般粗上下两个面是完全相同的圆,有一个面是曲面从生活中找圆柱圆柱的认识 2.名称:底面、高(直圆柱) 两底面之间的距离叫高,有无数条高手段:以上通过观察、操作、交流等活动1.生活中的圆锥圆锥的认识 2.特征 1个顶点底面是一个圆侧面是一个曲面3.名称: 1个底面 1个侧面 1条高(从圆锥顶点到底面圆心的距离)手段:观察操作交流等活动圆锥的体积: 1.利用已有知识自主探究圆锥的体积公式手段:通过实验、操作、观察、猜想、验证等活动2.应用公式正确计算圆锥体积解决相关问题三、解决问题策略第1课时解决问题的策略11.从不同角度理解条件,进一步感受转化,将分数转化成比或将比转化成分数。
2.能根据问题特点灵活选择学过的策略解决问题的思路及解答方法,有效地解决关于分数、百分数和比的实际问题。
第2课时解决问题的策略21.进一步理解并掌握画图、列举、分高等各种策略的解决过程,灵活选择不同策略,解决实际问题,说明应用策略思考的过程。
2.存在三种策略都可以解决有关大船小船的问题。
四、比例1.在具体情境中认识和理解图形的放大和缩小的含义,学会1.图形的放大与缩小用方格纸把简单的图形按指定的比放大或缩小2.体会图形的相似变换1.联系图形的放大和缩小认识和理解比例的意义,表示两个比相等的2.比例的意义式子2.会判断怎样的两个比能否组成比例:依据比例的意义(比值相等) 1.认识和理解比例尺的意义:图上距离和实际距离的比3.比例尺 2.会求平面图的比例尺3.能看懂线段比例尺,并进行数值比例尺和线段比例尺的转换4.比例尺是一个比,并不是一个测量工具,通常前项为11.结合实例进一步理解比例尺的意义,能根据比例尺求相应的实际4.比例尺的应用距离和图上距离(前提:先统一单位,实际距离=图上距离/比例尺)图上距离=实际距离×比例尺2.特殊:实际距离小于图上距离的,如精密零件等的比例尺():1五、确定位置1.用方向和距离描述位置:在具体情况中认识北偏东(西)、南偏东(西)方向的含义,会用方向和距离确定物体的位置,感受用方向和距离确定物体位置的准确性。
苏教版小学六年级总复习思维导图
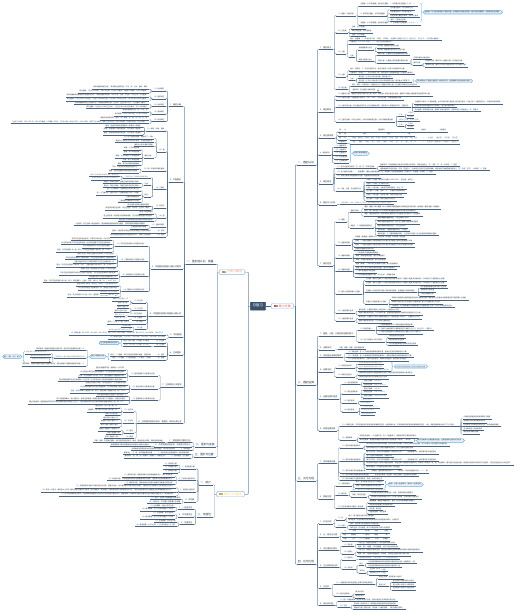
(6)圆
通过圆心并且两端都在圆的线段叫做圆的直径
一些图形,把它沿着一条直线对折,直线两侧的图形能够完全重合,这样的图形就是轴对称图形 这条直线叫做对称轴
(7)轴对称图形
围成一个图形的所有边长的总和就是这个图形的周长
(8)周长
物体的表面或围成的平面图形的大小,叫做它们的面积
(9)面积
把平行四边形通过剪切、平移可以转化成一个长方形
分类:
在一个三角形中,任意两边之和大于第三边
(4)三角形
2、平面图形
在一个三角形中,最多只有一个直角或最多只有一个钝角 三角形具有稳定性
特征:
三角形的内角和等于180度
四边形是由四条边围成的图形 常见的特殊四边形有:平行四边形、长方形、正方形、梯形
(5)四边形
圆是一种曲线图形
圆上的任意一点到圆心的距离都相等,这个距离就是圆的半径的长
(1)长方体 (2)正方体
5、常用数据
等积等底:圆锥的高是圆柱高的3倍,圆柱高与圆锥高的比是1︰3
锥1、差2、柱3、和4
圆柱体积与圆锥体积的比是3︰1 圆柱体积比圆锥体积多2倍 圆锥体积比圆锥体积少
等底等高:圆柱的体积是圆锥体积的3倍
圆柱与圆锥的关系
特征:一个侧面、两个完全相同的圆形底面、无数条高 特征:一个侧面、一个圆形底面、一个顶点、一条高
找来等底等高的空圆锥3个和空圆柱1个
将3个圆锥装满水,倒入圆柱中,发现正好装满,将圆柱里的水倒入3个圆锥中,发现正好倒完
平角:等于180度的角
周角:等于360度的角是周角
平行:不相交的两条直线互相平行 垂直:相交成直角的两条直线互相垂直
(3)同一平面内的两条直线
围成三角形的每条线段叫做三角形的边 每两条线段的交点叫做三角形的顶点
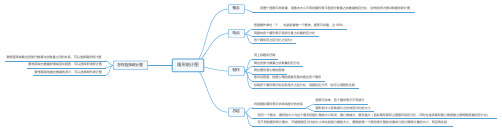
苏教版六年级数学下册一至六单元思维导图
圆柱从上到下一样粗解决问题的策略转化策略列举策略假设策略先假设再调整策略画图策略方程策略分数转化为比推导图形公式有序列举总量不变的情况下,依次调整两部分量的大小假设小的,先算出来的是大的经典问题:鸡兔同笼“假想构成法”:假设大的,先算出来的是小的先假设两种量同样多或差不多再根据计算结果对比调整结果相等停止调整直观清楚费时费力分析题意找等量关系式设未知数列出方程分数转化为份数不重复不遗漏主要类型具体问题具体分析主要步骤优缺点主要步骤结果相等停止调整计算每一次调整的结果并对比先进行假想的构成,然后在假想的条件下,探索解决问题的对策(1)已知总头数和总腿数,求鸡、兔各多少:(2)已知总头数和鸡兔脚数的差数,当鸡的总脚数比兔的总脚数多时,求鸡、兔 各多少:(3)已知总头数与鸡兔脚数的差数,当兔的总脚数比鸡的总脚数多时,求鸡、兔各多少:方法一:假设全是鸡,兔数 =(总腿数-总头数×2)÷(4-2);鸡数 = 总头数-兔数方法二: 假设全是兔,鸡数 =(总头数×4-总腿数)÷(4-2);兔数 = 总头数-鸡数方法一: 假设全是鸡,兔数 =(总头数×2-鸡兔脚数之差)÷(2+4);鸡数 = 总头数-兔数方法二: 假设全是兔,鸡数 =(总头数×4+鸡兔脚数之差)÷(2+4);兔数 = 总头数-鸡数方法一: 假设全是鸡,兔数 =(总头数×2+鸡兔脚数之差)÷(2+4);鸡数 = 总头数-兔数方法二: 假设全是兔,鸡数 =(总头数×4-鸡兔脚数之差)÷(2+4);兔数 = 总头数-鸡数依据:E表示东两种相关联的量,一种量变化,另一种量也随着变化。
