广东省茂名市2017届高三第一次质量监测考试理综物理试题 打印
2017年高考全国Ⅰ理综试题及答案解析(物理精校版)WORD版

2017年普通高等学校招生全国统一考试(全国Ⅰ)理科综合能力测试(物理)第一部分(选择题 共48分)二、选择题:本题共8小题,每小题6分,共48分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.【2017年全国Ⅰ,14,6分】将质量为1.00kg 的模型火箭点火升空,50g 燃烧的燃气以大小为600m的速度从火箭喷口在很短时间内喷出。
在燃气喷出后的瞬间,火箭的动量大小为( )(喷出过程中重力和空气阻力可忽略)A .30kg m/s ⋅B .25.710kg m/s ⨯⋅C .26.010kg m/s ⨯⋅D .26.310kg m/s ⨯⋅【答案】A【解析】开始总动量为零,规定向向下为正方向,根据动量守恒定律得,110m v P =+,解得火箭的动量110.05600kg m s 30kg m s P m v =-=-⨯⋅=-⋅,负号表示方向,故选A 。
15.【2017年全国Ⅰ,15,6分】发球机从同一高度向正前方依次水平射出两个速度不同的乒乓球(忽略空气的影响)。
速度较大的球越过球网,速度较小的球没有越过球网,其原因是( )A .速度较小的球下降相同距离所用的时间较多B .速度较小的球在下降相同距离时在竖直方向上的速度较大C .速度较大的球通过同一水平距离所用的时间较少D .速度较大的球在相同时间间隔内下降的距离较大【答案】C【解析】发球机发出的球,速度较大的球越过球网,速度度较小的球没有越过球网,原因是发球机到网的水平距离一定,速度大,则所用的时间较少,球下降的高度较小,容易越过球网,故选C 。
16.【2017年全国Ⅰ,16,6分】如图,空间某区域存在匀强电场和匀强磁场,电场方向竖直向上(与纸面平行),磁场方向垂直于纸面向量,三个带正电的微粒a ,b ,c 电荷量相等,质量分别为a m ,b m ,c m ,已知在该区域内,a 在纸面内做匀速圆周运动,b 在纸面内向右做匀速直线运动,c 在纸面内向左做匀速直线运动。
【新课标Ⅰ卷】2017届高三第一次全国大联考物理卷(Word版,含答题卡)

绝密★启用前|学易教育教学研究院命制2017年第一次全国大联考【新课标卷Ⅰ】理科综合物理试题(考试时间:150分钟试卷满分:300分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
可能用到的相对原子质量:H—1 C—12 N—14 O—16 Na—23 S—32 Fe—56 Ni—59 Ga—70第Ⅰ卷二、选择题:本题共8小题,每小题6分。
在每小题给出的四个选项中,第14~17题只有一项符合题目要求,第18~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.下列说法正确的是A.库仑定律的公式和万有引力的公式在形式上非常相似,说明这两种力的性质相同B.弗兰克和赫兹实验证明了汞原子的能量确实是量子化的C.在国际单位制中,力的单位是力学中基本单位D.能量守恒定律是最普遍的自然规律之一,英国物理学家牛顿对能量守恒定律的建立作出了突出贡献15.A、B两个物体在同一条直线上做直线运动,它们a–t图象如图所示,规定水平向右为正方向。
已知在t=0时,两物体的速度均为零,且A在B的左边1.75 m处,则A追上B的时间是A .t =0.5 sB .t =1.5 sC .t =2.5 sD .t =3.5 s16.有重力不计的A 、B 、C 、D 四种带电粒子,它们的质量之比是m A ∶m B ∶m C ∶m D =11∶21∶31∶41,它们的电荷量之比是q A ∶q B ∶q C ∶q D =1∶3∶5∶7,现让这四种带电粒子的混合物经过同一加速电场由静止开始加速,然后在同一偏转电场里偏转,如图所示。
2017年广东省理科综合试题(理综)Word版高考真题试卷含答案

绝密★启用前2017年普通高等学校招生全国统一考试理科综合能力测试广东卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
可能用到的相对原子质量:H 1 C 12 N 14 O 16 S 32 Cl 35.5 K 39 Ti 48 Fe 56 I 127一、选择题:本题共13个小题,每小题6分,共78分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.细胞间信息交流的方式有多种。
在哺乳动物卵巢细胞分泌的雌激素作用于乳腺细胞的过程中,以及精子进入卵细胞的过程中,细胞间信息交流的实现分别依赖于A.血液运输,突触传递B.淋巴运输,突触传递C.淋巴运输,胞间连丝传递D.血液运输,细胞间直接接触2.下列关于细胞结构与成分的叙述,错误的是A.细胞膜的完整性可用台盼蓝染色法进行检测B.检测氨基酸的含量可用双缩脲试剂进行显色C.若要观察处于细胞分裂中期的染色体可用醋酸洋红液染色D.斐林试剂是含有Cu2+的碱性溶液,可被葡萄糖还原成砖红色3.通常,叶片中叶绿素含量下降可作为其衰老的检测指标。
为研究激素对叶片衰老的影响,将某植物离体叶片分组,并分别置于蒸馏水、细胞分裂素(CTK)、脱落酸(ABA)、CTK+ABA 溶液中,再将各组置于光下。
一段时间内叶片中叶绿素含量变化趋势如图所示,据图判断,下列叙述错误的是A.细胞分裂素能延缓该植物离体叶片的衰老B.本实验中CTK对该植物离体叶片的作用可被ABA削弱C.可推测ABA组叶绿体中NADPH合成速率大于CTK组D.可推测施用ABA能加速秋天银杏树的叶由绿变黄的过程4.某同学将一定量的某种动物的提取液(A)注射到实验小鼠体内,注射后若干天,未见小鼠出现明显的异常表现。
茂名市高三级第一次综合测试

2017年茂名市高三级第一次综合测试数学试卷(理科)本试题卷分选择题和非选择题,共6页,23小题, 全卷满分150分,考试时时间120分钟.第一部分 选择题(共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|20}M x x x =--≤,{|2}xN y y ==,则M N =( )A .(0,2]B .(0,2)C .[0,2]D .[2,)+∞2.设i 为虚数单位,复数(2)1i z i -=+,则z 的共轭复数z 在复平面中对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3.如图1,函数)2sin()(φ+=x A x f 2||,0(πφ<>A )的图象过点)3,0(,则)(x f 的图象的一个对称中心是( ) A .(,0)3π- B .(,0)6π-C .(,0)6πD .(,0)4π4.设命题p :若定义域为R 的函数()f x 不是偶函数,则x R ∀∈,()()f x f x -≠. 命题 q :()||f x x x =在(,0)-∞上是减函数,在(0,)+∞上是增函数.则下列判断错误..的是( )A .p 为假B .q 为真 C .p ∨q 为真 D. p ∧q 为假5.我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金箠,一头粗,一头细,在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”根据上题的已知条件,若金箠由粗到细的重量是均匀变化的,问第二尺与第四尺的重量之和为( )A. 6 斤B. 9 斤C. 9.5斤D. 12 斤6. 已知定义域为R 的偶函数()f x 在(,0]-∞上是减函数,且(1)2f =,则不等式2(log )2f x >的解集为( )A . (2,)+∞B . 1(0,)(2,)2+∞ C. (0,(2,)2+∞ D. )+∞ 7. 执行如图2所示的程序框图,若输出的结果是3132,则输入的a 为 ( )A. 3B. 4C. 5D. 6 8. 一个几何体的三视图如图3所示,其表面积为6π,则该几何 体的体积为( )A .4πB .2πC .113π D . 3π 9. 学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座, 每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有 ( )A . 6种B .24种C .30种D .36种10.过球O 表面上一点A 引三条长度相等的弦AB 、AC 、AD ,且两两夹角都为60︒,若球半径为R ,则弦AB 的长度为( )A .3R BC . RD 11. 过双曲线的右焦点2(,0)F c 作圆的切线,切点为M ,延长2M F 交抛物线24y cx =-于点,P 其中O 为坐标原点,若21()2OM OF OP =+,则双曲线的离心率为( )()0,012222>>=-b a by a x 222a y x =+A .B .C .D .12.已知()||xf x xe =,又)()()(2x tf x f x g -=()t R ∈,若满足()1g x =-的x 有四个,则t 的取值范围是( )A. 21(,)e e+-∞- B. 21(,)e e ++∞ C. 21(,2)e e +-- D. 21(2,)e e+ 第二部分 非选择题(共90分)本卷包括必考题和选考题两部分. 第13~21题为必考题,每个试题考生都必须作答. 第22、23题为选考题,考生根据要求作答.二、填空题:本题共4小题,每小题5分,共20分,把答案填在答题纸上.13. 如图4为某工厂工人生产能力频率分布直方 图, 则估计此工厂工人生产能力的平均值 为 .14.已知22cos a xdx ππ-=⎰,则二项式6(x +展开式中的常数项是 ; 15. 若圆2240x y x my +-+-=关于直线0=-y x 对称,动点P ()b a ,在不等式组2000x y x my y +-≤⎧⎪+≥⎨⎪≥⎩表示的平面区域内部及边界上运动,则21b z a -=-的取值范围是 16.已知数列{}n a 是各项均不为零的等差数列,n S 为其前n项和,且n a =(n *∈N ).若不等式1(1)2(1)nn nn a nλ+-+-≤对任意n *∈N 恒成立,则实数λ的取值范围是 ;三、解答题:本大题共7小题,共70分.其中17至21题为必做题,22、23题为选做题.解答过程应写出文字说明、证明过程或演算步骤.7224-7224+231+251+17.(本小题满分12分)已知函数()sin(2)cos 2()6f x x x x R π=--∈.(Ⅰ)求函数f (x )的最小正周期、最大值及取得最大值时x 的集合;(Ⅱ)设△ABC 内角A 、B 、C 的对边分别为a b c 、、,若()22Bf =-,b =1,c = 且a b >,求角B 和角C .18.(本小题满分12分)调查表明:甲种农作物的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为x ,y ,z ,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标ω=x+y+z 的值评定这种农作物的长势等级,若ω≥4,则长势为一级;若2≤ω≤3,则长势为二级;若0≤ω≤1,则长势为三级,为了了解目前这种农作物长势情况,研究人员随机抽取10块种植地,得到如下表中结果:(Ⅰ)在这10块该农作物的种植地中任取两块地,求这两块地的空气湿度的指标z 相同的概率;(Ⅱ)从长势等级是一级的种植地中任取一块地,其综合指标为A ,从长势等级不是一级的种植地中任取一块地,其综合指标为B ,记随机变量X=A -B ,求X 的分布列及其数学期望.19.(本小题满分12分)AD 、BC 的中点,沿 EO 上,2BG GC =, M 、20.(本小题满分12分)设,x y R ∈,向量,i j 分别为直角坐标平面内,x y 轴正方向上的单位向量,若向量(3)a x i y j =++, (3)b x i y j =-+,且||||4a b +=.(Ⅰ)求点(,)M x y 的轨迹C 的方程;(Ⅱ)设椭圆22:1164x y E +=,P 为曲线C 上一点,过点P 作曲线C 的切线=+y kx m 交椭圆E 于A 、B 两点,试证:∆OAB 的面积为定值.21. (本小题满分12分)已知函数x x x x f 2)(3+-=.(Ⅰ)求函数()y f x =在点))1(,1(f 处的切线方程; (Ⅱ)令x xx f ax ax x g ln 2)()(2+-+=,若函数()y g x =在),(+∞e 内有极值,求实数a 的取值范围;(Ⅲ)在(Ⅱ)的条件下,对任意(1,),(0,1)t s ∈+∞∈,求证: 1()()2g t g s e e->+- .22.(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线1C 的参数方程为,,x y α⎧=⎨=⎩(α为参数). 在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线22:4cos 2sin 40.C ρρθρθ+-+= (Ⅰ)写出曲线21C C ,的普通方程; (Ⅱ)过曲线1C 的左焦点且倾斜角为4π的直线l 交曲线2C 于B A ,两点,求AB . 23.(本小题满分10分)选修4-5:不等式选讲已知函数|32||2|)(++-=x a x x f ,2|1|)(+-=x x g . (Ⅰ)若1a =,解不等式()6f x <;(Ⅱ)若对任意1x ∈R ,都有2x ∈R ,使得12()()=f x g x 成立,求实数a 的取值范围.绝密★启用前试卷类型:A 2017年茂名市高三级第一次综合测试数学试卷(理科)参考答案及评分标准一、选择题(本大题共12小题,每小题5分,共60分)提示:1.A 解:依题意得[1,2]M=-,(0,)N=+∞(0,2]M N∴=.2.D 解:12izi+=-(1)(2)22113(2)(2)555i i i iii i++++-===+-+,共轭复数为1355i-,对应点为13(,)55-,在第四象限.故选D.3.B 解:由函数图象可知:A = 2,由于图象过点(0),可得:2sinφ=即s i nφ=由于|φ|<2π,解得:φ=3π,即有:f(x)=2sin(2x+3π).由2 x +3π=kπ,k∈Z可解得:x =2kπ-6π,k∈Z,故f(x)的图象的对称中心是:(26kππ-,0),k∈Z,当k=0时,f(x)的图象的对称中心是:(6π-,0).4. C 解:函数()f x不是偶函数,仍然可,(-)()x f x f x∃=使,p为假;()||f x x x==22(x0)(x0)xx⎧≥⎪⎨-<⎪⎩在R上都是增函数,q为假;以p∨q为假,选C.5. A 解:每段重量构成等差数列,1524152,4,246a a a a a a ==+=+=+=6. B 解:()f x 是R 的偶函数,在(,0]-∞上是减函数,所以()f x 在[0,)+∞上是增函数, 所以2(log )2(1)f x f >=2(|log |)(1)f x f ⇔>2|log |1x ⇔>2log 1x ⇔>或2log 1x <-2x ⇔>或102x <<. 答案B. 7. C 解:执行程序框图,第1次运算有n =1,S = 12; 第2次运算有n =2,S = 1124+, …第5次运算有n =5,S = 511[1()]111113122124816323212-++++==-, 故输入的a 为5 . 8.D 解:该几何体是一个圆锥、一个圆柱、一个半球的组合体,其表面积为:22)2(2)2(6)61r r r r r r πππππ++=+=+∴=,该几何体的体积为22312(2)333r r r r r ππππ++=. 9. C 解:由于每科一节课,每节至少有一科,必有两科在同一节,先从4科中任选2科看作一个整体,然后做3个元素的全排列,共2343C A 种方法,再从中排除数学、理综安排在同一节的情形,共33A 种方法,故总的方法种数为2343C A -33A =36-6=30. 10. A 解:由条件可知A-BCD 是正四面体,法1:如图7:A 、B 、C 、D 为球上四点,则球心O 在正四面体中心,设AB=a ,则过点B 、C 、D的截面圆半径12233r O B BE ====, 正四面体A-BCD的高1AO ==,则截面BCD与球心的距离1d OO R ==-,所以222))R R =--,解得R a 362= . 法2:如图8:把正四面体A-BCD 放置于正方体1111AD BC A D BC - 中,则正方体边长x 与正四面体棱长a 满足2x a =,又正方体外接球半径R 满足:222222(2)3=32R x x x x =++=(),可解得:R a 362=11. D 解:如图9,∵21M (OP)2O OF =+,∴M 是2F P 的中点. 设抛物线的焦点为F 1,则F 1为(- c ,0),也是双曲线的焦点. 连接PF 1,OM .∵O 、M 分别是12F F 和2PF 的中点,∴OM 为 △PF 2F 1的中位线.∵OM =a ,∴|PF 1|=2 a .∵OM ⊥2PF ,∴2PF ⊥PF 1,于是可得|2PF 2b =,设P (x ,y ),则 c -x =2a , 于是有x =c -2a , y 2=-4c (c -2 a ),过点2F 作x 轴的垂线,点P 到该垂线的距离为2a . 由勾股定理得 y 2+4a 2=4b 2, 即-4c (c -2a )+4 a 2=4(c 2- a 2),变形可得c 2-a 2=ac ,两边同除以a 2有 210e e --=, 所以12e +=,负值已经舍去. 故选D . 12.B 解:令xy xe =,则'(1)xy x e =+,由'0y =,得1x =-,当(,1)x ∈-∞-时,'0y <,函数y 单调递减,当(1,)x ∈-+∞时,'0y >,函数y 单调递增. 作出x y xe =图象,利用图象变换得()||x f x xe =图象(如图10),令()f x m =,则关于m 方程2()10h m m tm =-+=两根分别在11(0,),(,)e e +∞时(如图11),满足()1g x =-的x 有4个,由2111()10h t e e e=-+<解得ee t 12+>.二、填空题(本大题共4个小题,每小题5分,共20分)13.133.8 14. 240 15. ),2[]2,(+∞⋃--∞ 16. [3,0]- 提示:13. 解:由频率分布直方图得 (0.008+0.02+0.048+x )⨯10=1,解得x =0.024.估计工人生产能力的平均数为:=x 115⨯0.008⨯10+125⨯0.020⨯10+135⨯0.048⨯10+145⨯0.024⨯10=133.8 .14.解:22cos a xdxππ-=⎰=22sin 2xππ-=,则二项式6(x =6)2(xx +展开式的通项公式为r rrr xC T 236612-+=,令0236=-r ,求得4=r,所以二项式6(x +展开式中的常数项是46C ×24=240.15.圆2240x y x my +-+-=关于直线0=-y x 对称,所以圆心 1(,)22m -在直在线0=-y x 上,1122m m =-⇒=-,2000x y x y y +-≤⎧⎪-≥⎨⎪≥⎩表示的平面区域如图21b z a -=- 表示区域OAB 内点P ()b a ,与点Q (1,2)连线的斜率.202,10OQ K -==- 022,21AQ K -==-- 所以答案: ),2[]2,(+∞⋃--∞16.解:n n a a =2(21)nn a n a ⇒=- 21n a n ⇒=-,*∈N n ⇒112(1)2(1)(1)(21)n n nn n n a n n nλ+++-+--≤=-(Ⅰ)当n 为奇数时, 2(2)(21)232223n n n n n n n nλ+-+--≤==-+2()23f n n n=-+是关于n(*n N ∈)的增函数.所以n=1时()f n 最小值为(1)2233f =-+=,这时 3,3,λλ-≤≥-(Ⅱ)当n 为偶数时, 2(2)(21)252225n n n n n n n nλ---+≤==+-恒成立,n 为偶数时,2()25g n n n=+-是增函数,当n=2时,()g n 最小值为(2)4150g =+-=,这时0λ≤ 综上(Ⅰ)、 (Ⅱ)实数λ的取值范围是[3,0]-.三、解答题(本大题共7小题,共70分.其中17至21题为必做题,22、23题为选做题. 解答过程应写出文字说明,证明过程或演算步骤) 17. 解:(Ⅰ)()sin 2coscos 2sincos 266f x x x ππ=-- ……………………………1分32cos 2)223x x x π=-=- ……………………………2分 函数f (x )的最小正周期为22T ππ== …………………………………………3分 当2232x k πππ-=+,即5,12x k k Z ππ=+∈时,f (x ………4分 这时x 的集合为5{|,}12x x k k Z ππ=+∈ …………………………………………5分(Ⅱ)1())sin(),23232B f B B ππ=-=-∴-=- ………………………6分 20,333B B ππππ<<∴-<-<………………………………………………7分,=366B B πππ∴-=-即, ………………………………………………8分1,sin sin b c b c BC==∴=又由正弦定理得:sin sin ,c B C b==2…………………………………………………………9分 2=33C C ππ∴又为三角形的内角,或…………………………………10分==32C A ππ当时,;…………………………………………………………………11分2==366C A a b A B A πππ=>>∴当时,, 不合题意舍去=,=63B C ππ∴ ……………………………………………………………………12分【点评】此题考查了两角和与差的正弦、余弦函数公式,正弦定理,正弦函数的单调性,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.18. 解:(Ⅰ)由表可知:空气湿度指标为1的有A 2, A 4,A 5,A 7, A 9,A 10 ………1分空气湿度指标为2的有A 1,A 3,A 6,A 8, …………………………………………2分 在这10块种植地中任取两块地,基本事件总数n=210109452C ⨯== ………………3分 这两块地的空气温度的指标z 相同包含的基本事件个数226465432122m C C ⨯⨯=+=+= ……………………………………………………5分 ∴这两地的空气温度的指标z 相同的概率2174515m P n ===………………………6分 (Ⅱ)由题意得10块种植地的综合指标如下表:其中长势等级是一级(ω≥4)有A 1 , A 2,A 3,A 5, A 6,A 8, A 9,共7个,长势等级不是一级(ω<4)的有A 4, A 7, A 10,共3个, ………………………………7分 随机变量X =A-B 的所有可能取值为1, 2,3,4, 5, ………………………………8分 w =4的有A 1 , A 2,A 5, A 6,A 9共5块地,w =3的有A 7, A 10共2块地,这时有X =4﹣3=1所以1152117310(1)21C C P x C C ===, …………………………………………………………9分同理111211732(2)21C C P x C C === ,1111511211737(3)21C C C C P x C C +===111111731(4)21C C P x C C === , 111111731(5)21C C P x C C === ……………………………10分∴X 的分布列为:11分1027114412345212121212121EX =⨯+⨯+⨯+⨯+⨯= ……12分 19.(Ⅰ)证明:法一如图13取OG 中点F ,连结BF 、FN ,则中位线FN ∥12OE 且FN 12=OE , 又BM ∥12OE 且BM 12=OE ……………………1分所以FN ∥BM 且FN = BM ,所以四边形BFNM 是平行四边形,所以MN ∥BF , ……2分又MN ⊄平面OBC ,BF ⊂平面OBC ,所以MN ∥平面OBC . …………………… 4分 法二:如图14,延长EM 、OB 交于点Q ,连结GQ ,因为BM ∥OE 且BM = OE ,所以12QM BM QE OE ==, M 为EQ 中点, ……………………………… 1分 所以中位线MN ∥QG …………………………2分又MN ⊄平面OBC ,QG ⊂面OBC ,所以MN ∥平面OBC.………………………4分 120BOC ∠=︒ , 所以3BC =, ……………………………5分 又2BG =1OG =,22290OB OG BG BOG ∴+=∴∠=︒,OG OB ⊥, ……………………………………6分又,,OE OB OE OC OB OC O OE ⊥⊥=∴⊥平面OBC ,OG ⊂面OBCOE OG ∴⊥ …………………………………………………………………………………7分又OBOE O =,所以OG ⊥平面OBE ,QE ⊂面OBE OG ⊥QE ………………8分又M 为EQ 中点,所以OQ =OE = ,所以,OM QE ⊥ OMOG O =,所以QE ⊥平面OMG , QE MG ⊥,OMG ∠为二面角G ME B --的平面角. ………9分所以Rt MOG ∆中,OM ==MG ==, ……11分cos OM OMG MG ∠===, ∴二面角 G ME-- (12)分法二:如图15,,120BOC ∠=︒ ,3BC ∴=,………………………………………………………5分 又2BG GC =,22,13BG BC GC ∴===, 1OG =22290OB OG BG BOG ∴+=∴∠=︒,OG OB ⊥, ………………………………………………………………………………6分又,,OE OB OE OC OB OC O OE ⊥⊥=∴⊥平面OBC ,OG OBC ⊂面 O E O G ∴⊥ ………………………………………………………7分又OBOE O =,所以OG ⊥平面OBE ,OE OBE ⊂面,OG OE ∴⊥ …………8分建立如图所示的空间直角坐标系Oxyz -,则M,G (0,1,0) ,E (0,0,,(3,1,3),(3,0,MG ME =--=- ………………………………………………9分而 1(0,1,0)n =是平面BOE 的一个法向量………………………………………11分设平面MGE 的法向量为2(,,)nx y z = 则223030n MG y n ME ⎧∙=-+=⎪⎨∙=-=⎪⎩,令 z 1=,则1,23,x y ==面MGE 的一个法向量为(1n =,……………10分 所以121212cos ,||||1n n n n n n <>====+ 所以,二面角G ME --………………………………………12分 20. (Ⅰ)解:∵ (3)a x i y j =++ , (3)b x i y j =-+ ,且||||4a b +=4=∴ 点M (x ,y )到两个定点F 1(0),F 2,0)的距离之和为4…………2分 ∴ 点M 的轨迹C 是以F 1、F 2为焦点的椭圆,设所求椭圆的标准方程为22221(0),x y a b a b +=>>则c =, 2a = ∴2221b a c =-= ………………3分 其方程为2214x y += …………………………………………………………………4分(Ⅱ)证明:设11(,)A x y ,22(,)B x y,将=+y kx m 代入椭圆E 的方程,消去x 可得222(14)84160+++-=k x kmx m显然直线与椭圆C 的切点在椭圆E 内,由韦达定理则有,0>∆∴:122814+=-+kmx x k ,212241614-=+m x x k . ……………………………………………5分所以12||-=x x…………………………………………………6分因为直线=+y kx m 与y 轴交点的坐标为(0,)m ,所以∆OAB 的面积121||||2=-=S m x x …………………7分== …………8分设2214=+m t k 将=+y kx m 代入椭圆C 的方程,可得222(14)8440+++-=k x kmx m ………10分由0∆=,可得2214=+m k 即1=t , …………………………………………11分又因为==S故=S . …………………………………………………………………12分 21.(Ⅰ)解: 21211)1(3=⨯+-=f . ………………………………………………1分2'()31x x f =-+2(1)313'f =⨯-= …………………………………2分∴函数()y f x =在点))1(,1(f 处的切线方程为:)1(32-=-x y ,即013=--y x ………………………………………………3分 (Ⅱ)解:x x ax x x x x ax x x x ax ax x ln 1ln )1)(1()1(ln )(g 32+-=+-++=+-+= 定义域为0,11+∞()(,)22222)1(1)2()1(12)1(1)(g -++-=--+-=--='∴x x x a x x x ax x x x a x x …………………4分 2()(2)1,()()h x x a x y g x e =-++=+∞设要使在,上有极值,则2h ()(2)10x x a x =-++= 12,,x x 有两个不同的实根 2(2)4004a a a ∴∆=+->∴><-或① ……………5分 212121(),x 1,0e e x e x x x e+∞>=∴<<<<而且一根在区间,上,不妨设又因为21111h(0)1,h()0,(2102e e a a e e e =∴<-++<∴>+-又只需即)②联立①②可得:21-+>e e a ……………………………6分(Ⅲ)证明:由(Ⅱ)知,单调递减则时,)(,0)('),1(2x g x g x x <∈ 2'()0,g()x x g x x ∈+∞>()时,单调递增2g()1()x g x ∴+∞在(,)上有最小值2t 1g ()()t g x ∀∈+∞≥即(,),都有 …………………………………………………7分 单调递增又当)(0)(),,0(1x g x g x x ∴>'∈单调递减当)(,0)(),1,(1x g x g x x ∴<'∈1g()01)g()x x ∴在(,上有最大值1s (0,1),g()()s g x ∀∈≤即对都有 ……………………………………………………8分又),e ),1,0(,1,2212121+∞∈∈=+=+(x e x x x a x x212121g()()()()ln ln 11a at g s g x g x x x x x ∴-≥-=+---- 11l 1212---+=x a x a x x n)(1ln 22222e x x x x >-+=………………………………10分 )0(1ln 21ln )(2>-+=-+=x x x x x x x x k 设 0112)(k 2>++='∴x x xe e e k x k x k 12)()(),e )(-+=>∴+∞∴上单调递增,在(…………………11分 e e s g t g 12)()(-+>-∴………………………………………………………12分请考生在第22、23两题中任选一题做答,如果多做,则按所做的第一题计分,作答时请写清题号.22. 解: (Ⅰ)2222()cos sin 122sin y x y αααα⎧=⎪⇒+=+=⎨=⎪⎩ ………………1分即曲线1C 的普通方程为221204x y+=…………………………………………………2分222,c o s ,s i n ,x y x y ρρθρθ=+== 曲线2C 的方程可化为224240x y x y ++-+= ……………………………………3分 即1)1()2(:222=-++y x C . ………………………………………………4分(Ⅱ)曲线1C 左焦点为(4-,0) ……………………………………………5分直线l 的倾斜角为4πα=, sin cos αα==…………………………………………6分 所以直线l 的参数方程为: 为参数)t t y t x (22224⎪⎪⎩⎪⎪⎨⎧=+-=………………………………7分将其代入曲线2C 整理可得:04232=+-t t , ……………………………………8分 设A,B 对应的参数分别为21,t t 则 所以4,232121==+t t t t . ………………………9分所以12AB t t =-===………………………10分解法二:(Ⅰ)同解法一. ………………………………………………………………4分 (Ⅱ)曲线1C 左焦点为(4-,0) ………………………………………………………5分直线l 的斜率为tan14k π==, ………………………………………………………6分直线l 的普通方程为4y x =+. 即40x y -+= …………………………………7分圆2C 的圆心坐标为:(-2,1). ……………………………………………………8分 圆心2C 到直线l的距离2d ==……………………………9分故AB === …………………………………………10分 解法三:(Ⅰ)同解法一. …………………………………………4分(Ⅱ)曲线1C 左焦点为(4-,0) …………………………………………5分 直线l 的斜率为tan14k π==, ……………………………………………6分直线l 的普通方程为4y x =+ …………………………………………………7分2122212423560(2)(1)121y x x x x x x y y y =+⎧⎧⎧=-=-⇒++=⇒⎨⎨⎨++-===⎩⎩⎩或,…………9分AB =| ………………………………………10分23. 解:(Ⅰ)当1a =时,()6f x <,即21236x x -++<,21 即3212236x x x ⎧≤-⎪⎨⎪---<⎩或312223126x x x ⎧-<<⎪⎨⎪++-<⎩或1221236x x x ⎧≥⎪⎨⎪-++<⎩ …………3分322x ∴-<≤-或3122x -<<或112x ≤< …………………………………4分 21x ∴-<< 所以不等式()6f x <的解集为{}|21x x -<< ………………5分 (Ⅱ)对任意R x ∈1,都有R x ∈2,使得)()(21x g x f =成立,则有{|()}{|()}y y f x y y g x =⊆=, …………………………………………………6分 又()|2||23|f x x a x =-++|(2)(23)||3|x a x a ≥--+=+ ……………………………7分 ()|1|22g x x =-+≥, ………………………………8分 从而|3|2a +≥,解得15a a ≥-≤-或, …………………………………………………9分 故[1,)(,5]a ∈-+∞-∞-U ………………………………………………………………10分。
2017届高三理科综合一诊试题(附答案)

2017届高三理科综合一诊试题(附答案)秘密★启用前【考试时间:2016年12月21日9:00~11:30】高中2017届毕业班第一次诊断性考试理科综合能力测试可能用到的相对原子质量:H-l N-14 0-16 Na-23第I卷一、选择题:本题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.线粒体是细胞的“动力车间”。
下列关于线粒体的叙述,正确的是A 线粒体外膜的表面积大于其内膜的表面积B.线粒体基质中含有分解葡萄糖和丙酮酸的酶.有氧呼吸过程中产生2的场所是线粒体内膜D.活细胞中的线粒体能定向运动到代谢旺盛的部位2.下列关于植物激素调节的叙述,正确的是A 植物体内激素的合成量与环境因子的变化无关B.植物激素直接参与细胞代谢同时传达调节信息.植物体内多种激素能对基因组的表达进行调节D植物所有的生命活动都由植物激素调节控制3.获得性免疫缺陷综合征( AIDS),是由人类免疫缺陷病毒(HIV)引起的,死亡率极高。
下列相关叙述错误的是A H IV的增殖需要宿主细胞提供营养物质和能量B.HIV侵人人体后对B细胞的增殖分化没有影响.AIDS病人后期往往会出现严重感染或恶性肿瘤D 切断HIV的传播途径是预防AIDS的有效措施4.科学家用伞形帽和菊花形帽两种伞藻做嫁接实验,结果如下图所示。
该实验能够得出的结论是A 伞帽形态结构的建成与细胞质没有关系B.伞帽形态结构的建成主要与细胞核有关.伞藻的细胞核具有发育成完整个体的潜能D 细胞核是遗传物质储存和复制的主要场所.用二倍体西瓜植株做父本与另一母本植株进行杂交,得到的种子种下去,就会长出三倍体植株。
下列叙述正确的是A父本植株杂交前需去除雄蕊,杂交后需套袋处理B.母本植株正常体细胞中最多会含有四个染色体组.三倍体植株的原始生殖细胞中不存在同染色体D三倍体无子西瓜高度不育,但其无子性状可遗传6.下图为甲、乙两种不同类型遗传病的家系图。
已知I1和Ⅱ4都不携带甲病致病基因,I4和Ⅱ3都携带乙病致病基因。
2017年茂名市高三级第一次综合测试

2017年茂名市高三级第一次综合测试数学试卷(理科)本试题卷分选择题和非选择题,共6页,23小题, 全卷满分150分,考试时时间120分钟.第一部分 选择题(共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|20}M x x x =--≤,{|2}xN y y ==,则M N =( )A .(0,2]B .(0,2)C .[0,2]D .[2,)+∞2.设i 为虚数单位,复数(2)1i z i -=+,则z 的共轭复数z 在复平面中对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3.如图1,函数)2sin()(φ+=x A x f 2||,0(πφ<>A )的图象过点)3,0(,则)(x f 的图象的一个对称中心是( ) A .(,0)3π-B .(,0)6π-C .(,0)6πD .(,0)4π4.设命题p :若定义域为R 的函数()f x 不是偶函数,则x R ∀∈,()()f x f x -≠. 命题 q :()||f x x x =在(,0)-∞上是减函数,在(0,)+∞上是增函数.则下列判断错误..的是( )A .p 为假B .q 为真 C .p ∨q 为真 D. p ∧q 为假5.我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金箠,一头粗,一头细,在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”根据上题的已知条件,若金箠由粗到细的重量是均匀变化的,问第二尺与第四尺的重量之和为( )A. 6 斤B. 9 斤C. 9.5斤D. 12 斤6. 已知定义域为R 的偶函数()f x 在(,0]-∞上是减函数,且(1)2f =,则不等式2(log )2f x >的解集为( )A . (2,)+∞B . 1(0,)(2,)2+∞ C . (0,(2,)2+∞ D . )+∞ 7. 执行如图2所示的程序框图,若输出的结果是3132,则输入的a 为 ( )A. 3B. 4C. 5D. 6 8. 一个几何体的三视图如图3所示, 其表面积为6π,则该几何体的体积为( )A .4πB .2πC .113π D . 3π 9. 学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座, 每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有 ( )A . 6种B .24种C .30种D .36种10.过球O 表面上一点A 引三条长度相等的弦AB 、AC 、AD ,且两两夹角都为60︒,若球半径为R ,则弦AB 的长度为( )A RB . 3RC . R D11. 过双曲线的右焦点2(,0)F c 作圆的切线,切点为M ,延长2M F 交抛物线24y cx =-于点,P 其中O 为坐标原点,若21()2OM OF OP =+,则双曲线的离心率为( ) A .B .C .D .12.已知()||xf x xe =,又)()()(2x tf x f x g -=()t R ∈,若满足()1g x =-的x 有四个,则t 的取值范围是( )A. 21(,)e e+-∞- B. 21(,)e e ++∞ C. 21(,2)e e +-- D. 21(2,)e e+ 第二部分 非选择题(共90分)本卷包括必考题和选考题两部分. 第13~21题为必考题,每个试题考生都必须作答. 第22、23题为选考题,考生根据要求作答.二、填空题:本题共4小题,每小题5分,共20分,把答案填在答题纸上.13. 如图4为某工厂工人生产能力频率分布直方 图, 则估计此工厂工人生产能力的平均值 为 .14.已知22cos a xdx ππ-=⎰,则二项式6(x 展开式中的常数项是 ; 15. 若圆2240x y x my +-+-=关于直线0=-y x 对称,动点P ()b a ,在不等式组2000x y x my y +-≤⎧⎪+≥⎨⎪≥⎩表示的平面区域内部及边界上运动,则21b z a -=-的取值范围是 16.已知数列{}n a 是各项均不为零的等差数列,n S 为其前n项和,且n a =()0,012222>>=-b a by a x 222a y x =+7224-7224+231+251+(n *∈N ).若不等式1(1)2(1)nn nn a nλ+-+-≤对任意n *∈N 恒成立,则实数λ的取值范围是 ;三、解答题:本大题共7小题,共70分.其中17至21题为必做题,22、23题为选做题.解答过程应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知函数()sin(2)cos 2()6f x x x x R π=--∈.(Ⅰ)求函数f (x )的最小正周期、最大值及取得最大值时x 的集合; (Ⅱ)设△ABC 内角A 、B 、C 的对边分别为a b c 、、,若()2Bf =,b =1,c =, 且a b >,求角B 和角C .18.(本小题满分12分)调查表明:甲种农作物的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为x ,y ,z ,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标ω=x+y+z 的值评定这种农作物的长势等级,若ω≥4,则长势为一级;若2≤ω≤3,则长势为二级;若0≤ω≤1,则长势为三级,为了了解目前这种农作物长势情况,研究人员随机抽取10块种植地,得到如下表中结果:(Ⅰ)在这块该农作物的种植地中任取两块地,求这两块地的空气湿度的指标z相同的概率;(Ⅱ)从长势等级是一级的种植地中任取一块地,其综合指标为A,从长势等级不是一级的种植地中任取一块地,其综合指标为B,记随机变量X=A-B,求X的分布列及其数学期望.19.(本小题满分12分)如图5,在边长为E、O分别为AD、BC的中点,沿EO将矩形ABOE 折起使得120BOC ∠=︒ ,如图6所示,点G 在BC 上,2BG GC =, M 、N 分别为AB 、EG 中点.(Ⅰ)求证:MN ∥平面OBC ; (Ⅱ)求二面角 G ME B --的余弦值.20.(本小题满分12分)设,x y R ∈,向量,i j 分别为直角坐标平面内,x y 轴正方向上的单位向量,若向量(3)a x i y j =++, (3)b x i y j =-+,且||||4a b +=.(Ⅰ)求点(,)M x y 的轨迹C 的方程;(Ⅱ)设椭圆22:1164x y E +=,P 为曲线C 上一点,过点P 作曲线C 的切线=+y kx m 交椭圆E 于A 、B 两点,试证:∆OAB 的面积为定值.21. (本小题满分12分)已知函数x x x x f 2)(3+-=.(Ⅰ)求函数()y f x =在点))1(,1(f 处的切线方程;(Ⅱ)令x xx f ax ax x g ln 2)()(2+-+=,若函数()y g x =在),(+∞e 内有极值,求实数a 的取值范围;(Ⅲ)在(Ⅱ)的条件下,对任意(1,),(0,1)t s ∈+∞∈,求证: 1()()2g t g s e e->+- .22.(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线1C 的参数方程为,,x y α⎧=⎨=⎩(α为参数). 在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线22:4cos 2sin 40.C ρρθρθ+-+= (Ⅰ)写出曲线21C C ,的普通方程; (Ⅱ)过曲线1C 的左焦点且倾斜角为4π的直线l 交曲线2C 于B A ,两点,求AB . 23.(本小题满分10分)选修4-5:不等式选讲已知函数|32||2|)(++-=x a x x f ,2|1|)(+-=x x g . (Ⅰ)若1a =,解不等式()6f x <;(Ⅱ)若对任意1x ∈R ,都有2x ∈R ,使得12()()=f x g x 成立,求实数a 的取值范围.绝密★启用前 试卷类型:A2017年茂名市高三级第一次综合测试数学试卷(理科)参考答案及评分标准一、选择题(本大题共12小题,每小题5分,共60分)提示:1.A 解:依题意得[1,2]M =-,(0,)N =+∞(0,2]M N ∴=.2.D 解:12i z i +=-(1)(2)22113(2)(2)555i i i i i i i ++++-===+-+,共轭复数为1355i -,对应点为13(,)55-,在第四象限.故选D .3.B 解:由函数图象可知:A = 2,由于图象过点(0,可得:2sin φ=即s i n φ=,由于|φ|<2π,解得:φ=3π,即有:f (x )=2sin (2x +3π ).由2 x +3π =k π,k ∈Z 可解得:x =2k π-6π,k ∈Z ,故f (x )的图象的对称中心是:(26k ππ-,0),k ∈Z ,当k =0时,f (x )的图象的对称中心是:(6π-,0).4. C 解:函数()f x 不是偶函数, 仍然可,(-)()x f x f x ∃=使, p 为假;()||f x x x ==22(x 0)(x 0)x x ⎧≥⎪⎨-<⎪⎩ 在R 上都是增函数, q 为假; 以 p ∨q 为假,选C .5. A 解:每段重量构成等差数列,1524152,4,246a a a a a a ==+=+=+=6. B 解:()f x 是R 的偶函数,在(,0]-∞上是减函数,所以()f x 在[0,)+∞上是增函数, 所以2(log )2(1)f x f >=2(|log |)(1)f x f ⇔>2|log |1x ⇔>2log 1x ⇔>或2log 1x <-2x ⇔>或102x <<. 答案B. 7. C 解:执行程序框图,第1次运算有n =1,S = 12; 第2次运算有n =2,S = 1124+, …第5次运算有n =5,S = 511[1()]111113122124816323212-++++==-, 故输入的a 为5 . 8.D 解:该几何体是一个圆锥、一个圆柱、一个半球的组合体,其表面积为:22)2(2)2(6)61r r r r r r πππππ++==+∴=,该几何体的体积为22312(2)333r r r r r ππππ++=. 9. C 解:由于每科一节课,每节至少有一科,必有两科在同一节,先从4科中任选2科看作一个整体,然后做3个元素的全排列,共2343C A 种方法,再从中排除数学、理综安排在同一节的情形,共33A 种方法,故总的方法种数为2343C A -33A =36-6=30.10. A 解:由条件可知A-BCD 是正四面体,法1:如图7:A 、B 、C 、D 为球上四点,则球心O 在正四面体中心,设AB=a ,则过点B 、C 、D 的截面圆半径12233r O B BE ====,正四面体A-BCD 的高1AO ==,则截面BCD 与球心的距离1d OO R ==-,所以222)()33a R a R =--,解得R a 362= .法2:如图8:把正四面体A-BCD 放置于正方体1111AD BC A D BC - 中,则正方体边长x 与正四面体棱长a 满足x =,又正方体外接球半径R 满足:222222(2)3=32R x x x x a =++=),可解得:R a 362=11. D 解:如图9,∵21M (OP)2O OF =+,∴M 是2F P 的中点. 设抛物线的焦点为F 1,则F 1为(- c ,0),也是双曲线的焦点. 连接PF 1,OM .∵O 、M 分别是12F F 和2PF 的中点,∴OM 为 △PF 2F 1的中位线.∵OM =a ,∴|PF 1|=2 a .∵OM ⊥2PF ,∴2PF ⊥PF 1,于是可得|2PF 2b =,设P (x ,y ),则 c -x =2a , 于是有x =c -2a , y 2=-4c (c -2 a ),过点2F 作x 轴的垂线,点P 到该垂线的距离为2a . 由勾股定理得 y 2+4a 2=4b 2, 即-4c (c -2a )+4 a 2=4(c 2- a 2),变形可得c 2-a 2=ac ,两边同除以a 2有 210e e --=, 所以e =,负值已经舍去. 故选D .12.B 解:令x y xe =,则'(1)xy x e =+,由'0y =,得1x =-,当(,1)x ∈-∞-时,'0y <,函数y 单调递减,当(1,)x ∈-+∞时,'0y >,函数y 单调递增. 作出x y xe =图象,利用图象变换得()||x f x xe =图象(如图10),令()f x m =,则关于m 方程2()10h m m tm =-+=两根分别在11(0,),(,)e e+∞时(如图11),满足()1g x =-的x 有4个,由2111()10h t e e e=-+<解得e e t 12+>.二、填空题(本大题共4个小题,每小题5分,共20分)13.133.8 14. 240 15. ),2[]2,(+∞⋃--∞ 16. [3,0]- 提示:13. 解:由频率分布直方图得 (0.008+0.02+0.048+x )⨯10=1,解得x =0.024.估计工人生产能力的平均数为:=x 115⨯0.008⨯10+125⨯0.020⨯10+135⨯0.048⨯10+145⨯0.024⨯10=133.8 .14.解:22cos a xdx ππ-=⎰=22sin 2xππ-=,则二项式6(x =6)2(xx +展开式的通项公式为r rrr xC T 236612-+=,令0236=-r ,求得4=r,所以二项式6(x 展开式中的常数项是46C ×24=240.15.圆2240x y x my +-+-=关于直线0=-y x 对称,所以圆心 1(,)22m -在直在线0=-y x 上,1122m m =-⇒=-,2000x y x y y +-≤⎧⎪-≥⎨⎪≥⎩表示的平面区域如图21b z a -=- 表示区域OAB 内点P ()b a ,与点Q (1,2)连线的斜率.202,10OQ K -==- 022,21AQ K -==-- 所以答案: ),2[]2,(+∞⋃--∞16. 解:n n a a =2(21)n n a n a ⇒=- 21n a n ⇒=-,*∈N n ⇒112(1)2(1)(1)(21)n n n n n n a n nnλ+++-+--≤=-(Ⅰ)当n 为奇数时, 2(2)(21)232223n n n n n n n nλ+-+--≤==-+2()23f n n n=-+是关于n(*n N ∈)的增函数.所以n=1时()f n 最小值为(1)2233f =-+=,这时 3,3,λλ-≤≥-(Ⅱ)当n 为偶数时, 2(2)(21)252225n n n n n n n nλ---+≤==+-恒成立,n 为偶数时,2()25g n n n=+-是增函数,当n=2时,()g n 最小值为(2)4150g =+-=,这时 0λ≤ 综上(Ⅰ)、 (Ⅱ)实数λ的取值范围是[3,0]-.三、解答题(本大题共7小题,共70分.其中17至21题为必做题,22、23题为选做题. 解答过程应写出文字说明,证明过程或演算步骤) 17. 解:(Ⅰ)()sin 2coscos 2sincos 266f x x x ππ=-- ……………………………1分3sin 2cos 2)223x x x π=-=- ……………………………2分 函数f (x )的最小正周期为22T ππ== …………………………………………3分 当2232x k πππ-=+,即5,12x k k Z ππ=+∈时,f (x ………4分这时x 的集合为5{|,}12x x k k Z ππ=+∈ …………………………………………5分(Ⅱ)1()),sin(),23232B f B B ππ=-=∴-=- ………………………6分 20,333B B ππππ<<∴-<-<………………………………………………7分,=366B B πππ∴-=-即,………………………………………………8分1,sin sin b c b c BC==∴=又由正弦定理得:sin sin ,c B C b==2…………………………………………………………9分2=33C C ππ∴又为三角形的内角,或…………………………………10分==32C A ππ当时,;…………………………………………………………………11分2==366C A a b A B A πππ=>>∴当时,, 不合题意舍去=,=63B C ππ∴ ……………………………………………………………………12分【点评】此题考查了两角和与差的正弦、余弦函数公式,正弦定理,正弦函数的单调性,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.18. 解:(Ⅰ)由表可知:空气湿度指标为1的有A 2, A 4,A 5,A 7, A 9,A 10 ………1分空气湿度指标为2的有A 1,A 3,A 6,A 8, …………………………………………2分 在这10块种植地中任取两块地,基本事件总数n=210109452C ⨯== ………………3分 这两块地的空气温度的指标z 相同包含的基本事件个数226465432122m C C ⨯⨯=+=+= ……………………………………………………5分∴这两地的空气温度的指标z 相同的概率2174515m P n ===………………………6分 (Ⅱ)由题意得10块种植地的综合指标如下表:其中长势等级是一级(ω≥4)有A 1 , A 2,A 3,A 5, A 6,A 8, A 9,共7个,长势等级不是一级(ω<4)的有A 4, A 7, A 10,共3个, ………………………………7分 随机变量X =A-B 的所有可能取值为1, 2,3,4, 5, ………………………………8分 w =4的有A 1 , A 2,A 5, A 6,A 9共5块地,w =3的有A 7, A 10共2块地,这时有X =4﹣3=1所以1152117310(1)21C C P x C C ===, …………………………………………………………9分同理111211732(2)21C C P x C C === ,1111511211737(3)21C C C C P x C C +=== 111111731(4)21C C P x C C === , 111111731(5)21C C P x C C === ……………………………10分∴X 的分布列为:11分1027114412345212121212121EX =⨯+⨯+⨯+⨯+⨯= ……12分 19.(Ⅰ)证明:法一如图13取OG 中点F ,连结BF 、FN ,则中位线FN ∥12OE 且FN 12=OE , 又BM ∥12OE 且BM 12=OE ……………………1分 所以FN ∥BM 且FN = BM ,所以四边形BFNM 是平行四边形,所以MN ∥BF , ……2分又MN ⊄平面OBC ,BF ⊂平面OBC ,所以MN ∥平面OBC . …………………… 4分法二:如图14,延长EM 、OB 交于点Q ,连结GQ , 因为BM ∥OE 且BM = OE ,所以12QM BM QE OE ==, M 为EQ 中点, ……………………………… 1分 所以中位线MN ∥QG …………………………2分又MN ⊄平面OBC ,QG ⊂面OBC ,所以MN ∥平面OBC. ………………………4分120BOC ∠=︒ ,所以3BC =, ……………………………5分 又2BG =1OG =,22290OB OG BG BOG ∴+=∴∠=︒,OG OB ⊥, ……………………………………6分又,,OE OB OE OC OB OC O OE ⊥⊥=∴⊥平面OBC ,OG ⊂面OBCOE OG ∴⊥ …………………………………………………………………………………7分又OBOE O =,所以OG ⊥平面OBE ,QE ⊂面OBE OG ⊥QE ………………8分又M 为EQ 中点,所以OQ =OE = ,所以,OM QE ⊥ OMOG O =,所以QE ⊥平面OMG , QE MG ⊥,OMG ∠为二面角G ME B --的平面角. ………9分所以Rt MOG ∆中,OM ==MG == ……11分cos7OMOMGMG∠===,∴二面角G ME--……12分法二:如图15, 120BOC∠=︒,3BC∴=,………………………………………………………5分又2BG GC=,22,13BG BC GC∴===,1OG=22290OB OG BG BOG∴+=∴∠=︒,OG OB⊥,………………………………………………………………………………6分又,,OE OB OE OC OB OC O OE⊥⊥=∴⊥平面OBC,OG OBC⊂面O E O G∴⊥………………………………………………………7分又OB OE O=,所以OG⊥平面OBE,OE OBE⊂面,OG OE∴⊥…………8分建立如图所示的空间直角坐标系O xyz-,则M,G(0,1,0),E (0,0,,(3,1,3),(3,0,MG ME=--=-………………………………………………9分而1(0,1,0)n =是平面BOE的一个法向量………………………………………11分设平面MGE的法向量为2(,,)n x y z=则223030n MG yn ME⎧∙=-+=⎪⎨∙=-+=⎪⎩,令z1=,则1,23,x y==面MGE 的一个法向量为(1n=,……………10分所以121212cos ,7||||1n nn nn n<>====+所以,二面角G ME--………………………………………12分20.(Ⅰ)解:∵(3)a x i y j=++,(3)bx i y j=-+,且||||4a b+=4=∴点M(x,y)到两个定点F1(,0),F20)的距离之和为4…………2分∴ 点M 的轨迹C 是以F 1、F 2为焦点的椭圆,设所求椭圆的标准方程为22221(0),x y a b a b +=>>则c =, 2a = ∴2221b a c =-= ………………3分 其方程为2214x y += …………………………………………………………………4分(Ⅱ)证明:设11(,)A x y ,22(,)B x y ,将=+y kx m 代入椭圆E 的方程,消去x 可得222(14)84160+++-=k x kmx m显然直线与椭圆C 的切点在椭圆E 内,由韦达定理则有,0>∆∴:122814+=-+km x x k ,212241614-=+m x x k . ……………………………………………5分所以12||-=x x …………………………………………………6分因为直线=+y kx m 与y 轴交点的坐标为(0,)m ,所以∆OAB 的面积121||||2=-=S m x x …………………7分== …………8分设2214=+m t k 将=+y kx m 代入椭圆C 的方程,可得222(14)8440+++-=k x kmx m ………10分由0∆=,可得2214=+m k 即1=t , …………………………………………11分又因为==S故=S . …………………………………………………………………12分 21.(Ⅰ)解: 21211)1(3=⨯+-=f . ………………………………………………1分2'()31x xf =-+2(1)313'f =⨯-= …………………………………2分∴函数()y f x =在点))1(,1(f 处的切线方程为:)1(32-=-x y ,即013=--y x ………………………………………………3分 (Ⅱ)解:x x ax x x x x ax x x x ax ax x ln 1ln )1)(1()1(ln )(g 32+-=+-++=+-+= 定义域为0,11+∞()(,)22222)1(1)2()1(12)1(1)(g -++-=--+-=--='∴x x x a x x x ax x x x a x x …………………4分2()(2)1,()()h x x a x y g x e =-++=+∞设要使在,上有极值,则2h ()(2)10x x a x =-++= 12,,x x 有两个不同的实根 2(2)4004a a a ∴∆=+->∴><-或① ……………5分 212121(),x 1,0e e x e x x x e+∞>=∴<<<<而且一根在区间,上,不妨设又因为21111h(0)1,h()0,(2102e e a a e e e=∴<-++<∴>+-又只需即)②联立①②可得:21-+>ee a ……………………………6分 (Ⅲ)证明:由(Ⅱ)知,单调递减则时,)(,0)('),1(2x g x g x x <∈ 2'()0,g()x x g x x ∈+∞>()时,单调递增2g()1()x g x ∴+∞在(,)上有最小值2t 1g ()()t g x ∀∈+∞≥即(,),都有 …………………………………………………7分 单调递增又当)(0)(),,0(1x g x g x x ∴>'∈单调递减当)(,0)(),1,(1x g x g x x ∴<'∈1g()01)g()x x ∴在(,上有最大值1s (0,1),g()()s g x ∀∈≤即对都有 ……………………………………………………8分又),e ),1,0(,1,2212121+∞∈∈=+=+(x e x x x a x x212121g()()()()ln ln 11a at g s g x g x x x x x ∴-≥-=+---- 11l 1212---+=x a x a x x n)(1ln 22222e x x x x >-+=………………………………10分 )0(1ln 21ln )(2>-+=-+=x x x x x x x x k 设 0112)(k 2>++='∴x x xe e e k x k x k 12)()(),e )(-+=>∴+∞∴上单调递增,在(…………………11分 e e s g t g 12)()(-+>-∴………………………………………………………12分请考生在第22、23两题中任选一题做答,如果多做,则按所做的第一题计分,作答时请写清题号. 22. 解:(Ⅰ)2222()cos sin 122sin y x y αααα⎧=⎪⇒+=+=⎨=⎪⎩ ………………1分即曲线1C 的普通方程为221204x y+=…………………………………………………2分222,c o s ,s i n ,x y x y ρρθρθ=+== 曲线2C 的方程可化为224240x y x y ++-+= ……………………………………3分 即1)1()2(:222=-++y x C . ………………………………………………4分(Ⅱ)曲线1C 左焦点为(4-,0) ……………………………………………5分 直线l 的倾斜角为4πα=, sin cos αα==…………………………………………6分 所以直线l 的参数方程为: 为参数)t t y t x (22224⎪⎪⎩⎪⎪⎨⎧=+-=………………………………7分将其代入曲线2C 整理可得:04232=+-t t , ……………………………………8分 设A,B 对应的参数分别为21,t t 则 所以4,232121==+t t t t . ………………………9分所以12AB t t =-===………………………10分解法二:(Ⅰ)同解法一. ………………………………………………………………4分 (Ⅱ)曲线1C 左焦点为(4-,0) ………………………………………………………5分直线l 的斜率为tan 14k π==, ………………………………………………………6分 直线l 的普通方程为4y x =+. 即40x y -+= …………………………………7分 圆2C 的圆心坐标为:(-2,1). ……………………………………………………8分 圆心2C 到直线l的距离2d == ……………………………9分故AB === …………………………………………10分 解法三:(Ⅰ)同解法一. …………………………………………4分(Ⅱ)曲线1C 左焦点为(4-,0) …………………………………………5分 直线l 的斜率为tan 14k π==, ……………………………………………6分 直线l 的普通方程为4y x =+ …………………………………………………7分 2122212423560(2)(1)121y x x x x x x y y y =+⎧⎧⎧=-=-⇒++=⇒⎨⎨⎨++-===⎩⎩⎩或, …………9分AB =| ………………………………………10分23. 解:(Ⅰ)当1a =时,()6f x <,即21236x x -++<, 即3212236x x x ⎧≤-⎪⎨⎪---<⎩或312223126x x x ⎧-<<⎪⎨⎪++-<⎩或1221236x x x ⎧≥⎪⎨⎪-++<⎩ …………3分322x ∴-<≤-或3122x -<<或112x ≤< …………………………………4分 21x ∴-<< 所以不等式()6f x <的解集为{}|21x x -<< ………………5分 (Ⅱ)对任意R x ∈1,都有R x ∈2,使得)()(21x g x f =成立,则有{|()}{|()}y y f x y y g x =⊆=, …………………………………………………6分 又()|2||23|f x x a x =-++|(2)(23)||3|x a x a ≥--+=+ ……………………………7分 ()|1|22g x x =-+≥, ………………………………8分 从而|3|2a +≥,解得15a a ≥-≤-或, …………………………………………………9分故[1,)(,5]a ∈-+∞-∞-U ………………………………………………………………10分。
2017年广东高考物理试题及答案
2017年普通高等学校招生全国统一考试理科综合能力测试二、选择题:本题共8小题,每小题6分,共48分。
在每小题给出的四个选项中,第14~17题只有一项符合题目要求,第18~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.将质量为1.00kg 的模型火箭点火升空,50g 燃烧的燃气以大小为600 m/s 的速度从火箭喷口在很短时间内喷出。
在燃气喷出后的瞬间,火箭的动量大小为(喷出过程中重力和空气阻力可忽略) A .30kg m/s ⋅B .5.7×102kg m/s ⋅C .6.0×102kg m/s ⋅D .6.3×102kg m/s ⋅15.发球机从同一高度向正前方依次水平射出两个速度不同的乒乓球(忽略空气的影响)。
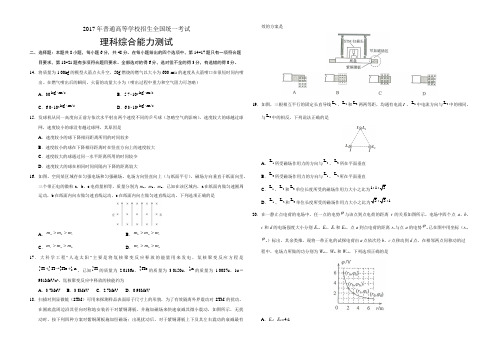
速度较大的球越过球网,速度较小的球没有越过球网,其原因是 A .速度较小的球下降相同距离所用的时间较多B .速度较小的球在下降相同距离时在竖直方向上的速度较大C .速度较大的球通过同一水平距离所用的时间较少D .速度较大的球在相同时间间隔内下降的距离较大16.如图,空间某区域存在匀强电场和匀强磁场,电场方向竖直向上(与纸面平行),磁场方向垂直于纸面向里,三个带正电的微粒a ,b ,c 电荷量相等,质量分别为m a ,m b ,m c ,已知在该区域内,a 在纸面内做匀速圆周运动,b 在纸面内向右做匀速直线运动,c 在纸面内向左做匀速直线运动。
下列选项正确的是A .a b c m m m >>B .b a cm m m >>C .a c bm m m >>D .c b a m m m >>17.大科学工程“人造太阳”主要是将氚核聚变反应释放的能量用来发电,氚核聚变反应方程是22311120H H He n++→,已知21H的质量为 2.0136u ,32He的质量为3.0150u ,1n的质量为 1.0087u ,1u =931MeV/c 2。
2017年广东理综物理高考卷

2017年广东物理高考卷一、单选题1.将质量为1.00 kg的模型火箭点火升空,50 g燃烧的燃气以大小为600 m/s的速度从火箭喷口在很短时间内喷出。
在燃气喷出后的瞬间,火箭的动量大小为( )(喷出过程中重力和空气阻力可忽略)A. 30B. 5.7×102C. 6.0×102D. 6.3×1022.发球机从同一高度向正前方依次水平射出两个速度不同的乒乓球(忽略空气的影响)。
速度较大的球越过球网,速度较小的球没有越过球网;其原因是( )A. 速度较小的球下降相同距离所用的时间较多B. 速度较小的球在下降相同距离时在竖直方向上的速度较大C. 速度较大的球通过同一水平距离所用的时间较少D. 速度较大的球在相同时间间隔内下降的距离较大3.如图,空间某区域存在匀强电场和匀强磁场,电场方向竖直向上(与纸面平行),磁场方向垂直于纸面向里,三个带正电的微粒a、b、c电荷量相等,质量分别为ma、mb、mc。
已知在该区域内,a在纸面内做匀速圆周运动,b在纸面内向右做匀速直线运动,c在纸面内向左做匀速直线运动。
下列选项正确的是( )A.B.C.D.4.大科学工程“人造太阳”主要是将氘核聚变反应释放的能量用来发电。
氘核聚变反应方程是。
已知的质量为2.013 6 u,的质量为3.015 0 u,的质量为1.008 7 u,1 u=931 MeV/c2。
氘核聚变反应中释放的核能约为( )A. 3.7 MeVB. 3.3 MeVC. 2.7 MeVD. 0.93 MeV5.扫描隧道显微镜(STM)可用来探测样品表面原子尺度上的形貌。
为了有效隔离外界振动对STM的扰动,在圆底盘周边沿其径向对称地安装若干对紫铜薄板,并施加磁场来快速衰减其微小振动,如图所示。
无扰动时,按下列四种方案对紫铜薄板施加恒磁场;出现扰动后,对于紫铜薄板上下及左右振动的衰减最有效的方案是( )二、多选题6.如图,三根相互平行的固定长直导线L 1、L2和L3两两等距,均通有电流,L1中电流方向与L2中的相同,与L3中的相反,下列说法正确的是( )A. L1所受磁场作用力的方向与L2、L3所在平面垂直B. L3所受磁场作用力的方向与L1、L2所在平面垂直C. L1、L2和L3单位长度所受的磁场作用力大小之比为D. L1、L2和L3单位长度所受的磁场作用力大小之比为7.在一静止点电荷的电场中,任一点的电势与该点到点电荷的距离r的关系如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、选择题:本题共有8小题,每小题6分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第18~21题有多项符合要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.如图,物体P 静止于固定的斜面上,P 的上表面水平,现把物体Q 轻轻地叠放在P 上,由此可求出A .P 与斜面的摩擦力B .P 与Q 的摩擦力C .P 对斜面的正压力D .斜面的倾角15.在光滑水平面上,有一竖直向下的匀强磁场分布在宽为L 的区域内,磁感应强度为B 。
正方形闭合线圈的边长为L ,沿x 轴正方向运动,未进入磁场时以速度v 0匀速运动,并能垂直磁场边界穿过磁场,那么A .bc 边刚进入磁场时bc 两端的电压为04BLvB .线圈进入磁场过程中的电流方向为顺时针方向C .线圈进入磁场做匀减速直线运动D .线圈进入磁场过程产生的焦耳热大于离开磁场过程产生的焦耳热16.一理想变压器原、副线圈匝数比n 1∶n 2=55∶3,原线圈输入电压u 随时间t 的变化规律u =2202sin 100πt V 。
理想交流电压表V 、理想交流电流表A 按所示方式连接,副线圈接入一个R =6 Ω的电阻,则A .经过1分钟电阻产生的热量是24JB .与电阻并联的电压表的示数约为20.0VC .电流表A 的示数约为0.11 AD .当再将一个电阻与电阻R 并联时,变压器的输出电压减小17.在t =0时,A 、B 两物体在同一地点以相同的初速度沿同一方向运动,A 物体的v -t 图象如图,B 物体做匀减速直线运动,直到停止,两物体的位移相同,下列说法正确的是A .B 运动的时间可能等于A B .在途中B 始终在A 的前方C .在途中任一时刻两物体的速度不可能相同D .在途中任一时刻两物体的加速度不可能相同 18. 下列说法正确的是A.当氢原子从n =2的能级跃迁到n =6的能级时,发射出光子B.放射性元素的半衰期是指大量该元素的原子核中有半数发生衰变需要的时间C.同一元素的两种同位素具有相同的质子数D.中子与质子结合成氘核时吸收能量19.如图在同一轨道平面上的两颗人造地球卫星A 、B 同向绕地球做匀速圆周运动,A 、B 和地球恰好在一条直线上,周期分别为T A 、T B ,由图中位置开始A 、B 和地球再次共线的时间间隔为T ,下列说法中正确的是A .A 、B 卫星的线速度v A >v BB .A 、B 卫星受到的万有引力一定有F A > F BC .T 可能小于T AD .T 一定大于2AT 20.如图,在△ABP 为等边三角形,在A 、B 两点分别放上一个点电荷,在P 处的合场强方向如图中箭头所示,与PB 连线的夹角为300, 下列说法正确的是A .A 处点电荷为正电荷,B 处点电荷为负电荷 B .两电荷的电荷量A B q qC .两电荷在P 点产生的场强大小A B E E >D .从P 点沿着AB 中垂线向外移动正电荷,电场力做负功21.如图所示,在粗糙水平地面上,弹簧一端固定在竖直墙壁上,另一端连着物块,弹簧处于原长时物块处于O 点位置。
现用外力缓慢把物块向左压至P 点不动,此时弹簧的弹性势能为Ep 。
撤去外力后物块向右运动至Q (图中未有标出)点停下。
下列说法正确的是A .外力所做的功等于E PB .物块到达PQ 中点时速度最大C .Q 点可能在O 点的左侧D .从P 到Q 的过程摩擦产生的热量一定小于E P22.(6分)如图是某同学研究小球下落时的频闪照片,频闪仪每隔0.1s 闪光一次并进行拍照。
照片中小球静止时在位置1,某时刻释放小球,下落中的小球各位置与位置1的距离如图中所标的数据(单位:cm )。
实验过程并没有错误,但该同学发现图中数据存在以下问题:根据22119.80.1 4.9022h gt m cm ==⨯⨯=,而图中标出的位置1和位置2的距离为1.23cm ,比4.90cm 小很多,你对此问题的解释是 。
下落中小球在位置3的速度为 m/s ,小球做自由落体运动的加速度为 m/s 2。
(计算结果保留3位有效数字)23.(9分)为了测量待测电阻R X 的阻值(约为200 Ω),备有以下器材: A.电源E :电动势约为1.5V ,内阻可忽略不计; B.电流表A 1:量程为0~10m A ,内电阻r 1=20 Ω; C.电流表A 2:量程为0~30m A ,内电阻r 2≈6 Ω; D.定值电阻R 0:阻值R 0=80 Ω;E.滑动变阻器R 1:最大阻值为20 Ω;F.滑动变阻器R 2:最大阻值为2 000 Ω;G.单刀单掷开关S ,导线若干;①滑动变阻器应选择____________。
②为了尽量准确地测量电阻R X ,在图甲、乙两图中,应选择图______(填图号)。
③合理选择电路后,某次测量中电流表A 1的示数为I 1,电流表A 2的示数为I 2。
则R X 的表达式为:R X =______________。
④某次测量时,其中一个电流表指针位置如图丙所示,其读数为=________m A 。
⑤本实验中,设滑动触头P 从b 端开始向左移动的距离为x ,P 、b 两点电压为U ,若图丁A 、B 、C 、D 中有两条是R 1、R 2的U —x 关系图线,则对应R 2的是______线。
24.(12分)直角坐标系中,在x 负半轴上x d =-位置有一发射源,可沿着x 轴正方向发射速度均为v 0的相同带电粒子(忽略重力),空间只存在沿y 轴负方向的匀强电场时,发射出的粒子经过y 轴上4d y =-的点。
空间同时加一垂直纸面向里的匀强磁场时,发射出的粒子沿x 轴正方向匀速直线运动。
若撤去电场,空间只存在匀强磁场,求发射出的粒子经过y 轴时的纵坐标。
25.(20分)如图,光滑轨道ABCO 固定在竖直平面内,圆弧AB 的圆心角为600,O 为圆心,半径为R =7.5cm ,OB 为半圆BCO 的直径,光滑平台与轨道相切于A 点。
质量为M =2kg ,长度为L =1.82m 的木板静止在水平地面上,木板与水平地面的动摩擦因数为μ 2 =0.1,木板上表面与平台上表面处于同一水平面上。
物体P 静止在木板上的某处,物体q 在水平向左的恒力F =4N 作用下,以V 0=4m/s 的初速度从木板右端向左运动,经过0.2s 与p 相碰并结合成一整体Q ,P 、q 、Q 与木板上表面的动摩擦因数为μ 1=0.3。
当木板与平台相碰时被牢固粘连,Q 滑离木板时立刻撤去恒力F ,Q 恰好能通过圆轨道BCO 的最高点。
P 、q 质量均为m =1kg ,P 、q 、Q 可看作质点,所有接触面的最大静摩擦力与滑动摩擦力大小相等,取g=10 m/s 2,求:(1)结合体Q 刚过A 点时轨道对它支持力; (2)物体q 开始运动时P 、q 的距离;(3)木板与平台相碰时,结合体Q 的速度大小。
(二)选考题33、[物理-选修3-3] (15分)(1) (5分)下列说法正确的是__________(填正确答案标号,选对1个得2分,选对2个得4分,选对3个得5分。
每错选1个扣3分,最低得0分)。
A.布朗运动就是液体分子的无规则运动B.当氧气与氢气的温度相同时,它们分子的平均动能相同C.小草上的露珠呈球形的主要原因是因为液体表面张力的作用D.分子间距离增大时,分子间的势能一定增大E.气体向真空的自由膨胀是不可逆的(2) (10分)如图所示,一圆柱形绝热气缸竖直放置,通过绝热活塞封闭着一定质量的理想气体。
活塞的质量为m,横截面积为S,与容器底部相距h ,此时封闭气体的温度为T1。
现通过电热丝缓慢加热气体,当气体吸收热量Q时,气体温度上升到T2。
已知大气压强为P0,重力加速度为g ,不计活塞与气缸的摩擦,求:①活塞上升的高度;②加热过程中气体的内能增加量。
物理试题参考答案14、B 15、D 16、C 17、B 18、BC 19、ACD 20、AD 21、BC 22、小球在位置2时下落的时间小于0.1s (2分),1.47(2分),9.80(2分); 23、① E(或R 1)(2分); ②乙(2分); ③10121I (R r )(I I )+-(2分);④ 20.0(1分);⑤ D(2分)。
24、解:只存在匀强电场时:0d v t = (1分) 2142d at = (1分) qE ma = (2分)空间同时存在匀强电场和匀强磁场时: 0qE qv B = (2分)空间只存在匀强磁场时:200v qv B m r= (2分)222()r y d r -+= (2分)解得2dy = (2分)25、解:(1) 恰好通过圆轨道BCO 的最高点且速度为V 42422V mg m r= ① (1分)其中2R r =05(1c o s 60)24R R h R =+-= ② (1分) 结合体由A 到最高点机械能守恒 2241122222A mV mgh mV ⨯+=⨯ ③ (1分) 222A V N mg m R-= ④ (1分)联立①~④得结合体刚过A 点时轨道对它支持力为 N=8mg=80N ⑤ (1分) (2)q 开始滑动时 113f mg N μ== ⑥ (1分)木板与地面的最大静摩擦力 22(2)4f m m m g N μ=++= ⑦ (1分) 因为12f f <所以木板和p 静止不动 (1分)根据牛顿第二定律得 1F f m a -=⑧ (1分) 物体q 开始运动时p 、q 的距离 2012s v t at =+ ⑨ (1分)由⑥~⑨解得 0.82s m= ⑩ (1分) (3)q 、P 相碰前q 的速度 V 1=V 0+at ⑪ (1分) 物体q 与p 相碰,动量守恒 mV 1=2mV 2 ⑫ (1分)又因为1226f N f =>,木板开始滑动 (1分) 设结合体Q 与木板未共速,木板与平台相碰对木板,木板与平台碰撞前木板速度为V 3,由动能定理21231(2)2f f x MV -=⑬ (1分) 对结合体Q ,从碰后到圆轨道BCO 的最高点2214211(2)()22222F f x L s mgh mV mV -+--=⨯-⨯ ⑭ (1分)由于2F f =,木板开始滑动到与平台碰撞前,结合体Q 和木板动量守恒,设此时结合体速度为V 5,则23522mV MV mV =+ ⑮(1分) 联立⑪~⑮解得:V 3=0.4m/s (1分) V 5=1.7m/s (1分)V 5=1.7m/s >V 3=0.4m/s ,所以设结合体Q 与木板未共速,木板就与平台相碰,相碰时的速度为1.7/m s 。
(1分)33、(1)BCE(2)解:①T 1时气体体积hs V =1 (1分) T 2时气体体积s h h V )(2'+= (1分) 由盖—吕萨克定律得2211T V T V = (2分) 解得活塞上升的高度h T T h )1(12-=' (1分) ②由热力学定律U Q W ∆=+ (2分)外界对系统做功W Fh '=- (1分) 活塞处于平衡0F P S mg =+ (1分) 解得加热过程中气体的内能增加量2011T U Q (P S mg )()h T ∆=-+- (1分)。
