尾部指标估计中的阈值选择
指标组合 权重 阈值

指标组合权重阈值全文共四篇示例,供读者参考第一篇示例:指标是评价一个事物或者情况的重要依据,也是衡量一个事物或者情况优劣的标准之一。
在实际应用中,往往需要将多个指标进行组合,以便更全面地评价或真实地反映事物或情况的特征。
这就引入了指标组合的概念。
指标组合是将多个指标综合在一起,形成一个综合指标。
通常来说,指标组合可以通过加权平均或者多指标决策方法来实现。
加权平均是指根据各指标的重要性设定权重,然后将各指标的观测值乘以对应的权重,再将各项结果加总得到最终的综合指标值;而多指标决策方法则是通过一些特定的数学模型,比如TOPSIS、AHP等来综合考虑各指标的观测值,从而得到最终的综合指标值。
权重是指标组合中的重要概念,它反映了各指标在综合评价中的重要性。
权重的设定直接影响到最终的综合指标值,因此权重的确定十分关键。
一般来说,权重的确定可以通过专家赋值法、层次分析法、熵权法等方法来实现。
在实际应用中,选取合适的权重确定方法对于指标组合的结果至关重要。
除了指标组合和权重的确定,阈值也是评价一个事物或情况的关键要素。
阈值是指一个事物或情况在某个指标上的最低值或最高值,如果超过或者达到了这个阈值,则可以认为这个事物或情况是合格的或者不合格的。
阈值的确定可以根据具体情况进行设定,一般来说,阈值的设定应该具有理论依据,并且符合实际情况。
在实际应用中,指标组合、权重和阈值的确定往往是一个复杂而繁琐的过程。
需要确定评价的目标是什么,需要综合评价的指标有哪些,然后需要确定权重的设定方法,以及最后确定阈值的设定方法。
在整个过程中,需要考虑到各种因素的影响,确保最终的综合评价结果是科学、准确、客观和可靠的。
指标组合、权重和阈值是评价一个事物或情况的主要手段,通过合理的组合和设定,可以更好地反映事物或情况的特征,为决策提供科学的依据。
在今后的研究和实践中,我们应该加强对指标组合、权重和阈值的研究,提高其在实际应用中的效果和效率,为社会发展和进步做出更大的贡献。
选择重尾阈值k的Bootstrap方法

选择重尾阈值k的Bootstrap方法刘维奇;赫英迪;邢红卫【摘要】详细讨论了重尾指数估计中选取k的Sum-plot方法和Bootstrap方法,并对Hall提出的Bootstrap方法作了改进,称为M-Bootstrap方法.并利用上述三种方法对已知重尾分布进行Monte-Carlo模拟,研究它们的可行性,比较它们的稳健性,改进的M-Bootstrap方法对重尾指数的估计在某些情况下优于Bootstrap 方法.【期刊名称】《山西大学学报(自然科学版)》【年(卷),期】2010(033)004【总页数】5页(P508-512)【关键词】重尾指数;重尾阈值;Sum-plot方法;Bootstrap方法;M-Bootstrap方法【作者】刘维奇;赫英迪;邢红卫【作者单位】山西大学,管理科学与工程研究所,山西,太原,030006;山西大学,数学科学学院,山西,太原,030006;山西大学,数学科学学院,山西,太原,030006;广东茂名职业技术学院,广东,茂名,525000;山西大学,数学科学学院,山西,太原,030006【正文语种】中文【中图分类】O212重尾指数估计方法总体上分为参数估计和半参数估计,都与重尾阈值或估计中所用次序统计量的个数k有关.k的选取关系到估计的精确性,k的偏大或偏小都会造成估计的极大误差.学者们从理论上提出了许多选取k的方法.其中一类是作图法,比如Hill[1]提出的Hill-plot,Kratz和Resnick[2]提出的qq-plot,Beirlant等[3]提出的Pareto分位数图,Resnick和Starica[4]给出的对Hill-plot改进的s mooHill-plot以及deHaan 和Resnick[5]给出的对Hill-plot改进的AltHill-plot等,这些作图法都有一定的优越性,但整体而言它们都不能适用于所有情况的重尾分布.像Hill-plot,qq-plot,当随机变量服从Pareto分布时,这两种方法表现出十分优良的性质,能够很容易选取k 值.一旦随机变量不服从Pareto分布,而是广义Pareto分布时,它们却不能很好地选取k,甚至无法选取k.Pareto分位数图,s mooHill-plot和AltHill-plot相对于Hillplot估计精度稍高一些,但是也不能对所有的重尾分布较好地选择k.Sousa[6]在其博士论文中提出的Sumplot方法在一定程度上克服了前几种方法中选取k所遇到的困难,而且具有比较好的性质.但是由于Sumplot方法是以观察图形得到k,因此选择k有一定的猜测性,因而会对重尾指数估计造成一定误差.另一类方法就是以估计重尾指数的均方误差(MSE)最小为标准来确定k,最优的k应该与均方误差一致.理论上MSE与k有关,增大k,方差减小,偏差增大.反之,减小k,方差增大,偏差减小.只有权衡方差和偏差使MSE最小,选取的k才是最优的.但是,MSE还与未知分布尾部指数α和二阶参数ρ有关,不能直接应用到实际问题中.基于此,1990年Hall[7]提出了利用Bootstrap方法来选取k,Danielsson[8]在2001年又对Hall的方法作了进一步改进,Gomes和Oliveira[9]在2001年给出了一个选取Bootstrap方法子样本的准则,Gomes等①GomesM I,Mendonca S,Pestana D.The bootstrap methodolgy and adaptive reduced-bias tail index and Value-at-Risk estimation.Working paper,2009.在2009年给出了针对降偏差重尾指数估计的Bootstrap方法.由于该方法计算量很大,有必要在保证估计特性的前提下提高估计的收敛速率以减少计算量.Sum-plot方法[6]是基于{(k,Sk),1≤k≤n}应该是一条直线的理论依据来选取k.Sousa通过对不同样本容量的不同分布进行模拟,得出无论是分布的尾部指数0<α<2还是α≥2,Sum-plot方法对绝大多数分布而言都较其它方法优越,并且不受样本异常值影响,即具有稳健性.这里随机变量其中Xn(1)≥Xn(2)≥…Xn(k+1)为次序统计量.如果选择k,使Xn(k+1)足够大,那么对任意x>Xn(k+1),有Sk~α-1k.近似式表明图形中直线的斜率等于α-1,而且Sousa证明了α-1可以通过如下线性回归模型估计出来.容易发现参数α-1的估计值等于回归模型的斜率^β1,即进一步,如果β0=0,则就是Hill估计.由于Sum-plot方法需要观察以坐标{(k,Sk),1≤k≤n}画成的散点图在哪一点偏离直线,因此选择的k有一定的猜测性,因而会对重尾指数估计造成不可避免的误差. Danielsson等[8]对Hall的方法作了改进,使用新的统计量Mn(k)来代替γn(k).引入统计量已经证明,当k→∞,k/n→0时,Mn(k)/(2γn(k))依概率收敛于γ,统计量Mn(k)/(2γn(k))-γn(k)和γn(k)-γ有相似的渐近性质,并且在一定条件下极小化AMSE和极小化AsyE(Mn(k)-2(γn(k))2)2可以得到同阶量的k(相对于n).因此,根据Bootstrap子样本X*n1,选用统计量:其中通过最小化Q(n1,k1)来确定k1.为了确定k,还需要另一个Bootstrap子样本然后利用与确定k1相同的程序来确定k2.再利用k,k1和k2之间的关系来确定k.我们受Danielsson等[8]提出的Bootstrap方法的启发,用γ的相合估计~γn(k)代替γn(k),渐近均方误差变为根据Bootstrap子样本X*n1,通过极小化AMSEM(n1,k1)和关系k=k1(n/n1)μ来确定k1与k.定理1 假设k→∞,k/n→0.k(n)由AMSE(n,k)最小确定.则S-1是函数S的反函数,A2(t)=∫∞tS(u)du(1+o(1)),t→∞.假设A(t)=ctρ,c≠0,ρ>0,则定理2 假设k1→∞,k1/n1→∞.假设A(t)=ctρ,c≠0,ρ<0,n1=O(n1-ε)(0<ε<1),由k1)最小确定k1.则由定理1和定理2可知,k与n,k1与n1存在同样的幂指数关系式.这与Hall所预设的关系一致.所以我们仍旧取来确定k.我们取μ=,无形中假设了二阶形状参数ρ=-1,这证实了Hall的Bootstrap方法与ρ=-1有关.随机变量Y1,Y2,…,Yn是i.i.d.,其共同分布为G(y)=1-y-1(y≥1),Yn,1≥…≥Yn,n是Y1,Y2,…,Yn的顺序统计量.引理1 0<k<n,且k→∞,则有定理1的证明:U(t)的定义等价于正则变化函数|logU(t)-γlogt-C0|以指数ρ正则变化,其中C0为常数.令A(t)=ρ(logU(t)-γlogt-C0).由Potter不等式,可得对任意0<ε<1,存在t0>0,对于t0>0,tx≥t0有,(2)n→∞,(Pn,Qn)渐近正态,它们的均值为0,方差分别为1,20,协方差为4,其中用Yn,k代替t,Yn,i/Yn,k+1代替x迭代不等式(i=1,2,…,k),然后乘以,得到又而Y1,…,Yki.i.d具有共同分布函数1-,于是由弱大数定律得即我们求(12)中右边的最小值点,得到定理1的结论,定理证毕.定理2的证明:令Gn表示独立变量的均匀分布的经验分布函数.令n足够大,n1=O(n1-ε),则有于是因此,对所有的4≤t≤n1(lognn)2,用Fn表示Xn的经验分布函数.,由(11),(13),(14)得,所以对任意的0<ε<1,总存在t0>4,对于t0<t<n1(logn1)2及t0<tx<n1(logn1)2,有同理用Yn1,k1+1,Yn1,i(i=1,…,k1)分别代替t和tx,则不等式(15),(16)是以概率成立的.于是有以概率成立.我们极小化E((γ*n1(k1)-γn(k))2|Xn).由定理1的证明过程可以得到又¯γn是γ的相合估计,.定理2得证,定理证毕.为了更好地说明问题,我们选用三种熟知的重尾分布,稳定分布Stable(1.5)分布、t-分布t(3)以及逆Γ分布IGa(1.5,1),分别采用Sum-plot方法、Danielsson等提出的Bootstrap方法(D-Bootstrap方法)和改进的Bootstrap方法(M-Bootstrap方法)进行模拟.结果表明,Sum-plot方法、Bootstrap方法和M-Bootstrap方法都能作为Hill估计中选择k的有力工具,它们和Hill估计结合起来估计重尾指数将是有效的.为便于比较,我们将三种方法的模拟结果列表如下(P512见表1).根据表1可以看出,应用三种方法得到的结果是令人满意的.相比之下,Sum-plot方法的精确性优于两种Bootstrap方法.从整体上看,两种Bootstrap方法估计的结果误差也是比较小的,都可以使用.从k选择上看,改进的M-Bootstrap方法更接近Sum-plot方法结果,对重尾指数的估计在某些情况下优于Bootstrap方法,特别是在计算量上明显优于Bootstrap方法.所以,M-Bootstrap方法是适用的,有意义的.两种Bootstrap方法个别情形下出现了较大偏差,这与方法本身的特点有关.基于两个子样本的Bootstrap方法受异常值的影响,我们所用的数据都是随机生成的,不免有异常值的出现.Bootstrap方法受样本容量的影响很大,这也是出现偏差的原因.【相关文献】[1] H I LL B.A Simple GeneralApproach to Infererce about The Tail of aDistribution[J].Annals of Statistics,1975,3:1163-1174.[2] KRATZM,RESN ICK S.The qq-estimator and Heavy Tails[J].Stochastic models,1996,12(4):699-724.[3] BEIRLANT J,VYNCKIER P,TEUGELSJ L.Tail Index Estimation,ParetoQuantileplots,and RegressionDiagnostics[J].Journal of the Am erican Statistical Association,1996,436:1659-1667.[4] RESN ICK S,STAR I CA C.Smoothing the Hill Estimator[J].Advances in Applied Probability,1997,29:271-293.[5] DREES H,HAAN L D,RESN I CK S.How toMake a Hill Plot[J].Annals ofStatistics,2000,28:254-274.[6] SOUSA B.A Contribution to the Estimation of the Tail Indexof Heavy-tailedDistributions[D].TheUniversityof Michigan,2002.[7] HALL ing the Bootstrap to Estimatemean Square Error and Select Smoothing Parameters in Non-parametricproblems[J]. Journal of M ultivariate Analysis,1990,32:177-203.[8] DAN IELSSON ing a Bootstrap Method Choosethe Sample Fraction in Tail Index Estimation[J].Journal ofM ultivariateAnalysis,2001,76:226-248.[9] GOMESM I,OL I VEIRA O.The Bootstrap Methodology in Statistics of Extremes-choice of the Optimal Sample Fraction[J].Extremes,2001,4(4):331-358.。
敏感指标中的阈值

敏感指标中的阈值敏感指标的阈值是指在某种条件下,经过量化的测量结果、计算结果或规定的准确度达到一定的数值,就会触发某种机制或导致特定后果的设定值。
这些敏感指标的阈值涉及到广泛的领域,包括环境保护、卫生安全、金融风险、信息安全等等。
在这些领域中,阈值的设置对于预警、预防和治理措施的制定起着很重要的作用。
敏感指标的阈值的设定需要考虑到伦理、政治和社会等多种因素。
对于某些环境保护和卫生安全指标的阈值,需要考虑到经济成本和公共利益之间的平衡,因为一些污染物或危险物质的减排或禁用可能会对某些企业或行业的利益产生不利影响。
对于金融风险指标的阈值,需要考虑到市场稳定和政策效果之间的平衡,因为调控措施过于激进可能会导致市场情绪波动和金融系统的不稳定。
对于信息安全指标的阈值,需要考虑到安全和隐私之间的平衡,因为过于严格的安全要求可能会对个人自由和社会开放产生负面影响。
敏感指标的阈值设置还需要考虑到不同政策目标和不同行业和领域背景下的特定情况。
例如,对于空气质量指标的阈值,不同国家和地区可能会根据自己的经济发展水平、气象条件、人口密度等因素来设定,以达到一定的空气质量目标。
对于医学诊断指标的阈值,也需要考虑到不同年龄、性别、族群等人群的特定情况,以保证准确诊断和治疗。
敏感指标的阈值设置需要基于可靠的数据和科学的方法。
在制定阈值时,需要分析大量的相关数据和信息,并结合科学的统计和模型分析方法,确保阈值的设定具有客观性、可复现性和科学性。
此外,为了确保阈值的准确度和可靠性,对敏感指标的阈值设定需要进行持续的监测和评估,以检测和修正阈值的错误和不合理性,以及应对不断变化的环境和条件。
敏感指标的阈值设置对于制定有效的预警和预防措施,对降低风险和防止损失都非常重要。
然而,敏感指标的阈值设置上也存在一些问题和挑战,例如阈值设定过于保守或激进、数据不足或不可靠、统计模型不准确、政策执行不到位等,这些问题都可能导致阈值的不准确和不可靠,从而影响到预警和预防措施的实施,甚至会使风险得不到有效控制。
统计学阈值

统计学阈值
统计学阈值是指在统计学中使用的一种阈值,用以判断样本数据是否显著地不同于总体数据。
在进行假设检验时,需要根据样本数据计算出统计量,并与设定的阈值进行比较,以确定是否拒绝原假设。
常见的统计学阈值包括显著性水平、p值和置信区间。
显著性水平一般设定为0.05或0.01,表示在原假设成立的情况下,样本数据中出现显著差异的概率不超过5%或1%。
p值是指在原假设成立的情况下,观察到比样本数据更极端的结果出现的概率,通常将p值小于0.05或0.01的结果视为拒绝原假设。
置信区间是指在一定置信水平下,总体参数的估计范围,通常将95%置信区间作为估计结果的参考。
在实际应用中,选择合适的统计学阈值需要根据问题的具体情况进行权衡。
过高的显著性水平会增加犯错率,而过低的显著性水平会增加漏检率;p值的选择需考虑样本大小、效应大小和多重比较等因素;置信区间的宽度与样本大小和置信水平有关,需要根据实际情况进行选择。
- 1 -。
基于样本分块的重尾指数估计

基于样本分块的重尾指数估计1. 介绍重尾指数(Tail Index)是用于描述随机变量尾部极端事件发生概率的指标。
在金融、保险、环境科学等领域中,对极端事件的研究和预测具有重要意义。
基于样本分块的重尾指数估计方法可以通过分析样本数据中的极值情况,对总体的重尾指数进行估计。
在本文中,我们将详细介绍基于样本分块的重尾指数估计方法及其应用。
首先,我们将解释什么是重尾指数以及为什么需要进行估计。
然后,我们将介绍基于样本分块的方法,并详细说明其步骤和计算公式。
最后,我们将通过一个实例来演示如何使用这种方法进行重尾指数的估计。
2. 什么是重尾指数?在概率论和统计学中,重尾(Heavy-tailed)是指随机变量具有较大概率产生极端值或离群值的特征。
相反,轻尾(Light-tailed)则表示随机变量产生极端值或离群值的概率较小。
重尾指数是用于衡量随机变量尾部分布特征的一个指标。
它通常用符号α表示,取值范围为(0,∞)。
当α>2时,表示随机变量具有轻尾分布;当α<2时,表示随机变量具有重尾分布。
当α=2时,表示随机变量服从指数分布。
重尾指数的估计对于风险管理、投资组合优化、极端事件预测等具有重要意义。
因此,研究人员提出了多种方法来估计重尾指数,其中基于样本分块的方法是一种常用且有效的方法之一。
3. 基于样本分块的方法基于样本分块的重尾指数估计方法是通过将样本数据划分为多个块,并对每个块进行极值统计,然后利用极值进行参数估计。
下面是该方法的详细步骤:1.将样本数据按照时间顺序划分为若干个块。
2.对每个块进行极值统计,例如选择最大值或最小值作为极值。
3.根据所选取的极值构建一个新的样本序列。
4.利用新样本序列进行参数估计,得到重尾指数的估计值。
基于样本分块的方法的优点在于可以减小样本数据中极端值对估计结果的影响,并提高估计的准确性。
此外,该方法还能够考虑到样本数据的时序性,更好地反映出随机变量的演化规律。
预测概率阈值选择

预测概率阈值选择
预测概率阈值的选择是一个重要的决策过程,它可以根据特定的业务需求和目标来调整模型的预测精度和覆盖率。
以下是一些可能有用的方法:
1、根据历史数据确定阈值:使用历史数据来确定一个适当的阈值是一种常见的方法。
通过对历史数据进行统计分析,可以确定一个适当的阈值,以便在模型预测时区分真正的正例和负例。
2、交叉验证:交叉验证是一种评估模型性能的统计方法,也可以用于确定预测概率的阈值。
通过将数据集分成多个部分,并使用其中的一部分数据进行训练,然后使用另一部分数据进行验证,可以找到一个最佳的阈值,以最大化模型的预测精度和覆盖率。
3、业务规则和常识:在某些情况下,业务规则和常识可以用来确定预测概率的阈值。
例如,某些行业可能已经有了公认的阈值标准,或者根据实际情况可以设定一个合理的阈值。
4、实验和调整:确定阈值的过程也可以是一个试错的过程。
通过对不同的阈值进行实验,并观察模型性能的变化,可以找到一个最佳的阈值。
如果需要的话,可以进行一些调整以获得更好的模型性能。
容量规划的关键性能指标与阈值设置

容量规划的关键性能指标与阈值设置在现代IT系统中,容量规划是保障系统正常运行的关键环节。
通过合理的容量规划,可以帮助企业实现资源优化配置,提高系统性能,并避免因资源不足而导致的故障和服务中断。
而在容量规划中,关键性能指标和阈值设置的确定则是确保规划有效性的重要步骤。
一、容量规划的概念和作用容量规划是指基于当前和预测的工作负载,对系统资源的需求进行估计和管理的过程。
其旨在确保系统能够满足正常的业务运行需求,并在需求增长时及时扩展资源,保持良好的性能表现。
容量规划的作用主要有三个方面:1. 预测与规划:通过观察历史数据、分析趋势和业务需求,预测未来工作负载的增长情况,并进行相应的资源规划。
这样可以确保不会因为资源不足而导致性能下降或服务中断的情况发生。
2. 优化资源配置:容量规划可以帮助企业发现资源利用率低的问题,及时进行资源再分配或优化,从而提高资源利用效率,降低系统运行成本。
3. 预测性维护:通过对系统进行容量规划,可以及时发现潜在问题,预测资源耗尽的时间,并提前进行维护和升级,从而避免系统性能的恶化或宕机。
二、关键性能指标的选择和意义在容量规划中,选择合适的性能指标是至关重要的。
它们能够客观地反映系统资源的使用情况和性能状况,并为容量规划提供必要的数据支持。
以下是几个常用的关键性能指标:1. CPU利用率:CPU是系统中最基本、最核心的资源之一,一般来说,CPU利用率高说明系统负载较重,容易导致性能下降,进而影响业务的正常运行。
2. 内存利用率:内存是用来存储程序和数据的关键资源,其利用率过高可能会导致系统交换内存,严重影响性能。
因此,合理的内存利用率是保证系统正常运行的关键。
3. 磁盘空间利用率:磁盘空间是存储数据和文件的关键资源,合理的磁盘空间利用率可以保证系统稳定运行。
过高的磁盘空间利用率可能导致日志文件无法写入、数据库崩溃等问题。
4. 网络带宽利用率:网络带宽是保障系统与外界通信的重要资源,合理的网络带宽利用率可以保证系统正常与外界交互。
图像二值化阈值选取常用方法汇总
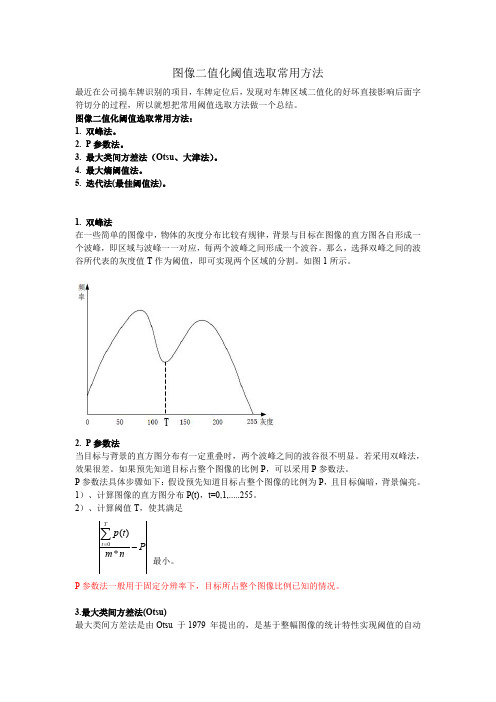
图像二值化阈值选取常用方法最近在公司搞车牌识别的项目,车牌定位后,发现对车牌区域二值化的好坏直接影响后面字符切分的过程,所以就想把常用阈值选取方法做一个总结。
图像二值化阈值选取常用方法:1.双峰法。
2.P 参数法。
3.最大类间方差法(Otsu 、大津法)。
4.最大熵阈值法。
5.迭代法(最佳阈值法)。
1.双峰法在一些简单的图像中,物体的灰度分布比较有规律,背景与目标在图像的直方图各自形成一个波峰,即区域与波峰一一对应,每两个波峰之间形成一个波谷。
那么,选择双峰之间的波谷所代表的灰度值T 作为阈值,即可实现两个区域的分割。
如图1所示。
2.P 参数法当目标与背景的直方图分布有一定重叠时,两个波峰之间的波谷很不明显。
若采用双峰法,效果很差。
如果预先知道目标占整个图像的比例P ,可以采用P 参数法。
P 参数法具体步骤如下:假设预先知道目标占整个图像的比例为P ,且目标偏暗,背景偏亮。
1)、计算图像的直方图分布P(t),t=0,1,.....255。
2)、计算阈值T ,使其满足0()*Tt p t Pm n =-∑最小。
P 参数法一般用于固定分辨率下,目标所占整个图像比例已知的情况。
3.最大类间方差法(Otsu)最大类间方差法是由Otsu 于1979年提出的,是基于整幅图像的统计特性实现阈值的自动选取的,是全局二值化最杰出的代表。
Otsu 算法的基本思想是用某一假定的灰度值t 将图像的灰度分成两组,当两组的类间方差最大时,此灰度值t 就是图像二值化的最佳阈值。
设图像有L 个灰度值,取值范围在0~L-1,在此范围内选取灰度值T ,将图像分成两组G0和G1,G0包含的像素的灰度值在0~T ,G1的灰度值在T+1~L-1,用N 表示图像像素总数,i n 表示灰度值为i 的像素的个数。
已知:每一个灰度值i 出现的概率为/i i p n N =;假设G0和G1两组像素的个数在整体图像中所占百分比为01ϖϖ、,两组平均灰度值为01μμ、,可得概率:00=T ii p ϖ=∑11011L i i T p ωω-=+==-∑平均灰度值:00T i i ipμ==∑111L ii T i p μ-=+=∑图像总的平均灰度值:0011μϖμϖμ=+类间方差:()()()22200110101()g t ωμμωμμωωμμ=-+-=-最佳阈值为:T=argmax(g(t))使得间类方差最大时所对应的t 值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
部指标规定了分布尾部“ 的程度和趋近于零 的速 厚” 度.尾部指标越大, 则尾部越厚, 趋近于零 的速度越
慢.特别地 , > / 时, 当 12 分布的方差不存在 ; 当 >
的厚尾数据及估计极端分位数和尾部 概率时, 尾部 指标 的 Hl估计 是一种重要估 计 , i l 它在保险和金
几年许多人都在研究 的一个 问题 , 提出 了许 多方法 和工具 , 如平 均超 出量 图, a t 位 数 图及各 种 P ro分 e Hl图.本文以美元对 日元的汇率 为例 , i l 分别用 自助 法, 直接估计 Hl估计的渐近均方误方法 , H l族 i l 对 a l
据这些数据 , 如何合理地估计 日对数 回报为 一 .3 00 ,
甚至更低回报的概率呢? 从极值理论看 , 这种高分位数和尾部概率 是 由
底分布的一个重要参数一尾部指标 一决定的.尾
1 时, ¥ 分布的均值也不存在.当尾部指标 > 0时 , 称此底分布是厚 尾分布.大量实证研究表 明: 大部
S a- , H N h nyn HI oj Z A G C u -ig D i
(ntueo Sine Taj nvrt, ini 30 7 , hn ) Istt f c c , i i U iesy Taj 0 0 2 C ia i e nn i n
Ab ta t sr c :Ho t ee t n a a t etrs od i no t lwa rm at ua e f aaa a d i ad l aematr w s lc d pi he h l n a pi yfo ap r c lrsto t th n s ei t t . o a v ma i d c e T i p p r o ue eHi si tr rtee t mevleidcso al x h n ert eun fteU. .d l rrlt e hs a e mp tst l et osf xr au ie fd i e c a g aertr so S ol ai c h l ma o h e n y h a e v
融等包含许多厚尾现象的领域中有着广泛应用. i Hl l
收稿 日期 : 050-8 20 -32 .
第一作者 : 史道济(9 2 1 4一 )男 , , 教授 , 博士生导师
维普资讯
20 年 1 月 06 2
史道济 , 尾部指标估计中的阈值选择 等:
F g I Dal x h n e r t e u n ft e i. i e c a g a e r t r so h y U. .d l r r l t e t e S ol ea v o y n a i
l P , 中 是第 t 0 川 其 g 的保费或测量投资风险时, 通
常需要预测那些很少 发生 、 但后果极其严重 的事件
的可能性.近年来 , a V R已经成为金融 风险度量 的
重要工具之一 , 而资产组合 的 V R实际上就是其损 a
益分布( 取相反数) 的一个高分位数.当投资者或资 金管理者评估或预测 不利事件时 , 这样 的风险测量
日元的汇率为例 , 明方法的使用. 说
关键词: 渐近均方误;自 助法; i估计; Hl l 序贯方法; 尾部指标 ; 最优阈值
中图分类号 : 2 4 7 F 2 . 文献标识码 : A
Th e h l ee t n i ali d x e t r s o d s l ci n t i n e si t n o ma i o
t e t i e n h e h l ee t n me h d h c y h n c mp r d o y n wi df r tt rs od s lc i t o s w ih a e t e o a e . h e o
Ke r s y wo d :AMS b osrpmeh d; l et tr sq e t l rc d r ;alid x teo tma h sod E; o tt to Hi 8j 0 ;e u ni o e ue ti n e ;h pi ltr h l a l ma ap e
文章编号 : 7 -9 X 2 0 )6 0 7 .4 1 3 05 (0 6 0 -0 80 6
尾 部 指 标 估计 中 的 阈值 选 择
史道 济 , 张春英
( 天津大学 理学院 , 天津 3 07 ) 0 0 2 摘 要:本文研 究如何 用较好的方法选择一个适 当的 闽值 , 算尾部指标 的 Hl估计 , 计 i l 然后 加 以比较 , 并以美元对
是非常有用 的.例如 , 1为 20 图 00年 1 1日到 月
20 04年 1 8日 2月 美元对 日 元的汇率.由图 1 可知, 近两年美元对 日 元的汇率有下降趋势.特别在 20 00 年 4月 1 日, 汇率 的 日对 数 回 报 置 =l P 一 该 o g
图 1 美元对 日元 的汇率
・ 9・ 7
估计简单且具有渐近正态性 , 但在实际应用 中, 的 它
元汇率 的 80 E 5个 t 对数 回报损失 ( 取相反数 ) P- 的 a
性质在很大程度上依赖于 阈值 的选择.给定一个数 rt 分位数 图, e o 右上角呈现较好的线性 , 可以认 为这 l l 据集 , 如何用较好 的方法选择一个适当的阈值 , 是近 组数据来 自厚尾分布.一般用 Hi 估计量尾部来估
维普资讯
第2 2卷 第 6期 20 0 6年 1 2月
天
津
理
工
大
学
学
报
V 12 . 0. 2 No 6
J OURNAL I OF T ANJ N I UNI VERS TY I OF TECHN0LOGY
D c2 o e.0 6
