2020-2021学年高一数学必修第一册(人教A版(2019))(试卷+答案)
1.1.1 物质的分类(练好题)(解析版)-2020-2021学年高一化学新教材(人教2019必修第一册)

1.1.1物质的分类(练好题)解析版A-基础过关1.碳酸氢钠是焙制糕点所用的发酵粉的主要成分之一,碳酸氢钠属于()A.混合物B.酸C.盐D.碱【答案】 C【解析】碳酸氢钠是碳酸的钠盐,属于盐,故选C。
2.将下列各组物质按酸、碱、盐分类顺序排列正确的是()A.硫酸、纯碱、石膏B.氢硫酸、烧碱、绿矾C.碳酸、生石灰、醋酸钠D.磷酸、熟石灰、苛性钾【答案】 B【解析】A项中纯碱是Na2CO3,属于盐而不是碱;C项中生石灰不属于碱;D项中苛性钾不属于盐。
3.下列物质中属于纯净物、化合物、无机化合物、盐、钙盐的是()A.石灰石B.Ca(OH)2C.CaCO3D.CH4【答案】 C【解析】A项,石灰石的主要成分是碳酸钙,但属于混合物,错误;B项,氢氧化钙不属于盐,错误;C 项,碳酸钙是纯净物、化合物,且是无机化合物,属于盐,含有钙元素,所以属于钙盐,正确;D项,甲烷不是无机化合物,属于有机化合物,错误,【答案】选C。
4.符合如图中阴影部分的物质是()A.NaHCO3B.Cu2(OH)2CO3C.NaClD.Na2CO3【答案】 D【解析】:A项属于酸式盐,B项为碱式盐、铜盐,C项不属于碳酸盐。
5.将下列各组物质,按酸、碱、盐顺序排列正确的是()A.硫酸、纯碱(Na2CO3)、食盐B.氢硫酸(H2S)、烧碱(NaOH)、硫酸铜C.碳酸、氧化铜、碳酸钠D.醋酸、熟石灰、苛性钾(KOH)【答案】 B【解析】A项中纯碱属于盐类而不属于碱类;B项符合题意;C项中氧化铜不属于碱类;D项中苛性钾属于碱类而不属于盐类。
6.某校实验室将试剂分类后放在不同的试剂柜里,已存放的部分试剂如下:该实验室新购进部分生石灰和纯碱应将它们分别放在()A.③和①B.④和①C.①和②D.③和④【答案】 D【解析】根据表中信息可判断①是碱,②是酸,③是氧化物,④是盐。
生石灰是氧化钙,放在③中;纯碱是碳酸钠,属于盐,放在④中。
7.下列各组物质,按化合物、单质、混合物顺序排列的是()A.烧碱、液态氧、碘酒B.生石灰、白磷、熟石灰C.干冰、铁、氯化氢D.空气、氮气、明矾【答案】 A【解析】A项,烧碱是氢氧化钠,属于化合物,液态氧是单质,碘酒是碘的酒精溶液,属于混合物,正确;B项,熟石灰是氢氧化钙,属于纯净物,错误;C项,氯化氢是纯净物,错误;D项,空气是混合物,胆矾是纯净物,错误。
1.3集合的基本运算-2020-2021学年高一数学同步课堂(人教A版2019必修第一册)

第一章集合与函数概念1.3 集合的基本运算一、并集【思考1】“x∈A或x∈B”包含哪几种情况?【思考2】集合A∪B的元素个数是否等于集合A与集合B的元素个数和?二、交集【特别提醒】交集有下列运算性质:A∩B=;A∩A=;A∩∅=。
三、全集1.定义:如果一个集合含有所研究问题中涉及的,那么就称这个集合为.2.记法:全集通常记作.【思考】全集一定是实数集R吗?四、补集(1)补集是相对于全集而言的,它与全集不可分割.一方面,若没有定义全集,则不存在补集的说法;另一方面,补集的元素逃不出全集的范围.(2)补集既是集合之间的一种关系,同时也是集合之间的一种运算.求集合A 的补集的前提是A 为全集U 的子集,随着所选全集的不同,得到的补集也是不同的. (3)符号∁U A 有三层意思: ①A 是U 的子集,即A ⊆U ; ②∁U A 表示一个集合,且(∁U A )⊆U ;③∁U A 是U 中不属于A 的所有元素组成的集合,即∁U A ={x |x ∈U ,且x ∉A }. (4)若x ∈U ,则x ∈A 或x ∈∁U A ,二者必居其一.一、1.提示: “x ∈A 或x ∈B”这一条件包括下列三种情况:x ∈A ,但x ∉B ;x ∈B ,但x ∉A ;x ∈A ,且x ∈B.用Venn 图表示如图所示.2. 提示:不等于,A ∪B 的元素个数小于或等于集合A 与集合B 的元素个数和. 二、 B ∩A A ∅ 三、1.所有元素 全集 2. U提示:全集是一个相对概念,因研究问题的不同而变化,如在实数范围内解不等式,全集为实数集R ,而在整数范围内解不等式,则全集为整数集Z. 四、不属于集合A ∁U A {x |x ∈U ,且x ∉A }1.并集的运算 求集合并集的方法(1)两集合用列举法给出:①依定义,直接观察求并集;②借助Venn 图写并集. (2)两集合用描述法给出:①直接观察,写出并集;②借助数轴,求出并集.(3)一个集合用描述法,另一个用列举法:①直接观察,找出并集;②借助图形,观察写出并集.(1)设集合M ={x |x 2+2x =0,x ∈R },N ={x |x 2-2x =0,x ∈R },则M ∪N =( )A .{0}B .{0,2}C .{-2,0}D .{-2,0,2}【答案】D【解析】M ={x |x 2+2x =0,x ∈R}={0,-2},N ={x |x 2-2x =0,x ∈R}={0,2},故M ∪N ={-2,0,2},故选D.(2)已知集合M ={x |-3<x ≤5},N ={x |x <-5或x >5},则M ∪N =( )A .{x |x <-5或x >-3}B .{x |-5<x <5}C .{x |-3<x <5}D .{x |x <-3或x >5} 【答案】A【解析】在数轴上表示集合M ,N ,如图所示,则M ∪N ={x |x <-5或x >-3}.【跟踪训练】设集合A ={-1,0,-2},B ={x |x 2-x -6=0},则A ∪B 等于( ) A.{-2} B.{-2,3}C.{-1,0,-2}D.{-1,0,-2,3}【答案】D【解析】因为A ={-1,0,-2},B={x |x 2-x -6=0}={-2,3}, 所以A ∪B ={-1,0,-2,3}.故选D.2.交集的运算求两个集合的交集的方法(1)对于元素个数有限的集合,逐个挑出两个集合的公共元素即可.(2)对于元素个数无限的集合,一般借助数轴求交集,两个集合的交集等于两个集合在数轴上的相应图形所覆盖的公共范围,要注意端点值的取舍.(1)若A ={x ∈N |1≤x ≤10},B ={x ∈R |x 2+x -6=0},则图中阴影部分表示的集合为( )A.{2}B.{3}C.{-3,2}D.{-2,3}【答案】A【解析】易知A ={1,2,3,4,5,6,7,8,9,10},B ={-3,2},图中阴影部分表示的集合为A ∩B ={2},故选A.(2)已知集合A ={x |x >-1},B ={x |x <2},则A ∩B =( )A .{x |x >-1}B .{x |x <2}C .{x |-1<x <2}D .∅【答案】C【解析】在数轴上标出集合A ,B ,如图所示,故A ∩B ={x |-1<x <2}.【跟踪训练】(1)设集合A ={1,2,6},B ={2,4},C ={1,2,3,4},则(A ∪B )∩C =( ) A.{2}B.{1,2,4}C.{1,2,4,6}D.{1,2,3,4,6}【答案】B【解析】由题意可得:A ∪B ={1,2,4,6},∴(A ∪B )∩C ={1,2,4}.故选B. (2)若集合A ={x |-2<x <1},B ={x |x <-1或x >3},则A ∩B =( ) A.{x |-2<x <-1} B.{x |-2<x <3} C.{x |-1<x <1} D.{x |1<x <3} 【答案】A【解析】∵A ={x |-2<x <1},B ={x |x <-1或x >3},∴A ∩B ={x |-2<x <-1},故选A. 3.集合交、并运算的性质及综合应用利用集合交集、并集的性质解题的依据及关注点 (1)依据:A ∩B =A ⇔A ⊆B ,A ∪B =A ⇔B ⊆A .(2)关注点:当集合A ⊆B 时,若集合A 不确定,运算时要考虑A =∅的情况,否则易漏解(易错题)已知集合A ={x |-3<x ≤4},集合B ={x |k +1≤x ≤2k -1},且A ∪B =A ,试求k 的取值范围.【解析】 (1)当B =∅,即k +1>2k -1时,k <2,满足A ∪B =A .(2)当B ≠∅时,要使A ∪B =A ,只需31,421,121,k k k k -<+⎧⎪≥-⎨⎪+≤+⎩解得2≤k ≤52综合(1)(2)可知k ≤52. 【名师点拨】因为∅是任何集合的子集,所以当作为子集的集合中含有字母时,要考虑该集合是否可以为∅。
2020-2021学年数学新教材人教A版必修第一册:5.2.3 同角三角函数的基本关系(2)
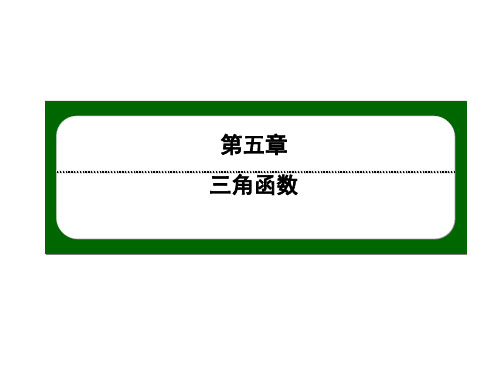
为( C )
A.-
3 2
B.±
3 2
C.-
5 2
D.±
5 2
解析:∵A为三角形的一个内角,且sinAcosA=-18,
∴A为钝角.∴cosA-sinA<0.
∴cosA-sinA=- cosA-sinA2
=- sin2A+cos2A-2sinAcosA=-
1+14=-
5 2.
8.已知θ是第三象限角,且sin4θ+cos4θ=
16 5
.
解析:tan2xsin2x=tan2x(1-cos2x)=tan2x-tan2xcos2x=tan2x- sin2x=156.
11.若0<α<π2,则 α
果是 2cos2 .
1-2sinα2cosα2+
1+2sinα2cosα2的化简结
解析:由0<α<2π,得0<α2<4π,
所以0<sinα2<cosα2.
故原式= sinα2-cosα22+ =cosα2-sinα2+sinα2+cosα2
sinα2+cosα22
=2cosα2.
三、解答题(共25分) 12.(12分)已知tanα=3,求下列各式的值: (1)34ssiinnαα+-5ccoossαα; (2)sin2α-4co2ss2inαα-co3ssαin-2αcos2α; (3)34sin2α+12cos2α.
-
sinα+cosα sin2α-cos2α
=
sin2α sinα-cosα
-
cos2αsinα+cosα sin2α-cos2α
=
sin2α sinα-cosα
-
cos2α
sinαco-s2cαosα=ssinin2αα--ccoossα2α=sinα+cosα=右边,∴原式成立.
专题04 充分条件与必要条件(练)(解析版).pdf

《2020-2021学年高一数学同步讲练测(新教材人教A 版必修第一册)》专题04充分条件与必要条件(练)1.a ,b 中至少有一个不为零的充要条件是( )A .ab =0B .ab>0C .a 2+b 2=0D .a 2+b 2>0【参考答案】D 【解析】,ab =0是a ,b 中至少有一个不为零的非充分非必要条件;A ab>0是a ,b 中至少有一个不为零的充分非必要条件;,B ,a 2+b 2=0是a ,b 中至少有一个不为零的非充分非必要条件;C ,a 2+b 2>0,则a ,b 不同时为零;a ,b 中至少有一个不为零,则a 2+b 2>0.所以a 2+b 2>0是a ,b 中至少有一个不D 为零的充要条件.故选:D2.a >b 的一个充分不必要条件是( )A .a 2>b 2B .|a |>|b |C .D .a -b >111a b <【参考答案】D 【解析】,,,则ABC 错误;22a b a b >⇒>/11b a a b <⇒/>||||a b a b>⇒>/a -b >1⇒a -b >0而a -b >0⇏a -b >1,则D正确;故选:D3.一元二次函数的图像的顶点在原点的必要不充分条件是( )2y ax bx c =++A .B .C .D .0,0b c ==0a b c ++=0b c +=0bc =【参考答案】D 【解析】若一元二次函数的图像的顶点在原点,则,且,所以顶点在2y ax bx c =++02b a -=0c =原点的充要条件是故A 是充要条件,B 、C 既不充分也不必要,D 是必要条件,非充分条件.0,0,b c ==故选:D.4.【黑龙江省海林市朝鲜族中学人教版高中数学同步练习】设集合,,则“”是“{}1,2M ={}2N a =1a =-”的( )N M ⊆A .充分不必要条件B .必要不充分条件.C .充分必要条件D .既不充分又不必要条件【参考答案】A 【解析】解:当时,,满足,故充分性成立;1a =-{}1N =N M ⊆当时,或,所以不一定满足,故必要性不成立.N M ⊆{}1N ={}2N =a 1a =-故选:A.5.【浙江省湖州市2019-2020学年高二上学期期中】已知,那么“”是“”的()a R ∈1a >21a >A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【参考答案】A 【解析】当时,成立,1a >21a >取,此时成立,但是不成立,2a =-21a >1a >“”是“”的充分不必要条件,1a >21a >故选:A.6.【必修第一册 逆袭之路】若,则“且”是“且”的( ),a b ∈R 1a >1b >1ab >2a b +≥A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件【参考答案】A 【解析】因为且,所以根据同向正数不等式相乘得,根据同向不等式相加得,即成1a >1b >1ab >2a b +>2a b +≥立,因此充分性成立;当时满足且,但不满足且,即必要性不成立;1,2a b ==1ab >2a b +≥1a >1b >从而“且”是“且”的充分不必要条件,1a >1b >1ab >2a b +≥故选:A7.【必修第一册 逆袭之路】设,则“”是“”的( )x ∈R 250x x -<|1|1x -<A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【参考答案】B 【解析】化简不等式,可知 推不出;05x <<11x -<由能推出,11x -<05x <<故“”是“”的必要不充分条件,250x x -<|1|1x -<故选B .8.若“”是“”的必要不充分条件,则实数的最大值为_______.21x >x m <m 【参考答案】1-【解析】由得,21x >-11x x <>或“”是“”的必要不充分条件,21x >x m <,(,)(,1)(1,)m ∴-∞⊆-∞-⋃+∞.1m ∴≤-故参考答案为.1-9.“方程没有实数根”的充要条件是________.220x x a --=【参考答案】1a <-【解析】解析因为方程没有实数根,所以有,解得,因此“方程没220x x a --=440a ∆=+<1a <-220x x a --=有实数根”的必要条件是.反之,若,则,方程无实根,从而充分性成立.故“方1a <-1a <-∆<0220x x a --=程没有实数根”的充要条件是“”.220x x a --=1a <-故参考答案为:1a <-10.已知a 、b 是实数,则“a >1,且b >1”是“a +b >2,且ab >1”的____条件.【参考答案】充分不必要【解析】解:a 、b 是实数,则“a >1,且b >1”⇒“a +b >2,且ab >1”正确,当a =10,b =0.2时,a +b >2,且ab >1,所以a >1,且b >1不成立,即前者是推出后者,后者推不出前者,所以a 、b 是实数,则“a >1,且b >1”是“a +b >2,且ab >1”的充分而不必要条件.故参考答案为:充分而不必要.11.设集合A ={x |x (x ﹣1)<0},B ={x |0<x <3},那么“m ∈A ”是“m ∈B ”的____条件(填“充分不必要”、“必要不充分”、“充要”或“既不充分又不必要”).【参考答案】充分不必要【解析】解:由于A ={x |0<x <1},则A ⊊B ,由m ∈B 不能推出m ∈A ,如x =2时,故必要性不成立.反之,根据A ⊊B ,“m ∈A ”⇒“m ∈B ”.所以“m ∈A ”是“m ∈B ”的充分不必要条件.故参考答案为:充分不必要12.“a >1且b >1”是“ab >1”成立的____条件.(填充分不必要,必要不充分,充要条件或既不充分也不必要.【参考答案】充分不必要【解析】解:若a >1且b >1时,ab >1成立.若a =﹣2,b =﹣2,满足ab >1,但a >1且b >1不成立,∴“a >1且b >1”是“ab >1”成立的充分不必要条件.故参考答案为:充分不必要.13.试判断“”是“”的充分条件还是必要条件?并给出证明.:1p x =32:10q x x x --+=【参考答案】充分条件,证明见解析【解析】是充分条件,但不是必要条件,证明如下由()()()()2322111110x x x x x x x x --+=---=-+=得或1x =1x =-或,或不能.:1:1p x q x =⇒=1x =-:1q x =1x =-:1p x ⇒=所以是充分条件,但不是必要条件.14.已知是实数,求证:成立的充分条件是,该条件是否为必要条件?试证,a b 44221a b b --=221a b -=明你的结论.【参考答案】必要条件,证明见解析.【解析】由,即44221a b b --=442210a b b ---=由()()()()244242222221111a b b a b a b a b -++=-+=++--则由()()222222442111021a b a b a b a b b -=⇒++--=⇒--=所以成立的充分条件是44221a b b --=221a b -=另一方面如果()()442222221110a b b a b a b --=⇒++--=因为,2210a b ++≠故,()()2222221101a b a b a b ++--=⇒-=所以成立的必要条件是.44221a b b --=221a b -=15.不等式x 2﹣3x +2>0的解集记为p ,关于x 的不等式x 2+(a ﹣1)x ﹣a >0的解集记为q ,若p 是q 的充分不必要条件,求实数a 的取值范围.【参考答案】﹣2<a ≤﹣1【解析】解:由不等式x 2﹣3x +2>0得,x >2或x <1;不等式x 2+(a ﹣1)x ﹣a >0等价为(x ﹣1)(x +a )>0,①当﹣a ≤1,即a ≥﹣1时,不等式的解是x >1或x <﹣a ,∵p 是q 的充分不必要条件,∴﹣a ≥1,即a =﹣1,②若﹣a >1,即a <﹣1时,不等式的解是x >﹣a 或x <1,∵p 是q 的充分不必要条件,∴﹣a <2,即﹣2<a <﹣1,综上﹣2<a ≤﹣1.1.【必修第一册(上) 重难点知识清单】已知a ,b ∈R,则“0≤a ≤1且0≤b ≤1”是“0≤ab ≤1”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【参考答案】A 【解析】若“0≤a ≤1且0≤b ≤1”,则“0≤ab ≤1”.当a =-1,b =-1时,满足0≤ab ≤1,但不满足0≤a ≤1且0≤b ≤1,∴“0≤a ≤1且0≤b ≤1”是“0≤ab ≤1”成立的充分不必要条件.故选A.2.【必修第一册(上) 重难点知识清单】“不等式在上恒成立”的充要条件是( )A .B .C .D .【参考答案】A 【解析】∵“不等式x 2﹣x +m >0在R 上恒成立”,∴△=(﹣1)2﹣4m <0,解得m ,又∵m ⇒△=1﹣4m <0,所以m是“不等式x 2﹣x +m >0在R 上恒成立”的充要条件,故选:A .3.【浙江省杭州二中检测】“”的一个充分但不必要的条件是( )260x x --<A .B .23x -<<03x <<C .D .32x -<<33x -<<【参考答案】B 【解析】由解得,260x x --<23x -<<要找“”的一个充分但不必要的条件,260x x --<即是找的一个子集即可,{}23x x -<<易得,B 选项满足题意.故选B4.【必修第一册 逆袭之路】设且,则是的( ),a b ∈R 0ab ≠1ab >1a b >A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要【参考答案】D 【解析】若“ab >1”当a =﹣2,b =﹣1时,不能得到“”,1a b >若“”,例如当a =1,b =﹣1时,不能得到“ab >1“,1a b >故“ab >1”是“”的既不充分也不必要条件,1a b >故选:D .5.【河南省6月联考】关于的不等式成立的一个充分不必要条件是,则的取x ()()30x a x -->11x -<<a 值范围是( )A .B .C .D .1a ≤-0a <2a ≥1a ≥【参考答案】D 【解析】由题可知是不等式的解集的一个真子集.()1,1-()()30x a x -->当时,不等式的解集为,此时 ;3a =()()30x a x -->{}3x x ≠()1,1-{}3x x ≠当时,不等式的解集为,3a >()()30x a x -->()(),3,a -∞⋃+∞,合乎题意;()1,1- (),3-∞当时,不等式的解集为,3a <()()30x a x -->()(),3,a -∞⋃+∞由题意可得,此时.()1,1-(),a -∞13a ≤<综上所述,.1a ≥故选:D.6.【河南省开封市2020届高三第三次模拟】设a ,b ∈R ,则“a >b ”是“a |a |>b |b |”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件【参考答案】C 【解析】由a >b ,①当a >b ≥0时,不等式a |a |>b |b |等价为a •a >b •b ,此时成立.②当0>a >b 时,不等式a |a |>b |b |等价为﹣a •a >﹣b •b ,即a 2<b 2,此时成立.③当a ≥0>b 时,不等式a |a |>b |b |等价为a •a >﹣b •b ,即a 2>﹣b 2,此时成立,即充分性成立;由a |a |>b |b |,①当a >0,b >0时,a |a |>b |b |去掉绝对值得,(a ﹣b )(a +b )>0,因为a +b >0,所以a ﹣b >0,即a >b .②当a >0,b <0时,a >b .③当a <0,b <0时,a |a |>b |b |去掉绝对值得,(a ﹣b )(a +b )<0,因为a +b <0,所以a ﹣b >0,即a >b .即必要性成立,综上可得“a >b ”是“a |a |>b |b |”的充要条件,故选:C .7.【必修第一册 过关斩将】设,则“”是“”的( )R x ∈11||22x -<31x <A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【参考答案】A 【解析】绝对值不等式,1122x -<⇔111222x -<-<⇔01x <<由.31x <⇔1x <据此可知是的充分而不必要条件.1122x -<31x <本题选择A 选项.8.【必修第一册 过关斩将】设集合,,那么“或”是“{|2}M x x =>{|3}P x x =<x M ∈x P ∈x P M ∈⋂”的________条件.(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)【参考答案】必要不充分【解析】解:条件是或等价于;结论是.:p x M ∈x P ∈x P M ∈⋃:q x P M ∈⋂依题意得是的真子集,所以“”能推出“”,反之不成立,P M ⋂P M ⋃x P M ∈⋂x P M ∈⋃即结论条件p ,必要性成立;条件结论q ,充分性不成立.q ⇒p ⇒综上,“或”是“”的必要不充分条件.x M ∈x P ∈x P M ∈⋂故参考答案为:必要不充分9.【必修第一册 逆袭之路】设,则“”是“”的______条件选填“充分不必要”,“必要不充a R ∈1a >1a >.(分”,“充要”,“既不充分也不必要”之一)【参考答案】充分不必要条件【解析】解:解绝对值不等式“”,得或,1a >1a >1a <-又“”是“或”的充分不必要条件,1a >1a >1a <-即“”是“”的充分不必要条件,1a >1a >故参考答案为充分不必要条件.10.【必修第一册 过关斩将】已知,若是p 的一个必要条件,则使:13p x -<<1(0)a x a a -<-<>恒成立的实数b 的取值范围是________.a b >【参考答案】{|2}b b <【解析】∵,111a x a a x a -<-<⇔-<<+∴,所以解得{|13}{|11}x x x a x a -<<⊆-<<+11,13,a a -≤-⎧⎨+≥⎩2a ≥又使恒成立,因此,故实数b 的取值范围是.a b >2b <{|2}b b <故参考答案为:.{|2}b b <11.【必修第一册 过关斩将】若M 是N 的充分不必要条件,N 是P 的充要条件,Q 是P 的必要不充分条件,则M 是Q 的________条件.【参考答案】充分不必要【解析】命题的充分必要性具有传递性.根据题意得,但,,且,因此M N P Q ⇒⇔⇒Q P ⇒N P ⇔N M ⇒,但,故M 是Q 的充分不必要条件.M Q ⇒Q M ⇒故参考答案为:充分不必要12.【必修第一册 过关斩将】若实数a ,b 满足,,且,则称a 与b 互补记0a ≥0b ≥0ab =,那么“”是“a 与b 互补”的________条件.(填“充分不必要”“必要不充(,)a b a b ϕ=--(,)0a b ϕ=分”“充要”或“既不充分也不必要”)【参考答案】充要【解析】解析若,,平方得,当时,所以;(,)0a b ϕ=a b =+0ab =0a =b =0b ≥当时,所以,故a 与b 互补;0b =a =0a ≥若a 与b 互补,易得.(,)0a b ϕ=故“”是“a 与b 互补”的充要条件(,)0a b ϕ=故参考答案为:充要条件13.【必修第一册(上) 重难点知识清单】已知,.{}2320P x x x =-+≤{}11S x m x m =-≤≤+(1)是否存在实数,使是的充要条件?若存在,求出的取值范围,若不存在,请说明理由;m x P ∈x S ∈m (2)是否存在实数,使是的必要条件?若存在,求出的取值范围,若不存在,请说明理由.m x P ∈x S ∈m 【参考答案】(1)不存在实数,使是的充要条件m x P ∈x S ∈(2)当实数时,是的必要条件0m ≤x P ∈x S ∈【解析】(1).{}{}232012P x x x x x =-+≤=≤≤要使是的充要条件,则,即 此方程组无解,x P ∈x S ∈P S =11,12,m m -=⎧⎨+=⎩则不存在实数,使是的充要条件;m x P ∈x S ∈(2)要使是的必要条件,则 ,x P ∈x S ∈S ⊆P 当时,,解得;S =∅11m m ->+0m <当时,,解得S ≠∅11m m -≤+0m ≥要使 ,则有,解得,所以,S ⊆P 11,1+2m m -≥⎧⎨≤⎩0m ≤0m =综上可得,当实数时,是的必要条件.0m ≤x P ∈x S ∈14.已知两个关于的一元二次方程和,求两方程的根都是x 2440mx x -+=2244450x mx m m -+--=整数的充要条件.【参考答案】1m =【解析】∵是一元二次方程,∴.2440mx x -+=0m ≠又另一方程为,且两方程都要有实根,2244450x mx m m -+--=∴()()212224160,1644450,m m m m ⎧∆=--≥⎪⎨∆=---≥⎪⎩解得.5,14m ⎡⎤∈-⎢⎥⎣⎦∵两方程的根都是整数,∴其根的和与积也为整数,即24,4,445,Z m m Z m m Z ⎧∈⎪⎪∈⎨⎪--∈⎪⎩∴为的约数.m 4又∵,5,14m ⎡⎤∈-⎢⎥⎣⎦∴或.1m =-1当时,第一个方程可化为,其根不是整数;1m =-当时,两方程的根均为整数,∴两方程的根均为整数的充要条件是.1m =1m =15.设集合,,若“”是“”的充分不必要条件,试求满足条{}2|320A x x x =-+={}|1B x ax ==x B ∈x A ∈件的实数组成的集合.a 【参考答案】10,1,2⎧⎫⎨⎬⎩⎭【解析】∵,{}{}2|3201,2A x x x =-+==由于“”是“”的充分不必要条件.∴ .x B ∈x A ∈B A 当时,得;B =∅0a =当时,由题意得或.B ≠∅{}1B ={}2B =当时,得;当时,得.{}1B =1a ={}2B =12a =综上所述,实数组成的集合是.a 10,1,2⎧⎫⎨⎬⎩⎭。
2020-2021学年第一学期10月份第一次月考试卷答案

2020-2021学年第一学期10月份第一次月考试卷高一数学试卷参考答案2020.10考试范围:人教A 版必修第一册第一、二章考试时间:120分钟一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.D 解析:由(6)(1)0x x -+<,得16x -<<,从而有{}16B x x =-<<,所以{}14A B x x ⋂=-<<,故选:D .2.B 解析:集合{}0,1,2,3,4,5A =,{{}2B x y x x ===≥,所以{}U 2B x x =<ð.图中阴影部分表示的集合为(){}U 0,1A B ⋂=ð.故选:B 3.A 解析:因为甲是乙的充要条件,所以乙⇔甲;又因为丙是乙的充分条件,但不是乙的必要条件,所以丙⇒乙,但乙⇒丙.综上,丙⇒甲,但甲⇒丙,即丙是甲的充分条件,但不是甲的必要条件.故选A .4.A 解析:因为全称命题的否定是特称命题,所以命题“[]1,3x ∀∈-,2320x x -+≤”的否定为“[]01,3x ∃∈-,200320x x -+>”.故选A .5.B 解析:对于A ,若22ac bc >,则0c ≠,2222ac bc c c >,即a b >,故正确;对于B ,根据不等式的性质,若0a b <<,不妨取2,1a b =-=-,则22a b >,故题中结论错误;对于C ,若0a b >>,则a b ab ab>,即11a b <,故正确;对于D ,若0a b <<,0c d >>,则0a b ->->,故ac bd ->-,ac bd <,故正确.故选B .6.B 解析:0a > ,0b >,且21a b +=,120b a ∴=->,解得102a <<.∴12122(1)1212122(1)(2321111a a a a a a a a b a a a a a a a a ---+=+=+-=+-+-=++-+----11+=+ ,当且仅当1a =,3b =-时取等号.∴12aa a b++有最小值1+.故选:B .7.C 解析:解:不等式210x mx -+<的解集为空集,所以0∆≤,即240m -≤,解得22m -≤≤.故选:C .8.B 解析:依题意2() 4.914.717h t t t =-++234.928.0252t ⎛⎫=--+ ⎪⎝⎭,故当32t =时,()max 28.02528m h t =≈.故选B .二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.ABD 解析:由于M N ⊆,即M 是N 的子集,故M N M ⋂=,M N N ⋃=,从而M M N ⊆⋂(),()M N N ⋃⊆.故选ABD .10.AC 解析:对于选项A ,由327x =-得293x x =-⇒=,但是3x =适合29x =,推出32727x =≠-,故A 正确;对于选项B ,在ABC ∆中,222AB AC BC ABC +=⇒∆为直角三角形,但ABC ∆为直角三角形222AB AC BC ⇒+=或222AB BC AC +=或2221BC AC AB +=,故B 错误;对于选项C ,由220,a b a b +≠⇒不全为0,反之,由a ,b 不全为2200a b ⇒+≠,故D 正确;对于选项D ,结论“四边形是菱形”推不出条件“四边形是正方形”,因此必要条件不成立.故选:AC .11.AB 解析:对A ,2211224a b ab +⎛⎫⎛⎫≤== ⎪ ⎪⎝⎭⎝⎭,当且仅当12a b ==时取等号.故A 正确.对B ,22a b a b a b =+++++=≤,当且仅当12a b ==时取等号.故B 正确.对C ,()1111224b a a b a b a b a b ⎛⎫+=++=++≥+⎝= ⎪⎭.当且仅当12a b ==时取等号.所以11a b+有最小值4.故C 错误.对D ,()222121a b a ab b +=⇒++=≤2a +()222a b b ++,即2212a b +≥,故22a b +有最小值12.故D 错误.故选:AB 12.ABD 解析:由23344x x b -+≤得23121640x x b -+-≤,又1b <,所以()4810b ∆=-<,从而不等式23344a x x b ≤-+≤的解集为∅,故A 正确.当1a =时,不等式23344a x x ≤-+就是2440x x -+≥,解集为R ,当4b =时,不等式23344x x b -+≤就是240x x -≤,解集为{}04x x ≤≤,故B 正确.由23344a x x b ≤-+≤的解集为{}x a x b ≤≤,知min a y ≤,即1a ≤,因此当x a =,x b =时函数值都是b .由当x b=时函数值是b ,得23344b b b -+=,解得43b =或4b =.当43b =时,由2343443a a b -+==,解得43a =或83a =,不满足1a ≤,不符合题意,故C 错误.当4b =时,由233444a ab -+==,解得0a =或4a =,0a =满足1a ≤,所以0a =,此时404b a -=-=,故D 正确.故选:A B D三、填空题:本题共4小题,每小题5分,共20分.13.4解析:由题得满足关系式{}{}2,31,2,3,4A ⊆⊆的集合A 有:{2,3},{1,2,3},{2,3,4},{1,2,3,4}.所以集合A 的个数为4.故答案为414.充分非必要解析:令命题:2p x y +≠-,命题:q x ,y 不都为1-;:2p x y ⌝+=-,:q x ⌝,y 都是1-,则当x ,y 都是1-时,满足2x y +=-,反之当1x =,3y =-时,满足2x y +=-,但x ,y 都是1-不成立,即q ⌝是p ⌝充分非必要条件,则根据逆否命题的等价性知p 是q 的充分非必要条件,故答案为:充分非必要.15.16解析:0a >,1b >且210a b b +=⇒->且()11a b +-=∴()()91919111010616111b a a b a b a b a b -⎛⎫+=++-=++≥+=⎡⎤ ⎪⎣⎦---⎝⎭当且仅当()911b a a a -=-取等,又2a b +=,即34a =,54b =时取等号,故所求最小值16.故答案为:1616.0解析:由根与系数的关系可知()11{0,01m m m b b m m a++=∴==+=四、解答题:本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.17.解:(1)若1A ∈,则210,1m m -+=∴=1a ∉ ,∴实数m 的取值范围为:{}1m m ∈≠R ……………4分(2)选①:若A =∅,则关于x 的方程2210mx x -+=没有实数解,所以0m ≠,且440m ∆=-<,所以1m >……………10分选②:若A 恰有两个子集,则A 为单元素集,所以关于x 的方程2210mx x -+=恰有一个实数解,讨论:①当0m =时,12x =,满足题意;②当0m ≠时,Δ440m =-=,所以1m =.综上所述,m 的集合为{}0,1……………10分选③:若1,22A ⎛⎫⋂≠∅ ⎪⎝⎭,则关于x 的方程221mx x =-在区间1,22⎛⎫ ⎪⎝⎭内有解,等价于当1,22x ⎛⎫∈ ⎪⎝⎭时,求2221111m x x x ⎛⎫=-=-- ⎪⎝⎭的值域,所以](0,1m ∈……………10分18.解:(1)122x x +>-等价于()()12220x x x ⎧+->⎨-≠⎩,解得25x <<:25p x ∴<<,由p ⌝为真知:2x ≤或5x ≥……………6分(2)q ⌝是p ⌝的充分不必要条件,则q 是p 的必要不充分条件.故2:50q x ax -+>对于任意25x <<恒成立,故5a x x<+,由基本不等式可知5x x+≥x =a <……12分19.解:(1)因为0x >,0y >,所以x y +≥,由2x y xy +=,得2xy ≥1≥,1xy ≥,当且仅当1x y ==时,等号成立……………6分(2)由2x y xy +=得112x y+=.2111223222x x x y y y x x x x y x x ⎛⎫+=++=++≥+≥ ⎪⎝⎭.当且仅当2x y x=,且0x <时,两个等号同时成立.即当且仅当12x =-且14y =,2y x x +的最小值是32……………12分20.(1)由题意可知,月处理成本y (元)与月处理量x (吨)之间的函数关系可近似地表示为()21200800004006002y x x x =-+≤≤,所以,每吨二氧化碳的平均处理成本为1800002002y x x x =+-,由基本不等式可得200200y x ≥=(元),当且仅当1800002x x=时,即当400x =时,等号成立,因此,该单位每月处理量为400吨时,才能使每吨的平均处理成本最低……………6分(2)()()222111100200800003008000030035000222f x x x x x x x ⎛⎫=--+=-+-=--- ⎪⎝⎭400600x ≤≤ ,函数()f x 在区间[]400,600上单调递减,当400x =时,函数()f x 取得最大值,即()()max 40040000f x f ==-.所以,该单位每月不能获利,国家至少需要补贴40000元才能使该单位不亏损……12分21.解:(1)()()2210⎡⎤-+-=---≤⎣⎦x x a a x a x a ,当1a a <-(12a <)时,不等式解集为{|1}x a x a ≤≤-;当1a a >-(12a >)时,不等式解集为{|1}x a x a -≤≤;当1a a =-(12a =)时,不等式解集为1{|}2x x =.所以,当1 2a <时,不等式解集为{|1}A x a x a =≤≤-;当1 2a =时,不等式解集为12A ⎧⎫=⎨⎬⎩⎭;当1 2a >时,不等式解集为{|1}A x a x a =-≤≤……………8分(2)由上(1),1 2a >时,() {|1}1,1A x a x a =-≤≤⊆-,所以111a a ->-⎧⎨<⎩,得1a <,所以,实数a 的取值范围112a <<……………12分22.解:(1)函数24y x mx =++的图象开口向上,对称轴为2m x =-,在区间[]1,2上的最大值,分两种情况:①322m -<(3m >-)时,根据图象知,当2x =时,函数取得最大值82max y m =+;②322m -≥(3m ≤-)时,当1x =时,函数取得最大值5max y m =+.所以,当3m >-时,82max y m =+;当3m ≤-时,5max y m =+……………7分(2)[] 1,20x y ∈<,恒成立,只需在区间[]1,2上的最大值0max y <即可,所以(1)0(2)0f f <⎧⎨<⎩,得45m m <-⎧⎨<-⎩,所以实数m 的取值范围是5m <-……………12分。
2020-2021学年高一数学(人教A版2019必修第一册)集合的基本运算重难点突破(解析版)
突破1.3 集合的基本运算重难点突破一、考情分析二、经验分享【知识点1、并集】 1.并集的概念一般地,由___________属于集合A 或属于集合B 的元素所组成的集合,称为集合A 与B 的并集,记作:___________(读作“A 并B ”),即{},AB x x A x B =∈∈或.用Venn 图表示如图所示:(1) (2) (3) 由上述图形可知,无论集合A ,B 是何种关系,AB 恒有意义,图中阴影部分表示并集.注意:并集概念中的“或”指的是只需满足其中一个条件即可,这与生活中的“或”字含义不同.生活中的“或”字是或此或彼,必居其一,而并集中的“或”字可以是兼有的.2.并集的性质对于任意两个集合A ,B ,根据并集的概念可得: (1)()A A B ⊆,()B A B ⊆; (2)A A A =;(3)AA ∅=; (4)AB BA =.【知识点2、交集】 1.交集的概念一般地,由___________的所有元素组成的集合,称为A 与B 的交集,记作:___________(读作“A 交B ”),即{|},AB x x A x B =∈∈且.用Venn 图表示如图所示:(1)A 与B 相交(有公共元素) (2)A B ⊂≠,则AB A = (3)A 与B 相离(A B =∅)注意:(1)交集概念中的“且”即“同时”的意思,两个集合的交集中的元素必须同时是两个集合的元素.(2)定义中的“所有”是指集合A 和集合B 中全部的公共元素,不能是一部分公共元素. 2.交集的性质 (1)(),()A B A A B B ⊆⊆; (2)A A A =; (3)A∅=∅; (4)A B BA =.【知识点3、全集与补集】 1.全集的概念一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集,通常记作U ,是相对于所研究问题而言的一个相对概念.学+科网说明:“全集”是一个相对的概念,并不是固定不变的,它是依据具体的问题来加以选择的.例如:我们常把实数集R 看作全集,而当我们在整数范围内研究问题时,就把整数集Z 看作全集. 2.补集的概念对于一个集合A ,由全集U 中___________集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集,简称为集合A 的补集,记作UA ,即{},U A x x U x A =∈∉且.用Venn 图表示如图所示:说明:(1)补集既是集合之间的一种关系,同时也是集合之间的一种运算.求集合A 的补集的前提是A 是 全集U 的子集,随着所选全集的不同,得到的补集也是不同的,因此,它们是互相依存、不可分割的两个 概念.(2)若x U ∈,则x A ∈或Ux A ∈,二者必居其一.3.全集与补集的性质设全集为U ,集合A 是全集U 的一个子集,根据补集的定义可得: (1)U U =∅; (2)UU ∅=; (3)()UUA A =;(4)()UAA U =; (5)()UAA =∅.三、题型分析重难点1 并集及其运算例1.(1)已知集合A ={1,2,3},B ={x |(x +1)(x -2)<0,x ∈Z },则A ∪B =( ) A .{1} B .{1,2} C .{0,1,2,3} D .{-1,0,1,2,3} 【答案】C【解析】因为B ={x |(x +1)(x -2)<0,x ∈Z }={x |-1<x <2,x ∈Z }={0,1},A ={1,2,3},所以A ∪B ={0,1,2,3}.故选C.(2)已知{}A 3,4=,B {1,=3,5},则A B (⋃= ) A. {}3 B. {1,4,5}C. {1,2,3,4,5}D. {1,3,4,5}【答案】D 【解析】,3,,3,4,,故选D .【变式训练1】.(多选题)若集合,,且,则m 的值可能为A. B. 0 C.D. 1【答案】ABD 【解析】集合,当时,当时,因为,所以,所以或,即或或0.故选ABD .【变式训练2】.(多选题)已知2A {0}x x ax b =|2-+=,2B {(2)50}x x a x b =|6++++=,且1A B {}2=,则A B 中的元素是( )A .-4B . 1C .D .【答案】ABD 【解析】由已知得:①;②则1{4,}2A =-,11{,}32B =,11{4,,}32AB =-,故选ABD.【变式训练3】.(2020·黑龙江省大庆中学高一期末)已知集合{1,2,3}A =,{|(1)(2)0,}B x x x x Z =+-<∈,则A B ⋃=( )A .{1}B .{12},C .{0123},,,D .{10123}-,,,, 【答案】C【解析】集合{}{|12,}0,1B x x x Z =-<<∈=,而{}1,2,3A =,所以{}0,1,2,3A B ⋃=,故选C. 【变式训练4】.(2020届山东省泰安市肥城市一模)已知集合A ={x |﹣1<x <1},B ={x |0<x <2},则A ∪B =( ) A .(﹣1,2) B .(﹣1,0)C .(0,1)D .(1,2)【答案】A【解析】由题意得{}()121,2A B x x ⋃=-<<=-.故选:A.【变式训练5】.(2020徐州期中模拟)已知集合{}2|20A x x x =--≤,{|21}B x x =-<≤,则A B =( )A .{|12}x x -B .{|22}x x -<C .{|21}x x -<D .{|22}x x -≤≤ 【答案】B【解析】}{|12},{|21A B x x x x =-≤≤=-<≤,{|22}A B x x ⋃=-<≤.故选:B. 重难点2 交集及其运算例2.(1).(2020·济南市历城第二中学高一期末)设集合A {}3,5,6,8=,集合B {}4,5,7,8=,则A B 等于( ) A .{}5,8 B .{}3,,6C .{}4,7D .{}3,5,6,8【答案】A【解析】集合A {}3,5,6,8=,集合B {}4,5,7,8=,又集合A 与集合B 中的公共元素为5,8,{}5,8A B ∴⋂=,故选A.(2).设集合{}1,2,4A =,{}1,2,3B = ,则A. {}1,2B. {}1,2,4C. {}2,3,4D. {}1,2,3,4【答案】A 【解析】集合{}1,2,4A =,集合{}1,2,3B =,∴集合A 与集合B 的共同元素为1和2,所以由集合交运算定义知,.故选: A【变式训练1】.集合A ={x |x 2–4≤0},B ={x |2x +a ≤0},且A ∩B ={x |–2≤x ≤1},则a =( ) A .–4 B .–2 C .2 D .4【答案】B【解析】求解二次不等式240x -≤可得{}2|2A x x -=≤≤,求解一次不等式20x a +≤可得|2a B x x ⎧⎫=≤-⎨⎬⎩⎭.由于{}|21A B x x ⋂=-≤≤,故12a -=,解得2a =-.故选B .【变式训练2】.(2020届山东省菏泽一中高三2月月考)已知集合(1,3]A =-,201x B xx ⎧⎫+=≤⎨⎬-⎩⎭,则A B =( )A .[2,1)-B .(]1,1-C .(1,1)-D .[2,3]-【答案】C 【解析】201x B xx ⎧⎫+=≤⎨⎬-⎩⎭,解201x x +≤-,得21x ,所以[)2,1B =-因为(]1,3A =-,所以()1,1A B ⋂=-,故选:C.【变式训练3】.(2019启东市期末)(多选题)已知全集U R =,集合A ,B 满足A B ,则下列选项正确的有( ) A .AB B =B .A B B =C .()U A B =∅ D .()U AB =∅【答案】BD . 【解析】AB ,AB A ∴=,AB B =,()U C A B =≠∅,()U AC B =∅,故选:BD .【变式训练4】.((2020·广东省高三月考(理))(多选题)对任意A ,B ⊆R ,记A ⊕B ={x |x ∈A ∪B ,x ∉A ∩B },并称A ⊕B 为集合A ,B 的对称差.例如,若A ={1,2,3},B ={2,3,4},则A ⊕B ={1,4},下列命题中,为真命题的是( )A .若A ,B ⊆R 且A ⊕B =B ,则A =∅ B .若A ,B ⊆R 且A ⊕B =∅,则A =BC .若A ,B ⊆R 且A ⊕B ⊆A ,则A ⊆BD .存在A ,B ⊆R ,使得A ⊕B =A R⊕B RE.存在A ,B ⊆R ,使得A B ⊕B A ≠⊕ 【答案】ABD【解析】根据定义[()][()]R R A B A B A B ⊕=,A.若A B B ⊕=,则RA B B =,R A B ⋂=∅,RA B B =RB A ⇒⊆,R A B ⋂=∅A B ⇒⊆,∴A =∅,A 正确; B.若A B ⊕=∅,则R AB =∅,R A B ⋂=∅,A B A B ==,B 正确; C. 若A B A ⊕⊆,则RA B =∅,RAB A ⊆,则B A ⊆,C 错;D.A B =时,A B ⊕=∅,()()R R A B A B ⊕=∅=⊕,D 正确;E.由定义,[()][()]R R A B A B A B ⊕=B A =⊕,E 错.故选:ABD .重难点3 全集与补集及其运算例3.(1)(2020·湖南省长郡中学高一期末)已知集合U ={1,3,4,5,7,9},A ={1,4,5},则∁U A =( ) A .{3,9} B .{7,9} C .{5,7,9} D .{3,7,9}【答案】D【解析】因为集合U ={1,3,4,5,7,9},A ={1,4,5},所以{3,7,9}UA =.故选:D .(2).(多选题)已知集合{}2|20A x x x =∈--≥Z ,则中的元素是( )A .0B .2C .1D .-2【答案】AC【解析】由集合{}2|20A x x x =∈--≥Z ,解得:{}|21A x x x =∈≥≤-Z 或,}{z 0,1C A =,故答案选AC.【变式训练1】.(2020·浙江省学军中学高一期中)设集合{}2S x x =>-,{}41T x x =-≤≤,则()RS T =________.【答案】{}42x x -≤≤-【解析】因为集合{}2S x x =>-,所以{}2RS x x =≤-,因为集合{}41T x x =-≤≤,所以(){}42RS T x x ⋂=-≤≤-故答案为:{}42x x -≤≤-【变式训练2】.(2019·广东省增城中学高一期中)设全集U =R ,集合{}13A x x =-≤<,{}242B x x x =-≥-.(1)求()UA B ;(2)若集合{}0C x x a =->,满足C C =B ∪,求实数a 的取值范围. 【答案】(1){2x x <或}3x ≥;(2)(),2-∞【解析】(1)解不等式242x x -≥-可得:2x ≥,{}2B x x ∴=≥又集合{}13A x x =-≤<, 故{}23A B x x ⋂=≤< 又U =R 从而(){|2U C A B x x ⋂=<或3}x ≥ (2)易知集合{}{}0C x x a x x a =->=> 由C C =B ∪可得:B C ⊆ 故有2a < 即所求实数a 的取值范围是(),2-∞【变式训练3】.(江苏如皋中学期中)设全集I R =,已知集合2{|690}M x x x =++≤,2{|60}N x x x =+-=.(1)求()I C M N ;(2)记集合()I A C M N =,已知集合{|15,}B x a x a a R =-≤≤-∈,若BA A =,求实数a 的取值范围.【解析】:(1) 因为{}{}26903M x x x =++≤=-,{}{}2603,2N x x x =+-==-,所以{},3M x x R x =∈≠-且,从而{}()2M N =.(2){}()2A M N ==.由B A A =知B A ⊆,所以B =∅或{}2B =.若B =∅,则15a a ->-,解得3a >;若{}2B =,则1252a a -=⎧⎨-=⎩,解得3a =综上所述,所求实数a 的取值范围是[3,)+∞. 重难点4 交集、并集与补集混合运算例4.(1)已知全集{}1,0,1,2,3U =-,集合{}0,1,2A =,{}1,0,1B =-,则 =( )A .{}1-B .{}0,1C .{}1,2,3-D .{}1,0,1,3- 【答案】A 【解析】∵,∴.故选A.(2)设集合{}2S x x =>-,{}41T x x =-≤≤,则________.【答案】{}42x x -≤≤-【解析】因为集合{}2S x x =>-,所以{}2RS x x =≤-,因为集合{}41T x x =-≤≤,所以(){}42RS T x x ⋂=-≤≤-故答案为:{}42x x -≤≤-【变式训练1】.设集合2{|40,}A x x x x R =+=∈,22{|2(1)10,}B x x a x a x R =+++-=∈. (1)若A B B ⋃=,求实数a 的值; (2)若AB B =,求实数a 的范围.【解析】(1)∵A B B ⋃=,∴A ⊆B ,又B 中最多有两个元素,∴A=B ,∴x=0,﹣4是方程x 2+2(a +1)x+a 2﹣1=0的两个根,故a =1; (2)∵A={x |x 2+4x =0,x ∈R}∴A={0,﹣4}, ∵B={x |x 2+2(a +1)x+a 2﹣1=0},且B ⊆A .故①B=时,△=4(a +1)2﹣4(a 2﹣1)<0,即a <﹣1,满足B ⊆A ; ②B≠时,当a =﹣1,此时B={0},满足B ⊆A ;当a >﹣1时,x =0,﹣4是方程x 2+2(a+1)x+a 2﹣1=0的两个根, 故a =1;综上所述a =1或a ≤﹣1.【变式训练2】.已知全集U =R ,集合A ={x |x 2-x -6<0},集合B ={x |x 2+2x -8>0},集合C ={x |x 2-4ax +3a 2<0}.(1)试求实数a 的取值范围,使C ⊇(A ∩B ); (2)试求实数a 的取值范围,使C ⊇(∁U A )∩(∁U B ).【解析】 U =R ,A =(-2,3),B =(-∞,-4)∪(2,+∞),故A ∩B =(2,3),∁U A = (-∞,-2]∪[3,+∞),∁U B =[-4,2],(∁U A )∩(∁U B )=[-4,-2]. ∵x 2-4ax +3a 2<0,即(x -3a )(x -a )<0,∴当a <0时,C =(3a ,a );当a =0时,C =∅;当a >0时,C =(a ,3a ).(1)要使C ⊇(A ∩B ),结合数轴知0a 23a 3a ⎧⎪⎨⎪⎩>,≤,≥,解得1≤a ≤2.(2)类似地,要使C ⊇(∁U A )∩(∁U B ),必有a 03a -4a -2⎧⎪⎨⎪⎩<,≤,≥,解得-2≤a ≤-43.四、迁移应用1、(2020·浙江省学军中学高一期末)设全集为R ,集合A ={x |0<x <2},B ={x |x ≥1},则A ∩B =( ) A .{x |1≤x <2} B .{x |0<x <2} C .{x |0<x ≤1} D .{x |0<x <1}【答案】A【解析】由集合{}|02A x x =<<,{}|1B x x =≥,所以{}|12A B x x =≤<.故选:A.2、(2020届江苏昆山调研)已知集合{}1,2,3,4A =,{}2,B y y x x A ==-∈,则AB =______.【答案】{}1,2【解析】由题得{}1,0,1,2B =-,所以{1,2}AB =.故答案为:{}1,2.3、(2020届江苏四校期中联考)已知R 为实数集,集合{}1,0,1A =-,集合{}0B x x =≤,则RAB =______.【答案】{}1 【解析】{}0B x x =≤,{}0R B x x ∴=>,因此,{}1RAB =.故答案为:{}1.4、(2020届江苏盐城中学高三月考)设集合{}1,A x =,{}2,3,4B =,若{}4A B ⋂=,则x =______ . 【答案】4【解析】由题意,集合{}1,A x =,{}2,3,4B =,因为{}4A B ⋂=,所以4A ∈,故4x =.故答案为4. 5. 设全集为R ,}{37A x x =≤<,}{510B x x =<<.求()R C A B ⋃. 【解析】因为}{37A x x =≤<,所以由补集定义知,}{73R C A x x x =≥<或, 因为}{510B x x =<<, 所以作图如下:由图可知,()}{35R C A B x x x ⋃=<>或.故答案为:{|3x x <或}5x > 6. 设全集U =R ,集合{}13A x x =-≤<,{}242B x x x =-≥-. (1)求;(2)若集合{}0C x x a =->,满足C C =B ∪,求实数a取值范围.【解析】(1)解不等式242x x -≥-可得:2x ≥,{}2B x x ∴=≥ 又集合{}13A x x =-≤<, 故{}23A B x x ⋂=≤< 又U =R 从而(){|2U C A B x x ⋂=<或3}x ≥韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档 1 (2)易知集合{}{}0C x x a x x a =->=> ,由C C =B ∪可得:B C ⊆故有2a < 即所求实数a 的取值范围是(),2-∞7. 已知全集U =R ,集合{}2|450A x x x =--≤,{}|24B x x =≤≤. (1)求()U A C B ⋂;(2)若集合{}|4,0C x a x a a =≤≤>,满足,,求实数a 的取值范围.【解析】(1)由题{}|15A x x =-≤≤,{|2U C B x x =<或}4x >,,(){|12U A C B x x ⋂=-≤<或}45x <≤;(2)由C A A =得C A ⊆,则145a a ≥-⎧⎨≤⎩,解得514a -≤≤, 由C B B =得B C ⊆,则244a a ≤⎧⎨≥⎩,解得12a ≤≤, ∴实数a 的取值范围为5|14a a ⎧⎫≤≤⎨⎬⎩⎭.。
2020-2021学年新教材人教A版高一数学必修第一册 第五章 三角函数 单元测试

2020-2021学年新教材高一数学人教A 版必修第一册第五章 三角函数 单元测试题一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知扇形的圆心角为2 rad ,弧长为4 cm ,则这个扇形的面积是( )A .4 cm 2B .2 cm 2C .4π cm 2D .1 cm 22.已知a =tan 5π12,b =cos 3π5,c =cos ⎝ ⎛⎭⎪⎫-17π4,则( )A .b >a >cB .a >b >cC .b >c >aD .a >c >b3.要得到函数y =cos ⎝⎛⎭⎪⎫2x +π3的图象,只需将函数y =cos 2x 的图象( )A .向左平移π3个单位长度B .向左平移π6个单位长度C .向右平移π6个单位长度D .向右平移π3个单位长度4.已知sin ⎝ ⎛⎭⎪⎫π3-x =35,则cos ⎝ ⎛⎭⎪⎫x +7π6等于( ) A.35 B.45C .-35D .-455.函数f (x )=x sin x 的图象大致是( )6.化简⎝ ⎛⎭⎪⎫1sin α+1tan α(1-cos α)的结果是( )A .sin αB .cos αC .1+sin αD .1+cos α7.如图所示,某摩天轮设施,其旋转半径为50米,最高点距离地面110米,开启后按逆时针方向匀速旋转,转一周大约21分钟.某人在最低点的位置坐上摩天轮的座舱,并开始计时,则第7分钟时他距离地面的高度大约为( )A .75米B .85米C .(50+253)米D .(60+253)米8.已知函数f (x )=sin x -sin 3x ,x ∈[0,2π],则函数f (x )的所有零点之和等于( )A .4πB .5πC .6πD .7π二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)9.下列函数中,最小正周期为π,且为偶函数的有( )A .y =tan ⎝ ⎛⎭⎪⎫x +π3B .y =sin ⎝ ⎛⎭⎪⎫2x -π2C .y =sin|2x |D .y =|sin x |10.已知sin θ=-23,且cos θ>0,则( )A .tan θ<0B .tan 2θ>49C .sin 2θ>cos 2θD .sin 2θ>011.已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π4,则下列结论正确的是( )A .函数f (x )的最小正周期为πB .函数f (x )在[0,π]上有三个零点C .当x =π8时,函数f (x )取得最大值D .为了得到函数f (x )的图象,只要把函数y =2sin ⎝ ⎛⎭⎪⎫x +π4图象上所有点的横坐标变为原来的2倍(纵坐标不变)12.若函数f (x )=1+4sin x -t 在区间⎝ ⎛⎭⎪⎫π6,2π上有2个零点,则t 的可能取值为( )A .-2B .0C .3D .4三、填空题(本题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.tan 15°=________.14.如图,某港口一天中6时到18时的水深变化曲线近似满足函数y =3sin ⎝ ⎛⎭⎪⎫π6x +φ+k ,据此可知,这段时间水深(单位:m)的最大值为________.15.在△ABC 中,若sin(2π-A )=-2sin(π-B ),3cos A =-2cos(π-B ),则A =________.16.已知函数f (x )=3sin 3x -a cos 3x +a ,且f ⎝ ⎛⎭⎪⎫29π=3,则实数a =________,函数f (x )的单调递增区间为________.四、解答题(本题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)在平面直角坐标系xOy 中,锐角α的顶点在坐标原点O ,始边与x 轴非负半轴重合,终边与单位圆交于点A ,且点A 的纵坐标为45.(1)求cos α和sin α; (2)求tan 2α的值.18.(12分)已知函数f (x )=3sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,-π2≤φ<π2的图象关于直线x =π3对称,且图象上相邻两个最高点的距离为π.(1)求ω和φ的值;(2)若f ⎝ ⎛⎭⎪⎫α2=34⎝ ⎛⎭⎪⎫π6<α<2π3,求cos ⎝ ⎛⎭⎪⎫α+3π2的值.19.(12分)(1)已知cos ⎝ ⎛⎭⎪⎫π2+α=2sin ⎝ ⎛⎭⎪⎫α-π2,求sin 2(π-α)+2sinαsin ⎝ ⎛⎭⎪⎫3π2-α+1的值; (2)已知cos ⎝ ⎛⎭⎪⎫π6-θ=13,求cos ⎝ ⎛⎭⎪⎫5π6+θ+2sin ⎝ ⎛⎭⎪⎫5π3-θ的值.20.(12分)在①tan α=43,②7sin 2α=2sin α,③cos α2=277这三个条件中任选一个,补充在下面问题中,并解决问题.已知α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝ ⎛⎭⎪⎫0,π2,cos(α+β)=-13,________,求cosβ.注:如果选择多个条件分别解答,按第一个解答计分.21.(12分)已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π3+1.(1)求f (x )的单调递增区间;(2)求f (x )在区间⎣⎢⎡⎦⎥⎤-π4,π4上的最值,并求出取最值时x 的值;(3)求不等式f (x )≥2的解集.22.(12分)已知函数f (x )=A sin(ωx +φ)⎝ ⎛⎭⎪⎫A >0,ω>0,|φ|≤π2的部分图象如图所示.(1)求函数y =f (x )的表达式;(2)将函数y =f (x )的图象向左平移π6个单位长度得到函数g (x )的图象,若关于x 的方程f (x )+g (x )-a =0在⎣⎢⎡⎦⎥⎤0,π2上有实数解,求实数a的取值范围.三角函数单元测试参考答案1.解析:设半径为R ,由弧长公式得4=2R ,即R =2 cm ,则S =12×2×4=4 (cm 2),故选A.答案:A2.解析:a =tan 5π12>1,b =cos 3π5<0,1>c =cos ⎝ ⎛⎭⎪⎫-17π4=cosπ4>0.∴a >c >b .则12<t -14<1或-1<t -14<0,解得3<t <5或-3<t <1,故选ABD. 答案:ABD13.解析:tan 15°=tan(45°-30°)=1-tan 30°1+tan 30°=1-331+33=2- 3.答案:2- 314.解析:由图象可知:当sin ⎝ ⎛⎭⎪⎫π6x +φ=-1时,y min =k -3=2,∴k =5,当sin ⎝ ⎛⎭⎪⎫π6x +φ=1时,y max =5+3=8. 答案:8 15.解析:由sin(2π-A )=-2sin(π-B ),得sin A =2sin B ①. 由3cos A =-2cos(π-B ),得3cos A =2cos B ②. 由①2+②2得:sin 2A +3cos 2A =2,即2cos 2A =1.由②和A ,B 为三角形的内角,可知角A ,B 均为锐角,则cos A =22.所以A =π4.答案:π416.解析:①因为f ⎝ ⎛⎭⎪⎫29π=3,所以f ⎝ ⎛⎭⎪⎫2π9=3sin 2π3-a cos 2π3+a =3,解得:a =1;②将a =1代入,得f (x )=3sin 3x -cos 3x +1,化简得f (x )=2sin ⎝ ⎛⎭⎪⎫3x -π6+1,故-π2+2k π≤3x -π6≤π2+2k π,k ∈Z。
全称量词与存在量词-2020-2021学年高一数学尖子生同步培优(人教A版2019必修第一册)

专题1.5 全称量词与存在量词姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分100分,考试时间45分钟,试题共16题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.下列命题中是全称量词命题并且是真命题的是()A.∃x>1,x2-2x-3=0B.若2x为偶数,则x∈NC.所有菱形的四条边都相等D.π是无理数2.命题“每一个四边形的四个顶点共圆”的否定是()A.存在一个四边形,它的四个顶点不共圆B.存在一个四边形,它的四个顶点共圆C.所有四边形的四个顶点共圆D.所有四边形的四个顶点都不共圆3.下列命题为真命题的是()A.存在x∈Q,使方程2x-2=0有解B.存在一个实数x,使x2+2x+4=0C.有些整数只有两个正因数D.所有的质数都是奇数4.设非空集合P,Q满足P∩Q=P,则()A .∀x ∈Q ,有x ∈PB .∀x ∉Q ,有x ∉PC .∃x ∉Q ,使得x ∈PD .∃x ∈P ,使得x ∉Q5.已知命题p :∃x >0,x +a -1=0,若p 为假命题,则a 的取值范围是( )A .{a |a <-1}B .{a |a ≥1}C .{a |a >1}D .{a |a ≤-1}6.(2020·沈阳二中北校高三模拟)已知命题“x R ∃∈,使212(1)02x a x +-+≤”是假命题,则实数a 的取值范围是( )A .(,1)-∞-B .(1,3)-C .(3,)-+∞D .(3,1)-7.(多选)下列命题的否定中,是全称量词命题且为真命题的有( )A .∃x ∈R ,x 2-x +41<0 B .所有的正方形都是矩形C .∃x ∈R ,x 2+2x +2≤0D .至少有一个实数x ,使x 3+1=08.(多选)下列命题错误的是( )A .∀x ∈{-1,1},2x +1>0B .∃x ∈Q ,x 2=3C .∀x ∈R ,x 2-1>0D .∃x ∈N ,|x |≤0二、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)9.下列存在量词命题是真命题的序号是________.①有些不相似的三角形面积相等;②存在实数x ,使x 2+2<0;③存在实数a ,使函数y =ax +b 的值随x 的增大而增大;④有一个实数的倒数是它本身.10.若命题p :∀x ∈R ,21 x <0,则綈p :________________. 11.若命题p :∀a ,b ∈R ,方程ax 2+b =0恰有一解,则綈p :________________.12.某中学开展小组合作学习模式,某班某组小王同学给组内小李同学出题如下:若命题“∃x ∈R ,x 2+2x +m ≤0”是假命题,求m 范围.小李略加思索,反手给了小王一道题:若命题“∀x ∈R ,x 2+2x +m >0”是真命题,求m 范围.你认为,两位同学题中m 范围是否一致?________(填“是”“否”中的一种)三、解答题(本大题共4小题,共40分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)13.判断下列命题的真假,并写出这些命题的否定:(1)三角形的内角和为180°;(2)每个二次函数的图象都开口向下;(3)存在一个四边形不是平行四边形.14.写出下列命题的否定,并判断真假:(1)正方形都是菱形;(2)∃x ∈R ,使4x -3>x ;(3)∀x ∈R ,有x +1=2x ;(4)集合A 是集合A ∩B 或集合A ∪B 的子集.15.写出下列命题的否定并判断真假:(1)所有自然数的平方都是正数;(2)任何实数x 都是方程5x -12=0的根;(3)∀x ∈R ,x 2+3<0;(4)有些质数不是奇数.16.已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},且B≠∅.(1)若命题p:“∀x∈B,x∈A”是真命题,求m的取值范围;(2)命题q:“∃x∈A,x∈B”是真命题,求m的取值范围.专题1.5 全称量词与存在量词姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分100分,考试时间45分钟,试题共16题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.下列命题中是全称量词命题并且是真命题的是()A.∃x>1,x2-2x-3=0B.若2x为偶数,则x∈NC.所有菱形的四条边都相等D.π是无理数【答案】C【解析】对于A,是存在量词命题,故A不正确;对于B,是真命题,但不是全称量词命题,故B不正确;对于C,是全称量词命题,也是真命题,故C正确;对于D,是真命题,但不是全称量词命题,故D不正确,故选C.2.命题“每一个四边形的四个顶点共圆”的否定是()A.存在一个四边形,它的四个顶点不共圆B.存在一个四边形,它的四个顶点共圆C.所有四边形的四个顶点共圆D.所有四边形的四个顶点都不共圆【答案】A【解析】根据全称量词命题的否定是存在量词命题,得命题“每一个四边形的四个顶点共圆”的否定是“存在一个四边形的四个顶点不共圆”,故选A.3.下列命题为真命题的是()A.存在x∈Q,使方程2x-2=0有解B.存在一个实数x,使x2+2x+4=0C.有些整数只有两个正因数D.所有的质数都是奇数【答案】C【解析】A.2x-2=0⇔x=2∉Q,故A错误;B.∵x2+2x+4=(x+1)2+3≥3,∴存在一个实数x,使x2+2x+4=0错误.C.∵2=1×2,∴有些整数只有两个正因数正确,D.2是质数,但2不是奇数,故D错误,故选C.4.设非空集合P,Q满足P∩Q=P,则()A.∀x∈Q,有x∈P B.∀x∉Q,有x∉PC.∃x∉Q,使得x∈P D.∃x∈P,使得x∉Q【答案】B【解析】∵P∩Q=P,∴P⊆Q,如图,∴A错误;B正确;C错误;D错误.故选B.5.已知命题p:∃x>0,x+a-1=0,若p为假命题,则a的取值范围是()A .{a |a <-1}B .{a |a ≥1}C .{a |a >1}D .{a |a ≤-1}【答案】B【解析】∵p 为假命题, ∴綈p 为真命题,即:∀x >0,x +a -1≠0,即x ≠1-a ,∴1-a ≤0,则a ≥1.∴a 的取值范围是a ≥1,故选B.6.(2020·沈阳二中北校高三模拟)已知命题“x R ∃∈,使212(1)02x a x +-+≤”是假命题,则实数a 的取值范围是( )A .(,1)-∞-B .(1,3)-C .(3,)-+∞D .(3,1)-【答案】B 【解析】因为命题“x R ∃∈,使212(1)02x a x +-+≤”是假命题,所以212(1)02x a x +-+>恒成立,所以2()114202a ∆=--⨯⨯<,解得13a -<<,故实数a 的取值范围是(1,3)-, 故选B, 7.(多选)下列命题的否定中,是全称量词命题且为真命题的有( )A .∃x ∈R ,x 2-x +41<0 B .所有的正方形都是矩形C .∃x ∈R ,x 2+2x +2≤0D .至少有一个实数x ,使x 3+1=0【答案】AC【解析】命题的否定是全称量词命题,即原命题为存在量词命题,故排除B.再根据命题的否定为真命题,即原命题为假命题.又D 为真命题,故选A 、C.8.(多选)下列命题错误的是( )A .∀x ∈{-1,1},2x +1>0B .∃x ∈Q ,x 2=3C .∀x ∈R ,x 2-1>0D .∃x ∈N ,|x |≤0【答案】ABC【解析】对于A ,x =-1时,不合题意,A 错误;对于B ,x =±3,B 错误;对于C ,比如x =0时,-1<0,C 错误;D 选项正确.二、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)9.下列存在量词命题是真命题的序号是________.①有些不相似的三角形面积相等;②存在实数x ,使x 2+2<0;③存在实数a ,使函数y =ax +b 的值随x 的增大而增大;④有一个实数的倒数是它本身.【答案】①③④【解析】①为真命题,只要找出等底等高的两个三角形,面积就相等,但不一定相似;②中对任意x ∈R ,x 2+2>0,所以不存在实数x ,使x 2+2<0,为假命题;③中当实数a 大于0时,结论成立,为真命题;④中如1的倒数是它本身,为真命题.故真命题的序号是①③④. 10.若命题p :∀x ∈R ,21-x <0,则綈p :________________. 【答案】∃x ∈R ,21-x >0或x -2=0 11.若命题p :∀a ,b ∈R ,方程ax 2+b =0恰有一解,则綈p :________________.【答案】∃a,b∈R,方程ax2+b=0无解或至少有两解12.某中学开展小组合作学习模式,某班某组小王同学给组内小李同学出题如下:若命题“∃x∈R,x2+2x+m≤0”是假命题,求m范围.小李略加思索,反手给了小王一道题:若命题“∀x∈R,x2+2x+m>0”是真命题,求m范围.你认为,两位同学题中m范围是否一致?________(填“是”“否”中的一种)【答案】是【解析】∵命题“∃x∈R,x2+2x+m≤0”的否定是“∀x∈R,x2+2x+m>0”.而命题“∃x∈R,x2+2x+m≤0”是假命题,则其否定“∀x∈R,x2+2x+m>0”为真命题.∴两位同学题中m范围是一致的.三、解答题(本大题共4小题,共40分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)13.判断下列命题的真假,并写出这些命题的否定:(1)三角形的内角和为180°;(2)每个二次函数的图象都开口向下;(3)存在一个四边形不是平行四边形.【解析】(1)是全称量词命题且为真命题.命题的否定:三角形的内角和不全为180°,即存在一个三角形其内角和不等于180°.(2)是全称量词命题且为假命题.命题的否定:存在一个二次函数的图象开口不向下.(3)是存在量词命题且为真命题.命题的否定:所有的四边形都是平行四边形.14.写出下列命题的否定,并判断真假:(1)正方形都是菱形;(2)∃x∈R,使4x-3>x;(3)∀x∈R,有x+1=2x;(4)集合A是集合A∩B或集合A∪B的子集.【解析】(1)命题的否定:正方形不都是菱形,是假命题.(2)命题的否定:∀x∈R.有4x-3≤x.因为当x=2时,4×2-3=5>2,所以“∀x∈R,有4x-3≤x”是假命题.(3)命题的否定:∃x∈R.使x+1≠2x.因为当x=2时,x+1=2+1=3≠2×2,所以“∃x∈R,使x+1≠2x”是真命题.(4)命题的否定:集合A既不是集合A∩B的子集也不是集合A∪B的子集,是假命题.15.写出下列命题的否定并判断真假:(1)所有自然数的平方都是正数;(2)任何实数x都是方程5x-12=0的根;(3)∀x∈R,x2+3<0;(4)有些质数不是奇数.【解析】(1)命题的否定:至少存在一个自然数的平方不是正数.真命题.(2)命题的否定:∃x∈R,5x-12≠0.真命题.(3)命题的否定:∃x∈R,x2+3≥0.真命题.(4)命题的否定:所有的质数都是奇数.假命题.16.已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},且B≠∅.(1)若命题p:“∀x∈B,x∈A”是真命题,求m的取值范围;(2)命题q:“∃x∈A,x∈B”是真命题,求m的取值范围.【解析】(1)由于命题p:“∀x∈B,x∈A”是真命题,所以B⊆A,B≠∅,所以⎪⎩⎪⎨⎧≤--≥+-≤+51221121m m m m ,解得2≤m ≤3.(2)q 为真,则A ∩B ≠∅,因为B ≠∅,所以m ≥2.所以⎪⎩⎪⎨⎧≥-≥-≤+221251m m m ,解得2≤m ≤4.。
