小学奥数专题计算综合
小学奥数思维训练-整数计算综合通用版

2014年四年级数学思维训练:整数计算综合1.计算:(1)121×32÷8;(2)4×(250÷8);(3)25×83×32×125.2.计算:(1)56×22+56×33+56×44;(2)222×33+889×66.3.计算:(1)37×47+36×53;(2)123×76﹣124×75.4.计算:100﹣99+98﹣97+96﹣95+…+12﹣11+10.5.计算:50+49﹣48﹣47+46+45﹣44﹣43+…﹣4﹣3+2+1.6.计算:(1+3+5+7+…+199+201)﹣(2+4+6+8+…+198+200).7.计算:1+2+3+4+…+48+49+50+49+48+…+4+3+2+1.8.下面是一个叫做“七上八下”的数字游戏.游戏规则是:对一个给定的数,按照由若干个7和8组成的口令进行一连串的变换.口令“7”是指在这个数中插入一个数字,使得新生成的数尽量大;口令“8”是指将这个数中的一个数字去掉,也要使新生成的数尽量大.例如:给出的数是1995,口令是“8→7,”在第一个口令“8”发出后变成995,在第二个口令“7”发出后变成9995.如果给出数“6595”以及口令“8→7→8→7→8→8”,问:变换后依次得到的6个数的和是多少?9.规定运算“▽”为:a▽b=(a+1)×(b﹣1),请计算:(1)8▽10;(2)10▽8.10.规定运算“☺”为:a☺b=a×b﹣(a+b),请计算:(1)5☺8;(2)8☺5;(3)(6☺5)4;(4)6☺(5☺4)11.计算:(1)72×27×88÷(9×11×12);(2)31×121﹣88×125÷(1000÷121).12.计算:(1)555×445﹣556×444;(2)42×137﹣80÷15+58×138﹣70÷15.13.计算:20092009×2009﹣20092008×2008﹣20092008.14.计算:1+2﹣3+4+5﹣6+7+8﹣9+…+97+98﹣99.15.计算:100×99﹣99×98+98×97﹣97×96+96×95﹣95×94+…+4×3﹣3×2+2×1.16.在不大于1000的自然数中,A为所有个位数字为8的数之和,B为所有个位数字为3的数之和.A与B的差是多少?17.求图中所有数的和.18.已知平方差公式:a2﹣b2=(a+b)×(a﹣b),计算:202﹣192+182﹣172+162﹣152+…+22﹣12.19.计算:951×949﹣52×48.20.规定运算“Θ”为:aΘb=a+2b﹣2,计算:(1)(8Θ7)Θ6;(2)8Θ(7Θ6)21.规定运算“○”为:a○b=(a+1)×(b﹣2).如果6○(□○5)=91,那么方格内应该填入什么数?22.规定:符号“△”为选择两数中较大的数的运算,“▽”为选择两数中较小的数的运算,例如:3△5=5,3▽5=3,请计算:1△2△3▽4△5△6▽7△…▽100.(运算的顺序是从左至右)23.观察下面算式的规律:2000+1991﹣1988﹣1982+1976+1970﹣1964﹣1958+1952+1946﹣1940﹣1934+…一直这样写下去,那么最后4个自然数分别是哪4个?符号分别是加还是减?算式最终的结果为多少?24.从1,2,…,9,10 中任意选取一个奇数和一个偶数,并将两数相乘,可以得到一个乘积,把所有这样的乘积全部加起来,总和是多少?25.计算:1﹣3+6﹣10+15﹣21+28﹣ (4950)26.已知平方差公式:a2﹣b2=(a+b)×(a﹣b),计算:1002+992﹣982﹣972+962+952﹣942﹣932+…+42+32﹣22﹣12.27.aΘb表示从a开始依次增加的b个连续自然数的和,例如:4Θ3=4+5+6=15,5Θ4=5+6+7+8=26,请计算:(1)4Θ15;(2)在算式(□Θ7)Θ11=1056中,方框里的数应该是多少?28.定义两种运算:aΩb=a﹣b+1,a∀b=a×b+1,用“Ω”、“∀”和括号填入下面的式子,使得等式成立(不能用别的计算符号):7 3 4 5=3.29.现定义四种操作的规则如下:①“一分为二”:如果一个自然数是偶数,就把它除以2;如果是奇数,就先加上1,然后除以2.例如从16可以得到8,从27可以得到14.②“丢三落四”:如果一个自然数中包含数字“3”或“4”,就将其划掉,例如从5304可以得到50,从408可以得到8.(不含数字3和4的自然数不能进行“丢三落四”操作)③“七上八下”:如果一个自然数中包含数字“7”,就将所有“7”移到最左边;如果一个自然数中包含数字“8”,就将所有“8”移到最右边.例如从98707可以得到77908,从802可以得到28.(不含数字7和8的自然数不能进行“七上八下”操作)④“十全十美”:将一个自然数的个位数字换成0.例如从111可以得到110,从905可以得到900.(个位是0的自然数不能进行“十全十美”操作)(1)请写出对4176依次进行③①③②④操作后的结果;(2)从655687开始,最少经过几次操作以后可以得到0?(3)一个三位数除了“丢三落四”外,其他三个操作各进行一次之后得到的结果是;求有多少个这样的三位数?30.如图是同学们都很熟悉的九九乘法口诀表,表中所有乘积的总和是多少?参考答案1.484;125;8300000;【解析】试题分析:(1)按照从左到右的顺序计算;(2)先算除法,再算乘法;(3)把32=4×8,利用乘法交换律与结合律简算.解:(1)121×32÷8=3872÷8=484;(2)4×(250÷8)=4×31.25=125;(3)25×83×32×125=25×4×(8×125)×83=100×1000×83=8300000.点评:整数混合运算的关键是抓住运算顺序,正确按运算顺序计算,适当利用运算定律简算..2.5544;66000.【解析】试题分析:(1)根据乘法分配律,把这几个乘式的公因数56提出来放在括号外,括号内的数相加是99,再把99看作(100﹣1),再应用乘法分配律解答.(2)把66看作2×33,即可用乘法分配律解答.解:(1)56×22+56×33+56×44=56×(22+33+44)=56×99=56×(100﹣1)=56×100﹣56)=5600﹣56=5544;(2)222×33+889×66=33×(222+889×2)=33×(222+1778)=33×2000=66000.点评:此题是整数的四则混合运算的简便算法,主要是考查乘法分配律的灵活运用.3.3647;48.【解析】试题分析:(1)把37×7看作(36+1)×47,根据乘法分配律,(36+1)×47=36×47+47,原式=36×47+47+36×53,再用乘法分配律,36×47+47+36×53=36×(47+53)+47,即可解答.(2)把123×76看作123×75+123,124×75看作123×75+75,原式═(123×75+123)﹣(123×75+75),去括号解答即可.解:(1)37×7+36×53=(36+1)×47+36×53=36×47+47+36×53=36×(47+53)+47=36×100+47=3600+47=3647;(2)123×76﹣124×75=(123×75+123)﹣(123×75+75)=123×75+123﹣123×75﹣75=123﹣75=48.点评:此题是考查整数的四则混合运算,两个小题看似没有简便算法,只要将原式适当变形,即可用乘法分配律,使计算简便.4.55【解析】试题分析:通过观察,相邻两个数字相差1,因此原式变为(100﹣99)+(98﹣97)+(96﹣95)+…+(12﹣11)+10,共有(100﹣12)÷2+1=45个1,然后加上10即可.解:100﹣99+98﹣97+96﹣95+…+12﹣11+10=(100﹣99)+(98﹣97)+(96﹣95)+…+(12﹣11)+10=1+1+1+…+1+10=45+10=55点评:此题解答的关键仔细分析数据,根据数字特点进行合理分组,达到简算的目的.5.51【解析】试题分析:此题中的隔项相差2,因此把原式变成(50﹣48)+(49﹣47)+…+(6﹣4)+(5﹣3)+2+1,计算即可.解:50+49﹣48﹣47+46+45﹣44﹣43+…﹣4﹣3+2+1=(50﹣48)+(49﹣47)+…+(6﹣4)+(5﹣3)+2+1=2+2+2+…+2+1=2×25+1=51点评:认真观察,根据数字特点进行组合,从而达到巧算的目的.6.101【解析】试题分析:通过观察,括号内的算式都是公差为2的等差数列,运用等差数列公式解答即可.解:(1+201)×101÷2﹣(2+200)×100÷2=202×101÷2﹣202×50=10201﹣10100=101点评:仔细观察数据,运用等差数列公式进行解答.7.2500【解析】试题分析:把1+2+3+…+49+50+49+48+…+3+2+1分成两段来计算,即原式=(1+2+3+…+49+50)+(49+48+…+3+2+1),把第二段加上50再减去50,每部分运用高斯求和公式计算即可.解:1+2+3+…+49+50+49+48+…+3+2+1=(1+2+3+…+49+50)+(50+49+48+…+3+2+1﹣50)=(1+50)×50÷2+(1+50)×50÷2﹣50=1275+(1275﹣50)=1275+1225=2500点评:此题主要运用了高斯求和公式进行计算.8.22478【解析】试题分析:先根据口令,6595在8发出后变为695,7发出后变为9695,8发出后为995,7发出后为9995,6发出后为999,最后一次8发出后为99,把这六个数加起来即可.解:根据游戏规则得:6595”以及口令“8→7→8→7→8→8分别变为:695→9695→995→9995→999→99695+9695+995+9995+999+99=(695+995)+(9695+9995)+1000﹣1+100﹣1=1690+19690+1100﹣2=22478点评:解答本题的根据是根据题意先把这6个数照出来,然后加起来即可.9.81;77.【解析】试题分析:规定运算“▽”为:a▽b=(a+1)×(b﹣1),也就是等于第一个因数与1的和乘第二个因数与1的差的乘积,据此解答即可.解:1)8▽10=(8+1)×(10﹣1)=9×9=81(2)10▽8=(10+1)×(8﹣1)=11×7=77点评:根据新运算的规则,等于第一个因数与1的和乘第二个因数与1的差的乘积.10.27;27;53;49.【解析】试题分析:a☺b=a×b﹣(a+b)表示两数的乘积减去这两个数的和,据此解答即可.解:因为a☺b=a×b﹣(a+b),所以:(1)5☺8=5×8﹣(5+8)=40﹣13=27(2)8☺5=8×5﹣(8+5)=40﹣13=27(3)(6☺5)☺4=(6×5﹣6﹣5)☺4=19☺4=19×4﹣(19+4)=76﹣23=53(4)6☺(5☺4)=6☺(5×4﹣5﹣4)=6☺11=6×11﹣(6+11)=66﹣17=49点评:根据新运算的法则:这种新运算等于两数的乘积减去这两个数的和.11.144;2420.【解析】试题分析:(1)利用a÷(b×c)=a÷b÷c即可;(2)88×125=8×125×11=11×1000,再利用a÷(b÷c)=a÷b×c即可.解:(1)72×27×88÷(9×11×12)=72×27×88÷(9×11×12)=(72÷12)×(27÷9)×(88÷11)=6×3×8=18×8=144(2)31×121﹣88×125÷(1000÷121)=31×121﹣8×125×11÷1000×121=31×121﹣11×121=121×(31﹣11)=121×20=2420点评:巧妙的利用合适的简便方法使计算简便.12.111;13748.【解析】试题分析:(1)利用555=5×111,444=4×111,然后利用乘法分配律即可;(2)58×138=58×137+58,80÷15+70÷15=(80+70)÷15,再利用乘法分配律即可.解:(1)555×445﹣556×444=111×5×445﹣4×111×556=111×2225﹣111×2224=111×(2225﹣2224)=111(2)42×137﹣80÷15+58×138﹣70÷15=42×137﹣(80+70)÷15+58×137+58=137×(42+58)﹣150÷15+58=137×100﹣10+58=13700+48=13748点评:解决本题的关键是注意对原题的恒等变形.13.2009.【解析】试题分析:每项都有20092008,那么利用20092009×2009=(20092008+1)×2009后,再利用乘法分配律即可.解:20092009×2009﹣20092008×2008﹣20092008=(20092008+1)×2009﹣20092008×2008﹣20092008=20092008×(2009﹣2008﹣1)+2009=2009点评:解答本题的关键是把20092009×2009转化为:(20092008+1)×2009.14.1584.【解析】试题分析:先进行分组,从前往后分别把三个数分为一组,即(1+2﹣3)+(4+5﹣6)+(7+8﹣9)…+(97+98﹣99)=0+3+6+…+96,变成首项为0,公差是3的前33项和,用等差公式计算即可.解:1+2﹣3+4+5﹣6+7+8﹣9+…+97+98﹣99=(1+2﹣3)+(4+5﹣6)+(7+8﹣9)…+(97+98﹣99)=0+3+6+…+96=(0+96)×33÷2=96×33÷2=1584.点评:合理分组,运用运算技巧或公式,进行简便计算.15.4182.【解析】试题分析:通过仔细观察,此题可通过数字变形,即原式变为100×(100﹣1)﹣98×(98﹣1)+96×(96﹣1)﹣94×(94﹣1)+...+4×(4﹣1)﹣2×(2﹣1)=(1002﹣100)﹣(982﹣98)+(962﹣96)+...+(42﹣4)﹣(22﹣2),运用平方差公式和加法结合律,进一步变为(1002﹣982+962﹣942+...+42﹣22)﹣(100+98+96+ (2),运用高斯求和公式,解决问题.解:100×99﹣98×97+96×95﹣94×93+…+4×3﹣2×1=100×(100﹣1)﹣98×(98﹣1)+96×(96﹣1)﹣94×(94﹣1)+…+4×(4﹣1)﹣2×(2﹣1)=(1002﹣100)﹣(982﹣98)+(962﹣96)+…+(42﹣4)﹣(22﹣2)=(1002﹣982+962﹣942+...+42﹣22)﹣(100+98+96+ (2)=(1002﹣982)+(962﹣942)﹣…+(42﹣22)﹣(100+2)×50÷2=198×2+190×2+…+6×2﹣2550=(198+190+182+…+6)×2﹣2550=(198+6)×33÷2×2﹣2550=6732﹣2550=4182点评:通过转化的数学思想,巧妙灵活地运用运算定律,使复杂的问题简单化.16.500.【解析】试题分析:分析:从1到10有2,8;,从11到20,即这样每10个数中有一个个位数是3的数,一个个位数是8的数.如1到10里,有3和8;11到20里有13和18,这两个数的差都是5,如8﹣3=5,18﹣13=5.又1000÷10=100,所以A与B的差是5×100=500.解:8﹣3=51000÷10=100,100×5=500.答:A与B的差是500.点评:完成此类题目要注意分析数据,从中找出规律后解答.17.510.【解析】试题分析:每一行把第一个与第九个相加,第二个与第把个相加,第三个与第七个相加,第四个与第六个相加,再加第五个,第一行是4个18与9;第二行4个20与10;第三行4个22与11;第四行4个24与12;第五行4个26与13相加即可.解:18×4+9+20×4+10+22×4+11+24×4+12+26×4+13=72+9+80+10+88+11+96+12+104+13=510.点评:本题考查了数字和问题,关键是得出第一行是4个18与9;第二行4个20与10;第三行4个22与11;第四行4个24与12;第五行4个26与13.18.210.【解析】试题分析:把算式进行必要的变形,进而利用平方差公式计算得解.解:202﹣192+182﹣172+162﹣152+…+22﹣12=(20+19)(20﹣19)+(18+17)(18﹣17)+(16+15)(16﹣15)+…+(2+1)(2﹣1)=39+35+31+…+3=(39+3)+(35+7)+(31+11)+(27+15)+(23+19)=42+42+42+42+42=210.点评:本题考查了平方差公式的应用.关键是把原式化为(20+19)(20﹣19)+(18+17)(18﹣17)+(16+15)(16﹣15)+…+(2+1)(2﹣1).19.900003.【解析】试题分析:先算乘法,再算减法,由此顺序计算即可.解:951×949﹣52×48=902499﹣2496=900003.点评:整数混合运算的关键是抓住运算顺序,正确按运算顺序计算即可.20.30;40.【解析】试题分析:规定运算“Θ”为:aΘb=a+2b﹣2,第一个数加上第二个数的2倍再减去2,按照这个规律即可;有括号先算括号里面的.解:因为aΘb=a+2b﹣2,所以:(1)(8Θ7)Θ6=(8+2×7﹣2)Θ6=20Θ6=20+2×6﹣2=32﹣2=30(2)8Θ(7Θ6)=8Θ(7+2×6﹣2)=8Θ17=8+2×17﹣2=8+34﹣2=40点评:本题考查根据新运算规则计算:正确找准计算规则是关键.21.4.【解析】试题分析:根据题意a○b=(a+1)×(b﹣2),即为第一个加1与第二个数减去2的差的乘积;设□○5=x,6○(□○5)=91就变为6○x=91,据此解出x,然后代入即可求得□.解:设□○5=x因为:a○b=(a+1)×(b﹣2)所以:6○(□○5)=91即为:6○x=91(6+1)×(x﹣2)=917x﹣14=917x﹣14+14=91+147x=1057x÷7=105÷7x=15所以:□○5=15(□+1)×(5﹣2)=153□+3=153□+3﹣3=15﹣33□=123□÷3=12÷3□=4答:方格内应该填4.点评:本题考查根据新运算规则计算:正确找准计算规则是关键.22.99.【解析】试题分析:因为符号“△”为选择两数中较大的数的运算,“▽”为选择两数中较小的数的运算,而△2△3▽4△5△6▽7△…▽100,两个向上的,一个向下的,3个是一周期,△取大,▽取小,所以正好是取3的倍数,到最后还剩99,据此解答即可.解:因为3△5=5,3▽5=31△2△3▽4△5△6▽7△…▽100两个向上的,一个向下的,3个是一周期,△取大,▽取小,所以正好是取3的倍数,到最后还剩99,所以:1△2△3▽4△5△6▽7△…▽100=2△3▽4△5△6▽7△…▽100=3▽4△5△6▽7△…▽100=3△5△6▽7△…▽100=6▽7△…▽100=6△8…▽100=99▽100=99点评:本题考查根据新运算规则计算:正确找准计算规则是关键.23.这四个数为24,18,12,6;24+18﹣12﹣6;24.【解析】试题分析:通过分析可知,每四个数为一循环,每一循环的第一个数相差24,后边的数相差6,所以最后4个自然数分别24,18,12,6,为24+18﹣12﹣6,据解答即可.解:根据规律可知,这四个数为24,18,12,6,算式为24+18﹣12﹣6结果为:24+18﹣12﹣6=24答:这四个数为24,18,12,6;24+18﹣12﹣6;24.点评:先找到各数量之间的关系,再根据这个关系求解.24.750.【解析】试题分析:在1、2、3、4、5、6、7、8、9、10这10个数中,奇数为1,3,5,7,9;偶数为2,4,6,8,10.奇数与偶数各5个,则每个奇数都可与其它5个偶数相乘得到5个不同的积,它们的和为:1×2+1×4+1×6+1×8+1×10=(2+4+6+8+10)×1,同理3与这五个偶数相乘积的和为(2+4+6+8+10)×3,由此可我们根据乘法分配律即求出在1、2、3、4、5、6、7、8、9、10这10个数中,每次取一个奇数和一个偶数相乘,它们所有积和的大小.解:(1×2+1×4+1×6+1×8+1×10)+(3×2+3×4+…+3×10)+…+(9×2+9×4+…+9×10)=(2+4+6+8+10)×1+(2+4+6+8+10)×3+…+(2+4+6+8+10)×9,=(1+3+5+7+9)×(2+4+6+8+10),=25×30,=750.点评:在列出算式的基础上通过分析找出算式中数据之间的特点及内在联系,然后连续运用乘法分配律是完成本题的关键.25.2500.【解析】试题分析:我们观察这个算式中的每一项,3=1+2,6=1+2+3,10=1+2+3+4,....4990=1+2+3 (99)那么原式变为:1﹣(1+2)+(1+2+3)﹣(1+2+3+4)+…+(1+2+3+…+99),计算即可.解:1﹣3+6﹣10+15﹣21+28﹣…+4950=1﹣(1+2)+(1+2+3)﹣(1+2+3+4)+...+(1+2+3+ (99)=1+3+5+…+99=(1+99)×50÷2=2500点评:仔细观察算式,根据数据特点,把数据进行拆分,变成从第二项开始相邻两式部分相同的式子,通过加减相互抵消,变成1+3+5+…+99,运用高斯求和公式计算求得结果.26.10100.【解析】试题分析:解答此题先运用平方差公式把相邻两个偶数或两个奇数平方的差转化成因数相乘的形式进行计算即可求解.解:1002+992﹣982﹣972+962+952﹣942﹣932+…+42+32﹣22﹣12=(1002﹣982)+(992﹣972)+(962﹣942)+(952﹣932)+…+(42﹣22)+(32﹣12)=(100﹣98)×(100+98)+(99﹣97)×(99+97)+…+(4﹣2)×(4+2)+(3﹣1)×(3+1)=2×(100+98)+2×(99+97)+…+2×(4+2)+2×(3+1)=2×(100+98+99+97+4+2+3+1)=2×=101×100=10100.点评:解答此题主要运用平方差公式、乘法分配律、加法结合律,高斯求和公式进行计算.27.165;10.【解析】试题分析:由题意可知:这种新运算是从第一个数开始,连续自然数相加,加数的个数就是后一个数;(2)设□Θ7=x,根据条件求出x,然后根据新运算规则再求得方框即可.解:因为4Θ3=4+5+6=15,5Θ4=5+6+7+8=26,所以:(1)4Θ15=4+5+6+7+ (18)=(4+17)×7+18=21×7+18=147+18=165(2)因为:(□Θ7)Θ11=1056设□Θ7=x,原算式变为:x+(x+1)+…(x+10)=105611x+(1+10)×5=105611x+55=105611x+55﹣55=1056﹣5511x=100111x÷11=1001÷11x=91所以□Θ7=91□+(□+1)+…(□+6)=917□+21=917□+21﹣21=91﹣217□=707□÷7=70÷7□=10答;方框里的数应该是10.点评:本题考查根据新运算规则计算:正确找准计算规则是关键.28.﹣7Ω{﹣[( 3∀4 )Ω 5]}=3.【解析】试题分析:根据aΩb=a﹣b+1,a∀b=a×b+1,要多次实验到底用几个Ω,几个∀,或者是单独用其中一个符号,让右边等于3即可.解:因为aΩb=a﹣b+1,a∀b=a×b+13∀4=3×4+1=1313Ω5=13﹣5+1=9﹣7Ω(﹣9)=﹣7+9+1=3所以:﹣7Ω{﹣[( 3∀4 )Ω 5]}=3.点评:本题考查根据新运算规则计算:正确找准计算规则是关键.29.(1)4176﹣7416﹣3708﹣7308﹣708﹣700(2)即经过7次可以得到0.(3)234经过①得117,再经过③得711,再经过④得710.【解析】试题分析:(1)(2)根据操作规则进行分析操作即可得出相应结果.(3)第一问可选择一个数根据操作规则进行操作得出结果即可,第二问可按不同的操作顺序分析完成.解:(1)4176依次进行③①③②④操作后的结果:4176﹣7416﹣3708﹣7308﹣708﹣700(2)从655687开始,655687经过“一分为二”的操作,得到327844;再经过“丢三落四”的操作,得到278;再经过“七上八下”的操作,得到728;再经过经过“一分为二”的操作,得到364;再经过“丢三落四”的操作,得到6;最后经过“十全十美”的操作,得到0.共6步完成操作,得到0.655687经过①得327844﹣经过②得278﹣经过①得139﹣经过②得19﹣经过①得10﹣经过①得5﹣经过④得0.即经过7次可以得到0.(3)一个三位数除了“丢三落四”外,其他三个操作各进行一次之后得到的结果是如:234经过①得117,再经过③得711,再经过④得710.步骤①③④,经过步骤①之后个位含有7,百位含有1的,有10个;分别是214,234,254,274,294,314,334,354,374,394;经过步骤①之后十位含有7,百位为1,有10个;分别是340,342,344,346,348,350,352,354,356,358.重复354;总共有10+10﹣1=19个.步骤①④③,经过步骤①之后十位含有7,百位含有1,有10个;分别是340,342,344,346,348,350,352,354,356,358步骤③①④,③④①,都没有步骤④①③,个位数有10种可能,分别是340,341,342,343,344,345,346,347,348,349步骤④③①,没有.根据上面的分类,除去重复的数据,那么总共有:19+5=24个.故答案为:710.点评:完成本题要注意条件中所给的操作规则,然后按操作规则分析即可.30.1155.【解析】试题分析:根9的乘法口诀表,把表中的各个乘积相加即可得出结论.解:(1+2+3+4+5+6+7+8+9)+(4+6+8+10+12+14+16+18)+(9+12+15+18+21+24+27)+(16+20+24+28+32+36)+(25+30+35+40+45)+(36+42+48+54)+(49+56+63)+(64+72)+81=[(1+9)×4+5]+[(4+18)×4]+[(9+27)×3+18]+[(16+36)×3]+[(25+45)×2+35]+[(36+54)×2]+168+136+81=45+88+126+156+175+180+168+136+81=1155点评:此题也可以按行累计九九乘法表里共有:1个1,1+2个2,1+2+3个3…以此类推,得1个1,3个2,6个3,10个4,15个5,21个6,28个7,36个8,45个9,由此解答即可.。
高思奥数导引小学五年级含详解答案第17讲:计算综合一

第17讲计算综合一内容概述了解等比数列的基本概念,学会利用错位相减的方法进行求和;灵活使用各种方法简化比较复杂的分数算式;具有一定综合性的“定义新运算”问题;较复杂的数列与数表问题。
典型问题兴趣篇1.计算:(1)1248163264128256++++++++;(2)111111111248163264128256 ++++++++。
2.计算:23456333333+++++。
3.计算:199519951995199519951995 200920092009200920092009 ++++。
4.计算:131435 415263 342556⨯+⨯+⨯。
5.计算:1111111111 123456789100 2342342342+-++-++-++。
6.规定新运算“*”为:*32a b a b=⨯-⨯。
(1)计算:456**345⎛⎫⎪⎝⎭;(2)已知456**345x⎛⎫=⎪⎝⎭,求x。
7.图17-1中除了每行两端的数之外,其余每个数都是与它相连的上一行的两个数的平均数,例如:2.75是2.5和3的平均数。
请问:第100行中的各数之和是多少?8.有这样一列数,前两个数分别是0和1,从第三个数开始,每一个数都是前两个数的和:0,1,1,2,3,5,8,13,21,34,…。
请问:这个数列的第1000个数除以8所得的余数是多少?9.观察下面的数阵:根据前五行数所表达的规律,求(1)3367这个数在由上至下的第几行?在这一行中,它是由左向右第几个?(2)第28行第19个数是什么?10.观察数列11,12,22,12,13,23,33,13,14,24,34,44,34,24,14,…,求:(1)数列中第150项;(2)数列中前300项的和。
拓展篇1.如图17-2,有一个边长为81厘米的等边三角形,将它每条边三等分,以中间那一份为边向外作等边三角形,得到图17-3。
由图17-3通过同样方法又得到图17-4。
六年级奥数专题 数论综合二(学生版)

学科培优数学“数论综合二”学生姓名授课日期教师姓名授课时长知识定位在整个数学领域,数论被当之无愧的誉为“数学皇后”。
翻开任何一本数学辅导书,数论的题型都占据了显著的位置。
在小学各类数学竞赛和小升初考试中,我们系统研究发现,直接运用数论知识解题的题目分值大概占据整张试卷总分的30%左右,而在竞赛的决赛试题和小升初一类中学的分班测试题中,这一分值比例还将更高。
知识梳理涉及知识点多、解题过程比较复杂的整数综合题,以及基本依靠数论手段求解的其他类型问题.例题精讲【试题来源】【题目】一台计算器大部分按键失灵,只有数字“7”和“0”以及加法键“+”尚能使用,因此可以输入77,707这样只含数字7和0的数,并且进行加法运算.为了显示出222222,最少要按“7”键多少次?【试题来源】【题目】有一批图书总数在1000本以内,若按24本书包成一捆,则最后一捆差2本;若按28本书包成一捆,最后一捆还是差2本书;若按32本包一捆,则最后一捆是30本.那么这批图书共有本.【试题来源】【题目】一个五位数恰好等于它各位数字和的2007倍,则这个五位数是 .【试题来源】【题目】在纸上写着一列自然数1,2,…,98,99.一次操作是指将这列数中最前面的三个数划去,然后把这三个数的和写在数列的最后面.例如一次操作后得到4,5,…,98,99,6;而两次操作后得到7,8,…,98,99,6,15.这样不断进行下去,最后将只剩下一个数,则最后剩下的数是 .【试题来源】【题目】有两种规格的9箱钢珠,每箱300个,甲种钢珠每个10克,乙种钢珠每个11克,将这9箱钢珠编为1~9号,然后依次从1~9号箱中取出20,21,22,23,24,25,26,27,28,个钢珠,这些钢珠共重5555克。
问:哪几箱是甲种钢珠?【试题来源】【题目】把除1外的所有奇数依次按一项,二项,三项,四项循环的方式进行分组:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,3l,33),(35,37,39,41),(43),…….那么,第1994个括号内的各数之和是多少?【试题来源】【题目】2001个球平均分给若干人,恰好分完。
六年级奥数专题 排列组合综合(学生版)

排列组合综合,掌握几种基本的排列组合相关问题的方法:特殊位置特殊元素优先分析法、捆绑法、插空法、隔板法我们在完成一件事时往往要分为多个步骤,每个步骤又有多种方法,当计算一共有多少种完成方法时就要用到乘法原理.乘法原理:一般地,如果完成一件事需要n个步骤,其中,做第一步有m1种不同的方法,做第二步有m2种不同的方法 ,…,做第n步有mn种不同的方法,则完成这件事一共有N=m1×m2×…×mn种不同的方法.乘法原理运用的范围:这件事要分几个彼此互不影响的独立步骤来完成,这几步是完成这件任务缺一不可的,这样的问题可以使用乘法原理解决.我们可以简记为:“乘法分步,步步相关”.加法原理无论自然界还是学习生活中,事物的组成往往是分门别类的,例如解决一件问题的往往不只一类途径,每一类途径往往又包含多种方法,如果要想知道一共有多少种解决方法,就需要用到加法原理.加法原理:一般地,如果完成一件事有k类方法,第一类方法中有m1种不同做法,第二类方法中有m2种不同做法 ,…,第k类方法中有mk种不同的做法,则完成这件事共有N= m1 + m2 +…+mk 种不同的方法.加法原理运用的范围:完成一件事的方法分成几类,每一类中的任何一种方法都能完成任务,这样的问题可以使用加法原理解决.我们可以简记为:“加法分类,类类独立”.特殊位置特殊元素优先分析法把有限制条件的元素(位置)称为特殊元素(位置),对于这类问题一般采取特殊元素(位置)优先安排的方法。
捆绑法在解决对于某几个元素要求相邻的问题时,先整体考虑,将相邻元素视作一个大元素进行排序,然后再考虑大元素内部各元素间顺序的解题策略就是捆绑法.插空法元素相离(即不相邻)问题,可以先将其他元素排好,然后再将不相邻的元素插入已排好的元素位置之间和两端的空中。
隔板法隔板法就是在n个元素间插入(b-1)个板,即把n个元素分成b组的方法。
【题目】①有5个人排成一排照相,有多少种排法?②5个人排成两排照相,前排2人,后排3人,共有多少种排法?③5个人排成一排照相,如果某人必须站在中间,有多少种排法?④5个人排成一排照相,某人必须站在两头,共有多少种排法【试题来源】(1)(迎春杯决赛)(2)(兴趣杯少年数学邀请赛决赛)【题目】(1)如右图(1)是中国象棋盘,如果双方准备各放一个棋子,要求它们不在同一行,也不在同一列,那么总共有多少种不同的放置方法?(2)在右图(2)中放四个棋子“兵”,使得每一列有一个“兵”,每一行至多有一个“兵”.有多少种不同的放法?【试题来源】【题目】大林和小林共有小人书不超过50本,他们各自有小人书的数目有多少种可能的情况?【试题来源】【题目】把13拆成三个数的和,请问有几种拆法?【试题来源】【题目】用数码0,1,2,3,4可以组成多少个小于1000的没有重复数字的自然数?【试题来源】【题目】用1~9可以组成______个不含重复数字的三位数:如果再要求这三个数字中任何两个的差不能是1,那么可以组成______个满足要求的三位数.【试题来源】【题目】数3可以用4种方法表示为1个或几个正整数的和,如3,1+2,2+1,1+1+1。
高思奥数导引小学六年级含详解答案第9讲计算综合二
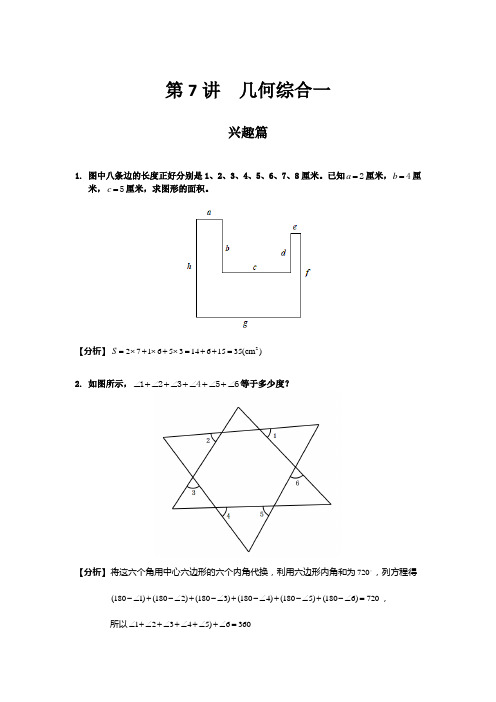
第7讲几何综合一兴趣篇1. 图中八条边的长度正好分别是1、2、3、4、5、6、7、8厘米。
已知a=2厘米,b=4厘米,c=5厘米,求图形的面积。
【分析】2S=⨯+⨯+⨯=++=2716531461535(cm)2. 如图所示,∠+∠+∠+∠+∠+∠123456等于多少度?【分析】将这六个角用中心六边形的六个内角代换,利用六边形内角和为720,列方程得(1801)(1802)(1803)(1804)(1805)(1806)720-∠+-∠+-∠+-∠+-∠+-∠=,所以12345)6360∠+∠+∠+∠+∠+∠=3. 如图,平行四边形ABCD 的周长为75厘米。
以BC 为底时高是14厘米,以CD 为底时高是16厘米。
求平行四边形ABCD 的面积。
【分析】 75237.5BC CD +=÷=,根据面积相等,底的比与高的比成反比例,所以:16:148:7BC CD ==,因此37.5(87)820BC =÷+⨯=,平行四边形ABCD 的面积是2014280⨯=平方厘米4. 如图所示,一个边长为1米的正方形被分成4个小长方形,它们的面积分别是310平方米、25平方米、15平方米和110平方米。
已知图中的阴影部分是正方形,那么它的面积是多少平方米?【分析】 1251110CH HD ==,因此23CH =,13HD =,3310245AE EB ==,所以37AE =,47EB =,因此2353721FG =-=,那么它的面积是252521441⎛⎫= ⎪⎝⎭平方米5. 如图,红、黄、绿三块大小一样的正方形纸片,放在一个正方体盒内,它们之间相互重叠。
已知露在外面的部分中,红色的面积是20,黄色的面积是14,绿色的面积是10。
那么,正方体盒子的底面积是多少?绿黄红【分析】 将黄色纸片推到左边,则每块纸片露出的形状如右上图.黄、绿两色的面积之和保持14+10=24不变,则在右图中这两块面积相等,均为24212÷=.根据公式可知,空白处面积=黄⨯绿÷红=1212207.2⨯÷=,则正方形盒底面积是7.212122051.2+++=.6. 如图,在三角形ABC 中,IF 和BC 平行,GD 和AB 平行,HE 和AC 平行。
小学奥数35个专题汇总

小学奥数35个专题汇总②一次不足,另一次有余数;③两次都有余数;④两次都不足;基本公式:①总量=(A×B)÷(A-C)=(B×C)÷(A-C);②总量=(A×B)÷(B-C)=(A×C)÷(B-C);③总量=(A×B)÷(A+B-C);④总量=(A×B)÷(C-B)=(A×C)÷(B-C);关键问题:根据题目给出的条件,确定分组的标准和分配方案,从而求出对象的总量。
7.分桃问题基本概念:分桃问题是一种典型的递归问题,即把一个问题分解成若干个相同或相似的子问题,然后把子问题分解成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并.基本思路:先假设有n个桃子,从而确定第一天分得的桃子数,然后根据第二天剩下的桃子数,确定第二天分得的桃子数,以此类推,直到最后一天分得的桃子数可以直接计算出来,从而求出总共分了几天.基本公式:设第n天分得的桃子数为x,则第n-1天剩下的桃子数为(x+1)×2,第n-2天剩下的桃子数为((x+1)×2+1)×2,以此类推,设第一天分得的桃子数为y,则有:x=y-1y-1+1)×2=x+1y-1+1)×2+1)×2+1)×2=(y-1+1)×2关键问题:确定第一天分得的桃子数,从而递推出每天分得的桃子数,直到最后一天分得的桃子数可以直接计算出来,从而求出总共分了几天.8.数位问题基本概念:数位问题是指对一个数的各个数位进行分析、计算的问题,主要涉及到数位的个数、各数位上数字的性质、各数位上数字之间的关系等.基本思路:先把问题中给出的数按位分解,然后根据题目要求,对各数位上的数字进行操作,最后把结果合并起来.基本题型:①给出一个数的各数位上的数字,求这个数;②给出一个数和它的各数位上的数字,求这个数的某个性质;③给出一个数和它的某些数位上的数字,求这些数位上的数字;④给出一个数和它的各数位上的数字,求这个数的某种变形;基本公式:①一个n位数的各数位上的数字之和为S,则有S=an×10n-1+an-1×10n-2+…+a1×10^0;②一个n位数的各数位上的数字之积为P,则有P=an×an-1×…×a1;③一个n位数的各数位上的数字之和为S,则有S=(a1+an)×n÷2;④一个n位数的各数位上的数字之和为S,则有S=(a1+an)×n÷2+(a2+an-1)×(n-2)÷2+…;关键问题:根据题目要求,确定对各数位上的数字进行何种操作,从而求出所需的结果.抽屉原理是一种基本的数学原理,可以用来解决许多问题。
小学奥数 设数法解题综合练习

设数法解题综合练习1、已知甲校学生数是乙校学生数的52,甲校女生数是甲校学生数的103,乙校的 男生数是乙校学生数的5021,那么两校女生总数占两校学生总数的几分之几?2、在一城市中,中学生数是居民的51,大学生数是中学生数的41,那么占大学 生总数的52的理工科大学生是居民数的几分之几?3、某人在一次选举中,需43的选票才能当选,计算32的选票后,他得到的选票 已达到当选票数的65,他还要得到剩下选票的几分之几才能当选?4、某校有53的学生是男生,男生的201想当医生,全校想当医生的学生的43是男 生,那么全校女生的几分之几想当医生?5、在阅览室看书的学生中,男生占25%,又来了一些学生后,学生总人数增加 20%,男生占总人数的30%,男生增加百分之几?6、某班男生人数是女生人数的65,女生的平均身高比男生的高10%,全班平均 身高116厘米,求男、女生的平均身高各是多少厘米?7、六年级三个班的人数相等,一班的男生人数和二班的女生人数相等,三班的男生人数是全部男生人数的83,全年级女生人数占全年级总人数的几分之 几?8、甲、乙两班人数相同,甲班男生人数与女生人数的比是3:4,乙班男生人数 与女生人数的比是4:5,求甲、乙两班总人数中男、女生人数的比是多少?9、某公司彩电按原价格销售,每台可获利润600元,现在降价销售,结果彩电 的销量增加一倍,获得的总利润增加0.5倍,则每台彩电降价多少元?10、有一批饼干平均分给幼儿园大、小两个班,每人分得12块;如果只分给大班的同学,每人可分得21块。
如果只分给小班的同学,每人可分得多少块?11、体育馆入场券18元一张,降价后观众增加一半,收入增加31,那么每张入 场券降价多少元?。
小学奥数:小数四则混合运算综合.专项练习及答案解析

1-1-1-1.小数四则混合运算(由K12教材中心【小学部】题库提供) 教师版本讲主要是通过一些速算技巧,培养学生的数感,并通过一些大数运算转化为简单运算,让学生感受学习的成就感,进而激发学生的学习兴趣一、运算定律 ⑴加法交换律:a b b a +=+的等比数列求和⑵加法结合律:()()a b c a b c ++=++⑶乘法交换律:a b b a ⨯=⨯⑷乘法结合律:()()a b c a b c ⨯⨯=⨯⨯⑸乘法分配律:()a b c a b a c ⨯+=⨯+⨯(反过来就是提取公因数)⑹减法的性质:()a b c a b c --=-+⑺除法的性质:()a b c a b c ÷⨯=÷÷()a b c a c b c +÷=÷+÷()a b c a c b c -÷=÷-÷上面的这些运算律,既可以从左到右顺着用,又可以从右到左逆着用.二、要注意添括号或者去括号对运算符号的影响⑴在“+”号后面添括号或者去括号,括号内的“+”、“-”号都不变;⑵在“-”号后面添括号或者去括号,括号内的“+”、“-”号都改变,其中“+”号变成“-”号,“-”号变成“+”号;⑶在“⨯”号后面添括号或者去括号,括号内的“⨯”、“÷”号都不变,但此时括号内不能有加减运算,只能有乘除运算;⑷在“÷”号后面添括号或者去括号,括号内的“⨯”、“÷”号都改变,其中“⨯”号变成“÷”号,“÷”号变成“⨯”号,但此时括号内不能有加减运算,只能有乘除运算.【例 1】 计算:200.920.08200.820.07⨯-⨯【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【解析】 原式200.920.0820.08200.7=⨯-⨯20.08(200.9200.7)=⨯-20.080.2=⨯4.016=【答案】4.016小数四则混合运算综合例题精讲 知识点拨教学目标【巩固】 计算:20.0931.5 2.009317200.9 3.68⨯+⨯+⨯= .【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【关键词】学而思杯,4年级【解析】 原式 2.009315 2.009317 2.009368=⨯+⨯+⨯()2.009315317368=⨯++2.00910002009=⨯=【答案】2009【巩固】 计算:2.009×43+20.09×2.9+200.9×0.28= .【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【关键词】希望杯,6年级,一试【解析】 原式20.09 4.320.09 2.920.09 2.8=⨯+⨯+⨯20.09(4.3 2.9 2.8)200.9=⨯++= 【答案】200.9【巩固】 计算:1999 3.14199.931.419.99314⨯+⨯+⨯.【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【关键词】第十届,小数报【解析】 原式1999 3.143=⨯⨯200019.4218830.58=-⨯=() 【答案】18830.58【巩固】 计算:199.919.98199.819.97⨯-⨯【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【解析】 (法1)原式199.919.9819.98199.7=⨯-⨯19.98(199.9199.7)=⨯-19.980.2=⨯3.996=(法2)也可以用凑整法来解决.原式(2000.1)19.98(2000.2)19.97=-⨯--⨯20019.980.119.9820019.970.219.97=⨯-⨯-⨯+⨯2 1.996=+3.996=【答案】3.996【巩固】 计算:....⨯+⨯=103734171926 .【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【关键词】希望杯,5年级,1试【解析】 10.37 3.4 1.719.26⨯+⨯()10.37 3.4 3.49.6310.379.63 3.420 3.468=⨯+⨯=+⨯=⨯=【答案】68【例 2】 计算:6.258.2716 3.750.8278⨯⨯+⨯⨯【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【解析】 原式 6.25168.27 3.750.88.27=⨯⨯+⨯⨯8.27(6.2516 3.750.8)=⨯⨯+⨯8.27(1003)=⨯+8.271008.273=⨯+⨯851.81=【答案】851.81【巩固】 计算:20.0962200.9 3.97 2.87⨯+⨯-⨯= .【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【关键词】学而思杯,5年级,第1题【解析】 原式20.096220.093920.09=⨯+⨯-()20.0962391=⨯+-20.091002009=⨯=【答案】2009【巩固】 计算:2.8947 1.53 1.4 1.1240.112880.530.1=⨯+-⨯+⨯+⨯- .【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【关键词】走美杯,5年级,决赛【解析】 原式=2.88×(0.47+0.53)+0.47+1.53+(24-14)×0.11-0.1=288+2+1=291【答案】291【巩固】 计算:2237.522.312.523040.7 2.51⨯+⨯+÷-⨯+= .【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【关键词】走美杯,5年级,决赛【解析】 原式2237.5223 1.252300.2570.251=⨯+⨯+⨯-⨯+2238.752230.251223912008=⨯+⨯+=⨯+= 【答案】2008【巩固】 计算:19.9837199.8 2.39.9980⨯+⨯+⨯【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【关键词】第三届,兴趣杯,5年级【解析】 原式19.983719.982319.9840=⨯+⨯+⨯19.983723401998=⨯++=() 【答案】1998【巩固】 计算:3790.000381590.00621 3.790.121⨯+⨯+⨯【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【关键词】迎春杯,5年级【解析】 原式 3.790.0381590.00621 3.790.121=⨯+⨯+⨯3.790.0380.1210.159 6.21=⨯++⨯()=51.28.1119.25⨯+⨯+(51225+)0.1951.28.1119.255120.19250.19⨯=⨯+⨯+⨯+⨯51.28.151.2 1.9119.250.251951.210110.251190.2519=⨯+⨯+⨯+⨯=⨯+⨯+⨯+⨯5120.2530996117.5618.5=+⨯+=+=【答案】618.5【例 6】 计算:2237.522.312.523040.7 2.51⨯+⨯+÷-⨯+【考点】四则混合运算之提取公因数 【难度】3星 【题型】计算【关键词】走美杯,决赛【解析】 原式2233 2.522.35 2.523 2.50.7 2.50.4 2.5=⨯⨯+⨯⨯+⨯-⨯+⨯2.5(223322.35230.70.4)=⨯⨯+⨯+-+2.5(669111.5230.70.4)=⨯++-+2.5803.2=⨯803.2104=⨯÷80324=÷2008=【答案】2008【巩固】 1.2517.6360.8 2.6412.5⨯+÷+⨯=【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【关键词】走美杯,初赛,六年级【解析】 1.2517.6360.8 2.6412.5⨯+÷+⨯=1.25(17.626.4)360.8=1.2544360.8=55+45=100⨯++÷⨯+÷【答案】100【例 7】 计算:[20078.58.5 1.5 1.510]1600.3-⨯-⨯÷÷-().【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【关键词】迎春杯【解析】 原式[20078.5 1.58.5 1.510]1600.3=-+⨯-÷÷-()()()200771600.320001600.312.50.312.2=-÷-=÷-=-=【答案】12.2【巩固】 计算(98065320)(669864)⨯-÷+⨯【考点】四则混合运算之提取公因数 【难度】3星 【题型】计算【解析】 注意到在被除数和除数的表达式中均出现了98,而且分别有相近的数64与65,我们可以考虑把被除数做如下变形:被除数980(641)320=⨯+-98064(980320)=⨯+-98064660=⨯+(986466)10=⨯+⨯所以被除数是除数的10倍,所以这道题的答案是10.【答案】10【巩固】 ⑴ 2004.051997.052001.051999.05⨯-⨯⑵ (873477198⨯-)÷(476874199⨯+)【考点】四则混合运算之提取公因数 【难度】3星 【题型】计算【解析】 (1)原式=(32001.05+)⨯(1999.052-)2001.051999.05-⨯=31999.0522001.05631999.0521999.052261989.05⨯-⨯-=⨯-⨯-⨯-=(2)原式=(873476873198⨯+-)÷(873476476199⨯++)=(873476675⨯+)÷(873476675⨯+)1=【答案】(1)1989.05 (2)1【例 8】 计算:221.23450.7655 2.4690.7655++⨯.【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【关键词】2014全国小学数学奥林匹克【解析】 原式21.23450.76550.7655 2.469=+⨯+()21.23450.7655 1.234521.2345 1.23450.76550.765521.234520.765521.23450.76552224=+⨯+=⨯++⨯=⨯+⨯=+⨯=⨯=()()()【答案】4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学奥数专题第1讲计算综合(一)繁分数的运算,涉及分数与小数的定义新运算问题,综合性较强的计算问题.1.繁分数的运算必须注意多级分数的处理,如下所示:甚至可以简单地说:“先算短分数线的,后算长分数线的”.找到最长的分数线,将其上视为分子,其下视为分母.2.一般情况下进行分数的乘、除运算使用真分数或假分数,而不使用带分数.所以需将带分数化为假分数.3.某些时候将分数线视为除号,可使繁分数的运算更加直观.4.对于定义新运算,我们只需按题中的定义进行运算即可.5.本讲要求大家对分数运算有很好的掌握,可参阅《思维导引详解》五年级[第1讲循环小数与分数].1.计算:71147 182621358 1333416⨯+⨯-÷【分析与解】原式=712372317 461224 1488128 131233+⨯=⨯=-2.计算:【分析与解】注意,作为被除数的这个繁分数的分子、分母均含有5199.于是,我们想到改变运算顺序,如果分子与分母在5 199后的两个数字的运算结果一致,那么作为被除数的这个繁分数的值为1;如果不一致,也不会增加我们的计算量.所以我们决定改变作为被除数的繁分数的运算顺序.而作为除数的繁分数,我们注意两个加数的分母相似,于是统一通分为1995×0.5.具体过程如下:原式=5919(3 5.22)19930.41.6 910() 52719950.51995 19(6 5.22)950+-⨯÷+⨯-+=5191.3219930.440.40.5 9() 519950.419950.5 191.329-⨯⨯⨯÷+⨯⨯-=199320.41()19950.5+÷⨯=0.410.5÷=1143.计算:1111111987 -+-【分析与解】原式=11198711986-+=198613973-=198739734.计算:已知=181111+12+1x+4=,则x等于多少?【分析与解】方法一:1118x68114x112x711 1+11148x62+214x1x+4+====+++++++交叉相乘有88x+66=96x+56,x=1.25.方法二:有11131118821x4+==+++,所以18222133x4+==++;所以13x42+=,那么x =1.25.5.求944,43,443,...,44...43个这10个数的和.【分析与解】方法一: 944+43+443...44...43++个=1044(441)(4441)...(44...41)+-+-++-个=104444444...44...49++++-个=1094(999999...999...9)99⨯++++-个 =1004[(101)(1001)(10001)...(1000...01)]99⨯-+-+-++--个 =914111.1009=49382715919⨯-个.方法二:先计算这10个数的个位数字和为39+4=31⨯;再计算这10个数的十位数字和为4×9=36,加上个位的进位的3,为36339+=; 再计算这10个数的百位数字和为4×8=32,加上十位的进位的3,为32335+=; 再计算这10个数的千位数字和为4×7=28,加上百位的进位的3,为28331+=; 再计算这10个数的万位数字和为4×6=24,加上千位的进位的3,为24327+=; 再计算这10个数的十万位数字和为4×5=20,加上万位的进位的2,为20222+=; 再计算这10个数的百万位数字和为4×4=16,加上十万位的进位的2,为16218+=; 再计算这10个数的千万位数字和为4×3=12,加上百万位的进位的1,为12113+=; 再计算这10个数的亿位数字和为4×2=8,加上千万位的进位的1,为819+=;最后计算这10个数的十亿位数字和为4×1=4,加上亿位上没有进位,即为4. 所以,这10个数的和为4938271591.6.如图1-1,每一线段的端点上两数之和算作线段的长度,那么图中6条线段的长度之和是多少?【分析与解】 因为每个端点均有三条线段通过,所以这6条线段的长度之和为: 1173(0.60.875)1+0.75+1.8+2.625=6.175=63440⨯+++=7.我们规定,符号“○”表示选择两数中较大数的运算,例如:3.5○2.9=2.9○3.5=3.5.符号“△”表示选择两数中较小数的运算,例如:3.5△2.9=2.9△3.5=2.9.请计算:23155(0.625)(0.4)333841235(0.3)( 2.25)3104⨯+ 【分析与解】原式1550.6255155725384218384122562.253⨯=⨯÷=+8.规定(3)=2×3×4,(4)=3×4×5,(5)=4×5×6,(10)=9×10×11,….如果111(16)(17)(17)-=⨯,那么方框内应填的数是多少?【分析与解】111(17)()1(16)(17)(17)(16)=-÷=-=161718111516175⨯⨯-=⨯⨯.9.从和式11111124681012+++++中必须去掉哪两个分数,才能使得余下的分数之和等于1?【分析与解】因为1116124+=,所以12,14,16,112的和为l,因此应去掉18与110.10.如图1-2排列在一个圆圈上10个数按顺时针次序可以组成许多个整数部分是一位的循环小数,例如1.892915929.那么在所有这种数中。
最大的一个是多少?【分析与解】有整数部分尽可能大,十分位尽可能大,则有92918……较大,于是最大的为9.291892915.11.请你举一个例子,说明“两个真分数的和可以是一个真分数,而且这三个分数的分母谁也不是谁的约数”.【分析与解】有11461015+=,11110156+=,111351410+=评注:本题实质可以说是寻找孪生质数,为什么这么说呢?注意到11c aa b c b a b c++=⨯⨯⨯⨯,当a c b+=时,有11c a1a b c b a b c a c++==⨯⨯⨯⨯⨯.当a、b、c两两互质时,显然满足题意.显然当a、b、c为质数时一定满足,那么两个质数的和等于另一个质数,必定有一个质数为2,不妨设a为2,那么有2c b+=,显然b、c为一对孪生质数.即可得出一般公式:1112(c2c(c2)2c+=⨯+⨯+⨯),c与c+2均为质数即可.12.计算:111 (11 (1)22331010 -⨯-⨯⨯-⨯⨯⨯)()【分析与解】原式=(21)(21)(31)(31)(101)(101) (22331010)-⨯+-⨯+-⨯+⨯⨯⨯⨯⨯⨯=13243546576879810911223344 (1010)⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=12334455...991011223344...991010⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=121011221010⨯⨯⨯⨯⨯⨯=1120.13.已知11661267136814691570a=10011651266136714681569⨯+⨯+⨯+⨯+⨯⨯⨯+⨯+⨯+⨯+⨯.问a 的整数部分是多少?【分析与解】11661267136814691570a=10011651266136714681569⨯+⨯+⨯+⨯+⨯⨯⨯+⨯+⨯+⨯+⨯=11(651)12(661)13(671)14(681)1569110011651266136714681569⨯++⨯++⨯++⨯++⨯+⨯⨯+⨯+⨯+⨯+⨯()=1112131415110011651266136714681569+++++⨯⨯+⨯+⨯+⨯+⨯() =11121314151001001165+1266136714681569+++++⨯⨯⨯+⨯+⨯+⨯. 因为11121314151001165+1266136714681569++++⨯⨯⨯+⨯+⨯+⨯<111213141510010011121314+156565++++⨯=+++⨯()所以a <10035100+1016565=. 同时111213141510011651266136714681569++++⨯⨯+⨯+⨯+⨯+⨯>111213141510010011121314+156969++++⨯=+++⨯()所以a >100311001016969+=. 综上有3110169<a <3510165.所以a 的整数部分为101.14.问135799...2468100⨯⨯⨯⨯⨯与110相比,哪个更大,为什么?。
