(完整版)解二元一次方程组练习题(经典)
二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题一.解答题(共16小题) 1.解下列方程组 (1)(2)(3))(6441125为已知数a a y x ay x ⎩⎨⎧=-=+(4)!(5)(6).&(7)(8)⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x/(9)(10) ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x,2.求适合的x ,y 的值.!,3.已知关于x ,y 的二元一次方程y=kx+b 的解有和.(1)求k ,b 的值.(2)当x=2时,y 的值. (3)当x 为何值时,y=3."1.解下列方程组(1)(2);(3);(4)|(5).(6);(7)(8)`(9)(10);、$2.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么(2)求出原方程组的正确解.二元一次方程组解法练习题精选参考答案与试题解析<一.解答题(共16小题)1.求适合的x,y的值.考点:解二元一次方程组.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出y的值,继而求出x的值.解答:*解:由题意得:,由(1)×2得:3x﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点评:;本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:>(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.,(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,、①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.|所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:*考点:解二元一次方程组.专题:计算题.分析:先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.解答:解:原方程组可化为,—①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点评:;二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.@4.解方程组:考点:解二元一次方程组.专题:计算题.分析:把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.(解答:解:(1)原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.#5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:|本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.!点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3》考点:解二元一次方程组.专题:计算题.分析:(1)将两组x,y的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k、b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.~解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.(2)由y=x+,^把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:—(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.解答:#解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,*①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.{根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.。
二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题精选(含答案)一.解答题(共16小题)1.求适合的x,y的值.2.解下列方程组(1)(2)(3)(4).3.解方程组:4.解方程组:5.解方程组:6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?7.解方程组:(1);(2).8.解方程组:9.解方程组:10.解下列方程组:(1)(2)11.解方程组:(1)(2)12.解二元一次方程组:(1);(2).13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.14.15.解下列方程组:(1);(2).16.解下列方程组:(1)(2)二元一次方程组解法练习题精选(含答案)参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.解二元一次方程组.考点:分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求y的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.评:2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:考点:解二元一次方程组.专题:计算题.分析:先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.解答:解:原方程组可化为,①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点评:注意:二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.4.解方程组:考点:解二元一次方程组.专题:计算题.分把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.析:解答:解:(1)原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?考点:解二元一次方程组.专题:计算题.分析:(1)将两组x,y的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.(2)由y=x+,把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y)+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:(1);(2).考点:解二元一次方程组.专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=,∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程.16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解.点评:。
解二元一次方程组练习题(经典)

解二元一次方程组练习题1.(2013•梅州)解方程组.2.(2013•淄博)解方程组.3.(2013•邵阳)解方程组:.4.(2013•遵义)解方程组.5.(2013•湘西州)解方程组:.6.(2013•荆州)用代入消元法解方程组.7.(2013•汕头)解方程组.8.(2012•湖州)解方程组.9.(2012•广州)解方程组.10.(2012•常德)解方程组:11.(2012•南京)解方程组.12.(2012•厦门)解方程组:.13.(2011•永州)解方程组:.14.(2011•怀化)解方程组:.15.(2013•桂林)解二元一次方程组:.16.(2010•南京)解方程组:.17.(2010•丽水)解方程组:18.(2010•广州)解方程组:.19.(2009•巴中)解方程组:.20.(2008•天津)解方程组:21.(2008•宿迁)解方程组:.22.(2011•桂林)解二元一次方程组:.23.(2007•郴州)解方程组:24.(2007•常德)解方程组:.25.(2005•宁德)解方程组:26.(2011•岳阳)解方程组:.27.(2005•苏州)解方程组:.28.(2005•江西)解方程组:29.(2013•自贡模拟)解二元一次方程组:.30.(2013•黄冈)解方程组:.解二元一次方程组练习题参考答案与试题解析一.解答题(共30小题)1.(2013•梅州)解方程组.,∴原方程组的解为2.(2013•淄博)解方程组.,故此方程组的解为:3.(2013•邵阳)解方程组:.,所以,方程组的解是4.(2013•遵义)解方程组.,所以,方程组的解是5.(2013•湘西州)解方程组:.,则原方程组的解为:.,所以,方程组的解是7.(2013•汕头)解方程组.,.8.(2012•湖州)解方程组.∴原方程组的解是9.(2012•广州)解方程组.,所以方程组的解是10.(2012•常德)解方程组:11.(2012•南京)解方程组.故原方程组的解是12.(2012•厦门)解方程组:.,故此方程组的解为:13.(2011•永州)解方程组:.,.14.(2011•怀化)解方程组:.,∴方程组的解集是:15.(2013•桂林)解二元一次方程组:.,故此方程组的解为16.(2010•南京)解方程组:..所以原方程组的解是17.(2010•丽水)解方程组:..18.(2010•广州)解方程组:.,所以方程组的解是19.(2009•巴中)解方程组:.,20.(2008•天津)解方程组:∴原方程组的解为21.(2008•宿迁)解方程组:.,∴原方程组的解是22.(2011•桂林)解二元一次方程组:.所以此二元一次方程组的解为故答案为:23.(2007•郴州)解方程组:解:原方程组化为:故原方程组的解为24.(2007•常德)解方程组:.因此原方程组的解为25.(2005•宁德)解方程组:∴原方程组的解是∴原方程组的解是26.(2011•岳阳)解方程组:.方程组的解集是:27.(2005•苏州)解方程组:.解:原方程组可化为.故原方程组的解为28.(2005•江西)解方程组::由原方程组得∴原方程组的解为:由得:∴原方程组的解为29.(2013•自贡模拟)解二元一次方程组:.,,所以,方程组的解是30.(2013•黄冈)解方程组:.解:方程组可化为.只要下功夫,一定有收获!。
完整版)二元一次方程组应用题经典题及答案

完整版)二元一次方程组应用题经典题及答案实际问题与二元一次方程组题型归纳(练题答案)类型一:列二元一次方程组解决——行程问题变式1】甲、乙两人相距36千米,相向而行,如果甲比乙先走2小时,那么他们在乙出发2.5小时后相遇;如果乙比甲先走2小时,那么他们在甲出发3小时后相遇,甲、乙两人每小时各走多少千米?解:设甲、乙速度分别为x、y千米/时,依题意得:2.5+2)x+2.5y=363x+(3+2)y=36解得:x=6,y=3.6答:甲的速度是6千米/每小时,乙的速度是3.6千米/每小时。
变式2】两地相距280千米,一艘船在其间航行,顺流用14小时,逆流用20小时,求船在静水中的速度和水流速度。
解:设这艘轮船在静水中的速度x千米/小时,则水流速度y千米/小时,有:20(x-y)=28014(x+y)=280解得:x=17,y=3答:这艘轮船在静水中的速度17千米/小时、水流速度3千米/小时。
类型二:列二元一次方程组解决——工程问题变式】小明家准备装修一套新住房,若甲、乙两个装饰公司合作6周完成需工钱5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周完成,需工钱4.8万元。
若只选一个公司单独完成,从节约开支的角度考虑,小明家应选甲公司还是乙公司?请你说明理由。
解:设甲、乙公司每周的工钱分别为x、y万元,依题意得:6(x+y)=5.24x+9y=4.8解得:x=0.8,y=0.4若只选一个公司单独完成,小明家应选择乙公司,因为乙公司每周工钱更少,从节约开支的角度考虑更优。
类型三:列二元一次方程组解决——商品销售利润问题变式1】(2011湖南衡阳)李大叔去年承包了10亩地种植甲、乙两种蔬菜,共获利元,其中甲种蔬菜每亩获利2000元,乙种蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜各种植了多少亩?解:设甲、乙两种蔬菜各种植了x、y亩,依题意得:①x+y=10②2000x+1500y=解得:x=6,y=4答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩。
解二元一次方程50道练习题(带答案)

解二元一次方程50道练习题(带答案)
1. 解方程组:
{2x - y = 3
{3x + 2y = 8
解答:
首先,可以通过消元法来解决这个问题。
将第一个方程乘以2,并将第二个方程乘以3,得到:
{4x - 2y = 6
{9x + 6y = 24
接下来,将第一个方程的两倍加到第二个方程上,得到:
{4x - 2y = 6
{13x + 4y = 30
然后,将第一个方程的2倍加到第二个方程上,得到:
{4x - 2y = 6
{8x - 8y = 12
接下来,将第二个方程的两倍加到第一个方程上,得到:
{36x = 18
{8x - 8y = 12
最后,解方程得到:
{x = 0.5
{y = 2
2. 解方程组:
{3x + 2y = 7
{5x + 3y = 11
解答:
可以使用消元法来解决这个方程组。
将第一个方程乘以3,并将第二个方程乘以2,得到:
{9x + 6y = 21
{10x + 6y = 22
接下来,将第二个方程的两倍减去第一个方程,得到:
{9x + 6y = 21
{2x = 1
最后,解方程得到:
{x = 0.5
{y = 2
3. ...
...
50. ...
...
这是前面五道解二元一次方程的练习题,你可以根据相同的方法解答剩下的题目。
希望这些练习题对你有帮助!。
二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题精选(含答案) 二元一次方程组解法练题精选(含答案)一.解答题(共16小题)1.求适合 $3x-2y=2$ 和 $6x+y=3$ 的 $x$,$y$ 的值。
解答:由 $(1)\times2$ 得:$3x-2y=2$(3),由$(2)\times3$ 得:$6x+y=3$(4),$(3)\times2$ 得:$6x-4y=4$(5),$(5)-(4)$ 得:$y=-\frac{1}{2}$,把 $y$ 的值代入 $(3)$ 得:$x=\frac{1}{2}$,故原方程组的解为$(x,y)=(\frac{1}{2},-\frac{1}{2})$。
2.解下列方程组:begin{cases} \frac{x}{2}+\frac{y}{3}=1 \\\frac{x}{3}+\frac{y}{2}=2 \end{cases}$$解答:由题意得:$\frac{x}{2}+\frac{y}{3}=1$(1),$\frac{x}{3}+\frac{y}{2}=2$(2),先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法解二元一次方程组。
把 $(1)\times3$ 减去 $(2)\times2$,得到 $x=-1$,把$x=-1$ 代入 $(1)$,得到 $y=6$,故原方程组的解为 $(x,y)=(-1,6)$。
3.解方程组:begin{cases} 3x+2y=7 \\ 2x+3y=8 \end{cases}$$解答:把两方程相加得到 $5x+5y=15$,即 $x+y=3$,把$x+y=3$ 代入其中一个方程,如 $(1)$,得到 $x=-1$,再把$x=-1$ 代入 $(1)$ 或 $(2)$ 中的一个方程,如 $(1)$,得到$y=4$,故原方程组的解为 $(x,y)=(-1,4)$。
4.解方程组:begin{cases} x+y=5 \\ 2x-y=4 \end{cases}$$解答:把两方程相加得到 $3x=9$,即 $x=3$,把$x=3$ 代入其中一个方程,如 $(1)$,得到 $y=2$,再把 $x=3$,$y=2$ 代入原方程组检验,发现符合,故原方程组的解为$(x,y)=(3,2)$。
(完整版)二元一次方程组练习题(含答案)

二元一次方程组练习题一.解答题(共16小题) 1.解下列方程组(1)(2)(3)(4))(6441125为已知数a a y x ay x ⎩⎨⎧=-=+(5)(6).(7)(8)⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x (9)(10) ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x 2.求适合的x ,y 的值.3.已知关于x ,y 的二元一次方程y=kx+b 的解有和.(1)求k ,b 的值.(2)当x=2时,y 的值.(3)当x 为何值时,y=3?1.解下列方程组(1)(2);(3);(4)(5).(6)(7)(8)(9)(10);2.在解方程组时,由于粗心,甲看错了方程组中的a ,而得解为,乙看错了方程组中的b ,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解. a t a nd Al l th i ng si nh ei r be i ng a 二元一次方程组解法练习题精选参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.考点:解二元一次方程组.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出y的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点评:本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:t h i n gt a t i mA l lt h in gs inh ei r be i ng ar ef o rs om et h②其中一个未知数的系数为1时,宜用代入法.3.解方程组:考点:解二元一次方程组.专题:计算题.分析:先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.解答:解:原方程组可化为,①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点评:;二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.4.解方程组:考点:解二元一次方程组.专题:计算题.分析:把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.解答:解:(1)原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?考点:解二元一次方程组.专题:计算题.h i ng at h i n ga ta ti m分析:(1)将两组x,y的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k、b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.(2)由y=x+,把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.解答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.t h i n ga ta ti n gs inh ei r be i ng ar eg oo df o rs om e点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y)+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.t h i n ga ta ti me an dA lh ei ro od fo rs om e解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:(1);(2).考点:解二元一次方程组.专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;i n g a ta ti me an dA l lt h in gs inh ei r be i ng ar eg oo df o rs om et h in g(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程. 16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.点评:解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解. 。
专题解二元一次方程组(计算题50题)(原卷版)
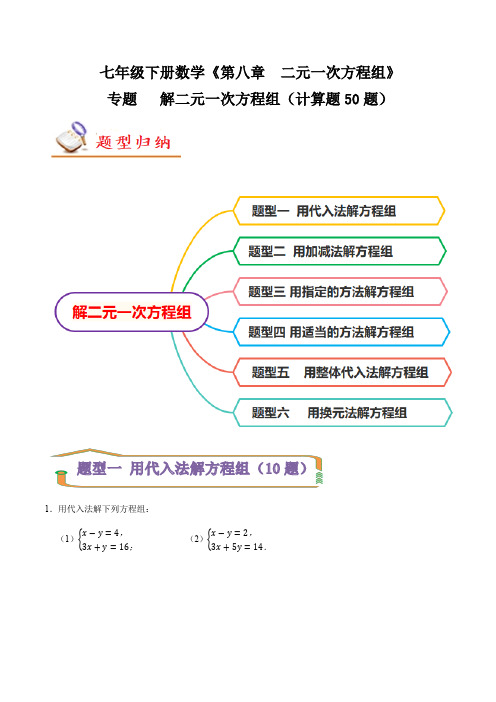
七年级下册数学《第八章二元一次方程组》专题解二元一次方程组(计算题50题)1.用代入法解下列方程组:(1){x−y=4,3x+y=16;(2){x−y=2,3x+5y=14.2.用代入法解下列方程组:(1){2x −y =33x +2y =8; (2){u +v =103u −2v =5.3.用代入法解下列方程组: (1){3x −y =2,9x +8y =17;(2){3x −4y =10x +3y =12.4.用代入法解下列方程组.(1){x +2y =4y =2x −3;(2){x −y =44x +2y =−2.5.用代入法解下列方程组:(1){5x +4y =−1.52x −3y =4 (2){4x −3y −10=03x −2y =06.用代入法解下列方程组: (1){x −y =42x +y =5;(2){3x −y =29x +8y =17;(3){3x +2y =−86x −3y =−9.7.用代入法解下列方程组:(1){3x +2y =11,①x =y +3,② (2){4x −3y =36,①y +5x =7,② (3){2x −3y =1,①3x +2y =8,②8.用代入法解下列方程组: (1){5x +2y =15①8x +3y =−1②; (2){3(y −2)=x −172(x −1)=5y −8.9.用代入法解下列方程组:(1){x =6−5y 3x −6y =4 (2){5x +2y =15x +y =6(3){3x +4y =22x −y =5 (4){2x +3y =73x −5y =110.用代入法解下列方程组:(1){2x +y =3x +2y =−6; (2){x +5y =43x −6y =5;(3){2x −y =63x +2y =2; (4){5x +2y =113y −x =−9;1.用加减法解下列方程组:(1){4x −y =143x +y =7(2){12x −2y =712x −3y =−82.用加减法解下列方程组: (1){2m +7n =53m +n =−2(2){2u −5v =124u +3v =−2(3){x 3−y 7=12x 3+y 7=133.用加减法解下列方程组:(1){x −y =52x +y =4;(2){x −2y =33x +4y =−1.4.用加减法解下列方程组: (1){4x −3y =11,2x +y =13;(2){x −y =3,2y +3(x −y)=115.用加减法解下列方程组:(1){3μ+2t =76μ−2t =11 (2){2a +b =33a +b =4.6.(2023•市北区校级开学)用加减法解下列方程组:(1){3y −4x =04x +y =8; (2){2x +y =312x −32y =−1.7.(2022秋•陕西期末)用加减法解下列方程组:(1){x −y =33x −8y =14; (2){3x +2y =10x 2=1+y+13.8.用加减法解下列方程组: (1){x +3=y ,2(x +1)−y =6; (2){x +y =2800,96%x +64%y =2800×92%.9.用加减法解下列方程组: (1){x −y =5,①2x +y =4;②(2){x −2y =1,①x +3y =6;②(3){2x −y =5,①x −1=12(2y −1).②10.用加减法解下列方程组:(1){x +3y =62x −3y =3 (2){7x +8y =−57x −y =4(3){y −1=3(x −2)y +4=2(x +1) (4){x3+y4=1x 2−y 3=−1.1.(2022春•新田县期中)用指定的方法解下列方程组: (1){2x −5y =14①y =−x②(代入法); (2){2x +3y =9①3x +5y =16②(加减法).2.(2022春•安岳县校级月考)解下列方程组:(1){3x −y =75x +2y =8(用代入法); (2){m4+n3=10m 3−n 4=5(用加减法).3.(2022春•大连期中)用指定的方法解下列方程组:(1){x −3y =42x +y =13(代入法); (2){5x +2y =4x +4y =−6(加减法).4.(2022春•宁远县月考)请用指定的方法解下列方程组 (1){5a −b =113a +b =7(代入消元法); (2){2x −5y =245x +2y =31(加减消元法).5.(2021秋•蒲城县期末)请用指定的方法解下列方程组: (1){2x +3y =11①x =y +3②(代入消元法); (2){3x −2y =2①4x +y =10②(加减消元法).6.(2022秋•历下区期中)请用指定的方法解下列方程组:(1){m −n2=22m +3n =12(代入法); (2){6s −5t =36s +t =−15(加减法).7.(2022春•泰安期中)用指定的方法解下列方程组 (1){3x +4y =19x −y =4(代入消元法);(2){2x +3y =−53x −2y =12(加减消元法);(3){5(x −9)=6(y −2)x 4−y+13=2.8.(2021秋•历下区期中)请用指定的方法解下列方程组:(1){3x +2y =14x =y +3;(代入法) (2){2x +3y =123x +4y =17.(加减法)9.(2021春•沙河口区期末)用指定的方法解下列方程组:(1){y =2x −33x +2y =8(代入法); (2){3x +4y =165x −6y =33(加减法).10.用指定的方法解下列方程组:(1){3x +4y =19x −y =4(代入法); (2){2x +3y =−53x −2y =12(加减法).1.(2022•苏州模拟)用适当的方法解下列方程组.(1){x +2y =9y −3x =1; (2){23x −34y =14(x −y)−(y −4x)=4.2.(2022秋•锦江区校级期末)用适当的方法解下列方程组.(1){x =2y −14x +3y =7; (2){3x +2y =22x +3y =28,.3.用适当的方法解下列方程组: (1){x +2y =0,3x +4y =6;(2){x+13=2y2(x +1)−y =11(3){x +0.4y =40,0.5x +0.7y =35; (4){m+n 3+n−m 4=−14,m+86−5(n+1)12=2.4.(2022•天津模拟)用适当的方法解下列方程组:(1){x +y =52x −y =4; (2){x+13=y+24x−34−y−33=112.5.(2021•越城区校级开学)用适当的方法解下列方程组: (1){2x −3y =7x −3y =7. (2){0.3p +0.4q =40.2p +2=0.9q .6.(2022春•东城区校级月考)用适当的方法解下列方程组 (1){x +y =52x +y =8; (2){2x +3y =73x −2y =4.7.(2021春•哈尔滨期末)用适当的方法解下列方程组 (1){x +2y =93x −2y =−1 (2){2x −y =53x +4y =28.(2022春•椒江区校级期中)用适当的方法解下列方程组: (1){2x +3y =16①x +4y =13②; (2)2s+t 3=3s−2t 8=3.9.(2022春•诸暨市期中)用适当的方法解下列方程组:(1){y =2x −1x +2y =−7 (2){x 4+y 3=7x 3+y 2=810.(2021春•南湖区校级期中)用适当的方法解下列方程组: (1){3x +2y =9x −y =8; (2){x−y3=x+y22x −5y =7.1.先阅读材料,然后解方程组: 材料:解方程组{x +y =4①3(x +y)+y =14②在本题中,先将x +y 看作一个整体,将①整体代入②,得3×4+y =14,解得y =2.把y =2代入①得x =2,所以{x =2y =2这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此法解答,请用这种方法解方程组{x −y −1=0①4(x −y)−y =5②.2.(2021秋•乐平市期末)解方程组{3x −2y =8⋯⋯⋯①3(3x −2y)+4y =20⋯.②时,可把①代入②得:3×8+4y =20,求得y =﹣1,从而进一步求得{x =2y =−1这种解法为“整体代入法“,请用这样的方法解下列方程组{2x −3y =123(2x −3y)+5y =26.3.先阅读,然后解方程组.解方程组{x −y −1=0①4(x −y)−y =5②时,可由①得x ﹣y =1.③,然后再将③代入②得4×1﹣y =5,求得y =﹣1,从而进一步求得{x =0y =−1这种方法被称为“整体代入法”,请用这样的方法解下列方程组:{2x −3y +5=06y−4x+37=2y +1.4.(2022春•太和县期末)先阅读,然后解方程组.解方程组{x −y −1=0①4(x −y)−y =5②时, 可由 ①得x ﹣y =1,③然后再将③代入②得4×1﹣y =5,求得y =﹣1,从而进一步求得{x =0①y =−1②这种方法被称为“整体代入法”, 请用这样的方法解下列方程组{2x −3y −2=02x−3y+57+2y =9.5.先阅读,然后解方程组.解方程组{x −y −1=0①4(x −y)−y =5②时,可由①得x ﹣y =1③, 然后再将③代入②得4×1﹣y =5,求得y =﹣1,从而进一步求得x 这种方法被称为“整体代入法”,请用这样的方法解下列方程组:{2x −3y −2=03(2x −3y)+y =7.1.用换元法解下列方程组{2x +2y =125x −1y =342.用换元法解下列方程组:(1){3(x +y)+2(x −y)=36(x +y)−4(x −y)=−16 (2){x−4y 2+x+5y 3=2x−4y 3−(x +5y)=5.3.(2022春•云阳县期中)阅读探索:解方程组{(a −1)+2(b +2)=62(a −1)+(b +2)=6解:设a ﹣1=x ,b +2=y 原方程组可以化为{x +2y =62x +y =6,解得{x =2y =2,即:{a −1=2b +2=2∴{a =3b =0,此种解方程组的方法叫换元法.(1)拓展提高运用上述方法解下列方程组{(a 4−1)+2(b 5+2)=102(a 4−1)+(b 5+2)=11; (2)能力运用已知关于x ,y 的方程组{a 1x +b 1y =c 1a 2x +b 2y =c 2的解为{x =6y =7,求关于m 、n 的方程组{a 1(m −2)+b 1(n +3)=c 1a 2(m −2)+b 2(n +3)=c 2的解.4.在学过了二元一次方程组的解法后,课堂上老师又写出了一个题目:{x+y 6+x−y 10=3①x+y 6−x−y 10=−1②,你会解这个方程组吗?小明、小刚、小芳争论了一会儿,他们分别写出了一种方法:小明:把原方程组整理得{8x +2y =90③2x +8y =−30④④×4﹣③得30y =﹣210,所以y =﹣7把y =﹣7代入③得8x =104,所以x =13,即{x =13y =−7小刚:设x+y 6=m ,x−y 10=n ,则{m +n =3③m −n =−1④③+④得m =1,③﹣④得m =2,即{x+y 6=1x−y 10=2,所以{x +y =6x −y =20,所以{x =13y =−7. 小芳:①+②得2(x+y)6=2,即x +y =6.③ ①﹣②得2(x−y)10=4,即x ﹣y =20.④③④组成方程组得x =13③﹣④得y =﹣7,即{x =13y =−7. 老师看过后,非常高兴,特别是小刚的方法独特,像小刚的这种方法叫做换元法,你能用换元法解下列方程组吗?{3x−2y 6+2x+3y 7=13x−2y 6−2x+3y 7=5.5.(2022春•卧龙区校级月考)阅读探索(1)知识积累解方程组{(a −1)+2(b +2)=62(a −1)+(b +2)=6. 解:设a ﹣1=x ,b +2=y .原方程组可变为{x +2y =62x +y =6,解这个方程组得{x =2y =2,即{a −1=2b +2=2,所以{a =3b =0,这种解方程组的方法叫换元法.(2)拓展提高运用上述方法解下列方程组:{(m 3−1)+2(n 5+2)=43(m 3−1)−(n 5+2)=5. (3)能力运用已知关于x ,y 的方程组{a 1x +b 1y =c 1a 2x +b 2y =c 2的解为{x =3y =4,请直接写出关于m 、n 的方程组{a 1(m +2)−b 1n =c 1a 2(m +2)−b 2n =c 2的解是 .。
