C语言求素数(质数)Eratosthenes经典算法
C语言求素数(质数)Eratosthenes经典算法

//使用Erato sthene s方法找出指定范围内的所有质数#include <stdlib.h>#defineSIZE 500 //该方法能够求出2*SIZE 之内的质数#defineTRUE 1#defineFALSE 0intmain(){char sieve[ SIZE ]; /* the sieve */char *sp; /* pointer to accessthe sieve */int number; /* numberwe’re computi ng *//*** Set the entiresieve to TRUE.*/for(sp = sieve; sp<&sieve[ SIZE ]; )*sp++ = TRUE;/*** Process each numberfrom 3 to as many as the sieve holds. (Note: the** loop is termina ted from inside.)*/for( number= 3; ; number+= 2 ){/*** Set the pointer to the properelement in the sieve, and stop** the loop if we’ve gone too far.*/sp = &sieve[ 0 ] + ( number-3 ) / 2;if(sp>= &sieve[ SIZE ] )break;/*** Now advance the pointer by multipl es of the numberand set** each subsequ ent entry FALSE.*/while(sp += number, sp<&sieve[ SIZE ] )*sp = FALSE;}/*** Go through the entiresieve now and print the numbers corresp onding** to the locatio ns that remainTRUE.*/printf( "2\t" );for( number= 3, sp = &sieve[ 0 ];sp<&sieve[ SIZE ];number+= 2, sp++ ){if( *sp )printf( "%d\t", number);}system("pause");returnEXIT_SU CCESS; }。
C语言常用数值计算算法(素数、公约数、级数、方程根和定积分)
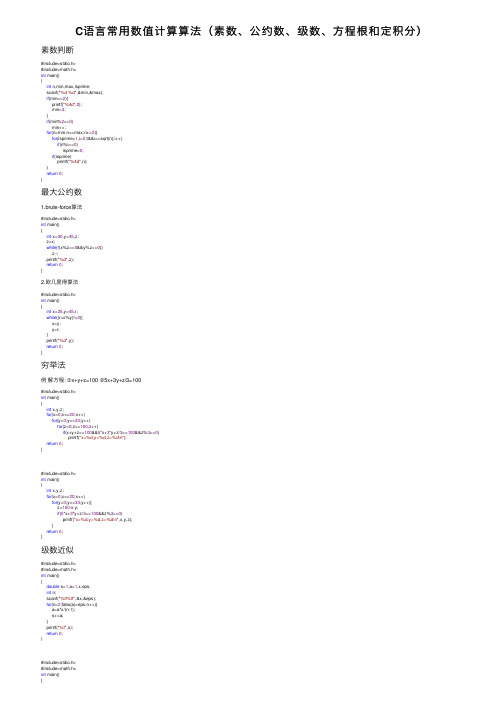
C语⾔常⽤数值计算算法(素数、公约数、级数、⽅程根和定积分)素数判断#include<stdio.h>#include<math.h>int main(){int n,min,max,isprime;scanf("%d %d",&min,&max);if(min<=2){printf("%4d",2);min=3;}if(min%2==0)min++;for(n=min;n<=max;n+=2){for(isprime=1,i=2;t&&i<=sqrt(n);i++)if(n%i==0)isprime=0;if(isprime)printf("%4d",n);}return0;}最⼤公约数1.brute-force算法#include<stdio.h>int main(){int x=30,y=45,z;z=x;while(!(x%z==0&&y%z==0))z--;printf("%d",z);return0;}2.欧⼏⾥得算法#include<stdio.h>int main(){int x=35,y=45,r;while((r=x%y)!=0){x=y;y=r;}printf("%d",y);return0;}穷举法例解⽅程: ①x+y+z=100 ②5x+3y+z/3=100#include<stdio.h>int main(){int x,y,z;for(x=0;x<=20;x++)for(y=0;y<=33;y++)for(z=0;z<=100;z++)if(x+y+z==100&&5*x+3*y+z/3==100&&z%3==0)printf("x=%d,y=%d,z=%d\n");return0;}#include<stdio.h>int main(){int x,y,z;for(x=0;x<=20;x++)for(y=0;y<=33;y++){z=100-x-y;if(5*x+3*y+z/3==100&&z%3==0)printf("x=%d,y=%d,z=%d\n",x,y,z);}return0;}级数近似#include<stdio.h>#include<math.h>int main(){double s=1,a=1,x,eps;int n;scanf("%lf%lf",&x,&eps);for(n=2;fabs(a)>eps;n++){a=a*x/(n-1);s+=a;}printf("%f",s);return0;)#include<stdio.h>#include<math.h>int main(){double sum,x,eps=1e-6,fn,tn;int s=1,n=2;scanf("%lf",&x);s=fn=x;do{s=-s;fn=fn*(2*n-3)/(2*n-2)*x*x;tn=sign*fn/(2*n-1);sum=sum+tn;n++;}while(fabs(tn)>eps);printf("%f",sum);⼀元⾮线性⽅程求根⼀、⽜顿迭代法 1.基本概念:如果函数连续,且待求零点孤⽴,那么在零点周围存在⼀个区域,当初值在这个邻域内时,⽜顿法收敛。
c语言求素数最快方法

c语言求素数最快方法摘要:1.引言2.最快方法:埃拉托斯特尼筛法(Sieve of Eratosthenes)3.算法原理4.C语言实现5.代码解析6.性能测试与优化7.结论正文:**引言**在计算机科学和编程领域,寻找素数是一种常见的任务。
素数是指大于1的自然数中,除了1和它本身以外,不能被其他自然数整除的数。
求解素数问题有助于理解数论、密码学等领域。
本文将介绍求解素数的最快方法——埃拉托斯特尼筛法(Sieve of Eratosthenes)及其C语言实现。
**最快方法:埃拉托斯特尼筛法(Sieve of Eratosthenes)**埃拉托斯特尼筛法是一种基于二维数组的算法,用于找出小于等于上限的素数。
该算法利用了素数的性质:如果一个数是素数,那么它的平方模小于等于上限的数也是素数。
通过不断标记数组中的素数,最终得到小于等于上限的素数。
**算法原理**1.创建一个二维数组,用于存储小于等于上限的数。
2.初始化数组中的所有元素为1,表示都是素数。
3.从2开始,遍历数组,将数组中的所有素数两两相乘,得到的结果大于上限的,将其对应的元素标记为0,表示该数不是素数。
4.重复步骤3,直到数组中的所有元素都被标记或遍历到上限。
**C语言实现**以下是一个简单的C语言实现:```c#include <stdio.h>#include <stdbool.h>void sieve_of_eratosthenes(int limit) {bool *prime = (bool *)malloc((limit + 1) * sizeof(bool));for (int i = 0; i <= limit; i++) {prime[i] = true;}for (int p = 2; p * p <= limit; p++) {if (prime[p]) {for (int i = p * p; i <= limit; i += p) {prime[i] = false;}}}for (int i = 2; i <= limit; i++) {if (prime[i]) {printf("%d ", i);}}free(prime);}int main() {int limit;printf("请输入一个上限:");scanf("%d", &limit);sieve_of_eratosthenes(limit);return 0;}```**代码解析**1.首先,我们需要一个布尔数组来存储小于等于上限的数是否为素数。
c++素数判定法

c++素数判定法素数是一个大于1的自然数,它的正因子只有1和它本身。
在计算机科学中,我们经常需要判断一个数是否为素数。
本文将介绍在C++中实现素数判定的一些方法。
1. 直接遍历法直接遍历法是最简单的素数判定方法,它依次检查从2到n-1的所有整数,看是否为该数的因子。
如果所有因子都只有1和本身,那么该数就是素数。
以下是使用直接遍历法的C++代码实现:```cpp#include <iostream>using namespace std;bool isPrime(int n) {if (n <= 1) {return false;}for (int i = 2; i * i <= n; i++) {if (n % i == 0) {return false;}}return true;}int main() {int n;cout << "Enter a number: ";cin >> n;if (isPrime(n)) {cout << n << " is a prime number." << endl;} else {cout << n << " is not a prime number." << endl;}return 0;}```2. 埃拉托斯特尼筛选法(Sieve of Eratosthenes)埃拉托斯特尼筛选法是一种更高效的素数判定方法,它通过逐次筛选出素数,从而判断一个数是否为素数。
以下是使用埃拉托斯特尼筛选法的C++代码实现:```cpp#include <iostream>#include <vector>using namespace std;vector<bool> sieve(int n) {vector<bool> prime(n + 1, true);prime[0] = prime[1] = false;for (int i = 2; i * i <= n; i++) {if (prime[i]) {for (int j = i * i; j <= n; j += i) {prime[j] = false;}}}return prime;}bool isPrime(int n, const vector<bool>& prime) {if (n <= 1) {return false;}if (prime[n]) {return true;} else {return false;}}3. 基布尔算法(Karatsuba's algorithm)基布尔算法是一种快速判定素数的方法,它利用了素数的性质:如果p是素数,那么p-1和p+1都是素数。
c语言求质数个数的古老方法

c语言求质数个数的古老方法古老的方法求质数个数质数是指大于1的整数,除了1和它本身之外,没有其他因数的数。
求质数个数是数论中的一个重要问题,古代数学家们通过一些简单但有效的方法来解决这个问题。
我们来看一个最简单的方法——试除法。
这是古代数学家们最早使用的方法之一。
试除法的思路是,对于给定的一个数n,我们从2开始,逐个除以小于等于n的所有数,如果能整除,则说明n不是质数;反之,如果不能整除,则说明n是质数。
试除法的代码如下所示:```c#include <stdio.h>int isPrime(int n) {if (n <= 1) {return 0;}for (int i = 2; i < n; i++) {if (n % i == 0) {return 0;}}return 1;}int countPrimes(int n) {int count = 0;for (int i = 2; i <= n; i++) {if (isPrime(i)) {count++;}}return count;}int main() {int n;printf("请输入一个正整数:");scanf("%d", &n);int count = countPrimes(n);printf("小于等于%d的质数个数为:%d\n", n, count); return 0;}上述代码中,我们定义了两个函数isPrime和countPrimes。
isPrime函数用于判断一个数是否为质数,countPrimes函数用于计算小于等于给定数n的质数个数。
在主函数中,我们通过用户输入一个正整数n,然后调用countPrimes函数计算质数个数,并输出结果。
然而,试除法虽然简单,但对于较大的数,效率较低。
因此,古代数学家们还发展了其他更高效的方法。
c语言埃氏筛求素数

c语言埃氏筛求素数埃氏筛是一种用于求解素数的经典算法,它以法国数学家埃拉托斯特尼斯(Eratosthenes)的名字命名。
这个算法的基本思想是通过不断筛除合数来得到素数。
我们需要明确什么是素数。
素数是指大于1且只能被1和自身整除的正整数。
例如,2、3、5、7、11等都是素数,而4、6、8、9等都不是素数。
那么,我们如何使用埃氏筛来求解素数呢?首先,我们需要一个足够大的范围来筛选,假设我们要求解小于等于N的素数。
我们可以创建一个长度为N+1的布尔数组,初始时将所有元素都标记为true,表示都是素数。
然后,从2开始,我们将素数2的倍数(除了2本身)全部标记为false,因为它们都可以被2整除,所以不是素数。
接着,我们找到下一个没有被标记为false的数,也就是3,将素数3的倍数(除了3本身)全部标记为false。
依次类推,直到我们找到第一个没有被标记为false的数x,那么x就是素数,我们再将x的倍数(除了x 本身)全部标记为false。
重复上述步骤,直到我们找到的最后一个素数的平方小于等于N为止。
此时,数组中所有标记为true的元素就是小于等于N的素数。
下面,我们来具体实现一下这个算法。
```c#include <stdio.h>#include <stdbool.h>void sieveOfEratosthenes(int N) {bool isPrime[N+1];memset(isPrime, true, sizeof(isPrime));for (int i = 2; i * i <= N; i++) {if (isPrime[i]) {for (int j = i * i; j <= N; j += i) { isPrime[j] = false;}}}printf("小于等于%d的素数有:\n", N); for (int i = 2; i <= N; i++) {if (isPrime[i]) {printf("%d ", i);}}printf("\n");}int main() {int N;printf("请输入一个正整数N:");scanf("%d", &N);sieveOfEratosthenes(N);return 0;}```以上是一个基于C语言的埃氏筛算法的实现。
c语言中判断素数的方法

c语言中判断素数的方法1. 嘿,你知道吗?在 C 语言里可以用循环来判断素数呢!就像警察一个个排查嫌疑人一样。
比如你要判断 7 是不是素数,就从 2 到 6 依次检查能不能整除它。
哎呀,多有趣呀!2. 哇哦,还可以通过判断一个数只有 1 和它本身能整除来确定它是素数哦!这就好像找朋友,只有那一个特别的和它自己才是它的真朋友。
比如11,除了 1 和 11 就没别的朋友能整除它啦,这不就是素数嘛!3. 嘿呀,你有没有想过用平方根的方法来判断素数呀?这可厉害了,就像抄近道一样。
比如要判断25,只需要检查到5 就行了,不用再往后找啦,多省事儿!4. 呀,还能根据素数的特性来写代码判断呢!这就好比是识别一个人的独特标志一样。
就像 13,有了这些特性就能确定它是素数,多神奇!5. 哇塞,其实可以写一个很巧妙的算法来专门判断素数哟!就如同有一双锐利的眼睛能一眼看穿是不是素数。
比如说 17,算法一上,马上就知道它是素数啦!6. 哈哈,你能想到用函数来封装判断素数的过程吗?这就好像把宝藏装在一个盒子里。
然后你想用的时候就拿出来,多方便呀!就像判断 19 是不是素数,用这个函数轻松搞定!7. 哎呀呀,还有一种特别的思路来判断素数呢!就像是找到了一条秘密通道。
比如对某个数进行各种测试,最后确定它是素数,是不是很有意思?8. 咦,你知道吗?通过一些巧妙的条件判断也能知道是不是素数呢!就像一道谜题,解开了就知道答案啦。
试试判断 23 是不是,你就明白啦!9. 好啦,其实判断素数的方法有好多好多呢,每一种都有它的奇妙之处!我觉得啊,这些方法真的让编程变得超级有趣,让我们能发现数字世界里的各种秘密!。
C语言超经典算法大全

C语言经典算法大全老掉牙河内塔费式数列巴斯卡三角形三色棋老鼠走迷官(一)老鼠走迷官(二)骑士走棋盘八个皇后八枚银币生命游戏字串核对双色、三色河内塔背包问题(Knapsack Problem)数、运算蒙地卡罗法求 PIEratosthenes筛选求质数超长整数运算(大数运算)长 PI最大公因数、最小公倍数、因式分解完美数阿姆斯壮数最大访客数中序式转后序式(前序式)后序式的运算关于赌博洗扑克牌(乱数排列)Craps赌博游戏约瑟夫问题(Josephus Problem)集合问题排列组合格雷码(Gray Code)产生可能的集合m元素集合的n个元素子集数字拆解排序得分排行选择、插入、气泡排序Shell 排序法 - 改良的插入排序Shaker 排序法 - 改良的气泡排序Heap 排序法 - 改良的选择排序快速排序法(一)快速排序法(二)快速排序法(三)合并排序法基数排序法搜寻循序搜寻法(使用卫兵)二分搜寻法(搜寻原则的代表)插补搜寻法费氏搜寻法矩阵稀疏矩阵多维矩阵转一维矩阵上三角、下三角、对称矩阵奇数魔方阵4N 魔方阵2(2N+1) 魔方阵1.河内之塔说明河内之塔(Towers of Hanoi)是法国人(Lucas)于1883年从泰国带至法国的,河内为越战时北越的首都,即现在的胡志明市;1883年法国数学家 Edouard Lucas曾提及这个故事,据说创世纪时Benares有一座波罗教塔,是由三支钻石棒(Pag)所支撑,开始时神在第一根棒上放置64个由上至下依由小至大排列的金盘(Disc),并命令僧侣将所有的金盘从第一根石棒移至第三根石棒,且搬运过程中遵守大盘子在小盘子之下的原则,若每日仅搬一个盘子,则当盘子全数搬运完毕之时,此塔将毁损,而也就是世界末日来临之时。
解法如果柱子标为ABC,要由A搬至C,在只有一个盘子时,就将它直接搬至C,当有两个盘子,就将B当作辅助柱。
如果盘数超过2个,将第三个以下的盘子遮起来,就很简单了,每次处理两个盘子,也就是:A->B、A ->C、B->C这三个步骤,而被遮住的部份,其实就是进入程式的递回处理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
//使用Eratosthenes方法找出指定范围内的所有质数
#include <stdlib.h>
#define SIZE 500 //该方法能够求出2*SIZE 之内的质数#define TRUE 1
#define FALSE 0
int
main()
{
char sieve[ SIZE ]; /* the sieve */
char *sp; /* pointer to access the sieve */
int number; /* number we’re computing */
/*
** Set the entire sieve to TRUE.
*/
for(sp = sieve; sp<&sieve[ SIZE ]; )
*sp++ = TRUE;
/*** Process each number from 3 to as many as the sieve holds. (Note: the
** loop is terminated from inside.)
*/
for( number = 3; ; number += 2 ){
/*
** Set the pointer to the proper element in the sieve, and stop
** the loop if we’ve gone too far.
*/
sp = &sieve[ 0 ] + ( number-3 ) / 2;
if(sp>= &sieve[ SIZE ] )
break;
/*
** Now advance the pointer by multiples of the number and set
** each subsequent entry FALSE.
*/
while(sp += number, sp<&sieve[ SIZE ] )
*sp = FALSE;
}
/*
** Go through the entire sieve now and print the numbers corresponding
** to the locations that remain TRUE.
*/
printf( "2\t" );
for( number = 3, sp = &sieve[ 0 ];
sp<&sieve[ SIZE ];
number += 2, sp++ ){
if( *sp )
printf( "%d\t", number );
}
system("pause");
return EXIT_SUCCESS; }。
