初中数学几何题100条秘籍——三角形篇
经典初中数学三角形专题训练及例题解析

经典《三角形》专题训练知识点梳理考点一、三角形1、三角形的定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2、三角形的分类. ⎪⎩⎪⎨⎧钝角三角形直角三角形锐角三角形 ⎪⎪⎩⎪⎪⎨⎧)(等边三角形等腰三角形不等边三角形 3、三角形的三边关系:三角形任意两边之和大于第三边,任意两边之差小于第三边.4、三角形的重要线段①三角形的中线:顶点与对边中点的连线,三条中线交点叫重心②三角形的角平分线:内角平分线与对边相交,顶点和交点间的线段,三个角的角平分线的交点叫内心③三角形的高:顶点向对边作垂线,顶点和垂足间的线段.三条高的交点叫垂心(分锐角三角形,钝角三角形和直角三角形的交点的位置不同)5、三角形具有稳定性6、三角形的内角和定理及性质定理:三角形的内角和等于180°.推论1:直角三角形的两个锐角互补。
推论2:三角形的一个外角等于不相邻的两个内角的和。
推论3:三角形的一个外角大于与它不相邻的任何一个内角。
7、多边形的外角和恒为360°8、多边形及多边形的对角线①正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.②凸凹多边形:画出多边形的任何一条边所在的直线,若整个图形都在这条直线的同一侧,这样的多边形称为凸多边形;,若整个多边形不都在这条直线的同一侧,称这样的多边形为凹多边形。
③多边形的对角线的条数:A.从n 边形的一个顶点可以引(n-3)条对角线,将多边形分成(n-2)个三角形。
B.n 边形共有2)3(-n n 条对角线。
9、边形的内角和公式及外角和①多边形的内角和等于(n-2)×180°(n ≥3)。
②多边形的外角和等于360°。
三角形 (按角分) 三角形 (按边分)10、平面镶嵌及平面镶嵌的条件。
①平面镶嵌:用形状相同或不同的图形封闭平面,把平面的一部分既无缝隙,又不重叠地全部覆盖。
②平面镶嵌的条件:有公共顶点、公共边;在一个顶点处各多边形的内角和为360°。
(完整版)三角形全等添加辅助线口诀

三角形全等添加辅助线口诀人说几何很困难,难点就在辅助线,辅助线,如何添加?把握定理和概念,还要刻苦加钻研,找出规律凭经验,图中有角平分线,可向两边引垂线,也可将图对折看,对称以后关系现,角平分线平行线,等腰三角形来添,角平分线加垂线,三线合一试试看,线段垂直平分线,常向两边把线连,要证线段倍与半,延长缩短可试验,三角形中两中点,连接则成中位线,三角形中有中线,延长中线等中线。
几何,不谈战术谈战略学而思中考研究中心施佳辰作为和代数并列为初中数学两大知识点的几何,常常因为图形变化多端,方法多种多样而被称为数学中的变形金刚。
话虽如此,变形金刚也不是无敌的,最终仍旧是人类的智慧更胜一筹。
实际上,每一道几何题目背后都有着一定的法则和规律,每一类题都有着相似的解题思想,这种思想的集中体现,便是模型(变形金刚的原力所在)。
对于几何,我们不仅仅要在战术上坚定执行,在战略层面上也要对几何在初中三年的整体学习有一个明确的了解。
得模型者得几何,而模型思想的建立又并非一朝一夕,是需要同学们在大量的实战做题和不断总结方法中培养出来的。
对于模型的理解和认识,分为很多层面,最浅的是基本的形似,看到图形相仿或相似的题目,能够有意识的联想以前学过的题型并加以运用,套用,这是最简单的模型思想。
高一些的是神似,看到一些关键点,关键线段或是题目所给条件的相似便能够联想到所学知识点,通过推理和演绎逐步取得正确的解法,记住的是一些具体模型,这,是第二种层次。
最高的境界是,心中只有很少几种基本模型,这些模型就像种子,看到一道题目就会发芽,开花结果,随着对于题目的深入理解,不断地寻找适合的花朵,每一朵花上面都有着一种具体的模型,而每种模型之间,都会有树枝相连,相互间并不是孤立的,而是借由其他条件贯穿连接的。
达到这样的理解才能算是包罗万象,驾轻就熟。
我们对于模型的把控能不应当仅限于会用于具有明显模型特征的题目,对于一些特征并不明显的题目,我们要有能力添加辅助线去挖掘图形当中的隐藏属性。
初中数学复习几何部分——三角形
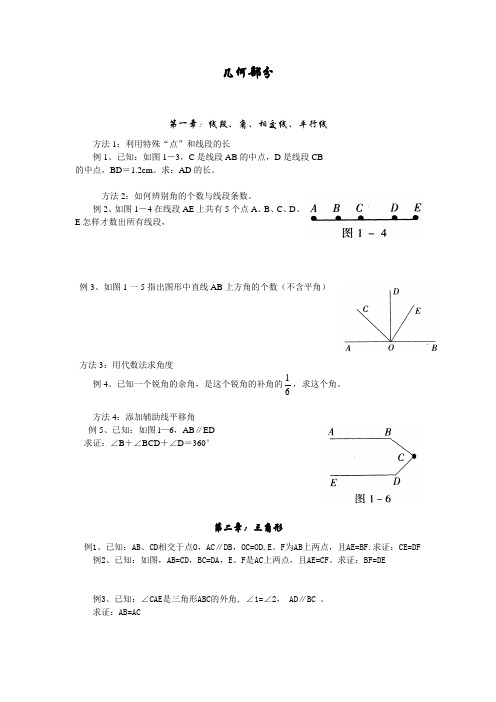
几何部分第一章:线段、角、相交线、平行线方法1:利用特殊“点”和线段的长例1、已知:如图1-3,C 是线段AB 的中点,D 是线段CB的中点,BD =1.2cm 。
求:AD 的长。
方法2:如何辨别角的个数与线段条数。
例2、如图1-4在线段AE 上共有5个点A 、B 、C 、D 、E 怎样才数出所有线段,例3、如图1一5指出图形中直线AB 上方角的个数(不含平角)方法3:用代数法求角度例4、已知一个锐角的余角,是这个锐角的补角的61,求这个角。
方法4:添加辅助线平移角例5、已知:如图l —6,AB ∥ED求证:∠B +∠BCD +∠D =360°第二章:三角形例1、已知:AB 、CD 相交于点O ,AC ∥DB ,OC=OD,E 、F 为AB 上两点,且AE=BF.求证:CE=DF 例2、已知:如图,AB=CD ,BC=DA ,E 、F 是AC 上两点,且AE=CF 。
求证:BF=DE例3、已知:∠CAE 是三角形ABC 的外角, ∠1=∠2, AD ∥BC 。
求证:AB=AC例4、已知:如图 3- 89,OE平分∠AOB,EC⊥OA于 C,ED⊥OB于 D.求证:(1)OC=OD;(2)OE垂直平分CD.第三章:四边形例1、如图41-2,求∠B+∠C+∠D的度数和。
例2、一个多边形的每一个外角都等于45°,那么这个多边形的内角和是多少度。
分析:用多边形外角和公式就可以求解。
例3、已知:如图43-1,在□ABCD中,AE⊥BC于E,AF⊥DC于F,∠EAF=60°,BE=2cm,DF=3cm。
求□ABCD内角的度数与边长。
例4、如图45-4,在□ABCD中,对角线AC、BD交于O点,EF过O分别交BC、AD于点E、F,且AE⊥BC,求证:四边形AECF是矩形。
例5、如图48-3,已知在梯形ABCD 中,AB∥CD,M 、N 分别为CD 、AB 的中点,且MN⊥AB。
求证:梯形ABCD 是等腰梯形。
初中数学三角形知识点典型例题解析都在这了,太全了,中考必备!

初中数学三角形知识点典型例题解析都在这了,太全了,中考必备!初中数学三角形的初步认识复习指导三角形是最简单、最基本的几何图形,在生活中随处可见。
三角形不仅是研究其他图形的基础,而且在解决实际问题中也有着广泛的应用。
因此,认识三角形就显得非常必要。
一、知识要点归纳(一)三角形的概念与性质(1)由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.(2)三角形的两边之和大于第三边,两边之差小于第三边。
(3)三角形的内角和等于180°;三角形的外角和等于360°。
(4)三角形按角分类:直角三角形、锐角三角形、钝角三角形。
(5)三角形中的“三线”是指的中线、高线和角平分线。
任意一个三角形都有三条中线、三条高和三条角平分线,其中三角形的三条中线、三条角平分线分别交于三角形内一点,三角形的三条高所在直线也相交于一点,这个点的位置视三角形的形状而定,它可能在三角形的内部、外部或三角形的顶点上。
(想一想:三角形的三条高线是否相交于一点?为什么?)(二)全等三角形概念与性质(1)能够重合的两个三角形称为全等三角形.(2)全等三角形的对应边相等,对应角相等.(三)三角形全等的条件(1)三角形全等的判别方法有四种:①边角边(SAS);②角边角(ASA);③角角边(AAS);④边边边(SSS)。
例1.已知四组线段的长分别如下,以各组线段为边,能组成三角形的是()。
A. l,2,3 B. 2,5,8 C. 3,4,5 D.4,5,10 分析:本题主要考查三角形的三边关系,应运用“三角形任何两边之和大于第三边”即可解决。
解:观察四个选项,满足两边之和大于第三边的只有3,4,5,故选C。
思路点拨:涉及三角形三边关系的问题时,只要符合“较小两边的和大于第三边”即可。
三、数学思想回顾1.转化思想:将实际问题转化数学问题(全等三角形)解决;2.方程思想:通过设未知数,根据三角形内(外)角和之间的关系构造方程解决角度问题;3.类比思想:说明两个三角形全等时,根据已知条件选择三角形全等的判别方法。
初中几何经典培优题型(三角形)

全等三角形辅助线找全等三角形的方法:〔1〕可以从结论出发,看要证明相等的两条线段〔或角〕分别在哪两个可能全等的三角形中;〔2〕可以从已知条件出发,看已知条件可以确定哪两个三角形相等;〔3〕从条件和结论综合考虑,看它们能一同确定哪两个三角形全等;〔4〕若上述方法均不行,可考虑添加辅助线,构造全等三角形.三角形中常见辅助线的作法:①延长中线构造全等三角形;②利用翻折,构造全等三角形;③引平行线构造全等三角形;④作连线构造等腰三角形.常见辅助线的作法有以下几种:1)遇到等腰三角形,可作底边上的高,利用"三线合一"的性质解题,思维模式是全等变换中的"对折".2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的"旋转".3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的"对折",所考知识点常常是角平分线的性质定理或逆定理.4)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的"平移"或"翻转折叠"5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答.常见辅助线写法:⑴过点A作BC的平行线AF交DE于F⑵过点A作BC的垂线,垂足为D⑶延长AB至C,使BC=AC⑷在AB上截取AC,使AC=DE⑸作∠ABC的平分线,交AC于D⑹取AB中点C,连接CD交EF于G点例1如图,AB=CD=1,∠AOC=60°,证明:AC+BD≥1.例2<2007年中考〕如图,已知△ABC⑴请你在BC边上分别取两点D、E〔BC的中点除外〕,连接AD、AE,写出使此图中只存在两对面积相等的三角形的相应条件,并表示出面积相等的三角形;⑵请你根据使⑴成立的相应条件,证明AB+AC>AD+AE.例3已知线段OA、OB、OC、OD、OE、OF.∠AOB=∠BOC=∠COD=∠DOE=∠EOF=60°.且AD=BE=CF=2.求证:S△OAB+S△OCD+S△OEF3.例4如图1,在四边形ABCD中,连接对角线AC、BD,如果∠1=∠2,那么∠3=∠4.仔细阅读以上材料,完成下面的问题.如图2,设P为□ABCD内一点,∠P AB=∠PCB,求证:∠PBA=∠PDA.图1图2⑴集散思想:有些几何题,条件与结论比较分散,通过添加适当的辅助线,将图形中分散,远离了的元素聚集到有关的图形上,使它们相对集中,便于比较,建立关系,从而找出问题的解决途径.⑵平移只能用来作为作辅助线的思路,具体做辅助线的时候不能直接说将△ABC 平移至△DEF .1.在正方形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 边上的点,且EG ⊥FH ,求 证:EG =FH .2.如图所示,P 为平行四边形ABCD 内一点,求证:以AP 、BP 、CP 、DP 为边可以构成一个四边形,并且所构成的四边形的对角线的长度恰好分别等于AB 和BC .3.如图,已知△ABC 的面积为16,BC =8,现将△ABC 沿直线BC 向右平移a 个单位到△DEF 的位置.⑴当a =4时,求△ABC 所扫过的面积;⑵连接AE 、AD ,设AB =5,当△ADE 是以DE 为一腰的等腰三角形时,求a 的值.4.如图,AA ′=BB ′=CC ′=1,∠AOB ′=∠BOC ′=∠COA ′=60°,求证:34AOB BOC COA SS S '''++<.例1 如图,E 、F 分别是正方形ABCD 的边BC 、CD 上的点,且∠EAF =45°,AH ⊥EF ,H 为垂足,求证:AH =AB .例2△ABC 中,∠ACB =90°,AC =BC ,P 是△ABC 内的一点,且AP =3,CP =2,BP =1,求∠BPC 的度数.例3已知在△ABC 中,AB =AC ,P 为三角形内一点,且∠APB >∠APC ,求证:PB <PC .有边相等或者有角度拼起来为特殊角的时候可以用旋转⑴边相等时常见图形为正方形,等腰三角形和等边三角形等等 ⑵角度能拼成的特殊角指的是180°,90°等等例4已知△ABC ,∠1=∠2,AB =2AC ,AD =BD .求证:DC ⊥AC .例5△ABC 为等腰直角三角形,∠ABC =90°,AB =AE ,∠BAE =30°,求证:BE =CE .例6在△ABC 中,E 、F 为BC 边上的点,已知∠CAE =∠BAF ,CE =BF ,求证:AC =AB .出现轴对称的时候可以考虑翻折,尤其注意有角平分线,有角相等或者出现特殊角的一半的时候,翻折是常用添加辅助线的思想.强调:旋转和翻折只能是一种作辅助线的思路,具体做辅助线的时候不能直接说将△ABC旋转或翻折至△DEF.1.如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心角为直角的扇形纸板的圆心方在O点处,并将纸板绕O点旋转,其半径分别交AB、AD于点M、N,求证:正方形ABCD的边被纸板覆盖部分的总长度为定值a.2.〔2008##〕在梯形ABCD中,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点,试判断EC与EB的位置关系,并写出推理过程.3.如图,P是等边△ABC内一点,若AP=3,PB=4,PC=5,求∠APB的度数.4.已知:在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别为线段BC上两动点,∠DAE=45°.⑴猜想BD、DE、EC三条线段之间存在的数量关系式,并对你的猜想给予证明;⑵当动点E在线段BC上,动点D运动在线段CB延长线上时,其它条件不变,⑴中探究的结论是否发生改变?请说明你的猜想并给予证明.5.如图,已知等腰直角三角线ABC,BD平分∠ABC,CE⊥BD,垂足为E,求证:BD=2CE.6.如图,折叠长方形的一边AD,使点D落在BC边的点F处,如果AB=8,BC=10,求EC的长.中点的妙用一、倍长中线法例1<文汇中学2009-2010期中测试题>,AD是△ABC中BC边上的中线,若AB=2,AC=4,则AD的取值范围是___________.例2已知在△ABC中,AD是BC边上的中线,E是AD上一点,延长BE交AC于F,AF=EF,求证:AC=BE.例3⑴如图1,△ABC与△BDE均为等腰直角三角形,BA⊥AC,ED⊥BD,点D在AB边上.连接EC,取EC中点F,连接AF,DF,猜测AF,DF的数量关系和位置关系,并加以证明.图1⑵如图2,将△BDE旋转至如图位置,使E在AB延长线上,D在CB延长线上,其他条件不变,则⑴中AF,DF的数量关系和位置关系是否发生变化,并加以证明.图2例4已知四边形ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点,求证EFGH为平行四边形.例5如图,已知四边形ABCD中,AB=CD,M、N分别为BC、AD中点,延长MN与AB、CD延长线交于E、F,求证∠BEM=∠CFM例6已知△ABD和△ACE都是直角三角形,且∠ABD=∠ACE=90°,连接DE,设M为DE的中点.⑴求证:MB =MC ;⑵设∠BAD =∠CAE ,固定Rt △ABD ,让Rt △ACE 移至图示位置,此时MB =MC 是否成立?请证明你的结论.出现中点的时候一般有以下作辅助线的方法⑴倍长中线法⑵构造中位线⑶如果是直角三角形,经常还会构造斜边上的中线例7如图,已知△ABC 和△ADE 都是等腰直角三角形,点M 为EC 中点,求证△BMD 为等腰直角三角形.1.在△ABC 中,AB =12,AC =30,求BC 边上的中线AD 的范围.2.在△ABC 中,D 为BC 边上的点,已知∠BAD =∠CAD ,BD =CD ,求证:AB =AC .3.如图,在△ABC 中,AD ⊥BC ,M 是BC 中点,∠B =2∠C ,如图,求证:DM =12AB 4.已知△ABC 中,AC =7,BC =4,D 为AB 中点,E 为边AC 上一点,且102AED C ∠=︒+∠9,求CE 的长.5.在任意五边形ABCDE 中,M,N,P,Q 分别为AB 、CD 、BC 、DE 的中点,K 、L 、分别为MN 、PQ 的中点,求证:KL 平行且等于14AE . 6.如图,已知△ABC 中,AB =AC ,CE 是AB 边上的中线,延长AB 到D ,使BD =AB ,那么CE 是CD 的几分之几?7.四边形ABCD 四边中点分别为E 、F 、G 、H ,当四边形ABCD 满足时,EFGH 为菱形;当四边形ABCD 满足时,EFGH 为矩形;当四边形ABCD 满足时,EFGH 为正方形.例1在△ABC 中,∠B =2∠C ,∠BAC 的平分线AD 交BC 与D .求证:AB +BD =AC .例2 ABCD 是正方形,P 为BC 上任意一点,∠P AD 的平分线交CD 于Q ,求证:DQ =AP -BP . 例3已知△ABC ,∠ABC =90°,以AB 、AC 为边向外做正方形ABDE 和ACFG ,延长BA 交EG 于H ,则BC =2AH .例4 AD 是△ABC 的角平分线,BE ⊥AD 交AD 的延长线于E ,EF //AC 交AB 于F .求证:AF =FB .截长补短法补形法例5如图,六边形ABCDEF的六个内角都相等,已知BC+CD=11,DE-AB=3,求DC+EF的值. 例6如图所示:BC>AB,AD=AC,BD平分∠ABC,求证:∠A+∠C=180°.1.如图,在△ABC中,AB+BD=AC,∠BAC的平分线AD交BC与D,求证:∠B=2∠CAB CD已知△ABC,以AB、AC为边向外作正方形ABGF、ACDE,M是BC中点,连接AM求证:EF=2AM且AM⊥EF.3.在△ABC中,AB=AC,∠A=100°,BE评分∠B交AC与E,如图,求证:AE+BE=BC 4.在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交与F,如图所示.求证:AF⊥BF5.在△ABC中,MB、NC分别是三角形的外角∠ABE、∠ACF的角平分线,AM⊥BM,AN⊥CN,垂足分别是M,N.求证:MN∥BC,MN=12<AB+AC+BC>6.在△ABC中,MB、NC分别是三角形的内角∠ABC、∠ACB的角平分线,AM⊥BM,AN⊥CN,垂足分别是M,N.求证:MN∥BC,MN=12<AB+AC-BC>例1在四边形ABCD中,已知AB=BC=CD,∠ABC=70°,∠BCD=170°,求∠BAD的度数.例2如图,△ABC中,AB=AC,AD=BC,∠A=20°,求∠DCA的度数.例3任意△ABC,试在△ABC内找一点P,使得P A+PB+PC的值最小例4<2000 初二数学竞赛〕,在等腰△ABC中,延长边AB到点D,延长边CA到点E,连接DE, 恰有AD=BC=CE=DE.求证:∠BAC=100°.例5如图所示,在△ABC中,∠B=60°∠A=100°,E为AC的中点,∠DEC=80°,D是BC边上的点,BC=1,求△ABC的面积与△CDE的面积的两倍的和.例6如图所示,在△ABC中,∠ACB=2∠ABC,P为三角形内一点,AP=AC,PB=PC,求证:∠BAC=3∠BAP.1.如图所示,在四边形ABCD中,BC CD=,60BCA ACD∠-∠=︒,求证:AD CD AB+≥.2.在ABC∆中,AB AC=,60120A︒<∠<︒,P为ABC∆内部一点,PC AC=,120PCA A∠=︒-∠,求CBP∠的度数.巧构等边3.在等边△ABC内有一点P,它到三个顶点A、B、C的距离分别为1求∠APB的度数.4.在凸四边形ABCD中,∠DAC=30°,∠CAB=20°,∠ADB=50°,∠BDC=30°,四边形的对角线交于点P,求证:PB=PC5.在等腰△ABC中,∠B=∠C=40°,延长AB至点D,使AD=BC,求∠BCD的度数. 6.如图,D是△ABC外一点,AB=AC=BD+CD,∠ABD=60°.求∠ACD的度数.。
初中几何辅助线口诀和秘籍

初中几何辅助线口诀和秘籍初中几何是数学学科中的一块重要内容,而几何辅助线是解决几何问题时常用的一种方法。
下面我将为大家介绍一些初中几何辅助线的口诀和秘籍。
一、角平分线角平分线是指将一个角分为两个相等的角的线段。
在解决几何问题时,我们常常需要用到角平分线来帮助我们求解。
如何画角平分线呢?下面是一个简单的口诀:“角平分线,一刀两半,角分两相等,求解题简单。
”二、三角形的中线三角形的中线是连接三角形的一个顶点与对边中点的线段。
在解决三角形相关问题时,中线也是一个常用的辅助线。
我们可以通过以下口诀来记忆中线的特点:“三角形中线,一条有三,中点连顶点,两边相等。
”三、垂直平分线垂直平分线是指将一个线段垂直分割并且分成两个相等部分的线段。
垂直平分线在解决线段相关问题时非常有用。
下面是一个简洁的口诀来帮助我们记忆垂直平分线的画法:“垂直平分线,画在线上,两边相等,线段垂直。
”四、角的对称线角的对称线是指将一个角按照对称轴对折后,得到的两个相等角的辅助线。
在解决角相关问题时,角的对称线可以帮助我们找到一些相等角。
以下是一个简单的口诀来帮助我们记忆角的对称线:“角的对称线,轴线中间,两边相等,角对称分。
”五、相似三角形的辅助线在解决相似三角形问题时,有一些特殊的辅助线可以帮助我们找到相似三角形之间的对应关系。
例如,高线可以帮助我们找到相似三角形的对应边的比例关系。
以下是一个简单的口诀来帮助我们记忆相似三角形的辅助线:“相似三角形辅助线,高线找比例,边线对应比例,找答案简单。
”通过以上口诀和秘籍,我们可以更加方便地使用几何辅助线来解决初中几何问题。
当然,在实际解题的过程中,我们还需要根据具体问题的要求灵活运用这些辅助线,以达到解题的目的。
总结起来,初中几何辅助线是解决几何问题时的重要工具。
通过记忆和掌握一些几何辅助线的特点和画法,我们能够更加高效地解决几何问题,提高我们的数学水平。
希望以上口诀和秘籍能够帮助到大家,让我们在初中几何学习中取得更好的成绩!。
中考数学直角三角形,三角函数解题方法总结,中考经典真题解析!

中考数学直角三角形,三角函数解题方法总结,中考经典真题
解析!
初中数学直角三角形(勾股定理、三角函数)
【知识点】
勾股定理、勾股定理的逆定理、三角函数的定义、特殊角的三角函数、解直角三角形
【规律方法】
1、直接利用勾股定理进行计算,当已知直角三角形的三边中任意两边的长,可以直接求第三边的长。
2、利用勾股定理建立方程:勾股定理是表示三边之间的关系,只有在两边确定的情形下,才可以直接利用公式求第三边,但有时题目的条件,却不能满足这点,这时可以引入未知数,让未知数参与运算,最后通过立方程求解。
3、利用勾股定理判断三角形是否为直角三角形,当三角形三边关系满足勾股定理时,三角形一定是直角三角形。
4、将一般的几何问题构造出直角三角形,再用勾股定理求解。
5、将现实问题转化为数学问题,建立直角三角形模型;
6、根据条件特点,选用适当的锐角三角函数解决问题;
【中考集锦】
一、选择题
4.(2016湖北襄阳第9题)如图,△ABC的顶点是正方形网格的格点,则sinA的值为()。
初二三角形所有知识点总结和常考题提高难题压轴题练习含答案解析

初二三角形所有知识点总结和常考题知识点:1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2.三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边.3.高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高.4.中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.5.角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.6.三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性.7.多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.8.多边形的内角:多边形相邻两边组成的角叫做它的内角.9.多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.10.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.11.正多边形:在平面内,各个角都相等,各条边都相等的多边形叫正多边形.12.平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面,13.公式与性质:⑴三角形的内角和:三角形的内角和为180°⑵三角形外角的性质:性质1:三角形的一个外角等于和它不相邻的两个内角的和.性质2:三角形的一个外角大于任何一个和它不相邻的内角.⑶多边形内角和公式:n边形的内角和等于(2)n-·180°⑷多边形的外角和:多边形的外角和为360°.⑸多边形对角线的条数:①从n边形的一个顶点出发可以引(3)n-条对角线,把多边形分成(2)n-个三角形.②n边形共有(3)2n n-条对角线.常考题:一.选择题(共13小题)1.已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是()A.13cm B.6cm C.5cm D.4cm2.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=()A.90°B.100°C.130° D.180°3.已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()A.315°B.270°C.180° D.135°4.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.5.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=()A.90°﹣αB.90°+αC.D.360°﹣α6.如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=()A.40°B.30°C.20°D.10°7.如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=50°,则∠BPC=()A.150°B.130°C.120° D.100°8.如图,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是()A.20米B.15米C.10米D.5米9.将一个n边形变成n+1边形,内角和将()A.减少180°B.增加90°C.增加180°D.增加360°10.一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是()A.27 B.35 C.44 D.5411.一个多边形的边数每增加一条,这个多边形的()A.内角和增加360°B.外角和增加360°C.对角线增加一条 D.内角和增加180°12.一个三角形三个内角的度数之比为2:3:7,这个三角形一定是()A.等腰三角形B.直角三角形C.锐角三角形D.钝角三角形13.如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为()A.13 B.14 C.15 D.16二.填空题(共13小题)14.若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是.15.如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,…,照这样走下去,他第一次回到出发地A点时,一共走了米.16.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为度.17.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为.18.若一个多边形内角和等于1260°,则该多边形边数是.19.如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=.20.一个多边形的内角和比外角和的3倍多180°,则它的边数是.21.若正多边形的一个内角等于140°,则这个正多边形的边数是.22.在△ABC中,三个内角∠A、∠B、∠C满足∠B﹣∠A=∠C﹣∠B,则∠B=度.23.如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC 和∠A1CD的平分线交于点A2,得∠A2;…∠A2012BC和∠A2012CD的平分线交于点A2013,则∠A2013=度.24.如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=度.25.用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=度.26.平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1﹣∠2=.三.解答题(共14小题)27.如图,直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.28.如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.29.已知△ABC中,∠ACB=90°,CD为AB边上的高,BE平分∠ABC,分别交CD、AC 于点F、E,求证:∠CFE=∠CEF.30.如图,AD为△ABC的中线,BE为△ABD的中线,(1)若∠ABE=25°,∠BAD=50°,则∠BED的度数是度.(2)在△ADC中过点C作AD边上的高CH.(3)若△ABC的面积为60,BD=5,求点E到BC边的距离.31.如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.(1)若∠B=35°,∠ACB=85°,求∠E的度数;(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.32.如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=158°,求∠EDF的度数.33.如图,AD平分∠BAC,∠EAD=∠EDA.(1)∠EAC与∠B相等吗?为什么?(2)若∠B=50°,∠CAD:∠E=1:3,求∠E的度数.34.(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB=,∠XBC+∠XCB=.(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.35.已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.(1)如图1,若AB∥ON,则①∠ABO的度数是;②当∠BAD=∠ABD时,x=;当∠BAD=∠BDA时,x=.(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.36.平面内的两条直线有相交和平行两种位置关系(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD 的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.37.如下几个图形是五角星和它的变形.(1)图(1)中是一个五角星,求∠A+∠B+∠C+∠D+∠E.(2)图(2)中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化说明你的结论的正确性.(3)把图(2)中的点C向上移到BD上时(1)如图(3)所示,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化说明你的结论的正确性.38.Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2=°;(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为:;(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为:.39.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.40.将纸片△ABC沿DE折叠使点A落在A′处的位置.(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是.(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.初二三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)参考答案与试题解析一.选择题(共13小题)1.(2008?福州)已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是()A.13cm B.6cm C.5cm D.4cm【分析】此题首先根据三角形的三边关系,求得第三边的取值范围,再进一步找到符合条件的数值.【解答】解:根据三角形的三边关系,得:第三边应大于两边之差,且小于两边之和,即9﹣4=5,9+4=13.∴第三边取值范围应该为:5<第三边长度<13,故只有B选项符合条件.故选:B.【点评】本题考查了三角形三边关系,一定要注意构成三角形的条件:两边之和>第三边,两边之差<第三边.2.(2013?河北)一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=()A.90°B.100°C.130° D.180°【分析】设围成的小三角形为△ABC,分别用∠1、∠2、∠3表示出△ABC的三个内角,再利用三角形的内角和等于180°列式整理即可得解.【解答】解:如图,∠BAC=180°﹣90°﹣∠1=90°﹣∠1,∠ABC=180°﹣60°﹣∠3=120°﹣∠3,∠ACB=180°﹣60°﹣∠2=120°﹣∠2,在△ABC中,∠BAC+∠ABC+∠ACB=180°,∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°,∴∠1+∠2=150°﹣∠3,∵∠3=50°,∴∠1+∠2=150°﹣50°=100°.故选:B.【点评】本题考查了三角形的内角和定理,用∠1、∠2、∠3表示出△ABC的三个内角是解题的关键,也是本题的难点.3.(2010?西藏)已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()A.315°B.270°C.180° D.135°【分析】利用三角形内角与外角的关系:三角形的任一外角等于和它不相邻的两个内角之和解答.【解答】解:∵∠1、∠2是△CDE的外角,∴∠1=∠4+∠C,∠2=∠3+∠C,即∠1+∠2=2∠C+(∠3+∠4),∵∠3+∠4=180°﹣∠C=90°,∴∠1+∠2=2×90°+90°=270°.故选:B.【点评】此题主要考查了三角形内角与外角的关系:三角形的任一外角等于和它不相邻的两个内角之和.4.(2015?长沙)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.【分析】根据三角形高线的定义:过三角形的顶点向对边引垂线,顶点和垂足之间的线段叫做三角形的高线解答.【解答】解:为△ABC中BC边上的高的是A选项.故选A.【点评】本题考查了三角形的角平分线、中线、高线,熟记高线的定义是解题的关键.5.(2014?达州)如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=()A.90°﹣αB.90°+αC.D.360°﹣α【分析】先求出∠ABC+∠BCD的度数,然后根据角平分线的性质以及三角形的内角和定理求解∠P的度数.【解答】解:∵四边形ABCD中,∠ABC+∠BCD=360°﹣(∠A+∠D)=360°﹣α,∵PB和PC分别为∠ABC、∠BCD的平分线,∴∠PBC+∠PCB=(∠ABC+∠BCD)=(360°﹣α)=180°﹣α,则∠P=180°﹣(∠PBC+∠PCB)=180°﹣(180°﹣α)=α.故选:C.【点评】本题考查了多边形的内角和外角以及三角形的内角和定理,属于基础题.6.(2009?荆门)如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=()A.40°B.30°C.20°D.10°【分析】由三角形的一个外角等于与它不相邻的两个内角的和,得∠A′DB=∠CA'D﹣∠B,又折叠前后图形的形状和大小不变,∠CA'D=∠A=50°,易求∠B=90°﹣∠A=40°,从而求出∠A′DB的度数.【解答】解:∵Rt△ABC中,∠ACB=90°,∠A=50°,∴∠B=90°﹣50°=40°,∵将其折叠,使点A落在边CB上A′处,折痕为CD,则∠CA'D=∠A,∵∠CA'D是△A'BD的外角,∴∠A′DB=∠CA'D﹣∠B=50°﹣40°=10°.故选:D.【点评】本题考查图形的折叠变化及三角形的外角性质.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.解答此题的关键是要明白图形折叠后与折叠前所对应的角相等.7.(2004?陕西)如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=50°,则∠BPC=()A.150°B.130°C.120° D.100°【分析】根据垂直的定义和四边形的内角和是360°求得.【解答】解:∵BE⊥AC,CD⊥AB,∴∠ADC=∠AEB=90°,∴∠BPC=∠DPE=180°﹣50°=130°.故选B.【点评】主要考查了垂直的定义以及四边形内角和是360度.注意∠BPC与∠DPE互为对顶角.8.(2009?黑河)如图,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是()A.20米B.15米C.10米D.5米【分析】根据三角形的三边关系,第三边的长一定大于已知的两边的差,而小于两边的和,求得相应范围,看哪个数值不在范围即可.【解答】解:∵15﹣10<AB<10+15,∴5<AB<25.∴所以不可能是5米.【点评】已知三角形的两边,则第三边的范围是:>已知的两边的差,而<两边的和.9.(2014?临沂)将一个n边形变成n+1边形,内角和将()A.减少180°B.增加90°C.增加180°D.增加360°【分析】利用多边形的内角和公式即可求出答案.【解答】解:n边形的内角和是(n﹣2)?180°,n+1边形的内角和是(n﹣1)?180°,因而(n+1)边形的内角和比n边形的内角和大(n﹣1)?180°﹣(n﹣2)?180=180°.故选:C.【点评】本题主要考查了多边形的内角和公式,是需要识记的内容.10.(2015?莱芜)一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是()A.27 B.35 C.44 D.54【分析】设出题中所给的两个未知数,利用内角和公式列出相应等式,根据边数为整数求解即可,再进一步代入多边形的对角线计算方法,即可解答.【解答】解:设这个内角度数为x°,边数为n,∴(n﹣2)×180﹣x=1510,180n=1870+x=1800+(70+x),∵n为正整数,∴n=11,∴=44,故选:C.【点评】此题考查多边形的内角和计算公式以及多边形的对角线条数的计算方法,属于需要识记的知识.11.(2011春?滨城区期末)一个多边形的边数每增加一条,这个多边形的()A.内角和增加360°B.外角和增加360°C.对角线增加一条 D.内角和增加180°【分析】利用多边形的内角和定理和外角和特征即可解决问题.【解答】解:因为n边形的内角和是(n﹣2)?180°,当边数增加一条就变成n+1,则内角和是(n﹣1)?180°,内角和增加:(n﹣1)?180°﹣(n﹣2)?180°=180°;根据多边形的外角和特征,边数变化外角和不变.故选:D.【点评】本题主要考查了多边形的内角和定理与外角和特征.先设这是一个n边形是解题的关键.12.(2012?滨州)一个三角形三个内角的度数之比为2:3:7,这个三角形一定是()A.等腰三角形B.直角三角形C.锐角三角形D.钝角三角形【分析】已知三角形三个内角的度数之比,根据三角形内角和定理,可求得三角的度数,由此判断三角形的类型.【解答】解:三角形的三个角依次为180°×=30°,180°×=45°,180°×=105°,所以这个三角形是钝角三角形.【点评】本题考查三角形的分类,这个三角形最大角为180°×>90°.本题也可以利用方程思想来解答,即2x+3x+7x=180,解得x=15,所以最大角为7×15°=105°.13.(2014?毕节市)如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为()A.13 B.14 C.15 D.16【分析】根据多边形内角和公式,可得新多边形的边数,根据新多边形比原多边形多1条边,可得答案.【解答】解:设新多边形是n边形,由多边形内角和公式得(n﹣2)180°=2340°,解得n=15,原多边形是15﹣1=14,故选:B.【点评】本题考查了多边形内角与外角,多边形的内角和公式是解题关键.二.填空题(共13小题)14.(2015?资阳)若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是8.【分析】任何多边形的外角和是360°,即这个多边形的内角和是3×360°.n边形的内角和是(n﹣2)?180°,如果已知多边形的边数,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.【解答】解:设多边形的边数为n,根据题意,得(n﹣2)?180=3×360,解得n=8.则这个多边形的边数是8.【点评】已知多边形的内角和求边数,可以转化为方程的问题来解决.15.(2006?镇江)如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,…,照这样走下去,他第一次回到出发地A点时,一共走了120米.【分析】由题意可知小亮所走的路线为一个正多边形,根据多边形的外角和即可求出答案.【解答】解:∵360÷30=12,∴他需要走12次才会回到原来的起点,即一共走了12×10=120米.故答案为:120.【点评】本题主要考查了多边形的外角和定理.任何一个多边形的外角和都是360°.16.(2014?随州)将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为75度.【分析】根据三角形三内角之和等于180°求解.【解答】解:如图.∵∠3=60°,∠4=45°,∴∠1=∠5=180°﹣∠3﹣∠4=75°.故答案为:75.【点评】考查三角形内角之和等于180°.17.(2013?上海)当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为30°.【分析】根据已知一个内角α是另一个内角β的两倍得出β的度数,进而求出最小内角即可.【解答】解:由题意得:α=2β,α=100°,则β=50°,180°﹣100°﹣50°=30°,故答案为:30°.【点评】此题主要考查了新定义以及三角形的内角和定理,根据已知得出β的度数是解题关键.18.(2013?遂宁)若一个多边形内角和等于1260°,则该多边形边数是9.【分析】根据多边形内角和定理及其公式,即可解答;【解答】解:∵一个多边形内角和等于1260°,∴(n﹣2)×180°=1260°,解得,n=9.故答案为9.【点评】本题考查了多边形的内角定理及其公式,关键是记住多边形内角和的计算公式.19.(2015?北京)如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=360°.【分析】首先根据图示,可得∠1=180°﹣∠BAE,∠2=180°﹣∠ABC,∠3=180°﹣∠BCD,∠4=180°﹣∠CDE,∠5=180°﹣∠DEA,然后根据三角形的内角和定理,求出五边形ABCDE 的内角和是多少,再用180°×5减去五边形ABCDE的内角和,求出∠1+∠2+∠3+∠4+∠5等于多少即可.【解答】解:∠1+∠2+∠3+∠4+∠5=(180°﹣∠BAE)+(180°﹣∠ABC)+(180°﹣∠BCD)+(180°﹣∠CDE)+(180°﹣∠DEA)=180°×5﹣(∠BAE+∠ABC+∠BCD+∠CDE+∠DEA)=900°﹣(5﹣2)×180°=900°﹣540°=360°.故答案为:360°.【点评】此题主要考查了多边形内角和定理,要熟练掌握,解答此题的关键是要明确:(1)n边形的内角和=(n﹣2)?180 (n≥3)且n为整数).(2)多边形的外角和指每个顶点处取一个外角,则n边形取n个外角,无论边数是几,其外角和永远为360°.20.(2014?自贡)一个多边形的内角和比外角和的3倍多180°,则它的边数是9.【分析】多边形的内角和比外角和的3倍多180°,而多边形的外角和是360°,则内角和是3×360°+180°.n边形的内角和可以表示成(n﹣2)?180°,设这个多边形的边数是n,得到方程,从而求出边数.【解答】解:根据题意,得(n﹣2)?180°=3×360°+180°,解得:n=9.则这个多边形的边数是9.故答案为:9.【点评】考查了多边形内角与外角,此题只要结合多边形的内角和公式寻求等量关系,构建方程即可求解.21.(2015?徐州)若正多边形的一个内角等于140°,则这个正多边形的边数是9.【分析】首先根据求出外角度数,再利用外角和定理求出边数.【解答】解:∵正多边形的一个内角是140°,∴它的外角是:180°﹣140°=40°,360°÷40°=9.故答案为:9.【点评】此题主要考查了多边形的外角与内角,做此类题目,首先求出正多边形的外角度数,再利用外角和定理求出求边数.22.(2013?黔东南州)在△ABC中,三个内角∠A、∠B、∠C满足∠B﹣∠A=∠C﹣∠B,则∠B=60度.【分析】先整理得到∠A+∠C=2∠B,再利用三角形的内角和等于180°列出方程求解即可.【解答】解:∵∠B﹣∠A=∠C﹣∠B,∴∠A+∠C=2∠B,又∵∠A+∠C+∠B=180°,∴3∠B=180°,∴∠B=60°.故答案为:60.【点评】本题考查了三角形的内角和定理,是基础题,求出∠A+∠C=2∠B是解题的关键.23.(2013?达州)如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2012BC和∠A2012CD的平分线交于点A2013,则∠A2013=度.【分析】利用角平分线的性质、三角形外角性质,易证∠A1=∠A,进而可求∠A1,由于∠A1=∠A,∠A2=∠A1=∠A,…,以此类推可知∠A2013=∠A=°.【解答】解:∵A1B平分∠ABC,A1C平分∠ACD,∴∠A1BC=∠ABC,∠A1CA=∠ACD,∵∠A1CD=∠A1+∠A1BC,即∠ACD=∠A1+∠ABC,∴∠A1=(∠ACD﹣∠ABC),∵∠A+∠ABC=∠ACD,∴∠A=∠ACD﹣∠ABC,∴∠A1=∠A,∴∠A1=m°,∵∠A1=∠A,∠A2=∠A1=∠A,…以此类推∠A2013=∠A=°.故答案为:.【点评】本题考查了角平分线性质、三角形外角性质,解题的关键是推导出∠A1=∠A,并能找出规律.24.(2012春?金台区期末)如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD ⊥AB于D,DF⊥CE,则∠CDF=74度.【分析】利用三角形的内角和外角之间的关系计算.【解答】解:∵∠A=40°,∠B=72°,∴∠ACB=68°,∵CE平分∠ACB,CD⊥AB于D,∴∠BCE=34°,∠BCD=90﹣72=18°,∵DF⊥CE,∴∠CDF=90°﹣(34°﹣18°)=74°.故答案为:74.【点评】主要考查了三角形的内角和外角之间的关系.(1)三角形的外角等于与它不相邻的两个内角和;(2)三角形的内角和是180度,求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;(3)三角形的一个外角>任何一个和它不相邻的内角.注意:垂直和直角总是联系在一起.25.(2006?临安市)用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=36度.【分析】利用多边形的内角和定理和等腰三角形的性质即可解决问题.【解答】解:∵∠ABC==108°,△ABC是等腰三角形,∴∠BAC=∠BCA=36度.【点评】本题主要考查了多边形的内角和定理和等腰三角形的性质.n边形的内角和为:180°(n﹣2).26.(2015?河北)平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1﹣∠2=24°.【分析】首先根据多边形内角和定理,分别求出正三角形、正方形、正五边形、正六边形的每个内角的度数是多少,然后分别求出∠3、∠1、∠2的度数是多少,进而求出∠3+∠1﹣∠2的度数即可.【解答】解:正三角形的每个内角是:180°÷3=60°,正方形的每个内角是:360°÷4=90°,正五边形的每个内角是:(5﹣2)×180°÷5=3×180°÷5=540°÷5=108°,正六边形的每个内角是:(6﹣2)×180°÷6=4×180°÷6=720°÷6=120°,则∠3+∠1﹣∠2=(90°﹣60°)+(120°﹣108°)﹣(108°﹣90°)=30°+12°﹣18°=24°.故答案为:24°.【点评】此题主要考查了多边形内角和定理,要熟练掌握,解答此题的关键是要明确:(1)n边形的内角和=(n﹣2)?180 (n≥3)且n为整数).(2)多边形的外角和指每个顶点处取一个外角,则n边形取n个外角,无论边数是几,其外角和永远为360°.三.解答题(共14小题)27.(2013春?临清市期末)如图,直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.【分析】先根据三角形的内角和定理求出∠A的度数,再根据三角形外角的性质求出∠BDF的度数.【解答】解:因为∠A+∠B+∠ACB=180°,所以∠A=180°﹣67°﹣74°=39°,所以∠BDF=∠A+∠AED=39°+48°=87°.【点评】本题考查三角形外角的性质及三角形的内角和定理,解答的关键是外角和内角的关系.28.(2013?湖州校级模拟)如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F 交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.【分析】根据三角形外角与内角的关系及三角形内角和定理解答.【解答】解:∵∠AFE=90°,∴∠AEF=90°﹣∠A=90°﹣35°=55°,∴∠CED=∠AEF=55°,∴∠ACD=180°﹣∠CED﹣∠D=180°﹣55°﹣42°=83°.答:∠ACD的度数为83°.【点评】三角形外角与内角的关系:三角形的一个外角等于和它不相邻的两个内角的和.三角形内角和定理:三角形的三个内角和为180°.29.(2015秋?全椒县期中)已知△ABC中,∠ACB=90°,CD为AB边上的高,BE平分∠ABC,分别交CD、AC于点F、E,求证:∠CFE=∠CEF.【分析】题目中有两对直角,可得两对角互余,由角平分线及对顶角可得两对角相等,然后利用等量代换可得答案.【解答】证明:∵∠ACB=90°,∴∠1+∠3=90°,∵CD⊥AB,∴∠2+∠4=90°,又∵BE平分∠ABC,∴∠1=∠2,∴∠3=∠4,∵∠4=∠5,∴∠3=∠5,即∠CFE=∠CEF.【点评】本题考查了三角形角平分线、中线和高的有关知识;正确利用角的等量代换是解答本题的关键.30.(2010春?横峰县校级期末)如图,AD为△ABC的中线,BE为△ABD的中线,(1)若∠ABE=25°,∠BAD=50°,则∠BED的度数是度.(2)在△ADC中过点C作AD边上的高CH.(3)若△ABC的面积为60,BD=5,求点E到BC边的距离.【分析】(1)根据三角形的一个外角等于与它不相邻的两个内角和,∠BED=∠ABE+∠BAE=75°;(2)三角形高的基本作法:用圆规以一边两端点为圆心,任意长为半径作两段弧,交于角的两边,再以交点为圆心,用交轨法作两段弧,找到两段弧的交点,连接两个交点,并过另一端点作所成直线的平行线,叫该边所在直线一点,连接该点和另一端点,则为高线;(3)我们通过证明不难得出三角形中线将三角形分成面积相等的两个三角形,那么可依据D是BC中点,E是AD中点,求出三角形BED的面积.三角形BDE中,E到BD的距离就是BD边上的高,有了三角形BDE的面积,BD的长也容易求得.那么高就求出来了.【解答】解:(1)∠BED=∠ABE+∠BAE=75°;(2)CH为所求的高.(3)解:如图,过点E作EF⊥BD于点F,∵AD是BC的中线∴BD=CD=S△ACD==×60=30∴S△ABD同理S=S△ABE==×30=15△BED=BD?EF=×5EF=15又∵S△BED∴EF=6即点E到BC边的距离为6.【点评】本题主要考查了基本作图中,三角形高的作法,三角形的内角和外角等知识点.31.(2015春?单县期末)如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.(1)若∠B=35°,∠ACB=85°,求∠E的度数;(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.【分析】(1)中,首先根据三角形的内角和定理求得∠BAC的度数,再根据角平分线的定义求得∠DAC的度数,从而根据三角形的内角和定理即可求出∠ADC的度数,进一步求得∠E的度数;(2)中,根据第(1)小题的思路即可推导这些角之间的关系.【解答】解:(1)∵∠B=35°,∠ACB=85°,∴∠BAC=60°,∵AD平分∠BAC,∴∠DAC=30°,∴∠ADC=65°,∴∠E=25°;(2).设∠B=n°,∠ACB=m°,∵AD平分∠BAC,∴∠1=∠2=∠BAC,∵∠B+∠ACB+∠BAC=180°,∵∠B=n°,∠ACB=m°,∴∠CAB=(180﹣n﹣m)°,∴∠BAD=(180﹣n﹣m)°,∴∠3=∠B+∠1=n°+(180﹣n﹣m)°=90°+n°﹣m°,∵PE⊥AD,∴∠DPE=90°,∴∠E=90°﹣(90°+n°﹣m°)=(m﹣n)°=(∠ACB﹣∠B).【点评】运用了三角形的内角和定理以及角平分线的定义.特别注意第(2)小题,由于∠B和∠ACB的大小不确定,故表达式应写为两种情况.32.(2010春?朝阳区期末)如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=158°,求∠EDF的度数.【分析】要求∠EDF的度数,只需求出∠BDE和∠FDC的度数即可,由FD⊥BC,得∠FDC=90°;而∠BDE在Rt△BDE中,故只需求出∠B的度数.因∠B=∠C,只需求出∠C 的度数即可.因∠AFD是△CDF的外角,∠AFD=158°∴∠C=∠AFD﹣∠FDC=158°﹣90°=68°.【解答】解:∵FD⊥BC,所以∠FDC=90°,∵∠AFD=∠C+∠FDC,∴∠C=∠AFD﹣∠FDC=158°﹣90°=68°,∴∠B=∠C=68°.∵DE⊥AB,∵∠DEB=90°,∴∠BDE=90°﹣∠B=22°.又∵∠BDE+∠EDF+∠FDC=180°,∴∠EDF=180°﹣∠BDE﹣∠FDC=180°﹣22°﹣90°=68°.【点评】考查三角形内角和定理,外角性质,垂直定义等知识.33.(2014春?岱岳区期末)如图,AD平分∠BAC,∠EAD=∠EDA.(1)∠EAC与∠B相等吗?为什么?(2)若∠B=50°,∠CAD:∠E=1:3,求∠E的度数.【分析】(1)由于AD平分∠BAC,根据角平分线的概念可得∠BAD=∠CAD,再根据三角形的一个外角等于和它不相邻的两个内角和,结合已知条件可得∠EAC与∠B相等;(2)若设∠CAD=x°,则∠E=3x°.根据(1)中的结论以及三角形的内角和定理及其推论列方程进行求解即可.【解答】解:(1)相等.理由如下:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
个三角形外角的位置上,小角处在内角的位置上,再利用外角定理证题.
例:已知 D 为△ABC 内任一点,求证:∠BDC>∠BAC
证法(一):延长 BD 交 AC 于 E, ∵∠BDC 是△EDC 的外角, ∴∠BDC>∠DEC
A
D
E
ቤተ መጻሕፍቲ ባይዱ
同理:∠DEC>∠BAC ∴∠BDC>∠BAC
B
CB
证法(二):连结 AD,并延长交 BC 于 F
求证:∠EAD = 1 (∠C-∠B) 2
证明:∵AE 平分∠BAC
∴∠BAE =∠CAE = 1 ∠BAC 2
∵∠BAC =180°-(∠B+∠C)
∴∠EAC = 1 [180°-(∠B+∠C)] 2
∵AD⊥BC
∴∠DAC = 90° -∠C
∵∠EAD = ∠EAC-∠DAC
∴∠EAD = 1 [180°-(∠B+∠C)]-(90°-∠C) 2
∵∠BDF 是△ABD 的外角, ∴∠BDF>∠BAD 同理∠CDF>∠CAD
A
D
E
A D
∴∠BDF+∠CDF>∠BAD+∠BCAD 即:∠BDC>∠BAC
CB
F
C
A
D
F
C
规律 21.有角平分线时常在角两边截取相等的线段,构造全等三角形.
例:已知,如图,AD 为△ABC 的中线且∠1 = ∠2,∠3 = ∠4,
①AB+AF>BD+DG+GF
②GF+FC>GE+CE
③DG+GE>DE
∴①+②+③有
AB+AF+GF+FC+DG+GE>BD+DG+GF+GE+CE+DE
∴AB+AC>BD+DE+CE
注意:利用三角形三边关系定理及推论证题时,常通过引辅助线,把求证的量(或与求
证有关的量)移到同一个或几个三角形中去然后再证题.
练习:已知:如图 P 为△ABC 内任一点,
求证: 1 (AB+BC+AC)<PA+PB+PC<AB+BC+AC 2
规律 16.三角形的一个内角平分线与一个外角平分线相交所成的锐角,等于第 三个内角的一半.
例:如图,已知 BD 为△ABC 的角平分线,CD 为△ABC 的外角∠ACE 的平分线,它与 BD 的延长线交于 D. 求证:∠A = 2∠D 证明:∵BD、CD 分别是∠ABC、∠ACE 的平分线
三角形部分
规律 15.在利用三角形三边关系证明线段不等关系时,如果直接证不出来,可 连结两点或延长某边构造三角形,使结论中出现的线段在一个或几个三角形中,
再利用三边关系定理及不等式性质证题.
例:如图,已知 D、E 为△ABC 内两点,求证:AB+AC>BD+DE+CE.
证法(一):将 DE 向两边延长,分别交 AB、AC 于 M、N
2
规律 18. 三角形的两个外角平分线相交所成的锐角等于 90o 减去第三个内角的一 半.
例:如图,BD、CD 分别平分∠EBC、∠FCB, 求证:∠BDC = 90°- 1 ∠A 2
证明:∵BD、CD 分别平分∠EBC、∠FCB ∴∠EBC = 2∠1、∠FCB = 2∠2 ∴2∠1 =∠A+∠ACB ① 2∠2 =∠A+∠ABC ② ①+②得 2(∠1+∠2)= ∠A+∠ABC+∠ACB+∠A 2(∠1+∠2)= 180°+∠A
求证:BE+CF>EF
证明:在 DA 上截取 DN = DB,连结 NE、NF,则 DN = DC 在△BDE 和△NDE 中, DN = DB ∠1 = ∠2 ED = ED ∴△BDE≌△NDE
A
N
E
F
B
1 2 34
D
C
∴BE = NE
同理可证:CF = NF
在△EFN 中,EN+FN>EF
∴BE+CF>EF
证明:∵BD、CD 分别平分∠ABC、∠ACB ∴ A 21 22 180
∴ 2(1+2) 180 A ①
∵ BDC 180 (1 2)
∴ (1+2) 180 BDC ②
把②式代入①式得 2(180 BDC) 180 A 即: 360 2BDC 180 A ∴ 2BDC 180 A ∴ BDC 90o 1 A
∴∠ACE =2∠1, ∠ABC =2∠2 ∵∠A = ∠ACE -∠ABC ∴∠A = 2∠1-2∠2 又∵∠D =∠1-∠2 ∴∠A =2∠D
规律 17. 三角形的两个内角平分线相交所成的钝角等于 90o 加上第三个内角的一 半.
例:如图,BD、CD 分别平分∠ABC、∠ACB, 求证:∠BDC = 90°+ 1 ∠A 2
= 90°- 1 (∠B+∠C)-90°+∠C 2
= 1 (∠C-∠B) 2
如果把 AD 平移可以得到如下两图,FD⊥BC 其它条件不变,
结论为:∠EFD = 1 (∠C-∠B). 2
规律 20.在利用三角形的外角大于任何和它不相邻的内角证明角的不等关系时,
如果直接证不出来,可连结两点或延长某边,构造三角形,使求证的大角在某
在△AMN 中, AM+ AN>MD+DE+NE ①
在△BDM 中,MB+MD>BD
②
在△CEN 中,CN+NE>CE
③
①+②+③得
AM+AN+MB+MD+CN+NE>MD+DE+NE+BD+CE
∴AB+AC>BD+DE+CE
证法(二)延长 BD 交 AC 于 F,延长 CE 交 BF 于 G,
在△ABF 和△GFC 和△GDE 中有,
E
F
B
1 2 34
D5
C
∴CM = BE
M
又∵∠1 = ∠2,∠3 = ∠4
∠1+∠2+∠3 + ∠4 = 180o
∴∠3 +∠2 = 90o
即∠EDF = 90o
∴∠FDM = ∠EDF = 90o
∴(∠1+∠2)= 90°+ 1 ∠A 2
∵∠BDC = 180°-(∠1+∠2)
∴∠BDC = 180°-(90°+ 1 ∠A) 2
∴∠BDC = 90°- 1 ∠A 2
规律 19. 从三角形的一个顶点作高线和角平分线,它们所夹的角等于三角形另 外两个角差(的绝对值)的一半.
例:已知,如图,在△ABC 中,∠C>∠B, AD⊥BC 于 D, AE 平分∠BAC.
规律 22. 有以线段中点为端点的线段时,常加倍延长此线段构造全等三角形.
例:已知,如图,AD 为△ABC 的中线,且∠1 = ∠2,∠3 = ∠4,求证:BE+CF>EF
证明:延长 ED 到 M,使 DM = DE,连结 CM、FM
A
△BDE 和△CDM 中,
BD = CD ∠1 = ∠5 ED = MD ∴△BDE≌△CDM
