力学第十四章 压杆稳定
简明工程力学14章压杆稳定

1 Fcr ' = Fcr ' ' , tgα = , α = 18.43o 3
§14-4 欧拉公式的应用范围 · 临界应力总图
一、 欧拉公式的应用范围 1.临界应力:压杆处于临界状态时横截面上的平均应力。
σ cr
Fcr = A
w Fcr
w=0;
代表了压杆的直线平衡状态。 代表了压杆的直线平衡状态。
此时A可以不为零。 此时 可以不为零。 可以不为零
l
w l 2 x
M (x)= Fcrw
x
B y (a)
B y (b)
w = A sin kx ≠ 0 失稳 失稳!!!
失稳的条件是: 失稳的条件是: sin kl = 0
kl = nπ
§14–1 压杆稳定性的概念
构件的承载能力: ①强度 ②刚度 ③稳定性 工程中有些构 件具有足够的强度、 刚度,却不一定能 安全可靠地工作。
P
一、稳定平衡与不稳定平衡 :
1. 不稳定平衡
2. 稳定平衡
3. 稳定平衡和不稳定平衡
二、压杆失稳与临界压力 :
1.理想压杆:材料绝对理想;轴线绝对直;压力绝对沿轴线作用。 1.理想压杆:材料绝对理想;轴线绝对直;压力绝对沿轴线作用。 理想压杆
y
B y (c)
B (d)
x
§14-3 不同杆端约束下细长压杆临界力的 欧拉公式 · 压杆的长度系数
各种支承约束条件下等截面细长压杆临界力的欧拉公式
支承情况 两端铰支 一端固定 两端固定 另端铰支 Fcr 失 稳 时 挠 曲 线 形 状 A C— D C B Fcr B Fcr B 一端固定 另端自由 Fcr 两端固定但可沿 横向相对移动 Fcr
工程力学——压杆稳定

欧拉公 式
其中:i
I — 截面的惯性半径;为截 面的几何性质; A
=
l
i
称为压杆的柔度(长细 比);反映压杆的柔软 程度。
15N
32 mm
1mm
第一节
压杆稳定的概念
FP<FPcr :直线平衡形式(稳定平衡)
在扰动作用下,直线平衡形式转为弯曲平衡形式,扰动除 去后,能够恢复到直线平衡形式,则称原来的直线平衡构形是 稳定的。 FP>FPcr :弯曲平衡形式(不稳定平衡) 在扰动作用下,直线平衡形式转为弯曲平衡形式,扰动除去 后,不能恢复到直线平衡形式,则称原来的直线平衡形式是不稳 定的。
F
F
1.
计算柔度判断两杆的临界荷载
5m
d
9m
d
d 4 64 d I i 4 d 2 4 A 1 5 L a 125 d i 0 .5 9 4 112.5 b d 4
(a)
(b )
a b
1
0.5
2. 计算各杆的临界荷载
b a P 101
(n ) EI Fcr 2 L Fcr
n 1
kL sin 2
A
适用条件: •理想压杆(轴线为直线,压力 与轴线重合,材料均匀) •线弹性,小变形 •两端为铰支座
y sin
x 挠曲线中点的挠度 l
挠曲线为半波正弦曲线
由此得到两个重要结果:
临界载荷
(a)
z
b
h
正视图:
工程力学:14第十四章 压杆稳定

π2EI π2EI
Fcr 4l 2 2l2
w 1 cos x
2l
14-4 欧拉公式的适用范 围中小柔度杆的临界应力
1.临界应力和柔度
临界应力可用临界力Pcr 除 以横截面面积A 来求得。
cr
cr
2EI
l2
令
iy
Ιy , Α
iz
Ιz Α
式中,iy和iz 分别称为截面图形对y轴和z轴的惯性半 径。
s p
cr
2 2
3. 中、小柔度杆的临界应力
经验公式: cr a b
压杆的临界应力图
s
a
b
s
经验公式的 适用范围:
s p
cr
cr s
s p
cr a b
cr
2 2
小柔度杆
S
欧拉公式
s p
实际是强度问题 cr s
一些常用材料的a、b值:
例14-1 截面为1220cm2,l = 7m,E = 10GPa,试求木柱的临
令 l
i
式中:--称为压杆的柔度或长细比
压杆临界应力的计算公式:
cr
cr
2EI
l2
cr
2Ε 2
2.欧拉公式的适用范围
cr
2 2
p
材料在线弹性范围内工作 压杆的临界应力图
比例极限的柔度值: cr
Ε p σp
s p
当 p时,欧
拉公式才适用。
这类压杆称为
大柔度杆或细 长杆。
欧拉公式
w Ak coskx Bksin kx
边界条件
x 0 w 0, w 0
xl w
积分常数 挠曲线近似方程
材料力学之压杆稳定

材料力学之压杆稳定引言材料力学是研究物体内部受力和变形的学科,压杆稳定是其中的一个重要内容。
压杆稳定是指在受到压力作用时,压杆能够保持稳定,不发生失稳或破坏的现象。
本文将介绍压杆稳定的基本原理、稳定条件以及一些常见的失稳形式。
压杆的受力分析在进行压杆稳定分析前,我们首先需要对压杆受力进行分析。
压杆通常是一根长条形材料,两端固定或铰接。
在受到外部压力作用时,压杆会受到内部的压力,这些压力会导致杆件产生变形和应力。
在分析压杆稳定性时,我们主要关注压杆的弯曲和侧向稳定性。
压杆的基本原理压杆的稳定性是由杆件的弯曲和侧向刚度共同决定的。
当压杆弯曲和侧向刚度足够大时,压杆能够保持稳定。
所以,为了提高压杆的稳定性,我们可以采取以下几种措施:1.增加杆件的截面面积,增加抗弯能力;2.增加杆件的高度或长度,增加抗弯刚度;3.增加杆件的横向剛性,增加抗侧向位移能力;4.添加支撑或加固结构,增加整体稳定性。
压杆的稳定条件压杆稳定的基本条件是在承受外部压力时,内部应力不超过材料的极限强度。
当内部应力超过材料的极限强度时,压杆将会发生失稳或破坏。
在实际工程中,我们一般采用压杆的临界压力比来判断压杆的稳定性。
临界压力比是指杆件在失稳前的临界弯曲载荷与临界弯曲载荷之比。
当临界压力比大于1时,压杆是稳定的;当临界压力比小于1时,压杆是不稳定的。
临界压力比的计算可以采用欧拉公式或者Vlasov公式等方法。
这些方法能够给出压杆在不同边界条件下的临界压力比。
在工程实践中,我们可以根据具体问题选择合适的方法来计算临界压力比。
压杆的失稳形式压杆失稳通常有两种形式:弯曲失稳和侧向失稳。
弯曲失稳压杆的弯曲失稳是指杆件在受到外部压力作用时,发生弯曲变形并导致失稳。
在弯曲失稳中,压杆的弯曲形态可以分为四种:1.局部弯曲失稳:杆件出现弯曲局部失稳,形成凸起或凹陷;2.局部弯扭失稳:杆件出现弯曲和扭曲共同失稳;3.全截面失稳:整个杆件截面均发生失稳;4.全体失稳:整个杆件完全失稳并失去稳定性。
材料力学答案- 压杆稳定
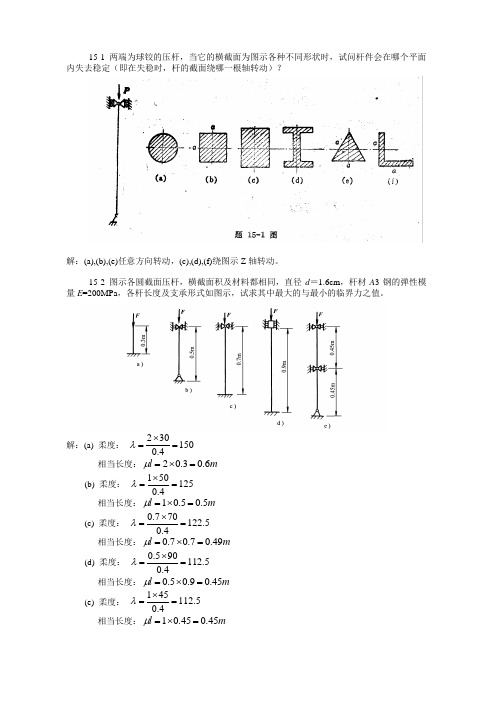
15-1 两端为球铰的压杆,当它的横截面为图示各种不同形状时,试问杆件会在哪个平面内失去稳定(即在失稳时,杆的截面绕哪一根轴转动)?解:(a),(b),(e)任意方向转动,(c),(d),(f)绕图示Z 轴转动。
15-2 图示各圆截面压杆,横截面积及材料都相同,直径d =1.6cm ,杆材A 3钢的弹性模量E =200MPa ,各杆长度及支承形式如图示,试求其中最大的与最小的临界力之值。
解:(a) 柔度: 2301500.4λ⨯== 相当长度:20.30.6l m μ=⨯=(b) 柔度: 1501250.4λ⨯== 相当长度:10.50.5l m μ=⨯=(c) 柔度: 0.770122.50.4λ⨯== 相当长度:0.70.70.49l m μ=⨯=(d) 柔度: 0.590112.50.4λ⨯== 相当长度:0.50.90.45l m μ=⨯=(e) 柔度: 145112.50.4λ⨯== 相当长度:10.450.45l m μ=⨯=由E=200Gpa 及各柔度值看出:各压杆的临界力可用欧拉公式计算。
即:()22cr EIF l πμ=各压杆的EJ 均相同,故相当长度最大的压杆(a)临界力最小,压杆(d)与(e)的临界力最大,分别为:()2948222320010 1.610640.617.6410cr EFF l N πππμ-⨯⨯⨯⨯⨯===⨯()2948222320010 1.610640.4531.3010cr EIF l Nπππμ-⨯⨯⨯⨯⨯===⨯15-3 某种钢材P σ=230MPa ,s σ=274MPa ,E =200GPa ,直线公式λσ22.1338-=cr ,试计算该材料压杆的P λ及S λ值,并绘制1500≤≤λ范围内的临界应力总图。
解:92.633827452.5p s s a λπσλ===--===15-4 6120型柴油机挺杆为45钢制成的空心圆截面杆,其外径和内径分别为,12mm 和10mm ,杆长为383mm ,两端为铰支座,材料的E =210GPa ,P σ=288MPa ,试求此挺杆的临界力cr F 。
《结构力学》压杆稳定

(1)计算柔度: L
i
惯性半径 i
I 。 A
( 2 )确定临界应力的求解方 法:
比较, p , s的大小( p , s的值根据 力学性质确定 )
(3)代入相应的公式,求解 压杆稳定的临界荷载;
§12-3 压杆的稳定计算- 系数法 一.稳定条件
为了防止压杆失稳,则必须使压杆的工作应力 小于或等于许用应力 cr ,即:
/
2.25 1.78 1.44 1.15 1.00 1.05
作 业1
预习本章下几节!
P176 1. 习题1 2. 习题2
二、欧拉公式的应用范围
1.压杆的临界应力公式 (临界应力欧拉公式)
压杆受临界力Pcr作用而仍在直线平衡形态下维持稳 定的平衡时,横截面上的压应力可按 = P/A 计算。
cr
查表2得:
3 2 105 402
54.83kN
s 62 s P ,为中柔度杆,其临界应 力用经验公式求。
查表2得:a=304, b=1.12
cr a b
Pcr cr A (a b )
d 2
4
269.4kN
例11-2:一两端铰支的圆截面受压柱d=40mm, E 200GPa ① l=1.2m, ② l=0.8m, ③l=0.5m; 试求:三者的临界力。
iz
Iz A
1 =
12 bh
=
bh3
h = 12
12 bh hb 3
iy
Iy A
1
b = 12
圆形截面的惯性 半径i:
i z=i y I = A
1
1 d 2 4
d4 64
d = 4
材料力学-压杆稳定

1.直线型经验公式
对于柔度(λs≤λ<λp)的中柔 度杆(中长压杆),临界应力 与λ的关系采用直线公式:
cr a b 13 8
式(13-8)中的系数a,b可查书中表 13-1。 λ的最低界限:
s
a
s
b
(塑性材料)
b
a
b
b
(脆性材料)
---------(13-9)
图13-3
2.抛物线型经验公式
式中有c1,c2,k三个未知量。根据边界条件:当x=0时, yA=0;代入式(c)得c2=0。式(c)成为
y c1 sinkx (d )
当x=l时,yB=0;代入式(d)后可得 c1 sinkl 0 (e)
要满足式(e),必然是c1或sinkl等于零,若c1=0,则压杆 上各点的位移都为零,这显然与压杆在微弯状态下保持平衡 的前提不符,故必须是sinkl=0。要满足这一条件的kl值为:
kl 0, ,2 ,L ,n (n为正整数)
由k P n 可得:
EI l
P
n2 2 EI
l2
(
f
)
使压杆可能在微弯状态下保持平衡的最大轴向压力,应
该是式(f) 中n=1时的P值,这就是所求的两端铰支压杆的临
界力Pcr,即
Pcr
2 EI
l2
(13 1)
式(13-1)习惯上称为两端铰支压杆的欧拉公式。当各个 方向的支承情况相同时(如两端为球铰),压杆总是在它的 抗弯能力最小的纵向平面内失稳,所以式(13-1)中的EI是压 杆的最小抗弯刚度,即I应取截面的最小形心主惯性矩Imin。
2
图13-4 对于柔度(λ<λc)的杆件,临界应力与λ的关系采用抛物线公式:
第十四章压杆稳定

中小柔度杆的临界应力计算 1.直线型经验公式 直线型经验公式 ①σP<σ<σS 时:
σ cr =a−bλ
Qσ cr = a − b λ ≤σ s a −σs ∴λ ≥ = λ0
λ0 ≤λ <λP
b
中柔度杆, 中柔度杆,应力用经验公式计算
②σS<σ 时:
σ cr
σS
σP
σ cr =σ s
λ < λ 0 小柔度杆,临界应力为屈服应力 小柔度杆,
=
cr
≥ nst
[ Fst ]
稳定许用压力
二、压杆的稳定容许应力: 压杆的稳定容许应力: 安全系数法确定容许应力: 安全系数法确定容许应力:
σ≤
σ cr
nst
= [σ st ]
二 折减系数法
[σ st ]
稳定条件是
= ϕ [σ ]
ϕ→折减系数, 它是λ的函数。
σ ≤ ϕ [σ ]
三 压杆的合理设计 1 压杆的合理设计 2 合理选择截面
解:压杆在正视图平面 两端约束为铰支,屈 内,两端约束为铰支 屈 曲时横截面将绕 z 轴转 动:x y平面 平面
λz=µz l / iz ,
iz =Izຫໍສະໝຸດ AIz=bh3/12λz=132.6
λy=µy l / iy , Iy=hb3/12
iy
压杆在俯 压杆在俯视图平面 内,两端约束为固 定端,屈曲时横截面 定端 屈曲时横截面 将绕 y 轴转动:x、z 轴转动: 、 平面 Iy = A
λy=99.48
因此,压杆将在正视图平面内屈曲(弯曲)。 因此,压杆将在正视图平面内屈曲(弯曲)。 屈曲 而且λ λz=132.6 > λy=99.48 而且λz=132.6 > λp=100
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
压杆2为中柔度杆,对于Q235钢,a=310MPa,b=1.24MPa,临界应力为
临界力为
σcr
Fcr
cr
A
cr
d 4
2
414 KN
压杆3为小柔度杆,因为Q235钢为塑性材料,故其临界应力为
临界力为
σcr
Fcr
sA s
d 2 4
461KN
§14-2 临界力和临界应力
例14-2 如图所示,一长度l=750mm的压杆,两端固定,横 截面为矩形,尺寸如图。压杆的材料为Q235钢,其弹性 模量E=200GPa,计算压杆的临界应力和临界力
压杆的临界力越大,稳定性越强
§14-2 临界力和临界应力
临界力的欧拉公式
2EI
Fcr l2
EI ——压杆的抗弯刚度。 μ——与支承情况有关的长度系数 l ——压杆的长度,单位为mm。 欧拉公式表明: 1)压杆的临界力与其抗弯刚度成正比 2)压杆的临界力与压杆长度的平方成正比 3)压杆的临界力与压杆的支承情况有关,压杆两端的支 承越牢固,压杆抵抗弯曲变形的能力越强,临界力越大。
§14-1 压杆稳定的概念及失稳分析
压杆失稳分析
对于细长压杆,其直线平 衡状态是否稳定,与轴向 压力F的大小有关。当压 力为某一数值FQ时,压杆 处于稳定的直线平衡状 态和不稳定的直线平衡 状态之间,这一状态称 为临界状态
压杆的失稳过程
压杆处于临界状态的压力值,称为压杆的临界压力,简称临界力, 用符号F1j表示
§14-2 临界力和临界应力
临界应力的欧拉公式
cr
2E 2
i——压杆横截面的惯性半径,单位为mm; λ——压杆的柔度,无量纲,柔度越大,则临界应力越小,压 杆越容易失稳。
压杆越细长、支承情况越不牢固、横截 面尺寸越小则柔度越大,临界应力越小
§14-2 临界力和临界应力
欧拉公式的适用范围
故圆形截面的惯性半径为
各压杆的柔度分别为
§14-2 临界力和临界应力
(2) 计算各压杆的临界应力和临界力
对于Q235钢λ p=100, λ s=60。对于压杆1,其柔度λ 1=160> λ p,所以压杆 1为大柔度杆,临界应力用欧拉公式计算。
临界力为
Fccrr21c2Er A77c.r1Md4P2a 151KN
第十四章 压杆稳定
主要内容:
压杆稳定的概念及失稳分析 临界力和临界应力 压杆的稳定性计算 提高压杆稳定性的措施
§14-1 压杆稳定的概念及失稳分析
压杆稳定的概念
压杆保持其原有直线平衡状态的能力,称为压杆的稳定性;反之, 压杆丧失其原有直线平衡状态而破坏的现象,称为压杆的失稳。
条形钢板的失稳
机械中的细长压杆
例14-1 如图所示,用Q235钢制成的三根压杆,两端均为铰链支承, 横截面为圆形,直径d=50mm,长度分别为l1=2m, l2=1m, l3=0.5m,材料的弹性模量E=200GPa,屈服点σs=235MPa,求三 根压杆的临界应力和临界力。
§14-2 临界力和临界应力
解 (1)计算各压杆的柔度 因压杆两端为铰链支承,查表得长度系数μ=1。圆形截 面对y轴和z轴的惯性矩相等,均为
Fcr—压杆的临界压力 F —压杆的工作压力 N —压杆工作安全系数 σcr —压杆的临界应力 σ —压杆的工作压应力 [nW] —规定的稳定安全系数,它表示要求受 压杆件必须达到的稳定储备程度。
§14-3 压杆的稳定性计算
几种常用零件稳定安全系数的参考值
压杆的临界压力取决于整个杆件的弯曲刚度。 但在工程实际中, 压杆局部有截面削弱的情况, 在确定临界压力 或临界应力时,此时可以不考虑杆件局部截面削弱的影响, 仍按 未削弱的截面面积、最小惯性矩和惯性半径等进行计算。但对这 类杆件,还需对削弱的截面进行强度校核。
λp为临界应力等于材料比例极限时的柔度,是允许应用欧拉公式 的最小柔度值 例如:Q235钢,其弹性模量E=200GPa,比例极限σp =200MPa, 则λp值为
对于Q235钢制成的压杆,当其柔度λ≥100时,才能应用欧拉公式。 λ ≥ λp的压杆称为大柔度杆或细长杆,其临界力或临界应力可用欧拉 公式计算。
§14-3 压杆的稳定性计算
例14-3 空气压缩机的活塞杆由45钢制成σs=350MPa,σs=280MPa, E=210GPa。长度l=-703mm,直径d=45mm。最大压力Fmax=41.6kN, 规定的安全系数为[nW] = 8~10。试校核其稳定性 解 (1)确定压杆类型。
活塞杆可简化为两端铰支压杆,μ=1。截面为圆形,i=d/4,柔度为 λ= μ l i =62.5 λ <λp
(2)计算临界应力和临界力 对于Q235钢λ p=100,则λ > λ p,故临界应力用欧拉公式计算。 σcr
临界力为 Fcr cr A 40.3KN
§14-3 压杆的稳定性计算
压杆稳定计算,通常采用安全系数法。为了保证压杆不失
稳,并具有一定的稳定储备,压杆的稳定条件可表示为
n=Fcr/F=σcr/σ≥[nW]
§14-2 临界力和临界应力
中、小柔度杆临界应力的计算
λ ≤ λp的压杆称为小柔度杆或短粗杆
小柔度杆的临界应力按其制作材料不同分为两种情况:
对塑性材料
cr s
对脆性材料 cr by
λs ≤ λ ≤ λp的压杆称为中柔度杆
中柔度杆临界应力的计算,通常采用建立在实验基础上的经验公式
解 (1)计算压杆的柔度 压杆两端固定,查表得长度系 数μ= 0.5。矩形截面对y轴和z轴 的惯性矩分别为
I y hb3 12 2880mm4 Iz hb3 12 8000mm4
Iy<Iz,所以压杆的横截面必定绕着y轴转动而失稳
§14-2 临界力和临界应力
截面对y轴的惯性半径为
得压杆的柔度为
cr a b
§14-2 临界力和临界应力
归纳:
(1)对于大柔度杆( λ≥λp ),用欧a b
(3)对于小柔度杆( λ≤λp ), 材料为塑性材料时,σcr= σs 材料为脆性材料时, σcr= σby
§14-2 临界力和临界应力
