搜索与或图搜索实例算法
合集下载
AI03-2与或图搜索

E H 5 4
F I
G
反向更新代价 g(E)=5, g(D)=9, g(Q0)=10 g(I)=0, g(F)=1, g(D)=8, g(Q0)=9
3.3.3 启发式与或树搜索
例 3.18
A D Q0
B
C K L
E H 5 4
F I
J
G
反向更新代价 g(J)=0, g(K)=0, g(B)=2, g(A)=7, g(Q0)=8 g(L)=0, g(C)=1, g(A)=5, g(Q0)=6
Q21 Q22 Q23
Q’21 Q’22 Q’23
3.3.1 与或图
与或图/与或树
n0 n1 n2 n4 初始节点
n3
n5
n6
n8 目标 n7 目标
3.3.1 与或图
问题求解
状态图/或图
一个问题可以有几种求解方法 只要其中一种方法可以求解问题,则该问题被求解,方法之 间是"或"的关系
与图:
在用一种方法求解时,又可能需要求解几个子问题 这些子问题必须全部求解,才可能用该方法求解原始问题, 这些子问题之间是"与"的关系
3.3.3 启发式与或树搜索
例 3.18
A D Q0
B 3 3
C
E 3 2
F
左局部树: g(B)=3, g(C)=3, g(A)=8, g(Q0)=9 右局部树: g(E)=3, g(F)=2, g(D)=7, g(Q0)=8
希望树
3.3.3 启发式与或树搜索
例 3.18
A D Q0
B 3 3
C
3.3.3 启发式与或树搜索
例 3.18
A √ D √ √ K √ C √ L E H 5 4 F I Q0 √
人工智能第4章图搜索技术

OPEN表的首部,转步2。
例4.4 对于八数码问题,应用
深度优先搜索策略,可得如图4—
6所示的搜索树。
283
深度优先搜索亦称为纵向搜 1 4 765
索。由于一个有解的问题树可能
含有无穷分枝,深度优先搜索如
果误入无穷分枝(即深度无限,但
解不在该分支内),则不可能找到
目标节点。所以,深度优先搜索
策略是不完备的。另外,应用此
例4.6 设A城是出发地,E城是目的地,边上的数字代表 两城之间的交通费。试求从A到E最小费用的旅行路线。
B 4
6
A
3
4
A
E
C 3
D1
3
4
D2 23
E1 3
C
D
2
(a)
E2
B2 6
深度优先搜索算法:
步1 把初始节点S0放入OPEN表中; 步2 若OPEN表为空,则搜索失败,退出。
步3 取OPEN表头节点N放入CLOSED表中,并冠以顺序编号n;
步4 若目标节点Sg=N,则搜索成功,结束。 步5 若N不可扩展,则转步2; 步6 扩展N,将其所有子节点配上指向N的返回指针依次放入
2831 14 765
第4章 图搜索技术
2 283
14 765
6 83
214 765
7 283 714 65
14 83 214 765
15 283 714 65
22 83 214 765
23 813 24 765
3 23 184 765
8 23
1 84 7 65
9 23 184 765
16 1 23
第4章 图搜索技术
步1 把S0放入OPEN表中,置S0的深度d(S0)=0; 步2 若OPEN表为空,则失败,退出。 步3 取OPEN表头节点N,放入CLOSED表中,并 冠以顺序编号n; 步4 若目标节点Sg=N,则成功,结束。 步5 若N的深度d(N)=dm(深度限制值),或者若N无 子节点,则转步2; 步6 扩展N,将其所有子节点Ni配上指向N的返回 指针后依次放入OPEN表中前部,置d(Ni)=d(N)+1,转 步2。
例4.4 对于八数码问题,应用
深度优先搜索策略,可得如图4—
6所示的搜索树。
283
深度优先搜索亦称为纵向搜 1 4 765
索。由于一个有解的问题树可能
含有无穷分枝,深度优先搜索如
果误入无穷分枝(即深度无限,但
解不在该分支内),则不可能找到
目标节点。所以,深度优先搜索
策略是不完备的。另外,应用此
例4.6 设A城是出发地,E城是目的地,边上的数字代表 两城之间的交通费。试求从A到E最小费用的旅行路线。
B 4
6
A
3
4
A
E
C 3
D1
3
4
D2 23
E1 3
C
D
2
(a)
E2
B2 6
深度优先搜索算法:
步1 把初始节点S0放入OPEN表中; 步2 若OPEN表为空,则搜索失败,退出。
步3 取OPEN表头节点N放入CLOSED表中,并冠以顺序编号n;
步4 若目标节点Sg=N,则搜索成功,结束。 步5 若N不可扩展,则转步2; 步6 扩展N,将其所有子节点配上指向N的返回指针依次放入
2831 14 765
第4章 图搜索技术
2 283
14 765
6 83
214 765
7 283 714 65
14 83 214 765
15 283 714 65
22 83 214 765
23 813 24 765
3 23 184 765
8 23
1 84 7 65
9 23 184 765
16 1 23
第4章 图搜索技术
步1 把S0放入OPEN表中,置S0的深度d(S0)=0; 步2 若OPEN表为空,则失败,退出。 步3 取OPEN表头节点N,放入CLOSED表中,并 冠以顺序编号n; 步4 若目标节点Sg=N,则成功,结束。 步5 若N的深度d(N)=dm(深度限制值),或者若N无 子节点,则转步2; 步6 扩展N,将其所有子节点Ni配上指向N的返回 指针后依次放入OPEN表中前部,置d(Ni)=d(N)+1,转 步2。
第三章与或图搜索

例2
在边长为2的正方形内,任意放置5个点
,求证其中必存在两个点,它们之间的距
离不大于2。
.
问题可转化为:
.
在四个单位正方形内,
.
任意放置5个点,至少
.
.
有两个点在同一正方形内。
①I 1
III ③ 23 II
②
例3
假定我们已经会求 矩形的面积,现在要 求如图所示的五边形 的面积。
求解步骤:
求五边形面积
– 若干概念
终节点 可解节点 不可解节点 解图 耗散值 最佳解图 可解过程 不可解过程
与或图中某一个节点n到节点集N的一个解图类似于普 通图中的一条解路径。
解图的求法:从节点n开始,正确选择一个外向
连接符,在从该连接符所指的每一个后继节点出
发,继续选一个外向连接符,如此进行下去直到
由此产生的每一个后继节点成为集合N中的一个
MOVE(B,2,3) (3 3 1)
MtOVE(A,1
(2 2 2)
(2 1 3)
(3 1 1)
(3 3 2) (3 3 3)
(2 2 3)
(2 1 1)
(3 1 2)
采用归约法
– 要把所有圆盘移至柱3,必须先把C盘移至 柱3,而在移动C盘至柱3前,柱3必须为空。
– 只有把A、B移至柱2后,才能将C移到柱3。 – 在C移至柱3后,再解决将A、B移至柱3。
P6 BAD BCD DBA= DBC, BAAD, BCCD,
DB, BAD, BCD
DB=DB|T P2
P4 DBA= DBC
BAD= BCD| T
P1
BAD= 90°| BAAD, ... BCD= 90°| BCCD, ...
人工智能之与或图搜索问题
(3,1,1,1,1)
(2,2,1,1,1) 我方必胜
(2,1,1,1,1,1) 30
对于比较复杂的博弈问题,只能模拟人的思维 “向前看几步”,然后作出决策,选择最有利自 己的一步。即只能给出几层走法,然后按照一定 的估算办法,决定走一好招。
31
中国象棋
一盘棋平均走50步,总状态数约为10的161 次方。
(2,2,2,1,MAX)
(2,2,1,1,1,MIN)
(2,1,1,1,1,1,MAX)
注:如果MAX走红箭头的分法,必定获胜。 29
分钱币问题
对方先走
(7)
(6,1) (5,2)
(4,3)
(5,1,1) (4,2,1) (3,2,2)
(3,3,1)
(4,1,1,1) (3,2,1,1) (2,2,2,1)
6
普通图搜索的情况
s
n
f(n) = g(n) + h(n) 对n的评价实际是对从s到n这条路 径的评价
7
与或图: 对局部图的评价
初始节点
c
a b
目标
目标
8
两个过程
图生成过程,即扩展节点
从最优的局部途中选择一个节点扩展
计算耗散值的过程
对当前的局部图从新计算耗散值
9
n1 n3 n6
n7 目标
44
步2
Open为空,即已经扩展完节点
5、若CLOSED表为空,则转8;否则取出
CLOSED表中的第一个节点,记为 np;
45
6、若 np 属于MAX层,且对于它的属于MIN层
的子节点 nci 的 e ( nci )有值,则: e ( np ) =max { nci }
与或图

与或图的搜索 及应用
北京信息科技大学 孙骏 2014.05.13
与或图的搜索策略
1 与或图的一般搜索过程 2 与或图的广度优先搜索
3 与或图的深度优先搜索
4 与或图的有序搜索 5 博弈树的启发式搜索
1 与或图的一般搜索过程
与图: 把一个原问题分解为若干个子问题,P1,P2, P3,…可用“与图”表示;P1,P2,P3,…对应的子问
S0 2
A 6 t1 5 t2 E C 1 t3 2 F 3 1 2 B 2
D 1 G 1
t4 2 t5
解:左边解树, 按和代价:h(A)=11 h(S0)=13; 按最大代价:h(A)=6 h(S0)=8; 右边解树, 按和代价:h(G)=3, h(D)=4, h(B)=6, h(S0)=8; 按最大代价:h(G)=2, h(D)=3, h(B)=5, h(S0)=7
P
E
F
2
G
0 0 2 2 0 0
H
3
2
h(N)=2, h(P)=7, h(C)=3, h(A)=8 左子树h(S0)=9
3
2
2
2
三阶梵塔问题
1 2 3 1 2 3
A
A
B C
B C
初始配置
目标配置
问题描述: 采用三元组表示状态: S=(i,j,k) 其中,i, j, k分别表示金片C,B,A所在的钢针号。 初始状态(1,1,1),目标状态(3,3,3)
a
4-5=-1 b
5-4=1
5-5=0
5-5=0
6-6=0
程可用一个“与或图”来表示
P P1 P11 P12 P2 P31 P3 P32 P33
北京信息科技大学 孙骏 2014.05.13
与或图的搜索策略
1 与或图的一般搜索过程 2 与或图的广度优先搜索
3 与或图的深度优先搜索
4 与或图的有序搜索 5 博弈树的启发式搜索
1 与或图的一般搜索过程
与图: 把一个原问题分解为若干个子问题,P1,P2, P3,…可用“与图”表示;P1,P2,P3,…对应的子问
S0 2
A 6 t1 5 t2 E C 1 t3 2 F 3 1 2 B 2
D 1 G 1
t4 2 t5
解:左边解树, 按和代价:h(A)=11 h(S0)=13; 按最大代价:h(A)=6 h(S0)=8; 右边解树, 按和代价:h(G)=3, h(D)=4, h(B)=6, h(S0)=8; 按最大代价:h(G)=2, h(D)=3, h(B)=5, h(S0)=7
P
E
F
2
G
0 0 2 2 0 0
H
3
2
h(N)=2, h(P)=7, h(C)=3, h(A)=8 左子树h(S0)=9
3
2
2
2
三阶梵塔问题
1 2 3 1 2 3
A
A
B C
B C
初始配置
目标配置
问题描述: 采用三元组表示状态: S=(i,j,k) 其中,i, j, k分别表示金片C,B,A所在的钢针号。 初始状态(1,1,1),目标状态(3,3,3)
a
4-5=-1 b
5-4=1
5-5=0
5-5=0
6-6=0
程可用一个“与或图”来表示
P P1 P11 P12 P2 P31 P3 P32 P33
(搜索推理技术-与或树搜索)

7、无判断起始节点1可解
8、从OPEN中删除含有可解先辈节点的节点
删除
OPEN= { B, C, t1, 10, 11, 12, A, t2, t3 }
CLOSED= { 1, 2, 3, 4, 5, 6, 7, 8, 9 } OPEN= {t1, 10, 11, 12, t2, t3}
CLOSED= {1, 2, 3, 4, 5, 6, 7, 8, 9} 说明:对于OPEN表中的叶节点直接移到 CLOSED表,不作任何处理
OPEN= {9, B, C, t1, 10, 11, 12, A} CLOSED= {1, 2, 3, 4, 5, 6, 7, 8}
第九大循环(3、4、5、6、7、8步): 3、从OPEN表中取出节点9,并送到CLOSED表 4、扩展节点9,生成后继节点 t2、t3,并送到 OPEN表的末端 5、有叶节点 6、实现可解标志过程(可以判断节点9、4、2可解)
即OPEN是堆栈
注意
由于深度限制,深度优先搜索算法有可能找不 到解
例:
深度界限为4
√
2
1
√
√
6
√
3
Ⅹ A √ √
7 √
C
Ⅹ
4
5
8
t
√
Ⅹ B
t
t
t
t
√
√
√
√
注:后生成的节点画在左边
课堂练习:用宽度和深度优先搜索算法找出解树
提示:对于宽度优先搜索,先生成的节点画在左;
对于深度优先搜索,后生成的节点画在左
CLOSED= { 1, 2, 3, 4, 5, 6, 7, 8, 9, t1, 10 }
搜索过程演示
√
第二章与或图搜索问题

15
耗散值(代价值)的计算:示例
• 解树:S0, A, t1和t2。S0, B, D, G, t4和t5。
S0
2
2
• 由左边的解树可得: • 和代价:h(A)=11,h(S0)=13
A
6
5
1
• 最大代价: h(A)=6,h(S0)=8
t1
t2
C
• 由右边的解树可得: • 和代价:h(G)=3,h(D)=4,h(B)=6,h(S0)=8
3
2
2
2
H(G)=7, h(H)=6, h(E)=7, h(D)=11, S0的右
子树算出的h(S0)=12,而左子树的h(S0)=9,
因此左子树为希望树
22
与或树的有序搜索:示例
S0
A
D
B L
C 3
M
E
F
2
G
H
0
0
2
2
3
2
2
2
h(L)=2, h(M)=6, h(B)=3, h(A)=8, L、B均为可解节点。但节
• 1. 把初始节点S0放入OPEN表。
• 2. 把OPEN表中的第一个节点(记为节点n)取出放入CLOSED 表。
• 3. 如果节点n可扩展,则作下列工作: • 3.1 扩展节点n,将其子节点放入OPEN 表的尾部,并为每
个子节点配置指向父节点的指针,以备标识过程使用。
• 3.2 考察这些子节点中有否终止节点。若有,则标识这些终 止节点为可解节点,并应用可解标识过程对其父节点、祖父 节点等先辈节点中的可解节点进行标识。如果初始节点S0也被 标识为可解节点,就得到了解树,搜索成果,退出搜索过程; 如辈果的不节能点确。定S0为可解节点,则从OPEN表中删去具有可解先
人工智能中图搜索算法(PDF 159页)

图4—5 八数码问题的广度优先搜索
第9页
第4章 图搜索技术
以上两个问题都是在某个有向图中寻找目标或路径问 题,这种问题图搜索问题。把描述问题的有向图称为状态 空间图,简称状态图。图中的节点代表问题中的一种格局, 一般称为问题的一个状态,边表示两个状态之间的联系。 在状态图中,从初始节点到目标节点的一条路径或者所找 到的目标节点,就是问题的解(路径解)。
谓搜索,顾名思义,就是从初始节点出发,沿着与之相连 的边试探地前进,寻找目标节点的过程(也可以反向进行)。 搜索过程中经过的节点和边,按原图的连接关系,形成树 型的有向图,称为搜索树。搜索过程应当随时记录搜索痕 迹。
1.搜索方式 用计算机来实现状态图的搜索,有两种最基本的方式: 树式搜索和线式搜索。 所谓树式搜索,形象地讲就是以“画树”的方式进行 搜索。 即从树根(初始节点)出发一笔一笔地描出来的。
状态图实际上是一类问题的抽象表示。事实上,有许
多智力问题(如梵塔问题、旅行商问题、八皇后问题、农
夫过河问题等)和实际问题(如路径规划、定理证明、演
绎推理、机器人行动规划等)都可以归结为在某一状态图
中寻找目标或路径的问题。因此,研究状态图搜索具有普
遍意义。
第10页
第4章 图搜索技术
4.1.2 状态图搜索 在状态图中寻找目标或路径的基本方法就是搜索。所
第4章 图搜索技术
3. 搜索算法 由于搜索的目的是为了寻找初始节点到目标节点 的路径,所以在搜索过程中就得随时记录搜索轨迹。 为此,我们用一个称为CLOSED表的动态数据结构来 专门记录考查过的节点。显然,对于树式搜索来说, CLOSED表中存储的正是一棵不断成长的搜索树;而 对于线式搜索来说,CLOSED表中存储的是一条不断 伸长的折线,它可能本身就是所求的路径(如果能找到 目标节点的话)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
q=43 n0 初始节点
第二个大循环(扩展结点),直到n0是SOLVED: 1. 找到待扩展的局部图G’{n0,n1}
q=5 n1
连接符1
n2
连接符2
2. n=G’中非终结点, 此时n=n1
3. 扩展结点n=n1, 生成后继结点集合{n2,n3},
q(n2)=4, q(n3)=4, 都不是终结点,把结点加到
q(n4)=1, q(n5)=1, q(n1)=2, 都不是终结点, 把结点加到G中
n4
4. 小循环(修改结点耗散值),直到S为空: a. S={n=n0}
b. 保证n的后代不在S中
c. m=n0的连接符有两条,
n5
计算q1(m)=1+q(n1)=1+2=3
q2(m)=2+q(n5)+q(n4)=2+1+1=4
与或图: 对局部图的评价
初始节点
c
a b
目标
目标
与或图搜索:AO*算法
两个过程
• 图生成过程,即扩展节点
自顶向下, 从最优的局部途中选择一个节点扩展
• 计算耗散值的过程
自下向顶, 对当前的局部图重新计算耗散值
AO*算法搜索例子
n0 初始节点
n1
n2
n4
n3
n5
n6
n7 目标
n8
目标
其中: h(n0)=3 h(n1)=2 h(n2)=4 h(n3)=4 h(n4)=1 h(n5)=1 h(n6)=2 h(n7)=0 h(n8)=0
与或图搜索
与或图表示
弧线 与节 点
终结点
父பைடு நூலகம்点
或节
点
A
子节
点
N MH
BC D E FG
• 与或图是一个超图,节点间通过连 接符连接。
• K-连接符:
…... K个
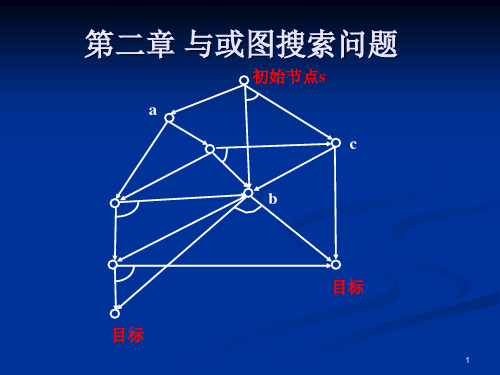
与或图搜索问题
a 目标
初始节点s c
b 目标
n0→ {n7,n8}的3个解图
初始节 点n0
初始节 点n0
目标n7 (a)
目标n8
初始节 点n0
• 没有后裔的非终节点是不能解节点。
• 若非终节点有“或”子节点,当且仅当所有子节点均不能解时,该非终节点才不 能解。
• 若非终节点有“与”子节点时,当至少有一个子节点不能解时,该非终节点才不 能解。
耗散值的计算
1.若n是N的一个元素, 则k(n, N) =0 2.若n是一个外向连接符指向后继结点{n1,..ni}
…
AO*算法搜索例子
q=4q=5 n0
初始节点
q=5
n1
连接符1
连接符2
n2
n4
qq==12
n3
n5
n6 n8
n7
G={n0,n1,n2,n3,n4,n5} 第三个大循环(扩展结点),直到n0是SOLVED: 1. 找到待扩展的局部图G’{n0,n4,n5} 2. n=G’中非终结点, 此时n=n5 3. 扩展结点n=n5, 生成后继结点集合
目标n7
(c)
目标n8
目标n7
(b)
目标n8
无解节点
有解节点
终结点
t
t
t
t
t
t
能解节点(a) t
t t (b)
• 终节点是能解节点
• 若非终节点有“或”子节点时,当且仅当其子节点至少有一能解时,该非终节点 才能解。
• 若非终节点有“与”子节点时,当且仅当其子节点均能解时,该非终节点才能解。
不能解节点
{n6,n7,n8}, q(n6)=2, q(n7)=0, q(n8)=0 把结点加到G中 4. 小循环(修改结点耗散值),直到S为空: a. S={n=n5} b. 保证n的后代不在S中 c. m=n5的连接符有两条,
计算q1(m)=1+q(n6)=1+2=3 q2(m)=1+q(n7)+q(n8)=2+0+0=2
k(n, N) = Cn+k(n1, N)+…+k(ni, N) 其中:N为终节点集
Cn为连接符的耗散值
n
…...
n1 n2
ni
i个
目标n7
初始节 点n0
搜索解图耗散值的递归计算:
n0=2+k(4, N)+k(5, N)
n4
k(5, N)= min(2+k(7,N)+k(8,
n5
N),…)
=2
k(4, N)= min(1+k(5, N),
令q(m)=q(n0)=min(q1,q2)=3
d.修改指针到q1对应的连结符上去
e.如果n1为非SOLVED,则m=n0也为非
SOLVED
f.如果m=n0为SOLVED,或者q(m)被修改过,则
需要也对m的父结点进行修改, 即将m的父结点
加到S中
g.小循环结束
5.大循环结束
AO*算法搜索例子 G={n0,n1,n4,n5}
n4
G中 4. 小循环(修改结点耗散值),直到S为空:
a. S={n=n1}
n3
b. 保证n的后代不在S中
n5
c. m=n1的连接符有两条,
计算q1(m)=1+q(n3)=1+4=5
q2(m)=1+q(n2)=1+4=5
d继令.q修…cq1续.q改2(m(m小(指mm=)循)=针n)==环01到q1的+:(+qhn连2h(1n对接()n1=应符5)m=)的有+1inh+连两((q54结条=1),=符6,q计42上算)=去45.大fdeg行....循如令q修小修(环果q改循m改(结n指m环=,3束n即)结针非=1将到束)qS被O(mqn修L10=V对改)nE=应1D过m的,的则,i则n父连m(需q结结=1要点n,符q也1n2上也0对)=加去为m5到非的SS父中O结LV点ED进
令q(m)=q(n5)=min(q1,q2)=2 d.修改指针到q2对应的连结符上去 e.n7,n8为SOLVED,则m=n5也为SOLVED f. q(m=n5)被修改过,则需要也对m的父结点 进行修改, 即将m=n5的父结点n0加到S中 g.小循环结束 5.大循环结束
AO*算法搜索例子
q=5 n0
设:K连接符 的耗散值为K
AO*算法搜索例子
G中只有一个结点n0
第一个大循环(扩展结点),直到n0是SOLVED:
q=3 n0 初始节点
1. 找到待扩展的局部图G’{n0} 2. n=G’中任意结点, 此时n=n0
3. 扩展结点n=n0, 生成后继结点集合{n1,n4,n5},
n1
连接符1
连接符2
1+k(8,N))
目标n8
= min(3, 1)=1
N0= 2+1+2=5
(c)
(a)的解图耗散值为8
(b)的解图耗散值为7
具有最小耗散值的解图称为最佳解 图,其值也用h*(n)标记.上例中的 h*(n)=5
普通图搜索的情况
s
n f(n) = g(n) + h(n) 对n的评价实际是对从s经过n到目的地这条路径的评价
初始节点
q=5 n1
连接符1
n2
连接符2
q=1 n4
n3
q=2 n5
n6 n8
