高中数学第三章统计案例2独立性检验教学案北师大版选修2_3
北师大版选修2《独立性检验的应用》教案及教学反思
北师大版选修2《独立性检验的应用》教案及教学反思一、教学目标1.了解独立性检验的概念及其应用；2.能够运用卡方检验进行独立性检验；3.能够使用SPSS软件进行数据分析及独立性检验；4.培养学生独立思考和数据分析的能力。
二、教学内容1. 独立性检验的概念1.1 独立性检验的定义1.2 独立性检验的假设1.3 独立性检验的统计量1.4 卡方分布的性质2. 卡方检验2.1 单个样本的卡方检验2.2 独立样本的卡方检验3. 数据分析3.1 数据预处理3.2 数据分析方法3.3 数据分析实例4. SPSS软件操作4.1 SPSS软件简介4.2 数据导入4.3 数据描述性统计4.4 独立性检验使用SPSS进行分析三、教学过程1. 独立性检验的概念1.1 独立性检验的定义教师向学生讲解独立性检验的定义，即根据样本数据来检验两个变量是否独立。
1.2 独立性检验的假设教师向学生介绍独立性检验的假设，即H0表示两个变量不独立，Ha表示两个变量独立。
1.3 独立性检验的统计量教师向学生介绍独立性检验的统计量，即卡方值。
1.4 卡方分布的性质教师向学生介绍卡方分布的性质，包括非负、单峰且右偏、分布形态取决于自由度等内容。
2. 卡方检验2.1 单个样本的卡方检验教师向学生介绍单个样本的卡方检验，包括计算方法、自由度等内容。
2.2 独立样本的卡方检验教师向学生介绍独立样本的卡方检验，包括计算方法、自由度、卡方检验的步骤等内容。
3. 数据分析3.1 数据预处理教师向学生介绍数据预处理的步骤，包括数据清洗、数据变换、数据标准化等内容。
3.2 数据分析方法教师向学生介绍数据分析的方法，包括描述性统计分析、推断性统计分析、因果关系分析、分类分析等内容。
3.3 数据分析实例教师选择一个实例，向学生介绍如何进行数据分析和独立性检验。
4. SPSS软件操作4.1 SPSS软件简介教师向学生介绍SPSS软件的基本信息，包括软件界面、数据菜单、统计菜单等内容。
高中数学3.2独立性检验一教案北师大选修23
研卷知古今；藏书教子孙。
一、基础知识运用（共24分，每小题3分）1、下列各组词语中，加点字的读音全部正确且没有错别字的一项是（）A喟．（kuì）然长叹举一返三暴虎冯．（pínɡ）河祸起萧墙B屏．（pínɡ）气凝神发奋忘食箪食．（sì）瓢饮循循善诱C粢盛．（chéng）既洁礼崩乐坏斐．（fěi）然成章文质彬彬D色厉内荏．（rěn）耰而不辍曲肱．（hónɡ）而枕杀身成仁2、下列各项中不全有通假现象的一项是（）A.乡也吾见夫子而问知且而从辟人之士也B.由也好勇过我良人出，则必餍酒肉而后反C. 莫春者，春服既成无欲速，无见小利D. 女闻六言六蔽矣乎蚤起，施从良人之所之3、选出下列划横线之词活用情况不同于其他三句的一项（）A、风．乎舞雩B、七十者可以衣．帛食肉C、饭．疏食饮水D、约．我以礼4、下列加横线的字解释错误的一项是（）A、思而不学则殆．(通“怠”，懈怠)B、恭而无礼则劳．（劳累、辛苦）C、小人之过必文．(掩饰)D、就．(接近，靠近)有道而正焉5、选出下列各项中不全是古今异现象的一项（）A、①子路问成人②尝独立，鲤趋而过庭B、①子路从而后，遇丈人②颠沛必于是C、①至于他邦②古之学者为己，今之学者为人D、①子路从而后②必不得已而去，于斯二者何先6、下列各项中，“之”的意义，用法与例句相同的一项是（）例句：子之武城A、天下之无道也久矣B、非其鬼而祭之C、今之成人者何必然D、先生将何之7、选出对下列加点字的意义与用法判断正确的一项（）①未知，焉．得仁②二王我将有所遇焉．③为国以．礼④二三子以．我为隐乎A、①②不同，③④不同B、①②同，③④不同C、①②同，③④同D、①②不同，③④同8、下列各项中，句式与例句相同的一项是（）例句：仁以为己任。
A、他人之贤者，丘陵也 B、子路宿于石门C、非夫人之为恸而谁为D、孟子遇于石丘二、文言诗文阅读鉴赏（共21分）阅读下面文字，完成9-11小题（共9分，每小题3分）万章曰：“尧以天下与舜，有诸？”孟子曰：“否。
高中数学 第三章 统计案例整合学案 北师大版选修2-3(2021年最新整理)
高中数学第三章统计案例整合学案北师大版选修2-3编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学第三章统计案例整合学案北师大版选修2-3）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学第三章统计案例整合学案北师大版选修2-3的全部内容。
高中数学第三章统计案例整合学案北师大版选修2—3知识建构综合应用专题一确定回归直线方程的策略准确确定回归直线方程，有利于进一步加强数学应用意识,培养运用所学知识解决实际问题的能力，正确地求出回归直线方程是本节的重点,现介绍求回归直线方程的三种方法.一、利用回归直线过定点确定回归直线方程回归直线方程y=a+bx经过样本的中心（x,y)点，（x,y）称为样本点的中心,回归直线一定过此点.【例1】观察两个相关变量的如下数据:x—1-2-3—4—554321y-0.9-2—3。
1—3。
9-5。
15 4.12。
9 2.10.9则两个变量间的回归直线为（ )A。
y=0。
5x—1 B。
y=x C。
y=2x+0.3 D。
y=x+1答案:B二、利用公式求a，b，确定回归直线方程利用公式求回归直线方程时应注意以下几点:①求b 时利用公式b=2111)())((∑∑==---ni ini i x xy y x x,先求出x =n 1（x 1+x 2+x 3+…+x n ），y =n1（y 1+y 2+y 3+…+y n ）。
再由a=y —b x 求a 的值，并写出回归直线方程。
②线性回归方程中的截距a 和斜率b 都是通过样本估计而来，存在着误差,这种误差可能导致预报结果的偏差.③回归直线方程y=a+bx 中的b 表示x 每增加1个单位时y 的变化量,而a 表示y 不随x 的变化而变化的量。
高中数学 第三章 统计案例 2 独立性检验学案 北师大版选修2-3(2021年最新整理)
高中数学第三章统计案例2 独立性检验学案北师大版选修2-3编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学第三章统计案例2 独立性检验学案北师大版选修2-3）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学第三章统计案例2 独立性检验学案北师大版选修2-3的全部内容。
§2独立性检验学习目标重点难点1。
通过对典型案例的探究，了解独立性检验(只要求2×2列联表)的基本思想．2．会求χ2，及利用χ2判断两个变量的把握程度(两个变量是否有关系）。
重点:独立性检验的基本思想．难点：利用χ2判断两个变量的关联程度。
独立性检验设A，B为两个变量，每一个变量都可以取两个值,变量A：A1，A2＝错误!；变量B:B1,B2＝错误!.其中，a表示变量A取A1,且变量B取B1时的数据，b表示变量A取A1，且变量B取B2时的数据,c表示变量A取A2，变量B取B1时的数据，d表示变量A取A2,变量B取B2时的数据．设n＝a＋b＋c＋d,χ2＝错误!.（1)χ2≤2。
706时，没有充分证据判定变量A，B有关联；(2）χ2＞2。
706时，有90%的把握判定变量A,B有关联；（3）χ2＞3.841时，有95%的把握判定变量A，B有关联；（4）χ2＞6。
635时，有99％的把握判定变量A，B有关联．预习交流独立性检验的基本思想是什么？提示：把假设检验的基本思想具体化到独立性检验中，就可以通过随机变量χ2把两个分类变量的独立性检验的基本思想表述为:χ2＝错误!(n＝a＋b＋c＋d)．独立性检验的基本思想为观察药物A，B治疗某病的疗效,某医生将100例该病病人随机地分成两组，一组40人,服用A药;另一组60人，服用B药，结果发现：服用A药的40人中有30人治愈；服用B药的60人中有11人治愈，问A，B两种药对该病的治愈率是否有显著差别?思路分析：首先应考查该资料取自什么样的试验设计，由于100个病人完全随机地被分成两组，而且，事先不知道任何一个病人的治疗结果是治愈还是不能治愈，故该资料取自完全随机统计，符合2×2列联表的要求．解：为了便于将数据代入公式计算,先列出2×2列联表：由公式得：χ2＝错误!≈31。
高中数学 第3章 统计案例 3.2 独立性检验学业分层测评 北师大版选修23
【课堂新坐标】2016-2017学年高中数学 第3章 统计案例 3.2 独立性检验学业分层测评 北师大版选修2-3(建议用时：45分钟)学业达标]一、选择题1．有两个分类变量X 与Y 的一组数据，由其列联表计算得χ2≈4.523，则认为“X 与Y 有关系”犯错误的概率为( )A ．95%B ．90%C ．5%D ．10%【解析】 χ2≈4.523＞3.841.这表明认为“X 与Y 有关系”是错误的可能性约为0.05，即认为“X 与Y 有关系”犯错误的概率为5%.【答案】 C2．在调查中发现480名男人中有38名患有色盲，520名女人中有6名患有色盲．下列说法正确的是( )A ．男、女患色盲的频率分别为0.038,0.006B ．男、女患色盲的概率分别为19240，3260C ．男人中患色盲的比例比女人中患色盲的比例大，患色盲与性别是有关的D ．调查人数太少，不能说明色盲与性别有关 【解析】 男人中患色盲的比例为38480，要比女人中患色盲的比例6520大，其差值为⎪⎪⎪⎪⎪⎪38480－6520≈0.067 6，差值较大．【答案】 C3．为了探究生的学习成绩是否与学习时间长短有关，在调查的500名学习时间较长的生中有39名学习成绩比较好，500名学习时间较短的生中有6名学习成绩比较好，那么你认为生的学习成绩与学习时间长短有关的把握为( )A ．0B ．95%C ．99%D ．都不正确【解析】 计算出χ2与两个临界值比较， χ2＝－245×955×500×500≈25.340 3＞6.635.所以有99%的把握说生的学习成绩与学习时间长短有关，故选C. 【答案】 C4．某卫生机构对366人进行健康体检，其中某项检测指标阳性家族史者糖尿病发病的有16人，不发病的有93人；阴性家族史者糖尿病发病的有17人，不发病的有240人，有________的把握认为糖尿病患者与遗传有关系．( )【导学号：62690057】A ．99.9%B ．99.5%C ．99%D ．97.5%【解析】 可以先作出如下列联表(单位：人)：糖尿病患者与遗传列联表χ2＝－2109×257×33×333≈6.067＞5.024.故我们有97.5%的把握认为糖尿病患者与遗传有关系． 【答案】 D5．假设有两个分类变量X 与Y ，它们的可能取值分别为{x 1，x 2}和{y 1，y 2}，其2×2列联表为：( )A ．a ＝5，b ＝4，c ＝3，d ＝2B ．a ＝5，b ＝3，c ＝4，d ＝2C ．a ＝2，b ＝3，c ＝4，d ＝5D ．a ＝2，b ＝3，c ＝5，d ＝4 【解析】 比较⎪⎪⎪⎪⎪⎪a a ＋b －c c ＋d .选项A 中，⎪⎪⎪⎪⎪⎪59－35＝245；选项B 中，⎪⎪⎪⎪⎪⎪58－46＝124；选项C 中，⎪⎪⎪⎪⎪⎪25－49＝245；选项D 中，⎪⎪⎪⎪⎪⎪25－59＝745.故选D.【答案】 D 二、填空题6．调查者通过随机询问72名男女生喜欢文科还是理科，得到如下列联表(单位：名) 性别与喜欢文科还是理科列联表【解析】 通过计算χ2＝－236×36×44×28≈8.42＞7.879.故我们有99.5%的把握认为生的性别和喜欢文科还是理科有关系． 【答案】 有7．某高校“统计初步”课程的教师随机调查了选该课的一些学生情况，具体数据如下表：χ2＝－223×27×20×30≈4.844，因为χ2≥3.841，所以判定主修统计专业与性别有关系，那么这种判断出错的可能性为________．【解析】 ∵χ2＞3.841，所以有95%的把握认为主修统计专业与性别有关，出错的可能性为5%.【答案】 5%8．在吸烟与患肺病是否相关的判断中，有下面的说法：①若统计量χ2>6.635，则在犯错误的概率不超过0.01的前提下，认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病；②从独立性检验可知在犯错误的概率不超过0.01的前提下，认为吸烟与患肺病有关系时，若某人吸烟，则他有99%的可能患有肺病；③从独立性检验可知在犯错误的概率不超过0.05的前提下，认为吸烟与患肺病有关系时，是指有5%的可能性使得推断错误．其中说法正确的是________．(填序号)【解析】统计量χ2是检验吸烟与患肺病相关程度的量，是相关关系，而不是确定关系，是反映有关和无关的概率，故说法①错误；说法②中对“确定容许推断犯错误概率的上界”理解错误；说法③正确．【答案】③三、解答题9．在一次天气恶劣的飞行航程中，调查了男女乘客在飞机上晕机的情况：男乘客晕机的有24人，不晕机的有31人；女乘客晕机的有8人，不晕机的有26人．请你根据所给数据判定：在天气恶劣的飞行航程中，男乘客是否比女乘客更容易晕机？【解】根据题意，列出2×2列联表如下：由公式可得χ2＝55×34×32×57≈3.689＞2.706，故我们有90%的把握认为“在天气恶劣的飞行航程中，男乘客比女乘客更容易晕机”．10．(2016·郑州模拟)有甲乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的列联表.已知在全部105人中随机抽取1人为优秀的概率为7.(1)请完成上面的列联表；(2)根据列联表的数据，若按95%的可靠性要求，能否认为“成绩与班级有关系”？(3)若按下面的方法从甲班优秀的学生中抽取一人：把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号．试求抽到6或10号的概率．参考公式：χ2＝n ad－bc2a＋b c＋d a＋c b＋d【解】(2)根据列联表中的数据，得到χ2＝55×50×30×75≈6.109＞3.841，因此有95%的把握认为“成绩与班级有关系”．(3)设“抽到6或10号”为事件A，先后两次抛掷一枚均匀的骰子，出现的点数为(x，y)．所有的基本事件有(1,1)，(1,2)，(1,3)，…，(6,6)，共36个．事件A包含的基本事件有：(1,5)，(2,4)，(3,3)，(4,2)，(5,1)，(4,6)，(5,5)，(6,4)，共8个，∴P(A)＝836＝29.能力提升]1．硕士学位与博士学位的一个随机样本给出了关于所获取学位类别与学生性别的分类数据如表所示：A．性别与获取学位类别有关B．性别与获取学位类别无关C．性别决定获取学位的类别D．以上都是错误的【解析】由列联表可得χ2＝－2305×35×189×151≈7.34>6.635，所以有99%的把握认为性别与获取学位的类别有关．【答案】 A2．某班主任对全班50名学生进行了作业量的调查，数据如下表：( ) A．0.01 B．0.025C．0.10 D．0.05【解析】χ2＝－226×24×27×23≈5.059＞5.024，因为P(χ2＞5.024)＝0.025，所以这种推断犯错误的概率不超过0.025.【答案】 B3．某研究小组为了研究生的身体发育情况，在某随机抽出20名15至16周岁的男生将他们的身高和体重制成2×2列联表，根据列联表中的数据，可以在犯错误的概率不超过________的前提下认为该学校15至16周岁的男生的身高和体重之间有关系.【解析】根据公式χ2＝a ＋b c＋d a＋c b＋d得，χ2＝－25×15×7×13≈5.934，因为χ2>5.024，因此在犯错误的概率不超过0.025的前提下认为该学校15至16周岁的男生的身高和体重之间有关系．【答案】0.0254．(2016·延安二检)为了研究“教学方式”对教学质量的影响，某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样)．以下茎叶图321为甲、乙两班(每班均为20人)学生的数学期末考试成绩.图321(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学，求成绩为87分的同学至少有一名被抽中的概率；(2)学校规定：成绩不低于75分的为优秀．请填写下面的2×2列联表，并判断有多大把握认为“成绩优秀与教学方式有关”.(参考公式：χ2＝a ＋b c＋d a＋c b＋d)【解】(1)记成绩为87分的同学为A，B，其他不低于80分的同学为C，D，E，“从甲班数学成绩不低于80分的同学中随机抽取两名同学”的一切可能结果组成的基本事件有(A，B)，(A，C)，(A，D)，(A，E)，(B，C)，(B，D)，(B，E)，(C，D)，(C，E)，(D，E)，共10个．“至少有一个87分的同学被抽到”所组成的基本事件有(A，B)，(A，C)，(A，D)，(A，E)，(B，C)，(B，D)，(B，E)，共7个，所以P＝710.(2)χ2＝＝6.4＞5.024，20×20×20×20因此，我们有97.5%的把握认为成绩优秀与教学方式有关．。
2017_2018版高中数学第三章统计案例2独立性查验学案北师大版选修2_3
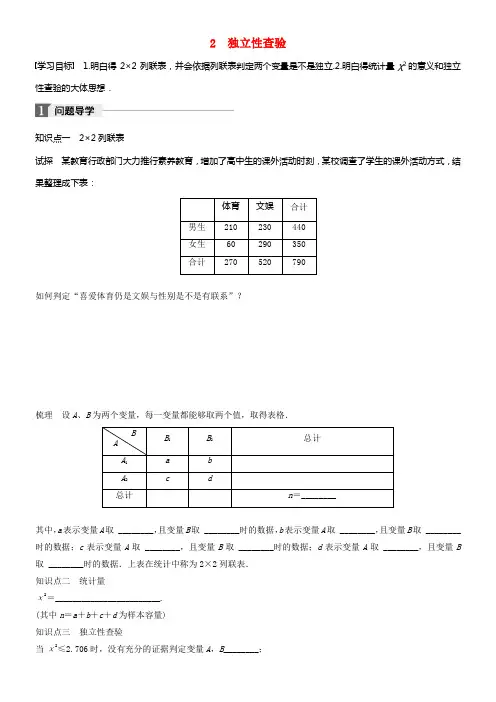
2 独立性查验学习目标 1.明白得2×2列联表，并会依据列联表判定两个变量是不是独立.2.明白得统计量χ2的意义和独立性查验的大体思想．知识点一2×2列联表试探某教育行政部门大力推行素养教育，增加了高中生的课外活动时刻，某校调查了学生的课外活动方式，结果整理成下表：体育文娱合计男生210230440女生60290350合计270520790如何判定“喜爱体育仍是文娱与性别是不是有联系”？梳理设A、B为两个变量，每一变量都能够取两个值，取得表格．BB1B2总计AA1 a bA2 c d总计n＝________其中，a表示变量A取 ________，且变量B取 ________时的数据，b表示变量A取 ________，且变量B取 ________时的数据；c表示变量A取 ________，且变量B取 ________时的数据；d表示变量A取 ________，且变量B 取 ________时的数据．上表在统计中称为2×2列联表．知识点二统计量χ2＝________________________.(其中n＝a＋b＋c＋d为样本容量)知识点三独立性查验当χ2≤2.706时，没有充分的证据判定变量A，B________；当χ2>2.706时，有__________的把握判定变量A，B有关联；当χ2>3.841时，有__________的把握判定变量A，B有关联；当χ2>6.635时，有__________的把握判定变量A，B有关联．类型一2×2列联表和统计量χ2例1 某企业为了更好地了解设备改造与生产合格品的关系，随机抽取了180件产品进行分析，其中设备改造前生产的合格品有36件，不合格品有49件；设备改造后生产的合格品有65件，不合格品有30件，请依照数据，列出2×2列联表，并说明能够用本列表研究什么问题？反思与感悟2×2列联表将文字语言转换为图表语言，使问题更为清楚，可为进一步研究问题作充分的预备．跟踪训练1 已知药物成效与动物实验列联表如下所示：患病未患病总计服用药104555未服药203050总计3075105则χ2≈________.(结果保留3位小数)类型二独立性查验的方式例2 研究人员选取170名青年男、女大学生作为样本，对他们进行一种心理考试，发觉有60名女生对该心理考试中的最后一个题目的反映是：确信的有22名，否定的有38名；男生110名在相同的题目上确信的有22名，否定的有88名．问：性别与态度之间是不是存在某种关系？用独立性查验的方式判定．反思与感悟独立性查验能够通过2×2列联表计算χ2的值，然后和临界值对照作出判定．跟踪训练2 为了研究人的性别与患色盲是不是有关系，某研究所进行了随机调查，发此刻调查的480名男性中有39名患有色盲，520名女性中有6名患有色盲，试问人的性别与患色盲有关系吗？1．当χ2>3.841时，以为事件A与事件B( )A．有95%的把握有关B．有99%的把握有关C．没有理由说它们有关D．不确信2．为了考察中学生的性别与是不是喜爱数学课程之间的关系，在某校中学生中随机抽取了300名学生，取得如以下联表：喜欢数学不喜欢数学总计男3785122女35143178合计72228300你以为性别与是不是喜爱数学课程之间有关系的把握有( )A．0 B．95% C．99% D．100%3．某大学在研究性别与职称(分正教授、副教授)之间是不是有关系时，你以为应该搜集哪些数据？4．2021年世界杯期间，某一电视台对年龄高于40岁和不高于40岁的人是不是喜爱西班牙队进行调查，对高于40岁的调查了50人，不高于40岁的调查了50人，所得数据制成如以下联表：不喜欢西班牙队 喜欢西班牙队 总计 高于40岁 pq50 不高于40岁153550 总计a b100假设工作人员从所有统计结果中任取一个，取到喜爱西班牙队的人的概率为35，那么有超过________的把握以为年龄与西班牙队的被喜爱程度有关．5．某省进行高中新课程改革已经四年了，为了解教师对新课程教学模式的利用情形，某一教育机构对某学校的教师关于新课程教学模式的利用情形进行了问卷调查，共调查了50人，其中有老教师20人，青年教师30人．老教师对新课程教学模式赞同的有10人，不赞同的有10人；青年教师对新课程教学模式赞同的有24人，不赞同的有6人．(1)依照以上数据成立一个2×2列联表；(2)判定是不是有99%的把握说明对新课程教学模式的赞同情形与教师年龄有关系．1．独立性查验的思想：先假设两个事件无关，计算统计量χ2的值．假设χ2值较大，那么拒绝假设，以为两个事件有关．2．独立性查验的步骤 (1)画列联表． (2)计算χ2.(3)将取得的χ2值和临界值比较，下结论．答案精析问题导学 知识点一试探 可通过表格与图形进行直观分析，也可通过统计分析定量判定． 梳理 a ＋b c ＋d a ＋c b ＋d a ＋b ＋c ＋d A 1 B 1 A 1 B 2 A 2 B 1 A 2 B 2 知识点二n ad －bc 2a ＋bc ＋d a ＋cb ＋d知识点三有关联 90% 95% 99% 题型探讨例1 解 依照题意列出2×2列联表如下：产品设备 合格 不合格 总计 设备改造前 36 49 85 设备改造后 65 30 95 总计10179180通过研究此2×2列联表能够研究设备改造对产品合格率是不是有阻碍． 跟踪训练1 6.109解析 χ2＝105×10×30－20×45230×75×55×50≈6.109.例2 解 依照题目所给数据成立如下2×2列联表：肯定 否定 总计 男生 22 88 110 女生 22 38 60 总计44126170依照2×2列联表中的数据，得χ2＝170×22×38－22×882110×60×44×126≈5.622>3.841，因此有95%的把握以为性别与态度有关系． 跟踪训练2 解 由题意列出2×2列联表：患色盲 未患色盲 总计 男性 39 441 480 女性6514520总计45 955 1 000由公式得χ2＝1 000×39×514－441×62480×520×45×955≈28.225.因为28.225＞6.635，因此有99%的把握以为人的性别与患色盲有关系． 当堂训练 1．A 2.B3．女正教授人数、男正教授人数、女副教授人数、男副教授人数 4．95%5．解 (1)2×2列联表如下所示：赞同 不赞同 总计 老教师 10 10 20 青年教师 24 6 30 总计341650(2)假设“对新课程教学模式的赞同情形与教师年龄无关”． 由公式，得χ2＝50×10×6－24×10234×16×20×30≈4.963<6.635，因此没有99%的把握以为对新课程教学模式的赞同情形与教师年龄有关．。
高中数学新北师大版精品教案《北师大版高中数学选修2-3 2.2独立性检验的基本思想》2
《独立性检验的基本思想及初步应用》教学设计江西省永修县第一中学胡玲玲【教材分析】《独立性检验的基本思想及初步应用》这节课是北师大版高中数学《选修2—3》第三章第2节，是概率与统计的重要内容。
在此之前，学生已经学习了随机事件发生的概率、相互独立事件等概念，本节课不仅是对前面所学知识的巩固和检测，更为学生进一步学习概率与统计奠定一定的理论基础，更有利于培养学生用数学的眼光去认识世界，用数学的思维去思考世界，用数学的方法去解决问题。
【教学目标】1知识与技能：通过对典型案例的探究,了解独立性检验的基本思想，会对两个分类变量进行独立性检验，明确独立性检验的基本步骤，并能解决实际问题。
2、过程与方法：让学生通过数据统计、分析和计算过程，从具体实例中学会用样本来估计总体的统计思想．通过主动探究、自主学习、小组合作交流，从具体实例“节目喜欢与性别是否相关”中抽象、概括、总结出独立性检验的基本原理和基本步骤，同时让学生充分体会知识的发现过程．3、情感、态度与价值观：通过本节课学习，让学生体会统计方法在决策中的作用；合作探究的学习过程，使学生感受发现、探索的乐趣及成功展示的成就感，培养学生学习数学知识的积极态度。
4、数学核心素养目标及落实途径：通过对实际问题的抽象与分析，引导学生建立数学模型，培养学生的数学建模能力；通过对数学模型的分析与解决，培养学生的数学运算能力和逻辑推理能力；培养学生的数据分析能力，从而掌握独立性检验的方法和思想，并能用这些方法解决一些实际问题，凸显数学的应用价值。
【教学重点】了解独立性检验的基本思想及实施步骤。
【教学难点】独立性检验的基本思想；随机变量2 的含义；临界值表的含义【学情分析】一方面，学生学习了相关关系之后，明白两个变量之间可能会存在一种相关关系，但这种关系是强还是弱？作出这种判断有无出错的可能？出错率是多少？把握性又是多少？这些都有待于进一步解决，所以通过情景设置和问题导向可以激发学生的学习兴趣另一方面，有了频率与概率、相互独立事件等知识做铺垫和准备，学生在学习本节课就具备了一定的知识基础但理解独立性检验的思想包括卡方及其临界值的含义是本节课的难点，因此教师要通过温故知新、由浅入深、层层递进、循序善诱的方法给学生做足够的铺垫和启发才可以突破这一难点，还需要设置相应的练习加深理解、巩固新知识【教学方式】多媒体辅助，以教师引导，学生合作探究式为主的教学方式。
高中数学 第三章 统计案例 3.2 独立性检验课件 北师大版选修2-3
χ2＝1 63235×4×310×3719×35554－×21245×79242≈68.033.
∵68.033>6.635，∴有 99%的把握认为每一晚都打鼾与患心
脏病有关．
休息时间到啦
同学们，下课休息十分钟。现在是休息时间，你们休息一 看看远处，要保护好眼睛哦~站起来动一动，久坐对身体
规律方法 “每一晚都打鼾与患心脏病有关”指的是统计上 的关系，不要误以为是因果关系．具体到某一个每一晚都打鼾的 人，并不能说他一定患心脏病．其实从 2×2 列联表中也可以看 出，每一晚都打鼾的人群中，患心脏病的概率也只有23504，稍微 超过十分之一．至于他患不患心脏病，应该由医学检查来确定．
解：计算得 χ2＝1 0004×742×585×262×845－002×425×002162≈7.075， ∵χ2＝7.075>6.635， 所以我们有 99%的把握认为该种血清能起到预防感冒的作 用．
7．为了研究患慢性气管炎与吸烟量的关系，调查了 228 人， 其中每天的吸烟支数在 10 支以上的 20 支以下的调查者中，患者 人数有 98 人，非患者人数有 89 人，每天的吸烟支数在 20 支以 上的调查者中，患者人数有 25 人，非患者人数有 16 人．
60 分以 61～70 71～80 81～90 91～100
下
分
分
分
分
甲班(人数) 3
6
11
18
12
乙班(人数) 4
8
13
15
10
现规定平均成绩在 80 分以上(不含 80 分)的为优秀．
(1)试分别估计两个班级的优秀率；
(2)由以上统计数据填写下面 2×2 列联表，并问是否有 95%
高中数学 第三章 统计案例教案 北师大版选修23
第三章统计案例§1回归分析1．1 回归分析(教师用书独具)●三维目标1．知识与技能(1)了解回归分析的基本思想，会对两个变量进行回归分析．(2)明确建立回归模型的基本步骤，并对具体问题进行回归分析．(3)会解决实际问题．2．过程与方法(1)通过实际问题去理解回归分析的必要性，明确回归分析的基本思想．(2)从散点图中的点的分布上，发现直接求回归直线方程存在明显不足，从中引导学生去发现解决问题的新思路——进行回归分析．3．情感、态度与价值观(1)培养学生用整体的观点和互相联系的观点，来分析问题．(2)进一步加强数学的应用意识，培养学生学好数学、用好数学的信心．(3)加强与现实生活中的联系，以科学的态度评价两个变量的相关关系．●重点难点重点：掌握回归分析的步骤、相关系数、建立回归模型的步骤；体会有些非线性模型通过变换，可以转化为线性回归模型；在解决实际问题的过程中寻找更好的建型方法．难点：求线性回归方程的系数a，b；相关系数；选择不同的模型建模．回归分析主要是研究两个变量间的关系，是在必修三的基础上学习，教材的1.1回归分析是复习必修三的内容，为了使建立回归方程有意义，提出了相关系数，这与回归直线中b的系数有关联，教师可通过实例，让学生了解相关系数的大小与线性相关的关系；在现实中又有一种非线性的相关性，如何解决引导学生转化为线性关系，主要通过数形结合思想、函数思想，使问题化归为线性关系，教学中可通过提醒、猜想、练习等方法，使学生掌握本节的重点内容．(教师用书独具)●教学建议建议本节课用3课时讲解完成．教学中通过组织学生自己动手操作计算、观察、分析、交流、讨论、归纳让他们在探究学习中经历知识形成的全过程，从而形成“自主探究、合作交流”的数学学习方法．教师在课堂上可以用计算机软件进行参数的估计、相关系数的计数，让学生掌握利用计算器进行线性回归方程的求解和评价．●教学流程第1课时以实际问题作为课题引入．⇒回顾建立回归直线方程的基本步骤．⇒通过实例巩固、体验线性回归直线方程的求法及应用．⇒第2课时提出新问题，如何用其他方法刻画变量之间的线性相关．⇒师生共同探究，得出相关系的概念及相关系数的大小与线性相关之间的关系．⇒通过例题，巩固验证相关系数刻画变量之间的线性相关的特点．⇒第3课时引导学生探究如果不是线性回归模型，如何估计参数，能否利用线性回归模型．⇒对数据进行分析变换后，对新数据建立线性模型．⇒转化为原来变量模型，得出结论，总结建模思想，补充拓展．⇒课堂小结并完成当堂双基达标，巩固本节所学知识.课标解读 1.通过实例掌握回归分析的基本思想方法．2．利用最小二乘法会求线性回归直线方程，并能用线性回归直线方程进行预报.变量之间的相关关系【问题导思】1．正方形的面积S 与其边长a 是什么关系？圆的周长l 与半径r 是什么关系？ 【提示】 ∵S ＝a 2，l ＝2πr ， ∴它们都是确定的函数关系．2．父亲的身高与儿子的身高之间有何关系？耕种深度与水稻产量之间有何关系？ 【提示】 非确定关系．1．变量之间有一定的联系，但不能完全用函数来表达．如人的体重y 与身高x .一般来说，身高越高，体重越重，但不能用一个函数来严格地表示身高与体重之间的关系．相关关系是非确定性关系，因变量的取值具有一定的随机性．2．在考虑两个变量的关系时，为了对变量之间的关系有一个大致的了解，人们通常将变量所对应的点描出来，这些点就组成了变量之间的一个图，通常把这种图叫作变量之间的散点图．线性回归方程【问题导思】1．确定线性回归方程，只需得出哪两个量？【提示】 确定线性回归直线方程，只需确定a ，b 两个量即可．2．在线性回归方程y ＝a ＋bx 中，当一次项系数b 为正数时，说明两个变量有何相关关系？在散点图上如何反映？ 【提示】 说明两个变量正相关，在散点图上自左向右看这些点呈上升趋势．假设样本点为(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )，设线性回归方程为y ＝a ＋bx ，要使这n 个点与直线y ＝a ＋bx 的“距离”平方之和最小，即使得Q (a ，b )＝(y 1－a －bx 1)2＋(y 2－a －bx 2)2＋…＋(y n －a －bx n )2达到最小，a ，b 需满足b ＝∑nb ＝1x i y i －n x y∑ni ＝1x 2i －n x2，a ＝y －b x .由数据求线性回归方程已知x ，y 之间一组数据：x 0 1 2 3 y1357(1)分别计算：x 、y 、x 1y 1＋…＋x 4y 4，x 21＋x 22＋…＋x 24； (2)求出线性回归方程y ＝bx ＋a .【思路探究】 可利用表格的数直接计算，然后把这些结果代入线性回归方程系数公式，分别求得a ，b ，再求出线性回归方程． 【自主解答】 (1)x ＝0＋1＋2＋34＝1.5，y ＝1＋3＋5＋74＝4，x 1y 1＋…＋x 4y 4＝0×1＋1×3＋2×5＋3×7＝34，x 21＋x 22＋…＋x 24＝02＋12＋22＋32＝14；(2)b ＝x 1y 1＋x 2y 2＋x 3y 3＋x 4y 4－4x yx 21＋x 22＋x 23＋x 24－4x 2＝34－4×1.5×414－4×1.52＝2；a ＝y －b x ＝4－2×1.5＝1.故y ＝2x ＋1.答：(1)所求的值分别为：1.5,4,34,14； (2)所求的线性回归方程是：y ＝2x ＋1.求线性回归方程的步骤：(1)列表求出x ，y ，∑ni ＝1x 2i ，∑ni ＝1x i y i ；(2)利用公式b ＝∑ni ＝1x i y i －n x y∑ni ＝1x 2i －n x2，a ＝y －b x ，求出b ，a ；(3)写出线性回归方程．观察两相关量得如下数据：x －1 －2 －3 －4 －5 5 3 4 2 1 y－9－7－5－3－115379求两变量间的回归方程． 【解】 列表i 12345678910 x i－1－2－3－4－55342 1 y i－9－7－5－3－115379 x2i1491625259164 1 x i y i9141512551512149由此可得x＝0，y＝0，∑10i＝1x2i＝110，∑10i＝1x i y i＝110，b＝∑10i＝1x i y i－10x y∑10 i＝1x2i－10x2＝110－10×0110－10×0＝1，a＝y－b x＝0，∴所求回归方程为y＝x.求实际问题的回归方程某企业想通过做广告来提高自己的知名度，经预测可知本企业产品的广告费支出x 与销售额y(单位：百万元)之间有如下对应数据：x 24568y 3040605070(1)判断y与x是否具有线性相关关系；(2)求回归直线方程．【思路探究】先画出散点图，即可判断y与x是否具有相关关系，如果y与x具有相关关系可将有关数据代入公式求得回归直线方程．【自主解答】(1)散点图如图所示：根据散点图可知，所给的数据点都在一条直线的附近，所以y与x具有线性相关关系．(2)列出下表，并且科学地的进行有关计算．i 1234 5x i24568y i3040605070x i y i60160300300560x＝5，y＝50，∑5 i＝1x2i＝145，∑5i＝1y2i＝135 000，∑5i＝1x i y i＝1 380于是可得，b＝∑5i＝1x i y i－5x y∑5 i＝1x2i－5x2＝1 380－5×5×50145－5×52＝6.5，a＝y－b x＝50－6.5×5＝17.5，于是所求的回归直线方程是y＝6.5x＋17.5.对一级数据进行线性回归分析时，应先画出其散点图，看其是否呈直线形，再依系数a、b的计算公式，算出a、b.由于计算量较大，所以在计算时应借助技术手段，认真细致，谨防计算中产生错误．某医院用光电比色计检验尿汞时，得尿汞含量(毫克/升)与消光系数如下表：汞含量x 2 4 6 8 10 消光系数y64138205285360(1)作散点图；(2)如果y 与x 之间具有线性相关关系，求线性回归方程． 【解】 (1)散点图如图．(2)由散点图可知，y 与x 呈相关关系，设线性回归方程为：y ＝bx ＋a .经计算：得x ＝6，y ＝210.4，∑5i ＝1x 2i ＝220，∑5i ＝1x i y i ＝7 790.∴b ＝7 790－5×6×210.4220－5×62＝36.95， a ＝210.4－36.95×6＝－11.3.∴线性回归方程为y ＝36.95x －11.3.利用回归直线方程进行统计某商场经营一批进价是30元/台的小商品，在市场试验中发现，此商品的销售单价x (x 取整数)元与日销售量y 台之间有如下关系：x 35 40 45 50 y 56 41 28 11(1)画出散点图，并判断y 与x 是否具有线性相关关系； (2)求日销售量y 对销售单价x 的线性回归方程；(3)设经营此商品的日销售利润为P 元，根据(2)写出P 关于x 的函数关系式，并预测当销售单价x 为多少元时，才能获得最大日销售利润．【思路探究】 两个变量呈现近似的线性关系，可通过公式计算出其线性回归方程，并根据方程求出其预测值．【自主解答】 (1)散点图如图所示，从图中可以看出这些点大致分布在一条直线附近，因此两个变量线性相关．(2)∵x ＝14×(35＋40＋45＋50)＝42.5，y ＝14×(56＋41＋28＋11)＝34，∑4i＝1x i y i＝35×56＋40×41＋45×28＋50×11＝5 410，∑4i＝1x2i＝352＋402＋452＋502＝7 350，∴b＝∑4i＝1x i y i－4x·y∑4 i＝1x2i－4x2＝5 410－4×42.5×347 350－4×42.52＝－370125＝－2.96.∴a＝y－b x＝34－(－2.96)×42.5＝159.8.∴y＝－2.96x＋159.8.(3)依题意有P＝(－2.96x＋159.8)(x－30)＝－2.96x2＋248.6x－4 794，∴当x＝248.62×2.96≈42时，P有最大值，约为426，即预测销售单价为42元时，能获得最大日销售利润．1．b＝－2.96是斜率的估计值，说明单价每增加一个单位，日销售量就减少2.96. 2．借助于回归方程对实际问题的估计值是个近似值，不是一个准确值．假设关于某设备的使用年限x 和所支出的维修费y (万元)有如下的统计资料：x 2 3 4 5 6 y2.23.85.56.57.0若由资料可知y 对x 呈线性相关关系． (1)求线性回归方程；(2)估计使用年限为10年时，维修费用是多少万元？ 【解】 (1)列表如下：ix iy ix 2ix i y i1 2 2.2 4 4.4 2 3 3.8 9 11.4 3 4 5.5 16 22.0 4 5 6.5 25 32.5 5 6 7.0 36 42.0 ∑202590112.3由此可得：x ＝4，y ＝5.进而可以求得b ＝∑5i ＝1x i y i －5x y∑5i ＝1x 2i －5x2＝1.23，a ＝y －b x ＝0.08.∴线性回归方程为y ＝0.08＋1.23x .(2)当x ＝10时，y ＝0.08＋1.23×10＝12.38(万元)，即估计使用10年时维修费用是12.38万元.数形结合思想在回归分析中的应用(12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨标准煤)与相应的生产能耗y(吨标准煤)的几组对照数据．x 345 6y 2.534 4.5(1)请画出上表数据的散点图；(2)请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程y＝bx＋a；(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？(参考数值：3×2.5＋4×3＋5×4＋6×4.5＝66.5)【思路点拨】(1)可直接由表格提供的点，列出散点图；(2)可利用线性回归方程中a，b公式直接求解；(3)直接用方程来估计所求值．【规范解答】(1)图形如图所示．3分(2)x ＝3＋4＋5＋64＝4.5；y ＝2.5＋3＋4＋4.54＝3.5；∑4i ＝1x i y i ＝3×2.5＋4×3＋5×4＋6×4.5＝66.5.∑4i ＝1x 2i ＝32＋42＋52＋62＝86. 6分∴b ＝∑4i ＝1x i y i －4x ·y ∑4i ＝1x 2i －4x2＝66.5－4×4.5×3.586－4×4.52＝0.7， 8分 a ＝y －b x ＝3.5－0.7×4.5＝0.35. 9分∴y ＝0.7x ＋0.35. 10分 (3)现在生产100吨甲产品用煤y ＝0.7×100＋0.35＝70.35，∴降低90－70.35＝19.65吨标准煤. 12分线性回归方程的应用(1)描述两变量间的依存关系；(2)利用回归方程可进行预测；(3)利用回归方程还可以进行统计控制．1．作回归分析要有实际意义．2．回归分析前，最好先做出散点图．3．应用回归分析预测时，最好先作出散点图．1．下列说法正确的是( )A．任何两个变量都具有相关关系B．球的体积与该球的半径具有相关关系C．农作物的产量与施化肥量之间是一种确定性的关系D．某商品的生产量与该商品的销售价格之间是一种非确定性的关系【解析】两个变量之间的关系有两种，即函数关系与相关关系，故A错误．B中球的体积与该球的半径是函数关系．C中农作物的产量与施化肥量之间不是严格的函数关系，但是具有相关关系，因而是非确定性的关系．D中商品的生产量还和市场需求有关，故商品的生产量与该商品的销售价格之间是非确定性的关系．故选D.【答案】 D2．一位母亲记录了儿子3岁～9岁的身高(数据略)，由此建立的身高y(单位：cm)与年龄x(单位：岁)的回归模型为y＝7.19x＋73.93.用这个模型预测这个孩子10岁时的身高，则下列叙述正确的是( )A．身高一定是145.83 cmB．身高在145.83 cm以上C．身高在145.83 cm以下D．身高在145.83 cm左右【解析】x＝10时，y＝7.19×10＋73.93＝145.83，但这是预测值而不是精确值，所以只能选D.【答案】 D3．在一次实验中，测得(x，y)的四组值分别是A(1,2)，B(2,3)，C(3,4)，D(4,5)，则y与x之间的线性回归方程为________．【解析】通过检验A，B，C，D四点共线，都在直线y＝x＋1上．【答案】y＝x＋14．已知一个回归直线方程为y＝1.5x＋45，x∈{1,7,5,13,19}，求y.【解】由已知可知：x＝1＋7＋5＋13＋195＝9.又∵回归直线过点(x，y)，∴y ＝1.5x ＋45，即y ＝1.5×9＋45＝58.5.一、选择题1．对具有线性相关关系的两个变量建立的线性回归方程y ＝a ＋bx 中，回归系数b ( ) A ．可以小于0 B ．只能大于0 C ．可能等于0D ．只能小于0【解析】 b 可能大于0，也可能小于0，但当b ＝0时，x ，y 不具有线性相关关系． 【答案】 A2．下列两个变量间的关系不是函数关系的是( ) A ．正方体的棱长与体积 B ．角的弧度数与它的正弦值C ．单产为常数时，土地面积与粮食总产量D ．日照时间与水稻亩产量【解析】 ∵A 、B 、C 都可以得出一个函数关系式，而D 不能写出确定的函数关系式，它只是一个不确定关系． 【答案】 D3．某产品的广告费用x 与销售额y 的统计数据如下表：广告费用x (万元) 4 2 3 5 销售额y (万元)49263954根据上表可得回归方程y ＝bx ＋a 中的b 为9.4，据此模型预报广告费用为6万元时销售额为( ) A ．63.36万元 B ．65.5万元 C ．67.7万元D ．72.0万元【解析】 x ＝4＋2＋3＋54＝3.5，y ＝49＋26＋39＋544＝42，∴a＝y－b x＝42－9.4×3.5＝9.1，∴回归方程为y＝9.4x＋9.1，∴当x＝6时，y＝9.4×6＋9.1＝65.5，故选B.【答案】 B4．由一组样本数据(x1，y1)，(x2，y2)，…，(x n，y n)得到回归直线方程y＝bx＋a，那么下列说法中不正确的是( ) A．直线y＝bx＋a必经过点(x，y)B．直线y＝bx＋a至少经过点(x1，y1)(x2，y2)，…，(x n，b n)中的一个点C．直线y＝bx＋a的斜率为∑ni＝1x i y i－n x·y∑ni＝1x2i－n x2D．直线y＝bx＋a的纵截距为y－b x【解析】回归直线可以不经过任何一个点．其中A：由a＝y－b x代入回归直线方程y＝bx＋y－a x，即y＝b(x－x)＋y过点(x，y)．∴B错误．【答案】 B5．已知两个变量x和y之间具有线性相关性，甲、乙两个同学各自独立地做了10次和15次试验，并且利用线性回归的方法求得回归直线分别为l1和l2，已知两个人在试验中发现对变量x的观测数据的平均数都为s，对变量y的观测数据的平均数都是t，则下列说法正确的是( )A．l1与l2一定有公共点(s，t)B．l1与l2相交，但交点一定不是(s，t)C．l1与l2必定平行D．l1与l2必定重合【解析】由于回归直线y＝bx＋a恒过(x，y)点，又两人对变量x的观测数据的平均值为s，对变量y的观测数据的平均值为t，所以l1和l2恒过点(s，t)．【答案】 A二、填空题6．从某大学随机选取8名女大学生，其身高x(cm)和体重y(kg)的线性回归方程为y＝0.849x－85.712，则身高172 cm的女大学生，由线性回归方程可以预测其体重约为________．【解析】将x＝172代入线性回归方程y＝0.849x－85.712，有y＝0.849×172－85.712＝60.316(kg)．【答案】60.316 kg7．面对竞争日益激烈的消费市场，众多商家不断扩大自己的销售市场，以降低生产成本．某白酒酿造企业市场部对该企业9月份的产品销量(单位：千箱)与单位成本的资料进行线性回归分析，结果如下：x＝72，y＝71，∑6i＝1x2i＝79，∑6i＝1x i y i＝1 481.b ＝1 481－6×72×7179－6×722≈－1.818 2，a ＝71－(－1.818 2)×72≈77.36，则销量每增加1 000箱，单位成本下降________元．【解析】 由上表可得，y ＝－1.818 2x ＋77.36，销量每增加1千箱，则单位成本下降1.818 2元． 【答案】 1.818 28．调查了某地若干户家庭的年收入x (单位：万元)和年饮食支出y (单位：万元)，调查显示年收入x 与年饮食支出y 具有线性相关关系，并由调查数据得到y 对x 的回归直线方程：y ＝0.254x ＋0.321.由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加________万元．【解析】 由题意知[0.254(x ＋1)＋0.321]－(0.254x ＋0.321)＝0.254. 【答案】 0.254 三、解答题9．某电脑公司有6名产品推销员，其工作年限与年推销金额数据如下表：推销员编号 1 2 3 4 5 工作年限x /年 3 5 6 7 9 推销金额y /万元23345(1)求年推销金额y 关于工作年限x 的线性回归方程；(2)若第6名推销员的工作年限为11年，试估计他的年推销金额． 【解】 (1)设所求的线性回归方程为y ＝bx ＋a ，则b ＝∑i ＝15x i －xy i －y∑i ＝15x i －x2＝1020＝0.5， a ＝y －b x ＝0.4.所以年推销金额y 关于工作年限x 的线性回归方程为y ＝0.5x ＋0.4. (2)当x ＝11时，y ＝0.5x ＋0.4＝0.5×11＋0.4 ＝5.9(万元)．所以可以估计第6名推销员的年推销金额为5.9万元．10．一种机器可以按各种不同速度运转，其生产物件中有一些含有缺点，每小时生产有缺点物件的多少随机器运转速度而变化，用x 表示转速(单位：转/秒)，用y 表示每小时生产的有缺点物件个数．现观测得到(x ，y )的4组值为(8,5)，(12,8)，(14,9)，(16,11)．(1)假设y 与x 之间存在线性相关关系，求y 与x 之间的线性回归方程．(2)若实际生产中所容许的每小时最大有缺点物件数为10，则机器的速度不得超过多少转/秒？(精确到1) 【解】 (1)设回归方程为y ＝a ＋bx ，则x ＝8＋12＋14＋164＝12.5，y ＝5＋8＋9＋114＝8.25， ∑4i ＝1x 2i ＝660，∑4i ＝1x i y i ＝438，b ＝∑4i ＝1x i y i －4x y∑4i ＝1x 2i －4x2＝438－4×12.5×8.25660－4×12.52≈0.73， a ＝y －b x ＝8.25－0.73×12.5＝－0.875，所以所求回归方程为y ＝－0.875＋0.73x .(2)由y ≤10，即－0.875＋0.73x ≤10，得x ≤10.8750.73≈15，即机器速度不得超过15转/秒．11．高二(3)班学生每周用于数学学习的时间x (单位：小时)与数学成绩y (单位：分)之间有如下数据：x 24 15 23 19 16 11 20 16 17 13 y92799789644783687159若某同学每周用于数学学习的时间为18小时，试预测该同学的数学成绩．【解】 显然学习时间与学习成绩间具有相关关系，可以列出下表，并用科学计算器进行计算．i 1 2 3 4 5 6 7 8 9 10 x i 24 15 23 19 16 11 20 16 17 13 y i 927997896447 83687159 x i y i2 208 1 185 2 231 1 691 1 024 5171 660 1 088 1 207767∑10i ＝1x 2i＝3 182，∑10i ＝1x i y i＝13 578于是可得b ＝∑10i ＝1x i y i －10x y∑10i ＝1x 2i －10x2＝545.4154.4≈3.53，a＝y－b x＝74.9－3.53×17.4≈13.5.因此可求得回归直线方程为y＝3.53x＋13.5.当x＝18时，y＝3.53×18＋13.5≈77.故该同学预计可得77分左右.(教师用书独具)在一段时间内，某种商品的价格x(万元)和需求量y(t)之间的一组数据如下表所示：价格x 1.4 1.6 1.82 2.2需求量y 121075 3(1)画出散点图；(2)求出y对x的回归直线方程；(3)如价格定为1.9万元，预测需求量大约是多少．(精确到0.01 t)【思路探究】先根据所给数据画出散点图，判断y与x是否具有线性相关关系，在此基础上利用回归方程系数的有关公式，求出相应的系数，然后结合函数知识预测需求量．【自主解答】(1)散点图如图所示．(2)采用列表的方法计算a与回归系数b.序号x i y i x2i x i y i1 1.412 1.9616.82 1.610 2.56163 1.87 3.2412.64 25 4 105 2.2 3 4.84 6.6Σ9 37 16.6 62x＝15×9＝1.8，y＝15×37＝7.4，b＝62－5×1.8×7.416.6－5×1.82＝－11.5，a＝7.4＋11.5×1.8＝28.1.所以y对x的回归直线方程为y＝a＋bx＝28.1－11.5x.(3)当x＝1.9时，y＝28.1－11.5×1.9＝6.25，所以价格定为1.9万元时，需求量大约是6.25 t.解答本类题目的关键首先应先通过散点图来分析两变量间的关系是否相关，然后再利用求回归方程的公式求解回归方程，在此基础上，借助回归方程对实际问题进行预测．已知10只狗的血球体积x(单位：mm3)及红血球数y(单位：百万)的测量值如下：x 45424648423558403950y 6.53 6.309.257.50 6.99 5.909.49 6.20 6.557.72(1)画出散点图；(2)求出y对x的回归线性方程；(3)若血球体积为49 mm3，预测红血球数大约是多少？【解】(1)散点图如图(2)设线性回归方程为y ＝bx ＋a ，由表中数据代入公式，得b ＝∑i ＝110x i y i －10x y∑i ＝110x 2i －10x2≈0.16，a ＝y －b x ≈0.12.所以所求线性回归方程为y ＝0.16x ＋0.12. (3)把x ＝49代入线性回归方程得：y ＝0.16×49＋0.12≈7.96(百万)，计算结果表明，当血球体积为49 mm 3时，红血球数大约为7.96百万．拓展阅读GDDS 和SDDS随着世界经济一体化的加快，各国间的交流与合作越来越频繁，为加强国际组织对各国经济运行状况的监督，国际社会在各领域纷纷建立了国际通行标准，其中国际货币基金组织(简称IMF)制定的数据公布通用系统(简称GDDS)和数据公布特殊标准(简称SDDS)．GDDS 的主要内容和要求：在统计范围内，它将国民经济活动划分为5大经济部门，对每一部门各选定一组能够反映其活动实绩和政策以及可以帮助理解经济发展和结构变化的最为重要的数据．系统提出了五大部门综合框架和相关的数据类别和指标编制、公布的目标．选定的数据类别和指标中规定为主要部分．SDDS 将国民经济活动划分为4大经济部门．选定的数据类别分为：必须的、受鼓励的和“视相关程度”三类．必须的数据类别包括：综合统计框架、跟踪性数据、与部门有关的其他数据.IMF 为什么制定GDDS 和SDDS 呢？进入20世纪90年代以来，世界一些地区金融危机频繁爆发.1994年墨西哥的金融危机、1997年东南亚金融危机都导致国际金融市场剧烈动荡．两次金融危机给IMF 一个深刻的教训，也对其职能提出了挑战，在总结经验教训的基础上，IMF 认为，在新的国际经济、金融形势下，必须制定统一的数据发布标准，使各成员国按照统一程序提供全面、准确的经济金融信息，从而可以有效及时地对各国的经济进行正确的分析预测，从宏观上来作出调控，减少金融危机的发生和影响．1．2 相关系数课标解读 1.了解两个随机变量间的线性相关系数r ，并能利用公式求出相关系数r ；了解正相关、负相关、不相关的概念． 2．能利用相关系数r 判断两个随机变量间线性相关程度的大小，从而判断回归直线拟合的效果.相关系数【问题导思】1．有什么办法判断两个变量是否具有线性相关关系？【提示】 作出散点图，看这些点是否在某一直线的附近，计算线性相关系数． 2．线性相关系数与最小误差有何关系？ 【提示】 Q (误差)＝l yy (1－r 2)．3．相关系数r 的绝对值的大小对相关性有何影响？【提示】 |r |越大，变量之间的相关程度越高；|r |越小，变量间线性相关程度越低；当r ＝0时，两个变量线性不相关．4．r 的正负对相关性的影响． 【提示】 r >0，b ＝l xyl xx>0两变量正相关； r <0，b ＝l xyl xx<0，两变量负相关．1．判断两个变量之间的线性相关关系的方法有： (1)计算线性相关系数r . (2)画散点图．2．假设两个随机变量的数据分别为(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )，则变量间线性相关系数r 的计算公式为r ＝l xyl xx l yy＝∑ni＝1x i－x y i－y∑ni＝1x i－x2i＝1ny i－y2＝∑ni＝1x i y i－n x y∑ni＝1x2i－n x2∑ni＝1y2i－n y2相关系数及其应用维尼纶纤维的耐热水性能的好坏可以用指标“缩醛化度”y来衡量，这个指标越高，耐热水性能就越好，而甲醛浓度是影响“缩醛化度”的重要因素，在生产中常用甲醛浓度x(克/升)去控制这一指标，为此必须找出它们之间的关系，现安排一批试验，获得如下表数据．甲醛浓度18202224262830(克/升)缩醛化度26.8628.3528.7528.8729.7530.0030.36(克分子%)求相关系数r.【思路探究】可直接利用相关系数r的公式直接计算．【自主解答】列表如下：i x i y i x2i x i y i y2i11826.86324483.48721.459 622028.35400567803.722 532228.75484632.5826.562 542428.87576692.88833.476 952629.75676773.5885.062 562830.0078484090073030.36900910.80921.729 6∑168202.94 4 144 4 900.16 5 892.013 6 x＝24，y＝28.99，r＝∑7i＝1x i y i－7x y∑7i＝1x2i－7x2∑7i＝1y2i－7y2＝4 900.16－7×24×28.994 144－7×242×5 892.013 6－7×28.992≈0.94.当相关系数|r|越接近1时，两个变量的线性相关程度越高，当相关系数|r|越接近0时，两个变量的线性相关程度越低．下列是小麦产量与施化肥量的一组观测数据：施化肥量15202530354045小麦产量320330360410460470480 判断施化肥量与水稻产量是否有相关关系．【解】i x i y i x2i y2i x i y i115320225102 400 4 800220330400108 900 6 600325360625129 6009 000430410900168 10012 300535460 1 225211 60016 100640470 1 600220 90018 800745480 2 025230 40021 600∑210 2 8307 000 1 171 90089 200∴r＝∑i＝17x i y i－7x y∑i＝17x2i－7x2∑i＝17y2i－7y2＝4 300700×27 771.43≈0.975.由于r＝0.975>0，因此施化肥量和水稻产量近似成线性正相关关系．线性回归分析的综合应用“阿曼德匹萨”是一个制作和外卖意大利匹萨的餐饮连锁店，其主要客户群是在校大学生，为研究各店铺的销售额与店铺附近地区大学生人数的关系，随机抽取十个分店的样本，得到数据如下：店铺编号 区内大学生数(万人)季度销售额(万元)1 0.2 5.8 2 0.6 10.53 0.8 8.84 0.8 11.85 1.2 11.76 1.6 13.7 7 2 15.78 2 16.9 9 2.2 14.9 10 2.620.2(1)试对区内大学生人数与店铺的销售额的关系进行相关性检验；(2)试根据这些数据建立回归模型，然后再进一步根据回归方程预测一个区内大学生人数1万人店铺的季度销售额； (3)若店铺的季度销售额低于10万元则亏损，试求建店区内大学生人数至少约多少人？【思路探究】 先根据表中的数据作相关检验，然后判断是否具有相关关系，再根据所给的数据解出线性回归方程，最后进行预测． 【自主解答】 (1)根据数据我们对区内大学生人数x 与店铺季度销售额y 作相关检验．根据数据可知：x ＝110(0.2＋0.6＋…＋2.6)＝1.4；y ＝110(5.8＋10.5＋…＋20.2)＝13，∑10i ＝1x 2i －10x 2＝5.68，∑10i ＝1x i y i －10x y ＝28.4，∑10i ＝1y 2i －10y 2＝157.3，因此r ＝28.45.68×157.3≈0.95；|r |接近1，因此有把握认为区内大学生人数x 与店铺季度销售额y 具有线性相关关系，求y 对x 的回归直线方程有意义．(2)回归系数b ＝28.45.68＝5，a ＝13－5×1.4＝6.因此回归直线方程是y＝bx＋a＝5x＋6.当x＝1时，y＝5×1＋6＝11，即区内大学生人数1万元店铺的季度销售额约11万元．(3)由回归直线方程是y＝5x＋6.令y≥10，解得x≥0.8，所以当建店区内大学生人数至少8 000人时才适合建店．进行相关性检验主要有两种常用方法，一是作散点图，观察所给的数据点是否在一条直线的附近，作散点图的优点是既直观又方便，是解决相关性检验问题比较常用的方法；缺点是作图总是存在误差，有时很难判断这些点是不是分布在一条直线的附近．二是利用样本相关系数对其进行相关性检验，优点是判断准确，缺点是计算繁琐，但可以借助计算器进行处理．在我国某地的一个县城，近期发现了好几个癌症村．政府部门十分震惊，马上组成调查组调查病因，经调查发现致癌的罪魁祸首是水源中的金属砷，它们来自附近的几家化工厂，化工厂排出的废水中含有金属砷，废水污染了水源，人食用了这种水就会致癌．下面就是调查组对几个癌症村水源中的砷超标的倍数和患癌症的人数统计的数据：砷超标的倍数x 34 5.5 4.2 5.86 3.5患癌症人数y 15202824354434(1)画出表中数据的散点图； (2)求y 对x 的回归方程；(3)若一个村的水源中砷超标的倍数为7，试估计这个村的患癌症的人数． 【解】 (1)散点图如图所示：(2)观察散点图，可知x 、y 成线性相关关系． 计算得x ＝327，y ＝2007，根据求b 公式代入数据计算得b ≈6.065，a ＝2007－6.065×327≈0.846. 所以患癌症人数y 对水源中砷超标的倍数x 的回归直线方程为y ＝6.065x ＋0.846.(3)根据上面求得的回归直线方程，当水源中砷超标的倍数为7时，y ＝6.065×7＋0.846＝43.301. 即该村患癌症的人数约为43人．对误差的大小与变量相关关系的理解有误对两个变量y和x进行回归分析，得到一组样本数据：(x1，y1)，(x2，y2)，…，(x n，y n)，则下列说法中不正确的是( )A．由样本数据得到的回归方程y＝bx＋a必过样本点的中心(x，y)B．在回归分析中，误差Q越小，变量之间的线性相关程度越高C．相关系数r越小，说明变量之间的线性相关程度越小D．在散点图中，若n个点在一条直线上，说明变量之间的相关性强【错解】 B【错因分析】对误差Q与变量间的相关关系理解错误．【防范措施】正确理解回归方程、相关系数r、误差Q、散点图等概念是解决概念题的基础．【正解】∵误差Q越小，|r|越大，变量之间的线性相关程度越高，而相关系数r的范围为－1≤r≤1，∴C错误．【答案】 C1．相关系数是用来刻画两个变量相关关系的强与弱的．2．相关系数的计算公式r＝∑ni＝1x i－x y i－y∑ni＝1x i－x2∑ni＝1y i－y2＝∑ni＝1x i y i－n x y∑ni＝1x2i－n x2∑ni＝1y2i－n y21．在对变量y和x进行线性相关检验时，已知n是观测值组数，r是相关系数，且已知：①n＝7，r＝0.953 3；②n＝15，r＝0.301 2；③n＝17，r＝0.499 1；④n＝3，r＝0.9950.则变量y和x具有较高线性相关程度的是( )A．①和②B．①和④C．②和④D．③和④【解析】相关系数r的绝对值越大，变量x，y的线性相关程度越高，故选B.【答案】 B2．对相关系数r，下列说法正确的是( )A．|r|越大，相关程度越大B．|r|越小，相关程度越大C．|r|越大，相关程度越小，|r|越小，相关程度越大D．|r|≤1且|r|越接近于1，相关程度越大，|r|越接近0，相关程度越小【解析】由两个变量相关系数公式。
高中数学第三章统计案例3.2独立性检验课件北师大版选
B A A1 A2
总计
B1
B2
总计
a
b
a+b
c
d
c+d
a+c
b+d
n=a+b+c+d
其中,a 表示变量 A 取 A1,且变量 B 取 B1 时的数据;b 表示变量 A 取 A1,且变量 B 取 B2 时的数据;c 表示变量 A 取 A2,且变量 B 取 B1 时 的数据;d 表示变量 A 取 A2,且变量 B 取 B2 时的数据.
因为 χ2≈27.1>6.635,
所以我们有 99%的把握认为性别与色盲有关系.
题型一
题型二
反思1. 先确定a,b,c,d,n的值,再求出χ2的值,并与临界值相比较,注意 正确运用公式,准确代入数据.
2.当χ2>3.841时,有95%的把握认为两个变量有关;当χ2>6.635时, 有99%的把握认为两个变量有关.
,
������+������ ������表示的是频率,不同于概
率.即使变量之间独立,式子两边也不一定恰好相等.但是当两边相差
很大时,变量之间就不独立.
12
【做一做1-1】 下面是一个2×2列联表:
x1 x2 总计
y1
y2
a
21
8
25
b
46
总计
73 33
则表中a,b处的值分别为( ) A.94,96 B.52,50 C.52,60 答案:C
分析:本题应首先作出调查数据的列联表,再利用独立性检验作 出判断.
解:根据题目所给的数据作出如下的列联表:
男 女 合计
色盲
38 6 44
不色盲
2019_2020学年高中数学第三章统计案例2独立性检验课件北师大版选修2_3
巴西医生马廷思收集的犯有各种贪污、受贿罪的官员与廉洁官员的寿命的调查资 料如下：500 名贪官中有 348 人的寿命小于平均寿命，152 人的寿命大于或等于平 均寿命；590 名廉洁官员中有 93 人的寿命小于平均寿命，497 人的寿命大于或等于 平均寿命．这里，平均寿命是指“当地人均寿命”．试分析官员在经济上是否清 廉与他们的寿命长短是否有关？
本题是利用公式求出 χ2 的值，再利用其与临界值的大小关系来判断独立性，解题 时应注意准确代入数据与计算，不可错用公式，要准确地进行比较与判断．
1．从发生汽车碰撞事故的司机中抽取 2 000 名．根据他们的血液中是否含有酒精
以及他们是否对事故负有责任．将数据整理如下：
有无责任 有
有无酒精
无 总计
P(χ2≥k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
[解析] (1)χ2＝100×58×404×2×275－5×184×5152＝224233030≈10.88>10.828， 所以有 99.9%的把握认为收看新闻节目的观众与年龄有关． (2)抽取的比例为455＝19，所以大于 40 岁的观众应该抽取19×27＝3(名)． (3)在年龄 20 至 40 岁的 2 名观众和年龄大于 40 的 3 名观众中任取 2 名，恰有 1 名观众的年龄为 20 至 40 岁的概率为CC21C25 13＝35.
患 A 疾病 不患 A 疾病 合计
服用该药品
5
100
105
不服用该药品 18
400
高中数学第三章统计案例3.2独立性检验课件北师大版选修23
答案:无
第二十六页，共26页。
第八页，共26页。
一
二
【 做一做2】 想要检验(jiǎnyàn)喜欢参加体育活动是不是与性
别有关,应该检验(jiǎnyàn)(
)
A.H0:男性喜欢参加体育活动
B.H0:女性不喜欢参加体育活动
C.H0:喜欢参加体育活动与性别有关
D.H0:喜欢参加体育活动与性别无关
答案D
第九页，共26页。
一
二
思考辨析
探究
(tànjiū)二
思维(sīwéi)辨
析
反思感悟 独立性检验的具体做法
(1)根据实际问题作出两个分类变量的2×2列联表.
2
(2)利用公式
(-)
2
χ=
计算随机变量 χ2 .
(+)(+)(+)(+)
(3)比较χ2与临界值的大小,推断有多大把握认为两个分类变量之间有
关系.
第十六页，共26页。
答案A
第十三页，共26页。
)
探究
(tànjiū)一
探究(tànjiū)
二
思维(sīwéi)辨
析
探究二
独立性检验的基本思想
【例2】 为了调查某生产线上质量监督员甲对产品质量的好坏
有无影响,现统计数据如下:甲在生产现场时,990件产品中有合格品982
件,次品8件;甲不在生产现场时,510件产品中有合格品493件,次品17件.能
晕船情况
性别
男性
女性
合计
晕船
不晕船
合计
32
8
40
51
24
75
83
高中数学 第三章 统计案例 2 独立性检验知识导航 北师大版选修2-3(2021年最新整理)
高中数学第三章统计案例2 独立性检验知识导航北师大版选修2-3 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学第三章统计案例2 独立性检验知识导航北师大版选修2-3）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学第三章统计案例2 独立性检验知识导航北师大版选修2-3的全部内容。
§2 独立性检验自主整理1.设A ，B 为两个变量，每一个变量都可以取两个值, 变量A ：A 1,A 2=A 1； 变量B ：B 1，B 2=B 1.通过观察得到下表所示数据：其中,a 表示变量A 取A 1，且变量B 取B 1时的数据；b 表示变量A 取A 1,且变量B 取B 2时的数据；c 表示变量A 取A 2，且变量B 取B 1时的数据；d 表示变量A 取A 2，且变量B 取B 2时的数据.设n=a+b+c+d,用_______________估计P （A 1B 1), ______________估计P （A 1）， __________估计P(B 1). 若有式子nca nb a n a +•+=， 则可以认为______________独立。
同理,若n d b n b a n b +•+=，则可以认为______________独立;若nca n d c n c +•+=，则可以认为______________独立；若ndb n dc nd +•+=，则可以认为______________独立.但是，在n c a n b a n a +•+=中,由于nca nb a n a ++,,表示的是______________，不同于概率，即使变量之间独立，式子两边也不一定恰好相等。
高中数学第三章统计案例2独立性检验的应用教案北师大版选修2
2 独立性检验的应用一、教学目标通过对典型案例的探究，进一步巩固独立性检验的基本思想、方法，并能运用2χ统计量进行独立性检验。
二、教学重点，难点：独立性检验的基本方法是重点．基本思想的领会及方法应用是难点． 三、教学方法：讨论交流，探析归纳 四、教学过程 （一）、学生活动 练习：（1）某大学在研究性别与职称(分正教授、副教授)之间是否有关系，你认为应该收集哪些数据？ ．（2）某高校“统计初步”课程的教师随机调查了选该课的一些学生情况，具体数据如下表：为了判断主修统计专业是否与性别有关系，根据表中的数据，得到2χ250(1320107) 4.84423272030⨯⨯-⨯=≈⨯⨯⨯，∵χ2 3.841≥， 所以判定主修统计专业与性别有关系，那么这种判断出错的可能性为 ．（答案：5%） 附：临界值表（部分）：（二）运用探析 1、例题：例1、在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人。
女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动。
（1）根据以上数据建立一个2× 2列联表；（2）判断性别与休闲方式是否有关系。
解：（1）2× 2的列联表：（2）假设“休闲方式与性别无关”2χ2124(43332721) 6.20170546460⨯⨯-⨯=≈⨯⨯⨯ 因为2χ 5.024≥，所以有理由认为假设“休闲方式与性别无关”是不合理的，即有97.5%的把握认为“休闲方式与性别有关”。
例2、气管炎是一种常见的呼吸道疾病，医药研究人员对两种中草药治疗慢性气管炎的疗效进行对比，所得数据如表所示．问它们的疗效有无差异（可靠性不低于99%）？分析：由列联表中的数据可知，服用复方江剪刀草的患者的有效率为75%245≈，服用胆黄片的患者的有效率为9191%100=，可见，服用复方江剪刀草的患者与服用胆黄片的患者的有 效率存在较大差异．下面用2χ进行独立性检验，以确定能有多大把握作出这一推断． 解：提出假设0H ：两种中草药的治疗效果没有差异，即病人使用这两种药物中的何种药物对疗效没有明显差异。
2017-2018版高中数学第三章统计案例章末复习课学案北师大版选修2_3
第三章统计案例学习目标 1.能通过相关系数判断两变量间的线性相关性.2.掌握建立线性回归模型的步骤.3.理解条件概率的定义及计算方法.4.能利用相互独立事件同时发生的概率公式解决一些简单的实际问题.5.掌握利用独立性检验解决一些实际问题．知识点一线性回归分析1．线性回归方程在线性回归方程y＝a＋bx中，b＝____________＝____________，a＝____________.其中x ＝____________，y＝____________.2．相关系数(1)相关系数r的计算公式r＝∑ni＝1x i y i－n x y∑ni＝1x2i－n x2∑ni＝1y2i－n y2.(2)相关系数r的取值范围是________，|r|值越大，变量之间的线性相关程度越高．(3)当r>0时，b________0，称两个变量正相关；当r<0时，b________0，称两个变量负相关；当r＝0时，称两个变量线性不相关．知识点二独立性检验1．2×2列联表设A、B为两个变量，每一变量都可以取两个值，得到表格其中，a表示变量A取 ________，且变量B取 ________时的数据，b表示变量A取 ______，且变量B取________时的数据；c表示变量A取 __________，且变量B取 ________时的数据；d表示变量A取________，且变量B取________时的数据．上表在统计中称为2×2列联表．2．统计量χ2＝____________________.3．独立性检验当χ2≤2.706时，没有充分的证据判定变量A，B有关联，可以认为变量A，B是没有关联的；当χ2>2.706时，有________的把握判定变量A，B有关联；当χ2>3.841时，有________的把握判定变量A，B有关联；当χ2>6.635时，有________的把握判定变量A，B有关联．类型一线性回归分析例1 某城市理论预测2010年到2014年人口总数与年份的关系如表所示：(1)请画出上表数据的散点图；(2)请根据上表提供的数据，求出y关于x的线性回归方程y＝bx＋a；(3)据此估计2018年该城市人口总数．反思与感悟解决回归分析问题的一般步骤(1)画散点图．根据已知数据画出散点图．(2)判断变量的相关性并求回归方程．通过观察散点图，直观感知两个变量是否具有相关关系；在此基础上，利用最小二乘法求回归系数，然后写出回归方程．(3)实际应用．依据求得的回归方程解决实际问题．跟踪训练1 在一段时间内，某种商品的价格x元和需求量y件之间的一组数据为：且知x与y具有线性相关关系，求出y关于x的线性回归方程．类型二 独立性检验思想与应用例2 为了解某班学生喜爱打篮球是否与性别有关，对本班48人进行了问卷调查得到了如下的2×2列联表：已知在全班48人中随机抽取1人，抽到喜爱打篮球的学生的概率为23.(1)请将上面的2×2列联表补充完整；(不用写计算过程)(2)能否在犯错误的概率不超过0.05的前提下认为喜爱打篮球与性别有关？说明你的理由．反思与感悟 独立性检验问题的求解策略 χ2统计量法：通过公式 χ2＝n ad －bc 2a＋bc ＋d a ＋cb ＋d先计算统计量，再用以下结果对变量的独立性进行判断．(1)当χ2≤2.706时，没有充分的证据判定变量A，B有关联，可以认为变量A，B是没有关联的．(2)当χ2>2.706时，有90%的把握判定变量A，B有关联．(3)当χ2>3.841时，有95%的把握判定变量A，B有关联．(4)当χ2>6.635时，有99%的把握判定变量A，B有关联．跟踪训练2 某学生对其亲属30人的饮食习惯进行了一次调查，并用茎叶图表示30人的饮食指数，如图所示．(说明：图中饮食指数低于70的人，饮食以蔬菜为主；饮食指数高于70的人，饮食以肉类为主)．(1)根据茎叶图，帮助这位同学说明其亲属30人的饮食习惯；(2)根据以上数据完成如下2×2列联表；(3)在犯错误的概率不超过0.01的前提下，是否能认为“其亲属的饮食习惯与年龄有关”？1．“回归”一词是在研究子女的身高与父母的身高之间的遗传关系时由高尔顿提出的，他的研究结果是子代的平均身高向中心回归．根据他的结论，在儿子的身高y与父亲的身高x的线性回归方程y＝bx＋a中，b( )A．在(－1,0)内B．等于0C．在(0,1)内D．在[1，＋∞)内2．已知线性回归方程中斜率的估计值为1.23，回归方程过点(4,5)，则线性回归方程为( ) A．y＝1.23x＋0.08 B．y＝0.08x＋1.23C．y＝1.23x＋4 D．y＝1.23x＋53．为了解高中生作文成绩与课外阅读量之间的关系，某研究机构随机抽取了60名高中生，通过问卷调查，得到以下数据：由以上数据，计算得到χ2≈9.643，则以下说法正确的是( )A．没有充足的理由认为课外阅读量大与作文成绩优秀有关B．有1%的把握认为课外阅读量大与作文成绩优秀有关C．有99.9%的把握认为课外阅读量大与作文成绩优秀有关D．有99%的把握认为课外阅读量大与作文成绩优秀有关4．考察棉花种子经过处理与生病之间的关系，得到下表中的数据：根据以上数据可得出( )A．种子是否经过处理与是否生病有关B．种子是否经过处理与是否生病无关C．种子是否经过处理决定是否生病D．有90%的把握认为种子经过处理与生病有关5．对于线性回归方程y＝bx＋a，当x＝3时，对应的y的估计值是17，当x＝8时，对应的y的估计值是22，那么，该线性回归方程是________，根据线性回归方程判断当x＝________时，y的估计值是38.1．建立回归模型的基本步骤(1)确定研究对象，明确变量．(2)画出散点图，观察它们之间的关系．(3)由经验确定回归方程的类型．(4)按照一定的规则估计回归方程中的参数．2．独立性检验是对两个分类变量间是否存在相关关系的一种案例分析方法．答案精析知识梳理 知识点一1.∑ni ＝1x i －xy i －y∑n i ＝1x i －x 2∑ni ＝1x i y i －n x y∑n i ＝1x 2i －n x2y －b x 1n ∑ni ＝1x i 1n ∑ni ＝1y i2．(2)[－1,1] (3)> < 知识点二1．a ＋b c ＋d a ＋c b ＋d a ＋b ＋c ＋d A 1 B 1 A 1 B 2 A 2 B 1 A 2 B 2 2.n ad －bc 2a＋bc ＋d a ＋cb ＋d3．90% 95% 99% 题型探究例1 解 (1)散点图如图．(2)因为x ＝0＋1＋2＋3＋45＝2，y ＝5＋7＋8＋11＋195＝10，∑5i ＝1x i y i ＝0×5＋1×7＋2×8＋3×11＋4×19＝132，∑5i ＝1x 2i ＝02＋12＋22＋32＋42＝30， 所以b ＝132－5×2×1030－5×22＝3.2， a ＝y －b x ＝3.6.所以线性回归方程为y ＝3.2x ＋3.6. (3)令x ＝8，则y ＝3.2×8＋3.6＝29.2， 故估计2018年该城市人口总数为292万人．跟踪训练1 解 x ＝15×(14＋16＋18＋20＋22)＝18，y ＝15×(12＋10＋7＋5＋3)＝7.4，∑i ＝15x 2i ＝142＋162＋182＋202＋222＝1 660， ∑i ＝15y 2i ＝122＋102＋72＋52＋32＝327， ∑i ＝15x i y i ＝14×12＋16×10＋18×7＋20×5＋22×3＝620，所以b ＝∑i ＝15x i y i －5x y∑i ＝15x 2i －5x 2＝620－5×18×7.41 660－5×182＝－1.15，所以a ＝7.4＋1.15×18＝28.1，所以y 对x 的线性回归方程为y ＝－1.15x ＋28.1. 例2 解 (1)列联表补充如下：(2)由χ2＝－228×20×32×16≈4.286.因为4.286>3.841，所以能在犯错误的概率不超过0.05的前提下认为喜爱打篮球与性别有关． 跟踪训练2 解 (1)30位亲属中50岁以上的人多以食蔬菜为主，50岁以下的人多以食肉类为主．(2)2×2列联表如下：(3)χ2＝－212×18×20×10＝10>6.635，故在犯错误的概率不超过0.01的前提下认为“其亲属的饮食习惯与年龄有关”．当堂训练1．C 2.A 3.D 4.B5．y＝x＋14 24。
高中数学 第3章 2独立性检验课件 北师大版选修23
• [答案] C
[解析] 由题意得 2×2 列联表： 色盲 不色盲 合计
男 39 461 500 女 6 494 500 合计 45 955 1000 χ2＝100500×0×395×004×944－5×6×9545612≈25.34， ∵25.34＞6.635， ∴有 99%把握认为色盲与性别有关．
2．2×2 列联表的独立性检验 根据 2×2 列联表计算出频率值，用频率估计概率进行独立 性检验． 用an估计 P(A1B1)，a＋n b估计 P(A1)，a＋n c估计 P(B1)．
若有式子an＝a＋n b·a＋n c，则可以认为 A1 与 B1 独立． 同理，若bn＝a＋n b·b＋n d，则可以认为 A1 与 B2 独立． 若nc＝c＋n d·a＋n c，则可以认为 A2 与 B1 独立； 若dn＝c＋n d·b＋n d，则可以认为 A2 与 B2 独立． 但在an＝a＋n b·a＋n c中，由于an、a＋n b、a＋n c表示的是频率， 不同于概率，即使变量之间独立，式子两边也不一定恰好相 等．但是当两边相差很大时，变量之间就不独立．
3．独立性检验的基本思想 利 用 2×2 列 联 表 检 验 变 量 之 间 是 否 独 立 ， 当 an－a＋n b·a＋n c 、 bn－a＋n b·b＋n d 、 nc－c＋n d·a＋n c 、 dn－c＋n d·b＋n d大时，变量之间不独立．但不能解释这些量究竟 要多大才能说明变量之间不独立． 为此，统计学家引入统计量 χ2＝a＋bcn＋add－ab＋cc2b＋d， 用它的大小来检验变量之间是否独立．当 χ2 较大时，说明变量 之间不独立．
• 1.在吸烟与患肺病是否相关的计算中，有下面的说法：( )
• ①若χ2＝6.635，我们有99%的把握判定吸烟与患肺病有关 联，那么在100个吸烟的人中必有99个人患肺病；
高中数学 第三章 统计案例 2 独立性检验同步测控 北师大版选修2-3(2021年最新整理)
高中数学第三章统计案例2 独立性检验同步测控北师大版选修2-3 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学第三章统计案例2 独立性检验同步测控北师大版选修2-3）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学第三章统计案例2 独立性检验同步测控北师大版选修2-3的全部内容。
高中数学 第三章 统计案例 2 独立性检验同步测控 北师大版选修2-3我夯基，我达标1.如果有99%的把握认为“X 与Y 有关系”，那么具体算出的数据满足（ ）A.χ2＞6.635 B 。
χ2＞5.024 C.χ2＞7。
879 D.χ2＞3。
841解析：当χ2＞6。
635时,有99%的把握认为“X 与Y 有关系". 答案：A2。
分类变量X 和Y 的列联表如下：则下列说法正确的是（ ） A 。
adbc 越小，说明X 与Y 关系越弱 B 。
adbc 越大，说明X 与Y 关系越强 C.（adbc ）2越大，说明X 与Y 关系越强 D 。
（adbc ）2越接近于0，说明X 与Y 关系越强解析:因为χ2=))()()(()(2d c d b c a b a bc ad n ++++-，当(ad-bc ）2越大时,χ2越大，说明X 与Y 关系越强。
答案:C3。
对于分类变量X 与Y 的随机变量χ2的观测值k,下列说法正确的是（ ） A 。
k 越大,“X 与Y 有关系”可信程度越小 B 。
k 越小,“X 与Y 有关系"可信程度越小C 。
k 越接近于0，“X 与Y 无关”程度越小D 。
k 越大，“X 与Y 无关”程度越大解析：χ2的值越小时，“X 与Y 有关系”的可信程度越小。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§2独立性检验
[对应学生用书P40]
1．2×2列联表
设A ，B 为两个变量，每个变量都可以取两个值，变量A ：A 1，A 2＝A －
1；变量B ：B 1，B 2
＝B －
1，用下表表示抽样数据
并将此表称为2．χ2
的计算公式 χ2
＝
n ad －bc 2a ＋b
c ＋
d a ＋c
b ＋d
.
3．独立性判断的方法
(1)当χ2
≤2.706时，没有充分的证据判定变量A ，B 有关联，可以认为变量A ，B 是没有关联的；
(2)当χ2>2.706时，有90%的把握判定变量A ，B 有关联； (3)当χ2>3.841时，有95%的把握判定变量A ，B 有关联； (4)当χ2>6.635时，有99%的把握判定变量A ，B 有关联．
(1)独立性检验是一种假设检验，在对总体的估计中，通过抽取样本，构造合适的统计量，对假设的正确性进行判断．
(2)使用χ2统计量作2×2列联表的独立性检验时，一般要求表中的4个数据都大于5，数据越大，越能说明结果的普遍性．
[对应学生用书P41]
[例1] 在调查的6名患有色盲，试作出性别与色盲的列联表．
[思路点拨] 在2×2列联表中，共有两类变量，每一类变量都有两个不同的取值，然后出相应的数据，列表即可．
[精解详析] 根据题目所给的数据作出如下的列联表：
[一点通]
1．下面是一个2×2列联表：则表中a ，b 处的值分别为( )
A.32,40 B C ．74,82 D ．64,72
解析：a ＝53－21＝32，b ＝a ＋8＝40. 答案：A
2．某学校对高三学生作一项调查后发现：在平时的模拟考试中，性格内向的426名学生中有332名在考前心情紧张，性格外向的594名学生中在考前心情紧张的有213人．试作出2×2列联表．
解：列联表如下：。