球的密堆积和
实验二十四 等径圆球的密堆积

实验二十四等径圆球的密堆积一、实验目的1. 通过等径圆球的堆积来模拟金属单质中原子的堆积,了解金属单质的若干典型结构型式,加深对金属结构的了解。
2. 掌握A1、A2、A3型堆积的特点;3. 掌握A1和A3型堆积中,每个晶胞中摊到的金属原子数、正四面体空隙数和正八面体空隙数及其分布情况;4. 计算A1、A2、A3型堆积中,原子体积的空间占有率;5. 计算A4型堆积(金刚石结构)中,C原子体积的空间占有率。
二、实验原理固体可分为晶体、非晶体和准晶体三大类。
固态物质是否为晶体,一般可由X射线衍射法予以鉴定。
晶体内部质点在三维空间周期性重复有序排列,使其具有各自特別的晶体结构与形状。
晶体按其内部结构可分为七大晶系和14种晶格类型。
晶体结构与组成粒子排列的紧密程度,会影响其熔点、密度、延展性等性质。
以立方晶系为例,简单立方、体心立方和面心立方晶格的排列方式、粒子的配位數(每原子邻接之原子数)、单位晶胞中所含粒子粒及填充紧密度均不相同。
晶体结构中,单层晶格点排列的情形可如图1所示。
每一个代表晶格点的圆球配位数为4,晶格点间的空隙较大,这种排列方式称为四方堆积。
图中第二列粒子排列在第一列相邻两个粒子的空隙间,排列较紧密,每一圆球的配位数为6,这种排列方式称为最密堆积。
最密堆积依层与层排列的差异又分为两种。
如图34-2(B)为ABAB…二层重复叠排,则为六方最密堆积。
如图34-2(C)为ABCABC…三层重复叠排,則为立方最密堆积或称为面心立方。
至于离子晶体,一般是较大的离子(通常为阴离子,以r- 表示)以最密堆积的形式排列,然后半径较小的离子(通常为阳离子,以r+ 表示)依离子半径比(r+/r-)安置于较大大离子的空隙间,如四面体空隙、八面体空隙或立方体空隙中,使阳离子与阴离子间的吸引力最大、排斥力最小。
以NaCl 为例,氯离子以面心立方晶形排列,钠离子位于八面体空隙。
本实验以圆球代表晶体结构中各晶格点的原子、分子或离子,通过小棍堆叠成各式晶体模型,观察其立体形状及填充紧密度。
等径圆球密堆积与非等径圆球密堆积的区别

等径圆球密堆积与非等径圆球密堆积的区别
山东省邹平县长山中学256206 吴贵智
在金属晶体、离子晶体和分子晶体的结构中,由于金属键、离子键和分子间作用力均没有方向性,使得晶体中的每一个原子或分子都能吸引尽可能多的其他原子或分子于周围,并以密堆积的方式降低体系的能量,使晶体结构变得比较稳定。
根据组成晶体的原子或分子的大小将密堆积的方式分为等径圆球密堆积和非等径圆球密堆积。
等径圆球密堆积:在金属晶体中,金属原子中的电子分布呈球对称,且金属键没有方向性,又由于金属原子的大小相等,所以金属原子按照等径圆球的密堆积。
首先,等径圆球在一列上呈直线排列,在同一平面上,每个圆球于周围的六个圆球紧密接触,形成密置层。
密置层与密置层的圆球之间平行的错开,使每个圆球的球心恰好对应另一层相邻三个球所围成的空隙的中心,并使两层紧密接触,形成密置双层。
在密置双层的基础上,根据堆积第三层时出现不同的排列方式,将堆积方式分为“…ABAB…”和“…ABCABC…”两种形式。
其中“…ABAB…”是在密置双层的基础上,隔层圆球的球心相对应,例如金属镁;而“…ABCABC…”则是相邻三层圆球的球心位置均不同,但此后都按照如此相邻的三层重复排列,例如金属铜。
非等径圆球密堆积:在离子晶体中,离子中的电子分布基本上也是球对称的,由于离子间存在无方向性的静电作用,每个离子周围都会尽可能多地吸引带相反电荷的离子,使体系的能量最低。
但由于阴、阳离子的半径不相同,在排列时,半径大的离子先按一定方式做等径圆球的密堆积,半径小的离子再填充到半径大的离子所形成的空隙中。
例如,NaCl晶体中,由于氯离子的半径大于钠离子的半径,氯离子先按等径圆球的密堆积,然后钠离子再填充到氯离子所构成的空隙中。
矿石的晶体化学分析——球体的最紧密堆积

书山有路勤为径,学海无涯苦作舟矿石的晶体化学分析——球体的最紧密堆积在晶体结构中,质点之间趋于尽可能地相互靠近,形成最紧密堆积,以达到内能最小,而使晶体处于最稳定状态。
尽管对于具有共价键的晶体来说,原子的排列会受到化学键的方向性和饱和性的影响,但是,在具有离子键和金属键的晶体中,由于离子键和金属键没有方向性和饱和性,因而用球体最紧密堆积的观点来进行分析,还是合适的。
球体的最紧密堆积,有等大球体的最紧密堆积和不等大球体的最紧密堆积两种。
一、等大球体的最紧密堆积等大球体(单一质点)在一个平而内作最紧密排列时,只能构成一种形式(图1)。
这时每个球周围有6 个球围绕,并在球与球之间形成三角孔,其中一半三角孔的尖端指向下方(图1 的B 处),而另一半三角孔的尖端指向上方(图1 的C 处)。
图1 一层球的最紧密堆积继续堆积第二层球时,球只能置于第一层球的三角孔上才是最紧密的,即置于图2 的B 处(图2—a)或C 处(图2—b)。
但无论置于B 处或C 处,其结果是一样的,因为将图2—a 旋转180°与图2—b 完全相同。
所以说两层球作最紧密堆积的方式依然只有一种。
图2 两层球的最紧密堆积a—第二层球(虚线)置于尖端向下的三角孔上;b—第二层球(虑线)置于尖端向上的三角孔上再继续堆积第三层球时则有两种不同的方式。
第一种方是第三层球的中心与第一层球的中心相对,即第三层球重复了第一层球的位置;另一种方式是第三层球置于第一层和第二层重叠的三角孔之上,即第三层球与第一层球和第二层球的位置都不重复。
如果在上述第一种方式的基础上,使第四层球与第二层球重复,并按这种ABABAB……二层重复一次的规律连续堆积(图3—a),其结果是球在空间的分布与空间格子中六方格子一致(图3—b),故称之为六方最紧密堆积。
图3 六方最紧密堆积a—球堆积的方式;b—球中心的分布(与六方格子相。
典型离子晶体地各种堆积-填隙模型的堆积球和填隙球的半径比-概述说明以及解释

典型离子晶体地各种堆积-填隙模型的堆积球和填隙球的半径比-概述说明以及解释1.引言1.1 概述离子晶体在自然界中广泛存在,并且在许多领域中具有重要的应用价值。
研究离子晶体的结构堆积方式对于理解其物理化学性质以及开发新型功能材料具有重要意义。
在离子晶体的结构中,堆积模型是其中一种重要的研究对象。
堆积模型是指离子晶体中离子排列的方式和顺序。
通过研究和分析不同类型的离子堆积模型,可以了解离子晶体的几何构型、离子间距以及孔隙结构等重要特征。
在典型离子晶体中,常见的堆积模型包括六方最密堆积、立方最密堆积和体心立方堆积等。
填隙模型是一个与堆积模型密切相关的概念。
填隙模型描述了离子晶体中离子球和填隙球之间的相互作用关系。
填隙球指的是在堆积模型中离子之间形成的孔隙,而离子球则是指堆积模型中的离子。
通过研究填隙模型,可以进一步了解离子晶体中的空位、孔径大小以及离子的配位数等重要性质。
本文将重点研究填隙模型的堆积球和填隙球的半径比。
理论上,填隙球的半径与堆积球的半径之间存在一定的关系,这对于准确描述离子晶体的结构和性质非常重要。
通过实验和模拟方法,我们将探讨不同离子晶体中填隙球和堆积球的半径比的变化规律,以期揭示离子晶体材料中的微观结构和宏观性质之间的关联性。
本研究具有重要的理论和实践意义。
首先,对填隙模型的深入研究可以为离子晶体的结构设计和制备提供理论指导。
其次,填隙模型的研究可以为新型功能材料的开发和设计提供参考。
最后,对填隙球和堆积球半径比的研究有助于揭示离子晶体的结构特征与其性质之间的内在联系,为相关领域的进一步研究提供基础和支持。
由于离子晶体的复杂性和多样性,填隙模型的研究还存在一些挑战和尚未解决的问题。
未来的研究可以进一步探索不同离子晶体中填隙球和堆积球的半径比的影响因素,并寻求更精确的描述方法和模型。
希望本研究能够为离子晶体结构与性质的研究提供新的思路和方法,促进相关领域的进一步发展。
1.2文章结构文章结构部分的内容可以按照以下方式编写:1.2 文章结构本文按照以下结构进行展开:第二部分为正文,共分为两个小节。
典型晶体结构

一个球体积:4/3πr3=4/3π×( 2/4 a )3=
3 4/3π× 2 2/64 a =
2 /24 πa 3
立方最密堆积一个单胞中球的数目: 8×1/8+6×1/2= 4个 球体积= 4× 2/24 πa 3 = 2 /6 πa 3 空间利用率= 2 a 3 / a 3 2 / 6 74.05% 6
(3) 体心立方bcc
密排面和密排方向: 密排面为{110},密排方向<111>
体心立方密排面
原子半径:
bcc的晶胞体积为a3,晶胞内含2个原子。 原子体积
空间利用率
=
单胞体积
4 æ 3 ö 2´ pç a÷ 3 è 4 ø a3
3
=
3 = p = 68.02% 8
空间利用率:68.02%
(4) 金刚石型堆积(A4) 在这种堆积方式中,等径圆球的排布与金刚石中 碳原子排布类似,所以称为金刚石型堆积。从金刚 石型堆积中可抽出面心立方晶胞,如下图所示
所以密堆积结构至少具有3m1点群对称性
其最低空间群对称性为P3m1和R3m1
密堆结构共有8个空间群:
P3m1, P3m1, P 6m2, P63 mc, P 63 mc m
R3m1, R3m1, Fm3m
能容纳3次旋转对称的点阵只有: 菱面体点阵 R 3层为周期密堆积结构的 六角点阵 H R点阵等价于cF(立方面 心)点阵
A
C A B
A
表示:方法一:四层:…ABAC ABAC… 五层:…ABCAB ABCAB… 六层: …ABCACB ABCACB ABCACB… …h c c h c c h c c h c c … 方法二 …ABABAC ABABAC ABABAC… …c h h h c h c h h h c h …
第二章 球的密堆积与结晶化学定律
近似地用球的紧密堆积来描述。
开普勒对固体结构的推测
冰的结构
A
A
B
最密堆积
(ccp)
二、空间利用率
3
π
2/24)a
1/8+6×1/2= 4
三、原子半径四、最密堆积中的空隙类型
1. 立方最密堆积中的空隙
2.六方最密堆积中的空隙
§2.2不等径球的密堆积1. 三配位
二、离子半径
1.离子的接触半径
2.离子的晶体半径
§2.3 结晶化学定律1、离子大小与晶体结构
2、离子的极化
极化对晶体结构的影响
§2.4 鲍林规则二、鲍林规则
Ca2+
Ca
Ti O
四面体和八面体分别公用顶点、棱和面的情况
46
中心阳离子间距越小,阳离子与阳离子间的静电斥
力越大,结构越不稳定。
SiO2,四面体以顶点连接SiS2,四面体以棱连接
配位多面体之间倾向于不公用几何元素。
5.第五规则(吝惜规则)。
总结均匀尺寸球的6种排列的规律

总结均匀尺寸球的6种排列的规律均匀尺寸的球体可以按照不同的方式排列,每种排列方式都遵循其特定的几何规律。
以下是六种常见的球体排列方式及其规律的总结:1.线性排列:●球体沿一直线排列。
●相邻两球中心的距离等于球的直径。
●这是最简单的排列方式,没有空隙。
2.方形排列:●球体在一个平面上沿正方形的格点排列。
●相邻球体中心的距离在水平和垂直方向上均等于球的直径。
●这种排列在两个方向上都是规律性的,但会在球体间留下空隙。
3.三角形排列:●球体在平面上沿等边三角形的格点排列。
●每三个相邻球体形成一个等边三角形。
●这种排列比方形排列更紧密,减少了空隙。
4.正四面体排列:●这是一种三维排列方式,球体排列成正四面体的结构。
●每四个球体形成一个正四面体,每个球体接触其他三个球体。
●这种排列是三维空间中最紧凑的排列之一。
5.立方体排列:●球体在三维空间中沿立方体的格点排列。
●每个球体在其六个面方向上各接触一个球体。
●这种排列在三维空间中是规则的,但与正四面体排列相比,有更多的空隙。
6.密堆积排列:●密堆积排列可以是面心立方(FCC)或六方密堆积(HCP)。
●在FCC排列中,每个球体被12个其他球体所包围,形成最密排列。
●在HCP排列中,球体同样形成紧密的结构,但排列方式略有不同。
●这两种排列都是三维空间中最紧密的排列方式,最大限度地减少了空间中的空隙。
这些排列方式在材料科学、化学和物理等领域有广泛的应用,比如在研究晶体结构、分子排列和材料打包等方面。
2-密堆积
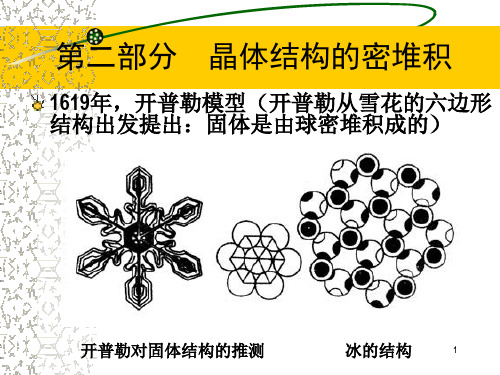
S a a sin 60 3 a2 2
平行六面体的高:
h 2边长为a的四面体高
2 6 a 2 6 a
3
3
20
V晶胞
3 a2 2 6 a
2
3
2a3 8 2r3
V球
2
4
3
r3
(晶胞中有2个球)
V球 V晶胞 100% 74.05%
21
22
23
隙上方,其排列方式与第一层相同,但与第
二层错开,形成ABAB…堆积。这种堆积方式
可以从中划出一个六方单位来,所以称为六
方最密堆积(A3)。
9
三维等径圆球的堆积(A3)
能量较低 密置层
A B A B A
B
A
10
A3最密堆积形成的六方晶胞
A3最密堆积形成后, 从中可以划分 出什么晶胞? 六方晶胞.
11
47
(4)六方ZnS晶胞图
48
六方ZnS
(1)六方晶系,简单六方晶胞 (2)Z=1 (3)Zn2+和S2- 六方最密堆积周期|AaBb|。 (4)配位数4:4。 (6)2s:0 0 0,2/3 1/3 1/2;
2Zn:0 0 5/8,2/3 1/3 1/8。
49
(5) CsCl型:
(1)立方晶系,简单立方晶胞。 (2)Z=1。 (3)Cs+,Cl-,离子键。 (4)配位数8:8。 (5) Cs+离子位于简单立方点阵的阵点上
3 30
A2型密堆积图片
31
金刚石型堆积(A4)
配位数为4,空间利用率为
34.01%,不是密堆积。这
种堆积方式的存在因为原
子间存在着有方向性的共
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)六方最密堆积 A3 :
按照ABABAB……最密堆积,重复周期为2层,按垂 直方向可取出六方晶胞,简称为 hcp(Hexagoal Closet packing)---A3。
A3型堆积可抽出六方晶胞,晶胞中心两个球的分数坐标 为(0,0,0,)、(2/3、1/3、1/2),密置层的晶面坐标为 (001)。
a
4r
V晶胞 = a 3 = (2 2r ) 3 = 16 2r 3 4 3 πr 3 4 3 16 3 V球 = 4 × πr = πr 3 3 V球 16πr 3 / 3 = = 74.05% 3 V晶胞 16 2r
立方最密堆积虽晶胞大小不同,每个晶胞中含球数不 同。但计算得到空间占有率相同。
体心立方堆积(bcp): 体对角线长为 晶胞体积
正八面体空隙
正四面体空隙
第二种放法,将第三层球放在第一层未被覆 盖的空隙上,形成C层,以后堆积按 ABCABC……重复下去,这种堆积称为立方最 密堆积。 这两种堆积,每个球在同一层与6个球相切, 上下层各与3个球接触,配位数均为12。
密置三层
(1)立方最密堆积 A1 :
按ABCABC……最密堆积,重复周期为3层,若将某 一平面层取为晶胞的(111)面,则可以从ABCABC堆积 中取出立方面心晶胞,简称ccp(Cubic Closest packing)--A1。
(4)金刚石堆积 A4 :
二. 密堆与空隙
1.空间占有率
等径球两种最密堆积具有相同的堆积密度,晶胞中圆 球体积与晶胞体积之比称空间占有率,六方最密堆积 (hcp)与立方最密堆积(ccp)空间占有率均为74.05%。
立方最密堆积(ccp): 设圆半径为r,晶胞棱长为a 晶胞面对角线长 4r = 2a, a = 2 2r 晶胞体积 每个球体积为 4个球体积 空间占有率
密置单层Biblioteka 第二层球堆上去,为了保持最密堆积,应放在 第一层的空隙上。每个球周围有6个空隙,只可能 有3个空隙被第二层球占用;
密置双层
正八面体空隙(a) 和正四面体空隙(b)
第三层球有2种放法: 第一种是每个球正对第一层:若第一层为A, 第二层为B,以后的堆积按ABAB……重复下去, 这样形成的堆积称六方最密堆积。
a
六 方 晶 胞
1 b 3
b
2 a 3
六方晶胞中的圆球位置
(3)立方体心堆积 A2 :
有些金属单质采取体心立方密堆形式。采用这种堆积 形式,每个金属原子最近邻有8个金属原子,次近邻有6个 金属原子,不是最密堆积。这种现象说明金属正离子并不 是完全象个圆球,在成键过程中,原子会发生形变,圆球 模型又是一种近似。体心立方密堆积可简写为bcp(Body Cubic Packing),符号记为A2。
三、金属单质结构
金属元素中具有面心立方,密集六方和体心立 方三种典型结构的金属占了绝大多数。许多金属中 存在多种结构转变现象,这说明三种结构之间能量 差异不大。 碱金属一般具有体心立方结构(A2),但在低 温时可转变为密堆六方。碱土金属大多是密堆六方 结构(A3)。过渡金属d壳层电子半满以上的,一 般是面心立方(A1),d壳层未半满的,大多是体 心立方结构(A2)。
4r = 3a, a = V晶胞 = a =
3
4 3
r
64 3 3
r3
4 3 8 3 体心立方晶胞含2个球 V球 = 2 × πr = πr 3 3 V球 8πr 3 / 3 = = 68.02% 3 空间占有率 V晶胞 16r / 3 3
2.最密堆积中的空隙(A1,A3)
密置双层 球数:八面体空隙数:四面体空隙数 = 2N:1N:2N =2:1:2 密置3层 球数:八面体空隙数:四面体空隙数 =3N:2N:4N= 3:2:4 密置4层 球数:八面体空隙数:四面体空隙数 =4N:3N:6N= 4:3:6 …. 密置n层 球数:八面体空隙数:四面体空隙数 =nN:(n-1)N:(2nN-2)= 1:1:2
金属的晶体构型(无色为复杂构型或无晶体结构)
第九章作业
7, 8, 9, 10, 11, 16, 17,19
9-2 球的密堆积和 金属单质的结构
金属原子堆积在一起,形成金属晶体。金属原 子最外层价电子脱离核的束缚,在晶体中自由运动, 形成“自由电子”,留下的金属正离子都是满壳层电 子结构,电子云呈球状分布,所以在金属结构模型 中,人们把金属正离子近似为等径圆球。
一.等径球密堆积
等径圆球平铺成最密的一层只有一种形式, 即每个球都和六个球相切;
