四川省眉山市东坡区多悦高级中学校2020-2021学年高一12月月考数学试题 Word版含答案
四川省眉山市高一上学期数学12月份月考试卷

四川省眉山市高一上学期数学12月份月考试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共12分)1. (1分)tan750°的值为()A . -B .C .D . -2. (1分) (2020高三上·海淀期末) 已知集合,,,则集合是()A .B .C .D .3. (1分) (2019高一上·屯溪期中) 若函数,则()A . -10B . 10C . -2D . 24. (1分) (2018高三上·赣州期中) 幂函数的图像经过点,则()A .B .C .D .5. (1分)一扇形的中心角为2,中心角所对的弦长为2,则此扇形的面积为()A . 2B . 1C .D .6. (1分)函数的零点所在的区间为()A . (1,)B . (, 2)C . (2,e)D . (e,+∞)7. (1分)已知某帆船中心比赛场馆区的海面上每天海浪高度y(米)可看作是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t),经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b,下表是某日各时的浪高数据:t/时03691215182124y/米2120.992则最能近似地表示表中数据间对应关系的函数是()A . y= cos t+1B . y= cos t+C . y=2cos t+D . y= cos6πt+8. (1分) (2018高一上·凯里月考) 函数的单调递增区间为()A .B .C .D .9. (1分)函数f(x)=﹣(cosx)|lg|x||的部分图象是()A .B .C .D .10. (1分)已知函数(其中)的部分图象如图所示,为了得到g(x)=sin2x 的图象,则只需将f(x0的图象()A . 向右平移个长度单位B . 向右平移个长度单位C . 向左平移个长度单位D . 向左平移个长度单位11. (1分) (2018高一下·宁夏期末) 定义在上的函数既是偶函数又是周期函数,若的最小正周期是,且当时,,则的值为()A .B .C .D .12. (1分)如图,偶函数f(x)的图像形如字母M,奇函数g(x)的图像形如字母N,若方程f(f(x))=0,f(g(x))=0,g(g(x))=0,g(f(x))=0的实根个数分别为a,b,c,d,则a+b+c+d=()A . 27B . 30C . 33D . 36二、填空题 (共4题;共4分)13. (1分) (2019高二上·浙江期中) 已知函数,则 ________,的解集为________.14. (1分) (2017高一上·鞍山期中) 函数f(x)对任意实数x,y满足f(x)+f(y)=f(x+y),则f(﹣1)+f(0)+f(1)=________.15. (1分)若函数y=loga(x2﹣ax+2)在区间(﹣∞,1]上为减函数,则a的取值范围是________.16. (1分)设集合A={|2a﹣1|,2},B={2,3,a2+2a﹣3}且∁BA={5},则实数a的值是________.三、解答题 (共6题;共12分)17. (1分) (2017高一下·乾安期末) 在△ABC中,已知=3 .(1)求证:tanB=3tanA;(2)若cosC=,求A的值.18. (2分)化简:19. (1分) (2016高一上·万州期中) 已知函数f(x)=x﹣.(1)判断函数f(x)的奇偶性,并加以证明;(2)用定义证明函数f(x)在区间[1,+∞)上为增函数;(3)若函数f(x)在区间[2,a]上的最大值与最小值之和不小于,求a的取值范围.20. (2分) (2018高二上·赣榆期中) 如图所示的是自动通风设施该设施的下部ABCD是等腰梯形,其中米,高米,米上部CmD是个半圆,固定点E为CD的中点是由电脑控制其形状变化的三角通风窗阴影部分均不通风,MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.(1)设MN与AB之间的距离为x米,试将三角通风窗的通风面积平方米表示成关于x的函数;(2)当MN与AB之间的距离为多少米时,三角通风窗的通风面积最大?求出这个最大面积.21. (3分)(2017·嘉兴模拟) 已知,(1)求函数y=f(x)的单调递增区间;(2)设△ABC的内角A满足f(A)=2,而,求边BC的最小值.22. (3分)已知定义域为R的函数是奇函数.(Ⅰ)求m,n的值;(Ⅱ)当时,f(kx2)+f(2x﹣1)>0恒成立,求实数k的取值范围.参考答案一、选择题 (共12题;共12分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共12分) 17-1、17-2、18-1、19-1、19-2、19-3、20-1、20-2、21-1、21-2、22、答案:略。
四川省眉山市东坡区多悦高级中学校2019-2020学年高一下学期期末模拟考试数学试题+扫描版含答案

二、填空题 (本题共 4 小题,每小题 5 分,共 20 分)
13.
2a1b 33
1 14. - 3
15.3
三、解答题 (本题共 6 小题,共 70 分)
16.②④
17. 解:(1)由已知得 a 0 ,且1,b 是方程 ax2-4x + 3 = 0 的两根,
即
1
b
b
3 a
4
a
…………………………………………3 分
因为{an }为等差数列,所以 a1、a2、a3 也是等差数列
……1 分
2a2 a1 a3 ,即 0 2x 2 8x 6 ,解得 x 1, 或x 3
数列{an }为递增的等差数列, x 1,
……2 分
a1 -2,a2 0,a3 2 ,
数列{an}的通项公式 an 2n 4
19. 解:(1) m n sin Acos B sin B cos A sin(A B), …………………2 分
对于 ABC, A B π C,0 C π,
∴ sin( A B) sin C
∴ m n sin C, 又 m n sin 2C,
∴ sin C sin 2C,cosC 1 ,C π 23
(2)由(1)得 bn
2n 1 2n
Tn
1 21
3 22
5 23
2n 3 2 n 1
2n 1 2n
①
1 2
Tn
1 22
3 23
2n 5 2 n 1
2n 3 2n
2n 1 2 n 1
②
……3 分
①——②得
1 2
Tn
1 21
2 22
2 23
2 2 n1
2020年四川省眉山市多悦中学高一数学理下学期期末试卷含解析

2020年四川省眉山市多悦中学高一数学理下学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 若那么下列各式中正确的是()A. B. C. D.参考答案:C2. 已知数列{a n}的通项公式,前n项和为S n,若,则的最大值是()A. 5B. 10C. 15D. 20参考答案:B【分析】将{a n}的通项公式分解因式,判断正负分界处,进而推断的最大最小值得到答案.【详解】数列{a n}的通项公式当时,当或是最大值为或最小值为或的最大值为故答案为B【点睛】本题考查了前n项和为的最值问题,将其转化为通项公式的正负问题是解题的关键.3. 若=,且,则=( )A.- B.- C. D.参考答案:C4. 下列叙述随机事件的频率与概率的关系中正确的是()A.频率就是概率B.频率是客观存在的,与试验次数无关C.随着试验次数的增加,频率一般会稳定在一个常数附近D.概率是随机的,在试验前不能确定参考答案:C考点:概率的意义;随机事件.专题:概率与统计.分析:利用频率与概率的意义及其关系即可得出.解答:解:随着试验次数的增加,频率一般会稳定在一个常数附近,这个常数就是此试验的事件的概率.因此C正确.故选C.点评:熟练掌握频率与概率的意义及其关系是解题的关键.5. 已知,且等于()A、 B、 C、 D、参考答案:D略6.已知f(x-1)=log a x(a>1),则函数f-1(x)的图象是参考答案:C 解析:令x -1=t ,∴x =t +1. f(t)=log a (t +1),∴f(x)=log a (x +1), 即y =log a (x +1).∴x +1=a y ,即x =a y -1. ∴f -1(x)=a x-1. 观察图象选C.7. 下列各组函数是同一函数的是( )A .与B .与C .与D .与参考答案:D考点:函数及其表示试题解析:因为的定义域为的定义域为R ,故A 错;的定义域为R ,的定义域为故B 错;与不同,故C 错。
四川省眉山市东坡区多悦高级中学校2021学年上学期高二年级12月月考数学试卷
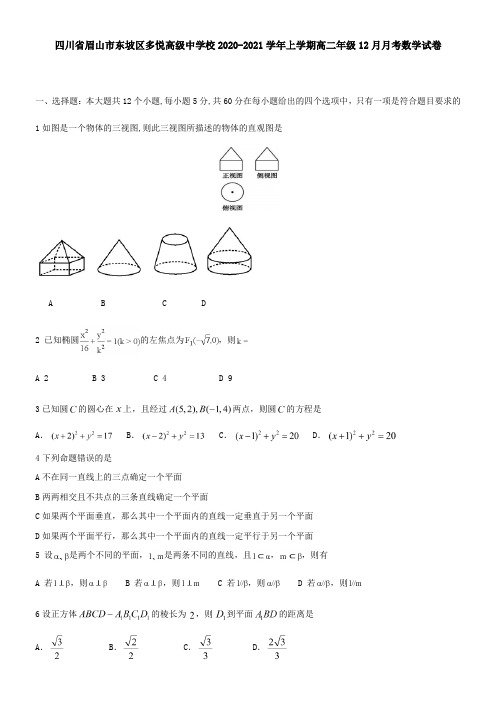
四川省眉山市东坡区多悦高级中学校2020-2021学年上学期高二年级12月月考数学试卷一、选择题:本大题共12个小题,每小题5分,共60分在每小题给出的四个选项中,只有一项是符合题目要求的1如图是一个物体的三视图,则此三视图所描述的物体的直观图是A B C D2 已知椭圆的左焦点为,则A 2B 3C 4D 93已知圆的圆心在上,且经过两点,则圆的方程是A. B. C. D.4下列命题错误的是A不在同一直线上的三点确定一个平面B两两相交且不共点的三条直线确定一个平面C如果两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面D如果两个平面平行,那么其中一个平面内的直线一定平行于另一个平面5 设是两个不同的平面,是两条不同的直线,且,,则有A 若,则B 若,则C 若,则D 若,则6设正方体的棱长为,则到平面的距离是A. B. C. D.7 已知椭圆的两个焦点是,点在椭圆上,若,则的面积是A B C D 8 已知正三棱柱中,各棱长均相等,则与平面所成角的余弦值为A BC D1:y=-14-1;l 2:y=2-2,则“=2”是“l 1⊥l 2”的A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件1,F 2分别是椭圆C :错误!+错误!=1a >b >0的左、右焦点,点20x 1≤0,命题q:∀∈R,2m1>0,若的取值范围是________ 16如图,在梯形中,,,,分别是的中点,将四边形沿直线进行翻折给出四个结论:①;②;③平面平面;④平面平面在翻折过程中,可能成立的结论序号是__________.三、解答题(本大题共6小题,共70分解答应写出文字说明、证明过程或演算步骤)17(10分)已知△ABC 的顶点是A-1,-1,B3,1,C1,6,直线l 平行于AB,且分别交AC,BC 于点E,F,且△CEF 的面积是△ABC 的面积的14倍21,l l 21,k k k 0422=+-m k k 21l l ⊥=m 21//l l =m1求点E,F 的坐标; 2求直线l 的方程18 12分命题与M 的轨迹交于G 、H 两点,当(O 为坐标原点)的面积最大时,求直线m 的方程并求出面积的最大值22(12分)如图,四棱锥中,底面为矩形,平面,为中点(1)证明:平面;(2)设,,三棱锥的体积求AB 与平面2222:1x y C a b+=(0)a b >>342y kx =+C A B AOB ∠O C ||AB 3,0()()22316x y ++=1,1C()GOH ∆GOH∆2-2过点,,∴O 到直线m 的距离为,当直线m 斜率不存在时,O 到m 的距离为1不满足,令故直线m 的方程为: 22(1)见解析;(2)【分析】(1)设与的交点为,连接,通过直线与平面平行的判定定理证明平面;(2)通过,,三棱锥的体积,求出,作交于,说明是到平面的距离,通过解三角形求解即可 (1)证明:设与的交点为,连接因为为矩形,所以为的中点,又为的中点,所以又因为平面,平面,所以平面(2)解:由,可得作交于由题设知,,且,所以平面,又平面,所以,又,做平面1452725272527522y --020x --24a =2a ∴=32c a =3c ∴=2221b ac =-=2214x y +=()11,A x y ()22,B x y 2y kx =+2214x y +=22(41)16120k x kx +++=AOB ∠12120OA OB x x y y =+=1212(2)(2)0x x kx kx +++=24420k +=24k =12216324117k x x k +=-=±+12212124117x x k ==+221211AB kx x k=+-=+21212()4x x x x +-232484565171717⎛⎫=⨯-= ⎪⎝⎭AB 46517()()00,,,A x y M x y 0000323222x x x x y y y y +⎧=⎪=-⎧⎪⇒⎨⎨=⎩⎪=⎪⎩()00,A x y ()22316x y ++=224x y +=GOH θ∠=211sin 22sin 2sin 22GOH S r θ=θθ∆=⋅⨯⨯⨯=sin θ=12GOH π∠=ABC S ∆()1,12GOH π∠=2:1m L x =()21:11,211m k L y k x d k k--=-===-+2y x =-+∵平面,∴,在中,由勾股定理可得,所以,所以到平面的距离为①② 点睛:本题主要考查了立体几何及其运算,对于⑴,运用一条直线平行于平面内一条直线,那么这条直线平行于该平面,即可证得;对于⑵,运用一条直线垂直于面上两条相交直线,那么这条直线垂直于该平面以及三角形面积公式即可求得。
四川省眉山市东坡区眉山中学2020届高三数学12月月考试题 文(无答案)

眉山中学校高三12月数学(文)月考试卷本试卷共3页,分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟,第I 卷(选择题共50分)注意事项:l .答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每题选出答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再改涂其他答案标号.一、选择题(本题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.复数i 2+i 1-2i 等于 ( ). A .i B .-i C .1 D .-12.已知向量)6,(),2,1(x b a ==,且b a //,则x 的值为( )A .1B .2C .3D .43.交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查.假设四个社区驾驶员的总人数为N ,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N 为( ).A .101B .808C .1 212D .2 0124. 设,x R ∈则“12x >”是“2210x x +->”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件5.设3log ,21log ,2log 253===c b a ,则( ) A .b c a >> B .a c b >> C .a b c >> D .b a c >>6.已知集合{}0342≤++=x x x A ,{}02≤-=ax x x B ,若B A ⊆,则实数a 的取值范围是( )A .33≤≤-aB .0≥aC .3-≤aD .R7.已知函数()sin (0,)2y x πωϕωϕ=+><的部分图象如图所示,则A. ω=1 ϕ= 6πB. ω=1 ϕ=- 6π C. ω=2 ϕ= 6π D. ω=2 ϕ= -6π 8. 如图所示的程序框图输出的S 是126,则①应为( )A .n ≤5?B .n ≤6?C .n ≤7?D .n ≤8?9. 设,x y 满足的约束条件3602000x y x y x y --≤⎧⎪-+≥⎪⎨≥⎪⎪≥⎩,若目标函数00(,)z ax by a b =+>>的最大值为12,则23a b+的最小值为( ) A.256 B. 83 C. 113 D.4 10.设定义在R 上连续的偶函数()f x 满足(2)()f x f x +=,'()f x 是()f x 的导函数,当[]0,1x ∈时,0()1f x ≤≤;当(0,2)x ∈且1x ≠时,(1)'()0x x f x -<.则方程()lg f x x = 根的个数为( )A .12B .1 6C .18D .20第Ⅱ卷(非选择题,共100分)注意事项:请用黑色0.5毫米的黑色墨迹签字笔在答题卡上作答,不能答在试卷上。
眉山市东坡区多悦高级中学校高一数学上学期期中试题

四川省眉山市东坡区多悦高级中学校2020—2021学年高一数学上学期期中试题本试卷分选择题和非选择题两部分。
第Ⅰ卷(选择题)1至2页,第Ⅱ卷(非选择题)3至4页,共4页,满分150分,考试时间120分钟。
注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}B=-,则集合A B=( )2,0,2A=-,{}1,0,1A .0B .∅C .{}0D .{}12.设全集U =R ,集合22{|}M y y x x U ∈==+,,集合3{|}N y y x x U ∈==,,则M N等于( ) A .{1,3,2,6} B .{(1,3),(2,6)} C .MD .{3,6}3.如图所示,阴影部分表示的集合是( )A .()ABC UB .()B AC UC .()B A C UD .()B A C U4.设全集U ={x |0〈x <10,x ∈Z },A ,B 是U 的两个真子集,()()}{9,1=B C A C U U,A ∩B ={2},()}{8,6,4=B AC U,则( )A .5A ∈,且B ∉5 B 。
A ∉5,且B ∉5C .5A ∈,且5B ∈D .A ∉5,且5B ∈5.下列各图中,可表示函数y =f (x )的图象的只可能是( )6.函数()132f x x x =+++的定义域是( )A .[)3,-+∞B .[)3,2--C .[)()3,22,---+∞D .()2,-+∞7.数()f x ,()g x 由下列表格给出,则()3f g =⎡⎤⎣⎦( )A .4B .3C .2D .18.已知函数()2,0,0x x f x x x ≥⎧⎪⎨<⎪⎩=,则2[()]f f -的值是( ) A .2 B .2-C .4D .4-9.函数223y x x -=+,12x -≤≤的值域是( )A .RB .[3,6]C .[2,6]D .[2,)+∞10.已知函数f (x )是定义在()()00,∞∞-,+上的奇函数,且当x 〈0时,函数的部分图象如图所示,则不等式xf(x)〈0的解集是()A.()--+∞)(2,(1)(),--B.()2,1122,10,C.(),21,00,12,∞-D.()()()()∞-+∞--)()--,21,01(,211.定义在R上的偶函数f(x)在[0,7]上是增函数,在[7,)+∞上是减函数,f(7)=6,则f(x)( )A.在[]7,0-上是增函数,且最大值是6 B.在[]7,0-上是减函数,且最大值是6C.在[]7,0-上是增函数,且最小值是6 D.在[]7,0-上是减函数,且最小值是612.定义在R上的偶函数f(x)满足:对任意12(,]0,(x1≠x2),∈∞x x-都有2121>0x xf x f x -()-(),则( )A .5()f -<f (4)<f (6)B .f (4)<5()f -<f (6)C .f (6)<5()f -<f (4)D .f (6)〈f (4)<5()f -二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.设P 和Q 是两个集合,定义集合{|}P Q x x P x Q -=∈∉,且,若P ={1,2,3,4},{}R x x x Q ∈<=,4则P Q -=________. 14.函数223y x x =+-的单调递减区间是________.15.若函数()2(12)f x kx k x -=++是偶函数,()x f 则的递减区间是________. 16.设函数()1,0221,02x x x x f x x ⎧-<<⎪=⎨--≤≥⎪⎩或,则函数y =()x f ,y =错误! 的图象交点个数是________.三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(10分)已知集合A ={x |2≤x ≤8},B ={x |1<x <6},C ={x |x >a },U =R .(1)求A ∪B ,()B A C U;(2)若AC ≠∅,求a 的取值范围.18.(12分)设A ={x |x 2+2(a +1)x +a 2-1=0},{|(02)14B x x x x ⎛⎫ ⎪⎝-⎭=+=,x ∈Z}. 若A ∩B =A ,求a 的取值范围.19.(12分)已知函数f (x )=-2x +m ,其中m 为常数. (1)求证:函数f (x )在R 上是减函数;(2)当函数f (x )是奇函数时,求实数m 的值.20.(12分)已知函数f (x )是正比例函数,函数g (x )是反比例函数,且f (1)=1,g (1)=2, (1)求函数f (x )和g (x );(2)判断函数f (x )+g (x )的奇偶性.21。
四川省眉山市东坡区多悦高级中学校2021学年高一数学上学期期中试题.doc

四川省眉山市东坡区多悦高级中学校2020-2021学年高一数学上学期期中试题本试卷分选择题和非选择题两部分。
第Ⅰ卷(选择题)1至2页,第Ⅱ卷 (非选择题)3至4页,共4页,满分150分,考试时间120分钟。
注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}1,0,1A =-,{}2,0,2B =-,则集合AB =( )A .0B .∅C .{}0D .{}12.设全集U =R ,集合22{|}M y y x x U ∈==+,,集合3{|}N y y x x U ∈==,,则M N 等于( )A .{1,3,2,6}B .{(1,3),(2,6)}C .MD .{3,6}3.如图所示,阴影部分表示的集合是( ) A .()A B C U B .()BA C UC .()B A C UD .()B A C U姓名 准考证号 考场号 座位号4.设全集U ={x |0<x <10,x ∈Z },A ,B 是U 的两个真子集,()()}{9,1=B C A C U U , A ∩B ={2},()}{8,6,4=B A C U ,则( )A .5A ∈,且B ∉5 B. A ∉5,且B ∉5C .5A ∈,且5B ∈D .A ∉5,且5B ∈5.下列各图中,可表示函数y =f (x )的图象的只可能是( )6.函数()132f x x x =+++的定义域是( ) A .[)3,-+∞ B .[)3,2--C .[)()3,22,---+∞D .()2,-+∞7.数()f x ,()g x 由下列表格给出,则()3f g =⎡⎤⎣⎦( )A .4B .3C .2D .18.已知函数()2,0,0x x f x x x ≥⎧⎪⎨<⎪⎩=,则2[()]f f -的值是( )A .2B .2-C .4D .4-9.函数223y x x -=+,12x -≤≤的值域是( ) A .RB .[3,6]C .[2,6]D .[2,)+∞10.已知函数f (x )是定义在()()00,∞∞-,+上的奇函数,且当x <0时,函数的部分图象 如图所示,则不等式xf (x )<0的解集是( )A .()2,112(),--B .()2,10,)(2,(1)--+∞C .()(),21,01(,2)--∞- D .(),21,00,12,()()()∞-+∞--11.定义在R 上的偶函数f (x )在[0,7]上是增函数,在[7,)+∞上是减函数,f (7)=6,则f (x )( ) A .在[]7,0-上是增函数,且最大值是6 B .在[]7,0-上是减函数,且最大值是6 C .在[]7,0-上是增函数,且最小值是6 D .在[]7,0-上是减函数,且最小值是612.定义在R 上的偶函数f (x )满足:对任意12(,]0x x -∈∞, (x 1≠x 2),都有2121>0x x f x f x -()-(),则( )A .5()f -<f (4)<f (6)B .f (4)<5()f -<f (6)C .f (6)<5()f -<f (4)D .f (6)<f (4)<5()f -二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.设P 和Q 是两个集合,定义集合{|}P Q x x P x Q -=∈∉,且,若P ={1,2,3,4},{}R x x x Q ∈<=,4则P Q -=________.14.函数223y x x =+-的单调递减区间是________. 15.若函数()2(12)f x kx k x -=++是偶函数,()x f 则的递减区间是________.16.设函数()1,0221,02x x x x f x x ⎧-<<⎪=⎨--≤≥⎪⎩或,则函数y =()x f ,y =12 的图象交点个数是________.三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(10分)已知集合A ={x |2≤x ≤8},B ={x |1<x <6},C ={x |x >a },U =R . (1)求A ∪B ,()B A C U ;(2)若A C ≠∅,求a 的取值范围.18.(12分)设A ={x |x 2+2(a +1)x +a 2-1=0},{|(02)14B x x x x ⎛⎫ ⎪⎝-⎭=+=,x ∈Z}.若A ∩B =A ,求a 的取值范围.19.(12分)已知函数f (x )=-2x +m ,其中m 为常数. (1)求证:函数f (x )在R 上是减函数; (2)当函数f (x )是奇函数时,求实数m 的值.20.(12分)已知函数f (x )是正比例函数,函数g (x )是反比例函数,且f (1)=1,g (1)=2, (1)求函数f (x )和g (x );(2)判断函数f (x )+g (x )的奇偶性.21.(12分)经过市场调查,超市中的某种小商品在过去的近40天的日销售量(单位:件)与价格(单位:元)为时间t (单位:天)的函数,且日销售量近似满足()1002g t t=-,价格近似满足()4020f t t =--.(1)写出该商品的日销售额y (单位:元)与时间t (040t ≤≤)的函数解析式并用分段函数形式表示该解析式(日销售额=销售量⨯商品价格); (2)求该种商品的日销售额y 的最大值和最小值.22.(12分)函数f (x )=21ax bx++是定义在()1,1-上的奇函数,且1225f ⎛⎫= ⎪⎝⎭. (1)求f (x )的解析式;(2)证明f (x )在()1,1-上为增函数; (3)解不等式f (t -1)+f (t )<0.多悦高中2023届第一期半期考试数 学 答 案一、选择题 1.【答案】C【解析】因为集合{}1,0,1A =-,{}2,0,2B =-,所以{}0A B =,故选C .2.【答案】C【解析】,[)2M ∞=+,N =R ..故选C . 3.【答案】A【解析】因为阴影部分既在集合UB 中又在集合A 中,所以阴影部分为()UB A ,故选A .4.【答案】A【解析】可借助Venn 图(如图2)解决,数形结合.故选A .图25.【答案】A【解析】根据函数的概念知,只有“一对一”或“多对一”对应才能构成函数关系. 故选A . 6.【答案】C【解析】由题可得:30320x x x ⎧⎨≥≠⎩+⇒≥-+且2x ≠-,故选C . 7.【答案】A【解析】由表可知()32g =,()()324f g f ==⎡⎤⎣⎦,故选A . 8.【答案】C【解析】∵2x =-,而20-<,∴2()(224)f --==. 又4>0,∴()[()244]f f f -==.故选C . 9.【答案】C【解析】画出函数223y x x -=+,12x -≤≤的图象,如图3所示,观察函数的图象可得图象上所有点的纵坐标的取值范围是[2,6],所以值域是[2,6].故选C . 10.【答案】D【解析】xf (x )<0⇔x 与f (x )异号,由函数图象及奇偶性易得结论.故选D . 11.【答案】B【解析】∵f (x )是偶函数,∴f (x )的图象关于y 轴对称. ∴f (x )在[]7,0-上是减函数,且最大值为6.故选B . 12.【答案】C【解析】∵对任意12(,]0x x -∈∞,(x 1≠x 2),都有2121>0x x f x f x -()-(),∴对任意12(,]0x x -∈∞,,若x 1<x 2,总有f (x 1)<f (x 2), ∴f (x )在(]0-∞,上是增函数.∴()()()456f f f --->>. 又∵函数f (x )是偶函数,∴()()66f f -=,()()44f f -=, ∴f (6)<5()f -<f (4).故选C .二、填空题 13.【答案】{4}【解析】因为x Q ∉,所以x Q ∈R ,故}{R x x x Q C R ∈≥=,4,故P Q -={4}.14.【答案】(],3-∞-【解析】由2230x x +-≥,得x ≥1或3x ≤-, ∴函数减区间为(],3-∞-. 15.【答案】(]0-∞,【解析】∵f (x )是偶函数,∴()2212()(12)()f x kx k x kx k x f x -+=-+-==-+. ∴1k =.∴f (x )=x 2+2,其递减区间为(]0-∞,. 16.【答案】4【解析】函数y =f (x )的图象如图5所示, 则函数y =f (x )与y =12的图象的交点个数是4.图5三、解答题17.【答案】(1){}|18AB x x =<≤,()UA B ={x |1<x <2};(2)a <8.【解析】(1)A ∪B ={x |2≤x ≤8}∪{x |1<x <6}={x |1<x ≤8}. U A ={x |x <2或x >8}.∴()UA B ={x |1<x <2}.(2)∵A C ≠∅,∴a <8. 18.【答案】1,{}1|a a a ≤-或=.【解析】由{|(02)14B x x x x ⎛⎫ ⎪⎝-⎭=+=,x ∈Z},得,0{}4B =-.由A ∩B =A ,得A ⊆B .于是,A 有四种可能, 即A ∅=,4{-}A =,A ={0},,{}40A -=. 以下对A 分类讨论:(1)若A ∅=,则Δ=4(a +1)2-4a 2+4=8a +8<0,解得a <-1; (2)若4{-}A =,则Δ=8a +8=0,解得a =-1. 此时x 2+2(a +1)x +a 2-1=0可化为x 2=0, 所以x =0,这与x =-4是矛盾的; (3)若A ={0},则由(2)可知,a =-1;(4)若A ={-4,0},则()288021410a a a ∆⎧=+>⎪-+=-⎨⎪-=⎩,解得a =1.综上可知,a 的取值范围1,{}1|a a a ≤-或=. 19.【答案】(1)见解析;(2)0.【解析】(1)证明:设x 1,x 2是R 上的任意两个实数,且x 1<x 2, 则f (x 1)-f (x 2)=(-2x 1+m )-2()2x m -+=2(x 2-x 1), ∵x 1<x 2,∴x 2-x 1>0.∴f (x 1)>f (x 2)∴函数f (x )在R 上是减函数.(2)∵函数f (x )是奇函数,∴对任意x ∈R ,有f (-x )=-f (x ).∴2x +m =-(-2x +m ).∴m =0.20.【答案】(1)f (x )=x ,g (x )=2x;(2)奇函数. 【解析】(1)设()1f x k x =,g (x )=2k x,其中k 1k 2≠0. ∵f (1)=1,g (1)=2,∴111k ⨯=,221k =. ∴k 1=1,k 2=2.∴f (x )=x ,g (x )=2x. (2)设h (x )=f (x )+g (x ),则()2h x x x +=, ∴函数h (x )的定义域是()()0,,0∞-∞+. ∵h (-x )=-x +2x -=-2x x ⎛⎫+ ⎪⎝⎭=-h (x ), ∴函数h (x )是奇函数,即函数f (x )+g (x )是奇函数.21.【答案】(1)由题意知()()()()•10024020y g t f t t t ==--- ()()()()100220,020100260,2040t t t y t t t ⎧-+≤<⎪∴=⎨--≤≤⎪⎩. (2)当2040t ≤≤时,()()100260y t t =--在区间[]20,40上单调递减,故[]400,2400y ∈;当020t ≤<时,()()100220y t t =-+在区间[)0,15上单调递增,在区间[)15,20上单调递减,故[]2000,2450y ∈∴当40t =时,y 取最小值400,当15t =时,y 取最大值2450.22.【答案】(1)f (x )=21xx +;(2)见解析;(3)1t|0<t<2⎧⎫⎨⎬⎩⎭. 【解析】(1)由题意得001225f f ()=⎧⎪⎨⎛⎫= ⎪⎪⎝⎭⎩,解得10a b =⎧⎨=⎩,所以f (x )=21x x+. (2)证明:任取两数x 1,x 2,且-1<x 1<x 2<1, 则12121212222212121()()=1111x x x x x x f x f x x x x x (-)(-)--=++(+)(+). 因为-1<x 1<x 2<1,所以x 1-x 2<0,x 1x 2<1,故1-x 1x 2>0, 所以f (x 1)-f (x 2)<0,故f (x )在()1,1-上是增函数.(3)因为f (x )是奇函数,所以由f (t -1)+f (t )<0,得f (t -1)<-f (t )=f (-t ). 由(2)知,f (x )在()1,1-上是增函数, 所以-1<t -1<-t <1,解得0<t <12, 所以原不等式的解集为1t|0<t<2⎧⎫⎨⎬⎩⎭.。
四川省眉山市东坡区多悦高级中学校2020-2021学年高二12月月考数学试题

多悦高中2022届高二上12月月考一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图是一个物体的三视图,则此三视图所描述的物体的直观图是(D)2. 已知椭圆的左焦点为,则()A. 2B. 3C. 4D. 9B【解析】椭圆的左焦点为,故选3.已知圆的圆心在上,且经过两点,则圆的方程是()A. B. C. D.C4.下列命题错误的是()A.不在同一直线上的三点确定一个平面B.两两相交且不共点的三条直线确定一个平面C.如果两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面D.如果两个平面平行,那么其中一个平面内的直线一定平行于另一个平面解析:选择C,如果两个平面垂直,那么其中一个平面内的直线不一定垂直于另一个平面,可能相交或平行于另一个平面,故命题错误.试题立意:本小题考查空间直线和平面的位置关系,直线与平面垂直的判定与性质定理等基础知识;意在考查学生空间想象能力.5. 设是两个不同的平面,是两条不同的直线,且,,则有()A. 若,则B. 若,则C. 若,则D. 若,则A6.设正方体的棱长为,则到平面的距离是()A. B. C. D.D【解析】试题分析:,若,则.该命题是两个平面垂直的判定定理,显然成立.故选A.两个平面垂直,一个平面内的直线不一定垂直另一个平面,故答案B错误.依次判断答案C、D也是错误的.7. 已知椭圆的两个焦点是,点在椭圆上,若,则的面积是()A. B. C. D.D【解析】,,可得,,是直角三角形,的面积,故选D.8. 已知正三棱柱中,各棱长均相等,则与平面所成角的余弦值为()A. B. C. D.C【解析】取的中点,连接,底面,是正三角形,平面,是与平面所成角,设棱长为,则在中,,,故选C.9.已知直线l1:y=-14x-1;l2:y=k2x-2,则“k=2”是“l1⊥l2”的(A)(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件10.设F1,F2分别是椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点,点P在椭圆C上,若线段PF1的中点在y轴上,∠PF1F2=30°,则椭圆的离心率为(A)A.33 B.36 C.13D.1 611.如图所示是一个几何体的三视图,则这个几何体外接球的表面积为( C )A.8πB.16πC.32πD.64π解析:由三视图可知,几何体为一横放的四棱锥,其底面是边长为4的正方形,高为2,平面SAB⊥平面ABCD,易知SA=SB=2 2.如图所示.故可补全为以DA、SA、SB为棱的长方体,故2R=DA2+SA2+SB2=32=42,∴R=22,∴S表=4πR2=32π.12. 椭圆的左、右顶点分别为,点在上且直线斜率的取值范围是,那么直线斜率的取值范围是()A. B. C. D.C【解析】由椭圆的方程可得,由椭圆的性质可知:,则故选点睛:本题主要考查的知识点是椭圆的简单性质以及直线的斜率问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一(上)数学月考试题2020.12一.选择题1、设集合,则( )A .B .C .D . 2、函数的定义域是( ) A . B . C . D .3、已知集合,,则( ) A . B . C . D .4、已知,,则函数的图象不经过( )A .第一象限B .第二象限C .第三象限D .第四象限5、函数(且)的图象恒过定点( ) A . B .C .D . 6、已知函数,在下列区间中,包含零点的区间是( ) A . B .C .D . 7、函数的定义域为( ) A B ={}123,4,,{}123,,{}234,,{}134,,()13f x x =-[)2,+∞()3,+∞[)()2,33,+∞()()2,33,+∞{|ln 1}A x x =<{|12}B x x =-<<AB =(0,)e (1,2)-(1,)e -(0,2)01a <<10b -<<x y a b =+()12x f x a-=+0a >1a ≠()0,3()1,3()1,2-()1,3-()26log f x x x=-()f x 0,11,2()2,4()4,+∞y =A .(,1)B .(,∞)C .(1,+∞)D .(,1)∪(1,+∞) 8、已知a =log 0.53,b =30.5,c =0.50.5,则( )A .a <b <cB .b <a <cC .a <c <bD .c <a <b9、方程的实数解的个数是( )A .0个B .1个C .2个D .3个10、函数的单调递减区间是( ) A . B . C . D .11、已知函数则f(1+log 23)=( ) A . B . C . D . 12、已知函数是定义域为的奇函数,当时,.函数,若存在3个零点,则的取值范围是( )A .B .C .D .二. 填空题13、函数是幂函数且为偶函数,则m 的值为_________.34343423x x =-()212()log 23f x x x =--(,)-∞+∞(,1)-∞(3,)+∞(1,)+∞1,3()2(1),3xx f x f x x ⎧⎛⎫≥⎪ ⎪=⎨⎝⎭⎪+<⎩,,1241121838()f x R0x >()2,01ln ,1x x x f x x x ⎧-+<<=⎨-≥⎩()()g x f x a =-()g x a 11,44⎛⎫- ⎪⎝⎭11,22⎡⎤-⎢⎥⎣⎦11,22⎛⎫- ⎪⎝⎭11,44⎡⎤-⎢⎥⎣⎦()22211m m y m m x --=--14、计算 . 15、已知,则______. 16、函数的图象与直线有两个不同的交点,则的取值范围为______.三.解答题17、已知集合,集合.(1)若,求a 的取值范围;(2)若全集,且,求a 的取值范围.70.5log 29lg 25lg 474⎛⎫+++= ⎪⎝⎭2336m n ==11m n +=()|21|x f x =-y m =m {|42}A x x =-≤≤-{|0}B x x a =-≥A B ⊆U =R C U A B ⊆18、已知函数是定义在R 上的奇函数. (1)求的解析式及值域;(2)判断在R 上的单调性,并用单调性定义.....予以证明.19、已知函数(,).(1)求的定义域;(2)判断的奇偶性并予以证明.20、设函数,且,若的图象过点.(1)求的值及的零点. (2)求不等式的解集.()212xa f x =-+()f x ()f x ()log (1)log (1)a a f x x x =+--0a >1a ≠()f x ()f x21、已知函数,且,.(1)求a ,b 的值;(2)求在上的值域. ()2ln x f x a b x =⋅+()12f =()24ln 2f =+()f x 1,42⎡⎤⎢⎥⎣⎦22、已知函数.(1)求函数的定义域;(2)设,若函数在上有且仅有一个零点,求实数的取值范围;(3)设,是否存在正实数,使得函数在内的最大值为4?若存在,求出的值;若不存在,请说明理由.2()log (31)x f x =-()f x ()()g x f x a =+()g x (1,2)a ()()()m h x f x f x =+m ()y h x =[1,2]m参考答案1、【答案】A2、【答案】C3、【答案】D4、【答案】C5、【答案】B6、【答案】C7、【答案】A8、【答案】C9、【答案】B10、【答案】C11、【答案】B12、【答案】A13、【答案】 14、【答案】 15、【答案】16、【答案】(0,1)17、【答案】(1)(2)试题分析:(1)结合数轴得到满足条件的不等式,即得;(2),那么,结合数轴得到满足条件的不等式,即得.1-11212{|4}a a ≤-{|2}a a {|}B x x a =≥C {|}U B x x a =<详解:解:,.(1)由,结合数轴(如图所示),可知,因此a 的取值范围为.(2)∵,∴,要使,结合数轴(如图所示),可知故a 的取值范围为.【点睛】 本题考查集合的子集和补集,结合数轴来求出变量取值范围.18、【答案】(1),(2)在R 上是增函数.见解析 试题分析:(1)由是定义在R 上的奇函数,则有,即可解得,即可得出的解析式,由,可知,即,进而可求出值域;(2)设,,再利用作差法判断的大小关系即可得证.详解:由题知,,即:, ∴,∴. 此时, {|42}A x x =-≤≤-{|}B x x a =≥A B⊆4a ≤-{|4}a a ≤-U =R C {|}U B x x a =<C U A B⊆2a >-{|2}a a4()212xf x =-+()(2,2)f x ∈-()f x ()212x a f x =-+(0)0f =4a =()f x 2(0,)x ∈+∞12(1,)x +∈+∞4(0,4)12x ∈+()f x 12,x x R ∀∈12x x <()()21,f x f x (0)0f =2012a a -=+4a =4()212x f x =-+4422222224()222()1221212121x x x x x x x x f x f x -⋅-⋅⋅-⎛⎫-=-=-==-=--=- ⎪+++++⎝⎭∴为奇函数.∵∴∴∴ (2)在R 上是增函数.证明:设,, 则, ∵,∴,, ∴,∴函数在R 上是增函数.【点睛】本题考查函数奇偶性,求函数解析式,求函数的值域,利用定义法证明函数的单调性等问题,难度一般.19、【答案】(1)(2)为奇函数,证明见解析试题分析:(1)使函数各部分都有意义的自变量的范围,即列出不等式组,,解此不等式组求出范围就是函数的定义域;(2)根据函数奇偶性的定义进行证明即可.试题解析:(1)要使函数(,)有意义,则解得,故函数的定义域为.(2)为奇函数,()f x 2(0,)x ∈+∞12(1,)x +∈+∞4(0,4)12x ∈+()(2,2)f x ∈-()f x 12,x x R ∀∈12x x <()()()()()211212214224412121212x x x x x x f x f x --=-=++++12x x <21220x x ->()()1212120x x ++>()()210f x f x ->()f x {}|11x x -<<()f x 10,{10,x x +>->x ()log (1)log (1)a a f x x x =+--0a >1a ≠10,{10,x x +>->11x -<<{}|11x x -<<()f x,故为奇函数.考点:函数的定义域;函数奇偶性的判断及证明20、【答案】(1);.(2).试题分析:分析:(1)直接把点代入函数解析式即可求出a 的值;从而求得函数的准确解析式,令,即可求出零点.(2)关于不等式,可化为,由此求出不等式的解集.解析:(1)∵经过点, 即, 又∵, ∴, ∴时,解得,零点为.(2)∵即,∴, ()log (1)log (1)a a f x x x -=-+-+[]log (1)log (1)()a a x x f x =-+--=-()f x∴, ∴,∴不等式解集为. 点睛:本题考查函数解析式的求法,零点的求法,指数不等式的解法,考查转化思想以及计算能力,函数与方程思想的运用.21、【答案】(1);(2);(3)存在,.试题分析:(1)根据对数函数的定义域列不等式求解即可.(2)由函数的单调性和零点存在定理,列不等式求解即可.(3)由对勾函数的性质可得函数的单调区间,利用分类讨论的思想讨论定义域与单调区间的关系,再利用函数的最值存在性问题求出实数的值.详解:(1)由题意,函数有意义,则满足,解得, 即函数的定义域为.(2)由,且,可得,且为单调递增连续函数,又函数在上有且仅有一个零点,所以,即,解得,所以实数的取值范围是.(3)由,设, {|0}x x >(3,1)--3m 2()log (31)x f x =-310x ->0x >()f x {|0}x x >()()g x f x a =+2()log (31)x f x =-2log (31)(),(1,2)x g x a x -=+∈()g x ()g x (1,2)()()120g g ⋅<(1)(3)0a a +⋅+<31a -<<-a (3,1)--()()()m h x f x f x =+(),[1,2]t f x x =∈则, 易证在为单调减函数,在为单调增函数,时,函数在上为增函数,所以最大值为, 解得,不符合题意,舍去;时,函数在上为减函数,所以最大值为, 解得,不符合题意,舍去; 当时,函数在上减函数,在上为增函数,所以最大值为或,解得,符合题意,综上可得,存在使得函数的最大值为4.【点睛】本题考查了对数函数的定义域问题、零点存在定理、对勾函数的应用,考查了理解辨析的能力、数学运算能力、分类讨论思想和转化的数学思想,属于一般题目.22、【答案】(1);(2) 试题分析:(1)由,.代入得到方程组,解得.(2)由(1)知,根据函数的单调性即可得解. 【详解】(),[1,3],0m h t t t m t=+∈>()h t ()+∞1≤()h t [1,3](3)343m h =+=3m =3≥()h t [1,3](1)141m h =+=3m =13<<()h t (1)4h =()34h =3m =3m =()y h x =11a b =⎧⎨=⎩ln 2,162ln 2⎤+⎦()12f =()24ln 2f =+()2ln xf x x =+解:(1)因为,,所以解得 (2)由(1)知.因为,都是上的增函数, 所以在上也是增函数, 又,, 所以在上的值域为. 【点睛】本题考查待定系数法求函数解析式,指数、对数函数的单调性的应用,属于基础题.()12f =()24ln 2f =+22,4ln 24ln 2,a a b =⎧⎨+⋅=+⎩1,1.a b =⎧⎨=⎩()2ln xf x x =+2x y =ln y x =()0,∞+()2ln x f x x =+1,42⎡⎤⎢⎥⎣⎦1ln 22f ⎛⎫= ⎪⎝⎭()4162ln 2f =+()f x 1,42⎡⎤⎢⎥⎣⎦ln 2,162ln 2⎤+⎦。
