高一三角同步练习6(化简与证明)
学年高中数学第章三角恒等变换...求值化简与证明课后课时精练新人教A版必修

3.1.2.2 求值、化简与证明A 级:根底稳固练一、选择题1.假设sin α+cos αsin α-cos α=12,那么tan ⎝ ⎛⎭⎪⎫α+π4=( ) A .-2 B .2 C .-12D .12答案 C解析 因为sin α+cos αsin α-cos α=12,所以tan α+1tan α-1=12,因为tan α+1tan α-1=tan α+tanπ4tan αtan π4-1=-tan ⎝⎛⎭⎪⎫α+π4=12,所以tan ⎝⎛⎭⎪⎫α+π4=-12. 2.函数y =sin ⎝ ⎛⎭⎪⎫2x +π4+sin ⎝ ⎛⎭⎪⎫2x -π4的最小值为( )A . 2B .-2C .- 2D . 3 答案 C解析 因为y =sin ⎝ ⎛⎭⎪⎫2x +π4+sin ⎝ ⎛⎭⎪⎫2x -π4=sin2x cos π4+cos2x sin π4+sin2x cos π4-cos2x sin π4=2sin2x ,所以所求函数的最小值为- 2.3.向量a =(cos75°,sin75°),b =(cos15°,sin15°),那么|a -b |的值为( ) A .12 B .22 C .32D .1答案 D解析 因为|a -b |2=a 2-2a ·b +b 2=2-2(cos75°cos15°+sin75°sin15°)=2-2cos(75°-15°)=2-2cos60°=1.所以|a -b |=1.4.sin(65°-x )cos(x -20°)+cos(65°-x )cos(110°-x )的值为( )A . 2B .22 C .12 D .32答案 B解析 原式=sin(65°-x )cos(x -20°)-cos(65°-x )·sin(20°-x )=sin(65°-x )·cos(x -20°)+cos(65°-x )·sin(x -20°)=sin[(65°-x )+(x -20°)]=sin45°=22. 5.tan α和tan ⎝ ⎛⎭⎪⎫π4-α是方程ax 2+bx +c =0的两个根,那么a ,b ,c 的关系是( )A .b =a +cB .2b =a +cC .c =b +aD .c =ab答案 C解析 由韦达定理可知tan α+tan ⎝ ⎛⎭⎪⎫π4-α=-b a 且tan αtan ⎝ ⎛⎭⎪⎫π4-α=ca ,∴tan π4=tan ⎣⎢⎡⎦⎥⎤α+⎝ ⎛⎭⎪⎫π4-α=-ba 1-c a=1.∴-b a =1-c a .∴-b =a -C .∴c =a +B .应选C . 二、填空题6.计算1-tan 5π12·ta nπ4tan 5π12+tanπ4的值等于________.答案 -33解析 原式=1tan ⎝ ⎛⎭⎪⎫5π12+π4=1tan 2π3=-33.7.13sin α+5cos β=9,13cos α+5sin β=15,那么sin(α+β)=________. 答案5665解析 将条件平方并两式相加,得169+25+130(sin αcos β+cos αsin β)=81+225,∴sin(α+β)=112130=5665.8.tan ⎝ ⎛⎭⎪⎫α-β2=12,tan ⎝⎛⎭⎪⎫β-α2=-13,那么tan α+β2的值等于________.。
沪教版(上海) 高一第二学期 新高考辅导与训练 第6章 三角函数 6.11 最简三角方程(2)

沪教版(上海) 高一第二学期新高考辅导与训练第6章三角函数
6.11 最简三角方程(2)
一、解答题
(★★) 1. 解下列三角方程:
(1);
(2);
(3).
(★★) 2. 已知关于 x的方程在区间内有两个相异的实数根,求实
数 k的取值范围及两根之和.
(★★) 3. 根据条件,求下列方程的解集:
(1);
(2).
(★★★) 4. 已知关于 x的方程.
(1)当时,求方程的解;
(2)要使此方程有解,试确定 m的取值范围.
(★★) 5. 已知函数在一个周期内的图像如图所示,求直线与函数图像的交点坐标.
(★★★) 6. 方程在上有两个不间的实数根,求实数 a的取值范围及两实数根之和.
二、填空题
(★) 7. 方程的解集为___________.
(★) 8. 方程的解集为____________.
(★★) 9. 方程的解集为________.
(★) 10. 方程的解集为__________.
(★★) 11. 方程的解集为 _________ .
(★★) 12. 方程的解集为___________.
(★) 13. 函数,的图象与直线y=k有且仅有两个不同的交点,则k 的取值范围是_____.
三、单选题
(★★) 14. 方程的解集是()
A.B.
C.D.
(★★) 15. 设方程的解集为 M,方程的解集为 N,则().A.B.C.D.以上都不对(★★) 16. 方程的解集是().
A.B.
C.D.。
(完整版)三角函数化简求值证明技巧
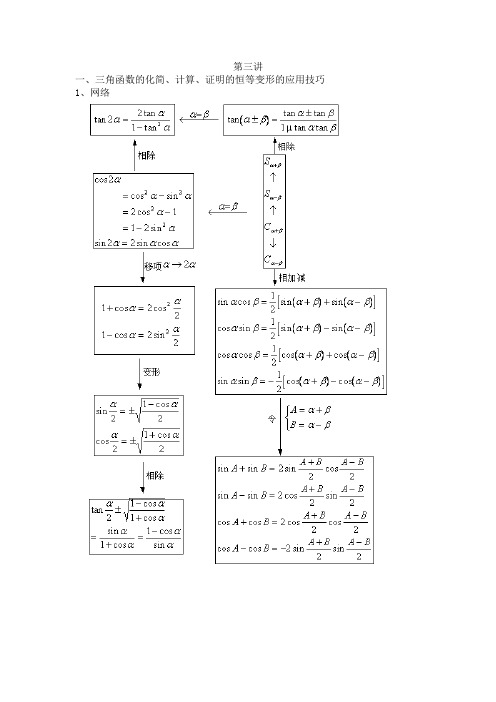
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结(1)变换函数名对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。
练习:已知sin(α+β)=,cos(α-β)=,求的值。
2)变换角的形式对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。
练习已知,求的值【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=提示:sin[(α+β)-β]=Asin (α+β)(3)以式代值利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
【例4】化简:(4)和积互化积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。
高一数学 三角函数 三角恒等变化 解三角形 专题练习及答案精析版(76页)

高一数学 三角函数 三角恒等变化 解三角形 专题练习1.在ABC ∆中,内角,,A B C 对边的边长分别是,,a b c ,若()()(),a c a c b b +-=+则cos A = A.2-B.2 C .12D.3- 2.函数ππln cos 22y x x ⎛⎫=-<< ⎪⎝⎭的图象是( )3.已知角α的终边上一点的坐标为(12,则角α的正弦值为( )A.-2B.2 C .-12 D.124.在ABC ∆中,若20sin A sin BcosC -=,则ABC ∆必定是 ( )A 、钝角三角形B 、等腰三角形C 、直角三角形D 、锐角三角形 5.把函数sin(2)6y x π=+的图象向右平移6π个单位长度得到函数 A .sin 2y x =B .sin(2)6y x π=-C .sin(2)3y x π=+ D .cos 2y x = 6.= 2010sin ( )A.21 B.21- C. 23- D.2377..已知m =αtan 化简αα22sin 2cos 1+得结果为:( )A. 22211m m ++ B.m m 211++C.m 211+ D. 211m+ 8. 将分针拨快10分钟,则分针转过的弧度数是( )xxA .B .C .D .A .3π B .3π- C .6π D .6π- 9.在ABC ∆中,若sinA ︰sinB ︰sinC=1:2:3,则::a b c 等于( )A.1:2:3B.3:2:1C.2D.2 10.要得到一个偶函数,只需将函数)3sin()(π-=x x f 的图象A.向左平移3π个单位 B.向右平移3π个单位 C.向左平移6π个单位 D.向右平移6π个单位 11.设0)3cos )(sin sin cos 2(=++-x x x x ,则xxx tan 12sin cos 22++的值为( )A .52 B .85 C .58 D .25 12.函数1sin 6cos 22++=x x y 的最大值为( ) A . 10 B .9 C .8 D . 713.半径为5cm ,面积为252cm 的扇形中,弧所对的圆心角为 A . ︒2 B.π2弧度 C .2弧度 D .4弧度 14.化简sin()2απ+等于( ). A.cos α B.sin α C.cos α- D.sin α-15.函数y =sin(ωx +ϕ)(x ∈R,ω>0,0≤ϕ<2π)的部分图象如右图,则 ( ) A.ω=π2,ϕ=π4 B.ω=π3,ϕ=π6C.ω=π4,ϕ=π4D.ω=π4,ϕ=π5416.为了得到函数sin(2)6y x π=-的图像,可以将函数cos 2y x =的图像A 、向右平移6π个单位 B 、 向左平移3π个单位 C 、向左平移6π个单位 D 、向右平移3π个单位17.在ABC ∆中,120A =︒5AB =,7BC =,则sin sin BC的值为 A .85 B .58 C .53 D .3518. △ABC 中,若030C =,8a =,b =S ABC 等于( )A.19.已知tan x =x 的集合为( )A .4{|2,}3x x k k Z ππ=+∈B .{|2,}3x x k k Z ππ=+∈C .4,33ππ⎧⎫⎨⎬⎩⎭D .{|,}3x x k k Z ππ=+∈20.已知α为锐角,2cos sin m=αα,则ααcos sin +的值是 ( ) A .1-m B .1+m C .1-±m D .1+±m21.若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比值为m,则m 的范围是( )A.(1,2)B.(2,+∞)C.[3,+∞)D.(3,+∞) 22.求0sin 600的值是 ( )A 、12 B、D 、12-23.下列关系式中正确的是( )A .sin11cos10sin168︒<︒<︒B .sin168sin11cos10︒<︒<︒C .sin11sin168cos10︒<︒<︒D .sin168cos10sin11︒<︒<︒ 24.若2π-≤x ≤2π,则()cos f x x x =+的取值范围是 ( ) A .[1,2]- B .[1,1]- C.[2] D.[ 25.已知x x x tan 1tan 14tan -+=⎪⎭⎫⎝⎛+π⎪⎭⎫⎝⎛+≠4ππk x ,那么函数x y tan =的周期为π。
6-三角函数的化简与求值(练习)

值为1,求常数a的值.
【解析】f(x)=sin(x+ )+sin(x- )+cos x+a
6 6
= 3 sin x+cos x+a=2sin(x+ )+a.
6
由a+2=1,得a=-1.
1.三角函数的求值类型有三类 (1)给角求值:一般所给出的角都是非特殊角,要观察所给角 与特殊角之间的关系,利用三角变换消去非特殊角,转化为求 特殊角的三角函数值问题;
3 6 3 3
(2)化简
2 2 tan α tan 2α + 3 (sin α-cos α). tan 2α tan α
【分析】此三角函数式出现两类函数,利用两角和与差公式 统一函数成为化简的主要目标. 【解析】(1)sin(3x+ )cos(x- )+cos(3x+ )cos(x+ )
3 6 3 3
4 2 4
3
由sin(β- )= ,知cos(β- )=- , 4 13 4 13
cos(α+ )=cos [(α+β)-(β- )]
4 4
12
5
=cos(α+β)cos(β- )+sin(α+β)sin(β- )
4 4
= ×(- )+(- )× =- .
4 5
5 13
3 5
(2)给值求值:给出某些角的三角函数式的值,求另外一些角
的三角函数值,解题的关键在于“变角”,如α=(α+β)-β,2α=(α +β)+(α-β)等,把所求角用含已知角的式子表示,求解时要注意
《高考风向标》高考数学一轮复习 第六章 第6讲 三角函数的求值、化简与证明课件 理

【互动探究】 3.求证:sin(2α+β)-2cos(α+β)sinα=sinβ. 证明:sin(2α+β)-2cos(α+β)sinα =sin[(α+β)+α]-2cos(α+β)sinα =sin(α+β)cosα+cos(α+β)sinα-2cos(α+β)sinα =sin(α+β)cosα-cos(α+β)sinα=sin[(α+β)-α]=sinβ. 故等式成立.
sin70°1-
3sin50°
cos50°
=sin70°cos50°c-os503°sin50°=221cos50°-co2s35s0i°n50°sin70° =2sin30°cos50°-cocso5s03°0°sin50°sin70°=-2sicno2s05°0s°in70° =-2sicno2s05°0c°os20°=-cossin5400°°=-cocso5s05°0°=-1.
=cos22x-xsin22xsin2x=
cosx·sin2x x
=tan2x.
cos2·cosx
cos2·cosx
使用升次公式的一个技巧为 1+sin2α+cos2α= (1+cos2α)+sin2α=2cos2α+2sinαcosα=2cosα(cosα+sinα).
【互动探究】
2.若 tanx= 2,求2cossi2n2xx-+scionsxx-1的值.
解题思路:首先要使角要统一,所以分母使用二倍角公式. 解析:原式=sinx+1-2sin22x-s1in2sxinx-1+2sin22x+1 =2sin2xcos2x-2sinx22x2xsin2xcos2x+2sin22x
2021上海沪教新版高一数学下学期同步练习6.3.1正弦定理详解版(01)

6.3.1正弦定理(作业)一、单选题1.(2020·上海高一课时练习)在ABC 中,2a =,1c =,则C 的取值范围是( ).A .0,6π⎛⎤ ⎥⎝⎦B .,62ππ⎡⎤⎢⎥⎣⎦C .,62ππ⎛⎫ ⎪⎝⎭D .0,2π⎛⎫ ⎪⎝⎭2.(2020·上海高一课时练习)在ABC 中,5a =,45B =,105C =,则b 等于( )A .2B .10C .D .3.(2020·上海高一课时练习)在ABC 中,80a =,100b =,30A ︒=,则B 的解的个数是( ) A .无解B .两个解C .一个解D .不确定4.(2020·上海高一课时练习)在ABC 中,若2C B =,则b 等于( )A .2sin cBB .2cos cBC .2sin cCD .2cos cC5.(2020·上海高一课时练习)在ABC 中,用三个角A ,B ,C 或三条边长a ,b ,c 及外接圆半径R 表示三角形的面积S ,下列式子中正确的是( ) ①4abcS R =;②22sin sin sin =S R A B C ;③sin sin =S aR B C ;④1sin sin sin 2S A B C =. A .①②B .①②③C .①④D .②③6.(2020·上海高一课时练习)在ABC 中,45,60,1︒︒===B C c ,则最小边长等于( ).A B C .12D 7.(2020·上海高一课时练习)已知下列条件解三角形,其中有唯一解的是( ) A .20,28,40︒===a b A B .18,20,150︒===a b A C .20,34,70︒===b c BD .60,50,45︒===b c B8.(2020·上海高一课时练习)在ABC 中,3,30︒===a c A ,则ABCS=_________.9.(2020·上海高一课时练习)在ABC 中,若30,10︒===A a b ,则B =________. 10.(2020·上海高一课时练习)在ABC 中,若3,10,30︒===a b C ,则ABCS=__________.11.(2020·上海高一课时练习)在ABC 中,若20a =,11b =,30B =,则sin A =_________. 12.(2020·上海高一课时练习)半径为1的圆内接三角形的面积为14,则三边之积abc =________.13.(2020·上海高一课时练习)在ABC 中,若45,15,2︒︒===B C b ,则该三角形的最长边等于________.14.(2020·上海高一课时练习)在ABC 中,若30,45,10︒︒===A B a ,则b =________. 15.(2020·上海高一课时练习)ABC 的三内角为A ,B ,C ,且方程2()0+++=Bx A C x B 有两个相等的实数根,若cos cos =a C c A ,则ABC 是________三角形. 16.(2020·上海高一课时练习)若ABC 的外接圆半径为12,则2sin sin b C B c+=_________. 17.(2020·上海高一课时练习)若三角形的三个内角之比为1∶2∶3,则它们所对的边长之比为_______18.(2020·上海高一课时练习)在ABC 中,满足条件4,45a b A ︒===的ABC 的个数是________.19.(2020·上海高一课时练习)在ABC 中,若30,8,︒===A a b ,则ABC 的面积等于_________. 三、解答题20.(2020·安徽宣城市·高一期中)△ABC 中,a =7,c =3,且sin sin C B =35. (1)求b ;21.(2020·广东深圳市·红岭中学高一月考)在ABC ∆中,已知4B π=,c =3C π=,求,,A a b 的值.22.(2020·贵港市覃塘区覃塘高级中学高一月考)(1)等比数列{}n a 中,210S =,315S =,求n S .(2)在ABC ∆中,已知030,2B c b ===,求ABC ∆的面积23.(2020·全国高一专题练习)在ABC ∆中,若cos b a C =,试判断ABC ∆的形状.24.(2019·四川眉山市·仁寿一中高一月考)已知ABC 的内角,,A B C 所对的边分别为,,a b c ,若sin cos a C A =.(1)求角A .(2)若a =2c =,求ABC 的面积.25.(2020·四川成都市·成都外国语学校高一期中(文))在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,满足a b c bc a b c-+=+-. (1)求角A ;(2)若ABC 的外接圆半径为1,求ABC 的面积S 的最大值.26.(2020·四川省成都市盐道街中学高一期中)已知A 、B 、C 为ABC 的三内角,且其对边分别为a 、b 、c ,若cos (2)cos 0a C c b A ++=. (1)求A .(2)若a =4b c +=,求ABC 的面积.27.(2019·四川成都市·成都七中高一月考)已知△ABC 中,,33BAC AB π∠==,BD DC λ=,且ACD ∆. (1)若3λ=,求AC 的长;(2)当线段BC 的长度最小时,求λ的值.28.(2021·江苏省锡山高级中学高一期末)如图,已知正方形ABCD 的边长为1,点P ,Q 分别是边BC ,CD 上的动点(不与端点重合),在运动的过程中,始终保持4PAQ π∠=不变,设BAP α∠=.(1)将APQ 的面积表示成α的函数,并写出定义域; (2)求APQ 面积的最小值.29.(2020·辽河油田第二高级中学高一期中)ABC ∆的内角A ,B ,C 所对边分别为a ,b ,c .已知sinsin()2A Ca b B C +=+. (1) 求B ;(2) 若ABC ∆为锐角三角形,且2c =,求ABC ∆面积的取值范围。
2021上海沪教新版高一数学下学期同步练习6.1.4同角三角函数基本关系详解版(01)

6.1.4同角三角函数基本关系(作业)一、单选题1.(2021·上海市行知中学高一期末)1sin()2πθ+=是2()6k k Z πθπ=-∈的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件2.(2020cos 0x x +=的解集是( ) A .{|,}x x k k Z π=∈B .{|2,}6x x k k Z ππ=-∈C .{|,}6x x k k Z ππ=-∈ D .{|,}6x x k k Z ππ=+∈3.(2020·上海市川沙中学高一期末)下列命题中,错误的命题是( ) A .若(5,12)(0)P t t t ->为α终边上一点,则5cos 13α=; B .α是ABC 的一个内角,且2sin cos 3αα+=,则ABC 必为钝角三角形; C .存在无数个α,满足sin cos 2αβ+=,且cos cos 0αβ⋅= D .存在无数个α,满足sec 3α=且2sin 3α=4.(2020·上海高一课时练习)已知4sin 5α,并且α是第二象限的角,那么tan α的值等于( ) A .43-B .34-C .34D .435.(2020·上海奉贤区·高一期中)若α是第二象限的角,4sin25α=,则sin α的值为( )A .925B .2125C .2425D .2425-二、填空题6.(2021·上海浦东新区·华师大二附中高一期末)已知1cos 3α=,,02πα⎛⎫∈- ⎪⎝⎭,则tan α等于________.7.(2020·华东师范大学第三附属中学高一期末)已知tan 2x =,则22sin cos 3cos sin 1x xx x ++的值为________.8.(2020·上海市金山中学高一期中)已知tan 2θ=,则3sin 2cos sin 3cos θθθθ-=+____________________________. 9.(2020·上海高一课时练习)函数sin |cos ||sin |cos =+x x y x x的值域是_________.10.(2020·上海高一课时练习)已知α在第三、第四象限内,23sin 4-=-m mα那么m 的取值范围是______.11.(2020·上海高一课时练习)若1tan 2θ=,则2sin2sin +=θθ________. 三、解答题12.(2020·上海高一课时练习)化简:sin tan tan (cos sin )cot csc +-++ααααααα.13.(2020·上海高一课时练习)根据下列条件确定角θ的终边所在象限. (1)sin 0θ<且tan 0θ>;(2)cos cot 0θθ>.14.(2021·上海普陀区·曹杨二中高一期末)已知1sin cos 5αα+=,0απ<<. (1)求sin cos αα-的值; (2)求tan cot αα-的值.15.(2020·上海市杨浦高级中学高一期末)已知4tan 3α=-,且α是第四象限角,求cot ,cos ,csc ααα的值.16.(2020·上海高一课时练习)求下列方程的解集:(1)1cos ,(0,2)42⎛⎫+=∈ ⎪⎝⎭x x ππ;(2)3tan (0,)3⎛⎫+=∈ ⎪⎝⎭x x ππ.17.(2020·上海高一课时练习)根据下列条件,求角x :(1)已知tan [0,2)=∈x x π;(2)已知sin x =,x是第三象限角.18.(2020·上海高一课时练习)已知2222sin cos cos 1sin +⋅=ααγβ,求证:222tan cot sin ⋅=αβγ.19.(2020·上海高一课时练习)若tan 2θ=,求下列各式的值:(1)sin cos sin cos θθθθ-+;(2)23cos 2sin cos -θθθ.20.(2020·上海高一课时练习)已知1tan 2θ=-,求:(1)sin 3cos sin 2cos ++θθθθ;(2)222sin 3sin cos 5cos -+θθθθ.6.1.4同角三角函数基本关系(作业)一、单选题1.(2021·上海市行知中学高一期末)1sin()2πθ+=是2()6k k Z πθπ=-∈的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【答案】B【分析】根据1sin()2πθ+=,可求得θ的表达式,根据充分、必要条件的定义,即可得答案. 【详解】因为1sin()2πθ+=, 所以2,()6k k Z ππθπ+=+∈或52,()6k k Z ππθπ+=+∈, 所以,52,()6k k Z πθπ=-∈或2,()6k k Z πθπ=-∈, 所以1sin()2πθ+=是2()6k k Z πθπ=-∈的必要不充分条件. 故选:B2.(2020cos 0x x +=的解集是( ) A .{|,}x x k k Z π=∈B .{|2,}6x x k k Z ππ=-∈C .{|,}6x x k k Z ππ=-∈ D .{|,}6x x k k Z ππ=+∈【答案】C【分析】把方程化为tan x =.cos 0x x +=,可化为tan 3x =-, 解得,6=+∈x k k Z ππ,即方程的解集为{|,}6x x k k Z ππ=-∈.故答案为:C.【点睛】本题主要考查了三角函数的基本关系式,以及三角方程的求解,其中解答中熟记正切函数的性质,准确求解是解答的关键,着重考查了推理与运算能力,属于基础题. 3.(2020·上海市川沙中学高一期末)下列命题中,错误的命题是( ) A .若(5,12)(0)P t t t ->为α终边上一点,则5cos 13α=; B .α是ABC 的一个内角,且2sin cos 3αα+=,则ABC 必为钝角三角形; C .存在无数个α,满足sin cos 2αβ+=,且cos cos 0αβ⋅= D .存在无数个α,满足sec 3α=且2sin 3α=【答案】D【分析】根据三角函数定义计算即可判断A;根据同角三角函数关系即可判断B;根据三角函数有界性可判断C; 根据同角三角函数关系即可判断D. 【详解】若(5,12)(0)P t t t ->为α终边上一点,则55cos 1313t t α===,A 正确; 245sin cos 12sin cos 2sin cos 0399αααααα+=∴+=∴=-<(0,)sin 0,cos 0απαα∈∴>∴<∴ABC 必为钝角三角形;B 正确;sin cos 2sin cos 1cos 0αβαβα+=∴==∴=,cos cos 0αβ∴⋅=,C 正确;22114sec 3cos cos sin 1399αααα=∴=∴+=+<,所以D 错误;故选:D【点睛】本题考查三角函数定义、同角三角函数关系、三角函数有界性,考查基本分析求解能力,属基础题,4.(2020·上海高一课时练习)已知4sin 5α,并且α是第二象限的角,那么tan α的值等于( ) A .43-B .34-C .34D .43【答案】A【分析】根据同角三角函数关系,进行求解即可.【详解】因为45sin α=,故35cos α==± 又因为α是第二象限的角,故3cos α5=-故43sin tan cos ααα==-.故选:A. 【点睛】本题考查同角三角函数关系的简单使用,属基础题. 5.(2020·上海奉贤区·高一期中)若α是第二象限的角,4sin25α=,则sin α的值为( ) A .925B .2125C .2425D .2425-【答案】C【分析】α是第二象限的角,根据sin 2α的值,利用三角函数的基本关系求出cos2α的值,再用二倍角公式即可求出sin α的值.【详解】解:α是第二象限的角,所以22,2k k k Z ππαππ+<<+∈,∴422k k παπππ+<<+,k Z ∈所以2α是第一或第三象限的角,又4sin 025α=>,2α是第一象限的角, 所以3cos25α=,由二倍角公式可得4324sin 2sin cos 2225525ααα==⨯⨯=. 故选:C【点睛】本题主要考查三角函数求值问题,解答本题需用到同角三角函数基本关系,和而二倍角角公式. 二、填空题6.(2021·上海浦东新区·华师大二附中高一期末)已知1cos 3α=,,02πα⎛⎫∈- ⎪⎝⎭,则tan α等于________.【答案】-【分析】利用同角三角函数的基本关系可求得sin α的值,进而利用商数关系可求得tan α的值.【详解】,02πα⎛⎫∈-⎪⎝⎭,sin α∴==sin tan cos ααα==-故答案为:-7.(2020·华东师范大学第三附属中学高一期末)已知tan 2x =,则22sin cos 3cos sin 1x xx x ++的值为________.【答案】16【分析】利用正弦、余弦、正切之间的商关系,分式的分子、分母同时除以2cos x 即可求出分式的值. 【详解】22222222222sin cos sin cos sin cos tan 1cos .4cos 2sin 3cos sin 13cos sin cos sin 42tan 6cos x xx x x x x x x x x x x x x x x x====+++++++ 【点睛】本题考查了同角三角函数的平方和关系和商关系,考查了数学运算能力. 8.(2020·上海市金山中学高一期中)已知tan 2θ=,则3sin 2cos sin 3cos θθθθ-=+____________________________.【答案】45【分析】分子、分母同除以cos θ,将tan 2θ=代入化简即可. 【详解】因为tan 2θ=,所以3sin 2cos 3tan 23224sin 3cos tan 3235θθθθθθ--⨯-===+++,故答案为45.【点睛】本题主要考查同角三角函数之间的关系的应用,属于基础题. 同角三角函数之间的关系包含平方关系与商的关系,平方关系是正弦与余弦值之间的转换,商的关系是正余弦与正切之间的转换.9.(2020·上海高一课时练习)函数sin |cos ||sin |cos =+x x y x x的值域是_________.【答案】{2,0,2}-【分析】分别讨论x 在第一象限,第二象限,第三象限,第四象限四种情况,计算得到答案. 【详解】根据题意知:2k x π≠,k Z ∈,当x 在第一象限时,sin |cos |sin cos 2|sin |cos sin cos x x x xy x x x x =+=+=;当x 在第二象限时,sin |cos |sin cos 0|sin |cos sin cos x x x xy x x x x=+=-=;当x 在第三象限时,sin |cos |sin cos 2|sin |cos sin cos x x x xy x x x x =+=--=-;当x 在第四象限时,sin |cos |sin cos 0|sin |cos sin cos x x x xy x x x x=+=-+=;综上所述:值域为{2,0,2}-.故答案为:{2,0,2}-.【点睛】本题考查了三角函数的值域,意在考查学生的计算能力和分类讨论能力. 10.(2020·上海高一课时练习)已知α在第三、第四象限内,23sin 4-=-m mα那么m 的取值范围是______.【答案】31,2⎛⎫- ⎪⎝⎭【详解】∵角α在第三、四象限内,∴()sin 10α∈-,,可得23104m m--<<-, ①当40m ->时,即4m <时,原不等式可化为4230m m -<-<, 解之得312m -<<;②当40m -<时,即4m >时,原不等式可化为4230m m ->->, 此不等式组的解集为空集,综上可得312m -<<,可 得m 的取值范围是31,2⎛⎫- ⎪⎝⎭,故答案为31,2⎛⎫- ⎪⎝⎭.11.(2020·上海高一课时练习)若1tan 2θ=,则2sin2sin +=θθ________. 【答案】1【分析】由二倍角公式结合商数关系和平方关系,即可得出答案.【详解】2222221122sin cos sin 2tan tan 24sin 2sin 11sin cos tan 114θθθθθθθθθθ⨯+⋅+++====+++ 故答案为:1【点睛】本题主要考查了商数关系,平方关系的应用,属于中档题.三、解答题12.(2020·上海高一课时练习)化简:sin tan tan (cos sin )cot csc +-++ααααααα.【答案】sin α【分析】利用同角三角函数的基本关系式借助切化弦,割化弦,对表达式化简即可.【详解】sin 1cos 1tan ,cot ,csc cos tan sin sin ααααααααα====, ∴sin tan tan (cos sin )cot csc +-++ααααααα=sin (cos sin sin sin cos cos 1cos si sin )n αααααααααα+-++=()()21cos si si n n cos sin 1cos cos 1sin sin ααααααααα+-++ =()()2cos sin cos sin 1cos cos 1sin sin 1αααααααα-+++ =22sin sin sin cos cos ααααα+-=sin α. 【点睛】本题主要考查同角三角函数之间的关系在化简中的应用,考查了利用商数关系式切化弦,割化弦,属于基础题.13.(2020·上海高一课时练习)根据下列条件确定角θ的终边所在象限. (1)sin 0θ<且tan 0θ>; (2)cos cot 0θθ>.【答案】(1)第三象限;(2)第一象限或第二象限. 【分析】(1)根据三角函数符号规律确定象限; (2)先解不等式,再根据符号确定象限.【详解】(1)由sin 0θ<可知θ的终边在第三象限或第四象限或y 轴的负半轴上, 由tan 0θ>可知θ的终边在第一象限或第三象限, 所以角θ的终边在第三象限.(2)由题意,得cos 0cot 0θθ>⎧⎨>⎩或cos 0cot 0θθ<⎧⎨<⎩,所以角θ的终边在第一象限或第二象限.【点睛】本题考查三角函数符号规律,考查基本分析判断能力,属基础题. 14.(2021·上海普陀区·曹杨二中高一期末)已知1sin cos 5αα+=,0απ<<. (1)求sin cos αα-的值; (2)求tan cot αα-的值. 【答案】(1)75;(2)712-. 【分析】(1)对已知条件两边同时平方结合22sin cos 1αα+=可得12sin cos 025αα=-<,结合0απ<<,可得2παπ<<,进而可得sin cos 0αα->,计算()2sin cos αα-即可求解;(2)将tan cot αα-化切为弦再通分,利用整体代入即可求解.【详解】(1)由1sin cos 5αα+=可得()21sin cos 25αα+=, 即221sin cos 2sin cos 25αααα++=,解得12sin cos 025αα=-<, 因为0απ<<,所以2παπ<<,可得sin 0,cos 0αα><,sin cos 0αα->所以()2221249sin cos sin cos 2sin cos 122525αααααα⎛⎫-=+-=-⨯-=⎪⎝⎭, 所以7sin cos 5αα-=, (2)22sin cos sin cos tan cot cos sin sin cos αααααααααα--=-=()()sin cos sin cos sin 1775cos 5121225αααααα+=-⨯=--=.【点睛】关键点点睛:本题解题的关键点是利用已知条件求出sin cos αα,根据其符号判断α所在的象限,可判断sin cos αα-的符号.15.(2020·上海市杨浦高级中学高一期末)已知4tan 3α=-,且α是第四象限角,求cot ,cos ,csc ααα的值.【答案】335cot ,cos ,csc 454ααα=-==-. 【分析】根据同角三角函数的基本关系计算可得; 【详解】解:因为4tan 3α=-,且α是第四象限角, 所以41cot tan 3αα==-,因为22sin tan cos sin cos 1ααααα⎧=⎪⎨⎪+=⎩,解得3cos 54sin 5αα⎧=⎪⎪⎨⎪=-⎪⎩或3cos 54sin 5αα⎧=-⎪⎪⎨⎪=⎪⎩因为α是第四象限角,所以3cos 54sin 5αα⎧=⎪⎪⎨⎪=-⎪⎩所以15csc sin 4αα==- 16.(2020·上海高一课时练习)求下列方程的解集:(1)1cos ,(0,2)42⎛⎫+=∈ ⎪⎝⎭x x ππ; (2)3tan (0,)3⎛⎫+=∈ ⎪⎝⎭x x ππ.【答案】(1)17,1212⎧⎫⎨⎬⎩⎭ππ;(2)56⎧⎫⎨⎬⎩⎭π 【分析】(1)根据(0,2)x π∈可得4x π+的范围,再根据1cos 42x π⎛⎫+= ⎪⎝⎭求解即可. (2)根据(0,)x π∈可得3x π+的范围,再根据tan 3x π⎛⎫+= ⎪⎝⎭求解即可. 【详解】(1)因为(0,2)x π∈,故9,444x πππ⎛⎫+∈ ⎪⎝⎭,又1cos 42x π⎛⎫+= ⎪⎝⎭,故43x ππ+=或543x ππ+=,解得12x π=或1712π. 故解集为17,1212⎧⎫⎨⎬⎩⎭ππ(2)因为(0,)x π∈,故4,333x πππ⎛⎫+∈ ⎪⎝⎭,又tan 3x π⎛⎫+= ⎪⎝⎭,故736x ππ+=,解得56x π=.故解集为56⎧⎫⎨⎬⎩⎭π【点睛】本题主要考查了已知三角函数值求角的问题,需要注意角度的范围以及特殊的三角函数值,属于基础题.17.(2020·上海高一课时练习)根据下列条件,求角x :(1)已知tan [0,2)=∈x x π;(2)已知sin 2x =-,x是第三象限角. 【答案】(1)3π或43π;(2)52,4+∈k k Z ππ 【分析】(1)根据特殊角所对应的三角函数值,以及角的范围,即可得出结果; (2)根据特殊角所对应的三角函数值,以及角的范围,即可得出结果;【详解】(1)由tan x =,3x k k Z ππ=+∈,因为[0,2)x π∈,所以023k πππ≤+<,因此0k =或1,故3x π=或43π;(2)由sin 2x =-得24=-+x k ππ或52,4x k k Z ππ=+∈, 又x 是第三象限角,所以52,4x k k Z ππ=+∈. 【点睛】本题主要考查由三角函数值求角,熟记特殊角所对应的三角函数值即可,属于基础题型.18.(2020·上海高一课时练习)已知2222sin cos cos 1sin +⋅=ααγβ,求证:222tan cot sin ⋅=αβγ. 【分析】利用同角间的三角函数关系,将已知等式分离出γ角的三角函数,再把,αβ角化弦为切,即可证明结论.【详解】22222222sin sin cos cos 1,cos cos 1sin sin αααγαγββ+⋅=∴⋅=-, 22221tan cos cos sin αγαβ=-,2222222221tan cos 1tan cos s o sin 1co in c s sin s 1ααααβαβγγ∴=-=--+=+ 22222221sin 1tan (1)tan tan cot sin sin βαααβββ-=--=-⋅=⋅, ∴等式成立.【点睛】本题考查条件等式的证明,熟练应用同角间的三角函数关系是解题的关键,属于中档题.19.(2020·上海高一课时练习)若tan 2θ=,求下列各式的值:(1)sin cos sin cos θθθθ-+;(2)23cos 2sin cos -θθθ. 【答案】(1)13;(2)15-【分析】(1)利用商数关系,化弦为切,代入所给正切值即可; (2)巧用平方关系,转为二次齐次式,化弦为切,代入计算即可. 【详解】(1)∵tan 2α=∴tan sin cos sin c 1211tan 121os 3θθθθθθ--===++-+;(2)∵tan 2α=222223cos 2sin cos 32tan 3413cos 2sin cos sin cos tan 1415θθθθθθθθθθ---∴-====-+++ 【点睛】本题主要考查了同角基本三角函数间的关系,弦化切的思想,考查了运算能力,属于中档题.20.(2020·上海高一课时练习)已知1tan 2θ=-,求:(1)sin 3cos sin 2cos ++θθθθ;(2)222sin 3sin cos 5cos -+θθθθ. 【答案】(1)53;(2)285. 【分析】(1)直接利用齐次式计算得到答案.(2)变换原式22222sin 3sin cos 5cos sin cos θθθθθθ-+=+,再利用齐次式计算得到答案.【详解】(1)原式sin 3cos 13tan 35cos 2sin 2cos 1tan 232cos 2θθθθθθθθ+-++====++-+. (2)原式2222222sin 3sin cos 5cos 2sin 3sin cos 5cos 1sin cos -+-+==+θθθθθθθθθθ2213252tan 3tan 528421tan 1514θθθ⨯++-+===++.【点睛】本题考查了同角三角函数关系,齐次式求值,意在考查学生的计算能力和转化能力.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一三角同步练习6(化简与证明)
一、选择题
1、已知cos α= -
1213 ,α∈(π,2π),则tan α嘚值是 ( ) A .513 B .512 C .125 D .± 512
2、化简 160tan 11
2+嘚结果为 ( )
A .-cos160°
B .cos160°
C .±cos160°
D .-sec160°
3、若是α第二象限角,则1sin 1tan 2-α
α化简嘚结果是 ( ) A .1 B .-1 C .tan 2α D .-tan 2α
4、若0cot tan cos cos sin sin 22=++θθθθθθ,则θ不可能是 ( )
A .第一、第二、第三象限角
B .第一、第二、第四象限角
C .第一、第三、第四象限角
D .第二、第三、第四象限角
5、如果角θ满足1cos sin =+θθ,那么θθcot tan +嘚值是 ( )
A .1-
B .0
C .1
D .不存在
6、若θ为二象限角,且2cos 2sin 212sin 2cos θ
θ
θ
θ
-=-,那么2
θ是 A .第一象限角 B .第二象限角
C .第三象限角
D .第四象限角 7、若2tan =x , 则
()()x x x x sin cos cos 3sin 1--嘚值为: A .3- B .5- C .3 D .5
8、函数()=x f 1cos 1tan 2tan 1cos 1
22-++x x x
x 值域中元素嘚个数是( ) A .1个 B .2个 C .3个 D .4个
二、填空题
1、化简sin 2α+sin 2β-sin 2αsin 2β+cos 2αcos 2β=
. 2、化简
40sin 140sin 40cos 40sin 212---= .
3、若α是第四象限角,化简ααtan 2sec 2-=________________.
4、若ααααsin 1sin 1sin 1sin 1+---+ = -2 tan α,则角α嘚取值范围是 .
三、解答题
1、化简:tan α(cos α-sin α)+
ααααcos 1)tan (sin sin ++.
2、求证:
1
tan 1tan cos sin cos sin 2122-+=-+αααααα.
3、求证:ααααααααcot tan cos sin 2cot cos tan sin 22+=++.
4、已知cosB = cosθsinA , cosC = sinθsinA ,求证:sin2A+sin2B+sin2C = 2.
参考答案
一、选择题
BABB DCDD
二、填空题
1、1;
2、-1;
3、αtan 1-;
4、
()Z k k k ∈+<<+,22
322ππαππ 三、解答题
1、αsin
2、左边α
ααααα2222cos sin cos sin 2cos sin -++=()αααα222
cos sin cos sin -+= =-+=-+=1tan 1tan cos sin cos sin αααααα右边. 3、
∵
()()()
ααααααααααcot cos 1tan sin 1cot cos tan sin cot tan 2222-+-=+-+ ααααααααααcos sin 2cos sin sin cos cot sin tan cos 22=+=+= ∴ααααααααcot tan cos sin 2cot cos tan sin 22+=++. 4、
∵A B 222sin cos cos θ=,A C 222sin sin cos θ=,
∴()A C B 22222sin sin cos cos cos θθ+=+,
即:A C B 222sin sin 1sin 1=-+-,
∴2sin sin sin 222=++C B A .。
