曲线与方程(轨迹方程)
曲线运动轨迹方程

曲线运动轨迹方程1. 引言曲线运动轨迹方程是高中数学中的重要内容之一,也是物理学、工程学等学科中必须掌握的基本知识之一。
曲线运动轨迹方程是描述物体在曲线运动过程中位置随时间的关系公式,能够真实地反映物理规律。
本文将深入探讨曲线运动轨迹方程的相关概念、性质和应用。
2. 曲线运动轨迹方程的定义和概念曲线运动是指物体在其运动过程中沿曲线路径运动。
在物理学中,曲线运动常常表现为物体绕一个固定的中心旋转,或者物体在重力、电场等作用下做曲线运动。
曲线运动轨迹方程是描述物体在曲线运动过程中位置随时间的关系公式,通常使用代数符号表达,可以是一个方程、多个方程组成的一组方程,也可以是一个参数式方程等。
3. 曲线运动轨迹方程的性质曲线运动轨迹方程具有以下性质:3.1 显示物体位置的函数曲线运动轨迹方程是一组显示物体在不同时刻位置的函数。
通过该方程可以得知物体在运动过程中每个时刻的位置坐标,进而获得物体位置随时间的规律。
3.2 显示物体速度和加速度的函数曲线运动轨迹方程除了能够显示物体在不同时刻的位置信息外,还能够显示物体在不同时刻的速度和加速度。
通过对曲线运动轨迹方程求导,可以得到物体在不同时刻的速度和加速度。
3.3 曲线的切线方向与导数曲线运动轨迹方程可以描述曲线在不同点的切线方向。
曲线在某一点处的切线与曲线方程在该点处的导数有关。
曲线在该点处的切线方向与导数在极限意义下相等。
3.4 曲率半径和二阶导数曲线运动轨迹方程也可以描述曲线的曲率半径,它与曲线的二阶导数有关。
因此,通过对曲线运动轨迹方程求两次导,可以得到曲线在不同点上的曲率半径。
3.5 物理规律的体现曲线运动轨迹方程是物理规律在运动中的具体体现。
这一点在工程学、物理学等领域得到了广泛的应用。
4. 应用实例曲线运动轨迹方程在物理学、工程学等领域中具有广泛的应用。
以下是几个实例:4.1 行星轨道分析行星轨道分析是物理学中的一个重要研究领域。
通过对曲线运动轨迹方程的求解,可以得到一个行星绕太阳的椭圆轨道方程。
高考一轮复习第8章解析几何第8讲曲线与方程
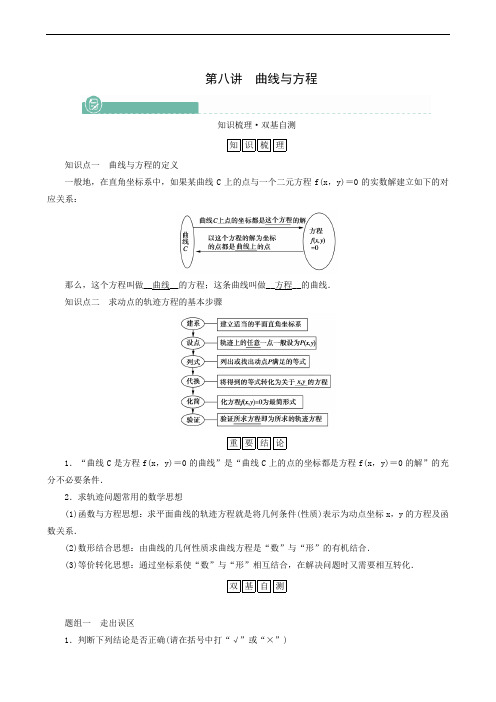
第八讲曲线与方程知识梳理·双基自测知识梳理知识点一曲线与方程的定义一般地,在直角坐标系中,如果某曲线C上的点与一个二元方程f(x,y)=0的实数解建立如下的对应关系:那么,这个方程叫做__曲线__的方程;这条曲线叫做__方程__的曲线.知识点二求动点的轨迹方程的基本步骤重要结论1.“曲线C是方程f(x,y)=0的曲线”是“曲线C上的点的坐标都是方程f(x,y)=0的解”的充分不必要条件.2.求轨迹问题常用的数学思想(1)函数与方程思想:求平面曲线的轨迹方程就是将几何条件(性质)表示为动点坐标x,y的方程及函数关系.(2)数形结合思想:由曲线的几何性质求曲线方程是“数”与“形”的有机结合.(3)等价转化思想:通过坐标系使“数”与“形”相互结合,在解决问题时又需要相互转化.双基自测题组一走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)方程x 2+xy =x 的曲线是一个点和一条直线.( × )(2)到两条互相垂直的直线距离相等的点的轨迹方程是x 2=y 2.( × ) (3)y =kx 与x =1ky 表示同一直线.( × )(4)动点的轨迹方程和动点的轨迹是一样的.( × ) 题组二 走进教材2.(必修2P 37T3)已知点F ⎝ ⎛⎭⎪⎫14,0,直线l :x =-14,点B 是l 上的动点,若过点B 垂直于y 轴的直线与线段BF 的垂直平分线交于点M ,则点M 的轨迹是( D )A .双曲线B .椭圆C .圆D .抛物线[解析] 由已知|MF|=|MB|,根据抛物线的定义知,点M 的轨迹是以点F 为焦点,直线l 为准线的抛物线.3.(选修2-1P 37T1改编)已知A(-2,0),B(1,0)两点,动点P 不在x 轴上,且满足∠APO =∠BPO ,其中O 为原点,则点P 的轨迹方程是__x 2+y 2-4x =0(y≠0)__.[解析] 设P(x ,y),∵∠APO =∠BPO , ∴|PA||PB|=|OA||OB|=2, 即|PA|=2|PB|,∴(x +2)2+y 2=4[(x -1)2+y 2],(y≠0)化简整理得P 的轨迹方程为x 2+y 2-4x =0(y≠0). 题组三 走向高考4.(多选题)(2020·山东)已知曲线C :mx 2+ny 2=1.( ACD ) A .若m >n >0,则C 是椭圆,其焦点在y 轴上 B .若m =n >0,则C 是圆,其半径为nC .若mn <0,则C 是双曲线,其渐近线方程为y =±-m nx D .若m =0,n >0,则C 是两条直线[解析] A .若m >n >0,则1m <1n ,则根据椭圆定义,知x 21m +y21n =1表示焦点在y 轴上的椭圆,故A 正确;B .若m =n >0,则方程为x 2+y 2=1n ,表示半径为1n的圆,故B 错误;C .若m <0,n >0,则方程为x21m+y21n =1,表示焦点在y 轴的双曲线,故此时渐近线方程为y =±-m n x ,若m >0,n <0,则方程为x 21m +y 21n=1,表示焦点在x 轴的双曲线,故此时渐近线方程为y =±-mnx ,故C 正确;D .当m =0,n >0时,则方程为y =±1n表示两条直线,故D 正确;故选ACD . 5.(2019·北京卷)数学中有许多形状优美、寓意美好的曲线,曲线C :x 2+y 2=1+|x|y 就是其中之一(如图).给出下列三个结论:①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ②曲线C 上任意一点到原点的距离都不超过2; ③曲线C 所围成的“心形”区域的面积小于3. 其中,所有正确结论的序号是( C ) A .① B .② C .①②D .①②③[解析] 将x 换成-x 方程不变,所以图形关于y 轴对称, 当x =0时,代入得y 2=1,∴y =±1,即曲线经过(0,1),(0,-1); 当x >0时,方程变为y 2-xy +x 2-1=0,所以Δ=x 2-4(x 2-1)≥0,解得x ∈⎝⎛⎦⎥⎤0,233,所以x 只能取整数1,当x =1时,y 2-y =0, 解得y =0或y =1,即曲线经过(1,0),(1,1), 根据对称性可得曲线还经过(-1,0),(-1,1), 故曲线一共经过6个整点,故①正确. 当x >0时,由x 2+y 2=1+xy 得x 2+y 2-1=xy≤x 2+y22,(当x =y 时取等),∴x 2+y 2≤2,∴x 2+y 2≤2,即曲线C 上y 轴右边的点到原点的距离不超过2,根据对称性可得:曲线C 上任意一点到原点的距离都不超过2;故②正确.在x 轴上图形面积大于矩形面积=1×2=2,x 轴下方的面积大于等腰直角三角形的面积=12×2×1=1,因此曲线C 所围成的“心形”区域的面积大于2+1=3,故③错误.故选C .考点突破·互动探究考点一 曲线与方程——自主练透例1 (多选题)关于x ,y 的方程x 2m 2+2+y 23m 2-2=1,⎝⎛⎭⎪⎫其中m 2≠23对应的曲线可能是( ABCD ) A .焦点在x 轴上的椭圆 B .焦点在y 轴上的椭圆 C .焦点在x 轴上的双曲线 D .圆[解析] 由题,若m 2+2>3m 2-2,解得-2<m <2,3m 2-2>0,解得m <-63或m >63,则当x ∈⎝ ⎛⎭⎪⎫-2,-63∪⎝ ⎛⎭⎪⎫63,2时,曲线是焦点在x 轴上的椭圆,A 正确;若3m 2-2>m 2+2,解得m <-2或m >2,此时曲线是焦点在y 轴上的椭圆,B 正确;若3m 2-2<0,解得-63<m <63,此时曲线是焦点在x 轴上的双曲线,C 正确;当m 2=2时,方程为x 2+y 2=4,所以D 正确.故选ABCD .〔变式训练1〕(多选题)(2021·山东青岛一中期末)已知点F(1,0)为曲线C 的焦点,则曲线C 的方程可能为( AD )A .y 2=4x B .x 2=4yC .x 2cos 2θ+y 2sin 2θ=1⎝ ⎛⎭⎪⎫0<θ<π2 D .x 2cos 2θ-y 2sin 2θ=1⎝⎛⎭⎪⎫0<θ<π2 [解析] y 2=4x 的焦点坐标为(1,0);x 2=4y 的焦点坐标为(0,1);当θ=π4时,sin 2θ=cos 2θ=12,x 2cos 2θ+y 2sin 2θ=1表示圆;双曲线x 2cos 2θ-y 2sin 2θ=1⎝⎛⎭⎪⎫0<θ<π2的焦点在x 轴上,且c =cos 2θ+sin 2θ=1,其焦点坐标为(1,0),(-1,0),故选AD .考点二 定义法求轨迹方程——自主练透例2 (1)(2021·长春模拟)如图所示,A 是圆O 内一定点,B 是圆周上一个动点,AB 的中垂线CD 与OB 交于点E ,则点E 的轨迹是( B )A .圆B .椭圆C .双曲线D .抛物线(2)(2021·福州模拟)已知圆M :(x +5)2+y 2=36,定点N(5,0),点P 为圆M 上的动点,点Q 在NP 上,点G 在线段MP 上,且满足NP →=2NQ →,GQ →·NP →=0,则点G 的轨迹方程是( A )A .x 29+y24=1B .x 236+y231=1 C .x 29-y24=1D .x 236-y231=1 (3)(2021·江苏南京二十九中调研)已知两圆C 1:(x +3)2+y 2=1,C 2:(x -3)2+y 2=9,动圆M 同时与圆C 1和圆C 2外切,则动圆圆心M 的轨迹方程为( D )A .x 2-y28=1B .x 28-y 2=1C .x 2-y28=1(x≥1)D .x 2-y28=1(x≤-1)[解析] (1)由题意知,|EA|+|EO|=|EB|+|EO|=r(r 为圆的半径)且r >|OA|,故E 的轨迹为以O ,A 为焦点的椭圆,故选B .(2)由NP →=2NQ →,GQ →·NP →=0知GQ 所在直线是线段NP 的垂直平分线,连接GN ,∴|GN|=|GP|,∴|GM|+|GN|=|MP|=6>25,∴点G 的轨迹是以M ,N 为焦点的椭圆,其中2a =6,2c =25,∴b 2=4,∴点G 的轨迹方程为x 29+y24=1,故选A .(3)设动圆M 的半径为r ,则|C 1M|=r +1,|C 2M|=3+r ,∴|C 2M|-|C 1M|=2<6=|C 1C 2|.∴动圆圆心M 的轨迹是以C 1、C 2为焦点的双曲线左支,且c =3,a =1,∴b 2=c 2-a 2=8,∴其轨迹方程为x 2-y28=1(x≤-1).故选D .[引申1]本例(3)中,若动圆M 与圆C 1内切,与圆C 2外切,则动圆圆心M 的轨迹方程为__x 24-y25=1(x≤-2)__.[引申2]本例(3)中,若动圆M 与圆C 1外切,与圆C 2内切,则动圆圆心M 的轨迹方程为__x 24-y25=1(x≥2)__.[引申3]本例(3)中,若动圆M 与圆C 1、圆C 2都内切,则动圆圆心M 的轨迹方程为__x 2-y28=1(x≥1)__.[引申4]本例3中,若动圆M 与圆C 1、圆C 2中一个内切一个外切,则动圆圆心M 的轨迹方程为__x 24-y25=1__.名师点拨定义法求轨迹方程及其注意点(1)在利用圆锥曲线的定义法求轨迹方程时,若所求的轨迹符合某种圆锥曲线的定义,则根据曲线的方程,写出所求的轨迹方程.(2)利用定义法求轨迹方程时,还要看轨迹是否是完整的圆、椭圆、双曲线、抛物线,如果不是完整的曲线,则应对其中的变量x 或y 进行限制.〔变式训练2〕(1)动圆M 经过双曲线x 2-y23=1的左焦点且与直线x =2相切,则圆心M 的轨迹方程是( B )A .y 2=8x B .y 2=-8x C .y 2=4xD .y 2=-4x(2)(多选题)(2021·湖南娄底质检)在水平地面上的不同两点处竖有两根笔直的电线杆,假设它们都垂直于地面,则在水平地面上视它们上端仰角相等的点P 的轨迹可能是( AB )A .直线B .圆C .椭圆D .抛物线[解析] (1)双曲线x 2-y23=1的左焦点为F(-2,0),由题意可知点M 的轨迹是以F 为焦点、原点为顶点、对称轴为x 轴的抛物线,故其方程为y 2=-8x .故选B .(2)如图两根电杆AB ,CD ,①当|AB|=|CD|时,∵∠BPA =∠DPC ,∴|PA|=|PC|, ∴P 的轨迹是AC 的中垂线,②当|AB|=λ|CD|(λ≠1,λ>0)时, 由∠BPA =∠DPC 知Rt △ABP ∽Rt △CDP , ∴|AP||CP|=|AB||CD|=λ, 以AC 所在直线为x 轴,线段AC 的中垂线为y 轴建立平面直角坐标系, 记A(-1,0),C(1,0),P(x ,y), 则x +12+y 2x -12+y2=λ,即⎝ ⎛⎭⎪⎫x -λ2+1λ2-12+y 2=⎝ ⎛⎭⎪⎫2λλ2-12, 轨迹为圆,故选AB .考点三 直接法求轨迹方程——师生共研例3 (1)(2021·四川、云南、贵州、西藏四省四校联考)已知圆C 过点A(0,2)且与直线y =-2相切,则圆心C 的轨迹方程为( B )A .x 2=4y B .x 2=8y C .x 2=-4yD .x 2=-8y(2)(2021·山东菏泽模拟)已知动圆过定点A(4,0),且在y 轴上截得的弦MN 的长为8. ①求动圆圆心的轨迹C 的方程;②已知点B(-1,0),设不垂直于x 轴的直线l 与轨迹C 交于不同的两点P ,Q ,若x 轴是∠PBQ 的角平分线,证明:直线l 过定点.[解析] (1)设圆心C(x ,y), 由题意知x 2+y -22=|y +2|,化简得x 2=8y ,故选B .(2)①设动圆圆心P(x ,y),线段MN 的中点为E , 则|PA|2=|PE|2+42,即(x -4)2+y 2=x 2+16,化简得y 2=8x , ∴动圆圆心的轨迹C 的方程为y 2=8x . ②设直线l 的方程为y =kx +b ,联立⎩⎪⎨⎪⎧y 2=8x ,y =kx +b ,得k 2x 2+2kbx +b 2=8x ,k 2x 2-(8-2kb)x +b 2=0(其中Δ>0), 设P(x 1,kx 1+b),Q(x 2,kx 2+b), 则x 1+x 2=8-2kb k 2,x 1x 2=b 2k 2, 若x 轴是∠PBQ 的角平分线, 则k PB +k QB =kx 1+b x 1+1+kx 2+bx 2+1=kx 1+b x 2+1+kx 2+b x 1+1x 1+1x 2+1=2kx 1x 2+k +b x 1+x 2+2bx 1+1x 2+1=8k +bk2x 1+1x 2+1=0,即k =-b .故直线l 的方程为y =k(x -1),直线l 过定点(1,0).名师点拨直接法求曲线方程的一般步骤(1)建立合适的直角坐标系.(2)设出所求曲线上点的坐标,把几何条件或等量关系用坐标表示为代数方程.(3)化简整理这个方程,检验并说明所求方程就是曲线的方程.直接法求曲线方程时最关键的就是把几何条件或等量关系“翻译”为代数方程,要注意“翻译”的等价性.(4)运用直接法应注意的问题①在用直接法求轨迹方程时,在化简的过程中,有时破坏了方程的同解性,此时就要补上遗漏的点或删除多余的点,这是不能忽视的.②若方程的化简过程是恒等变形,则最后的验证可以省略. 〔变式训练3〕(1)已知两定点A(-2,0),B(1,0),如果动点P 满足|PA|=2|PB|,则动点P 的轨迹是( B ) A .直线 B .圆 C .椭圆D .双曲线(2)(2021·湖南湘潭模拟)在平面直角坐标系xOy 中,已知点Q(1,0),直线l :x =2.若动点P 在直线l 上的射影为R ,且|PR →|=2|PQ →|,设点P 的轨迹为C .①求C 的轨迹方程;②设直线y =x +n 与曲线C 相交于A 、B 两点,试探究曲线C 上是否存在点M ,使得四边形MAOB 为平行四边形,若存在,求出点M 的坐标;若不存在,请说明理由.[解析] (1)设P(x ,y), 则x +22+y 2=2x -12+y 2,化简得x 2+y 2-4x =0,即(x -2)2+y 2=4, 其表示以(2,0)为圆心,4为半径的圆,故选B . (2)①设P(x ,y),由|PR →|=2|PQ →|, 得|2-x|=2·x -12+y 2,平方化简得C 的轨迹方程为x 22+y 2=1.②设A(x 1,y 1),B(x 2,y 2),M(x 3,y 3), 联立⎩⎪⎨⎪⎧y =x +n x 22+y 2=1,得x 2+2(x +n)2-2=0,即3x 2+4nx +2n 2-2=0,所以x 1+x 2=-4n 3,y 1+y 2=x 1+x 2+2n =2n3.假设存在点M 使得四边形MAOB 为平行四边形, 则OM →=OA →+OB →,所以(x 3,y 3)=(x 1,y 1)+(x 2,y 2), 所以x 3=x 1+x 2=-4n 3,y 3=y 1+y 2=2n3.由点M 在曲线C 上得x 232+y 23=1,代入得8n 29+4n29=1,解得n 2=34,n =±32.所以当n =±32时,曲线C 上存在点M 使得四边形MAOB 为平行四边形, 此时点M 的坐标为⎝ ⎛⎭⎪⎫-233,33或者M ⎝ ⎛⎭⎪⎫233,-33,当n≠±32,曲线C 上不存在点M 使得四边形MAOB 为平行四边形. 考点四 代入法(相关点法)求轨迹方程——师生共研例4 (2021·河南新乡模拟)在直角坐标系xOy 中,点M(-2,0),N 是曲线x =14y 2+2上的任意一点,动点C 满足MC →+NC →=0.(1)求点C 的轨迹方程;(2)经过点P(1,0)的动直线l 与点C 的轨迹交于A ,B 两点,在x 轴上是否存在定点D(异于点P),使得∠ADP =∠BDP ?若存在,求出D 的坐标;若不存在,请说明理由.[解析] (1)设C(x ,y),N(x 0,y 0), 则MC →=(x +2,y),NC →=(x -x 0,y -y 0), MC →+NC →=(2x -x 0+2,2y -y 0).又MC →+NC →=0,则⎩⎪⎨⎪⎧2x -x 0+2=0,2y -y 0=0,即⎩⎪⎨⎪⎧x 0=2x +2,y 0=2y.因为点N 为曲线x =14y 2+2上的任意一点,所以x 0=14y 20+2,所以2x +2=14(2y)2+2,整理得y 2=2x ,故点C 的轨迹方程为y 2=2x . (2)设存在点D(t,0),使得∠ADP =∠BDP , 所以k DA +k DB =0.由题易知,直线l 的倾斜角不可能为0°, 故设直线l 的方程为x =my +1,将x =my +1代入y 2=2x ,得y 2-2my -2=0. 设A(x 1,y 1),B(x 2,y 2),则y 1+y 2=2m ,y 1y 2=-2. 因为k DA +k DB =y 1x 1-t +y 2x 2-t =y 1my 1+1-t +y 2my 2+1-t =0,所以2my 1y 2+(1-t)(y 1+y 2)=0, 即-4m +2m·(1-t)=0,所以t =-1. 故存在点D(-1,0),使得∠ADP =∠BDP .名师点拨代入法(相关点法)求轨迹方程(1)当题目中的条件同时具有以下特征时,一般可以用相关点法求其轨迹方程: ①某个动点P 在已知方程的曲线上移动; ②另一个动点M 随P 的变化而变化;③在变化过程中P 和M 满足一定的规律.(2)代入法(相关点法)的基本步骤①设点:设被动点坐标为(x ,y),主动点坐标为(x 1,y 1);②求关系式:求出两个动点坐标之间的关系式⎩⎪⎨⎪⎧ x 1=f x ,y ,y 1=g x ,y ;③代换:将上述关系式代入已知曲线方程,便可得到所求动点的轨迹方程;④检验:注意检验所求方程是否符合题意.〔变式训练4〕(2021·河北石家庄模拟)已知点Q 在椭圆C :x 216+y 210=1上,点P 满足OQ →=12(OF 1→+OP →)(其中O 为坐标原点,F 1为椭圆C 的左焦点),则点P 的轨迹为( D )A .圆B .抛物线C .双曲线D .椭圆 [解析] 设P(x ,y),Q(x 0,y 0),椭圆C 的左焦点F 1(-2,0),由题意知⎩⎪⎨⎪⎧ x 0=x -22,y 0=y 2 又x 2016+y 2010=1,∴x -2264+y 240=1,故选D . 考点五,参数法求轨迹方程——师生共研例5 (2021·河北衡水中学调研)已知圆C 1:x 2+y 2=2,圆C 2:x 2+y 2=4,如图,C 1,C 2分别交x 轴正半轴于点E ,A .射线OD 分别交C 1,C 2于点B ,D ,动点P 满足直线BP 与y 轴垂直,直线DP 与x 轴垂直.(1)求动点P 的轨迹C 的方程;(2)过点E 作直线l 交曲线C 与点M ,N ,射线OH ⊥l 于点H ,且交曲线C 于点Q .问:1|MN|+1|OQ|2的值是否是定值?如果是定值,请求出该定值;如果不是定值,请说明理由.[分析] 显然点P(x ,y)的变动由∠AOD 的大小α(或k OD )决定,故可通过α(或k OD )建立x ,y 间的关系,即点P 的轨迹方程.[解析] (1)解法一:如图设∠BOE =α,则B(2cos α,2sin α),D(2cos α,2sin α),所以x P =2cos α,y P =2sin α.所以动点P 的轨迹C 的方程为x 24+y 22=1. 解法二:当射线OD 的斜率存在时,设斜率为k ,OD 方程为y =kx ,由⎩⎪⎨⎪⎧ y =kx x 2+y 2=2得y 2P =2k 21+k 2, 同理得x 2P =41+k 2, 所以x 2P +2y 2P=4即有动点P 的轨迹C 的方程为x 24+y 22=1. 当射线OD 的斜率不存在时,点(0,±2)也满足.(2)由(1)可知E 为C 的焦点,设直线l 的方程为x =my +2(斜率不为0时)且设点M(x 1,y 1),N(x 2,y 2),由⎩⎨⎧x =my +2x 2+2y 2=4,得(m 2+2)y 2+22my -2=0, 所以⎩⎪⎨⎪⎧y 1+y 2=-22m m 2+2y 1y 2=-2m 2+2, 所以1|MN|=11+m 2|y 1-y 2|=m 2+24m 2+1, 又射线OQ 方程为y =-mx , 代入椭圆C 的方程得x 2+2(mx)2=4, 即x 2Q =41+2m 2,y 2Q =4m 21+2m 2,1|OQ|2=1+2m 24m 2+1, 所以1|MN|+1|OQ|2=m 2+24m 2+1+1+2m 24m 2+1=34, 又当直线l 的斜率为0时,也符合条件.综上,1|MN|+1|OQ|2为定值,且为34.名师点拨(1)在选择参数时,参数可以具有某种物理或几何意义,如时间、速度、距离、角度、直线的斜率、点的横(纵)坐标等,也可以没有具体的意义,但要特别注意它的取值范围对动点坐标取值范围的影响.(2)参数法求轨迹方程的适用条件动点所满足的条件不易得出或不易转化为等式,也没有明显的相关点,但却较易发现(或经过分析可发现)这个动点的运动与某一个量或某两个变量(角、斜率、比值、截距等)有关.〔变式训练5〕若过点P(1,1)且互相垂直的两条直线l 1,l 2分别与x 轴、y 轴交于A 、B 两点,则AB 中点M 的轨迹方程为__x +y -1=0__.[解析] 当直线l 1的斜率存在时,l 2的斜率也存在,设直线l 1的方程是y -1=k(x -1),则直线l 2的方程是y -1=-1k (x -1),所以直线l 1与x 轴的交点为A ⎝ ⎛⎭⎪⎫1-1k ,0,l 2与y 轴的交点为B ⎝⎛⎭⎪⎫0,1+1k ,设AB 的中点M 的坐标为(x ,y),则有⎩⎪⎨⎪⎧ x =12⎝ ⎛⎭⎪⎫1-1k ,y =12⎝ ⎛⎭⎪⎫1+1k ,两式相加消去k ,得x +y =1⎝ ⎛⎭⎪⎫x ≠12,即x +y -1=0(x≠12),所以AB 中点M 的轨迹方程为x +y -1=0⎝ ⎛⎭⎪⎫x ≠12. 当直线l 1(或l 2)的斜率不存在时,点M 的坐标为⎝ ⎛⎭⎪⎫12,12,此点在直线x +y -1=0上. 综上,AB 中点M 的轨迹方程为x +y -1=0.另解:由题意易知|MP|=|MO|,∴M 的轨迹为线段OP 的中垂线,其方程为y -12=-⎝ ⎛⎭⎪⎫x -12, 即x +y -1=0.名师讲坛·素养提升高考中的轨迹问题例6 (2019·课标Ⅱ)已知点A(-2,0),B(2,0),动点M(x ,y)满足直线AM 与BM 的斜率之积为-12.记M 的轨迹为曲线C . (1)求C 的方程,并说明C 是什么曲线;(2)过坐标原点的直线交C 于P ,Q 两点,点P 在第一象限,PE ⊥x 轴,垂足为E ,连接QE 并延长交C 于点G .①证明:△PQG 是直角三角形;②求△PQG 面积的最大值.[解题思路] (1)由题直译得关系→化简,观察方程形式得结论(2)①设直线PQ :y =kx →与C 的方程联立得P ,Q 两点坐标→得直线QG 的方程→与C 的方程联立得G 的坐标→求PG 的斜率→得结论 ②利用公式求面积→得关于k 的函数→判断单调性求最值→得结论 [解析] (1)由题设得y x +2·y x -2=-12, 化简得x 24+y 22=1(|x|≠2), 所以C 为中心在坐标原点,焦点在x 轴上的椭圆,不含左右顶点.(2)①证明:设直线PQ 的斜率为k ,则其方程为y =kx(k >0),由⎩⎪⎨⎪⎧ y =kx ,x 24+y 22=1得x =±21+2k 2. 记u =21+2k 2,则P(u ,uk),Q(-u ,-uk),E(u,0).于是直线QG 的斜率为k 2,方程为y =k 2(x -u). 由⎩⎪⎨⎪⎧ y =k 2x -u x 24+y 22=1, 得(2+k 2)x 2-2uk 2x +k 2u 2-8=0.①设G(x G ,y G ),则-u 和x G 是方程①的解,故x G =u 3k 2+22+k 2,由此得y G =uk 32+k 2.从而直线PG 的斜率为uk 32+k 2-uk u 3k 2+22+k 2-u =-1k . 所以PQ ⊥PG ,即△PQG 是直角三角形.②由①得|PQ|=2u 1+k 2,|PG|=2uk k 2+12+k 2, 所以△PQG 的面积S =12|PQ||PG|= 8k 1+k21+2k 22+k 2=8⎝ ⎛⎭⎪⎫1k +k 1+2⎝ ⎛⎭⎪⎫1k +k 2. 设t =k +1k,则由k >0得t≥2,当且仅当k =1时取等号, 因为S =8t 1+2t2在[2,+∞)单调递减,所以当t =2, 即k =1时,S 取得最大值,最大值为169. 因此,△PQG 面积的最大值为169. [解题关键] ①利用方程思想得出点P 、Q 的坐标,进而利用换元法及整体代换法简化运算过程是顺利解决本题的关键;②正确利用基本不等式及函数单调性是求解△PQG 面积最值的关键.〔变式训练6〕(2020·新课标Ⅲ)在平面内,A ,B 是两个定点C 是动点,若OC →·BC →=1,则点C 的轨迹为( A )A .圆B .椭圆C .抛物线D .直线[解析] 不妨以AB 所在直线为x 轴,AB 的中点为原点,建立平面直角坐标系,设C(x ,y),A(-c,0),B(c,0),c >0,则AC →=(x +c ,y),BC →=(x -c ,y),由AC →·BC →=1,得(x +c)(x -c)+y·y=1,即x 2+y 2=c 2+1>0,∴点C 的轨迹为圆.故选A .。
曲线与方程

曲线与方程一、曲线与方程的关系:一般地,在坐标平面内的一条曲线C 与一个二元方程(,)0F x y =之间, 如果具有以下两个关系:1.曲线C 上的点的坐标,都是 的解;2.以方程(,)0F x y =的解为坐标的点,都是 的点,那么,方程(,)0F x y =叫做这条曲线C 的方程;曲线C 叫做这个方程(,)0F x y =的曲线.二、求轨迹方程的常用方法有:直接法,定义法,待定系数法,参数法,相关点法(代入法),交轨法等.三、求曲线的方程的步骤:①建立适当的坐标系,用(,)M x y 表示曲线上的任意一点的坐标;②写出适合条件P 的点M 的集合{|()}P M p M =;③用坐标表示条件P ,列出方程(,)0f x y =;④将方程(,)0f x y =化为最简形式;⑤说明以化简后的方程的解为坐标的点都在曲线上.四、直线系 具有某种共同属性的一类直线的集合,称为直线系.它的方程称直线系方程.(1)共点直线系:过已知点 P (x 0 , y 0 ) 的直线系方程 y − y 0 = k (x − x 0 ) (k 为参数) (2)平行直线系:斜率为 k 的直线系方程 y = kx + b (b 是参数)与已知直线 Ax + By + C = 0 平行的直线系方程 Ax + By + λ = 0 (λ 为参数)(3)垂直直线系:与已知直线 Ax + By + C = 0 垂直的直线系方程Bx − Ay + λ = 0(λ 为参数)(4)过直线 l 1 :A 1 x + B 1 y + C 1 = 0 与 l 2 :A 2 x + B 2 y + C 2 = 0 的交点的直线系方程:A 1 x + B 1 y + C 1 + λ(A 2 x + B 2 y + C 2 ) = 0(λ 为参数),此直线系不含直线 l 2例1: “ 以方程 f(x, y) = 0 的解为坐标的点都在曲线 C 上” 是 “ 曲线 C 的方程是 f(x,y) = 0 ” 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件下列方程各表示什么曲线?① 29y x -=② 0324222=++-+y x y x 0)9)(2(22=-+-+y x y x例2: 设圆 C : (x − 1)2 + y 2 = 1 ,过原点 O 作圆的任意弦,求所作弦的中点的轨迹方程.练习1:(直接法)已知线段AB 的长度为10,它的两个端点分别在x 轴,y 轴上滑动,求AB 的中点P 的轨迹方程。
10.5 曲线与方程-5年3年模拟北京高考

10.5 曲线与方程五年高考考点轨迹与轨迹方程 1.(2013福建.18,13分)如图,在正方形OABC 中,O 为坐标原点,点A 的坐标为(10,0),点C 的坐标为(O ,10).分别将线段OA 和AB 十等分,分点分别记为921,,,A A A 和,,,21 B B ⋅9B 连结,i OB 过i A 作x 轴的垂线与i OB 交于点≤∈1*,(N i P i ).9≤i(1)求证:点)91,(≤≤⋅∈i N i p i 都在同一条抛物线上,并求该抛物线E 的方程;(2)过点C 作直线L 与抛物线E 交于不同的两点M ,N ,若AOCM 与△OCN 的面积比为4:1,求直线L 的方程.2.(2013四川.20 ,13分)已知椭圆)0(1:2222>>=+b a by a x C 的两个焦点分别为),0,1(),0,1(21F F -且椭圆C 经过点⋅)31,34(P(1)求椭圆C 的离心率;(2)设过点A(O ,2)的直线L 与椭圆C 交于M ,N 两点,点Q 是线段MN 上的点,且,||1||1||2222AN AM AQ +=求点Q 的轨迹方程.3.(2012辽宁.20,12分)如图,椭圆,0(1:220>>=+b a by a x C a ,b 为常数),动圆.,:121221a t b t y x C <<=+点21,A A 分别为0C 的左,右顶点,1C 与0C 相交于A ,B ,C ,D 四点.(1)求直线1AA 与直线B A 2交点M 的轨迹方程;(2)设动圆22222:t y x C =+与0C 相交于D C B A ,,,四点,其中b ⋅=/<<212,t t a t 若矩形ABCD 与矩形ABCD 的面积相等,证明:222t t l +为定值.智力背景斯太纳——从牧童或长为几何学家 斯太纳是瑞士的大数学家,是世界数学史上具有传奇色彩的一个人物.1796年出生于瑞士北部伯尔尼州的一个小镇上,斯太纳到了14岁还是个一字不识的文盲,但 他不甘于这种状况,经过长期的勤奋研究,出版了《几何图形相互关系的系统发展》和《用直尺和一个固 定圆完成的几何作图》两本书.1834年,他被选为柏林科学院院士;同年又被聘为柏林大学教授,直到他 逝世,后人把他评为“自欧几里得以来最伟大的几何学家”.4.(2011天津,18.13分)在平面直角坐标系xOy 中,点P(a ,b)(a>b>0)为动点,21,F F 分别为椭圆122=+by a x 的左、右焦点,已知21PF F ∆为等腰三角形. (1)求椭圆的离心率e ;(2)设直线2PF 与椭圆相交于A ,B 两点,M 是直线2PF 上的点,满足,2.-=BM AM 求点M 的轨迹方程.5.(2011安徽.21,13分)设A>0,点A 的坐标为(1,1),点B 在抛物线2x y =上运动,点p 满足,B λ= 经过点Q 与x 轴垂直的直线交抛物线于点M ,点P 满足,MP λ=QM求点P 的轨迹方程.解读探究知识清单1.“曲线的方程”与“方程的曲线”在直角坐标系中,如果某曲线C(看作适合某种条件的点的集合或轨迹)上的点与一个二元方程f(x ,y )=0的实数解建立了如下的关系:(1)曲线上的点的坐标都是这个方程的解.(2)以这个方程的解为坐标的点都是曲线上的点.那么,这个方程叫做曲线的方程,这条曲线叫做方程的曲线.事实上,曲线可以看作一个点集C ,以一个二元方程的解作为坐标的点组成一个点集F 上述定义中C CF F C ⇔⎩⎨⎧⊆⇔⊆⇔)2(,)1(条件条件.F = 2直接法求动点的轨迹方程的步骤 (1)①____——建立适当的坐标系;(2)②____——设轨迹上的任一点P (x ,y ); (3)③____——列出动点P 所满足的关系式;(4)④ ——依条件式的特点,选用距离公式、斜率公式等将其转化为x 、y 的方程式,并化简;(5)⑤ 一-证明所求方程即为符合条件的动点轨迹方程 【知识拓展】1.求轨迹方程时,要注意检验曲线上的点与方程的解是否为一一对应的关系,若不是,则应对方程加上一定的限制条件,检验可以从以下两个方面进行;一是方程的化筒是否为同解变形;二是是否符合题目的实际意义.2.求点的轨迹与求轨迹方程是不同的要求,求轨迹时,应先求轨迹方程,然后根据方程说明轨迹的形状、位置、大小等.·知识清单答案智力背景姜伯驹 1937年生,浙江苍南A.1957年毕业于北京大学数学力学系,曾任美国普林斯顿高等研究所、巴黎高等科学研究所研究员、联邦德国海德堡大学客座教授,1985年当选第三世界科学院院士.姜氏空间:数学家姜伯驹关于尼尔森数计算的研究成果被国际上命名为“姜氏空间”,另外还有以他命名的“姜氏子群”.突破方法方法1 定义法求轨迹方程运用解析几何中一些常用定义(例如圆锥曲线的定义),可从曲线定义出发直接写出轨迹方程,或从曲线定义出发建立关系式,从而求出轨迹方程.例1 (2012山东青岛二模,18,12分)等腰三角形的顶点是A(4,2),底边一个端点是B(3,5),求另一个端点C 的轨迹方程,并说明它的轨迹是什么. 解题思路解析 设另一端点C 的坐标为(x ,y).依题意,得|AC |=|AB |,由两点间距离公式,得,)52()34()2()4(2222-+-=-+-y x整理得 .10)2()4(22=-+-y x这是以点A(4,2)为圆心,以10为半径的圆,如图所示,又因为A 、B 、C 为三角形的三个顶点,所以A 、B 、C 三点不共线,即点B 、C 不能重合且B 、C 不能为圆A 的一直径的两个端点.因为点B 、C 不能重合,所以点C 不能为(3,5). 又因为点B 、C 不能为一直径的两个端点, 所以,225,423=/+=/+y x 且即点C 不能为(5,-1). 故端点C 的轨迹方程是10)2()4(22=-+-y x (除去点(3,5)和( 5, -1). 它的轨迹是以点A(4,2)为圆心,10为半径的圆,但除去(3,5)和(5,-1)两点.【方法点拨】 定义法求轨迹方程的步骤:方法2 相关点法例2(2011陕西.17,12分)如图,设P 是圆2522=+y x 上的动点,点D 是P 在x 轴上的投影,M 为PD 上一点,且=||MD .||.54PD (1)当P 在圆上运动时,求点M 的轨迹C 的方程; (2)求过点(3,0)且斜率为54的直线被C 所截线段的长度,解题思路解析 (1)设M 的坐标为(x ,y ),P 的坐标为),,(P P y x 由已知得⎪⎩⎪⎨⎧==,45,y y x x P P∵ P 在圆上 ,∴,25)45(22=+y x 即C 的方程为.1162522=+y x (4分) (2)过点(3,0)且斜率为54的直线方程为),3(54-=x y (6分)设直线与C 的交点为),,(),,(2211y x B y x A 将直线方程)3(54-=x y 代入C 的方程,得 ,125)3(2522=-+x x 即.0832=--x x 2413,241321+=-=∴x x (10分) ∴ 线段AB 的长度为221221221))(25161()()(||x x y y x x AB -+=-+-=⋅=⨯=541412541 注:求AB 长度时,利用韦达定理或弦长公式求得正确结果,同样给分.【方法点拨】 相关点法求轨迹芳程的步骤:智力背景从倒数第一到数学大师的转变(一) 季理真,1964年出生在浙江温州一个普通的农村家庭.1980 年,季理真参加了在温州进行的全国统考.除了英语,他的数学是所有科目中考得最差的,化学最好.但在体检中,季理真因辨色能为差而被诊断为色弱,只能学数学和物理他被杭大的数学专业录取,“我不喜欢数学,在年级里成绩也比较差,对我而言,数学之路从来不是平坦的,但绝对是充满乐趣的!”方法3 参数法求轨迹方程例3(2012河南鹤壁二模.20,12分)设椭圆方程为+2x ,142=y 过点M(O ,1)的直线L 交椭圆于点A 、B ,0是坐标原点,L 上的动点P 满足),P (21P O OA O +=点N 的坐标为⋅)21,21(当L 绕点M 旋转时,求:(1)动点P 的轨迹方程;||)2(N 的最小值与最大值.解题思路解析 (1)直线L 过点M(O ,1),当直线L 的斜率存在时,设其斜率为也k 则L 的方程为.1+=kx y设),,(),(2211y x B y x A 、由题设得点A 、B 的坐标分别为,(1x ),).(221⋅y x y 是方程组⎪⎩⎪⎨⎧=++=②①14,122y x kx y 的解. (2分)将①代入②并化简得,,032)4(22=-++kx x k所以⎪⎪⎩⎪⎪⎨⎧+=++-=+,48,42221221k y y k k x x于是⋅++-=++=+=)44,4()2,2()(21222121k k k y y x x设点P 的坐标为(x ,y),则⎪⎪⎩⎪⎪⎨⎧+=+-=,44,422k y kk x消去参数k 得.0422=-+y y x ③(5分)当直线L 的斜率不存在时,A 、B 的中点坐标为原点(0,0),也满足方程③,所以动点P 的轨迹方程为.0422=-+y y x (6分) (2)由点P 的轨迹方程知,1612≤x 即⋅≤≤-4141x (7分) 所以22222441)21()21()21(||x x y x NP -+-=-+-=,127)61(32++-=x (10分)故当41=x 时,||NP 取得最小值,最小值为;41(11分)当61-=x 时,||取得最大值,最大值为⋅621 (12分) 【方法点拨】 参数法求轨迹方程的步骤:三年模拟A 组 2011-2013年模拟探究专项基础测试时间:45钟 分值:50分 一、选择题(每题5分,共10分)1.(2013青海玉树一模,3)方程022=-y x 对应的图象是( )2.(2013河北廊坊二模.6)有一动圆P 恒过定点F(a ,0)(a>0)且与y 轴相交于点A 、B ,若△ABP 为正三角形,则点P 的轨迹为 ( )A .直线B .圆C .椭圆D .双曲线 二、填空题(每题5分,共15分) 3.(2013山东聊城一模,13)在平面直角坐标系中,0为坐标原点,A(l ,0)、B(2,2),若点C 满足),0(OA B t OA OC -+=其中,R t ∈则点C 的轨迹方程是4.(2013广东阳江5月,12)已知点),0,3(),0,2(B A -动点),(y x P 满足,62-=⋅x 则动点P .的轨迹是 5.(2012山东枣庄一模.14)已知△ABC 的顶点B(O ,0,C(5,0),AB 边上的中线长l CDl =3,则顶点A 的轨迹方程为智力背景从倒数第一到数学大师的转变(二) 人到中年的他,说自己做事做人终于开始从容起来,“对于数学终于找到了感觉,就像从大一时数学成绩的倒数第一前进到大四的名列前茅,需要一个过程,数学是 很好玩的,并且是会有收获的,当数学家是一件美事,”2007年12月17日,杭州第四届世界华人数学家 大会晨兴数学奖颁奖仪式上,美国密歇根大学数学系教授、第四届晨兴奖银奖获得者季理真在发表获奖感言时这样表达对数学的热爱.三、解答题(共25分)6.(2013北京大兴一模)已知动点P 到点A (-2,0)与点B(2,0)的斜率之积为,41-点P 的轨迹为曲线C . (1)求曲线C 的方程;(2)若点Q 为曲线C 上的一点,直线AQ 、BQ 与直线x=4分别交于M 、N 两点,直线BM 与椭圆的交点为D .求证,A 、D 、N 三点共线.7.(2013北京东城一模.19)如图所示,直线1l 与2l 相交于点,,21l l M ⊥ 点,1l N ∈以A 、B 为端点的曲线段C 上的任一点到2l 的距离与到点N 的距离相等,若△AMN 为锐角三角形,||AM ,3||,17==AN 且,6||=NB 建立适当的坐标系,求曲线段C 的方程.B 组 2011-2013年模拟探究专项提升测试时间:45分钟 分值:50分 一、选择题(每题5分,共10分)1.(2013陕西延安3月.7)已知函数1)(2+=x x f 的定义域为[a ,b](a<b ),值域为[1,5],则在平面直角坐标系内,点(a ,b)的运动轨迹与两坐标轴围成的图形的面积是 ( )A .8B .6C .4D .2 2.(2013福建厦门二模.8)到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是 ( )A .直线B .椭圆C .抛物线D .双曲线 二、填空题(每题5分,共15分)3.(2013云南保山一模.14)动圆与1:221=+⋅y x OC 外切,与0128:222=+-+x y x C 内切,则动圆圆心的轨迹是4.(2013四川成都二模.15)P 是椭圆12222=+by a x 上的任意一点,21F F 、是它的两个焦点,0为坐标原点,有一动点Q 满足,21PF PF O +=则动点Q 的轨迹方程是 5.(2013吉林长春5月.16)设集合y x y x A (+-=2)3(|),{(},54)42=-==-+-=C y x y x B },51)4()3(|),{(622},|41|3|2|),{(λ=-+-y x y x 若,)(;∅=/C B A 则实数λ的取值范围是 . 三、解答题(共25分)6.(2013黑龙江绥化一模,20)已知定点F(O ,1)和直线=y l :1,1-过定点F 与直线1l 相切的动圆的圆心为点C .(1)求动点C 的轨迹方程;(2)过点F 的直线2l 交轨迹于两点P 、P ,交直线1l 于点R ,求Q R RP .⋅的最小值. 7.(2013湖北恩施二模.21)在直角坐标平面上,0为原点,M 为动点,.552,5||OM ON OM ==过点y MM M ⊥1作轴于点,1M 过N 作x NN ⊥1轴于点.N 0,111+=M N 记点T 的轨迹为曲线C,点A(5,0)、B(l,O),过点A作直线L交曲线C于两个不同的点P、Q(点Q在A与P之间).(1)求曲线C的方程;(2)是否存在直线L,使得|BP|=|BQ|,并说明理由,智力背景谷超豪的数学人生(一)谷超豪,1926年生,浙江温州人.1948年毕业于浙江大学.1959年获苏联莫斯科大学物理数学科学博士学位,在苏联留学的时候,谷超豪就因为研究K展空间的新方法而受到了学术界的关注,当时他的主攻方向是微分几何,在1956年中国制订科学发展规划时,谷超豪就是规划的参与制订者之一,当时他和数学界的一些学者联合提出数学领域要重点发展微分方程、概率论和计算数学.。
高二数学曲线和方程

曲线和方程 曲线和方程(1)一、知识小结1.曲线和方程的概念:在直角坐标系中,如果曲线C (看作适合某种条件的点的集合或轨迹)与方程(),0F x y =的实数解集之间具有以下两个关系:(1)曲线C 上的点的坐标都是方程(),0F x y =的解;(2)以方程(),0F x y =的解为坐标的点都是曲线C 上的点,那么曲线C 上的点与方程(),0F x y =的解是一一对应的,此时把方程(),0F x y =叫做曲线C 的方程,曲线C 叫做方程(),0F x y =的曲线.定义中条件(1)说明曲线上没有哪个点的坐标不满足方程,即曲线上所有点都适合这 个条件而毫无例外,即曲线具有纯粹性;条件(2)说明适合条件的点都有在这条曲线上而无一遗漏,也就是说曲线具有完备性.由曲线与方程的关系可以知道,曲线的方程实质就是这条曲线上的任意一点的横坐标x 与纵坐标y 之间的等量关系. 注意点:数形结合分析问题.2.点与曲线的关系的判断:若曲线C 的方程(),0F x y =,则点()()()0000000,,,0P x y C F x y C F x y ∈⇔∈⇔=,即要判断一个点是否在曲线上,只要把点的坐标代入曲线方程,如果满足方程,则点在曲线上;如果不满足方程,则点不在曲线上.注意点:用代入法来解决问题.3.求曲线的方程的一般步骤:(1)建立适当的直角坐标系(建系); (2)设曲线上任意一点的坐标为(),x y (设点);(3)根据曲线上点所适合的条件,写出等式(列式);(4)用坐标x ,y 表示这个等式,并化方程为最简形式(化简);(5)证明以化简后的方程的解为坐标的点都是曲线上的点(证明).注意点:要检验,防止出现增解或失解.4.求曲线的方程的一般方法:(1)直接法:根据题意与条件,设出动点坐标,直接列出相关等式,然后化简得结果;(2)代入法:设出动点坐标,然后找出相关点的了解,利用相关点的规律,从而得出动点之间关系的等式;注意点:过程中要保持等价变形,这样可省略检验环节.5.曲线的交点的求法:如果曲线1C 、2C 的方程分别为()1,0F x y =、()2,0F x y =,则点()00,0P x y =是曲线1C 、2C 交点的充要条件是()()100200,0,0F x y F x y ⎧=⎪⎨=⎪⎩. 由曲线上点的坐标和它的方程的实数解之间的对应关系可知,两条曲线交点的坐标应该是这两条曲线的方程所组成的方程组的实数解.方程组有几组实数解,两条曲线就有几个交点;方程组没有实数解,两条曲线就没有交点.因此,求曲线的交点坐标就是求曲线的方程所组成的方程组的解.注意点:代数与几何方法要结合.6.解析几何的本质:用代数的方法来研究几何问题,具体来说就是用方程的思想来解决曲线的问题.其中会涉及两个主要问题:(1)已知曲线,求相应的方程;(2)已知方程,画出相应的曲线,并研究其相关的性质.二、应用举例:例1、方程()()211y a x b x c =-+-+的曲线过原点的条件是 .例2、到两坐标轴距离的积为2的动点轨迹方程是 .例3、已知定点()4,0Q ,P 为曲线224x y +=上一个动点,那么线段PQ 中点的轨迹方程是_____________.曲线和方程 曲线和方程(2)一、应用举例例4、设P 为曲线2214x y -=上一动点,O 为坐标原点,M 为线段OP 中点,则点M 的轨迹方程是_____________.例5、直线53y x =-被曲线22y x =截得的线段长是___________.例6、已知直线y kx k =-+与曲线22y x x =-. (1程是________________;(2)直线与曲线相交而得交点的中点轨迹方程是____________.例7、长为a 的线段的两端点分别在直线y x =和y x =-上运动,则线段中点的轨迹为 .例8、若直线0mx y m -+=与抛物线243y x x =-+的取值范围为__________.例9、已知两点()()2,02,0M N -、,点P 0MN MP MN NP ⋅+⋅=,则动点P 的轨迹方程为例10、直线2y kx =-交曲线28y x =于A 、B 两点,若弦AB 中点的横坐标为2,则k =________.一、应用举例:1.选择题例11、直线210x y -+=关于直线1x =对称的直线方程是( ). (A )210x y +-= (B )210x y +-= (C )230x y +-= (D )230x y +-=例12、设有一组圆()()()224:1320k C x k y k k k -++-=≠,则下列四个命题中正确的是( ).(A )存在一条定直线与所有的圆均相切 (B )所有的圆均不经过原点(C )存在一条定直线与所有的圆均不相交 (D )存在一条定直线与所有的圆均相交例13、设过点(),P x y 的直线分别与x 轴的正半轴和y 轴的正半轴交于A ,B 两点,点Q 与点P 关于y 轴对称,O 为坐标原点,若2BP PA =且1OQ AB ⋅=,则点P 的轨迹方程是( ). (A )()223310,02x y x y +=>> (B )()223310,02x y x y -=>> (C )()223310,02x y x y -=>>(D )()223310,02x y x y +=>>例14、直线2y k =与曲线2222918k x y k x +=(),0k k ∈≠R 且且0)k ≠的公共点的个数为( ). (A )1 (B )2(C )3(D )42.解答题例15、(1)求曲线(,)0C f x y =:关于点(),a b 对称的曲线的方程;(2)若直线1y kx =+与曲线220x y x ky ++-=的两个交点的横坐标之和为零,求k 的值.例16、已知动点P 到定点()1,0F 和直线3x =的距离之和等于4,求点P 的轨迹方程.一、应用举例:1.解答题例17、已知△ABC 的两个顶点()8,0B -,()0,0C ,顶点A 在曲线22160x y x +-=上运动,求△ABC 的重心的轨迹方程.例18、过原点作曲线21y x =+的割线12OPP ,求弦12P P 的中点P 的轨迹方程.例19、k 为何值时,直线2y kx =+和曲线22236x y +=有两个公共点?有一个公共点?没有公共点?例20、(1)画出方程1x -(2)曲线)122y x =-≤≤与直线()24y k x =-+有两个交点时,试求出实数k 的取值范围.例21、若两条曲线的方程是()1,0F x y =和()2,0F x y =,交点为()000,P x y , (1)证明:方程()()12,,0F x y F x y λ+=的曲线也经过0P (λ为任意实数); (2)求经过曲线2230x y x y ++-=和22330x y y ++=的交点的直线方程.例22、已知曲线2:1C y x mx =-+-,点()3,0A ,()0,3B ,求曲线C 与线段AB 有两个不同交点的充要条件.曲线和方程(4)一、应用举例:1.解答题例17、已知△ABC 的两个顶点()8,0B -,()0,0C ,顶点A 在曲线22160x y x +-=上运动,求△ABC 的重心的轨迹方程.例18、过原点作曲线21y x =+的割线12OPP ,求弦12P P 的中点P 的轨迹方程.例19、k 为何值时,直线2y kx =+和曲线22236x y +=有两个公共点?有一个公共点?没有公共点?例20、(1)画出方程1x -(2)曲线)122y x =-≤≤与直线()24y k x =-+有两个交点时,试求出实数k 的取值范围.例21、若两条曲线的方程是()1,0F x y =和()2,0F x y =,交点为()000,P x y , (1)证明:方程()()12,,0F x y F x y λ+=的曲线也经过0P (λ为任意实数); (2)求经过曲线2230x y x y ++-=和22330x y y ++=的交点的直线方程.例22、已知曲线2:1C y x mx =-+-,点()3,0A ,()0,3B ,求曲线C 与线段AB 有两个不同交点的充要条件.友情提示:部分文档来自网络整理,供您参考!文档可复制、编制,期待您的好评与关注!。
曲线与方程圆的方程

曲线与方程、圆的方程1.曲线C的方程为:f(x,y)=o 曲线C上任意一点P (X o,y o)的坐标满足方程f(x,y)=O,即f(x o,y o)=0 ;且以f(x,y) =0的任意一组解(x o,y o)为坐标的点P (x o,y o)在曲线C上。
依据该定义:已知点在曲线上即知点的坐标满足曲线方程;求证点在曲线上也只需证点的坐标满足曲线方程。
求动点P(x,y)的轨迹方程即求点P的坐标(x,y)满足的方程(等式)。
求动点轨迹方程的步骤:①建系,写(设)出相关点的坐标、线的方程,动点坐标一般设为(x,y),②分析动点满足的条件,并用等式描述这些条件,③化简,④验证:满足条件的点的坐标都是方程的解,且以方程的解为坐标的点都满足条件。
解析:原方程等价于: x y 1 0 2 2 2 2 ',或x y 4;x y 4其中当x y 1 0需;x2y24有意义,等式才成立,即x2y24,此时它表示直线x y 1 0上不在圆x2y? 4内的部分,这是极易出错的一个环节。
选[举例2]已知点A (- 1 , 0), B (2, 0),动点M满足2 / MAB2 MBA求点M的轨迹方程。
解析:如何体现动点M满足的条件2/ MAB M MBA是解决本题的关键。
用动点M的坐标体现2 / MAB M MBA 的最佳载体是直线MA MB的斜率。
设M(x, y), / MAB=,则/ MBA=2,它们是直线MA MB的倾角还是倾角的补角,与点M在x轴的上方还是下方有关;以下讨论:① 若点M在x轴的上方,(00,900), y 0 ,此时,直线MA的倾角为,MB的倾角为-2 ,tan k MA xV an( 2)七(2 900)[举例1]方程(x y 1). x2y2 4 0所表示的曲线是:( )[巩固2]已知点R (-3, 0),点P 在y 轴上,点 Q 在x 轴的正半轴上,点 M 在直线PQ 上, PM =0 , 2 PM +3MQ =0,当点P 移动时,求M 点的轨迹方程。
求曲线方程方法讲解

y ( x, y) 由中点坐标公式可知
x1 y1
x 2 y 2
A
∵AB 边上的中线 CD=3
D
∴ (x1 4)2 y12 9
B
化简整理得 (x 8)2 y2 36
∴点 A 的轨迹方程为 (x 8)2
y2
0
36
.
y
0C
Mx
法二: 添辅助线 MA,巧用图形性质, 妙极了! 注:这种求轨迹方程的方法叫做相关点坐标分析法(代入法)
变式练习
若三角形ABC的两顶点C,B的坐标分别是C(0,0),
B(6,0),顶点A在曲线y=x2+3上运动,求三角形ABC
重心G的轨迹方程.
y 10
8
y=x2+3
6
A
4
2
M
OB
x
-2
-4
四 例 3.经过原点的直线 l 与圆 x2 y2 6x 4 y 9 0 相交于
√√ 4.化简方程 f (x, y) 0 为最简形式;
5.证明(查漏除杂).
以上过程可以概括为一句话:建.设.现.(.限.).代.化..
知识回顾
在什么条件下,方程f(x,y)=0是曲线C 的方程,同时曲线C是该方程的曲线?
(1)曲线C上的点的坐标都是方程 f(x,y)=0的解;(纯粹性)
(2)以方程f(x,y)=0的解为坐标的点 都在曲线C上. (完备性)
简单地说:利用所求曲线上的动点与某一已知曲 线上的动点的关系,把所求动点转换为已知动点 满足的曲线的方程,由此即可求得动点坐标x,y之 间的坐标。
变 变式 .△ABC 的顶点 B、C 的坐标分别为(0,0)、(4,0), 式 A B 边上的中线的长为 3,求顶点 A 的轨迹方程.
求曲线的轨迹方程

第九章
平面解析几何
解析:由题设知|x1|> 2,A1(- 2,0),A2( 2,0),则有 y1 直线 A1P 的方程为 y= (x+ 2),① x1+ 2 - y1 直线 A2Q 的方程为 y= (x- 2),② x1- 2 2 2 x=x1, x1=x, 联立①②,解得 所以 ③ 2 y 2 y 1 y= y1 = , x , x1
栏目 导引
第九章
平面解析几何
直接法求曲线方程的一般步骤 (1)建立合理的直角坐标系; (2)设出所求曲线上点的坐标,把几何条件或等量关系用坐标 表示为代数方程; (3)化简整理这个方程,检验并说明所求的方程就是曲线的方 程.
栏目 导引
第九章
平面解析几何
直接法求曲线方程时最关键的就是把几何条件或等量关系 “翻译”为代数方程,要注意“翻译”的等价性. [提醒] 对方程化简时, 只要前后方程解集相同, 证明一步可
栏目 导引
第九章
平面解析几何
栏目 导引
第九章
平面解析几何
利用相关点法(代入法)求轨迹方程 [典例引领] x2 y2 (2018· 杭州模拟)已知点 Q 在椭圆 C: + =1 上, 点 16 10 → 1 → → P 满足OQ= (OF1+OP)(其中 O 为坐标原点,F1 为椭圆 C 的 2 左焦点),则点 P 的轨迹为( A.圆 C.双曲线 ) B.抛物线 D.椭圆
栏目 导引
第九章
平面解析几何
直接法求轨迹方程(高频考点) 直接法求点的轨迹方程是求轨迹方程的一种重要方法, 也是高考考查的重要内容.主要命题角度有: (1)已知动点满足的关系式求轨迹方程(或判断轨迹); (2)无明确等量关系求轨迹方程.
栏目 导引
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学第二章曲线与方程学案
学习目标:
1、理解平面直角坐标中“曲线的方程”和“方程的曲线”的含义;
2、掌握求曲线的方程的方法及一般步骤;
学习重点:理解曲线和方程的概念,掌握求曲线的方程的方法及一般步骤; 学习难点:曲线和方程概念的理解; 学习过程:
完成教学目标1:理解平面直角坐标中“曲线的方程”和“方程的曲线”的含义;
新授知识:曲线的方程与方程的曲线的概念
一般地,在直角坐标系中,如果其曲线C 上的点与一个二元方程f (x ,y )=0的实数解建立了如下的关系:(1)曲线上的点的坐标都是这个方程的解;
(2)以这个方程的解为坐标的点都是曲线上的点;
那么,这个方程叫做曲线的方程;这条曲线叫做方程的曲线.
例1、判断下列结论的正误并说明理由
(1)过点A (3,0)且垂直于x 轴的直线为x=3 ;
(2)到x 轴距离为2的点的轨迹方程为y=2 ;
(3)到两坐标轴距离乘积等于1的点的轨迹方程为xy=1 ;
练习:1、到两坐标轴距离相等的点组成的直线方程是0=-y x 吗?
2、已知等腰三角形三个顶点的坐标是)3,0(A ,)0,2(-B ,)0,2(C ,中线O AO (为原点)的 方程是0=x 吗?为什么?
3、若曲线C 上的点的坐标满足方程(,)0f x y =,则下列说法正确的是( ) A.曲线C 的方程是(,)0f x y = B.方程(,)0f x y =的曲线是C C.坐标不满足方程(,)0f x y =的点都不在曲线C 上 D.坐标满足方程(,)0f x y =的点都在曲线C 上
例2、已知方程252
2=+by ax 的曲线经过点)3
5,0(A 和点)1,1(B ,求a 、b 的值。
练习:已知方程 2
2
25x y +=表示的曲线C
经过点)A m ,求m 的值。
完成教学目标2:掌握求曲线的方程的方法及一般步骤;
类型一:待定系数法求轨迹方程(设出标准方程,根据题意求出a ,b ,p ) 例1:已知A,B,C 是长轴长为4的椭圆上的三点,点A 是长轴的一个顶点,BC 过椭圆的中心O ,
且0=∙,||2||=,求椭圆的方程。
练习:已知椭圆C 的中心在坐标原点,焦点在x 轴上,椭圆C 上的点到焦点距离的最大值为3,最小值为1.求椭圆C 的标准方程;
类型二:直接法求轨迹方程(根据题目条件,直译为关于动点的几何关系,即把这种关系“翻译”成含x ,y 的等式就得到曲线的轨迹方程了。
注意:是否应该建立适当的坐标系) 例2:已知点F(1,0),直线l:x =-1,P为平面上的动点,过点P作直线l的垂线,垂
足为点Q,且FQ FP QF QP ∙=∙,求动点P的轨迹C的方程;
**练习:已知动点M 到定点A (1,0)与到定直线l :x=3的距离之和等于4,求动点M 的轨迹方程,并说明轨迹是什么曲线?
**例3、线段AB 与CD 互相垂直平分,|AB|=2a,|CD|=2b,动点M 满足|MA|·|MB|=|MC|·|MD|,求动点M 的轨迹方程.
练习:已知两个定点A , B 的距离为6,点M 到A , B 的距离的平方和等于26,求点M 的轨迹方程.
类型三:定义法求轨迹方程(若动点轨迹满足已知曲线的定义,可先设定方程,再确定其中的基本量,求出动点的轨迹方程。
)
例4:如图,已知圆A :(x+2)2+y 2
=1与点B(2,0),分别求出满足下列条件的动点P 的轨迹方程.
(1)△PAB 的周长为10;
(2)圆P 过点B(2,0)且与圆A 外切(P 为动圆圆心);
(3)圆P 与圆A 外切且与直线x=1相切(P 为动圆圆心).
练习:如图,已知圆B :(x+1)2+y 2=16及点A(1,0),C 为圆B 上任意一点,则线段AC 的垂直平分l 与线段CB 的交点P 的轨迹方程
类型四:相关点法(动点满足的条件不便用等式列出,但动点是随着另一动点(称之为相关点)而运动的,根据相关点所满足的方程即可求得动点的轨迹方程。
)
例5:设P 是圆x 2+y 2=25上的动点,点D 是P 在x 轴上的投影,M 为PD 上一点,且 MD =4
5PD .当P 在圆上运动时,求点M 的轨迹C 的方程;
练习:双曲线2
219
x y -=有动点P ,F 1, F 2是曲线的两个焦点,求△PF 1F 2的重心M 的轨迹方程。
课堂小结:
课堂检测:1、“点M 在曲线x y 42
=上”是“点M 的坐标满足方程x y 2-=”的( ) A. 充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2、已知椭圆的焦点是F 1、F 2,P 是椭圆上的一个动点,如果延长F 1P 到Q ,使得|PQ |=|PF 2|,
那么动点Q 的轨迹是( ) A. 圆 B. 椭圆 C. 双曲线的一支 D. 抛物线。
